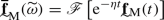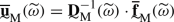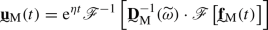Abstract
A computational homogenization framework is presented to study the dynamics of locally resonant acoustic metamaterial structures. Modelling the resonant units at the microscale as representative volume elements and building on well-established scale transition relations, the framework brings as a main novelty a reduced-order macroscopic homogenized continuum whose governing equations involve no additional variables to describe the microscale dynamics unlike micromorphic homogenized continua obtained by alternative computational homogenization approaches. This model-order reduction is obtained by formulating the governing equations of the micro- and macroscale problems in the frequency domain, introducing a finite-element discretization of the two problems and performing an exact dynamic condensation of all the degrees of freedom at the microscale. An appropriate inverse Fourier transform approach is implemented on the frequency-domain equations to capture transient dynamics as well; notably, the implementation involves the Exponential Window Method, here applied for the first time to calculate the time-domain response of undamped locally resonant acoustic metamaterial structures. The framework may handle arbitrary geometries of micro- and macro-structures, any transient excitations and any boundary conditions on the macroscopic domain.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Locally resonant acoustic metamaterials (LRAMs) are emerging as a remarkably versatile concept in the field of metamaterials. The term LRAM refers to an artificially-structured material, typically a heterogeneous elastic medium consisting of a matrix with embedded resonant inclusions or substructures, which may be tailored to obtain exotic properties such as near zero transmissibility [1], enhanced energy absorption [2], negative dynamic mass density and/or bulk modulus [3,4,5,6,7], super anisotropy, zero rigidity [7], etc. These properties make LRAMs ideal candidates for band-stop filtering of low-frequency elastic waves [1, 5,6,7,8,9], seismic protection of civil structures [10, 11], super lenses with a resolution beyond the Rayleigh limit [12, 13] and guided wave propagation.
Developing accurate and computationally efficient methods to study the dynamics of LRAMs is the subject of ongoing research. Direct numerical simulations (DNS) based on the finite-element (FE) method may become extremely demanding from a computational point of view because of the large difference of scales that can be involved. Seeking for alternatives to DNS, phenomenological approaches and various homogenization techniques were developed in the literature.
Phenomenological models are usually formulated at the macroscale, with additional macroscopic kinematic variables accounting for the internal dynamics at the microscale. Starting from the seminal work by Mindlin [14], several studies proposed phenomenological models especially tailored for LRAM media [15] and LRAM beam lattices [16, 17], focusing on wave dispersion analyses [15,16,17].
Homogenization techniques for LRAMS were developed based on different concepts. For example, some studies proposed asymptotic techniques, which consist in expanding and computing relevant local (or microscopic) fields and in constructing macroscopic fields and effective constitutive properties by appropriate volume averages over a unit cell. In this context, wave dispersion was analyzed in LRAM media [18, 19] and in LRAM beam lattices assembled by rectangular framed unit cells [20, 21]. Further homogenization techniques obtained effective equivalent media for LRAMs building on the pioneering volume averaging technique by Willis [22]. Examples in this respect are the averaging techniques proposed by Nemat-Nasser and coworkers [23, 24] and by Pernas-Salomón and Shmuel [25] for wave dispersion analysis in LRAM media [23, 24] and in Euler-Bernoulli beams with spring-mass resonators [25]. Alternative averaging techniques delivering effective medium properties for LRAM media were proposed by Torrent et al. [26] and by Zhou and Hu [27] based on the scattering properties of the resonators and by Chen et al. [28]; again, these studies focused on wave dispersion analysis of LRAMs [26,27,28]. In this context, various dynamic homogenization techniques targeting the computation of the band structure of periodic composites are also noteworthy [29,30,31,32].
Although phenomenological approaches and homogenization techniques were successful in studying LRAMs, especially for wave dispersion analysis, alternative numerical approaches are of great importance for a more general description of LRAMs capable of capturing the transient response, considering finite macroscopic domains with arbitrary boundary conditions, as well as complex microstructure geometries. To this aim, in the past few years a considerable research effort turned to the development of the so-called computational homogenization approaches, i.e., approaches that involve, in a broad sense, the formulation of two nested boundary value problems at the macroscale and at the microscale [33,34,35,36]. Upon introducing an enriched description of the micro–macro kinematics, where the microscopic displacement within a representative volume element (RVE) may exhibit large spatial fluctuations relative to the macroscopic displacement as a result of transient microstructural behaviour, downscaling and upscaling relations dictating the coupling between the two scales were derived; while downscaling relations involve periodic kinematic boundary conditions on the RVE, upscaling relations consist essentially in an extended Hill-Mandel macrohomogeneity condition [33,34,35,36]. The distinctive feature of this approach is that a coupling of the macroscopic stress to the microscopic momentum was found, as a result of the transient microstructural behavior [33,34,35,36]. The approach was combined with FE techniques, allowing complex microstructure topologies to be incorporated within finite macrostructure geometries, considering arbitrary transient excitations and sophisticated boundary conditions. Specifically, homogenized constitutive relations for the macroscopic stress were obtained in ref. [35], depending on additional kinematic degrees of freedom representing the internal dynamics of the microstructure, which enrich the macroscopic continuum with micro-inertia effects in a micromorphic sense. Indeed, the additional degrees of freedom are generalized coordinates associated with local resonance modes of a Craig-Bampton representation of the internal dynamics of the RVE. The approach in ref. [35] did not require a solution of the microscale problem at each time step as, it is the case, in ref. [33, 34]. The study in ref. [36] proposed a similar approach but especially tailored to LRAM beams and shells. Consistent variational formulations of computational homogenization approaches were presented by de Souza Neto et al. [37] and Blanco et al. [38]. Again in the context of a variational framework, a computational approach was proposed by Roca et al. [39], which involves reformulating the Hill-Mandel principle in a constrained variational form with Lagrange multipliers associated with kinematic restrictions on the RVE and representing, respectively, the homogenized macroscopic D’Alembert force density and stress. The Lagrange multipliers were obtained by solving the FE equations governing the dynamics of the RVE, upon representing the microstructural response as the sum of a quasistatic solution and an inertial solution under some assumptions on the effects of macroscopic strains and displacements on the inertial microscopic response and microscopic reactive stress. Macroscale equations were obtained with additional kinematic degrees of freedom given as generalized coordinates associated with local resonance modes of the RVE. The approach proposed in ref. [39] was also applied to develop a topological optimization procedure [40]. Further computational homogenization approaches were also developed [41,42,43], with focus on frequency-domain and wave dispersion analyses. Specifically, the study in ref. [42] introduced a generalized homogenization operator based on a family of weighted projection functions, to be constructed using Floquet-Bloch eigenvectors obtained in the desired frequency regime. Using a generalized Hill-Mandel relation, a micromorphic continuum was derived assuming linear elasticity and material periodicity. Assuming a high-order spatial-temporal gradient expansion with respect to the macroscale displacements as ansatz for the full-scale displacements, the global problem was localized to a problem on a single unit cell and reverted to a series of recursive local unit cell problems solved by a FE method. Recently, a computational homogenization approach focusing on transient dynamics was proposed by Zhi et al. [44]; the approach involves only a single boundary value problem with coupled macroscopic and microscopic degrees of freedom, avoiding the two concurrent finite element simulations and information interchange that are necessary in some classical computational homogenization approaches [33, 34, 45]. Indeed, solving a single boundary value problem at the macroscale instead of two concurrent ones at the macroscale and the microscale is a relevant feature of the computational homogenization approach developed in ref. [44] as well as in ref. [35, 36, 39], which deliver veritable effective continua enriched with additional variables describing the microscale dynamics.
Given the existing interest in computational homogenization approaches that may efficiently deal with the dynamic response of LRAM structures, this paper builds on the framework presented in ref. [35] introducing two main novelties:
-
1.
The formulation of a reduced-order macroscopic homogenized continuum for LRAM structures, whose governing equations do not involve additional variables describing the microscale dynamics. This is a considerable novelty and advantage over micromorphic homogenized continua obtained by alternative computational homogenization approaches [35, 36, 39, 44], which is particularly relevant for the design of engineering applications using LRAM structures. In particular, the model-order reduction is obtained assuming the well-established scale transition relations in ref. [35], formulating the governing equations of the micro- and macroscale problems in the frequency domain, introducing a FE discretization of the two problems and performing an exact dynamic condensation of all the degrees of freedom at the microscale.
-
2.
The introduction of a pertinent inverse Fourier transform approach, based on the Exponential Window Method (EWM) [46], to calculate the transient response of the reduced-order macroscopic homogenized continuum. The EWM is a numerical technique especially suitable for undamped (or lightly damped) systems and, to the best of the authors’ knowledge, this paper is the first to demonstrate its suitability for calculating the dynamic response of undamped LRAM structures. Notably, it allows to obtain results in the time domain, next to the frequency domain.
The proposed computational homogenization framework is readily implementable in a FE code and may handle arbitrary geometries of the micro- and macro-structures, any transient excitations and any arbitrary boundary conditions.
The paper is organized as follows. Section 2 outlines the fundamental scale transition relations of the computational homogenization framework. Section 3 describes the exact dynamic condensation at the microscale and derives the equations governing reduced-order macroscopic homogenized continuum without additional variables describing the microscale dynamics. The implementation of the computational homogenization framework in frequency and time domains is discussed in Sect. 4. Finally, a numerical example demonstrating the method is presented in Sect. 5.
The following notation is used throughout the paper. The standard Cartesian basis vectors are \(\textbf{e}_k\), with \(k=1,2,3\). Unless otherwise stated, scalars and vectors are denoted as a (or A) and \(\textbf{a}\), respectively; second, third and fourth order Cartesian tensors as \(\textbf{A}\) (or \(^{(2)}\bullet \)), \(^{(3)}\bullet \) and \(^{(4)}\bullet \); column matrices consisting of scalars as  (or
(or  ), column matrices consisting of vectors as
), column matrices consisting of vectors as  and matrices consisting of second-order tensors as
and matrices consisting of second-order tensors as  , that in general may be composed of subcolumns or submatrices. The tensor operations are denoted as follows: conjugate of a second order tensor \(\textbf{A}^{\textrm{C}} = A_{ji} \textbf{e}_{i}\otimes \textbf{e}_{j}\), dot product \(\textbf{A}\cdot \textbf{b} = A_{ij}b_j \textbf{e}_i\), double contraction \(\textbf{A}:\textbf{B} = A_{ij}B_{ji}\) and \(^{(4)}\textbf{A}:\textbf{B} = A_{ijhk}B_{kh}\textbf{e}_i \otimes \textbf{e}_j\), dyadic product \(\textbf{a}\otimes \textbf{b} = a_{i}b_{j}\textbf{e}_{i}\otimes \textbf{e}_j\) (Einstein notation is used here for all tensor operations). Further, \(\textbf{a}\cdot \textbf{b} = a_i b_i\).
, that in general may be composed of subcolumns or submatrices. The tensor operations are denoted as follows: conjugate of a second order tensor \(\textbf{A}^{\textrm{C}} = A_{ji} \textbf{e}_{i}\otimes \textbf{e}_{j}\), dot product \(\textbf{A}\cdot \textbf{b} = A_{ij}b_j \textbf{e}_i\), double contraction \(\textbf{A}:\textbf{B} = A_{ij}B_{ji}\) and \(^{(4)}\textbf{A}:\textbf{B} = A_{ijhk}B_{kh}\textbf{e}_i \otimes \textbf{e}_j\), dyadic product \(\textbf{a}\otimes \textbf{b} = a_{i}b_{j}\textbf{e}_{i}\otimes \textbf{e}_j\) (Einstein notation is used here for all tensor operations). Further, \(\textbf{a}\cdot \textbf{b} = a_i b_i\).
2 Scale transition relations
The multiscale problem governing the dynamics of LRAMs is built within the classical first order homogenization framework [35]. The relation governing the transition from the macroscale to the microscale (downscaling) is built on the basis of a suitable first order approximation of the microscopic kinematics at a given point. The relation governing the transition from the microscale to the macroscale (upscaling) is based on the Hill-Mandel principle. Full balance of linear momentum is accounted for at both scales.
The first order homogenization framework is formulated by assuming a relaxed principle of separation of scales. In particular, denoting with \(n_{het}\) and \(n_{mat}\) the number of microstructural phases constituting the heterogeneities and the host matrix, respectively, the following inequalities are assumed:
where \(\lambda _{j}^{mat}\) and \(\lambda _{k}^{het}\) are, respectively, the shortest characteristic wavelengths in the \(j^{\textrm{th}}\) and \(k^{\textrm{th}}\) constituents of the matrix and the heterogeneities for a given excitation, while \(l_j\) and \(l_k\) denote their typical sizes. Eq. (1) means that, for a given excitation, the sizes of the microstructural constituents of the matrix are much smaller than the shortest characteristic wavelength associated to the matrix (long wavelength approximation), while the sizes of the microstructural constituents of the heterogeneities can be of the same order of the shortest characteristic wavelengths associated to the heterogeneities.
Consider at the macroscale a solid occupying a closed domain \({\widehat{\Omega }}_{\textrm{M}} = \Omega _{\textrm{M}} \cup \partial \Omega _\textrm{M}\), \(\partial \Omega _{\textrm{M}}\) being its boundary, subjected to external boundary tractions \(\textbf{t}_{\textrm{M}}\) and neglecting the external body forces. The dynamics at the macroscale is governed by the following set of differential equations:
\(\varvec{\sigma }_{\textrm{M}}\) being the Cauchy stress tensor, \(\textbf{p}_{\textrm{M}}\) the linear momentum vector, \(\textbf{u}_{\textrm{M}}\) the displacement field vector and \(\varvec{\epsilon }_{\textrm{M}}\) the linear infinitesimal strain tensor at the macroscale, \(\nabla ^{s}_{\textrm{M}}\) denotes the symmetric gradient operator and the superimposed “\(~\dot{}~\)” denotes the time derivative. As for constitutive behavior at the macroscale, no constitutive (closure) relations are assumed for \(\varvec{\sigma }_{\textrm{M}}\) and \(\textbf{p}_\textrm{M}\); they will be obtained from the microscale problem, as explained in the following.
Assuming that each field varies harmonically in time, e.g., \(\varvec{\sigma }_{\textrm{M}} = \overline{\varvec{\sigma }}_{\textrm{M}}(\omega )\textrm{e}^{\textrm{i}\omega t}\), Eq. (2) can be written as follows in the frequency domain (for conciseness, \(\omega \)-dependence of the symbols will be omitted in the equations of this paper whenever is possible):
with \(\overline{\textbf{q}}_{\textrm{M}}(\omega ) = \textrm{i}\omega \overline{\textbf{p}}_\textrm{M}(\omega )\). The application of the principle of virtual work to Eq. (3) leads to the weak formulation
being \(\overline{\textbf{t}}_{\textrm{M}}(\omega ) = \overline{\varvec{\sigma }}_\textrm{M}(\omega ){\cdot }\textbf{n}\) with \(\textbf{n}\) the outward unit normal vector to the boundary \(\partial \Omega _{\textrm{M}}\).
To each material point \(\textbf{x}_{\textrm{M}}\) of the macroscopic domain \(\Omega _{\textrm{M}}\) a microscale domain \({\widehat{\Omega }} = \Omega \cup \partial \Omega \) is associated, selected to capture the local microstructural effects at the given material point of the macroscopic domain and known as a representative volume element (RVE). The RVE identifies physical and geometrical properties of the microstructure [47] and, for periodic LRAMs, it coincides with the unit cell, consistently with the Bloch theorem stating that the elastic wave propagation properties of a periodic medium are fully described from its single unit cell. A typical example of an RVE is given in Fig. 1. The dynamics of the RVE is governed by the following elastodynamics problem:
In the frequency domain, Eq. (5) takes the form
having defined \(\overline{\textbf{q}}(\omega ) = \textrm{i}\omega \overline{\textbf{p}}(\omega )\). The corresponding weak formulation of equilibrium resulting from the principle of virtual work is
At the microscale, the constitutive relations of the classical elastodynamics are supposed to hold, i.e., for each microstructural component it holds:
and furthermore
where \(^{(4)}\textbf{C}_{\alpha }\) and \(\rho _{\alpha }\) are the elastic material tensor and mass density of the \(\alpha ^{\textrm{th}}\) RVE constituent. Next, the focus is on the scale transition relations.
The kinematics of the RVE associated to a material point of the macroscopic domain is represented by the following downscaling relation:
\(\overline{\textbf{u}}(\textbf{x},\omega )\) being the displacement field within the RVE and \(\overline{\textbf{w}}(\textbf{x},\omega )\) the microfluctuation field, which represents the fine scale variations due to the microstructure heterogeneities; \(\textbf{x}_\textrm{R}\) is the position vector of a reference point.
The upscaling relations can be determined by making use of the Hill-Mandel principle, which equates the macroscale virtual work density at a material point to the volume averaged virtual work of the RVE and, in turn, to the virtual work of the external boundary tractions on the RVE
where Eq. (7) is taken into account. From Eq. (11) the following upscaling relations can be derived [35]:
with \(\Delta \textbf{x} = \textbf{x} - \textbf{x}_{\textrm{R}}\). The Hill-Mandel principle was used in several computational homogenization approaches to allow the upscaling transition from the microscale to the macroscale and also holds if no inertia forces are present, as typically the case for static computational homogenization (e.g., see [47, 48]). Here, it enables an energy-consistent derivation of the macroscopic stress–strain constitutive law and macroscopic inertia terms from the corresponding ones at the microscale via Eqs. (12)-(13), as detailed next.
3 Reduced-order macroscopic homogenized continuum
This section contains the core novelties of this study. The first step is a standard FE discretization of Eq. (6) governing the dynamics of the RVE. Upon introducing the FE discretization, an exact dynamic condensation of the RVE degrees of freedom is performed in the frequency domain. The dynamic condensation method is well established in classical continuum mechanics [49,50,51]; here, for the first time to the best of authors’ knowledge, it is applied for model order reduction of a macroscopic homogenized continuum. Remarkably, as a result of the dynamic condensation, a reduced-order macroscopic homogenized continuum is formulated, the governing equations of which involve no additional variables describing the microscale dynamics.
3.1 Dynamic condensation at the microscale
The RVE governing equations (5) can be discretized by means of the FE method, which leads to

Assuming harmonically varying solutions, Eq. (14) yields the equilibrium equation of the RVE in the frequency domain

where  denotes the dynamic stiffness tensor matrix of the RVE. Assuming a 2-dimensional (2D) RVE for illustration purposes, the displacement column matrix can be conveniently partitioned (see Fig. 1) as
denotes the dynamic stiffness tensor matrix of the RVE. Assuming a 2-dimensional (2D) RVE for illustration purposes, the displacement column matrix can be conveniently partitioned (see Fig. 1) as 
 , where the subscripts ‘T’, ‘B’, ‘L’, ‘R’ denote the displacements of the nodes along the top, bottom, left and right boundary of the RVE, the subscripts ‘\(p_k\)’ and ‘i’ denote the displacements of the \(k^{\textrm{th}}\) vertex and internal nodes, respectively. Following ref. [35], it is assumed that the microfluctuations are periodic. Under this assumption, the downscaling relations in Eq. (10) lead to the following identities:
, where the subscripts ‘T’, ‘B’, ‘L’, ‘R’ denote the displacements of the nodes along the top, bottom, left and right boundary of the RVE, the subscripts ‘\(p_k\)’ and ‘i’ denote the displacements of the \(k^{\textrm{th}}\) vertex and internal nodes, respectively. Following ref. [35], it is assumed that the microfluctuations are periodic. Under this assumption, the downscaling relations in Eq. (10) lead to the following identities:

where  , \(\textbf{I}\) being a second order unit tensor.
, \(\textbf{I}\) being a second order unit tensor.
Equation (16) can be written in the form of a linear transformation acting on the nodal displacements of the RVE (see Fig. 1)

being  the column matrix collecting the displacements of the retained nodes, i.e., the displacements of the unconstrained nodes
the column matrix collecting the displacements of the retained nodes, i.e., the displacements of the unconstrained nodes  , which can be partitioned in the column matrix of prescribed displacements
, which can be partitioned in the column matrix of prescribed displacements  and in the column matrix of free displacements
and in the column matrix of free displacements  . Therefore, by making use of the transformation in Eq. (17), the displacements of the dependent nodes
. Therefore, by making use of the transformation in Eq. (17), the displacements of the dependent nodes  are eliminated and Eq. (15) becomes
are eliminated and Eq. (15) becomes

Note that the column matrix of the nodal forces associated with retained nodes  and the column matrix of the external (reaction) nodal forces
and the column matrix of the external (reaction) nodal forces  associated with the prescribed nodes are related by
associated with the prescribed nodes are related by

Next, Eq. (18) can be partitioned with respect to the column matrix of prescribed displacements  and the column matrix of free displacements
and the column matrix of free displacements  within the column matrix of retained displacements
within the column matrix of retained displacements 

Performing the exact dynamic condensation of the free displacements yields

where  is the Schur complement of the block
is the Schur complement of the block  of the matrix
of the matrix 

Eq. (21) can be further partitioned with respect to each prescribed node of the RVE
It is noticed that the downscaling relation (10) for the nodal displacements \(\overline{\textbf{u}}_{p_i}(\omega )\) at the vertices of the RVE reads [35]
being \(\Delta \textbf{x}_{p_i} = \textbf{x}_{p_i}- \textbf{x}_{\textrm{R}}\), i.e., the microfluctuations in the prescribed nodes are equal to zero in agreement with ref. [35].
3.2 Governing equations at the macroscale
The upscaling relations, Eqs. (12)-(13), allow to recover the inertial force \(\overline{\textbf{q}}_{\textrm{M}}(\omega )\) and Cauchy stress tensor \(\overline{\varvec{\sigma }}_{\textrm{M}}(\omega )\) in the frequency domain at the macroscale from the RVE governing equations, Eq. (6). Likewise, the discretization of Eqs. (12)-(13) enables to recover these quantities from the discretized RVE governing equation, Eq. (21). In particular, let \(\delta \overline{\textbf{u}}(\textbf{x},\omega )\) be the virtual displacement represented by the following isoparametric expansion:

where  is the column matrix of the FE shape functions and
is the column matrix of the FE shape functions and  the column matrix of virtual displacements of the RVE nodes. Substituting Eq. (25) in the r.h.s of Eq. (11) leads to
the column matrix of virtual displacements of the RVE nodes. Substituting Eq. (25) in the r.h.s of Eq. (11) leads to

Substituting Eq. (24) in Eq. (26) gives
Substituting Eq. (27) in Eq. (11) leads to the discrete upscaling relations
Making use of Eq. (24) and substituting Eq. (23) in Eqs. (28)-(29) yield
where “\((\cdot )^{\textrm{LC}}\)” denotes the left conjugate of a high order tensor \(A^{\textrm{LC}}_{jihk} = A_{ijhk}\). In Eq. (28), the \(2^{\textrm{nd}}\) and \(3^{\textrm{rd}}\) order dynamic density mass tensors are respectively defined as
Likewise, in Eq. (29), the \(3^{\textrm{rd}}\) and \(4^{\textrm{th}}\) order elastic tensors are defined, respectively, as
A few comments on Eq. (23) and Eq. (28) are of interest. If \(\omega = 0\),  ,
,  ,
,  , and the matrix
, and the matrix  in Eq. (23) reverts to the condensed static stiffness matrix
in Eq. (23) reverts to the condensed static stiffness matrix  (\(= \underline{\textbf{K}}_\textrm{qs}\) in ref. [35]). Bearing in mind the downscaling relations (24), the following relation is obtained in static conditions:
(\(= \underline{\textbf{K}}_\textrm{qs}\) in ref. [35]). Bearing in mind the downscaling relations (24), the following relation is obtained in static conditions:
In Eq. (36), the term \(\sum _{j=1}^{3}\textbf{K}_{p_{ij}}^{\textrm{qs}}\cdot \textbf{u}_{\textrm{M}} = \textbf{0}\) as it describes a rigid body motion of the RVE while, in general, the second term \(\sum _{j=1}^{3}\textbf{K}_{p_{ij}}^\textrm{qs}\cdot {(\nabla _{\textrm{M}}\textbf{u}_{\textrm{M}})^{\textrm{C}}}\cdot \Delta \textbf{x}_{p_{j}} \ne \textbf{0}\) and, as a result, the nodal forces \(\textbf{f}_{p_i} \ne \textbf{0}\). However, \(\sum _{i=1}^{3} \textbf{f}_{p_i} = \textbf{0}\) because of equilibrium; therefore, \(\textbf{q}_{\textrm{M}} = \textbf{0}\) in Eq. (28) consistently with the fact that no inertia forces arise at the macroscale for a static response of the RVE; on the other hand, \(\sum _{i=1}^{3}\textbf{f}_{p_i}\otimes \Delta \textbf{x}_{p_i}\ne 0\) implies \(\varvec{\sigma }_{\textrm{M}} \ne \textbf{0} \) (see Eq. (29) in the frequency domain). If \(\omega \ne 0 \), the nodal forces \(\textbf{f}_{p_i} \ne \textbf{0}\) as well as the sum of the nodal forces \(\sum _{i=1}^{3}\textbf{f}_{p_i} \ne \textbf{0}\) because of the balance with the inertia forces in the RVE; therefore, \(\textbf{q}_{\textrm{M}}\ne \textbf{0}\) in Eq. (28) meaning that inertia forces arise at the macroscale for a dynamic response of the RVE.
4 Numerical implementation in the frequency and time domains
The numerical solution of the elastodynamics problem Eq. (3) is built by means of the FE method. The time domain solution is retrieved from the frequency response taking full advantage of the EWM [46]; to the best of authors’ knowledge, here the EWM is applied for the first time to calculate the transient response of a 2D solid within the context of a computational homogenization framework.
4.1 Frequency domain response
The displacement field vector at the macroscale \(\overline{\textbf{u}}_{\textrm{M}}\) is represented through the following isoparametric expansion:

whereby  is the column matrix collecting all the nodal displacements of the discretized model at the macroscale and
is the column matrix collecting all the nodal displacements of the discretized model at the macroscale and  is the column matrix of the FE shape functions. The application of the standard Galerkin method to the weak formulation in Eq. (4), with account for the Eqs. (32)-(35), yields
is the column matrix of the FE shape functions. The application of the standard Galerkin method to the weak formulation in Eq. (4), with account for the Eqs. (32)-(35), yields

where  is the discretized strain operator. Equation (38) can be conveniently recast in matrix form as follows:
is the discretized strain operator. Equation (38) can be conveniently recast in matrix form as follows:

where  is the dynamic stiffness tensor matrix of the macroscopic homogenized continuum. Solving Eq. (39) in terms of
is the dynamic stiffness tensor matrix of the macroscopic homogenized continuum. Solving Eq. (39) in terms of  for a given frequency \(\omega \) gives the frequency response function corresponding to a load
for a given frequency \(\omega \) gives the frequency response function corresponding to a load  . The frequency response function allows to recover the time domain solution through the inverse Fourier transform as detailed in the following Section.
. The frequency response function allows to recover the time domain solution through the inverse Fourier transform as detailed in the following Section.
4.2 Time domain response
A time-dependent load  can be represented in the frequency domain by its Fourier transform
can be represented in the frequency domain by its Fourier transform  . The frequency response under this load follows from the solution of Eq. (39) as
. The frequency response under this load follows from the solution of Eq. (39) as

The dynamic response in the time domain is then reconstructed by computing the inverse Fourier transform of Eq. (40)

At this stage, it is worth to note that the Fourier transform  in Eq. (40) is a complex function of frequency including amplitude and phase information of the excitation, as indeed
in Eq. (40) is a complex function of frequency including amplitude and phase information of the excitation, as indeed  , being
, being  the amplitude and
the amplitude and  the phase. This means that, correspondingly, both amplitude and phase information are included in the response given by Eq. (40), allowing a complete reconstruction of the response in the time domain as well from Eq. (41).
the phase. This means that, correspondingly, both amplitude and phase information are included in the response given by Eq. (40), allowing a complete reconstruction of the response in the time domain as well from Eq. (41).
For displacement boundary conditions, the column matrix collecting the nodal displacements  is partitioned in two column matrices of prescribed displacements
is partitioned in two column matrices of prescribed displacements  along the macroscopic domain boundary and unknown displacements
along the macroscopic domain boundary and unknown displacements  , therefore Eq. (39) reads
, therefore Eq. (39) reads

Consequently, the column matrix of unknown displacements  is readily given as
is readily given as

Upon defining the column matrix of the prescribed displacements in the time domain  , the corresponding column matrix of unknown displacements can be obtained as follows:
, the corresponding column matrix of unknown displacements can be obtained as follows:

Finally, the inverse Fourier transform yields the column matrix of unknown displacements in the time domain

As for numerical implementation, in this study the Fourier transform  in Eq. (40) and the inverse Fourier transform in Eq. (41) are calculated by the EWM [46], which is specifically suitable for undamped (or lightly damped) systems. The EWM applies for arbitrary excitations and captures the typical time offset of the dynamic response at different points of the system as elastic waves propagate through the system, as shown in ref. [46]. For completeness, some details on the implementation of the EWM are reported in the Appendix. Similar comments hold for the Fourier transform
in Eq. (40) and the inverse Fourier transform in Eq. (41) are calculated by the EWM [46], which is specifically suitable for undamped (or lightly damped) systems. The EWM applies for arbitrary excitations and captures the typical time offset of the dynamic response at different points of the system as elastic waves propagate through the system, as shown in ref. [46]. For completeness, some details on the implementation of the EWM are reported in the Appendix. Similar comments hold for the Fourier transform  in Eq. (44) and the inverse Fourier transform in Eq. (45) and therefore not repeated here for brevity.
in Eq. (44) and the inverse Fourier transform in Eq. (45) and therefore not repeated here for brevity.
4.3 Internal dynamics of the RVE
If the dynamics of the RVE is to be studied in addition to the macroscale problem, the following steps can be adopted within the computational homogenization framework.
Once the displacement vector \(\textbf{u}_{\textrm{M}}(t)\) of a material point at the macroscale is known, the column matrix of displacements  of the underlying RVE can be easily retrieved by the prescribed displacements at the microscale by means of Eq. (24) rewritten as follows:
of the underlying RVE can be easily retrieved by the prescribed displacements at the microscale by means of Eq. (24) rewritten as follows:
whereby  is the column matrix collecting the prescribed displacements. The column matrix of the free displacements
is the column matrix collecting the prescribed displacements. The column matrix of the free displacements  can be obtained from Eq. (20) as
can be obtained from Eq. (20) as

Making use of Eq. (17), the column matrix  collecting the displacements of the RVE in the frequency domain is given as
collecting the displacements of the RVE in the frequency domain is given as

The internal dynamics of the RVE in the time domain can be finally retrieved by means of the inverse Fourier transform

4.4 Remarks
Now, a few remarks are in order.
Remark 1
The proposed computational homogenization framework is a multiscale technique involving the derivation of the local macroscopic constitutive behavior from the underlying microstructure, via construction and solution of a microscale boundary value problem defined on a RVE identifying physical and geometrical properties of the microstructure. That is, the local macroscopic constitutive behavior is neither assumed a priori nor obtained from asymptotic convergence of the microscopic one. Therefore, the proposed framework differs from any classical mathematical homogenization where the microscopic structural behavior asymptotically converges to the material behavior at the macroscopic material point.
Irrespectively of the size of the RVE, the proposed framework is meaningful and provides accurate results as long as the relaxed principle of separation of scales is fulfilled, i.e., as long as the sizes of the microstructural constituents (matrix and heterogeneities) are within the ranges expressed by Eq. (1), for a given excitation. As explained in previous work by some of the authors [33], the relaxed principle of separation of scales is especially suitable for the frequency range of excitation at which LRAMs exhibit exotic properties and, consistently with the assumption that the characteristic wavelengths associated to the heterogeneities can be comparable to the sizes of the microstructural constituents of the heterogeneities (see Eq. (1)), inertia effects at the microscale cannot be neglected in Eq. (5) and shall be reflected in the local macroscopic response. Indeed, coupling of the macroscopic stress to the microscopic inertia forces is inherent in Eq. (13) (see also corresponding Eqs. (17)-(19) in ref. [35]).
The question may arise on whether inertia terms at the microscale will always play a role if, for a fixed frequency of the excitation, the size of the RVE is progressively reduced. Since, in this case, the characteristic wavelengths are fixed while the sizes of the microstructural constituents reduce with the size of the RVE, it is evident that, for a certain reduced size of the RVE, the long wavelength approximation will hold for both host matrix and heterogeneities, i.e., the sizes of the microstructural constituents of both host matrix and heterogeneities will be very small compared to the associated characteristic wavelengths. At this stage, the responses of all the microstructural constituents will be quasistatic, inertia effects at the microscale will be negligible and the proposed framework will automatically revert to a quasistatic computational homogenization, i.e., a homogenization where inertia effects at the microscale are neglected. In this respect, the proposed framework mirrors the computational homogenization approach developed in ref. [33], which was shown to provide the same results of the classical quasistatic homogenization if, for a constant size of the macroscale domain and the frequency of the excitation, the size of the RVE is reduced until the long wavelength approximation holds for all the microstructural constituents of both host matrix and heterogeneities. However, it is important to remark that, in this case, inertia forces will be negligible because the response is quasistatic and not because the size of the RVE is “very small”. This means that, even for that very small size of the RVE, high-frequency excitations with characteristic wavelengths comparable to the sizes of the microstructural constituents of the heterogeneities will cause inertia effects at the microscale that, again, cannot be neglected and shall be reflected in the macroscopic response.
Recognize that, in the proposed framework, the upscaling of inertia effects at the microscale is obtained via the Hill-Mandel principle (11), which delivers Eq. (13) coupling the macroscopic stress to the microscopic inertia forces.
2-dimensional LRAM structure consisting of \(40 \times 10\) unit cells under two different loading conditions at the left edge: harmonic excitation in compression induced by prescribed displacement fields \(u_{\textrm{M},b_x}(t) = u_{\textrm{M},b}(t)\) and \(u_{\textrm{M},b_y}(t) =0\) (no contraction is possible in y-direction), with time function \(u_{\textrm{M},b}(t)\) shown in Fig. 2a; transient shear load induced by prescribed uniform y-displacement field \(u_{\textrm{M},b_y}(t) = u_{\textrm{M},b}(t)\) (x-displacements are free), with time function \(u_{\textrm{M},b}(t)\) shown in Fig. 2b
Remark 2
The proposed computational homogenization framework enables a remarkable model order reduction, since the equations governing the macroscopic homogenized continuum involve only the degrees of freedom associated with the macroscale displacement field and no additional degrees of freedom or additional variables describing the internal dynamics of the RVE. This is not the case, instead, for other macroscopic homogenized continua obtained by alternative homogenization approaches [35, 36, 39, 44]. Therefore, N being the number of nodes at the macroscale, the FE model of the macroscopic homogenized continuum involves only 2N or 3N degrees of freedom depending on whether the LRAM structure is 2- or 3-dimensional.
Moreover, the internal dynamics of the RVE can readily be reconstructed from the macroscale response, in either the frequency domain using Eq. (48) or the time domain using Eq. (49). That is, a full description of the microscale response is possible, although no related additional degrees of freedom/variables are involved in the solution of the macroscale problem.
Remark 3
The proposed dynamic condensation of the internal degrees of freedom of the RVE removes the need to approximate the internal dynamics of the RVE by means of dynamic substructuring techniques as, e.g., the Craig-Bampton method [35]. Consequently, the solution is not affected by modal truncation errors inherent to the numerical implementation of this technique and, within the relaxed principle of separation of scales (1), is accurate to the extent provided by the FE method. Note that removing the need to approximate the internal dynamics of the RVE by a finite number of modes makes the proposed computational homogenization framework especially suitable for those applications where, depending on the loading conditions, it is not straightforward to predict which modes contribute to the internal dynamics of the RVE.
Remark 4
A dynamic condensation approach in the frequency domain could be applied, in principle, to alternative computational homogenization approaches in the literature, e.g., the approach proposed in ref. [35]. In this case, the dynamic condensation would remove the additional degrees of freedom describing the internal dynamics of the RVE according to the Craig-Bampton technique from the microscale system of equations, written in the frequency domain. Moreover, the EWM could also be applied to calculate the response in the time domain. As pointed in the previous Remark #3, however, the dynamic condensation approach proposed in this study is of particular interest as it does not require any modal truncation to represent the internal dynamics of the RVE.
Remark 5
A dynamic condensation of the internal degrees of freedom of the RVE was proposed by some of the authors in ref. [34]. It was implemented in the time domain to solve the microscale problem in the context of a computational homogenization approach requiring the concurrent solutions, at each time step, of two nested boundary value problems at the microscale and the macroscale. Differently, the proposed dynamic condensation approach in the frequency domain leads to formulating and solving only the boundary value problem of the reduced-order macroscopic homogenized continuum without additional variables describing the microscale dynamics, and its solution in the time domain is made particularly efficient by adopting the EWM.
Remark 6
Provided that the relaxed principle of separation of scales (1) holds, the proposed computational homogenization framework applies for any geometry at the microscale and any geometry at the macroscale. Any transient excitation can be considered in the time domain. Further, any time-dependent boundary conditions can be considered at both transient and steady states. Transient excitations in the time domain and time-dependent boundary conditions can be handled by the inverse Fourier transform approach in conjunction with the EWM, as devised in Sect. 4.2.
Remark 7
The proposed computational homogenization framework can handle spatial damping in different ways. A possible approach involves redefining the constitutive laws of the microstructural phases in the RVE and deriving the corresponding macroscopic constitutive behavior by the Hill-Mandel principle. Assuming, for example, a Kelvin-Voigt viscoelastic behavior for the microstructural phases, this approach would lead to rewriting the \(3^{\textrm{rd}}\) and \(4^\textrm{th}\) order frequency-dependent elastic tensors (34)-(35) at the macroscale as frequency-dependent complex stiffness tensors. For this approach to be applicable, however, an accurate mathematical model of the actual damping mechanism within the microstructural constituent materials is necessary. An alternative approach is to introduce proportional damping in the FE discretized equations governing the microscale dynamics, on a purely numerical basis. For instance, a damping matrix proportional to the mass matrix can be introduced in Eq. (14) for the RVE. For both approaches, the main implementation steps of the proposed framework would mirror those for the undamped case developed in Sect. 4, i.e., the governing equations should be formulated, first, in the frequency domain, while the transient response could be obtained by the inverse Fourier transform. In particular, in presence of damping, the Fourier transform and the inverse Fourier transform could be calculated by standard techniques and not by the EWM, which is especially devised for undamped (or lightly damped) systems. That is, the inclusion of spatial damping would not require substantial modifications in the main implementation steps of the proposed framework and, on the other hand, no special novelties will be introduced in the formulation to calculate the transient response, as standard Fourier transform techniques could be implemented. It is important to remark that, in contrast, standard Fourier transform techniques cannot be applied to calculate the transient response of undamped systems (see ref. [46]) and this issue motivates the use of the EWM introduced in Sect. 4.2.
5 Numerical application
To assess the effectiveness of the proposed computational homogenization framework, consider a LRAM structure consisting of a 2-dimensional array of \(40 \times 10\) contiguous unit cells as shown in Fig. 2.
Each unit cell consists of an epoxy matrix with an embedded lead inclusion coated with silicone rubber; one microstructural phase constitutes the host matrix (\(n_{mat} =1\) in Eq. (1)) and two microstructural phases constitute the heterogeneities (\(n_{het} =2\) in Eq. (1)). Material composition and the geometry of each unit cell of the LRAM are illustrated in Fig. 3a, while the material properties of each constituent are reported in Table 1. Data are taken from ref. [35].
Considered LRAM unit cell in Fig. 2: (a) composition and geometry of the unit cell, (b) FE mesh of the unit cell
As for the boundary conditions of the LRAM structure in Fig. 2, the right edge is clamped, top and bottom edges are free, the left edge is subjected to prescribed time-dependent displacements to be detailed in Sects. 5.1 and 5.2.
The proposed computational homogenization framework is implemented considering a macroscale computational domain of \(40 \times 10\) 4-node plane strain FEs and 451 nodes, totalling \(902 = 2 \times 451\) degrees of freedom. The RVE, whose geometry coincides with that of the unit cell, is discretized by 524 FEs as shown in Fig. 3b; the associated degrees of freedom, however, are removed by the dynamic condensation introduced in Sect. 3.1 and, as a result, the reduced-order FE model of the macroscopic homogenized continuum features only 902 degrees of freedom of the macroscale computational domain. The model is implemented in an in-house Matlab code.
Time response of the LRAM in Fig. 2: (a) horizontal displacement along the line at \(y = 0.105\hspace{1.5pt}\text {m}\) for \(t = 4\pi /\omega = 2/f\), (b) horizontal displacement at the point \(\textbf{x}_{\textrm{M},1} = (0.21,0.105)\,\hspace{1.5pt}\text {m}\) for \(t \in [0,4\pi /\omega ]\) and excitation frequencies (i) \(f = 200\hspace{1.5pt}\text {Hz}\), (ii) \(f = 450\hspace{1.5pt}\text {Hz}\), (iii) \(f = 800\hspace{1.5pt}\text {Hz}\), (iv) \(f = 1200\hspace{1.5pt}\text {Hz}\)
For comparison in the time domain, two alternative solutions are built. The first solution is the direct numerical simulation (DNS) solution obtained from a fully resolved FE model, implemented in Abaqus employing 4-node plane strain elements (CPE4). Considering 192416 FEs and 193318 nodes, the full FE model includes \(386636 = 2 \times 193318\) degrees of freedom. The time integration scheme called “Hilber-Hughes-Taylor operator” is used to calculate the time response in Abaqus. The second solution is a quasistatic computational homogenization solution built as explained in ref. [35], i.e., by omitting the mass contribution in the following equilibrium equations of the RVE and solving for the free degrees of freedom using a static condensation procedure:

In Eq. (50), “ ” and “
” and “ ” denote prescribed and free degrees of freedom, superscripts “p” and “f” denote the related blocks of the stiffness and mass matrices
” denote prescribed and free degrees of freedom, superscripts “p” and “f” denote the related blocks of the stiffness and mass matrices  and
and  ; further, “
; further, “ ” denotes the forces acting on the prescribed nodes, “
” denotes the forces acting on the prescribed nodes, “ ” is a column matrix (whose length is equal to the number of free nodes) where every entry is a zero vector. To construct the quasistatic solution, the macroscale and microscale computational domains mirror those used in the proposed computational homogenization framework, i.e., \(40 \times 10\) 4-node plane strain FEs, 451 nodes and \(902 = 2 \times 451\) degrees of freedom at the macroscale, 524 FEs to discretize the RVE as shown in Fig. 3b. The model is implemented in an in-house Matlab code and the time response is obtained solving the system of equations of the macroscopic homogenized continuum by a generalized \(\alpha \)-method (Newmark algorithm). The proposed computational homogenization framework, the DNS solution and the quasistatic solution are built on a HP Zbook 15v G5 Workstation (Intel i5-9300 H 2.40 GHz CPU with 8GB of memory).
” is a column matrix (whose length is equal to the number of free nodes) where every entry is a zero vector. To construct the quasistatic solution, the macroscale and microscale computational domains mirror those used in the proposed computational homogenization framework, i.e., \(40 \times 10\) 4-node plane strain FEs, 451 nodes and \(902 = 2 \times 451\) degrees of freedom at the macroscale, 524 FEs to discretize the RVE as shown in Fig. 3b. The model is implemented in an in-house Matlab code and the time response is obtained solving the system of equations of the macroscopic homogenized continuum by a generalized \(\alpha \)-method (Newmark algorithm). The proposed computational homogenization framework, the DNS solution and the quasistatic solution are built on a HP Zbook 15v G5 Workstation (Intel i5-9300 H 2.40 GHz CPU with 8GB of memory).
Deformed shape (scale magnified for visualization purposes) of the LRAM in Fig. 2 at \(t = 4\pi /\omega = 2/f\) with: (a) \(f = 200\hspace{1.5pt}\text {Hz}\), (b) \(f = 450\hspace{1.5pt}\text {Hz}\), (c) \(f = 800\hspace{1.5pt}\text {Hz}\), (d) \(f = 1200\hspace{1.5pt}\text {Hz}\); contour map with black continuous mesh denotes the displacement magnitude (proposed framework), red dots (outline of the unit cells from DNS)
Local deformed shape of the LRAM unit cell in Fig. 2 at four time instants: (i) \(t = T/4\), (ii) \(t = T/2\), (iii) \(t = 3T/4\), (iv) \(t = T\) with \(T=2/f\) and \(f=450\hspace{1.5pt}\text {Hz}\); (a) response of the RVE in the point \(\textbf{x}_{\textrm{M},2} = (0.2205,0.1155)\hspace{1.5pt}\text {m}\) obtained by the proposed framework, (b) response of the unit cell at \(\textbf{x}_{2} = (0.2205,0.1155)\hspace{1.5pt}\text {m}\) from the DNS. Contour map denotes the total displacement magnitude
Figure 4 shows the dispersion curves of the infinite LRAM corresponding to the finite LRAM in Fig. 2 calculated along the irreducible Brillouin zone, using the FE model in Abaqus. Two stopbands can be clearly identified.
5.1 Harmonic load
Assume that the LRAM in Fig. 2 is subjected to prescribed displacement fields \(u_{\textrm{M},b_x}(t) = u_{\textrm{M},b}(t)\) and \(u_{\textrm{M},b_y}(t) =0\) at the left edge as shown in Fig. 2a, being \(u_{\textrm{M},b}(t)\) a harmonic function \( u_{\textrm{M},b}(t) = 1\times 10^{-5}(1-\cos (\omega t))\;{(\mathrm m)}\). That is, the horizontal displacements of the left edge induce a harmonic excitation in compression while no contraction of the left edge is possible in the vertical direction.
Figure 5 shows the time response of the LRAM for several excitation frequencies \(\omega \) (indicated in the dispersion graph for completeness, see Fig. 4), as computed by the proposed computational homogenization framework, including the DNS solution and the quasistatic solution for comparison. For both the DNS and the quasistatic solution, the simulation is carried out until \(t_{tot} = 2T\), being \(T=2\pi /\omega \) the period of the excitation, while the time step is always selected as \(\Delta t=t_{tot}/800\) for all excitation frequencies. Specifically, Fig. 5 shows the displacement of the LRAM at different locations, as detailed in the following: (a) along the line at half height, i.e., at \(y = 0.105\hspace{1.5pt}\text {m}\) (indicated in Fig. 2 by a red line), at time \(t = 2T = 4\pi /\omega \), i.e., two times the period T of the excitation; (b) at the point \(\textbf{x}_{\textrm{M},1} = (0.21,0.105)\hspace{1.5pt}\text {m}\) of the macroscopic homogenized continuum and at the corresponding point \(\textbf{x}_{1} = (0.21,0.105)\hspace{1.5pt}\text {m}\) in the DNS model for t spanning two times the period T of the excitation. The perfect agreement between the DNS solution and that obtained by the proposed framework again confirms its accuracy. Moreover, it is noticed that the quasistatic solution is not able to correctly capture the dynamic response of the LRAM, especially for higher frequency excitations.
Furthermore, Fig. 6 shows the deformed configurations of the LRAM at time \(t = 2T\) computed by the proposed computational homogenization framework and the DNS results for excitations with different frequencies. The displacements along the whole LRAM are in perfect agreement, confirming again the accuracy of the proposed method.
An additional insight into the dynamics of the LRAM can be offered by the time response of the RVE underlying a given material point. Indeed, employing the procedure described in Sect. 4.3, the internal dynamics of the RVE can be obtained efficiently from the time response in each point of the macroscopic homogenized continuum. For example, Fig. 7 shows the time response of the RVE in the point \(\textbf{x}_{\textrm{M},2} = (0.2205,0.1155)\hspace{1.5pt}\text {m}\) shown in Fig. 2 for an excitation frequency \(f = 450\hspace{1.5pt}\text {Hz}\) at time instants \(t = T/4\), \(T = T/2\), \(t = 3T/4\) and \(t = T\). Specifically, Fig. 7 shows the dynamical response computed by the proposed computational homogenization framework and the dynamical response of the unit cell with its centroid at the point \(\textbf{x}_{2} = (0.2205,0.1155)\hspace{1.5pt}\text {m}\) in the DNS model. The two solutions are in excellent agreement, confirming the accuracy of the proposed framework and its capability of capturing the internal dynamics of the RVE, without any additional degrees of freedom in the macroscopic homogenized continuum. Further, it is worth remarking that the two solutions in Fig. 7 agree very well even if the meshes are slightly different, these small differences being due to the automatic meshing of the DNS model in Abaqus.
Time response of the LRAM in Fig. 2: (a) vertical displacement along the line at \(y = 0.105\hspace{1.5pt}\text {m}\) for \(t = 0.0021438\hspace{1.5pt}\text {s}\), (b) vertical displacement at the point \(\textbf{x}_{\textrm{M},1} = (0.21,0.105)\,\hspace{1.5pt}\text {m}\) for \(t \in [0,0.0025]\,\hspace{1.5pt}\text {s}\)
Deformed shape (scale magnified for visualization purposes) of the LRAM in Fig. 2 at \(t = 0.0021438\hspace{1.5pt}\text {s}\) for a prescribed shear y-displacement varying according to the law shown in Fig. 2b; contour map with black continuous mesh denotes the displacement magnitude (proposed framework), red dots (outline of the unit cells from DNS)
Local deformed shape of the LRAM in Fig. 2 at four time instants: (i) \(t = T/4\), (ii) \(t = T/2\), (iii) \(t = 3T/4\), (iv) \(t = T\) for \(T = 2.5 \times 10^{-5}\hspace{1.5pt}\text {s}\); (a) response of the RVE in the point \(\textbf{x}_{\textrm{M},2} = (0.2205,0.1155)\hspace{1.5pt}\text {m}\) obtained by proposed framework, (b) response of the unit cell with its centroid at the point \(\textbf{x}_{2} = (0.2205,0.1155)\hspace{1.5pt}\text {m}\) from the DNS. Contour map denotes the total displacement magnitude
5.2 Transient load
Next, assume that the LRAM in Fig. 2 is subjected to prescribed uniform y-displacement field \(u_{\textrm{M},b_y}(t) = u_{\textrm{M},b}(t)\) at the left edge as shown in Fig. 2b, where \(u_{\textrm{M},b}(t)\) is a transient function given by:
That is, the vertical displacements of the left edge induce a transient shear load while the horizontal displacements of the left edge are free. This loading condition is of particular interest to highlight a main advantage of the proposed computational homogenization framework and, specifically, the fact that it does not require approximating the internal dynamics of the RVE by a finite number of modes, the selection of which would not be immediate, in this case, as a result of shear effects and transient nature of the load. Moreover, this loading condition is useful to demonstrate that the inverse Fourier transform approach in conjunction with the EWM is capable of handling arbitrary time-dependent boundary conditions (see Remark #6 in Sect. 4.4).
Fig. 8 shows the time response of the LRAM, as computed by the proposed computational homogenization framework, along with the DNS solution and the quasistatic solution. In this case, to build both the DNS and the quasistatic solution the simulation is carried out until \(t_{tot} = 2.5\times 10^{-3}\hspace{1.5pt}\text {s}\) (see Fig. 2b), while the time step is again \(\Delta t= t_{tot}/800\). In particular, Fig. 8 shows the displacement of the LRAM: (a) along the line at half height, i.e., at \(y=0.105\hspace{1.5pt}\text {m}\) (indicated in Fig. 2 by a red line) at time \(t = 0.0021438\hspace{1.5pt}\text {s}\), i.e., the time instant at which the response attains the maximum at the point \(\textbf{x}_{\textrm{M},1} = (0.21,0.105)\,\hspace{1.5pt}\text {m}\); (b) at the point \(\textbf{x}_{\textrm{M},1} = (0.21,0.105)\,\hspace{1.5pt}\text {m}\). Again, the perfect agreement between the DNS solution and that obtained by the proposed framework confirms its accuracy. Moreover, it is evident that the quasistatic solution is completely unable to capture the correct dynamic response.
Figure 9 shows the deformed configuration of the LRAM at time \(t = 0.0021438\hspace{1.5pt}\text {s}\). Again, the DNS results and those computed by the proposed computational homogenization framework are in excellent agreement.
Further, the time response of the RVE in the point \(\textbf{x}_{\textrm{M},2} = (0.2205,0.1155)\hspace{1.5pt}\text {m}\) is calculated by the proposed computational homogenization framework and compared with that of the unit cell having its centroid at the point \(\textbf{x}_{2} = (0.2205,0.1155)\,\hspace{1.5pt}\text {m}\) in the DNS model. The two solutions, shown in Fig. 10 at four time instants, are in a perfect agreement, substantiating once again the accuracy of the proposed framework.
Finally, Table 2 reports the wall-clock times associated with the execution of the time domain analyses under the transient shear load (results in Figs. 8-9-10), by means of the DNS and the proposed computational homogenization framework. The proposed framework offers a remarkable speed-up of about \(70\times \) compared to the DNS execution time. Notice that computational savings are similar for the time domain analyses under the harmonic excitation in compression, for all the excitation frequencies considered in Sect. 5.1.
6 Conclusions
This paper presented a reduced-order computational homogenization framework for LRAM structures. The main novelty is the formulation of a macroscopic homogenized continuum whose governing equations involve no additional variables describing the microscale dynamics that, in contrast, are typically required in micromorphic homogenized continua obtained by alternative computational homogenization approaches. Specifically, this relevant model-order reduction is obtained formulating the governing equations of the micro- and macroscale problems in the frequency domain, as derived from well-established scale transition relations, introducing a FE discretization of the microscale and macroscale problems and performing an exact dynamic condensation of all the degrees of freedom at the microscale. A further relevant novelty is the introduction of an appropriate inverse Fourier transform of the frequency-domain equations, in conjunction with the EWM, which allows to analyze transient dynamics as well. Under the assumption that the relaxed principle of separation of scales holds, arbitrary geometries of micro- and macro-structures, any transient excitations and any boundary conditions can be readily handled. Accuracy and computational advantages of the proposed reduced-order homogenized model have been demonstrated for a typical 2-dimensional LRAM structure.
Abbreviations
- \(^{(3)}\textbf{C}_{\textrm{M}}\) :
-
Macroscopic homogenized \(3{\textrm{rd}}\) order elastic material tensor
- \(^{(4)}\textbf{C}_{\textrm{M}}\) :
-
Macroscopic homogenized \(4{\textrm{th}}\) order elastic material tensor
- \(^{(4)}\textbf{C}_{\alpha }\) :
-
\(4{\textrm{th}}\) order elastic material tensor of the \(\alpha ^{\textrm{th}}\) RVE constituent
- \({\widehat{\textbf{D}}}_{p_{ij}}\) :
-
\(2{\textrm{nd}}\) order tensors within
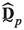
-
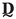 :
: -
Dynamic stiffness tensor matrix of the RVE
-
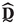 :
: -
Transformed dynamic stiffness tensor matrix of the RVE
-
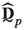 :
: -
Schur complement of
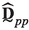
-
 :
: -
Blocks of the transformed dynamic stiffness tensor matrix
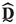 of the RVE
of the RVE -
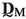 :
: -
Dynamic stiffness tensor matrix of the macroscopic homogenized continuum
-
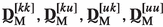 :
: -
Blocks of the dynamic stiffness tensor matrix
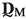 of the macroscopic homogenized continuum
of the macroscopic homogenized continuum - E :
-
Young’s modulus
- \(\textbf{e}_{k}\) :
-
Standard Cartesian basis
- \(\overline{\textbf{f}}_{p_1}\), \(\overline{\textbf{f}}_{p_2}\), \(\overline{\textbf{f}}_{p_3}\) :
-
Nodal force vectors associated with the prescribed nodes in the frequency domain
-
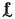 :
: -
Column matrix of the nodal forces of the RVE
-
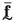 :
: -
Column matrix of the nodal forces of the RVE in the frequency domain
-
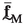 :
: -
Column matrix of the nodal forces at the macroscale in the frequency domain
-
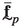 :
: -
Column matrix of the nodal forces associated with the prescribed nodes of the RVE in the frequency domain
-
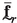 :
: -
Column matrix of the nodal forces associated with the retained nodes of the RVE in the frequency domain
- \(\textbf{I}\) :
-
Second order unit tensor
-
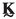 :
: -
Stiffness tensor matrix of the RVE
-
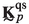 :
: -
Condensed static stiffness tensor matrix of the RVE
-
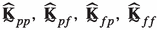 :
: -
Blocks of the transformed stiffness tensor matrix of the RVE
- \(l_k\) :
-
Typical size of the \(k{\textrm{th}}\) constituent of the heterogeneities
- \(l_j\) :
-
Typical size of the \(j{\textrm{th}}\) constituent of the matrix
- \(n_{het}\) :
-
Number of microstructural phases constituting the heterogeneities
- \(n_{mat}\) :
-
Number of microstructural phases constituting the host matrix
- N :
-
Number of nodes at the macroscale
-
 :
: -
Column matrix of FE shape functions at the microscale
-
 :
: -
Column matrix of FE shape functions at the macroscale
-
 :
: -
Mass tensor matrix of the RVE
-
 :
: -
Blocks of the transformed mass tensor matrix of the RVE
- \(\textbf{n}\) :
-
Outward unit normal vector to the boundary of the macroscale solid
- \(\textbf{p}\) :
-
Linear momentum vector at the microscale
- \(\textbf{p}_{\textrm{M}}\) :
-
Linear momentum vector at the macroscale
- \(\textbf{p}_{\alpha }\) :
-
Linear momentum vector of the \(\alpha {\textrm{th}}\) constituent of the RVE
- \(\overline{\textbf{p}}\) :
-
Linear momentum vector at the microscale in the frequency domain
- \(\overline{\textbf{p}}_{\textrm{M}}\) :
-
Linear momentum vector at the macroscale in the frequency domain
- \(\overline{\textbf{q}}\) :
-
Inertia force vector at the microscale in the frequency domain
- \(\overline{\textbf{q}}_{\textrm{M}}\) :
-
Inertia force vector at the macroscale in the frequency domain
-
 :
: -
Transformation matrix
- t :
-
Time
- \(t_{tot}\) :
-
Final time instant of the numerical simulation
- \(\Delta t\) :
-
Time step
- T :
-
Period of the excitation
- \(\textbf{t}\) :
-
Traction vector along the boundary of the RVE
- \(\overline{\textbf{t}}\) :
-
Traction vector along the boundary of the RVE in the frequency domain
- \(\textbf{t}_{\textrm{M}}\) :
-
Traction vector along the boundary of the macroscale solid
- \(\overline{\textbf{t}}_{\textrm{M}}\) :
-
Traction vector along the boundary of the macroscale solid in the frequency domain
- \(u_{\textrm{M},b}\) :
-
Prescribed displacement field time function at the macroscale
- \(u_{\textrm{M},b_x}\) :
-
Prescribed displacement field time function at the macroscale along the x-direction
- \(u_{\textrm{M},b_y}\) :
-
Prescribed displacement field time function at the macroscale along the y-direction
- \(\textbf{u}\) :
-
Displacement field vector within the RVE
- \(\textbf{u}_{\textrm{M}}\) :
-
Displacement field vector at the macroscale
- \(\textbf{u}_{\alpha }\) :
-
Displacement field vector within the \(\alpha {\textrm{th}}\) constituent of the RVE
- \(\overline{\textbf{u}}\) :
-
Displacement field vector within the RVE in the frequency domain
-
 :
: -
Column matrix of the nodal displacements of the RVE
-
 :
: -
Column matrix of the nodal displacements of the RVE in the frequency domain
- \(\overline{\textbf{u}}_{\textrm{M}}\) :
-
Displacement field vector at the macroscale in the frequency domain
-
 :
: -
Column matrix of the nodal displacements at the macroscale
-
 :
: -
Column matrix of the nodal displacements at the macroscale in the frequency domain
-
 :
: -
Column matrix of the prescribed nodal displacements at the macroscale in the frequency domain
-
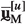 :
: -
Column matrix of the unknown nodal displacements at the macroscale in the frequency domain
-
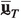 ,
, 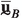 ,
, 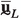 ,
,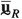 :
: -
Column matrices of the displacements of the nodes along the top, bottom, left and right edges of the RVE in the frequency domain
- \(\overline{\textbf{u}}_{p_1}\), \(\overline{\textbf{u}}_{p_2}\), \(\overline{\textbf{u}}_{p_3}\), \(\overline{\textbf{u}}_{p_4}\) :
-
Displacement vectors of the vertex nodes of the RVE in the frequency domain
-
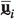 :
: -
Column matrix of the displacements of the interior nodes of the RVE in the frequency domain
-
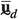 :
: -
Column matrix of the displacements of the dependent nodes of the RVE in the frequency domain
-
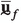 :
: -
Column matrix of the free displacements of the RVE in the frequency domain
-
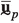 :
: -
Column matrix of the prescribed displacements of the RVE in the frequency domain
-
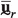 :
: -
Column matrix of the displacements of the retained nodes of the RVE in the frequency domain
- \(\textbf{w}\) :
-
Microfluctuation field vector
- \(\overline{\textbf{w}}\) :
-
Microfluctuation field vector in the frequency domain
- V :
-
Volume of the RVE
- \(\textbf{x}\) :
-
Position vector at the microscale
- \(\textbf{x}_{\textrm{M}}\) :
-
Position vector at the macroscale
- \(\textbf{x}_{\textrm{R}}\) :
-
Position vector of a reference point within the RVE
- \(\Delta \textbf{x} = \textbf{x} -\textbf{x}_{\textrm{R}}\) :
-
Difference between the position vector at the microscale and the position vector of a reference point within the RVE
- \(\Delta \textbf{x}_{p_i} = \textbf{x}_{p_i} - \textbf{x}_\textrm{R}\) :
-
Difference between the position vector of the vertex nodes of the RVE and the position vector of a reference point within the RVE
-
 :
: -
Column matrix where every entry is a zero vector
-
 :
: -
Unit tensor matrix
- \(\varvec{\epsilon }\) :
-
Linear infinitesimal strain tensor at the microscale
- \(\varvec{\epsilon }_{\alpha }\) :
-
Linear infinitesimal strain tensor of the \(\alpha {\textrm{th}}\) constituent of the RVE
- \(\overline{\varvec{\epsilon }}\) :
-
Linear infinitesimal strain tensor at the microscale in the frequency domain
- \(\varvec{\epsilon }_{\textrm{M}}\) :
-
Linear infinitesimal strain tensor at the macroscale
- \(\overline{\varvec{\epsilon }}_\textrm{M}\) :
-
Linear infinitesimal strain tensor at the macroscale in the frequency domain
- \(\lambda _{k}^{het}\) :
-
Shortest characteristic wavelength of the \(k{\textrm{th}}\) constituent of the heterogeneities
- \(\lambda _{j}^{mat}\) :
-
Shortest characteristic wavelength of the \(j{\textrm{th}}\) constituent of the matrix
- \(\nu \) :
-
Poisson’s ratio
- \(\rho \) :
-
Mass density
- \(\rho _{\alpha }\) :
-
Mass density in the \(\alpha {\textrm{th}}\) RVE costituent
- \(^{(2)}\varvec{\rho }_{\textrm{M}}\) :
-
Macroscopic homogenized \(2{\textrm{nd}}\) order dynamic density mass tensor
- \(^{(3)}\varvec{\rho }_{\textrm{M}}\) :
-
Macroscopic homogenized \(3{\textrm{rd}}\) order dynamic density mass tensor
- \(\varvec{\sigma }\) :
-
Cauchy stress tensor at the microscale
- \(\varvec{\sigma }_{\alpha }\) :
-
Cauchy stress tensor of the \(\alpha {\textrm{th}}\) constituent of the RVE
- \(\overline{\varvec{\sigma }}\) :
-
Cauchy stress tensor at the microscale in the frequency domain
- \(\varvec{\sigma }_{\textrm{M}}\) :
-
Cauchy stress tensor at the macroscale
- \(\overline{\varvec{\sigma }}_{\textrm{M}}\) :
-
Cauchy stress tensor at the macroscale in the frequency domain
- \(\Omega \) :
-
Interior of the domain occupied by the RVE
- \({\widehat{\Omega }}\) :
-
Domain occupied by the RVE
- \(\Omega _{\textrm{M}}\) :
-
Interior of the domain occupied by the macroscale solid
- \({\widehat{\Omega }}_{\textrm{M}}\) :
-
Domain occupied by the macroscale solid
- \(\partial \Omega \) :
-
Boundary of the domain occupied by the RVE
- \(\partial \Omega _{\textrm{M}}\) :
-
Boundary of the domain occupied by the macroscale solid
- \(\omega \) :
-
Frequency
-
 :
: -
Discretized strain operator
- \({\text {div}}\) :
-
Divergence operator in the the microscale coordinate system
- \({\text {div}}_{\textrm{M}}\) :
-
Divergence operator in the macroscale coordinate system
- \({\mathscr {F}}\) :
-
Fourier transform
- \({\mathscr {F}}^{-1}\) :
-
Inverse Fourier transform
- \(\nabla ^{s}\) :
-
Symmetric gradient operator in the microscale coordinate system
- \(\nabla ^{s}_{\textrm{M}}\) :
-
Symmetric gradient operator in the macroscale coordinate system
References
Liu Z, Zhang X, Mao Y, Zhu YY, Yang Z, Chan CT, Sheng P (2000) Locally resonant sonic materials. Science 289(5485):1734–1736
Wen J, Zhao H, Lv L, Yuan B, Wang G, Wen X (2011) Effects of locally resonant modes on underwater sound absorption in viscoelastic materials. J Acoust Soc Am 130(3):1201–1208
Sheng P, Mei J, Liu Z, Wen W (2007) Dynamic mass density and acoustic metamaterials. Phys B Condens Matter 394(2):256–261
Ding Y, Liu Z, Qiu C, Shi J (2007) Metamaterial with simultaneously negative bulk modulus and mass density. Phys Rev Lett 99:093904
Huang HH, Sun CT, Huang GL (2009) On the negative effective mass density in acoustic metamaterials. Int J Eng Sci 47(4):610–617
Huang HH, Sun CT (2009) Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J Phys 11(1):013003
Lai Y, Wu Y, Sheng P, Zhang Z-Q (2011) Hybrid elastic solids. Nat Mater 10(8):620–624
Bigoni D, Guenneau S, Movchan AB, Brun M (2013) Elastic metamaterials with inertial locally resonant structures: application to lensing and localization. Phys Rev B 87(17)
Krushynska AO, Kouznetsova VG, Geers MGD (2014) Towards optimal design of locally resonant acoustic metamaterials. J Mech Phys Solids 71:179–196
Mitchell SJ, Pandolfi A, Ortiz M (2014) Metaconcrete: designed aggregates to enhance dynamic performance. J Mech Phys Solids 65:69–81
Miniaci M, Krushynska A, Bosia F, Pugno NM (2016) Large scale mechanical metamaterials as seismic shields. New J Phys 18(8):083041
Zhu R, Liu XN, Hu GK, Sun CT, Huang GL. (2014) Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat Commun 5(1)
Pendry JB (2000) Negative refraction makes a perfect lens. Phys Rev Lett 85:3966–3969
Mindlin RD (1964) Micro-structure in linear elasticity. Arch Ration Mech Anal 16(1):51–78
Zhu R, Huang HH, Huang GL, Sun CT (2011) Microstructure continuum modeling of an elastic metamaterial. Int J Eng Sci 49(12):1477–1485
Bacigalupo A, Gambarotta L (2016) Simplified modelling of chiral lattice materials with local resonators. Int J Solids Struct 83:126–141
Bacigalupo A, Gambarotta L (2017) Wave propagation in non-centrosymmetric beam-lattices with lumped masses: discrete and micropolar modeling. Int J Solids Struct 118–119:128–145
Smyshlyaev VP (2009) Propagation and localization of elastic waves in highly anisotropic periodic composites via two-scale homogenization. Mech Mater 41(4):434–447
Auriault J-L, Boutin C (2012) Long wavelength inner-resonance cut-off frequencies in elastic composite materials. Int J Solids Struct 49(23–24):3269–3281
Chesnais C, Boutin C, Hans S (2012) Effects of the local resonance on the wave propagation in periodic frame structures: generalized Newtonian mechanics. J Acoust Soc Am 132(4):2873–2886
Zhou Q, Zha S, Bian L-A, Zhang J, Ding L, Liu H, Liu P (2019) Independently controllable dual-band terahertz metamaterial absorber exploiting graphene. J Phys D Appl Phys 52(25):255102
Willis JR (2009) Exact effective relations for dynamics of a laminated body. Mech Mater 41(4):385–393
Nemat-Nasser S, Willis JR, Srivastava A, Amirkhizi AV (2011) Homogenization of periodic elastic composites and locally resonant sonic materials. Phys Rev B 83(10)
Srivastava A, Nemat-Nasser S (2014) On the limit and applicability of dynamic homogenization. Wave Motion 51(7):1045–1054
Pernas-Salomón R, Shmuel G (2018) Dynamic homogenization of composite and locally resonant flexural systems. J Mech Phys Solids 119:43–59
Torrent D, Pennec Y, Djafari-Rouhani B (2014) Effective medium theory for elastic metamaterials in thin elastic plates. Phys Rev B 90(10)
Zhou X, Hu G (2009) Analytic model of elastic metamaterials with local resonances. Phys Rev B 79(19)
Chen Y, Hu G, Huang G (2017) A hybrid elastic metamaterial with negative mass density and tunable bending stiffness. J Mech Phys Solids 105:179–198
Hu R, Oskay C (2019) Multiscale nonlocal effective medium model for in-plane elastic wave dispersion and attenuation in periodic composites. J Mech Phys Solids 124:220–243
Mei C, Li L, Li X, Tang H, Han X, Wang X, Hu Y (2022) A nonlocality-based homogenization method for dynamics of metamaterials. Comp Struct 295:115716
Deshmukh K, Breitzman T, Dayal K (2022) Multiband homogenization of metamaterials in real-space: higher-order nonlocal models and scattering at external surfaces. J Mech Phys Solids 167:104992
Ganghoffer JF, Reda H (2022) Variational formulation of dynamical homogenization towards nonlocal effective media. Eur J Mech A/Solids 93:104487
Pham K, Kouznetsova VG, Geers MGD (2013) Transient computational homogenization for heterogeneous materials under dynamic excitation. J Mech Phys Solids 61(11):2125–2146
van Nuland TF, Silva PB, Sridhar A, Geers MG, Kouznetsova VG (2019) Transient analysis of nonlinear locally resonant metamaterials via computational homogenization. Math Mech Solids 24(10):3136–3155
Sridhar A, Kouznetsova VG, Geers MG (2016) Homogenization of locally resonant acoustic metamaterials towards an emergent enriched continuum. Comput Mech 57(3):423–435
Liu L, Sridhar A, Geers MGD, Kouznetsova VG (2021) Computational homogenization of locally resonant acoustic metamaterial panels towards enriched continuum beam/shell structures. Comput Methods Appl Mech Eng 387:114161
de Souza Neto EA, Blanco PJ, Sánchez PJ, Feijóo RA (2015) An RVE-based multiscale theory of solids with micro-scale inertia and body force effects. Mech Mater 80:136–144
Blanco PJ, Sánchez PJ, Souza Neto EA, Feijóo RA (2016) Variational foundations and generalized unified theory of RVE-based multiscale models. Arch Comput Methods Eng 23(2):191–253
Roca D, Lloberas-Valls O, Cante J, Oliver J (2018) A computational multiscale homogenization framework accounting for inertial effects: application to acoustic metamaterials modelling. Comput Methods Appl Mech Eng 330:415–446
Roca D, Yago D, Cante J, Lloberas-Valls O, Oliver J (2019) Computational design of locally resonant acoustic metamaterials. Comput Methods Appl Mech Eng 345:161–182
Sridhar A, Kouznetsova VG, Geers MGD (2017) A semi-analytical approach towards plane wave analysis of local resonance metamaterials using a multiscale enriched continuum description. Int J Mech Sci 133:188–198
Sridhar A, Kouznetsova VG, Geers MGD (2018) A general multiscale framework for the emergent effective elastodynamics of metamaterials. J Mech Phys Solids 111:414–433
Sridhar A, Kouznetsova VG, Geers MGD (2020) Frequency domain boundary value problem analyses of acoustic metamaterials described by an emergent generalized continuum. Comput Mech 65(3):789–805
Zhi J, Raju K, Tay T-E, Tan VBC (2021) Transient multi-scale analysis with micro-inertia effects using direct FE\(^{2}\) method. Comput Mech 67(6):1645–1660
Yuan Z, Fish J (2008) Toward realization of computational homogenization in practice. Int J Numer Methods Eng 73(3):361–380
Kausel E, Roësset JM (1992) Frequency domain analysis of undamped systems. J Eng Mech 118(4):721–734
Kouznetsova VG, Geers MGD, Brekelmans WAM (2009) Computational homogenisation for non-linear heterogeneous solids. Comput Exp Methods Struct 3:1–42. Imperial College Press
Kouznetsova V, Geers MGD, Brekelmans WAM (2002) Multi-scale constitutive modelling of heterogeneous materials with a gradient-enhanced computational homogenization scheme. Int J Numer Meth Eng 54(8):1235–1260
Failla G, Santoro R, Burlon A, Russillo AF (2020) An exact approach to the dynamics of locally-resonant beams. Mech Res Commun 103:103460
Russillo AF, Failla G, Fraternali F (2021) Free and forced vibrations of damped locally-resonant sandwich beams. Eur J Mech A/Solids 86:104188
Russillo AF, Failla G (2022) A novel reduced-order dynamic-stiffness formulation for locally resonant metamaterial plates. Comp Struct 280:114811
Acknowledgements
Author Andrea Francesco Russillo gratefully acknowledges the financial support of NextGenerationEU, TECH4YOU, Pilot Project 4.7.1: “Open Platform “Phigital Space” (physical and digital) of the Type “User Profiling” for the Advanced and Dynamic Codesign of Interventions on the Built and ex Novo”. Author Giuseppe Failla gratefully acknowledges the financial support of the Italian Ministry of University and Research (MUR), PRIN 2022: “Innovative Metamaterial Components and Absorbers for Vibration Mitigation (METAVIBRA)”, grant number: 2022LA43E2.
Funding
Open access funding provided by Università degli Studi Mediterranea di Reggio Calabria within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Brief note on the exponential window method
Brief note on the exponential window method
In absence of damping, care should be paid to the calculation of the Fourier transform in Eq. (40) and the inverse Fourier transform in Eq. (41). In particular, computing the time response (41) requires the application of the Exponential Window Method [46], consisting in the following steps:
-
Computation of the Fourier transform of the external load on the line \({\widetilde{\omega }} = \omega - \textrm{i}\eta \) in the complex plane, where \(\eta \) is a coefficient to be chosen suitably large for the implementation of the method.
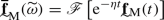 (A1)
(A1) -
Computation of the frequency response (40) on the line \({\widetilde{\omega }} = \omega - \textrm{i}\eta \) in the complex plane
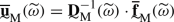 (A2)
(A2) -
Calculation of the inverse Fourier transform as
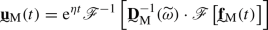 (A3)
(A3)
In the numerical applications of this study, the parameter \(\eta \) has been chosen equal to 1200 and results do not change as the value of this parameter increases.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Russillo, A.F., Kouznetsova, V.G., Failla, G. et al. A reduced-order computational homogenization framework for locally resonant metamaterial structures. Comput Mech (2024). https://doi.org/10.1007/s00466-024-02453-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00466-024-02453-9



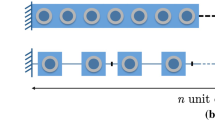











 :
: :
: :
:
 :
: of the RVE
of the RVE :
: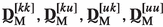 :
: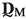 of the macroscopic homogenized continuum
of the macroscopic homogenized continuum :
: :
: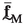 :
: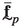 :
: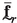 :
: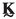 :
: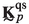 :
: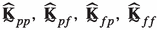 :
: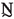 :
: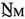 :
: :
: :
: :
: :
: :
: :
: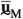 :
: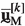 :
: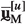 :
: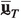 ,
, 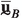 ,
, 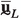 ,
,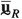 :
: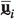 :
: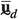 :
: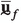 :
: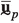 :
: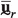 :
: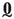 :
: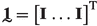 :
: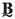 :
: