1 Introduction

The main objective of this contribution is to establish a computational framework for CPD that is versatile and devoid of-often overly complex-analytical derivatives for residuals and tangents using HDN. A brief overview of CPD and HDN are given in Sects. 1.1 and 1.2, respectively. Section 1.3 elaborates on the key features of the manuscript. The notations and definitions that are employed throughout the manuscript are listed in Sect. 1.4, followed by Sect. 1.5 explaining the organization of the remainder of the manuscript.

1.1 Peridynamics

Peridynamics (PD) is a nonlocal framework to formulate continuum mechanics which assumes that physical points within a continuum body interact with each other across a finite distance called horizon [1]. In PD, the governing equations are formulated based on integral equations without spatial derivatives, which makes the framework suitable for the analysis of problems involving discontinuities and singularities such as fracture [2,3,4,5,6,7,8,9]. However, the spectrum of PD applications is considerably broad and not limited to fracture mechanics, see Javili et al. [10] for a comprehensive review. In bond-based PD, the interaction between two points within the continuum is only described by a two-point force density vector. Such simplified assumption for the interactions leads to failure in capturing the Poisson’s effect. That is, the Poisson’s ratio is restricted to 1/4 for isotropic materials. To overcome this limitation, state-based PD was developed [3] where the force density vector can be defined based on the stress tensors which allows the use of constitutive models in PD [11]. Recently, Javili et al. [12] established an alternative formulation for PD called “continuum-kinematics-inspired peridynamics (CPD)” wherein the underlying kinematics are reminiscent to classical continuum mechanics. The nonlocal material behavior in CPD is governed by three interactions types; one-neighbor interaction which occurs between a point and all of its neighbors; two-neighbor interaction which occurs between a point and all pairs of its neighbors; and three neighbor interaction which occurs between a point and all triplets of its neighbors. Since the interactions are defined by the change of pair-length, triplet-area and tetrad-volume, CPD build upon classical continuum mechanics kinematics. Additionally, constrained Poisson’s ratio or zero-energy modes are absent in CPD. Owing to its great versatility and advantages, CPD has been growing rapidly. The computational framework for the implementation of CPD was developed in [13], see also [14]. Afterwards, Javili et al. [15] investigated the thermodynamic restrictions on the interaction energies in CPD and derived thermodynamically consistent constitutive laws through a Coleman–Noll-like procedure. Schaller et al. [16] reexamined the governing equations in CPD for open systems and demonstrated how the balances of momentum, energy and entropy are modified in the presence of an additional mass source. Zhou and Tian [17] investigated the concept of constitutive correspondence in CPD. Ekiz et al. [18, 19] established relationships between the material parameters of CPD and isotropic linear elasticity. For further studies on CPD, the reader is referred to the following references with applications to wrinkling and instabilities [20], bone remodeling [21], elasto-plasticity [22], damage and fracture [23, 24] and interfacial modeling in multi-phase materials [25, 26].

1.2 Hyper-dual numbers

In computational mechanics, modeling and simulation of the mechanical behavior of materials undergoing large deformations is a challenging task. Further complexities arise if accounting for inelasticity or anisotropy is required. The material behavior is commonly described by a potential energy function whose derivatives with respect to certain fields yields the stresses and tangent moduli. Accurate calculation of derivatives of the potential energy function is essential and considerably influences the simulation results. In particular, accurate calculation of the residual guarantees the precision in the physics of the problem and accurate calculation of the tangent influences the convergence of the Newton–Raphson scheme for solving the nonlinear system of equations [27, 28].

There exist various methods for the calculation of derivatives. At this stage of development on the subject, it seems virtually impossible to propose a classification that precisely addresses all aspects objectively. However, for the sake of representation and better conveying the ideas of the manuscript, we aim to propose a somewhat fair classification. Figure 1 shows a schematic classification of the differentiation schemes.Footnote 1 The first differentiation scheme is approximate differentiation which is mainly numerical and is based on the Taylor series expansion [29]. A well-known example of approximate differentiation is the finite difference method which is usually classified, for example, into the backward, forward or central difference method. However, finite difference methods have two major drawbacks; first, they are approximations in essence and second, the derivative accuracy depends on the perturbation values. Small perturbations could yield instabilities due to machine precision and large perturbations yield inaccuracy especially for the second-order derivatives. Aside from the finite difference method, the complex-step derivative approximation method [30, 31], the double number method [32] have been proposed which do not suffer from the aforementioned disadvantages, see [33,34,35,36,37,38,39] for further studies on both methods. The second differentiation scheme is accurate differentiation which calculates the differentiation precisely. The first and most-well known accurate differentiation scheme is the analytical differentiation which is an ideal method due to its efficiency. However, for complex material models such as anisotropic materials, analytical calculation of derivatives can become excessively complicated and is an arduous task, if not impossible. In such cases, symbolic and automatic differentiations become handy since they are computer based [40]. Recently Fike and Alonso [41], based on the theory of quaternions developed by Clifford [42], developed an automatic differentiation tool employing “hyper-dual numbers” for the exact calculation of first and second derivatives, see also [43]. Hyper-dual numbers (HDN) are basically an extension of the dual numbers which are able to calculate the up to the second-derivatives precisely. Due due their promising accuracy and versatility, hyper-dual numbers (HDN) have been utilized in various research areas. Fundamentals of matrix representation of hyper-dual numbers were presented by Imot er al. [44] where higher-order derivatives could be calculated using hyper-dual numbers. Cohen and Shoham [45] introduced the algebra of hyper-dual numbers and hyper-dual vectors of higher orders. Endo et al. [46] developed a new variant of hyper-dual numbers called diagonal hyper-dual numbers which are computationally more efficient for the calculation of Hessian matrices. Kiran and Khandelwal [47] utilized hyper-dual numbers in finite strain anisotropic hyperelasticity in order to automatically calculate the Piola stress tensor and the corresponding tangent moduli from the potential energy function. A similar study was carried out by Tanaka et al. [48] for elasto-plasticity, who compared the performance of the incremental variational formulation and hyper-dual numbers, see also [49]. Further studies with applications to hyper-dual numbers include rigid body kinematics [50,51,52], modelling equations of state [53], reduced order modeling [54], plate and shell buckling [55], gradient-enhanced elasto-plasticity [56] and topology optimization [57, 58].

Fig. 1
figure 1

A classification of the differentiation schemes. Note that such a classification is introduced for the sake of representation and better conveying the ideas of the manuscript

Full size image

1.3 Objectives and key features

CPD is a novel continuum formulation to explain the nonlocal behavior of materials. However, further exploration is required to fully grasp its potential. As any novel model, a crucial aspect to harness the capabilities of CPD lies in evaluating its utility to predict the material response for a wide range of energy densities and to identify their key properties. On the other hand - even for fairly simple energy densities - the derivations of the residuals and tangents in CPD become lengthy and intricate. This, in turn makes the computational implementation of CPD cumbersome and prone to errors. This manuscript aims to facilitate investigating arbitrary energies via a versatile framework that remains independent of the given energy model. To do so, we develop a computational framework furnished with automatic differentiation for a generic implementation of CPD via employing hyper-dual numbers (HDN). Although the governing equations of CPD are in integral form, calculation of derivatives are necessary to solve the system of non-linear equations in an implicit manner. In addition, the accuracy of the derivative calculation is important since it might influence the solution path in the case of non-convex potential energy functions [59] that can be encountered when modeling various physical phenomena such as in multi-scale modeling of carbon nano-tube foams [60], bi-stable elastic structures [61], mechanical transmission lines [62], narrow magnetic domain materials [63] and chemical surface adsorption [64]. Very few studies have been carried out on automatic differentiation methods in peridynamics [65,66,67,68]. However, to the best of the authors’ knowledge, there exist no contribution on implementation of hyper-dual numbers for CPD. Such computational framework paves the way for analysis of a wide range peridynamics material models which provides significant insights towards better understanding of complex material behaviors such as anisotropic materials or composites.

1.4 Notations and definitions

Throughout this manuscript, scalars are denoted by lower case Greek letters, first-order tensor quantities are denoted by lowercase bold letters and second-order tensor quantities are denoted by uppercase bold letters. For instance \(\alpha \) is a scalar, \(\varvec{a}\) is a first-order tensor, \(\varvec{A}\) is a second-order tensor. The cross product of two vectors \(\varvec{a}\) and \(\varvec{b}\) is a vector \(\varvec{c}=\varvec{a}\times \varvec{b}\) with \([\varvec{c}]_{k}=[\varvec{a}]_{i} [\varvec{b}]_{j}[{{\mathbbm {e}}}]_{ijk}\) where \([{{\mathbbm {e}}} ]_{ijk}\) is the third-order Levi-Civita permutation tensor. The action of a second-order tensor \(\varvec{A}\) on a vector \(\varvec{b}\) results in a vector \(\varvec{c}=\varvec{A}\cdot \varvec{b}\) with \([\varvec{c}]_{i}=[\varvec{A}]_{ij}[\varvec{b}]_{j}\). The standard dot product of a vector \(\varvec{a}\) to a third-order tensor \({{\mathbbm {a}}} \) results in a second-order tensor \(\varvec{A}=\varvec{a}\cdot {{\mathbbm {a}}} \) with \([\varvec{A}]_{ij}=[\varvec{a}]_{k}[{{\mathbbm {a}}} ]_{kij}\). The non-standard dot product of a vector \(\varvec{a}\) to a third-order tensor \({{\mathbbm {a}}} \) results in a second-order tensor \(\varvec{A}=\varvec{a}\,\overline{\cdot }\,{{\mathbbm {a}}} \) with \([\varvec{A}]_{ij}=[\varvec{a}]_{k}[{{\mathbbm {a}}} ]_{ikj}\). The imaginary (non-real) and the real operators are denoted as \(\Im \) and \(\Re \). For instance, for an arbitrary complex number \(\alpha + \beta i\), the imaginary (non-real) operator \(\Im \) extracts the imaginary part as \(\Im (\alpha + \beta i) = \beta \) and the real operator extracts the real part as \(\Re (\alpha + \beta i) = \alpha \). As will be discussed later, for double numbers, dual numbers and hyper-dual numbers, the non-real unit has different properties than the well-known imaginary unit i and shall generally be addressed as a non-real unit. To avoid confusing terminologies, we also refer to the imaginary unit i as non-real.

Fig. 2
figure 2

Problem definition in CPD. A continuum body \({\mathcal {B}}_{0}\) in the material configuration is mapped to its spatial counterpart \({\mathcal {B}}_t\) via the nonlinear deformation map \(\varvec{y}\). The point a interacts with its neighbors within a horizon \({\mathcal {H}}_0\) and \({\mathcal {H}}_t\) in both material and spatial configurations, respectively. There exist three interaction types in CPD. One-, two- and three-neighbor interactions which correspond to the relative position vector, area and volume, respectively. \(\varvec{\Xi }^{ai}\) is the relative position between the points a, i. \(\varvec{A}^{aij}\) is the area formed between the points a, i, j. \(V^{aijk}\) is the volume formed between the points a, i, j, k

Full size image

1.5 Organization of the manuscript

The remainder of the manuscript is organized as follows. In Sect. 2, the fundamentals of CPD and its computational implementation are briefly reviewed. Hyper-dual numbers and their algebra are introduced in Sect. 3 where numerical differentiation using hyper-dual numbers with respect to scalar, vector and tensor arguments is elaborated. In Sect. 4, CPD is furnished with hyper-dual numbers and a general framework for calculation of the residual and tangents in CPD is developed. Section 5 details on a family of potential energy functions employed in this manuscript. The proposed framework is evaluated through a set of numerical examples in Sect. 6. Finally, Sect. 7 concludes the work and provides further outlooks. Table 1 summarizes the notation and terminology adopted in this manuscript.

2 Continuum-kinematics-inspired peridynamics

2.1 Kinematics

Let \({\mathcal {B}}_{0}\) be a continuum body with material configuration at time \(t=0\) which is mapped to its spatial counterpart \({\mathcal {B}}_t\) via the nonlinear deformation map as \(\varvec{x} = \varvec{y} (\varvec{X},t)\) , as shown in Fig. 2. In the material configuration, the point \(\varvec{X}^{a}\) interacts with its neighbors \(\varvec{X}^{i}\), \(\varvec{X}^{j}\), \(\varvec{X}^{k}\), etc within the Horizon \({\mathcal {H}}_{0}\). Similarly, the point \(\varvec{x}^{a}\) interacts with its mapped neighbors \(\varvec{x}^{i}\), \(\varvec{x}^{j}\), \(\varvec{x}^{k}\), etc within the Horizon \({\mathcal {H}}_{t}\). The relative positions between the points and their neighbors in the material and spatial configurations are defined as

$$\begin{aligned} \varvec{\Xi }^{ai} := \varvec{X}^{i} {-} \varvec{X}^{a} \qquad \text {and} \qquad \varvec{\xi }^{ai} := \varvec{x}^{i} {-} \varvec{x}^{a} {=} \varvec{y}(\varvec{X}^{i}) {-} \varvec{y}(\varvec{X}^{a}) \,.\nonumber \\ \end{aligned}$$
(1)

Similar to classical continuum mechanics, there exist three relative deformation measures in CPD. The first relative deformation measure is the relative position vector \(\varvec{\xi }^{ai}\) which describes one-neighbor interactions and is defined as

$$\begin{aligned} \varvec{\xi }^{ai} := \varvec{x}^{i} - \varvec{x}^{a} \,. \end{aligned}$$
(2)

This relative deformation measure mimics the deformation gradient \(\varvec{F}\) which maps infinitesimal material line elements \(\textrm{d} \varvec{X}\) to their spatial counterparts \(\textrm{d} \varvec{x}\). Note, the superscript \(``ai''\) implies that the relative position vector corresponds to points \(\left\{ a,i\right\} \) and shall not be confused with tensor indices. The second relative deformation measure is the relative area vector \(\varvec{a}^{aij}\) which describes two-neighbor interactions and is defined as

$$\begin{aligned} \varvec{a}^{aij} := \left[ \varvec{x}^{i} -\varvec{x}^{a}\right] \times \left[ \varvec{x}^{j} -\varvec{x}^{a}\right] = \varvec{\xi }^{ai} \times \varvec{\xi }^{aj} \,. \end{aligned}$$
(3)

This relative deformation measure mimics the cofactor of the deformation gradient \(\text {Cof}\varvec{F}=J\varvec{F}^{-T}\) which maps infinitesimal material area elements \(\textrm{d} \varvec{A}\) to their spatial counterparts \(\textrm{d} \varvec{a}\). Similarly, the superscript \(``aij''\) implies that the area is spanned between points \(\left\{ a,i,j\right\} \) and shall not be confused with tensor indices. The third relative deformation measure is the relative volume \(v^{aijk}\) which describes three-neighbor interactions and is defined as

$$\begin{aligned} v^{aijk}&:= \left[ \left[ \varvec{x}^{i} - \varvec{x}^{a}\right] \times \left[ \varvec{x}^{j} - \varvec{x}^{a}\right] \right] \nonumber \\&\quad \cdot \left[ \varvec{x}^{k} - \varvec{x}^{a}\right] = \left[ \varvec{\xi }^{ai} \times \varvec{\xi }^{aj} \right] \cdot \varvec{\xi }^{ak}\,. \end{aligned}$$
(4)

This relative deformation measure mimics the determinant of the deformation gradient \(J=\text {Det}(\varvec{F})\) which maps infinitesimal material volume elements \(\textrm{d} V\) to their spatial counterparts \(\textrm{d} v\). The superscript \(``aijk''\) implies that the volume is spanned between points \(\left\{ a,i,j,k\right\} \) and shall not be confused with tensor indices. In the limit of vanishing horizon the following relations hold between the relative deformation measures

$$\begin{aligned}&\left. \begin{array}{l} \varvec{\xi }^{ai} := \varvec{x}^{i} - \varvec{x}^{a}\\ \varvec{a}^{aij} := \varvec{\xi }^{ai} \times \varvec{\xi }^{aj}\\ v^{aijk} := \left[ \varvec{\xi }^{ai} \times \varvec{\xi }^{aj} \right] \cdot \varvec{\xi }^{ak} \end{array}\right\} \nonumber \\&\quad {\Rightarrow }^{\delta _{0}\rightarrow 0} \qquad \left\{ \begin{array}{l} \varvec{\xi }^{ai} := \varvec{F} \cdot \varvec{\Xi }^{ai}\\ \varvec{a}^{aij} := \text {Cof}\varvec{F}\, \cdot \varvec{A}^{aij}\\ v^{aijk} := \text {Det}\varvec{F}\, V^{aijk} \end{array}\right. \,. \end{aligned}$$
(5)
Table 1 Summary of notation and terminology
Full size table

2.2 Governing equations

The next step is to elaborate the governing equations. In order to obtain the governing equations, the total potential energy functional is minimized via setting its variation to zero. The total potential energy \(\Pi \) is composed of the internal potential energy \(\Psi \) and the external potential energy \(\Upsilon \) as

$$\begin{aligned} \Pi = \Psi + \Upsilon \qquad \Longrightarrow \qquad \delta \Pi = \delta \Psi + \delta \Upsilon \qquad \forall \, \delta \varvec{y}\,. \end{aligned}$$
(6)

It shall be noted that our analysis will be carried out for non-dissipative processes in a variational setting. The variation of the external potential energy reads

$$\begin{aligned} \delta \Upsilon = - \int _{{\mathcal {B}}_0} \varvec{b}_{\textrm{ext}}^{a} \cdot \delta \varvec{y}^{a} \, \textrm{d} V - \int _{\partial {\mathcal {B}}_0} \varvec{t}_{\textrm{ext}}^{b} \cdot \delta \varvec{y}^{b} \, \textrm{d} A \,, \end{aligned}$$
(7)

with \(\varvec{b}_{\textrm{ext}}^{a}\) being the external force density and \(\varvec{t}_{\textrm{ext}}^{a}\) being the external traction on the boundary.

2.2.1 Internal potential energy

The internal potential energy consists of the contribution of one-, two- and three-neighbor interactions as

$$\begin{aligned}&\Psi = \Psi _{1} + \Psi _{2} + \Psi _{3}= \int _{{\mathcal {B}}_{0}} \left[ \displaystyle \frac{1}{2} \int _{{\mathcal {H}}_{0}} {\psi }_{1}^{ai} \, \textrm{d} V_{1}\right. \nonumber \\&+ \left. \displaystyle \frac{1}{3} \int \!\!\!\! \int _{{\mathcal {H}}_{0}} {\psi }_{2}^{aij} \, \textrm{d} V_{2} \, \textrm{d} V_{1}\displaystyle \frac{1}{4} \int \!\!\!\! \int \!\!\!\! \int _{{\mathcal {H}}_{0}} {\psi }_{3}^{aijk} \, \textrm{d} V_{3} \, \textrm{d} V_{2} \, \textrm{d} V_{1} \right] \textrm{d} V\,. \end{aligned}$$
(8)

The factors 1/2, 1/3 and 1/4 are associated with equivalent energies encountered for the same pairs, triplets and quadruples, respectively. The variation of the internal potential energy reads

$$\begin{aligned}&\delta \Psi _{1} = \int _{{\mathcal {B}}_{0}} \int _{{\mathcal {H}}_{0}} \delta {\psi }_{1}^{ai} \, \textrm{d} V_{1} \, \textrm{d} V \,,\nonumber \\&\delta \Psi _{2} = \int _{{\mathcal {B}}_{0}} \int \!\!\!\! \int _{{\mathcal {H}}_{0}} \delta {\psi }_{2}^{aij} \, \textrm{d} V_{2} \, \textrm{d} V_{1} \, \textrm{d} V \,,\nonumber \\&\delta \Psi _{3} = \int _{{\mathcal {B}}_{0}} \int \!\!\!\! \int \!\!\!\! \int _{{\mathcal {H}}_{0}} \delta {\psi }_{3}^{aijk} \, \textrm{d} V_{3} \, \textrm{d} V_{2} \, \textrm{d} V_{1} \, \textrm{d} V \,, \end{aligned}$$
(9)

where the pre-factors disappear. The one-, two- and three-neighbor interactions potential energy densities are a function of the relative position vector between point a and its neighbor i, the area vector formed by point a and its neighbor pairs \(\{i,j\}\) and the volume formed by point a and its neighbor triplets \(\{i,j,k\}\), respectively, as

$$\begin{aligned}&{\psi }_{1}^{ai} = {\psi }_{1}^{ai}(\varvec{\xi }^{ai})\,, \nonumber \\&{\psi }_{2}^{aij} = {\psi }_{2}^{aij}(\varvec{a}^{aij})\,, \nonumber \\&{\psi }_{3}^{aijk} = {\psi }_{3}^{aijk}(v^{aijk})\,. \end{aligned}$$
(10)

Using the relation \(\delta \varvec{\xi }^{ai} =\delta \varvec{y}^{i} - \delta \varvec{y}^{a}\) and the following identities

$$\begin{aligned} \delta \varvec{\xi }^{ai}&= \delta \varvec{y}^{i} - \delta \varvec{y}^{a} \,,\nonumber \\ \delta \varvec{a}^{aij}&= \left[ \delta \varvec{\xi }^{ai} \times \varvec{\xi }^{aj} \right] + \left[ \varvec{\xi }^{ai} \times \delta \varvec{\xi }^{aj} \right] \,,\nonumber \\ \delta v^{aijk}&= \left[ \delta \varvec{\xi }^{ai} \times \varvec{\xi }^{aj} \right] \cdot \varvec{\xi }^{ak} + \left[ \varvec{\xi }^{ai} \times \delta \varvec{\xi }^{aj} \right] \cdot \varvec{\xi }^{ak} \nonumber \\&\quad + \left[ \varvec{\xi }^{ai} \times \varvec{\xi }^{aj} \right] \cdot \delta \varvec{\xi }^{ak} \,, \end{aligned}$$
(11)

the final form of the variation of the internal potential energy variation reads

$$\begin{aligned} \delta \Psi&= \int _{{\mathcal {B}}_{0}} \int _{{\mathcal {H}}_{0}} \underbrace{\left[ \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}} + \int _{{\mathcal {H}}_{0}} \left[ 2\varvec{\xi }^{aj} \times \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}} \right] \, \textrm{d} V_{2} + \int \!\!\!\! \int _{{\mathcal {H}}_{0}} \left[ 3\displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}} \left[ \varvec{\xi }^{aj} \times \varvec{\xi }^{ak} \right] \right] \, \textrm{d} V_{3} \, \textrm{d} V_{2} \right] }_{\varvec{p}^{ai}} \cdot \delta \varvec{y}^{i} \, \textrm{d} V_{1} \textrm{d} V\nonumber \\&\quad - \int _{{\mathcal {B}}_{0}} \underbrace{\left[ \int _{{\mathcal {H}}_{0}} \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}} \, \textrm{d} V_{1} + \int \!\!\!\! \int _{{\mathcal {H}}_{0}} \left[ 2\varvec{\xi }^{aj} \times \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}} \right] \, \textrm{d} V_{2} \, \textrm{d} V_{1} + \int \!\!\!\! \int \!\!\!\! \int _{{\mathcal {H}}_{0}} \left[ 3\displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}} \left[ \varvec{\xi }^{aj} \times \varvec{\xi }^{ak} \right] \right] \, \, \textrm{d} V_{3} \textrm{d} V_{2} \, \textrm{d} V_{1} \right] }_{\varvec{b}_{\textrm{int}}^{a}} \cdot \delta \varvec{y}^{a} \textrm{d} V\,, \end{aligned}$$
(12)

with \(\varvec{p}^{ai}\) being the force density per volume squared and \(\varvec{b}_{\textrm{int}}^{a}\) being the internal force density per volume. Thus, the compact form of the internal potential energy potential variation boils down to

$$\begin{aligned} \delta \Psi = \int _{{\mathcal {B}}_{0}} \int _{{\mathcal {H}}_{0}} \varvec{p}^{ai} \cdot \delta \varvec{y}^{i} \, \textrm{d} V_{1} \textrm{d} V - \int _{{\mathcal {B}}_{0}} \varvec{b}_{\textrm{int}}^{a} \cdot \delta \varvec{y}^{a} \textrm{d} V\,. \end{aligned}$$
(13)

2.2.2 Equilibrium and balance equations

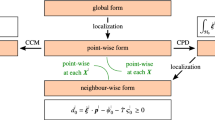
Via setting the variation of the total potential energy with respect to admissible variations \(\delta \varvec{y}\) at a fixed material point to zero, the governing equations for equilibrium are obtained. Inserting Eqs. (13) and (7) into Eq. (6) yields

$$\begin{aligned}&\int _{{\mathcal {B}}_{0}} \int _{{\mathcal {H}}_{0}} \varvec{p}^{ai} \cdot \delta \varvec{y}^{i} \, \textrm{d} V_{1} \textrm{d} V - \int _{{\mathcal {B}}_{0}} \varvec{b}_{\textrm{int}}^{a} \cdot \delta \varvec{y}^{a} \textrm{d} V \nonumber \\&\quad - \int _{{\mathcal {B}}_0} \varvec{b}_{\textrm{ext}}^{a} \cdot \delta \varvec{y}^{a} \, \textrm{d} V - \int _{\partial {\mathcal {B}}_0} \varvec{t}_{\textrm{ext}}^{b} \cdot \delta \varvec{y}^{b} \, \textrm{d} A = 0 \,. \end{aligned}$$
(14)

Due to arbitrariness of \(\delta \varvec{y}\), we can readily extract the governing equations as

$$\begin{aligned}&\int _{{\mathcal {B}}_{0}} \varvec{b}_{\textrm{int}}^{a} \textrm{d} V + \int _{{\mathcal {B}}_{0}} \varvec{b}_{\textrm{ext}}^{a} \textrm{d} V = {\varvec{0}}\,, \qquad \text {subject to} \nonumber \\&\quad \int _{{\mathcal {B}}_{0}} \int _{{\mathcal {H}}_{0}} \varvec{p}^{ai} \cdot \delta \varvec{y}^{i} \, \textrm{d} V_{1} \textrm{d} V - \int _{\partial {\mathcal {B}}_0} \varvec{t}_{\textrm{ext}}^{b} \cdot \delta \varvec{y}^{b} \, \textrm{d} A = 0 \,, \end{aligned}$$
(15)

in global form and as

$$\begin{aligned} \varvec{b}_{\textrm{int}}^{a} + \varvec{b}_{\textrm{ext}}^{a} = {\varvec{0}}\,, \end{aligned}$$
(16)

in point-wise local form. The obtained relations formulate the linear momentum balance which is the underlying governing equation in CPD. The angular momentum balance is a priori satisfied if the internal potential energy densities satisfy material frame indifference or more precisely, if they are defined as functions of \(|\varvec{\xi }^{ai}|\), \(|\varvec{a}^{aij}|\) and, \(|v^{aijk}|\).

2.3 Computational implementation of CPD

The first step towards computational implementation of CPD is to transform the equations from their continuous form to a discrete form. In doing so, the integrals over the horizon are transformed to summation over neighbors and using quadrature rule, integrals over the body are transformed to summation over collocation points. In our case, the collocations points and the quadrature points coincide, thus, we refer to them collectively as grid points henceforth, see [13].

For the linear momentum balance equation, we here assume that external body forces are zero for the sake of presentation. Accordingly the local form of the linear momentum balance can be expressed in discretized form as

$$\begin{aligned} \varvec{b}_{\textrm{int}}^{a}&= \sum ^{\#{\mathcal {N}}}_{i=1} \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}} {\mathcal {V}}^{i} + \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \left[ 2\varvec{\xi }^{aj} \times \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}} \right] {\mathcal {V}}^{ij} \nonumber \\&\quad + \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \sum _{{\begin{array}{c} k=1 \\ k\ne i \\ k\ne j \end{array}}}^{\#{\mathcal {N}}} \left[ 3\displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}} \left[ \varvec{\xi }^{aj} \times \varvec{\xi }^{ak} \right] \right] {\mathcal {V}}^{ijk} = {\varvec{0}} \,, \end{aligned}$$
(17)

with \({\mathcal {V}}^{i}\), \({\mathcal {V}}^{ij}\), \({\mathcal {V}}^{ijk}\) accounting for volume integrals. We define the point-wise residual vector for collocation point \({\mathcal {P}}^{a}\) as \(\varvec{R}^{a}\), which is composed of three parts; one-neighbor interactions contributions, two-neighbor interactions contributions and three-neighbor interactions contributions. That is

$$\begin{aligned} \varvec{R}^{a} = \varvec{R}^{a}_{1} + \varvec{R}^{a}_{2} + \varvec{R}^{a}_{3} = {\varvec{0}}\,, \end{aligned}$$
(18)

with

$$\begin{aligned}&\varvec{R}^{a}_{1} = \sum ^{\#{\mathcal {N}}}_{i=1} \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}} {\mathcal {V}}^{i}\,,\nonumber \\&\varvec{R}^{a}_{2} = \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \left[ 2\varvec{\xi }^{aj} \times \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}} \right] {\mathcal {V}}^{ij}\,,\nonumber \\&\varvec{R}^{a}_{3} = \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \sum _{{\begin{array}{c} k=1 \\ k\ne i \\ k\ne j \end{array}}}^{\#{\mathcal {N}}} \left[ 3\displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}} \left[ \varvec{\xi }^{aj} \times \varvec{\xi }^{ak} \right] \right] {\mathcal {V}}^{ijk}\,. \end{aligned}$$
(19)

The global discretized residual vector \({{\mathbbm {R}}} \) is composed of point-wise discretized residual vectors \(\varvec{R}^a\) assembled into a global vector formally represented as \({{\mathbbm {R}}} = \left[ \varvec{R}^{1} \,\, \varvec{R}^{2} \,\, \ldots \,\, \varvec{R}^{a} \right. \)\(\left. \,\, \ldots \,\, \varvec{R}^{\#{\mathcal {P}}} \right] ^{T}\). Similar to the point-wise residual, the point-wise tangent can be decomposed into three parts associated with one-, two- and three-neighbor interactions as \(\varvec{K}^{ab} =\partial \varvec{R}^{a}/\partial \varvec{x}^{b} = \varvec{K}^{ab}_1 +\varvec{K}^{ab}_2 + \varvec{K}^{ab}_3\) with

$$\begin{aligned} \varvec{K}^{ab}_1&= \displaystyle \frac{\partial \varvec{R}^a_1}{\partial \varvec{x}^b} = \displaystyle \frac{\partial }{\partial \varvec{x}^{b}} \left( \sum ^{\#{\mathcal {N}}}_{i=1} \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}} {\mathcal {V}}^{i}\right) \,,\nonumber \\ \varvec{K}^{ab}_2&= \displaystyle \frac{\partial \varvec{R}^a_2}{\partial \varvec{x}^b} = \displaystyle \frac{\partial }{\partial \varvec{x}^{b}} \left( \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \left[ 2\varvec{\xi }^{aj} \times \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}} \right] {\mathcal {V}}^{ij} \right) \,,\nonumber \\ \varvec{K}^{ab}_3&= \displaystyle \frac{\partial \varvec{R}^a_3}{\partial \varvec{x}^b} = \displaystyle \frac{\partial }{\partial \varvec{x}^{b}}\nonumber \\&\quad \left( \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \sum _{{\begin{array}{c} k=1 \\ k\ne i \\ k\ne j \end{array}}}^{\#{\mathcal {N}}} \left[ 3 \left[ \varvec{\xi }^{aj} \times \varvec{\xi }^{ak} \right] \displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}}\right] {\mathcal {V}}^{ijk}\right) \,. \end{aligned}$$
(20)

The fully discrete nonlinear system of governing equations can be stated as \({{\mathbbm {R}}} {\mathop {=}\limits ^{\cdot }} {{\mathbbm {O}}} \) which could be solved using an iterative Newton–Raphson scheme. The consistent linearization of the resulting system at iteration n reads

$$\begin{aligned}&{{\mathbbm {R}}} _{n+1} = {{\mathbbm {R}}} _{n} + {{\mathbbm {K}}} _{n} \cdot \Delta {\mathbbm {x}} _n \doteq \varvec{0} \qquad \text {thus}\nonumber \\&\quad \Delta {\mathbbm {x}} _{n} = - {{\mathbbm {K}}} ^{\text {-}1}_{n} \cdot {{\mathbbm {R}}} _{n} \qquad \text {with} \qquad {{\mathbbm {K}}} _{n} :=\displaystyle \frac{\partial {{\mathbbm {R}}} }{\partial {\mathbbm {x}} } \bigg |_{n}\,, \end{aligned}$$
(21)

where \(\Delta {\mathbbm {x}} \) is the incremental global deformation vector. After each iteration, the global deformation vector \({\mathbbm {x}} \) is updated by \(\Delta {\mathbbm {x}} \) according to \({\mathbbm {x}} _{n+1} = {\mathbbm {x}} _{n} + \Delta {\mathbbm {x}} _{n}\). Obviously, equations (19) and (20) require calculations of the first and second derivatives of the potential energy function, respectively, which is gathered in Table 2. Such calculations are carried out in a generic form using the hyper-dual numbers in the next Section.

Table 2 Derivatives required for calculation of the residual and tangents in CPD
Full size table

3 Hyper-dual numbers

In computational mechanics, it is crucial to calculate the derivatives of the potential energy function accurately since it has a significant impact on simulation outcomes. Precise computation of the residual is particularly essential to ensure the accuracy of the physics involved in the problem, while calculating the tangent with precision affects the ability of the Newton–Raphson method to converge in solving the nonlinear system of equations. Numerical differentiation is a common technique to approximate the derivative of a function using various methods. One of the disadvantages of numerical differentiation methods compared to analytical differentiation is that they suffer from numerical errors. There exist two main sources of error in numerical differentiation. The first error type is the truncation error which arises when higher-order terms in approximations or derivative calculations are neglected. The truncation error can be minimized by making the perturbation value h very small. The second error type is the subtractive cancellation error which occurs because in computers the numbers are only stored up to a certain precision. For example, in double precision arithmetic, the numbers are stored up to 15 decimal digits. If the numbers that are being subtracted from each other are too close, the computer fails to distinguish them hence the zero difference. This leads to an incorrect approximation of the derivatives. The subtractive cancellation error increases by making the perturbation value h very small. Therefore, both errors cannot be minimized simultaneously via decreasing the perturbation value h. Various numerical differentiation techniques have been developed to minimize these errors, among which, hyper-dual numbers have proven to be one of the most accurate methods. Appendix A provides a unifying study on various numerical differentiation techniques and highlights the advantages and disadvantages of each method.

Hyper-dual numbers are a number system developed based on the theory of quaternions to calculate exact first and second derivatives. The derivation calculation involves converting a real-valued function evaluation to operate on hyper-dual numbers. The hyper-dual numbers are characterized by one real part and three non-real parts. A hyper-dual number \(\overline{a}\) is defined as

$$\begin{aligned}&\overline{a} = a_{0} + a_{1}\epsilon _{1} + a_{2}\epsilon _{2} +a_{12}\epsilon _{12} \qquad \text {with} \nonumber \\&\quad \epsilon _{12} =\epsilon _{21} = \epsilon _{1}\epsilon _{2} = \epsilon _{2}\epsilon _{1} \ne 0 \qquad \text {and} \qquad \epsilon _{1}^{2}=\epsilon _{2}^{2}=0\,. \end{aligned}$$
(22)

Accordingly, the real and non-real operators are defined as

$$\begin{aligned}&\Re \left( \overline{a}\right) = \Re \left( a_{0} + a_{1} \epsilon _{1} + a_{2} \epsilon _{2} + a_{12} \epsilon _{12} \right) =a_{0} \,,\nonumber \\&\Im _{\epsilon _{1}} \left( \overline{a}\right) = \Im _{\epsilon _{1}} \left( a_{0} + a_{1} \epsilon _{1} + a_{2} \epsilon _{2} + a_{12} \epsilon _{12} \right) = a_{1} \,,\nonumber \\&\Im _{\epsilon _{2}} \left( \overline{a}\right) = \Im _{\epsilon _{2}} \left( a_{0} + a_{1} \epsilon _{1} + a_{2} \epsilon _{2} + a_{12} \epsilon _{12} \right) = a_{2} \,,\nonumber \\&\Im _{\epsilon _{12}} \left( \overline{a}\right) = \Im _{\epsilon _{12}} \left( a_{0} + a_{1} \epsilon _{1} + a_{2} \epsilon _{2} + a_{12} \epsilon _{12} \right) = a_{12} \,. \end{aligned}$$
(23)

When operations are performed on the real component of a hyper-dual number, the derivative information for those operations is created and stored in the non-real parts of the number. The non-real elements of the number contain derivative information with regard to the input at every stage of the function evaluation. Cohen and Shoham [45] demonstrated that hyper-dual numbers are indeed an extended version of dual numbers of order two. For the sake of simplicity, it is usually assumed that \(a_{1}=a_{2}=h\) and \(a_{12}=0\) hence \(\overline{a} = a_{0} + h\epsilon _{1} +h\epsilon _{2}\). Therefore, the Taylor series expansion of the smooth function \(f(x+h\epsilon _{1}+h\epsilon _{2})\) reads

$$\begin{aligned} f(x+h\epsilon _{1}+h\epsilon _{2})&= f(x) +h\epsilon _{1}\displaystyle \frac{\partial f(x)}{\partial x} +h\epsilon _{2}\displaystyle \frac{\partial f(x)}{\partial x}\nonumber \\&\quad + h^2\epsilon _{12} \displaystyle \frac{\partial ^2 f(x)}{\partial x^2} \,, \end{aligned}$$
(24)

that could be rewritten as

$$\begin{aligned} f(x+h\epsilon _{1}+h\epsilon _{2})&= f(x) + \left[ h\displaystyle \frac{\partial f(x)}{\partial x} \right] \epsilon _{1}\nonumber \\&\quad + \left[ h\displaystyle \frac{\partial f(x)}{\partial x} \right] \epsilon _{2} + \left[ h^2 \displaystyle \frac{\partial ^2 f(x)}{\partial x^2} \right] \epsilon _{12} \,, \end{aligned}$$
(25)

The first and second derivatives of f(x) can be calculated as

$$\begin{aligned} \displaystyle \frac{\partial f(x)}{\partial x}&=\displaystyle \frac{\Im _{\epsilon _{1}} \Big (f(x+h\epsilon _{1}+h\epsilon _{2}) \Big )}{h}\nonumber \\&= \displaystyle \frac{\Im _{\epsilon _{2}} \Big (f(x+h\epsilon _{1}+h\epsilon _{2}) \Big )}{h} \qquad \text {and} \nonumber \\ \displaystyle \frac{\partial ^2 f(x)}{\partial x^2}&=\displaystyle \frac{ \Im _{\epsilon _{12}}\Big ( f(x+h\epsilon _{1}+h\epsilon _{2}) \Big )}{h^2}\,. \end{aligned}$$
(26)

Note that the operators \(\Im _{\epsilon _{1}}\), \(\Im _{\epsilon _{2}}\) and \(\Im _{\epsilon _{12}}\) extract the multiples to the non-real parts \(\epsilon _{1}\), \(\epsilon _{1}\) and \(\epsilon _{12}\), respectively. It is observed that the first and the second derivatives neither suffer from truncation errors nor from subtractive cancellation errors. As a result, both derivatives are calculated in an exact manner.

3.1 Algebra and tensor analysis with hyper-dual numbers

Table 3 Algebra of hyper-dual numbers
Full size table

This section briefly elaborates the algebra of hyper-dual numbers. Table 3 summaries the definitions for basic algebraic operations for hyper-dual numbers. As mentioned in the previous section, it is usually assumed that for a typical hyper-dual number \(a_{1}=a_{2}=h\) and \(a_{12}=0\). Therefore, a hyper-dual number can be represented as \(\overline{a} = a_{0} + h\epsilon _{1} + h\epsilon _{2}\). Another equally important feature of differentiation with hyper-dual numbers is that the derivatives do not depend on the perturbation magnitude h, thus one could assume \(h=1\). Accordingly, we henceforth continue our analysis with hyper-dual numbers defined as \(\overline{a} = a_{0} + \epsilon _{1} +\epsilon _{2}\). Assume that f(x) is a scalar valued function of a scalar variable x. The first and second derivatives of f(x) with respect to x can be obtained as

$$\begin{aligned} \displaystyle \frac{\partial f(x)}{\partial x}&=\Im _{\epsilon _{1}}\Big ( f(x+\epsilon _{1}+\epsilon _{2}) \Big ) =\Im _{\epsilon _{2}}\Big ( f(x+\epsilon _{1}+\epsilon _{2}) \Big )\,,\nonumber \\ \displaystyle \frac{\partial ^2 f(x)}{\partial x^2}&=\Im _{\epsilon _{12}}\Big ( f(x+\epsilon _{1}+\epsilon _{2}) \Big )\,. \end{aligned}$$
(27)

Similarly, for a two variable scalar function f(x, y), the derivatives with respect to scalar independent variables are obtained as

$$\begin{aligned} \frac{\partial f(x,y)}{\partial x}&= \Im _{\epsilon _{1}} \Big (f(x+\epsilon _{1}\,,\,y+\epsilon _{2}) \Big ) \,,\nonumber \\ \frac{\partial f(x,y)}{\partial y}&= \Im _{\epsilon _{2}} \Big (f(x+\epsilon _{1}\,,\,y+\epsilon _{2}) \Big ) \,,\nonumber \\ \frac{\partial ^2 f(x,y)}{\partial x \partial y}&= \Im _{\epsilon _{12}}\Big ( f(x+\epsilon _{1} \,,\,y+\epsilon _{2}) \Big )\,,\nonumber \\ \frac{\partial ^2 f(x,y)}{\partial x^2}&= \Im _{\epsilon _{12}} \Big (f(x+\epsilon _{1}+\epsilon _{2}\,,\,y) \Big )\,,\nonumber \\ \frac{\partial ^2 f(x,y)}{\partial y^2}&= \Im _{\epsilon _{12}} \Big (f(x\,,\,y+\epsilon _{1}+\epsilon _{2}) \Big )\,. \end{aligned}$$
(28)

As shown in Eq. (28), in order to find the whole set of first and second derivatives, three different combinations of the hyper-dual forms for the independent variables need to be used. Thus, the function f(x, y) needs to be evaluated three times.

3.2 Differentiation with respect to tensor arguments

Another important aspect of hyper-dual numbers is differentiation with respect to first- and second-order tensors, which will be elaborated in this section. In doing so, we provide a systematic scheme in order to define the derivatives of an arbitrary function with respect to zero-, first- and second-order functions. In order to facilitate the terminology, henceforth we refer to zero-order tensors as scalars, first-order tensors as vectors and second-order tensors simply as tensors. Also, to avoid confusing notation, we denote an independent scalar variable as z, vector variable as \(\varvec{z}\) and tensor variable as \(\varvec{Z}\). Similar to classical continuum mechanics, in peridynamics the problem is associated with a potential energy function whose first and second derivatives are required in order to employ the Newton–Raphson method. Therefore, we present our framework here for scalar-valued functions with scalar, vector or tensor arguments. Such a function could represent a potential energy function. Assume \(\phi \) is a scalar-valued function whose independent variables could be scalars \(\phi (z)\), vectors \(\phi (\varvec{z})\) or tensors \(\phi (\varvec{Z})\). For the scalar variable z, using Eq. (27), the first and second derivatives of \(\phi (z)\) can be obtained as

$$\begin{aligned} \frac{\partial \phi (z)}{\partial z}&= \Im _{\epsilon _{1}}\Big ( \phi (z+\epsilon _{1}+\epsilon _{2}) \Big ) = \Im _{\epsilon _{2}}\Big ( \phi (z+\epsilon _{1}+\epsilon _{2}) \Big )\,,\nonumber \\ \frac{\partial ^2 \phi (z)}{\partial z^2}&= \Im _{\epsilon _{12}}\Big ( \phi (z+\epsilon _{1}+\epsilon _{2}) \Big )\,. \end{aligned}$$
(29)

Next, let \(\varvec{a}_{1}\) and \(\varvec{a}_{2}\) be two arbitrary vectors. Then, for the vector variable \(\varvec{z}\), the first and second directional derivatives of \(\phi (\varvec{z})\) in the directions \(\varvec{a}_{1}\) and \(\varvec{a}_{2}\) are calculated as

$$\begin{aligned} \frac{\partial \phi (\varvec{z})}{\partial \varvec{z}} \cdot \varvec{a}_{1}&= \Im _{\epsilon _{1}} \Big (\phi (\varvec{z}+\epsilon _{1}\varvec{a}_{1}) \Big )\,,\nonumber \\ \varvec{a}_{1} \cdot \displaystyle \frac{\partial ^2 \phi (\varvec{z})}{\partial \varvec{z}^2} \cdot \varvec{a}_{2}&= \Im _{\epsilon _{12}} \Big (\phi (\varvec{z}+\epsilon _{1}\varvec{a}_{1} +\epsilon _{2}\varvec{a}_{2}) \Big )\,. \end{aligned}$$
(30)

Similarly, we assume \(\varvec{A}_{1}\) and \(\varvec{A}_{2}\) to be two arbitrary tensors. Then, for the tensor variable \(\varvec{Z}\), the first and second directional derivatives of \(\phi (\varvec{Z})\) in the directions \(\varvec{A}_{1}\) and \(\varvec{A}_{2}\) are calculated as

$$\begin{aligned} \frac{\partial \phi (\varvec{Z})}{\partial \varvec{Z}} : \varvec{A}_{1}&= \Im _{\epsilon _{1}} \Big (\phi (\varvec{Z}+\epsilon _{1}\varvec{A}_{1}) \Big )\,,\nonumber \\ \varvec{A}_{1} : \displaystyle \frac{\partial ^2 \phi (\varvec{Z})}{\partial \varvec{Z}^2} : \varvec{A}_{2}&= \Im _{\epsilon _{12}}\Big ( \phi (\varvec{Z}+\epsilon _{1} \varvec{A}_{1}+\epsilon _{2}\varvec{A}_{2}) \Big )\,. \end{aligned}$$
(31)

For further details and application of tensorial derivatives in hyperelasticity see [48, 49].

Fig. 3
figure 3

Comparison of the computational time when differentiating using hyper-dual numbers versus analytical differentiation. The vertical axis represents the ratio of the assembly time over the solution time and horizontal axis represents the number of DOFs

Full size image

3.3 Comments on computational efficiency

The computational efficiency in derivative calculation between available methods is ranked sequentially as: analytical methods, finite difference method, complex numbers method, dual numbers method and hyper-dual numbers method, respectively [48, 49, 69]. However, the gap between the performance of methods decreases as the number of degrees of freedom in the problem increases. This is due to the fact that instead of the derivative calculation and assembly procedure, it is the solution time (inverse computation) that dominates in the computational efficiency. Figure 3 compares the computational effort required when differentiation is carried out using hyper-dual numbers (blue line) versus analytical method (red line) for our implementation. The vertical the vertical axis represents the ratio of the assembly time over the solution time and horizontal axis represents the number of DOFs. It is observed that as the number of degrees of freedom increases, the computational effort gap between the analytical scheme and hyper-dual numbers decreases. As shown in Table 3, it is observed that the summation of two hyper-dual numbers requires four real summations. Also, multiplication of two hyper-dual numbers require nine real multiplications plus five real summations. Such extended algebraic calculations are the main sources of computational cost associated with hyper-dual numbers. For example, the calculation of the Hessian using hyper-dual numbers is 2.5 times slower than the central difference method and 5 times slower than the forward difference method [41]. However, via adopting a mixed approach, the differentiation efficiency using hyper-dual numbers can be significantly improved in case of iterative methods such as the Newton–Raphson method. That is, instead of obtaining the convergence using hyper-dual numbers, the convergence can be obtained using real numbers and then the derivatives can be calculated via a single step hyper-dual evaluation. Such a strategy could lead the hyper-dual differentiation to be even more robust than the finite difference schemes, see [41, 43] for further details.

4 CPD with hyper-dual numbers

The final step to complete our proposed generic computational framework is to calculate the derivatives required for residual and tangents. In doing so, we carry out the differentiations using hyper-dual numbers. This strategy has three main advantages; it is compact, exact and model-independent. Thus, as the framework is implemented, any other material model can be incorporated via modifying the potential energy function solely. As mentioned before, there exist three interaction potential energy densities as

$$\begin{aligned}&{\psi }_{1}^{ai} = {\psi }_{1}^{ai}(|\varvec{\xi }^{ai}|) \,,\nonumber \\&{\psi }_{2}^{aij} = {\psi }_{2}^{aij}(|\varvec{a}^{aij}|) \,,\nonumber \\&{\psi }_{3}^{aijk} = {\psi }_{3}^{aijk}(v^{aijk}) \,, \end{aligned}$$
(32)

associated with one-, two- and three-neighbor interactions. All the potential energies are scalar-valued functions. The first two potential energies have vectors as their argument and the third potential energy has a scalar argument. Note, Eq. (32) is a more specific form of Eq. (10). All the derivations in this section are expressed in index notation. To begin, we rewrite the three relative deformation measures as

$$\begin{aligned} \left[ \varvec{\xi }^{ai} \right] _{m}&:= \left[ \varvec{x}^{i} \right] _{m} - \left[ \varvec{x}^{a} \right] _{m} \,,\nonumber \\ \left[ \varvec{a}^{aij} \right] _{m}&:= \left[ \varvec{\xi }^{ai} \right] _{n} \left[ \varvec{\xi }^{aj} \right] _{r} {{\mathbbm {e}}} _{nrm} \,,\nonumber \\ v^{aijk}&:= \left[ \varvec{\xi }^{ai} \right] _{n} \left[ \varvec{\xi }^{aj} \right] _{r} \left[ \varvec{\xi }^{ak} \right] _{m} {{\mathbbm {e}}} _{nrm}\,. \end{aligned}$$
(33)

Similarly, for the residual we have

$$\begin{aligned} \left[ \varvec{R}^{a}_{1} \right] _{m}&= \sum ^{\#{\mathcal {N}}}_{i=1} \left[ \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}}\right] _{m} \! {\mathcal {V}}^{i}\,,\nonumber \\ \left[ \varvec{R}^{a}_{2} \right] _{m}&= \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \left[ 2 \left[ \varvec{\xi }^{aj} \right] _{s} \left[ \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}}\right] _{r} {{\mathbbm {e}}} _{srm} \right] {\mathcal {V}}^{ij}\,,\nonumber \\ \left[ \varvec{R}^{a}_{3} \right] _{m}&= \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \sum _{{\begin{array}{c} k=1 \\ k\ne i \\ k\ne j \end{array}}}^{\#{\mathcal {N}}} \nonumber \\&\quad \left[ 3 \left[ \varvec{\xi }^{aj} \right] _{s} \left[ \varvec{\xi }^{ak} \right] _{r} \left[ \displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}}\right] {{\mathbbm {e}}} _{srm} \right] {\mathcal {V}}^{ijk}\,, \end{aligned}$$
(34)

for which the first derivatives of the potential energy with respect to the relative deformation measures are required. Using the formulation presented in Eqs. (29) and (30) we have

$$\begin{aligned} \left[ \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}}\right] _{m}&= \Im _{\epsilon _{1}} \Big ({\psi }_{1}^{ai}(\varvec{\xi }^{ai} +\epsilon _{1}\varvec{e}_{m}) \Big ) \nonumber \\&\quad = \Im _{\epsilon _{2}}\Big ({\psi }_{1}^{ai} (\varvec{\xi }_{m}^{ai}+\epsilon _{1} \varvec{e}_{m})\Big ) \,,\nonumber \\ \left[ \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}}\right] _{m}&= \Im _{\epsilon _{1}} \Big ({\psi }_{2}^{aij}(\varvec{a}^{aij}_{m} +\epsilon _{1}\varvec{e}_{m}) \Big ) \nonumber \\&\quad = \Im _{\epsilon _{2}}\Big ({\psi }_{2}^{aij} (\varvec{a}_{m}^{aij}+\epsilon _{1}\varvec{e}_{m})\Big ) \,,\nonumber \\ \left[ \displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}}\right]&= \Im _{\epsilon _{1}} \Big ({\psi }_{3}^{aijk}(v^{aijk}+\epsilon _{1}) \Big )\nonumber \\&\quad = \Im _{\epsilon _{2}}\Big ( {\psi }_{3}^{aijk} (v^{aijk}+\epsilon _{1}) \Big )\,, \end{aligned}$$
(35)

with \(\varvec{e}_{m}\) being the unit vector in the mth coordinate direction. To proceed with the calculation of tangents, we rewrite Eq. (20) in index notation as

$$\begin{aligned} \left[ \varvec{K}^{ab}_1\right] _{mn}&= \left[ \displaystyle \frac{\partial \varvec{R}^a_1}{\partial \varvec{x}^b}\right] _{mn}\nonumber \\&= \left[ \displaystyle \frac{\partial }{\partial \varvec{x}^{b}}\right] _{n} \left( \sum ^{\#{\mathcal {N}}}_{i=1} \left[ \displaystyle \frac{\partial {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai}}\right] _{m} {\mathcal {V}}^{i}\right) \,,\nonumber \\ \left[ \varvec{K}^{ab}_2\right] _{mn}&= \left[ \displaystyle \frac{\partial \varvec{R}^a_2}{\partial \varvec{x}^b} \right] _{mn} = \left[ \displaystyle \frac{\partial }{\partial \varvec{x}^{b}}\right] _{n} \nonumber \\&\quad \left( \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} 2 \left[ \varvec{\xi }^{aj} \right] _{s} \left[ \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}}\right] _{r} {{\mathbbm {e}}} _{srm} {\mathcal {V}}^{ij} \right) \,,\nonumber \\ \left[ \varvec{K}^{ab}_3 \right] _{mn}&= \left[ \displaystyle \frac{\partial \varvec{R}^a_3}{\partial \varvec{x}^b} \right] _{mn} = \left[ \displaystyle \frac{\partial }{\partial \varvec{x}^{b}}\right] _{n} \nonumber \\&\quad \left( \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \sum _{{\begin{array}{c} k=1 \\ k\ne i \\ k\ne j \end{array}}}^{\#{\mathcal {N}}} 3 \left[ \varvec{\xi }^{aj} \right] _{s} \left[ \varvec{\xi }^{ak} \right] _{r} \left[ \displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}}\right] {{\mathbbm {e}}} _{srm} {\mathcal {V}}^{ijk}\right) \,. \end{aligned}$$
(36)

Moreover, to use the chain rule, the following constitutive model-independent, geometric relations prove to be useful

$$\begin{aligned} \left[ \displaystyle \frac{\partial \varvec{\xi }^{ai}}{\partial \varvec{x}^b}\right] _{mn}&= \left[ { \delta ^{ib} - \delta ^{ab} } \right] \, \delta _{mn} \,,\nonumber \\ \left[ \displaystyle \frac{\partial \varvec{a}^{aij}}{\partial \varvec{x}^b} \right] _{mn}&= \left[ \displaystyle \frac{\partial \left[ \varvec{\xi }^{ai}\times \varvec{\xi }^{aj}\right] }{\partial \varvec{x}^b} \right] _{mn}\nonumber \\&= \Bigg [\left[ { \delta ^{ib} - \delta ^{ab} } \right] \left[ \varvec{\xi }^{aj} \right] _{s}\nonumber \\&\quad -\left[ { \delta ^{jb}}{- \delta ^{ab} }\right] \, \left[ \varvec{\xi }^{ai} \right] _{s} \Bigg ]\,{{\mathbbm {e}}} _{mns}\,,\nonumber \\ \left[ \displaystyle \frac{\partial v^{aijk}}{\partial \varvec{x}^b}\right] _{m}&=\left[ \displaystyle \frac{\partial \left[ \varvec{\xi }^{ai}\!\cdot [\varvec{\xi }^{aj} \!\times \varvec{\xi }^{ak}]\right] }{\partial \varvec{x}^b}\right] _{m}\nonumber \\&= \bigg [\left[ { \delta ^{ib} \!\!- \delta ^{ab} } \right] \, \left[ \varvec{\xi }^{aj}\right] _{n} \left[ \varvec{\xi }^{ak}\right] _{s}\nonumber \\&\quad +\left[ { \delta ^{jb} \!\!- \delta ^{ab} } \right] \, \left[ \varvec{\xi }^{ak}\right] _{n} \left[ \varvec{\xi }^{ai}\right] _{s} \nonumber \\&\quad + \left[ { \delta ^{kb} \!\!- \delta ^{ab} } \right] \, \left[ \varvec{\xi }^{ai}\right] _{n} \left[ \varvec{\xi }^{aj}\right] _{s} \bigg ]\,{{\mathbbm {e}}} _{mns}\,. \end{aligned}$$
(37)

for the details on the derivations, see Appendix B. Accordingly, using relations in Eq. (37), the final form of the tangents read

Table 4 Convergence behavior associated with the right set in Fig. 5 with \(C_{2}/C_{1}\gg 1\) at different deformations. The top segment corresponds to the case with differentiation with hyper-dual numbers and the bottom segment corresponds to the case with analytical differentiations
Full size table
Fig. 4
figure 4

Illustration of the behavior of the functions \(S_{1}\) and \(\psi ^{ai}_{1}\) with respect to \(\lambda _{\varvec{\xi }}\) for different values of n. For the bottom plot, it is assumed \(C_{1}=1\) and \(|\varvec{\Xi }^{ai}|=1\). Similar behavior can be observed for the pair \(S_{2}\) and \(\psi ^{aij}_{2}\) and the pair \(S_{3}\) and \(\psi ^{aijk}_{3}\)

Full size image
Fig. 5
figure 5

Deformation of a unit square undergoing \(100\%\) extension in compressible and nearly compressible regimes. The left set corresponds to the compressible material behavior with the ratio \(C_{2}/C_{1}=0\) and the left set corresponds to the nearly incompressible material behavior with the ratio \(C_{2}/C_{1}\gg 1\)

Full size image
Fig. 6
figure 6

Deformation of a unit cube undergoing \(100\%\) extension in for three different material behaviors. The left set corresponds to the compressible or length-preserving material behavior with the ratios \(C_{2}/C_{1}=0\) and \(C_{3}/C_{1}=0\). The middle set corresponds to the area-preserving material behavior with the ratios \(C_{2}/C_{1}\gg 1\) and \(C_{3}/C_{1}=0\). The right set corresponds to the volume-preserving material behavior with the ratios \(C_{2}/C_{1}=0\) and \(C_{3}/C_{1}\gg 1\)

Full size image
$$\begin{aligned} \left[ \varvec{K}^{ab}_1 \right] _{mn}&= \sum ^{\#{\mathcal {N}}}_{i=1} \left[ \, \left[ \delta ^{ib} - \delta ^{ab} \right] \left[ \displaystyle \frac{\partial ^2{\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai^2}}\right] _{mn} \right] {\mathcal {V}}^{i}\,,\nonumber \\ \left[ \varvec{K}^{ab}_2 \right] _{mn}&= \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}}\nonumber \\&\quad \left[ 2 \left[ \delta ^{jb} - \delta ^{ab} \right] \left[ \displaystyle \frac{\partial {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij}} \right] _{r} {{\mathbbm {e}}} _{nrm} + 2 \left[ \xi ^{aj}\right] _{s}\right. \nonumber \\&\qquad \quad \Bigg [\left[ \delta ^{ib} - \delta ^{ab} \right] \left[ \xi ^{aj}\right] _{t} - \left[ \delta ^{jb} - \delta ^{ab} \right] \left[ \xi ^{ai}\right] _{t} \Bigg ]\nonumber \\&\qquad \quad \left. \left[ \displaystyle \frac{\partial ^2 {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij^2}} \right] _{rq} \!\!\!\! {{\mathbbm {e}}} _{qnt} {{\mathbbm {e}}} _{srm}\right] {\mathcal {V}}^{ij}\,,\nonumber \\ \left[ \varvec{K}^{ab}_3 \right] _{mn}&= \sum ^{\#{\mathcal {N}}}_{i=1} \sum _{{\begin{array}{c} j=1 \\ j\ne i \end{array}}}^{\#{\mathcal {N}}} \sum _{{\begin{array}{c} k=1 \\ k\ne i \\ k\ne j \end{array}}}^{\#{\mathcal {N}}} \nonumber \\&\quad \left[ 3 \bigg [ \left[ \delta ^{jb} - \delta ^{ab} \right] \left[ \xi ^{ak}\right] _{r} - \left[ \delta ^{kb} - \delta ^{ab} \right] \left[ \xi ^{aj}\right] _{r} \bigg ] \right. \nonumber \\&\quad \left[ \displaystyle \frac{\partial {\psi }_{3}^{aijk}}{\partial v^{aijk}}\right] {{\mathbbm {e}}} _{mnr} + 3 \left[ \varvec{\xi }^{aj} \right] _{s} \left[ \varvec{\xi }^{ak} \right] _{r}\nonumber \\&\quad \Bigg [\left[ { \delta ^{ib} \!\!- \delta ^{ab} } \right] \, \left[ \varvec{\xi }^{aj}\right] _{q} \left[ \varvec{\xi }^{ak}\right] _{t} \nonumber \\ {}&\quad + \left[ { \delta ^{jb} \!\!- \delta ^{ab} } \right] \, \left[ \varvec{\xi }^{ak}\right] _{q} \left[ \varvec{\xi }^{ai}\right] _{t}\nonumber \\&\qquad \quad + \left[ { \delta ^{kb} \!\!- \delta ^{ab} } \right] \, \left[ \varvec{\xi }^{ai}\right] _{q} \left[ \varvec{\xi }^{aj}\right] _{t}\Bigg ]\nonumber \\&\qquad \quad \left. \left[ \displaystyle \frac{\partial ^2{\psi }_{3}^{aijk}}{\partial v^{aijk^2}}\right] {{\mathbbm {e}}} _{msr} {{\mathbbm {e}}} _{nqt} \right] {\mathcal {V}}^{ijk}\,. \end{aligned}$$
(38)

The last step to determine the tangents is to calculate the second derivatives of the potential energy with respect to the relative deformation measures. Using the formulations presented in Eqs. (29)–(31) we have

$$\begin{aligned}&\left[ \displaystyle \frac{\partial ^2 {\psi }_{1}^{ai}}{\partial \varvec{\xi }^{ai^2}}\right] _{mn} \nonumber \\&\quad = \Im _{\epsilon _{12}}\Big ({\psi }_{1}^{ai}(\varvec{\xi }^{ai} +\epsilon _{1}\left[ \varvec{e}_{m}\otimes \varvec{e}_{n}\right] +\epsilon _{2} \left[ \varvec{e}_{m}\otimes \varvec{e}_{n}\right] \Big ) \,,\nonumber \\&\left[ \displaystyle \frac{\partial ^2 {\psi }_{2}^{aij}}{\partial \varvec{a}^{aij^2}}\right] _{mn} \nonumber \\&\quad = \Im _{\epsilon _{12}}\Big ({\psi }_{2}^{aij} (\varvec{a}^{aij}_{m}+\epsilon _{1} \left[ \varvec{e}_{m}\otimes \varvec{e}_{n}\right] +\epsilon _{2}\left[ \varvec{e}_{m} \otimes \varvec{e}_{n}\right] ) \Big ) \,,\nonumber \\&\left[ \displaystyle \frac{\partial ^2 {\psi }_{3}^{aijk}}{\partial v^{aijk^2}}\right] = \Im _{\epsilon _{12}} \Big ({\psi }_{3}^{aijk}(v^{aijk}+\epsilon _{1}+\epsilon _{2}) \Big ) \,. \end{aligned}$$
(39)

As mentioned earlier, the main advantage of our proposed framework is that it is model-independent. That is, once it is implemented, any other material model can be incorporated via modifying the potential energy function solely.

5 Internal potential energy

The last step to complete our proposed framework is to define an internal energy potential. In this manuscript, we define a family of internal potential energies based on the Seth–Hill strain measures. To proceed, it proves convenient to define scalar-valued ratios of the deformation measures in CPD as

$$\begin{aligned}&\lambda _{\varvec{\xi }} = \displaystyle \frac{|\varvec{\xi }^{ai}|}{|\varvec{\Xi }^{ai}|}\,,\nonumber \\&\lambda _{\varvec{a}} = \displaystyle \frac{|\varvec{a}^{aij}|}{|\varvec{A}^{aij}|}\,,\nonumber \\&\lambda _{v} = \displaystyle \frac{v^{aijk}}{V^{aijk}}\,. \end{aligned}$$
(40)

As mentioned before, the internal potential energy consists of the contribution of one-, two- and three-neighbor interactions. Accordingly we define the discretized energies as

$$\begin{aligned}&\psi _{1}^{ai} = \displaystyle \frac{1}{2} C_{1} \, |\varvec{\Xi }^{ai}| \, S_1^2 \,,\nonumber \\&\psi _{2}^{aij} = \displaystyle \frac{1}{2} C_{2} \, |\varvec{A}^{aij}| \, S_2^2 \,, \nonumber \\&\psi _{3}^{aijk} = \displaystyle \frac{1}{2} C_{3} \, V^{aijk} \, S_3^2 \,, \end{aligned}$$
(41)

with the sufficient but not necessary conditions \(C_{1}>0\), \(C_{2}\ge 0\) and \(C_{3}\ge 0\) to guarantee positiveness of the energy, where

$$\begin{aligned}&S_1= {\left\{ \begin{array}{ll} \displaystyle \frac{1}{n} \left[ \lambda _{\varvec{\xi }}^{n}-1 \right] &{}n\ne 0\,,\\ \ln \lambda _{\varvec{\xi }} &{}n=0\,, \end{array}\right. }\nonumber \\&S_2= {\left\{ \begin{array}{ll} \displaystyle \frac{1}{n} \left[ \lambda _{\varvec{a}}^{n}-1 \right] &{}n\ne 0\,,\\ \ln \lambda _{\varvec{a}} &{}n=0\,, \end{array}\right. }\nonumber \\&S_3= {\left\{ \begin{array}{ll} \displaystyle \frac{1}{n} \left[ \lambda _{v}^{n}-1 \right] &{}n\ne 0\,,\\ \ln \lambda _{v} &{}n=0\,, \end{array}\right. } \,. \end{aligned}$$
(42)

Figure 4 illustrates the behavior of the functions \(S_{1}\) and \(\psi ^{ai}_{1}\) with respect to \(\lambda _{\varvec{\xi }}\) for different values of n. Note, for the potential energy (bottom plot) we assume \(C_{1}=1\) and \(|\varvec{\Xi }^{ai}|=1\). For \(\lambda _{\varvec{\xi }}<1\), smaller values of n render higher energy potentials whereas for \(\lambda _{\varvec{\xi }}>1\) the opposite behavior is observed.

6 Numerical examples

The objective of this section is to illustrates the performance of our proposed computational framework enabled by hyper-dual numbers. In doing so, three different studies are carried out with different combinations of the internal potential energies introduced in Eqs. (41) and (42). Our simulations demonstrate the influence of multi-neighbor interactions on the material response together with the robustness of the framework and its consistent quadratic convergence even at very large deformations. All the examples are solved using our in-house CPD code written in C++.

6.1 Uniaxial tension

Table 5 Convergence behavior associated with the left set in Fig. 5 with \(C_{2}/C_{1}=0\) at different deformations. The top segment corresponds to the case with differentiation with hyper-dual numbers and the bottom segment corresponds to the case with analytical differentiations
Full size table

The objective of this study is to evaluate the accuracy of the computations using hyper-dual numbers. In doing so, a unit specimen is subject to \(100\%\) uniaxial tension and the convergence behaviors due to analytical derivatives and hyper-dual numbers derivatives are compared. Figure 5 illustrates a 2D analysis where two different material behaviors are considered. The left column corresponds to a compressible material behavior where \(C_{2}/C_{1}=0\) and the right column corresponds to the case with nearly incompressible material behavior where \(C_{2}/C_{1}\gg 1\) .Footnote 2 The grid spacing for both cases is \(\Delta =0.01\) and the ratio of the horizon size over grid spacing is \(\delta /\Delta =3\). For this study, we consider the potential energy introduced in Eqs. (41) and (42) with \(n=1\). Thus, \(S_1 = \left[ \lambda _{\varvec{\xi }}-1 \right] \), \(S_2 = \left[ \lambda _{\varvec{a}}-1 \right] \) and \(S_3 = \left[ \lambda _{v}-1 \right] \). The undeformed configurations are depicted at the top and the deformed configurations at the intermediate steps are shown subsequently. The vertical displacement distribution is shown throughout each specimen. It is observed that the case with \(C_{2}/C_{1}\gg 1\) renders more lateral contraction compared to the case with \(C_{2}/C_{1}=0\) which is justifiable since larger values of \(C_{2}/C_{1}\) indicate more incompressibility. Table 5 compares the convergence behavior associated with Fig. 5-left for the compressible material behavior. The top segment corresponds to the case where the differentiation is carried out using hyper-dual numbers and the bottom segment corresponds to the case where the differentiation is calculated analytically. Columns correspond to different deformation magnitudes whereas rows show the normalized \(L_{2}\)-norm of the residual at each Newton–Raphson iteration. A quadratic convergence rate is observed for both cases which is expected due to the use of Newton–Raphson scheme. The convergence due to hyper-dual numbers is identical to the one obtained by analytical derivations for the first few steps. Minor differences are observed at the last steps which originate from machine precision induced round-off. Table 4 is the counter part of Table 5 for the nearly incompressible material behavior associated with Fig. 5-right. Similar to the previous case, an identical trend is observed for the convergence due to the hyper-dual numbers and the analytical derivatives.

Table 6 Convergence behavior associated with the left set in Fig. 6 with \(C_{2}/C_{1}=0\) and \(C_{3}/C_{1}=0\) at different deformations. The top segment corresponds to the case with differentiation with hyper-dual numbers and the bottom segment corresponds to the case with analytical differentiations
Full size table
Table 7 Convergence behavior associated with the middle set in Fig. 6 with \(C_{2}/C_{1}\gg 1\) and \(C_{3}/C_{1}=0\) at different deformations. The top segment corresponds to the case with differentiation with hyper-dual numbers and the bottom segment corresponds to the case with analytical differentiations
Full size table
Table 8 Convergence behavior associated with the right set in Fig. 6 with \(C_{2}/C_{1}=0\) and \(C_{3}/C_{1}\gg 1\) at different deformations. The top segment corresponds to the case with differentiation with hyper-dual numbers and the bottom segment corresponds to the case with analytical differentiations
Full size table

Figure 6 illustrates a 3D analysis where a unit cube is subject to \(100\%\) uniaxial tension. The grid spacing for this study is \(\Delta =0.05\) and the ratio of the horizon size over grid spacing is \(\delta /\Delta =3\). Three different types of interactions are considered for this example. One-neighbor interactions with \(C_{2}/C_{1}=0\) and \(C_{3}/C_{1}=0\) render compressible or length-preserving material behavior, one- and two-neighbor interactions with \(C_{2}/C_{1}\gg 1\) and \(C_{3}/C_{1}=0\) render nearly area-preserving behavior, and one- and three-neighbor interactions with \(C_{2}/C_{1}\gg 1\) and \(C_{3}/C_{1}\gg 1\) rendering volume-preserving behavior Footnote 3. As demonstrated in [13], we emphasize that it is not possible to have only two-neighbor interactions or only three-neighbor interactions. When only one neighbor interactions are taken into account, the least contraction is obtained which leads to increased compressibility. More incompressibility is observed when one- and two-neighbor interactions or one- and three-neighbor interactions are considered. It is important to note that although accounting for both two-neighbor interactions and three-neighbor interactions result in decreased compressibility, the solutions are different indicating that they indeed correspond to a different deformations. Tables 6, 7, 8 exhibit the convergence behavior for the three material behaviors in Fig. 6. Similarly, the residual obtained via hyper-dual number differentiation and analytical differentiation are almost identical where only minor differences are observed at the very last steps.

6.2 Bending

In this study we exhibit the capability of CPD to tackle with problems involving large deformations. In doing so, a cantilever beam is subject to rotation and compression at its free end as shown in Fig. 7. The top row corresponds to a 3D analysis and the bottom row corresponds to a 2D analysis. For both cases, the grid spacing for this study is \(\Delta =0.02\) and the ratio of the horizon size over grid spacing is \(\delta /\Delta =3\). The material constants in this example are \(C_{1}=1\) and \(C_{2}=10^4\). The colors indicate the deflection in y-direction and the intermediate deformed configurations are depicted for each case. For this study, we consider the potential energy introduced in Eqs. (41) and (42) with \(n=2\). Thus, \(S_1 = \tfrac{1}{2} \left[ \lambda _{\varvec{\xi }}^2-1 \right] \) and \(S_{2} = \tfrac{1}{2} \left[ \lambda ^{2}_{a}-1\right] \) For all the cases, the aspect ratio of the beam is 25 and one- and two-neighbor interactions are considered representing a compressible material response. The deformation is applied such that at each increment the points are incrementally rotated with respect to the clamped end and then are vertically compressed proportional to their initial displacement. For instance, if a point’s vertical displacement due to the initial rotation is x, then after the rotation it is vertically compressed with a magnitude of ax with \(0<a<1\). Three different values for a are considered in this study. In the left column the compression magnitude is \(a=0.1\), in the middle column the compression magnitude is \(a=0.3\) and in the right column the compression magnitude is \(a=0.5\). As the compression magnitude increases, it is observed that the beams tend to increase their curvature in order to maintain their length.

Fig. 7
figure 7

Deformation of cantilever beam subject to \(90^{\circ }\) rotation and three different magnitudes of compression in 3D and 2D settings. In the left column the compression magnitude is 0.1, in the middle column the compression magnitude is 0.3 and in the right column the compression magnitude is 0.5. Colors represent deflection in y-direction

Full size image

6.3 Torsion

The final example is devised to compare the robustness of our computational framework for bulk-dominated and surface-dominated geometries. Figures 8 and 9 exhibit two blocks with slenderness ratios of 2 and 4, respectively, that are subject to \(180^{\circ }\) torsion. For both cases the material constants are \(C_{1}=1\), \(C_{2}=0\) and \(C_{3}=10^8\). The deformed bodies together with their corresponding convergence are shown at different twisting angles. The colors indicate the deflection in y-direction. For both cases, the grid spacing for this study is \(\Delta =0.02\) and the ratio of the horizon size over grid spacing is \(\delta /\Delta =3\). For this study, we consider the potential energy introduced in Eqs. (41) and (42) with \(n=0\), thus, \(S_1 = \ln \lambda _{\varvec{\xi }}\) and \(S_3=\ln \lambda _{v}\). For the block with slenderness ratio 2, since the value of the horizon is small compared to the block’s cross-section, the problem is more of a bulk-dominated type. On the other hand, for the block with slenderness ratio of 4, the problem is more of a surface-dominated type due to comparable values of the horizon and cross-section. Fewer steps are required to obtain the convergence for the case with larger slenderness ratio which is understandable since there are less collocations points hence less degrees of freedom. Nonetheless, it is observed that our computational framework can deal with large deformations without losing its robustness.

Fig. 8
figure 8

Deformation of a block with slenderness ratio of 2 under \(180^{\circ }\) torsion. The deformed bodies together with their corresponding convergence are shown at different twisting angles. Colors represent deflection in y-direction

Full size image
Fig. 9
figure 9

Deformation of a block with slenderness ratio of 4 under \(180^{\circ }\) torsion. The deformed bodies together with their corresponding convergence are shown at different twisting angles. Colors represent deflection in y-direction

Full size image

6.4 Nonlocality

Fig. 10
figure 10

CPD nonlocality study on stress concentration in an L-shaped specimen undergoing infinitesimal vertical displacement. The post processed von Mises stress through the highlighted arrow in the domain is plotted. For the left plot, the horizon-to-lattice size ratio is fixed \(\delta /\Delta =3.0\) and the lattice size is decreased. For the right plot, the lattice size ratio is fixed \(\Delta =0.005\) and the horizon-to-lattice size is decreased. Stress-like quantities in CPD can be computed in post processing via an integral over the horizon, similar to the customary practice in computational homogenization  [70]

Full size image
Fig. 11
figure 11

A cut-out of brain sample undergoing small shear deformation

Full size image

Finally, as the last study, we aim to demonstrate the nonlocality of CDP. In doing so, as depicted in Fig. 10, an infinitesimal vertical displacement is applied to an L-shaped specimen and the value of the von Mises stress in the vicinity of the sharp corner highlighted in Fig. 10 is investigated in both vertical and horizontal directions. For this study, the ratio of the horizon size to grid spacing is fixed \(\delta /\Delta =3.0\) and the value of the grid spacing \(\Delta \) is increased, leading to a more nonlocal behavior. This example is carried out for a compressible material behavior where \(\nu =0.33\), thus we set the material constant \(C_{2}\) to zero and change \(C_{1}\) in accordance with \(\Delta \) in order to satisfy \(\nu =0.33\), see [18] for further details. In Fig. 10 left, the von Mises stress in the horizontal direction is plotted and in Fig. 10 right, the von Mises stress in the vertical direction is plotted. It is observed that as the value of grid spacing \(\Delta \) increases, the stress concentration at the vicinity of the corner decreases which indicates a more nonlocal response. Similarly, the highest stress concentration occurs for the case with the most local effect which is associated with smallest \(\Delta \). Note that for this study, we consider the potential energy introduced in Eqs. (41) and (42) with \(n=1\). Thus, \(S_1=\left[ \lambda _{\varvec{\xi }}-1 \right] \).

Motivated by the previous observation regarding the capability of CPD to capture nonlocal effects, our methodology can be adopted to determine the overall response materials with complex micro-structures. A well-known example of such material is brain tissue. Several studies has been carried out to determine the mechanical properties of brain tissue [71,72,73]. Figure 11 shows a brain sample with its cut-out which is subject to infinitesimal shear deformation. Such specimen is utilized to carry out rheometry analysis in order to determine the mechanical properties of brain matter. Undoubtedly, investigation of the nonlocal effects in brain matter and determining the proper potential energy together with parameter identification seems desirable. However, such analysis is beyond the scope of this manuscript and shall be carried out in a separate contribution. For relevant studies on applications of peridynamics in biomechanics see [74,75,76].

7 Conclusion

Continuum-kinematics-inspired peridynamics (CPD) has been briefly introduced as a geometrically exact alternative to PD to formulate nonlocal continuum mechanics. Next, hyper-dual numbers and their underlying algebra were recapitulated and the associated differentiations with respect to scalar, vector and tensor arguments were elaborated. Based thereon, we developed a computational framework furnished with automatic differentiation for implementation of CPD via employing hyper-dual numbers. The proposed computational framework is compact and model-independent, and suitable to incorporate any sophisticated material model via modifying the potential energy solely. Using the Seth–Hill strain measures, we proposed a family of internal potential energies that could be utilized for various material modelings. Through a set of numerical examples the performance and versatility of our proposed computational framework was evaluated while considering various loadings and material models. The convergence due to hyper-dual numbers proved to be highly accurate and identical to the one obtained by analytical derivations. The numerical implementation and solution procedure were robust and showed the asymptotically quadratic rate of convergence associated with the Newton–Raphson scheme. Taken together, differentiation via hyper-dual numbers renders CPD as a compelling computational framework to study a broad variety of nonlocal materials.