1 Introduction

In general, biological systems are considered to be complex and optimized. The complexity arises from multiphysical phenomena. The transportation of water is described by fluid mechanics, and the loads imposed by environmental factors, like wind, are depicted by solid mechanics, for instance. The biological systems achieve an optimal state by adapting themselves to environmental challenges through evolution. Since in the environment only a limited supply of nutrients, sunlight, water etc. exists, a competition with the surrounding organisms arises. Based upon the principles of evolution, the organism, which is better adapted to the surroundings, has a higher probability of producing descendants. Therefore, in nature, an optimization process occurs with respect to the environmental boundary conditions of the organisms.

Plant like biological systems provide a source of inspiration to overcome engineering challenges. In general, these systems are able to generate arbitrary shapes. The process of growth is mainly based upon cell elongation and division. These effects do not take place at the macroscale. Therefore, no limitations are present in the shape and topology of the plant like systems. As a consequence, the biological principles describing these growth phenomena can be utilized as inspiration to model engineering structures in an optimal and efficient manner.

A method of gaining quantitative insights into the inner mechanisms of biological systems is intended to describe the governing biological principles within the framework of continuum mechanics. As a direct result, a description of the process of finding the optimal three-dimensional shape and topology can be obtained. Furthermore, using the continuum mechanical description of biological systems, engineering challenges can be overcome.

To model growth, the deformation gradient is split into mechanical and growth parts. The set of constitutive equations describing the material behavior, only depends on the mechanical part of the deformation. Nevertheless, the choice of the material model influences growth. The basis for modeling growth are the balance laws of continuum mechanics. The internal energy is chosen to be the driving force of growth as one constitutive assumption. Consequently, the growth formulation is developed via the balance of energy. As a consequence, the stresses influence the growth deformations.

In the literature, different descriptions of growing organisms are presented. The focus of current research are bacteria films [1, 31, 32], biological soft tissues [4, 9, 23, 25], muscle tissues [14], tumors [6, 35] and bones [7, 18] for instance. To the authors knowledge, the application to plant like systems is not yet presented in the literature. Therefore, the focus of the contribution at hand is to introduce a framework to consider growth in such systems. Furthermore, different principles depicting the growth, for example the growth rate and split into primary and secondary growth direction are described. Additionally, formulations for tropisms, defining the main growth direction based upon environmental influences, are stated. As a consequence, a novel approach for modeling growth is obtained.

To achieve an efficient numerical solution scheme, an energy based description of continuum mechanical growing processes is shown. To the authors knowledge, this approach is not yet described in the literature. The formulation is based upon the internal energy of the system, characterized by the first law of thermodynamics. This approach is chosen, since it only introduces one additional degree of freedom. The internal energy is assumed to be influenced by the factors inducing growth.

In Sect. 2, the continuum mechanical principles for thermodynamically open systems are presented. Therefore, an exchange of matter and energy with the environment is possible. The following formulations only consider the growing system. As a consequence, the assumptions yield physically meaningful results. In Sect. 3, the constitutive equations arising from the continuum mechanical fundamentals are specified. These equations are chosen in such a way that the main influences on growth are incorporated. Additionally, in Sect. 4, the basics of solving the initial boundary value problem are presented. A common challenge of numerical simulations of growth is the increasing element volume during the solution process. Therefore, a structural generator is presented in Sect. 5, which consists of the introduced constitutive formulations to model growth processes and a remeshing algorithm. As a consequence, a more detailed depiction of growth processes is achieved. Subsequently, numerical examples are given in Sect. 6. The examples are chosen to demonstrate interactions of different growth principles. Finally, a conclusion and an outlook are stated in Sect. 7.

2 Continuum mechanical fundamentals of growth

In this section, a short depiction of growth based on to continuum mechanical balance laws, stress and deformation measures is presented. The content of this chapter is mainly based upon the research presented in the works of [9, 11, 14, 30, 31].

2.1 Configuration and movement

In the contribution at hand, a solid body B is investigated. The reference position \( {\mathcal {B}}_0 \) at time \(t=0\) is considered to be stress free and is also a subset of the Euclidean space \(B \subset \mathbb {R}^3\). Each material point \(P\in B\) possesses a position \({\varvec{x}} \in {\mathcal {B}}_t\) in the configuration at time \( t \in {\mathcal {T}} \ \vert \ {\mathcal {T}} \subset \mathbb {R}_+ \). The deformation \(\varvec{\varphi }_t: {\mathcal {B}}_0 \times {\mathcal {T}}\) maps the position of a material point in the reference configuration \({\varvec{X}}\in {\mathcal {B}}_0\) to the position in the current configuration. Taking the gradient of the deformation map, the deformation gradient is obtained, reading

$$\begin{aligned} {\varvec{F}}:= \textrm{Grad}(\varvec{\varphi }_t) = \frac{\partial \varvec{\varphi }_t }{\partial {\varvec{X}}}. \end{aligned}$$
(2)

Taking the determinant of Eq. (1), \(J:=\det ({\varvec{F}})\) can be defined.

2.2 Stress, density, growth deformation, internal energy and flux

In this section, the fundamental quantities describing the growing process of biological materials are briefly summarized.

2.2.1 Density and deformation measures

Density is a fundamental quantity in continuum mechanics. It relates infinitesimal changes in the mass to the corresponding changes in volume. The density in the reference configuration is given as

$$\begin{aligned} \rho _0 = \frac{\textrm{d}M}{\textrm{d}V}, \end{aligned}$$
(3)

where the relation of the infinitesimal mass element \(\textrm{d}M\) and the infinitesimal volume element in the reference configuration \(\textrm{d}V\) is considered. The density in the current configuration is defined as

$$\begin{aligned} \rho = \frac{\textrm{d}m}{\textrm{d}v}, \end{aligned}$$
(5)

the relation between the infinitesimal mass element \(\textrm{d}m\) and the infinitesimal volume element in the current configuration \(\textrm{d}v\). In growing biological systems, multiple effects are observed. At first, an influx of material in cells occurs, which leads to an expansion of the cells. Subsequently, cells undergo division, to prevent damage. To be able to model this process, growth is split into two processes. The influx of material results in a change in the density at the material point on the macroscale. The elongation and subdivision of cells is modeled by the introduction of growth deformations \({\varvec{F}}^{gr}\). In finite strain kinematics, the deformation gradient is split multiplicatively into mechanical and growing parts as

$$\begin{aligned} {\varvec{F}} = {\varvec{F}}^{mech}{\varvec{F}}^{gr}. \end{aligned}$$
(6)

Therefore, the existence of a growing intermediate configuration is assumed. The growth deformations need to evolve. The evolution is described in Sect. 3, since further constitutive relations are required. In Eq. (4), the mechanical part of the deformation is introduced. In general, different phenomena, like thermal expansion or plasticity can be included. In the contribution at hand, inelastic phenomena are not investigated. Therefore, the mechanical part of the deformation gradient only consists of elastic deformations

$$\begin{aligned} {\varvec{F}}^{mech} = {\varvec{F}}^e. \end{aligned}$$
(8)

The deformation gradient includes rigid body motions in general. Therefore, it is not an admissible strain measure. Since only elastic deformations are assumed to induce stresses, the elastic part of the left Cauchy-Green-tensor is stated as

$$\begin{aligned} {\varvec{b}}^e = {\varvec{F}}^e({\varvec{F}}^e)^T. \end{aligned}$$
(9)

Using the split of the deformation gradient into volumetric and isochoric parts

$$\begin{aligned} {\varvec{F}} = {\varvec{F}}^{vol}{\varvec{F}}^{iso} = J^{\frac{1}{3}} \bar{{\varvec{F}}}, \end{aligned}$$
(11)

the purely isochoric elastic part of the left Cauchy-Green-tensor can be derived

$$\begin{aligned} \bar{{\varvec{b}}}^e = (J^e)^{-\frac{2}{3}}{{\varvec{b}}}^e. \end{aligned}$$
(14)

For the parts of the deformation gradient describing growth, no further decomposition is utilized.

2.2.2 Internal energy

The internal energy depicts the total energy, which is stored in the thermomechanical system under observation. It is defined as the volume integral over the mass specific internal energy e and the density, and reads

$$\begin{aligned} {\mathcal {E}}:= \int \rho e \textrm{d}v. \end{aligned}$$
(20)

It is assumed that the internal energy of biological systems is influenced by growing processes. In biological systems, a phenomenon, that often occurs, is the production of glucose via photosynthesis. To be able to capture the production of glucose, the source of internal energy h is introduced.

2.2.3 Flux of internal energy

The flux of internal energy \({\varvec{J}}\) is assumed to capture phenomena like the flux of nutrients in biological systems or the directed flux of growth hormones within the body under observation based upon environmental factors. Growth hormones are known to influence the growth response of plants significantly, see [8, 10, 29] among others. The flux of internal energy at a surface can be expressed as

$$\begin{aligned} J_n:= {\varvec{J}}\cdot {\varvec{n}}. \end{aligned}$$
(21)

In Eq. (10), the outward normal vector \({\varvec{n}}\) is utilized. Furthermore, Eq. (10) can be used to describe the transport of internal energy through a point \({\varvec{x}} \in \partial {\mathcal {B}}\) according to

$$\begin{aligned} J_n\textrm{d}a = {\varvec{J}}\cdot {\varvec{n}}\textrm{d}a. \end{aligned}$$
(25)

2.3 Balance of mass

For thermodynamically closed systems, the mass is constant in time. This assumption does not hold true for biological systems undergoing growth, see [16]. For instance, in plants, an increase of mass is observed. Therefore, thermodynamically open systems are investigated. Consequently, the time derivative of the mass at a material point reads

$$\begin{aligned} \frac{\textrm{d}m}{\textrm{d}t} = \left( \frac{\textrm{d}\rho }{\textrm{d}t} + \underbrace{\textrm{div}({\varvec{v}})\rho }_{\approx 0}\right) \ \textrm{d}v. \end{aligned}$$
(27)

In Eq. (12), the divergence of the velocity \(\textrm{div}({\varvec{v}})\) is stated. In general, growth deformations are considered to be slow. Therefore, the part containing the velocity vector \({\varvec{v}}\) can be neglected. As a consequence, the material time derivative of the density is expressed as

$$\begin{aligned} \frac{\textrm{d}\rho }{\textrm{d}t} = {\dot{\rho }} + {\varvec{v}}\cdot \textrm{grad}(\rho ). \end{aligned}$$
(28)

Again, the assumption of slow growth is considered. Therefore, Eq. (13) is reformulated as

$$\begin{aligned} \frac{\textrm{d}\rho }{\textrm{d}t} = {\dot{\rho }}. \end{aligned}$$
(29)

Subsequently, the remaining partial time derivative is considered in a constitutive equation.

2.4 Balance of linear momentum

The balance of linear momentum also needs to be adjusted for open systems. The formulation depends on the body forces \({\varvec{b}}\) and the Cauchy stresses \(\varvec{\sigma }\), reading

$$\begin{aligned} \rho \dot{{\varvec{v}}} = \rho {\varvec{b}} + \textrm{div}(\varvec{\sigma }). \end{aligned}$$
(31)

The formulation is taken from [15]. Considering the aforementioned assumption of slow growth, Eq. (15) is simplified to

$$\begin{aligned} {\varvec{0}} = \rho {\varvec{b}} + \textrm{div}(\varvec{\sigma }). \end{aligned}$$
(33)

2.5 Balance of energy

The balance of energy is utilized to calculate the internal energy of the system. The internal energy is assumed to be the driving quantity for growth deformations. It is numerically efficient to combine all driving factors of growth, water, nutrients among others into one scalar field. In reality, plant like structures are influenced by many different factors, see [28]. The local form of the balance of energy yields

$$\begin{aligned} \rho {\dot{e}} = \varvec{\sigma }:{\varvec{d}} + \rho h - \textrm{div}({\varvec{J}}). \end{aligned}$$
(38)

In this formulation, the source h and flux terms \({\varvec{J}}\) are incorporated. Therefore, fluxes and sources of internal energy can be calculated in numerical simulations. For the sake of brevity, only constant source terms are considered. The formulations of these terms are detailed in Sect. 3. The derivation of the balance of energy for growing systems is further depicted in [15].

3 Constitutive equations of growth formulations

Subsequently, formulations are chosen for the constitutive equations.

3.1 Free Helmholtz energy

Recalling the kinematic assumptions from Eq. (7), the free energy formulation is split into a volumetric and an isochoric part

$$\begin{aligned} \rho \psi = \rho \psi ^{vol} + \rho \psi ^{iso}. \end{aligned}$$
(49)

Here, the strain energy is given per unit mass. From [12], the specific formulation of the volumetric part is utilized, reading

$$\begin{aligned} \rho \psi ^{vol}(J^e) = \frac{\varkappa }{2} \ln (J^e)^2, \end{aligned}$$
(50)

where \(\varkappa \) refers to the compression modulus. The remaining, isochoric part reads

$$\begin{aligned} \rho \psi ^{iso} = a ({\bar{I}}_1 - 3). \end{aligned}$$
(52)

Here, a Neoh-Hooke material model is utilized. Since the main focus is modeling of the growth of plants, a standard material model is sufficient. Therefore, the abbreviation \(a = \frac{\mu }{2}\) is defined. \(\mu \) denotes the shear modulus. The first invariant is given as

$$\begin{aligned} {\bar{I}}_1 = \textrm{tr}(\bar{{\varvec{b}}}^e). \end{aligned}$$
(1)

3.2 Cauchy stresses

For thermodynamically open systems, the formulation of the Cauchy stresses is stated as

$$\begin{aligned} \varvec{\sigma } = 2\rho \frac{\partial \psi }{\partial {\varvec{g}}} = 2 \rho \frac{\rho _0}{\rho _0}\frac{\partial \psi }{\partial {\varvec{g}}} = 2 \frac{\rho }{\rho _0}\frac{\partial \rho _0\psi }{\partial {\varvec{g}}}. \end{aligned}$$
(4)

In Eq. (22), \({\varvec{g}}\) refers to the metric tensor in the current configuration. According to Eq. (18), the stress tensor can be divided additively into two parts. The purely volumetric part of the stresses reads

$$\begin{aligned} \varvec{\sigma }^{vol} = \frac{\rho }{\rho _0}\varkappa \ln (J^e) {\varvec{g}}^{-1}. \end{aligned}$$
(7)

The purely isochoric part reads

$$\begin{aligned} \varvec{\sigma }^{iso} = 2 \frac{\rho }{\rho _0} a \textrm{dev}(\bar{{\varvec{b}}}^e). \end{aligned}$$
(10)

In Eq. (24), the deviatoric operator \(\textrm{dev}(\square )\) is given.

3.3 Density production

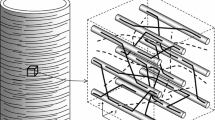
As pointed out in Sect. 2.3, the production of density needs to be constitutively specified. The driving force for growth is the internal energy. Biological systems consist of cells. Therefore, each material point on the macroscale represents a conglomerate of cells on the microscale. On the microscopic level, an influx of nutrients and water into the cells occurs. As a result, cell elongation and cell division occur. Furthermore, an increase of mass is observed. Since the conglomerate is represented as a point on the macroscale, the density of the material point is subjected to change. This assumption is schematically depicted in Fig. 1. The water and nutrients are assumed to be part of the internal energy. Therefore, the formulation of the density change is a function of the internal energy

$$\begin{aligned} {\dot{\rho }} = f(e). \end{aligned}$$
(12)

For the sake of brevity, the relation is assumed to be linear, and is given by

$$\begin{aligned} {\dot{\rho }} = \frac{H_{gr}}{J} e. \end{aligned}$$
(13)

Here, the mass production modulus \(H_{gr}\) is defined, relating the internal energy with the production of density. In Eq. (26), the determinant of the total deformation gradient is included, to obtain a formulation for the growth rate \(\Gamma \), see Eq. (37), which does not depend on deformations. Therefore, the growth rate depends only on the internal energy. Furthermore, Eq. (26) is constitutively chosen to depend on the total internal energy, which consists partially of the free Helmholtz energy. Therefore, the accumulation of matter depends on the stresses. Consequently, processes like the forming of reaction wood can be captured. It is shown in the literature, see [3, 33], that wooden structures like trees accumulate matter at points of stress concentrations, which is called reaction wood. The time integration is further described in Sect. 4.

Fig. 1
figure 1

Model assumptions of the macroscopic density production

Full size image

3.4 Flux of internal energy

In Eq. (17), the flux of the internal enegy \({\varvec{J}}\) is introduced. In order to model the growth of plants by continuum mechanics, this flux is split into three different parts

$$\begin{aligned} {\varvec{J}} = {\varvec{J}}^F + {\varvec{J}}^P + {\varvec{J}}^G, \end{aligned}$$
(15)

describing separate mechanisms. The Fickean part \({\varvec{J}}^F\), the portion which governs phototropism \({\varvec{J}}^P\) and the contribution, which describes graviotropism \({\varvec{J}}^G\) of the flux, are considered. In general, tropisms depict the directed growth response with respect to environmental influences. Phototropism describes the influence of the light on the growth direction, while graviotropism denotes the influence of gravity on the growth direction. The Fickean part is thought to model the osmotic and diffusion processes inside of plants. The formulation for this part yields

$$\begin{aligned} {\varvec{J}}^F = -\frac{\rho }{\rho _0} {\varvec{m}}\cdot \textrm{grad}(e). \end{aligned}$$
(16)

It is a function of the current gradient of the internal energy distribution \(\textrm{grad}(e)\) and the anisotropic material tensor \({\varvec{m}}\). For the sake of brevity, the Fickean flux is chosen to depend on the whole internal energy distribution. The formulation depends on the directional vectors for the primary \({\varvec{D}}\) and secondary \({\varvec{E}}\) and \({\varvec{H}}\) growth directions

$$\begin{aligned} {\varvec{m}} = m_{prim} {\varvec{D}}\otimes {\varvec{D}} + m_{sec} ({\varvec{E}}\otimes {\varvec{E}} + {\varvec{H}}\otimes {\varvec{H}}). \end{aligned}$$
(17)

Furthermore, the conductivity coefficients \(m_{prim}\) and \(m_{sec}\) are stated. The calculation of the growth directions is provided in Sect. 3.6. For the computation of the phototropistic flux term, the logic from the work [13, 26] is utilized. From [13], the idea of modeling the flux of internal energy by a unit vector combined with a related transportation velocity is taken. The calculation of the directional vector is based upon [26]. It is assumed that the internal distribution of growth hormones depends on the influence of a light source. This source induces an enrichment of growth hormones on the side facing away from the light source. The assumptions hold true, only if positive phototropism is investigated. For negative tropistic effects, the enrichment of growth hormones takes place at the side facing towards the light source. The directed flux of growth hormones is captured by

$$\begin{aligned} {\varvec{J}}^P = \frac{\rho }{\rho _0} v^P e \frac{{\varvec{p}}}{\vert {\varvec{p}}\vert }. \end{aligned}$$
(18)

In Eq. (30), the phototropistic transportation velocity of the internal energy \(v^P\) and the direction vector of the phototropistic effect \({\varvec{p}}\) are given. The position vector can be calculated by

$$\begin{aligned} {\varvec{p}} = {\varvec{x}} - {\varvec{P}}^{\textrm{sun}}. \end{aligned}$$
(19)

Here, \({\varvec{P}}^\textrm{sun}\) is the position vector of the light source. The third part of the flux term is the graviotropistic flux of internal energy

$$\begin{aligned} {\varvec{J}}^G = \frac{\rho }{\rho _0} v^G e (-{\varvec{e}}^3). \end{aligned}$$
(22)

The reasoning, as in the work of [20], is followed for the direction of the unit vector. The basic modeling approach is taken from [13]. In Eq. (32), the velocity of internal energy transportation induced by graviotropism \(v^G\) and the direction vector of the acceleration due to gravity \({\varvec{e}}^3\) are stated. The direction can be calculated via

$$\begin{aligned} {\varvec{e}}^3 = -\frac{{\varvec{g}}_a}{\vert {\varvec{g}}_a\vert }. \end{aligned}$$
(23)

Here, \({\varvec{g}}_a\) denotes the vector of the acceleration acting upon the body under observation. A depiction of the enrichment caused by tropistic phenomena is illustrated in Fig. 2.

Fig. 2
figure 2

Influence of the tropisms on the growth hormone distribution

Full size image

3.5 Growth deformation gradient

Growth deformations are represented via the growth part of the deformation gradient. For plants, it can be observed that there is a preferred direction of spatial expansion. This topic is further discussed in [2, 5, 24]. Therefore, the growth deformation gradient is split into the primary and secondary growth directions. Consequently, the deformation gradient depends on the primary \({\varvec{D}}\) and secondary \({\varvec{E}}\) and \({\varvec{H}}\) growth directions. Following [14], an anisotropic formulation for the growth deformation is obtained as

$$\begin{aligned} {\varvec{F}}^{gr} = \beta _{p}^{\frac{1}{3}} {\varvec{D}} \otimes {\varvec{D}} + \beta _s^{\frac{1}{3}} ({\varvec{E}}\otimes {\varvec{E}} + {\varvec{H}}\otimes {\varvec{H}}). \end{aligned}$$
(24)

Here, \(\beta _{p}\) is the expansion coefficient of the primary growth direction and \(\beta _s\) is the expansion coefficient of the secondary growth direction, respectively. The calculation of growth directions based upon environmental influences is further described in Sect. 3.6. The expansion coefficients need to be specified. Following [1], the time derivatives depend on the growth rate \(\Gamma \), reading

$$\begin{aligned} \dot{\beta _{p}} = \Gamma H_{p} \beta _{p} \end{aligned}$$
(26)

and

$$\begin{aligned} \dot{\beta _s} = \Gamma H_s \beta _s. \end{aligned}$$
(30)

In Eqs. (35) and (36), the material constants \(H_p\) and \(H_s\) relate the spatial expansion to the growth. The growth rate is often utilized to quantify growth, see [19, 21, 22]. It is formulated as the change of mass in relation to the total mass

$$\begin{aligned} \Gamma = \frac{\dot{\textrm{d}m}}{\textrm{d}m} = \frac{{\dot{\rho }}\textrm{d}v}{\rho \textrm{d}v} = \frac{{\dot{\rho }}}{\rho }. \end{aligned}$$
(32)

In the contribution at hand, a formulation is proposed, which describes the density change and the spatial expansion by adding one more field variable.

3.6 Primary and secondary growth direction for stems

In Sects. 3.4 and 3.5, the vectors of the primary and secondary growth directions are introduced. The primary growth is often related to one distinct spatial direction. On the contrary, the secondary growth is often related to the surface perpendicular to the primary growth. The growth directions are influenced by the tropisms. In the contribution at hand, the photo- and graviotropism are investigated. For modeling of phototropism, the directional vector towards the source of light

$$\begin{aligned} {\varvec{r}} = {\varvec{P}}^{\textrm{sun}} - {\varvec{x}} \end{aligned}$$
(34)

is utilized. The formulation of the primary growth direction reads

$$\begin{aligned} {\varvec{I}} = \alpha _{tr} {\varvec{e}}^3 + \beta _{tr} \frac{{\varvec{r}}}{\vert {\varvec{r}}\vert }. \end{aligned}$$
(35)

Here, the weighting coefficients for the graviotropism \(\alpha _{tr}\) and phototropism \( \beta _{tr}\) are given. The amount of spatial expansion is controlled by Eqs. (35) and (36) only. Therefore, the vector of primary growth needs to be normalized

$$\begin{aligned} {\varvec{D}} = \frac{{\varvec{I}}}{\vert {\varvec{I}}\vert }. \end{aligned}$$
(36)

The two remaining direction vectors can be calculated as

$$\begin{aligned} {\varvec{E}} = \frac{{\varvec{T}}^{ED}\cdot {\varvec{D}}}{\vert {\varvec{T}}^{ED}\cdot {\varvec{D}}\vert } \end{aligned}$$
(37)

and

$$\begin{aligned} {\varvec{H}} = {\varvec{D}}\times {\varvec{E}}. \end{aligned}$$
(39)

In Eq. (41), the matrix

$$\begin{aligned} {\varvec{T}}^{ED} = \begin{bmatrix} 0 &{} 0 &{} -1 \\ 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 \end{bmatrix} \end{aligned}$$
(40)

is introduced to ensure that \({\varvec{E}}\) will always be perpendicular to \({\varvec{D}}\). The algorithm consisting of Eqs. (41)–(43) will not work for the specific formulation of \({\varvec{D}}^T = \begin{bmatrix} 0&1&0 \end{bmatrix}\). To avoid implausible results, Eq. (41) is exchanged with \({\varvec{E}}^T = \begin{bmatrix} 1&0&0 \end{bmatrix}\), if the vector of the primary growth direction takes the form \({\varvec{D}}^T = \begin{bmatrix} 0&1&0 \end{bmatrix}\). A schematic representation of the primary growth direction being influenced by tropisms is depicted in Fig. 3. The influence of the ratio of \(\beta _{tr}\) to \(\alpha _{tr}\) on the primary growth direction is further investigated. Therefore, the resulting angle between \({\varvec{I}}\) and \({\varvec{e}}^3\) in dependence on the ratio of the two weighting factors is shown in Fig. 4. As it can be seen, a nonlinear relation is obtained.

Fig. 3
figure 3

Determination of the primary growth direction

Full size image
Fig. 4
figure 4

Angle between the primary growth direction and graviotropistic growth direction

Full size image

3.7 Primary growth direction of branches

In Sect. 3.6, the primary and secondary growth directions are introduced for a stem. For branch materials, the formulations need to be adjusted accordingly. In branches, the main driving force for growth is the maximization of photosynthesis. Therefore, the most stable supply of nutrients for the whole plant is ensured. As a consequence, the objective is to maximize the area subjected to sunlight, because it is a catalyst for photosynthesis. Therefore, Eq. (39) is further manipulated. The influence of the maximization of photosynthesis is considered, by adding the directional vector \({\varvec{p}}^{br}\) and the weighting factor \(\gamma _{tr}\)

$$\begin{aligned} {\varvec{I}}^{br} = \alpha _{tr} {\varvec{e}}^3 + \beta _{tr} \frac{{\varvec{r}}}{\vert {\varvec{r}}\vert } + \gamma _{tr} {\varvec{p}}^{br}. \end{aligned}$$
(41)

The directional vector is perpendicular to the surface of the stem. The vector needs to be a unit vector. The calculation of the vector is described in Sect. 5.4. Alternatively, the vector can be treated as a material parameter.

3.8 Fiber growth

The mechanical response of plants is mainly characterized by fibers. Therefore, a model is developed, which enables the calculation of the fiber direction at the individual integration point. The fiber direction is obtained from the fiber growth processes. It is assumed that the fiber direction can be obtained by considering flow of nutrients and water (Fig. 5). In plants, transportation processes occur, because nutrients need to be delivered to and from the leaves. In reality, only small velocities are observed. Nevertheless, good approximations of fiber directions can be obtained from this assumption, see [17]. To capture this mechanism in numerical simulations, the calculation of the fiber direction as gradient of the internal energy is utilized

$$\begin{aligned} {\varvec{A}}_{n+1} = -\textrm{grad}(e)_n. \end{aligned}$$
(42)

\({\varvec{A}}_{n+1}\) denotes the fiber direction at the current time step \(n+1\). \(\textrm{grad}(e)_n\) is the gradient in the current configuration of the internal energy distribution at the previous time step n. In nature, growing processes are slow, and, thus, the gradient of the previous time step can be utilized.

4 Finite element formulation of growth

In this section the implementation of the proposed formulations in a finite element algorithm is further elaborated.

Fig. 5
figure 5

Schematic fiber growth inside a structure

Full size image

4.1 Backward Euler integration scheme

In Sect. 3, Eqs. (26), (35) and (36) are formulated as time dependent equations. For an implementation of these equations into a numerical solution scheme, time integration needs to be carried out. Here, a backward Euler scheme is chosen. Therefore, Eq. (26) can be rewritten as

$$\begin{aligned} \rho _{n+1} = \frac{H_{gr}}{J} e \Delta t + \rho _{n}. \end{aligned}$$
(43)

In Eq. (46), \(\rho _{n+1}\) and \(\rho _{n}\) denote the density at the current and previous time step respectively. Furthermore, \(\Delta t\) is introduced as the time step of the numerical simulation. Equations (35) and (36) need to be integrated by the exponential integration scheme, which is further explained in [34]. Applying this procedure, the Eqs. (35) and (36) can be re-written as

$$\begin{aligned} \beta _{p}^{n+1} = \exp (\Gamma H_{p} \Delta t)\beta _{p}^n \end{aligned}$$
(44)

and

$$\begin{aligned} \beta _{s}^{n+1} = \exp (\Gamma H_{s} \Delta t)\beta _{s}^n. \end{aligned}$$
(45)

The implementation of the constitutive equations into the finite element method is depicted by Algorithm 1.

Algorithm 1
figure a

Growth material model at every Gauss point

Full size image

4.2 Galerkin functional

The solution of the coupled boundary value driven problem is achieved by the finite element method. The displacement field is driven by the balance of linear momentum, see Sect. 2.4. The internal energy evolves via the balance of energy, see Sect. 2.5. The driving partial differential equations (PDEs) are processed via Galerkin functionals. To be able to apply the solution procedure, the test functions

$$\begin{aligned} \delta {\varvec{u}}:= \{ \delta {\varvec{u}}({\varvec{x}})\in {\mathcal {B}}_t \ \vert \ \delta {\varvec{u}} = 0 \forall {\varvec{x}} \in \partial {\mathcal {B}}_{t,u} \} \end{aligned}$$
(46)

and

$$\begin{aligned} \delta e:= \{ \delta e ({\varvec{x}})\in {\mathcal {B}}_t \ \vert \ \delta e = 0 \forall {\varvec{x}} \in \partial {\mathcal {B}}_{t,e} \} \end{aligned}$$
(47)

are defined. Furthermore, the domain, which is considered, needs to be decomposed into multiple finite elements. Using Eqs. (15) and (17), multiplying by the test functions, integrating over the volume of each individual element \({\mathcal {B}}_{tE}\), utilizing the Gaussian theorem and the divergence theorem, the governing equations can finally be formulated as

$$\begin{aligned} \begin{aligned} G&= \int _{{\mathcal {B}}_{tE}} \textrm{grad}(\delta {\varvec{u}})_{ij}:\varvec{\sigma }_{ij}\textrm{d}v - \int _{{\mathcal {B}}_{tE}}\rho {\varvec{b}}_i\cdot \delta {\varvec{u}}_i\textrm{d}v\\&\quad - \int _{{\mathcal {B}}_{tE}} \delta e \varvec{\sigma }_{ij}: {\varvec{d}}_{ij}\textrm{d}v - \int _{{\mathcal {B}}_{tE}} \delta e \rho h \textrm{d}v \\&\quad + \int _{{\mathcal {B}}_{tE}}\delta e \rho {\dot{e}}\textrm{d}v - \int _{{\mathcal {B}}_{tE}}\textrm{grad}(\delta e)_i\cdot {\varvec{J}}_i\textrm{d}v. \end{aligned} \end{aligned}$$
(48)

Within the finite element framework, the initial condition at \(t=0\) needs to be specified. In general, the prescription of energy distributions, energy fluxes, displacements and tractions is possible. As a result, the boundary of the observed body is divided into \(\partial {\mathcal {B}} = \{\partial {\mathcal {B}}_u,\ {\mathcal {B}}_e \} = \{{\mathcal {B}}_\sigma ,\ {\mathcal {B}}_J\}\) parts. The structure of the functional is non-linear in general, necessitating an iterative solution for each time step.

4.3 Linearization of the Galerkin functional

For a fast and reliable solution of Eq. (51), a Newton-type solver is applied. As a consequence, the linearization operator is introduced as the total derivative

$$\begin{aligned} \Delta [\dots ] = \frac{\textrm{d}[\dots ]}{\textrm{d}{\varvec{u}}}: \Delta {\varvec{u}} + \frac{\textrm{d}[\dots ]}{\textrm{d}e}: \Delta e. \end{aligned}$$
(51)

The linearization of the Galerkin functional yields

$$\begin{aligned} \begin{aligned} \Delta G&= \int _{{\mathcal {B}}_{tE}}\Delta \textrm{grad}(\delta {\varvec{u}}): \varvec{\sigma }\textrm{d}v + \int _{{\mathcal {B}}_{tE}} \textrm{grad}(\delta {\varvec{u}}): \Delta \varvec{\sigma }\textrm{d}v \\&\quad + \int _{{\mathcal {B}}_{tE}} \textrm{grad}(\delta {\varvec{u}}):\varvec{\sigma }\Delta \textrm{d}v - \int _{{\mathcal {B}}_{tE}} \Delta \rho {\varvec{b}}\cdot \delta {\varvec{u}}\textrm{d}v - \int _{{\mathcal {B}}_{tE}}\rho {\varvec{b}}\cdot \delta {\varvec{u}}\Delta \textrm{d}v \\&\quad - \int _{{\mathcal {B}}_{tE}} \delta e \Delta \varvec{\sigma }: {\varvec{d}} \textrm{d}v - \int _{{\mathcal {B}}_{tE}} \delta e \varvec{\sigma }: \Delta {\varvec{d}} \textrm{d}v - \int _{{\mathcal {B}}_{tE}} \delta e \varvec{\sigma }: {\varvec{d}} \Delta \textrm{d}v \\ {}&\quad - \int _{{\mathcal {B}}_{tE}}\delta e \Delta \rho h \textrm{d}v - \int _{{\mathcal {B}}_{tE}}\delta e \rho \Delta h \textrm{d}v - \int _{{\mathcal {B}}_{tE}} \delta e \rho h \Delta \textrm{d}v \\&\quad + \int _{{\mathcal {B}}_{tE}} \delta e \Delta \rho {\dot{e}}\textrm{d}v + \int _{{\mathcal {B}}_{tE}} \delta e \rho \Delta {\dot{e}}\textrm{d}v + \int _{{\mathcal {B}}_{tE}} \delta e \rho {\dot{e}}\Delta \textrm{d}v \\&\quad - \int _{{\mathcal {B}}_{tE}} \Delta \textrm{grad}(\delta e)\cdot {\varvec{J}} \textrm{d}v - \int _{{\mathcal {B}}_{tE}}\textrm{grad}(\delta e) \cdot \Delta {\varvec{J}} \textrm{d}v \\ {}&\quad - \int _{{\mathcal {B}}_{tE}}\textrm{grad}(\delta e)\cdot {\varvec{J}}\Delta \textrm{d}v. \end{aligned} \end{aligned}$$
(53)

Further simplifications of Eq. (53) based upon the balance of mass are not possible because the system is thermodynamically open.

5 Structural generator

In this section, the structural generator is elaborated in more detail. The structural generator consists of growth formulations and an adaptive meshing algorithm. In a classical finite element simulation, the element size is an indicator for the quality of the simulation. If the elements are too large, the approximation is not realistic. In the simulation of growing systems, the element size increases due to growth deformations. Thus, to prevent unrealistic results, an adaptive meshing algorithm needs to be employed. The described algorithm is only valid for hexahedral elements consisting of 8 nodes. As a consequence, only linear ansatz functions can be utilized in the isoparametric space. Consequently, trilinear element formulations are utilized. These elements are chosen, due to its simplicity. This yields an advantage, since the important part are the physical formulations of the contribution at hand. Nevertheless, a common deformation state of plants is bending. The 8 node hexahedral elements are known to work well for bending.

5.1 Initialization of the structural generator simulation

Inside the structural generator, no investigation of the processes below ground level is conducted. Therefore, the starting point is an initial structure above ground. Since the finite element method is generally not capable of handling 3D finite elements with exactly zero volume, an initial geometry needs to be established. Therefore, in the implementation of the algorithms proposed in the contribution at hand, a circular surface is chosen, which is extended with an initial height \(h_{\text {init}}\) in growing direction. \(h_{\text {init}}\) is denoted as a process parameter and can be set individually for each simulation. Furthermore, the surface is meshed in a predefined way. A method is chosen, which requires the specification of the elements in only radial direction of the circle. Therefore, another process parameter \(n_{\text {r}}\) is introduced. Additionally, the radius of the initial structure needs to be provided, denoted as \(r_{\text {init}}\). A graphical representation of the result of the algorithm is given in Fig. 6. The meshing algorithm is carried out by initializing the first node at the middle of the surface. Next, one linear quadrilateral element per quarter of the circle is meshed. One node of each element is located at the middle of the structure. Per quarter circle, three nodes are equidistantly distributed along the circumference. A resulting element can be seen in Fig. 6 labeled as number 1. The next circle of nodes is constructed by doubling the amount of nodes and, again, distributing them along the circumference. The nodes are only connected to form quadrilateral elements. The elements are created in a repeatable pattern. The first and last element per quarter of a circle are created by connecting two nodes from the new circle of nodes and two from the already existing outermost layer of nodes. Such an element can be seen in Fig. 6 labeled as number 2. The connection procedure has to alternate along the circumference. Only quadrilateral elements are created. The alternative connection procedure is obtained by connecting three nodes from the newly created circle of nodes and only one of the already existing circle. An element of this shape is given in Fig. 6 obtaining label 3. This pattern is repeated for all quarters of a circle. Afterwards, the next layer of elements is connected similarly. To achieve a three dimensional structure, the obtained surface is copied and shifted by the amount of \(h_{\text {init}}\) in the initial growth direction. Therefore, a mesh only consisting of linear hexahedral elements is obtained.

Fig. 6
figure 6

Graphical depiction of the initialization of the mesh

Full size image

5.2 Boundary conditions

For the initialization of the numerical solution, boundary conditions need to be specified. The boundary conditions are only applied at the lowest surface of nodes. This layer of nodes is supposed to represent the part of the plant interacting with the soil. The displacements in the initial primary growing direction are prescribed. To represent the flux of nutrients and water from the roots into the growing system, the internal energy is prescribed at the lowest surface of the structure. Therefore, the maximum internal energy \(e_{\text {max}}\) is introduced. For the sake of brevity, only constant or linearly increasing loading functions are considered. Subsequently, the plane perpendicular to the initial primary growth direction needs to be fixed. It is sufficient to fix all displacements of the node in the middle of the structure. Alternatively, all displacements of all nodes in the lowest surface can be prescribed. The option mentioned firstly, will lead to softer responses compared to reality, and the second option to a stiffer behavior. Soil is normally modeled as elastic springs allowing a certain amount of displacements before the restoring force counteracts the displacement. For the sake of brevity, the modeling strategy restraining all nodes is applied.

5.3 Adaptive meshing

Growth leads to spatially expanding elements. The solution quality gets worse, if the elements exhibit larger volumes. Therefore, an adaptive meshing algorithm needs to be included. The total volume of each element is utilized as an error approximation. If the volume exceeds a threshold, denoted as \(v_{\text {r}}\), remeshing is initialized. The newly created elements are placed outside of the structure in growing direction. The initial height of this element is specified as a process parameter, denoted as \(h_{\text {r}}\). If the height of the newly included elements is small compared to the existing elements, and the nodal unknowns are given as smooth functions, a negligible error is obtained. For the new elements, eight nodes are necessary to form a linear hexahedral element. In Sect. 5.1, an algorithm is explained creating a circular surface. Therefore, the growing structure consists of quadrilateral surfaces at the top boundary. As a consequence, a layer of new nodes can be created by taking the position vector in the reference configuration and shift the position of each node by the amount of \(h_{\text {r}}\) in the primary growth direction. Therefore, the nodal vector in the reference configuration \({\varvec{X}}\) is obtained for the new nodes. Next, the global unknown fields are initialized. Due to a negligible small initial height and linear ansatz functions, the values of the existing nodes are copied to the new nodes. Subsequently, a Newton iteration is performed, to obtain the equilibrium state.

Elements are not allowed to exceed a certain volume to limit the approximation error. Therefore, the maximum volume of an element \(v_{\text {f}}\) is introduced. In elements exceeding the threshold, growth deformations are prohibited. Therefore, a transition of the growing zone of the biological system is achieved. The transition is motivated by the so-called cambial layer. This layer can be formed by multiple layers of cells in the growing system. It characterizes the zone undergoing cell elongation and division. In general, plant like structures are able to perform cell elongation outside of the cambial layer. This phenomenon is caused by influence from the environment. In the structural generator, growth is limited to the cambial layer.

5.4 Initialization of branches

In the contribution at hand, a growth formulation for branches is presented in Sect. 3.7. The initialization of branches is included in the structural generator. For the sake of brevity, only the initial part is considered, referred to as buds in literature. For the generalization of the proposed approach, an additional remeshing strategy needs to be employed, enabling the development of full branches. Nevertheless, interactions of different growth processes can be demonstrated by the inclusion of branches. A phenomenon, that often occurs in plant like structures, is the initialization of branches with a repeating time interval. For instance, spruce creates a ring of branches every year, see [27]. Therefore, the modeling strategy is based upon time. The interval in which branching occurs is denoted as \(t_\text {b}\). At every integer multiple of \(t_{\text {b}}\), a new layer of branches is introduced. Branching at the start of the simulation is neglected. The number of layers, where branching is skipped, is denoted by \(n_\text {b}\). Branching is not limited to just the uppermost element layer in the simulation, resulting in a more flexible approach. The branches are assumed to produce internal energy. It is postulated that plants strive to achieve an even distribution of internal energy. Therefore, the position of the branch is determined by the node possessing the least amount of internal energy. Three remaining nodes need to be chosen to initialize the branch element. The neighboring node containing lesser internal energy is chosen. Furthermore, the nodes possessing the same circumferential direction of the layer below are considered. Therefore, a quadrilateral surface is obtained. The position of four new nodes is calculated by shifting the positional vector of the aforementioned nodes. The direction of the shift is given by the surface normal. The length of the new branch is a process parameter denoted as \(h_{\text {b}}\). Subsequently, \({\varvec{p}}^{br}\) is chosen as the surface normal. To obtain an equilibrium state, a Newton iteration is performed. A graphical representation of the process is given in Fig. 7.

Fig. 7
figure 7

Graphical representation of the initialization of a branch

Full size image

5.5 History terms

History terms are introduced by the applied backward Euler integration scheme. These terms pose a challenge in the structural generator. The amount of history terms and the initial values depend on the material formulation. In the structural generator, the amount of branch and stem elements cannot be determined during initial mesh creation. The pattern in which branch and stem elements are incorporated may differ depending on the chosen material and process parameters. For the sake of simplicity, the maximum number of elements is chosen during mesh creation stage itself. The mesh is split into activated and deactivated elements. During mesh refinement, elements are activated. Deactivated elements are stored in a reservoir, and are not considered during calculation. On activation, the material model is specified. Therefore, the history terms are initialized with the initial values during activation. As a consequence, every element represents material neglecting previous growth deformations on activation. This assumption yields a good agreement with reality for the buds. The stem is treated similarly. To enable a better agreement with reality for the stem, the initialization might be adjusted.

6 Numerical examples

In this section, numerical examples are presented to demonstrate the capabilities of the proposed formulations to capture growth phenomena of plant organs.

6.1 Growth response of stems

In this section, a numerical example is investigated to demonstrate the capabilities of modeling the combination of phototropism and graviotropism in stems. The structure is shown in Fig. 8. The lower surface is completely fixed. Furthermore, an internal energy distribution of \( 90\frac{{\text {J}}}{{{\text {kg}}}} \) is prescribed at the lowest surface of the structure. Two material parameter sets are utilized. Set 1 undergoes growth deformation. For set 2, growth is prohibited by the chosen material parameters. The upper part of the structure, which is plotted in green in Fig. 8, undergoes growth. The second set of material parameters is employed in the portion of the mesh colored with the brighter color. Three simulations are investigated. The position of the light source is varied, to demonstrate the influence of the phototropism on the growth process. The position of the light source for the simulations is listed in Table 1. It should be mentioned that the origin of the coordinate system is the middle point of the lower surface of the structure. Additionally, in simulation (c), a force is applied to the structure. The force is applied at every node, which has the maximum \({\varvec{x}}_1\)-value. The direction of the force counteracts the phototropistic growth response. The absolute value of the force applied at every node is 0.005 N. In these simulations, no body forces are considered. The material parameters are stated in Table 2.

The growth response of the three simulations is depicted in Fig. 9. Here, the elongation in the primary growth direction is shown by the expansion coefficient \(\beta _{p}\). As it can be seen, the force causes the plant to bend away from the light source in simulation (c) initially. Over time, the impact of the force becomes negligible. The bending of the plant is induced by the phototropism in two separate ways. Firstly, the primary growth direction is directly influenced in the calculation of the growth deformation gradient. Secondly, the phototropistic flux terms cause an enrichment of internal energy at the shaded side of the structure. Consequently, the growth takes place mainly at this side of the structure. This is indicated by the distribution of the \(\beta _p\) field in Fig. 9. Furthermore, the adapted position of the light source in simulation (b) leads to an entirely different bending behavior compared to simulation (a). The bending is limited to the height of the light source. In the other two simulations, the height of the light source is not reached. The maximum displacement in \({\varvec{x}}_1\)-direction at the tip of the structure is around 59 mm for cases (a) and (c). For case (b), this value is limited to 45 mm. The convergence behavior of the time step with the most iterations is shown in Fig. 10. This particular time step occurs in the simulation (c), where two counteracting mechanisms and a large time step of 2 seconds are present. Nevertheless, a stable convergence is obtained. The convergence behavior of the simulation in the vicinity of the root is quadratic. Thus, it may be stated that the implementation of the proposed formulation is satisfactory.

Fig. 8
figure 8

Boundary conditions for the phototropistic responses, the green color indicates the region, where growth is allowed, while the brighter color indicates prevented growth

Full size image
Table 1 Position of the light source in the three simulation
Full size table
Table 2 Material parameters of the growth simulations
Full size table
Fig. 9
figure 9

Evolution of phototropistic growth response to different boundary conditions; a reference solution; b higher position of the light source; c application of additional force boundary conditions

Full size image

6.2 Growth response of branches

In this section, a numerical example regarding phototropism and graviotropism in branches is investigated. The structure is depicted in Fig. 11. One stem with four branches is investigated. Two branches connect only to another branch, and not to the stem. The stem exhibits a quadratic cross-section of 20 \(\times \) 20 mm. The branches directly connecting to the stem have a cross-section of 15 \(\times \) 15 mm. While the branches, which are not in contact with the stem, exhibit a cross-section of 10 \(\times \) 10 mm. The coordinate origin is located at the fixed surface of the stem. Specifically, the vertex, which is not visible in Fig. 11, is the coordinate origin. The length of the branches within one layer is constant. The material parameter sets are shown in Fig. 11. All displacements are fixed for the bottom surface. Additionally, an internal energy of is prescribed. The utilized material parameters are stated in Table 3. In general, different plant organs can be influenced by different light sources. Therefore, to study this phenomenon, different light sources are applied to the stem and branches in this simulation. The position vectors of the light sources are given in Table 4.

The growth of the stem is prevented by the given material parameters. In Fig. 12, the evolution of the growth response is displayed. As it can be seen, the branches bend upwards, and slightly towards the specified source of light. The behavior is reasonable, since the material parameters describing graviotropism are of a higher magnitude compared to the material parameters describing phototropism. The bending out of plane, due to phototropism, can be seen in the top view in Fig. 12. Here, the expansion factor in the primary growth direction \(\beta _{p}\) is plotted over the structure. The flux terms of the graviotropism reduce the internal energy transported to the tip of the branches. Therefore, the most growth energy is located at the bottom of the branch. Consequently, the largest values of \(\beta _{p}\) are found at the bottom of the branches. The material parameters for the stem are chosen such that no graviotropism is present. Therefore, the stem exhibits only fluxes of internal energy caused by the Fickean law and the phototropism. The upwards bending of the lower branch, connecting to the stem, causes a displacement of the stem in \({\varvec{x}}_1\)-coordinate direction. In Fig. 13, the displacements of material point (b) are given. As it can be seen, a slight upward curvature is obtained.

In Fig. 11, the location of the material point (a) is shown. In Fig. 14, the nodal displacements of the point (a) are given. As it can be seen, the displacement behavior of the node in the FE mesh is complex, due to a combination of different effects. The \({\varvec{u}}_1\)-displacement is mainly influenced by graviotropism of the branch with material parameter set 4, see Table 3. The displacement curve is increasingly upwards at first, but the movement is reduced as the simulation progresses. The \({\varvec{u}}_2\)-displacement is mainly influenced by the phototropistic growth response of the branch with material set 5. Initially, the branch elongates slightly, which causes positive displacements. The more internal energy is transported by the phototropism, the more bending towards the light source occurs. This phenomenon causes the reduced increase of the displacements, since a rotation towards the light source is induced. Finally, the curvature of the \({\varvec{u}}_3\)-displacements can be explained by considering the flux terms. The upwards movement, induced by graviotropism, causes the displacements in \({\varvec{x}}_3\)-coordinate direction. As a consequence, the graviotropism reduces the energy, which is transported to higher regions in the structure. This relation can be seen in Fig. 15. The graviotropistic transport results in a reduction of the rate of increase of displacements in \({\varvec{x}}_3\)-direction.

Fig. 10
figure 10

Convergence behavior of the time step with maximum number of iterations

Full size image
Fig. 11
figure 11

Boundary conditions and material parameter sets, material parameter set 1 denotes the branch material, while the sets 2–5 denote the branch materials

Full size image
Table 3 Material parameters of the growth simulations
Full size table

6.3 Structural generator

In this section, the combination of different biological principles in the structural generator is highlighted. Therefore, four simulations are conducted. The process parameters for the numerical examples are given in Table 8. Two simulations are carried out in which branching is allowed and two simulations are carried out in which branching is prohibited. In Table 5, the material parameters for the structural generator simulations not considering phototropism are given. The material parameters utilized in the simulation of the stem with branches and phototropism are given in Table 6. In Table 7, the parameters are given, which are utilized in the simulation without branching but considering phototropism. All simulations in this section are conducted to highlight the influence of the growth principles on the acquisition of matter. All displacements are fixed in the lowest face of the growing structure. Additionally, internal energy of is prescribed at every node in this surface. The stem material is identified as material parameter set 1 and the branches as set 2, in Tables 5, 6, and 7. A graphical depiction of the boundary conditions and material parameter sets is shown in Fig. 16. Additionally, the element reservoir containing deactivated elements is shown. All plots in this section are shown with a scaling factor of the displacements by 1.5. The branches are scaled with an additional factor of 0.8 along their primary growth direction.

Table 4 Positional vector of the light sources
Full size table
Fig. 12
figure 12

Evolution of gravio- and phototropistic growth response in perspective and top view

Full size image
Fig. 13
figure 13

Displacement in \({\varvec{x}}_1\)-direction of material point (b)

Full size image
Fig. 14
figure 14

Displacement components of the branch at point (a)

Full size image
Fig. 15
figure 15

Internal energy of the branch at point (a)

Full size image

The first simulations are compared in Fig. 17. The upper simulation presents the solution obtained while neglecting phototropism. Therefore, the growing structure distributes buds across the whole cross-section over different heights. There is no phenomenon, which directs the growth of the stem or buds. The results for the simulation considering phototropistic growth are given in the lower part of Fig. 17. If phototropism is considered, the buds are mainly directed towards the source of light. The phototropism causes an enrichment of internal energy at the side opposite to the light source. Therefore, the nodes obtaining the least amount of internal energy are located at the side facing the source of light. As a consequence, the buds point towards the light source. Additionally, internal energy is produced by the buds. However, the production is small compared to the impact of the phototropism.

In Fig. 18, results of simulations in which no branching is present are displayed. Therefore, the influence of phototropism without the influence of buds is investigated. In the upper simulation, no phototropistic growth is allowed due to the material parameters. In the lower simulation, phototropism is pronounced. As it can be seen, the bending towards the light source develops over time. A significant deflection of the primary growth direction is achieved, compared to the solely graviotropistic response.

The third example is presented, to highlight the influence of the buds on the deflection of the growth direction. The results are shown in Fig. 19. The upper simulation exhibits only phototropism, while the lower simulation also undergoes branching. As it can be seen, the behavior of the structure is significantly different. The observed response can be explained by a property of the buds. The specific energy source term h produces energy in the buds. As a consequence, the flux term, which would induce bending towards the source of light is countered. Subsequently, the growth response of the structure is nearly straight.

To summarize the comparison of the different structural generator examples, the influence of phototropism and buds is different compared to the examples in the previous sections. In the previously demonstrated examples, the influence of phototropism is present in the flux terms and in the growth deformation gradient. For the structural, generator only the parts in the flux terms are present. Nevertheless, a significant phototropistic response is obtained.

Table 5 Material parameters of the structural generator simulations without phototropism
Full size table
Table 6 Material parameters of a structural generator simulation
Full size table
Table 7 Material parameters of a structural generator simulation
Full size table
Fig. 16
figure 16

Boundary conditions, material parameter sets and element reservoir for the structural generator, material parameter set 1 denotes the stem material, while material set 2 denotes the branch material

Full size image
Table 8 Process parameters of the structural generator simulations
Full size table
Fig. 17
figure 17

Evolution in time of the structural generator example with and without phototropism, including branching

Full size image
Fig. 18
figure 18

Evolution in time of the structural generator with and without phototropism, neglecting branches

Full size image
Fig. 19
figure 19

Evolution in time of the structural generator with the effects of branches on phototropistic growth responses

Full size image

7 Conclusion and outlook

To conclude, in the contribution at hand, a first formulation for biological growing processes of plant like systems is shown within the framework of continuum mechanics. The most significant influence on the fully developed shape of the biological system is posed by tropisms. To the authors knowledge, the tropisms are not depicted in a continuum mechanical framework considering growth so far. The newly introduced formulations yield physically meaningful results. The capabilities of modeling different growth principles are demonstrated. Furthermore, plausible interactions of different principles are shown. Additionally, the influence of certain material parameters on the result of the grown structure is highlighted. The proposed formulation is thus shown to produce realistic results.

Further research needs to be conducted, for expanding the proposed formulations to different plants organs. Additionally, the interpolation of the history field can be included, enhancing the initialization of history variables in the structural generator. Furthermore, remeshing of the branches is another process worth investigating. Finally, the proposed formulations can be expanded to include the multi-physical phenomena in the biological system in more detail.