1 Introduction

The Lattice Boltzmann Method (LBM) was first established as a viable simulation method in the context of fluid mechanics–in which the LBMs’ distribution functions are most directly subject to physical interpretation, and technologically relevant transient phenomena are commonplace [2]. However, solid mechanics also features its share of such phenomena–stress wave superposition and dynamic overshoots in the displacement under dynamic loading can result in significantly higher stresses than those predicted by quasistatic calculations–with far-reaching consequences for mining and crash-proofing, for example [4]. Since analytical calculations are often impossible and efficiency is a bottleneck for numerical computation in these cases, researchers have recently begun developing LBM algorithms for the simulation of solids: Marconi et al. [5] approximated crack propagation with one such algorithm, and O’Brien et al. [6] based another on a wave equation for Poisson solids to model wave propagation. More recently, Murthy et al. [1] and Escande et al. [2] extended the solid LBM to the more general class of isotropic, linear elastic solids. In the latter work, a first-order convergence rate was observed [2]. For the static case, second-order convergent methods for the modelling of the bulk and boundary behaviour of linear elastic solids were recently proposed in [7] and [8]. Given further developments, it may become feasible to perform coupled fluid–structure simulations using the LBM as both a fluid and a solid solver.

Thus, the groundwork for LBM-based transient solid simulations has been laid, but much work remains to be done if LBM algorithms are to become viable tools for applied solid mechanics. While efficient, these algorithms are not yet sufficiently stable [2]. Additionally, only rudimentary boundary conditions–for periodic, free, and fixed boundaries–may be modelled in the dynamic case at this point [2].

This work takes aim at the latter obstacle. Prototypes for simple local bounce-back-type boundary rules which may be used to model arbitrarily valued Dirichlet and Neumann boundaries in the solid case are presented. While only first order accuracy can be obtained with these prototypes at present, they highlight a possible pathway to the consistent implementation of boundary conditions for solid simulations with the LBM. Improvements to the stability of the algorithms outlined in [1] and [2], while ultimately necessary for their viability, are beyond the scope of this work.

Before the formulation of the boundary rules are addressed, however, Sect. 2 discusses the reformulation of the underlying solid mechanical equations required by the LBM. The Lamé-Navier equation is restated as a moment chain and boundary conditions are adjusted consistently with this formulation. Section 3 outlines the Lattice Boltzmann Method for solids briefly, and Sect. 4 presents the novel boundary rules. In Sect. 5, we perform an empirical convergence study for a simple example problem, and evaluate the performance of the LBM algorithm and the boundary rules on one analytical and one numerical benchmark problem in Sect. 6. Consistency studies for the LBM algorithm by Murthy et al. [1] and the boundary rules presented here are included in the appendix. While the modified boundary rules are easily generalised to the three-dimensional case, for ease of visualisation and validation we limit the discussion to two-dimensional (plane strain) problems here.

2 A moment chain formulation for linear elastodynamics

For sufficiently small displacements and displacement derivatives (see e.g. [9, p.3]), the Lamé-Navier equation

$$\begin{aligned} \rho _0 d_t^2 u_\alpha = (\lambda + \mu ) d_\alpha d_\beta u_\beta + \mu d_\beta d_\beta u_\alpha + \rho _0 b_\alpha \end{aligned}$$
(1)

approximates the temporal and spatial evolution of the displacement \(\varvec{u}\) in isotropic, elastic continua [10, p.39]. Here, \(\rho _0\) denotes the (reference) density, \(\lambda \) and \(\mu \) are the Lamé parameters, and \(\varvec{b}\) is a bulk force per unit mass. The d symbols indicate the material time derivative (\(d_t (\cdot ) = d (\cdot )/d t\)) and the spatial derivative in the reference configuration (\(d_\alpha (\cdot ) = d (\cdot )/d x_\alpha \)), respectively. Furthermore, Einstein summation convention is used. Note that, in contrast to [1], we choose a presentation in the reference configuration–as is common in solid mechanics–which simplifies derivations in the following. Of course, the current and reference configurations coincide in the small strain limit, but it proves convenient to approach this limit from the reference configuration here. Furthermore, elasticity implies reversibility, which has implications for solid modelling via the LBM. These are discussed in Sect. 3.

For a solution to be determined on a domain \(\Omega _0\) with boundary \(\partial \Omega _0\), initial conditions as well as boundary conditions (BCs) for the displacement (Dirichlet boundary conditions)

$$\begin{aligned} u_\alpha (\varvec{x},t) = u_\alpha ^*(\varvec{x},t), \, \varvec{x} \in \partial \Omega _{0,u}\,, \end{aligned}$$
(2)

with displacement boundary values \(\varvec{u^*}\) and/or for the surface traction (Neumann boundary conditions)

$$\begin{aligned} \sigma _{\alpha \beta }(\varvec{x},t) n_\beta = t_\alpha ^*(\varvec{x},t), \, \varvec{x} \in \partial \Omega _{0,t}\,, \end{aligned}$$
(3)

with traction boundary values \(\varvec{t^*}\) and surface normal \(\varvec{n}\) on regions \(\partial \Omega _{0,u}\) and \(\partial \Omega _{0,t}\), respectively, must further be defined, where \({\partial \Omega _{0,u} \cup \partial \Omega _{0,t} = \partial \Omega }\) [11, p.7].

While boundary conditions are easily specified, accounting for them in a simulation method is often non-trivial, and the LBM makes no exception [12, p.155]. Moreover, because boundary conditions are central to engineering problems–much of the information relevant to an engineering design process is contained in boundary conditions–their importance is hard to overstate.

Note that, where explicit reference is made to the space- and time dependence of variables, it will be assumed to be of the form \((\varvec{x},t)\). For the sake of conciseness, this reference is omitted unless necessary.

2.1 A moment chain of conservation laws

As shown by [1] and as demonstrated below, the Lamé-Navier equation can be restated as a moment chain. This allows us to use the LBM–which acts as a solver for moment chains, as detailed in appendix A–to model small-strain elastodynamics. Here, in contrast to [1], a presentation in the reference configuration is chosen

$$\begin{aligned}&d_t \rho + d_\alpha j_\alpha = 0\,, \nonumber \\&d_t j_\alpha + d_\beta P_{\alpha \beta } = \rho _0 b_\alpha + \frac{\mu -\lambda }{\rho _0} d_\alpha \rho \,, \nonumber \\&d_t P_{\alpha \beta } + d_\gamma \Big ( \frac{\mu }{\rho _0} ( j_\alpha \delta _{\beta \gamma } + j_\beta \delta _{\alpha \gamma } + j_\gamma \delta _{\beta \alpha } ) \Big ) = 0 \,. \end{aligned}$$
(4)

In the above, \(\rho \) is a linearised approximation of the density in the current configuration, \(\varvec{j}\) is the linear momentum density, and \(\varvec{P}\) a stress tensor (though not the established Cauchy stress). These variables are outlined in more detail below, in equations (5) to (8). In keeping with the formulation in the reference configuration, the spatial derivatives \(d_\alpha \) are taken with respect to the reference configuration, and the time derivatives \(d_t\) denote material derivatives. However, \(\rho \) is a linearised approximation of the density in the current configuration, defined (in terms of quantities in the reference configuration) as

$$\begin{aligned} \rho = \rho _0 (1- d_\alpha u_\alpha )\,. \end{aligned}$$
(5)

Meanwhile, \(\varvec{j}\) is the linear momentum density in the reference configuration,

$$\begin{aligned} j_\alpha = \rho _0 v_\alpha = \rho _0 d_t u_\alpha \,. \end{aligned}$$
(6)

As is readily verified by differentiation, the definition of these first two moments is consistent with the first equation of the moment chain,

$$\begin{aligned} d_\alpha j_\alpha&= d_\alpha ( \rho _0 v_\alpha ) = d_\alpha ( \rho _0 d_t u_\alpha ) \\&= d_t d_\alpha (\rho _0 u_\alpha ) = d_t (\rho _0 d_\alpha u_\alpha ) = - d_t \rho \,, \end{aligned}$$

which models mass conservation. \(\varvec{P}\), meanwhile, denotes a stress tensor which is generally not equivalent to the established Cauchy stress \(\varvec{\sigma }\). Via the third equation in (4),

$$\begin{aligned} -d_t P_{\alpha \beta } = d_\gamma \Big ( \frac{\mu }{\rho _0} ( j_\alpha \delta _{\beta \gamma } + j_\beta \delta _{\alpha \gamma } + j_\gamma \delta _{\beta \alpha } ) \Big )\,, \end{aligned}$$

the stress tensors are related by

$$\begin{aligned} -d_t P_{\alpha \beta }&= d_t \Big ( \mu ( d_\beta u_\alpha + d_\alpha u_\beta + d_\gamma u_\gamma \delta _{\beta \alpha } ) \Big ) \nonumber \\&= d_t \Big ( \lambda d_\gamma u_\gamma \delta _{\alpha \beta } + \mu ( d_\beta u_\alpha + d_\alpha u_\beta ) \nonumber \\&\quad \quad - (\lambda -\mu ) d_\gamma u_\gamma \delta _{\alpha \beta } \Big )\nonumber \\&= d_t \Big ( \sigma _{\alpha \beta } - (\lambda -\mu ) d_\gamma u_\gamma \delta _{\alpha \beta } \Big )\,, \end{aligned}$$
(7)

and, assuming an adequate initialisation with \(P_{\alpha \beta }(\varvec{x},0) = - \sigma _{\alpha \beta }(\varvec{x},0) + ( \lambda - \mu ) d_\gamma u_\gamma (\varvec{x},0) \delta _{\alpha \beta }\),

$$\begin{aligned} P_{\alpha \beta }&= - \mu ( d_\beta u_\alpha + d_\alpha u_\beta + d_\gamma u_\gamma \delta _{\beta \alpha } )\nonumber \\&= - \sigma _{\alpha \beta } + ( \lambda - \mu ) d_\gamma u_\gamma \delta _{\alpha \beta }\,, \end{aligned}$$
(8)

i.e. the stress tensor \(\varvec{P}\) is equivalent to a negated Cauchy stress tensor \(\varvec{\sigma }\), with an additional displacement derivative term with coefficient \(\lambda -\mu \). The latter disappears for Poisson solids with \(\mu =\lambda \) and Poisson’s ratio \(\nu =1/4\), which is why \(\varvec{P}\) is termed the Poisson stress tensor in the following.

With (5), the gradient of \(\rho \) can be written as

$$\begin{aligned} d_\alpha \rho = d_\alpha ( \rho _0 (1- d_\beta u_\beta ) ) = - \rho _0 d_\alpha d_\beta u_\beta \,. \end{aligned}$$
(9)

Note that \(\rho \), as defined in (5), can be viewed as a scalar variable encoding information about dilatational strains. This allows information about these dilatational strains to be introduced into the linear momentum balance in (4) via the gradient of \(\rho \), without the displacement \(\varvec{u}\) being required.

Finally, substitution of (6), (8), and (9) into the second equation of the moment chain (4)–which accounts for the linear momentum balance

$$\begin{aligned}&d_t j_\alpha + d_\beta P_{\alpha \beta } = \rho _0 b_\alpha + \frac{\mu -\lambda }{\rho _0} d_\alpha \rho \,, \\&\quad \Leftrightarrow d_t ( \rho _0 d_t u_\alpha ) - \mu d_\beta ( d_\beta u_\alpha + d_\alpha u_\beta + d_\gamma u_\gamma \delta _{\beta \alpha } ) \\&\quad \quad = \rho _0 b_\alpha + \frac{\mu -\lambda }{\rho _0} (- \rho _0 d_\alpha d_\beta u_\beta )\,,\\&\quad \Leftrightarrow \rho _0 d_t^2 u_\alpha - \mu ( d_\beta d_\beta u_\alpha + d_\alpha d_\beta u_\beta + d_\alpha d_\gamma u_\gamma ) \\&\quad \quad = \rho _0 b_\alpha - (\mu -\lambda ) d_\alpha d_\beta u_\beta \,, \\&\quad \Leftrightarrow \rho _0 d_t^2 u_\alpha = (\lambda + \mu ) d_\alpha d_\beta u_\beta + \mu d_\beta d_\beta u_\alpha + \rho _0 b_\alpha \,, \end{aligned}$$

yields the Lamé-Navier equation

$$\begin{aligned} \rho _0 d_t^2 u_\alpha = (\lambda + \mu ) d_\alpha d_\beta u_\beta + \mu d_\beta d_\beta u_\alpha + \rho _0 b_\alpha \,. \end{aligned}$$

The presentation in the reference configuration simplifies the derivations (and the analysis in the following) somewhat: in contrast to the calculations in [1], there are no convective terms which need to be eliminated with small-strain assumptions. Smallness assumptions are only required in the formulation of the material law, which neglects material and geometric nonlinearities at the outset.

The first equation of the moment chain (4) is a mass conservation equation which accounts for the evolution of the linearised density in the current configuration, \(\rho \). As discussed in the context of (9), \(\rho \) is used to embed information about dilatational strains without reference to the displacements. The second equation accounts for the linear momentum balance, with the contribution due to the Cauchy stress \(\varvec{\sigma }\) partially modeled via the Poisson stress \(\varvec{P}\) and partially via the gradient of \(\rho \). \(\rho \) introduces information about the non-Poisson contribution to the dilatational strain into the linear momentum balance. The final equation determines the evolution of the Poisson stress tensor \(\varvec{P}\). Together, these equations were shown to be equivalent to the Lamé-Navier equation, which is commonly used to model the dynamic behaviour of isotropic solids subject to small strains. As the LBM acts as a solver for moment chains like (4), it may be used to tackle isotropic, small-displacement elastodynamics.

The introduction of the Poisson tensor \(\varvec{P}\) as in [1] is necessary as the LBM can not account for the Cauchy stress \(\varvec{\sigma }\) easily: the reasons for this are discussed in Sect. 3.

2.2 Reformulating the boundary conditions

In accordance with the reformulation of the Lamé-Navier equation as a moment chain in \(\rho \), \(\varvec{j}\), and \(\varvec{P}\), boundary conditions (BCs) must of course also be rephrased in terms of these variables. For Dirichlet boundary conditions, this is comparatively straightforward: with the definition of the linear momentum density \(\varvec{j}=\rho _0 d_t \varvec{u}\), boundary values in the linear momentum density \(\varvec{j^*}\) can be obtained from boundary values in the displacement

$$\begin{aligned} j_\alpha (\varvec{x},t) = j_\alpha ^*(\varvec{x},t) = \rho _0 d_t u_\alpha ^*(\varvec{x},t), \quad \varvec{x} \in \partial \Omega _{0,u}\,. \end{aligned}$$
(10)

With (8), boundary values in the Poisson stress tensor \(P^*\) could be computed from boundary values in the Cauchy stress tensor \(\varvec{\sigma }^*\) and from values of the divergence of the displacement at the boundary, via

$$\begin{aligned}&P_{\alpha \beta }(\varvec{x},t) = P_{\alpha \beta }^*(\varvec{x},t)\\&\quad = - \sigma _{\alpha \beta }^*(\varvec{x},t) + ( \lambda - \mu ) d_\gamma u_\gamma (\varvec{x},t) \delta _{\alpha \beta }\,, \quad \varvec{x} \in \partial \Omega _{0,t}\,. \end{aligned}$$

However, Neumann boundary conditions enforce boundary values in the Cauchy stress vector \(\varvec{t}^* =\varvec{\sigma }^*\varvec{n}\) rather than the Cauchy stress tensor \(\varvec{\sigma }^*\) directly. Furthermore, the displacement \(\varvec{u}\) does not appear in the moment chain (4), and is thus not directly available in the LBM algorithm.

The latter of these issues could be circumvented by integrating the linear momentum density \(\varvec{j}=\rho _0 d_t \varvec{u}\) to obtain the displacement \(\varvec{u}\). However, the linearised density \(\rho \) embeds information about the displacement divergence via (5), which can be exploited

$$\begin{aligned} d_\alpha u_\alpha = \frac{\rho _0-\rho }{\rho _0}\,, \end{aligned}$$
(11)

to compute \(d_\alpha u_\alpha \) more efficiently.

Meanwhile, Neumann boundary conditions can be transformed into a coordinate system normal to the boundary with a rotation matrix \(\varvec{T}\)

$$\begin{aligned} t_\alpha ^{*n}(\varvec{x},t) = T_{\beta \alpha } t_\beta ^*(\varvec{x},t) \quad x \in \partial \Omega _{0,t} \,. \end{aligned}$$

The entries of the orthonormal transformation tensor \(\varvec{T}\) are simply given by the normal and tangential vectors \(\varvec{e}^n\) and \(\varvec{e}^t\) of the boundary, i.e. \(T_{1\alpha } = e_\alpha ^n\) and \(T_{2\alpha }=e_\alpha ^t\) for the two-dimensional case [13, p.28].

For the two-dimensional case, (3) becomes, in this normal coordinate system

$$\begin{aligned} \begin{pmatrix} \sigma _{nn}^n &{} \sigma _{nt}^n \\ \sigma _{nt}^n &{} \sigma _{tt}^n \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} t_n^{*n} \\ t_t^{*n} \end{pmatrix}\,. \end{aligned}$$

As is apparent, the first column of the Cauchy stress tensor \(\varvec{\sigma }^n\) is fully determined by the Cauchy stress vector that is prescribed via the boundary condition, i.e.

$$\begin{aligned} \sigma _{nn}^n&= t_n^{*n}:=\sigma _{nn}^{*n}\,, \\ \sigma _{nt}^n&= t_t^{*n}:=\sigma _{nt}^{*n}\,, \end{aligned}$$

meaning that, with the symmetry of the Cauchy tensor, the Neumann boundary condition determines all entries of \(\varvec{\sigma }^n\) save for \(\sigma _{tt}^n\). This remaining entry should remain unaffected by the Neumann boundary condition. In the boundary rules suggested in Sect. 4, we extrapolate from (known) values of \(\sigma _{tt}^n(\varvec{x},t), \varvec{x} \in \Omega _0 {\setminus } \partial \Omega _0\) within the material domain to the boundary to obtain an approximation of \(\sigma _{tt}^n(\varvec{x},t), \varvec{x} \in \partial \Omega _{0,t}\)–see (23) for details. Thus, we obtain boundary values for the Cauchy stress \(\varvec{\sigma }^{*n}\) in the normal coordinate system. A subsequent inverse transformation yields boundary values for \(\varvec{\sigma }^*\) in the original (global) coordinate system,

$$\begin{aligned} \sigma _{\alpha \beta }^*(\varvec{x},t) = T_{\alpha \gamma } \sigma _{\gamma \zeta }^{*n}(\varvec{x},t) T_{\beta \zeta }\quad x \in \partial \Omega _{0,t}\,. \end{aligned}$$
(12)

Using (8), we finally obtain the desired boundary values for the Poisson stress tensor \(\varvec{P}\)

$$\begin{aligned}&P_{\alpha \beta }(\varvec{x},t) = P_{\alpha \beta }^*(\varvec{x},t) \nonumber \\&\quad = - \sigma _{\alpha \beta }^*(\varvec{x},t) + ( \lambda - \mu ) d_\gamma u_\gamma (\varvec{x},t) \delta _{\alpha \beta }\,, \quad \varvec{x} \in \partial \Omega _{0,t}\,. \end{aligned}$$
(13)

where \(\varvec{\sigma }^*\) is determined via (12) and the displacement divergence may be obtained from (11). With (10) and (13), Dirichlet and Neumann boundary conditions for elastodynamic problems described by the Lamé-Navier equation can now be stated consistently with the moment chain form in (4). This completes the reformulation required to make elastodynamic problems amenable to solutions with the LBM.

3 The solid LBM in a nutshell

For the sake of compactness, only a brief overview of the LBMs key features will be given here. An in-depth discussion can be found in [12]. In keeping with [14], we treat the Lattice Boltzmann algorithm as a numerical solver for PDEs described by moment chains, independently from any associations with kinetic theory.Footnote 1

The algorithm operates on a lattice L consisting of regularly spaced lattice sites \(\varvec{x} \in L \subset \Omega \) (the dark grey points in Fig. 1) which are in turn connected by lattice links (the light grey lines in the same diagram) [12, p.94]. Furthermore, several lattice velocity vectors \(\varvec{c}_i, i \in 0, \ldots ,q-1\) (indicated by the blue arrows in Fig. 1) cover the distance between any lattice site \(\varvec{x}\) and its neighbours \(\varvec{x}+\varvec{c}_i \Delta t\) along a lattice link i in one time step \(\Delta t\) [12, p.94]. The simplicity of this spatial discretisation makes for easy pre- and post-processing.

Generally, LBM discretisations are classed by the dimension d and the number of lattice velocities q, as DdQq lattices. For ease of visualisation and validation, we only consider D2Q9 lattices - exemplified in Fig. 1 - here. Note that among the \(q=9\) lattice velocities, there is a zero velocity \(\varvec{c}_0=\varvec{0}\).

Fig. 1
figure 1

(Part of) a D2Q9 lattice for the LBM

Full size image

The LBM encapsulates information about the tensors to be modelled (the linearised density in the current configuration \(\rho \), the linear momentum density \(\varvec{j}\), and the Poisson stress \(\varvec{P}\) in our case) in distribution functions. On each site of the lattice, a distribution function vector with one entry \(\bar{f}_i\) per lattice velocity \(\varvec{c}_i\) is introduced [12, p.63]. Here and in the following, we utilise distribution functions resulting from the second-order accurate discretisation by He et al. [15], which is denoted by the overbar \(\bar{\cdot }\).

In each iteration, the distribution functions \(\bar{f}_i\) at each lattice site are locally relaxed toward the value of the equilibrium distribution function \(f_i^{\text {eq}}\) [12, p.64], and a contribution due to a source term is added [12, p.239]. The choice of equilibrium distribution function determines the PDE modelled by the LBM algorithm - as shown in appendix A, the equilibrium distribution function by Murthy et al. [1]

$$\begin{aligned} f_i^{\text {eq}}{} & {} = w_i \Big (\rho + \frac{1}{c_s^2} c_{i \alpha } j_\alpha \nonumber \\{} & {} \quad + \frac{1}{2c_s^4} ( P_{\alpha \beta } - \rho c_s^2 \delta _{\alpha \beta } ) ( c_{i \alpha } c_{i \beta } - c_s^2 \delta _{\alpha \beta } ) \Big ) \end{aligned}$$
(14)

may be used to recover the Lamé-Navier equation. Here, \(c_s=\sqrt{\mu /\rho _0}\) denotes the speed of shear waves, and \(w_i\) is a lattice weight associated with lattice link i [2].

In the solid LBM algorithm by Murthy et al. [1] and Escande et al. [2], a BGK collision operator with relaxation time \(\bar{\tau }\) is utilised. Together with the contribution due to the source term \(\psi _i\), this results in the following expression for the post-collision (i.e., post-relaxation) distribution functions [12, p.239]

$$\begin{aligned} \bar{f}_i^{\text {col}} = \bar{f}_i - \frac{\Delta t}{\bar{\tau }}( \bar{f}_i - f_i^{\text {eq}} ) + \Delta t \Big (1 - \frac{\Delta t}{2 \bar{\tau }} \Big ) \psi _i\,. \end{aligned}$$
(15)

The locality of this collision step makes parallelisation relatively easy [12, p.579], contributing to the efficiency which makes the LBM attractive as a PDE solver.

The source term

$$\begin{aligned} \psi _i = \frac{1}{c_s^2} w_i c_{i\alpha } S_\alpha ^{\text {FD}}\,, \end{aligned}$$
(16)

meanwhile, is used to model bulk forces, where

$$\begin{aligned} S_\alpha ^{\text {FD}} = \rho _0 b_\alpha + \frac{\mu -\lambda }{\rho _0} d^{\text {FD}}_\alpha \rho \,, \end{aligned}$$
(17)

accounts both for the volumetric loads \(\varvec{b}\) and the part of the material law not contained in the Poisson stress tensor [2] - recall the moment chain (4). The finite difference stencil used to evaluate the gradient of \(\rho \)–denoted by \(d^{\text {FD}}_\alpha \rho \) above–must at least be second-order accurate for the LB algorithm to be second-order consistent with the target moment chain in the bulk, as demonstrated in appendix A. The source term is crucial for P-wave modelling in non-Poisson solids: the Lamé constant \(\lambda \) does not appear in the equilibrium distribution function by Murthy et al. [1]; the source term ensures that the correct dilatational wave speed \(c_d=\sqrt{(\lambda + 2 \mu )/\rho _0}\) is recovered.

The post-collision distribution functions are subsequently propagated to neighbouring lattice sites along the associated lattice velocities \(\varvec{c}_i\) in the streaming step [12, p.66]

$$\begin{aligned} \bar{f}_i(\varvec{x}+\varvec{c}_i \Delta t,t+\Delta t) = \bar{f}_i^{\text {col}}\,. \end{aligned}$$
(18)

Together, the collision and streaming steps define the Lattice Boltzmann equation

$$\begin{aligned}&\bar{f}_i(\varvec{x}+\varvec{c}_i \Delta t,t+\Delta t) = \nonumber \\&\quad \bar{f}_i - \frac{\Delta t}{\bar{\tau }}( \bar{f}_i - f_i^{\text {eq}} ) + \Delta t \Big (1 - \frac{\Delta t}{2 \bar{\tau }} \Big ) \psi _i\,, \end{aligned}$$
(19)

which describes the evolution of the distribution functions on the lattice [12, p.239]. From the distribution functions, the desired tensors may finally be post-processed as moments

$$\begin{aligned} \rho&=\sum _i \bar{f}_i\,, \nonumber \\ j_\alpha&= \sum _i \bar{f}_i c_{i \alpha } + \frac{1}{2} \Delta t S_\alpha ^{\text {FD}}\,, \nonumber \\ P_{\alpha \beta }&= \sum _i \bar{f}_i c_{i \alpha } c_{i \beta }\,. \end{aligned}$$
(20)

Appendix A uses the method suggested by Farag et al. [14] to demonstrate that the resulting algorithm is consistent with the target equations (4) up to the second order. Note that, to obtain second-order consistency, the bulk force term \(\varvec{S}^{\text {FD}}\) in (20) must be evaluated at time \(t+\Delta t\) for an iteration starting at time t. Despite \(\rho \) influencing \(\varvec{S}^{\text {FD}}\) via (17), this is unproblematic. \(\rho (\varvec{x},t+\Delta t)\) may be computed via the first equation in (4), and subsequently used to compute \(\varvec{S}^{\text {FD}}(\varvec{x},t+\Delta t)\) for use in the second moment.

In contrast to the fluid LBM (see e.g. [14]), the solid LBM algorithm outlined above models the stress tensor \(\varvec{\sigma }\) (see equation (8)) entirely via the equilibrium moments. This is because the momentum transfer described by the Cauchy stress \(\varvec{\sigma }\) is non-dissipative and reversible in elastic solids, in contrast to the Navier–Stokes fluid case, where viscous terms play a role [12, p.6].

On account of this reversibility, the non-dissipative, non-viscous limit \(\bar{\tau }\rightarrow \Delta t/2_+\) (from above) of the LBM (see e.g. [12, p.65,101]) is of interest for linear elastic solid modelling. As simulations with \(\bar{\tau } = \Delta t/2\) (and no damping) are unstable, \(\bar{\tau }=0.55\Delta t\) is chosen in keeping with [2]. In contrast to the fluid case, \(\bar{\tau }\) is treated as a numerical parameter and does not determine the evolution of the stress tensor.

The introduction of the Poisson tensor \(\varvec{P}\) as in [1] is necessary as the LBM can not account for the Cauchy stress \(\varvec{\sigma }\) directly without significant structural changes: the terms of the third-order moment \(\varvec{Q}\) (which determines the evolution of the second moment) that are affected by the isotropy defect in a D2Q9 lattice are inconsistent with an evolution equation for the Cauchy stress, i.e.

$$\begin{aligned} Q_{A A A}= & {} \sum _i c_{iA} c_{iA} c_{iA} f_i^{\text {eq}} = \sum _i \Big (\frac{\Delta x}{\Delta t}\Big )^2 c_{iA} f_i^{\text {eq}}\nonumber \\= & {} 3 c_s^2 \bar{j}_A = 3\frac{\mu }{\rho _0} j_A \ne \frac{\lambda +2\mu }{\rho _0} j_A \,, \end{aligned}$$

where summation over the latin index A is not implied. However, \(Q_{AAA}=j_A (\lambda +2\mu )/\rho _0\) must hold for \(d_t \sigma _{\alpha \beta } - d_\gamma Q_{\alpha \beta \gamma }=0\) to hold for all \(\alpha \) and \(\beta \). Therefore, \(\varvec{\sigma }\) can not be modelled directly as a moment, unless modifications are made to the equilibrium distribution function and the wave speed \(c_s\).

Note that the displacement \(\varvec{u}\) is not required at any point in the LBM algorithm outlined above (it is also not required at any stage in the boundary rules discussed below). If displacements are required for postprocessing, they may be computed from the linear momentum density \(\varvec{j}\) by numerical integration, e.g.

$$\begin{aligned}{} & {} u_\alpha (\varvec{x},t+\Delta t) = \nonumber \\{} & {} \quad u_\alpha (\varvec{x},t) + \frac{1}{\rho _0} j_\alpha (\varvec{x},t+\Delta t)\Delta t + \mathcal {O}(\Delta t^2)\,. \end{aligned}$$

Of course, higher-order integration is also possible.

The operations constituting the LB algorithm–the local relaxation in the collision step (15), the simple memory swap in the streaming step (18), and the local array operations in the moment computation (20) can be evaluated very efficiently, which makes the LBM attractive from a computational point of view.

4 Local boundary rules for the solid LBM

While the LBE accounts for the evolution of the distribution functions in the interior of the lattice, the collision and streaming steps leave some distribution functions in the vicinity of the boundary \(\partial \Omega _0 \subset \Omega _0\) undefined. As illustrated in Fig. 2, these need to be ‘streamed’ from across the boundary to each boundary lattice site \(\varvec{x} \in \partial L\), i.e. each lattice site with lattice links crossing the boundary [12, p.165]. For convenience, let the set of boundary lattice sites \(\partial L \subset L\) be divided into \(\partial L_u\) and \(\partial L_t\) depending on whether the nearby boundary is subject to Dirichlet or Neumann boundary values, respectively.Footnote 2

Fig. 2
figure 2

Lattice-conforming boundary (dotted line) with lattice velocities leading out of the domain (blue) and lattice velocities for which distribution functions are missing (red) for a boundary lattice site at \(\varvec{x}\)

Full size image

Specifying the missing distribution functions in accordance with the boundary conditions of the underlying PDE is a non-trivial task: while boundary conditions are formulated in terms of the tensors appearing in the moment chain (\(\rho \), \(\varvec{j}\), \(\varvec{P}\)), a boundary rule specification with respect to \(\bar{f}_i\) is sought [12, p.155]. Furthermore, the number of unknown distribution functions \(\bar{f}_i\) at some \(\varvec{x} \in \partial L\) is sometimes higher than the number of boundary condition equations available to specify them, leaving boundary rules for the LBM under-determined. An example in the D2Q9 case are Dirichlet boundary conditions (10) at a straight boundary as in Fig. 2, with three unknown distribution functions but two entries of \(\varvec{j}^*\) determined as boundary values. Conversely, boundary rules might also be over-determined, as in the case of a concave boundary with, for example, only one missing distribution function.

As a first step, Escande et al. [2] appropriated the popular bounce-back [12, p.175] and anti-bounce-back [12, p.200] rules from the fluid case, to model lattice-conforming fixed and free boundaries respectively. In the scope of this work, these rules are extended, to approximate the behaviour in the vicinity of boundaries with arbitrary Dirichlet and Neumann boundary conditions.

The modified bounce-back rule

$$\begin{aligned} \bar{f}_{\bar{i}}(\varvec{x},t+\Delta t) = \bar{f}_i^{\text {col}} - \frac{2}{c_s^2} w_i c_{i \alpha } j_\alpha ^{*}\,, \end{aligned}$$
(21)

first reverses the direction of motion for the post-collision distribution functions \(\bar{f}_i^{\text {col}}(\varvec{x},t)\) which would be streamed out of the bulk: the missing distribution functions \(\bar{f}_{\bar{i}}(\varvec{x},t+\Delta t)\) for directions \(\bar{i}\) are set to the values of the post-collision distribution functions \(\bar{f}_i^{\text {col}}(\varvec{x},t)\) associated with the opposite direction i. Then, a term depending on the linear momentum density boundary values \(\varvec{j}^*\) is subtracted, and the distribution functions are sent back into the interior of the lattice, in direction \(\bar{i}\). The distribution function \(\bar{f}_{\bar{5}}(\varvec{x},t+\Delta t)= \bar{f}_7(\varvec{x},t+\Delta t)\) in Fig. 2, for example, is set to the value of the post-collision distribution function \(\bar{f}_5^{\text {col}}(\varvec{x},t)\), minus the boundary value term \(\frac{2}{c_s^2}w_5c_{5\alpha } j_\alpha ^*\).

The required boundary values in the linear momentum density \(\varvec{j}^*\) can be obtained from Dirichlet boundary values in the displacement \(\varvec{u}^*\) via (10). As these are typically known a priori, the necessary differentiation can be performed analytically.

In appendices B and C, the simple bounce-back rule suggested by Escande et al. [2] and extended here is shown to replicate the target behaviour at the boundary (10) with first-order accuracy.

The modified anti-bounce-back boundary rule - used here to model Neumann boundaries - operates similarly. The sign of the post-collision distribution function \(\bar{f}_i^{\text {col}}(\varvec{x},t)\) at \(\varvec{x} \in \partial L_t\) is first inverted and a contribution depending on the linearised density \(\rho ^*\) in the current configuration and the Poisson stress \(\varvec{P}^{*}\) at the boundary is added, before the distribution functions are sent back into the direction whence they came

$$\begin{aligned}&\bar{f}_{\bar{i}}(\varvec{x},t+\Delta t) = -\bar{f}_i^{\text {col}} + 2 w_i \Big ( \rho ^*\nonumber \\&\qquad \qquad + \frac{1}{2 c_s^4}( P_{\alpha \beta }^{*} - \rho ^* c_s^2 \delta _{\alpha \beta } ) ( c_{i \alpha }c_{i \beta } - c_s^2 \delta _{\alpha \beta } ) \Big )\,. \end{aligned}$$
(22)

While Escande et al. [2] extrapolate \(\rho \) and \(\varvec{P}\) normal to the boundary, we use (13) to determine boundary values in the Poisson stress tensor \(\varvec{P}^*\) from Neumann boundary conditions on the Cauchy traction vector \(\varvec{t}^*\). The entry of the Cauchy stress at the boundary \(\sigma _{tt}^{*n}\) which is left undetermined by the boundary conditions in a normal coordinate system, is extrapolated along the current lattice link i to \(\varvec{x}^{\text {bd}}=\varvec{x}+\frac{1}{2}\varvec{c}_i\Delta t\),

$$\begin{aligned}&\sigma _{tt}^{*n} = \sigma _{tt}^{n}(\varvec{x}^{\text {bd}},t) \nonumber \\&\qquad = \frac{1}{2} \Big ( 3 \sigma _{tt}^{n}(\varvec{x},t) - \sigma _{tt}^{n}(\varvec{x}-\varvec{c}_i \Delta t,t) \Big ) + \mathcal {O}(\Delta t^2) \,. \end{aligned}$$
(23)

Similarly, the linearised density in the current configuration at the boundary, \(\rho ^*\)–for which there are no boundary values–is similarly extrapolated to the boundary along the current lattice link i

$$\begin{aligned}&\rho ^* = \rho (\varvec{x}^{\text {bd}},t) \\&\qquad = \frac{1}{2} \Big ( 3 \rho (\varvec{x},t) - \rho (\varvec{x}-\varvec{c}_i \Delta t,t) \Big ) + \mathcal {O}(\Delta t^2)\,. \end{aligned}$$

Figure 2 indicates, using \(i=1\) as an example, how the location of the boundary lattice site \(\varvec{x}\), neighbouring lattice site \(\varvec{x}-\varvec{c}_i \Delta t\), and boundary site \(\varvec{x}^{\text {bd}}=\varvec{x}+\frac{1}{2}\varvec{c}_i \Delta t\) are defined in the lattice-conforming case.

The consistency study in appendices B and C indicates that the modified anti-bounce-back boundary rule (22) reproduces the desired boundary values in the Poisson stress \(\varvec{P}^*\), and thus, by (12) and (13), the desired Cauchy traction \(\varvec{t}^*\) with first-order accuracy.

5 Empirical convergence study

As demonstrated in appendix A, the LBM by Murthy et al. [1] should act as a second-order solver for solid-mechanical problems written in the moment chain form discussed in Sect. 2. The analysis in appendix C, meanwhile, suggests that the simple boundary rules suggested in Sect. 4 should enforce Dirichlet and Neumann boundary values with first-order accuracy, respectively.

In this section, an empirical mesh refinement study is performed to investigate the convergence rate of the LBM algorithm outlined above on a simple example problem.

To this end, we consider the material domain and load case illustrated in Fig. 3: the rectangular region with side length l is subjected to a plane strain state, the upper and lower boundaries being loaded with a traction of \(t^*\) in their respective normal directions. Note that the variables used here are non-dimensionalised, with \(u_{\text {ref}}=10^{-3}l\) (arbitrary units). The traction is increased linearly from \(t^*=0.0 \mu u_{\text {ref}}/l\) at time \(t=0.0l/c_s\) to \(t^*\approx 4.385 \mu u_{\text {ref}}/l\) at \(t=1.155l/c_s\), and subsequently held at this level until the end of the simulation at \(t=2.281l/c_s\). The left and right sides of the domain are stress-free, i.e. subject to homogeneous Neumann boundary conditions. The material to be simulated is characterised by \(c_d^2/c_s^2\approx 2.769\) and \(\nu \approx 0.2174\), which is typical for certain types of concretes and glasses [16].

Fig. 3
figure 3

Square domain subjected to an in-plane tension load

Full size image

Lattice Boltzmann simulations are run for a range of lattice spacings \(\Delta x \in [0.003125,0.05]l\), i.e. \(\Delta x \in [1/320,1/20]l\). In each case, the time step is determined to satisfy the lattice isotropy conditions via [12, p.64]

$$\begin{aligned} \frac{1}{\sqrt{3}} \frac{\Delta x}{\Delta t} = c_s\,. \end{aligned}$$

A relaxation time of \(\bar{\tau }=0.55\Delta t\) is chosen, as in [2]. In the absence of analytical solutions, the convergence study is performed relative to a solution of a high-fidelity FEM simulation for the resulting displacement fields. The FE analyses were run using the FEAP FE program (see e.g. [17]). For the FEM simulations, we use bilinear shape functions, a regular mesh consisting of quadratic elements, an element edge length of \(\Delta x^{\text {FEM}}\approx 0.001563l\), and an explicit central difference integrator with time step \(\Delta t^{\text {FEM}}\approx 3.956 \times 10^{-4} l/c_s\). Convergence rates for elastodynamic FEM simulation can be quite low–examples with linear or superlinear convergence, even for geometrically simple problems, can be found, see e.g. [18]. However, fourth-order convergence has been observed for the FEM in similar well-behaved, regularly discretised elastodynamic problems [18]. Furthermore, the FE solution does not change appreciably, relative to the error between LBM and FEM solutions, upon further refinement. We therefore assume that the displacement field computed by the FEM with this discretisation is sufficiently indistinct from the exact solution for use in the convergence study.

Fig. 4
figure 4

\(x_2\)-components of dimensionless displacements at the top right corner post-processed from LBM (shades of gray) and FE (red) simulations of the square plane strain domain used for the convergence study. Simulations with 320, 160, 80, 40, and 20 lattice sites along an edge were used for the LBM, while the higher-fidelity FEM reference simulation is shown for comparison. The time values for which convergence studies were performed are shown as dashed lines

Full size image

Figure 4 illustrates the tensile response of the plane strain domain as predicted by the FEM and the LBM: the \(x_2\)-displacement values at the top right corner (\(x_1=x_2=0.5 l\)) are postprocessed from simulation runs with the LBM at different discretisations, as well as from the higher-fidelity reference FEM solution.

In both simulations, the displacement first increases gradually, then peaks (with the LBM yielding a slightly higher peak value), and then oscillates around the static solution. As dissipation is not considered in linear elastic theory, the oscillation would continue indefinitely if there were no artificial numerical damping. This behaviour is apparent in the first three dynamic overshoots in the displacement until \(t\approx 4 l/c_s\). Both simulations are initially in acceptable agreement, with a disparity that decreases as the lattice used for the LB simulation runs is refined. At some point, however, instabilities in the LB algorithm (which were already noted by [2]) cause the solution to diverge. For the higher-fidelity simulations, instabilities appear earlier in time, but after a similar number of time-steps. In appendix D, a series of contour plots of the displacement magnitude are shown to highlight how instabilities arise near the corners of the simulated domain. While this instability ultimately needs to be addressed in the further development of the method, this is beyond the scope of the current work.

As the oscillations exhibited by the plane strain domain continue indefinitely with little change to their amplitude or frequency, almost all of the mechanical behaviour of interest is captured by simulations of the first transient overshoot. In the following, attention will thus be confined to this interval, \(t \in [0,2.5] l/c_s.\)

A mean error with respect to the reference solution is computed over the displacement field obtained via the LBM for each discretisation, at times \(t\approx \{0.5775,1.155,1.703,2.281\}l/c_s\) (noted as dashed lines in Fig. 4). The resulting convergence plot in Fig. 5 shows that the LBM solution converges linearly toward the reference FE solution. Eventually, instabilities cause a reduction in the rate of convergence, as already noted by [2]. This indicates that the LBM by Murthy et al. [1] and the boundary rules presented here capture the transient behaviour of the Lamé-Navier equation and the chosen boundary values as suggested in the consistency studies in appendices A and C, though improvements must be made to the stability of the method. Furthermore, higher-order convergence would be desirable to achieve higher accuracy with a coarser discretisation. To achieve this with bounce-back-type boundary rules, the error terms in equations (C20) and (C21) in appendix C would have to be eliminated. However, the grid refinement study and the consistency studies in appendices A and C indicate that solid-mechanical boundary rules can be modeled consistently via bounce-back-type boundary rules. Furthermore, the additional linear momentum density source suggested by Murthy et al. - see (4) - seems to model the non-Poisson part of the material law successfully in this application. Despite the linear convergence rate and the eventual instabilities, the relative error of the LBM relative to the FEM solution can be reduced below \(0.1\%\) with moderate mesh refinement.

Fig. 5
figure 5

Convergence study for several times t during the LBM simulation of a quadratic domain. The Euclidean norm of the error over the displacement field \(e/u_{\text {ref}}\) (non-dimensionalised and normalised with the number of evaluation points) is plotted over the non-dimensionalised lattice spacing \(\Delta x/l\)

Full size image

The LBM simulations for the convergence study outlined above were run using an in-house Python code. These simulations runs result in a slightly lower runtime than explicit FEAP simulations with an equivalent discretisation: an FEM simulation run with \(\Delta x \approx 6.250 \times 10^3\,l\) took 49 seconds on a Intel (R) Core(TM) i5-8500 CPU @ 3.00GHz, while the equivalent LBM simulation required only 24 seconds on the same hardware, with the same time step being used for both. A detailed performance benchmarking study would be necessary to investigate relative runtime advantages further, but the rough preliminary comparison is encouraging.

6 Numerical and analytical examples

This section considers two further benchmark examples to illustrate how the LBM can be used to approach elastodynamic problems. A dynamically tension-loaded rectangular domain with a circular hole is modeled first. In the latter example, results produced by the LBM are compared against an analytical solution for the sudden loading of a finite crack. In both cases, moderately coarse discretisations are used to investigate whether the LB algorithm and the boundary rules suggested above produce acceptable results at low resolution – and thus at low computational cost.

6.1 Tension loading of a rectangular domain with a circular hole

Firstly, we consider a rectangular domain (side length l) with a central circular hole (radius \(r=0.133l)\), as illustrated in Fig. 6. This domain is subjected to a plane strain state, the upper and lower boundaries being loaded with a traction of \(t^*\) in their respective normal directions. Note that at the boundary of the circular hole, the condition for the determinacy of Neumann boundary conditions–discussed at the end of appendix C–is not met everywhere. The example serves to broadly illustrate the behaviour of the solid LBM in this scenario. Again, all variables used here are non-dimensionalised, with \(u_{\text {ref}}=10^{-3}l\) (arbitrary units).

Fig. 6
figure 6

Square domain with circular hole subjected to an in-plane tension load

Full size image

The traction is increased linearly from \(t^*=0.0 \mu u_{\text {ref}}/l\) at time \(t=0.0l/c_s\) to \(t^*=5.0 \mu u_{\text {ref}}/l\) at \(t=1.0l/c_s\), and subsequently held at this level until the end of the simulation at \(t=2.0l/c_s\). The left and right sides of the rectangle as well as the circular hole are stress-free, i.e. subject to homogeneous Neumann boundary conditions.

To describe the simulated material, we use both parameters corresponding to a Poisson solid (\(c_d^2/c_s^2=3.0\), \(\nu =0.25\)) and a non-Poisson solid (\(c_d^2/c_s^2=2.8\), \(\nu =0.\bar{2}\)). The former is often encountered in seismological wave modelling [6] and the latter is typical for certain concretes and glasses [16].

LBM and FEM simulations with lattice spacing/element size \(\Delta x=0.0125l\) and time step \(\Delta t \approx 7.217\times 10^{-3}l/c_s\) are compared qualitatively.

Fig. 7
figure 7

\(x_2\)-components of dimensionless displacements at \(P_1\) post-processed from LBM (blue) and FE (red) simulations of a Poisson- and non-Poisson solid under tension loading

Full size image

After the simulation run, the \(x_2\)-component \(u_2\) of the displacement at the point \(P_1=(-0.5l+\Delta x/2,0.5l-\Delta x/2)\) in the top-left corner and the \(x_1\)-component \(u_1\) of the displacement at the point \(P_2=(-0.15l+\Delta x/2,\Delta x/2)\) near the hole are post-processed from the linear momentum density \(\varvec{j}\). These points are chosen as they yield relatively high displacements that vary comparatively strongly in time.

Figure 7 plots the vertical displacement (\(u_2\)) predicted at \(P_1\) by the LBM and the FEM for the Poisson case in blue, and the non-Poisson case in red. The reference results produced by the FEM are displayed as dotted lines, while the continuous curves indicate the LBM’s prognosis. As is apparent in the figure, the LBM and the FEM are in acceptable agreement throughout the simulation, in view of the moderate discretisation.

Fig. 8
figure 8

\(x_1\)-components of dimensionless displacements at \(P_2\) postprocessed from LBM (blue) and FE (red) simulations of a Poisson- and a non-Poisson solid under tension loading

Full size image

Similarly, Fig. 8 visualises the change of horizontal displacement (\(u_1\)) at \(P_2\) computed via the LBM and the FEM. As above, the displacements are in decent agreement throughout the simulation. Interestingly, the LBM seems to predict a slightly lower and later peak in the displacement \(u_1\).

The displacements shown in Figs. 7 and 8 for Poisson and non-Poisson material parameters reveal a slight difference in the displacement amplitude due to the differing ratio of shear and volumetric stiffnesses. As is apparent, both the LBM and the FEM predict similar magnitudes for this effect.

Finally, the deformation predicted by the LBM and FEM simulations at \(t=1.5l/c_s\) is visualised in Fig. 9, for the non-Poisson solid with \(c_d^2/c_s^2=2.8\). A contour plot for the vertical displacements \(u_2\) is superimposed on the warped surface indicating the current configuration as determined by the FEM. The position of lattice sites in the current configuration is indicated by black dots. The agreement in the computed displacements throughout the simulated domain is apparent.

Fig. 9
figure 9

Deformed configurations predicted at \(t=1.5l/c_s\) by FEM and LBM simulations. A contour plot for the vertical displacement \(u_2\) is superimposed on the warped FEM domain, while the lattice sites of the LBM simulation are indicated by black dots. The deformation is scaled by a factor of 20

Full size image

The agreement between the two simulation methods in this example is generally encouraging. The LBM and the FEM produce a very similar qualitative behaviour and the error in the displacement fields remains in the low single-digit percentage range, despite the underdeterminacy issues arising from the non-lattice-conforming interior boundary. Though instabilities are a common issue with the BGK-LBM [2], the transient LBM simulations here remain stable for a sufficiently long duration to capture the transient overshoots in the displacement of the dynamically loaded solid. However, further development in non-lattice conforming boundary conditions is necessary, as is apparent via the offset in the peaks of the postprocessed displacements, which appears to a considerably lesser extent in the example with lattice-conforming boundaries considered in Sect. 5.

6.2 Sudden loading of a stationary crack

Fig. 10
figure 10

Square domain with a crack (length \(l_c\)) subjected to tensile crack face traction. Side length not to scale

Full size image

In the second numerical example, the LBM is used to treat a problem of dynamic fracture mechanics: the square cross-section in Fig. 10 with side length \(l=4.0l_c\) and free boundaries features a stationary crack of length \(l_c\). The finite material domain modelled here is sufficiently large for our purposes: no P waves reflected by the exterior boundaries can return to and influence the crack within the simulated time. We non-dimensionalised this problem with \(l_{\text {ref}}=l_c=1.0\) (arbitrary units). Here, we use the dilatational wave speed \(c_d\) for non-dimensionalisation, as it determines the time of arrival of the P waves which are most characteristic for this problem.

The crack is oriented in the y-direction and centred at the origin \((0l/l_{c},0l/l_{c})\). Both crack faces are suddenly loaded with a traction \(t^*=0.009615\mu u_{\text {ref}}/l\) in their negative normal directions at time \(t=0.0l/c_d\), and the traction remains constant until the end of the simulation at \(t=2.0l/c_d\). The LBM is used to simulate the consequences of this sudden so-called ‘mode I’ loading of the crack for a non-Poisson solid with \(c_d^2/c_s^2=2.769\), \(\nu =0.2174\). A spatial discretisation with \(\Delta x=0.01l_c\) is chosen, leading to a time-step of \(\Delta t \approx 2.669\times 10^{-3}l/c_d\). We again use a relaxation time of \(\bar{\tau }=0.55\Delta t\).

Following the simulation, the \(x_1\)-component of the Cauchy stress \(\sigma _{11}\) at a point \(P_1=(0.0l_c,0.52l_c)\) just in front of one of the crack tips is evaluated via the second moment (20) and the formula relating the Poisson and Cauchy tensors (8). The result is used to calculate the mode I stress intensity factor \(K_I\) for each time step via [19, 74]

$$\begin{aligned} K_I = \lim _{r\rightarrow 0} \sigma _{11}(r,\varphi ) \sqrt{2 \pi r}\,. \end{aligned}$$
(24)

Here, r is the distance from the crack tip to \(P_1\) and \(\varphi =0\) the angle with which \(P_1\) is offset from the crack plane (see Fig. 11).

Fig. 11
figure 11

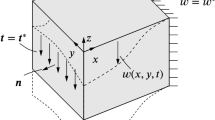
Cylindrical coordinate system at the crack tip and definition of the displacement. Adapted from [10, p.71]

Full size image

The results are compared to the exact analytical solution from Freund [3, p.117], which yields

$$\begin{aligned} K_I^0 = 2t^* \frac{\sqrt{1-2\nu }}{1-\nu } \sqrt{\frac{c_d t}{\pi }}\,, \end{aligned}$$
(25)

for the mode-I stress intensity factor from \(t=0.0l_c/c_d\) to \(t=1.0l_c/c_d\), i.e. until the first dilatational waves scattered by one crack tip arrive at the other [3, p.119]. The stress intensity factor from \(t=l_c/c_d\) to \(t=2l_c/c_d\) (i.e., until the dilatational waves return to the other crack tip once more) is given by the nested integral [3, p.122]

$$\begin{aligned}&K_I^1 = K_I^0 +\frac{2 t^* F_+(0)}{\pi } \sqrt{\frac{2l_c}{\pi }} \cdot \cdot \nonumber \\&\quad \int _a^{\frac{t}{l_c}} {\text {Im}} \Big ( \sqrt{\frac{t}{l_c}-\eta } \sqrt{\frac{a-\eta }{a+\eta }} \frac{c_r+\eta }{c_r-\eta } \frac{1}{\eta } \exp \Big ( \cdot \cdot \nonumber \\&\quad \frac{1}{\pi } \int _a^b \arctan \Big ( 4 \xi ^2 \frac{\sqrt{(\xi ^2-a^2)(b^2-\xi ^2)}}{(b^2-2 \xi ^2)^2} \Big ) \cdot \cdot \nonumber \\&\quad \frac{2 \eta }{\xi ^2-\eta ^2} d \xi \Big ) d \eta \Big )\,, \end{aligned}$$
(26)

with \(a=1/c_d\) and \(b=1/c_s\). \(c_r=1/c\) is the inverse of the Rayleigh (surface) wave speed. In contrast to [3, p.83], where an approximation is used, we compute c via the roots of the equation [20]

$$\begin{aligned} 0 = \Big ( 2 - \Big ( \frac{c}{c_s} \Big )^2 \Big )^2 - 4 \sqrt{ \Big ( 1 - \Big ( \frac{c}{c_d} \Big )^2 \Big ) \Big ( 1 - \Big ( \frac{c}{c_s} \Big )^2 \Big )}\,. \end{aligned}$$

The meaning of the function \(F_+(\xi )\) is explained in [3, p.90]. Here, it suffices to know that it assumes the value of \(F_+(0)\approx 0.8774\) in (26).

Crucially, the inner and outer integrands feature poles at \(\xi =\eta \) and \(\eta =c_r\), respectively. Since the integrands are sufficiently well-behaved and change sign as the variable of integration crosses the pole, Cauchy principal values exist [3, p.122]. Here, we evaluate (26) using a trapezoidal rule with an adaptive integration step near the poles, and we integrate around the inner singularity \(\xi =\eta \) along a small semi-circular contour in the upper complex half-plane. A tolerance of \(2\times 10^{-5}\) at the singularities seems sufficient for convergence. A lower tolerance does not visibly change the computed analytical solution. The MATLAB script for the evaluation of the Cauchy principal value integrals is provided with the supplementary material (Online Resource 1).

Fig. 12
figure 12

Mode-I stress intensity factor postprocessed from the LBM simulation of a non-Poisson solid with a shock-loaded crack at \(P_1=(0.005,0.52)\), compared with an analytical solution calculated using the Wiener-Hopf method. Stress intensity factor normalised with the quasistatic solution \(K_I^s = t^* \sqrt{\pi l_c/2}\)

Full size image

The numerically integrated analytical solution for \(K_I\) is plotted against the results postprocessed from the LBM simulation run at \(P_1\) in Fig. 12. The analytical solution is not exact after \(t=2l_c/c_d\), and the plot is continued with a dashed line. The exact solution, however, is expected to deviate only slightly from this dashed line [3, p.123]. The LBM produces results that generally agree well with the analytical solution and a reference FE calculation: the stress intensity factor rises steeply initially, with the rate of change decreasing gradually. After \(t=\frac{l_c}{c_d}\) the solutions both behave almost linearly in time as stress waves from the other end of the crack arrive, with a notable uptick just before \(t=2\frac{l_c}{c_d}\) due to the arrival of Rayleigh surface waves [21]. \(K_I\) then levels off. The LBM (with the modified boundary rules) and the FEM produce a smoother behaviour than the exact solution.

However, the solution produced by the LBM captures key aspects of the behaviour in the vicinity of the crack tip roughly as well as the FEM, both qualitatively and quantitatively. The proposed computation of the Cauchy stress \(\varvec{\sigma }\) via Poisson stress \(\varvec{P}\) and density in the current configuration \(\rho \) (see (8)) appears to work as desired in this example. Encouragingly, the simulation remains stable in the considered interval despite the discontinuous loading and the singular stress field in the vicinity of the crack tip.

7 Conclusions

In this work, local boundary rules for the LBM algorithm by Murthy et al. [1] and Escande et al. [2] were proposed. These approximate the behaviour of Dirichlet and Neumann boundary conditions with first-order accuracy.

In Sect. 2, the Lamé-Navier equation and the associated boundary conditions were first rephrased in moment chain form. In contrast to the presentation chosen by Murthy et al. [1], the reformulation was performed in the reference configuration. The relationship between the Poisson stress tensor \(\varvec{P}\) appearing in this moment chain and the established Cauchy stress tensor \(\varvec{\sigma }\) was explored, and a convenient formula for the calculation of one from the other derived. Section 3 then very briefly outlined the Lattice Boltzmann Method for solids, and Sect. 4 presented the boundary rules used to model arbitrarily valued Dirichlet and Neumann boundary conditions. In Sect. 5, an empirical convergence study was performed for a simple benchmark example, showing linear convergence towards a high-fidelity FEM reference solution. In Sect. 6 two further examples–featuring a circular hole and a finite crack, respectively–were considered to illustrate the application of the LBM to elastodynamic problems. In appendix A, the LBM proposed by Murthy et al. [1] was shown to act as a second-order Crank-Nicolson scheme for the moment chain formulated in Sect. 2; in appendix C the simple bounce-back and anti-bounce-back rules were shown to replicate the desired boundary values with formal first-order accuracy.

While only first-order accuracy could be achieved here, the results indicate that solid-mechanical (Dirichlet and Neumann) boundary conditions can be modeled consistently via bounce-back-type boundary rules in the LB algorithm by Murthy et al. [1]. Despite the linear convergence rate and the eventual instabilities, the relative error of the LBM solution could be reduced below \(0.1\%\) with moderate mesh refinement, which is satisfactory for many engineering applications. Further improvements must be made to the stability of the method, as only finite-time simulations are possible to date. This issue is especially pronounced for material parameters which deviate significantly for the Poisson case (\(\lambda = \mu \)), as highlighted by [2]. Simulations of incompressible or nearly incompressible materials are therefore impossible currently. Furthermore, higher-order convergence would be desirable to achieve higher accuracy at lower resolutions.

Beyond this, the algorithm outlined here only facilitates the modelling of materially and geometrically linear solid behaviour. For an extension to the nonlinear regime, nonlinear terms in the material law must be accounted for. This may be challenging, as nonlinear terms can not easily be modeled via the third equation of the moment chain (4). As a first approach, source terms could be used to account for nonlinear terms in the material law, but depending on the finite difference stencils required to this end, this may interfere with the computational efficiency of the LBM.

On the other hand, the LBM seems promising as an elastodynamic solver: because the interaction between neighbouring lattice sites in the streaming step is linear, and the nonlinear behaviour enters the local collision step [12, p.55], the LBM can be implemented efficiently and parallelised easily. In particular, the LBM lends itself to modelling dynamic phenomena which call for fine spatial and temporal resolutions–an area of application in which computational efficiency becomes crucial. As discussed in Sect. 5, our in-house Python implementation required half the simulation time of an equivalently discretised explicit FE simulation using FEAP for a simple example problem. While a thorough performance study would be necessary to asses the relative performance of the LBM in detail, the preliminary results are encouraging. Furthermore, spatially discretising - ‘meshing’ - a material domain is comparatively easy. If the solid LBM can be turned into a practicable simulation method, much time might be saved in engineering design processes.

The numerical solutions to the dynamic example problems considered here are generally encouraging: the solid LBM by Murthy et al. [1] and the boundary rules presented here are able to consistently model elastodynamic problems described by the Lamé-Navier equation and Dirichlet and Neumann boundary conditions.

However, a need for further development is apparent in several key areas. Firstly, the stability of the method must be improved. Schemes with multiple relaxation times [12, p.407] and multi-reflection boundary rules [22] seem promising first places to start. Second-order accurate boundary rules could further improve the accuracy of the method. A possible approach to implement these may be to derive bounce-back-type boundary rules which eliminate the error terms arising in the consistency study in appendix C. Finally, extensions to material nonlinearity and large deformations are desirable.

If these shortcomings are addressed, however, fascinating areas of application beckon: the LBM could be used to study stresses caused by the propagation, reflection, and superposition of waves under highly dynamic loading. Crashproofing and mining are fields that might benefit from such studies. If an extension to the nonlinear regime can be achieved, simulations of polymer components (such as seals and tires) or tissue (such as muscle) under transient loads further become feasible. Here, also, the LBM might be useful on account of its efficiency and ease of parallelisation. The formulation in the reference configuration chosen here circumvents one key obstacle in the extension to the geometrically nonlinear regime: a formulation with respect to material rather than spatial coordinates means that no re-discretisation is necessary to deal with the large topological changes that may occur at finite strains.

8 Supplementary information

The MATLAB script for the evaluation of the analytical solution from [3, p.117] is provided with the supplementary material (Online Resource 1).