1 Introduction

Concrete undergoes time-dependent deformation mainly due to creep and shrinkage, which affects the performance and the design life of concrete structures. Both creep and shrinkage are complex phenomena that are not fully understood yet. Creep represents the continuous increase of deformation under sustained load and for concrete it is generally divided into basic creep and drying creep. Basic creep represents the time-dependent strain developed in a sealed specimen or one that is in hygral equilibrium with the ambient environment. Drying creep is the additional strain developed in a specimen that is subjected to simultaneous drying environment, this is also known as the Pickett effect. Several well accepted mechanisms were proposed for creep including the seepage theory [1], viscous flow [2], and the microprestress-solidification [3] theory. Shrinkage represents the change in volume measured on a load free specimen as a result of drying shrinkage and autogenous shrinkage. For normal strength concrete, the latter one is negligible and total shrinkage is assumed to be equal to the drying shrinkage only which is taken as the strain measured in a specimen that is exposed to a drying environment [4, 5]. Drying shrinkage is commonly associated with mechanisms include capillary pressure, surface tension, disjoining pressure and interlayer water movement [6, 7]. Both drying creep and drying shrinkage develop with the presence of a dry atmosphere which is typical under service conditions. Cracking is also commonly seen in concrete structures over time. These cracks can be caused by external loading, or by the time-dependent deformation, especially shrinkage, in internally or externally restrained structural members. Cracking of concrete increases its permeability, making it more susceptible to sulfate [8] and chloride attacks [9, 10].

Macro-scale models are typically used for concrete and they consider it as a homogeneous material. Extensive experimental research on creep and shrinkage of concrete has been conducted. A collection of the experimental data in the literature can be found in Hubler et al. [11]. By calibrating experimental data, empirical creep and shrinkage models have been developed in design codes, such as the ACI model [4], fib model [12] and B4 model [13] and they allow the prediction of creep and shrinkage from a simple formula. For drying creep and drying shrinkage, these design code models adopted a sectional approach, in which only the mean effects of drying over the cross section of the structural member are considered. Both drying creep and drying shrinkage are assumed to be uniformly distributed within the section. Other more sophisticated models have also been proposed to model drying creep and drying shrinkage [3, 14,15,16,17]. Extensive applications of creep and shrinkage models for structural analysis have been made in the past, including on plane specimens [18, 19], beams and girders [20,21,22] and other members.

Concrete is a composite consisting of cement paste, fine aggregates and coarse aggregates. The time-dependent deformation observed in concrete is well accepted to originate from the cement paste and it is restrained by the presence of aggregates. The restraint depends on properties of the aggregates, such as their elastic modulus, content, distribution, shape etc. This restraint mechanism which is essential for predicting creep and shrinkage of concrete cannot be explicitly captured by homogeneous models. Attempts have been made to simulate creep and shrinkage using composite homogenisation models [23,24,25,26]. These models were developed by making some simplified assumptions on the distribution of aggregates, and they allow the prediction of the deformation of concrete based on the material properties and volume fraction of the constituents. Nevertheless, the random distribution of the aggregates, their size gradation and shape cannot be explicitly modelled.

Meso-scale modelling of concrete has become increasingly popular in recent years due to its capability to explicitly model the different components of concrete. On the meso-scale, concrete is typically treated as a composite of mortar and coarse aggregates. The interfacial transition zone (ITZ) may also be considered with meso-scale models which is a thin layer (around 50\(\mu \)m) of porous region formed around the aggregates due to wall effect [27, 28]. One key step of meso-scale modelling is the acquisition of the concrete meso-structure. Due to difficulty of obtaining the internal structure of concrete, numerically generated meso-structures have been adopted by most of the studies which was obtained by making certain simplified assumptions regarding to the aggregate shape, size, distribution and etc [29, 30]. Alternatively, the internal structure of concrete may be obtained from X-ray microCT scanning, which can be used to run direct image analysis [31, 32].

Most of the existing meso-scale models of concrete focused on simulating its crack pattern under load [29, 33] without the consideration of the time-dependent deformation. Continuum models based on the finite element method (FEM) are adopted by most of the studies in which the concrete meso-structure is discretised into finite elements with different material properties and constitutive relations assigned to them. The ITZ has been typically modelled as either a thin lay of elements [32, 34] or through cohesive zone models [35, 36]. Other than FEM, discrete modelling approaches such as the beam lattice model [37, 38] and the lattice discrete particle model [39] have also been proposed in which the concrete meso-structure is characterised by a grid of beam elements. A comprehensive review of these studies can be found in Thilakarathna et al. [40]. Investigations have been made in recent years to model individual aspects of the time-dependent behaviour of concrete, including creep [41,42,43], shrinkage and shrinkage induced tensile cracking [38, 44, 45]. However, only limited attempts [35, 46, 47] have been made to integrate creep, shrinkage and cracking into a single model. Idiart et al. [35] extended the meso-scale model developed by López et al. [30] to simulate the time-dependent behaviour of concrete. The model accounts for creep using a viscoelastic Maxwell chain and shrinkage as an additional stress-independent strain. The cracking of the mortar phase and ITZ is captured using a cohesive zone model. Despite that cohesive zone models are commonly adopted for ITZ modelling, they may not be suitable for the modelling of cracks within the mortar phase due to their mesh dependency. Havlásek and Jirásek [46] investigated the relation between ultimate shrinkage and the ambient relative humidity using a meso-scale hygro-mechanical model. The creep and shrinkage strain components are modelled using the Microprestress-Solidification theory [3], and cracking of mortar is captured using a scalar damage model. However, the debonding of ITZ has not been accounted for in this study. Another meso-scale hygro-mechanical model is proposed by Ožbolt et al [47]. The model accounts for basic creep, shrinkage and cracking. Drying creep was not considered as it is assumed to be caused by the interaction between damage and the time-dependent strain components only, and the debonding of ITZ was not considered either.

Most meso-scale studies have been carried out based on FEM as mentioned above. Meshes generated based on Delaunay triangulation have been adopted by many studies [35, 47]. However, it can be difficult and time consuming to generate a quality mesh especially when the meso-structure contains aggregates with a large quantity and irregular shapes. To simplify the mesh generation procedure, a uniform finite element mesh was adopted by many studies [32, 42]. Similar procedures have also been adopted in typical beam lattice models for the generation of lattice structure [31, 38]. Another powerful tool capable of running meso-scale analysis that has not been fully utilised for this purpose is the scaled boundary finite element method (SBFEM). The SBFEM is a continuum based semi-analytical numerical method developed by Song and Wolf [48]. The model can be coupled with a fast and automatic quadtree decomposition algorithm that converts digital images of concrete meso-structures into meshes [49]. The generated quadtree meshes cannot be directly analysed using FEM due to the presence of hanging nodes. However, the SBFEM is highly complementary with quadtree meshes due to its ability to handle polygonal elements with arbitrary number of sides. By coupling SBFEM with the quadtree algorithm, this method serves as a more efficient alternative for the meso-scale analysis of concrete.

In previous works by the authors, a novel simplified two-scale model based on SBFEM was proposed to predict the creep [50, 51] and shrinkage [52] of concrete from the cement paste scale. The two-scale refers to the mortar scale which consists of cement paste and fine aggregates, and the concrete scale which consists of mortar and coarse aggregates. The model was simplified in a sense that drying of the specimens were not explicitly modelled. Instead drying creep and drying shrinkage were assumed to be uniform within the structure. In the present study, a more advanced and integrated hygro-mechanical model based on 2D SBFEM formulation is proposed to account for the coupled effects of basic creep, drying creep, drying shrinkage, aging and cracking simultaneously. The non-uniform internal humidity field within the concrete specimen or member is also considered. In this study, we will focus on the concrete scale. The coarse aggregates are assumed to be elastic, whereas the mortar is subjected to time-dependent deformation including creep and shrinkage. The basic creep response is assumed to be viscoelastic with aging which is simulated using a rate-type Kelvin chain model with time-dependent model parameters. Drying shrinkage and drying creep are addressed using the model proposed by Bažant and Chern [14], in which drying shrinkage is directly linked to the humidity and drying creep is linked to both humidity and stress. The moisture movement in cementitious material is assumed to be driven by a non-linear diffusion equation developed by Bažant and Najjar [53], which leads to the humidity distribution within the structure. In addition to the time-dependent strain components, cracking and softening of mortar under tensile load is accounted for through an isotropic damage model. The modelling of the time-dependent deformation and damage are combined through the use of an effective stress approach. The debonding of ITZ is considered through the cohesive zone model.

In the following sections, the constitutive relations of the materials on the meso-scale are presented in Sect. 2. Afterwards, the image-based mesh generation and the SBFEM formulation are introduced in Sect. 3. For clarity, section 4 provides a summary of the overall solution procedure for the present hygro-mechanical model. Then in Sect. 5, numerical examples are carried out to demonstrate the capability of the proposed model. Finally, this paper is concluded with a summary of the presented findings.

2 Constitutive relations

2.1 Time-dependent strain components

The proposed meso-scale model accounts for deformation caused by mechanical loading, as well as the change of moisture conditions. Aggregates are assumed to be linear elastic, whereas the mortar matrix is assumed to exhibit time-dependent deformation. The total strain in the mortar matrix \(\epsilon (t)\) at a given time t is assumed to be the sum of instantaneous strain \(\epsilon _{ins}(t)\), basic creep strain \(\epsilon _{bc}(t)\), drying creep \(\epsilon _{dc}(t)\) and shrinkage strain \(\epsilon _{sh}(t)\) as expressed in Eq. (1).

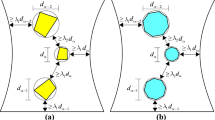
$$\begin{aligned} \epsilon (t)=\epsilon _{ins}(t)+\epsilon _{bc}(t)+\epsilon _{dc}(t)+\epsilon _{sh}(t) \end{aligned}$$
(1)

The rheological model used to simulate the time-dependent deformation of mortar is shown in Fig. 1. The deformation of the rheological model is assumed to be controlled by an effective stress \(\bar{\sigma }\). The mortar matrix is assumed to be linear under compression. In this case, the effective stress \(\bar{\sigma }\) is equivalent to the nominal stress \(\sigma \). Under tension, mortar undergoes cracking which is captured using a scalar damage model. In this case, the effective stress becomes larger than the actual stress, leading to larger deformation of the entire rheological model as compared to the linear case. Alternatively, the other approach of incorporating damage into a creep analysis of concrete rely on the use of nonlinear viscoelastic models like the modified principle of superposition [54]. This approach yields a rheological model with stress-dependent spring and dashpot constants and it was used in past studies by the authors [21, 55] for the creep analysis of reinforced concrete beams. Nevertheless, it assumes recoverable strain at unloading, which is not a characteristic of the drying creep component of concrete. More details of the damage model is presented in Sect. 2.3.

There are four strain components involved in the rheological model as shown in Fig. 1. For conciseness, these strain components are categorised into viscoelastic strain \(\epsilon _{ve}(t)\) and moisture induced strain \(\epsilon _{mis}(t)\). The viscoelastic strain \(\epsilon _{ve}(t)\) consists of the elastic strain \(\epsilon _{e}(t)\) and basic creep \(\epsilon _{bc}(t)\). The viscoelastic behaviour is modelled using a Kelvin chain model consisting of a spring and a number of Kelvin units. The constants of the springs and dashpots vary with time due to aging. The moisture induced strain \(\epsilon _{mis}(t)\) consists of drying creep \(\epsilon _{dc}(t)\) and shrinkage \(\epsilon _{sh}(t)\). Drying creep is treated as viscous and modelled using a dashpot unit. Shrinkage is described with a stress-independent unit. The detailed formulations of these strain components are presented in the subsequent sections.

Fig. 1
figure 1

Illustration of the constitutive model

Full size image

2.1.1 Viscoelasticity

Following the principal of superposition, the stress and strain relation of a viscoelastic material is expressed as

$$\begin{aligned} \epsilon _{ve}(t)=\int _0^t J(t,t')\textrm{d}\sigma (t') \end{aligned}$$
(2)

where \(J(t,t')\) is the compliance function that describes the strain at time t caused by a sustained unit stress \(\sigma \) applied at time \(t'\). The following form of compliance function is adopted in this study [50]

$$\begin{aligned} J(t,t')=\frac{1}{E(t')}+\frac{c_1\ln {(1+c_2(t-t'))}}{E(t')} \end{aligned}$$
(3)

where \(c_1\) and \(c_2\) are constants to be fitted against experimental data and \(E(t')\) is the elastic modulus at loading age. A rate type formulation is adopted to facilitate time-stepping analysis. Following the concepts of continuous retardation spectrum [56], the fitted compliance function is approximated with a Dirichlet series corresponding to a Kelvin chain model (see Fig. 1). The Kelvin chain model is then converted into an incremental form following the exponential algorithm proposed by Yu et al. [57]. For a given time increment \(\Delta t_k=t_{k+1}-t_k\), the incremental stress–strain relation is expressed as

$$\begin{aligned} \Delta \epsilon _{ve,k}=\frac{1}{E_{ve,k}''}\Delta \bar{\sigma }_k+\Delta \epsilon _{ve,k}'' \end{aligned}$$
(4)

where \(E_{ve,k}''\) is the incremental pseudo modulus for viscoelasticity and \(\Delta {\varvec{\epsilon }}''_{ve,k}\) is the strain increment due to basic creep, expressed as

$$\begin{aligned} E_{ve,k}''&=\left( \frac{1}{E_{0,k+1/2}}+\sum _{\mu =1}^{M}\frac{1-\lambda _{\mu ,k}}{E_{\mu ,k+1/2}}\right) ^{-1} \end{aligned}$$
(5)
$$\begin{aligned} \Delta \epsilon ''_{ve,k}&=\sum _{\mu =1}^{M}(1-\beta _{\mu ,k})\gamma _{\mu ,k} \end{aligned}$$
(6)

The stiffness moduli of the Kelvin chain \(E_{0,k+1/2}\) and \(E_{\mu ,k+1/2}\) are evaluated at the middle of each time step \(t_{k+1/2}\) to account for aging, \(\beta _{\mu ,k}\) and \(\lambda _{\mu ,k}\) are factors that need to be evaluated for every Kelvin unit, \(\gamma _{\mu }\) is the internal variable that needs to be updated at the end of every time step as

$$\begin{aligned} \gamma _{\mu ,k+1}=\frac{\lambda _{\mu ,k}}{E_{\mu ,k+1/2}}\Delta \bar{\sigma }_k+\beta _{\mu ,k}\gamma _{\mu ,k} \end{aligned}$$
(7)

2.1.2 Moisture induced strain

Following the work of Bažant and Chern [14], the rate of moisture induced strain \(\dot{\epsilon }_{mis}\) is directly linked to the humidity rate \(\dot{h}\), expressed as

$$\begin{aligned} \dot{\epsilon }_{mis}=\left[ -\epsilon _s^\infty g_{sh}(t_e)\frac{\textrm{d}k_h}{\textrm{d}h}\left( 1+r\bar{\sigma }\ \textrm{sgn}(\dot{h})\right) \right] \dot{h} \end{aligned}$$
(8)

where \(\epsilon _s^\infty \) is the ultimate free shrinkage at zero humidity, \(g_{sh}(t_e)\) characterises the reduction of shrinkage due to hydration and aging. It is defined as the ratio of the elastic modulus at the start of drying \(t_0\) over the elastic modulus at the hydration time \(t_e\)

$$\begin{aligned} g_{sh}(t_e)=\frac{E(t_0)}{E(t_e)} \end{aligned}$$
(9)

The hydration time \(t_e\) depends on the moisture condition and its formulation will be discussed later in Sect. 2.2, \(k_h\) is a function that defines the relation between the normalised shrinkage and humidity. Under typical environmental conditions where the humidity is generally above 50%, function \(k_h\) exhibits an approximately inverse linear relationship to the humidity with the expression of \(k_h=1-h\). By substituting this into Eq. (8), it can be simplified to

$$\begin{aligned} \dot{\epsilon }_{mis}=\left[ k_{sh} g_{sh}(t_e)\left( 1+r\bar{\sigma }\ \textrm{sgn}(\dot{h})\right) \right] \dot{h} \end{aligned}$$
(10)

in which \(k_{sh}\) is the shrinkage ratio defined as the shrinkage strain developed per percentage of humidity drop. Equation (10) may be rearranged to represent the drying shrinkage \(\epsilon _{sh}\) (the stress-independent part) and drying creep \(\epsilon _{dc}\) (the stress-dependent part) component respectively, expressed as

$$\begin{aligned} \dot{\epsilon }_{sh}&=k_{sh}g_{sh}(t_e) \dot{h} \end{aligned}$$
(11)
$$\begin{aligned} \dot{\epsilon }_{dc}&=k_{sh}g_{sh}(t_e) r \bar{\sigma }\textrm{sgn}(\dot{h})\dot{h} \end{aligned}$$
(12)

By assuming the factor \(g_{sh}(t_e)\) to be a constant within each time step, the incremental shrinkage strain \(\Delta \epsilon ''_{sh,k}\) can be simply derived from Eq.(11) as

$$\begin{aligned} \Delta \epsilon ''_{sh,k}=k_{sh}g_{sh,k+1/2} \Delta h_k \end{aligned}$$
(13)

where \(g_{sh,k+1/2}\) is evaluated at the middle of each time step \(t_{k+1/2}\). For drying creep (Eq. 12), its rate form is directly related to the stress which is equivalent to a dashpot unit (see Fig. 1) with viscosity of \(\eta =(k_{sh}g_{sh}(t_e) r \textrm{sign}(\dot{h})\dot{h})^{-1}\). The incremental formulation of drying creep strain may be determined by integration over the time step as

$$\begin{aligned} \Delta \epsilon _{dc,k}&=\int _{t_{e,k}}^{t_{e,k+1}} k_{sh}g_{sh}(t_{e}) r\bar{\sigma }\textrm{sgn}\left( \dot{h}\right) \dot{h}\ \textrm{d}t_e \end{aligned}$$
(14)
$$\begin{aligned}&=\frac{1}{E_{dc,k}''}\Delta \bar{\sigma }_{k}+\Delta \epsilon _{dc,k}'' \end{aligned}$$
(15)

where \(E_{dc,k}''\) is the incremental pseudo modulus for drying creep and \(\Delta \epsilon _{dc,k}''\) is the incremental drying creep strain. They are expressed as

$$\begin{aligned} E_{dc,k}''&=\frac{1}{2}k_{sh}g_{sh,k+1/2}r\ \textrm{sgn}\left( \Delta h_k\right) \Delta h_k \end{aligned}$$
(16)
$$\begin{aligned} \Delta \epsilon _{dc,k}''&=k_{sh}g_{sh,k+1/2}r\ \textrm{sgn}\left( \Delta h_k\right) \Delta h_k \end{aligned}$$
(17)

2.1.3 Integrated incremental formulation

The overall incremental stress–strain relation may be obtained by summing and rearranging Eqs. (4), (13) and (15), which leads to

$$\begin{aligned} \Delta \bar{\sigma }_k=E_k''\left( \Delta \epsilon _k-\Delta \epsilon _k''\right) \end{aligned}$$
(18)

where \(E_k''\) and \(\Delta \epsilon _k''\) are the overall incremental pseudo modulus and incremental strain respectively, expressed as

$$\begin{aligned} E_k''&=\left( \frac{1}{E_{ve,k}''}+\frac{1}{E_{dc,k}''}\right) ^{-1} \end{aligned}$$
(19)
$$\begin{aligned} \Delta \epsilon _k''&=\Delta \epsilon _{ve,k}''+\Delta \epsilon _{sh,k}''+\Delta \epsilon _{dc,k}'' \end{aligned}$$
(20)

2.2 Aging and hygral effects

The mortar phase undergoes a continuous aging process that leads to an increase of its elastic modulus and tensile strength over time. Their variation is assumed to take the following form [12]:

$$\begin{aligned} E(t)&=[\beta _{cc}(t)]^{0.5}E(28) \end{aligned}$$
(21)
$$\begin{aligned} f_{t}(t)&=\beta _{cc}(t)f_{t}(28) \end{aligned}$$
(22)
$$\begin{aligned} \beta _{cc}(t)&=\exp \left\{ s\cdot \left[ 1-\left( \frac{28}{t}\right) ^{0.5}\right] \right\} \end{aligned}$$
(23)

where s is a constant that governs the magnitude of aging.

In order to account for the effect of humidity on the aging and viscoelastic process, Bažant [58] proposed the introduction of a hydration time \(t_e\) and a reduced time \(t_r\) respectively. The hydration time \(t_e\) replaces the actual time in Eqs. (21) to (23), and the reduced time \(t_r\) is used in the incremental form which replaces the actual incremental time used in the computation of the factors \(\beta _{\mu ,k}\) and \(\lambda _{\mu ,k}\). They are adopted in this work as follows [58]

$$\begin{aligned} t_e&=\int _0^t\beta _{eh}(h)\textrm{d}t'&\beta _{eh}(h)=\frac{1}{1+[\alpha _e(1-h)]^4} \end{aligned}$$
(24)
$$\begin{aligned} t_r&=\int _0^t\beta _{rh}(h)\textrm{d}t'&\beta _{rh}(h)=\alpha _r+(1-\alpha _r)h^2 \end{aligned}$$
(25)

where \(\beta _{eh}\) characterises the effect humidity on aging, and \(\beta _{ch}\) characterises the the effects of humidity on basic creep; \(\alpha _e\) and \(\alpha _r\) are material constants that can be calibrated from experimental data. Following the trapezoidal rule, the incremental form of the hydration time \(\Delta t_{e,k}\) and reduced time \(\Delta t_{r,k}\) may be derived as

$$\begin{aligned} \Delta t_{e,k}&=\frac{\beta _{eh}(h_{k})+\beta _{eh}(h_{k+1})}{2}\Delta t_k \end{aligned}$$
(26)
$$\begin{aligned} \Delta t_{r,k}&=\frac{\beta _{rh}(h_{k})+\beta _{rh}(h_{k+1})}{2}\Delta t_k \end{aligned}$$
(27)

2.3 Continuum damage model

2.3.1 Damage criterion

As mentioned in Sect. 2.1, the instantaneous stress–strain relation of mortar in compression is taken as linear elastic with aging material properties. In tension it is nonlinear due to cracking. In the present study, a continuum isotropic scalar damage model is adopted to model cracking, with the following stress–strain relation [59]

$$\begin{aligned} \sigma =(1-\omega )\bar{\sigma }=(1-\omega )D\epsilon \end{aligned}$$
(28)

where \(\omega \) is a variable that characterises the degree of damage or stiffness reduction. By rearranging this equation, we can see that Hooke’s law still applies for a damaged material, except that it links between the effective stress and the strain. The effective stress \(\bar{\sigma }\) is expressed as

$$\begin{aligned} \bar{\sigma }=\frac{\sigma }{1-\omega } \end{aligned}$$
(29)

The damage variable \(\omega \) takes values between 0 when undamaged to 1 when completely damaged. The damage evolution is assumed to follow a typical exponential softening curve [60] (see Fig. 2)

$$\begin{aligned} \omega =\left\{ \begin{array}{c c} 0 &{} \;\hbox {if}\, \kappa \le \epsilon _0\\ 1-\frac{\epsilon _0}{\kappa }\exp \left( -\frac{\kappa -\epsilon _0}{\epsilon _f-\epsilon _0}\right) &{}\; \hbox {if}\, \epsilon _0<\kappa \end{array}\right. \end{aligned}$$
(30)

where \(\epsilon _0=f_t/E\) is the limit elastic strain under uniaxial tension which changes with time due to aging, \(\epsilon _f\) is a parameter that affects the softening response and \(\kappa =\max \{\tilde{\epsilon }(t): t=0,\dots ,t_k\}\) is the maximum equivalent strain reached in the loading history assuming irrecoverable damage in tension. The equivalent strain \(\tilde{\epsilon }\) adopted here is based on the Rankine’s criterion of maximum principal stress

$$\begin{aligned} \tilde{\epsilon }=\frac{1}{E}\max _{I=1,2,3}\left<\bar{\sigma }_I\right> \end{aligned}$$
(31)

where E is the elastic modulus and \(\left<\bar{\sigma }_I\right>\) denotes the positive parts of the effective principal stress. In the case of unloading or reloading, the stress–strain relation follows a linear function between the origin and the point on the stress–strain diagram corresponding to the maximum equivalent strain \(\kappa \).

Fig. 2
figure 2

Stress–strain diagram with exponential softening

Full size image

2.3.2 Non-local damage regularisation

It is well accepted that local continuum damage models are sensitive to the domain discretisation. To circumvent this issue, the integral-type non-local damage model [60] or the crack band model [61] have been typically adopted. The former approach is adopted in this study which is based on replacing a state variable with its non-local counterpart through weighted averaging over a given space. In this approach, a local field f(x) in a domain V can be replaced by a non-local field \(\bar{f}(x)\) as

$$\begin{aligned} \bar{f}(x)=\int _V\alpha (x,\xi )f(\xi )\textrm{d}\xi \end{aligned}$$
(32)

where \(\alpha (x,\xi )\) is a non-local weight function, defined as

$$\begin{aligned} \alpha (x,\xi )=\frac{\alpha _0(||x-\xi ||)}{\int _V\alpha _0(||x-\xi ||)\textrm{d}\xi } \end{aligned}$$
(33)

\(\alpha _0\) is a monotonically decreasing non-negative weight function of the distance \(r=||x-\xi ||\) from each point in consideration. A truncated quartic polynomial function [60] is adopted here:

$$\begin{aligned} \alpha _0(r)=\left<1-\frac{r^2}{R^2}\right>^2 \end{aligned}$$
(34)

in which R is the interaction radius corresponds to the largest distance from point \(\xi \) that affects the non-local average at point x.

2.3.3 Damage with aging material properties

The continuum damage model has been typically applied to cementitious material for short-term analysis. Since the material properties do not vary much in a short period, the damage evolution is governed by a static stress–strain curve as presented in Sect. 2.3.1. However, in a time-dependent long-term analysis, such an assumption no longer holds due to aging. As described in Sect. 2.2, both the elastic modulus and tensile strength of the mortar increase with time. In the context of incremental analysis, it is assumed that all the parameters are constant within each time step with their values evaluated at the middle of the time step. For two consecutive time steps k and \(k+1\), the stress–strain relation for a mortar specimen that has not been previously loaded is assumed to be governed by its elastic modulus and tensile strength at the middle of these two time steps respectively as shown in Fig. 3a.

In the case when the mortar has been previously loaded, we assume that both the stress and damage state of the material remain unchanged due to aging when moving from time step k to \(k+1\). Figure 3b illustrates the load path of the mortar that carries load from a previous time step. When a change of load happens at time step \(k+1\), it follows the same aging stress–strain curve presented in Fig. 3a except that the curve has been shifted horizontally to coincide with its previous stress and damage state. In this case, the maximum equivalent strain at the current time step \(\kappa _k\) cannot be simply adapted from the previous step. Based on the assumption that the damage state does not change due to aging when moving to a new time step, the starting position of the maximum equivalent strain at time step \(k+1\) is determined from the damage index at the previous time step \(\omega _{k}\) by rearranging Eq. (30) as

$$\begin{aligned} \kappa _{k+1}= & {} (\epsilon _{f,k+1}-\epsilon _{0,k+1})\nonumber \\{} & {} W\left( \frac{\epsilon _{0,k+1}\exp {\left( \frac{\epsilon _{0,k+1}}{\epsilon _{f,k+1}-\epsilon _{0,k+1}}\right) }}{(1-\omega _{k})(\epsilon _{f,k+1}-\epsilon _{0,k+1})}\right) \end{aligned}$$
(35)

where \(W(\ )\) is the Lambert W function. It can also be seen from Fig. 3b that when the material is unloaded back to a stress-free state, it still carries some residual strain. The equivalent strain \(\tilde{\epsilon }_k\) for an aging material is still determined using Eq. (31) except that the constant elastic modulus is replaced with the one at the middle of the current time step \(E_{k+1/2}\).

Fig. 3
figure 3

Stress–strain diagram with aging material properties

Full size image

2.4 Cohesive zone model

The cohesive zone model is used to simulate the debonding of the ITZ. The model was first developed by Dugdale [62] and later applied to concrete by Hillerborg [63]. It is a phenomenological model in which the crack opening is characterised with a softening traction-separation law that starts once the maximum tensile stress of the material is reached. The model follows an exponential softening as shown in Fig. 4a and described in Eq. (36) [50].

$$\begin{aligned} \sigma (\zeta )=\left\{ \begin{array}{ll} K_{pen}\zeta &{}\; \zeta <\lambda _{cr}=f_t/K_{pen} \\ f_te^{\frac{-f_t(\zeta -\lambda _{cr})}{G_f}} &{}\;\hbox {otherwise} \end{array}\right. \end{aligned}$$
(36)

where \(G_f\) is the critical fracture energy, \(K_{pen}\) is a large penalty stiffness that minimises the crack opening before reaching \(f_t\) and \(\zeta =\max \{\lambda (t): t=0,\dots ,t_k\}\) is the maximum value of the equivalent crack opening \(\lambda \) in the loading history. The equivalent crack opening \(\lambda \) is defined as a function of the normal displacements \(u_n\) and tangential displacements \(u_t\) [64, 65]

$$\begin{aligned} \lambda =\sqrt{u_n^2+u_t^2} \end{aligned}$$
(37)

The normal traction \(T_n\) and tangential traction \(T_t\) are expressed as a function of the normal crack opening \(u_n\) and tangential crack opening \(u_t\) respectively as

$$\begin{aligned} T_t&=\frac{\partial \Phi }{\partial u_t}=\sigma (\zeta )\frac{u_t}{\zeta } \end{aligned}$$
(38)
$$\begin{aligned} T_n&=\frac{\partial \Phi }{\partial u_n}=\sigma (\zeta )\frac{u_n}{\zeta } \end{aligned}$$
(39)
Fig. 4
figure 4

Traction-separation law under different loading conditions

Full size image

Similar to the damage model, the traction-separation law also needs to be adjusted to account for aging, which can also influence the critical fracture energy \(G_f\). Due to the lack of research on the variation of \(G_f\) for cementitious materials over time, in the present study, it is assumed to follow the change of the tensile strength over time following Eq. (22). Figure 4b illustrates the load path of the traction separation law that carries load from a previous time step. When loaded at different ages, the traction separation law is assumed to behave following the same concept as in the damage model in which we assume that the stress state and damage level do not change during aging. For ITZ, the damage level is determined as the reduction of secant stiffness with respect to the initial penalty stiffness.

2.5 Moisture diffusion

Problems involving moisture or temperature field are typically modelled using diffusion equations. In this study, the non-linear moisture diffusion equation proposed by Bažant and Najjar [53, 66] is adopted to determine the moisture profile within a concrete meso-structure. The governing differential equation for moisture transport of cementitious materials is expressed as

$$\begin{aligned} \dot{h}=\nabla \cdot \left[ C(h)\nabla h\right] \end{aligned}$$
(40)

where C(h) is the moisture diffusivity that depends on the pore relative humidity and \(\nabla \) is the differential operator. The dependency of C(h) on humidity is expressed as

$$\begin{aligned} C(h)=C_1\left( \alpha _0+\frac{1-\alpha _0}{1+\left( \frac{1-h}{1-h_c}\right) ^r}\right) \end{aligned}$$
(41)

where \(C_1\) is the diffusivity when fully saturated, \(\alpha _0\) is the ratio of \(C(0)/C_1\) (approximately), \(h_c\) is the humidity at which \(C(h_c)=[C(0)+C(1)]/2\), and r is a parameter that affects the shape of the diffusivity curve. This expression has been adopted in many past studies [18, 46, 67], and it has also been recommended by the fib model code [12].

3 Hygro-mechanical time-dependent analysis using SBFEM

3.1 Concrete meso-structure and quadtree mesh generation

In the present study, the concrete meso-structures used for the analysis are numerically generated. They are generated based on a take-and-place algorithm presented in Guo et al. [68]. The aggregates are assumed to be in circular shape. The size distribution of aggregates is assumed to follow Fuller’s grading curve.

As highlighted in the introduction section, most of the existing meso-scale studies were carried out on meshes consisting of a uniform element size or elements with similar sizes (from Delaunay triangulartion). Such an approach limits the scale of the analysis as large meso-structures would be discretised into meshes containing a substantial number of elements. In this study, a quadtree decomposition algorithm is adopted for image-based mesh generation which is a powerful alternative for the meshing of composite domains such as concrete meso-structures in 2D [49]. It is based on the recursive subdivision of cells into four smaller ones of equal size until only one material exists in one cell. The generated quadtree meshes contain hanging nodes between adjacent cells of different sizes which cannot be modelled directly by traditional FEM. Modifications are needed to enforce their compatibility in FEM which is typically achieved by further decomposing the cells next to the hanging nodes into smaller triangular and quadrilateral elements [69, 70]. However, the SBFEM serves as an efficient alternative to solve this problem. The quadtree cells can be directly modelled using SBFEM due to its ability to handle arbitrarily sided polygons. The adopted hierarchical quadtree meshes consist of elements of different sizes which reduces the elements needed for computation comparing to the algorithms adopted by existing meso-scale studies. In addition, the quadtree mesh contains only six unique patterns and all the quadtree cells in a mesh can be generated by scaling and rotating these six cells. This feature makes the analysis of quadtree meshes using SBFEM computationally more efficient, as the information of the six unique cells can be pre-computed and quickly retrieved during the analysis. The concept of quadtree mesh generation algorithm outlined in this section may also be applied for 3D problems. For more details of the quadtree algorithm and its coupling with SBFEM, see Saputra et al. [49].

3.2 Geometry representation

Unlike in FEM where the integral over an element is approximated using Gaussian quadrature, an SBFEM element is integrated analytically along the radial direction and approximated by polynomials in the circumferential direction. The modelling of an arbitrary n-sided polygonal element in SBFEM has been illustrated by Song [71] and it has also been presented in a previous work by the authors [50], so only a brief introduction is provided here.

For each polygonal element, a scaling centre is defined such that it is visible to every point on the boundary. The boundary of a polygon is discretised using line elements with shape function \([N(\eta )]\) and natural coordinates \(-1\le \eta \le 1\). The surface of the polygonal element which consists of multiple triangular sectors is obtained by scaling the discretised boundary towards the scaling centre along the radial direction. A radial coordinate \(\xi \) is introduced, with \(\xi =0\) at the scaling centre and \(\xi =1\) at the boundary. The Cartesian coordinates of an arbitrary point (x, y) within a triangular sector are expressed as

$$\begin{aligned}&x=\xi [N(\eta )]\{x\} y=\xi [N(\eta )]\{y\} \end{aligned}$$
(42)

where \(\{x\}=[x_1\ x_2\ \cdots \ x_M]^\textrm{T}\) and \(\{y\}=[y_1\ y_2\ \cdots \ y_M]^\textrm{T}\) are the nodal coordinate vectors of an M-node line element, and \([N(\eta )]=[N_1(\eta )\ N_2(\eta )\ \cdots \ N_M(\eta )]\) is the corresponding one dimensional shape function.

3.3 SBFEM formulation for diffusion

3.3.1 Diffusion equation

The detailed derivation of SBFEM for linear diffusion was originally presented by Song and Wolf [72]. In the present study, it is extended to solve for nonlinear diffusion problems. Since most of the formulations remain unchanged, only the essential steps are presented here for brevity.

The governing equation for nonlinear diffusion takes the following form in two-dimension:

$$\begin{aligned} \{L_h\}^\textrm{T}\{q\}+\{\dot{h}\}=0 \end{aligned}$$
(43)

where \(\{L_h\}\) is the differential operator

$$\begin{aligned} \{L_h\}^\textrm{T}=\begin{Bmatrix} \frac{\partial }{\partial x}&\frac{\partial }{\partial y} \end{Bmatrix} \end{aligned}$$
(44)

and \(\{q\}\) is the flux vector related to humidity h as

$$\begin{aligned} \{q\}=-[\kappa _h]\{L_h\}h \end{aligned}$$
(45)

with the isotropic diffusion matrix \([\kappa _h]\) that depends on the humidity

$$\begin{aligned} {[}\kappa _h]=\begin{bmatrix} C(h) &{} 0 \\ 0 &{} C(h) \end{bmatrix} \end{aligned}$$
(46)

3.3.2 General solution

The humidity field \(h(\xi ,\eta )\) at any point along the circumference may be interpolated as

$$\begin{aligned} h(\xi ,\eta )=[N_h(\eta )]\{h(\xi )\} \end{aligned}$$
(47)

By applying the weighted residual method to the governing equation in the circumferential direction \(\eta \), the SBFEM equation for diffusion in terms of \(h(\xi )\) is expressed as

$$\begin{aligned}{} & {} \left[ E^0\right] \xi ^2\{h(\xi )\}_{,\xi \xi }+\left( \left[ E^0 \right] -\left[ E^1 \right] +\left[ E^1 \right] ^T \right) \xi \{h(\xi )\}_{,\xi }\nonumber \\{} & {} \qquad \qquad \qquad \qquad -\left[ E^2 \right] \{h(\xi )\}-\xi ^2\left[ M_0 \right] \{\dot{h}(\xi )\}=0 \end{aligned}$$
(48)

where \(\{\}_{,\xi }\) and \(\{\}_{,\xi \xi }\) denote the first and second order derivatives of a variable with respect to \(\xi \) respectively. \(\left[ E^0 \right] \), \(\left[ E^1 \right] \), \(\left[ E^2 \right] \) and \(\left[ M^0 \right] \) in Eq. (48) are the coefficient matrices, expressed as:

$$\begin{aligned} \left[ E^0 \right]&=\sum _e\int _{-1}^{+1}\left[ B^1 \right] ^\textrm{T}[\kappa ]\left[ B^1 \right] |J|\textrm{d}\eta \end{aligned}$$
(49)
$$\begin{aligned} \left[ E^1 \right]&=\sum _e\int _{-1}^{+1}\left[ B^2 \right] ^\textrm{T}[\kappa ]\left[ B^1 \right] |J|\textrm{d}\eta \end{aligned}$$
(50)
$$\begin{aligned} \left[ E^2 \right]&=\sum _e\int _{-1}^{+1}\left[ B^2 \right] ^\textrm{T}[\kappa ]\left[ B^2 \right] |J|\textrm{d}\eta \end{aligned}$$
(51)
$$\begin{aligned} \left[ M^0 \right]&=\sum _e\int _{-1}^{+1}\left[ N \right] ^\textrm{T}[N]|J|\textrm{d}\eta \end{aligned}$$
(52)

in which \(\left[ B^1 \right] \) and \(\left[ B^2\right] \) are the SBFEM strain-displacement matrices. The steady state of Eq. (48) can be transformed into a set of first-order ordinary differential equations with twice the number of unknowns as

$$\begin{aligned} \xi \begin{bmatrix} \{h(\xi )\}\\ \{Q(\xi )\} \end{bmatrix} _{,\xi }=-[Z]\begin{bmatrix} \{h(\xi )\}\\ \{Q(\xi )\} \end{bmatrix} \end{aligned}$$
(53)

where [Z] is a Hamiltonian matrix

$$\begin{aligned} {[}Z]=\begin{bmatrix} \left[ E^0 \right] ^{-1}\left[ E^1 \right] ^\textrm{T}&{} -\left[ E^0 \right] ^{-1} \\ \left[ E^1 \right] \left[ E^0 \right] ^{-1}\left[ E^1 \right] ^\textrm{T}-\left[ E^2 \right] &{} -\left[ E^1 \right] \left[ E^0 \right] ^{-1} \end{bmatrix} \end{aligned}$$
(54)

and \(\{Q(\xi )\}\) is the internal nodal flux

$$\begin{aligned} \{Q(\xi )\}=\left[ E^0 \right] \xi \{u(\xi )\}_{,\xi }+\left[ E^1 \right] \{u(\xi )\} \end{aligned}$$
(55)

A block diagonal Schur decomposition of [Z] is then performed, which results in

$$\begin{aligned} {[}Z]\begin{bmatrix} [\Phi _{11}] &{} [\Phi _{12}] \\ [\Phi _{21}] &{} [\Phi _{22}] \end{bmatrix} = \begin{bmatrix} [\Phi _{11}] &{} [\Phi _{12}] \\ [\Phi _{21}] &{} [\Phi _{22}] \end{bmatrix} \begin{bmatrix} [S_\textrm{n}] &{} \\ &{} [S_\textrm{p}] \end{bmatrix} \end{aligned}$$
(56)

where \([S_\textrm{n}]\) and \([S_\textrm{p}]\) are upper triangular matrices that contain eigenvalues with negative and positive real parts along the diagonal respectively. For bounded domains, only \([S_\textrm{n}]\) leads to finite humidity at the scaling centre. The variables \([\Phi _{11}]\) and \([\Phi _{12}]\) are transformation matrices that correspond to the humidity, whereas the variables \([\Phi _{21}]\) and \([\Phi _{22}]\) are transformation matrices that correspond to the flux. The general solutions for humidity and flux vector are then derived as

$$\begin{aligned} \{h(\xi )\}&=[\Phi _{11}]\xi ^{-[S_\textrm{n}]}\{c_\textrm{n}\} \end{aligned}$$
(57)
$$\begin{aligned} \{Q(\xi )\}&=[\Phi _{21}]\xi ^{-[S_\textrm{n}]}\{c_\textrm{n}\} \end{aligned}$$
(58)

where the integration constants \(c_n\) are determined by the nodal humidity on the boundary \(\{h\}=\{h(\xi =1)\}\) as

$$\begin{aligned} \{c_\textrm{n}\}=[\Phi _{11}]^{-1}\{h\} \end{aligned}$$
(59)

The steady state stiffness matrix [K] can then be obtained by substituting Eq. (59) into Eq. (58) and set \(\xi =1\), which is expressed as

$$\begin{aligned} {[}K]=[\Phi _{21}][\Phi _{11}]^{-1} \end{aligned}$$
(60)

3.3.3 Shape function

By substituting Eq. (59) into Eq. (57), the humidity field along the radial direction is expressed as

$$\begin{aligned} \{h(\xi )\}=[\Phi _{11}]\xi ^{-[S_\textrm{n}]}[\Phi _{11}]^{-1}\{h\} \end{aligned}$$
(61)

By substituting Eq. (61) in Eq. (47), the humidity field at any point within the element can be interpolated as

$$\begin{aligned} \{h(\xi ,\eta )\}=[N_\Phi ]\{h\} \end{aligned}$$
(62)

where \([N_\Phi ]\) is the scaled boundary shape function, expressed as

$$\begin{aligned} {[}N_\Phi ]=[N_h][\Phi _{11}]\xi ^{-[S_\textrm{n}]}[\Phi _{11}]^{-1} \end{aligned}$$
(63)

3.3.4 Governing equation for diffusion

The diffusion equation of an SBFEM element takes the same form as the standard FEM, expressed as

$$\begin{aligned} {[}K]\{h\}+[M]\{\dot{h}\}=0 \end{aligned}$$
(64)

where [K] is the stiffness matrix and [M] is the mass matrix with unit density. The formulation for stiffness matrix has been derived in Eq. (60). The mass matrix is formulated as

$$\begin{aligned} {[}M]=[\Phi _{11}]^{-T}[m][\Phi _{11}]^{-1} \end{aligned}$$
(65)

where [m] satisfies the Lyapunov equation

$$\begin{aligned}{} & {} ([I]-[S_\textrm{n}])[m]+[m]([I]-[S_\textrm{n}])\nonumber \\{} & {} \quad =[\Phi _{11}]^\textrm{T}[M^0][\Phi _{11}] \end{aligned}$$
(66)

The time derivation in Eq. (64) shall be discretised in order to run incremental analysis. For time step \(\Delta t_k=t_{k+1}-t_k\), the diffusion equation in Eq. (64) is approximated using finite differences and the backward Euler method as

$$\begin{aligned} {[}M]\left( \frac{\{h\}_{k+1}-\{h\}_{k}}{\Delta t_k}\right) +[K]_{k+1}\{h\}_{k+1}=0 \end{aligned}$$
(67)

The backward Euler method is adopted here as it was found to be unconditionally stable. For clarity, Eq. (67) can then be rearranged to separate the humidity field at different time steps as

$$\begin{aligned} \left( [K]_{k+1}+\frac{[M]}{\Delta t_k}\right) \{h\}_{k+1}=\left( \frac{[M]}{\Delta t}\right) \{h\}_k \end{aligned}$$
(68)

3.4 SBFEM formulation for displacement

3.4.1 General solution

Similar to the humidity field, the displacement field \(u(\xi ,\eta )\) at any point within an SBFEM element is interpolated as

$$\begin{aligned} \{u(\xi ,\eta )\}=[N_u]\{u(\xi )\} \end{aligned}$$
(69)

where \([N_u(\eta )]\) is the shape function for displacement. The SBFEM equation for displacement shares the same form as the steady state diffusion equation, expressed as

$$\begin{aligned}{} & {} \left[ E^0 \right] \xi ^2\{u(\xi )\}_{,\xi \xi }+\left( \left[ E^0 \right] -\left[ E^1 \right] +\left[ E^1 \right] ^T\right) \xi \{u(\xi )\}_{,\xi }\nonumber \\{} & {} \quad -\left[ E^2\right] \{u(\xi )\}=0 \end{aligned}$$
(70)

For displacement problems, the diffusion matrix \([\kappa _h]\) in Eqs. (49) to (51) is replaced with the elasticity matrix [D]. The SBFEM equation for displacement in Eq. (70) can be solved following the same procedures presented in Eqs. (53) to (63). The general solutions appeared in Eqs. (57) and (58) in this case are for the displacement \(\{u(\xi )\}\) and internal force vector \(\{q(\xi )\}\) respectively. The stiffness matrix formulation remains the same as presented in Eq. (60)

3.4.2 Shape function and B-matrix of SBFEM elements

For displacement problems, the strain–displacement relationship is governed by

$$\begin{aligned}&\{\epsilon \}=[L_u]\{u\} \qquad [L_u]^\textrm{T}= \begin{bmatrix} \frac{\partial }{\partial x} &{} 0 &{} \frac{\partial }{\partial y}\\ 0 &{} \frac{\partial }{\partial y} &{} \frac{\partial }{\partial x} \end{bmatrix} \end{aligned}$$
(71)

where \([L_u]\) is the differential operator for displacement and its expression in terms of the scaled boundary coordinate system takes the following form.

$$\begin{aligned} {[}L_u]=[b^1]\frac{\partial }{\partial \xi }+[b^2]\frac{1}{\xi }\frac{\partial }{\partial \eta } \end{aligned}$$
(72)

where \([b_1]\) and \([b_2]\) are matrices that depend on the geometry of the elements only. By substituting Eqs. (69) and (72) into Eq. (71), the strain field is expressed as

$$\begin{aligned} \{\epsilon \}=&[B]\{u\} \end{aligned}$$
(73)
$$\begin{aligned} =&\left( -[B^1][\Phi _{11}][S_\textrm{n}]+[B^2][\Phi _{11}]\right) \xi ^{-[S_\textrm{n}]-[I]}[\Phi _{11}]^{-1} \end{aligned}$$
(74)

where [B] is equivalent to the B-matrix in FEM, \([B^1]\) and \([B^2]\) are the SBFEM strain–displacement matrices.

3.4.3 Governing equation for time-dependent displacement

The incremental SBFEM formulation is derived from Eq. (18) by applying the principal of virtual work. It shares the same form as the one presented by the authors for the simulation of creep and shrinkage [50,51,52]. For an undamaged SBFEM element, the incremental force-displacement relation at a given time step k with time increment of \(\Delta t_k=t_{k+1}-t_k\) is given as

$$\begin{aligned} {[}K]_k\{\Delta u\}_k=\{\Delta F_{ext}\}_k+\{\Delta F''\}_k \end{aligned}$$
(75)

where \([K]_k\) is the stiffness matrix as expressed in Eq. (60). In this case, the coefficient matrices in Eqs. (49) to (51) that are used to construct the stiffness matrix is formulated using the pseudo modulus \(E''_k\) (see Eq. (19)) instead of \([\kappa ]\). \(\{\Delta F_{ext}\}_k\) is the external load vector, and \(\{\Delta F''\}_k\) is the equivalent load vector due to time-dependent strain components, expressed as

$$\begin{aligned} \left\{ \Delta F''\right\} _k=\int _\Omega [B][D]_{k+1/2}\{\Delta \epsilon ''\}_k\textrm{d}\Omega \end{aligned}$$
(76)

From the above equation, [B] is the strain–displacement matrix, \([D]_{k+1/2}\) is the material constitutive matrix evaluated at the middle of each time step. For two-dimensional problems, \(\textrm{d}\Omega \) is expressed as

$$\begin{aligned} \textrm{d}\Omega =|J|\xi \textrm{d}\xi \textrm{d}\eta \end{aligned}$$
(77)

The equations presented above shares the same form as the ones presented by the authors for the simulation of creep and shrinkage [50,51,52], except that the formulation has been extended in the present study to explicitly account for drying creep. In addition, the variation of the prescribed strain \(\{\Delta \epsilon ''\}_k\) within an SBFEM element was approximated by a polynomial function in previous works. However, due to the complexity of the problem in this study, it is assumed that \(\{\Delta \epsilon ''\}_k\) is a constant within each element and it is evaluated at the scaling centre of each element.

3.5 SBFEM formulation for coupled time-dependent deformation and damage

Previous works conducted by the third author accounted for damage using SBFEM [73]. Here, the same concepts are used and further extended to cover damage in structures that undergo time-dependent deformations. Due to the complexity of the problem, the damage index \(\omega \) is assumed to be uniform within each element. Such an approach significantly simplifies the formulation and it is justified as long as sufficiently fine elements are used. By combining Eqs. (18) and (29), the total force-displacement relation for coupled isotropic damage and time-dependent deformation analysis is formulated as

$$\begin{aligned}{} & {} (1-\omega _k)\sum _{i=1}^{k}[K]_i\{\Delta u\}_i=\{F_{ext}\}_k\nonumber \\{} & {} \quad +(1-\omega _k)\{\bar{F}''\}_k \end{aligned}$$
(78)

where the external load vector \(\{F_{ext}\}_k\) and effective equivalent load vector \(\{\bar{F}''\}_k\) are obtained by summing their incremental values up to time step k

$$\begin{aligned} \{F_{ext}\}_k&=\sum _{i=1}^k\{\Delta F_{ext}\}_i \end{aligned}$$
(79)
$$\begin{aligned} \{\bar{F}''\}_k&=\sum _{i=1}^k\{\Delta \bar{F}''\}_i \end{aligned}$$
(80)

The term ’effective’ depicts variables formulated using undamaged material properties, and \(\{\Delta \bar{F}''\}\) is determined following Eq. (76). To facilitate time-stepping analysis, Eq. (78) needs to be converted into an incremental form. For a small time step, the incremental force-displacement relation is linearised as

$$\begin{aligned}{} & {} {[}K_{dmg}]_k\{\Delta u\}_k=\{F_{ext}\}_k+(1-\omega _k)\{\bar{F}''\}_k\nonumber \\{} & {} \quad -(1-\omega _{k-1})\{\bar{F}_{int}\}_{k-1} \end{aligned}$$
(81)

where \([K_{dmg}]_k\) is the stiffness matrix used for the iterative procedures and the tangent stiffness is adopted typically. \(\{\bar{F}_{int}\}_{k-1}\) is the effective internal load vector at step \(k-1\) with expression of

$$\begin{aligned} \{\bar{F}_{int}\}_{k-1}=\sum _{i=1}^{k-1}\{\Delta \bar{F}_{int}\}_i=\sum _{i=1}^{k-1}[K]_i\{\Delta u\}_i \end{aligned}$$
(82)

Newton-Raphson iterative procedures are used to solve the nonlinear problem. Due to complexity of the derivation of the tangent stiffness matrix and the computational cost associated with its formulation at every time step and iteration, the secant stiffness matrix is adopted for the iterative procedures in this study. At step k, the secant stiffness matrix for each element can be formulated as

$$\begin{aligned}{}[K_{sec}]_k=(1-\omega _k)[K]_k \end{aligned}$$
(83)

The secant stiffness matrix can be quickly computed in each iteration by directly scaling the pre-computed stiffness matrix.

3.6 Interface elements

Interface elements are used to accommodate the cohesive zone model which is used to simulate the debonding of the ITZ. A secant modulus approach is also used for the interface elements. Their secant stiffness matrix \(K_{z}\) is assembled as

$$\begin{aligned} {[}K_{z}]_k=\int [B_{z}]^\textrm{T}[R]^\textrm{T}[D_{z}]_{k}[R][B_{z}]\textrm{d}\eta \end{aligned}$$
(84)

where \([D_{z}]_{k+1/2}\) is the material’s secant stiffness evaluated at the middle of each time step following Sect. 2.4, [R] is the rotation matrix that transforms the vectors from global coordinate system to local coordinate system and \([B_{z}]\) is the shape function matrix. Their formulations can be found in Zhang et al. [50]. The internal load vector of interface elements at any time step k is expressed as

$$\begin{aligned} \{F_{int,z}\}_k=\int [B_z]\begin{bmatrix} T_t&T_n \end{bmatrix}^\textrm{T}_k\textrm{d}\eta \end{aligned}$$
(85)

The Newton-Cotes integration scheme is adopted in the formulation of the interface elements because the standard Gaussian integration scheme leads to spurious oscillations when a high penalty stiffness is used [74].

4 Solution procedure

As mentioned in Section. 3.1, a two-dimensional quadtree mesh only has six unique cell patterns. For each material that could appear in the meso-scale analysis, a set of six master cells is defined by considering the cells to have a unit edge length and a unit Young’s modulus. The stiffness matrix [K], and mass matrix [M] can be pre-computed for each master cell and each material type before the analysis. Other important matrices including \(\left[ B^1 \right] \), \(\left[ B^2 \right] \), \([S_\textrm{n}]\) and \([\Phi _{11}]\) can also be pre-computed to speed up the formulation of the equivalent load vector \(\{\Delta F''\}_k\). During the analysis, these matrices can be quickly retrieved and scaled to account for cells with different side length and material properties.

The present hygro-mechanical model carries out analysis on two layers including the hygral layer which determines the distribution of humidity within a structure and a mechanical layer which determines the deformation due to time-dependent behaviour. For clarity, the computational procedures involved in the two layers are presented separately.

4.1 Hygral layer

Box 1 shows the procedures for the analysis of moisture movement. Due to the dependence of the stiffness matrix on diffusivity C(h), iterations are carried out (see steps b to f). In each iteration, the stiffness matrix [K] of each element is updated based on the current humidity at the scaling centre and the respective diffusivity C(h). A residual vector \(R_h\) is defined by rearranging Eq. (68) as

$$\begin{aligned} R_h= & {} \left( [K]_{k+1}+\frac{[M]}{\Delta t_k}\right) \{h\}_{k+1}-\left( \frac{[M]}{\Delta t_k}\right) \{h\}_k \end{aligned}$$
(86)

and the iterations stop once the norm of the residual vector \(|R|\) is smaller than a tolerance value \(R_{h,tol}\)

figure a

4.2 Mechanical layer

Box 2 shows the procedures for analysis of the time-dependent deformation. This is again a nonlinear problem that requires iterations due to material damage and ITZ debonding. Steps a to f are computed only once at the beginning of each time step. The iterations happen between steps h to k. The damage index \(\omega _k\) is updated every iteration from which the secant stiffness and residual load vector are determined. The residual load vector for SBFEM elements \(R_{u,e}\) and interface elements \(R_{u,z}\) are determined as

$$\begin{aligned} R_{u,e}&=\{F_{ext}\}_k+(1-\omega _k)\{\bar{F}''\}_k-(1-\omega _{k})\{\bar{F}_{int}\}_k \end{aligned}$$
(87)
$$\begin{aligned} R_{u,z}&=\{F_{ext}\}_k-\{F_{int,z}\}_k \end{aligned}$$
(88)

Similar to the hygral layer, the iterations stop once the norm of the residual vector \(|R_u|\) is smaller than the tolerance value \(R_{u,tol}\). After convergence is attained, the internal variables \(\gamma _{\mu ,k}\) are updated, which will be used in the subsequent time step to compute the incremental strain due to basic creep \(\Delta \epsilon _{ve,k+1}''\).

figure b

5 Numerical examples

This section starts with a numerical example that simulates the experiment by Bažant and Xi [75]. This example aims to demonstrate the capability of the proposed model in modelling drying creep with account of changes in the humidity distribution over time. This is followed by the simulation of the experiment by Idiart et al. [76] which demonstrates the capability of the proposed model in capturing shrinkage-induced cracks in concrete that is subjected to uniform drying. This section concludes with a numerical simulation of the differential drying of a concrete slab. The effect of boundary conditions and aggregate size on shrinkage-induced cracks are investigated through a parametric study.

5.1 Simulation of drying creep

Bažant and Xi [75] carried out a set of experiments to demonstrate that both drying creep and microcracking contribute to the apparent strain measured on drying creep specimens. The experimental setup of Bažant and Xi [75] is illustrated in Fig. 5 which includes testing of specimens under eccentric loads. The equivalent stress distributions of the eccentric loads have also been shown in the figure. The specimens tested were square prisms with length of 406.4 mm and side of 101.6 mm. Two load eccentricities were considered, a small one of 5.3 mm and a large one of 24.6 mm. For each set of tests, sealed and unsealed specimens were tested. The sealed specimens undergo basic creep only, whereas the unsealed specimens undergo basic creep, drying creep and drying shrinkage. For these specimens, drying was only allowed in one dimension that is on two of the opposite side surfaces. The specimens loaded with small eccentricity were under compression, whereas the specimens that were loaded with large eccentricity were subjected to tension on the left side that is less than the tensile capacity of concrete \(f_t\). Nevertheless, this tensile stress when combined with internal restrained shrinkage and differential drying can cause microcracking that can be simulated with the proposed meso-scale model, but cannot be captured using macro-scale homogeneous models. The environmental humidity was kept at 50% throughout the experiment.

Fig. 5
figure 5

Experimental set up of Bažant and Xi [75]

Full size image

The concrete used for the test was made from weight ratio of water: cement: sand: gravel = 0.5:1.0:2.5:3.0. The coarse aggregates used for the mix have a maximum size of 19 mm. Based on the mix proportion and the typical weight density of the materials, the proportion of mortar and coarse aggregates for the meso-scale analysis is estimated to be 61.1% and 38.9% respectively. The concrete meso-structure generated for the analysis is shown in Fig. 6 which is represented by an image with a resolution of 4096 by 1024 pixels. The quadtree decomposition criteria is set to give element sizes between 1 pixel and \(4^2\) pixels. The produced quadtree mesh contains 488,209 elements with a total number of 553,712 nodes. A small section of the quadtree mesh is presented in Fig. 6. The ratio of the number of elements generated to the total number of pixels is around 11.6%. An overall fine mesh is adopted in this study for the convergence and accuracy of the simulation because the crack pattern is not known a priori and it propagates or change with time due to the time-dependent deformations. It should be noted that the SBFEM approach allows for adaptive local mesh refinement without the need to regenerate the entire mesh [77], which can further reduce the computational cost. However, this feature of the SBFEM approach is not adopted in this study.

Fig. 6
figure 6

Generated concrete meso-structure

Full size image

The material parameters adopted for the meso-scale analysis are shown in Table 1. For an ideal validation of the proposed model, all of the input parameters should be obtained or calibrated from experimental data on the same or similar mortar mix. However, due to the lack of experimental data on mortar, some of the parameters adopted in this example are back calibrated in a way that they give a good fit against the experimental results of the concrete specimens. In existing meso-scale studies, the elastic modulus of mortar is well accepted to be in the range of 20–30 GPa, whereas the aggregates have an elastic modulus of 60–70 GPa [29, 35, 46]. The Poisson’s ratio of both mortar and aggregates are commonly assumed to be 0.2 [35, 43]. The aging coefficient s is adopted from Zhang et al. [51] which was calibrated for a similar mortar mix. The coefficients that relate moisture to hydration and creep are adopted from Bažant and Chern [14]. The basic creep properties of mortar are calibrated such that the simulated deflection agrees well with the experimental results. The validity of meso-scale models for the prediction of basic creep of concrete from mortar has already been demonstrated in a previous work by the authors [51] through comparison with accompanied experimental program. Both drying creep and drying shrinkage are related to the humidity which is obtained from the nonlinear diffusion analysis. For diffusion, the parameters \(\alpha _0\), \(h_c\) and r take the values from the fib model [12]. \(C_1\) is back calculated from that of the concrete which is estimated based on the fib model [12]. A simple formula based on the proportion of mortar is adopted to determine \(C_1\) for mortar assuming that aggregates are impermeable. For parameters relating drying shrinkage and drying creep, \(k_{sh}\) is estimated based on the shrinkage results presented in [78]. Due to the lack of relevant data, the parameter r governing drying creep is back calibrated to ensure a good agreement between the simulation and experimental results. For damage parameters, the tensile strength of mortar is assumed to be 10% the compressive strength of typical mortar mixes and the remaining damage parameters are back calibrated. The tensile strength and fracture energy of the ITZ are assumed to be \(f_t=1.5\) MPa and \(G_c=0.01\) N/mm following [46]. It should be noted that due to the fact that some of the parameters are not adopted from relevant experiment data, the comparison between test and numerical results as shown subsequently is not a quantitative validation of the model. It is rather a qualitative verification of its ability to predict a physical response that was obtained in tests.

Table 1 Adopted parameters for mortar and aggregates in Example 1
Full size table

In the work of Bažant and Xi [75], eccentric loads were applied through pins at the two ends of the specimen with steel plates attached between the specimen and the pins for load transfer. Since the exact dimensions of the plates were not reported, we assume that the eccentric point load is transferred to the entire section of the specimen at the edges, which is simulated through a linearly distributed load on the top and bottom surfaces. The simulated results under sealed condition (basic creep only) along with the experimental results are shown in Fig. 7. Figure 7a shows the results under load with small eccentricity and Fig. 7b shows the results under load with large eccentricity. The calibrated model parameters for basic creep is able to replicate the test results under both loading scenarios as observed from the figure.

Fig. 7
figure 7

Mid-span deflection over time under sealed condition

Full size image

For the specimens that are subjected to drying, all the time-dependent strain components need to be considered in the simulation, including basic creep, drying creep and shrinkage. The last two are directly related to the internal humidity. Figure 8 shows the simulated change of humidity over time in the mortar phase. Mortar is assumed to be in fully humid condition at the start of drying and aggregates are assumed to be impermeable. After 1 day, it can be observed from the figure that drying only occurred close to the exposed surfaces and the majority of the mortar remains fully humid. Drying propagates to the interior of the specimen over time and the centre of the specimen reaches a humidity of around 75% after 200 days of simulation. Please notice that the humidity at the surface is equal to the external relative humidity of 50%.

Fig. 8
figure 8

Internal humidity after 1, 10 and 200 days of drying

Full size image

The effect of damage caused by tension at the meso-scale was found to be insignificant for the specimen that was loaded with small eccentricity. Figure 9a shows the damage level of the mortar phase at 200 days after loading for the specimen that was loaded with large eccentricity. It can be observed that cracking is more significant on the left edge. This is due to the combined effects of the eccentric load and differential drying. Concrete is subjected to differential shrinkage due to the non-uniform distribution of humidity. Shrinkage is higher on the surface of the specimen than the interior, which introduces large tensile stress on the surface and cracking. When these tensile stresses are combined with eccentric loading, the cracking pattern becomes different at the two edges of the specimen. In the examined case, cracking is more severe at the left edge. Most of the observed cracks are surface cracks that are developed between the exposed surface and the outer layer of aggregates, and they are generally perpendicular to the drying surface. On the left edge, some of the cracks are also observed to penetrate further into the specimen. It can be seen that cracks generally propagate next to the aggregates which restrain the shrinkage deformation of mortar and introduce stress concentrations. Figure 9b shows the decohesion of the ITZ in the deformed meso-structure. Only minor ITZ decohesion is observed on the left side of the specimen. The above observations were not reported in the tests, and in general, they can hardly be measured.

Fig. 9
figure 9

Fracture of concrete under large eccentric load (t = 200 days)

Full size image

Figure 10 shows the comparison between simulated and measured mid-span deflections when the specimens are subjected to drying. A good agreement is obtained for the specimen loaded under small eccentricity. For the specimen loaded with large eccentricity, good correlations are observed up to about 40 days. After that, the rate of the increase of deflection over time observed from the experimental results decreases which leads to some minor difference between the simulated and test results. Nevertheless, an overall good agreement is obtained.

Fig. 10
figure 10

Mid-span deflection over time under drying condition

Full size image

It should be noted the presented study is in 2D which is not accurately representative of real concrete specimens. Concrete specimens and aggregates are generally 3D in nature which can affect the stress field and damage pattern. It has been demonstrated in previous works by the authors [51, 52] that the use of 2D meso-scale models is sufficient for the prediction of creep and shrinkage strain in typical laboratory size concrete specimens that are loaded in one direction only as the out-of-plain restraint is generally small. This was shown through good comparison between simulated and measured responses. However, the accuracy of 2D simulations in predicting crack patterns and humidity distribution requires further validation. Nevertheless, the present model serves as a meaningful tool for clarifying the effect of various factors on the time-dependent response, and as a basis for the development of 3D models in the future.

5.2 Simulation of shrinkage-induced cracks under uniform drying

The experimental program of Idiart et al. [76] is used for this simulation. The experiment involves testing of 2 mm thin plate of cementitious composite subjected to drying. The plate is made of cement paste with cylindrical aggregates made from stainless steel. The cement paste was made with a water-to-cement ratio of 0.5 and the specimens were allowed to dry after 28 days of wet curing. The crack patterns were recorded at the end of the drying period and were reported in the study. The exact positions of the aggregates have also been given which allows a qualitative comparison with the experimental results.

The idea of using thin samples in the tests was to simulate uniform drying scenario which in turn produces 2D crack-patterns. Under uniform drying, shrinkage induced cracks develop as a result of the restraint caused by the aggregates. The environmental humidity started at 100% and was gradually decreased to \(60\%\) humidity over the course of 7 days and then kept constant for an additional 31 days. Due to the specimens being very thin, we can safely assume that the internal humidity of the specimen follows that of the environment. The gradual decrease of humidity was not specified in the study, and so it is assumed to take the shape of Fig. 11 with a drying rate of 1% per hour between the various humidity levels.

Fig. 11
figure 11

Humidity evolution

Full size image

The experiment considered two aggregate distributions with 10% and 35% aggregate volume fraction respectively. In addition, four different sizes of the sample are considered with edge length of 21.5 mm, 32.4 mm, 43.3 mm and 65 mm. The aggregate sizes were scaled along with the samples with diameters of 2 mm, 3 mm, 4 mm and 6 mm respectively, to ensure a uniform geometry on the meso-scale. The distribution of aggregates adopted by the experiment [76] are shown in Fig. 12. Digital images with a resolution of 2048 by 2048 pixels are generated to represent the adopted meso-structures. The quadtree decomposition criteria is again set to give element sizes between 1 and \(4^2\) pixels. The produced quadtree mesh contains 291094 elements with a total number of 300574 nodes for the meso-structure with 10% aggregate volume fraction, and 363880 elements with 394694 nodes for the meso-structure with 35% aggregate volume fraction. The ratio of the number of elements generated to the total number of pixels is 6.9% and 8.7% for the two meso-structures respectively. Similar to the previous example, a fine mesh is adopted here to ensure the damage zone is accurately captured.

Fig. 12
figure 12

Cementitious composite used in the experiment of Idiart et al. [76]

Full size image

The crack patterns were reported for meso-structures with 2 mm and 10% aggregates, 6 mm and 10% aggregates, and 4 mm and 35% aggregates. Despite that the specimens were thin and the humidity was carefully controlled, a uniform crack pattern across the thickness was not obtained in the tests. Two types of crack patterns were reported, including middle-section cracks and through-going cracks. In the present study, because of the 2D characteristics of the model, the simulated results are compared with the measured cracks at middle-section.

The material properties adopted in this example are summarised in Table 2. The elastic properties of cement paste and steel aggregates are adopted from Idiart et al. [76]. The parameters related to the time-dependent deformation are calibrated from experimental data reported in Zhang et al. [51] for a similar type of mix. Due to the lack of relevant data, the damage parameters are calibrated such that the computed cracks patterns agree reasonably well with the measured cracks. It is worth noting that the crack path is mainly governed by the elastic properties of the steel aggregates and the time-dependent properties of cement paste, whereas the damage parameters mainly affect the length of the developed cracks. It was found that the predicted response will only slightly change with varying the input damage parameters within the logical range, which provides a level of validation to the proposed model. Figure 13 shows the comparison between computed and measured crack patterns. In the simulated results, crack patterns are presented using damage levels and they are manifested as a band of damaged region. It can be seen that the simulated crack patterns agree reasonably well with the measured crack patterns. It should be noted that an exact prediction of the crack patterns is very difficult considering that cement paste is a highly heterogeneous material.

Table 2 Adopted parameters for cement paste and steel aggregates - Idiart’s experiment
Full size table

5.3 Simulation of shrinkage-induced cracks under differential drying

In this example, a concrete specimen subjected to differential drying is considered in order to simulate real scenarios in construction where only the upper surface is typically exposed to the environment. Under this condition, shrinkage-induced cracks develop due to the combined effect of aggregate restraint and differential drying. A parametric study is carried out to investigate the effect of various parameters on shrinkage-induced cracking. A component of a concrete slab with thickness of 100 mm by 200 mm length is considered. For brevity, we will consider the same concrete mix and material properties as adopted in Sect. 5.1. However, typical 10 mm grade aggregates in compliance with the Australian Standard AS2758.0 [79] is used. All the aggregates are assumed to be circular. Drying of the slab is only allowed on the top surface, while all the other surfaces are assumed to be impermeable. The simulations are run for 200 days and there is no external loading on the slab considered.

Fig. 13
figure 13

Comparison between computed damage level and measured crack pattern for meso-structures with 10% 2 mm aggregates (left), 10% 6 mm aggregates (middle) and 35% 4 mm aggregates (right)

Full size image
Fig. 14
figure 14

Generated meso-structure for Example 3

Full size image
Fig. 15
figure 15

Simulated crack pattern under various environmental humidity (top: 30%, middle: 50%, bottom: 70%)

Full size image

The effect of ambient humidity is investigated first. The generated digital image of concrete meso-structure is shown in Fig. 14 with a resolution of 1024 by 2048 pixels. The quadtree decomposition criteria is set to be the same as previous examples. Three constant environmental humidity levels are considered, including 30%, 50% and 70%. The slab is supported on the bottom surface against vertical movement and only one point is restrained in the horizontal direction. The simulated crack patterns under the three different cases are shown in Fig. 15. Only the top 30 mm of the slabs are presented in the figure as no damage is observed in the inner part of the slab. It can be clearly observed from the figure that a lower environmental humidity leads to more pronounced cracking. This can be attributed to the higher tensile stress induced on the drying surface as a result of the steeper humidity gradient between the exposed surface and the interior of the slab. It can be seen that for the case with 30% humidity, a more severe crack pattern is observed in which the cracks penetrated deeper inside the slab and cracks between aggregates start to develop.

In the second part, the effect of aggregate size on shrinkage-induced cracking is investigated. Three concrete meso-structures are generated containing aggregates with uniform sizes of 5 mm, 10 mm and 15 mm respectively while keeping the overall aggregate content unchanged. The slab is subjected to an environmental humidity of 50%. Figure 16 shows the simulated crack pattern on the top 30 mm of the slabs with different aggregate sizes. More cracks are observed in the concrete with smaller aggregate. This can be attributed to the increase of the quantity of aggregates which created more locations with stress concentrations for cracks to develop. On the other hand, concrete with larger aggregates is observed to have wider damaged zone or in other words larger cracks. A similar observation has also been made in the numerical study by Grassl et al. [80].

Fig. 16
figure 16

Simulated crack pattern under various aggregate sizes (top: 5 mm, middle: 10 mm, bottom: 15 mm)

Full size image

Another simulation is carried out here to investigate the effect of horizontal restraint on shrinkage-induced cracks. In addition to the restraint on the bottom surface, the slab is restrained from horizontal movement on the left and right surface in this case. The slab is subjected to an environmental humidity of 50%. The simulated crack patterns in this case are shown in Fig. 17. When the slab is restrained from horizontal movements, one localised cracking path is observed in addition to the typical surface cracks observed in Fig. 15. This is due to the tensile stress introduced in the horizontal direction as a result of the structural restraint. In this case, the debonding of the ITZ is also clearly visible especially around the localised crack as shown in Fig. 18. As already highlighted in the first numerical example, the observations obtained from this example are qualitative ones due to the 2D nature of the proposed model.

Fig. 17
figure 17

Simulated crack pattern under 50% humidity and restrained horizontal movement

Full size image
Fig. 18
figure 18

Simulated ITZ debonding under 50% humidity and restrained horizontal movement

Full size image

6 Conclusions

An SBFEM based 2D meso-scale hygro-mechanical model has been presented in this paper for the modelling of the time-dependent behaviour of concrete. The model takes digital images of concrete meso-structures as input and converts them into meshes through a quadtree decomposition algorithm that is compatible with SBFEM analysis. Concrete is treated as a two-phase composite consisting of aggregates and mortar, and the ITZ between mortar and aggregates are modelled using the cohesive zone model.

The model accounts for basic creep, drying creep, drying shrinkage and cracking. Basic creep is treated as viscoelastic, and it is modelled using a rate-type Kelvin chain model. Drying creep is modelled using a viscous unit which depends on the current stress level. Both drying creep and drying shrinkage are related to the internal humidity level. The internal humidity distribution within the concrete meso-structure is obtained from a diffusion analysis in which moisture movement in mortar is governed by a nonlinear diffusion equation and aggregates are assumed to be impermeable. Cracking of concrete on the meso-scale is modelled through the combination of a continuum damage model for mortar, and a cohesive zone model for the ITZ.

The capability of the proposed model in predicting the time-dependent deformations and cracking patterns was verified through comparison with experimental observations from the literature. A parametric study was also carried out which demonstrated the effect of ambient humidity, aggregate size and restraining condition on the development of shrinkage-induced cracks in a concrete specimen subjected to differential drying. It was found that an increase of aggregate size reduces the number of surface cracks observed, but it generates larger cracks. Given the capability of the proposed model, it serves as an effective tool for the simulation and understanding of the time-dependent behaviour and cracking of concrete under various realistic conditions, i.e. variable loading and variable drying condition. The model may also serve as a powerful tool to examine the role of various components of concrete and their properties on the time-dependent behaviour of concrete, which can assist in the optimisation of concrete mix for serviceability.

In future works, the proposed meso-scale hygro-mechanical mode will be extended to simulate the time-dependent behaviour on 3D concrete specimens in which a more accurate representation of the humidity and damage fields can be obtained. The model will also be coupled with an adaptive mesh refinement technique to reduce the computational cost.