Abstract
This paper develops two-step methods for solving contact problems with uncertainties. In the first step, we propose stochastic Lagrangian multiplier/penalty methods to compute a set of reduced basis. In the stochastic Lagrangian multiplier method, the stochastic solution is represented as a sum of products of a set of random variables and deterministic vectors. In the stochastic penalty method, the problem is divided into the solutions of non-contact and possible contact nodes, which are represented as sums of the products of two different sets of random variables and deterministic vectors, respectively. The original problems are then transformed into deterministic finite element equations and one-dimensional (corresponding to stochastic Lagrangian multiplier method)/two-dimensional (corresponding to stochastic penalty method) stochastic algebraic equations. The deterministic finite element equations are solved by existing numerical techniques, and the one-/two-dimensional stochastic algebraic equations are solved by a sampling method. Since the computational cost for solving stochastic algebraic equations does not increase dramatically as the stochastic dimension increases, the proposed methods avoid the curse of dimensionality in high-dimensional problems. Based on the reduced basis, we propose semi-reduced order Lagrangian multiplier/penalty equations with two components in the second step. One component is a reduced order equation obtained by smooth solutions of the reduced basis and the other is the full order equation for the nonsmooth solutions. A significant amount of computational cost is saved since the sizes of the semi-reduced order equations are usually small. Numerical examples of up to 100 dimensions demonstrate the good performance of the proposed methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Contact problems play important roles in many practical applications [26, 27]. However, uncertainties are unavoidable for many problems in practical engineering. The consideration of uncertainties in systems behavior has become an essential part of the analysis and design of engineering applications. Although mathematical theories and numerical methods for the treatment of contact problems are well understood for the analysis of deterministic problems [6, 9, 27, 28], there is only limited experience in the treatment of stochastic contact problems.
This paper focuses on solving two-body contact problems with random parameters, e.g. random material properties. There are several methods for solving stochastic contact problems. The Monte Carlo method (MC) is a powerful tool for many kinds of stochastic problems. Although MC can be readily implemented by use of the already existing deterministic codes, a large number of deterministic contact problems need to be solved in order to achieve high-accuracy solutions, which is prohibitively expensive for large-scale problems in practice [7]. As an extension of MC, the multilevel Monte Carlo method (MLMC) has been developed to save the computational cost of MC. It has been applied to the model of contact between a deformable body and a rough uncertain substrate in [5] and the effect of uncertainties on quantities of interest related to contact mechanics of rough surfaces in [24]. The adaptive MLMC is also presented to solve the stochastic obstacle problem in [16].
Another approach is the polynomial chaos (PC)-based method [12, 29]. In this method, the stochastic solution is projected onto a stochastic space spanned by (generalized) PC basis. The stochastic Galerkin projection is used to transform the original stochastic problem into a system of deterministic equations whose size is much larger than the original stochastic problem. However, the accuracy and efficiency of this method need to be further improved. On one hand, since the computational effort increases dramatically as the number of random variables and/or the number of expansion terms increase, the PC-based method suffers from the curse of dimensionality [2], which is prohibitively expensive, especially for large-scale and high-dimensional stochastic problems. On the other hand, the classical PC-based method cannot accurately capture the discontinuous solutions of stochastic contact problems, thus it usually works in conjunction with other methods, e.g. the stochastic collocation method [2, 3, 10]. Other methods have also been proposed to solve related problems. The stochastic variational inequality problem (SVIP) is solved by stochastic projections and reformulations of SVIP in [14]. Low-rank tensor methods are used to solve parametrized SVIP of the obstacle type in [11].
As described so far, efficient methods for solving stochastic contact problems are still insufficient and further investigations are needed. In this paper we propose efficient two-step algorithms to solve (high-dimensional) stochastic contact problems. In the first step, the stochastic Lagrangian multiplier method and the stochastic penalty method are developed to compute a set of reduced basis. The stochastic solution in the stochastic Lagrangian multiplier method is expanded as a sum of products of a set of random variables and deterministic vectors. The stochastic solution in the stochastic penalty method is divided into the solutions of non-contact and possible contact nodes, which are represented as sums of the products of two different sets of random variables and deterministic vectors, respectively. Similar expansions of stochastic solutions have been widely used in the proper generalized decomposition (PGD)/generalized spectral decomposition (GSD) methods [19, 22]. In this kind of method, priori tensor product constructions and separated variables representations are adopted to approximate the solutions. The components of the approximations are calculated by several dedicated iterations [8, 17]. PGD-based methods have been widely applied to various problems with great success [8, 25] and the applications on contact problems can be found in [13, 18].
The improvements of the approximations used in this paper include two aspects: one is that the non-intrusive representation of expanded random variables allows complexly nonlinear stochastic problems to be dealt with in a weak-intrusive way and to avoid the curse of dimensionality successfully, and the other is that a dedicated expansion is developed for the stochastic penalty method, which overcomes the poor convergence of solutions using the same extended random variables for both non-contact and possible contact nodes.
Based on the two proposed expansions, original stochastic finite element equations are transformed into deterministic finite element equations and one-dimensional (corresponding to the stochastic Lagrangian multiplier method)/two-dimensional (corresponding to the stochastic penalty method) stochastic algebraic equations including all random variables. They are computed in their individual spaces, that is, deterministic finite element equations are solved by existing finite element methods and corresponding one-/two-dimensional stochastic algebraic equations are solved by a sampling method, the computational cost of which does not increase dramatically as the stochastic dimension increases. Hence the curse of dimensionality in high-dimensional stochastic spaces is circumvented with great success. The effectiveness of the proposed approaches is demonstrated on numerical examples of up to 100 dimensions.
As the so far obtained full-reduced order equations directly constructed by the reduced basis cannot capture the nonsmooth solutions of stochastic contact problems immediately, semi-reduced order Lagrangian multiplier/penalty equations are proposed to overcome that obstacle. This strategy consists of the reduced order model into two components. One component is a reduced basis model obtained by smooth solutions and the other is the full order equation for the nonsmooth solutions. The size of the semi-reduced order equation is small since the possible contact region is small compared to the whole domain in many applications, thus the computational effort is significantly saved. Similar ideas have been discussed for the static condensation process of deterministic contact problems [21, 26] and problems with localized solution behavior [1, 15], in which the reduced approximation basis is adopted in the region with smooth solutions and a standard finite element approximation is used in the region with high gradient or discontinuous solutions. In this paper, the reduced basis in the first step is still considered as global approximations and smooth parts of the reduced basis are used to generate the semi-reduced order equations in the second step.
The paper is organized as follows: The basic setting of stochastic contact problems is introduced in Sect. 2. In Sect. 3, we propose the stochastic Lagrangian multiplier method to solve stochastic contact problems, including the construction of stochastic solutions, the iterative algorithm and the algorithm implementation. Following that, a stochastic penalty method is developed in Sect. 4. In Sect. 5, two numerical examples of low- and high-dimensional cases are given to demonstrate the performance of the proposed methods. Section 6 gives conclusions and discussions.
2 Stochastic contact problems
In this paper, we consider linear elastic two-body normal contact problems without friction and adopt the finite element method to discretize the problem. The total energy of the deterministic system is given by
where U, W are the strain and kinetic energy and G comes from the contribution of the contact traction. Let \(( {\Theta , \Sigma , {{\mathcal {P}}}} )\) be a complete probability space, where \(\Theta \) denotes the space of elementary events, \(\Sigma \) is the \(\sigma \)-algebra defined on \(\Theta \) and \({{\mathcal {P}}}\) is the probability measure. Considering random parameters \(\theta \in \Theta \) and extending Eq. (1) to the stochastic case, the total energy of the stochastic system is described as
where \(U\left( \theta \right) \), \(W\left( \theta \right) \) and \(G\left( \theta \right) \) are considered as the stochastic strain energy, the stochastic kinetic energy and the stochastic contact contribution. They have similar forms to the deterministic cases but are related to the random input \(\theta \). The solution of Eq. (2) is obtained by minimizing the total potential energy \(\Pi \left( \theta \right) \), that is
Several methods can be used to formulate \(G\left( \theta \right) \), e.g. Lagrangian multiplier method, penalty method and augmented Lagrangian method, etc [26]. In this paper we only focus on the Lagrangian multiplier method and the penalty method. Other methods are beyond the scope of this article and will be studied in subsequent research.
Similar to the deterministic case, \({G}_L\left( \theta \right) \) of the stochastic Lagrangian multiplier method (SLMM) is given by
where \(s\left( \theta \right) \) is the stochastic contact interface, \(\gamma {\left( \theta \right) }\) is the vector of stochastic Lagrangian multipliers and coincides with the normal contact traction, \(g\left( \theta \right) \) is the random gap vector. Corresponding the first variation \(\delta {G}_L\left( \theta \right) \) in Eq. (3) is
Similar to the classical penalty method, the stochastic \({G}_P\left( \theta \right) \) of stochastic penalty method (SPM) is given by
where \(\alpha \) is the penalty parameter and the corresponding first variation \(\delta {G}_P\left( \theta \right) \) in Eq. (3) is calculated as
Analogous to the deterministic cases [26], the advantage of SLMM is that it meets contact constraint conditions exactly. The drawback is that finite element matrices based on SLMM are not positive definite and have augmented sizes due to introducing additional variables. It may present difficulties in dealing with some cases with friction. SPM has no additional variables but leads to very small physical penetration. We will develop numerical algorithms for solving the stochastic solutions based on SLMM and SPM in subsequent sections.
3 Stochastic Lagrangian multiplier method
In this section, we solve stochastic contact problems by adopting SLMM. By use of Eqs. (3) and (4) and the classical finite element discretization, a stochastic finite element equation regarding SLMM is obtained
where \(K(\theta ) \in {\mathbb {R}}^{n \times n}\) is the stochastic stiffness matrix, \(F(\theta ) \in {\mathbb {R}}^{n}\) is the stochastic force vector and \(Q \in {\mathbb {R}}^{n_c \times n}\) is the matrix related to \(n_c\) contact constraints and Lagrangian multipliers. The details of above finite element discretization can be found in [26].
It is noted that the coefficient matrix of Eq. (8) is not positive definite since
is indefinite. In order to avoid this difficulty, we rewrite Eq. (8) in the form
where \({{\widetilde{u}}}\left( \theta \right) = {\left[ {u{{\left( \theta \right) }^T},\gamma {{\left( \theta \right) }^T}} \right] ^T} \in {\mathbb {R}}^{n+n_c}\),
The stochastic matrix \({{\widetilde{K}}}\left( \theta \right) \) in Eq. (11) is positive definite since
holds. In the next subsection, to take advantage of the positive definiteness of the matrix \({{{\widetilde{K}}}}\left( \theta \right) \), we solve the reduced basis based on Eq. (10) rather than Eq. (8).
3.1 Stochastic solutions of SLMM
To efficiently solve the stochastic solution \({{{\widetilde{u}}}}\left( \theta \right) \) of Eq. (10), we introduce the following approximation
where the deterministic vectors \({{{{\widetilde{d}}}}_k} = {\left[ {d_k^T,q_k^T} \right] ^T} \in {\mathbb {R}}^{n + n_c}\), \(d_k \in {\mathbb {R}}^{n}\), \(q_k \in {\mathbb {R}}^{n_c}\), the scalar random variable \({\lambda _k}\left( \theta \right) \in {\mathbb {R}}\), the matrix \({{\widetilde{D}}} = \left[ {{{{{\widetilde{d}}}}_1}, \ldots ,{{{{\widetilde{d}}}}_k}} \right] \in {\mathbb {R}}^{ \left( {n + {n_c}} \right) \times k}\), the random variable vector \(\Lambda (\theta ) = \left[ \lambda _1(\theta ), \ldots , \lambda _k(\theta ) \right] ^T \in {\mathbb {R}}^{k}\) and the previous approximation \({{{\widetilde{u}}}_{k - 1}}\left( \theta \right) \) is given by
For the stochastic components \(u(\theta )\) and \(\gamma (\theta )\) of \({{\widetilde{u}}}\left( \theta \right) \), Eq. (13) is equivalent to \(u\left( \theta \right) = \sum \nolimits _{i = 1}^k {{\lambda _i}\left( \theta \right) {d_i}}\) and \(\gamma \left( \theta \right) = \sum \nolimits _{i = 1}^k {{\lambda _i}\left( \theta \right) {q_i}}\), where the vectors \(d_i \in {\mathbb {R}}^n\), \(q_i \in {\mathbb {R}}^{n_c}\) and each pair \(\left( {{d_i},{q_i}} \right) \) shares the same random variable coefficient \(\lambda _i(\theta )\). It is noted that all of them are unknown and iterative algorithms are used to compute them one by one. The expansion Eq. (13) has been widely used in the context of PGD/GSD methods [8, 19, 22, 32]. We develop improved expansions in this paper to deal with stochastic contact problems and high-dimensional random variables involved.
Based on Eq. (13), Eq. (10) is written as
where \({{{\widetilde{u}}}_{k - 1}}\left( \theta \right) \) is assumed to be known and the couple \(\{ {\lambda _k}\left( \theta \right) , {{{\widetilde{d}}}_k} \}\) is the unknown solution to be solved. However, it is not easy to determine the random variable \({\lambda _k}\left( \theta \right) \) and the vector \({{\widetilde{d}}}_k\) simultaneously. We adopt the following iterative algorithm [8, 22] to solve \({\lambda _k}\left( \theta \right) \) and \({{\widetilde{d}}}_k\):
If the random variable \({\lambda _k}\left( \theta \right) \) has been known (or given an initial value), the vector \({{{\widetilde{d}}}_k}\) is solved via the following deterministic finite element equation obtained by stochastic Galerkin method [12, 29],
where \({{\mathbb {E}}}\left\{ \cdot \right\} \) is the expectation operator and which can be rewritten as a compact form,
where the deterministic matrix and vector are given by
Equation (17) can be considered as a finite element equation for deterministic contact problems, thus existing contact FEM solver can be used to solve it efficiently [26, 27, 34]. Recalling Eq. (13), we approximate the stochastic solution by random linear combinations of the deterministic basis functions \(\left\{ {{{\widetilde{d}}}_k} \right\} \). Repeated or close modes of \(\left\{ {{{\widetilde{d}}}_k} \right\} \) make the number of retained terms for the stochastic solution large. Therefore, in practice, we only want to retain the vector \({{\widetilde{d}}}_k\) in dominant modes, so that the number of retained terms is as small as possible, which will also reduce the size of subsequent reduced order stochastic finite element equations. For this purpose, we let the solution \({{\widetilde{d}}}_k\) orthogonal to the obtained vectors \(\left\{ {\widetilde{d}}_i \right\} _{i=1}^{k-1}\) via Gram-Schmidt orthogonalization, which is corresponding to
If the deterministic vector \({{{\widetilde{d}}}_k}\) has been solved by use of Eqs. (17) and (20), the random variable \(\lambda _k(\theta )\) is updated via the following deterministic Galerkin procedure
where the simplification \({{{\widetilde{d}}}_k^T{{\widetilde{K}}}\left( \theta \right) {{{{\widetilde{d}}}}_k}} = { d_k^T K\left( \theta \right) {{d}_k}}\) holds based on Eq. (12). A commonly used method to solve Eq. (21) is the polynomial chaos (PC)-based method, which expands \(\lambda _k(\theta )\) by use of PC basis and solves the unknown expanded coefficients using a system of linear equations. However, this kind of method suffers from the curse of dimensionality when dealing with high-dimensional problems. It is noted that Eq. (21) is a one-dimensional stochastic algebraic equation of the random variable \(\lambda _k(\theta )\). In this paper, we propose a sampling method to compute \(\lambda _k(\theta )\) [32, 33], which is corresponding to,
where \(\star \left( {\widehat{\varvec{\theta }}} \right) \in {\mathbb {R}}^{\Box \times \Box \times n_s}\) is the sample representation of stochastic matrix (or vector, variable) \(\star \left( {\theta } \right) \in {\mathbb {R}}^{\Box \times \Box }\), \(n_s\) is the number of random samples, the vector \({{{\widetilde{d}}}_k^T\left[ {{{\widetilde{F}}}\left( { {\widehat{\varvec{\theta }}} } \right) - {{\widetilde{K}}}\left( {\widehat{\varvec{\theta }}} \right) {{{{\widetilde{u}}}}_{k - 1}}\left( {\widehat{\varvec{\theta }}} \right) } \right] }\! \in \!{\mathbb {R}}^{n_s}\), the vector \({d_{k}^TK\left( {\widehat{\varvec{\theta }}} \right) {d_{k}}} \in {\mathbb {R}}^{n_s}\), the vector \({\lambda _{k}}\left( {\widehat{\varvec{\theta }}} \right) \in {\mathbb {R}}^{n_s}\) represents the random sample vector of \({\lambda _{k}}\left( {{\theta }} \right) \). In practical calculations, Eq. (22) is performed by the element-wise division of the two vectors, which is similar to the Hadamard division operator. Equation (22) is less sensitive to the stochastic dimension and the computational effort is very low even for high stochastic dimensions, which avoids the curse of dimensionality successfully. Further, statistical methods can be used to compute probability characteristics of \({\lambda _{k}}\left( {{\theta }} \right) \) from the random samples \({\lambda _{k}}\left( {\widehat{\varvec{\theta }}} \right) \).
In this way, we calculate the k-th couple \(\left\{ \lambda _k\left( \theta \right) , {{{\widetilde{d}}}_k} \right\} \) by iteratively solving Eqs. (17) and (22) until a specified precision is reached, the details of which will be discussed in Algorithm 1. Also, the same iteration is used to calculate the next couple \(\left\{ \lambda _{k+1}\left( \theta \right) , {{{\widetilde{d}}}_{k+1}} \right\} \) until all couples are obtained. However, it is noted that the above iteration solves each couple \(\left\{ \lambda _k\left( \theta \right) , {{{\widetilde{d}}}_k} \right\} \) in a sequential way and the stochastic solution \({{\widetilde{u}}}\left( \theta \right) \) in Eq. (13) is also approximated in a greedy way. The original stochastic finite element equation (10) is not exactly met by the stochastic solution \({{\widetilde{u}}}_k\left( \theta \right) \) obtained in this way. Low-accuracy stochastic solutions are obtained for some problems, as illustrated in Example 5.1. To improve the accuracy of the stochastic solution, we consider \({{\widetilde{D}}} = \left[ {{{{{\widetilde{d}}}}_1}, \ldots ,{{{{\widetilde{d}}}}_k}} \right] \) as a set of reduced basis and introduce reduced order equations to recalculate the random vector \(\Lambda (\theta ) = \left[ \lambda _1(\theta ), \ldots , \lambda _k(\theta ) \right] ^T \in {\mathbb {R}}^k\) in the next two sections.
3.2 Full-reduced order method based on SLMM
As discussed above, we first build a full-reduced order equation by applying the known reduced order matrix \({{\widetilde{D}}}\) obtained by the above iteration to Eq. (10)
which is equivalent to
where the random vector \(\Lambda \left( \theta \right) \in {\mathbb {R}}^{k}\) is the unknown solution to be recalculated, \({{{\widetilde{K}}}_{{{\widetilde{D}}}}}\left( \theta \right) = {{{\widetilde{D}}}^T}{{{\widetilde{K}}}}\left( \theta \right) {{\widetilde{D}}} \in {\mathbb {R}}^{k \times k}\) is the reduced order stochastic matrix and \({{\widetilde{F}}}_{{{\widetilde{D}}}}\left( \theta \right) = {{{\widetilde{D}}}^T}{{\widetilde{F}}}\left( \theta \right) \in {\mathbb {R}}^{k}\) is the reduced order stochastic force vector. In practice, we solve Eq. (24) by
for each random sample realization \(\theta ^ {\left( {{i}} \right) }\), \(i = 1,\ldots ,n_s\) and the random samples \(\Lambda \left( {\widehat{\varvec{\theta }}} \right) = \left[ {\Lambda \left( {{\theta ^{\left( 1 \right) }}} \right) , \ldots ,\Lambda \left( {{\theta ^{\left( {{n_s}} \right) }}} \right) } \right] \in {\mathbb {R}}^{k \times n_s}\) are obtained by \(n_s\) solutions of Eq. (25). It is noted that the random samples \({\widehat{\varvec{\theta }}}\mathrm{{ = }}\left\{ \theta ^ {\left( {{i}} \right) } \right\} _{i = 1}^{{n_s}} \in \Theta \) used for solving Eq. (25) are not necessary to be the same as that used for solving the reduced order matrix \({{\widetilde{D}}}\) since only the deterministic matrix \({{\widetilde{D}}}\) is inherited from the iteration and no random quantities are involved.
The size of Eq. (24) is usually small thanking to the small value k, thus the computational effort for solving a single Eq. (25) is very low and the total computational costs of \(n_s\) solutions are still low. However, the full-reduced order equation (24) cannot accurately capture the nonsmooth stochastic solutions on the contact interface, which will be verified in Example 5.2. Hence, it is necessary to improve the accuracy of Eq. (24).
3.3 Semi-reduced order method based on SLMM
In order to improve the computational accuracy of the stochastic solution of the full-reduced order equation and to capture the nonsmooth stochastic solution on the stochastic contact interface, we propose a semi-reduced order method to solve stochastic contact problems.
Recall the full order stochastic finite element equation (8) and rewrite it in the form,
where the vectors \(u_1(\theta ) \in {{{\mathbb {R}}}^{{n - n_c}}}\) and \(u_2(\theta ) \in {{{\mathbb {R}}}^{{n_c}}}\) are the stochastic solutions of non-contact and possible contact degrees of freedom, the deterministic matrices \(B_1 \in {\mathbb {R}}^{n \times \left( n-n_c \right) }\) and \(B_2 \in {\mathbb {R}}^{n \times n_c}\) are used to locate the non-contact and possible contact solutions and their elements are given by
where \(\delta _{ij}\) is the Kronecker delta that meets \(\delta _{ij} = 1\) for \(i=j\) and 0 for \(i \ne j\), the set \(c_{\textrm{con}} = \left[ c_{\textrm{con},1}, \ldots ,c_{\textrm{con},n_c} \right] \in {{{\mathbb {R}}}^{{n_c}}}\) contains the indices of the degrees of freedom on the possible contact interface and the set \(c_{\textrm{non}} = \left[ c_{\textrm{non},1}, \ldots ,c_{\textrm{non},n-n_c} \right] \in {{{\mathbb {R}}}^{{n-n_c}}}\) are the indices of the rest of degrees of freedom.
Let the submatrix \(D_1 = \left[ B_1^T, 0_{\left( n-n_c\right) \times n_c}\right] {{{\widetilde{D}}}} \in {\mathbb {R}}^{\left( {n - {n_c}} \right) \times k} \subset {{\widetilde{D}}}\) be the reduced basis matrix corresponding to the non-contact nodes. The stochastic solution of the non-contact nodes is thus represented as \(u_1(\theta ) = D_1 \Lambda _1(\theta ) \in {\mathbb {R}}^{n - {n_c}}\), where \(\Lambda _1(\theta ) = \left[ \lambda _{1,1}\left( \theta \right) , \ldots , \lambda _{1,k}\left( \theta \right) \right] ^T \in {\mathbb {R}}^{k}\) is the random vector to be solved. Hence, the solution vector of Eq. (26) can be rewritten as
where \(I_{n_c} \in {{{\mathbb {R}}}^{n_c \times n_c}}\) is the identity matrix. Based on Eq. (26), we introduce the following deterministic Galerkin procedure to build a semi-reduced order stochastic finite element equation
which is rewritten as a compact form
where the reduced order matrices and vectors are given by
It is noted that only the stochastic solution of non-contact degrees of freedom is approximated by a reduced order representation and the stochastic solution of possible contact degrees of freedom is still solved in a full order way, thus the proposed method is a semi-reduced order approach. Further, the size of the semi-reduced order equation (31) is \(k+2n_c\), which is slightly larger than the size k of Eq. (24), but still very small compared to the original stochastic problem Eq. (8) in most applications. Similar to Eq. (25), we still adopt the sampling method to solve (31) for each sample realization and total computational costs of \(n_s\) solutions are still very low.
3.4 Algorithm implementation of SLMM

The proposed SLMM for solving stochastic contact problems is summarized in Algorithm 1, which includes a double-loop iterative procedure. The inner-loop iteration from step 3 to 10 is used to compute the couple \(\left\{ {{\lambda _k}\left( \theta \right) ,{{{\widetilde{d}}}_k}} \right\} \) and the outer loop from step 2 to 15 corresponds to recursively approximate the stochastic solution \({{\widetilde{u}}}_k(\theta )\). In order to compute each couple \(\left\{ {{\lambda _k}\left( \theta \right) ,{{{\widetilde{d}}}_k}} \right\} \), the random sample vector \({\lambda _{k,0}}\left( {\widehat{\varvec{\theta }}} \right) = \left\{ {{\lambda _{k,0}}\left( {{\theta ^{\left( i \right) }}} \right) } \right\} _{i = 1}^{{n_s}} \in {{{\mathbb {R}}}^{{n_s}}}\) is initialized in step 3. In practical implementation, any nonzero vectors with size \(n_s\) can be used as the initialization and it almost has no influence on the proposed method. The vector \({{\widetilde{d}}}_{k,j}\) is determined by solving the deterministic finite element equations in step 5, where the subscript j represents the j-th round iteration of \(\left\{ {{\lambda _{k,j}}\left( \theta \right) ,{{{\widetilde{d}}}_{k,j}}} \right\} \). Following that, \({{\widetilde{d}}}_{k,j}\) requires to be orthogonalized and normalized along the whole iterative process. With the obtained vector \({{\widetilde{d}}}_{k,j}\), the random variable \(\lambda _{k,j}(\theta )\) is then updated in step 7. The iterative error in step 8 is given by
where \(\left\| {\Box } \right\| = {\mathbb {E}}\left\{ {{{\Box }^T}{\Box }} \right\} \). The outer-loop iteration then generates a new approximated stochastic solution \(u_k(\theta )\) in step 11 and updates the deterministic matrix \({{\widetilde{D}}}\) in step 12. The iterative error in step 13 is defined as
which measures the contribution of the k-th stochastic increment \(\lambda _k(\theta ) {{\widetilde{d}}}_k\) to the stochastic solution \(u_k(\theta )\). Based on the known matrix \({{\widetilde{D}}}\), the semi-reduced order stochastic finite element equation with the size \(k + 2n_c\) is obtained and solved in step 16. We highlight that the sample size \(n_s\) used for solving the reduced basis can be different from that for solving the semi-reduced order stochastic equation. In practice, we can adopt a small size in step 3 to calculate the reduced basis and after obtaining the matrix D, a large sample size is reset in step 16 to solve the semi-reduced order stochastic finite element equation, which saves computational costs.
4 Stochastic penalty method
In this section, we propose a SPM to solve stochastic contact problems. According to Eqs. (3) and (6) and the classical finite element discretization, the stochastic finite element equation obtained by the penalty method is described as
where \(K_0(\theta ) \in {\mathbb {R}}^{n \times n}\) is the stochastic stiffness matrix, \(\alpha \) is the penalty parameter, \(K_p \in {\mathbb {R}}^{n \times n}\) is a deterministic matrix related to possible contact constraints and the detail of its assembly can be found in [26].
In the approximation Eq. (13), the vectors \(\left\{ {{{{\widetilde{d}}}_k}} \right\} \) of possible contact and non-contact degrees of freedom share the same random variable coefficients \(\left\{ {{\lambda _k}\left( \theta \right) } \right\} \). It does not work well for SPM since a large penalty parameter biases the random variables \(\left\{ {{\lambda _k}\left( \theta \right) } \right\} \) towards the solution of the possible contact degrees of freedom. Let us give a simple explanation for this point. For the purpose, we still consider an Eq. (13)-like approximation used to SPM, that is, the coefficient of the deterministic vector \(d_k^* \in {\mathbb {R}}^{n}\) is a random variable \(\lambda _k^*\left( \theta \right) \in {\mathbb {R}}\). Similar to Eq. (21), \(\lambda _k^*\left( \theta \right) \) is solved under a known vector \(d_k^*\)
which is further rewritten as
the approximate equivalence in which holds for a large penalty parameter \(\alpha \). The penalty parameter biases \(\lambda _k^*\left( \theta \right) \) towards the contribution of \(d_k^{*T}K_pd_k^*\), which cannot capture the contribution of non-contact nodes well.
4.1 Stochastic solutions of SPM
In order to solve Eq. (35), we introduce the following approximation to avoid the difficulty suffering from the expansion Eq. (13),
where the vector \({u_{k - 1}}\left( \theta \right) \in {{\mathbb {R}}}^n\) is the previous approximation of the stochastic solution and it is usually already known, the vector \(\Delta {u_k}\left( \theta \right) \in {{\mathbb {R}}}^n\) is the unknown stochastic increment to be solved. The size of \(u_k\left( \theta \right) \) in Eq. (38) is the same as the original stochastic problem, which is different from the augmented vector \({{\widetilde{u}}}_k\left( \theta \right) \in {{\mathbb {R}}}^{n+n_c}\) in SLMM.
To calculate the unknown stochastic increment \(\Delta {u_k}\left( \theta \right) \), we introduce the following two equivalent approximations
where \(d_k \in {{\mathbb {R}}}^n\) is the unknown deterministic vector to be solved, the random variable vector \({\lambda _k}\left( \theta \right) = \left[ {\lambda _{k,1}}\left( \theta \right) ,{\lambda _{k,2}}\right. \left. \left( \theta \right) \right] ^T \in {{\mathbb {R}}}^{2}\) is also unknown, the index matrices \(Z_m = B_mB_m^T \in {\mathbb {R}}^{n \times n}\), \(m=1,2\), \(B_m\) have been given in Eqs. (27) and (28). They can also be calculated by \(Z_{1,ij} = \sum \limits _{k=1}^{n-n_c}{ {\delta _{i,c_{\textrm{non},k}}}{\delta _{j,c_{\textrm{non},k}}} }\) and \(Z_{2,ij} = \sum \limits _{k=1}^{n_c}{ {\delta _{i,c_{\textrm{con},k}}}{\delta _{j,c_{\textrm{con},k}}} }\) for \(i,j=1,\ldots ,n\). Equation (35) thus becomes as
where the matrix \(K\left( \theta \right) = {K_0}\left( \theta \right) \mathrm{{ + }}\alpha {K_p} \in {\mathbb {R}}^{n \times n}\) and the vector \({F_k}\left( \theta \right) = F\left( \theta \right) - K\left( \theta \right) {u_{k - 1}}\left( \theta \right) \in {\mathbb {R}}^n\).
Similar to SLMM, an alternating iteration is adopted in this section to solve the triplet \(\left\{ {{\lambda _{k,1}}\left( \theta \right) ,{\lambda _{k,2}}\left( \theta \right) ,{d_k}} \right\} \) in Eq. (39) one by one. Specially, for known random variables \({\lambda _{k,1}}\left( \theta \right) \) and \({\lambda _{k,2}}\left( \theta \right) \), the vector \({d_k}\) is solved via the following deterministic finite element equation obtained by the approximation Eq. (39) and stochastic Galerkin method
where the deterministic matrix and vector are given by
Further, Eq. (42) can be rewritten as
where the matrices \({{\widetilde{K}}}_{0,k}\) and \({{\widetilde{K}}}_{p,k}\) are obtained by Eq. (43)
In this way, Eq. (42) (or Eq. (45)) can also be considered as a finite element equation with penalty parameters for deterministic contact problems and existing contact FEM solvers are available. Similar to SLMM, we retain the dominant vector \(d_k\) and Eq. (20) is still adopted to orthogonalize the vector \(d_k\).
Based on the obtained vector \(d_k\), an updated random vector \({\lambda _k}\left( \theta \right) = {\left[ {{\lambda _{k,1}}\left( \theta \right) ,{\lambda _{k,2}}\left( \theta \right) } \right] ^T}\) is solved by Eq. (40) and the following deterministic Galerkin procedure
which is rewritten as
where the random variables \(c_{k,ij}\left( \theta \right) \) and \(h_{k,i}\left( \theta \right) \) are given by
for \(i,j=1,2\). By taking advantage of the proposed sampling method used in Eq. (22), the stochastic solutions \({\lambda _{k,1}}\left( \theta \right) \) and \({\lambda _{k,2}}\left( \theta \right) \) of Eq. (49) are solved via the following two decoupled equations
where the random sample vectors of the numerators \(s_{k,1}\left( {\widehat{\varvec{\theta }}} \right) , s_{k,2}\left( {\widehat{\varvec{\theta }}} \right) \in {\mathbb {R}}^{n_s}\) and the denominator \(s_{k,0}\left( {\widehat{\varvec{\theta }}} \right) \in {\mathbb {R}}^{n_s}\) are given by
Computational costs for solving Eqs. (52) and (53) are still very low. Also, similar to Eq. (22) used in SLMM, both Eq. (52) and (53) are insensitive to the stochastic dimension, thus SPM can also be applied to high-dimensional stochastic contact problems.
4.2 Semi-reduced order method based on SPM
In order to build a reduced order equation for SPM, we rewrite the approximate stochastic solution \(u_k(\theta )\) as
where \(\Lambda \left( \theta \right) = {\left[ {{\lambda _{1,1}}\left( \theta \right) , \ldots ,{\lambda _{k,1}}\left( \theta \right) ,u_2^T\left( \theta \right) } \right] ^T} \in {\mathbb {R}}^{k+n_c}\) is a random vector and \(u_2(\theta ) \in {{{\mathbb {R}}}^{{n_c}}}\) is the stochastic solution of the possible contact degrees of freedom. Similar to Eq. (30), the semi-reduced order stochastic finite element equation of SPM is then given as
where the sizes of the stochastic submatrices and subvectors are \({D^T}Z_1^TK\left( \theta \right) {Z_1}D \in {{{\mathbb {R}}}^{k \times k}}\), \({D^T}Z_1^TK\left( \theta \right) {B_2} \in {{{\mathbb {R}}}^{k \times {n_c}}}\), \(B_2^TK\left( \theta \right) {Z_1}D \in {{{\mathbb {R}}}^{{n_c} \times k}}\), \(B_2^TK\left( \theta \right) {B_2} \in {{{\mathbb {R}}}^{{n_c} \times {n_c}}}\), \({D^T}Z_1^TF\left( \theta \right) \in {\mathbb {R}}^k\) and \(B_2^TF\left( \theta \right) \in {\mathbb {R}}^{n_c}\). The sampling approach used in Eq. (25) is again adopted to solve the semi-reduced order stochastic finite element equation (56) for each sample realization. One-sample solution of Eq. (56) is cheaply solved since its size \(k+n_c\) is much smaller than the original stochastic problem. Total computational costs for \(n_s\) random samples \(\Lambda \left( {\widehat{\varvec{\theta }}} \right) = \left[ {\Lambda \left( {{\theta ^{\left( 1 \right) }}} \right) , \ldots ,\Lambda \left( {{\theta ^{\left( {{n_s}} \right) }}} \right) } \right] \in {\mathbb {R}}^{\left( {k + {n_c}} \right) \times n_s}\) of the solution are still low.
4.3 Algorithm implementation of SPM

The proposed stochastic penalty method for solving stochastic contact problems is summarized in Algorithm 2 and the procedure is similar to Algorithm 1. It is noted that samples of two random variables \(\lambda _{k,1}(\theta )\) and \(\lambda _{k,2}(\theta )\) need to be initialized in step 3 and corresponding updates of two random variables are processed in step 7. After the inner-loop iteration, the stochastic increment \(\Delta u_k(\theta )\) in step 11 is updated via Eqs. (39) or (40). Similar to Eq. (34), the iterative error in step 13 is now defined by use of random variables \({\left\{ {{\lambda _{k,1}}(\theta )} \right\} _k}\),
and the iterative error \({\varepsilon _{l,j}}\) in step 8 has been defined in Eq. (33).
5 Numerical examples
In this section, we test the proposed SLMM and SPM by two numerical examples. For both SLMM and SPM, the convergence errors are set as \({\varepsilon _{l}} = 1 \times 10^{-3}\) and \({\varepsilon _{g}} = 1 \times 10^{-6}\) in Algorithm 1 and . The number of random samples is \(n_s = 1 \times 10^4\) and the reference solutions are obtained by \(1 \times 10^4\) standard MCS. The penalty parameter is \(\alpha =10^{6}~\mathrm{{N/m^2}}\) in SPM.
5.1 Euler Bernoulli beam limited by a rigid block
This example considers a one-dimensional Euler Bernoulli beam shown in Fig. 1, which is clamped at one end and subjected to a distributed load q(x). The deflection of the free end of the beam is limited by a rigid block. There is a small random gap between the end of the beam and the rigid block. The bending rigidity \(EI\left( x, \theta \right) \) is considered as a Gaussian random field with the mean function \({{\overline{EI}}}\left( x \right) \) and the covariance function given by
By use of Karhunen–Loève (KL) expansion [4, 31], the random field \(EI\left( x, \theta \right) \) is approximated by the following series expansion
where r is the truncation number, \(\left\{ {{\xi _i}\left( \theta \right) } \right\} _{i = 1}^r\) are independent standard Gaussian random variables and \({\left\{ {{\kappa _i},{f_i}\left( x \right) } \right\} _i^r}\) are solved by the homogeneous Fredholm integral equation of the second kind,
In this example the following numerical parameters are adopted: the distributed load \(q(x)=1 \times 10^3~\mathrm {kN/m}\), the length of the beam \(L=1~\textrm{m}\), the mean value of the bending rigidity \({{\overline{EI}}}\left( x \right) = 1 \times 10^7~\mathrm {N \cdot m^2}\), the standard deviation \(\sigma _{EI} = 0.2{{\overline{EI}}}\left( x \right) \), the correlation length \(l_x=1~\textrm{m}\), the truncation number \(r=5\) and the random gap is a uniform random variable on \(\left[ {1,1.5} \right] \times 10^{-2}~\textrm{m}\). It is noted that the random samples \({\theta }^{\left( i \right) }\) such that \(\mathop {\min }\limits _{x} EI\left( x,\theta ^{\left( i \right) } \right) \le 1 \times 10^{-3}\) are dropped out to make sure that all realizations are positive, thus \(EI\left( x,\theta \right) \) is considered as a truncated Gaussian random field in the numerical implementation The model is discretized into 100 two-node Euler Bernoulli beam elements [23]. In this element, each node includes 2 degrees of freedom given by the vertical displacement and the rotation. Thus 101 nodes and \(n=202\) degrees of freedom (two of which are fixed at the left boundary) are defined totally, where the number of the possible contact degrees of freedom is \(n_c=1\).
Figure 2 shows the comparison between the probability density functions (PDFs) of the stochastic solution of the vertical displacement of the free end without the rigid block and the random gap. The free end is in the contact state for the stochastic solution exceeding 0.015 m and is in the non-contact state for the stochastic solution less than 0.01 m. The stochastic contact occurs for the solution in the random gap interval. In other words, the occurrence of the contact state between the free end and the rigid block is random since the stochastic solution and the gap are independent in the interval \(\left[ {1,1.5} \right] \times 10^{-2}\). It is necessary to check the stochastic contact state in practical computations.
We make use of the proposed Algorithm 1 and 2 to solve this problem. Iterative errors of the proposed SLMM and SPM are shown Fig. 3, which indicates that SPM is more efficient than SLMM in this case since only \(k=3\) retained items are needed to achieve the specified accuracy while SLMM needs nine items.
The PDFs of the stochastic vertical displacement of the free end obtained by SLMM, SPM and MCS are compared in Fig. 4, where the SLMM (initial) and SPM (initial) represent the solutions obtained by the iterative step 2 to 15 of Algorithm 1 and , i.e. the stochastic solution \(u_k(\theta )\) in step 11 after the last iteration, and the SLMM (final) and SPM (final) represent the solutions obtained by semi-reduced stochastic finite element equations in step 16 of Algorithm 1 and 2. As shown in Fig. 4a, b, the solutions of both SLMM (final) and SPM (final) have good agreement with MCS, which demonstrates the high accuracy of the proposed methods. SLMM (initial) shows less accuracy and the semi-reduced stochastic finite element equation is necessary to improve the approximation accuracy while SPM (initial) is already of high accuracy. It is noted that the PDFs in Fig. 4 are discontinuous at the boundary values 0.01 m and 0.015 m of the random gap. In fact, as shown in Fig. 5, for each sample realization of the random gap, the PDF of the vertical displacement of the free end is discontinuous at the value of the sample. If all samples of the gap are considered in the case of Fig. 5, we can obtain the PDF that is continuous in the interval of the random gap but still discontinuous at the boundary. The proposed methods can capture this characteristic well, as depicted in Fig. 4. Moreover, PDFs of contact forces of the free end obtained by SLMM and MCS are shown in Fig. 6, which indicates the proposed SLMM is in good accordance with MCS and accurately captures the discontinuous contact force around zero (i.e. the non-contact state).
5.2 Contact between hemisphere and rigid body
In this example we consider a hemisphere in contact with a rigid body shown in Fig. 7a where the radius is \(1.0~\textrm{m}\) and the force \(f(x,y) = 1.5 \times 10^3~\mathrm {MN/m}\). We only use a half model for the analysis by taking advantage of the symmetry. The finite element mesh is depicted in Fig. 77b, including 374 nodes and 672 triangular elements with linear shape functions. Poisson’s ratio of the hemisphere is \(\nu = 0.2\). The Young’s modulus \(E\left( x,y, \theta \right) \) is considered as a Gaussian random field with the mean value \({{\overline{E}}} (x,y) = 210~{\textrm{GPa}}\) and the covariance function
where the standard deviation \(\sigma _E = 0.1 {{\overline{E}}} (x,y)\) and the correlation lengths \(l_x = l_y = 1~\textrm{m}\). Similar to Eq. (59), we approximate the random filed \(E\left( x,y, \theta \right) \) by use of KL expansion. The number of the truncated item of KL expansion is adopted as \(r = 10\). Again, the sample realizations \({\theta }^{\left( i \right) }\) such that \(\mathop {\min }\limits _{x,y} E\left( x,y,\theta ^{\left( i \right) } \right) \le 1 \times 10^{-3}\) are dropped out to generate positive random samples.
The iterative errors of SLMM and SPM are shown in Fig. 8. The items \(k=11\) for SLMM and \(k= 9\) for SPM are retained to achieve the specified accuracy, which indicates that SPM is still more efficient than SLMM. In this sense, SPM is suggested to be a better choice for solving most stochastic contact problems.
The first six reduced basis in x and y directions obtained by SLMM and SPM are depicted in Fig. 9. As shown in Fig. 9a, b, the comparison of the reduced basis in the x direction between SLMM and SPM indicates that the reduced basis of possible contact nodes are more dominant components in SPM. It is seen from Fig. 9c, d that this conclusion is more obvious in the y direction since the contact boundary is closely related to the displacement in the y direction. Also, the first item \(d_{x1}\) and \(d_{y1}\) of SLMM are similar to that of SPM since both of them are solved by contactless stochastic problems.
To illustrate the accuracy of the proposed methods, we compare the solutions obtained by the proposed methods and MCS. As shown in Fig. 10, the solutions of five characteristic nodes are checked, including the contact nodes, the possible contact nodes and the non-contact nodes on the possible contact interface, the nodes near and far from the possible contact interface. For the contact nodes on the possible contact interface, SLMM matches contact boundary conditions accurately. The relative errors between the vertical displacements of contact nodes obtained by SPM and the gaps are shown in Table 1, where \(gap_i\) represents the initial gap value of the i-th contact node (i.e. the cyan points) shown in Fig. 10. The results in Table 1 show the high accuracy of SPM for solving the solutions of contact nodes. The possible contact nodes (i.e. the red points in Fig. 10) on the possible contact interface are the nodes that are in contact states for some samples of random parameters and in non-contact states for other samples, thus they are in ‘possible’ contact states. Accurately capturing possible contact states is a difficulty for stochastic contact problems since their PDFs are strongly discontinuous. PDFs of the solutions of the possible contact nodes are shown in Fig. 11, which indicates that both SLMM and SPM are in good accordance with MCS and can capture the discontinuities well. Figure 12 depicts PDFs of the solutions of the non-contact nodes (i.e. the blue points in Fig. 10) on the possible contact interface. The stochastic solutions are less than the corresponding gap values for all samples of random parameters, thus all of them are in non-contact states. All of the
above nodes are on the possible contact interface and their stochastic solutions are solved by the full order component of the semi-reduced order stochastic finite element equation. The proposed methods have good accuracy for these nodes. We also check the nodes that are not on the possible contact interface, whose stochastic solutions are solved by the reduced order component of the semi-reduced order stochastic finite element equation. PDFs of the solutions of the points A and B (as depicted in Fig. 10) in x and y directions are shown in Fig. 13. The good accuracy of SLMM and SPM is certified again.
For comparisons, we solve the stochastic solutions by use of the full-reduced order method proposed in section 3.2 and the PC-based stochastic Lagrangian multiplier method given in “Appendix”. The size of the full-reduced order equation is equal to the retained items \(k=11\). Two-order Hermite PC basis of ten standard Gaussian random variables are adopted. The number of PC basis is 66 and the size of the derived finite element equations is about \(5 \times 10^4\), which is much higher than the original stochastic problem. Solutions of the contact nodes on the possible contact interface obtained by the full-reduced order method and PC-based SLMM are seen in Fig. 14, which indicates that both the full-reduced order method and PC-based SLMM cannot meet the contact boundary exactly.
where \(t_S\) (second) is the computational time for computing the reduced basis, \(t_U\) is the computational time for solving the semi-reduced order stochastic finite element equation and \(t_T\) is the total time.
To verify the validity of the proposed methods for solving high-dimensional stochastic contact problems, different stochastic dimensions \(r=10\) and 100 are solved using SLMM and SPM. All of them are tested on a laptop (dual-core, Intel Core i7, 2.40GHz). Computational times are listed in Table 2, which indicates that the proposed SLMM and SPM are efficient even for the stochastic dimension 100. For both SLMM and SPM, as the stochastic dimension increases, the computational time \(t_U\) for solving the semi-reduced order stochastic finite element equations slightly increases since the retained item k is a bit larger than the low-dimensional case while the computational time \(t_S\) for computing reduced basis increases. In this paper, we adopt KL expansion (as shown in Eq. (59)) to approximate the random fields and the stochastic matrix \(K(\theta )\) in SLMM and SPM has the form \(K\left( \theta \right) = \sum \nolimits _{i = 0}^r {{\xi _i}\left( \theta \right) {K_i}}\). Extra computational effort and storage are needed for a large number of deterministic matrices \(\left\{ {{K_i}} \right\} _{i = 0}^r\), thus the computational time \(t_S\) is high for the high-dimensional case. High-performance computational equipment and parallel computing can be used to reduce the computational time furthermore.
Further, we study the influence of the sample size \(n_s\) on the proposed methods and only SLMM used for the case of 10 stochastic dimensions is tested as an illustration. In numerical implementation, the sample sizes \(n_s = 10^1, 10^2, 10^3, 10^4\) in step 3 of Algorithm 1 are first used to solve the reduced basis matrix D and \(n_s\) is then reset as \(10^4\) in step 16 to solve the semi-reduced order stochastic finite element equation. PDFs of stochastic displacements of the point A in the y direction obtained by different sample sizes \(n_s\) are compared in Fig. 15a and their absolute errors relative to the reference PDF obtained by MCS are seen from Fig. 15b, which indicates that the computational accuracy decreases slightly as the sample size \(n_s\) decreases. It is noted that the PDF accuracy is acceptable in most cases even only 10 samples are adopted to calculate the reduced basis, thus we do not need to carefully choose the sample size in many problems.
Further, computational costs of different sample sizes are listed in Table 3, where the times \(t_S\), \(t_U\) and \(t_T\) have the same meaning as that in Table 2. It is seen that for all cases, the computational times \(t_U\) for solving the semi-reduced order stochastic finite element equations are almost the same since the number of retained terms is very close. While the computational times \(t_S\) for calculating reduced basis decreases as the sample size decreases since the computational costs for performing Eqs. (18), (19) and (22) are reduced.
6 Conclusion
This paper develops two semi-reduced order stochastic finite element methods for solving stochastic contact problems and two numerical examples are used to certify their accuracy and efficiency. Based on the approximations of stochastic solutions proposed for SLMM and SPM and the corresponding iterative algorithms, the reduced basis are calculated by solving deterministic finite element equations and one-/two-dimensional stochastic algebraic equations. By use of the obtained reduced basis, the original problems are transformed into semi-reduced order stochastic finite element equations, whose solutions are solved by using a non-intrusive sampling method. The proposed methods can be applied to high-dimensional stochastic contact problems and avoid the curse of dimensionality successfully. In these senses, the proposed methods provide novel and efficient numerical strategies for solving stochastic contact problems.
We only focus on the stochastic Lagrangian multiplier method and stochastic penalty method in this paper. Extending other methods for solving deterministic contact problems to the stochastic cases is attractive, e.g. the augmented Lagrangian multiplier method. Also, we only consider linear elastic contact problems. Contact problems coupled with other nonlinearities should be further studied, e.g. material nonlinearity or large deformations.
References
Ammar A, Pruliere E, Férec J et al (2009) Coupling finite elements and reduced approximation bases. Eur J Comput Mech/Revue Européenne de Mécanique Numérique 18(5–6):445–463. https://doi.org/10.3166/ejcm.18.445-463
Arnst M, Ghanem R (2012) A variational-inequality approach to stochastic boundary value problems with inequality constraints and its application to contact and elastoplasticity. Int J Numer Methods Eng 89(13):1665–1690. https://doi.org/10.1002/nme.3307
Baroth J, Bressolette P, Chauvière C et al (2007) An efficient SFE method using Lagrange polynomials: application to nonlinear mechanical problems with uncertain parameters. Comput Methods Appl Mech Eng 196(45–48):4419–4429. https://doi.org/10.1016/j.cma.2007.04.017
Betz W, Papaioannou I, Straub D (2014) Numerical methods for the discretization of random fields by means of the Karhunen–Loève expansion. Comput Methods Appl Mech Eng 271:109–129. https://doi.org/10.1016/j.cma.2013.12.010
Bierig C, Chernov A (2015) Convergence analysis of multilevel Monte Carlo variance estimators and application for random obstacle problems. Numer Math 130(4):579–613. https://doi.org/10.1007/s00211-014-0676-3
Bostan V, Han W (2006) A posteriori error analysis for finite element solutions of a frictional contact problem. Comput Methods Appl Mech Eng 195(9–12):1252–1274. https://doi.org/10.1016/j.cma.2005.06.003
Chevalier L, Cloupet S, Soize C (2005) Probabilistic model for random uncertainties in steady state rolling contact. Wear 258(10):1543–1554. https://doi.org/10.1016/j.wear.2004.11.012
Chinesta F, Keunings R, Leygue A (2013) The proper generalized decomposition for advanced numerical simulations: a primer. Springer, New York. https://doi.org/10.1007/978-3-319-02865-1
Duong TX, De Lorenzis L, Sauer RA (2019) A segmentation-free isogeometric extended mortar contact method. Comput Mech 63(2):383–407. https://doi.org/10.1007/s00466-018-1599-0
Forster R, Kornhuber R (2010) A polynomial chaos approach to stochastic variational inequalities. J Numer Math. https://doi.org/10.1515/jnum.2010.012
Garreis S, Ulbrich M (2017) Constrained optimization with low-rank tensors and applications to parametric problems with PDEs. SIAM J Sci Comput 39(1):A25–A54. https://doi.org/10.1137/16M1057607
Ghanem RG, Spanos PD (2003) Stochastic finite elements: a spectral approach. Courier Corporation, North Chelmsford. https://doi.org/10.1007/978-1-4612-3094-6
Giacoma A, Dureisseix D, Gravouil A et al (2015) Toward an optimal a priori reduced basis strategy for frictional contact problems with LATIN solver. Comput Methods Appl Mech Eng 283:1357–1381. https://doi.org/10.1016/j.cma.2014.09.005
Jiang H, Xu H (2008) Stochastic approximation approaches to the stochastic variational inequality problem. IEEE Trans Autom Control 53(6):1462–1475. https://doi.org/10.1109/TAC.2008.925853
Kerfriden P, Passieux JC, Bordas SPA (2012) Local/global model order reduction strategy for the simulation of quasi-brittle fracture. Int J Numer Methods Eng 89(2):154–179. https://doi.org/10.1002/nme.3234
Kornhuber R, Youett E (2018) Adaptive multilevel Monte Carlo methods for stochastic variational inequalities. SIAM J Numer Anal 56(4):1987–2007. https://doi.org/10.1137/16M1104986
Ladevèze P, Passieux JC, Néron D (2010) The Latin multiscale computational method and the proper generalized decomposition. Comput Methods Appl Mech Eng 199(21–22):1287–1296. https://doi.org/10.1016/j.cma.2009.06.023
Néron D, Ladevèze P (2010) Proper generalized decomposition for multiscale and multiphysics problems. Arch Comput Methods Eng 17(4):351–372. https://doi.org/10.1007/s11831-010-9053-2
Néron D, Boucard PA, Relun N (2015) Time-space PGD for the rapid solution of 3D nonlinear parametrized problems in the many-query context. Int J Numer Methods Eng 103(4):275–292. https://doi.org/10.1002/nme.4893
Newberry F, Hampton J, Jansen K et al (2021) Bi-fidelity reduced polynomial chaos expansion for uncertainty quantification. Comput Mech. https://doi.org/10.1007/s00466-021-02096-0
Nour-Omid B, Wriggers P (1986) A two-level iteration method for solution of contact problems. Comput Methods Appl Mech Eng 54(2):131–144. https://doi.org/10.1016/0045-7825(86)90122-2
Nouy A (2007) A generalized spectral decomposition technique to solve a class of linear stochastic partial differential equations. Comput Methods Appl Mech Eng 196(45–48):4521–4537. https://doi.org/10.1016/j.cma.2007.05.016
Oñate E (2013) Structural analysis with the finite element method. Linear statistics: volume 2: beams, plates and shells. Springer, New York. https://doi.org/10.1007/978-1-4020-8743-1
Rey V, Krumscheid S, Nobile F (2019) Quantifying uncertainties in contact mechanics of rough surfaces using the multilevel Monte Carlo method. Int J Eng Sci 138:50–64. https://doi.org/10.1016/j.ijengsci.2019.02.003
Scanff R, Néron D, Ladevèze P et al (2022) Weakly-invasive LATIN-PGD for solving time-dependent non-linear parametrized problems in solid mechanics. Comput Methods Appl Mech Eng 396(114):999. https://doi.org/10.1016/j.cma.2022.114999
Wriggers P, Laursen TA (2006) Computational contact mechanics. Springer, New York. https://doi.org/10.1007/978-3-540-32609-0
Wriggers P, Nackenhorst U (2006) Analysis and simulation of contact problems. Springer, New York. https://doi.org/10.1007/3-540-31761-9
Wriggers P, Scherf O (1995) An adaptive finite element algorithm for contact problems in plasticity. Comput Mech 17(1):88–97. https://doi.org/10.1007/BF00356481
Xiu D, Karniadakis GE (2002) The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J Sci Comput 24(2):619–644. https://doi.org/10.1137/S1064827501387826
Zakian P, Khaji N (2019) A stochastic spectral finite element method for solution of faulting-induced wave propagation in materially random continua without explicitly modeled discontinuities. Comput Mech 64(4):1017–1048. https://doi.org/10.1007/s00466-019-01692-5
Zheng Z, Dai H (2017) Simulation of multi-dimensional random fields by Karhunen–Loève expansion. Comput Methods Appl Mech Eng 324:221–247. https://doi.org/10.1016/j.cma.2017.05.022
Zheng Z, Dai H (2021) Structural stochastic responses determination via a sample-based stochastic finite element method. Comput Methods Appl Mech Eng 381(113):824. https://doi.org/10.1016/j.cma.2021.113824
Zheng Z, Beer M, Dai H et al (2022) A weak-intrusive stochastic finite element method for stochastic structural dynamics analysis. Comput Methods Appl Mech Eng 399(115):360. https://doi.org/10.1016/j.cma.2022.115360
Zienkiewicz OC, Taylor RL (2005) The finite element method for solid and structural mechanics. Elsevier, New York. https://doi.org/10.1016/C2009-0-26332-X
Acknowledgements
The authors are grateful to the Alexander von Humboldt Foundation and the International Research Training Group 2657 (IRTG 2657) funded by the German Research Foundation (DFG) (Grant number 433082294).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 PC-based stochastic Lagrangian multiplier method
Although the PC-based methods are well-known for solving many stochastic problems [20, 30], there is only little effort in solving stochastic contact problems. We provide a comparative study between the proposed methods and the PC-based method in Example 5.2. In this section, we give a simple process to solve the stochastic finite element equation (8) using the PC-based stochastic Lagrangian multiplier method.
In the context of the PC-based method, the stochastic solution of Eq. (8) is represented as
where \(\{{\Psi _i}\left( \theta \right) \}_{i=1}^P\) are PC basis, the total number P of the PC basis is \(\left( {r + p} \right) !/r!/p!\), where \(\left( \cdot \right) !\) represents the factorial operator, r and p are the number of random variables and the order of PC basis, respectively, the unknown vector \({\left[ {u_i^T,\gamma _i^T} \right] ^T \in {\mathbb {R}}^{n+n_c}}\) are the deterministic expanded coefficients corresponding to the basis \({\Psi _i}\left( \theta \right) \). Although there are theoretical guidelines [29], the type of PC basis and the expansion order still need to be specified manually. Substituting Eq. (62) into Eq. (8) and applying stochastic Galerkin method we have
equivalently,
where the matrices \(K_{ji}={{{\mathbb {E}}}\left\{ {K\left( \theta \right) {\Psi _i}\left( \theta \right) {\Psi _j}\left( \theta \right) } \right\} }\) \(\in {\mathbb {R}}^{n \times n}\), the vectors \({F_j} = {{\mathbb {E}}}\left\{ {F\left( \theta \right) {\Psi _j}\left( \theta \right) } \right\} \in {\mathbb {R}}^{n}\), \({g_j} = {{\mathbb {E}}}\left\{ {g\left( \theta \right) {\Psi _j}\left( \theta \right) } \right\} \in {{{\mathbb {R}}}^{{n_c}}}\) and which can be rewritten as
where the solutions \({{\widetilde{u}}} = {\left[ {u_1^T, \ldots ,u_P^T} \right] ^T \in {\mathbb {R}}^{nP}}\), \({{\widetilde{\gamma }}} = {\left[ {\gamma _1^T, \ldots ,\gamma _P^T} \right] ^T \in {\mathbb {R}}^{n_cP}}\) and the deterministic matrices are given by
It is worth noting that the size of the PC-derived deterministic finite element equation (65) is \(nP = \left( n+n_c \right) \left( {r + p} \right) !/r!/p!\), which is significantly higher than the original stochastic problem. It is prohibitively expensive to solve Eq. (65) for high-dimensional and large-scale stochastic contact problems and thus leads to the curse of dimensionality.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zheng, Z., Nackenhorst, U. Semi-reduced order stochastic finite element methods for solving contact problems with uncertainties. Comput Mech 72, 991–1008 (2023). https://doi.org/10.1007/s00466-023-02323-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-023-02323-w



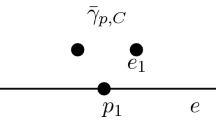











 ), the possible contact nodes (the red points
), the possible contact nodes (the red points  ) on the possible contact interface, the nodes near and far from the possible contact interface (the points A and B
) on the possible contact interface, the nodes near and far from the possible contact interface (the points A and B )
)



