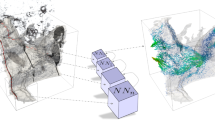
Abstract
In this contribution we propose a data-driven surrogate model for the prediction of permeabilities and laminar flow through two-dimensional random micro-heterogeneous materials; here Darcy’s law is used. The philosophy of the proposed scheme is to provide a large number of training sets through a numerically “cheap” (stochastic) model instead of using an “expensive” (FEM) one. In order to achieve an efficient computational tool for the generation of the database (up to \(10^3\) and much more realizations), needed for the training of the neural networks, we apply a stochastic model based on the Brownian motion. An efficient algebraic algorithm compared to a classical Monte Carlo approach is based on the evaluation of stochastic transition matrices. For the encoding of the microstructure and the optimization of the surrogate model, we compare two architectures, the so-called UResNet model and the Fourier Convolutional Neural Network (FCNN). Here we analyze two FCNNs, one based on the discrete cosine transformation and one based on the complex-valued discrete Fourier transformation. Finally, we compare the flux fields and the permeabilities for independent microstructures (not used in the training set) with results from the \(\hbox {FE}^2\) method, a numerical homogenization scheme, in order to demonstrate the efficiency of the proposed surrogate model.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
For several years now, data-driven science has become increasingly important for gaining scientific knowledge, see [38]. Starting from experimentally based knowledge about the phenomena of nature, the underlying laws have been explored for centuries by means of the theoretical sciences. Nowadays, ever-increasing computer performance enables detailed simulation-based predictions of complicated phenomena, which can be used purposefully by means of AI to assess and optimise complex boundary value problems. Especially supervised and unsupervised deep neural networks (DNNs) have emerged in this field. Supervised trained DNNs can also be used as efficient surrogate models as an alternative to e.g. traditional reduced order models. As a data based method DNNs need large training data sets, see e.g. [31], which can be obtained by simulations using artificial input data. For an overview of applications in material science where deep learning has become a game-changing technique for the prediction of material properties see [1]. For the philosophy of data-driven computations in solid mechanics, bypassing explicit constitutive models, we refer to [22].
As a model system we have chosen the laminar flow through a porous medium at low Reynolds numbers assuming a linear relation between the flux and the pressure gradient. This linear relation is governed by the permeability tensor \({\varvec{k}}\) which in an inhomogeneous material depends on its location. We assume that the laminar fluid flow can be modeled on both scales, the micro- and macroscale, with Darcy’s equation [6]. In order to characterize the effective flow behavior on the macroscale we have to determine the homogenized (effective) permeability tensor \({\bar{{\varvec{k}}}}\). One approach is to find heuristic or semi-analytical approximations for the estimation of the effective permeability as a function of geometrical and statistical properties of the micro-heterogeneous material, for an overview we refer to [28]. Furthermore the \(\text {FE}^2\) method, see e.g. [27, 35] and the references therein, is an established method to determine the homogenized properties of the underlying representative micro-structure. For a variationally consistent homogenization of flow through porous media we refer to [33, 34]. The \(\text {FE}^2\) method gives accurate results but is computationally very expensive.
Therefore we need another computational inexpensive simulation scheme (that is, from our motivation, an non Finite-Element-based method) for the generation of a sufficiently large training set for the DNN in order to obtain a predictive surrogate model. For an overview of general requirements to achieve surrogate models within a data based approach using large training sets in a deep learning framework see [23] and [9, 13, 14, 30] as examples of applications of trained DNNs as surrogate models in mechanics. Furthermore, e.g. in the context of optimization or parameter identification problems, where a large number of evaluations has to be performed, a fast surrogate model should be designed for efficiency reasons.
The solutions of Darcy’s flow problem can be considered as the stationary state of a diffusion process. In order to achieve a computational efficient scheme we use the fact that such processes can be formulated with a particle based atomistic description, the so called Brownian motion of particles, see [3]. This process is driven by a thermal induced stochastic motion of the particles and can in the averaged form be described by the Poisson equation [12]. Therefore the stationary state of the diffusion process is described by the Laplace equation. The advantage of this particle based approach to solve Darcy’s problems compared to Finite Element based methods is that no meshing is needed and the computation of the flux fields is computationally simple and fast. The resulting simulation performs random movements of particles to neighbored cells on a equidistant grid and can be realized either by a Monte Carlo method are by a pure algebraic method using the related stochastic transition matrices as described e.g. in [7]. This simulation method is used for fast generation of pairs of random geometries and resulting flux fields which can serve as a training set for machine learning algorithms.
In the growing scientific field of data driven mechanics DNNs serve e.g. as substitutes for constitutive laws, see e.g. [20, 37] for applications in elastic mechanics and [4, 8] for viscoelastic, viscoplastic and fracture problems. Physical informed Neural Networks, see e.g. [39, 40], are applied in order to take into account physical constraints during the training process. Furthermore, DNNs have also been succesfully used for the fast determination of quasi-optimal coupling constraints for the FETI-DP domain decomposition solver [19].
Deep Convolutional Neural Networks (DCNN) have been used for image classification and image segmentation at a pixel level with great success in the past, see e.g. [11]. Furthermore, DCNNs are used as fast surrogate models in computational fluid dynamics (CFD), see [10, 18]. The U-Net architecture was initially introduced by [31] for biomedical image segmentation and is based on a fully convolutional neural network. U-Net models were also used for steady-state and dynamic CFD applications, see [5, 10], as well as for the prediction of surface waves, [25]. A modified version of the UResNet model used for the prediction of the horizontal and vertical flux components per pixel using the nearest neighbor upsampling was proposed in [36]. It is well known that using spectral analysis for Darcy’s flow in inhomogenous media has several advantages, see e.g. [2]. Therefore, the application of a Fourier Convolutional Neural Network (FCNN) seems reasonable. A Fourier neural operator is a deep learning method that has been recently introduced and can outperform most existing machine learning approaches, see [24, 41]. It captures global interactions by convolution with low-frequency functions and yields high-frequency modes by composition with an activation function, so it can approximate functions with slow Fourier mode decay.
In this contribution we discuss, focussing on laminar flow through a micro-heterogenous medium, how training sets can be validated and generated in an efficient way. Furthermore we present and compare two different architectures of DNNs concerning their training behavior and approximation quality. For the efficient generation of training sets we apply a stochastic Brownian motion model and discuss its numerical treatment within a Monte Carlo approach. This model is then extended to an algebraic model based on stochastic transition matrices, Sect. 2. The applied DNNs are motivated and described in Sect. 3. The first one is a modified U-shaped residual network (UResNet) with an hierarchical structure. The second one is based on a Fourier Convolutional Neural Network (FCNN), where we compare the discrete Fourier Cosine transform (DCT-II) and the classical discrete complex-valued Fourier transform (DFT). Here, the FCNN architecture consists of two parallel branches, one path acting in the frequency space and a second one performing convolutions in euclidean space. Section 4 presents the \(\hbox {FE}^2\) homogenization scheme for the prediction of the effective permeabilities, used for the comparison with the predictions from the surrogate models. Representative numerical examples are discussed in Sect. 5, evaluating the training speed and the quality of the surrogate models, based on correlation coefficients and error measures.
2 Stochastic modeling of Darcy flow
2.1 Strong form of Darcy’s law
Let \(\mathcal {B} \subset \textrm{IR}^3\) be the body of interest parametrized in \({\varvec{x}}\), the surface of \(\mathcal {B} \) is denoted by \(\partial \mathcal {B} \). The later is subdivided into a part \(\partial \mathcal {B}_{q}\) where the flux across the surface is described and a remaining part \(\partial \mathcal {B}_p\) where the pressure is described. The decomposition of the boundary satisfies the relations \(\partial \mathcal {B} = \partial \mathcal {B}_{q} \cup \partial \mathcal {B}_p\) and \( \partial \mathcal {B}_{q} \cap \partial \mathcal {B}_p =\emptyset \,\). For a fully saturated porous medium the mass conservation law with constant density \(\rho \) and porosity appears as \(\textrm{div}(\rho \,{\varvec{q}}) = - f^*\,\) with the mass source density \(f^* \) and the flow rate \({\varvec{q}}\). This so-called Darcy’s law is suitable for the approximate solution of laminar flows. We use the reformulation
Here, the spatially constant permeability \({\varvec{k}}:= {\varvec{k}}^{*}/\mu \) is introduced, where \({\varvec{k}}^{*}\), measured in \(\hbox {N}^{-1}\) \(\hbox {s}^{-1}\), denotes the tensorial intrinsic permeability and \(\mu \) the fluid viscosity in Ns/\(\hbox {m}^2\).The boundary conditions have to be specified
where \({\varvec{n}}\) is the outward unit normal on \(\partial \mathcal{B}\), and \([p]_{SI} = \) Pa = N/m\(^2\), \([q]_{SI} = \) m/s. The Darcy equation is valid for a slow flux under isothermal conditions. In order to get a large number of trainings sets in reasonable time, we use a simple simulation tool based on a stochastic Brownian motion. The simulation generates random geometries and computes the resulting flux under given periodic boundary condition. These pairs of geometry with the resulting flux build the training set.
2.2 Brownian motion based on a Monte Carlo approach
In the following we consider a two dimensional micro-heterogenous structure consisting of two phases, an impermeable phase A and a permeable matrix. Phase A is given by the union of the inclusions which are defined by a given number of circles with random centers inside the considered domain \([0,l] \times [0,h]\) and with radii \(r \in [r_{min}, r_{max}]\) varying uniform randomly. The set S of admissible points, i.e. the matrix domain, is given by
where i and j are the indices of the equidistant \(L\cdot H\) grid points. At the initial state all fluid particles are positioned randomly at admissible points at the left boundary, i.e. at the left column of the discretized region given by \(j=1\) and \(i=1\ldots H\) and \((i,j) \in S\). Each particle can move potentially to all four directions provided the target position is admissible. In each iteration step the following rules of motion are applied to each particle:
-
1.
Exactly one of the four direct neighbors (left, right, lower, upper) can be visited with probability \(\frac{1}{4}\).
-
2.
This movement is rejected if the chosen neighbor is not in S.
-
3.
If the particle wants to cross a horizontal boundary edge \(i=1\) or \(i=H\) the particle is moved to the corresponding position on the upper/lower side, see Fig. 1 green lines.
-
4.
If the particle wants to cross a vertical boundary (\(j=1\) or \(j=L\)) the particle is moved to a randomly chosen admissible point on the left boundary, see Fig. 1 red lines.
If the move is rejected, i.e. the target position is not in S, the particle stays for this step at the current position. An iteration step inside this algorithm can be written in pseudo code, considering only rule 1. and 2., as:

Example of the definition of the transition matrix \(\textsf {M}\). The probabilities that a particle at position \(J=(2,1)\) moves to a position \(I=(i,j)\) are for \(I=(1,1)\) and \(I=(2,1)\) \(\frac{1}{4}+\frac{1}{4}\frac{1}{2}\), for \(I=(2,2)\):\(\frac{1}{4}\) and 0 for the remaining positions (left), the corresponding complete transition matrix \(\textsf {M}\) with highlighted column \(J=(2,1)\) (right)
These transition rules, see Fig. 1, assign a cylindrical topology and define the left edge as inflow and the right as outflow boundary. It is important to observe that this transition rules keep the number of moving particles constant and that the sum of probabilities for the possible moves of each particle is 1. Figure 2 shows two snapshots of a Monte Carlo simulation with \(1000 \times 1000\) grid points and 800.000 particles. The most time critical part of the algorithm is the generation of the random numbers. The simulation of 100.000 time steps needs on a standard laptop 10 min.
2.3 Brownian motion based on stochastic matrix approach
In the proposed framework the Brownian motion approach is implemented using the corresponding stochastic transition matrix \(\textsf {M}\) yielding a faster algebraic algorithm compared to the Monte Carlo implementation. Let for
be the probability that a particle located at position J moves to position I. \(\textsf {M}\in {\mathbb {R}}^{L\cdot H\times L\cdot H}\) is a sparse asymmetric matrix of dimension \(L\cdot H \times L\cdot H\), see Fig. 3 as an example. Let \(p_I\in [0,1]\) be the probability that a particle can be found at position I, \(\textsf {M}\, {\varvec{p}}\) with \({\varvec{p}}\in {\mathbb {R}}^{L\cdot H}\) is the probability distribution after applying the transition rules given above.
Due to the definition of \(\textsf {M}\) the vector \({\bar{1}} \in {\mathbb {R}}^{L\cdot H}\) (all entries are 1) is a left eigenvector of \(\textsf {M}\) with the eigenvalue 1. Because the 1-norm \(||\textsf {M}||_1\) is 1, the number 1 is also the largest eigenvalue of \(\textsf {M}\), see e.g. [16]. Having a left eigenvalue with eigenvalue 1 there must also exist a right eigenvector associated to this eigenvalue. This means there is a vector \(\overset{*}{{\varvec{p}}}\) with \(\textsf {M}\, \overset{*}{{\varvec{p}}}=\overset{*}{{\varvec{p}}}\), the so called stationary state, which can be computed by forward iteration starting with an arbitrary probability distribution \({\varvec{p}}_0\) and iterating \({\varvec{p}}_{n+1} = \textsf {M}\,{\varvec{p}}_n\). The initial probability distribution \({\varvec{p}}_0\) at position I is in correspondance to the Monte Carlo approach given by:
where m is the number of admissible positions at the left boundary. The computational complexity is nearly the same as in the Monte Carlo approach but due to the usage of fast sparse matrix–vector operations faster by a factor of three: to get a nearly converged stationary state on a grid with \(L=H=1000\), see Fig. 4, both methods get with 100.000 iteration comparable results. The matrix based implementation needed about 3 min on a standard laptop.
2.4 Extraction of flux and effective permeability from the stochastic model
We can identify the pressure as the density which is just the spatial probability distribution \({\varvec{p}}\). The probability that a single particle moves from position \(J=(i,j)\) to \(I=(i,j+1)\) is given by the number \(M_{IJ}\). The horizontal component of the macroscopic flux \(q_I\) at position I is the effective amount of particles moving from J to I given by
Setting the dynamic viscosity to 1, we have by Darcy’s law:
where \({\bar{q}}_x\) is the x-component of the averaged flux, \({\bar{q}}_x H\) is the total flow through the domain measured by the flow through the outflow boundary, \(\frac{p_{right}-{p}_{left}}{L}\) is the x-component of the averaged gradient of \({\varvec{p}}\) and \({p}_{left}\), \({p}_{right}\) are the averages of \({\varvec{p}}\) at the left and right edges respectivly. The \(\bar{k}_{yy}\) is extracted in the analogue manner. For the diagonal configuration we have the length:height ratio: \(\frac{L}{\sqrt{2}}:\sqrt{2}H = \frac{L}{2H}\). Figure 5 shows the stationary states of these configurations.
3 Deep convolutional neural network framework
3.1 Generated dataset
The generated data, consisting of 1000 cross-sectional images of porous media with an image size of \(64 \times 64\) pixels and the corresponding flux field, are divided into a training dataset and test dataset. The training dataset is used to optimize the parameters using stochastic gradient descent with momentum and an adaptive learning rate optimization to minimize the prediction error. Use of the test data set aims to detect overfitting during the training process and to evaluate the predictive performance of the trained model.
3.2 Deep convolutional neural network architecture
A modified version of the U-shaped residual neural network model based on [36] is established for predicting the effective permeability and the horizontal (\(q_x\)) and vertical (\(q_y\)) flux components per pixel. The detailed architecture set up is shown in Fig. 6. The binary cross-sectional image, in which a pixel with a value of 0 (1) corresponds to the solid phase (pore space), is the input of the model. Hereby noting that the desired pixel size of images in Deep Convolutional Neural Networks is mostly \(2^m\), in this case \(2^6\), pixels. From the UResNet model, we obtain a flux field as a \(64 \times 64\) matrix with the flux values per pixel, graphically shown below using density and stream plots.
The encoding part of the network consists of 5 downsampling blocks, which are used to reduce the number of variables and to compress the geometric information into a reduced dimension image. Each block includes a pooling layer, two convolutional layers each followed by a batch normalization layer, a rectified linear unit (RELU) activation function and a dropout layer. For the detailed structure of the second coding block, see Table 1. The pooling, which is located in the first layer of each block, leads to a reduction of the image size by half and thus decreases the training time and computational cost. There are different methods of pooling, whereby the most common max-pooling method was applied in this model, in which only the maximum output value is retained when reducing the dimensions for all further layers and calculations. Each convolutional layer has a number of output channels, which are also referred to as filters and a kernel of size \(3 \times 3\).The filters are used to extract important key features from the corresponding input. During the convolution, the input data is multiplied by the \(3 \times 3\) matrices of the filter kernels, and the result is summed and combined into one output pixel. This process is repeated for the entire image while shifting the filter along the image by a stride of one. The usage of dropout layers at the end of each block is a frequently performed regularization method in deep neural networks to reduce the risk of over-fitting. This involves inactivating 50% of the output neurons by randomly dropping connected nodes. This value is taken from literature, see e.g. [15], but has not been optimized here.
Located between the encoding and decoding blocks are 4 residual blocks, which can lead to an improvement in gradient flow during training and may simplify the network by effectively skipping connections. Unlike the traditional structure of neural networks, residual neural networks not only have all layers concatenated consecutively, but also have skip connections, whereby blocks of equal size from downsampling and upsampling are connected with one another. The blocks have a mirrored layer structure due to a chosen U-shaped design.
The 5 upsampling blocks for the decoding part of the network are supposed to gradually scale the image up to the pixel size of the original input. The first layer of each decoding block is concatenated with the corresponding encoding block. Convolutional neural networks employ several deconvolution layers in the process of image resampling and formation and iteratively resample a larger image from a number of lower resolution images. However, instead of a deconvolution layer, a resize layer is used to scale the image up by a factor of two using the nearest neighbor interpolation method to prevent checkerboard artifacts in the output images. Hence, each decoding block has a similar structure as the encoding block with two convolutional layers, each being followed by a batch normalization layer and a rectified linear unit activation function as shown in Table 2. The rectified linear unit (RELU) activation function is defined as
with \({\hat{x}}^{(i)}\) being the \(i_{th}\) pixel in the volume data to be trained and n being the total number of pixels.
In particular, each output neuron in the last layer is computed by the scalar product between their weights and a concatenated small domain of the input values, adding the bias and applying an activation function \(A_R\) of the form
with \({\hat{x}}_l^{(i)}\) denoting the neurons output calculated by the synaptic weights \(W_l^{(j)}\), a bias \(b_l^{(j)}\) and a total of M number of elements in the domain of the previous layer. Then, the final output values are calculated by the weighted inputs and a parametric RELU activation function \(A_R\) defined as
where \(a_i\) being a coefficient regulating the slope on the negative component. For the parametric RELU, \(a_i\) is a hyperparameter learned from the data, which can be obtained from the computation of the gradient with respect to \(a_i\). The parameter \(a_i\) is updated simultaneously with other parameters of the neural network during backpropagation.
3.3 Fourier convolutional neural network
The second approach is a Fourier Convolutional Neural Network (FCNN), first introduced by [26, 29], which provides a alternative to traditional DCNNs by computing convolutions in the Fourier domain instead of the spatial domain. Convolution in the spatial domain corresponds to an element-wise product in the Fourier domain, which can significantly reduce the computational cost of training. Fourier neural operators can model complex operators in partial differential equations, which often exhibit highly non-linear behavior and high frequencies, by the interaction of linear convolution, Fourier transformations, and the non-linear activation function, see [17].
3.3.1 Fourier Convolutional Neural Network Architecture
The Fourier Convolutional Neural Network consists of two fully connected layers (FC) in the first and last layers respectively, and four consecutive Fourier layers, see e.g. [17, 24]. In this model the architecture setup of the Fourier neural operator (FNO), introduced by [24], was adapted for the application of the prediction of velocity fields in microheterogeneous media. The network architecture is illustrated in Fig. 7.
For the application of the FNO numerical inputs are required. Hence, the binary structures of all images in the data set are encoded with a prior data preprocessing by transforming the input into a 2-D matrix of pixel data for the image input. Since the output of the velocity fields are stored in 2-D matrices, no further decoding is required in this special case.
Based on the preprocessed pixel data of the binary image, the network starts by transforming the input into higher dimensions using a Fully Connected (FC) Layer with 32 channels. Here, the channels represent the width of the FNO network, which can be interpreted as the number of features to be learned in each layer.
In the top path of each FNO layer, the input is encoded by applying the discrete Fourier transform (DFT) or a discrete Fourier cosine Transform (DCT). A linear transformation \({\mathcal {R}}\) is applied in the spectral domain to filter multiple high frequencies, since high frequencies often contain noise and imply abrupt changes in the image. Therefore, we define the number of low Fourier modes (wave numbers) which are used for the following analysis. Here, a number of 14 Fourier modes is chosen. A further reduction of the Fourier Modes leads to a lower resolution of the prediction. It should be noted that the maximum allowed number of retained modes depends on the size of the computer grid, see [17]. A well-balanced hyperparameter setting (namely the chosen number of channels, modes, training pairs, as well as the size and resolution of the discretization) could lead to an adjustment of the accuracy of the model.
While convolution is performed in frequency space in the top path of the FNO, the bottom path is implemented solely in the spatial domain. In the latter, the input is transformed by a one-dimensional spatial convolution \({\mathcal {C}}\), i.e. we have a kernel of size 1 and a stride of 1. The two paths are recombined after decoding the frequency domain values into the spatial dimension using the associated inverse Fourier Transform. Once the two paths are added, a non-linear activation function, the Rectified Linear Unit activation, is applied. Finally, the received feature maps are resized to the desired dimensions using a fully connected layer.
3.3.2 Discrete Fourier cosine transformations
The proposed scheme is a modified version of the Fourier neural operator introduced in [24]. The architecture set up of the Fourier Layer is illustrated in Fig. 7. Starting from the binarized image f(i, j), in the upper path the input is encoded by applying the Discrete Fourier Cosine Transform (DCT-II). We substitute in Fig. 7 the operator \(\mathcal{{F}}(u,v)\) by \({\tilde{F}}(u,v)\), the latter is defined as
The inverse transform \(\mathcal{{F}}^{-1}\), which is the inverse of the DCT-II, is here obtained through
3.3.3 Discrete Fourier transformations
The basic equation defining the complex valued discrete Fourier transformation \(\overset{*}{F}(u,v)\) are:
and its inverse is defined by
where \(\iota \) with \(\iota ^2=-1\) is the imaginary unit.
4 Two-scale formulation of Darcy flow through porous media
4.1 Definition of effective quantities and boundary conditions
At the macroscale an explicit constitutive model is not presumed. Instead of that we attach a representative volume element (RVE) at each macroscopic point. Therefore, at the macroscale the body of interest is denoted by \({\overline{\mathcal {B}}}\) and parametrized in \({\overline{{\varvec{x}}}} \); all macroscopic quantities are characterized by an overline. In order to compute the macroscopic (effective) permeability tensor \({\bar{{\varvec{k}}}}\) for the macroscopic Darcy flow
we start from the microscopic boundary value problem. Multiplying the strong form (1)\(_1\), neglecting volume sources, with the test function \(-\delta p\), inserting the constitutive relation (1)\(_2\) and integration over \(\mathcal {B}\) yields the weak form on the microscale \( G(p, \delta p) = -\int _{\mathcal {B}} \delta p \textrm{div}\left( {\varvec{k}}\cdot \nabla p\right) \text {d}v = 0 \,. \) The application of Gauss’ theorem leads to the weak form
In order to link the macroscopic quantities with their microscopic counterparts we define the macroscopic pressure gradient \(\overline{\nabla p}:= \nabla _{\overline{x}} \overline{p}\) and the macroscopic flux \({\overline{{\varvec{q}}}} \) as
where \({\varvec{q}}\) and \({\varvec{n}}\) are the flux vector and outward unit normal on the boundary \({\partial {\mathcal {B}}}\) of the RVE. Let us apply an additive decomposition of the microscopic pressure field in a constant \(\overline{p}\) and a fluctuation part \({\widetilde{p}}\), i.e. \( p = \overline{p} +{\widetilde{p}} \).
Substitution of the latter expression into (17)\(_1\) yields
In addition, the additive decomposition of flux tensor \({\varvec{q}}\) into a constant \({\overline{{\varvec{q}}}}\) and a fluctuation part \({\widetilde{{\varvec{q}}}}\), i.e. \( {\varvec{q}}= {\overline{{\varvec{q}}}} +{\widetilde{{\varvec{q}}}} , \) leads to
where \({\widetilde{q}} = {\widetilde{{\varvec{q}}}}\cdot {\varvec{n}}\) is the fluctuation part of the flux vector on the boundary \({\partial \mathcal {B}}\). Suitable boundary conditions can be derived from a postulated macro-homogeneity condition. Form this we obtain Dirichlet and Neumann boundary conditions
and periodic boundary conditions
The symbols \(p^\pm \) and \({\tilde{p}}^\pm \) denote opposing fluxes across the boundary and equal fluctuations of pressure at the corresponding points on the boundary, see Fig. 8. A derivation of the boundary conditions is given in the Appendix. A theroretical and numerical scheme for weak periodic boundary conditions of Stokes flow has been proposed by [32].
4.2 The discrete scale transition procedure: FE\(^2\)-scheme
In the first step we apply at each Gauss point of a macroscopic boundary value problem suitable boundary conditions on the microscopic boundary value problem. This is then solved with respect to the fluctuation of the pressure field \({\widetilde{p}}\).
For the discrete version of the weak form we use a conforming interpolation with finite element spaces for p and the triangulation of the \(\mathcal {B}\), i.e. \(p \in H^1( \mathcal {B}^h) \,\text {with}\, \displaystyle \mathcal {B}^h = \cup _{e=1}^{{num}_{ele}} \ \mathcal {B}^e \approx \mathcal {B}\) where \(\mathcal {B}^h\) denotes the discretization of \(\mathcal {B}\) with \(num_{ele}\) finite elements \(\mathcal {B}^e\). For the approximation of the pressure and the test function as well as their gradients
we introduce the matrix of ansatzfunctions \(\textsf {N}\) and \(\textsf {B}\) containing the derivatives of the ansatzfunctions. The discrete counterpart of the weak form (16) is \( G^h({\widetilde{p}}, \delta {\widetilde{p}}) = \sum _{e=1}^{{num}_{ele}} G^e({\widetilde{p}}, \delta {\widetilde{p}}) \) with \( G^e({\widetilde{p}}, \delta {\widetilde{p}}) = G^{e,int} ({\widetilde{p}}, \delta {\widetilde{p}}) + G^{e,ext} (\delta {\widetilde{p}}) \). The explicit expressions for \(G^{e,int} ({\widetilde{p}}, \delta {\widetilde{p}})\) and \(G^{e,ext} (\delta {\widetilde{p}})\) are
where \(\textsf {k}^e \) denotes the element stiffness matrix, and
The final set of algebraic equations follows from
with the global vector of unknowns \({\widetilde{{\varvec{D}}}} \) and the global stiffness matrix \(\textsf {K}\) and global residual vector \(\textsf {R}\) respectively. A formal linearization of \(G^h({\widetilde{p}}, \delta {\widetilde{p}})\), i.e.
at an equilibrium state on the microscale yields
where the stiffness matrix and generalized fluctuation influence matrix are

From (27) we compute the increments of the fluctuations of the pressure field:
The increment of the gradient of the pressure fluctuations are now obtained by
In order to derive the overall (algorithmic consistent) moduli \({\overline{{\varvec{k}}}}\), implicitly given in (15), we consider the linear increment of the macroscopic flux vector (17) and insert the constitutive relation (1)\(_2\):
Substituting the algebraic expression for \(\Delta \widetilde{\nabla p}\), (30), yields
In the last expression the terms and \(\textsf {K}\) and \(\textsf {L}\) are constant, thus we write \(\int _{\mathcal {B}} \, {\varvec{k}}\,\textsf{B} \, \textsf {K}^{-1} \, \textsf {L}\, \hbox {d}v = \int _{\mathcal {B}} \, {\varvec{k}}\,\textsf{B} \, \hbox {d}v \, \textsf {K}^{-1} \, \textsf {L}= \textsf {L}^T \, \textsf {K}^{-1} \, \textsf {L}\) and identify
For details on deriving the consistent macroscopic moduli we refer to [27, 35].
5 Numerical examples
5.1 Training process and regression loss metrics
For the training of the network, the ADAM optimization method (Adaptive Moment Estimation) [21] is applied. This is an extension to the stochastic gradient descent method (SGD) by calculating individual adaptive learning rates for the parameter \(\theta \). Let \(g_t = \nabla _{\theta }f(\theta _{t-1})\) denote the gradient of the objective function \(f(\theta )\). The objective function measures the deviation between the predicted \({\hat{{\varvec{q}}}}\) and the given (training set) \({\varvec{q}}\) flow, i.e. for a given member \(\tau \) of the training set we have \(f^{\tau }(\theta )= \frac{1}{n} \sum _{i=1}^n {\frac{1}{2}(\hat{{\varvec{q}}_i}(\theta )-{\varvec{q}}_i)^2}\), where n denotes the number of pixels and \({\hat{{\varvec{q}}}}, {\varvec{q}}\in \textrm{IR}^2\) the flow vector per pixel. Furthermore we define \(f(\theta )=\frac{1}{T}\sum _{\tau \in T} {f^{\tau }(\theta )}\), where T is the whole training set. A further improvement of ADAM of the SGD is the use of the unbiased estimators \({{\hat{m}}}\) and \({{\hat{V}}}\) for the expectation and variance. For given parameters \(\theta \), the update formula for a typical training round reads
where t indexes the current training epoch and the initializiation \(V_0=m_0=0\). The setting of the parameter \(\beta _1 = 0.9\), \(\beta _2 =0.999\) and \(\epsilon = 10^{-8}\), to prevent division by 0, is well established, whereby \(\alpha \) is a learning rate to be chosen.
In order to evaluate the quality of the trained system we define several error measures. The Mean Squared Error (MSE) is the sum of the squared distances between the predicted velocities by the DCNN and the measured flux components, while the Mean Absolute Error (MAE) is the absolute deviation and the normalized rooted MSE (NRMSE) is the normalized rooted MSE. Now considering and comparing several regression metrics for loss evaluation for each individual training pair \(\tau \)
with the mean flux value \({\overline{q}} = \frac{1}{n} \sum _{i=1}^n{||{\varvec{q}}_i||} \ne 0\). Whereas \({{\hat{{\varvec{q}}}}_i}\) is the predicted flux vector per pixel, \({\varvec{q}}_i\) the ground truth (flux vector) per pixel. In the following the solution obtained by the simulations of Brownian motion are referred to as ground truth.
5.1.1 Results UResNet and Fourier convolutional neural network
The final training process of the implemented network runs on a GPU (GeForce RTX 3090) with overall 100 epochs, see (34) and a batch size of 8. The duration of the training takes approximately 3 min when using 900 training examples, whereas a prediction of the trained model takes 0.014 s. Figure 9 (right) shows the loss plot of NMSE over 100 epochs averaged over 900 training sets and 100 validation sets. Obviously the loss decreases rapidly within the first 20 to 50 epochs. In the UResNet model, the two flux components have been trained simultaneously, while in the FCNN model, the x and y components have been trained individually. The computation has shown that an individual training of the components in the UResNet model leads to no significant improvement of the results. An exemplary binary image that served as test input is shown in Fig. 9.
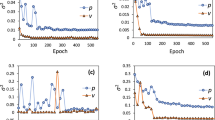
The training process for a lower (\(64 \times 64\)) and higher (\(128 \times 128\)) resolution of the binary input images are plotted in Fig. 10, whereby the errors after 100 epochs are at a comparable value for each of the two resolutions. For a number of about 844000 optimized parameters, the training of the higher resolution takes approximately 3 times longer than the lower resolution. Beside the simulation of the inflow on the left boundary (\(0^\circ \) rotation of microstructure, blue curve), the loss plots of the configurations for the inflow from the bottom (\(90^\circ \) rotation, red curve) and for the inflow for an \(45^\circ \) rotated structure (green curve) are depicted in Fig. 10. For all three setups, a decrease in the error of the training set, referred to as round loss, as well as a decrease in the error of the validation set can be observed.
Since the validation set is only used to evaluate the performance of the model on new data, it is not used for the training process. A significant gap between training and validation errors would indicate an over-fitting phenomenon, in which the model solely learns the training data to the best extent possible. Obviously, the performed training of the model yields reasonable error measures for the training and validation set, see Table 3.
The size of the training sets was varied and gradually reduced as illustrated in Fig. 11. While the predictive performance of the trained model increases with a larger number of training data, the accuracy of the model is reasonably reliable even with a rather small training set. The results indicate that reducing the size of the training dataset down to approximately 300 samples does not result in a significant decrease in the quality of the results.
The performance of the trained model in predicting the flow maps in the leading directions (flux in x-direction and y-direction) is illustrated in Fig. 13. The density plots of the flow fields for the developed and trained UResNet model with dimensions \(64 \times 64\) (Figs. 12a, 13a, d) and the calculated flow maps for the dimensions \(128 \times 128\) (Fig. 12d) as well as the Fourier Convolutional Neural Network (Fig. 14a) show a similar behavior.
A qualitative comparison of the predicted fluxes shows a high agreement with the reference data from the simulations based on Brownian motion. The per pixel calculated error of the fluxes, see Figs. 12, 13 and 14, is in the order of magnitude of about \(3.15\%\) (NMSE). To assess the quality of the results based on the prediction of the UResNet surrogate model, the \(x-\) and \(y-\)components of the fluxes are shown in Fig. 13. Since the main flow is in the horizontal direction, there are larger relative deviations for the y-component of the fluxes than for the x-components.
Cross plot of the predicted fluxes for \({\hat{q}}_x\) (left) and \({\hat{q}}_y\) (right) for each pixel (\(64 \times 64\)) versus the ground truth components \(q_x\) and \(q_y\) of the system depicted in Fig. 13a, d
The UResNet model has generally been more accurate in detecting the impermeable inclusions, while the FCNN prediction remains closer to the extreme flux values.
5.2 Pearson correlation coefficient (PCC)
The correlation between the predicted flow maps and their ground truths (Brownian Motion) is expressed with the Pearson Correlation Coefficient (PCC).
with \(\sigma _{\hat{{{\varvec{q}}}}}\) and \(\sigma _{{\varvec{q}}}\) being the standard deviations and Cov\(({\hat{{\varvec{q}}}},{\varvec{q}})\) as the covariance of the predicted flux values \({\hat{{\varvec{q}}}}\) and the ground truth values \({\varvec{q}}\). PCC values of \(-1\) indicate total disagreement and \(+1\) total agreement. For completely random predictions, the correlation coefficient is 0. In this context, a differentiation is made between the correlation of the entire dataset (900 training sets and 100 validation sets), the correlation of the training data (900 training sets), the correlation of the validation data (100 validation sets) and the worst and best results as listed in Table 4.
From the correlation results, the FCNN/DFT model gives the most accurate predictions for this example. Whereby the computational time of the FCNN and UResNet are comparable.
The cross plots of predicted flow values \({\varvec{q}}\) for test images vs. ground truth in Fig. 15 indicate that the surrogate model has a high PCC of 0.983 for \(q_x\) (left), a PCC of 0.938 for \(q_y\) (right).
5.3 Estimation of the effective permeabilities and FE\(^2\) comparison
From the resulting neural network evaluations, the flux fields are obtained. For each microstructure these can be used to estimate the permeabilities, see Sect. 2.4. For the 2D case, the permeabilities of a porous microstructure are described by a permeability tensor \({\varvec{k}}\). Thus, the evaluation of the microstructure for 3 orientations of the microstructure provide us with the scalar components
for the orientations \(\alpha = 0^\circ \), \(\alpha = 45^\circ \), \(\alpha = 90^\circ \), respectively. To determine the whole tensor, we start from the transformation relation
From this results, considering (35), the simple relation
with
For the exemplary microstructure in Fig. 9 (left), we obtain the scalar components
We thus derive the following permeability tensor for the case \(\alpha = 0^\circ \)
The Darcy flow simulation within the FE\(^2\)-scheme is based on the unit cell depicted in Fig. 16. The quadratic unit cell of dimension \(1\times 1\) consists of a permeable matrix and 9 nearly impermeable inclusions. The system is discretized with 24629 six-noded triangles.
For the simulation we apply a macroscopic pressure gradient \(\overline{\nabla p} = (-1,0)^T\) and periodic boundary conditions, see (21). While the matrix material is defined by a permeability of \({\varvec{k}}_{\text {matrix}} = {\varvec{I}}\), the inclusions are nearly impermeable with a permeability of \({\varvec{k}}_{\text {inclusion}} = 10^{-6} \, {\varvec{I}}\). These material parameters yield to an effective permeability tensor
Figure 16 shows the mesh and numerical results for the RVE. An illustration of the vector field of flux \({\varvec{q}}\) is displayed on the right and is plotted over the magnitude \(|{\varvec{q}}|\) and the pressure field \({\varvec{p}}\), respectively.
6 Conclusion
This work aims to propose an alternative approach to the determination of microscopic and macroscopic moduli of flow fields, using machine learning models to reduce computational cost. Using the generated data from Brownian molecular motion, we have proposed two data-driven Machine Learning approaches where numerical flow simulations are approximated by a spatial convolutional neural network. The deep residual neural U-Net (UResNet) consists of both encoding and decoding blocks, connected by skip connections and residual blocks. As an input, a binary image of any size can be used, whereas the output is constrained to a \(64 \times 64\) or \(128 \times 128\) grid through the formats of the training data. By transforming the spatial frequency space, the Fourier Convolutional Neural Network (FCNN) filters high Fourier modes and convolves the spatial domain to allow the prediction of flow simulations. In this context, the obtained outputs of both proposed surrogate models provide high accurate predictions and very good correlation for the obtained flow fields. The predicted permeability tensors are of the same order of magnitude as the permeabilities from the FE\(^2\) simulation, used to validate the surrogate models.
In the proposed algorithm scheme, we have restricted ourselves to Darcy’s law, i.e., to linear response. The extension to nonlinear rheologies is possible in principle, but would require further modifications. The application of CNNs to turbulent flows is directly possible (see e.g. [24]), but the application of our proposed stochastic matrices (Brownian motion) would require the evaluation of state-dependent matrices. In doing so, we would experience a significant loss of efficiency.
If we were only interested in estimating permeabilities, the question arises: Isn’t directly linking microstructure to permabilities (without training the NN with velocity fields) sufficient? We had actually also tried the prediction of the permeabilities alone, where no velocity distributions were provided to the NN when training the network. Here we had disappointing results compared to the proposed approach. Although the training sets were reproduced very well, validation sets (test sets) could not be approximated, they fail.
References
Agrawal A, Choudhary A (2019) Deep materials informatics: applications of deep learning in materials science. MRS Commun 9(3):779–792. https://doi.org/10.1557/mrc.2019.73
Bignonnet F, Dormieux L (2014) FFT-based bounds on the permeability of complex microstructures. Int J Numer Anal Methods Geomech 38:1707–1723. https://doi.org/10.1002/nag.2278
Brown R (1828) XXVII. A brief account of microscopical observations made in the months of June, July and, (1827) on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies. Philos Mag 4(21):161–173
Carrara P, De Lorenzis L, Stainier L et al (2020) Data-driven fracture mechanics. Comput Methods Appl Mech Eng 372(113):390. https://doi.org/10.1016/j.cma.2020.113390
Chen J, Viquerat J, Hachem E (2019) U-net architectures for fast prediction of incompressible laminar flows. arXiv preprint arXiv:1910.13532
Darcy H (1856) Les fontaines publiques de la ville de Dijon: exposition et application des principes à suivre et des formules à employer dans les questions de distribution d’eau: Ouvrage terminé par un appendice relatif aux fournitures d’eau de plusieurs villes, au filtrage des eaux et à la fabrication des tuyaux de fonte, de plomb, de tôle et de bitume. V. Dalmont, Libraire des Corps imperiaux des ponts et chaussees et des mines
Dynkin EB (1989) Kolmogorov and the theory of Markov processes. Ann Probab 17(3):822–832
Eggersmann R, Kirchdoerfer T, Reese S et al (2019) Model-free data-driven inelasticity. Comput Methods Appl Mech Eng 350:81–99. https://doi.org/10.1016/j.cma.2019.02.016
Egli FS, Straube RC, Mielke A et al (2021) Surrogate modeling of a nonlinear, biphasic model of articular cartilage with artificial neural networks. PAMM 21(1):e202100188. https://doi.org/10.1002/pamm.202100188
Eichinger M, Heinlein A, Klawonn A (2020) Surrogate convolutional neural network models for steady computational fluid dynamics simulations
Eidel B (2021) Deep convolutional neural networks predict elasticity tensors and their bounds in homogenization. https://doi.org/10.48550/arXiv.2109.03020
Einstein A (1905) Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann Phys 322(8):549–560
Fernández M, Rezaei S, Mianroodi JR et al (2020) Application of artificial neural networks for the prediction of interface mechanics: a study on grain boundary constitutive behavior. Adv Model Simul Eng Sci 7:1–27. https://doi.org/10.1186/s40323-019-0138-7
Fernández M, Fritzen F, Weeger O (2022) Material modeling for parametric, anisotropic finite strain hyperelasticity based on machine learning with application in optimization of metamaterials. Int J Numer Methods Eng 123(2):577–609. https://doi.org/10.1002/nme.6869
Garbin C, Zhu X, Marques O (2020) Dropout vs. batch normalization: an empirical study of their impact to deep learning. Multimed Tools Appl 79:1–39. https://doi.org/10.1007/s11042-019-08453-9
Golub G, Van Loan C (1996) Matrix computations. Johns Hopkins studies in the mathematical sciences, 3rd edn. Johns Hopkins University Press
Guan S, Hsu K, Chitnis PV (2021) Fourier neural operator networks: a fast and general solver for the photoacoustic wave equation. https://doi.org/10.48550/arXiv.2108.09374
Guo X, Li W, Iorio F (2016) Convolutional neural networks for steady flow approximation. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, pp 481–490. https://doi.org/10.1145/2939672.2939738
Heinlein A, Klawonn A, Lanser M et al (2021) Combining machine learning and adaptive coarse spaces—a hybrid approach for robust FETI-DP methods in three dimensions. In: Computer methods in applied mechanics and engineering, pp 816–838. https://doi.org/10.1137/20M1344913
Ibañez R, Abisset-Chavanne E, Aguado JV et al (2018) A manifold learning approach to data-driven computational elasticity and inelasticity. Arch Comput Methods Eng 25(1):47–57. https://doi.org/10.1007/s11831-016-9197-9
Kingma D, Ba J (2014) Adam: a method for stochastic optimization. https://doi.org/10.48550/arXiv.1412.6980
Kirchdoerfer T, Ortiz M (2016) Data-driven computational mechanics. Comput Methods Appl Mech Eng 304:81–101. https://doi.org/10.1016/j.cma.2016.02.001
Kollmannsberger S, d’Angella D, Jokeit M et al (2021) Deep learning in computational mechanics—an introductory course. Springer. https://doi.org/10.1007/978-3-030-76587-3
Li Z, Kovachki N, Azizzadenesheli K, et al (2020) Fourier neural operator for parametric partial differential equations. https://doi.org/10.48550/arXiv.2010.08895. arXiv:2010.08895v3
Lino M, Cantwell C, Fotiadis S et al (2020) Simulating surface wave dynamics with convolutional networks. arXiv preprint arXiv:2012.00718
Mathieu M, Henaff M, LeCun Y (2014) Fast training of convolutional networks through FFTs. Comput Res Repos. https://doi.org/10.48550/ARXIV.1312.5851
Miehe C, Koch A (2002) Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch Appl Mech 72:300–317. https://doi.org/10.1007/s00419-002-0212-2
Nemat-Nasser S, Lori M, Datta SK (1993) Micromechanics: overall properties of heterogeneous materials. North-Holland series in applied mathematics and mechanics. https://doi.org/10.1115/1.2788912
Pratt H, Williams B, Coenen F et al (2017) FCNN: Fourier convolutional neural networks. In: Machine learning and knowledge discovery in databases, pp 786–798. https://doi.org/10.1007/978-3-319-71249-9_47
Ribeiro M, Rehman A, Ahmed S et al (2020) DeepCFD: efficient steady-state laminar flow approximation with deep convolutional neural networks. https://doi.org/10.48550/arXiv.2004.08826
Ronneberger O, Fischer P, Brox T (2015) U-Net: convolutional networks for biomedical image segmentation. In: Navab N, Hornegger J, Wells WM et al (eds) Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015. Springer, pp 234–241. https://doi.org/10.1007/978-3-319-24574-4_28
Sandstöm C, Larsson F, Runesson K (2014) Weakly periodic boundary conditions for the homogenization of flow in porous media. Adv Model Simul Eng Sci 1(1):12. https://doi.org/10.1186/s40323-014-0012-6
Sandström C, Larsson F (2013) Variationally consistent homogenization of Stokes flow in porous media. J Multiscale Comput Eng 11(2):117–138. https://doi.org/10.1615/INTJMULTCOMPENG.2012004069
Sandström C, Larsson F, Runesson K et al (2013) A two-scale finite element formulation of Stokes flow in porous media. Comput Methods Appl Mech Eng 261–262:96–104. https://doi.org/10.1016/j.cma.2013.03.025
Schröder J (2014) A numerical two-scale homogenization scheme: the FE\(^2\)-method. In: Schröder J, Hackl K (eds) Plasticity and beyond, CISM courses and lectures, vol 550. Springer, pp 1–64. https://doi.org/10.1007/978-3-7091-1625-8
Takbiri A, Kazemi H, Nasrabadi N (2020) A data-driven surrogate to image-based flow simulations in porous media. Comput Fluids. https://doi.org/10.1016/j.compfluid.2020.104475
Thakolkaran P, Joshi A, Zheng Y et al (2022) NN-EUCLID: deep-learning hyperelasticity without stress data. https://doi.org/10.48550/arXiv.2205.06664
Tolle KM, Tansley DSW, Hey AJG (2011) The fourth paradigm: data-intensive scientific discovery. Proc IEEE 99(8):1334–1337. https://doi.org/10.1109/JPROC.2011.2155130
Wang K, Chen Y, Mehana M et al (2021) A physics-informed and hierarchically regularized data-driven model for predicting fluid flow through porous media. J Comput Phys 443(110):526. https://doi.org/10.1016/j.jcp.2021.110526
Wessels H, Weißenfels C, Wriggers P (2020) The neural particle method—an updated Lagrangian physics informed neural network for computational fluid dynamics. Comput Methods Appl Mech Eng 368:113–127. https://doi.org/10.1016/j.cma.2020.113127
Yan B, Harp DR, Chen B et al (2022) A gradient-based deep neural network model for simulating multiphase flow in porous media. J Comput Phys 463(111):277. https://doi.org/10.1016/j.jcp.2022.111277
Acknowledgements
We gratefully acknowledge the finanicial support of the German Research Foundation (DFG) in the framework of CRC/TRR 270, projekt ZINF “Management of data obtained in experimental and in silico investigations”, Project Number 405553726-TRR 270. Furthermore we would like to thank Simon Maike for his contribution to the FE\(^2\) calculation and simulation.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 A.1 Boundary conditions of the microscopic boundary value problem
To derive the appropriate boundary conditions of the boundary value problem at microscale the macro-homogeneity condition is considered. This macro-homogeneity condition also known as Hill condition or Hill-Mandel condi tion. Therein, they postulates that the macroscopic power is equal to the volumetric average of the microscopic powers, i.e.
Using the abbreviation \( \langle \bullet \rangle _V:= \displaystyle \dfrac{1}{V} \int _V \left( \bullet \right) \text {d}v\) and starting from (38)\(_2\) the equivalence of (38)\(_1\) and (38)\(_2\) can be proved as follows
Expression (38)\(_2\) is a priori fulfilled by the constraints conditions \( {\varvec{q}}= {\overline{{\varvec{q}}}} \;\forall \; {\varvec{x}}\in \mathcal {B} \) or \( \nabla p = \overline{\nabla p} \;\forall \; {\varvec{x}}\in \mathcal {B} \). Microscopic boundary conditions can be derived, exploiting \(\textrm{div}{\varvec{q}}= 0\), from
The latter condition is fulfilled by the microscopic boundary conditions
which characterize the Neumann and Dirichlet boundary conditions on the RVE, respectively. For the derivation of periodic boundary conditions we decompose \(\partial \mathcal {B}\) in two associated boundaries \(\partial \mathcal {B}^{\,+}\) and \(\partial \mathcal {B}^{\,-}\), see Fig. 8, with the associated points \({\varvec{x}}^+ \in \partial \mathcal {B}^{\,+}\) and \({\varvec{x}}^- \in \partial \mathcal {B}^{\,-}\). These points characterise the points to which the periodic complements of the unit cells are linked. Furthermore, we assume that at this points the outward unit normals are anti-parallel, i.e. \({\varvec{n}}^+ = -{\varvec{n}}^-\). Starting from the surface integral in (39) we write
With \( {\widetilde{p}}({\varvec{x}}^{\,+} ) = {\widetilde{p}} ({\varvec{x}}^{\,-})\), short \( {\widetilde{p}}^{\,+} = {\widetilde{p}}^{\,-}\), we get
where \({\varvec{q}}^\pm \) denote opposing flux vectors at the associated points. Thus the periodic boundary conditions are
The symbols \(q^\pm \) and \({\tilde{p}}^\pm \) denote opposing fluxes across and equal pressure fluctuations at the corresponding points on the boundaries, respectively.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Niekamp, R., Niemann, J. & Schröder, J. A surrogate model for the prediction of permeabilities and flow through porous media: a machine learning approach based on stochastic Brownian motion. Comput Mech 71, 563–581 (2023). https://doi.org/10.1007/s00466-022-02250-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-022-02250-2