Multiscale thermoelastic modelling of composite strands using the “fundamental solutions” method

Abstract

A novel computationally effective approach to multiscale thermoelastic modelling of composite structures and its application to a thermomechanical analysis of two ITER superconducting strands is presented. Homogenisation and recovering problems are solved by means of the “fundamental solutions” method, which was expanded to the case of thermoelastic analysis. We describe a general procedure of multiscale analysis on the basis of this method and apply it to recover stresses at the microscopic scale of a composite strands using a two-level procedure. The recovered micro-stresses are found to be in good correlation with the stresses obtained in the reference problem where the entire composite structure was modelled with a fine mesh.

1 Introduction

Practical impossibility of direct accounting for the entire microstructure when performing analysis of whole composite structures gave birth to the development of various multiscale analysis techniques. Such methods allow for consideration of the composite structure on different scales, and various kinds of techniques are used to ensure coupling between those scales [1, 2]. One of the widespread approaches is based on two procedures: homogenisation and recovering. The first one, homogenisation, implies calculation of effective properties of a composite medium, which eventually allows to replace the heterogeneous medium with a homogenous one in the framework of a given analysis. First attempts to solve this problem go back to more than a century ago with the pioneering studies of Voigt and Reuss [3, 4], and a number of different techniques have been introduced since then. Among the most popular ones for periodic structures are those based on the asymptotic expansion method for differential equation with oscillating coefficients [5, 6]. When finite element analysis is applied, solving boundary-value problems with periodic boundary conditions for a unit cell [7,8,9,10,11,12,13] has become arguably the most popular method for identifying effective mechanical properties of a composite medium. The ability to obtain effective properties of a composite medium and to perform the analysis on macroscopic scale (a homogenised solution) is, however, not always sufficient. The second procedure, recovering, which is also often referred to as unsmearing or heterogenization, is aimed at calculation of fields of interest on the microscopic scale starting from a homogenised solution. Typical applications of the recovering techniques are associated with situations where stress and strain states of individual components of a composite structure are required to account for non-linear behaviour. There are, however, problems where microscopic states affect the overall performance of the structure also in different ways. One of such examples is the composite superconducting strand of the ITER magnet coil considered below where superconductivity itself depends on the residual strain state.

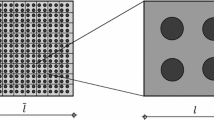
ITER (International Thermonuclear Experimental Reactor) [14] is a scientific and engineering project unique in its complexity, which has raised many challenges. Despite the fact that its design is primarily completed and assembly of the machine is ongoing, looking for new ways to tackle problems raised by the ITER project is still relevant, especially in light of the development of forthcoming new fusion devices. Among the most challenging ITER components is its magnet system, which has significantly pushed the limits of current superconducting technology. It is known [15,16,17] that the critical current of Nb₃Sn conductors, used for the generation of the strong toroidal magnetic field in ITER, substantially depends on the accumulated mechanical strains. The ability to predict strains in individual Nb₃Sn filaments in a superconducting cable becomes, therefore, crucial in the design of superconducting coils. In view of the multiscale structure of the strand [18] (Fig. 1), it is necessary to obtain effective properties of such a structure, perform a macroscopic analysis for the magnetic system, step back down to microscopic scale and evaluate microscopic fields at this scale. The knowledge of residual strains after cool-down operation, needed for the operation of the coils is crucial for evaluating their performance. Various homogenisation and recovering techniques have been used by researchers to solve these problems under different assumptions and with different computational cost [19,20,21,22].

Fig. 1

Copyright 2005, with permission from Elsevier

Multiscale composite structure of ITER superconducting strand, reprinted from Cryogenics Vol. 45, Boso D.P., Lefik M., Schrefler B.A. A multilevel homogenised model for superconducting strand thermomechanics., 259–271,

A novel method called “fundamental solutions and regular expansions” was proposed in 2006 by Palmov and Borovkov [23] for analysing stress and strain fields in periodic linear elastic heterogeneous media. The method is based on the idea that stress, strain, and displacement fields in a periodic medium can be represented as a linear combination of solutions of six problems for a unit cell. These solutions are called “fundamental solutions”, and the linear combinations—“regular expansions”. Beyond the inherent homogenisation abilities, the method features computationally effective recovering for the fields at microscopic scale.

This paper presents a generalization of the “fundamental solutions and regular expansions” method to thermoelastic problems by adding the seventh “fundamental problem” and acquiring thereby the ability to recover stress and strain fields in a composite medium subjected to mechanical and thermal loads simultaneously. The superconducting strand of the ITER magnetic system described above presents a good example of a complex composite structure in which both types of loads are essential, and hence the application of the presented method to a multiscale analysis of the strand was used to test the method and to estimate its accuracy.

2 “Fundamental solutions” in thermoelasticity

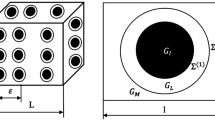
We assume that a periodic composite structure is characterized by a three-dimensional unit cell, which has three planes of symmetry. We use local coordinates, with the coordinate planes parallel to the sides of the unit cell, and the origin located in the geometric centre:

$$-\frac{{h}_{i}}{2}\le {x}_{i}\le \frac{{h}_{i}}{2}, i=1\div 3,$$

(1)

where ${h}_{1}$, ${h}_{2}$ and ${h}_{3}$ are dimensions of the unit cell.

Let us formulate seven fundamental boundary-value problems with simple mixed displacement-traction boundary conditions.

Fundamental problem 1. Stretching along OX₁ axis:

$$\begin{array}{cccc}{\mathrm{x}}_{1}=\pm {\mathrm{h}}_{1}/2:&{\mathrm{u}}_{1}=\pm \Updelta,& {\upsigma }_{12}=0,& {\upsigma }_{13}=0;\\ {\mathrm{x}}_{2}=\pm {\mathrm{h}}_{2}\text{/2:}& {\mathrm{u}}_{2}=0,&{\upsigma }_{23}=0,&{\upsigma }_{21}=0;\\ {\mathrm{x}}_{3}=\pm {\mathrm{h}}_{3}\text{/2:}&{\mathrm{u}}_{3}=0,&{\upsigma }_{31}=0,&{\upsigma }_{32}=0,\end{array}$$

(2)

Fundamental problem 2. Stretching along OX₂ axis:

$$\begin{array}{cccc}{\mathrm{x}}_{1}=\pm {\mathrm{h}}_{1}\text{/2:}& {\mathrm{u}}_{1}=0,& {\upsigma }_{12}=0,& {\upsigma }_{13}=0;\\ {\mathrm{x}}_{2}=\pm {\mathrm{h}}_{2}\text{/2:}& {\mathrm{u}}_{2}=\pm\Delta ,& {\upsigma }_{23}=0,& {\upsigma }_{21}=0;\\ {\mathrm{x}}_{3}=\pm {\mathrm{h}}_{3}\text{/2:}& {\mathrm{u}}_{3}=0,& {\upsigma }_{31}=0,& {\upsigma }_{32}=0,\end{array}$$

(3)

Fundamental problem 3. Stretching along OX₃ axis:

$$\begin{array}{cccc}{\mathrm{x}}_{1}=\pm {\mathrm{h}}_{1}\text{/2:}& {\mathrm{u}}_{1}=0,& {\upsigma }_{12}=0,& {\upsigma }_{13}=0;\\ {\mathrm{x}}_{2}=\pm {\mathrm{h}}_{2}\text{/2:}& {\mathrm{u}}_{2}=0,& {\upsigma }_{23}=0,& {\upsigma }_{21}=0;\\ {\mathrm{x}}_{3}=\pm {\mathrm{h}}_{3}\text{/2:}& {\mathrm{u}}_{3}=\pm\Delta ,& {\upsigma }_{31}=0,& {\upsigma }_{32}=0,\end{array}$$

(4)

Fundamental problem 4. Shear deformation in OX₁X₂ plane:

$$\begin{array}{cccc}{\mathrm{x}}_{1}=\pm {\mathrm{h}}_{1}\text{/2:}& {\mathrm{u}}_{2}=0,& {\upsigma }_{13}=0,& {\upsigma }_{11}=0;\\ {\mathrm{x}}_{2}=\pm {\mathrm{h}}_{2}\text{/2:}& {\mathrm{u}}_{1}=\pm\Delta ,& {\upsigma }_{22}=0,& {\upsigma }_{23}=0;\\ {\mathrm{x}}_{3}=\pm {\mathrm{h}}_{3}\text{/2:}& {\mathrm{u}}_{3}=0,& {\upsigma }_{31}=0,& {\upsigma }_{32}=0,\end{array}$$

(5)

Fundamental problem 5. Shear deformation in OX₂X₃ plane:

$$\begin{array}{cccc}{\mathrm{x}}_{1}=\pm {\mathrm{h}}_{1}\text{/2:}& {\mathrm{u}}_{1}=0,& {\upsigma }_{12}=0,& {\upsigma }_{13}=0;\\ {\mathrm{x}}_{2}=\pm {\mathrm{h}}_{2}\text{/2:}& {\mathrm{u}}_{3}=0,& {\upsigma }_{21}=0,& {\upsigma }_{22}=0;\\ {\mathrm{x}}_{3}=\pm {\mathrm{h}}_{3}\text{/2:}& {\mathrm{u}}_{2}=\pm\Delta ,& {\upsigma }_{31}=0,& {\upsigma }_{33}=0,\end{array}$$

(6)

Fundamental problem 6. Shear deformation in OX₁X₃ plane:

$$\begin{array}{cccc}{\mathrm{x}}_{1}=\pm {\mathrm{h}}_{1}\text{/2:}& {\mathrm{u}}_{3}=\pm\Delta ,& {\upsigma }_{12}=0,& {\upsigma }_{11}=0;\\ {\mathrm{x}}_{2}=\pm {\mathrm{h}}_{2}\text{/2:}& {\mathrm{u}}_{2}=0,& {\upsigma }_{21}=0,& {\upsigma }_{23}=\text{0;}\\ {\mathrm{x}}_{3}=\pm {\mathrm{h}}_{3}\text{/2:}& {\mathrm{u}}_{1}=0,& {\upsigma }_{32}=0,& {\upsigma }_{33}=0,\end{array}$$

(7)

Fundamental problem 7. Uniform heating:

$$\begin{array}{cccc}{\mathrm{x}}_{1}=\pm {\mathrm{h}}_{1}\text{/2:}& {\mathrm{u}}_{1}=0,& {\upsigma }_{12}=0,& {\upsigma }_{13}=0;\\ {\mathrm{x}}_{2}=\pm {\mathrm{h}}_{2}\text{/2:}& {\mathrm{u}}_{2}=0,& {\upsigma }_{23}=0,& {\upsigma }_{21}=0;\\ {\mathrm{x}}_{3}=\pm {\mathrm{h}}_{3}\text{/2:}& {\mathrm{u}}_{3}=0,& {\upsigma }_{31}=0,& {\upsigma }_{32}=0,\end{array}$$

$$-{\mathrm{h}}_{1}/2\le {\mathrm{x}}_{1}\le {\mathrm{h}}_{1}/2;\quad -{\mathrm{h}}_{2}/2\le {\mathrm{x}}_{2}\le {\mathrm{h}}_{2}/2;\quad-{\mathrm{h}}_{3}/2\le {\mathrm{x}}_{3}\le {\mathrm{h}}_{3}/2:\quad{{\Delta}}\mathrm{T}=\updelta $$

(8)

In (2)–(8) ${u}_{i}$ and ${\sigma }_{ij}$ are components of the displacement vector and of the Cauchy stress tensor; ∆ and δ are arbitrary non-zero constants, for which unit values can be taken due to the linear nature of the problems under consideration. The first six boundary-value problems here are the fundamental problems formulated in [23] except for slightly different boundary conditions in the shear deformation problems. In [23], for shear deformation problems, two components of the displacement vector tangential to the boundary and one normal component of the stress tensor were prescribed at each boundary of the cell. Here, in (5)–(7) we prescribe at each boundary only one component of the displacement vector and two components of the stress tensor. It can be proven that these boundary conditions provide exactly the same values of averaged components of the strain tensor and possess the same periodicity properties as the ones originally introduced in [23]. That modification was made to make the boundary conditions as relaxed as possible as well as to achieve some uniformity in the statements for stretching and shear deformation problems—in our case in all these statements one component of the displacement vector and two components of the stress tensor are prescribed at each boundary. The seventh boundary-value problem (8) was introduced to deal with linear thermal expansion.

3 «Regular expansions» in thermoelasticity

The seven boundary-value problems (2)–(8) above have an important property—their solutions are periodic in terms of stresses. It can be proven that values of all stress tensor components at the corresponding points of opposite faces are equal. That can be done, for example, using proof by contradiction in the manner of [24] as it is demonstrated below for one of the normal components of the stress tensor.

Let us consider the first fundamental problem (2) for a symmetric unit cell, and let us assume that the normal stress ${\sigma }_{11}$ has a part that takes opposite values at the corresponding points of the opposite faces. Stress vectors produced by this part of ${\sigma }_{11}$ on the opposite faces are denoted with ${\sigma }_{11}^{A}$ in Fig. 2a. Performing a reflection of the unit cell (together with all boundary conditions and internal forces) with respect to the vertical axis ${x}_{2}$ yields the system presented in Fig. 2b. The symmetry of the unit cell and of the boundary conditions (2) with respect to the vertical axis ${x}_{2}$ implies that the boundary value problems presented in Fig. 2a and b (after the reflection) are exactly the same. Opposite directions of ${\sigma }_{11}^{A}$ in these two identical boundary value problems yields ${\sigma }_{11}^{A}=0$, which means that ${\sigma }_{11}$ in the first fundamental problem (2) takes equal values at the two considered opposite faces of the unit cell.

Fig. 2

A unit cell in the first fundamental problem: a initial problem with the assumed antisymmetric component of ${\sigma }_{11}$; b after reflection with respect to ${x}_{2}$

Using similar arguments, it can be rigorously proven that all components of the stress tensor except for those prescribed as zeroes in the boundary conditions of (2)–(8), take equal values at the corresponding points of all opposite faces. The periodicity of stresses implies similar periodicity of strains and quasi-periodicity of displacements. Due to the linear nature of the equations and boundary conditions, any linear combination of the “fundamental solutions” can also be considered as a solution of elasticity equations for a periodic media—(9). Using the mentioned periodicity of the “fundamental solutions”, we can consider their linear combination (9) an approximation for any periodic solution.

$${\boldsymbol{\upsigma}}={\sum }_{\mathrm{k}=1}^{6}{\uplambda }^{(\mathrm{k})}{{\boldsymbol{\upsigma}}}^{(\mathrm{k})}+{\uplambda }^{(7)}{{\boldsymbol{\upsigma}}}^{(7)};$$

$${\boldsymbol{\upvarepsilon}}={\sum }_{\mathrm{k}=1}^{6}{\uplambda }^{(\mathrm{k})}{{\boldsymbol{\upvarepsilon}}}^{(\mathrm{k})}+{\uplambda }^{(7)}{{\boldsymbol{\upvarepsilon}}}^{(7)};$$

(9)

$$\mathbf{u}={\sum }_{\mathbf{k}=1}^{6}{\uplambda }^{(\mathrm{k})}{\mathbf{u}}^{(\mathrm{k})}+{\uplambda }^{(7)}{\mathbf{u}}^{(7)},$$

where ${{\boldsymbol{\upsigma}}}^{\left(\mathrm{k}\right)}({x}_{1},{x}_{2},{x}_{3})$, ${{\boldsymbol{\upvarepsilon}}}^{(\mathrm{k})}({x}_{1},{x}_{2},{x}_{3})$ and ${\mathbf{u}}^{(\mathrm{k})}({x}_{1},{x}_{2},{x}_{3})$ are the fields of stress tensor, strain tensor and displacement vector in the (k)-th fundamental problem, and ${\uplambda }^{(k)}$ are constant multipliers (weight coefficients, which determine contribution of the (k)-th fundamental problem). We will refer to expressions (9) as “regular expansions” in thermoelasticity.

Let us introduce an operator of averaging across the unit cell volume $<\dots >=\frac{1}{V}\int_{V}dV$ and apply it to Eqs. (9). It can be easily shown that for some of the stress and strain tensor components in the “fundamental solutions”, averaging results in zero values. For instance, for ${\varepsilon }_{xx}$ in the 4th fundamental problem (5):

$$ \langle \varepsilon _{{11}}^{{(4)}} \rangle = \frac{1}{V}\mathop {\mathop \smallint \limits^{{}} }\limits_{V} \varepsilon _{{11}} dV = \frac{1}{{{\text{h}}_{1} {\text{h}}_{2} {\text{h}}_{3} }}\mathop {\mathop \smallint \limits^{{\frac{{h_{3} }}{2}}} }\limits_{{ - \frac{{h_{3} }}{2}}} \mathop {\mathop \smallint \limits^{{\frac{{h_{2} }}{2}}} }\limits_{{ - \frac{{h_{2} }}{2}}} \mathop {\mathop \smallint \limits^{{\frac{{h_{1} }}{2}}} }\limits_{{ - \frac{{h_{1} }}{2}}} \frac{{\partial u_{1} }}{{\partial {\text{x}}_{1} }}d{\text{x}}_{1} d{\text{x}}_{2} d{\text{x}}_{3} = \frac{1}{{{\text{h}}_{1} {\text{h}}_{2} {\text{h}}_{3} }}\mathop {\mathop \smallint \limits^{{\frac{{h_{3} }}{2}}} }\limits_{{ - \frac{{h_{3} }}{2}}} \mathop {\mathop \smallint \limits^{{\frac{{h_{2} }}{2}}} }\limits_{{ - \frac{{h_{2} }}{2}}} u_{1} \left| {\begin{array}{*{20}c} {\frac{{h_{1} }}{2}} \\ { - \frac{{h_{1} }}{2}} \\ \end{array} } \right.d{\text{x}}_{2} d{\text{x}}_{3} $$

where only the values of ${u}_{1}$ at the faces of the unit cell are present. Using symmetry of the unit cell with respect to ${x}_{2}$ axis, it can be proven in similar manner as above that these values are bound to be equal. Indeed, a reflection with respect to ${x}_{2}$ axis results in the boundary value problem for the same unit cell but with opposite boundary conditions. This “reflected” boundary value problem, due to its linearity, must result in opposite displacements with respect to the initial one. That yields the conclusion that ${u}_{1}$ takes equal values at corresponding points of the faces ${x}_{1}=\frac{{h}_{1}}{2}$ and ${x}_{1}=-\frac{{h}_{1}}{2}$. The latter results in $\langle {\varepsilon }_{11}^{(4)}\rangle =0$ according to the equation above. Similarly, $\langle {\varepsilon }_{22}^{(4)}\rangle =0$ and $\langle {\varepsilon }_{33}^{(4)}\rangle =0.$ Repeating the same reasoning for fundamental problems (6) and (7), we come to the conclusions that in all these problems associated with shear deformation of the unit cell, averaged values of the normal components of the strain tensor take zero values. For the first three fundamental problems, which are associated with stretching of the unit cell, similar reasoning results in zero values of the averaged non-diagonal components of the strain tensor. Finally, for the 7th fundamental problem (8), all averaged components of the strain tensor are zero. That allows to represent the result of averaging (9) in the matrix form as follows (${\upgamma }_{\text{ij}}=2{\upvarepsilon }_{\text{ij}}$ are engineering shearing strains).

$$\langle {\boldsymbol{\upsigma}}\rangle =\langle {\boldsymbol{\Sigma}}\rangle \cdot{\boldsymbol{\Lambda}}+{\uplambda }^{(7)}\left[\begin{array}{c}\langle {\upsigma }_{11}^{(7)}\rangle \\ \langle {\upsigma }_{22}^{(7)}\rangle \\ \langle {\upsigma }_{33}^{(7)}\rangle \\ 0\\ 0\\ 0\end{array}\right];$$

(10)

$\langle {\boldsymbol{\upvarepsilon}}\rangle =\langle {\mathbf{E}}\rangle \cdot{\boldsymbol{\Lambda}},$

$$\langle {\varvec{\upsigma}}\rangle =\left[\begin{array}{c} <{\upsigma }_{11}> \\ <{\upsigma }_{22}>\\ <{\upsigma }_{33}>\\ <{\upsigma }_{12}>\\ <{\upsigma }_{23}> \\ <{\upsigma }_{31}>\end{array}\right];\quad < {\varvec{\upvarepsilon}}> =\left[\begin{array}{c} <{\upvarepsilon }_{11}>\\ <{\upvarepsilon }_{22}>\\ <{\upvarepsilon }_{33}> \\ \langle {\upgamma }_{12}\rangle \\ \langle {\upgamma }_{23}\rangle \\ \langle {\upgamma }_{31}\rangle \end{array}\right];\quad{\varvec{\Lambda}}=\left[\begin{array}{c}{\uplambda }^{(1)}\\ {\uplambda }^{(2)}\\ {\uplambda }^{(3)}\\ {\uplambda }^{(4)}\\ {\uplambda }^{(5)}\\ {\uplambda }^{(6)}\end{array}\right];$$

(11)

$$\langle{\boldsymbol{\Sigma}}\rangle =\left[\begin{array}{cccccc} <{\upsigma }_{11}^{(1)}> & <{\upsigma }_{11}^{(2)}> & <{\upsigma }_{11}^{(3)}> & 0& 0& 0\\ <{\upsigma }_{22}^{(1)}> & <{\upsigma }_{22}^{(2)}> & <{\upsigma }_{22}^{(3)}> & 0& 0& 0\\ <{\upsigma }_{33}^{(1)}> & <{\upsigma }_{33}^{(2)}> & <{\upsigma }_{33}^{(3)}> & 0& 0& 0\\ 0& 0& 0& <{\upsigma }_{12}^{(4)}> & 0& 0\\ 0& 0& 0& 0& <{\upsigma }_{23}^{(5)}> & 0\\ 0& 0& 0& 0& 0& <{\upsigma }_{31}^{(6)}> \end{array}\right];$$

(12)

$$\langle {\mathbf{E}}\rangle =\left[\begin{array}{cccccc} <{\upvarepsilon }_{11}^{(1)}> & <{\upvarepsilon }_{11}^{(2)}> & <{\upvarepsilon }_{11}^{(3)}> & 0& 0& 0\\ <{\upvarepsilon }_{22}^{(1)}>& <{\upvarepsilon }_{22}^{(2)}> & <{\upvarepsilon }_{22}^{(3)}> & 0& 0& 0\\ <{\upvarepsilon }_{33}^{(1)}> & <{\upvarepsilon }_{33}^{(2)}> & <{\upvarepsilon }_{33}^{(3)}> & 0& 0& 0\\ 0& 0& 0& <{\upgamma }_{12}^{(4)}> & 0& 0\\ 0& 0& 0& 0& <{\upgamma }_{12}^{(5)}> & 0\\ 0& 0& 0& 0& 0& <{\upgamma }_{31}^{(6)}> \end{array}\right].$$

(13)

The averaged normal strains in the first six fundamental problems can be calculated analytically using the corresponding boundary conditions in the same way as demonstrated above for $\langle {\varepsilon }_{11}^{(4)}\rangle$, which reveals that $\left\langle {\mathbf{E}} \right\rangle$ is a diagonal matrix. The column of multipliers ${\uplambda }^{(k)}$ can be calculated from the second expression in (10) as:

$${\boldsymbol{\Lambda}}={\langle \mathbf{E}\rangle }^{-1}\cdot \langle {\boldsymbol{\upvarepsilon}}\rangle .$$

(14)

Substitution of (14) into the first expression in (10) yields the following relation between averaged stresses and averaged strains in a periodic solution:

$$ \langle {\boldsymbol{\upsigma}}\rangle =\langle {\boldsymbol{\Sigma}}\rangle \cdot {\langle \mathbf{E}\rangle }^{-1}\cdot \langle {\boldsymbol{\upvarepsilon}}\rangle +{\uplambda }^{\left(7\right)}\left[\begin{array}{c}\langle {\upsigma }_{11}^{\left(7\right)}\rangle \\ \langle {\upsigma }_{22}^{\left(7\right)}\rangle \\ \langle {\upsigma }_{33}^{\left(7\right)}\rangle \\ 0\\ 0\\ 0\end{array}\right],$$

(15)

which can be written in the following form:

$$\langle {\boldsymbol{\upsigma}}\rangle =\langle {\boldsymbol{\Sigma}}\rangle \cdot {\langle \mathbf{E}\rangle }^{-1}\cdot \left(\langle {\boldsymbol{\upvarepsilon}}\rangle +{\uplambda }^{\left(7\right)}\langle \mathbf{E}\rangle \cdot {\langle {\boldsymbol{\Sigma}}\rangle }^{-1}\left[\begin{array}{c}\langle {\upsigma }_{11}^{\left(7\right)}\rangle \\ \langle {\upsigma }_{22}^{\left(7\right)}\rangle \\ \langle {\upsigma }_{33}^{\left(7\right)}\rangle \\ 0\\ 0\\ 0\end{array}\right]\right). $$

(16)

Equation (16) in fact represents a constitutive equation for averaged stresses and averaged strains in a thermoelastic medium:

$$\langle {\boldsymbol{\upsigma}}\rangle ={\mathbf{C}}^{*}\cdot \left(\langle {\boldsymbol{\upvarepsilon}}\rangle -\left[\begin{array}{c}{{\alpha }}_{1}^{*}\\ {{\alpha }}_{2}^{*}\\ {{\alpha }}_{3}^{*}\\ 0\\ 0\\ 0\end{array}\right]{{\Delta}}\mathrm{T}\right),$$

(17)

where ${\mathbf{C}}^{*}=\langle {\boldsymbol{\Sigma}}\rangle \cdot {\langle \mathbf{E}\rangle }^{-1}$ is the matrix of effective elastic moduli, which can be calculated on the basis of averaged solutions for the first six fundamental problems, and ${{\alpha }}_{1}^{*}$, ${{\alpha }}_{2}^{*}$, ${{\alpha }}_{3}^{*}$ are the effective thermal expansion coefficients, and ${{\Delta}}\mathrm{T}$ is the averaged change in temperature with respect to the reference one. (17) implies that the following substitution was made:

$$\left[\begin{array}{c}{{\alpha }}_{1}^{*}\\ {{\alpha }}_{2}^{*}\\ {{\alpha }}_{3}^{*}\\ 0\\ 0\\ 0\end{array}\right]=-\frac{{\uplambda }^{(7)}}{{{\Delta}}\mathrm{T}}\langle \mathbf{E}\rangle \cdot {\langle {\boldsymbol{\Sigma}}\rangle }^{-1}\cdot \left[\begin{array}{c}\langle {\upsigma }_{11}^{(7)}\rangle \\ \langle {\upsigma }_{22}^{(7)}\rangle \\ \langle {\upsigma }_{33}^{(7)}\rangle \\ 0\\ 0\\ 0\end{array}\right]$$

(18)

On the other hand, the column of effective thermal expansion coefficients can be found by applying averaged constitutive Eqs. (17) to the (7)-th fundamental problem and taking into account zero values of all averaged strains in the solution:

$$\left[\begin{array}{c}\langle {\upsigma }_{11}^{(7)}\rangle \\ \langle {\upsigma }_{22}^{(7)}\rangle \\ \langle {\upsigma }_{33}^{(7)}\rangle \\ 0\\ 0\\ 0\end{array}\right]={\mathbf{C}}^{*}\cdot \left(-\left[\begin{array}{c}{{\alpha }}_{1}^{*}\\ {{\alpha }}_{2}^{*}\\ {{\alpha }}_{3}^{*}\\ 0\\ 0\\ 0\end{array}\right]\updelta \right),$$

(19)

which yields:

$$\left[\begin{array}{c}{{\alpha }}_{1}^{*}\\ {{\alpha }}_{2}^{*}\\ {{\alpha }}_{3}^{*}\\ 0\\ 0\\ 0\end{array}\right]=-\frac{1}{\updelta }{{\mathbf{C}}^{*}}^{-1}\cdot \left[\begin{array}{c}\langle {\upsigma }_{11}^{(7)}\rangle \\ \langle {\upsigma }_{22}^{(7)}\rangle \\ \langle {\upsigma }_{33}^{(7)}\rangle \\ 0\\ 0\\ 0\end{array}\right]$$

(20)

Knowing ${\mathbf{C}}^{*}=\langle {\boldsymbol{\Sigma}}\rangle \cdot {\langle \mathbf{E}\rangle }^{-1}$ and comparing Eqs. (18) and (20), we conclude that ${\uplambda }^{(7)}=\frac{{{\Delta}}\mathrm{ T}}{\updelta }$. Finally, the homogenisation problem in thermoelasticity can be solved by means of “fundamental solutions” method as:

$${\mathbf{C}}^{*}=\langle {\boldsymbol{\Sigma}}\rangle \cdot {\langle \mathbf{E}\rangle }^{-1};$$

(21)

$\left[\begin{array}{c}{{\alpha }}_{1}^{*}\\ {{\alpha }}_{2}^{*}\\ {{\alpha }}_{3}^{*}\\ 0\\ 0\\ 0\end{array}\right]=-\frac{1}{\updelta }\langle {\mathbf{E}}\rangle \cdot {\langle {\boldsymbol{\Sigma}}\rangle }^{-1}\cdot \left[\begin{array}{c}\langle {\upsigma }_{11}^{(7)}\rangle \\ \langle {\upsigma }_{22}^{(7)}\rangle \\ \langle {\upsigma }_{33}^{(7)}\rangle \\ 0\\ 0\\ 0\end{array}\right]$

4 Recovering micro stresses and micro strains by use of the «fundamental solutions» method

An important advantage of the “fundamental solutions” method is that not only it allows calculation of effective moduli according to (21), but it can also be used for recovering of micro fields in the homogenised solution, i.e., the solution of a macroscopic problem, in which a homogeneous material model with effective properties was used for the composite media. Using the column notations for non-averaged stress and stress tensors analogous to the one introduced in (11), we write present expansions (9) in the matrix form:

$${\varvec{\upsigma}}={\varvec{\Sigma}}\cdot{\varvec{\Lambda}}+{\uplambda }^{(7)}\left[\begin{array}{c}{\upsigma }_{11}^{(7)}\\ {\upsigma }_{22}^{(7)}\\ {\upsigma }_{33}^{(7)}\\ {\upsigma }_{12}^{(7)}\\ {\upsigma }_{23}^{(7)}\\ {\upsigma }_{13}^{(7)}\end{array}\right] \quad {\varvec{\upvarepsilon}}={\mathbf{E}}\cdot{\varvec{\Lambda}}+{\uplambda }^{(7)}\left[\begin{array}{c}{\upvarepsilon }_{11}^{(7)}\\ {\upvarepsilon }_{22}^{(7)}\\ {\upvarepsilon }_{33}^{(7)}\\ {\upvarepsilon }_{12}^{(7)}\\ {\upvarepsilon }_{23}^{(7)}\\ {\upvarepsilon }_{13}^{(7)}\end{array}\right]$$

(22)

Matrix notations ${\boldsymbol{\Sigma}}$ and $\mathbf{E}$ in (22) are analogous to the ones introduced by (12)–(13), but are constructed for non-averaged stresses and strains in the “fundamental solutions”:

${\boldsymbol{\Sigma}}=\left[\begin{array}{cccccc}{{\boldsymbol{\upsigma}}}^{(1)}& {{\boldsymbol{\upsigma}}}^{(2)}& {{\boldsymbol{\upsigma}}}^{(3)}& {{\boldsymbol{\upsigma}}}^{(4)}& {{\boldsymbol{\upsigma}}}^{(5)}& {{\boldsymbol{\upsigma}}}^{(6)}\end{array}\right]$—the matrix of stresses in the first six fundamental problems;

$\mathbf{E}=\left[\begin{array}{cccccc}{{\boldsymbol{\upvarepsilon}}}^{(1)}& {{\boldsymbol{\upvarepsilon}}}^{(2)}& {{\boldsymbol{\upvarepsilon}}}^{(3)}& {{\boldsymbol{\upvarepsilon}}}^{(4)}& {{\boldsymbol{\upvarepsilon}}}^{(5)}& {{\boldsymbol{\upvarepsilon}}}^{(6)}\end{array}\right]$—the matrix of strains in the first six fundamental problems.

It was shown above that the first six multipliers ${\uplambda }^{(k)}$ can be calculated using the values of the strains averaged across the unit cell in the first six “fundamental solutions” (14). The 7th multiplier ${\uplambda }^{(7)}$ can be identified using the averaged change in temperature ${{\Delta}} \mathrm{T}$ and the value of temperature applied in the 7^th fundamental problem as ${\uplambda }^{(7)}=\frac{\Delta T}{\delta }$. By substitution of these expressions in (22) and using notations ${{\boldsymbol{\upsigma}}}^{(7)}$ and ${{\boldsymbol{\upvarepsilon}}}^{(7)}$ for the columns of stress and strains components in the 7th fundamental problem, we obtain:

$${\boldsymbol{\upsigma}}={\boldsymbol{\Sigma}}\cdot {\langle \mathbf{E}\rangle }^{-1}\cdot \langle {\boldsymbol{\upvarepsilon}}\rangle +\frac{{\Delta}\mathrm{T}}{\updelta }{{\boldsymbol{\upsigma}}}^{(7)};$$

(23)

$${\boldsymbol{\upvarepsilon}}={\mathbf{E}}\cdot {\langle \mathbf{E}\rangle }^{-1}\cdot \langle {\boldsymbol{\upvarepsilon}}\rangle +\frac{{\Delta}\mathrm{T}}{\updelta }{{\boldsymbol{\upvarepsilon}}}^{(7)}$$

It is necessary to note that Eq. (23) were obtained for perfectly periodic stresses and strains, which implies that strains averaged through the unit cell are constant across the whole composite medium. That is obviously not the case in most real applications, but we can expect that regular expansions (23) also provide a good estimate for stress and strain field in a composite if $\langle {\boldsymbol{\varepsilon}}\rangle$ is variable, but smooth across the composite medium. Under that assumption, we can use (23) for recovering microscopic fields on the basis of a homogenised solution by substituting strains from that solution for the averaged across the unit cell strains:

$${{\boldsymbol{\upsigma}}}_{\mathrm{rec}}={\boldsymbol{\Sigma}}\cdot {\langle \mathbf{E}\rangle }^{-1}\cdot {{\boldsymbol{\upvarepsilon}}}_{\mathbf{h}\mathbf{o}\mathbf{m}\mathbf{o}\mathbf{g}}+\frac{{{\Delta}}\mathrm{ T}}{\updelta }{{\boldsymbol{\upsigma}}}^{\left(7\right)};$$

(24)

$$ {{\boldsymbol{\upvarepsilon}}}_{\mathrm{rec}}=\mathbf{E}\cdot {\langle \mathbf{E}\rangle }^{-1}\cdot {{\boldsymbol{\upvarepsilon}}}_{\mathbf{h}\mathbf{o}\mathbf{m}\mathbf{o}\mathbf{g}}+\frac{{{\Delta}}\mathrm{T}}{\updelta }{{\boldsymbol{\upvarepsilon}}}^{(7)}$$

Note that in (24) we assume that strains from the homogenised solution ${{\boldsymbol{\varepsilon}}}_{{\boldsymbol{h}}{\boldsymbol{o}}{\boldsymbol{m}}{\boldsymbol{o}}{\boldsymbol{g}}}$ are no longer constant across the cell of periodicity, but depend on coordinates. That obviously violates the condition of periodicity of strains and stress in a unit cell and introduces some error in the values recovered according to (24). However, in view of the large ratio of macroscopic to microscopic dimensions in real composite structures, we can expect that even a non-homogenous distribution of strains in the homogenised solution leads to a small deviation of this field from a periodic one within a single unit cell. That provides grounds for using (24) for recovering microscopic stresses and stresses in real applications. With the purpose of estimating inaccuracy caused by the absence of periodicity in such applications, in the numerical examples presented below we use this method to recover microscopic stresses in regions of a composite structures that are relatively close to the boundary, and we compare results with those of the reference solutions obtained with a very fine mesh.

5 Recovering microscopic fields in three-scale thermoelastic problems

In this section we consider two thermomechanical problems for ITER superconducting strands. In the first problem, the ITER superconducting strand described briefly in the introduction is considered. As shown in Fig. 1, it is natural to identify several scales in the composite structure of the strand. Here we deal with three of them: the macroscopic scale M and two meso-scales m₁ and m₂. Unit cells corresponding to these meso-scales and their finite element (FE) models (we use conventional finite element method and ANSYS code to obtain “fundamental solutions” as well as to solve the homogenised problem) are presented in Fig. 3. Our procedure is applied here in series as explained below.

Fig. 3

FE models of the unit cells corresponding to two meso-scales: a m₁ scale; b m₂ scale. Images of the strand cross section reprinted from Cryogenics Vol. 45, Boso D.P., Lefik M., Schrefler B.A. A multilevel homogenised model for superconducting strand thermomechanics., 259–271, Copyright 2005, with permission from Elsevier

With the aim to illustrate the application of the “fundamental solutions” method to thermomechanical analysis, the following problem was investigated. A partial cool down process is considered—the temperature of the strand is decreasing from the cryostat temperature 80 K [25] down to the operating temperature of the Nb₃Sn superconductor 4.2 K [18]. Obviously, the strand is never used alone, but always as a part of a superconducting cable obtained with a twisting procedure to avoid eddy currents. To simulate the situation when a strand is in contact with three other strands, the strand is subjected to a distributed pressure at three regions—Fig. 4. The pressure is applied according to Hertz distribution:

$$P\left(s\right)={P}_{max}\sqrt{1-\frac{{s}^{2}}{{a}^{2}}},$$

where s is a local coordinate for each “contact” area, with the origin at its centre, and a defines the size of the area (Fig. 4). In the considered numerical example, ${P}_{max}$ was taken 200 MPa. In real conditions, due to the complex multiscale twisting of strands inside the cable, contact areas are usually located in a non-symmetrical way [26], but they are supposed to be symmetric within the problem under consideration with the goal to have a self-balanced system.

Fig. 4

A schematic of the application of pressure that imitates contact interaction with three other strands

Material properties of individual components of the strand were assumed according to [22]. The problem was treated under plane strain assumption, which corresponds to the situation when the strand is straight and its ends are fixed. This is another assumption that is to some extent violated in reality, but radii of curvature of real strands in the cable are very large in comparison to its dimensions in a cross section [26], so we can consider that assumption as a reasonable approximation.

The key benefit of the plane strain assumption is the possibility to solve the same problem with a reference model where the entire composite structure is reproduced. This model, developed for testing the accuracy of the recovering method, is presented in Fig. 5. The model includes 4675 Nb₃Sn filaments, consists of ~ 450,000 s-order elements and has ~ 2,680,000 degrees of freedom. We will refer to the solution obtained with this model as the “reference solution” while the solution obtained for a model in which the whole composite area was represented with a homogenous material with effective characteristics, will be referred to as the homogenised solution.

Fig. 5

Finite element model for obtaining the reference solution

The distribution of von Mises stresses in the cross section of the strand is presented in Fig. 6 for the reference solution. The stress field is due to both the mechanical loading and the cool down process.

The distribution of von Mises stresses in the reference solution (Fig. 6) reveals that whereas in the central zone of the cross section the stress field is nearly periodic, there are areas in the composite structure close to its boundaries where the periodicity condition is apparently violated. For the purpose to select reasonably difficult conditions for testing the recovering algorithm, we choose one of the unit cells located in such high-gradient area shown in Fig. 7.

Fig. 6

Von Mises stress distribution in the reference solution, units MPa

Fig. 7

A unit cell in the composite strand structure for controlling the recovering accuracy

The procedure of three-scale thermoelastic analysis for the composite strand using “fundamental solutions” method consists of the following steps.

Step 1:

Homogenisation at m₁ scale.

We develop a finite element model of the unit cell associated with m₁ scale of Fig. 3a. We solve seven fundamental problems (2)–(8) for this model and, after calculating averaged values of stress and strain components in each problem, apply Eqs. (21) to obtain effective thermoelastic parameters at the meso-scale m₁: ${\mathbf{C}}_{{m}_{1}}^{*}$, ${{\boldsymbol{\upalpha}}}_{{{m}}_{{1}}}^{*}={\left[\begin{array}{ccc}{{\alpha }}_{{{m}}_{1}1}^{*}& {{\alpha }}_{{{m}}_{1}2}^{*}& {{\alpha }}_{{{m}}_{1}3}^{*}\end{array}\right]}^{\mathrm{T}}$. We also store the distributions of stresses and strains in the seven fundamental problems for further use in the recovering of microscopic fields. Using the matrix notation introduced before, we can form the following matrices:

$${{\boldsymbol{\Sigma}}}_{{\mathrm{m}}_{1}}=\left[\begin{array}{cccccc}{{\boldsymbol{\sigma}}}_{{m}_{1}}^{(1)}& {{\boldsymbol{\sigma}}}_{{m}_{1}}^{(2)}& {{\boldsymbol{\sigma}}}_{{m}_{1}}^{(3)}& {{\boldsymbol{\sigma}}}_{{m}_{1}}^{(4)}& {{\boldsymbol{\sigma}}}_{{m}_{1}}^{(5)}& {{\boldsymbol{\sigma}}}_{{m}_{1}}^{(6)}\end{array}\right]; {\boldsymbol{ }{\boldsymbol{\sigma}}}_{{m}_{1}}^{(7)};$$

(25)

$${\mathbf{E}}_{{\mathrm{m}}_{1}}=\left[\begin{array}{cccccc}{{\boldsymbol{\varepsilon}}}_{{m}_{1}}^{(1)}& {{\boldsymbol{\varepsilon}}}_{{m}_{1}}^{(2)}& {{\boldsymbol{\varepsilon}}}_{{m}_{1}}^{(3)}& {{\boldsymbol{\varepsilon}}}_{{m}_{1}}^{(4)}& {{\boldsymbol{\varepsilon}}}_{{m}_{1}}^{(5)}& {{\boldsymbol{\varepsilon}}}_{{m}_{1}}^{(6)}\end{array}\right]; {\boldsymbol{ }{\boldsymbol{\varepsilon}}}_{{m}_{1}}^{(7)}.$$

Step 2:

Transformation of the effective moduli between two mesoscopic scales.

Boundary conditions in fundamental problems (2)–(8) are formulated in local coordinates associated with the unit cell. Therefore, due to the fact that unit cells of m₁ and m₂ meso-scales are oriented differently with respect to the strand, effective thermoelastic parameters ${\mathbf{C}}_{{m}_{1}}^{*}$, ${{\boldsymbol{\upalpha}}}_{{\mathbf{m}}_{1}}^{*}$ obtained at step 1 need to be translated into the local coordinates of the mese-scale m₂. For the components of the fourth-order tensor ${\mathbf{C}}_{{m}_{1}}^{*}$ the usual transformation takes the following form:

$${\mathrm{C}}_{({\mathrm{m}}_{1})\mathrm{ijkm}}^{*\mathrm{^{\prime}}}={\mathrm{l}}_{\mathrm{ip}}{\mathrm{l}}_{\mathrm{jq}}{\mathrm{l}}_{\mathrm{kr}}{\mathrm{l}}_{\mathrm{ms}}{\mathrm{C}}_{({\mathrm{m}}_{1})\mathrm{pqrs}}^{*},$$

(26)

where ${\mathrm{l}}_{\mathrm{ip}}$ are direction cosines of the angles between corresponding coordinate axes (ξ₁,η₁) of m₁ and (ξ₂,η₂) of m₂ scales, and the Einstein summation convention is used. A reduced form of the same transformation is applied for the diagonal second-order tensor composed of the effective coefficients of thermal expansion ${{\boldsymbol{\upalpha}}}_{{\mathbf{m}}_{1}}^{*}$. In the considered example, axes ξ₁ and ξ₂ have an angle of 73°.

Step 3:

Homogenisation at m₂ scale.

We develop a finite element model of the unit cell associated with m₂ scale of Fig. 3b. For the region corresponding to the structure considered at m₁ scale we use the effective moduli obtained at step 2. We solve seven fundamental problems (2)–(8) for this model and, after calculating averaged values of stress and strain components, apply Eqs. (21) to obtain effective thermoelastic parameters at the meso-scale m₂: ${\mathbf{C}}_{{m}_{2}}^{*}$, ${{\boldsymbol{\upalpha}}}_{{\mathbf{m}}_{2}}^{*}$. We also store the distributions of stresses and strains in the seven fundamental problems for this scale:

$${{\boldsymbol{\Sigma}}}_{{\mathrm{m}}_{2}}=\left[\begin{array}{cccccc}{{\boldsymbol{\upsigma}}}_{{\mathrm{m}}_{2}}^{(1)}& {{\boldsymbol{\upsigma}}}_{{\mathrm{m}}_{2}}^{(2)}& {{\boldsymbol{\upsigma}}}_{{\mathrm{m}}_{2}}^{(3)}& {{\boldsymbol{\upsigma}}}_{{\mathrm{m}}_{2}}^{(4)}& {{\boldsymbol{\upsigma}}}_{{\mathrm{m}}_{2}}^{(5)}& {{\boldsymbol{\upsigma}}}_{{\mathrm{m}}_{2}}^{(6)}\end{array}\right]; {{\boldsymbol{\upsigma}}}_{{\mathrm{m}}_{2}}^{(7)};$$

(27)

$${\mathbf{E}}_{{\mathrm{m}}_{2}}=\left[\begin{array}{cccccc}{{\boldsymbol{\upvarepsilon}}}_{{\mathrm{m}}_{2}}^{(1)}& {{\boldsymbol{\upvarepsilon}}}_{{\mathrm{m}}_{2}}^{(2)}& {{\boldsymbol{\upvarepsilon}}}_{{\mathrm{m}}_{2}}^{(3)}& {{\boldsymbol{\upvarepsilon}}}_{{\mathrm{m}}_{2}}^{(4)}& {{\boldsymbol{\upvarepsilon}}}_{{\mathrm{m}}_{2}}^{(5)}& {{\boldsymbol{\upvarepsilon}}}_{{\mathrm{m}}_{2}}^{(6)}\end{array}\right]; {{\boldsymbol{\upvarepsilon}}}_{{\mathrm{m}}_{2}}^{(7)}.$$

Step 4:

Solving the homogenised problem at macroscopic scale.

We develop a finite element model of the structure at macroscopic scale, in which the entire composite structure is modelled with a homogeneous material with effective characteristics ${\mathbf{C}}_{{m}_{2}}^{*}$, ${{\boldsymbol{\upalpha}}}_{{\mathbf{m}}_{2}}^{*}$ (Fig. 8a). For the considered example, the macroscopic problem may be solved in the coordinates (x,y) which are identical to (ξ₂,η₂) used for the homogenisation at m₂ scale, so there is no need for a transformation of effective moduli obtained at step 3. We solve the macroscopic problem and obtain the distribution of stresses and strains within the domain ${{\boldsymbol{\upsigma}}}_{\text{hom}}\text{, }{{\boldsymbol{\upvarepsilon}}}_{\text{hom}}$. The distribution of von Mises stresses in the cross section of the strand is presented in Fig. 8b to illustrate the “homogenised” solution.

Fig. 8

Homogenised model of the strand cross section (a) and the von Mises stress distribution in the homogenised solution, units MPa (b)

Step 5:

Recovering fields at m₂ scale.

Using Eqs. (24), we recover the distribution of stresses and strains at m₂ scale on the basis the homogenised solution and solutions of fundamental problems at m₂ scale:

$$\begin{gathered} {\boldsymbol{\sigma}} _{{rec~\left( {m_{2} } \right)}} = {\boldsymbol{\Sigma}} _{{m_{2} }} \cdot \langle {\bf E}_{{m_{1} }} \rangle ^{{ - 1}} \cdot {\boldsymbol{\varepsilon}} _{{\hom }} + \frac{{\Delta T_{{\hom }} }}{\delta }{\boldsymbol{\sigma}} _{{m_{2} }}^{{\left( 7 \right)}} ; \hfill \\ {\boldsymbol{\varepsilon}} _{{rec~\left( {m_{2} } \right)}} = {\bf{E}}_{{m_{2} }} \cdot \langle {\bf E}_{{m_{1} }} \rangle ^{{ - 1}} \cdot {\boldsymbol{\varepsilon}} _{{\hom }} + \frac{{\Delta T_{{\hom }} }}{\delta }{\boldsymbol{\varepsilon}} _{{m_{2} }}^{{\left( 7 \right)}} \hfill \\ \end{gathered} $$

(28)

Step 6:

Transformation of the recovered strains between two mesoscopic scales.

The recovered strains according to (28) at m₂ scale are further used for recovering microscopic fields at the lowest scale m₁. Due to the mentioned difference in orientation of the unit cells corresponding to these two mesoscopic scales, an appropriate transformation must be applied for ${{\boldsymbol{\upvarepsilon}}}_{\mathrm{rec }\left({m}_{2}\right)}$:

$${\upvarepsilon }_{\text{rec (}{\mathrm{m}}_{2}\text{) }\mathrm{ij}}^{\mathrm{^{\prime}}}={\mathrm{l}}_{\mathrm{ik}}{\mathrm{l}}_{\mathrm{jm}}{\upvarepsilon }_{\text{rec (}{m}_{2}\text{) }\mathrm{km}}.$$

(29)

where the same notations as in (26) are used.

Step 7:

Recovering fields at m₁ scale.

Using Eqs. (24), we recover the distribution of stresses and strains at m₂ scale on the basis the homogenised solution and solutions of fundamental problems at m₂ scale:

$$ \begin{aligned} {\boldsymbol{\sigma }}_{{{\text{rec}}\left( {m_{1} } \right)}} & = \pmb{\Sigma} _{{m_{1} }} \cdot \langle {\bf E}_{{m_{1} }} \rangle ^{{ - 1}} \cdot {{\boldsymbol{\upvarepsilon}}^{\boldsymbol{\prime}}}_{{{\text{rec}}(m_{2} )}} + \frac{{\Delta T_{{\hom }} }}{\delta }{\boldsymbol{\sigma }}_{{m_{1} }}^{{(7)}} ; \\ {\boldsymbol{\upvarepsilon }}_{{{\text{rec}}\left( {m_{1} } \right)}} & = {\bf E}_{{m_{1} }} \cdot \langle {\bf E}_{{m_{1} }} \rangle ^{{ - 1}} \cdot {{\boldsymbol{\upvarepsilon}} ^{\boldsymbol{\prime}}}_{{{\text{rec}}(m_{2} )}} + \frac{{\Delta T_{{\hom }} }}{\delta }{\boldsymbol{\upvarepsilon }}_{{m_{1} }}^{{(7)}} \\ \end{aligned} $$

(30)

The presented procedure of three-scale analysis on the basis of “fundamental solutions” was implemented in APDL (Ansys Parametric Design Language) and used with the ANSYS FE code. A comparison of the recovered homogenised solutions and the reference solution for the axial stress ${\upsigma }_{z}$ across the m₁-scale unit cell shown in Fig. 7, is presented in Fig. 9. Large positive values of ${\upsigma }_{z}$ are mostly caused by the cooldown from 80 to 4.2 K, but because of the difference in thermal expansion coefficients and in elastic moduli of Nb₃Sn filaments and bronze matrix, there are “jumps” in ${\upsigma }_{z}$ at the interface, which were successfully captured by the reference and recovered solutions. Contrary to that, the homogenised solution features approximately constant value of ${\upsigma }_{z}$ across the interface, which is between the maximum and minimum values of the reference solution. The difference between the recovered and reference solutions in this example does not exceed 2%, which is acceptable given that the considered unit cell is located relatively close to the boundary of the composite area in the strand (Fig. 7). However, both the recovered and reference solutions feature rather simple distribution of the axial stress, in which temperature-induced stresses clearly dominate.

Fig. 9

Distribution of the axial stress ${\upsigma }_{z}$ across the m₁-scale unit cell, comparison of the recovered, reference and homogenised solutions

A significantly more difficult situation for the recovering algorithm is observed for some other components of the stress tensor that are strongly influenced by the pressure imitating contact with other strands. Figure 10 presents results of recovering ${\upsigma }_{x}$ ${\upsigma }_{y}$ ${\upsigma }_{xy}$ component of the stress tensor in local coordinates of m₁-scale as well as the von Mises stress along the same line in the same unit cell as in Fig. 9. The recovered solutions for all normal components of the stress tensor (Figs. 9, 10a and b) are fairly close to the reference solution (maximum deviation is observed for ${\upsigma }_{x}$ (Fig. 10a), but is still less than 10%). The shear stress ${\upsigma }_{xy}$, however, appears to be recovered with much poorer accuracy in terms of relative deviation in % (Fig. 10c), which can be explained by small absolute values of this component—maximum values are roughly by an order of magnitude smaller than those for the normal components. That is illustrated by the comparison of recovered and reference values of the von Mises stress, which is important for predicting plastic deformations in such superconducting cables. In can be seen from Fig. 10d that in the considered example, the accuracy in recovering the von Mises stress is roughly as good as it is for the normal components of the stress tensor.

Fig. 10

Distribution of σ_x (a), σ_y (b), σ_xy (c) and von Mises stress (d) across the m₁-scale unit cell, comparison of the recovered, reference and homogenised solutions

Overall, for the considered example the solution obtained using the two-scale recovering procedure provides a reasonably good approximation given that periodicity conditions are apparently poorly satisfied. Furthermore, it needs to be mentioned that the homogenised solution in case of ${\upsigma }_{x}$ is clearly outside the range of reference and recovered values along the line. This can be explained by the three-scale nature of the composite structure of the strand combined with the choice of m₁-scale unit cell located close to the boundary of the homogenised area within the m₂-scale cell, which in turn is located close to the boundary of the homogenised area of the entire strand (Fig. 7). Nevertheless, the two-level recovering process based on “fundamental solutions” successfully captured that inhomogeneity, and the recovered ${\upsigma }_{x}$ is fairly close to the reference one.

To make sure that the method works well for other composite structures and other loading options, we considered another superconducting ITER strand with significantly different microstructure. Figure 11 presents a photo of the cross section of the Luvata (LUV) strand [21, 22] as well as the finite element models used for performing multiscale simulations and obtaining a reference solution.

Fig. 11

reproduced from Boso D.P., Lefik M., Schrefler B.A. Homogenisation methods for the thermo-mechanical analysis of Nb3Sn strand. Cryogenics 2006; 46 (7–8).—569–580 with permission from Elsevier

LUV superconducting strand. Finite element model for obtaining the reference solution and finite element models of unit cells for multiscale analysis. Image of the cross section of the strand, top left,

The LUV strand shown in Fig. 11 features a composite structure with less clear separation of scales—unit cells at both scales are not so small in comparison with the dimensions of the entire composite structure of the strand. Because of that reason, asymptotic homogenisation method is usually considered non applicable to such structure [21]. Nevertheless, with a purpose to test the proposed “fundamental solutions” approach in difficult conditions, the following problem was considered for the LUV strand. A partial cool down process when the temperature of the strand is decreasing from the cryostat temperature 80 K down to the operating temperature of the Nb₃Sn superconductor 4.2 K is considered, and the strand is subjected to external pressure simulating contact with other strands. To make the pressure boundary conditions different from those used in the previous example, only two areas of contact were introduced—Fig. 12. The pressure is applied according to Hertz distribution with the maximum value ${P}_{max}=200\,{\text{MPa}}$. Because of the symmetrical nature of the problem, one quarter of the cross section region is considered.

Fig. 12

A schematic of the pressure application used in the simulation for the LUV strand, also called OUK strand in [21]

Figure 13 shows on the reference model two paths across the unit cells where the recovered solution is studied. Path 1 represents a unit cell that is located relatively far from the boundaries of the composite structure, whereas Path 2 represents a cell located in one of the areas of high stress gradient and almost at the boundary of the composite structure.

Fig. 13

Paths in the composite structure for the control of recovering accuracy

Comparison of the recovered and reference solutions for all components of the stress tensor and for von Mises stress along Path 1 is presented in Fig. 14. A fairly good correlation can be observed for all components, including the shear ones, and for the von Mises stress. A better accuracy in the recovering shear stresses in comparison with the previous example can be explained by a “better” location of Path 1, which is located relatively far from the boundaries of the composite structure and from the area where external load is applied.

Fig. 14

Distribution of σ_x (a), σ_y (b), σ_z (c), σ_xy (d) and von Mises stress (e) along Path 1. Comparison of the recovered and reference solutions

To test the procedure in the worst possible within the considered problem scenario, a recovering along Path 2 was also studied. This path (Fig. 13) is located very close to the boundary of the composite structure and right under the area of pressure application—that makes gradients of stresses in this zone particularly large, and the periodicity assumption, which is the foundation of the method, is therefore poorly satisfied.

Comparison of the recovered and reference solutions for the stresses along Path 2 is presented in Fig. 15. The accuracy of the recovering decreased noticeably in comparison to what was observed on Path 1 for all components of the stress tensor except for σ_z, which is mostly determined by thermal stresses and not so much affected by the applied pressure. However, the accuracy in recovering the von Mises stress is still about 5%, which may be considered a good correlation and indicates applicability of the method even in situations when the solutions are not exactly periodic. To highlight the gradients in the stress field in the considered area, a contour plot of the von Mises stress in the reference solution is shown in Fig. 16.

Fig. 15

Distribution of σ_x (a), σ_y (b), σ_z (c), σ_xy (d) and von Mises stress (e) along Path 2. Comparison of the recovered and reference solutions

Fig. 16

Contour plot of the von Mises stress, MPa Reference solution, fragment of the strand cross section

6 Conclusions

An extension of the “fundamental solutions” method in the mechanics of periodic composites to thermoelastic problems is presented and its accuracy is studied using two different composite structures. The method allows for solving homogenisation and recovering problems in multiscale thermomechanical analysis of composite structures characterized by linear behaviour of their components.

A three-scale analysis was performed using this method for two different superconducting strands of the ITER magnet system, both of which feature a complex composite structure. A problem of the strand cool down from the cryostat temperature 80 K down to the working conditions 4.2 K with simultaneous side compression from other strands was simulated. Models of the strands with a very fine mesh, in which the entire composite structure was represented, were used to obtain reference solutions for controlling the accuracy of the recovered micro fields. The comparison revealed that the accuracy of the method depends on the extent, to which the distribution of stresses and strains in the composite structure can be considered periodic. In the considered examples, the recovered major stress tensor components were within 10% from the ones provided by the reference solution even in the most difficult conditions. The von Mises stress was found to be recovered with even better accuracy of about 5% even in the areas located close to the boundary of the composite structure. Since in the considered linear case stresses and strains are related by the generalised Hooke’s lay, one may expect that recovering the various strain functions used to describe the dependence of critical current superconducting cables on strains [27] may be carried out with good accuracy using the proposed method.

The method only requires seven fundamental problems to be solved once for unit cells representing each mesoscopic scale of a composite structure, and the recovery of microscopic fields is performed on the basis of algebraic calculations involving these solutions of fundamental problems and a homogenised solution on the macroscopic scale. Thereby, the method can be considered as computationally not expensive, whereas the main limitation of its application follows from the underlying idea of “regular expansions”, which requires linear behaviour of the composite components. However, an explicit incremental solution as in [20] may allow to include some nonlinearity if the nature of the problems allows considering the materials behaviour linear elastic within each increment. In that case the fundamental problems have to be solved at each step making the procedure more expensive. This will be further investigated.