Abstract
A new family of hybrid/mixed finite elements optimized for numerical stability is introduced. It comprises a linear hexahedral and quadratic hexahedral and tetrahedral elements. The element formulation is derived from a consistent linearization of a well-known three-field functional and related to Simo–Taylor–Pister (STP) elements. For the quadratic hexahedral and tetrahedral elements we derive (static reduced) discontinuous hybrid elements, as well as continuous mixed finite elements with additional primary unknowns for the hydrostatic pressure and the dilation, whereas the linear hexahedral element is of the discontinuous type. The elements can readily be used in combination with any isotropic, invariant-based hyperelastic material model and can be considered as being locking-free. In a representative numerical benchmark test the elements numerical stability is assessed and compared to STP-elements and the family of discontinuous hybrid elements implemented in the commercial finite element code Abaqus/Standard. The new elements show a significant advantage concerning the numerical robustness.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 State of the art
A hypothetical solid that changes only its shape when loaded while maintaining its original volume is called (fully or ideal) incompressible. Real world rubber-like materials are quasi-incompressible. The compressibility of a solid is in practice often quantified by the use of Poisson’s ratio \(\nu \). While ideal incompressibility corresponds to \(\nu =0.5\), a (fuzzy) classification of quasi-incompressibility might be given by the range \(0.47\le \nu <0.5\).
Standard finite elements (FEs) are displacement based, meaning that only the displacements are assembled primary unknowns, whereas strains and stresses are so-called secondary unknowns that are updated when a new displacement increment is computed. Since an applied hydrostatic pressure on an ideal incompressible solid would not lead to any strains, a small calculated displacement increment might cause huge changes in the resulting hydrostatic part of the strain and stress for a quasi-incompressible material. This renders the purely displacement-based formulation numerically ill-conditioned. Furthermore, since the condition of ideal incompressiblity represents a kinematic coupling between the displacement degrees of freedom, artificial stresses arise at integration points in the quasi-incompressible case, so that standard finite elements tend to be overly stiff. This effect is known as volumetric locking.
To overcome these deficiencies, several so-called mixed and hybrid element formulations were developed. Starting with modified displacement based finite elements, the simplest variant are uniform reduced-integration elements, which use a lower order (typically one order lower) numerical integration scheme. Since these elements suffer from rank deficiency, numerical stabilization is required, cf., e.g., [3, p. 452] or [39, p. 402]. To overcome this problem, selective reduced integration elements use a split of strains and stresses into volumetric and dilational parts. In order to prevent rank deficiency, the volumetric components are integrated an order lower than the dilational parts, cf. [15, p. 221]. Furthermore, the use of incompatible mode elements is advantageous in view of volumetric locking compared to standard displacement elements, but these come with the disadvantage of possibly non-monotonic convergence and may cause instabilities in geometrically nonlinear simulations that are physically not present, cf. [2, p. 268]. Other elements, like F-bar elements, de Souza Neto et al. [6], and B-Bar elements, Hughes [14], either use a modified deformation gradient or a modified matrix of form function derivatives (in finite element literature usually denoted by \(\varvec{F}\) and \(\varvec{B}\), respectively) to obtain a formulation that evaluates the volumetric part of the constitutive law in fewer points than the isochoric part. Since all these low-order modified pure displacement elements either suffer from bad convergence behavior or even instabilities, they are not capable to deal with quasi-incompressible materials in a satisfactory manner. Computationally more expensive higher-order element formulations based on integrated Legendre polynomials that can circumvent these problems have been proposed by Szabó and Babuška [38]; Heisserer et al. [12].
Furthermore, there are element formulations, based on elastic potentials augmented by terms with additional variables like independent dilation or pressure fields. The simplest formulation uses a Lagrange multiplier expression in order to enforce ideal incompressibility, cf. e.g. [39, p. 164]. To improve numerical stability a perturbation term which weakens this constraint can be added upon the aforementioned formulation. An appropriate choice thereof allows simulating compressible materials with the volumetric standard model, cf. [4] and [13, p. 406 sq.]. A well known element formulation using an independent pressure field was proposed by Sussman and Bathe [37]. However, the approach depends on a material specific constraint equation that was provided only for the volumetric standard model in the original publication. The restriction to a constant compression modulus holds also for the mixed-interpolation approaches, proposed by Pantuso and Bathe [22, 23]. Simo and Taylor [33] and Simo et al. [34] proposed a formulation using a three-field functional with independent dilation and pressure fields. This element formulation does not introduce a material-dependent constraint function. Hence, it can be combined with all invariant-based hyperelastic materials with minor effort.
To improve the convergence behavior there are numerous variants of enhanced assumed strain elements, using the same underlying functional, cf. [39, p. 421 sq.]. These use an enhanced deformation gradient, which is added upon the deformation gradient of the configuration in order to add extra parameters to the element formulation. This formulation has disadvantages regarding hourglassing, for what reason either stabilization techniques or modified interpolation terms have to be applied, cf. [7, p. 678 sq.]. Enhanced assumed strain elements have a rich history and are treated in e.g. [8,9,10, 18, 20, 24,25,26,27], albeit some of those treatises are more focused on the issue of shear locking.
Schröder et al. [31] proposed a further mixed-element formulation, based on a three-field functional. The formulation relies on a different approximation of the deformation gradients cofactor (compared to other displacement variables). Hence, the strain energy has to have a pronounced cofactor term in order to benefit from the formulation, which in turn restricts the class of material that may benefit from the usage of the formulation.
At the beginning of the 21st century, the discontinuous Galerkin method gained reasonable popularity in solid mechanics, which also gave rise to multiple hybrid-element formulations, cf. e.g. [5, 16, 40]. This method shows great potential in simulating quasi-incompressible material, but usually numerical stabilization is required as well.
To summarize, the three-field potential of [33, 34] played a key role in the history of hybrid-element formulations and this research field is far from being settled. Recent hybrid-element formulations often rely heavily on matching numerical stabilization techniques.
1.2 Objective of this contribution
We start this article with a revisit of the well established hybrid-element formulation of [33, 34]. Afterwards, novel contributions closely connected to the original formulation are presented in a threefold way.
First of all, more as a side note, we present the consistent linearization associated with the three-field potential introduced in [33] for a general hyperelastic material where the strain-energy density may be an arbitrary function of the right Cauchy–Green tensor. For this general setting the weak form was already given in [33], but the linearization was only provided for a more specialized setting. We simplify this new general linearization to the common special case of an isotropic, invariant-based, quasi-incompressible material. In this regard it is remarkable that the severe simplifications of the linearization in comparison to the general setting are mainly induced by key properties between the first and second-order derivatives of the isochoric invariants with respect to the modified right Cauchy–Green tensor. This relations have not yet been mentioned in the literature to our best knowledge, although their role (in the light of the general setting) is comparable to the decoupling of stress into isochoric and volumetric parts, which is—in contrast—extensively studied in the literature because the decoupling is already relevant for the derivation of the weak form. From our point of view this investigation completes the continuum mechanical foundation for the derivation of hybrid elements based on the three-field potential.
Secondly, as the main contribution, an implementation scheme for discontinuous hybrid elements that differs from the classical Simo–Taylor–Pister elements but is based upon the same three-field potential is introduced. We show by numerical benchmarks that the new elements retain the mesh convergence behavior of the original Simo–Taylor–Pister elements—especially they do not suffer from volumetric locking—whereas the numerical robustness is greatly improved. Their robustness allows these elements to be used without numerical stabilization in contrast to most recent hybrid-element formulations.
At last, we also implement and study continuous hybrid elements associated with the discontinuous implementation scheme mentioned before. Although the possibility of continuous mixed elements is frequently mentioned in the literature, this type of element is rarely implemented due to its limited applicability. In a matching setting we systemically compare discontinuous versus continuous type elements with the same displacement interpolation. Also, all the elements are compared to the state-of-the-art commercial, discontinuous hybrid-element family implemented in Abaqus/Standard.
1.3 Notation basics
The standard notational conventions of nonlinear continuum mechanics are used, especially Einstein’s summation convention. We restrict ourselves to Cartesian coordinate systems. In turn, the simplified tensor-index notation can be used, where it is unnecessary to distinguish between co- and contravariant indices. Material points in the undeformed body \(\Omega \) will be identified with their Cartesian coordinate vectors  . Due to the body’s deformation, a point \(\varvec{X}\) shifts by a displacement vector \(\varvec{U}\left( \varvec{X}\right) \) to its new destination
. Due to the body’s deformation, a point \(\varvec{X}\) shifts by a displacement vector \(\varvec{U}\left( \varvec{X}\right) \) to its new destination  in the so-called spatial (or deformed) configuration. With the configuration map \(\varvec{\varphi }\), the spatial points are given by \(\varvec{x}=\varvec{\varphi }(\varvec{X})=\varvec{X}+\varvec{U}\left( \varvec{X}\right) \). Hence, the deformed body is the image of \(\Omega \) under the configuration map \(\varvec{\varphi }\), i.e. \(\varvec{\varphi }(\Omega )\). The deformed body’s surface is indicated as \(\partial \varvec{\varphi }(\Omega )\), whereas an infinitesimal volume element in the spatial configuration is denoted by \({{\,\mathrm{d\!}\,}}v\) and the corresponding infinitesimal area element of the deformed body’s surface is denoted by \({{\,\mathrm{d\!}\,}}a\). The quantities for the undeformed body are denoted analogously by \(\partial \Omega \), \({{\,\mathrm{d\!}\,}}V\) and \({{\,\mathrm{d\!}\,}}A\).
in the so-called spatial (or deformed) configuration. With the configuration map \(\varvec{\varphi }\), the spatial points are given by \(\varvec{x}=\varvec{\varphi }(\varvec{X})=\varvec{X}+\varvec{U}\left( \varvec{X}\right) \). Hence, the deformed body is the image of \(\Omega \) under the configuration map \(\varvec{\varphi }\), i.e. \(\varvec{\varphi }(\Omega )\). The deformed body’s surface is indicated as \(\partial \varvec{\varphi }(\Omega )\), whereas an infinitesimal volume element in the spatial configuration is denoted by \({{\,\mathrm{d\!}\,}}v\) and the corresponding infinitesimal area element of the deformed body’s surface is denoted by \({{\,\mathrm{d\!}\,}}a\). The quantities for the undeformed body are denoted analogously by \(\partial \Omega \), \({{\,\mathrm{d\!}\,}}V\) and \({{\,\mathrm{d\!}\,}}A\).
2 A recap of the STP-hybrid-element formulation
In this section, we recap the Simo–Taylor–Pister (STP) hybrid-element formulation, originally provided in [33, 34], in some detail, in order to outline differences to the later introduced new CL3F-formulation.
2.1 The three-field formulation
A hyperelastic material is per definition a material that can be characterized by a given strain energy density W. In a very general setting we assume W to be given as a function of the components of the right Cauchy–Green tensor \(\varvec{C}\) which is itself a function of the deformation gradient \(\varvec{F}\).
In particular W might depend on the Jacobian J, i.e. the determinant of \(\varvec{F}\). In the undeformed body \(\Omega \), the overall potential \(\Pi \) is then given by
where \(\Pi _\mathrm {ext}\) is the potential of applied forces.
The standard overall potential (1) is modified into a three-field potential by the introduction of a modified displacement gradient \(\mathring{\varvec{F}}\) and in turn a modified version of the right Cauchy–Green tensor \(\mathring{\varvec{C}}\), defined by
Here, \(\varTheta \) is a newly introduced primary unknown scalar-field, we call the (volumetric) dilation. Since the determinant of \(\mathring{\varvec{F}}\) is \(\varTheta \), the usage of \(\mathring{\varvec{F}}\) instead of \(\varvec{F}\) will effectively replace the Jacobian J by the primary variable \(\varTheta \). The modified strain energy density \(\mathring{W}\) is defined by replacing \(\varvec{F}\) by \(\mathring{\varvec{F}}\) in the argument, i.e. \(\mathring{W}:=W(\mathring{\varvec{C}}(\mathring{\varvec{F}}))\). Due to this notational convention, we may omit the argument. Note that W and \(\mathring{W}\), regarded as a function of the (modified) strain, refer to the same mathematical function, but regarded as a continuum mechanical quantity, we have \(\mathring{W}=W\), if, and only if, we have \(J=\varTheta \). Therefore, we have to enforce this equality by a Lagrange-multiplier, in order to arrive at an equivalent potential. We denote this Lagrange-multiplier by p, which is another newly introduced, primary unknown scalar-field. Like the purely displacement based counterpart of \(\varTheta \) is J, the purely displacement based counterpart of p turns out to be the hydrostatic pressure. The final modified three-field potential, with the primary variables \(\varvec{\varphi },\,\varTheta \) and p reads
The weak form associated with the three-field potential (2) is derived by computing the first variation of the three-field potential \(\Pi _{\mathrm {mod}}\) at a current state defined by:
-
\(\hat{\varvec{\varphi }}\)—the current configuration (vector-field),
-
\(\hat{\varTheta }\)—the current dilation (scalar-field),
-
\(\hat{p}\)—the current (independent) hydrostatic pressure (scalar-field),
with respect to the associated virtual quantities denoted by:
-
\({\varvec{\eta }}\)—the virtual displacement (vector-field),
-
\({\psi }\)—the virtual dilation (scalar-field),
-
q—the virtual (independent) hydrostatic pressure (scalar-field),
leading to the following weak form for a total Lagrangian formulation



Despite notational differences equation (3) was already provided in Proposition 3.2 of [33]. (In addition there is an obvious typographical error in equation (3.18) of [33].)
2.2 A semi-discretized variant of the weak form
In [33], Proposition 3.5, a linearization of the weak form is provided for a more specialized setting (uncoupled case), where the strain energy density is assumed to have the structure \( W:=W^\text {vol}(\Theta )+W^\text {iso}(C^\text {iso}). \) However, for the proposed implementation of STP-elements this linearization is not used. Instead an approach, here referred to as “semi-discretization”, originally sketched in section 4.1 of [33] is utilized, which is recapped below.
The same inter-element discontinuous interpolation for the dilation and the pressure and their virtual counterparts is utilized

Regarding just the additive term of the weak form (3) that incorporates the virtual pressure q and only the contribution of a single finite element  , factoring out the coefficients of the virtual pressure leads to an intra-element interpolation for the dilation
, factoring out the coefficients of the virtual pressure leads to an intra-element interpolation for the dilation

that is written in terms of the configuration \(\hat{\varvec{\varphi }}\). The same procedure applied to the additive part of (3) that incorporates the virtual dilation \(\psi \) leads to a corresponding intra-element interpolation for the hydrostatic pressure

The elimination of the independent pressure and dilation in the remainder of (3) by insertion of (5) and (6) leads to the semi-discretized variant of the weak formulation depending solely on the configuration (or displacement). The spatial representation reads

(It is crucial to note that here  is not the independent hydrostatic pressure, but instead a shorthand notation for the insertion of (6), i.e.,
is not the independent hydrostatic pressure, but instead a shorthand notation for the insertion of (6), i.e.,  is a given function that only depends on the configuration. This also applies for
is a given function that only depends on the configuration. This also applies for  below.)
below.)
Since (7) only depends on the current configuration \(\hat{\varvec{\varphi }}\), it can be linearized by calculation of the Gateaux derivative in the direction of the displacement increment \(\varvec{u}\) only. The final spatial representation of the linearization reads

where

is the so-called “discrete divergence operator”, cf. [33]. (In Simo and Taylor [33] there is an obvious typographical error in the last term of the linearization,  ).
).
Finally, the introduction of an inter-element continuous interpolation for the not yet discretized displacement field leads to STP-elements. The implementation is very similar to purely displacement-based elements because just the remaining displacement degrees of freedom are assembled. Due to the used inter-element discontinuous pressure and dilation interpolation (4), STP-elements are classified as “discontinuous-type” hybrid elements.
3 The continuum-level linearization approach
Hybrid elements based directly on a consistent continuum-level linearization of the three-field potential’s weak form (3) with respect to all three primary unknowns—and hence denoted CL3F-elements—will be derived in this contribution. The continuum mechanical foundation is provided in this section, whereas the discretization schemes are discussed in Sect. 4.
3.1 The isotropic, quasi-incompressible case
The weak form (3) is given for a very general setting where the strain energy density is assumed to be a general function of the modified right Cauchy–Green tensor \(\mathring{W}:=W(\mathring{\varvec{C}}(\mathring{\varvec{F}}))\). For the special case of an isotropic, quasi-incompressible material, like rubber, one usually assumes for a purely displacement-based setting that W can be additively split into a volumetric part, that only depends on the third invariant, the determinant of \(\varvec{C}\) (or \(\varvec{F}\), since \(\det (\varvec{C})=\det (\varvec{F})^2\)) and an isochoric remainder. This remainder is assumed to depend on the first two invariants of the isochoric part of \(\varvec{C}\). (One often speaks of “modified invariants” in this case which we omit here to avoid confusion with the already introduced modification of \(\varvec{F}\).) In our case we consequently assume that \(\mathring{W}\) can be additively split into a volumetric part that depends only on the (volumetric) dilation \(\varTheta \) and an isochoric remainder

where the (modified) isochoric invariants are

i.e., the invariants of the isochoric part of the modified right Cauchy–Green tensor \(\mathring{\varvec{C}}\)
For an isotropic, quasi-incompressible material of type (9) straight forward calculations yield

which implies

Hence, by the standard definition of the Cauchy stress

we can calculate the isochoric part of the stress by

whereas, we obtain for the volumetric part of the stress

With the same argumentation one can also derive the two parts of the stiffness tensors by

and

With (10) and (11) we obtain the following spatial representation of the weak form (3):

The associated linearization of the weak form (Gateaux differential) on the deformed configuration is given by

where, we introduced the fourth-order tensors

and the denotations of the incremental quantities are:
-
\({\varvec{u}}\)—the displacement increment (vector-field),
-
\({\omega }\)—the (independent) dilation increment (scalar-field),
-
\({\gamma }\)—the (independent) hydrostatic pressure increment (scalar-field).
(A detailed derivation of the linearization can be found in the “Appendix”.) For the case of only dead loads, the contribution from the potential of applied loads \(\Pi _{\mathrm {ext}}\) is simply zero. However, we have a non-vanishing contribution for follower-loads like pressure, cf. [32].
It is noteworthy that the summand of (15) that comprises the current isochoric stress  is symmetric in \(\varvec{u}\) and \(\varvec{\eta }\), although the two summands that we would get by expanding the round bracket are not. In turn, the resulting tangent stiffness matrix will be actually symmetric.
is symmetric in \(\varvec{u}\) and \(\varvec{\eta }\), although the two summands that we would get by expanding the round bracket are not. In turn, the resulting tangent stiffness matrix will be actually symmetric.
Furthermore, note that (15) represents in contrast to the tangent stiffness used in [33], i.e. (8), a linearization with respect to all three primary unknowns. In the here presented CL3F-formulation consisting of the weak form (14) and its linearization (15), p and \(\Theta \) remained primary unknowns, whereas the STP-approach consisting of the weak form (7) and its linearization (8) is finally purely displacement-based: the configuration \(\varvec{\varphi }\) is the only primary unknown and \(\varvec{\eta }\) the only virtual quantity. p and \(\Theta \) in (8) are just shorthands for displacement terms and not independent unknowns anymore.
3.2 A remark on the linearization for the general case
In the preceding section as well as in [33] the linearization of the weak form is only given for the special case of an isotropic material. To our best knowledge a linearization for the general setting that was utilized to introduce the weak form, i.e. a setting where the strain energy density can be a general function of the modified right Cauchy–Green tensor \(\mathring{W}:=W(\mathring{\varvec{C}}(\mathring{\varvec{F}}))\), was never presented in the literature. This general linearization is provided in the “Appendix” of this contribution.
The general linearization is way more complex than the linearization for the special case (15). In this regard it is remarkable that the severe simplifications are induced by key properties between the first and second-order derivatives of the isochoric invariants with respect to the modified right Cauchy–Green tensor:



The properties (17) and (18) provide a possibility for stress and stiffness terms to cancel out each other that is not given for the general case. A detailed derivation of the linearization for the general and special case is provided in the “Appendix”.
4 Discretization for the CL3F-hybrid elements
At a given current state \((\hat{\varvec{\varphi }}, \hat{\varTheta }, \hat{p})\) the linearized problem of finding critical points reads
where g and \(\delta g\) are given by (14) and (15). This equation is iterated for a given load level after the here introduced discretization and assembling, which is the well-known classical Newton–Raphson scheme. While it is common and beneficial to use the configuration \(\varvec{\varphi }\) as the first primary unknown for theoretical derivation, usually the displacement \(\varvec{U}\) is chosen as the first primary unknown for implementations, cf. Sect. 1.3.
The key to locking-free hybrid elements are a well-chosen combinations of form functions for the displacement degrees of freedom on the one hand and the dilation and pressure degrees of freedom on the other hand, which is extensively discussed in the literature. For an introduction one may refer to e.g. [2, pp. 292 sqq.].
In this contribution well established combinations of form functions are chosen. Also, quadrature schemes are selected in a way so that the later derived discontinuous-type CL3F-elements will be one-on-one comparable to the Abaqus hybrid elements C3D8H, C3D10H and C3D20H, since the same interpolation and quadrature schemes are used. (However, it should be mentioned that the Abaqus elements are based on a two-field formulation rather than a three-field formulation.)
For the displacement degrees of freedom inter-element continuous interpolations with standard Lagrange form functions are used, that are explained in detail in basic text books on finite elements (cf. e.g [2, 39, 41])

Like it is common practice, we selected the same form functions for every coordinate direction i. For dilation and pressure, either Lagrange-type interpolation schemes (of lower order) are selected for continuous-type CL3F-elements, or inter-element discontinuous polynomial interpolation schemes are selected in order to derive discontinuous-type CL3F-elements that are directly comparable to STP-elements or the aforementioned Abaqus elements. In general the same scheme is selected for dilation and pressure, cf. (4). For the associated virtual quantities \(\varvec{\eta }\), \(\psi \) and q the same form functions  and
and  are used.
are used.
Problem (19) leads to a discrete linear system with the structure

Note that the submatrix  might, in addition to the first three summands on the right-hand side of Eq. (15), also contain load terms stemming from \(\varphi _*\{\delta ( \delta \Pi _\mathrm {ext}(\hat{\varvec{\varphi }},\varvec{\eta }),\varvec{u})\}\) in Eq. (15), if follower loads are considered. The overall element-tangent-stiffness matrix is symmetric, e.g., we have
might, in addition to the first three summands on the right-hand side of Eq. (15), also contain load terms stemming from \(\varphi _*\{\delta ( \delta \Pi _\mathrm {ext}(\hat{\varvec{\varphi }},\varvec{\eta }),\varvec{u})\}\) in Eq. (15), if follower loads are considered. The overall element-tangent-stiffness matrix is symmetric, e.g., we have  .
.
4.1 Continuous elements
The possibility of continuous hybrid elements is frequently noted in the literature. However, these types of elements are rarely implemented, since one has to be careful regarding multi-material interfaces especially if different types of finite elements are to be combined. Due to the fact that inhomogeneous solids have generally spoken a discontinuous pressure field, the discontinuous type elements have a wider rage of applicability. We are not aware of systematic continuous versus discontinuous type hybrid element comparisons like provided in this contribution, where matching elements—especially utilizing the same displacement interpolation—of different types (continuous/discontinuous) are directly compared. However, a noteworthy comparison of a continuous second-order L2/P1 tetrahedral with a discontinuous linear L1/P0 hexahedral element can be found in [30].
In this contribution we combine quadratic displacement elements with a linear Lagrange interpolation for the dilation and the pressure. For quadratic hexahedral elements a serendipidy-type Lagrange interpolation is utilized since this is the interpolation used by Abaqus CAE (although the usage of an incomplete second-order polynomial has a negative influence on the rate of convergence from a theoretical point of view). Since the additional dilation and pressure degrees of freedom (DOFs) are assembled just like displacement DOFs, the principle solution algorithm used for this kind of elements does not differ from the one used for simple displacement-based elements. However, besides the obvious difference that not all degrees of freedom have the same physical meaning, the treatment of a different number of DOFs per node has to be implemented.
For the continuous hybrid elements it is noteworthy that although the element tangent stiffness matrix (20) is singular, the assembled tangent stiffness matrix is not.
We implemented the following specific continuous mixed finite elements. The suffix L1 is used to indicate the first-order Lagrange-type interpolation for the dilation and the pressure.

CL3F-H2sG27-L1
-
hexahedral element
-
20 node, quadratic, serendipity-type Lagrange interpolation for the displacements
-
27 point Gauß quadrature (1D product rule)
-
linear Lagrange interpolation for dilation and pressure (assembled)
-
76 degrees of freedom

CL3F-T2G4-L1
-
tetrahedral element
-
10 node, quadratic, Lagrange interpolation for the displacements
-
4 point, second-order,
 : 2-1 quadrature, cf. [36, p. 307]
: 2-1 quadrature, cf. [36, p. 307] -
linear Lagrange interpolation for dilation and pressure (assembled)
-
38 degrees of freedom
4.2 Discontinuous elements
For the discontinuous type elements we either use zeroth-order or a linear (first-order) polynomial ansatz
for the dilation and pressure interpolation, which is indicated by the suffix P0 or P1 in the element name. While this leads to a smooth interpolation of the dilation and pressure inside every element, their values will in general jump between adjacent elements, i.e., the overall interpolation is (inter-element) discontinuous (but intra-element continuous). For this type of element, the dilation and pressure degrees of freedom can be removed from the tangent stiffness matrix by static condensation and only the displacement degrees of freedom will be assembled.
Due to the fact that we selected the same ansatz for the dilation and the pressure, the submatrix  is quadratic and can be inverted. The original system (20) is equivalent to the system
is quadratic and can be inverted. The original system (20) is equivalent to the system



The displacement degrees of freedom are assembled according to (21) for the implementation of discontinuous type CL3F-elements. However, since in contrast to the STP-approach, the current states values of the independent dilation and the pressure are needed in order to compute the replacement element stiffness and residual vector from (21), we need to keep track of these quantities. It is mandatory that every instance of a finite element has internal state variables for the dilation and pressure that are updated via (22) and (23) once the global tangent stiffness equation system, assembled from (21), is solved.
We implemented and tested the following specific discontinuous hybrid finite elements. Here the gray dots refer to the not assembled internal dilation and pressure degrees of freedom.

CL3F-H1G8-P0
-
hexahedral element
-
8 node, linear Lagrange interpolation for the displacements
-
8 point Gauß quadrature (1D product rule)
-
1 node, constant dilation and pressure ansatz (not assembled)
-
24 (assembled) degrees of freedom

CL3F-H2sG27-P1
-
hexahedral element
-
20 node, quadratic, serendipity-type Lagrange interpolation for the displacements
-
27 point Gauß quadrature (1D product rule)
-
4 node, linear polynomial dilation and pressure ansatz (not assembled)
-
60 (assembled) degrees of freedom

CL3F-T2G4-P0
-
tetrahedral element
-
10 node, quadratic, Lagrange interpolation for the displacements
-
4 point, second-order,
 : 2-1 quadrature, cf. [36, p. 307]
: 2-1 quadrature, cf. [36, p. 307] -
1 node, constant dilation and pressure ansatz (not assembled)
-
30 (assembled) degrees of freedom
4.3 The difference between the discontinuous type CL3F and STP hybrid elements
The major difference between continuous type CL3F-elements and the discontinuous CL3F-elements relies on the fact that the dilation and pressure degrees of freedom are only assembled for the continuous elements. This methodological difference also causes the interpolation schemes to differ, since we require a continuous dilation and pressure interpolation for the continuous elements and a discontinuous one for the discontinuous elements.
In contrast, to finally achieve a fair comparison, the exact same interpolation and discretization schemes are used for the discontinuous type STP-elements like introduced in the last section for the discontinuous type CL3F-elements. Like already outlined the schemes were selected in the first place to match the Abaqus hybrid elements. Therefore, all considered discontinuous type CL3F-elements are always one-on-one comparable to an STP and an Abaqus element. CL3F and STP-prefixes are used to distinguish the elements on a notational level. For example, the CL3F-H1G8-P0 and STP-H1G8-P0 are both of the discontinuous H1/P0 type, but nevertheless, the specific implementations are different, like we will shortly discuss in this section.
From a mathematical point of view the STP-elements are based on (7) and (8), whereas the discontinuous type CL3F-elements are based on the static condensation (21) of (14) and (15). The resulting systems are not equivalent and in turn the resulting finite elements are different as well.
Let us recall in this regard that we did not use any approximations in order to derive the (therefore consistent) continuum level linearization (15) of the original three-field potentials weak from (3). While only the continuous type CL3F-elements can utilize the resulting discretization (20) directly, the discontinuous type CL3F-elements utilize the system (21), (22), (23), which is however equivalent to (20). In contrast, the original STP-approach utilizes the pure displacement-based linearization (8) which is neither equivalent to the three-field linearization (15), nor its displacement part (21) (after discretization). At this point it should be pointed out that this is not due to a mistake in the STP-approach: Equation (8) is of course also a valid consistent linearization, but the weak form that is linearized is not (3) but instead the semi-discretized variant (7) where dilation and pressure are already eliminated. This elimination was performed with the help of the dilation/pressure interpolation which is already an approximation. So roughly spoken, the discontinuous CL3F-elements differ from the STP-elements because we followed the design paradigm of staying as long as possible in the realm of exact continuum mechanics—although it is of course inevitable to finally utilize the dilation/pressure interpolation.
Since finally the exact same dilation/pressure interpolations are utilized for the discontinuous CL3F-elements and the STP-elements and the weak form (7) is derived from (3) by the use of the dilation/pressure interpolation, we do not expect differences beside small round off errors in the resulting displacement field solutions (i.e., after the equilibrium iterations are converged) for comparable elements, even in the still mesh depended regime. However, since the elements differ from each other especially in the utilized tangent stiffness there can be (pronounced) differences concerning the numerical stability. In this regard, the authors found it plausible that the utilization of the (unexact) discretization as the very last step should influence the numerical stability in a positive way (if there is an influence). In the later introduced benchmark test, cf. Sect. 5.3, this influence turns out to be actually substantial.
On an implementation level, a major difference between the elements lies in the fact that \(\Theta \) and p were independent variables during the linearization for the CL3F-approach and are in turn secondary variables for the discontinuous type CL3F-elements. Thus every finite element instance stores internal state variables for the dilation and pressure degrees of freedom, which are updated via (22) and (23) in every increment. There is no need for such a secondary variable update-scheme for the purely displacement-based STP-elements. Here, in contrast to the incremental relations (22) and (23), the Eqs. (5) and (6) directly provide the current states \(\Theta \) and p in terms of displacement quantities and incremental quantities like \(\omega \) and \(\gamma \) do not appear in the STP-approach at all, since \(\Theta \) and p were eliminated from the weak form before the linearization. The differences in the update schemes are illustrated by the Algorithms 1 and 2.


Ignoring the fact that—due to the secondary variable update scheme—the pressures p in both approaches are not directly comparable, the element residual of the STP-approach equals the term  in the CL3F-approach—compare (7) and the first line of (14). Thus, the additional summands of the vector residual of (21) stemming from
in the CL3F-approach—compare (7) and the first line of (14). Thus, the additional summands of the vector residual of (21) stemming from  and
and  are simply missing in the STP-approach and are therefore implicitly assumed to vanish, which may be regarded as another difference between both approaches, cf. Algorithms 1 and 2.
are simply missing in the STP-approach and are therefore implicitly assumed to vanish, which may be regarded as another difference between both approaches, cf. Algorithms 1 and 2.
5 Numerical benchmarks
5.1 Basic benchmark setting
To benchmark the influence of the strength of the nonlinearity in the volumetric model, we combine the simple Neo-Hooke model for the isochoric part of the strain energy density (\(\mu _0 = 1.0316\,\text {MPa}\)) with three different compression models. All compression models were (least-square) fitted by Ricker et al. [28] to the same experimental data obtained by confined axial compression testing of an industrial NR/IR-blend (natural rubber/isoprene rubber) with strongly nonlinear compression behavior used for damping applications. Sorted by the strength of the uplift from weakest to strongest nonlinearity, the compression models are:
-
Ogden compression model, cf. [21], \(\mathring{W}_\mathrm {vol} = \frac{K_0}{\beta ^2}\left( \beta \ln {\varTheta } + \varTheta ^{-\beta } - 1\right) \), \(K_0=2781\ \text {MPa}\), \(\beta =-2\)
-
Standard compression model, \(\mathring{W}_\mathrm {vol} = \frac{1}{2}K_0\left( \varTheta -1 \right) ^2\), \(K_0=2816\ \text {MPa}\)
-
Hartmann–Neff model, cf. [11], \(\mathring{W}_\mathrm {vol}= \frac{K_0}{2\beta ^2}\left( \varTheta ^\beta + \varTheta ^{-\beta } - 2\right) \), \(K_0=2290\ \text {MPa}\), \(\beta =41\)
For the popular Ogden model the nonlinear parameter \(\beta \) was fixated to \(-2\) to avoid contradictions. Therefore, the volumetric part of the strain energy for the Ogden model grows asymptotically even slower than for the standard model. Since the measured rate of growth of the strain energy is not supported by the theoretical foundation of the Ogden compression model, this model has to be considered as being inadequate for the material at hand. The standard model is known to have a wrong asymptotic limit for the stresses under compression and is therefore also inadequate from a theoretical point of view, but is included in the investigation since the material model is the only one readily available in Abaqus. Only the “freely fitted” Hartmann–Neff model captures the energetic growth adequately. Because of the resulting high exponents (\(\beta =41\)) this model is very challenging from a numerical point of view.
As a first benchmark example, we selected the well known Cooks membrane, see Fig. 1. The membrane is loaded with a constant force of \(1\,\mathrm {N}\) pointing into positive y direction, distributed over the face at \(x=48\,\mathrm {mm}\). The nodes belonging to the face at \(x=0\,\mathrm {mm}\) are fixed in all directions.
For the second test, the geometry and boundary conditions are adapted from a standard block locking test, cf. [39, p. 458]: A cubic block, see Fig. 2, is loaded on a quarter of its upper surface with a pressure \(\tilde{p}\). All nodes on the upper surface are fixed in x and y direction. The bottom side is fixed in z direction. The faces \(x=0\) and \(y=0\) have symmetry constraints normal to their surfaces.
All simulation involving STP and CL3F elements were done using Sofeas, a Finite-Element code, mainly developed by P. Schneider (second author). A spatial formulation was used for the numerical benchmarks in conjunction with a full Newton–Raphson scheme. The \(L^2\)-norm of the (absolute) reaction-force error is used as the convergence criterion. Tolerance was set to \(10^{-5}\). Neither extrapolation nor any stabilization techniques based on augmentation are used. Python’s standard floating point arithmetic using 64-bit (double-precision) floats was used in general. (Abaqus/Standard always uses double-precision as well.)
In order to compare the CL3F-elements performance to standard industrial hybrid elements, Abaqus/Standard, Versions 2017 and 2020, Simulia (Dassault Systèmes SE, France) were used. The specifically used elements are C3D8H, C3D20H and C3D10H, cf. [35, chapter 28]. Like already outlined, the STP and discontinuous CL3F elements were designed to match the Abaqus elements interpolation and quadrature schemes. These elements are therefore one-on-one comparable. However, the continuous CL3F-elements have more DOFs than their Abaqus counterparts and different dilation/pressure interpolations by design. These elements are compared to elements with the same displacement interpolation. For all simulations in Abaqus default parameters were used including default convergence criteria, standard double-precision floating point accuracy and the Abaqus standard extrapolation. Abaqus only provides the standard volumetric extension for Neo-Hookean hyperelastic material. Therefore, user material subroutines (UMAT) have to be used in order to implement the Odgen and the Hartmann–Neff compression model. The routines were generated with AceGen [17] and provided to the authors by A. Ricker, “Deutsches Institut für Kautschuktechnologie e.V.” (German institute for rubber technology), Hannover, Germany. For further comparison, we also use an AceGen generated H1-P0 user element (UEL) in Abaqus, see [19, p. 204 ff], that is based on the same functional as utilized for the STP and CL3F elements, cf. (2). The hexahedral AceGen H1-P0 element uses linear Lagrange interpolation for displacements and an intra-element constant pressure and dilation ansatz. The AceGen source code for the Neo-Hooke standard model is provided in [19, Box 6.9] and was modified in order to implement the used compression models. The element was implemented by A. Ricker as an Abaqus user element (UEL) utilizing the AceGen method SMSSCondense to perform the static condensation. The material law is directly integrated into the element formulation and neither the built-in nor the user material subroutines (UMATs) used for the standard Abaqus hybrid elements are utilized.
5.2 Mesh convergence study
Hybrid/mixed elements are (within this context) only useful when they do not suffer from volumetric locking. To assess how stiff an element is, one has to perform mesh convergence studies, where the mesh is refined in several steps towards the point were the solution does not change anymore within a certain tolerance. To visualize this convergence the displacement of the point that undergoes the greatest displacement, which are in our case the points \(\varvec{X}=(48,60,0)\) for the Cook membrane and \(\varvec{X}=(0,0,50)\) for the block test (lengths in mm), are plotted versus the mesh size. (This is the standard way to evaluate mesh convergence studies for these tests, cf., e.g., [29].) The membranes edges are divided into \(2^n\) equal divisions in x and y direction and n equal divisions in z direction, where n is varied in between \(n=1\dots 5\), leading to \(4\dots 5120\) hexahedral sub-volumes. The block is divided into \(2^3\), \(4^3\), \(8^3\) or \(16^3\) equal sized cubic sub-volumes. Each sub-volume is either discretized by one hexahedral element, or once more subdivided into 6 tetrahedral elements. The load for the membrane was choosen as force of \(1\,\mathrm {N}\) and the block is loaded with a pressure of \(\tilde{p}=1.5\,\mathrm {MPa}\).
The block convergence simulations were done for all three volumetric parts of the strain energy. Due to the fact that all material models are fitted to the same data, the generated plots basically coincide and only the results for the Ogden model are provided below. In order to review the performance for various material stiffnesses, the Cook membrane convergence test is additionally performed using the block tests original material parameters provided by Wriggers [39, p. 459], which specify a Neo-Hookean material with standard compression model given by the parameters \(\lambda = 499.92568~\text {MPa}\) (first Lamé constant) and \(\mu _0 = 1.61148~\text {MPa}\). Note that this material is significantly softer in compression (\(K_0=501~\text {MPa}\)) than the NR/IR-blend, but is stiffer in shear direction.
The interpretation of the conformity in the plots is that the solution (displacement field) is not affected by the choice of the material model which is a perquisite for fairness of the later conducted stability investigation. The results are provided in the Figs. 3, 4 and 5.
Cook membrane mesh convergence study using the standard compression model with parameters provided by Wriggers [39, p. 459]. First row: linear and quadratic hexahedral elements. Second row: quadratic tetrahedral elements
The (discontinuous) STP-elements use the semi-discretized weak form where variables were eliminated from the weak form used by the discontinuous CL3F-elements and the same discretization schemes are used. The methodological differences should therefore only affect non-converged states. In turn, the elements should deliver essentially the same data points in the plot. This is also to be expected from the AceGen H1-P0 elements, which share the same basis, which is indeed observed, i.e. the STP-, the discontinuous CL3F- and the AceGen H1-P0-elements have the same mesh convergence behavior.
Regarding the shear dominated Cook membrane test, Abaqus’ linear hexahedral C3D8H-elements show a slightly slower convergence behavior, whereas the compression dominated block test gives comparable results. For quadratic elements, we observe that the discontinuous CL3F- and STP-elements show also a very good agreement in the results with the corresponding Abaqus elements. The Abaqus elements theoretical foundation is not further investigated in this paper, but its point of departure is also the three-field functional (2). This applies to the H1-P0 user element, generated by AceGen, too. The result from the numerical test is that the discontinuous CL3F-elements, STP-elements and (discontinuous) AceGen H1-P0, as well as in large parts the built-in Abaqus elements, basically have the same mesh convergence behavior.
Regarding the continuous CL3F-elements, we observe comparatively higher deviations for the coarsest discretizations, which might stem from the increased number of DOFs. Furthermore, in the block test, we see an oscillating mode of convergence. However, the convergence behavior is still very favorable. Probably, these deviations will have only a minor relevance in everyday use. The convergence characteristics of elements that are known to have “locking issues” are very far worst. To use a formulation which is very popular in the literature, we may therefore conclude that all the CL3F-elements considered here are “locking-free”. (However, note that there is no sharp definition of “being locking-free”.) In this regard it is fair to note that the increased number of DOFs of the continuous CL3F-elements and their slightly worse mesh convergence behavior is to some extent counterbalanced by a significantly lower number of equilibrium iterations.
As a side note, in contrast, we observed locking for the discontinuous linear tetrahedral CL3F-element that was therefore discarded, as well as for the also not further considered linear, tetrahedral hybrid element C3D4H from Abaqus.
5.3 Numerical stability benchmark
Now we will assess the numerical stability. Finite element programs are essentially based on a Newton–Raphson scheme, which is known to be locally converging. If the predictor step of a load step gets the algorithm close enough to the true solution, the scheme will converge and otherwise diverge. In order to finally obtain a solution for a desired load it is, therefore, a prerequisite that the load steps are selected small enough so that we stay within the stable range. So the maximum step size in a fixed setting can essentially serve as a measure for the numerical stability.
The basic setting for our stability tests is again the block locking test using the material parameters of the NR/IR blend. In order to quantify the influence of the element formulation as well as the material model on the stability, we assess every single combination of hybrid element and material model.
The aim is to find the maximum final load \(\tilde{p}\), that is always applied in 5 equidistant load steps, for which all steps converge. The idea behind the choice to always apply 5 equidistant load steps is that the first load step is a very special one since we start from the undeformed configuration. Therefore, in the first step many quantities are still zero and in turn not the whole element implementation is tested in the first step. Also the first step is often not the most challenging one. Hence, we wanted to apply more than one load step. However, the number 5 is arbitrary.
In order to save computation time, the first simulation for every specific element and material combination is performed with \(\tilde{p}=5~\text {MPa}\). In case all load steps converge, the final load \(\tilde{p}\) is gradually increased by \(3~\text {MPa}\) until for one of the 5 steps the equilibrium iterations diverge. Starting from the maximum previously converged load, the final load is increased by multiples of \(1~\text {MPa}\) until for one step the equilibrium iterations diverge. Then the procedure is once more repeated with multiples of \(0.1~\text {MPa}\). If for the first simulation with \(\tilde{p}=5~\text {MPa}\) no convergence is obtained, first, the maximum converging natural number pressure is sought by decreasing \(\tilde{p}\) in \(1~\text {MPa}\) steps. Then the final load is once more increased in multiples of \(0.1~\text {MPa}\) until for one of the 5 steps the equilibrium iterations diverge. The so obtained final maximum \(\tilde{p}\) for which we obtained a result (i.e. all 5 steps converged) is listed in Fig. 6.
For the remainder of this section we discuss Fig. 6 in detail. We start with a discussion of the Abaqus hybrid elements which are represented by the red bars. Note that these elements are used with standard parameters and provide therefore a good baseline result for what a user of commercial software has to expect who uses these elements “as provided”.
In general the Abaqus elements react very sensitive to the material model. For the standard volumetric model, we have two red bars per element: Since Neo-Hooke material with the standard volumetric part is the only material model that is readily available in Abaqus, we were in this case also able to use the internal material model (native) which is benchmarked against the same material model (with the same material parameters) implemented via the AceGen generated UMAT. Interestingly enough, here, the use of the UMAT already has a slightly negative effect on the stability of all Abaqus elements. On the other hand, by switching to the “well-behaving” nonlinear compression model of Ogden, we get indeed partially higher results than for the internal standard model. Hence, if there is a general negative effect that is connected to the usage of UMATs, at least it does not seem to be predominant over the general influence of the material model. Nevertheless, it is noteworthy that the native standard model of Abaqus is more stable than the same model implemented via an UMAT. However, comparing the standard model implemented via the UMAT with the Ogden compression model, we see a general advantage of the “well-behaving” Ogden model, like expected. (However, keep in mind that the Ogden model is basically used outside its applicability here.)
In contrast, the material model of Hartmann and Neff, which is in practice needed to obtain realistic simulation results once the “linear range” of the standard model is left, is problematic with regard to the numerical stability in combination with the Abaqus hybrid elements. For all types of Abaqus hybrid elements, the stable step-width decreases for the Hartmann–Neff model in comparison to the standard model. For the quadratic elements this effect is so pronounced that these elements are not an option for practical applications in combination with the Hartmann–Neff model. Only the linear hexahedral element (C3D8H) still retains a usable stable step-width and is hence the only choice for an Abaqus user who uses the Hartmann–Neff model. Of course this is especially a severe problem in combination with complex geometries that cannot be meshed (exclusively) by hexahedral elements.
The AceGen H1-P0 element (in green) shows a slightly better numerical stability compared to its built-in Abaqus counterpart C3D8H, with the greatest advantage observed for the numerically challenging Hartmann and Neff material. Since solely the Abaqus UEL implementation of the AceGen H1-P0 element was tested, no final statement on the theoretical performance of these elements may be issued. (It is conceivable, that the Abaqus Standard solver may influence the elements stability as well.) However, from a theoretical point of view a disadvantage of the AceGen-element in comparison to the CL3F-element is that the CL3F condensation explicitly accounts for the vanishing submatrices in (20). (Note that there are zero diagonal entries in (20), therefore, the block-diagonal-submatrix of variables to be condensed is singular. The CL3F-element implementation circumvents this problem by applying the scheme (21)–(23).)
The STP-elements (in gray) are implemented without any numerical stabilization using the (not augmented) formulations provided above. Also in contrast to Abaqus/Standard no extrapolation is used, i.e. the first guess to the incremental solution is simply zero. A production stage implementation of an STP-element would use (most probably) both concepts to improve the numerical stability. The here given STP-element results are hence not intended to provide a fair comparison between production stage hybrid element formulations. Instead, they document the baseline performance that we can expect if we implement the underlying formulation in its pure form.
In general, the stable step-width for these elements is—with at most \(0.2\,\mathrm {MPa}=1.0/5\,\mathrm {MPa}\)—very small, even for the Ogden and the standard model. In particular, it is in general way smaller than for the Abaqus elements, with the only exception of the quadratic tetrahedral element in combination with the Hartmann–Neff model. However, here the measured 0.1 MPa difference in the maximum load, corresponding to an 0.02 MPa advantage of the STP-element in terms of the stable step-width, is hardly of interest, since on the one hand the deviation equals the resolution of the benchmark and on the other hand the performance of both elements is poor anyway.
The new CL3F-elements (in blue) are also implemented in a pure, not augmented way, without extrapolation, i.e. with the exact same disadvantages of the STP-elements (in comparison to the Abaqus elements). However, the formulation generates a massive improvement of the stable step-width in comparison to the STP-element formulation. Since both formulations are implemented without any stabilization or extrapolation, it is clear that this advantage stems from the formulation itself (which is the reason the STP-elements formulation was implemented without both in the first place.) Indeed, this improvement is so significant that while the STP-elements cannot compete with the Abaqus hybrid elements, the CL3F-elements perform better than the (production stage) Abaqus as well as the AceGen H1-P0 Abaqus user element in general, despite the unfair advantage of the Abaqus elements. Already for the standard model, the edge of the CL3F-elements over their Abaqus counterparts is at least (i.e. in comparison to the better performing native standard model) \(+52\%\) for linear and \(+38\%\) for quadratic hexahedral elements and \(+51\%\) for quadratic tetrahedral elements. Note that for the discontinuous CL3F-elements, this edge could translate to an equal edge in terms of computation speed in combination with an assumed/hypothetical optimal working step-width control algorithm.
However, the greatest advantage of the CL3F-elements is that for all three considered material models every CL3F-element achieved the same maximum load, which means that—within the margin of error of the benchmark—the stable step-width of the CL3F-elements is independent of the choice of the material model. In turn, the edge of the CL3F-elements over the Abaqus elements rises significantly if the Hartmann–Neff model is used, reaching up to a maximum of \(+2200\%\) for quadratic tetrahedral elements. Especially the availability of a robust tetrahedral CL3F-element should be of great utility with respect to practical applications, since complex geometries often cannot be meshed (exclusively) by hexahedral elements.
Comparing the quadratic, continuous CL3F-elements with their discontinuous CL3F-counterparts, we see unsystematic deviations of at most 0.1 MPa in the maximum load, which equals the resolution of the benchmark. Hence, we might conclude that the continuous and discontinuous CL3F-elements of the same type, i.e. using the same displacement interpolation, perform equally good in regard of the stable step-width. However, keep in mind that the usage of continuous elements leads to a higher numerical effort per iteration, since the number of assembled DOFs is increased.
5.4 Massive element distortion
The block-locking test used for our benchmarks is often used in the literature to examine the elements’ capability to cope with bad aspect ratios and acute angles, which is sometimes also referred to as “numerical stability”. To this end, the original material parameters provided by Wriggers [39, p. 459], see Sect. 5.2, are used. Since this material is significantly softer in compression than the NR/IR-blend, it generates a more pronounced distortion of the elements.
We repeated the stability test with all CL3F-elements, which lead to a comparable result, but with increased absolute values for the maximum load that could be applied in five steps. Given the softness of the material, all CL3F-elements showed therefore their capability to handle the arising extreme distortions of the finite elements. To illustrate this exemplarily, Fig. 7, shows the distortions that emerged by the application of \(\tilde{p}=18\) MPa (maximum load) in five equidistant steps to the block meshed by 4096 C3LF-H1G8-P0 elements. The graphical representation of the simulation results was accomplished with Paraview, [1]. Here, the maximum displacement in load direction (of the upper-front-corner node) was \(45.8~\text {mm}\). (The initial height of the block is \(50~\text {mm}\), cf. Fig. 2.) The colors refer to the integration point Jacobians (for converged steps coinciding with the dilations), extrapolated to the element nodes. Clearly this exemplarily outlines the C3LF-elements superior ability to handle extreme element distortions as well as steep intra-element gradients of the Jacobian.
6 Conclusions
From our point of view, the consistent linearization for the general setting associated with the three-field potential introduced in [33] and the simplification to the common setting of a isotropic, quasi-incompressible material by the key relations ((16), (17) and (18)) provided in the “Appendix” represents an important step towards the completion of the continuum mechanical foundations for the derivation of hybrid elements.
The main contribution of this article is however the derivation of the CL3F-hybrid element formulation. We followed the design paradigm of staying as long as possible in the realm of exact continuum mechanics and utilized the dilation/pressure interpolation after the linearization of the problem with respect to all three primary unknowns, whereas the STP-formulation utilizes the dilation/pressure interpolation to eliminate variables from the weak form in order to arrive at a pure displacement-based semi-discretized variant of the weak form which is then consistently linearized by deriving the Gateaux derivative with respect to the displacements only. Whereas the CL3F approach naturally leads to continuous type mixed elements, discontinuous type hybrid elements can be derived by the utilization of static condensation and the implementation of a secondary variable update scheme. These discontinuous type CL3F-elements are one-on-one comparable to STP-elements utilizing the same interpolation and quadrature schemes, however, the resulting elements are different, especially the CL3F elements considers the dilation and pressure residuals  and
and  that are missing by design following the STP-approach.
that are missing by design following the STP-approach.
Since for the STP-elements the dilation and pressure degrees of freedom are eliminated in the weak form, we would not expect deviations in converged stages, i.e. critical points, between comparable STP and CL3F-elements. Indeed, the discontinuous CL3F-elements had the same mesh convergence behaviour like the STP-elements in the block locking test. Especially the CL3F-elements inherit the property of being free of volumetric locking from the STP-elements. We would expect the CL3F-elements to mimic the mesh convergenge behavior of comparable STP-elements in other test-cases as well. (Due to the theoretical argument; this was not tested.)
The benefit of the CL3F-elements is a greatly improved numerical stability in comparison to the STP-elements. In order to actually compare the formulations, both were implemented without any stabilizing augmentation and without extrapolation (i.e. a method to determine the first guess to the incremental solution), although usual production stage elements would utilize both concepts. To include a standard production stage environment for perspective, the elements from Abaqus are also tested and used “as provided”, partially in combination with AceGen generated UMATs. Especially since Abaqus/Standard uses extrapolation by default, cf. [35, pp. 6.1.2-6], the Abaqus elements have (intentionally) a huge theoretical advantage in the stability benchmark. Nevertheless, we observe a substantial advantage of the (pure) CL3F-elements in the benchmark—not only in comparison to the related STP-elements, but even over the production stage Abaqus elements and the H1-P0 Abaqus user element generated by AceGen. Extrapolation is a concept that can basically be freely combined with element formulations of all kind and therefore should be used by production stage implementations. Additional stabilization techniques (augmentation) on the other hand do not seem to be necessary for the CL3F-elements, especially since the benchmark results are not negatively affected by an increasing material nonlinearity. This is in particular an interesting observation since most recent hybrid element formulations in the literature heavily rely on matching stabilization techniques. However, additional testing is needed and planned by the authors for future contributions.
It is noteworthy in this regard that most standard tests for finite elements are mesh convergence studies, cf. e.g. [29]. In contrast the here performed stability benchmark, cf. Sect. 5.3, is not all a standard test and hence there is basically no comparable data in the literature, although the ability to apply reasonably big load steps is undeniably of great importance for finite element applications. Maybe this contribution also inspires other authors to do similar investigations.
Continuous mixed elements are often mentioned in the literature as a hypothetical option, but this type of elements is basically never implemented. Especially we are not aware of competitive studies between comparable discontinuous and continuous elements that utilize the same displacement interpolation. In this contribution we also assessed continuous type quadratic hexahedral and tetrahedral CL3F-elements. Concerning the mesh convergence behavior the continuous elements show a slight disadvantage, although we do not think that the difference will have a significant impact on the practical usage. A meaningful disadvantage of the continuous elements is the increased computation time per iteration, which simply stems from the increased number of assembled degrees of freedom. A counterbalancing advantage of the continuous elements is however that the number of iterations per step is significantly reduced. Although our stability focused study was not really designed to quantify this advantage, an assessment of the metadata of the mesh convergence study suggests a massive gain.
References
Ayachit U (2015) The ParaView guide: updated for ParaView version 4.3. Kitware, Clifton Park, New York
Bathe KJ (2014) Finite element procedures. Klaus-Jürgen Bathe, Berlin
Belytschko T (2000) Nonlinear finite elements for continua and structures. Wiley, Chichester, New York
Chang TYP, Saleeb AF, Li G (1991) Large strain analysis of rubber-like materials based on a perturbed Lagrangian variational principle. Comput Mech 8:221–233. https://doi.org/10.1007/bf00577376
Cockburn B, Shen J (2019) An algorithm for stabilizing hybridizable discontinuous Galerkin methods for nonlinear elasticity. Results Appl Math 1:100001. https://doi.org/10.1016/j.rinam.2019.01.001
de Souza Neto EA, Perić D, Dutko M, Owen DRJ (1996) Design of simple low order finite elements for large strain analysis of nearly incompressible solids. Int J Solids Struct 33:3277–3296. https://doi.org/10.1016/0020-7683(95)00259-6
de Souza Neto E, Perić D, Owen DRJ (2008) Computational methods for plasticity theory and applications. Wiley, Chichester, West Sussex. https://doi.org/10.1002/9780470694626
Djoko JK, Lamichhane BP, Reddy BD, Wohlmuth BI (2006) Conditions for equivalence between the Hu–Washizu and related formulations, and computational behavior in the incompressible limit. Comput Methods Appl Mech Eng 195:4161–4178. https://doi.org/10.1016/j.cma.2005.07.018
Eyck AT, Lew A (2010) An adaptive stabilization strategy for enhanced strain methods in non-linear elasticity. Int J Numer Methods Eng 81:1387–1416. https://doi.org/10.1002/nme.2734
Glaser S, Armero F (1997) On the formulation of enhanced strain finite elements in finite deformations. Eng Comput 14:759–791. https://doi.org/10.1108/02644409710188664
Hartmann S, Neff P (2003) Polyconvexity of generalized polynomial-type hyperelastic strain energy functions for near-incompressibility. Int J Solids Struct 40:2767–2791. https://doi.org/10.1016/s0020-7683(03)00086-6
Heisserer U, Hartmann S, Düster A, Yosibash Z (2008) On volumetric locking-free behaviour of p-version finite elements under finite deformations. Commun Numer Methods Eng 24:1019–1032
Holzapfel GA (2000) Nonlinear solid mechanics. Wiley, New York
Hughes TJR (1980) Generalization of selective integration procedures to anisotropic and nonlinear media. Int J Numer Methods Eng 15:1413–1418. https://doi.org/10.1002/nme.1620150914
Hughes TJR (1987) The finite element method: linear static and dynamic finite element analysis. Prentice-Hall, Englewood Cliffs
Kabaria H, Lew AJ, Cockburn B (2015) A hybridizable discontinuous Galerkin formulation for non-linear elasticity. Comput Methods Appl Mech Eng 283:303–329. https://doi.org/10.1016/j.cma.2014.08.012
Korelc J (2002) Multi-language and multi-environment generation of nonlinear finite element codes. Eng Comput 18:312–327. https://doi.org/10.1007/s003660200028
Korelc J, Wriggers P (1996) Consistent gradient formulation for a stable enhanced strain method for large deformations. Eng Comput 13:103–123. https://doi.org/10.1108/02644409610111001
Korelc J, Wriggers P (2016) Automation of finite element methods, 1st edn. Springer International Publishing, Cham
Korelc J, Šolinc U, Wriggers P (2010) An improved EAS brick element for finite deformation. Comput Mech 46:641–659. https://doi.org/10.1007/s00466-010-0506-0
Ogden RW (1972) Large deformation isotropic elasticity—on the correlation of theory and experiment for incompressible rubberlike solids. Proc R Soc A Math Phys Eng Sci 326:565–584. https://doi.org/10.1098/rspa.1972.0026
Pantuso D, Bathe KJ (1995) A four-node quadrilateral mixed-interpolated element for solids and fluids. Math Models Methods Appl Sci 5:1113–1128. https://doi.org/10.1142/s0218202595000589
Pantuso D, Bathe KJ (1997) On the stability of mixed finite elements in large strain analysis of incompressible solids. Finite Elem Anal Des 28:83–104. https://doi.org/10.1016/s0168-874x(97)81953-1
Puso MA (2000) A highly efficient enhanced assumed strain physically stabilized hexahedral element. Int J Numer Methods Eng 49:1029–1064. https://doi.org/10.1002/1097-0207(20001120)49:8\(<\)1029::aid-nme990\(>\)3.0.co;2-3
Reese S (2003) On a consistent hourglass stabilization technique to treat large inelastic deformations and thermo-mechanical coupling in plane strain problems. Int J Numer Methods Eng 57:1095–1127. https://doi.org/10.1002/nme.719
Reese S (2005) On a physically stabilized one point finite element formulation for three-dimensional finite elasto-plasticity. Comput Methods Appl Mech Eng 194:4685–4715. https://doi.org/10.1016/j.cma.2004.12.012
Reese S, Küssner M, Reddy BD (1999) A new stabilization technique to avoid hourglassing in finite elasticity. Int J Numer Methods Eng 44:79–109. https://doi.org/10.1002/(SICI)1097-0207(19990420)44:11\(<\)1617::AID-NME557\(>\)3.0.CO;2-X
Ricker A, Fehse A, Kröger NH (2020) Final report on IGF project No. 19916 N, characterization and modeling of compression moduli of technical rubber materials. (in German)
Schröder J, Wick T, Reese S et al (2021) A selection of benchmark problems in solid mechanics and applied mathematics. Arch Comput Methods Eng 28:713–751. https://doi.org/10.1007/s11831-020-09477-3
Schröder J, Wriggers P (eds) (2016) Advanced finite element technologies, vol 566. Springer, Berlin
Schröder J, Wriggers P, Balzani D (2011) A new mixed finite element based on different approximations of the minors of deformation tensors. Comput Methods Appl Mech Eng 200:3583–3600. https://doi.org/10.1016/j.cma.2011.08.009
Schweizerhof K, Ramm E (1984) Displacement dependent pressure loads in nonlinear finite element analyses. Comput Struct 18:1099–1114. https://doi.org/10.1016/0045-7949(84)90154-8
Simo JC, Taylor RL (1991) Quasi-incompressible finite elasticity in principal stretches. Continuum basis and numerical algorithms. Comput Methods Appl Mech Eng 85:273–310. https://doi.org/10.1016/0045-7825(91)90100-k
Simo JC, Taylor RL, Pister KS (1985) Variational and projection methods for the volume constraint in finite deformation elasto-plasticity. Comput Methods Appl Mech Eng 51:177–208. https://doi.org/10.1016/0045-7825(85)90033-7
Dassault Systèmes Simulia Corp. (2014) Abaqus 6.14 Analysis User’s Guide, Providence, RI, USA
Stroud AH (1971) Approximate calculation of multiple integrals. Prentice-Hall series in automatic computation. Prentice-Hall, London
Sussman T, Bathe KJ (1988) Some advances in the analysis of semideformable media. In: Noor AK, Dwoyer DL (eds) Computational structural mechanics and fluid dynamics. Elsevier, Amsterdam, pp 105–112. https://doi.org/10.1016/b978-0-08-037197-9.50015-2
Szabó B, Babuška I (1991) Finite element analysis. Wiley, New York
Wriggers P (2008) Nonlinear finite element methods. Springer-Verlag GmbH, Berlin
Wulfinghoff S, Bayat HR, Alipour A, Reese S (2017) A low-order locking-free hybrid discontinuous Galerkin element formulation for large deformations. Comput Methods Appl Mech Eng 323:353–372. https://doi.org/10.1016/j.cma.2017.05.018
Zienkiewicz OC, Taylor RL, Fox DD (2013) The finite element method for solid and structural mechanics. Butterworth-Heinemann, Oxford
Acknowledgements
The authors express their gratitude to Alexander Ricker from the “Deutsches Institut für Kautschuktechnologie e.V.” (German institute for rubber technology), Hannover, Germany, for providing the material parameters, the Abaqus user-material as well as the AceGen H1-P0 Abaqus user element subroutines used in this contribution.
Funding
Open Access funding enabled and organized by Projekt DEAL. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Josef Arthur Schönherr and Patrick Schneider: Formerly 3.
Appendix
Appendix
1.1 The linearization for the general case
First we provide the linearization of the weak form (3) for the general setting, i.e. the strain energy density is assumed to be a general function of the modified right Cauchy–Green tensor \(\mathring{W}:=W(\mathring{\varvec{C}}(\mathring{\varvec{F}}))\). To our best knowledge the linearization in this generality was never presented in the literature. In order to increase the clearness of the presentation we will note the specific variation that was computed on the right side of every summand, delimited by a “\(\longleftarrow \)”. Starting with the first summand (3a), we obtain

For the second summand of the weak form (3b), we derive

and finally we obtain from the third summand of the weak form (3c)

Due to the length of the equations we skip to denote the full linerization again, as well as we skip the transformation of the enclosing integral to the deformed configuration.
1.2 The isotropic, quasi-incompressible case
Now, we will simplify the linearization of the general case to the linearization for the special case of a hyperelastic material based on isotropic invariants with the usual additive split into an isochoric and volumetric part, cf. Eq. (9). This will lead to a much simpler tangent stiffness. Like mentioned here the key properties (16), (17) and (18) play an important role.
Like shown in Sect. 3.1, the stress can be expressed by the first-order derivatives of \(\mathring{W}\) with respect to \(\mathring{\varvec{C}}\) whereas the stiffness tensor is given by the second-order derivatives. Resolving this derivatives by the chain rule for a material of type (9), we obtain for the first-order derivatives

and

for the second-order derivatives. Only the derivatives of \(\mathring{W}\) with respect to the isochoric invariants and the dilation \(\varTheta \) remain material dependent. Therefore, in order to implement a custom material, solely simple scalar derivatives have to be implemented by the user.
The tensor-field valued quantities in (27) and (28) are calculated by successive application of the multidimensional chain rule. The pushed first-order derivatives are

whereas we get for the second-order derivatives


All the quantities are determined by J, \(\varTheta \) and the finger tensor  and are proper second-order or fourth-order tensors with all indices referring to the deformed configuration and hence suitable for the finally desired spatial formulation. All the second-order and forth-order tensors given before are symmetric in the sense
and are proper second-order or fourth-order tensors with all indices referring to the deformed configuration and hence suitable for the finally desired spatial formulation. All the second-order and forth-order tensors given before are symmetric in the sense
In order to derive the linearization of the weak form for the isotropic, quasi-incompressible setting (9) from the representation for the general case, cf. (24), (25) and (26), we have to use the defining equations for the stress and stiffness tensor parts (10), (11), (12) and (13) in combination with their chain rule expansions, cf. (27) and (28), with inserted tensorial parts (29)–(31). We will be able to reduce the complexity of the resulting formulation significantly by exploitation of the properties of the deviator operator, as well as the key relations (16), (17) and (18), which follow directly from the equations above.
We start with the first summand of (24) that reads

by using of (10) and (11). Because of the two deviatoric tensors in the inner product and (29) the  summand in
summand in  , cf. (28), has no contribution. Since this is actually the only occurrence of
, cf. (28), has no contribution. Since this is actually the only occurrence of  in the whole linearization, we might (but do not have to) drop the
in the whole linearization, we might (but do not have to) drop the  summand in
summand in  , as well as the first tensor summand in (30), leading to
, as well as the first tensor summand in (30), leading to

In the second, fifth and sixth summand of (24) we can replace \(\hat{\mathring{W}}\) with \(\hat{\mathring{W}}_{\text {iso}}\) because of (29), (16) and the deviatoric tensors in the product. Also, the contributions from the second-order derivatives with respect to the modified isochoric invariants, cf. (28), in the second summand of (24) drop out because of the hydrostatic tensor \(\delta _{kl}\) in the product. Finally, the remaining terms in the second, fifth and sixth summand of (24) sum up to zero because of the key properties (17) and (18).
The third and the forth summand of (24) can be added, leading to

Turning our attention to the so far derived volumetric parts of the stress and the stiffness appearing in (24), we find that by employing (11) and (32)

follows, so that they sum up to zero.
In the last summand of (24) the volumetric stress drops out because of the deviator in the product

In the first and forth summand of (25), we can again replace \(\hat{\mathring{W}}\) with \(\hat{\mathring{W}}_{\text {iso}}\). Also, in the first summand the contributions from the second-order derivatives with respect to the modified isochoric invariants, cf. (28), drop out again because of the hydrostatic tensor \(\delta _{ij}\) in the product. Finally, the remaining terms of the first and forth summand of (25) add up to zero because of the key properties (17) and (18).
In all remaining summands of (25) we can replace \(\hat{\mathring{W}}\) with \(\hat{\mathring{W}}_{\text {vol}}\). Furthermore, the contributions from the first-order derivative of \(\hat{\mathring{W}}\) with respect to \(\varTheta \) in the remaining summands of (25) sum up to zero. Finally, we obtain

No major simplifications are possible for (26). Summarizing the argumentation, adding (24), (25) and (26) and transforming the enclosing integral to the deformed configuration, we obtain the already given linearization (15) for the special case.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schönherr, J.A., Schneider, P. & Mittelstedt, C. Robust hybrid/mixed finite elements for rubber-like materials under severe compression. Comput Mech 70, 101–122 (2022). https://doi.org/10.1007/s00466-022-02157-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-022-02157-y



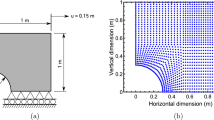

 : 2-1 quadrature, cf. [
: 2-1 quadrature, cf. [ : 2-1 quadrature, cf. [
: 2-1 quadrature, cf. [





