The concept of Representative Crack Elements (RCE) for phase-field fracture: transient thermo-mechanics

Abstract

The phase-field formulation for fracture based on the framework of representative crack elements is extended to transient thermo-mechanics. The finite element formulation is derived starting from the variational principle of total virtual power. The intention of this manuscript is to demonstrate the potential of the framework for multi-physical fracture models and complex processes inside the crack. The present model at hand allows to predict realistic deformation kinematics and heat fluxes at cracks. At the application of fully coupled, transient thermo-elasticity to a pre-cracked plate, the opened crack yields thermal isolation between both parts of the plate. Inhomogeneous thermal strains result in a curved crack surface, inhomogeneous recontact and finally heat flow through the crack regions in contact. The novel phase-field framework further allows to study processes inside the crack, which is demonstrated by heat radiation between opened crack surfaces. Finally, numerically calculated crack paths at a disc subjected to thermal shock load are compared to experimental results from literature and a curved crack in a three-dimensional application are presented.

1 Introduction

A crack contact criterion and the decomposition into degraded and transferred forces through the crack are approximated by splits of the deformation energy potential in phase-field models for fracture. Unphysical predictions of deformations at cracks are reported for common splits like the volumetric-deviatoric, the spectral and similar splits. Furthermore, the crack driving force of the phase-field variable is significantly controlled by the split approach and, thus, may result in unreliable predictions for the fracture process.

Artificial splits are replaced by Representative Crack Elements (RCE) in [1], which allows to overcome the kinematical deficiencies. After first application to anisotropic elasticity [1], the framework is successfully applied to phase-field fracture for visco-elastic materials [2], for inelastic materials, crack surface friction, finite deformations [3] and cohesive interface failure [4]. In the paper at hand, representative crack elements are developed towards phase-field fracture for transient coupled thermo-mechanics. The variational formulation is presented and derived into a finite element model. Through academic examples, the potential of representative crack elements is demonstrated for multi-physical applications and for processes, which take place inside the crack, e.g. heat radiation through the crack. It is also shown in the theoretical discussion, that the numerical solution scheme, which is introduced to solve the RCE model with heat radiation, can be used to model the reduced heat conductivity in closed cracks as a consequence of micro cavities, and to model heat convection at the crack surface.

2 Theory

The principle of total virtual power $\delta {\mathcal {P}^{\text {tot}}}= \delta {\mathcal {P}^{\text {int}}}- \delta {\mathcal {P}^{\text {ext}}}= 0$ balances the virtual power, which is associated with a thermodynamic system (internal and kinetic energy) and the virtual power transferred to the system from the exterior (mechanical work and heat) for all admissible generalised virtual velocities $\forall \delta v\in \text {Var}_{v}$ and their generalised local strain rate actions $\mathcal {D}(\delta v)$. Internal and external virtual powers are formed by dual products of the tensor valued virtual velocity components $\delta \varvec{v}^{i}$ and strain rate components $\mathcal {D}^{i}(\delta v)$ with their thermodynamically conjugated forces $\varvec{f}^{i}$ and stresses $\varvec{\Sigma }^{i}$, which yield

$$\begin{aligned} {\mathcal {P}^{\text {int}}}(\mathcal {D}(\delta v))&= \int _{\mathcal {B}} \langle \langle \mathcal {D}(\delta v), \Sigma \rangle \rangle ~\text {d}V\nonumber \\&= \int _{\mathcal {B}} \sum \limits _{i=1}^{m} \left\langle \varvec{\mathcal {D}}^{i}(\delta v), \varvec{\Sigma }^{i} \right\rangle ~\text {d}V, \end{aligned}$$

(1)

$$\begin{aligned} {\mathcal {P}^{\text {ext}}}(\delta v)&= \int _{\mathcal {B}} \langle \langle \delta v, f \rangle \rangle ~\text {d}V\nonumber \\&= \int _{\mathcal {B}} \sum \limits _{i=1}^{n} \left\langle \delta \varvec{v}^{i}, \varvec{f}^{i} \right\rangle ~\text {d}V. \end{aligned}$$

(2)

Displacements $\varvec{u}$, phase-field $p$ and absolute temperature $\theta$ are the state variables for transient thermo-mechanics of phase-field fracture. Thus, the virtual velocity $v=[\varvec{v},\dot{p},\dot{\theta }]$ and virtual strain rate action $\mathcal {D}(v)=[\varvec{v},\dot{\varvec{H}},\dot{p},\dot{\nabla p},\dot{\theta },\dot{\nabla \theta }]$ result in the total virtual power

(3)

where $\varvec{H}$ is the displacement gradient and the dot represents time derivative.

2.1 Constitutive relations

It is shown in [5] that the variational formulation in the form of Eq. (3) represents the weak form of the momentum balance, the entropy balance and von Neumann boundary conditions. Momentum rate ${\varvec{\Sigma }}^{\varvec{u}}$, 1. Piola-Kirchhoff stress ${\varvec{\Sigma }}^{\varvec{H}}$, entropy rate ${\Sigma }^{\theta }$, negative entropy flux ${\varvec{\Sigma }}^{\nabla \theta }$ and contributions to the phase-field driving force ${\Sigma }^{p}$, ${\varvec{\Sigma }}^{\nabla p}$ can be identified without additional assumptions on the constitutive relations. The variation of entropy balance in the form of [6] is obtained by accepting the relation of entropy flux to heat flux $\theta \,\varvec{h}=\varvec{q}$, and entropy source to heat source $\theta \,d=r$. The thermodynamically conjugated thermal stresses

$$\begin{aligned}&{\varvec{\Sigma }}^{\theta } = \rho \left[ - \theta \dfrac{\partial ^2 \psi }{\partial \theta ^2} \dot{\theta }- \theta \dfrac{\partial ^2 \psi }{\partial \varvec{H}\partial \theta } : \varvec{D}+ \left( \dfrac{\partial ^2 \psi }{\partial \alpha \partial \theta } + \beta \right) \dot{\alpha }\right] , \nonumber \\&{\varvec{\Sigma }}^{\nabla \theta } = -\varvec{q}\end{aligned}$$

(4)

and mechanical stresses

$$\begin{aligned} {\varvec{\Sigma }}^{\varvec{H}}&= \dfrac{\partial \psi }{\partial \varvec{H}},&{\Sigma }^{p}&= \dfrac{\partial \psi }{\partial p},&{\varvec{\Sigma }}^{\nabla p}&= \dfrac{\partial \psi }{\partial \nabla p} \end{aligned}$$

(5)

can be derived evaluating the first and second law of thermodynamics using Helmholtz free energy $\psi$. Fourier ’s empirical law of heat conduction states the relations between temperature and heat

$$\begin{aligned} c&= -\theta \dfrac{\partial ^2 \psi }{\partial \theta ^2},&\varvec{q}&= -\varvec{\mathbb K}\cdot \nabla \theta \end{aligned}$$

(6)

and is experimentally validated at various thermodynamic systems. Heat capacity c and thermal conductivity tensor $\varvec{\mathbb K}$ are material parameters. 1. Piola-Kirchhoff stress ${\varvec{\Sigma }}^{\varvec{H}}$ is known from standard thermo-mechanics and ${\Sigma }^{p}$ together with ${\varvec{\Sigma }}^{\nabla p}$ form the driving force for the phase-field.

The influence of the presence of a crack on the mechanical and thermal behaviour is considered through the postulation of a constitutive structure in the form

$$\begin{aligned} \psi&= {\psi ^{\text {m,c}}} + g(p) \left[ {\psi ^{\text {m,0}}} - {\psi ^{\text {m,c}}} \right] + {\psi ^{\text {ph}}} + {\psi ^{\text {th}}}, \end{aligned}$$

(7)

$$\begin{aligned} \varvec{q}&= {\varvec{q}^{\text {c}}} + g(p) \left[ {\varvec{q}^{\text {0}}} - {\varvec{q}^{\text {c}}} \right] . \end{aligned}$$

(8)

The degradation function $g(p)$ acts as interpolation weight between the material behaviour of intact material, represented by ${\psi ^{\text {m,0}}}$ and ${\varvec{q}^{\text {0}}}$, and fully degraded material, ${\psi ^{\text {m,c}}}$ and ${\varvec{q}^{\text {c}}}$, as introduced in [1]. The regularised fracture energy is given by ${\psi ^{\text {ph}}}$. ${\psi ^{\text {th}}}$ is the stored heat in the material. The reader is referred e.g. to [6] for further discussion on ${\psi ^{\text {th}}}$ at dissipative deformation processes.

2.2 A thermo-mechanical representative crack element

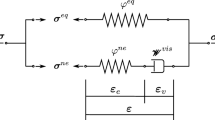
Whereas, constitutive laws for intact mechanical material ${\psi ^{\text {m,0}}}$, the regularised fracture energy ${\psi ^{\text {ph}}}$ and the heat storage ability ${\psi ^{\text {th}}}$ are defined using standard constitutive models, the behaviour for cracked material ${\psi ^{\text {m,c}}}$ and ${\varvec{q}^{\text {c}}}$ is determined by means of a Representative Crack Element, see Fig. 1. A local coordinate system $(\varvec{N}_{1},\varvec{N}_{2},\varvec{N}_{3})$ is introduced, where $\varvec{N}_{1}$ is the normal direction of the crack surface. The crack is modelled as discrete crack by the RCE, hence, the state variables are displacements and absolute temperature. Coupling operators between the cracked part of the phase-field model and the representative crack model are defined by

$$\begin{aligned} \bar{\varvec{u}}(\bar{\varvec{x}})&= \varvec{u}|_{\varvec{x}} + \varvec{H}|_{\varvec{x}} \cdot (\bar{\varvec{x}} - {\bar{\varvec{x}}^{\text {ref}}}) + \bar{{\tilde{\varvec{u}}}}, \end{aligned}$$

(9)

$$\begin{aligned} \bar{\theta }(\bar{\varvec{x}})&= \theta |_{\varvec{x}} + \nabla \theta |_{\varvec{x}} \cdot (\bar{\varvec{x}} - {\bar{\varvec{x}}^{\text {ref}}}) + \bar{{\tilde{\theta }}} \end{aligned}$$

(10)

following the concept of variational homogenisation of [7]. Quantities denoted by bar are associated with the RCE model, ${\bar{\varvec{x}}^{\text {ref}}}=\dfrac{1}{V} \int \nolimits _{\bar{\mathcal {B}}} \bar{\varvec{x}} ~\text {d}V$ is the geometric centre, $\bar{{\tilde{\varvec{u}}}}$ and $\bar{{\tilde{\theta }}}$ are the unknown displacement and temperature fluctuations, and V is the RCE volume. Homogenisation of the state variables is given by

$$\begin{aligned} \varvec{u}|_{\varvec{x}}&= \dfrac{1}{V} \int \limits _{\bar{\mathcal {B}}} \bar{\varvec{u}}~\text {d}V,&\varvec{H}|_{\varvec{x}}&= \dfrac{1}{V} \int \limits _{\bar{\mathcal {B}}} \bar{\varvec{H}} ~\text {d}V, \end{aligned}$$

(11)

$$\begin{aligned} \theta |_{\varvec{x}}&= \dfrac{1}{V} \int \limits _{\bar{\mathcal {B}}} \bar{\theta }~\text {d}V,&\nabla \theta |_{\varvec{x}}&= \dfrac{1}{V} \int \limits _{\bar{\mathcal {B}}} \bar{\nabla \theta } ~\text {d}V. \end{aligned}$$

(12)

Once, a solution for the unknown fluctuation fields $\bar{{\tilde{\varvec{u}}}}$ and $\bar{{\tilde{\theta }}}$ is determined, the thermodynamically conjugated forces, stresses and heat flux can be calculated as

(13)

(14)

(15)

(16)

(17)

(18)

where are volume forces and $\bar{f}^{\theta }$ volume heat sources. These relations are a result of the principle of multi-scale virtual power [7].

Fig. 1

Sketch of an RCE with a discrete crack and local coordinates in a reference configuration and b deformed configuration

A solution for the unknown displacement and temperature fluctuations of the RCE can be obtained numerically, for instance by application of the finite element method. The embedding of finite element problems into the material model of another finite element problem is called $\text {FE}^2$ and is computationally very expensive. That is why an analytical and a semi-analytical solution are derived for linear and non-linear bulk materials in the following. The computational costs of the resultant phase-field model are similar to standard phase-field models. Both RCE solutions are based on the assumptions of

• homogeneous displacement and temperature gradients in $\bar{\mathcal {B}}^1$ and $\bar{\mathcal {B}}^2$,

• weak thermo-mechanical coupling through homogeneous thermal expansion, and

• homogeneous volume forces , $\bar{f}^\theta$ and transient stresses $\bar{{\varvec{\Sigma }}^{}}^{\varvec{u}}$, $\bar{{\varvec{\Sigma }}^{}}^{\theta }$.

Based on these simplifications, the RCE can be divided into a quasi-static mechanical problem for the determination of the displacement discontinuity and a steady-state thermal problem for the determination of the temperature discontinuity .

The displacement field of the mechanical RCE for small deformations reads

(19)

The linearised strain tensor is $\varvec{E}=\tfrac{1}{2}\,(\varvec{H}+\varvec{H}^{\intercal })$. The normalised relative displacement of the crack surfaces is called crack deformation . The solution for the mechanical Representative Crack Element with thermal strains is presented in [1] for the first time. Thermal strains at the RCE are calculated based on the average temperature $\theta |_{\varvec{x}}$ in order to ensure homogeneous strain fields.

The thermal RCE for the heat conduction is determined with the absolute temperature field

(20)

where

$$\begin{aligned} \kappa (\bar{\varvec{x}})&= \dfrac{1}{2} l_1 \text {sgn}\left[ \varvec{N}_{1} \cdot (\bar{\varvec{x}} - {\bar{\varvec{x}}^{\text {ref}}}) \right] - \varvec{N}_{1} \cdot (\bar{\varvec{x}} - {\bar{\varvec{x}}^{\text {ref}}}). \end{aligned}$$

(21)

A solution for the unknown temperature gradient through the crack follows from the principle of virtual power of the RCE

$$\begin{aligned} \delta {\bar{\mathcal {P}}^{\text {tot}}}&= \quad \int _{\bar{\mathcal {B}}^1 \cup \bar{\mathcal {B}}^2} \delta \dot{\bar{\nabla \theta }} \cdot {\bar{{\varvec{\Sigma }}^{}}}^{\nabla \theta } ~\text {d}V\nonumber \\&\quad \,\, + \int _{\bar{{\partial \mathcal {B}}}^\Gamma } \delta \dot{\bar{\nabla \theta }} \cdot {\bar{{\varvec{\Sigma }}^{}}}^{\nabla \theta } ~\text {d}A{\mathop {=}\limits ^{!}}0. \end{aligned}$$

(22)

The linearisation and discretisation of the RCE with the nodal vector, shape function and the derivative of the shape function

$$\begin{aligned}&\hat{\varvec{\theta }} = \left[ \begin{array}{c} \theta |_{\varvec{x}} \\ \nabla \theta |_{\varvec{x}} \\ \Gamma _{\theta } \end{array} \right] ,&\bar{N}^\theta (\bar{\varvec{x}}) = \left[ \begin{array}{c} 1 \\ \bar{\varvec{x}} - {\bar{\varvec{x}}^{\text {ref}}} \\ \kappa (\bar{\varvec{x}}) \end{array} \right] , \nonumber \\&\quad \bar{B}^\theta (\bar{\varvec{x}}) = \left[ \begin{array}{c} \varvec{0} \\ \varvec{I}\\ -\varvec{N}_{1} \end{array} \right] \end{aligned}$$

(23)

result in the linear system of equations for the nodal updates

$$\begin{aligned} \left[ \begin{array}{lll} {\varvec{K}}^{{\theta \theta }} &{} {\varvec{K}}^{{\theta \nabla \theta }} &{} {\varvec{K}}^{{\theta \Gamma _{\theta }}} \\ {\varvec{K}}^{{\nabla \theta \theta }} &{} {\varvec{K}}^{{\nabla \theta \nabla \theta }} &{} {\varvec{K}}^{{\nabla \theta \Gamma _{\theta }}} \\ {\varvec{K}}^{{\Gamma _{\theta }\theta }} &{} {\varvec{K}}^{{\Gamma _{\theta }\nabla \theta }} &{} {\varvec{K}}^{{\Gamma _{\theta }\Gamma _{\theta }}} \end{array} \right] \cdot \left[ \begin{array}{l} \Delta \theta |_{\varvec{x}} \\ \Delta \nabla \theta |_{\varvec{x}} \\ \Delta \Gamma _{\theta } \end{array} \right]&= \left[ \begin{array}{l} {\varvec{R}}^{{\theta }} \\ {\varvec{R}}^{{\nabla \theta }} \\ {\varvec{R}}^{{\Gamma _{\theta }}} \end{array} \right] , \end{aligned}$$

(24)

where $\theta |_{\varvec{x}}$ and $\nabla \theta |_{\varvec{x}}$ are the quantities at the material point of the phase-field model and given by Dirichlet boundary conditions to the RCE.

2.2.1 Solution for thermally isolated cracks

The first analytical solution for the RCE model is derived under the assumptions of perfect heat conduction through a closed crack and that an opened crack behaves as thermal isolator, i.e. no heat flux through the crack exists (${\bar{{\varvec{\Sigma }}^{}}}^{\nabla \theta }(\bar{\varvec{x}})=0, \forall \bar{\varvec{x}}\in \bar{{\partial \mathcal {B}}}^\Gamma ,\text {for }\Gamma _1>0$). As introduced in [1], linear thermo-elastic material at small deformations with the Lamé constants $\lambda$, $\mu$ and the coefficient of thermal expansion $\alpha$ yield

(25)

where the thermal strain tensor is $\varvec{E}^\theta =\alpha \theta |_{\varvec{x}} \varvec{I}$. For the kinematic coupling holds $\bar{\varvec{E}}=\varvec{E}|_{\varvec{x}}-\tfrac{1}{2} \sum _{i=1}^3 \Gamma _i (\varvec{N}_i \otimes \varvec{N}_1 + \varvec{N}_1 \otimes \varvec{N}_i)$.

The solution for the temperature discontinuity reads

$$\begin{aligned} \Gamma _\theta = {\left\{ \begin{array}{ll} 0, &{} \Gamma _{1} = 0, \\ \dfrac{\varvec{N}_1 \cdot \varvec{\mathbb K}\cdot \nabla \theta |_{\varvec{x}}}{\varvec{N}_1 \cdot \varvec{\mathbb K}\cdot \varvec{N}_1}, &{} \Gamma _{1} > 0, \end{array}\right. } \end{aligned}$$

(26)

which results in the homogenised thermal stress and tangent

$$\begin{aligned} {\varvec{\Sigma }}^{\nabla \theta ,c}|_{\varvec{x}}&= \varvec{\mathbb K}\cdot \nabla \theta |_{\varvec{x}} \cdot \left( \varvec{I}- \varvec{N}_1 \otimes \varvec{N}_1 \right) , \end{aligned}$$

(27)

$$\begin{aligned} \dfrac{\partial {\varvec{\Sigma }}^{\nabla \theta ,c}|_{\varvec{x}}}{\partial \nabla \theta }&= \varvec{\mathbb K}\cdot \left( \varvec{I}- \varvec{N}_1 \otimes \varvec{N}_1 \right) \end{aligned}$$

(28)

for an opened crack ($\Gamma _{1}>0$). The thermal conductivity tensor for an isotropic material is $\varvec{\mathbb K}=k\varvec{I}$. The temperature gradient of both solid blocks of the RCE reads $\bar{\nabla \theta }=\nabla \theta |_{\varvec{x}}-\Gamma _\theta \varvec{N}_1$.

The solution of the mechanical and thermal RCE depends on the crack contact state, which is identified by $\Gamma _1$. A tolerance range is adopted from [3] in order to avoid contact oscillations. However, still some additional Newton iterations due to contact oscillations are observed for the thermo-mechanical formulation with a tolerance range in the subsequent examples. The reason is the bilinear character in both, mechanical and thermal behaviour, due to crack contact. Thus, the contact criterion is fixed in each time step after the first Newton iteration, which results in quick and robust convergence.

2.2.2 Solution for cracks with heat radiation

Heat transfer between bodies through radiation is discribed in [8]. This process depends on the absolute temperature at the body surfaces, the surface areas, the emissivity $\varepsilon$, the Stefan-Boltzmann constant $\sigma ^{B}$ and the geometrical view factor F. The emissivity relates the radiation absorption ability of the physical concept grey body (can reflect radiation) to those of a black body (no reflection). The view factor is the fraction of energy which leaves the first surface and reaches the second surface.

Crack surfaces are considered to be equally parallel planes and the radiation is approximately related to the average surface temperature in the following model. This simplification allows to avoid a numerical integration on the crack surfaces in the RCE for the calculation of radiation heat flux. Then, the heat flux reads

$$\begin{aligned} {q^{\text {r}}} = {\left\{ \begin{array}{ll} -\sigma ^{B} \varepsilon F \left[ (\bar{\theta }^{2})^{4} - (\bar{\theta }^{1})^{4} \right] , &{} \text {for } \Gamma _1 > 0, \\ \quad 0, &{} \text {else.} \end{array}\right. } \end{aligned}$$

(29)

The average temperature of the crack surfaces follows from Eq. (20)

$$\begin{aligned} \bar{\theta }^{1}(\bar{\varvec{x}})&= \theta |_{\varvec{x}} + \dfrac{1}{2} l_1 \Gamma ^\theta ,&\bar{\theta }^{2}(\bar{\varvec{x}})&= \theta |_{\varvec{x}} - \dfrac{1}{2} l_1 \Gamma ^\theta . \end{aligned}$$

(30)

Following [9], the view factor of identical parallel square facets of length $l_2$ and distance $l_1 \Gamma _1$ is given by

$$\begin{aligned} F&= \dfrac{1}{\pi w^2} \left( \ln {\dfrac{a^4}{1+2w^2}} + 4wb \right) \end{aligned}$$

(31)

with

$$\begin{aligned} w&= \dfrac{l_2}{l_1 \Gamma _1},&a&= \sqrt{1+w^2},&b&= a \arctan {\dfrac{w}{a}} - \arctan {w}. \end{aligned}$$

(32)

Then the iterative Newton-Raphson scheme for the unknown temperature discontinuity reads

$$\begin{aligned} \left[ \begin{array}{ccc} {\varvec{K}}^{{\Gamma _{\theta }\Gamma _{\theta }}} \end{array} \right] \cdot \left[ \begin{array}{c} \Delta \Gamma _{\theta } \end{array} \right]&= \left[ \begin{array}{c} {\varvec{R}}^{{\Gamma _{\theta }}} \end{array} \right] . \end{aligned}$$

(33)

The residuum is

$$\begin{aligned} {\varvec{R}}^{{\Gamma _{\theta }}} = -k \, \nabla \theta |_{\varvec{x}} \cdot \varvec{N}_1 + {q^{\text {r}}} \end{aligned}$$

(34)

and the algorithmic tangent is

$$\begin{aligned} {\varvec{K}}^{{\Gamma _{\theta }\Gamma _{\theta }}} = k - \dfrac{\partial {q^{\text {r}}}}{\partial \Gamma _{\theta }}. \end{aligned}$$

(35)

A numerical derivative based on finite differences is implemented for the view factor derivative

$$\begin{aligned} \dfrac{\partial F}{\partial \Gamma _{\theta }} \approx \dfrac{F(\Gamma _{\theta }+\Delta \Gamma _{\theta }) - F(\Gamma _{\theta })}{\Delta \Gamma _{\theta }} \end{aligned}$$

(36)

for the purpose of simplicity. The homogenised thermal stress and tangent read

$$\begin{aligned} {\varvec{\Sigma }}^{\nabla \theta ,c}|_{\varvec{x}}&= k \, \left( \nabla \theta |_{\varvec{x}} - \Gamma _\theta \varvec{N}_1 \right) , \end{aligned}$$

(37)

$$\begin{aligned} \dfrac{\partial {\varvec{\Sigma }}^{\nabla \theta ,c}|_{\varvec{x}}}{\partial \nabla \theta }&= k \, \left( \varvec{I}+ \dfrac{k}{{\varvec{K}}^{{\Gamma _{\theta }\Gamma _{\theta }}}} \varvec{N}_1 \otimes \varvec{N}_1 \right) \end{aligned}$$

(38)

for an opened cracked ($\Gamma _{1}>0$).

Note, that heat radiation and, thus, the solution of the RCE, depends on the value of the crack opening , whereas previously published solutions of the RCE depend only on the dimensionless crack deformation $\Gamma _i$. Thus, in contrast to the former RCE solutions, the model is not independent of the RCE size and $l_1$ becomes a model parameter.

2.2.3 Remarks on further heat flux processes at cracks

Perfect heat conduction behaviour through a closed crack is assumed for both solutions above, i.e. $\Gamma _{\theta }=0$ for $\Gamma _1=0$. However, the heat conduction in compressed cracks is typically less than in the bulk material due to spot contact, conduction in micro cavities and further effects. [10] has identified the following constitutive structure for the heat flux through a closed crack

$$\begin{aligned} {q^{\text {N}}} = {\hat{q}^{\text {N}}}(\bar{\theta }^{1}, \bar{\theta }^{2}, {p^{\text {N}}}), \end{aligned}$$

(39)

where ${q^{\text {N}}}$ is the heat flux normal to the crack surface and ${p^{\text {N}}}$ is the normal pressure of the crack surfaces in contact. Thus, the iterative solution scheme for the temperature discontinuity at the RCE model with heat radiation ($\Gamma _1>0$), given by Eqs. (33–35), (37) and (38), also applies to the proposed RCE model when Eq. (39) is considered for closed cracks ($\Gamma _1=0$).

It is further possible to consider heat convection at the crack surface, which depends on the temperature of the crack surfaces $\bar{\theta }^{1}$ and $\bar{\theta }^{2}$, and the temperature of the medium in the crack $\bar{\theta }^{c}$. Then, the heat flux at the crack surface can be given in the form

$$\begin{aligned} {q^{\text {N}}} = {\hat{q}^{\text {N}}}(\bar{\theta }^{1}, \bar{\theta }^{2}, \bar{\theta }^{c}). \end{aligned}$$

(40)

However, the medium temperature in the crack depends on the heat conduction and fluid mechanics of the medium in the whole crack in general, which is not part of the proposed phase-field model. Thus, heat convection at crack surfaces is restricted to slow processes, where $\bar{\theta }^{c}=\text {const.}$ can be assumed, or very quick processes, where $\bar{\theta }^{c}$ can be calculated from the heat capacity of the medium in the crack and the heat transferred through the crack surfaces.

2.3 Finite element formulation

The finite element method is applied to the phase-field model in Eq. (3). Thus, a solution is obtained iteratively starting at the state $(\varvec{u}^{i},p^{i},\theta ^{i})$ with

$$\begin{aligned} G^{i} = G(\varvec{u}^{i},p^{i},\theta ^{i}) {:}{=}\delta {\mathcal {P}^{\text {tot}}}\Big |_{\begin{array}{c} \varvec{u}=\varvec{u}^{i} \\ p=p^{i} \\ \theta =\theta ^{i} \end{array}} \rightarrow 0 \end{aligned}$$

(41)

and the linearisation by means of the first order Taylor expansion

$$\begin{aligned}&G(\varvec{u}^{i}+\Delta \varvec{u}^{i},p^{i}+\Delta p^{i},\theta ^{i}+\Delta \theta ^{i}) \nonumber \\&\quad \approx G(\varvec{u}^{i},p^{i},\theta ^{i})\nonumber \\&\quad + \left. \dfrac{\partial G}{\partial \varvec{u}}\right| _{\begin{array}{c} \varvec{u}=\varvec{u}^{i} \\ p=p^{i} \\ \theta =\theta ^{i} \end{array}} \cdot \Delta \varvec{u}^{i} + \left. \dfrac{\partial G}{\partial p}\right| _{\begin{array}{c} \varvec{u}=\varvec{u}^{i} \\ p=p^{i} \\ \theta =\theta ^{i} \end{array}} \Delta p^{i} + \left. \dfrac{\partial G}{\partial \theta }\right| _{\begin{array}{c} \varvec{u}=\varvec{u}^{i} \\ p=p^{i} \\ \theta =\theta ^{i} \end{array}} \Delta \theta ^{i}, \nonumber \\&\quad \approx G^{i} + \dfrac{\partial G^{i}}{\partial \varvec{u}} \cdot \Delta \varvec{u}^{i} + \dfrac{\partial G^{i}}{\partial p} \Delta p^{i} + \dfrac{\partial G^{i}}{\partial \theta } \Delta \theta ^{i} {\mathop {=}\limits ^{!}}0 \end{aligned}$$

(42)

with respect to the state variables. For the discretisation into finite elements, the same shape functions ${\varvec{N}}^{}(\varvec{x})$ and derivatives ${\varvec{B}}^{}(\varvec{x})$ are used for the state variables and their corresponding virtual velocities

$$\begin{aligned} \varvec{u}(\varvec{x})&= {\varvec{N}}^{\varvec{u}}(\varvec{x}) \cdot \hat{\varvec{u}}^{(e)},&\delta \varvec{v}(\varvec{x})&= {\varvec{N}}^{\varvec{u}}(\varvec{x}) \cdot \delta \hat{\varvec{v}}^{(e)}, \end{aligned}$$

(43)

$$\begin{aligned} p(\varvec{x})&= {\varvec{N}}^{p}(\varvec{x}) \cdot \hat{\varvec{p}}^{(e)},&\delta \dot{p}(\varvec{x})&= {\varvec{N}}^{p}(\varvec{x}) \cdot \delta \hat{\dot{\varvec{p}}}^{(e)}, \end{aligned}$$

(44)

$$\begin{aligned} \theta (\varvec{x})&= {\varvec{N}}^{\theta }(\varvec{x}) \cdot \hat{\varvec{\theta }}^{(e)},&\delta \dot{\theta }(\varvec{x})&= {\varvec{N}}^{\theta }(\varvec{x}) \cdot \delta \hat{{\dot{\varvec{\theta }}}}^{(e)}, \end{aligned}$$

(45)

$$\begin{aligned} \varvec{H}(\varvec{x})&= {\varvec{B}}^{\varvec{u}}(\varvec{x}) \cdot \hat{\varvec{u}}^{(e)},&\delta \dot{\varvec{H}}(\varvec{x})&= {\varvec{B}}^{\varvec{u}}(\varvec{x}) \cdot \delta \hat{\varvec{v}}^{(e)}, \end{aligned}$$

(46)

$$\begin{aligned} \nabla p(\varvec{x})&= {\varvec{B}}^{p}(\varvec{x}) \cdot \hat{\varvec{p}}^{(e)},&\delta \dot{\nabla p}(\varvec{x})&= {\varvec{B}}^{p}(\varvec{x}) \cdot \delta \hat{\dot{\varvec{p}}}^{(e)}, \end{aligned}$$

(47)

$$\begin{aligned} \nabla \theta (\varvec{x})&= {\varvec{B}}^{\theta }(\varvec{x}) \cdot \hat{\varvec{\theta }}^{(e)},&\delta \dot{\nabla \theta }(\varvec{x})&= {\varvec{B}}^{\theta }(\varvec{x}) \cdot \delta \hat{\dot{\varvec{\theta }}}^{(e)}. \end{aligned}$$

(48)

The total virtual power is required to vanish for all admissible virtual velocities,

$$\begin{aligned} G(\varvec{u}^{i}&+\Delta \varvec{u}^{i},p^{i}+\Delta p^{i},\theta ^{i}+\Delta \theta ^{i}) \approx \nonumber \\ \quad \delta \hat{\varvec{v}} \cdot&\left\{ -{\varvec{R}}^{{\varvec{u}}} + {\varvec{K}}^{{\varvec{u}\varvec{u}}} \cdot \Delta \hat{\varvec{u}}^{i} + {\varvec{K}}^{{\varvec{u}p}} \cdot \Delta \hat{\varvec{p}}^{i} + {\varvec{K}}^{{\varvec{u}\theta }} \cdot \Delta \hat{\varvec{\theta }}^{i} \right\} \nonumber \\ \quad + \delta \hat{\dot{\varvec{p}}} \cdot&\left\{ -{\varvec{R}}^{{p}} + {\varvec{K}}^{{p\varvec{u}}} \cdot \Delta \hat{\varvec{u}}^{i} + {\varvec{K}}^{{pp}} \cdot \Delta \hat{\varvec{p}}^{i} + {\varvec{K}}^{{p\theta }} \cdot \Delta \hat{\varvec{\theta }}^{i} \right\} \nonumber \\ \quad + \delta \hat{\dot{\varvec{\theta }}} \cdot&\left\{ -{\varvec{R}}^{{\theta }} + {\varvec{K}}^{{\theta \varvec{u}}}\cdot \Delta \hat{\varvec{u}}^{i} + {\varvec{K}}^{{\theta p}}\cdot \Delta \hat{\varvec{p}}^{i} + {\varvec{K}}^{{\theta \theta }} \cdot \Delta \hat{\varvec{\theta }}^{i} \right\} \text {,} \end{aligned}$$

(49)

which yields the linear system of equations for the nodal updates of the state variables

$$\begin{aligned} \left[ \begin{array}{ccc} {\varvec{K}}^{{\varvec{u}\varvec{u}}} &{} {\varvec{K}}^{{\varvec{u}p}} &{} {\varvec{K}}^{{\varvec{u}\theta }} \\ {\varvec{K}}^{{p\varvec{u}}} &{} {\varvec{K}}^{{pp}} &{} {\varvec{K}}^{{p\theta }} \\ {\varvec{K}}^{{\theta \varvec{u}}} &{} {\varvec{K}}^{{\theta p}} &{} {\varvec{K}}^{{\theta \theta }} \end{array} \right] \cdot \left[ \begin{array}{c} \Delta \hat{\varvec{u}}\\ \Delta \hat{\varvec{p}} \\ \Delta \hat{\varvec{\theta }} \end{array} \right] = \left[ \begin{array}{c} {\varvec{R}}^{{\varvec{u}}} \\ {\varvec{R}}^{{p}} \\ {\varvec{R}}^{{\theta }} \end{array} \right] \end{aligned}$$

(50)

Fig. 2

a Sketch of the thermo-mechanical boundary value problem and b the load history at the upper edge of the pre-cracked plate

with

(51)

(52)

(53)

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

is the assembly operator for the n finite elements towards the global system of equations.

Fig. 3

a, b Temperature and displacement profile along the vertical symmetry axis of the plate ($x={50}\,\mathrm{mm}$), and c temperature distribution on the deformed plate (scaling factor 5)

3 Application to linear thermo-elasticity

3.1 Pre-cracked plate

The proposed thermo-mechanical phase-field model for fracture is applied to a pre-cracked plate. For a plate of ${100}\,{\mathrm{mm}}$ length with an initial middle crack, a displacement of $u_y={4}\,{\mathrm{mm}}$ is applied to open the crack, cf. Fig. 2a. The temperature at one edge parallel to the crack is increased by ${6}\,{\mathrm{K}}$. The load history of the boundary conditions is given in Fig. 2b. The time is discretised into 100 time steps. The thermo-elastic material parameters are $\lambda ={19.6}\,{\mathrm{MPa}}$, $\mu ={2}\,{\mathrm{MPa}}$, $\alpha ={0.01}\,{\mathrm{mm}/\mathrm{K}}$, $\rho ={0.1}\,{\mathrm{kg}/\mathrm{mm}^3}$, $c={38.8}\,{\mathrm{J}/\mathrm{kg}/\mathrm{K}}$ and $k={1000}\,{\mathrm{W}/\mathrm{m}/\mathrm{K}}$, while thermal isolation is assumed for opened crack states.

The temperature distribution on the deformed plate is shown in Fig. 3c, and the temperature and displacement profile at the vertical symmetry axis ($x={50}\,\mathrm{mm}$) are given in Fig. 3a, b. The heat propagates from the plate edge towards the crack and causes thermal expansion. The heat cannot pass the opened crack and yields a curved crack surface, which propagates towards the opposite, straight crack surface. The first crack contact takes place at the middle of the plate and allows the heat to propagate through the region in contact into the second half of the plate. The ongoing thermal expansion in both halves of the plate increases the contact area of the crack until contact along the entire crack surface.

The example demonstrates realistic deformations at the crack for thermo-mechanical material behaviour and the influence of the crack state on the thermal conduction, while the opened crack is considered as thermal isolator. Convergence is obtained in three or less Newton iterations for all time steps.

Fig. 4

a Sketch of the thermo-mechanical boundary value problem, b temperature profile along the vertical symmetry axis of the plate ($x={50}\,\mathrm{mm}$) and c temperature distribution on the deformed plate (scaling factor 5) with and without heat radiation through the crack

Fig. 5

a Number of Newton-Raphson iterations per time step and relative residuum norm of three time steps (10, 27, 63) for the global system of equations, and b number of Newton-Raphson iterations per time step (first global iteration) and relative residuum norm of three time steps (8, 18, 25) for the heat radiation

The simulation of the pre-cracked plate is repeated and heat radiation between the crack surfaces is considered, cf. Fig. 4a. The boundary condition loads are changed to $u_y={7}\,\mathrm{mm}$ and ${6}\,{K}$ in order to prevent crack contact when only one plate half is thermally expanding. The emissivity is considered as $\varepsilon =1$, which represents heat radiation for black bodies. The heat is propagating from the plate edge to the crack. However, the temperature difference between the crack surfaces increases slowly and, thus, only a small amount of heat is transferred by radiation. With increasing temperature at the crack surface, also the distance between the crack surfaces reduces, which increases heat flux from radiation. The slightly curved crack yields an inhomogeneous distribution of the heat flux at the crack. The second half of the plate is heated up faster at the middle than at the plate sides. The temperature distribution on the deformed plate is given in Fig. 4c for a simulation with and without heat radiation at the opened cracked. The thermal expansion of the lower half plate yields crack contact after a while, which cannot be achieved without taking heat radiation into account.

The solution scheme of the non-linear problem consists of two Newton-Raphson loops, one applied to the global system of equations and one at the RCE model. The convergence behaviour in terms of the number of iterations is presented in Fig. 5. Up to nine iterations per time step at the global level are required due to the strongly non-linear radiation relation. Corresponding relative residuum norms of the iterations are given for three time steps at all phases of the simulation.

The local Newton loop for the radiation flux is plotted for an element in the centre of the plate in Fig. 5b and, thus, at the centre of the crack. Convergence is achieved within two to three iterations. Quadratic convergence is demonstrated by the relative residuum norms of three time steps. The local loop is not activated when the crack is in contact, which is the case from step 26 onwards for the investigated element.

3.2 Thermal shock of a circular specimen

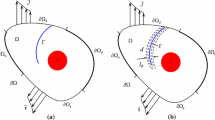
The second example examines the capability of the present phase-field model applied to a practical engineering problem. A recent experiment of [11] attempts to investigate crack evolution patterns of ceramic materials exposed to a thermal shock (quench treatment), which obtains a quasi periodical and hierarchical crack profile within a thin layer of circular specimen. Thereafter, a numerical method [12] using a thermal coupled phase-field fracture model studies the cracking pattern, showing good agreement with the experimental investigation in [11]. The work at hand reproduces this model problem using the proposed thermo-phase-field approach within an RCE framework based on the setup shown in Fig. 6. In particular, a two-dimensional boundary value problem, which is characterized as homogeneous and isotropically linear elastic, is taken into account. For the initial phase, the specimen is uniformly heated up by ${200}\,\mathrm{K}$, where the whole heating procedure yields a complete stress-free state of the specimen. In the sequel, the most outside surface is supposed to be cooling down in a significantly fast manner. Naturally, this process leads to material shrinkage at the outside layer and results in tensile stress along the tangential direction.

As long as the elastic strain potential sufficiently exceeds the critical energy release rate of the material, e.g. $\mathcal {G}_c={8}\times {10^{-3}}\,{\mathrm{GPa}/\mathrm{m}^2}$, multiple cracks are nucleated and start to propagate inwards along the radial direction. Due to the symmetry characteristics of the geometric setup and the temperature loading condition, the model problem is simplified as a quarter of the original one with proper boundary conditions, depicted in Fig. 6a. The simulation is performed by a standard parallel computation technique, where the finite element discretization is partitioned by 80 individual domains, see Fig. 6b. The material parameters are given as $\kappa ={196}\,{\mathrm{GPa}}$, $\mu ={20}\,{\mathrm{GPa}}$, $\rho ={1000}\,{\mathrm{kg}/\mathrm{m}^3}$, $k={50}\,{\mathrm{W}/\mathrm{m}/\mathrm{K}}$, $c={3.88 \times 10^{-3}}\,{\mathrm{kJ}/\mathrm{kg}/\mathrm{K}}$, $\alpha ={1.2 \times 10^{-4}}\,{\mathrm{mm}/\mathrm{K}}$, $l={1}\,{\mathrm{mm}}$. The simulation results, shown in Fig. 7, depict that multiple cracks are nucleated at the circular edge in an approximately periodical manner. In the sequel, cracks propagate with different growth speed. Some of them slowly evolve straightforwardly inwards, and some slightly change their directions. The simulation result shows good agreement with the experimental investigation in [11].

Fig. 6

Schematic description of thermal shock cracking of a circular specimen, a geometric setup and b finite element discretization for each partition domain of parallel computation

Fig. 7

Simulation of crack evolution induced by thermal shock versus the experimental investigations in [11]

Fig. 8

Schematic description of notched beam and perspective visualisation

3.3 Thermally induced cracking of a notched beam

This example studies the crack evolution induced by thermal shrinking within a beam with an initial notch. Similar to the aforementioned thermal shock cracking mechanism, sudden cooling is applied to the surface of the structure. Thus, the thermal shrinking yields a stress concentration at the notch tip, where the crack is supposed to be initiated. In order to demonstrate the propagation of curved cracks in a three-dimensional specimen, an inclined notch is taken into account. The geometrical setup of the boundary value problems is depicted in Fig. 8. The material parameters are given as $\kappa =196$ GPa, $\mu =20$ GPa, $\rho =3000$ kg$\cdot$m$^{-3}$, $k=520$ W/m/K, $c=1.66e^{-5}$ kJ/kg/K, $\alpha =1.2e^{-4}$ mm/K, $\mathcal {G}_c=5 e^{-2}$ GPa/m$^2$, $l=2$ mm. The maximum principal stress direction is used to approximate the crack normal orientation [1, 3].

The temperature loading is applied to the bottom surface, where the initial notch is located at, as a Dirichlet boundary condition. In the sequel, due to continuous heat conduction, the lower temperature propagates upwards reaching the notch tip. As a result, a concentrated elastic deformation occurs at the notch tip to initiate the phase-field crack. The inclined notch yields a curved crack surface, which reduces the crack surface area while dividing the beam into two parts, see Fig. 9. For the sake of better visualization, a post-processing technique generates the isosurface with $p=0.95$ to represent the evolved crack surfaces.

Fig. 9

Evolution of the curved crack surface as a result of thermal strains in a clamped beam, a perspective view and b top view

4 Conclusions and outlook

The abstract variational principle of total virtual power is applied to phase-field fracture for coupled thermo-mechanics. The state variables are chosen to be the displacement vector, the phase-field variable and the absolute temperature. The obtained variational problem represents the weak form of momentum balance, entropy balance and phase-field balance. A representative model for a portion of a crack is introduced in order to determine crack contact, force degradation, degradation of the heat conductivity and further processes inside the crack. This Representative Crack Element (RCE) is coupled to the phase-field formulation by means of variational homogenisation.

The presented framework is used to derive a phase-field fracture model for transient thermo-elasticity, where the crack acts either as thermal isolator or where heat radiation through the crack is considered. An iterative solution scheme to solve the non-linear RCE model is introduced. The possible application of the solution scheme to considered further thermal effects, e.g. spot contact, micro-cavity conduction or heat convection, is discussed. The derived models are applied to a plate with an initial crack, demonstrating the interaction of thermal strain and heat conduction with the crack with and without considering heat radiation. A thermal shock simulation is presented and the results are compared to experimental findings. The three-dimensional application is performed at a clamped beam with an inclined notch, which yields a curved crack surface.

The presented procedure to derive multi-physical models of phase-field fracture based on representative crack elements can be adopted to further formulations in future works, e.g. nonlocal material models, higher order continuum models, multi-scale problems and other multi-physical couplings.