Abstract
A great proportion of the existing architectural heritage, including historical and monumental constructions, is made of brick/block masonry. This material shows a strong anisotropic behaviour resulting from the specific arrangement of units and mortar joints, which renders the accurate simulation of the masonry response a complex task. In general, mesoscale modelling approaches provide realistic predictions due to the explicit representation of the masonry bond characteristics. However, these detailed models are very computationally demanding and mostly unsuitable for practical assessment of large structures. Macroscale models are more efficient, but they require complex calibration procedures to evaluate model material parameters. This paper presents an advanced continuum macroscale model based on a two-scale nonlinear description for masonry material which requires only simple calibration at structural scale. A continuum strain field is considered at the macroscale level, while a 3D distribution of embedded internal layers allows for the anisotropic mesoscale features at the local level. A damage-plasticity constitutive model is employed to mechanically characterise each internal layer using different material properties along the two main directions on the plane of the masonry panel and along its thickness. The accuracy of the proposed macroscale model is assessed considering the response of structural walls previously tested under in-plane and out-of-plane loading and modelled using the more refined mesoscale strategy. The results achieved confirm the significant potential and the ability of the proposed macroscale description for brick/block masonry to provide accurate and efficient response predictions under different monotonic and cyclic loading conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Brick/block masonry represents one of the most ancient building techniques, which is still used to build modern structures due to the simple way of construction and low material cost [1, 2]. Existing masonry structures, including historical buildings, monuments and bridges, constitute a high percentage of the architectural and cultural heritage worldwide playing an important economic and social role. To preserve these important assets, it is critical to employ realistic numerical descriptions to predict the response under different loading conditions, including extreme loadings like earthquakes, so as to direct the potential implementation of strengthening measures to enhance the performance of deficient structures.
Masonry shows a complex 3D anisotropic behaviour even under low loading levels due to the heterogeneous nature of the material. The response becomes even more complex in the nonlinear field under higher loading due to the development of damage and cracking. For these reasons, the numerical simulation of the response of masonry structures up to collapse still represents a challenging technical task [3,4,5].
The most popular approaches currently used to simulate the nonlinear behaviour of masonry are based upon micro, meso or macroscale representations. In the first two modelling strategies, masonry bond is explicitly represented utilising separate descriptions for units and mortar joints, and employing nonlinear interface elements to describe the development and propagation of cracks. This methodology is applied also for other quasi-brittle materials like concrete, and it is particularly suitable for regular masonries (e.g. brick/block masonry) where the localization of the cracks can be easily established a priori, as it generally follows the directions of the mortar joints. In finite element (FE) micromodels, masonry units and mortar joints are modelled with separate nonlinear continuum elements and the physical interfaces connecting the two main components are described by nonlinear interface elements [6, 7] providing a highly detailed representation of the masonry domain. In FE mesoscale models [8–16], masonry joints and mortar-unit physical interfaces are simulated by zero-thickness nonlinear interface elements. The Distinct Element Method (DEM) [17, 18] can be also used to develop masonry mesoscale descriptions. In this case, the masonry units are modelled by means of rigid or elastic solid elements, connected by discrete multi-directional contact-links. Sophisticated procedures are employed to identify contact, allowing the simulation of complete detachment of parts of the structure. The advantage of mesoscale FE and DEM models is to reduce the computational burden compared to detailed microscale models, while maintaining an explicit representation of the masonry meso-structure. Previous studies in the literature demonstrated the ability of mesoscale approaches to provide a realistic description of failure mechanisms of masonry components and realistic 3D structures including buildings [19] and bridges [20]. However, these models require a high computational cost, thus they are unsuitable for practical assessments using standard computational resources.
Continuous macroscale modelling approaches [21–24] assume masonry as an equivalent homogeneous material. They are not based upon an explicit description of masonry bond which guarantees a drastic reduction of the computational cost. However, macroscale models generally entail a high number of model material parameters which often require sophisticated calibration procedures [25]. Multi-layered models [23] represent a particular category of continuum macroscale models, where the average constitutive relation is derived by considering masonry as a two-phase material. In the main, they include an isotropic continuum matrix and a set of aligned vertical weak inclusions representing mortar head joints which are combined with continuous planes of weakness simulating mortar bed joints. In [24], a simplified multi-layered masonry model neglecting the head joint contribution is presented and applied to simulate the in-plane shear behaviour of masonry panels.
Another class of efficient macromodels is represented by hybrid discrete modelling strategies utilising rigid elements and nonlinear links as rigid body spring models (RBSM) [26, 27] and discrete macroelement models (DMEM) [28–30]. In these numerical descriptions, as for continuous macromodels, masonry is considered as an equivalent homogeneous material and the mesh is independent from the specific arrangement of units and mortar joints. On the other hand, discontinuities in the displacement field are modelled by zero-thickness nonlinear springs whose nonlinear constitutive relationships are determined following specific calibration procedures.
The efficiency of macroscale models and the ability of detailed meso- and micro-scale models to accurately represent realistic cracking and failure modes of brick/block masonry is combined in multi-scale formulations [31–35]. According to these strategies, the structural problem is analysed at two scales: at the structural-scale an equivalent homogeneous medium is considered, while at the micro-scale the complex heterogeneous masonry micro-structure is taken into account by solving the elasto-plastic problem on a representative portion of the micro-structure. Online or offline strategies are then adopted to connect the two scales of representations. Furthermore, enhanced accuracy can be achieved adopting improved continuum theories at the macroscale based upon second-order or micropolar (Cosserat) material models, where non-local homogenization or multi-scale techniques are used to link micro/meso to macroscale. Such numerical descriptions provide a more refined representation of the masonry micro-structure [36–38] describing size/scale effects and allowing for the finite dimensions of the masonry units and their potential relative rotations [39, 40].
In this paper, a novel simplified anisotropic continuum macromodel allowing for the intrinsic 3D meso-structure of masonry is presented. A two-scale approach is followed, where a homogeneous continuum model describes the masonry at the macroscale, while nonlinear embedded distributed interfaces, referred to as Internal Layers (ILs), represent the material at the meso-scale level. The ILs simulate the tensile (mode I), shear (model II) and crushing (mode III) failure modes of masonry joints and units. The advanced 3D damage-plasticity constitutive model for nonlinear interfaces presented in [41] is employed for the ILs. It enables a realistic representation of stiffness and strength degradation of mortar joints under cyclic loading. Objective calibration procedures are established for the material parameters of the ILs which consider the mechanical properties of masonry units, mortar joints and masonry bond characteristics. The accuracy and efficiency of the proposed model are investigated comparing the numerical results against experimental data and detailed mesoscale simulations, focusing on the nonlinear response up to collapse of masonry panels subjected to in-plane and out-of-plane monotonic and cyclic loadings.
2 Proposed two-level macroscale model
The proposed modelling strategy is based on a two-level description of the masonry domain. A homogeneous 3D continuum FE model with solid elements is considered at the macroscopic level, whilst a 3D distribution of ILs describes the masonry meso-structure at the local level. The ILs are assumed orthogonal to each other, and their orientation is established according to the main local material directions based on the specific masonry bond. As a result, a triad of mutual orthogonal ILs is associated to each integration point within the domain of a solid element, as schematically depicted in Fig. 1 with reference to a generic inner integration point p of a 20-noded solid element representing a portion of a masonry panel. In the figure, (X,Y,Z) represents the global reference system while (x,y,z) is the local reference system identifying the orientation of the ILs.
Two distinct strain–stress fields are considered at the macroscopic and local levels. The material constitutive relationships are defined at the local level linking the strain and stress parameters of the ILs, while the macroscopic strains allow for kinematic compatibility, and the macroscopic stresses are calculated based on macroscopic equilibrium.
A two-scale approach, schematically illustrated in Fig. 2, is followed at each integration point to transfer the response parameters from the macroscopic to the local level and vice versa. First, the macroscopic strains are evaluated from the nodal displacements of the element, according to the chosen shape functions. Subsequently, the local (internal) strains of the three ILs are determined based on local kinematic compatibility conditions (Step 1 in Fig. 2). From the internal strains, the local (internal) stresses of the three ILs are calculated by integrating the constitutive laws (Step 2 in Fig. 2). Finally, local Cauchy equilibrium is imposed to obtain the macroscopic stresses (Step 3 in Fig. 2). Due to the material nonlinearity, the procedure is iterative. Thus, Step 1 represents an elastic prediction and Step 3 a plastic correction, after which the residual internal unbalanced stresses required in the next iteration are evaluated. As specified in the following, the above iterative procedure is performed through a full Newton–Raphson strategy.
In the proposed model, only the macroscopic strain field is continuous, while the internal strain field is discontinuous presenting weak discontinuities. Based on this consideration, the prosed strategy can be classified as a FEM model with embedded discontinuity (ED-FEM) [42], where the distance between integration points represents the crack band width (Fig. 2). Comparing the proposed strategy with a standard mesoscale description [14], where nonlinear interface elements simulate the deformation and the failure of mortar joints, the ILs can be seen as embedded distributed interfaces. Referring to the previous multilayered material model developed by Pietruszczak and Niu [23], the ILs play the role of inclusions and weak planes distributions, while allowing for sophisticated nonlinear models and the description of damage accumulation due to cyclic loadings, which are not considered by standard multilayered material models [23]. However, in the proposed strategy, the deformability of the composite material comprising units and mortar joints is concentrated at the ILs, differently from multilayered models where an isotropic continuum matrix allows for the deformability of the masonry units. Thus, the ILs must be calibrated taking into account the stiffness characteristics of both bricks/blocks and mortar joints (Sect. 3).
An important difference between the proposed two-scale strategy and typical two-scale approaches [31–35] is related to the use of the representative periodic cell allowing for masonry bond, which is explicitly solved in standard multi-scale strategies, but is considered only for the evaluation of the mechanical properties of the ILs in the proposed approach (Sect. 3). This brings an important computational benefit compared to online multiscale approaches, where a significant computational effort is required to evaluate the nonlinear response of the periodic cells at each integration point and for each iteration of the nonlinear analysis solution procedure.
2.1 Kinematics and local equilibrium
The macroscopic strains at the element level include six components, collected in the vector. \({{\varvec{\upvarepsilon}}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } & {\varepsilon_{y} } & {\varepsilon_{z} } & {\gamma_{xy} } & {\gamma_{xz} } & {\gamma_{yz} } \\ \end{array} } \right]^{T}\), and are associated with six stress components, in the vector \({{\varvec{\upsigma}}} = \left[ {\begin{array}{*{20}c} {{\upsigma }_{x} } & {{\upsigma }_{y} } & {{\upsigma }_{z} } & {\tau_{xy} } & {\tau_{xz} } & {\tau_{yz} } \\ \end{array} } \right]^{T}\). Both vectors are expressed in the local referent system (x,y,z) indicated in Fig. 1.
At the local level, the deformation field is described by nine components, collected in three vectors \({\mathbf{d}}_{k}\) (\(k = x,y,z\)), where the subscript k indicates the direction in the element reference system normal to the layer \(\Gamma_{k}\). The corresponding stress field at the local level is described by the three vectors \({\mathbf{s}}_{k}\) (\(k = x,y,z\)) where, as for the strains, the subscript indicates the IL. In Eq. (1), the three vectors of local strains are reported where, \(d_{k}\) and \(d_{kh}\) \((k=x,y,z; h{\neq}k=x,y,z)\) are the normal strain and shear strain components along the local direction h of \(\Gamma_{k}\), respectively. In Eq. (2), the three local stress vectors are reported, where, as for the local strains, the first index specifies the IL while the second (in the shear components) designates the component direction. Figure 3 provides a schematic representation of the stress components for each IL, referred to the elementary volume (δx, δy, δz) at the generic Gauss integration point of the element.
The local stresses at each IL are obtained by integrating the nonlinear constitutive law of the IL. It is worth noting that the proposed methodology is independent from the constitutive laws adopted. In the present study, the plastic-damage constitutive law described in Sect. 3 is considered at the level of IL.
Equation (3) provides the vector \({\mathbf{d}}_{{{\varvec{int}}}}\) collecting the nine components of the local strains to which it is convenient to refer in the following. In the equation, \({\mathbf{d}}_{{\varvec{n}}} = \left[ {\begin{array}{*{20}c} {d_{x} } & {d_{y} } & {d_{z} } \\ \end{array} } \right]^{T}\) represents the normal strains, while \({\mathbf{d}}_{{{\varvec{t}}1}} = \left[ {\begin{array}{*{20}c} {d_{xy} } & {d_{xz} } & {d_{yz} } \\ \end{array} } \right]^{T}\) and \({\mathbf{d}}_{{{\varvec{t}}2}} = \left[ {\begin{array}{*{20}c} {d_{yx} } & {d_{zx} } & {d_{zy} } \\ \end{array} } \right]^{T}\) correspond to the shear strains. Equation (4) reports the dual local stress components, in the vector \({\mathbf{s}}_{{{\varvec{int}}}}\).
The local kinematic compatibility condition, linking the local deformations to the macroscopic deformations is obtained considering the following rules: (i) the local normal strains are identical to the macroscopic normal strains along the corresponding direction; (ii) each macroscopic shear deformation is additively decomposed into the two ILs acting on the same plane of the macroscopic deformation, as schematically illustrated in Fig. 4. Specifically, the macroscopic shear strain in the coordinated plane h–k (\(\gamma_{hk}^{{}}\)) includes the ILs \(\Gamma_{h}\) and \(\Gamma_{k}\). According to these assumptions, six kinematics relations hold. Equation (5a) indicate the relations linking the macroscopic normal strains to the local normal strains (Eq. (5a)) and the macroscopic shear strains to the local shear strains Eq. (5b)
By imposing internal Cauchy equilibrium conditions, three additional equilibrium equations, involving the local shear stress components, can be written:
Denoting \({\mathbf{D}}_{k} = \delta {\mathbf{s}}_{k} /\delta {\mathbf{d}}_{k}\) (k = x, y, z) as the 3 × 3 tangent stiffness matrix of the k-th IL, which can be obtained by integrating the constitutive law of the IL, the increments of the local shear stress can be expressed as:
Substituting Eqs. (5) in Eqs. (7) and enforcing the equilibrium conditions of Eq. (6) in the variational form, the following expressions linking the increment of the local strains to the macroscopic strains are obtained:
where \(\delta {{\varvec{\upgamma}}} = \left[ {\begin{array}{*{20}c} {\delta {\upgamma }_{xy} } & {\delta {\upgamma }_{xz} } & {\delta {\upgamma }_{yz} } \\ \end{array} } \right]^{T}, {\mathbf{0}_{3x3}}\) the 3x3 zero matrix, \({\mathbf{I}_{3x3}}\) the 3x3 Identity matrix, and:
and:
Finally, the variation of the local deformations, can be written in terms of the variation of the macroscopic strains as:
where \({\mathbf{C}}\) is the 9 × 6 tangent kinematic compatibility matrix allowing for Cauchy equilibrium, which thus depends on the tangent stiffness matrices of the ILs.
From the compatibility relation in Eq. (12) and considering the 9 × 9 \({\mathbf{D}}\) matrix, obtained by assembling the contributions of the three tangent stiffness matrices \({\mathbf{D}}_{k}\) (k = x,y,z) of the ILs, the variation of the local stress results:
2.1.1 Internal Newton–Raphson iteration procedure
The solution of Eq. (6) is achieved through an iterative Newton Raphson procedure, performed at the level of the integration point. Indicating with a subscript i the values at the generic i-th iteration, \({\boldsymbol{\Delta\varepsilon}}_{i} = {{\varvec{\upvarepsilon}}}_{i} - {{\varvec{\upvarepsilon}}}_{i - 1} = {\mathbf{0}}\) and \( {\boldsymbol{\Delta }}\mathbf{d}_{{{\varvec{t}}1,i}} = {\mathbf{d}}_{{{\varvec{t}}1,i}} - {\mathbf{d}}_{{{\varvec{t}}1,i - 1}}\), Eq. (6) becomes:
where \({\mathbf{R}}_{i}\) is the residual out-of-balance vector associated with Eq. (6):
Inverting Eq. (14), the current value \({{\varvec{\upgamma}}}_{1,i}\) is evaluated from the out-of-balance at the previous iteration:
with:
where \({{\varvec{\upvarepsilon}}}_{j}\) and \({{\varvec{\upvarepsilon}}}_{o}\) represent the macroscale strains for the current global structural equilibrium iteration j and at the end of the previous incremental equilibrium step, respectively.
The internal shear strains can be calculated from the three terms of Eq. (5b) as:
Finally, Eq. (19) reports the vector of the internal strains, which is used to perform the plastic corrector phase by integrating the constitutive laws of the ILs and evaluating the out-of-balance for the next iteration. Convergence at the material integration point level is reached when the norm of the out-of-balance vector is smaller than a prefixed tolerance, \(\left| {{\mathbf{R}}_{i} } \right| < toll\).
2.1.2 Tangent stiffness matrix and macroscopic stresses
Considering the equivalence of virtual work principle at the local and macroscopic levels:
Since Eq. (20) should hold for any \(\delta {{\varvec{\upvarepsilon}}}^{{\varvec{T}}}\), the macroscopic stress is obtained as:
Or, in alternative, directly from Eq. (6):
The 6 × 6 tangent stiffness matrix \({\mathbf{K}}\) at the macroscopic level is determined by differentiating the macroscopic stress given by Eq. (21a) with respect to the macroscopic strain. Considering Eqs. (13) and (21b):
2.2 Model yield domain
In this section, the model yield domain is investigated in the local and global stress spaces with reference to a simple 2D orthotropic material model to show how the mechanical parameters and orientation of the ILs influence the material ultimate behaviour.
In the following, a brick-masonry sample (Fig. 5a) belonging to the XY plane of the global reference system and subjected to a planar biaxial tension–compression stress pattern is considered.
According to the proposed description, the response is governed by the ILs Гx and Гy, (Fig. 5b) whose stress components, according to Eq. (2), are respectively (\(s_{x}^{{}} , s_{xy}^{{}}\)) and (\(s_{y}^{{}} , s_{yx}^{{}}\)). A shear Mohr–Coulomb yielding criterion \(\left| {s_{u,h} } \right| = c_{h} + s_{h} \eta_{h}\) (\(h = x,y\)) is assumed for each IL, where \(\tau_{u,h}\) is the ultimate tangential stress, \(c_{h}\) is the cohesion and \(\eta_{h}\) is the friction coefficient. Two strength limits in tension (\(f_{t,h}\)) and compression (\(f_{c,h}\)) are also considered. The following parameters: \(f_{t,x} = 0.1MPa; c_{x} = 0.15MPa; f_{c,x} = - 2.0MPa; \eta_{x} = 0.5\) are employed for Гx, while the parameters of Гy are defined by the ratios \(r_{t} = f_{t,y} /f_{t,x}\), \(r_{c} = f_{c,y} /f_{c,x}\) and \(r_{\eta } = \eta_{y} /\eta_{x}\). The orientation of the material main directions is defined by the angle β between the global X axes and the x axes of the local reference system.
The 3D yield domain in the local stress space sx-sy-sxy, for different values of \(r_{t}\), \(r_{c}\) and \(r_{\eta }\), is shown in Fig. 6. The case characterised by unit r-ratio values (\(r_{t} = r_{c} = r_{\eta } = 1\)) is representative of an isotropic masonry such as irregular masonry with a chaotic arrangement of units and mortar joints. Conversely, values of r-ratios greater than 1, represent regular masonries with brick interlocking, where the direction parallel to the bed joints is generally stronger than the orthogonal ones. In Fig. 6, three different sources of anisotropy are separately considered: different tensile strength, compressive strength or friction coefficient. It is possible to observe that the shape of the domain changes significantly moving from the isotropic to anisotropic material.
In Fig. 7, the 2D yield domain in the space of the global stress σx–σy (zero shear force stress) is shown considering the same values of r-ratios displayed in Fig. 6. Moreover, different masonry orientations are assumed by changing β (ranging from 0° to 60°). The domains are composed of linear piecewise segments, where the singular points correspond to the changing of the yield mechanism (tensile, shear or compression) or the yield layer. In the case of β = 0°, failure is associated to reaching the tensile or compressive strength of the IL, and the yield domain reduces to the Rankine’s domain. If β > 0°, the plastic envelope encompasses four edges in the case of isotropic tensile strength, \(r_{t} = 1\), and six edges for different tensile strengths for the two layers (\(r_{t} > 1\)). The domains associated with β > 0° are symmetric with respect to the bisectors of the first and third quadrants. Along these directions, failure is reached when the conditions \(\sigma_{X} = \sigma_{Y} = {\text{min}}\left\{ {f_{t,x} ,f_{t,z} } \right\}\) and \(\sigma_{X} = \sigma_{Y} = {\text{max}}\left\{ {f_{c,x} ,f_{c,z} } \right\}\) are met. In the case of isotropic material (\(r_{t} = r_{c} = r_{\eta } = 1\)), the domain for β = 45° contains those associated with β = 30° and β = 60°. In contrast, for the case of anisotropic masonry, the domains for β = 30° and β = 60° provide higher strengths than those corresponding to β = 45°.
3 Constitutive model
As noted before, the proposed macroscale material description with embedded discontinuities can be used with any constitutive model for the 2D nonlinear interfaces employing different material properties and even different constitutive laws for each material direction to take into account the effects of the masonry bond. In the present study, the same constitutive law is employed to represent all the ILs, for which the material properties are calibrated according to the procedure described in Sect. 4.
In the numerical simulations presented subsequently, the cyclic damage-plasticity model proposed in [41] is adopted. This model, which has been implemented in the FE code for advanced nonlinear analysis ADAPTIC developed at Imperial College London [43], has been extensively validated and employed for detailed mesoscale simulations of masonry components and structures [16, 20].
The material model for the 2D nonlinear interface elements is based upon a multi-surface elasto-hardening plasticity criterion which governs the evolution of plastic deformations, coupled with an anisotropic damage tensor which simulates strength and stiffness material degradation. According to [41], the elasto-plastic problem is solved first, then the damage variables are updated according to the current plastic work, which ensures a high level of robustness during the iterative process [44]. The most important mechanical aspects simulated by the model are: (i) the softening behaviour in tension and shear, (ii) the stiffness degradation depending on the level of damage, (iii) the recovery of normal stiffness in compression and (iv) the permanent (plastic) strains at zero stresses in presence of damage.
Appendix 1 provides a brief description of the adopted constitutive model, so as to introduce the main characteristics and parameters of the model, where the full model details can be found in [41].
4 Model calibration
One of the main merits of the proposed macroscale description is that it requires simple calibration of the model material parameters. This section presents a simple procedure to calibrate the linear and nonlinear parameters of the ILs with reference to regular brick/block masonry. The proposed calibration strategy, as typical mesoscale descriptions [14, 41], considers the main mechanical properties of bricks and mortar joints, which can be evaluated from in-situ or laboratory tests [45]. Figure 8 illustrates schematically the adopted approach with reference to a generic 2D periodic masonry cell (Fig. 8a) and its representation by the equivalent continuum macromodel through the ILs \({\Gamma }_{x}\) and \({\Gamma }_{z}\) simulating the masonry mechanical behaviour along the local directions parallel (x) and orthogonal (z) to the bed joints (Fig. 8b). In this figure, \(E_{m}\, {\text{and}}\, \nu_{m}\) are the Young’s modulus and Poisson’s ratio of mortar; \(E_{b}\, {\text{and}}\, \nu_{b}\) are the Young’s modulus and Poisson’s ratio of bricks; \(h_{m}\) is the average mortar thickness; and \(b \) and \(h\) are the length and height of bricks.
The elastic normal (\(E_{nk}\)) and shear (\(E_{tk}\)) moduli of the continuum model (k = x,z) are evaluated according to the homogenisation theory adopted in [23] with the simplification proposed in [24], neglecting the contribution of the head joints in the initial elastic deformability and assuming the same shear modulus for both the ILs. Equations (23 – 25) report the two equivalent normal moduli and the shear moduli. In the case of masonry arrangements with no brick interlocking, typically employed in multi-ring masonry arch bridges [20], the normal modulus \(E_{nx}\) can be evaluated according to Eq. (24) replacing the brick height h with the brick base b.
where \(\mu_{m} = \frac{{h_{m} }}{{\left( {h_{m} + h} \right)}}\) and \(\mu_{b} = \frac{h}{{\left( {h_{m} + h} \right)}}\).
The nonlinear parameters of the ILs associated with the tensile and shear failure mechanism are evaluated from the strength parameters for the mortar joints (in the following, the same mechanical properties are assumed for the bed and head joints) and for the bricks. Conversely, the compressive strengths and the corresponding fracture energies, along the direction parallel (\(f_{cx} ,G_{cx}\)) and orthogonal (\(f_{cz}\), \(G_{cz}\)) to the bed joints, are assumed known form the literature or based on experimental data. Hereafter, in accordance with the mesoscale mechanical description reported in [41], the tensile strength (\(f_{tj}\)), cohesion (\(c_{j}\)), friction angle (\(\phi_{j}\)) and the corresponding values of tensile and shear fracture energies (\(G_{tj}\),\( G_{sj}\)), are considered for the mortar joints, whilst the tensile strength (\(f_{tb}\)), cohesion (\(c_{b}\)), friction angle (\(\phi_{b}\)) and fracture energies (\(G_{tb}\), \(G_{sb}\)) are assumed for the bricks.
Following a simple phenomenological approach, two different normal and shear failure modes are utilised to describe the ultimate masonry behaviour along the directions normal and parallel to the bed joints (Fig. 9). According to this representation, the internal layer \(\Gamma_{z}\) inherits the same strength parameters of masonry joints, as reported in Eqs. (26), where the subscript z indicates that these parameters refer to the layer \(\Gamma_{z}\). To avoid mesh dependency of the solution in the presence of softening behaviour, the specific tensile and shear fracture energies in each direction of the solid elements are obtained by normalising the corresponding fracture energy values associated with mesoscale interfaces by the crack bandwidth (\(h_{bw}\)), which is assumed as the minimum value between the element mesh size and the distance between masonry joints in that direction.
Strength and degradation characteristics of the Internal Layer \(\Gamma_{x}\) are evaluated by imposing an equilibrium equivalence between the heterogeneous, mesoscale model and the continuum model considering the failure mechanisms showed in Fig. 9. This results in the following expressions:
where \(r_{b} = b/2h\) represents the masonry bond shape ratio (\(r_{b} = 0\) should be considered for running bond masonry).
In particular, Eqs. (27) are used for elements loaded in-plane. In the case of elements loaded out-of-plane, these nonlinear parameters in the x local direction are assumed equal to the nonlinear shear parameters of the joints.
4.1 Numerical simulation of brick-to-brick mortar joints
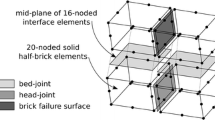
The ability of the proposed model to simulate the response of masonry joints is validated here by simulating the experimental tests performed by Van der Pluijm [47] on small-scale masonry specimens composed of two 100 × 50 × 50 mm3 (length × hight × width) bricks connected by a 15 mm mortar layer. Monotonic tensile tests and shear tests with different compression levels were performed. The specimen responses are numerically simulated by the proposed macromodel with a single 20-noded finite element and by a mesoscale model composed of two 20-noded elastic elements, representing the bricks, connected by a 16-noded zero-thickness interface element [14] with the nonlinear material model in [41].
The mechanical parameters of the joint employed in the analyses are assumed according to the experimental tests [46, 47] and numerical simulations presented in literature [6, 8]. In particular, the Young’s moduli for bricks \(E_{b} = 16700{\text{ MPa}}\) and mortar \(E_{m} = 2970{\text{ MPa}}\) with Poisson’s ratio 0.15 are employed in the analyses. The tensile strength \(f_{t} = 0.30\, MPa\) and fracture energy \(G_{t} = 0.012\,N/mm\) are assumed to simulate the Mode I failure mechanism. Cohesion \(c = 0.87MPa\), initial and residual friction factors \(\tan \phi = 1.01\) and fracture energy \(G_{s} = 0.13{\text{p}} + 0.058\,N/mm\) [8] are considered to represent the Mode II (shear) failure mechanism, where p = 0.1–0.5–1.0 MPa is the compression acting orthogonal to the mortar joint. The normal (\(k_{n}\)) and shear (\(k_{s}\)) stiffnesses of the interface and the moduli (\(E_{n}\), \(E_{t}\)) of the continuum macromodel are evaluated combining in series the elastic stiffness of bricks and the mortar joint, resulting in: \(K_{n} = 198{\text{ N}}/{\text{mm}}^{3}\), \(K_{s} = 86{\text{ N}}/{\text{mm}}^{3}\), \(E_{n} = 8080{\text{ MPa}}\) and \(E_{t} = 7026{\text{ MPa}}\).
The responses obtained by the proposed macro model are compared to those provided by the mesoscale model and the experimental observations. The results are shown in terms of average tensile stress \(F_{n} /A\) versus the normal displacement \(u_{n}\) (Fig. 10a) and average shear stress \(F_{s} /A\) versus the slip \(u_{s}\) (Fig. 10b), where \(F_{n}\) and \(F_{s}\) are the applied external traction and shear forces, and \(A\) is the transverse area of the brick. Both the tensile and shear responses of the proposed model are in a good agreement with the numerical predictions of the mesoscale model and the experimental observations, where the largest differences are observed in terms of peak-shear strength. More specifically, the macromodel predicts slightly lower shear capacities and smother responses than those predicted by the mesoscale model and experimental findings. These differences can be attributed to different internal distributions of the shear stresses predicted by the two models, where the deformed shapes and shear stresses at the peak-load of the shear test with compression p = 0.5 MPa are shown in Fig. 10c. In the macromodel, the peak shear stresses are concentrated along the diagonal of the element, while a uniform stress distribution is obtained by the mesoscale model due to the presence of the bricks.
After the peak-load, the shear capacity curves obtained by the macromodel converge towards those obtained by the mesoscale model. It is observed that both models overestimate the experimental residual shear strength, which can be ascribed mainly to the simplified assumption of a constant friction factor. However, the overall level of approximation guaranteed by the numerical predictions is satisfactory and suitable for engineering applications.
A numerical validation, aimed at demonstrating the ability of the proposed model to simulate the cyclic behaviour of masonry joints, is presented hereafter. Three load conditions, namely, unidirectional tension, shear and pure bending moment, are applied to the same specimen considered in the monotonic simulations discussed before.
The responses of the proposed model, compared to those obtained by the mesoscale model, are depicted in Fig. 11. In particular, Fig. 11a and b show the numerical responses under tension, whilst Fig. 11c displays the numerical prediction under bending moment in terms of \(M/W\) versus the relative rotation \(\phi\) of the opposite sections of the specimen, where M is the external applied moment, and \(W\) is the flexural stiffness of the brick transverse section. The comparisons in Fig. 11 confirm a good agreement between the mesoscale model and the proposed macromodel, which provides accurate response predictions of masonry joints subjected to cyclic loading allowing for (i) axial/flexural strength and stiffness degradation (Fig. 11a and c), (ii) stiffness recovery in compression after closure of tensile cracks (Fig. 11a) and (iii) shear frictional mechanism (Fig. 11b) after degradation of cohesion.
5 Numerical examples
In this section, the accuracy and potential of the proposed continuum macro modelling strategy for brick/block masonry are evaluated based on the response of masonry walls under monotonic and cyclic in-plane and out-of-plane loading. The numerical results obtained by the developed material model implemented in ADAPTIC [43] are compared against the outcome of previous experimental tests and numerical results obtained using detailed mesoscale models.
5.1 In-plane monotonic tests
In this section, the experimental tests carried out by Vermeltfoort and Raijmakers [48] are simulated. The physical experiments were performed on single-leaf solid-brick masonry panels 990 mm width, 1000 mm height and 98 mm thick, indicated as specimens J4D, J5D and J7D in [48]. The brick dimensions are 204 × 98 × 50 mm3 whereas the bed and head mortar joints are 12.5 mm thick. All the specimens were preloaded first with a vertical pressure pv. Subsequently, an in-plane horizontal force F was applied at the top of the panels with increasing magnitude up to collapse (Fig. 12). A pressure pv = 0.3 MPa was applied on the J4D and J5D specimens, while pv = 2.12 MPa was imposed on the J7D wall. During the tests, some horizontal cracks appeared at the top and bottom of the panels first, and then cracks suddenly propagated along the diagonal direction, mainly along the bed and head mortar joints. Shear failure of some bricks was also observed, mainly in the J7D specimen. A marked post-peak softening behaviour, which initiated with the formation of diagonal cracks at the centre of the panel, characterised the experimental responses of all tests at collapse.
According to the proposed macromodelling strategy, the panel is discretised by a 6 × 6 regular mesh of 20-noded solid elements. The mesoscale model utilises 153 20-noded elastic elements to represent each half brick and 144 nonlinear interface elements allowing for geometric and material nonlinearity [14] to represent mortar joints and potential cracks in the masonry units. Globally, the model requires 9180 degrees of freedom. The macroscale model is developed adopting a regular mesh of 36 solid elements with characteristic element size of about 165 mm. The model comprises 315 nodes and 945 degrees of freedom, corresponding to 10% of the degrees of freedom required by the mesoscale model.
Initially, a uniform vertical displacement is imposed at the top of panel giving rise to the same vertical pressure applied in the experiments. Then, nonlinear dynamic analysis is performed by applying a constant horizontal quasi-static velocity of 0.01 mm/sec at the same top nodes where the initial vertical displacements are prescribed. The mechanical properties of the mesoscale model are selected according to [14]. More specifically, the bricks are modelled with an elastic modulus \(E_{b} = 16700 MPa\), a Poisson’s coefficient \(\nu_{b} = 0.15\) and unit weight \(w_{b} = 19kN/m^{3}\), whereas material model parameters for the zero-thickness interface elements representing mortar joints and brick-to-brick interfaces are reported in Table 1. According to the proposed strategy, the macromodel material properties are obtained directly from the parameters of the mesoscale model following the procedure described in Sect. 4, where the relations in Eqs. (28 and 29) are used to evaluate the mortar Young’s and shear moduli \(E_{m} , G_{m}\) [45]. The complete set of macroscopic parameters adopted in the analysis is reported in Table 2.
Figure 13 shows the experimental failure mechanisms and the mesoscale predictions. During the tests, all the specimens showed shear failure with the activation of main diagonal cracks at the centre of the panel and horizontal cracks at the top and bottom sections (Fig. 13a, c). Brick failures are observed in the central part of the specimens, mainly in the panel J7D, due to the higher vertical pre-compression applied to the wall [48]. The mesoscale models are capable of simulating the experimental crack patterns of the two specimens with a good level of accuracy (Fig. 13b, d). As in the experimental tests, mesoscale models predict the development of shear failure of brick-to-brick interfaces at the centre of the panel, mainly for the panel J7D. Plastic sliding occurs at the bed joint interfaces, along the diagonal direction, while crushing in compression develops at the bottom and top corners (Fig. 13d).
The numerical curves of the mesoscale and continuum macroscale models are compared against the experimental results in Fig. 14 in terms of top horizontal displacement versus the applied external force F. In the case of the J4D and J5D specimens, a good agreement is observed between the numeric mesoscale and macromodel results and the experimental responses (Fig. 14a). The numerical peak loads predicted by the mesoscale model (52.3 kN) and macromodel (53.5 kN) are very close to the experimental value (52.4 kN). In the post-peak phase, the models show irregular responses, characterised by drops of strength followed by hardening, while the experiments showed a smoother response. These differences might be related to the simplified linearised yield surfaces, adopted to simulate the Mode I and Mode III failure mechanisms (Sect. 3). However, the global level of accuracy provides by both the mesoscale and macroscale models is satisfactory and suitable for engineering applications. In the case of J7D specimen, a good agreement is still observed between the mesoscale model and the experimental results, both in the pre-peak and post-peak stages with an accurate prediction of the ultimate strength of the panel, with 101.9 kN predicted by the mesoscale model against the experimental value of 95.8 kN. The macromodel provides a good numerical prediction of the lateral response up a top displacement of approximately 1.5 mm with a maximum load of 104 kN. After the peak-load, the continuum model underestimates the actual displacement capacity and the residual lateral strength of the panel.
This difference is mainly due to the simplified Cauchy description assumed by the proposed modelling strategy, which does not allow for the effects of potential local rotation of adjacent masonry units [26]. More sophisticated macroscale second-order or micropolar continuum descriptions combined with non-local homogenisation techniques [36, 39, 40] may provide more accurate predictions of the post-peak response but with higher computational effort associated with the material calibration and the enriched kinematics.
Figure 15 shows the deformed shapes and the von Mises equivalent stresses at the peak load (Fig. 15a, c) and the last step of the analyses (Fig. 15b, d) with macromodels. At the peak load step, both models show a single diagonal-strut mechanism which evolves to two different mechanisms for the post peak response of the two specimens: a multi-strut mechanism in the case of the panels J4D-J5D (Fig. 15b) and failure of the central part for panel J7D (Fig. 15d). These results are consistent with the experimental observations and the mesoscale predictions.
In the numerical investigation, the influence of the macroscale mesh characteristics on the numerical response has been also evaluated. Parametric simulations have been performed considering the same geometric layout reported in Fig. 13 and different mesh sizes, numbers of integration points and finite element type. Namely, a 6 × 6 (mesh A) and 10 × 10 mesh (mesh B), 27 and 125 integration points, 20-node quadratic elements and 8-node linear elements, are considered. Finally, two different values of vertical compression, 0.3 MPa and 1.2 MPa, kept constant during the analyses, are assumed.
The numerical curves, are reported in Fig. 17, with each model identified using the notation Mx-IPy-Ez, where x = A,B represents the mesh size; y = 3,5 represents the number of integration points; and z = 8,20 represents the number of nodes of the generic solid element of the mesh. Figure 16a shows the influence of the mesh discretization and the number of integration points, whereas Fig. 16b illustrates the influence of the element type used in the FE discretisation. From these analyses, a rather stable response can be observed for the two compression levels considered in the numerical investigation. A slight increase of the lateral strength and displacement capacity is observed for mesh A (larger mesh) and for the mesh with 8-noded linear elements. Conversely, a negligible influence of the number of integration points is observed. The computing time of the models employing quadratic (20-node) elements is approximately 3 times greater than the computing time required for the corresponding models employing 8-node linear elements. Considering quadratic elements, the computing time required for the models with mesh B and 5 integration points is approximately 2 times the computing time required for mesh A and 3 integration points. In Fig. 17, the ultimate deformed shapes and the Von-Mises stress patterns are reported for different values of the investigated parameters. Comparing the different meshes, it can be concluded that the coarser mesh (mesh A) with 27 integration points is adequate to achieve an accurate prediction of the ultimate failure mechanism. Besides, the use of 8-noded linear elements leads to a good representation of the failure mode and the overall force–displacement response but, as expected, to a less smooth stress prediction.
5.2 In-plane cyclic tests
In this section, the nonlinear response of two brick-masonry walls subjected to in-plane horizontal cyclic loading is analysed using the developed macroscale modelling strategy with embedded discontinuities.
The two English bond masonry panels built with clay bricks 250 × 120 × 55 mm3 and 10 mm mortar joints (Fig. 18), hereinafter referred to as Short Wall and Tall Wall, were tested in previous research [49]. They are 250 mm thick and characterised by the same length of 1000 m and different height values of 1350 mm (Short Wall) and 2000 mm (Tall Wall).
In the tests, a uniform vertical compressive pressure of 0.6 MPa was applied first on the top of each masonry panel through a steel spreader beam which was retained horizontally throughout the experiments. Subsequently, horizontal in-plane displacement cycles of increasing magnitude were imposed onto the beam maintaining the vertical load constant. The Short Wall specimen developed diagonal shear cracking and large hysteretic loops with significant strength degradation after reaching the lateral peak load. Conversely, the Tall Wall specimen developed horizontal cracks due to flexural bending which were mainly localised at the top and bottom bed joints and experienced rocking cyclic behaviour with no strength degradation.
Material tests [49] were also performed to characterise the masonry materials of the two specimens. The main strength parameters obtained in such tests are reported in Table 3 and include: tensile and compression strength of bricks (\(f_{bt}\),\({ }f_{bc}\)); tensile and compression strength of mortar (\(f_{mt}\),\({ }f_{mc}\)); tensile strength, cohesion and friction coefficient of masonry joints (\(f_{jt}\),\({ }c_{j}\),\({ }\phi\)) and masonry compression strength (\(f_{c}\)).
Detailed mesoscale models of the two masonry panels were developed and validated in [41] using a Young’s modulus \(E_{b} = 3000MPa\), a Poisson’s ratio υ = \(0.15\) and a density of \(19{\text{kN}}/{\text{m}}^{3}\) for the solid elements and the mechanical parameters for the nonlinear interfaces in Table 4. The same mesoscale mechanical properties used in [41] are considered in this study to calibrate the macromodel according to the procedure described in Sect. 3. The resulting material parameters of the macroscale description are evaluated according to [28] and [50] and are summarised in Table 5. Regular 6 × 8 and 6 × 12 meshes of 20-noded solid elements, with edge size approximately of 150 mm and 27 integration points have been adopted in the analyses for the Short Wall and the Tall Wall, respectively.
Nonlinear dynamic simulations representing monotonic and cyclical loading conditions have been performed on the two macroscale models up to the ultimate displacement of 12 mm for the Tall Wall and 6 mm for the Short Wall. The results of the numeric analyses are reported in Fig. 19, where they are compared against the experimental curves. The monotonic numerical predictions (dashed lines in Fig. 19) fit well the envelope of the experimental responses. In particular, the proposed model provides a good prediction of the peak and residual strengths of the Short Wall (Fig. 19a) and the ultimate strength of the Tall Wall (Fig. 19b). The deformed shapes at the last step of the monotonic analyses showing von Mises equivalent stresses are reported in Fig. 20. A marked shear failure mechanism for the Short Wall and a flexural rocking mechanism for the Tall Wall can be noted in the two figures, which is consistent with the experimental observations. The results of the cyclic analyses (continuous lines in Fig. 19) are in a good agreement with the experimental results, confirming the ability of the proposed model to simulate unloading/reloading stiffness degradation and the different hysteretic loops characteristics corresponding to the flexural rocking failure of the Tall Wall, and the shear failure of the Short Wall. In the case of the Short Wall, some differences can be noted between the numerical and experimental results, after 4 mm lateral displacement (approximately 2 times the peak-load displacement), where the macromodel underestimates the amplitude of the hysteretic loops if compared to the experimental findings (Fig. 21).
5.3 Out-of-plane response of masonry panels
The ability of the proposed macroscale modelling strategy to simulate the out-of-plane response of masonry panels has been also assessed for one-way and two-way bending conditions.
5.3.1 One-way bending
Two brick-masonry panels with 110 mm thickness and 1500 mm height, which were tested by Griffith and Lam [51] under one-way bending, have been considered for the first set of numerical-experimental comparisons. In the tests, to investigate the influence of gravity loads on the out-of-plane response of loadbearing masonry panels, one of the two wall specimens was subjected to an initial top vertical force giving rise to a uniform precompression of 0.15 MPa. After this initial loading stage, a line load uniformly distributed along the wall length was cyclically applied at the mid-height with increasing magnitude up to failure. The top end of each wall was connected to a stiff steel frame preventing horizonal out-of-plane displacements [51]. Material tests were performed on masonry samples leading to the evaluation of a Young’s modulus of 9400 MPa, a tensile strength of 0.49 MPa and compression strength equal to 3.4 MPa for the masonry material.
Macroscale models have been developed to simulate the two wall specimens. The mesoscale masonry characteristics for the walls which, according to the proposed modelling strategy, are required to determine macroscale material properties, have been estimated considering the results from the material tests and by fitting the experimental responses of the two panels by a detailed mesoscale description. The parameters for nonlinear interface elements of the calibrated mesoscale model are reported in Table 6. The elastic properties of the macroscale material model are obtained by combining the elastic properties of the solid and nonlinear interface elements resulting into En = 6475 MPa and Et = 2785 MPa, while the macroscale nonlinear parameters correspond to the strength characteristics assumed for the mortar joint nonlinear interfaces (Table 6).
In the numerical analyses, a constant vertical load is applied at the top of the two wall models preventing the out-of-plane horizontal displacements and rotations but allowing the vertical displacements to represent the actual boundary conditions adopted in the physical tests. A mesh of 14 20-noded solid elements with 115 mm characteristic length has been employed in the macroscale simulations of the two walls. The numerical cyclic responses obtained with the proposed macroscale model and by a detailed mesoscale description are shown in Fig. 21, where they are compared against the experimental ultimate loads. In both cases, the macromodel provides an accurate prediction of the experimental ultimate load, showing a good agreement with the mesoscale model, both in terms of response envelope and cyclic response. The unloading–reloading stiffness degradation is well simulated showing the typical flexural hysteretic loops associated with closing and reopening of tensile cracks. The deformed shape at the peak load displaying the vertical stresses in the solid elements are shown in Fig. 22, where a good agreement can be noticed between the mesoscale and the proposed macroscale models.
5.3.2 Two-way bending
In further numerical-experimental comparisons for model validation under out-of-plane loading, the response of two masonry panels with hollow concrete blocks 390 × 190 × 100mm3 subjected to two-way bending condition has been analysed. The two walls, which correspond to specimens WII and WF tested by Gazzola et al. [52], are characterised by the same dimensions: 2800 mm height, 5000 mm length and 100 mm thickness, but different boundary conditions. Panel WII is simply supported along its perimeter, while wall WF is supported at three edges only and has a top free edge (Fig. 23). In the tests, a uniform out-of-plane pressure p (Fig. 23) was applied with increasing amplitude until failure [52] through an air-bag sandwiched between the wall and a stiff reacting frame.
Brick-masonry panels investigated by Gazzola et al. [52]
In the following, as for the previous numerical-experimental comparisons, the results of the proposed macromodel are compared with the experimental ultimate load-capacity and the numerical results obtained by a detailed mesoscale model explicitly allowing for the actual masonry bond. The homogenised parameters characterising the masonry flexural behaviour along both the horizontal and vertical directions are reported in [22] and [29]. These values are considered hereafter to calibrate both the mesoscale and macroscopic model parameters. First, the unknown parameters, needed to characterise the mesoscale model are evaluated by fitting the experimental results. Subsequently, the macromodel is calibrated considering the data available in the literature and the calibrated mesoscale model.
A Young’s modulus equal to 9400 MPa and a Poisson’s coefficient of 0.15 are adopted for the masonry blocks. The complete set of mechanical properties for the nonlinear interfaces and the mechanical macromodel parameters are reported in Tables 7 and 8, respectively. Elastic 20-noded solid elements and 16-noded nonlinear interface elements with 49 integration points are employed in the mesoscale model. In the macromodel analyses, a mesh of 400 × 400 mm 20-noded solid elements, each corresponding approximately to two blocks, is adopted. For each model, 27 or 125 integration points within each element are considered. The model WII and WF require 1620 and 1806 degrees of freedom, while the mesoscale models with 175 solid elements is characterised by 10,500 degrees of freedom.
The failure mechanisms obtained by the mesoscale models are reported in Fig. 24. In the case of wall WI, a large horizontal crack is observed in the middle of the panel, while sliding develops along the panel diagonals and close to the corners. In the case of panel WF, a vertical crack forms at the top-centre of the panel, starting at the free edge and two diagonal cracks develop from the centre to the two bottom corners of the panel. These mechanisms are coherent to what observed experimentally and predicted numerically by other authors [22, 29].
The numerical responses of the mesoscale and macroscale models, expressed as a function of the maximum out-of-plane displacement versus the applied pressure (p), are shown in Fig. 25. A good agreement is observed between the macro and mesoscale models, both in terms of initial lateral stiffness and ultimate load. After the peak load, the mesoscale model shows a more brittle behaviour than the macromodel, due to the higher concentration of deformation at the interfaces (Fig. 25a). Finally, it is possible to notice that the use of a different number of integration points leads to very similar numerical predictions.
The ultimate deformed shapes of the macromodel (with 27 integration points) are reported in Figs. 26 and 27 for panels WII and WF, respectively. Comparing the results shown in Figs. 2627 and 24, it is possible to conclude that the proposed model is capable of simulating the two-way out-of-plane response of brick-masonry panels with very good accuracy also when using rather coarse meshes and a limited number of integration points per element.
Finally, in Fig. 28, the computational performance of the proposed masonry macroscale modelling strategy is assessed by comparing the computational time required for the simulation of the out-of-plane response of panel WII and panel WF against the time requested by the detailed mesoscale model. As shown in the figure, at 10 mm displacement the macroscale model requires 8.7% and 11.7% of the computational time needed by the mesoscale description for the WF and WII panels, respectively. Considering the entire displacement range, the time required by the macroscale model is shorter than 15% of the time required by the mesoscale simulations. These results confirm superior efficiency of the proposed macroscale modelling strategy.
6 Conclusions
This paper presents a novel macroscale material description for nonlinear FE simulations of brick/block masonry structures. A two-scale mechanical description is proposed, where a continuum strain–displacement field describes the material at the macroscopic level, while separate internal layers allow for the 3D anisotropic mesostructure of the material. The response parameters are transferred from the macroscopic to the local level and vice versa at each integration point of the domain. The nonlinear material behaviour is defined at the level of the sub-local layers enabling the use of different constitutive laws for each main material direction, which are calibrated according to the specific masonry bond and the characteristics of units and mortar joints. The use of local interface element kinematics enables an accurate representation of typical complex cracking and damage mechanisms of brick/block masonry associated with opening/closing of tensile cracks and shear sliding.
The proposed masonry material model guarantees enhanced computational efficiency compared to detailed mesoscale models, while leading to accurate response predictions for brick/block masonry walls subjected to in-plane and out-of-plane monotonic as well as cyclic loading conditions. Compared to previous masonry macroscale descriptions, the proposed approach requires simple calibration of the model material parameters, and it enables an effective representation of masonry anisotropy by using different material characteristics along the main material directions which are directly linked to the properties of the constituents (e.g. units and mortar joints) and the masonry bond. This paves the way for an effective use of the proposed approach for detailed simulations of realistic large brick/block masonry structures subjected to extreme loading conditions, including earthquakes.
References
Jaiswal K, Wald D, Porter K (2010) A global building inventory for earthquake loss estimation and risk management. Earthq Spectra 26(3):731–748
Tomaževič M (1999) Earthquake-resistant design of masonry buildings
Lourenço PB (2002) Computations on historic masonry structures. Prog Struct Mat Eng 4(3):301–319
Roca P, Cervera M, Gariup G (2010) Structural analysis of masonry historical constructions Classical and advanced approaches. Arch Comput Methods Eng. 17(3):299–325
D’Altri AM, Sarhosis V, Milani G, Rots J, Cattari S, Lagomarsino S, ... & de Miranda S (2019) Modeling strategies for the computational analysis of unreinforced masonry structures: review and classification Arch Comput Methods Eng 1–33
D’Altri AM, de Miranda S, Castellazzi G, Sarhosis V (2018) A 3D detailed micro-model for the in-plane and out-of-plane numerical analysis of masonry panels. Comput Struct 206:18–30
Petracca M, Pelà L, Rossi R, Zaghi S, Camata G, Spacone E (2017) Micro-scale continuous and discrete numerical models for nonlinear analysis of masonry shear walls. Constr Build Mater 149:296–314
Lourenço PB, Rots JG (1997) Multisurface interface model for analysis of masonry structures. J Eng Mech 123(7):660–668
Gambarotta L, Lagomarsino S (1997) Damage models for the seismic response of brick masonry shear walls Part I: the mortar joint model and its applications. Earthq Eng Struct Dyn 26(4):423–439
Oliveira DV, Lourenço PB (2004) Implementation and validation of a constitutive model for the cyclic behaviour of interface elements. Comput Struct 82(17–19):1451–1461
Alfano G, Sacco E (2006) Combining interface damage and friction in a cohesive-zone model. Int J Numer Meth Eng 68(5):542–582
Sacco E, Toti J (2010) Interface elements for the analysis of masonry structures. Int J Comput Methods Eng Sci Mech 11(6):354–373
Dolatshahi KM, Aref AJ (2011) Two-dimensional computational framework of meso-scale rigid and line interface elements for masonry structures. Eng Struct 33(12):3657–3667
Macorini L, Izzuddin BA (2011) A non-linear interface element for 3D mesoscale analysis of brick-masonry structures. Int J Numer Meth Eng 85(12):1584–1608
Macorini L, Izzuddin BA (2013) Nonlinear analysis of masonry structures using mesoscale partitioned modelling. Adv Eng Softw 60:58–69
Minga E, Macorini L, Izzuddin BA (2018) Enhanced mesoscale partitioned modelling of heterogeneous masonry structures. Int J Numer Meth Eng 113(13):1950–1971
Hart R, Cundall PA, Lemos J (1988) Formulation of a three-dimensional distinct element model-Part II mechanical calculations for motion and interaction of a system composed of many polyhedral blocks. Int J Rock Mech Min Sci Geomech (Pergamon) 25(3):117–125
Lemos JV (2007) Discrete element modeling of masonry structures. Int J Archit Herit 1(2):190–213
Chisari C, Macorini L, Izzuddin BA (2021) Mesoscale modelling of a masonry building subjected to earthquake loading. J Struct Eng 147:04020294
Tubaldi E, Macorini L, Izzuddin BA (2018) Three-dimensional mesoscale modelling of multi-span masonry arch bridges subjected to scour. Eng Struct 165:486–500
Pelà L, Cervera M, Roca P (2013) An orthotropic damage model for the analysis of masonry structures. Constr Build Mater 41:957–967
Lourenço PB (2000) Anisotropic softening model for masonry plates and shells. J Struct Eng 126(9):1008–1016
Pietruszczak S, Niu X (1992) A mathematical description of macroscopic behaviour of brick masonry. Int J Solids Struct 29(5):531–546
Gambarotta L, Lagomarsino S (1997) Damage models for the seismic response of brick masonry shear walls Part II: the continuum model and its applications. Earthq Eng Struct Dyn 26(4):441–462
Chisari C, Macorini L, Izzuddin BA (2020) Multiscale model calibration by inverse analysis for nonlinear simulation of masonry structures under earthquake loading Int J Multiscale Comput Eng
Casolo S (2009) Macroscale modelling of microstructure damage evolution by a rigid body and spring model. J Mech Mater Struct 4(3):551–570
Casolo S, Milani G (2010) A simplified homogenization-discrete element model for the non-linear static analysis of masonry walls out-of-plane loaded. Eng Struct 32(8):2352–2366
Caliò I, Marletta M, Pantò B (2012) A new discrete element model for the evaluation of the seismic behaviour of unreinforced masonry buildings. Eng Struct 40:327–338
Pantò B, Cannizzaro F, Caliò I, Lourenço PB (2017) Numerical and experimental validation of a 3D macro-model for the in-plane and out-of-plane behavior of unreinforced masonry walls. Int J Archit Herit 11(7):946–964
Pantò B, Caliò I, Lourenço PB (2018) A 3D discrete macro-element for modelling the out-of-plane behaviour of infilled frame structures. Eng Struct 175:371–385
Addessi D, Sacco E, Paolone A (2010) Cosserat model for periodic masonry deduced by nonlinear homogenization. Eur J Mech-A/Solids 29(4):724–737
Geers M, Kouznetsova VG, Brekelmans WAM (2003) Multiscale first-order and second-order computational homogenization of microstructures towards continua. Int J Multiscale Comput Eng 1(4):371–386
Massart TJ, Peerlings RHJ, Geers MGD (2007) An enhanced multi-scale approach for masonry wall computations with localization of damage. Int J Numer Meth Eng 69(5):1022–1059
Oliver J, Caicedo M, Roubin E, Huespe AE, Hernández JA (2015) Continuum approach to computational multiscale modeling of propagating fracture. Comput Methods Appl Mech Eng 294:384–427
Petracca M, Pelà L, Rossi R, Oller S, Camata G, Spacone E (2017) Multiscale computational first order homogenization of thick shells for the analysis of out-of-plane loaded masonry walls. Comput Methods Appl Mech Eng 315:273–301
Trovalusci P, Masiani R (2003) Non-linear micropolar and classical continua for anisotropic discontinuous materials. Int J Solids Struct 40(5):1281–1297
Bacigalupo A, Gambarotta L (2011) Non-local computational homogenization of periodic masonry. Int J Multiscale Comput Eng 9(5):565–578
De Bellis ML, Addessi D (2011) A Cosserat based multi-scale model for masonry structures. Int J Multiscale Comput Eng 9(5):543–563
Leonetti L, Fantuzzi N, Trovalusci P, Tornabene F (2019) Scale effects in orthotropic composite assemblies as micropolar continua: a comparison between weak-and strong-form finite element solutions. Materials 12(5):758
Tuna M, Trovalusci P (2020) Scale dependent continuum approaches for discontinuous assemblies:‘explicit’and ‘implicit’non-local models. Mech Res Commun 103:103461
Minga E, Macorini L, Izzuddin BA (2018) A 3D mesoscale damage-plasticity approach for masonry structures under cyclic loading. Meccanica 53(7):1591–1611
Jirásek M (2000) Comparative study on finite elements with embedded discontinuities. Comput Methods Appl Mech Eng 188(1–3):307–330
Izzuddin BA (1991) Nonlinear dynamic analysis of framed structures, Imperial College London (University of London)
Grassl P, Rempling R (2008) A damage-plasticity interface approach to the meso-scale modelling of concrete subjected to cyclic compressive loading. Eng Fract Mech 75(16):4804–4818
Chisari C, Macorini L, Amadio C, Izzuddin BA (2018) Identification of mesoscale model parameters for brick-masonry. Int J Solids Struct 146:224–240
van der Pluijm R (1992) Material properties of masonry and its components under tension and shear. 6th Canadian Masonry Symposium, 15–17 June, Saskatoon, Canada, 1992
van der Pluijm R (1993) Shear behaviour of bed joints. 6th North American Masonry Conference, 6–9 June, Philadelphia, Pennysylvania, USA
Vermeltfoort AT, Raijmakers TMJ (1993) Deformation controlled meso shear tests on masonry piers–Part 2 Draft Report, Department of BKO, TU Eindhoven
Anthoine A, Magonette G, Magenes G (1995) Shear-compression testing and analysis of brick masonry walls. In" Proceedings of the 10th European conference on earthquake engineering, vol 3, pp 1657–1662
Minga E, Macorini L, Izzuddin BA, Calio I (2020) 3D macroelement approach for nonlinear FE analysis of URM components subjected to in-plane and out-of-plane cyclic loading. Eng Struct 220:110951
Griffith MC, Lam NTK, Wilson JL, Doherty K (2004) Experimental investigation of unreinforced brick masonry walls in flexure. J Struct Eng 130(3):423–432
Gazzola EA, Drysdale RG and Essawy AS (1985) Bending of concrete masonry walls at different angles to the bed joints In JG Borchelt and John H Matthys (Eds) Proceedings of the Third North America Masonry Conference. Arlington, Texas: University of Texas at Arlington Paper 27
Acknowledgements
The first author gratefully acknowledges support from the Marie Skłodowska-Curie Individual fellowship under Grant Agreement 846061 (Project Title: Realistic Assessment of Historical Masonry Bridges under Extreme Environmental Actions, "RAMBEA", https://cordis.europa.eu/project/id/846061.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: Damage-plasticity formulation
Appendix 1: Damage-plasticity formulation
The interface model proposed and detailed in [41] is adopted in the present work at the local level, where it is used to link the local IL strains to the corresponnding stresses, as defined in Eq. (3) and Eqs. (4), denoted here by \({\mathbf{s}} = \left[ {\begin{array}{*{20}c} {\sigma} & {\tau_{1} } & {\tau_{2} } \\ \end{array} } \right]^{T}\) and \({\mathbf{d}} = \left[ {\begin{array}{*{20}c} \varepsilon & {\gamma_{1} } & {\gamma_{2} } \\ \end{array} } \right]^{T}\). The first components of the two vectors represent the normal strain and stress, while the second and third components represent the shear components along the local IL directions defined by the local reference system, as illustrated in Fig.
29.
A standard decomposition between elastic and plastic deformations \({\mathbf{d}} = {\mathbf{d}}_{e} + {\mathbf{d}}_{p}\) is assumed and the concept of effective stresses \({\tilde{\mathbf{s}}} = {\mathbf{E}}_{0} \left( {{\mathbf{d}} - {\mathbf{d}}_{p} } \right)\) is introduced, where \({\mathbf{E}}_{0}\) is the elastic matrix. The effective stresses represent the physical stress developing at the undamaged part of the element. The nominal stresses are evaluated from the effective stress by multiplying the damage matrix, as follows:
Equation (30) reports the elastic matrix which is assumed diagonal with \({\text{E}}_{n}\) and \({\text{E}}_{t}\) the equivalent normal and shear deformation moduli of masonry. in Eq. (32) shows the damage matrix \({\mathbf{D}}\) which defines an anisotropic damage state, containing \({\text{D}}_{n}\) the damage variable in tension/compression and \({\text{D}}_{t}\) the damage variable in shear. Zero values of these variables represent the undamaged material state.
The plastic yield surface (Fig. 29) is composed of three surfaces, (\(F_{t}\), \(F_{c}\), \(F_{s}\)) respectively associated to the tensile (mode I), shear (mode II) and compression (mode III) failure mode, defined in Eqs. (33–35). In the expressions, \(f_{t}\) and \(f_{c}\) are the tensile and compression material strengths, \(\phi\) the friction angle and \(q\) a linear hardening variable, ranging from 0 (initial value) to the limit value \(q_{lim} = \frac{c}{tan\left( \phi \right)} - f_{t}\). In Eq. (33), \(c^{\prime} = c\), with c the material cohesion, if \(q \le q_{lim}\) and \(c^{\prime} = c + \left( {q - q_{lim} } \right)tan\left( \phi \right)\) if \(q > q_{lim}\).
The variable \(q\) allow the control of the normal permanent strain in tension through the definition of a model parameter \(\eta = \varepsilon_{0} /\varepsilon_{u}\), where \(\varepsilon_{u}\) is the deformation at the beginning of the unloading and \({\varepsilon }_{0}\) is the residual deformation (0b).
With the increase the hardening parameter \(q\), the surface \({\text{F}}_{t} \) reduces until becoming a point when \(q\) reaches the value \(q_{lim}\). On the other hand, \({\text{F}}_{s}\) increases as represented in Fig. 29. Two associated plastic flows are associated to \({\text{F}}_{t}\) and \({\text{F}}_{c}\) while, in shear, a plastic potential (\({\text{G}}_{s}\)), with the same expression of \({\text{F}}_{s}\) and \(\phi_{g}\) in replacing the friction angle \(\phi\) is considered in order to take into account the effects of masonry dilatancy.
The three plastic works (\({\text{W}}_{pt} , {\text{W}}_{pc} , {\text{W}}_{ps}\)) of the effective stress by the plastic deformation flow through the surfaces \(F_{t}\), \(F_{c}\) and \(F_{s}\), rule the evolution of the damage parameters. In particular, three ratios are defined: \({\text{r}}_{t} = {\text{W}}_{pt} /{\text{G}}_{t}\), \({\text{r}}_{c} = {\text{W}}_{pc} /{\text{G}}_{c}\) and \({\text{r}}_{s} = {\text{W}}_{ps} /{\text{G}}_{s}\) where, \({\text{G}}_{t}\), \({\text{G}}_{c}\) and \({\text{G}}_{s}\) are the fracture energy in traction, compression and shear respectively.
The damage variable in the normal direction (\({\text{D}}_{n}\)) assumes two different expressions in relation to the sign of the normal effective stress (\(\tilde{\sigma }\)). In the case traction \({\text{D}}_{n} = {\text{D}}_{nt}\) as in Eq.(A7); in the case of compression, \({\text{D}}_{n} = {\text{D}}_{nc}\) as in Eq. (27). Two different damage variables for tension and compression in the normal direction allow the model to simulate the normal stiffness recovery in compression associated with the closing of the tensile cracking.
where the parameter \(0 \le a_{t} \le 1\) in Eq. (A7) controls the influence of the shear plastic work on the tensile damage.
The damage in shear is governed by the plastic in tension, shear and compression. It determines the residual frictional behaviour which is characterised by a residual friction factor (\(\phi_{r}\)) and zero cohesion.
The value of Dt is given by:
where:
The parameter \(0 \le a_{s} \le 1\) controls the influence of the tensile plastic work on the shear damage. The parameter \(q_{s}\) depends on the sign of the normal stress: \(q_{s} = 0\) if \(\sigma \le q_{lim}\); \(q_{s} = \left( {q - q_{lim} } \right)\tan \phi\) if \(\sigma > q_{lim}\). Finally, \(r_{t}^{*} = r_{t} \left( {2 - r_{t} } \right)\), \(r_{s}^{*} = r_{s} \left( {2 - r_{s} } \right)\) and \(r_{c}^{*} = r_{c} \left( {2 - r_{c} } \right)\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pantò, B., Macorini, L. & Izzuddin, B.A. A two-level macroscale continuum description with embedded discontinuities for nonlinear analysis of brick/block masonry. Comput Mech 69, 865–890 (2022). https://doi.org/10.1007/s00466-021-02118-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-021-02118-x