Residual stresses in gas tungsten arc welding: a novel phase-field thermo-elastoplasticity modeling and parameter treatment framework

Abstract

The fusion welding process of metallic components, such as using gas tungsten arc welding (GTAW), is often accompanied by detrimental deformations and residual stresses, which affect the strength and functionality of these components. In this work, a phase-field model, usually used to track the states of phase-change materials, is embedded in a thermo-elastoplastic finite element model to simulate the GTAW process and estimate the residual stresses. This embedment allows to track the moving melting front of the metallic material induced by the welding heat source and, thus, splits the domain into soft and hard solid regions with a diffusive interface between them. Additionally, temperature- and phase-field-dependent material properties are considered. The J2 plasticity model with isotropic hardening is considered. The coupled system of equations is solved in the FE package FEniCS, whereas two- and three-dimensional initial-boundary-value problems are introduced and the results are compared with reference data from the literature.

1 Introduction

In fusion welding processes, two or more metallic parts are permanently joined by applying a suitable heat source, e.g. arc, laser, or electron beam sources. Such a way of joining is of particular importance, especially for metallic structures, such as pressure vessels and piping systems. Due to the highly-localized nature of the heat source, the highest temperatures occur in the zone near the welding torch and decrease with increasing distance from the weld centerline. As a result, welded parts undergo higher nonuniform thermal expansion followed by contraction due to the heating-cooling cycle, which in turn leads to the generation of plastic deformations within and around the weld zone. The expansion and contraction result in high-level tensile residual stresses and distortions when the weld structure cools to the ambient temperature. The presence of weld-induced tensile residual stresses has detrimental effects on load-carrying capacity, fracture toughness, stress corrosion resistance, and fatigue crack initiation and propagation when subjected to cyclic loading [2, 11, 14, 54, 66]. Therefore, understanding and predicting weld-induced residual stresses and deformations in the welded structures are of high significance and should be accounted for in the early design stages to avoid possible reductions in their performance and reliability.

1.1 Thermo-elastoplastic models of residual stresses computation

The presence of residual stresses in the welded structures is complex to be only calculated by performing experiments or applying analytical formulations. For instance, the experimental measurements of residual stresses and distortions involve some shortcomings related to the complexity, cost, and difficulty of obtaining complete and detailed values. For these reasons and due to the advancements in numerical techniques and computational capacities, researchers have focused on developing and implementing numerical models. The developed models are then validated and calibrated with the experimental measurements using, e.g., the Finite Element Method (FEM). These FEM approaches have shown acceptable capabilities to perform computational analyses and to predict the residual stresses for different fusion welding processes in multi-dimensional space, e.g., [12, 22, 27, 79, 80, 110, 116,117,118]. Other works have intensively studied the effect of finite and small strain theory on the numerical results of the welding deformations, e.g., [28, 31, 76, 116].

In welding computational analysis, it is a common practice to use temperature-dependent material properties. However, at high temperatures, the complete temperature-dependent properties for many materials could be very difficult to measure and are not available in the literature [42, 115]. The parts being welded undergo complex multi-physical processes that involve heat transfer, material flow, and other metallurgical changes. As a result of these coupled phenomena, the physical and chemical properties of the final welded parts are usually changed. Therefore, the need for considering the dependency of material properties on temperature has been intensively investigated in the literature, where assumptions and simplification approaches could also be found. In most cases, numerical modeling approaches related to welding are evaluated by their accuracy and performance to predict the transient temperature field and the welding-induced residual stresses and permanent deformations [7, 8, 13, 15, 42, 55, 61, 67, 84, 115]. For instance, Little and Kamtekar [67] have found that varying the thermal properties, namely the heat capacity and the thermal conductivity, highly influence the computed temperature fields in the weld and its surrounding regions. Zhu and Chao [115] performed an analysis on welding of an aluminum plate using three different sets for the thermo-mechanical properties. The study showed that the temperature distribution, residual stresses, and distortions can be predicted with sufficient accuracy by taking constant room-temperature properties, except for the yield stress. Armentani et al. [8] showed how the residual stresses of butt-welded joints can be affected by thermal properties and concluded that varying the thermal conductivity has a significant influence on the calculated residual stresses. Barroso et al. [13] applied a simplified material model in their FEM simulations and found that the residual stresses in the longitudinal direction can be predicted with reasonable accuracy when the mechanical properties are taken as constant values. Joshi et al. [55] performed a FE analysis of two overlapping beads, where the chemical compositions of the base and deposited metal were used in the Weldware package to derive the equivalent material properties in the weld pool. Bhatti et al. [16] investigated the influence of thermo-mechanical material properties of various grades of steel on the predicted residual stresses and distortions. They found that considering constant properties, except for the yield stress, can provide good results for residual stresses. Additionally, they concluded that acceptable angular distortion can be achieved when the yield stress, the heat capacity, and the thermal expansion coefficient are functions of temperature. Similarly, Perić et al. [84] investigated the influence of the temperature-dependent properties on the FE model outputs, and suggested that using constants properties, except for the yield stress, is suitable for the prediction of the deformations. Moreover, temperature-dependent properties can be used for the assessment of the temperature distributions, the heat-affected zones, and the residual stresses. Kong and Kovacevi [61] reported that assigning a small value of the elastic modulus at the weld pool for temperatures exceeding the melting point can reduce the computational time and increase the solution convergence rate. Anca et al. [7] studied the melting-solidifying behavior on the residual stresses calculation during the liquid/solid and solid/liquid phase changes. For the mechanical analysis, the weld pool was assumed as a soft region with no further changes in the material properties above a specific cut-off or zero-strength temperature. He et al.[42] introduced an additional temperature-dependent internal state variable to capture the irreversible welding interfaces and accounted for the effects of the melting state on the thermo-mechanical properties during the lap joint welding process of two sheets. The aforementioned research works showed the importance of considering state- or temperature-dependent material parameters in the FE simulations to get reasonable numerical results, as for the residual stresses. They also showed that these considerations are associated with many challenges concerning the parameter values measurement or estimation. This leads to the conclusion that further investigations and reduction of model complexity are badly needed to achieve more accurate numerical computation of, e.g., residual stress calculations, at moderate efforts and assumptions.

While utilizing the phase-field method to capture the melting of metal during welding, the underlying work considers the phase-change effects in both the thermal and the mechanical analysis. In particular, it considers phase-field-dependent material properties, such that the model domain is divided into a hard (unmelted) and a soft (melted) region. These regions are separated by a diffusive transition interface, where the material properties can smoothly change. Hence, soft material properties are assigned to the fully melted region in the weld pool, whereas hard material properties are assigned to the material below the solidus temperature.

1.2 Phase-field modeling of thermally-induced phase transition

In the literature, several approaches exist to describe the process of phase transition of phase-change materials, such as during melting, and to determine the position of the corresponding interface between melted and unmelted phases. These methods, such as the level-set [81, 104], the volume-of-fluid [51], and the phase-field method (PFM) allow to describing the phase change within continuum mechanical framework as needed in the current research work. The developments and uses of the PFM have been discussed by many research groups [18, 23, 34, 58, 98, 109, 111, 114]. In this, the PFM is originally applied in the mechanics of materials to describe the complex microstructural evolution of the interfaces in non-equilibrium states [18, 58, 59, 98].

Here, we utilize the energy-based PFM to describe the melting of metals as a phase-change phenomenon between a hard state for temperatures below the melting point and a soft state for temperatures above the melting point, whereas the thermal energy during welding is the driving force for the phase change. To this, a phenomenological phase-field variable is used to indicate the state of the metal, which allows for a diffusive state change across the interface between the two states. Unlike the sharp-interface approaches for describing the phase-change materials, the diffusive-interface approaches allow a much easier and stable FE implementation, whereas the finite thickness of the interface has its origin in the lower-scale phase-change description, see, e.g., [18, 86]. In this regard, the PFM is applied in many research works to describe material phase change on the continuum scale, see, e.g., [101, 102, 112,113,114]. In this case, the macroscopic interface thickness, which is dictated by the FE mesh size, could be orders of magnitude larger than the physical interface thickness. However, studies related to the variation of the interface thickness parameter in the PFM on the macroscale show that below a certain limit, decreasing the value of this parameter will have an insignificant effect on the overall solution or the interface position [19, 103]. To this, references and overview of the origin of this method in the context of continuum mechanics can be found in, e.g., [57] and [102, 103]. Apart from PFM of phase-change materials, the PFM has recently been intensively applied within fracture mechanics for solids as well as for porous media as in, e.g., [3, 5, 44,45,46, 48, 82, 83], among others. It is also worth mentioning that several research works have recently employed the PFM to study the microstructure evolution, such as the investigation of the growth of the columnar grains accompanied by the solidification process in welding and additive manufacturing process, for example, the works done in [36, 63, 90, 107, 108]. Therefore, the underlying modeling framework together with the developed algorithms will be implemented in future works in the context of modeling direct metal laser melting (DMLM) in the additive manufacturing process. Additionally, future works will address the possible embedment of machine learning approaches, like in [35, 49, 50, 60, 99, 100], to capture the microscopic thermo-mechanical processes in the continuum modeling.

1.3 Highlights and content overview

In summary, the main objective of this work is to gain new insight into the challenging coupled inelastic thermo-mechanical processes that occur during gas tungsten arc welding (GTAW) via applying an advanced numerical study and comparison with experimental and numerical data from the literature. The proposed modeling methodology allows an accurate estimation of the spatial and temporal distribution of the residual stresses and the permanent plastic deformations. This approach includes: (1) Presenting and implementing a continuum mechanical framework with unified kinematics of the melted and unmelted phases of the solid metal. (2) Applying a thermodynamically consistent phase-field approach to describe study the effect of the phase transition during melting/solidification processes on the size and the shape of the weld pool. (3) Proposing a new ansatz for the phase-field-dependent material parameters, which reduces the modeling complexity and gives a realistic description of the properties’ change across the diffusive interface. (4) Investigating two different plasticity models and describing their implementation in the open-access/open-source FEniCS package to solve two- and three-dimensional initial-boundary-value-problems (IBVPs).

To give an overview, Sect. 2 describes the essential kinematics and the formulation of the coupled phase-field thermo-elastoplasticity within a thermodynamic framework. In Sect. 3, the material properties are properly formulated to be functions of the temperature field as well as the phase-field variable, so that their values change smoothly across the diffusive interface. The finite element implementation is discussed in Sect. 4, which includes writing the weak formulation and discussing the discretization with mixed finite elements and the time-stepping via the backward finite difference method. Two- and three-dimensional numerical examples are presented in Sect. 5, where the proposed models are implemented to solve IBVPs. These implementations allow to verify and validate the numerical model through comparison with reference data from the literature. This is followed by the conclusions in Sect. 6, where also a summary and an outlook of future works are presented. As the focus of the current work is to develop a themomechanical model for the prediction of residual stresses, currently small strain theory is considered and geometrical nonlinearity will be involved in future works.

2 Mathematical formulations of the phase-field thermo-elastoplasticity model

In this work, a coupled phase-field thermo-elastoplasticity problem is considered for the modeling of the GTAW welding process and the occurring residual stresses, where the material modeling is addressed within a thermodynamically consistent framework. The three primary fields considered in the following treatment are functions of the space ${\mathbf {x}}$ and time t. These are the vector-valued displacement field ${\mathbf {u}}={\mathbf {u}}({\mathbf {x}},\,t)$, the scalar-valued temperature field $\theta =\theta ({\mathbf {x}},\,t)$, and the scalar-valued phase-field variable $\phi =\phi ({\mathbf {x}},\,t)$. A brief description of the phase-field modeling of temperature-induced melting of metals is presented in (“Appendix A”). However, in the following treatment, the phase-field evolution equation along with the other constitutive formulations are derived based on the restrictions imposed by the Clausius–Duhem inequality.

2.1 Kinematics of the thermo-mechanical problem

The formulation of the thermo-elastoplasticity in the current contribution is restricted to the small deformations assumption. Therefore, the total strain tensor ${\varvec{\varepsilon }}$ can be expressed in terms of the displacement gradient and its transpose as

$$\begin{aligned} {\varvec{\varepsilon }}:=\frac{1}{2}\,(\mathrm {grad}\,{\mathbf {u}}+\mathrm {grad}^{\mathrm {T}}{\mathbf {u}}) \,. \end{aligned}$$

(1)

For the thermo-elastoplasticity treatment, ${\varvec{\varepsilon }}$ can additively be decomposed into an elastic strain tensor ${\varvec{\varepsilon }}^\text {e}$ and an inelastic (plastic) strain tensor ${\varvec{\varepsilon }}^\text {p}$ as

$$\begin{aligned} {\varvec{\varepsilon }}= {\varvec{\varepsilon }}^\text {e} +{\varvec{\varepsilon }}^\text {p}\,. \end{aligned}$$

(2)

2.2 Constitutive formulations of the phase-field thermo-mechanical problem

In analogy to the work presented in [4] in the context of gradient thermo-plasticity, the focus in the constitutive formulations will be on the following set of independent state variables

$$\begin{aligned}&\mathcal {V} =\{{\varvec{\varepsilon }}-{\varvec{\varepsilon }}^\text {p},\, \alpha ,\, \theta ,\, \text {grad}\,\theta ,\,\phi ,\, \text {grad}\,\phi \}, \end{aligned}$$

(3)

where $\alpha$  is the equivalent plastic strain, which is chosen to characterize the state of the material hardening and $\phi$ is the phenomenological phase-field variable (see, “Appendix A”). Therefore, the free energy function $\varPsi \,(\mathcal {V})$ for the coupled problem can be expressed as

$$\begin{aligned}&\varPsi \,(\mathcal {V}):= \varPsi ^\text {e}+\varPsi ^\text {p}+\varPsi ^\text {e-th}+\varPsi ^\phi +\varPsi ^\text {th}\nonumber \\&\quad \quad \text{ with }\quad \left\{ \begin{array}{ll} \varPsi ^\text {e}=\frac{1}{2}\mathrm {K}\,{e}^2 +\mu \,{\bar{\varvec{\varepsilon }}}^\text {e} \cdot {\bar{\varvec{\varepsilon }}}^\text {e}\,, \\ \varPsi ^\text {p}=\frac{1}{2}H\alpha ^2 \,, \\ \varPsi ^\text {e-th}= -3\mathrm {K}\, \alpha _{\theta }\, e (\theta -\theta _{\text {ref}})\, \,, \\ \varPsi ^{\phi }= f(\phi , \theta )+ \frac{l^2}{2}|\text {grad}\,\phi |^2\, \,,\\ \varPsi ^\text {th}=c_\varepsilon \Big [(\theta -\theta _\text {ref})-\theta \ln \Big ({\frac{\theta }{\theta _\text {ref}}}\Big )\Big ] \,. \end{array}\right. \end{aligned}$$

(4)

The above definitions of the free energy densities (per unit volume) can be found, e.g., in [4, 6, 78, 95]. In this, $\varPsi ^\text {e}$ is the elastic stored energy, $\varPsi ^\text {p}$ is the plastic contribution due to hardening, $\varPsi ^\text {e-th}$ is the energy term due to thermoelastic coupling, $\varPsi ^{\phi }$ is the phase-field contribution, and $\varPsi ^\text {th}$ is the purely thermal energy. H is the linear hardening modulus, which is taken $(H \approx 0.01E)$ in analogy to [92], $c_\varepsilon$ is the volumetric heat capacity, and $\mathrm {K}$, $\mu$ are the bulk and shear moduli, respectively. Moreover, $e = {{\,\mathrm{tr}\,}}{{\varvec{\varepsilon }}}^\text {e}$ and ${\bar{\varvec{\varepsilon }}}^\text {e}=({{\varvec{\varepsilon }}}^\text {e}- \frac{1}{3}e\,{\mathbf {I}})$ are, respectively, the trace and the deviatoric (isochoric) part of the elastic strain tensor ${\varvec{\varepsilon }}^\text {e}$. Furthermore, $\alpha _{\theta }$ is the temperature-dependent coefficient of linear expansion, $\theta _{\text {ref}}$ is a specified reference temperature, and ${\mathbf {I}}$ is the identity tensor. In connection with the temperature-related phase change of the metallic material, the phase-field related energy function $\varPsi ^{\phi }$ is expressed in terms of a bulk free energy contribution $f(\phi , \theta )$ and the interfacial energy terms. This can further be expressed, in analogy to [18], as

$$\begin{aligned}&\varPsi ^{\phi }(\phi ,\theta ) = W\,g(\phi ) + \rho \,L\,\frac{(\bar{\theta }^M-\theta )}{\bar{\theta }^M}\,p(\phi ) \!+\! \frac{l^2}{2}|\text {grad}\,\phi |^2 ,\nonumber \!\!\!\!\!\\ \end{aligned}$$

(5)

where W, $g(\phi )$, $p(\phi )$ and $\bar{\theta }^M$ are the energy barrier height at the interface, the double-well potential, the interpolation function, and the material melting temperature, respectively. Moreover, $\rho$, L and l are, respectively, the material density, the latent heat of fusion, and the gradient-energy coefficient that affects the width of the diffusive interface. In the current work, we consider a constant reference material density at room temperature. For the heat capacity, thermal conductivity, Young’s modulus, yield stress, and thermal expansion coefficient will be either temperature- or phase-depended as discussed later in Sect. 3 and given in Table 2 and Figs. 1 and 2.

2.3 Plasticity-related response and yield functions

We proceed in the following discussion with the dissipative force fields that represent the dual fields to the internal state variables of the plastic response, i.e. ${\varvec{\sigma }}^\text {D}$ dual to ${\varvec{\varepsilon }}^\text {p}$ and $\mathrm {q}^\alpha$ dual to $\alpha$ . For the J2 plasticity with isotropic hardening, the von Mises yield criterion can be defined according to, e.g., [70, 94, 96], as

$$\begin{aligned}&\chi ({\varvec{\sigma }}, \mathrm {q}^{\alpha }, \theta ):=\frac{1}{2}\,{{\varvec{\sigma }}}^\text {D} \cdot {{\varvec{\sigma }}}^\text {D}-\frac{1}{3} {\mathrm {q}}^2 \le 0\, \qquad \text {with}\nonumber \\&{{\varvec{\sigma }}}^\text {D} = {\varvec{\sigma }}-\frac{1}{3} \,(\text {tr}\, {\varvec{\sigma }}) \,{\mathbf {I}}\qquad \text {and}\nonumber \\&\mathrm {q} = \mathrm {y}_{0}(\theta )- {\mathrm {q}^{\alpha }} \,, \end{aligned}$$

(6)

where ${{\varvec{\sigma }}}^\text {D}$, $\mathrm {q}$, and $\mathrm {y}_{0}(\theta )$ are the deviatoric part of the stress tensor, the internal stress-like dynamic variable, and the initial yield stress, respectively.

2.4 The free energy and the entropy evaluation

With the given definitions of the energy contributions in Eqs. (4) and (5), the total free energy per unit volume can now be expressed as

$$\begin{aligned} \begin{aligned} \varPsi&= \frac{\mathrm {K}}{2}\,e^2+ \mu \,{\bar{\varvec{\varepsilon }}}^\text {e} \cdot {\bar{\varvec{\varepsilon }}}^\text {e}\,\\&\quad + \frac{1}{2} H \alpha ^2 - 3\mathrm {K}\, \alpha _{\theta }\,e\, (\theta -\theta _{\text {ref}})\,\\&\quad + c_{\varepsilon } \Big [(\theta -\theta _\text {ref})-\theta \ln \Big ({\frac{\theta }{\theta _\text {ref}}}\Big )\Big ] \\&\quad + W\,g(\phi ) + \rho \,L\,\frac{(\bar{\theta }^M-\theta )}{\bar{\theta }^M}\,p(\phi ) + \frac{l^2}{2}\,|\text {grad}\,\phi |^2 \,. \end{aligned} \end{aligned}$$

(7)

The time derivative of the energy formulation, needed for the entropy inequality evaluation, can be expressed as

$$\begin{aligned}&\dot{\varPsi } = \frac{\partial \varPsi }{\partial {\varvec{\varepsilon }}^\text {e}} \cdot \dot{\varvec{\varepsilon }}\, - \frac{\partial \varPsi }{\partial {\varvec{\varepsilon }}^\text {e}} \cdot {\dot{\varvec{\varepsilon }}^\text {p}} + \frac{\partial \varPsi }{\partial \alpha } \,\dot{\alpha }+ \frac{\partial \varPsi }{\partial \theta } \,\dot{\theta } \nonumber \\&\quad + \frac{\partial \varPsi }{\partial \,\text {grad}\,\theta }\cdot \text {grad}\,\dot{\theta } + \frac{\partial \varPsi }{\partial \phi } \,\dot{\phi } + \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\cdot \text {grad}\,\dot{\phi } \,. \end{aligned}$$

(8)

Using the divergence theorem in analogy to [32], the last term in the above derivative can be reformulated as follows

$$\begin{aligned}&\frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\cdot \text {grad}\,\dot{\phi }= \mathrm {div} \Big (\dot{\phi }\,\frac{\partial \varPsi }{\partial \,\text {grad}\,\phi } \Big ) - \mathrm {div}\Big ( \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) \dot{\phi }\,.\nonumber \\ \end{aligned}$$

(9)

Following this, we rely on the 2$^{nd}$ law of thermodynamics (entropy inequality) in order to generate thermodynamically consistent constitutive formulations for the coupled problem under consideration. This inequality can be expressed in the Clausius–Duhem general representation as

$$\begin{aligned} {\varvec{\sigma }}\cdot \dot{\varvec{\varepsilon }}- \dot{\varPsi } -\eta \,\dot{\theta }-\frac{{\mathbf {q}}^\theta }{\theta } \cdot \text {grad}\,\theta \,\ge 0 \,, \end{aligned}$$

(10)

where $\eta$ and ${\mathbf {q}}^\theta$ are the entropy and the heat flux vector. Substituting the formulation in (8) into the entropy inequality (10) and applying reformulation yields

$$\begin{aligned} \begin{aligned}&\Big ({\varvec{\sigma }}-\frac{\partial \varPsi }{\partial {\varvec{\varepsilon }}^\text {e}} \Big ) \cdot \dot{\varvec{\varepsilon }}-\, \Big (\eta +\frac{\partial \varPsi }{\partial \theta } \Big ) \dot{\theta }+\, \frac{\partial \varPsi }{\partial {\varvec{\varepsilon }}^\text {e}} \cdot {\dot{\varvec{\varepsilon }}^\text {p}} \\&\quad -\, \frac{\partial \varPsi }{\partial \alpha } \,\dot{\alpha }-\, \frac{\partial \varPsi }{\partial \,\text {grad}\,\theta }\cdot \text {grad}\,\dot{\theta }\, -\, \Big [\frac{\partial \varPsi }{\partial \phi }\\&\quad -\,\mathrm {div}\Big ( \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) \Big ] \dot{\phi } -\, \mathrm {div}\Big (\dot{\phi }\, \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) - \frac{{\mathbf {q}}^\theta }{\theta } \cdot \text {grad}\,\theta \,\ge 0 \,.\nonumber \end{aligned}\\ \end{aligned}$$

(11)

The evaluation of the entropy inequality (11) towards deriving thermodynamically consistent constitutive formulations is applied following the procedure presented in [24]. In this, the fulfillment of the inequality is guaranteed if each term is greater or equal to zero. Thus, we conclude the following equilibrium relations:

$$\begin{aligned}&\varvec{\sigma } := \frac{\partial \varPsi }{\partial {\varvec{\varepsilon }}^\text {e}} = p\, {\mathbf {I}} + {{\varvec{\sigma }}}^\text {D} \quad \text {where}\nonumber \\&p:= \mathrm {K} (e -3\,\alpha _{\theta }\,(\theta -\theta _{\text {ref}})) \quad \text {and} \nonumber \\&{{\varvec{\sigma }}}^\text {D}:=2 \mu {\bar{\varvec{\varepsilon }}}^\text {e} \,, \end{aligned}$$

(12a)

$$\begin{aligned}&\eta := -\frac{\partial \varPsi }{\partial \theta } = 3\mathrm {K}\, \alpha _{\theta }\,e + c_{\varepsilon }\ln \Big ({\frac{\theta }{\theta _\text {ref}}}\Big ) + \rho \,L\frac{1}{\bar{\theta }^M}\,p(\phi )\,, \end{aligned}$$

(12b)

$$\begin{aligned}&\frac{\partial \varPsi }{\partial \,\text {grad}\,\theta } =\varvec{0}\,, \end{aligned}$$

(12c)

$$\begin{aligned}&\mathrm {div}\Big (\dot{\phi }\, \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) = 0 \,. \end{aligned}$$

(12d)

Analogous to the continuity equation in fluid mechanics, relation (12d) describes the continuity of the vector term in the parentheses. Following this, integration of (12d) over the volume of the domain and applying the Gaussian integral theorem as presented in [32] yields

$$\begin{aligned}&\int _{\varOmega } \mathrm {div}\Big (\dot{\phi }\, \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big )\,\mathrm {d}v = \int _{{\varGamma _{N_\phi }}} \Big (\dot{\phi }\, \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big )\cdot {\mathbf {n}}\,\mathrm {d}a \,, \end{aligned}$$

(13)

where ${\mathbf {n}}$ is the outward unit surface normal. The resulting equation (13) can be realized in the numerical implementation through applying the following Neumann boundary condition:

$$\begin{aligned} \frac{\partial \, \varPsi }{\partial \,\text {grad}\,\phi } \cdot {\mathbf {n}}= 0 \,. \end{aligned}$$

(14)

Additionally, the evaluation of (11) results in the following three non-equilibrium (dissipative) restrictions

$$\begin{aligned}&-\frac{{\mathbf {q}}^\theta }{\theta } \cdot \text {grad}\,\theta \, \ge 0\,, \end{aligned}$$

(15a)

$$\begin{aligned}&-\Big [ \frac{\partial \varPsi }{\partial \phi } -\,\mathrm {div}\Big ( \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) \Big ] \dot{\phi } \ge 0 \,, \end{aligned}$$

(15b)

$$\begin{aligned}&{\varvec{\sigma }}\cdot \dot{\varvec{\varepsilon }}^\text {p} - \frac{\partial \varPsi }{\partial \alpha } \,\dot{\alpha }\, \ge 0\,, \end{aligned}$$

(15c)

representing the thermal, phase change, and mechanical dissipation contributions, respectively. In the case of the thermal dissipation or the so-called Fourier’s inequality in (15a), this is related to the existence of the temperature gradient with the restriction such that the heat must flow from warm material points to colder ones [26, 62]. In this regard, the constitutive equation for the heat flux vector may be given by Fourier’s law ${\mathbf {q}}^\theta :=-\kappa \, \text {grad}\,\theta \,$.

To satisfy the dissipation inequalities in (15b) and (15c), proper evolution equations should be formulated. First, an evolution equation for the phase-field variable can be introduced by assuming the following natural proportionality [32, 71]

$$\begin{aligned} \begin{aligned} \dot{\phi } \,&\varpropto \,\,-\,\left[ \frac{\partial \varPsi }{\partial \phi } -\mathrm {div}\Big ( \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) \right] , \\ \dot{\phi }&= -M \left[ W g^\prime (\phi ) + \rho \,L\,\frac{(\bar{\theta }^M-\theta )}{\bar{\theta }^M}\,p^\prime (\phi ) - \mathrm {div}(l^2\,\text {grad}\,\phi ) \right] ,\nonumber \end{aligned}\\ \end{aligned}$$

(16)

where $M>0$ can be interpreted as the interface mobility parameter, which is discussed in “Appendix A” and expressed according to [18] in Eq. (49). It is worth mentioning here that the phase-field evolution equation can be derived based on other approaches, such that presented by Gurtin [41] and proceeded from the microforce equilibrium laws. This approach is however beyond the scope of the current work. In addition, due to the time history of the plastic deformation, the first and second terms in (15c) do not vanish [29]. The thermodynamic variable $\mathrm {q}^{\alpha }$ conjugate to $\alpha$ can be expressed as

$$\begin{aligned} \mathrm {q}^{\alpha } := -\frac{\partial \varPsi }{\partial \alpha } = -H{\alpha }\,. \end{aligned}$$

(17)

Having the latter definitions, an expression for non-negative reduced dissipation, or the so-called mechanical dissipation, given by the Clausius-Planck inequality, can be written as

$$\begin{aligned} D_\text {loc}^\text {red} := {\varvec{\sigma }}\cdot \dot{{\varvec{\varepsilon }}}^\text {p} + \mathrm {q}^{\alpha }\,\dot{\alpha } \,\ge 0 \,. \end{aligned}$$

(18)

2.5 Evolution and governing balance equations

The starting point in the derivation of the evolution equations for $\dot{\varvec{\varepsilon }}^\text {p}$ and $\dot{\alpha }$ is the application of the principle of maximum plastic dissipation, which is widely used in connection with a plasticity variational formulation [96]. In this regard, the yield surface (6) of the associative plasticity model together with the plastic dissipation relation (18) are employed to transfer the maximum plastic dissipation into a minimization problem by introducing the Lagrangean functional [29]

$$\begin{aligned}&\mathcal {P}({\varvec{\sigma }}, \mathrm {q}^{\alpha }, \dot{{\varvec{\varepsilon }}}^\text {p}, \dot{\alpha }, \theta ) = -D_\text {loc}^\text {red} +\dot{\lambda }\, \chi ({\varvec{\sigma }}, \mathrm {q}^{\alpha }, \theta ) \nonumber \\&\quad \text {subject to}\qquad \dot{\lambda }\,\chi ({\varvec{\sigma }}, \mathrm {q}^{\alpha }, \theta )=0\,, \end{aligned}$$

(19)

where $\dot{\lambda } \ge 0$ is the Lagrange (or plastic) multiplier, which enforces the restriction $\chi \le 0$ on the yield surface potential. Finally, the evolution equations can be obtained by taking the derivative with respect to ${\varvec{\sigma }}$ and $\mathrm {q}^{\alpha }$ as

$$\begin{aligned}&\frac{\partial \mathcal {P}}{\partial {\varvec{\sigma }}} = -\dot{{\varvec{\varepsilon }}}^\text {p} +\dot{\lambda }\frac{\partial \chi }{\partial {\varvec{\sigma }}} = 0\,, \end{aligned}$$

(20)

$$\begin{aligned}&\frac{\partial \mathcal {P}}{\partial \mathrm {q}^{\alpha }} = -\dot{\alpha } +\dot{\lambda }\frac{\partial \chi }{\partial \mathrm {q}^{\alpha }} = 0\,. \end{aligned}$$

(21)

Following this, the governing balance equations in their local form will be introduced. The balance of linear momentum can in general be defined as

$$\begin{aligned} \rho \ddot{{\mathbf {u}}} -\mathrm {div}\,{\varvec{\sigma }}- \varvec{b} = \varvec{0}\,, \end{aligned}$$

(22)

where $\ddot{{\mathbf {u}}}$ is the acceleration vector and $\varvec{b}$ is the body force vector, defined per unit volume. Making use of the balance of internal energy, the scalar-valued local energy balance equation can be expressed as

$$\begin{aligned} \dot{\mathcal {E}}= {\varvec{\sigma }}\cdot \dot{\varvec{\varepsilon }}-\mathrm {div}\,{\mathbf {q}}^\theta + r \,. \end{aligned}$$

(23)

In this, $\dot{\mathcal {E}}$ and r are the internal energy rate and the internal energy supply per unit volume. A relationship between the energetically conjugate variables $\theta$ and $\eta$ is obtained via the application of Legendre transformation for the internal energy

$$\begin{aligned} \mathcal {E}= \varPsi + \theta \eta \, \quad \longrightarrow \quad \dot{\mathcal {E}}= \dot{\varPsi } + \dot{\theta }\eta + \theta \dot{\eta }. \end{aligned}$$

(24)

Recalling the reduced local dissipation relation (18), the definition of the time derivative Eq. (8) can be expressed as follows

$$\begin{aligned}&\dot{\varPsi }= {\varvec{\sigma }}\cdot \dot{{\varvec{\varepsilon }}} - D_\text {loc}^\text {red} - \eta \dot{\theta }+ \Big [\frac{\partial \varPsi }{\partial \phi } -\,\mathrm {div}\Big ( \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) \Big ] \dot{\phi }\,\nonumber \\&\quad \longrightarrow \quad \dot{\mathcal {E}}= {\varvec{\sigma }}\cdot \dot{{\varvec{\varepsilon }}} - D_\text {loc}^\text {red} + \theta \dot{\eta }\,+ \Big [\frac{\partial \varPsi }{\partial \phi } -\,\mathrm {div}\Big ( \frac{\partial \varPsi }{\partial \,\text {grad}\,\phi }\Big ) \Big ] \dot{\phi }.\nonumber \!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(25)

With the latter definition of the internal energy density $\dot{\mathcal {E}}$, Eq. (23) can be rewritten as

$$\begin{aligned}&\!\!\!\theta \dot{\eta } = D_\text {loc}^\text {red} -\Big [W g^\prime (\phi ) + \rho \,L\,\frac{(\bar{\theta }^M-\theta )}{\bar{\theta }^M}\,p^\prime (\phi ) - \mathrm {div}(l^2 \text {grad}\,\phi ) \Big ] \dot{\phi }\nonumber \\&\!\!\!\qquad - \mathrm {div}\,{\mathbf {q}}^\theta + r\,.\nonumber \!\!\!\!\!\!\!\!\!\\ \end{aligned}$$

(26)

Following this, we derive an explicit relationship to the entropy rate $\dot{\eta }$ in analogy to the procedure presented in [4]. In nutshell, we start from the general definition of the entropy $\eta := -\frac{\partial \varPsi \,(\mathcal {V})}{\partial \theta }$ with $\mathcal {V} =\{{\varvec{\varepsilon }}-{\varvec{\varepsilon }}^\text {p},\, \alpha ,\, \theta ,\, \text {grad}\,\theta ,\,\phi ,\, \text {grad}\,\phi \}$ and carry out the time derivative using the chain rule to obtain $\dot{\eta }$. This leads to the following relation

$$\begin{aligned} \begin{aligned} \dot{\eta }&= -\frac{\partial }{\partial \theta }\Big [{\varvec{\sigma }}\cdot \dot{\varvec{\varepsilon }}- D_\text {loc}^\text {red}\Big ] -\frac{\partial ^2 \varPsi }{\partial \theta ^2} \dot{\theta } \\&\quad - \frac{\partial }{\partial \theta }\Big [\,W g^\prime (\phi )+ \rho \,L\,\frac{(\bar{\theta }^M-\theta )}{\bar{\theta }^M}\,p^\prime (\phi )\\&\quad - \mathrm {div}(l^2 \text {grad}\,\phi ) \Big ]\dot{\phi } \, \\&= -\frac{\partial }{\partial \theta }\Big [{\varvec{\sigma }}\cdot \dot{\varvec{\varepsilon }}- D_\text {loc}^\text {red}\Big ]\\&\quad -\frac{\partial ^2 \varPsi }{\partial \theta ^2} \dot{\theta }+ \rho \, L \frac{1}{\bar{\theta }^M} p^\prime (\phi ) \, \dot{\phi }\,. \end{aligned} \end{aligned}$$

(27)

By subtitling Eq. (27) into (26), we finally obtain the governing energy balance equation in its local form

$$\begin{aligned} c\,\dot{\theta } = - \mathrm {div}\,{\mathbf {q}}^\theta + r + D_\text {loc}^\text {red} + {\mathcal {H}}^\text {ep} -{\mathcal {H}}^\text {pc}\, \end{aligned}$$

(28)

with

$$\begin{aligned} \begin{aligned} c:&= -\theta \frac{\partial ^2 \varPsi }{{\partial \theta }^2}\,,\\ {\mathcal {H}}^\text {ep} :&= \theta \frac{\partial }{\partial \theta }\Big [{\varvec{\sigma }}\cdot \dot{\varvec{\varepsilon }}- D_\text {loc}^\text {red}\Big ]\,,\\ {\mathcal {H}}^\text {pc} :&= \Big [ \rho L\,\frac{\theta }{\bar{\theta }^M}\,p^\prime (\phi ) +W g^\prime (\phi ) \\&\quad + \rho L\,\frac{(\bar{\theta }^M-\theta )}{\bar{\theta }^M}\,p^\prime (\phi ) - \mathrm {div}(l^2 \text {grad}\,\phi ) \Big ]\dot{\phi }\,,\\ \end{aligned} \end{aligned}$$

(29)

where c and ${\mathcal {H}}^\text {ep}$ represent the volumetric heat capacity and the structural elastoplastic heating effect. The term, ${{\mathcal {H}}^\text {pc}}$, represents the phase-change contribution.

For linear elastic isotropic materials with temperature-dependent elastic modulus , the stress given in Eq. (12a) can be expressed using the additive strain decomposition in Eq. (2) as

(30)

in this, ${\varvec{\varepsilon }}^\text {th}$ can be expressed within the isotropic small strains framework as

$$\begin{aligned} {\varvec{\varepsilon }}^\text {th} := \alpha _{\theta } (\theta -\theta _{\text {ref}})\,{\mathbf {I}}\,. \end{aligned}$$

(31)

Following (30), the rate form can be expressed as

(32)

Table 1 Summary of governing partial differential equations

Table 2 Material properties as functions of $\phi$

To account for plastic strains, a rate-independent associative plasticity model with J2 von Mises plasticity and isotropic strain hardening law is used. The derivation of the plasticity model is presented briefly in the following, whereas a detailed description can be found in, e.g., [1]. According to Eqs. (20) and (21) with the definition of the yield function in (6), the evolution for both plastic strain and equivalent plastic strain can be established as follows

$$\begin{aligned} \dot{\varvec{\varepsilon }}^\text {p} =\dot{\lambda }\frac{\partial \chi }{\partial {\varvec{\sigma }}} = \dot{\lambda }\,{{\varvec{\sigma }}}^\text {D}\,,\dot{\alpha } =\dot{\lambda }\frac{\partial \chi }{\partial \mathrm {q}^{\alpha }} = \dot{\lambda }\frac{2}{3}\mathrm {q}\,. \end{aligned}$$

(33)

Incorporating the consistency condition $\dot{\chi }= 0$ and using the rate of the yield stress function, one finds another relation for the rate of the equivalent plastic strain

$$\begin{aligned} \dot{\chi }= \frac{\partial \chi }{\partial {\varvec{\sigma }}}\cdot \dot{{\varvec{\sigma }}} + \frac{\partial \chi }{\partial \,\mathrm {q}} \,\dot{\mathrm {q}} =0\longrightarrow \quad \dot{\alpha } =\frac{{{\varvec{\sigma }}}^\text {D}\cdot \dot{{\varvec{\sigma }}}}{\frac{2}{3}H \mathrm {q}}. \end{aligned}$$

(34)

Fig. 1

Temperature and phase-field contours with $l= 10$ (mJ/mm)$^{1/2}$ (a) and phase-field-dependent derived properties (b)

Fig. 2

Temperature and phase-field contours with $l= 10$ (mJ/mm)$^{1/2}$ (a) and temperature-dependent properties adapted from [31] (b)

Combining equations of the equivalent plastic strain (33)$_2$ with (34) and using the stress rate Eq. (32) augmented with the flow rule (33)$_1$, the plastic multiplier evolution can finally be written as

(35)

Once $\dot{\lambda }$ is calculated, the rates of stress $\dot{{\varvec{\sigma }}}$ and equivalent plastic strain $\dot{\alpha }$ can be computed, as will be discussed in details in Sect. 4 within the numerical treatment.

2.6 Summary of the governing balance relations

Following the previous discussion, Table 1 summarizes the local system of coupled nonlinear partial differential equations (PDEs), which are needed to solve IBVPs of phase-change thermo-elastoplasticity.

3 Temperature and phase-field dependent material properties

In the numerical simulation of the welding process using the FEM, the choice of the material properties and their dependencies on the temperature or the material state (melted/unmelted) plays a vital role in the thermal and mechanical analysis [40, 64, 93]. For the transient temperature field computation, the material density ($\rho$), the thermal conductivity ($\kappa$ ), and the heat capacity (c) are of particular importance. The Young’s modulus (E), the yield stress ($\mathrm {y}_{0}$), the hardening parameter (H), the Poisson’s ratio ($\nu$), and thermal expansion coefficient ($\alpha _{\theta }$) play the major role in the calculation of elastoplastic deformations and, thus, the residual stresses. However, Poisson’s ratio has only a slight effect on the final state of the residual stress as discussed in [21, 105]. In the literature, it is a common practice in the thermomechanical analysis of the welding process in metals to consider the values of $\rho$ and $\nu$ to be independent of the temperature or the material state, whereas their values are usually taken equal to that measured at room temperature. This simplification will also be applied in the underlying work. However, the consideration of the dependency of the other material properties, i.e. E, c, $\mathrm {y}_{0}$, H, $\kappa$, and $\alpha _{\theta }$, on the temperature field or the material state via the phase-field is crucial for the accurate computation of the residual stresses. In this case, the dependency on the temperature can experimentally be figured out through conducting special measurement techniques as presented in, e.g, [85, 93]. Alternatively, to capture the variation of the parameter’s values during the welding process, we propose in this work an alternative and easier-to-implement approach, in which the phase-field variable is utilized to generate state-dependent material properties. In particular, depending on the state of the material, i.e. soft or hard, a state-dependent value is assigned to each parameter (one value for the soft state and one value for the hard state). In this case, a smooth transition between these two values is achieved via the utilization of a phase-field-dependent interpolation function. Table 2 summarizes the proposed expressions of the material properties for the nickel-based alloy IN718 with their soft/hard-state-related values.

To show the effect of the gradient-energy coefficient l on the resulted parameter curves given in Table 2, a transient one-directional melting analysis is performed. In this, the right-end of the rectangular FE domain is kept at a constant temperature of 1700 K above the melting point, while the left-end is kept at 293 K as illustrated in Fig. 1a.

In this way, the melting interface moves from the right to the left-hand side of the considered domain. Figure 1a shows the contour plots of the temperature distribution and the phase-field variable at time equals 50 s. The spatial variation of the phase-field-dependent properties with change of the gradient-energy coefficient is given in Fig. 1b. On the other hand, Fig. 2 shows the counterpart contours and curves when the temperature-dependent properties are used [31].

4 Finite element formulation

The following discussion focuses on the numerical solution of IBVPs related to residual stresses in gas tungsten arc welding using the finite element method (FEM). The primary variables in connection with the applied phase-field thermo-elastoplasticity modeling approach are $\{\theta ,\,\phi ,\,{\mathbf {u}}\}$ and the governing PDEs are summarized in Table 1. Let $\varOmega \subset \mathbb {R}^3$ be the homogenized spatial domain under consideration with $\partial \varOmega$ being its boundary, $\partial \varOmega$ is split for each variable into two parts, i.e. Dirichlet or essential ($\varGamma _D$) and Neumann or natural ($\varGamma _N$) boundaries. These boundaries fulfill the conditions $\partial \varOmega ={\varGamma _D \cup \varGamma _N}$ and ${\varGamma _D \cap \varGamma _N}=\emptyset$. More specifically, the Dirichlet and Neumann boundary conditions for each variable together with the initial values at $t=t_0$ can be specified as follows:

$$\begin{aligned} \begin{array}{llccl} -\kappa \, \text {grad}\,\theta \cdot {\mathbf {n}}&{}=\bar{q} &{}\text {on}&{} &{} {{\varGamma _{N_\theta }}}\times [\,t_0,\,t\,]\,,\\ \theta &{}= \bar{\theta } &{}\text {on}&{} &{} {\varGamma _{D_\theta }}\times [\,t_0,\,t\,]\,,\\ \text {grad}\,\phi \cdot {\mathbf {n}}&{}=0 &{}\text {on} &{} &{} {\varGamma _{N_\phi }}\times [\,t_0,\,t\,]\,,\\ \phi &{}= \bar{\phi } &{} \text {on}&{} &{} {\varGamma _{D_\phi }}\times [\,t_0,\,t\,]\,,\\ \varvec{\sigma }{\mathbf {n}}&{} = \bar{{\mathbf {t}}} &{} \text {on}&{} &{} {\varGamma _{N_u}}\times [\,t_0,\,t\,]\,,\\ {\mathbf {u}}&{}= \bar{{\mathbf {u}}} &{} \text {on}&{} &{} {\varGamma _{D_u}}\times [\,t_0,\,t\,]\,,\\ \theta =\theta _{0},\, \phi &{}=\phi _{0},\,\, {\mathbf {u}}={\mathbf {u}}_0 \qquad &{} \text {in}&{} &{} \varOmega \times \{t_0\} \,. \end{array} \end{aligned}$$

(36)

In this, ${\mathbf {n}}$ is the outward unit normal vector to $\partial \varOmega$ and $\bar{q}$ is a prescribed external heat flux.

4.1 Governing weak formulations

In connection with the implementation in the open-access/open-source FE package FEniCS, one needs to derive the weak or variational form of the governing PDEs, given in strong form in Table 1. The required trial spaces $V_\theta$, $V_\phi$, and $V_u$ for the primary variables and the related weighting functions can be defined as

$$\begin{aligned} \begin{aligned} V_\theta&:= \lbrace \theta ,\,\delta \theta \,:\varOmega \longrightarrow \mathbb {R} \,\vert \, \theta ,\,\delta \theta \, \in \mathrm {H}^1 (\varOmega ),\,\, \theta |_{\varGamma _{D_\theta }} \\&= \bar{\theta },\, \, \delta \theta |_{\varGamma _{D_\theta }} = 0\, \rbrace \,, \\ V_\phi&:= \lbrace \phi ,\,\delta \phi \,:\varOmega \longrightarrow \mathbb {R} \,\vert \, \phi ,\,\delta \phi \, \in \mathrm {H}^1 (\varOmega ), \,\, \phi |_{\varGamma _{D_\phi }} \\&= \bar{\phi },\,\, \delta \phi |_{\varGamma _{D_\phi }} = 0 \, \rbrace \,,\\ V_u&:= \lbrace {\mathbf {u}},\,\delta {\mathbf {u}}\,:\varOmega \longrightarrow \mathbb {R}^3 \, \vert \, {\mathbf {u}},\,\delta {\mathbf {u}}\, \in [\mathrm {H}^1 (\varOmega )]^3,\,\, {\mathbf {u}}|_{\varGamma _{D_u}} \\&= \bar{{\mathbf {u}}},\,\, \delta {\mathbf {u}}|_{\varGamma _{D_u}} = \mathbf{0}\, \rbrace \, \end{aligned} \end{aligned}$$

(37)

with $\mathrm {H}^1(\varOmega )$ denoting the Sobolev space of order one. For the numerical examples of welding process in Sect. 5, the energy balance equation will be simplified by ignoring the terms $D_\text {loc}^\text {red}$ and ${\mathcal {H}}^\text {ep}$ from the energy balance equation in Table 1. This is justified as the amount of heat produced by the mechanical deformations is too small in comparison with the heat provided by the welding heat source, see, e.g., [25, 89, 92] for analogous discussion. In this regard, investigations performed in [77] for entropic thermoelasticity showed also that the structural elastoplastic heating term has a negligible contribution. Following this, the variational problem after multiplying the governing equations in Table 1 by the test functions and applying integration by parts over the entire domain can be posed as: Find $\lbrace \theta , \phi , {\mathbf {u}}\rbrace$ $\in$ $V_u \times V_\theta \times V_\phi$ such that

$$\begin{aligned}&\int _{\varOmega } \Big [ c \, \dot{\theta }\,+ {{\mathcal {H}}^\text {pc}} \Big ]\delta \theta \, \mathrm {d}v +\int _{\varOmega } \kappa \,\mathrm {grad}\,\theta \cdot \mathrm {grad}\,\delta \theta \,\mathrm {d}v \nonumber \\&\quad +\int _{\varOmega } r\, \delta \theta \,\mathrm {d}v - \int _{{\varGamma _N}_\theta } \bar{q}\,\delta \theta \,\mathrm {d}a = 0\,,\nonumber \\&\int _{\varOmega } \Big [\frac{1}{M}\,\dot{\phi }\,\delta \phi {+} W\,g^{\prime }(\phi )\,\delta \phi {+} \rho \,L\,\frac{(\bar{\theta }^M{-}\theta )}{\bar{\theta }^M}\,p^{\prime }(\phi )\,\delta \phi \nonumber \\&\quad {+} l^2\,\mathrm {grad}\,\phi \cdot \mathrm {grad}\,\delta \phi \Big ]\,\mathrm {d}v {-}\int _{{\varGamma _{N_\phi }}}l^2\,\,\mathrm {grad}\,\phi \cdot {\mathbf {n}}\, \delta \phi \,\mathrm {d}a {=} 0\,,\nonumber \\&\quad \int _{\varOmega } \rho \,\ddot{{\mathbf {u}}}\cdot \delta {\mathbf {u}}\,\mathrm {d}v + \int _{\varOmega }{\varvec{\sigma }}\cdot \mathrm {grad}\,\delta {\mathbf {u}}\,\mathrm {d}v \nonumber \\&\quad - \int _{\varOmega } \,{\mathbf {b}} \cdot \delta {\mathbf {u}}\,\mathrm {d}v - \int _{{\varGamma _{N_u}}} \bar{\varvec{t}} \cdot \delta {\mathbf {u}}\,\mathrm {d}a = 0\,. \end{aligned}$$

(38)

4.2 Temporal and spatial discretization

In the numerical solution of time-dependent IBVPs in FEniCS, a time-stepping scheme based on the finite difference approximation over a time interval $\varDelta \,t=t_{n+1}-t_{n}$ is applied. This results in time-discrete (stationary) equations, where the time stepping is followed by constructing the variational formulation towards the spatial FE discretization, see, e.g., [68] for more details. In this work, an “isothermal split”-like strategy is applied in accordance to the descriptions presented in, e.g., [9, 72, 73], which results in a robust solution of the volumetrically-coupled problem. In particular, at each time step $t_{n+1}$, the solution of the coupled problem is carried out in two sequential steps: (i) The thermal and the phase-field problem are solved monolithically under a constant mechanical state to get $\theta _{n+1}$ and $\phi _{n+1}$. (ii) The mechanical subsystem of elastoplasticity is solved under an isothermal state, which allows computing the updated displacement $\mathbf {u}_{n+1}$ . For the spatial-discretization using the FEM, the continuous homogenized domain $\varOmega$ is transformed into a discrete domain $\varOmega ^\text {h}$ subdivided into $N_e$ finite elements. For an abstract representation, the primary unknowns of the problem are summarized in a vector $\mathbf {v}:= \mathbf {v}({\mathbf {x}},\mathrm {t})$ with $\mathbf {v}= [\,\theta , \phi , {\mathbf {u}}\,]$ . Thus, the trial and test functions read

$$\begin{aligned} \begin{aligned} \mathbf {v}^\text {h}({\mathbf {x}},\mathrm {t})&= \bar{\mathbf {v}}^\text {h} ({\mathbf {x}},\mathrm {t}) + \sum _{i=1}^{\mathrm {N}_\mathbf {v}} {{\mathbf {N}}_{\mathbf {v}(i)}}({\mathbf {x}})\, \mathbf {v}_{(i)}(\mathrm {t})\, \in {V}^\text {h}(\mathrm {t})\,,\\ \delta \mathbf {v}^\text {h}({\mathbf {x}})&= \sum _{i=1}^{\mathrm {M}_\mathbf {v}} {{\mathbf {M}}_{\mathbf {v}(i)}}({\mathbf {x}})\, \delta \mathbf {v}_{(i)} \,\, \, \in \, \hat{V}^\text {h}\,. \end{aligned} \end{aligned}$$

(39)

In this, $\bar{\mathbf {v}}^\text {h}$ are the approximated Dirichlet boundary conditions and $\mathrm {N}_\mathbf {v}$ denotes the total number of FE nodes. Additionally, ${{\mathbf {N}}_{\mathbf {v}(i)}}$ and ${{\mathbf {M}}_{\mathbf {v}(i)}}$ denote the global basis functions of the trial and test functions at node i, whereas $\mathbf {v}_{(i)}$ are the nodal degrees of freedom and $\delta \mathbf {v}_{(i)}$ represent the nodal values of the test functions. Moreover, ${V}^\text {h}$ and $\hat{V}^\text {h}$ are the discrete, finite-dimensional trial and test spaces, respectively. In this work, we follow the Continuous Galerkin (CG) approach with first-order basis functions, which provides standard linear Lagrange elements, e.g., a triangle with nodes at the three vertices of each element [68]. For the FE treatment of the last term in Eq. (29)$_3$, i.e. $\mathrm {div}(l^2 \text {grad}\,\phi )$, we carried out numerical studies employing second-order basis functions to check the importance of this term. The results showed that this term has a negligible value in comparison to the contribution of other terms in ${\mathcal {H}}^\text {pc}$. Thus, it is neglected in the later numerical treatments. Furthermore, the application of the Bubnov-Galerkin procedure, in which $\mathbf {v}$ and $\delta \mathbf {v}$ are approximated using the same basis functions ${{\mathbf {N}}_{\mathbf {v}(i)}} \equiv {{\mathbf {M}}_{\mathbf {v}(i)}}$, implies that ${V}^\text {h}$ and $\hat{V}^\text {h}$ coincide [74]. Moreover, for the implementation in FEniCS, a common space ${V}^\text {h}$ is used for both test and trial function as $\bar{\mathbf {v}}^\text {h}$ are not specified as part of this function space [68]. For further details on the finite element formulations, the interested reader is referred to, e.g., [10, 38, 43, 47, 52, 53, 68], among others.

4.3 Integration algorithms for plasticity

For the numerical solution of IBVPs of rate-independent plasticity with linear isotropic hardening, proper integration algorithms have to be specified to integrate the evolution equations of the plastic strain and the related hardening parameters. Adopting the FE package FEniCS in this contribution, a special focus is laid in the following on the implementation and comparison between two plasticity integration algorithms, which are the “return mapping algorithm” and an “incremental plasticity” approach.

4.3.1 The return mapping method (RM)

Proceeding with a known material state ${\{\theta ,\, \phi \}}_{n+1}$ at $t_{n+1}$ and ${\{ {\varvec{\varepsilon }},\, {\varvec{\sigma }},\, {{\varvec{\varepsilon }}}^\text {p},\,\alpha \}}_{n}$ at $t_n$, the RM applies a strain increment $\varDelta {\varvec{\varepsilon }}$ and aims to figure out the updated current state at $t_{n+1}$ as summarized in Algorithm (I).

In this, the updated values have to satisfy the yielding condition and the global equilibrium within a predefined tolerance. For this purpose, an iterative procedure is used to drive the residual (Res) between the internal forces and the external force vector. Furthermore, in the FEniCS implementation of plasticity, the solution of the internal variables is carried out at the quadrature points, which are interpreted as degrees of freedom when using the so-called “quadrature element”. This element type is developed within the FEniCS framework to avoid a suboptimal convergence rate for Newton’s method [17, 68]. The suboptimal convergence arises due to the linearization procedure followed by FEniCS Form Compiler (FFC) when nonlinear continuous weak forms are linearized using Newton’s method. Thus, the implementation of RM in FEniCS requires the definition of quadrature elements with the application of Newton’s method to compute the stress and its linearization at the quadrature points.

4.3.2 The incremental method (IM)

The incremental method (IM) is presented here as an alternative procedure to solve the plasticity problem. In the IM, the plasticity problem can be solved by avoiding the quadrature element definition and the nonlinear problem in step (4) given in Algorithm (I). The method simply uses the stress state ${\varvec{\sigma }}_{n}$ from the previous step $t_{n}$ to calculate the plastic multiplier ${\dot{\lambda }}_{n+1}$ and update the internal state variables. Then updated ${\varvec{\sigma }}_\text {n+1}$ and ${\varvec{\varepsilon }}^{\text {p}}_\text {n+1}$ at the current time $(t_\text {n+1})$ can be computed as

$$\begin{aligned} {\varvec{\sigma }}_\text {n+1}= & {} {\varvec{\sigma }}_\text {n} +\varDelta t\,\dot{{\varvec{\sigma }}}, {\alpha }_\text {n+1} = {\alpha }_\text {n} +\varDelta t\,\dot{\alpha } , \nonumber \\&{\varvec{\varepsilon }}^\text {p}_\text {n+1}= {\varvec{\varepsilon }}^\text {p}_\text {n} +\varDelta t\,\dot{\varvec{\varepsilon }}^\text {p}\,, \end{aligned}$$

(40)

where $(\bullet )_\text {n}$ denotes the value computed at the previous time step. The method provides an accurate numerical solution for small time increments [1]. The solution steps for the IM are presented in Algorithm (II).

5 Numerical examples

The proposed phase-field thermo-elastoplasticity model in the previous sections is adopted and tested against two representative numerical examples.These examples employ the material properties of nickel-based alloy IN718 for temperature-dependent and phase-field-dependent properties as given in Figs. 2 and 1, respectively. The first example involves a two-dimensional (2D) GTAW spot welding problem, while in the second example a three-dimensional (3D) analysis of the moving GTAW process is performed. The numerical implementation is carried out in the FE-package FEniCS Project according to the settings and assumptions discussed in the previous sections.

5.1 2D modeling of welding-induced residual stresses

In this section, the numerical simulations are carried out for an IBVP problem of GTAW spot welding in 2D plane strain settings. The focus in the phase-field thermo-elastoplastic model is laid on the performances of the two different algorithms for plasticity, i.e. the return mapping method (RM) and the incremental method (IM) previously discussed in Sect. 4.3. The phase-field-dependent material properties, depicted in Fig. 1, are employed in the analysis. Figure 3 illustrates the geometry of the symmetric 2D problem together with the mechanical and heat flux boundary conditions.

Fig. 3

Schematic illustration of the two-dimensional numerical model 18 $\times$ 10 mm$^2$

The left symmetry surface is thermally insulated, while the bottom and right surfaces are subjected to heat losses by convection according to

$$\begin{aligned} \bar{q}_{_\text {{loss}}} = h_\text {c} (\theta -\theta _{\text {amb}})\, \end{aligned}$$

(41)

with $\theta _{\text {amb}}$ being the surrounding ambient temperature 293 K and $h_\text {c}$ is the convective heat transfer coefficient of the surrounding air. The heat flux at the top surface represents the heat exchange between the top surface and the GTAW torch, i.e.

$$\begin{aligned} \bar{q}_{_\text {{heat}}} = \, -q_{_\text {{max}}}\exp \left( -\frac{x_1^2 }{r_0^2}\right) + h_\text {c} (\theta -\theta _{\text {amb}})\,, \end{aligned}$$

(42)

where $q_{_\text {{max}}}=81280\,$mW being the welding power and $r_0=1.4$ mm is the Gaussian radius of the heat source. Additionally, a constant value of the material density $\rho =7737\times 10^{-12}$ tonne$\cdot$mm$^{-3}$ is considered, and the value of convective heat transfer coefficient is chosen to be $h_c=700\,$ mW$\cdot$mm$^{-2}$ K$^{-1}$ . For the 2D analysis case, the gradient-energy coefficient is set to 3 (mJ/mm)$^{1/2}$ and the rest of the parameters used for solving the phase-field variable Eq. (38)$_2$ are listed in Table 3.

Table 3 Numerical and material parameters

Thermal analysis results are presented in Fig. 4, which depicts a contour plot of the phase-field variable after 5 s heating time with the melted weld pool as a soft region $\phi =1$ and the unmelted hard region with $\phi =0$.

Fig. 4

Contour of the phase-field variable after 5 s heating cycle. Whole domain right and enlarged section left

At each time step, the computed values of the temperature and phase-field variables are passed to the mechanical problem for the computation of the residual stresses. The distribution of the residual stress components in $x_1$ and $x_2$-directions are shown in Fig. 5 at the end of the analysis, i.e. at $t=50\,$s. For quantitative comparisons of the results obtained by RM and IM, Fig. 6 shows curves of $\sigma _{11}$ and $\sigma _{22}$ along the sections indicated in Fig. 5. It can be seen that a good agreement is obtained between the solutions by RM and IM. This indicates that both methods are reliable to be used for performing the mechanical analysis. However, they differ in the convergence behavior and computational costs, as will be discussed in the following.

Fig. 5

Contour plots of the residual stress components $\sigma _{11}$ and $\sigma _{22}$ after 100 s for the case of RM (a) and IM (b) of the 2D numerical analysis

Fig. 6

Curves for stress components along the cross sections 1-1 (left) and 2-2 (right)

Within the model sensitivity study, the implementation is tested with different time steps and mesh refinements. The results of the sensitivity study are summarized in Tables 4, 5 and 6. The computations are performed using a workstation of an Intel$^{\circledR }$ Core™  i7-8700 CPU@3.20 GHz $\times$12 and 16 GB RAM. The results presented in these tables show that both RM and IM have good stability and convergence behavior. However, IM attains convergence for a wider range of time steps and mesh refinements over RM, whereas the total time needed for the IM computation for a given time-step size is longer. Due to its stability and convergence characteristics for a relatively large time-step size, the IM will be used in the subsequent section for the simulation of residual stresses within a 3D IBVP.

Table 4 Elapsed time by RM and IM: coarse mesh (2677 elements$\times$ 1418 nodes) with different time steps

Table 5 Elapsed time by RM and IM implementation: $\varDelta t=0.05\,\text {s}$ with different mesh refinements

Table 6 RM and IM implementation: fine mesh (12,450 elements$\times$ 6396 nodes) with different time steps

5.2 Model validation by 3D bead-on-plate welding problem

5.2.1 Problem setup

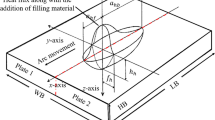
In the following, a 3D problem of the GTAW process will be studied. It represents bead-on-plate welding as illustrated in Fig. 7 (left). The boundary conditions, the geometry, and the material parameters are adopted from [31] for the case study on an autogenous welding process of a plate made from Nickel-based alloy IN718.

Fig. 7

Geometry (left) and finite element mesh (right) used for the bead-on-plate analysis

For the considered bead-on-plate welding IBVP and due to the symmetry of the surface heat source (illustrated in Fig. 8) along the welding central-line, only half of the domain is considered in the FE model. In this way, the computational time is reduced and, thus, the employed domain has the dimensions of $50\times 200 \times 2$mm$^3$, as shown in Fig. 7 (left). The unstructured FE mesh, which consists of four-node tetrahedral elements, is created by the mesh generator Gmsh [37] and illustrated in Fig. 7 (right). The mesh density is higher towards the welding zone and gradually decreases far away from this zone. The side length of the smallest elements utilized in the FE model is $(0.6 \text {mm})$, while the largest allowed element side has a size of $5 \text {mm}$. The FE mesh consists of 107,151 elements and 27,147 nodes. The same finite element mesh is used for the thermal and mechanical analyses choosing first-order Lagrange elements. Moreover, thermal and mechanical boundary conditions are defined on the considered domain. In the thermal analysis, the moving heat source model is applied as a surface heat flux at the top surface of the domain. For the plate with a small thickness of $2\,\text {mm}$, a 2D heat source with circular Gaussian distribution is a suitable choice for giving a good approximation of the heating process with few parameters [31, 92]. As indicated in Fig. 8, the maximum power density $\text {mW}/\text {mm}^2$ will be experienced at the center of the top surface of the plate and continuously decays as the distance increases. The surface heat flux is given as a Neumann boundary condition at the top surface of the considered FE model [33, 39, 106], which can be written as

$$\begin{aligned}&\bar{q}_{_\text {{sur}}} = \frac{\eta _s\, Q}{\pi \, r^2_0}\, \exp \Big (-\frac{(x_1-x_{01})^2 +(x_2 - x_{02}-v\,t)^2}{r^2_0}\Big )\,. \nonumber \!\!\!\!\!\!\\ \end{aligned}$$

(43)

In this, Q, $\eta _s$, and $r_0$, represent the input power provided by the moving welding torch, the arc welding efficiency, and the radius of the flux distribution, respectively. $x_{01}$ and $x_{02}$ refer to the initial position of the heat source and v and t are the torch velocity and time. The heat source parameters are listed in Table 7.

Table 7 GTAW heat source parameters used in the 3D analysis [31, 91]

Fig. 8

Circular Gaussian heat source with $r_0=4$ mm and $Q= 580\times 10^3$ mW

On the top of the plate, the heat source travels along the $x_2$-direction for 180 mm, where the start and the end locations are 10 mm distance from the edges. The heat losses due to the interaction with the surroundings are considered to occur through heat convection and modeled by Newton’s law. All external boundary surfaces, except for the symmetry plane, are assumed to interact with the surroundings by applying the Neumann boundary conditions given in Eq. (41). To prevent rigid body motion, artificial boundary constraints are applied during the mechanical analysis, as depicted in Fig. 7 (left). This includes a mechanical symmetry condition on the plane of symmetry $(\mathrm {u}_\mathrm {1}=\partial \mathrm {u}_\mathrm {2} / \partial x_1 =\partial \mathrm {u}_\mathrm {3} / \partial x_1 = 0\,\text {mm})$, constrained degree of freedoms $(\mathrm {u}_\mathrm {2}=\mathrm {u}_\mathrm {3}=0\, \text {mm})$ at point D, and $(\mathrm {u}_\mathrm {3} =0\,\text {mm})$ at point E. Furthermore, at the beginning of computation, the primary variables are initialized with the following values ($\phi _\text {init}=0$, $\theta _\text {init}=293 \,\text {K}$ and ${\mathbf {u}}_\text {0} =\varvec{0}\,\text {mm}$). The total simulation time is 300 s, which includes the heating time of 113 s. The time steps employed in the thermal and mechanical analysis are $\varDelta t=0.08$ s and $\varDelta t=0.16$ s, respectively.

5.2.2 Discussion of the thermal analysis results

The results of the 3D welding problem related to the temperature field and phase change are presented in Figs. 9, 10, 11 and 12. Figure 9 shows temperature profiles assembled at three different locations corresponding to points A, B and C, which are, respectively, at a distance of 6 mm, 8 mm, and 10 mm from the weld centerline. As shown in Fig. 9a, when temperature-dependent properties are used, the predictions of the thermal analysis have a good agreement with experimental measurements conducted in [31] with some deviations related to the peak temperatures. The deviations of the predicted peak temperatures are expressed by the relative errors¹ of ${ ERR}_{\theta , A }\approx 6\%$, ${ ERR}_{\theta , B }\approx 7\%$ and ${ ERR}_{\theta , C }\approx 7\%$ at points A, B and C, respectively.

Fig. 9

Temperature profiles of points A, B, and C compared to the experiment in [31] for temperature-dependent properties (a) and phase-field-dependent properties (b)

The corresponding temperature profiles at these points for the analysis based on phase-field-dependent properties are shown in Fig. 9b. In comparison with the experimental ones, higher peak temperature relative errors of ${ ERR}_{\theta , A }\approx 19\%$, ${ ERR}_{\theta , B }\approx 13\%$, and ${ ERR}_{\theta , C }\approx 10\%$ are observed. The increase in deviations is attributed to the lowered thermal conductivity at the hard state of the material, which in turn affects the flow of heat from the soft region (the weld pool) to the surrounding regions. Bhatti et al. [16] have also reported that more heat accumulation occurs at lower thermal conductivity values and thus it takes a longer time for the specimen to conduct heat to the surrounding material. As shown in Fig. 10, this effect can be mitigated if we use an averaged value for thermal conductivity of the hard phase, i.e., $\kappa ^H =(\kappa ^H +\kappa ^M)/2$. Reduced relative errors ${ ERR}_{\theta , A }\approx 10\%$, ${ ERR}_{\theta , B }\approx 8\%$, and ${ ERR}_{\theta , C }\approx 8\%$ can be achieved for the profiles at the specified points. Thus, the averaged value for thermal conductivity will be considered in the forthcoming thermal and mechanical analysis.

When it comes to the thermomechanical modeling of welding processes, several research works ignore the effect of the phase change term, ${\mathcal {H}}^\text {pc}$, occurring in the energy equation. Investigations of this term exhibits a sound effect on both size and shape of the weld pool, where a wider and shorter weld pool is observed if this term is neglected as shown in Fig. 11. Thus, by utilizing the phase-field approach, it is possible to account for the effect of energy release or absorption in the shape of latent heat during the phase change. Furthermore, this term has a prominent effect on the temperature evolution in the weld pool, which was also observed in, e.g., [56, 97]. The impact on the temperature profile is shown in Fig. 12 for the point $(0, 100,2)\text {mm}$ within the weld pool.

5.2.3 Discussion of the mechanical analysis results

The results of the 3D mechanical analysis are presented in Figs. 13 and 14. In this, the final states of the residual stress distributions for both transverse $\sigma _{11}$ and longitudinal $\sigma _{22}$ stress components are presented in Fig. 13 on a plane at $x_3=1\,\text {mm}$.

To closely investigate the stress state, Fig. 14 shows line plots for $\sigma _{11}$ and $\sigma _{22}$ at the mid-length and mid-depth of the FE model along the path P1 indicated Fig. 7 (left). The residual stress components are compared with the results in [31] as shown in Fig. 14a for the case of a small deformation assumption. From a qualitative point of view, the resulted stresses using the temperature-dependent properties are compared to the benchmark results by calculating the Weighted Mean Absolute Percentage Error (WMAPE). The definition of WMAPE can be expressed as [75]

$$\begin{aligned} \text {WMAPE}:= 100\times \frac{\sum _{t=1}^n | A_t - F_t |}{\sum _{t=1}^n | A_t|}\,, \end{aligned}$$

(44)

Fig. 10

Temperature profiles of points A, B, and C compared to the experiment in [31] for temperature-dependent properties using an averaged value of thermal conductivity

Fig. 11

Comparison of weld pool size and shape. Neglecting phase-change term (left) and considering phase-change term (right). Figures depict the top view of the weld pool

Fig. 12

Effect of the phase-change term on the calculated peak temperatures. Neglecting this term leads to a relative error of ${ ERR}_{\theta }\approx 6\%$

where $A_t$ and $F_t$ being the actual (reference) values and the predicted values by the proposed model. The transverse stress deviates by $16\%$ while the longitudinal stress shows $17\%$ deviation. Moreover, Fig. 14b depictes a comparison of the results obtained from the model and benchmark temperature-dependent analyses with the ones from the phase-field-dependent properties analysis. It is shown that, in the region of the weld bead, the longitudinal stress $\sigma _{22}$ starts decreasing earlier than in the case of the temperature-dependent analysis. The WMAPE deviation error is $24\%$ for the transverse stress and $8\%$ in the case of the longitudinal stress component. From both Fig. 14a and b, one observes that the region close to the weld centerline experiences tensile stress of the yield stress magnitude, which gradually decreases and turns to compressive stress as the distance from the weld centerline increases. However, in this region, it is noticed that the predicted longitudinal stress is lower than the one predicted in [31]. This can be attributed to the treatment of the plastic strain evolution in our model. We involve the annealing effect in the proposed model. The annealing effect accounts for the hardening reduction due to the change in the dislocation structure caused by the solid-liquid phase change [65]. This is modelled such that for any material point going through melting/re-melting effect, the artificial accumulated plastic strains are eliminated [25, 30]. From a quantitative point of view, the residual stresses predictions by the numerical model are in good agreement with the small deformation analysis given in [31].

Fig. 13

Contours of a transverse $\sigma _{11}$ and b longitudinal $\sigma _{22}$ residual stresses depicted at $x_3=1\,\text {mm}$

Fig. 14

Transverse $\sigma _{11}$ and longitudinal $\sigma _{22}$ stresses plotted along the path P1 indicated in Fig. 7 (left). Solid lines represent the results obtained from the 3D mechanical analysis and dashed lines for small-deformation results in [31], wherein case a temperature-dependent properties are used and case b phase-field-dependent properties are used

6 Conclusions and future works

The presented work proposes a modeling methodology for the phase-field thermo-elastoplasticity problem of gas tungsten arc welding in a thermodynamically consistent framework. The involvement of the phase-field method promotes the use of phase-field-dependent material properties for the melted (soft) and the unmelted (hard) material states. In this way, the thermomechanical properties are driven by the melting/solidification state with the phase-field variable. Two- and three-dimensional IBVP numerical examples are introduced to investigate the performance of the proposed model. In the two-dimensional example, two approaches (algorithms) are tested for the computation of the residual stresses using the von Mises isotropic hardening plasticity. The first approach relies on the conventional return-mapping method by solving a nonlinear problem using Newton’s method to correct the stress state. The second approach applies simplified “incremental plasticity”, in which the stress from the previous step is used to compute the plastic multiplier. The numerical models are implemented in the open-source finite element package FEniCS, where for the return-mapping algorithm the quadrature element type developed with the FEniCS framework is used.

The capability of the proposed model in capturing realistic scenarios of the gas tungsten arc welding process was investigated and a three-dimensional bead-on-plate analysis was performed. The numerical results of temperature profiles and residual stresses have good agreement with results available in the literature. The model shows that using phase-field-dependent parameters can provide reliable predictions for both thermal and mechanical analyses. Furthermore, as a matter of implementation in FEniCS, employing the described incremental plasticity approach gives accurate numerical results when compared to those obtained from the return-mapping method.

To this end, the proposed numerical treatment and modeling framework can serve as a base for future research works in related fields to GTAW and the prediction of residual stresses. As future works, the approach can be extended to consider thermo-elastoplasticity within finite deformations, which allows for more accurate description of the coupled processes if large deformations occur. One of the important extensions would also be the consideration of the material in a melted state as a fluid, which can be treated within a unified kinematics framework together with the solid phase. Another future aspect in connection with the proposed phase-field thermo-elastoplasticity approach is the application to predict residual stresses induced by additive layer manufacturing processes of metal parts. Moreover, modeling the weld-induced cracks can also be achieved by incorporating the phase-field fracture approach.

Appendix A: Phase-field modeling of heat-induced phase transition

Fig. 15

Schematic illustration using the spatial variation of $\phi$ to show the difference between the sharp interface approach (left) and the diffusive interface approach (right)

The phase change between unmelted (hard solid) state and a melted (soft solid or liquid-like) state is a common phenomenon in fusion welding processes [113]. In this work, the phase-field method (PFM) is applied to model the melting/solidification processes of the metal being welded. Applying the PFM is accompanied by many advantages, where two of them will be mentioned in the following: (1) No need to explicitly track the interface between the melted and the unmelted metal. Therefore, no need to explicitly fulfill the continuity equation or the force balance on the interface, which is considered then a part of the interior domain. (2) Applying the PFM allows for a unified-kinematics treatment of the melted and the unmelted metal. In particular, putting the material parameters as functions of the phase-field variable allows for a smooth variation of their values between the two metal states and across the diffusive interface. For illustration, Fig. 15 illustrates the concept of a diffusive interface in phase-change materials in comparison with the sharp-interface concept.

The first step in the PFM approach is the definition of the phenomenological phase-field variable that governs the smooth change across the interface. This is defined as

$$\begin{aligned} \phi ({\mathbf {x}},t)\,\in \,[0,\,1] \quad \text{ with }\quad \left\{ \begin{array}{ll} \phi =1&{}\text{: } \text{ melted } \text{(soft) } \text{ state }\,, \\ \phi =0&{}\text{: } \text{ unmelted } \text{(hard) } \text{ state }\,, \\ 0<\!\phi \!<1 &{}\text{: } \text{ diffusive } \text{ interface }\,.\nonumber \end{array}\right. \!\!\!\!\!\!\!\\ \end{aligned}$$

(45)

The treatment in the following assumes that the phase-change process occurs merely due to changing of the thermal energy and ignores the contribution of the mechanical energy in this process. Thus, in analogy to the thermodynamically consistent approach in [18] and following the Ginzburg-Landau theory, the global potential energy function $\mathcal {F}$ over the spatial domain $\varOmega$ is expressed as the sum of the bulk free energy term $f(\phi , \theta )$ and the interfacial energy terms as

$$\begin{aligned} \mathcal {F}(\phi , \theta )=\int _\varOmega \left[ {f(\phi , \theta )}+\frac{l^2}{2}|\text {grad}\,\phi |^2 \right] dV\, \end{aligned}$$

(46)

with l being a gradient-energy coefficient that influences the width of the diffusive zone. At equilibrium, the variational derivative of (46) results in the following restriction:

$$\begin{aligned} \frac{\delta \mathcal {F}}{\delta \phi }= \frac{\partial f}{\partial \phi } -l^2\, \nabla ^2\phi =0 \,. \end{aligned}$$

(47)

The phase-field evolution and the resulting migration of the diffusive interface is a time-dependent process. To describe this evolution, the application of the Allen-Cahn reaction-diffusion equation is a common practice. It can be expressed as

$$\begin{aligned}&\frac{\partial \phi }{\partial t} \,=\,\dot{\phi }\,=\, -M\frac{\delta \mathcal {F}}{\delta \phi } \,\nonumber \\&\qquad \quad \qquad =\, -M\left[ \frac{\partial f}{\partial \phi }-l^2\, \nabla ^2\phi \right] \,. \end{aligned}$$

(48)

In this, M represents the interface mobility parameter, which can be expressed according to [18] as

$$\begin{aligned} M= \frac{\mu _{\phi }\, \bar{\theta }^M}{6\,\delta \,\rho L}\, \end{aligned}$$

(49)

with $\mu _{\phi }$, $\bar{\theta }^M$, and $\delta$ as the kinetic coefficient, the material melting temperature and the interface width, respectively. In absence of the mechanical or chemical free energy contributions, the free energy density of the system is defined by

$$\begin{aligned} f(\phi ,\theta )= W g(\phi )+Q(\theta )\,p(\phi )\, , \end{aligned}$$

(50)

where the first term Wg represents the energy barrier related to the interface between the soft and hard phases of the metal. Moreover, W, $g(\phi )$, and $p(\phi )$ are the energy barrier height at the interface, the double-well potential, and the interpolation function, respectively:

$$\begin{aligned}&W = 3 \frac{\sigma _{\phi }}{\delta }\,\,,\quad g(\phi )=(\phi )^2(1-\phi )^2,\nonumber \\&p(\phi ) =(\phi )^3\left( 6(\phi )^2-15\phi +10\right) \, \end{aligned}$$

(51)

with $\sigma _{\phi }$ being the surface tension. For melting/solidification phase-change problems, the main thermal force driving for the evolution of the phase-field parameter, $Q(\theta )$, can be expressed as

$$\begin{aligned}&Q(\theta )=\rho \, L\frac{(\bar{\theta }^M-\theta )}{\bar{\theta }^M}\,. \end{aligned}$$

(52)

Using Eqs. (50) and (51), the evolution of the phase-field variable, Eq. (48), can be rewritten as

$$\begin{aligned} \begin{aligned} \dot{\phi }=&\,M\Big [l ^2\,\nabla ^2\phi -2\,W \phi \,(1-\phi )(1-2\phi )\\&-30\,Q(\theta )\,(\phi )^2(1-\phi )^2\Big ]. \end{aligned} \end{aligned}$$

(53)

More details, references, and applications can be found in [20, 69, 87, 88, 90, 98] among others.