MPM–FEM hybrid method for granular mass–water interaction problems

Abstract

The present study proposes an MPM (material point method)–FEM (finite element method) hybrid analysis method for simulating granular mass–water interaction problems, in which the granular mass causes dynamic motion of the surrounding water. While the MPM is applied to the solid (soil) phase whose motion is suitably represented by Lagrangian description, the FEM is applied to the fluid (water) phase that is adapted for Eulerian description. Also, the phase-field approach is employed to capture the free surface. After the accuracy of the proposed method is tested by comparing the results to some analytical solutions of the consolidation theory, several numerical examples are presented to demonstrate its capability in simulating fluid motions induced by granular mass movements.

Introduction

In the natural phenomenon known as submarine or/and subaerial landslide [25, 26], sediment on the slope slides down from shallower to deeper regions of the ocean, resulting in a series of hazardous events, such as the severing of submarine cables and submarine pipelines, obstacles obstructing the operation of resource development facilities, and large-scale tsunamis. The damage caused by such a tsunami has been considerable on a global scale, and the loss of life has also been significant. However, the process of such a landslide is not well understood. Since multiple physical phenomena simultaneously interact in the generation of tsunamis caused by a landslide (the collapse of the seabed, the interaction between soil and water), determining the mechanism has proven to be challenging. It is, however, extremely difficult to predict the behavior of the soil and seawater with high accuracy using conventional approaches [13]. Therefore, it is necessary to develop effective numerical simulation methods that can properly evaluate the complex mechanical behaviors involved in the generation of tsunami due to landslides.

Among the computational methods to solve the complex solid-liquid coupled problems, the traditional finite element method (FEM) is not good at solving the complex large deformation in solid phase such as debris flow and landslides due to severe grid distortion. In this context, the grid-free methods (including FEM with the Eulerian frame) have been developed as substitutes for FEM. The element-free Galerkin method [29], smooth particle hydrodynamic (SPH) method [8, 16, 37], multi-phase flow model [19, 30, 40], Particle-FEM [18], and material point method (MPM) [1, 3, 38] have recently become popular in this area of research. Notable among these methods is the MPM [32] for its contribution to remarkable progress in this area, and is the method of choice for many researchers.

Within the MPM framework, two approaches are proposed to study the interaction between solid and liquid phases: (1) the two-phase single-point approach [10, 11, 15, 31, 39] and (2) the two-phase double-point approach [1, 3, 22, 23, 38]. The governing equations used by the two approaches are not the same. Compared with the first approach, in which the formulation is derived by reference to the solid configuration, the second approach uses two sets of material points to separately represent the solid skeleton and the liquid phase. Thanks to this, the motions of each phase can be expressed separately and applied to solve more diverse problems, such as seepage [3, 23], over-topping [22] and transportation [38]. Since we have our sights set on simulating a tsunami generated by a submarine or/and subaerial landslide, which requires the rough movements of water and soil phases to be represented, the second approach is considered more suitable.

However, in most of the coupled solid-liquid MPM algorithms, see, e.g., [3, 22], the liquid phase is assumed to be weakly compressible, since the MPM was originally developed mainly with focus on large deformation problems for solids. Many of these existing analysis methods result in pressure oscillation, free surface instability and involve a high computational cost due to the large bulk modulus of water when an explicit time integration is adopted. For single phase problems, there have been some remedies for dealing with incompressibility that yield stable solution schemes for MPM calculations; see, e.g., [17, 42] for flow simulations of incompressible fluids. Nevertheless, only few attempts have so far been made at managing with incompressibility for solid–liquid MPM. In addition, the dynamic addition or deletion of water particles is more complicated when it comes to problems containing inflow or outflow boundaries [22, 43]. In view of such issues, a class of stabilization schemes with a Eulerian description provides a simpler process and therefore has clear advantages in terms of calculation cost and accuracy. Thus, a novel scheme needs to be developed to couple the FEM with MPM to simulate granular mass-water interactions. Here, the “granular mass” is a synonym for “soil structure” in this study.

In this study, we propose a hybrid method of MPM and FEM capable of expressing the complex interaction between granular masses and liquids. The proposed method is formulated based on porous media theory [4, 6], in which saturated soil is considered as a continuum composed of the soil skeleton and the liquid phase. The MPM is applied to the governing equation of the solid phase by the Lagrangian description, whereas the stabilized FEM [34] is applied to the governing equation of the liquid phase in the Eulerian frame. In addition, a free surface is captured by using the phase-field method [14]. Several numerical examples are presented to demonstrate the performance of the proposed hybrid MPM–FEM on suppressing the afore-mentioned instabilities in the liquid phase (pressure oscillation, free surface instability) often appearing in the conventional solid–liquid coupled MPM and the capability in dealing with landslide-triggered tsunamis involving complex granular mass–water interaction problems.

Fig. 1

Continuum assumption of porous medium

Governing equations

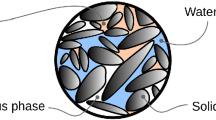
In this study, saturated soil is assumed to be a continuum consisting of a solid skeleton and a fluid phase, which are separately handled as shown in Fig. 1. It must be noted that either fully saturated or fully dry soils are considered in the present formulation.

Momentum balance and continuity equations

In the present formulation, the superscripts ‘s’ and ‘f’ are attached to involved variables and symbols to refer to the solid skeleton and fluid phase, respectively. In line with the methods established in a previous study [22, 23, 38], the momentum balance equations are solved to obtain the accelerations of the solid skeleton and the fluid phase separately. The momentum exchange term is considered in both of them.

In mixture theory, the momentum balance equation for the solid skeleton is written as

$$\begin{aligned} (1-n)\rho ^\text {s} a_i^\text {s}=\frac{\partial \bar{\sigma }_{ij}^\text {s}}{\partial x_j}+\hat{P_i}-p^\text {f}\frac{\partial n}{\partial x_i}+(1-n)\rho ^\text {s} b_i^\text {s}, \end{aligned}$$

(1)

where $\rho ^\text {s}$ is the true density of solid grains, n is the porosity, and $b_i^{\alpha }\, (\alpha = \text {s}, \text {f})$ is the body force. Here, the partial stress tensor of soil $\bar{\sigma }_{ij}^\text {s}$ is defined as

$$\begin{aligned} \bar{\sigma }_{ij}^\text {s}=\sigma _{ij}^\prime -(1-n) p^\text {f}\delta _{ij}, \end{aligned}$$

(2)

where $\sigma _{ij}^\prime$ is the effective stress of the soil skeleton, $p^\text {f}$ is the fluid pressure and $\delta _{ij}$ is the Kronecker’s delta. $\hat{P}_i$ is the drag force between the solid skeleton and the fluid phase, and the Forchheimer-like equation [23] is used to compute it as

$$\begin{aligned} \hat{P}_i=n^2\left( \frac{\mu ^\text {f}}{k}+\frac{1.75\rho ^\text {f}}{\sqrt{150k}}\frac{|v^\text {f}_i-v^\text {s}_i|}{n^{3/2}}\right) (v^\text {f}_i-v^\text {s}_i), \end{aligned}$$

(3)

where $\mu ^\text {f}$ is the dynamic viscosity of fluid and k is the intrinsic permeability. The intrinsic permeability of the soil is calculated according to the following Kozeny–Carman formula [9]:

$$\begin{aligned} k=\frac{D_{50}^2n^3}{150(1-n)^2}, \end{aligned}$$

(4)

which is a function of the porosity and the averaged diameter of the solid grains denoted by $D_{50}$. Using Eqs. (1)–(3), the final version of the momentum balance equation for the solid skeleton is written as

$$\begin{aligned} {\begin{matrix} (1-n)\rho ^\text {s}a_i^\text {s}=\frac{\partial \sigma _{ij}^\prime }{\partial x_j}-(1-n)\frac{\partial p^\text {f}}{\partial x_i}+\hat{P}_i+(1-n)\rho ^\text {s} b_i^\text {s}. \end{matrix}} \end{aligned}$$

(5)

The momentum balance equation for the fluid phase is expressed as

$$\begin{aligned} n\rho ^\text {f} a_i^\text {f}=\frac{\partial {\bar{\sigma }_{ij}^\text {f}}}{\partial x_j}-\hat{P}_i + p^\text {f}\frac{\partial n}{\partial x_i}+n\rho ^\text {f} b_i^\text {f}, \end{aligned}$$

(6)

where $\rho ^\text {f}$ is the true density of fluid, and $\bar{\sigma }_{ij}^\text {f}, a_i^\text {f}$ are the partial stress tensor and acceleration of fluid can be written as, respectively,

$$\begin{aligned}&\bar{\sigma }_{ij}^\text {f}=-np^\text {f}\delta _{ij}, \end{aligned}$$

(7)

$$\begin{aligned}&a_i^\text {f}=\frac{\partial v_{i}^\text {f}}{\partial t}+\bar{v}_{j}^\text {f} \frac{\partial v_{i}^\text {f}}{\partial x_j}. \end{aligned}$$

(8)

Here, the $a_i^\text {f}$ is in the Eulerian description so the advection velocity $\bar{v}_{j}^\text {f}$ also needs to be considered. Using Eqs. (6)–(8), the final version of the momentum balance equation for the fluid phase becomes

$$\begin{aligned} n\rho ^\text {f} \left( \frac{\partial v_{i}^\text {f}}{\partial t}+\bar{v}_{j}^\text {f}\frac{\partial v_{i}^\text {f}}{\partial x_j}\right) =-n\frac{\partial p^\text {f}}{\partial x_i}-\hat{P}_i+n\rho ^\text {f} b_i^\text {f}. \end{aligned}$$

(9)

On the other hand, solid grains can be regarded incompressible, the mass balance equation for the solid skeleton is given as

$$\begin{aligned} \rho ^\text {s}\frac{D^\text {s}(1-n)}{Dt}+(1-n)\frac{D^\text {s}\rho ^\text {s}}{Dt}+(1-n)\rho ^\text {s}\frac{\partial v_i^\text {s}}{\partial x_i}=0, \end{aligned}$$

(10)

in which the second term can be neglected. Also, on the assumption of the incompressibility the fluid phase, the mass balance equation for the fluid phase is given as

$$\begin{aligned} \rho ^\text {f}\frac{D^\text {f} n}{Dt}+n\frac{D^\text {f}\rho ^\text {f}}{Dt}+n\rho ^\text {f}\frac{\partial v_i^\text {f}}{\partial x_i}=0, \end{aligned}$$

(11)

in which the second term can also be neglected. In this study, the continuity equation of the fluid is solved together with the momentum equation of the fluid. Therefore, the material time derivatives on the left-hand side of Eqs. (10) and (11) read

$$\begin{aligned} {\begin{matrix}&\frac{D^\text {s}(1-n)}{Dt}=\frac{\partial (1-n)}{\partial t}+v_i^\text {s}\frac{\partial (1-n)}{\partial x_i}, \end{matrix}} \end{aligned}$$

(12)

$$\begin{aligned} {\begin{matrix}&\frac{D^\text {f} n}{Dt}=\frac{\partial n}{\partial t}+v_i^\text {f}\frac{\partial n}{\partial x_i}. \end{matrix}} \end{aligned}$$

(13)

Using Eqs. (10)-(13), the continuity equation for the whole mixture becomes

$$\begin{aligned} \frac{\partial \left( (1-n)v_i^\text {s}+nv_i^\text {f}\right) }{\partial x_i}=0. \end{aligned}$$

(14)

Constitutive model of soil skeleton

We employ a standard elasto-plastic constitutive model based on multiplicative decomposition of the deformation gradient such that

$$\begin{aligned} F_{ij}=F_{ik}^\text {e}F_{kj}^\text {p}, \end{aligned}$$

(15)

where $F_{ik}^\text {e}$ and $F_{kj}^\text {p}$ are the elastic and plastic components, respectively. The Hencky hyperelastic model is adopted to represent the elastic response of the solid keleton whose energy function is given as

$$\begin{aligned} \mathcal {H}(\lambda _{1}^\text {e},\lambda _{2}^\text {e},\lambda _{3}^\text {e})=\mu \left[ (\ln {\lambda _{1}^\text {e}})^2+(\ln {\lambda _{2}^\text {e}})^2+(\ln {\lambda _{3}^\text {e}})^2\right] +\frac{\lambda }{2}(\ln {J^\text {e}})^2, \end{aligned}$$

(16)

where $\lambda _{\alpha }^\text {e} \, (\alpha =1,2,3)$ are the three principal stretches of the elastic component of the left-Cauchy-Green deformation tensor, $\lambda , \, \mu$ are Lame constant, and $J^\text {e}$ is the determinant of $F_{ik}^\text {e}$. The plastic deformation of the solid phase is defined by the Drucker-Prager yield criterion whose plastic potential function is given as

$$\begin{aligned} \Phi =\sqrt{J_2(s_{ij})}+\eta p-\xi c, \end{aligned}$$

(17)

where $s_{ij}$ is the deviatoric stress defined as $s_{ij}=\sigma '_{ij}-\frac{1}{3}p\delta _{ij}$. Here, p is the hydrostatic pressure component and $J_2$ is the second invariant of the deviatoric stress tensor. Also, c is the cohesion, and $\eta , \, \xi$ are material constants defined as

$$\begin{aligned} \eta \equiv \frac{3\tan \psi }{\sqrt{9+12\tan ^2 \psi }}, \end{aligned}$$

(18)

$$\begin{aligned} \xi \equiv \frac{3}{\sqrt{9+12\tan ^2 \psi }}, \end{aligned}$$

(19)

where $\psi$ is the internal friction angle. In order to suppress excessive dilatancy, the non-associated flow rule is employed in this study. The corresponding plastic potential to determine the specific flow rule is formed by setting the second and third terms in the right hand side in Eq. (17) to zeros.

Weak forms

We adopt the direct method with the conventional FEM, in which the momentum balance and continuity equations, Eqs. (9) and (14), are solved together. The corresponding weak form is written as

$$\begin{aligned} {\begin{matrix} &{}\int _{\varOmega ^\text {f}}\omega _i n\rho ^\text {f}\left( \frac{\partial v_{i}^\text {f}}{\partial t}+\bar{v}_{j}^\text {f} \frac{\partial v_{i}^\text {f}}{\partial x_j}-b_i^\text {f} \right) d\varOmega +\int _{\varOmega ^\text {f}}\omega _i\hat{P}_id\varOmega \\ &{} \quad -\int _{\varOmega ^\text {f}}\frac{\partial \left( \omega _in\right) }{\partial x_i}p^\text {f} d\varOmega +\int _{\varOmega ^\text {f}}q\frac{\partial }{\partial x_i}\left( (1-n)v_i^\text {s}+n v_i^\text {f}\right) d\varOmega \\ &{}\quad =-\int _{\partial \varOmega ^\text {f}}\omega _in\bar{p}_i^\text {f} d\Gamma , \end{matrix}} \end{aligned}$$

(20)

where $v_i^\text {f}$, $\bar{v}_{j}^\text {f}$ ,$p^\text {f}$ and $\bar{p}_i^\text {f}$ are the velocity, advection velocity, pressure fields and prescribed pore pressure that acts on the part of the fluid phase boundary $\partial \varOmega ^\text {f}$, respectively, while $\omega _i$ and q are the corresponding test functions.

By multiplying Eq. (5) by a test function $\omega _i$ and then integrating over the domains $\varOmega ^\text {s}$ and $\varOmega ^\text {f}$, we also can derive the weak form of the momentum balance equation for the solid phase as

$$\begin{aligned} {\begin{matrix} &{}\int _{\varOmega ^\text {s}}\omega _i (1-n)\rho ^\text {s} a_i^\text {s}d\varOmega =-\int _{\varOmega ^\text {s}}\frac{\partial \omega _i}{\partial x_j}\sigma _{ij}^\prime d\varOmega +\int _{\partial \varOmega ^\text {s}}\omega _i t_i d\Gamma \\ &{}\quad +\int _{\varOmega ^\text {s}}\omega _i(1-n)\rho ^\text {s} b_i^\text {s} d\varOmega +\int _{\varOmega ^\text {f}}\frac{\partial \left( \omega _i (1-n)\right) }{\partial x_i} p^\text {f} d\varOmega \\ &{}\quad -\int _{\partial \varOmega ^\text {f}}\omega _i(1-n)\bar{p}_i^\text {f}d\Gamma +\int _{\varOmega ^\text {f}}\omega _i\hat{P}_i d\varOmega , \end{matrix}} \end{aligned}$$

(21)

in which the term involving the stress has been integrated by parts by the application of divergence theorem. Here, $t_i$ is the prescribed traction that acts on the part of the solid skeleton’s boundary $\partial \varOmega ^\text {s}$, and $\bar{p}_i^\text {f}$ is the same as that in Eq. (20).

Fig. 2

Schematic diagram of hybrid MPM–FEM

Hybrid MPM–FEM

In the proposed hybrid MPM–FEM, MPM is applied for deformation analyses of the solid skeleton using both Lagrangian and Eulerian frames, the latter of which is used together to apply FEM for flow simulations of the fluid phase. This section presents both of the discretized equations in some detail. For reference, Fig. 2 shows a schematic diagram illustrating the combination of these separate discretization schemes.

Spatial discretization

An arbitrary variable $\Phi (\varvec{x})$ in the solid skeleton and the fluid phase is approximated as integrated over every FE (finite element) and every solid material point as, respectively,

$$\begin{aligned}&\int _{\varOmega ^\text {f}}\Phi (\varvec{x})d\varOmega \approx \sum _{e=1}^{N^{e}}\int _{\varOmega ^{e}}\Phi (\varvec{x})d\varOmega , \end{aligned}$$

(22)

$$\begin{aligned}&\int _{\varOmega ^\text {s}}\Phi (\varvec{x})d\varOmega \approx \sum _{p=1}^{N^{p}}\int _{\varOmega ^{p}}\Phi (\varvec{x})d\varOmega \approx \sum _{p=1}^{N^{p}}\Phi (\varvec{x}^{p})\varOmega ^{p}, \end{aligned}$$

(23)

where superscripts ‘e’ and ‘p’ represent a FE and material point, respectively. Also, $\varOmega ^{e}$ is the domain of an element and $\varOmega ^{p}$ is the volume of a solid material point. The field variables such as velocity, pressure and their test functions can be approximated using the shape functions $N_{\alpha }(\varvec{x})$ associated with the Eulerian grid as

$$\begin{aligned} \Phi (\varvec{x})\approx \Phi ^h(\varvec{x})=\sum _{\alpha =1}^{N^n}N_{\alpha }(\varvec{x})\Phi _{\alpha }, \end{aligned}$$

(24)

where $N^n$ is the total number of nodes and $\Phi _{\alpha }$ is the nodal value at node $\alpha$. Here and hereafter, variables with superscript ‘h’ indicates their approximations in this manner. It should be noted that the same shape function and the same Eulerian grid are utilized to discretize both the variables associated with the solid skeleton and fluid phase. In this study, we employ the 2nd-order B-spline basis functions as shape functions, the details of which are presented in Appendix A.

The stabilized FEM with the SUPG/PSPG stabilization schemes [7, 34] is applied to the governing equation of the fluid phase, Eq. (20), to obtain the following discretized equation:

$$\begin{aligned}&\int _{\varOmega ^\text {f}}\omega _i^h n\rho ^\text {f} \left( \frac{\partial v_{i}^{\text {f},\,h}}{\partial t}+\bar{v}_{j}^{\text {f}, \, h}\frac{\partial v_{i}^{\text {f}, \, h}}{\partial x_j}-b_i^\text {f} \right) d\varOmega +\int _{\varOmega ^\text {f}}\omega ^h_i\hat{P}_i^hd \varOmega \nonumber \\&\quad -\int _{\varOmega ^\text {f}}\frac{\left( \partial \omega _i^h n\right) }{\partial x_i}p^{\text {f}, \, h}d\varOmega +\int _{\varOmega ^\text {f}}q^h\frac{\partial }{\partial x_i}\left( (1-n)v_i^{\text {s}, \, h}+nv_i^{\text {f}, \, h}\right) d\varOmega \nonumber \\&\quad \quad +\sum _{e=1}^{N^e}\int _{\varOmega ^{e}}\tau _\text {m}^e\left( \bar{v}_j^{\text {f}, \, h}\frac{\partial \omega _i^h}{\partial x_j}+\frac{1}{\rho ^\text {f}}\frac{\partial q^h}{\partial x_i}\right) \nonumber \\&\quad \quad \quad \cdot \left[ n\rho ^\text {f} \left( \frac{\partial v_{i}^{\text {f}, \, h}}{\partial t}+\bar{v}_{j}^{\text {f}, \, h}\frac{\partial v_{i}^{\text {f}, \, h}}{\partial x_j}-b_i^\text {f} \right) +\hat{P}_i^h + n\frac{\partial p^{\text {f}, \, h}}{\partial x_i}\right] d\varOmega \nonumber \\&\quad \quad +\sum _{e=1}^{N^e}\int _{\varOmega ^{e}}\tau _\text {cont}^e\frac{\partial \omega _i^h}{\partial x_i}\rho ^\text {f} \frac{\partial }{\partial x_j}\left( (1-n)v_j^{\text {s}, \, h}+nv_j^{\text {f}, \, h}\right) d\varOmega \nonumber \\&\quad \quad =-\int _{\partial \varOmega ^\text {f}}\omega _i^h n\bar{p}^{\text {f}, \, h}d\Gamma . \nonumber \\ \end{aligned}$$

(25)

The first four integral terms on the left-hand side and the integral term on the right-hand side are Galerkin items. On the other hand, the fifth term involves the SUPG and PSPG terms, which are introduced to stabilize the advection-induced unstable behavior and to suppress pressure oscillation, respectively. Also, the sixth term is the shock-capturing term[2] introduced to avoid the numerical instability of free surfaces. The stabilization parameters, $\tau _\text {m}^e$ and $\tau _\text {cont}^e$, are defined as, respectively,

$$\begin{aligned}&\tau _\text {m}^e\equiv \left[ \left( \frac{2}{\varDelta t}\right) ^2+\left( \frac{2\Vert \bar{v}_i^{\text {f}, \, h}\Vert }{h_e}\right) ^2+\left( \frac{4\nu }{h_e^2}\right) ^2\right] ^{-\frac{1}{2}} \end{aligned}$$

(26)

$$\begin{aligned}&\tau _\text {cont}^e\equiv \frac{h_e}{2}\Vert \bar{v}_i^{\text {f}, \, h}\Vert \xi (Re_e) \end{aligned}$$

(27)

$$\begin{aligned}&Re_e\equiv \frac{\Vert \bar{v}_i^{\text {f}, \, h}\Vert h_e}{2\nu } \end{aligned}$$

(28)

$$\begin{aligned}&\xi (Re_e)\equiv {\left\{ \begin{array}{ll} \dfrac{Re_e}{3}, &{}Re_e\le 3\\ 1, &{}Re_e > 3 \end{array}\right. } \end{aligned}$$

(29)

where $\varDelta t$, $h_e$, $\nu$, $\bar{v}_i^{\text {f}, \, h}$ and $Re_e$ are the time increment, the characteristic element length, the kinematic viscosity, the advection velocities, and the element Reynolds number, respectively.

Substituting Eqs. (22) and (24) into Eq. (25), we obtain the following FE equations for the fluid phase:

$$\begin{aligned}&(\varvec{M}+\varvec{M}_{\text {s}})\frac{\partial \varvec{v}_i^\text {f}}{\partial t}+(\varvec{A}+\varvec{A}_{\text {s}})\varvec{v}_i^\text {f}+(\varvec{G}_{\text {s},\,i}-\varvec{G}_i)\varvec{p}^\text {f}\end{aligned}$$

(30)

$$\begin{aligned}&\quad +(\varvec{Q}_{(i)}+\varvec{Q}_{\text {s}, \,{{(i)}}})(\varvec{v}_i^\text {f}-\varvec{v}_i^\text {s})+\varvec{S}_{\text {c},\, ij}^\text {s}\varvec{v}_{j}^\text {s}+\varvec{S}_{\text {c},\, ij}^\text {f}\varvec{v}_{j}^\text {f}=(\varvec{F}+\varvec{F}_\text {s})\varvec{b}_i^\text {f},\nonumber \\&\varvec{C}^\text {s}_{i}\varvec{v}_i^\text {s}+\varvec{C}^\text {f}_{i}\varvec{v}_i^\text {f}+\varvec{M}_{\text {p},\,i}\frac{\partial \varvec{v}_i^\text {f}}{\partial t}+\varvec{A}_{\text {p},\,i}\varvec{v}_i^\text {f}+\varvec{G}_{\text {p}}\varvec{p}^\text {f}+\varvec{Q}_{\text {p},\,i}(\varvec{v}_i^\text {f}-\varvec{v}_i^\text {s})\nonumber \\&\quad =\varvec{F}_{\text {p},\,i}\varvec{b}_i^\text {f}, \end{aligned}$$

(31)

which constitutes the set of the momentum balance and the continuity (mass conservation) equations, respectively. These discretized equations are to be solved for the nodal fluid velocity and pressure vectors at nodes, provided that the nodal solid velocity vectors are given as data. Here, $\varvec{M}$, $\varvec{A}$, $\varvec{G}$, $\varvec{Q}$, $\varvec{S}_\text {c}$, $\varvec{F}$ and $\varvec{C}$ are the mass matrix, advection matrix, pressure matrix, interaction matrix, shock-capturing matrix, force vector, and continuity matrix, respectively. Also, subscript ‘i’ indicates the component of a nodal velocity vector in the $x_i$-direction, and subscripts ‘s’ and ‘p’ indicate the SUPG and PSPG matrices, respectively. The specific forms of these matrices are written as follows:

$$\begin{aligned}&[\varvec{M}]^{e}_{\alpha \beta }=\int _{\varOmega ^{e}}\rho ^\text {f} n N_{\alpha }^{e}N_{\beta }^{e}d\varOmega , \end{aligned}$$

(32)

$$\begin{aligned}&[\varvec{A}]^{e}_{\alpha \gamma }=\int _{\varOmega ^{e}}\rho ^\text {f} n N_{\alpha }^{e}N_{\beta }^{e}\bar{v}_{j\beta }^{\text {f}, \, e}\frac{\partial N_{\gamma }^{e}}{\partial x_{j}}d\varOmega , \end{aligned}$$

(33)

$$\begin{aligned}&[\varvec{G}_i]^{e}_{\alpha \beta }=\int _{\varOmega ^{e}}\left( n \frac{\partial N_{\alpha }^{e}}{\partial x_i}+N_{\alpha }^{e}\frac{\partial n}{\partial x_i}\right) N_{\beta }^{e}d\varOmega , \end{aligned}$$

(34)

$$\begin{aligned}&[\varvec{Q}_i]^{e}_{\alpha \beta }=\int _{\varOmega ^{e}} \vartheta n^2N_{\alpha }^{e}\left( \frac{\mu ^\text {f}}{k}+\frac{1.75\rho ^\text {f}}{\sqrt{150 k}}\frac{|v^\text {f}_{i\beta }-v^\text {s}_{i\beta }|}{n^{3/2}}\right) N_{\beta }^{e}d\varOmega , \end{aligned}$$

(35)

$$\begin{aligned}&[{\varvec{C}_i^\text {s}}]^{e}_{\alpha \beta }=\int _{\varOmega ^{e}}\left( (1-n)N_{\alpha }^{e}\frac{\partial N_{\beta }^{e}}{\partial x_i}-N_{\alpha }^{e}\frac{\partial n}{\partial x_i}N_{\beta }^{e}\right) d\varOmega , \end{aligned}$$

(36)

$$\begin{aligned}&[{\varvec{C}_i^\text {f}}]^{e}_{\alpha \beta }=\int _{\varOmega ^{e}}\left( n N_{\alpha }^{e}\frac{\partial N_{\beta }^{e}}{\partial x_i}+N_{\alpha }^{e}\frac{\partial n}{\partial x_i}N_{\beta }^{e}\right) d\varOmega , \end{aligned}$$

(37)

$$\begin{aligned}&[{\varvec{F}}]^{e}_{\alpha }=\int _{\varOmega ^{e}}\rho ^\text {f} n N_{\alpha }^{e}d\varOmega , \end{aligned}$$

(38)

$$\begin{aligned}&[\varvec{M}_{\text {s}}]_{\alpha \gamma }^{e}=\tau _\text {m}^e\int _{\varOmega ^{e}}\rho ^\text {f} n \frac{\partial N_{\alpha }^{e}}{\partial x_{j}}N_{\beta }^{e}\bar{v}_{j\beta }^{\text {f}, \, e}N_{\gamma }^{e}d\varOmega , \end{aligned}$$

(39)

$$\begin{aligned}&[\varvec{A}_\text {s}]^{e}_{\alpha \delta }=\tau _\text {m}^e\int _{\varOmega ^{e}}\rho ^\text {f} n \frac{\partial N_{\alpha }^{e}}{\partial x_{j}}N_{\beta }^{e}\bar{v}_{j\beta }^{\text {f}, \, e}N_{\gamma }^{e}\bar{v}_{l\gamma }^{\text {f}, \, e}\frac{\partial N_\delta ^{e}}{\partial x_l}d\varOmega , \end{aligned}$$

(40)

$$\begin{aligned}&[\varvec{G}_{\text {s},\,i}]^{e}_{\alpha \gamma }=\tau _\text {m}^e\int _{\varOmega ^{e}} n \frac{\partial N_{\alpha }^{e}}{\partial x_{j}}N_{\beta }^{e}\bar{v}_{j\beta }^{\text {f}, \, e}\frac{N_{\gamma }^{e}}{\partial x_i}d\varOmega , \end{aligned}$$

(41)

$$\begin{aligned}&[\varvec{Q}_{\text {s},\,i}]^{e}_{\alpha \gamma }=\tau _\text {m}^e\int _{\varOmega ^{e}} \vartheta n^2\frac{\partial N_{\alpha }^{e}}{\partial x_{j}}N_{\beta }^{e}\bar{v}_{j\beta }^{\text {f}, \, e}\nonumber \\&\qquad \qquad \ \ \qquad \left( \frac{\mu ^\text {f}}{k}+\frac{1.75\rho ^\text {f}}{\sqrt{150 k}}\frac{|v^\text {f}_{i\gamma }-v^\text {s}_{i\gamma }|}{ n^{3/2}}\right) N_{\gamma }^{e}d\varOmega ,\end{aligned}$$

(42)

$$\begin{aligned}&[{\varvec{F}_\text {s}}]^{e}_{\alpha \beta }=\tau _\text {m}^e\int _{\varOmega ^{e}}\rho ^\text {f} n \frac{\partial N_{\alpha }^{e}}{\partial x_{j}}N_{\beta }^{e}\bar{v}_{j\beta }^{\text {f}, \, e}d\varOmega , \end{aligned}$$

(43)

$$\begin{aligned}&[\varvec{M}_{\text {p},\,i}]_{\alpha \gamma }^{e}=\tau _\text {m}^e\int _{\varOmega ^{e}} n \frac{\partial N_{\alpha }^{e}}{\partial x_i}N_{\beta }^{e}d\varOmega , \end{aligned}$$

(44)

$$\begin{aligned}&[\varvec{A}_{\text {p},\,i}]^{e}_{\alpha \gamma }=\tau _\text {m}^e\int _{\varOmega ^{e}} n \frac{\partial N_{\alpha }^{e}}{\partial x_i}N_{\beta }^{e}\bar{v}_{j\beta }^{\text {f}, \, e}\frac{\partial N_{\gamma }^{e}}{\partial x_{j}}d\varOmega , \end{aligned}$$

(45)

$$\begin{aligned}&[\varvec{G}_{\text {p}}]^{e}_{\alpha \beta }=\tau _\text {m}^e\int _{\varOmega ^{e}}\frac{n}{\rho ^\text {f}}\frac{\partial N_{\alpha }^{e}}{\partial x_{j}}\frac{\partial N_{\beta }^{e}}{\partial x_{j}}d\varOmega , \end{aligned}$$

(46)

$$\begin{aligned}&[\varvec{Q}_{\text {p},\,i}]^{e}_{\alpha \beta }=\tau _\text {m}^e\int _{\varOmega ^{e}}\frac{\vartheta n^2}{\rho ^\text {f}}\frac{\partial N_{\alpha }^{e}}{\partial x_i}\nonumber \\&\left( \frac{\mu ^\text {f}}{k}+\frac{1.75\rho ^\text {f}}{\sqrt{150k}}\frac{|v^\text {f}_{i\beta }-v^\text {s}_{i\beta }|}{ n^{3/2}}\right) N_{\beta }^{e}d\varOmega ,\end{aligned}$$

(47)

$$\begin{aligned}&[{\varvec{F}_{\text {p},\,i}}]^{e}_{\alpha }=\int _{\varOmega ^{e}} n \frac{\partial N_{\alpha }^{e}}{\partial x_i}d\varOmega , \end{aligned}$$

(48)

$$\begin{aligned}&[{\varvec{S}_{{\text {c},\,ij}}^\text {s}}]^{e}_{\alpha \beta }=\tau _\text {cont}^e\int _{\varOmega ^{e}}\rho ^\text {f}\frac{\partial N_{\alpha }^{e}}{\partial x_i}\left( (1-n)\frac{\partial N_{\beta }^{e}}{\partial x_{j}}-\frac{\partial n}{\partial x_{j}}N_{\beta }^{e}\right) d\varOmega , \end{aligned}$$

(49)

$$\begin{aligned}&[{\varvec{S}_{{\text {c},\,ij}}^\text {f}}]^{e}_{\alpha \beta }=\tau _\text {cont}^e\int _{\varOmega ^{e}}\rho ^\text {f}\frac{\partial N_{\alpha }^{e}}{\partial x_i}\left( n \frac{\partial N_{\beta }^{e}}{\partial x_{j}}+\frac{\partial n}{\partial x_{j}}N_{\beta }^{e}\right) d\varOmega . \end{aligned}$$

(50)

Here, subscripts ‘j’ and ‘l’ indicate the components of the nodal velocity vectors, ‘$\alpha$’, ‘$\beta$’, ‘$\gamma$’, and ‘$\delta$’ denote the values of the grid nodes. Also, the volume fraction of the solid material points in an element, $\vartheta$, has been introduced, because there is a possibility that the fluid phase and the solid skeleton do not overlap with each other. In these discretized equations, n, k, and $\vartheta$ are functions of space to be interpolated by use of the shape functions as

$$\begin{aligned} n \approx \sum _{\alpha =1}^{N^{n}} n_{\alpha } N_{\alpha }^{e}, \quad k \approx \sum _{\alpha =1}^{N^{n}} k_{\alpha } N_{\alpha }^{e}, \quad \vartheta \approx \sum _{\alpha =1}^{N^{n}} \vartheta _{\alpha } N_{\alpha }^{e}, \end{aligned}$$

(51)

where $n_{\alpha }$ and $k_{\alpha }$ are the nodal values of the porosity and permeability, respectively.

On the other hand, substituting Eqs. (22)$\sim$(24) into Eq. (21), we obtain the semi-discrete momentum balance equation for the solid skeleton as

$$\begin{aligned} \varvec{M}^\text {s}\varvec{a}_{i}^\text {s}=\varvec{F}_{\text {int}, \, i}^\text {s}+\varvec{F}_{\text {ext}, \, i}^\text {s}+\varvec{Q}_{(i)}\left( \varvec{v}^\text {f}_{i}-\varvec{v}^\text {s}_{i}\right) . \end{aligned}$$

(52)

This equation is solved for the solid acceleration at nodes by using the pressure of the fluid phase as input a datum, which is the solution of the momentum balance equation for the fluid phase in Eqs. (30) and (31). Here, the mass matrix for the solid skeleton is lumped as

$$\begin{aligned}{}[\varvec{M}^\text {s}]_{\alpha }=\sum _{p=1}^{N^{p}}m^{p}N_{\alpha }(\varvec{x}^{p}), \end{aligned}$$

(53)

where $m^{p}$ is the mass of the solid particle computed as $m^p=(1-n^p)\rho ^\text {s}\varOmega ^p$. Also, the nodal values of the internal and external forces are written as, respectively,

$$\begin{aligned}&[\varvec{F}_{\text {int}, \, i}^\text {s}]_{\alpha }=-\sum _{p=1}^{N^{p}}\frac{\partial N_{\alpha }(\varvec{x}^{p})}{\partial x_j}\sigma _{ij}^{\prime }\varOmega ^{p}\nonumber \\&\quad +\int _{\varOmega ^\text {f}}\left( (1-n)\frac{\partial N_{\alpha }^{e}}{\partial x_i}-N_{\alpha }^{e}\frac{\partial n}{\partial x_i}\right) p^\text {f} d\varOmega , \end{aligned}$$

(54)

$$\begin{aligned}&[\varvec{F}_{\text {ext}, \, i}^\text {s}]_{\alpha }=\sum _{p=1}^{N^{p}}N_{\alpha }(\varvec{x}^{p})m^{p}b_i^\text {s}+\int _{\partial \varOmega ^\text {s}}N_{\alpha }(\varvec{x}^\text {s})t_i(\varvec{x}^\text {s})d\Gamma , \end{aligned}$$

(55)

in which the fluid pressure must be interpolated as $p^\text {f} = \sum _{\beta =1}^{N^{n}}{N_\beta ^e p_{\beta }^\text {f}}$.

Time integration

The semi-discrete equations derived above are discretized with a discrete set of times, and the numerical solution is obtained at a current time. In what follows, the discrete approximation at time $t^L$ is indicated by superscript L and the time increment is defined as $\varDelta t\equiv t^{L+1}-t^{L}$.

The time discretized forms of the momentum balance and the mass balance equations for the fluid phase, Eqs. (30) and (31), can be written as

$$\begin{aligned}&(\varvec{M}+\varvec{M}_{\text {s}})\frac{\partial \varvec{v}_i^\text {f}}{\partial t}\bigg |^{L+\theta }+(\varvec{A}+\varvec{A}_{\text {s}})\varvec{v}_i^{\text {f}, \, L+\theta }+(\varvec{G}_{\text {s},\,i}-\varvec{G}_i)\varvec{p}^{\text {f}, \, L+\theta }\nonumber \\&\quad +(\varvec{Q}_{(i)}+\varvec{Q} _{\text {s}, {{(i)}}})(\varvec{v}_i^{\text {f}, \, L+\theta }-\varvec{v}_i^{s,L+\theta })+\varvec{S}_{\text {c},\, ij}^\text {s}\varvec{v}_{j}^{s,L+\theta }+\varvec{S}_{\text {c},\, ij}^\text {f}\varvec{v}_{j}^{\text {f}, \, L+\theta }\nonumber \\&\quad \quad =(\varvec{F}+\varvec{F}_{\text {s}})\varvec{b}_i^{\text {f}, \, L}, \nonumber \\ \end{aligned}$$

(56)

$$\begin{aligned}&\varvec{C}^\text {s}_{i}\varvec{v}_i^{s, L+\theta }+\varvec{C}^\text {f}_{i}\varvec{v}_i^{\text {f}, \, L+\theta }+\varvec{M}_{\text {p},\,i}\frac{\partial \varvec{v}_i^\text {f}}{\partial t}\bigg |^{L+\theta }+\varvec{A}_{\text {p},\,i}\varvec{v}_i^{\text {f}, \, L+\theta }+\varvec{G}_{\text {p}}\varvec{p}^{\text {f}, \, L+\theta }\nonumber \\&\quad +\varvec{Q}_{\text {p},\,i}(\varvec{v}_i^{\text {f}, \, L+\theta }-\varvec{v}_i^{s, L+\theta })=\varvec{F}_{\text {p},\,i}\varvec{b}_i^{\text {f}, \, L},\nonumber \\ \end{aligned}$$

(57)

which are simultaneously solved for the fluid phase velocities $v_i^{\text {f}, \, L+1}$ and fluid pressure $p^{\text {f}, \, L+1}$. Here, the range of $\theta$ is set to be $0\le \theta \le 1$. Also, the nodal variables (time derivative, velocities, pressure) are approximated as

$$\begin{aligned}&\frac{\partial \varvec{v}_i^\text {f}}{\partial t}\bigg |^{L+\theta }\approx \frac{\varvec{v}_i^{\text {f}, \, L+1}-\varvec{v}_i^{\text {f}, \, L}}{\varDelta t}, \end{aligned}$$

(58)

$$\begin{aligned}&\varvec{v}_i^{\text {f}, \, L+\theta }\approx \varvec{v}_i^{\text {f}, \, L+\frac{1}{2}}=\frac{\varvec{v}_i^{\text {f}, \, L+1}+\varvec{v}_i^{\text {f}, \, L}}{2}, \end{aligned}$$

(59)

$$\begin{aligned}&\varvec{v}_i^{\text {s}, \, L+\theta }\approx \varvec{v}_i^{\text {s}, \, L}, \end{aligned}$$

(60)

$$\begin{aligned}&\varvec{p}^{\text {f}, \, L+\theta }\approx \varvec{p}^{\text {f}, \, L+1}, \end{aligned}$$

(61)

where $\theta$ has been set at 1 in Eqs. (58) and (61), 1/2 in Eq. (59) and 0 in Eq. (60). To explicitly approximate the advection velocities $\bar{v}_i^\text {f}$, we adopt the Adams-Bashforth method [12], as

$$\begin{aligned} \varvec{\bar{v}}_i^\text {f}=\frac{3}{2}\varvec{v}_i^{\text {f}, \, L}-\frac{1}{2}\varvec{v}_i^{\text {f}, \, L-1}. \end{aligned}$$

(62)

Also, the continuity term $\varvec{C}_{i}^\text {f}\varvec{v}_i^{\text {f}, \, L+\theta }$ is implicitly represented, while the interaction terms, $\varvec{Q}_i\varvec{v}_i^{\text {f}, \, L+\theta }, \, \varvec{Q}_{\text {s},\,i}\varvec{v}_i^{\text {f}, \, L+\theta }$ and $\varvec{Q}_{\text {p},\,i}\varvec{v}_i^{\text {f}, \, L+\theta }$, are evaluated explicitly as

$$\begin{aligned}&\varvec{C}_{i}^\text {f}\varvec{v}_i^{\text {f}, L+\theta }=\varvec{C}_{i}^\text {f}\varvec{v}_i^{\text {f}, L+1}, \end{aligned}$$

(63)

$$\begin{aligned}&\varvec{Q}_{i}\varvec{v}_i^{\text {f}, L+\theta }=\varvec{Q}_i\varvec{v}_i^{\text {f}, \, L}, \end{aligned}$$

(64)

$$\begin{aligned}&\varvec{Q}_{\text {s},\,i}\varvec{v}_i^{\text {f}, L+\theta }=\varvec{Q}_{\text {s},\,i}\varvec{v}_i^{\text {f}, \, L}, \end{aligned}$$

(65)

$$\begin{aligned}&\varvec{Q}_{\text {p},\,i}\varvec{v}_i^{\text {f}, L+\theta }=\varvec{Q}_{\text {p},\,i}\varvec{v}_i^{\text {f}, \, L}. \end{aligned}$$

(66)

where $\theta$ has been set at 1 in Eq. (63) and 0 in Eqs. (64), (65) and (66). Using Eqs. (56)-(66) with some straightforward calculations, we obtain the final versions of Eqs. (56) and (57) as

$$\begin{aligned}&(\varvec{M}+\varvec{M}_{\text {s}})\frac{\varvec{v}_i^{\text {f}, \, L+1}}{\varDelta t}+\left( \varvec{A}+\varvec{A}_{\text {s}}+\varvec{S}_{\text {c},\, ij}^\text {f}\right) \frac{\varvec{v}_{j}^{\text {f}, \, L+1}}{2}+\left( \varvec{G}_{\text {s},\,i}-\varvec{G}_i\right) \varvec{p}^{\text {f}, \, L+1}\nonumber \\&\quad =(\varvec{M}+\varvec{M}_{\text {s}})\frac{\varvec{v}_i^{\text {f}, \, L}}{\varDelta t}-\left( \varvec{A}+\varvec{A}_{\text {s}}+\varvec{S}_{\text {c},\,ij}^\text {f}\right) \frac{\varvec{v}_{j}^{\text {f}, \, L}}{2}-\varvec{S}_{\text {c},\,ij}^\text {s}\varvec{v}_{j}^{\text {s}, \, L}\nonumber \\&\quad \quad +(\varvec{Q}_{(i)}+\varvec{Q}_{\text {s},\,({i})})(\varvec{v}_i^{\text {s}, \, L}-\varvec{v}_i^{\text {f}, \, L})+(\varvec{F}+\varvec{F}_{\text {s}})\varvec{b}_i^{\text {f}, \, L}, \nonumber \\ \end{aligned}$$

(67)

$$\begin{aligned}&\left( \varvec{C}^\text {f}_{i}+\frac{\varvec{M}_{\text {p},\,i}}{\varDelta t}+\frac{\varvec{A}_{\text {p},\,i}}{2}\right) \varvec{v}_i^{\text {f}, \, L+1}+\varvec{G}_{\text {p}}\varvec{p}^{\text {f}, \, L+1}=\left( \frac{\varvec{M}_{\text {p},\,i}}{\varDelta t}-\frac{\varvec{A}_{\text {p},\,i}}{2}\right) \varvec{v}_i^{\text {f}, \, L}\nonumber \\&\quad \quad +\varvec{Q}_{\text {p},\,i}(\varvec{v}_i^{\text {s}, \, L}-\varvec{v}_i^{\text {f}, \, L})-\varvec{C}^\text {s}_{i}\varvec{v}_i^{\text {s}, \, L}+\varvec{F}_{\text {p},\,i}\varvec{b}_i^{\text {f}, \, L},\nonumber \\ \end{aligned}$$

(68)

from which the fluid phase velocity and pressure are determined for the next time step.

The time-discretized form of the momentum balance equation for the solid phase (52) can be written as

$$\begin{aligned} \varvec{M}^{\text {s}, \, L+\theta }\varvec{a}_{i}^{\text {s}, \, L+\theta }=\varvec{F}_{\text {int}, \, i}^{\text {s}, \, L+\theta }+\varvec{F}_{\text {ext}, \, i}^{\text {s}, \, L+\theta }+\varvec{Q}_{(i)}\left( \varvec{v}^{\text {f}, \, L+\theta }_{i}-\varvec{v}^{\text {s}, \, L+\theta }_{i}\right) . \end{aligned}$$

(69)

Using the nodal pressure, $\varvec{p}^{\text {f}, \, L+1}$, obtained from Eqs. (67) and (68), this is solved for $\varvec{a}_{i}^{\text {s}, \, L}$ explicitly with $\theta =0$. After the nodal acceleration of the solid skeleton, $\varvec{a}_{i}^{\text {s}, \, L}$, is obtained, the nodal velocity vector in the $x_i$-direction is updated as

$$\begin{aligned} \varvec{v}_{i}^{\text {s}, \, L+1}=\varvec{v}_{i}^{\text {s}, \, L}+\varDelta t\varvec{a}_{i}^{\text {s}, \, L}, \end{aligned}$$

(70)

and then the velocity and position vectors of each solid material point can be updated by the following formulae:

$$\begin{aligned}&v_{i}^{p, \, L+1}=v_{i}^{p, \, L}+\varDelta t\sum _{\alpha =1}^{N^n} a_{i\alpha }^{\text {s}, \, L}N_{\alpha }(\varvec{x}^{p, \, L}), \end{aligned}$$

(71)

$$\begin{aligned}&x_{i}^{p, \, L+1}=x_{i}^{p, \, L}+\varDelta t\sum _{\alpha =1}^{N^n}v_{i\alpha }^{\text {s}, \, L+1}N_{\alpha }(\varvec{x}^{p, \, L}). \end{aligned}$$

(72)

Prior to updating the state valuables of each solid material point, we adopt the MUSL procedure [32] to “refine” the nodal velocity vector by an additional mapping process. Then, the deformation gradient of a solid material point can be computed as

$$\begin{aligned} F_{ij}^{p, \, L+1}=\left( \delta _{ik}+\varDelta t \sum _{\alpha =1}^{N^n}\frac{\partial N_{\alpha }(\varvec{x}^{p, \, L})}{\partial x_k}v_{i \alpha }^{\text {s}, \, L+1}\right) F_{kj}^{p, \, L},\quad \end{aligned}$$

(73)

and its determinant $J^{p, \, L+1}=\det \varvec{F}^{p, \, L+1}$ is used to update its volume and the porosity as, respectively,

$$\begin{aligned} \varOmega ^{p, \, L+1}&=J^{p, \, L+1} \varOmega ^{p, \, 0}, \end{aligned}$$

(74)

$$\begin{aligned} n^{p, \, L+1}&=1-\frac{(1-n^{p, \, 0})}{J^{p, \, L+1}}. \end{aligned}$$

(75)

According to Eq. (4), the permeability $k^{p, \, L+1}$ can also be calculated using $n^{p, \, L+1}$ as

$$\begin{aligned} k^{p, \, L+1}=\frac{D_{50}^2\left( n^{p, \, L+1}\right) ^3}{150\left( 1-n^{p, \, L+1}\right) ^2}. \end{aligned}$$

(76)

Here, the upper limit value of the solid porosity $n^{p, \, L+1}$ has to be set to suppress numerical instability. In this study, it will be set at $n^{p, \, L+1}=0.99$ in the numerical examples.

Mapping of state variables at node

Nodal values for the solid skeleton are calculated by the mapping procedures established in the previous studies [3, 38].

As is the case when using the conventional solid-fluid coupled MPM, the weighted least square approximation is adopted to evaluate the nodal velocity vector and the permeability at each node as

$$\begin{aligned}&\varvec{v}_{i}^{\text {s}, \, L+1}=\sum _{p=1}^{N^p}\frac{m^{p, \, L} \, v_i^{p, \, L+1} \, N_{\alpha }(\varvec{x}^{p, \, L})}{m^{p, \, L} \, N_{\alpha }(\varvec{x}^{p, \, L})}, \end{aligned}$$

(77)

$$\begin{aligned}&k_{\alpha }^{L+1}=\sum _{p=1}^{N^{p}}\frac{m^{p, \, L+1}k^{p, \, L+1}N_{\alpha }(\varvec{x}^{p, \, L+1})}{m^{p, \, L+1}N_{\alpha }(\varvec{x}^{p, \, L+1})}. \end{aligned}$$

(78)

The volume fraction of a grid node, $\vartheta _{\alpha }^{L+1}$, is computed using $\varOmega ^{p, \, L+1}$ as

$$\begin{aligned} \vartheta _{\alpha }^{L+1}=\frac{\sum _{p=1}^{N^{p}}\varOmega ^{p, \, L+1}N_{\alpha }(\varvec{x}^{p, \, L+1})}{\varOmega _{\alpha }}. \end{aligned}$$

(79)

Here, $\varOmega _{\alpha }$ is the nodal volume defined as

$$\begin{aligned} \varOmega _{\alpha }=\int _{\varOmega ^e} N_{\alpha }^e d\varOmega , \end{aligned}$$

(80)

which is carried out element-wise with the Gaussian quadrature rule [41]. Similarly, we map the porosities of solid particles onto the value at a node such that

$$\begin{aligned} n_{\alpha }^{L+1}=1-\frac{\sum _{p=1}^{N^{p}}(1-n^{p, \, L+1})\varOmega ^{p, \, L+1}N_{\alpha }(\varvec{x}^{p, \, L+1})}{\varOmega _{\alpha }}. \end{aligned}$$

(81)

to suppress numerical instability due to the interpolation of the porosity gradient [38].

Interface representation

It is assumed that the solid phase is homogeneous and that the fluid phase consists of liquid (water) and gas (air) phases, which are identified by superscripts “$\ell$” and “g” on their variables and symbols, respectively. Under this circumstance, the fluid phase has an interface with the solid skeleton or another fluid phase within an element, as illustrated in Fig. 2, and moves with time. The moving interface must be carefully handled to determine the domains of the phases involved so that the momentum balance and continuity equations derived above can properly be evaluated.

There are two kinds of methods to determine the geometry of a free surface that is an interface between either a liquid and a gas or a fluid and a solid. One is the interface tracking method, which uses a Lagrange description to directly express the geometry using a moving grid. The other one is the interface-capturing method, which uses an Eulerian or spatially fixed grid to track the time evolution of the interface. Since our target problems involve wave generation and propagation, and complex free surfaces, we employ the phase-field method, which is an interface-capturing method in this study. The details of this capturing method are provided in Appendix B.

Numerical algorithm

The numerical algorithm for the proposed hybrid MPM–FEM is summarized as follows:

• (i) Map the information carried by solid material points to the background grid. The nodal values of mass, velocity, volume fraction, porosity, and permeability

  $$\begin{aligned} \left( M_{\alpha }^{\text {s}, L},\varvec{v}_{i}^{\text {s}, \, L}, \vartheta _{\alpha }^{L},n_{\alpha }^{L},k_{\alpha }^{ L}\right) \end{aligned}$$

  are calculated using Eqs. (53), (77), (79), (81) and (78), respectively;

• (ii) Compute the volume fraction, porosity and permeability of the fluid phase $\left( \vartheta ^{L}, \, n^{L}, \, k^{L}\right)$ with Eqs. (51);

• (iii) Solve Eqs. (67) and (68) simultaneously for the velocities and pressure $\left( \varvec{v}_i^{\text {f}, L+1}, \, p^{\text {f}, L+1}\right)$ of the fluid phase for the next time step;

• (iv) Following the procedure provided in Appendix B, obtain the interface function $\phi ^{L+1}$ to capture the interface between different physical domains and then update the fluid density and viscosity around the interface between the gas and liquid phases according to Eqs. (89) and (90);

• (v) Solve Eq. (69) for the nodal acceleration vector of the solid skeleton $a_i^{\text {s}, \, L}$;

• (vi) Update the velocity and position of the solid material points using Eqs. (71) and (72), respectively;

• (vii) Initialize the computational grid of the solid skeleton for the next time step.

Some remarks

It is worth mentioning that both the FEM and MPM adopt weak formulations and therefore have almost the same mathematical structures. This is particularly advantageous for solid-liquid coupled problems, because the domains of solid and liquid phases overlaps with each other in most problems of interest. In fact, since the numerical algorithms of MPM are inevitably similar to that of FEM, the information exchanging between solid and liquid phases is easier than other CFD approaches such the finite difference method.

Nevertheless, surprisingly few studies have so far been made at combining FEM and MPM for solid-liquid coupled problems, for which liquid and solid phases are separately described in the Eularian and Lagrangian frames, respectively. Although there have been some studies to connect FEM and MPM with different goals in the literature [20, 21], they employ a sequential coupling method to transition between a moderately large deformation state that can be dealt with FEM and an extremely large deformation state that can more suitably be handled by MPM. Thus, the novelty of this study is obvious.

A remark is also made on the computational cost of time integration. Since the explicit time integration scheme is adopted for the solid phase, the time step size controlled by the CFL condition must be sufficiently small. Even though the implicit time integration is employed for fluid phase, the overall time step size must be controlled by that for the solid phase. Nevertheless, the size needs not be as small as that of the existing solid-liquid MPM that assumes large bulk modulus of elasticity to represent the weakly compressible liquid phase. This is another advantage over the previous explicit MPM-MPM framework for solid-liquid coupled problems.

However, the proposed method is still time-consuming and therefore not suitable for large-scale and long-duration phenomena that might include submarine landslide-induced tsunamis. This is one of the major limitations and remains to be resolved in future studies. The other major limitation is that the formulation is only applicable to either fully saturated or dry soils but not to unsaturated ones. Therefore, some important phenomena such as rainfall-induced landslides cannot be handled by the present scheme and give us a significant challenge.

Representative numerical examples

In this section, several numerical examples are presented to demonstrate the capability of the proposed hybrid MPM–FEM. First, the formulation is verified by solving the one-dimensional consolidation problem in comparison with the Terzaghi’s analytical solution. Second, a model experiment of the wave generated by an underwater granular collapse is simulated to assess the performance of the proposed method. Also, the model in which half of the soil column soaked in water and the other half in air is simulated to further explore the capability of our method. Finally, a model experiment of the wave induced by subaerial landslide over inclined plane to demonstrate the potential of the method to be applied to a diversity of problems. What has to be noticed here is that soils are all the way assumed to be either fully saturated or dry ones.

One-dimensional consolidation

The one-dimensional consolidation theory is used to verify the proposed method. The same verification is carried out in the literature [3, 38].

The Terzaghi’s analytical solution is given as

$$\begin{aligned} p^{\ell }&=\frac{4p^{0}}{\pi }\sum _{n=1}^{\infty }\frac{(-1)^{n-1}}{2n-1}\cos {\left[ \frac{(2n-1)\pi }{2}\frac{z}{h}\right] }\nonumber \\&\qquad \exp {\left[ \left( -\frac{(2n-1)\pi }{2}\right) ^2T_\text {v}\right] } \end{aligned}$$

(82)

where $T_\text {v}$ is the virtual time that defined as

$$\begin{aligned} T_\text {v}\equiv \frac{c_\text {v} t}{h^2}. \end{aligned}$$

(83)

Here, the normalized parameters are defined as

$$\begin{aligned} c_\text {v}\equiv \frac{k}{\mu ^{\ell } m_\text {v}}, \quad m_\text {v}\equiv \frac{(1+\nu )(1-2\nu )}{(1-\nu )E} \end{aligned}$$

(84)

where k is the intrinsic permeability in Eq. (4), and E and $\nu$ are the Young’s modulus and Poisson’s ratio of the solid skeleton, respectively. Fig. 3(a) shows the schematic diagram of the three-dimensional numerical model. The solid column consists of $150 \, (=3 \times 50 \times 1)$ cubic cells and 600 solid material points, and each cell has a side-length of 0.02 m and contains $4 \, (=4\times 1\times 1)$ solid material points. An isotropic linear elastic material is assumed for the solid skeleton, and the material parameters are provided in Table 1. The initial pore water pressure and effective stress in the whole domain are set at zeros, while the effect of gravity is neglected. A load of $p^0=10$ kPa is applied to the solid material points at the top layer. For both of the phases, slip boundaries are applied to the sides and bottom of the grid to realize the one-dimensional state. The total time for this simulation is 2 second, and the time increment is set at $1.0\times 10^{-5}$ s throughout the calculation.

Fig. 3

One-dimensional consolidation test. a Schematic diagram of the numerical model; b Comparison of pore pressure from coupled MPM–FEM with Terzaghi’s solution

Table 1 Parameters for simulation of consolidation test

Fig. 4

Schematic diagram of experiment setup: wave induced by underwater granular collapse

Figure 3(b) shows the obtained pore pressure distributions at different virtual times $T_\text {v}$ along with the corresponding analytical solutions. As can be seen in this figure, the numerical results with the proposed hybrid MPM–FEM are in perfect agreement with the analytical ones.

Wave induced by underwater granular collapse

We target the model experiment [28, 36] of a wave generated by the collapse of a granular mass that mimics a submarine granular collapse [26]. The schematic diagram of the experimental setup is shown in Fig. 4. A soil column is delimited by a removable vertical gate, which can be rapidly removed to simulate granular collapse, and the tank is partially filled with water. For the three-dimensional numerical model, the soil column is covered by a background grid consisting of $6,400 \, (=200 \times 32 \times 1)$ cubic cells and 12,288 solid material points, and each cell has a side-length of 0.0025 m and contains $16 \, (=4\times 4\times 1)$ solid material points. The material parameters used in this simulation are provided in Table 2. For both of the phases, the non-slip condition is considered on the bottom surface, and the slip condition is applied on the sides. The initial stresses in the soil and water are calculated by linearly increasing the gravity acceleration for 10 seconds. In this process, the soil is assumed to be elastic by giving sufficiently large cohesion. At time $t=0.0$ s, a cohesion of 0 kPa is instantaneously given to all the soil material points, while the vertical gate is removed upward within 0.1s in the experiment. The total time for this simulation is 2 second, and the time increment is set at $1.0\times 10^{-5}$ s throughout the calculation.

The obtained interface functions $\phi$ indicating the profiles of the granular mass and water surface, and the water pressures at some representative times are shown in Fig. 5. At the initial stage, the sinking of the column causes the sinking of the water surface above the column, and vortex can also be observed at the upper right corner. Then the water level rises near the wall on the left, and the waves start to propagate to the right side. At the later stages, the free surface is disturbed during the wave propagation. Despite this, the water pressure remains stable throughout the collapse, thanks to the stabilization scheme implemented in the stabilized FEM for incompressible fluids.

Fig. 6 shows the simulated deposition profiles at several representative times in comparison with the experimental measurements [28, 36]. The profile obtained at 1 second is slightly different from the experimental one. This is probably due to the fact that the initial condition adopted in this numerical analysis is not fully consistent with the experimental setup. Nevertheless, the subsequent profiles exhibit similar trends to those obtained experimentally. The final geometry with the sliding distance is very close to the measured one. From these results, it can be concluded that the proposed method is capable of assessing complex interactions between soil and water.

Table 2 Parameters for simulation of wave induced by underwater granular collapse

Fig. 5

Numerical results: wave induced by underwater granular collapse

Fig. 6

Comparison of deposition configurations between numerical and experimental results [28, 36]: Wave induced by underwater granular collapse

Table 3 Parameters: soil column half in water and half in air

In order to further explore the capability of the proposed method, another situation is simulated: no experimental data is available for this situation. The model is almost the same as that above, with only half of the soil column soaked in water and the other half in air. The schematic diagram of the model is shown in Fig. 7. The soil column consists of 7,680 solid material points with a background grid whose cell has a length of 0.005 m and contains $16 \, (= 4\times 4\times 1)$ material points. The parameters for this numerical analysis are provided in Table 3. For both of the phases, the non-slip condition is imposed on the bottom surface, and the slip condition is applied on the sides. The total time of this granular collapse simulation is 1 second, and the time increment is set at $1.0\times 10^{-4}$ s throughout the calculation.

The results are shown in Fig. 8. As can be seen from these figures, at the initial stage ($t=0.1$ s), the soil column collapses and causes the free surface rise. From 0.2 seconds on, the solid material points in the upper right corner are rolled up by the wave and as the waves return, the solid particles move to the left with the free surface. Then, after hitting the left wall, few solid particles are rolled up by the waves and fall. Throughout the simulation, the moving free surface and interface with complex geometries are properly captured without suffering numerical instabilities. In summary, it is safe to conclude that the proposed method is applicable to this type of complex interaction between soil and water.

Fig. 7

Schematic diagram of target model: soil column half in water and half in air

Fig. 8

Numerical results: soil column half in water and half in air

Fig. 9

Wave induced by subaerial granular slide: Schematic diagram of experimental setup

Wave induced by subaerial slide over inclined plane

In order to demonstrate that the proposed method can be applied to a variety of problems, we target the experiment [35], in which a granular mass drops into the water to generate impulse waves, mimicking a subaerial landslide-induced wave. The schematic diagram of the experimental setup is shown in Fig. 9. The tank is 2.2 m long, 0.3 m high and includes a 45-degree inclined plane on the right side. The initial water depth is 0.148 m. The granular mass is supported on the inclined plane with a vertical removable gate, and the bottom of the mass is located at the level of the free water surface.

When the vertical gate is opened, the granular mass slides down the inclined plane, impacts the water surface and generates impulse waves propagating leftward. The evolution of the generated impulse waves and the granular flow shape are recorded with a high speed camera. Four wave gauges is set at 0.45 m (G1), 0.75 m (G2), 1.05 m (G3) and 1.35 m (G4) from the vertical removable gate to measure the time-varying amplitudes of the generated waves.

For the numerical simulation by the proposed hybrid MPM–FEM, the granular mass consists of 10,368 solid material points with a background grid, each of whose cell has $16 \, (=4\times 4\times 1)$ material points and a length of 0.004 m. The material parameters used in the simulation are presented in Table 4. It is to be noted that the inclined plane is also regarded as a solid phase and made of an elastic material to realize the non-slip and undrained conditions on the interface with the granular mass. For both of the phases, the non-slip condition is considered on the bottom surface, and the slip condition is applied on the wall sides. The total time of simulation is 2 second, and the time increment is $1.0\times 10^{-5}$ s throughout the calculation.

The numerical results are compared with the experimental ones as shown in Fig. 10, in which the snapshots taken at three representative times are presented. As can be seen form these figures, the simulated profiles of the granular mass and wave are in good agreement with the experimental observations. At the beginning ($t=0.23$ s), the irruption of the granular mass into the water causes the upthrust of the water that subsequently wraps around the irruptive mass. At $t=0.41$ s, the wave crest is raised in front of the forefront of the granular slide, and then the leading wave is generated and begins to propagate away from the impact source. Also, similarly to the experimental observation, the vortex is formed around the upper part of the granular flow. In addition, the obtained sliding distance is in close agreement with the experimental one, while the forefront has not yet touched the bottom surface. After the granular slide has experienced a large deformation and turned along the bottom surface, its vortex makes a backward flow prominent at $t=0.52$ s. This simulated tendency is consistent with the experimental one. However, the simulated profile of the granular mass does not agree with the experimental one completely. Accuracy improvement must be a major challenge in future studies.

Table 4 Parameters for simulation of wave induced by subaerial granular slide

Fig. 10

Snapshots of the observed and simulated sliding processes at $t = 0.23$, 0.41 and 0.52 s. a PIV measured data borrowed from [35]; b Present simulations

Fig. 11

Numerical results: Wave induced by subaerial granular slide

Fig. 12

Comparison of computed and measured water level at four positions

Figure 11(a) shows the waveforms in the tank caused by the subaerial granular slide after the granular mass begins to deposit on the bottom, but the corresponding experimental data are not available. As can be seen from the figures, several waves are generated right after the irruption of the granular mass and propagate leftward. Among them, the first wave has the largest amplitude and mimics a tsunami induced by subaerial landslide [27]. Additionally, Fig. 11(b) demonstrates that the water pressure has been successfully stabilized during the event thanks to the stabilized FEM adopted for flow simulations of incompressible fluids. Tsunamis caused by sediment movement of granular masses are hazardous to the opposite shore [24] and therefore are first choices for our future targets to simulate.

Figure 12 shows the simulated waveforms in comparison with those measured at four different points. Here, the water surface identified with the air-water interface is determined by the narrow region with interface function $\phi =0.5$. As can be seen from the figures, the overall responses obtained by the simulation are in a reasonable agreement with the measurements. In particular, both the peak of the first wave level and its arrival time in each of the figures closely agree with the experimental ones. However, as time passed, the simulated subsequent wave is delayed and its amplitude declines more than the experimental one. A similar tendency is also reported in [30], in which by the multi-phase flow model is employed. The main reason for the discrepancy is probably due to the low spatial resolutions for both the MPM and FEM. By refining the FE mesh and increasing the number of solid material points, we expect that our simulations would be made more accurate than the present one. This must be open to further discussion. Nonetheless, the performance of the novel method of hybrid MPM–FEM has been satisfactorily confirmed in the presented numerical examples.

Conclusion

By combining MPM and FEM, we have proposed a new numerical method for solving granular mass-water interaction problems with a view to simulating tsunamis caused by submarine and subaerial landslides. Similar to the existing solid-liquid coupled MPM, the proposed method is formulated based on porous media theory, in which saturated soil is considered as a continuum composed of a soil skeleton and a liquid phase. The Lagrangian description is adopted for the governing equations of the solid skeleton to be handled with MPM, whereas the Eulerian one is for those of the fluid phase to be solved by the stabilized FEM. Also, the phase-field method is applied to represent the free surface. In addition, MPM and FEM use the same spatially fixed grid, to which B-spline basis functions are introduced for the spatial discretization. Four representative numerical examples were presented to demonstrate the promise and capability of the proposed hybrid MPM–FEM. In summary, the following conclusion can be drawn:

• Instead of the Lagrangian description, the Eulerian description can gain high precision of numerical solutions with larger time steps and greatly improves computational efficiency compared to the conventional solid-liquid coupled MPMs with the help of the stabilized FEM.

• The results from the numerical simulation of the model experiment of a granular collapse in a tank shows that the proposed method was able to simulate large deformation of the solid skeleton accompanied by complex solid-liquid interactions and complex free surface movement. Therefore, the proposed method has a great potential in understanding the mechanism of related events such as a tsunami induced by submarine or subaerial landslides.

• The results from the last two numerical examples reveal that the proposed method can also be applied to a variety of hazardous phenomena, in which the interface function drastically changes to represent the interaction among three different phases; air, water and solid.

Although the simulation results were not in a perfect agreement with the experimental measurements, the overall behavior was fairly satisfactory. It is expected that the accuracy would be improved by making the analysis conditions coincident with the experimental ones, and increasing the numbers of grid nodes and material points. It may also be worthwhile to point out that the laboratory data used to validate the proposed method were all obtained in small scale experiments. Validation analyses with reference to larger-scale real data will be conducted in the future.

Appendices

Appendix A: B-spline basis function

B-spline basis function are defined with the use of a knot vector $\Xi =\{\xi _1, \xi _2,\cdots , \xi _{n+p}, \xi _{n+p+1}\}$, $\xi _i$ is i-th knot with $i=1, 2,\cdots , n+p, n+p+1$, n is the number of basis functions, and p is the polynomial order. The first and last knot are repeated $p+1$ time to make the resulting B-spline interpolatory at both end points. The Cox-de Boor formula [5] defines B-spline basis functions recursively. The zeroth order basis functions $(p=0)$ are defined as follow

$$\begin{aligned} N_{i,0}(\xi )= {\left\{ \begin{array}{ll} 1, &{}\mathrm {if}\quad \xi _i\le \xi \le \xi _{i+1},\\ 0, &{}\mathrm {otherwise}, \end{array}\right. } \end{aligned}$$

(85)

For $p\ge 1$, the basis functions are defined by the follow recursion scheme.

$$\begin{aligned} N_{i,p}(\xi )=\frac{\xi -\xi _i}{\xi _{i+p}-\xi _{i}}N_{i,{p-1}}(\xi )+\frac{\xi _{i+p+1}-\xi }{\xi _{i+p+1}-\xi _{i+1}}N_{{i+1},{p-1}}(\xi ) \end{aligned}$$

(86)

where the 0/0 are defined as zero. Fig.13 shows quadratic basis functions with open knot vector $\Xi =\left\{ 0,0,0,1,2,3,3,3\right\}$. B-spline basis functions satisfy the following properties:

• (i) They form a partition of unity: $\sum _{i=1}^{n}N_{i,p}(\xi )=1$.

• (ii) They are non-negative, $N_{i,p}(\xi )\ge 0$, for all $\xi$.

• (iii) $N_{i,p}(\xi )$ is supported in the interval $[\xi _{i},\xi _{i+p+1}]$.

The gradient of $N_{i,p}(\xi )$ also can be computed by a recursive formula as follow

$$\begin{aligned} \frac{dN_{i,p}(\xi )}{d\xi }\!=\!\frac{p}{\xi _{i+p}-\xi _{i}}N_{i,{p-1}}(\xi )-\frac{p}{\xi _{i+p+1}-\xi _{i+1}}N_{{i+1},{p-1}}(\xi ) \end{aligned}$$

(87)

The gradient corresponding to the basis functions from Fig.13 are shown in Fig.14.

Fig. 13

Example of quadratic B-spline basis functions

Fig. 14

Example of gradient of quadratic B-spline basis function

The B-spline basis functions of order p by a uniform knot vector are $C_{p-1}$-continuous, they guarantee at least $C_0$ continuity of the gradients and hence, significantly reduce the cell crossing error.

The multi-dimensional B-spline basis factions can be built from the tensor product of one-dimensional basis functions. In three dimensional case, given knot vectors $\Xi =\{\xi _1,\xi _2,\cdots ,\xi _{n+p},\xi _{n+p+1}\}$, $H=\{\eta _1,\eta _2,\cdots ,\eta _{m+q},\eta _{m+q+1}\}$, and $Z=\{\zeta _1,\zeta _2,\cdots ,\zeta _{o+r},\zeta _{o+r+1}\}$ along the parametric coordinates of $\xi$, $\eta$, $\zeta$, respectively, where p, q, r are the polynomial order, and n, m, o are the number of basis functions along $\xi$, $\eta$, $\zeta$. The B-spline basis functions in three dimensional are given as

$$\begin{aligned} N_{(i,j,k),(p,q,r)}(\xi ,\eta ,\zeta )=N_{i,p}(\xi )N_{j,q}(\eta )N_{k,r}(\zeta ) \end{aligned}$$

(88)

where $i=1,2,\cdots ,n$, $j=1,2,\cdots ,m$, and $k=1,2,\cdots ,o$.

Appendix B: Phase-field method for free surface

This appendix is devoted to explaining the method to capture a moving interface between separate domain by applying the phase-field (PF) method [14].

In the PF method, the movement of a free-surface is defined as the time-variation of the interface function $\phi$, where $\phi$ takes 0.0 for gas, 1.0 for liquid and the intermediate value 0.5 represents the interface as shown in Fig.15. With the values of the interface function, the density $\rho$ and the viscosity $\mu$ of the fluid can be defined as

$$\begin{aligned} \rho ^\text {f} = \rho ^{\ell }\phi +\rho ^\text {g}(1-\phi ) \end{aligned}$$

(89)

$$\begin{aligned} \mu ^\text {f} = \mu ^{\ell }\phi +\mu ^\text {g}(1-\phi ) \end{aligned}$$

(90)

where $\rho ^{\ell }$ and $\rho ^\text {g}$ are the densities of liquid and gas, and $\mu ^{\ell }$ and $\mu ^\text {g}$ are the corresponding viscosity.

Fig. 15

Schematic diagram of phase-field model

In this study, we use the following Allen-Cahn equation [33] for the free surface

$$\begin{aligned}&\frac{\partial \phi }{\partial t}+v_i^\text {f}\frac{\partial \phi }{\partial x_i}=M_{\phi }\frac{\delta F}{\delta \phi } \end{aligned}$$

(91)

$$\begin{aligned}&\frac{\delta F}{\delta \phi }=a^2\frac{\partial ^2\phi }{\partial x_i^2}+4W\phi (1-\phi )(\phi -0.5) \end{aligned}$$

(92)

where a is the gradient coefficient, W is the energy barrier height, and $M_{\phi }$ is the PF mobility. The weak form of the interface equation using the Galerkin method can be written as

$$\begin{aligned} {\begin{matrix} \int _{\varOmega }&{}\psi \left( \frac{\partial \phi }{\partial t}+v_i^\text {f}\frac{\partial \phi }{\partial x_i}\right) d\varOmega +M_\phi a^2\int _{\varOmega }\frac{\partial \psi }{\partial x_i}\frac{\partial \phi }{\partial x_i}d\varOmega \\ -&{}4WM_\phi \int _{\varOmega }\psi \phi (1-\phi )(\phi -0.5) d\varOmega =0 \end{matrix}} \end{aligned}$$

(93)

where $\phi$ and $\psi$ are the FE approxiamtion of the interface function and it’s test function. Similar to the fluid phase, by applying the stabilized FE approximation with the SUPG method [2] to the Eq.(91), we obtain the discretized equation as follow

$$\begin{aligned} \int _{\varOmega }&\psi ^h\left( \frac{\partial \phi ^h}{\partial t}+v_i^{\text {f}, h}\frac{\partial \phi ^h}{\partial x_i}\right) d\varOmega +M_\phi a^2\int _{\varOmega }\frac{\partial \psi ^h}{\partial x_i}\frac{\partial \phi ^h}{\partial x_i}d\varOmega \nonumber \\ -&4WM_\phi \int _{\varOmega }\psi ^h\phi ^h(1-\phi ^h)(\phi ^h-0.5) d\varOmega \nonumber \\ +&\sum _{e=1}^{N^e}\int _{\varOmega ^e}\tau _{\phi }^ev_i^{\text {f}, h}\frac{\partial \psi ^h}{\partial x_i}\left( \frac{\partial \phi ^h}{\partial t}+v_j^{\text {f}, h}\frac{\partial \phi ^h}{\partial x_j}-M_\phi \frac{\delta F}{\delta \phi } \right) d\varOmega \nonumber \\ +&\sum _{e=1}^{N^e}\int _{\varOmega ^e}\tau _\text {LSIC}^e\frac{\partial \psi ^h}{\partial x_i}\frac{\partial \phi ^h}{\partial x_i}d\varOmega =0 \end{aligned}$$

(94)

where $\tau _{\phi }^e$ and $\tau _\text {LSIC}^e$ are the stabilized parameters defined by

$$\begin{aligned}&\tau _{\phi }^e=\left[ \left( \frac{2}{\varDelta t}\right) ^2+\left( \frac{2\Vert v_i^{\text {f}, h}\Vert }{h_e}\right) ^2\right] ^{-\frac{1}{2}} \end{aligned}$$

(95)

$$\begin{aligned}&\tau _\text {LSIC}^e=\frac{h_e}{2}\Vert v_i^{\text {f}, h}\Vert \end{aligned}$$

(96)

The last term of Eq.(94) is introduced to supress the numerical instability of interface function around the interface. Substituting (24) into (94), we obtain the following finite element equation

$$\begin{aligned} (\varvec{M}+\varvec{M}_{\text {s}})\frac{\partial \varvec{\phi }}{\partial t}+(\varvec{A}+\varvec{A}_{\text {s}}+\varvec{D}+\varvec{S}_{\text {c}})\varvec{\phi }=\varvec{P}+\varvec{P}_{\text {s}} \end{aligned}$$

(97)

where $\varvec{M}, \varvec{A}, \varvec{D}, \varvec{S}_{\text {c}}, \varvec{P}$ are the time matrix, advection matrix, diffusion matrix, shock-capturing matrix, phase-field matrix, respectively, and subscript ‘s’ indicates the SUPG matrices. The details of each matrix are written as follow

$$\begin{aligned}&[\varvec{M}]^{e}_{\alpha \beta }=\int _{\varOmega ^{e}}N_{\alpha }^{e}N_{\beta }^{e}d\varOmega \end{aligned}$$

(98)

$$\begin{aligned}&[\varvec{A}]^{e}_{\alpha \gamma }=\int _{\varOmega ^{e}}N_{\alpha }^{e}N_{\beta }^{e}v_{i\beta }^{\text {f}, \, e}\frac{\partial N_{\gamma }^{e}}{\partial x_i}d\varOmega \end{aligned}$$

(99)

$$\begin{aligned}&[\varvec{D}]^{e}_{\alpha \beta }=M_{\phi }a^2\int _{\varOmega ^{e}}\frac{\partial N_{\alpha }^{e}}{\partial x_i}\frac{\partial N_{\beta }^{e}}{\partial x_i}d\varOmega \end{aligned}$$

(100)

$$\begin{aligned}&[\varvec{P}]^{e}_{\alpha }=4WM_\phi \int _{\varOmega ^{e}}N_{\alpha }^{e}\phi ^e(1-\phi ^e)(\phi ^e-0.5) d\varOmega \end{aligned}$$

(101)

$$\begin{aligned}&[\varvec{M}_{\text {s}}]_{\alpha \gamma }^{e}=\tau _{\phi }^e\int _{\varOmega ^{e}}\frac{\partial N_{\alpha }^{e}}{\partial x_i}N_{\beta }^{e}v_{i\beta }^{\text {f}, \, e}N_{\gamma }^{e}d\varOmega \end{aligned}$$

(102)

$$\begin{aligned}&[\varvec{A}_{\text {s}}]^{e}_{\alpha \delta }=\tau _{\phi }^e\int _{\varOmega ^{e}}\frac{\partial N_{\alpha }^{e}}{\partial x_i}N_{\beta }^{e}v_{i\beta }^{\text {f}, \, e}N_{\gamma }^{e}v_{j\gamma }^{\text {f}, \, e}\frac{\partial N_\delta ^{e}}{\partial x_j}d\varOmega \end{aligned}$$

(103)

$$\begin{aligned}&[\varvec{P}_{\text {s}}]^{e}_{\alpha }=4WM_\phi \tau _{\phi }^e\int _{\varOmega ^{e}}\frac{\partial N_{\alpha }^{e}}{\partial x_i}N_{\beta }^{e}v_{i\beta }^{\text {f}, \, e}\phi ^e(1-\phi ^e)(\phi ^e-0.5) d\varOmega \end{aligned}$$

(104)

$$\begin{aligned}&[\varvec{S}_{\text {c}}]^{e}_{\alpha \beta }=\tau _\text {LSIC}^e\int _{\varOmega ^{e}}\frac{\partial N_{\alpha }^{e}}{\partial x_i}\frac{\partial N_{\beta }^{e}}{\partial x_i}d\varOmega \end{aligned}$$

(105)

About the Time integration, The approximation of the variables(time derivative, interface function) are using the similar approaches (see Eqs.(58) and (59)), and $\phi ^e$ in $\varvec{P}, \varvec{P}_s$ are using the current time step. The final version of time discretized form of Eq.(97) can be written as

$$\begin{aligned}&(\varvec{M}+\varvec{M}_{\text {s}})\frac{\varvec{\phi }^{L+1}}{\varDelta t}+(\varvec{A}+\varvec{A}_{\text {s}}+\varvec{D}+\varvec{S}_{\text {c}})\frac{\varvec{\phi }^{L+1}}{2}\nonumber \\&=(\varvec{M}+\varvec{M}_{\text {s}})\frac{\varvec{\phi }^{L}}{\varDelta t}-(\varvec{A}+\varvec{A}_{\text {s}}+\varvec{D}+\varvec{S}_{\text {c}})\frac{\varvec{\phi }^{L}}{2}+\varvec{P}+\varvec{P}_{\text {s}} \end{aligned}$$

(106)

From Eq.(106), we can obtain the interface function of the next time step.