Comparing field data using Alpert multi-wavelets

Abstract

In this paper we introduce a method to compare sets of full-field data using Alpert tree-wavelet transforms. The Alpert tree-wavelet methods transform the data into a spectral space allowing the comparison of all points in the fields by comparing spectral amplitudes. The methods are insensitive to translation, scale and discretization and can be applied to arbitrary geometries. This makes them especially well suited for comparison of field data sets coming from two different sources such as when comparing simulation field data to experimental field data. We have developed both global and local error metrics to quantify the error between two fields. We verify the methods on two-dimensional and three-dimensional discretizations of analytical functions. We then deploy the methods to compare full-field strain data from a simulation of elastomeric syntactic foam.

Appendix: Alpert multi-wavelets

Multi-wavelets and wavelets can be different types of bases where multiresolution functions can be represented by linear combinations. Wavelets encode all the scales in the data and their locations in space and/or time. Initial wavelets were developed for data defined on regular grids such as signal, image and video data. They are referred to as First generation wavelets (FGW) given by the approximation basis $\phi (x)$ and wavelet basis $\psi (x)$ to find the details in a function [33] following:

$$\begin{aligned} \phi _j (x)= & {} \sum _{k \in {\mathbb {Z}}} a_k \phi _{j-1} (2x - k) \end{aligned}$$

(25)

$$\begin{aligned} \psi _j(x)= & {} \sum _{k \in {\mathbb {Z}}} b_k \phi _{j-1} (2x - k) \end{aligned}$$

(26)

where x is the spatio-temporal coordinate, j and k are the detail level and location indices, respectively, and $a_k$ and $b_k$ are coefficients intrinsic to the FGW type. Each wavelet basis $\psi _j(x)$ models a finer resolution detail as j increases. Regular grids are dyadic such that the maximum number of detail levels $j_\text {max}$ is equal to log$_2(N)$ where N is the number of grid points in each dimension.

FGWs are not a suitable representation in our work because we analyze data represented on unstructured meshes [50]. Instead, non-traditional wavelet bases such as second generation wavelets [50, 51], diffusion wavelets [52] or Alpert multi-wavelets (AMW) [36, 38] are required; we use the latter type in in our work.

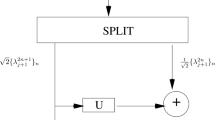
These types of wavelets have similar characteristics to FGWs. While Eqs. 25 and 26 are also used used to compute AMWs, there are two main differences between FGW and AMWs. First, $j_\text {max}$ is computed by recursive splitting of the non-dyadic mesh into separate subdomains that form a multiscale hierarchical tree [50]. Thus, AMWs can accommodate non-dyadic grids such as finite intervals and irregular geometries. Second, the AMW bases are not based on constant coefficients $a_k$ and $b_k$ as in FGWs but they are calculated according to the mesh coordinates $x_k$.

The major advantage of AMWs is they do not require any special treatment of irregular boundaries (e.g. holes) present in the domain and they avoid them by construction [36]. The discrete Alpert wavelets $\psi _j(x_k)$ are polynomials that are easy to compute; they are represented in a square sparse matrix $[\Psi ]$.

1.1 Building the wavelets matrix

It is unclear how to compute $[\Psi ]$ using Eqs. 25 and 26 in a systematic and practical manner. Instead, we employ a discrete methodology to build the Alpert wavelet matrix. We briefly present a technique for the case of one-dimensional (1D) non-uniform mesh for a polynomial order w. The 1D mesh is constituted of N points $x_1< \cdots< x_i< \cdots < x_N$.

First, the mesh is subdivided into P almost equally sized bins where the number of points n per bin is $2w \ge n \gtrsim w$. This subdivision operation is not required when FGW are used in a dyadic grid.

Second, the so-called initial moment matrices $[M]_{1,1 \le p \le P} \in {\mathbb {R}}^{n \times w}$ are computed for each bin:

$$\begin{aligned} {[}M]_{1,p}= \begin{bmatrix} 1 &{}\quad x_1 &{}\quad x_1^2 &{}\quad \ldots &{}\quad x_1^{w-1} \\ 1 &{}\quad x_2 &{}\quad x_2^2 &{}\quad \ldots &{}\quad x_2^{w-1} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 1 &{}\quad x_n &{}\quad x_n^2 &{}\quad \ldots &{}\quad x_n^{w-1} \end{bmatrix} \end{aligned}$$

(27)

$[M]_{1,p}$ contain the wavelet functions $\psi$ (see Eq. 26), assumed to be polynomials in AMW [38]. We also compute the matrices $[U]_{1,p} \in {\mathbb {R}}^{n \times n}$ for each bin by orthogonalizing the matrices [M] (e.g. using a QR operation).

Third, the matrices $[U]_{1,p}$ are assembled in a large matrix $[V]_1 \in {\mathbb {R}}^{N \times N}$ as illustrated in Fig. 12 (left column). The columns of the matrix [V] correspond to the N mesh points and the N rows correspond to the N wavelet coefficients.

Fourth, the finer detail levels in the mesh are accounted for. The P bins form a hierarchy of the details where $j_{max}=\text {log}_2(P)+1$ is the maximum number of detail levels. Matrices $[V]_{2 \le j \le j_{max}}$ are computed similarly to $[V]_1$ and the full wavelet matrix as is obtained as:

$$\begin{aligned} {[}\Psi ] = \prod _{j=1}^{j_\text {max}} [V]_j \end{aligned}$$

(28)

More details on these four steps are given in [36,37,38]. This procedure can be generalized to D-dimensional meshes. The procedure described above to build the wavelet matrix $[\Psi ]$ guarantees that it is orthonormal such that its matrix inverse is equal to its transpose, $[\Psi ]^{-1} = [\Psi ]^T$.