Computational stability investigations for a highly symmetric system: the pressurized spherical membrane

Abstract

Thin membranes are notoriously sensitive to instabilities under mechanical loading, and need sophisticated analysis methods. Although analytical results are available for several special cases and assumptions, numerical approaches are normally needed for general descriptions of non-linear response and stability. The paper uses the case of a thin spherical hyper-elastic membrane subjected to internal gas over-pressure to investigate how stability conclusions are affected by chosen material models and kinematic discretizations. For spherical symmetry, group representation theory leads to linearized modes on the uniformly stretched sphere, with eigenvalues obtained from the mechanics of a thin membrane. A complete three-dimensional geometric description allows non-axisymmetric shear modes of the sphere, and such instabilities are shown to exist. When the symmetry of the continuous sphere is broken by discretized models, group representation theory gives predictions on the effects on the critical states. Numerical simulations of the pressurized sphere show and verify stability conclusions for sets of meshing strategies and hyper-elastic models.

1 Introduction

A large variety of thin pressurized membranes are common in biology and engineering [31, 32, 34, 39]. The mechanical definition of a membrane implies that the structure will carry all loads acting on it by establishing normal force resultants. With the exception of cases where a plane membrane is subjected to tensile forces, this means that the membrane can only carry forces of distributed transversal intensities, i.e., pressure loads. With such loading situations, the response of a membrane to loading is fundamentally non-linear, when a combination of increasing stresses and increasing deformations carry an increasing pressure. This implies a need for smoothness and continuity in the deformed configuration of the membrane.

Rubber-like materials are commonly considered for membranes, and are then described by hyper-elastic material models. Due to computational convenience, the Mooney–Rivlin model, [35, 43], is often used in a two-parameter form related to the first two strain invariants [26]. Several studies have shown that the relation between the two constitutive parameters significantly affects the qualitative response of simulated membranes [14, 40]. Many other material models for the simulation of membrane structures exist in literature, where a common one is given by Ogden [38]. Comparisons of models are given in, e.g., [8]. Parametric material models give large flexibility in describing materials, but can also cause unexpected results, e.g., non-intuitive instabilities [15].

Being thin structures, membranes are strongly affected by instabilities. Common views demand for static stability a minimum total potential energy at the equilibrium state [4, 19, 30, 47]. Stability is, however, fundamentally dynamic, and can be evaluated from a Liapunov stability condition, i.e., a capacity to remain close to the static equilibrium situation after a minor disturbance [33]. A special aspect of membrane stability is wrinkling, when compressive forces create wavy transversal deformations with crest lines orthogonal to the principal compressive stress [18]. Relaxed strain energy forms allow the calculation of wrinkling as an average stress field, but lead to ill-defined problems under pressure loads [41].

For the stability of thin membranes, analytical results can be obtained only for simple geometries [23, 37, 45], but general treatments are also available [5, 7, 21]. Of particular interest has been the stability of pressurized spheres. This problem is frequently studied in literature [29, 36, 37, 48, 50, and many others]. An extensive treatment of this problem is given by Haughton and Ogden [24, 25], where an axi-symmetric analytical model and two hyperelastic material models provide detailed stability conclusions from the total potential energy in the deformed state. The first part of the present work can be seen as a review and an extension of this, with a more general kinematic description, a wider range of material models, and a stability analysis based on vibration properties [17]. As a motivation, the latter part of the work is also directed towards the representation of instabilities by numerical simulation models.

The stability analysis is in the present work restricted to the isolation of critical equilibrium states on the primary sequence, while secondary paths emanating from these are not a main objective. Both stable and unstable equilibria are thereby sought, as the treatment of bi-stable structures is considered as an interesting area for membranes [1, 2, 6].

The description of the geometry of a spherical surface is a well-known and frequently studied problem, not least in cartography, meteorology and oceanography [22, 42, 49, as examples]. When physical phenomena need be described on the spherical surface, the parameterized mapping of the surface causes problems [44], which can be handled by the Cubed sphere approach, with six local mappings together forming the sphere [46]. Another approach is to base the description of physics on the spherical harmonics functions [10]. The latter will be used in the present analysis, while the former is used as a tool to create one form of discretized mesh.

Nature shows many aspects of symmetry, and engineering frequently uses symmetric or repetitive designs, from both aesthetical and functional optimality reasons [11]. Symmetries of an object can be analyzed by group theory [9, 12, 13], where the elements of the symmetry group are the rigid transformations which bring a point on the sphere surface to another, leaving the center point unmoved, and keeping the spherical geometry [11].

In numerical simulations, symmetry is often introduced as mirror reflections in the main coordinate planes, or as rotational symmetry in axi-symmetric situations. A special aspect of symmetry is when an unsymmetric meshing of a fully symmetric domain can lead to surprising results [16]. As the present work utilizes flat triangular membrane elements to cover the complete sphere, this approximates the geometry by meshes of lower symmetry, which contain some, but not all, symmetry properties [28, 51]. Classifying the resulting meshes with respect to their respective symmetry groups gives further insights into how a discretized mesh can significantly affect simulation results.

The analytical treatment of an isotropic hyper-elastic uniformly pressurized sphere is given in Sect. 2, discussing the combination of geometric properties and material models, and deriving stability conclusions from the vibration frequencies of the pressurized sphere. The relation between the spherical continuum and discretized element meshes is given in Sect. 3. Section 4 presents results from numerical experiments with finite element models, focussing on two common incompressible hyper-elastic material models, and on effects from the discretization. Section 5 draws a set of conclusions from the study. Appendices give further details.

2 Analysis of pressurized sphere

This section considers the linearized problem of small incremental motions for a spherical membrane of original radius a and uniform thickness t, when inflated to a radius $\lambda a$ by an internal constant over-pressure p; $\lambda$ is then a uniform stretch. The membrane is assumed to be described by an isotropic hyper-elastic material model. For the dynamics, the inertia is assumed to come only from the membrane itself, with original uniform density $\rho$.

The motion around the equilibrium state is analyzed by finding all the eigenmodes of the membrane and the associated eigenvalues. The analysis is related to the primary equilibrium solution of uniform stretch, where critical solutions are found, with zero eigenvalues. At these, modes corresponding to vanishing eigenvalues exist, but secondary, non-spherical solutions are only very briefly mentioned here.

The discussion is related to two parts, where the first considers the conclusions that can be drawn from the geometry of the sphere alone, and the second considers the mechanics of a thin membrane formulation. These are brought together in a stability formulation, where stability of an equilibrium state is defined through the existence of vibration modes, i.e., positive eigenvalues for all modes of incremental displacements from the equilibrium state.

2.1 Spherical symmetry

The uniformly stretched sphere maintains the full spherical symmetry group O(3) of the original shape. The infinite-dimensional space of all small incremental displacements from this state can be split into a direct sum of finite-dimensional subspaces, each invariant under the spherical symmetry. For example, the 1-dimensional space of equal and purely radial displacement is clearly such a subspace. Group representation theory for O(3) classifies these subspaces as each corresponding to one of a list of known irreducible representations of the group, cf. “Appendix A”.

On the other hand, the subspace of eigenmodes belonging to a particular eigenvalue is clearly also an invariant subspace under spherical symmetry. The end result is that the space of small incremental displacements can be split into a direct sum of invariant eigenmode subspaces, each of which corresponds to a particular irreducible representation of O(3). These eigenmode spaces have finite dimensions, and thus eigenvalue multiplicities, given by the representation. For the stretched sphere, the degree of symmetry is so high that the mode shapes are almost entirely determined by symmetry alone.

When considering all possible modes of the sphere, and not only axi-symmetric ones, a small incremental displacement vector for a point of the stretched sphere will be represented by a scalar outward normal component u together with a 2D vector $\varvec{v}$ in the tangent space of the sphere. A basis for scalar functions is given by the set of real-valued scalar spherical harmonics $Y_{\ell m}$, where $\ell =0,1,2,3,\ldots$ and $m=-\ell ,-\ell +1,\ldots ,\ell -1,\ell$, cf. “Appendix A”. If further $\nabla ^{(S)}$ denotes the surface gradient of a scalar function on the stretched sphere, and $^*$ is the operation of rotating a tangent vector clockwise a right angle about the outward normal, then a basis for vector-valued functions on the stretched sphere is given by $\nabla ^{(S)}Y_{\ell m}$ and $^*\nabla ^{(S)}Y_{\ell m}$, where now $\ell =1,2,3,\ldots$, as a zero value for $\ell$ gives a zero gradient.

This basis is convenient since it corresponds to the irreducible representations of the group O(3). The representations will here be denoted $D_{\ell g}$, $D_{\ell u}$ for $\ell =0,1,2,3,\ldots$. In particular, for any given even $\ell$, the set of $2\ell +1$ scalar functions $Y_{\ell m}$ transforms as the representation $D_{\ell g}$, as does the set of vector functions $\nabla ^{(S)}Y_{\ell m}$ (for $\ell >0$), whereas the set $^*\nabla ^{(S)}Y_{\ell m}$ (for $\ell >0$) transforms as $D_{\ell u}$. For odd $\ell$, the first two sets instead transform as $D_{\ell u}$, while the third set transforms as $D_{\ell g}$. Since each eigenspace can be taken to correspond to one of the irreducible representations, the basis above is already close to an eigenmode basis, the exception being where a scalar and a vector set both transform according to the same representation. To summarise:

The $D_{0g}$ representation gives a radial mode

$$\begin{aligned} u=\alpha _{0} Y_{0 0} ,\quad \varvec{v}=\varvec{0}, \end{aligned}$$

(1)

where the mode amplitude $\alpha _{0}$ is an arbitary scaling, so this mode is unique. While this mode shape is fully determined by symmetry, the corresponding eigenvalue depends on the physics of the problem. The representation $D_{0u}$ would give $u=0,\quad \varvec{v}=\varvec{0}$, which means there are no modes for this representation.

For $\ell \ge 1$, we first get modes corresponding to the representations $D_{\ell u}$ for even $\ell$, and $D_{\ell g}$ for odd $\ell$, of the form

$$\begin{aligned} u=0,\quad \varvec{v}=\gamma _{\ell _{1}} \; (\lambda a) ^*\nabla ^{(S)}Y_{\ell m}, \end{aligned}$$

(2)

— a ($2\ell +1$)-fold shear mode for each $\ell$, again with an arbitrary scaling $\gamma _{\ell _{1}}$ and with a corresponding physics-dependent eigenvalue for each $\ell$. The factor $(\lambda a)$ compensates for the size of the stretched sphere and makes u and $\varvec{v}$ have the same physical dimension. Secondly, we get modes corresponding to the representations $D_{\ell g}$ for even $\ell$, and $D_{\ell u}$ for odd $\ell$, of the form

$$\begin{aligned} u=\alpha _{\ell _{i}} Y_{\ell m},\quad \varvec{v}=\beta _{\ell _{i}}\; (\lambda a) \nabla ^{(S)}Y_{\ell m}, \end{aligned}$$

(3)

two different ($2\ell +1$)-fold coupled modes (for $i=2,3$). Here, physics determines not only the two eigenvalues for each $\ell$, but also the ratio of the amplitude constants $\alpha _{\ell _{i}}$ and $\beta _{\ell _{i}}$. The relation between representations and mode types is summarised in Table 1.

Table 1 Correspondence between representations $D_{\ell s}$ of O(3) and mode types of incremental displacements for uniformly stretched sphere

2.2 Isotropic hyper-elastic membranes

The eigenproblem for solving the coefficients $\alpha _{\ell _{i}}$, $\beta _{\ell _{i}}$, and $\gamma _{\ell _{i}}$ in Eqs. (2)–(3) needs the consideration of the physics of a particular problem on the sphere. This section gives the general equations for an isotropic hyper-elastic membrane, and specializes them for a uniformly stretched sphere.

An isotropic hyper-elastic material is characterized by a strain energy density $W_{e}$, i.e., per material volume. This is a function of invariants of the right Cauchy–Green tensor $\varvec{C}$. For a membrane, two coordinates $X^\alpha$, such as the two spherical angles $\theta$ and $\varphi$ for the sphere, are introduced to describe points in its surface, while the third direction is taken to be its outwards normal. We will use the convention that lower case component indices run over the two in-plane directions, whereas an upper case index runs over all three directions. Using local plane stress, the covariant components of $\varvec{C}$ then have the property $C_{3\alpha }=C_{\alpha 3}=0$, and $C_{33}$ can be solved for in terms of the in-plane components $C_{\alpha \beta }$ from either incompressibility or plane stress, cf. the material model examples below. Thus, $W_e$ can be expressed in terms of $C_{\alpha \beta }$ and by isotropy, from two invariants of the in-plane part $\varvec{C}_{2}$ containing the components $C_{\alpha \beta }$

$$\begin{aligned} J_1=\mathrm {Tr}(\varvec{C}_{2})/2,\text { and }J_2=\sqrt{\mathrm {Det}(\varvec{C}_{2})} , \end{aligned}$$

(4)

The two invariants allow the definition of the strain energy density as

$$\begin{aligned} W_{e}=W_e(J_{1},J_{2}) . \end{aligned}$$

(5)

The general equation can be specialized for a spherical membrane of initial thickness t isotropically stretched by $\lambda$, for which $J_{1}=J_{2}=\lambda ^2$. This is expanded up to second order in small incremental displacements. As further shown in “Appendix B”, the first order terms in both $J_1$ and $J_2$ are equal, but the second order terms are not. This means that to find the second order terms in variations in $W_{e}$, it is enough to know the values of the fundamental material functions

$$\begin{aligned} e(\lambda )&=t\frac{\partial W_e}{\partial J_{1}}(\lambda ^2,\lambda ^2) , \nonumber \\ f(\lambda )&=t\frac{\partial W_e}{\partial J_{2}}(\lambda ^2,\lambda ^2) , \nonumber \\ g(\lambda )&=t\lambda ^2\left[ \frac{\partial ^2 W_e}{\partial J_{1}\partial J_{1}}+2\frac{\partial ^2 W_e}{\partial J_{1}\partial J_{2}} \right. \nonumber \\&\quad + \left. \frac{\partial ^2 W_e}{\partial J_{2}\partial J_{2}}\right] (\lambda ^2,\lambda ^2) , \end{aligned}$$

(6)

with t the initial thickness, and the arguments showing that the strain energy density derivatives should be evaluated for the arguments $(J_{1}=\lambda ^{2},J_{2}=\lambda ^{2})$.

The description based on three functions was also used in [25], using the linearly transformed forms

$$\begin{aligned} \varSigma _1= & {} \frac{\lambda ^2}{t}(e+f) \end{aligned}$$

(7)

$$\begin{aligned} \varSigma _2= & {} \frac{\lambda ^2}{t}(e+g)\end{aligned}$$

(8)

$$\begin{aligned} \varSigma _3= & {} 2\frac{\lambda ^2}{t}e \end{aligned}$$

(9)

In Eq. (6), the expressions e, f, and g have the same physical dimension, force per length. For the unstretched material with $\lambda =1$, $f=-e$ for a material in equilibrium, and e and g must both be positive for a stable material model. It is also obvious that the expressions in Eq. (6) are easily obtained for any hyper-elastic material model which can be written in the form of Eq. (5).

The three functions in Eq. (6) express the dependence on a particular material model, given the particular stretch state existing in the pressurized sphere. It is not surprising that the derived functions are identical to the ones for a bi-axially isotropically stretched plane square given in [15], but with other expansions of $J_{1},J_{2}$.

A few common material models are elaborated below.

2.3 Equation of motion for small deviations of the inflated sphere

Starting from the spherical geometry and symmetry, and introducing the mechanics of a uniformly stretched membrane, the equations of linearized motion around an equilibrium state are now presented.

The uniform tension needed to keep the membrane in equilibrium at radius $\lambda a$ is

$$\begin{aligned} \psi (\lambda )=\frac{p\lambda a}{2} , \end{aligned}$$

(10)

related to the internal over-pressure p. As shown in “Appendix B”, this can be related to the tension defined as the integral of the Cauchy normal stress over the current thickness as

$$\begin{aligned} \psi (\lambda )=e(\lambda )+f(\lambda ) . \end{aligned}$$

(11)

with the fundamental material functions from Eq. (6).

The linearized equations of motion for the small incremental displacements described by u and $\varvec{v}$ are derived in “Appendix B” as

$$\begin{aligned}&-h(\lambda ) \ddot{u} -\frac{2g(\lambda )}{\lambda a}\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) \nonumber \\&\quad + \psi (\lambda )\left( 2u/(\lambda a)^2+\varDelta ^{(S)}u\right) =0 , \nonumber \\&-h(\lambda ) \ddot{\varvec{v}} +e(\lambda )\left( \frac{1}{(\lambda a)^2}\varvec{v}+\Delta ^{(S)}\varvec{v}\right) \nonumber \\&\quad +g(\lambda )\nabla ^{(S)}\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) =\varvec{0} , \end{aligned}$$

(12)

where $\Delta ^{(S)}$ is the surface Laplacian, and the uniform mass per stretched area is

$$\begin{aligned} h(\lambda )=\frac{t\rho }{\lambda ^2} . \end{aligned}$$

(13)

The equations of motion are converted to an eigenvalue problem by replacing the second time derivatives through multiplication by $-\kappa$ (if $\kappa$ is positive, this corresponds to a harmonic time variation with angular frequency $\omega =\sqrt{\kappa }$), yielding one scalar and one vector equation

$$\begin{aligned}&\kappa h(\lambda )u -\frac{2g(\lambda )}{\lambda a}\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) \nonumber \\&\quad + \psi (\lambda )\left( 2u/(\lambda a)^2+\Delta ^{(S)}u\right) =0 , \nonumber \\&\kappa h(\lambda )\varvec{v} +e(\lambda )\left( \frac{1}{(\lambda a)^2}\varvec{v}+\Delta ^{(S)}\varvec{v}\right) \nonumber \\&\quad + g(\lambda )\nabla ^{(S)}\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) =\varvec{0}. \end{aligned}$$

(14)

2.3.1 Eigensolutions to equations of motion

The eigenmodes from Eqs. (1), (2) or (3) can be used to compute the corresponding eigenvalues. Using the properties of the spherical harmonics $Y_{\ell m}$, cf. “Appendix A”, the eigenvalues are dependent on the index $\ell$, but not on m. As in “Appendix A”, the short-hand notation $q=Y_{\ell m}$, $\varvec{r}=(\lambda a)\nabla ^{(S)}q$, $\varvec{s}={}^*\varvec{r}$ is used in this section.

First, considering the radial mode $\ell =0$ gives the single eigenmode $u=\alpha _{0} q$, $\varvec{v}=\varvec{0}$ from Eq. (1). After some algebra, cf. “Appendix A”, two equations are obtained, according to

$$\begin{aligned} \frac{1}{(\lambda a)^2}\left[ (\lambda a)^2\kappa _0 h +(2\psi -4g)\right] \alpha _0 q&=0 , \nonumber \\ \varvec{0}&=\varvec{0} , \end{aligned}$$

(15)

when dropping the $\lambda$ arguments to g, h and $\psi$, and noting by the index on $\kappa$ that the single eigenvalue belongs to $\ell =0$. Equation (15) gives, by introduction of Eq. (13), the eigenvalue

$$\begin{aligned} \kappa _{0}= \frac{2(2g(\lambda )-\psi (\lambda ))}{a^{2}t\rho } , \end{aligned}$$

(16)

corresponding to this mode. The eigenvalue is thereby related to the current stretch and the fundamental material functions in Eqs. (6) and (11), i.e., the material model and its parameters.

Next, the case $\ell \ge 1$ with the first form of eigenmodes from Eqs. (2), is considered. Again, after some algebra, the eigenvalue equations in Eq. (14) then become

$$\begin{aligned}&0=0 , \nonumber \\&\frac{1}{(\lambda a)^2}\left[ (\lambda a)^2\kappa _{\ell _{1}} h- \theta _{\ell } e\right] \gamma _{l_1}\varvec{s} =\varvec{0} , \end{aligned}$$

(17)

— where a simplified notation

$$\begin{aligned} \theta _\ell =\ell (\ell +1)-2 , \end{aligned}$$

(18)

is introduced.

This gives the final expression for the eigenvalue

$$\begin{aligned} \kappa _{\ell _{1}} =\frac{\theta _{\ell } e(\lambda )}{a^{2}t\rho } , \end{aligned}$$

(19)

now dependent on the mode order $\ell$. As these eigenvalues $\kappa _{\ell _{1}}$ do not depend on m, they have multiplicities $2\ell +1$. Since the corresponding eigenmodes have zero divergence, they were called pure shear modes above and correspond to purely circumferential incremental displacement in an axi-symmetric model. As a special case, when $\ell =1$, i.e., $\theta _{\ell }=0$, the triple eigenvalue $\kappa _{1_{1}}$ is vanishing, corresponding to three modes of rigid rotation.

Finally, the coupled modes $u=\alpha _{\ell _{2,3}} q$, $\varvec{v}=\beta _{\ell _{2,3}} \varvec{r}$ from Eq. (3) are considered. Equation (14) then gives the two coupled equations

$$\begin{aligned}&\frac{1}{(\lambda a)^{2}} \left\{ \left[ (\lambda a)^2\kappa _{\ell _{2,3}} h -4g -\psi \theta _{\ell }\right] \alpha _{\ell _{2,3}} \right. \nonumber \\&\quad \left. +\left[ 2g\ell (\ell +1)\right] \beta _{\ell _{2,3}}\right\} \;q =0 , \nonumber \\&\frac{1}{(\lambda a)^{2}} \left\{ \left[ 2g\right] \alpha _{\ell _{2,3}}+\left[ (\lambda a)^2\kappa _{\ell _{2,3}} h-e\left( \theta _{\ell }\right) \right. \right. \nonumber \\&\quad \left. \left. -g\ell (\ell +1)\right] \beta _{\ell _{2,3}}\right\} \;\varvec{r}=\varvec{0} , \end{aligned}$$

(20)

where indices on $\kappa$, $\alpha$, and $\beta$ include both the order $\ell$ and the 2, 3 notation, which indicates that two new eigenvalues are obtained, each of multiplicity $2\ell +1$. They require the solution to the $2\times 2$ eigenvalue problem

(21)

which can be ensured to give real eigenvalues.

For $\ell =1$, $\theta _1=0$, the triple eigenvalue

$$\begin{aligned} \kappa _{1_{2}}=0 \quad \text {for} \quad \begin{pmatrix}\alpha _{1_{2}}\\ \beta _{1_{2}} \end{pmatrix}= \begin{pmatrix}1\\ 1 \end{pmatrix} \end{aligned}$$

(22)

corresponds to three modes of rigid translation. Another triple mode is found from Eq. (21) for $\ell =1$ as

$$\begin{aligned} \kappa _{1_{3}}=\frac{6 g(\lambda )}{a^{2}t\rho } \quad \text {for} \quad \begin{pmatrix}\alpha _{1_{3}}\\ \beta _{1_{3}} \end{pmatrix}= \begin{pmatrix}-2\\ 1 \end{pmatrix} , \end{aligned}$$

(23)

The modes in Eq. (23) are commonly described as pear-shaped, as they primarily consist of an axial deformation where one pole moves outwards, and the opposite one inwards.

For $\ell \ge 2$, the eigenvalues and eigenmodes can be computed by solving a second order algebraic equation from Eq. (21). It may, however, be easier to discuss the eigenvalues in terms of the trace and determinant of Eq. (21), which can be written

$$\begin{aligned} a^2 t \rho (\kappa _{\ell _2}+\kappa _{\ell _3})&=\theta _\ell (\psi +e+g)+6g \nonumber \\ (a^2 t\rho )^2 \kappa _{\ell _2}\kappa _{\ell _3}&=\theta _\ell \left[ \theta _\ell \psi (e+g)+2g(2e+\psi )\right] . \end{aligned}$$

(24)

By considering Eqs. (16), (19) for $\ell >1$, (23) for $\ell =1$, and Eqs. (24) for $\ell > 1$, it is noted that all eigenvalues at a specific uniform stretch value $\lambda$ can be easily evaluated through the order number $\ell$, and the three fundamental material functions coming from the hyper-elastic model. This, and in particular when any of these eigenvalues vanishes, will be used for stability investigations below.

2.3.2 Wave-speed interpretation

As a further interpretation of the above expressions, it is seen that asymptotically for large $\ell$, and thus large $\theta _{\ell }$, the two equations (24) provide the solutions

$$\begin{aligned} a^2 t\rho \kappa _{\ell _{2}}\approx \theta _\ell \psi (\lambda ),\quad a^2 t\rho \kappa _{\ell _{3}}\approx \theta _\ell (e(\lambda )+g(\lambda )) , \end{aligned}$$

(25)

while Eq. (19) is still valid and can be expressed as

$$\begin{aligned} a^2 t\rho \kappa _{\ell _{1}}=\theta _\ell e(\lambda ). \end{aligned}$$

(26)

The expressions for the eigenvalues

$$\begin{aligned} \kappa _{\ell _{1}}&= \frac{\theta _\ell e(\lambda )}{a^{2}t\rho } , \nonumber \\ \kappa _{\ell _{2}}&\approx \frac{\theta _\ell \psi (\lambda )}{a^{2}t\rho } = \frac{\theta _\ell (e(\lambda )+f(\lambda ))}{a^{2}t\rho } , \nonumber \\ \kappa _{\ell _{3}}&\approx \frac{\theta _\ell (e(\lambda )+g(\lambda ))}{a^{2}t\rho } \end{aligned}$$

(27)

are thereby all valid in high $\ell$ and arbitrary m, i.e., in the limit of short wave length, where curvature is unimportant. The three expressions correspond to transverse in-plane, transverse out-of plane, and longitudinal in-plane short waves with wave speeds (on the deformed sphere)

$$\begin{aligned} c_{1}(\lambda )&=\sqrt{\frac{e(\lambda )}{h}},\nonumber \\ c_{2}(\lambda )&=\sqrt{\frac{\psi (\lambda )}{h}},\nonumber \\ c_{3}(\lambda )&=\sqrt{\frac{e(\lambda )+g(\lambda )}{h}} , \end{aligned}$$

(28)

respectively, and depending on the material model. The form of the equations is chosen to emphasize the similarity to common wave speed expressions for solids as the square root of a quotient of stiffness to density.

2.4 Stability

Rather than investigating the definiteness of the total potential energy, stability of an equilibrium state for a pressurized sphere is judged by the existence of vibration frequencies for linearized small motions around the state, considering the mass distribution of the model [17]. Stability thereby requires all eigenvalues to correspond to time harmonic modes, i.e., all $\kappa _{\ell _{i}}=\omega ^{2}$ positive, except the two sets of triple zero eigenvalues $\kappa _{1_{1}}$ and $\kappa _{1_{2}}$, which are related to rigid body motions.

The signs of the eigenvalues from Eqs. (16), (19), (23) and (24) only depend on the stretch and the material model through the values of $e(\lambda )$, $\psi (\lambda )$, and $g(\lambda )$. With e, $\psi$ and g considered as independent quantities, the signs of the eigenvalues can be computed for any point in $(e,\psi ,g)$ space. This will give regions in $(e,\psi ,g)$ space corresponding to stability, and surfaces corresponding to critical stability with any vanishing eigenvalue. Once these regions and surfaces have been established, the increasing stretch $\lambda$ of a sphere of any particular material will correspond to a curve in $(e,\psi ,g)$ space. These curves will pass through the regions and surfaces, thus giving the stability intervals and critical values for that material, in the particular situation of uniform stretch.

First, Eq. (27) is used to show that, with large enough $\ell$, there are an infinite number of negative eigenvalues whenever any of e, $\psi$, or $e+g$ is negative. Thus, any stable region must lie within a set A given by $e\ge 0$, $\psi \ge 0$, $g\ge -e$. Within this set A, critical states are sought, for all $\ell$.

The single mode for $\ell =0$ is critical according to Eq. (16) when

$$\begin{aligned} g=g_{0}(e,\psi )=\frac{\psi }{2}, \end{aligned}$$

(29)

The non-rigid-body mode for order $\ell =1$ is critical according to Eq. (23) when

$$\begin{aligned} g=g_{1}(e,\psi )=0. \end{aligned}$$

(30)

The critical surfaces for the $\ell _{2,3}$ modes with $\ell \ge 2$ is given by the vanishing determinant in Eq. (24), which for increasing $\ell$ is

$$\begin{aligned} g=g_{\ell }(e,\psi )=-\frac{\theta _\ell \psi e}{(\theta _\ell +2)\psi +4e}. \end{aligned}$$

(31)

As both $e>0$ and $\psi >0$ in the interior of the set A, the values $g_{\ell }(e,\psi )$ form a decreasing sequence with $\ell$ for fixed e and $\psi$. As $\ell$ becomes large, $g_{\ell }(e,\psi )$ converges to $g_{\infty }(e,\psi )=-e$. Thus, for given $e>0$ and $\psi >0$, a relation holds:

$$\begin{aligned} -e=g_{\infty }&<\cdots<g_{\ell +1}<g_{\ell }<\cdots \nonumber \\&<g_2<g_1=0<g_0=\frac{\psi }{2}. \end{aligned}$$

(32)

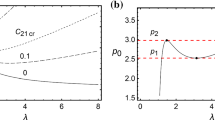
The relation shows that the critical surfaces $g=g_\ell (e,\psi )$ never intersect in the interior of A, but lie monotonously stacked below each other in $(e,\psi ,g)$ space for increasing $\ell$, and bound by the simple surfaces $g=\psi /2$ and $g=-e$, as shown in Fig. 1.

It can also be shown from Eq. (19) that no surfaces of type $\ell _{1}$ exist in the interior of A.

Fig. 1

Critical surfaces in $(e,\psi ,g)$ space. Plotted are the surfaces $g_{\ell }(e,\psi )$ for $\ell =0,1,2,4,10,\infty$, Eqs. (29)–(32), but also the critical surfaces $e=0$, and $\psi =0$. The quantity $\mu t$ in the axis labels is the product of linearized shear stiffness and thickness

The conclusion from Fig. 1 is that only the region above $g=g_0(e,\psi )$ is stable. For any point with $e>0$, $\psi =0$, and $g>0$, e.g., the undeformed sphere, Eqs. (19) and (24) immediately show that all non-rigid-body eigenvalues are stable The surface $g=g_0$ does, however, not belong to the stable region, nor does the boundary $e=0$, as all modes of type $\ell _1$ are critical there. This also shows that the more stable side of each of the surfaces $g=g_\ell$ is the upper side, in the sense that the number of negative eigenvalue is increased by $2\ell +1$ on the lower side.

To conclude, the stable region consists of points where

$$\begin{aligned} \psi \ge 0\text {, } e>0\text {, and } g>g_0(e,\psi )=\frac{\psi }{2}, \end{aligned}$$

(33)

while there are $\sum _{\ell =0}^n(2\ell +1)=(n+1)^2$ negative eigenvalues, all others being positive, in the region

$$\begin{aligned} \psi>0\text {, } e>0\text {, and } g_{n+1}(e,\psi )<g<g_n(e,\psi ), \end{aligned}$$

(34)

formed between the $g_n$ and $g_{n+1}$ surfaces. Finally, an infinite number of eigenvalues are negative for

$$\begin{aligned} \psi<0\text {, } e<0\text {, or } g<-e. \end{aligned}$$

(35)

This result agrees with the work in [25], except in the numbers of negative eigenvalues in the sub-regions, which are now higher due to the more comprehensive kinematic description.

As a final remark, it is noted that these stability conclusions are valid for the case of given pressure. Other situations, for example controlling the pressure implicitly by prescribing the gas amount or gas volume are possible. As long as these indirect ways of specifying the pressure retain full spherical symmetry, the only eigenvalue that could be influenced is $\kappa _0$, which would result in a different—or possibly absent—limit state surface $g_0$. For example, for fixed volume, the surface $g_{0}$ disappears, and the stability region is bounded by $g>g_{1}=0$ instead.

2.4.1 Response to increasing stretch

The above treatment, and Fig. 1, have assumed that e, g and $\psi$ are independent variables. Attention is now given to the curve in $(e,\psi ,g)$ space corresponding to a particular material when stretch $\lambda$ increases from $\lambda =1$ at a state with $e(1),g(1)>0$, $\psi (1)=0$. This belongs to the stable region, but is on the boundary, which defines the demands for an initially stable material. As the stretch $\lambda$ increases from 1, the value $\psi (\lambda )$ becomes positive, so the curve initially points into the stable region. Continuing on the curve with increasing $\lambda$, giving $e(\lambda )$, $g(\lambda )$, and $\psi (\lambda )$, stability can be lost through three different mechanisms.

The first is related to $g(\lambda )$ passing through $g_{0}(e(\lambda ),\psi (\lambda ))$ from above, when the single critical mode is the spherically symmetric one, according to Eq. (1). This corresponds to a limit state, where the pressure p has a local maximum with respect to the stretch $\lambda$, cf. [25]. If $g(\lambda )$ further decreases through $g_1(e(\lambda ),\psi (\lambda ))=0$, a bifurcation with a 3-fold zero eigenvalue occurs for $\ell =1$. If $g(\lambda )$ continues to move towards $g_{\infty }(e(\lambda ),\psi (\lambda ))=-e(\lambda )$, bifurcations occur, with an increasing number of unstable modes for $\ell =2,3,\ldots$, with increasing multiplicity. It is, however, fully possible that the function $g(\lambda )$ could reduce instability by starting to pass back through the $g_\ell (e(\lambda ),\psi (\lambda ))$ values from below for increasing $\ell$. It is even possible to regain stability at further increased stretch, cf. the Ogden model below.

A second mechanism for loss of stability is related to $e(\lambda )$ becoming negative. As this, through Eq. (27)${}_{1}$, is related to shear modes according to Eq. (2), this makes all in-plane shear modes become unstable at the same value of the stretch $\lambda$, and the material thereby collapses in shear.

A third mechanism is related to $\psi (\lambda )$ becoming negative. As this, through Eq. (27)${}_{2}$, is related to coupled modes according to Eq. (3), this makes all short wavelength out-of-plane modes unstable through a wrinkling behavior, which is also a collapse.

Figure 2 shows how the $e(\lambda )$, $\psi (\lambda )$, and $g(\lambda )$ functions vary during a uniform stretch variation $\lambda$ for a few specific material models discussed below. The models show qualitatively very different responses, as clearly seen from the crossings with the critical surfaces and the vanishing e and $\psi$ values. Note how the curve ‘Case 1’ will cross all critical surfaces before simultaneously reaching the $g=-e$ and $\psi =0$ surfaces.

Fig. 2

Examples of stretch-dependent fundamental material function values, allowing stability conclusions for increasing stretch $\lambda$ of the sphere. Case 1: Mooney–Rivlin material with $c_{2}/c_{1}=-1/2$, $\mu =2(c_{1}+c_{2})$. Case 2: Mooney–Rivlin material with $c_{2}/c_{1}=-2$, $\mu =2(c_{1}+c_{2})$. Case 3: Ogden material with $\mu _{1}=630\,\text {kPa}$, $\alpha _{1}=1.3$, $\mu _{2}=1.2\,\text {kPa}$, $\alpha _{2}=5$, $\mu _{3}=-10\,\text {kPa}$, $\alpha _{3}=-2$, cf. Sect. 2.5.3. Case 4: Ogden material with $\mu _{1}=803.2$ kPa, $\alpha _{1}=1.05$, $\mu _{2}=-0.8032,$ kPa, $\alpha _{2}=-2$, $\mu _{3}=0$, cf. Sect. 4.2.2

2.5 Common hyper-elastic material models

The discussion above has considered a general hyper-elastic material model, where the strain energy density is written as a function of the two invariants of the in-plane strain tensor, Eq. (5). Stability conclusions can thereby be drawn for the pressurized sphere under uniform stretch, for three common material models.

2.5.1 Saint Venant–Kirchhoff model

The Saint Venant–Kirchhoff material model extends the linear elastic material model to the non-linear Green-Lagrange strains

$$\begin{aligned} E^{A}_{B}=\frac{1}{2}\left( C^{A}_{B}-\delta ^{A}_{B}\right) \end{aligned}$$

(36)

with capital letters denoting 3D indices ($A,B=1,2,3$), and $\delta ^{A}_{B}$ the Kronecker delta function. Introducing local plane-stress assumptions and formulating deviatoric strains gives the strain invariants

$$\begin{aligned} E^{i}_{i}=J_{1}-1,\quad {\bar{E}}^{i}_{j}{\bar{E}}^{j}_{i}=\frac{1}{2}((J_{1})^{2}-(J_2)^2), \end{aligned}$$

(37)

with lower case letters denoting 2D indices, and overbars 2D deviatoric strains ${\bar{E}}^{j}_{i}=E^{j}_{i}-(1/2) E^{k}_{k}\delta ^{j}_{i}$. The strain energy density is then

$$\begin{aligned} W_e=\frac{G}{2}((J_{1})^{2}-(J_2)^2)+\frac{K_{\text {2D}}}{2}(J_1-1)^{2}, \end{aligned}$$

(38)

with G the shear modulus and $K_{\text {2D}}=(9 G K_{\text {3D}})/(4G+3 K_{\text {3D}})$ the 2D plane stress version of the bulk modulus $K_{\text {3D}}$. The fundamental material functions in Eq. (6) then become

$$\begin{aligned} e(\lambda )&=t \left[ G\lambda ^2+K_{\text {2D}}(\lambda ^2-1)\right] \nonumber \\ f(\lambda )&=-t G\lambda ^2 \nonumber \\ g(\lambda )&=t K_{\text {2D}}\lambda ^2. \end{aligned}$$

(39)

At unit stretch $\lambda =1$, this leads to $e(1)=tG$, $f(1)=-e(1)$, $\psi (1)=0$, and $g(1)=tK_{\text {2D}}$, identifying e(1) and g(1) as shear and 2D plane stress bulk moduli integrated over thickness. Also note, comparing to the cases below, that plane stress, but not incompressibility, is assumed here.

An example

Since the constants $G,K_{\text {2D}}>0$, the sphere is stable for all $\lambda \ge 1$ as

$$\begin{aligned}&e(\lambda )>0 , \nonumber \\&\psi (\lambda )=tK_{\text {2D}}(\lambda ^2-1) \ge 0 ,\nonumber \\&g(\lambda )-g_0(e(\lambda ),\psi (\lambda ))=tK_{\text {2D}}\frac{\lambda ^2+1}{2} >0 . \end{aligned}$$

(40)

2.5.2 Two-parameter incompressible Mooney–Rivlin model

A two-parameter Mooney–Rivlin model utilizes the incompressibility relation $I_3=1$, and defines a strain energy density as

$$\begin{aligned} W_e=c_1(I_1-3)+c_2(I_2-3). \end{aligned}$$

(41)

with two constants and the strain invariants, identified with the ones in Eq. (4),

$$\begin{aligned} I_{1}&=C^{I}_{I} =2J_1+\frac{1}{(J_{2})^{2}} \nonumber \\ I_{2}&=\frac{1}{2}(C^{I}_{I}C^{J}_{J} - C^{I}_{J}C^{J}_{I}) =(J_{2})^{2}+2\frac{J_1}{(J_{2})^{2}} , \end{aligned}$$

(42)

using that incompressibility gives $C^{3}_{3}=1/(J_{2})^2$. The strain energy density for the incompressible Mooney–Rivlin material model is thereby

$$\begin{aligned} W_e&=c_1\left( 2J_1+\frac{1}{(J_{2})^{2}}-3\right) \nonumber \\&\quad + c_2\left( (J_{2})^{2}+2\frac{J_1}{(J_{2})^{2}}-3\right) , \end{aligned}$$

(43)

and the fundamental material functions become

$$\begin{aligned} e(\lambda )&=2t\frac{c_1 \lambda ^6+c_2\lambda ^2}{\lambda ^6}, \nonumber \\ f(\lambda )&=-2t\frac{c_1+c_2\lambda ^2(2-\lambda ^6)}{\lambda ^6}, \nonumber \\ g(\lambda )&=2t\frac{3c_1+c_2\lambda ^2(2+\lambda ^6)}{\lambda ^6}. \end{aligned}$$

(44)

For a uniform stretch of $\lambda =1$, this gives $e(1)=2t(c_1+c_2)$, $f(1)=-e(1)$, and $g(1)=3e(1)$, which identifies $\mu =2(c_1+c_2)$ as the linearized shear modulus at unit stretch.

An example Stability at unit stretch demands $c_1+c_2>0$. Further

$$\begin{aligned} \psi (\lambda )=e(\lambda )+f(\lambda )=2t\frac{\lambda ^6-1}{\lambda ^6}(c_1+c_2\lambda ^2). \end{aligned}$$

(45)

When both $c_1,c_2>0$, then

$g(\lambda )>g_1(e(\lambda ),\psi (\lambda ))=0$ for $\lambda \ge 1$, but limit states $g(\lambda )=g_0(e(\lambda ),\psi (\lambda ))$ will be encountered two or zero times depending on whether $c_2/c_1$ is smaller than or larger than $(\sqrt{396}-9)/(15(\sqrt{396}+19)^{1/3})\approx 0.21446$.

When $c_{1}>0, c_{2}<0$, the system will pass through all $g(\lambda )=g_{\ell }(e(\lambda ),\psi (\lambda ))$ values and finally reach $g(\lambda )=-e(\lambda )$ and $\psi (\lambda )=0$ at the same stretch. For larger stretches, the material collapses. As an example, when $c_2/c_{1}=-1/2$, then $g(\lambda )=g_0(e(\lambda ),\psi (\lambda ))$ at $\lambda =1.1447$, $g(\lambda )=g_1(e(\lambda ),\psi (\lambda ))$ at $\lambda =1.1611$, and $g(\lambda )=g_{2}(e(\lambda ),\psi (\lambda ))$ at $\lambda =1.1874$. For higher $\ell$, e.g., $g(\lambda )=g_{10}(e(\lambda ),\psi (\lambda ))$ at $\lambda =1.3205$, while $g(\lambda )=-e(\lambda )$ (and $\psi (\lambda )=0$) at $\lambda =\sqrt{2}\approx 1.4142$. This is Case 1 in Fig. 2.

When $c_1<0$, the system will not pass any surface $g(\lambda )=g_\ell \left( e(\lambda ),\psi (\lambda )\right)$, but instead pass through $e(\lambda )=0$ at some stretch, when the material suddenly collapses. For example, when $c_{1}<0, c_{2}/c_{1}=-2$, this happens at $\lambda =\root 4 \of {2}\approx 1.1892$. This is Case 2 in Fig. 2.

As will be further shown by numerical examples below, the two-parameter Mooney–Rivlin material model can show three qualitatively different behaviors for positive $c_{1}$, in addition to the sudden collapse for $c_{1}<0$: a monotonously increasing pressure under stretch, a pair of pressure limit states, or one pressure limit state followed by an infinite sequence of bifurcations. To what extent these instabilities can be reproduced by discretized models will be further discussed below.

2.5.3 Incompressible Ogden model

The strain energy density for the incompressible N-term Ogden material model is expressed using the three principal stretches $\lambda _{J}$, [38],

$$\begin{aligned} W_e=\sum _{i}^{N}\frac{\mu _i}{\alpha _i} \left( \lambda _1^{\alpha _i}+\lambda _2^{\alpha _i}+\lambda _3^{\alpha _i}-3\right) , \end{aligned}$$

(46)

and 2N constitutive parameters $\mu _i$, $\alpha _i$.

As incompressibility gives $\lambda _1\lambda _2\lambda _3=1$, and, since $\lambda ^2_1+\lambda ^2_2=2J_1$ and $\lambda _1\lambda _2=J_2$, the relation between principal stretches and the sought invariants are expressed as

$$\begin{aligned} \lambda _1&=\sqrt{J_1+\sqrt{(J_{1})^{2}-(J_{2})^{2}}},\nonumber \\ \lambda _2&=\sqrt{J_1-\sqrt{(J_{1})^{2}-(J_{2})^{2}}},\nonumber \\ \lambda _3&=1/J_2. \end{aligned}$$

(47)

The derivative expressions need be evaluated as limits $J_2\rightarrow J_1$, due to the mild singularity at $J_2=J_1$, giving

$$\begin{aligned} e(\lambda )&=\frac{t}{2}\sum _{i}^{N}\mu _i\alpha _i\lambda ^{\alpha _i-2},\nonumber \\ f(\lambda )&=-\frac{t}{2}\sum _{i}^{N}\mu _i\left[ (\alpha _i-2)\lambda ^{\alpha _i-2} +2\lambda ^{-2\alpha _i-2}\right] , \nonumber \\ g(\lambda )&=\frac{t}{2}\sum _{i}^{N}\mu _i\left[ (\alpha _i-2) \lambda ^{\alpha _i-2}\right. \nonumber \\&\quad \left. +2(\alpha _i+1)\lambda ^{-2\alpha _i-2}\right] . \end{aligned}$$

(48)

At $\lambda =1$, the expressions give

$e(1)=t/2\sum _{i}^{N}\mu _i\alpha _i$, $f(1)=-e(1)$, and $g(1)=3e(1)$, which identifies $\mu =\sum _{i}^{N}\mu _i\alpha _i/2$ as the linearized shear modulus at unit stretch.

An example

For the well-known parameter values $\mu _1=630\;\text {kPa}$, $\alpha _1=1.3$, $\mu _2=1.2\text {kPa}$, $\alpha _2=5$, $\mu _3=-10\;\text {kPa}$, $\alpha _3=-2$ [26], the system will become unstable by passing through a limit state as $g(\lambda )=g_0(e(\lambda ),\psi (\lambda ))$ at $\lambda =1.3741$. For further stretches, there is a bifurcation when $g(\lambda )=g_1(e(\lambda ),\psi (\lambda ))$ at $\lambda =1.7719$ with $g(\lambda )$ decreasing, and one when again $g(\lambda )=g_1(e(\lambda ),\psi (\lambda ))$, but now with $g(\lambda )$ increasing, at $\lambda =2.5453$. Finally, the system will become stable again by passing through a limit state as $g(\lambda )=g_0(e(\lambda ),\psi (\lambda ))$ at $\lambda =4.3203$. This is Case 3 in Fig. 2.

A one-term restricted form of the model in Eq. (46) was studied in both [25, 37] with conclusions in Table 2. Results are numerically confirmed below.

Table 2 Stability properties for pressurized sphere, modelled by one-term Ogden material models with different exponents $\alpha _{1}$ in Eq. (46), $\mu _{2}=\mu _{3}=0$

In two-term form, with four parameters, the Ogden material model can give a more complex behavior than the Mooney–Rivlin material model, and is then strongly dependent on the $\alpha _{i}$ exponents. This will be further shown by numerical examples below. One example is Case 4 in Fig. 2.

3 Symmetries of structures and models

Previous work [16, 17] has shown how symmetry properties of a discretization can significantly affect the calculated response to loading. In discretized modelling, symmetry aspects will essentially appear in two contexts, where the first relates to a complete structure represented by a mesh which has, or does not have, particular symmetry properties. The second aspect is related to the modeling of a minimal part of the full structure, where sets of conditions are introduced on the subdomain boundaries [16]. For example, using a mesh with icosahedral symmetry, only a fundamental domain of 1/120 of the sphere need be modelled, but with a significant amount of bookkeeping needed to reconstruct the solutions and eigenmodes on the full sphere. The present work only considered modeling of the full sphere, and this section will discuss how the symmetry groups of a discretized mesh will affect the description of the critical eigenvectors of order $\ell$ on the sphere.

3.1 Splitting of representations

The representations $D_{\ell g}$ and $D_{\ell u}$ for $\ell =0,1,2,\ldots$ in Table 1 are irreducible for the full spherical symmetry group O(3). As noted above, the symmetry of a discretized mesh must be that of a finite subgroup G of O(3). While $D_{\ell g}$ and $D_{\ell u}$ are still representations for G, they are not necessarily irreducible, since the subset of group elements belonging to G also implies a subset of linear operators when testing for invariance. Like any reducible representation, it will split into a direct sum of irreducible representations of the group G.

“Appendix C” reviews how to use published character tables to compute the splitting. The conventional names for the irreducible representations follow a pattern, where A and B are one-dimensional representations, E two-dimensional, T three-dimensional, G four-dimensional, and H five-dimensional. Numerical indices denote different representations of the same dimension, whereas the indices $(\cdot )_{g}$ and $(\cdot )_{u}$ denote symmetry and anti-symmetry with respect to inversions.

As an example, “Appendix C” shows that a mesh with tetrahedral symmetry will split the 11-dimensional representation $D_{5u}$ into $E+T_1+2T_2$ with dimensions $2+3+2\cdot 3=11$. This shows that, for any reasonably fine mesh, a group of four close eigenvalues of multiplicities 2, 3, 3, 3 (in some order) will be observed instead of one eigenvalue of multiplicity 11. The same reasoning shows that the zero-crossings of the eigenvalues will not coincide.

For critical eigenvalues and modes, it is of special interest to identify whether a mode corresponds to the trivial representation¹ where each group element is associated with the one-dimensional identity operator. The eigenmode then has full symmetry, the same as the equilibrium solution. In general, a zero eigenvalue then shows a limit state on the primary branch. On the other hand, critical eigenmodes corresponding to non-trivial representations imply a symmetry-breaking bifurcation, where one or more secondary branches of lower symmetry can cross the primary branch.

Although several response aspects converge as expected with fineness of the meshing, some aspects like the capacity to reproduce bifurcations of higher orders are independent of the mesh refinement, and are purely effects from the mesh symmetry properties.

3.2 Meshes from regular geometries

A basic method to create a mesh on the sphere starts from a simple regular geometry, and refines it systematically. Only a few realistic instances exist, and the symmetry properties of three regular geometries are discussed below.

3.2.1 Icosahedron-based meshes $I_h$

The best modelling of the sphere based on a triangle mesh, i.e., the one with highest symmetry is using the icosahedron symmetry group $I_{h}$. The analysis of a mesh with $I_{h}$ symmetry results in the representation splittings in Table 3. Any mesh based on icosahedral symmetry will then represent the criticalities up to $\ell =2$ as isolated states with correct multiplicity, while the states for $\ell =3,4,5$ will be split into 2, 2, 3 closely spaced but separate bifurcations of lower orders, respectively. The presence of the trivial representation $A_{g}$ in the entry for $\ell =6$, corresponding to eigenvalues $\kappa _{6_2}$ and $\kappa _{6_3}$, shows that the $I_{h}$ models will here give a limit state—instead of a bifurcation—and thereby fail to follow the correct sequence of uniform stretch.

Table 3 Splitting of out-of-plane and in-plane modes by an $I_h$ (icosahedral) mesh, cf. Table 1

3.2.2 Tetrahedron-based meshes $T_d$

Conclusions can be reached similarly for discretizations based on the tetrahedron symmetry group $T_{d}$, Table 4. A tetrahedron-based mesh will therefore show vanishing eigenvalues of at most multiplicity 3. A conclusion is also that any mesh based on tetrahedral symmetry will split the $\ell =2$ bifurcation into two bifurcations of multiplicities 2 and 3, respectively, and will fail to represent the $\ell =3$ bifurcation state correctly.

Table 4 Splitting of out-of-plane and in-plane modes by a $T_d$ (tetrahedral) mesh, cf. Table 1

3.2.3 Octahedron-based meshes $O_h$

The analysis of meshes with $O_{h}$ symmetry is similar, and shows that any such mesh will split the $\ell =2$ and $\ell =3$ bifurcations into isolated bifurcations of multiplicities $2+3$ and $1+3+3$, respectively, and will fail to represent the $\ell =4$ bifurcation state correctly.

It is noted that a cube, which could be another possibility to create the mesh, is also of symmetry group $O_h$.

3.3 Axis-based meshes

Symmetry aspects are in engineering practice most commonly observed through mirror planes. This corresponds to the creation of a well-defined subdomain, followed by a repetition of this through simple geometric transformations. In the present context, it is rather natural to introduce an equator mirror plane, and to define as the basic subdomain one sector, limited by mirror planes of constant longitude, of the half-sphere. This introduces an axial direction, around which the initial mesh is rotated. Consequently, the meshes are not equal in the three global axis directions, and are of lower symmetry. With n sectors around the circumference, the symmetry will be from the dihedral group $D_{nh}$. In the present work, a basic mesh was created for $n=8$, i.e., from one eighth of the half-sphere, introducing eight vertices in the mirror plane, together with one apex point on each side. The symmetry group for these meshes was thereby $D_{8h}$.

3.3.1 Dihedral meshes $D_{8h}$

An analysis of a mesh with $D_{8h}$ symmetry will give results of the same form as above, and indicate that any mesh based on the $D_{8h}$ symmetry splits already the $\ell =1$ bifurcation into two bifurcations of multiplicities 1 and 2, respectively, and will fail to represent the $\ell =2$ bifurcation state correctly.

3.4 Systematic mesh refinement

With either of the two approaches above, a minimal basic mesh is created, consisting of a set of triangles. This mesh introduces the symmetry properties which will also be valid for recursive refinements to computational meshes. The basic meshes used here were created as a set of identical surfaces, but it is noted that meshes created from regular geometries consisted of equilateral triangular surfaces, while the axis-based mesh consisted of isosceles triangles.

A requirement for kept symmetry is a systematic procedure for the refinement from the basic mesh. Aiming at a general method for any domain, a recursive process divided each existing triangle into four, by introducing nodes at the midpoints of existing triangle edges. All new nodes were then radially moved to the unit sphere, before going to the next recursive step. This is essentially similar to the approaches in [3, 42]. It is noted that, although all vertices are correctly placed on the sphere, the recursive introduction of new vertices will lead to a hierarchy of nodes

Two steps of refinement of an equilateral triangle in Fig. 3 shows how new generations of nodes are created, with different positions in relation to the symmetry of the initial mesh; nodes with the same notation are symmetrically identical in the uniform stretch. Figure 4 shows how the initial regular tetrahedron with four flat surfaces and four vertices was refined to a $T_{d}$ mesh with 1024 surfaces and 514 vertices, keeping the initial symmetry.

Fig. 3

Two steps of recursive refinement of an equilateral triangular element, showing $1+1+2=4$ hierarchical classes of nodes. For an isosceles triangle, a similar refinement will give $2+2+5=9$ different classes of nodal placements

Fig. 4

Initial and refined tetrahedron-based $T_{d}$ meshes with 4 and 1024 flat surfaces, respectively

As discussed in [27], this method for meshing on the sphere is not perfect, as the sphere surface will be divided into elements of unequal sizes, with larger elements in the central regions of initial triangles. The effect is particularly visible for the tetrahedron-based meshes in Fig. 4. For the present purposes, and primarily focussing on the icosahedron-based meshes, the effects from non-uniform meshing are limited, as long as symmetry is kept.

Another non-iterative method for mesh generation is similar to the method shown in [46]. A cube is then regularly but non-uniformly divided into six side meshes. When the cube sides are mapped onto a circumscribed sphere, this mesh becomes slightly more uniform in element sizes.

A practical aspect of mesh refinement is that very high precision must be used, in order to keep the intended symmetry; a relative inaccuracy in nodal coordinates of $\approx 1\cdot 10^{-6}$ was in [17] shown to destroy symmetry in results.

3.5 Meshes for numerical tests

Simulations of the gas-pressurized spherical membrane were primarily performed with meshes of triangular elements from four different symmetry classes. These meshes are below denoted using the symmetry group name followed by the number of elements within parentheses. The four classes were:

• A regular icosahedron mesh $I_{h}(20)$ was created, using 12 nodes. The primarily used $I_{h}(5120)$ mesh with 2562 nodes needed 4 refinement steps, giving nodes of 30 hierarchical classes.

• A regular tetrahedron mesh $T_{d}(4)$ was created, using 4 nodes. The used $T_{d}(4096)$ mesh with 2050 nodes needed 5 refinement steps, which gave 102 different nodal classes.

• A regular octahedron mesh $O_{h}(8)$ was created, using 6 nodes. The used $O_{h}(8192)$ mesh with 4098 nodes needed 5 refinement steps, which gave 102 different nodal classes.

• A $D_{8h}(16)$ mesh was created according to the description above, and using 10 nodes. The used $D_{8h}(4096)$ mesh with 2050 nodes needed 4 refinement steps, which gave 81 different nodal classes, due to the isosceles initial triangles.

In addition, a variation of the cubed sphere mesh from [46] was created. The mesh was created from an internally symmetric mesh of $2N\times N$ (N even) triangular elements on each side of a cube, with the nodes then moved radially to correct radius. In particular, a C(3072) mesh was created with $N=16$ giving 1538 nodes of 45 different nodal classes. The resulting cube-based mesh maintains the $O_{h}$ symmetry of the cube.

4 Numerical verification

The previous sections have given an analytical treatment of the stability of gas-pressurized hyper-elastic spheres, and discussed how different discretizations for the continuous sphere will affect the obtained results. The present section will demonstrate how the analytical results and predictions are reproduced in element-based discretizations. Results are presented for parameter variations within two hyper-elastic material models discussed above, and for different meshes.

4.1 Problem setting, and basic formulation

The case studied was a thin sphere of midplane radius $a=50\,\text {mm}$ and thickness $t=0.05\,\text {mm}$ pressurized by an internal over-pressure p. Incompressible material models were considered, with linearized shear stiffness for the unstressed membrane $\mu =422.5\,\text {kPa}$. The material models were included in the formulation of a faceted triangular thin membrane element with linear interpolation of translations and local plane stress conditions [14]. No handling of wrinkling was included, but all presented results were verified to be wrinkling-free.

The numerical tests used meshes described in Sect. 3.5 above, with the $I_{h}(5120)$ mesh as default, and with one initial node at (0, 0, a). The radial displacement $u_{a}$ of this node is used to quantify stretch as $\lambda =(a+u_{a})/a$ in results.

Mainly solutions on the primary solution path for the discretized problem were obtained, i.e., the path where solutions maintain the full symmetry of the mesh. Results are represented by the relation between stretch $\lambda$ and over-pressure p. The non-linear equilibrium problem was set up as described in [17]. Stability of equilibrium states was evaluated from the Jacobian matrix, with no inertia associated to constraint equations. Bisection was used to high precision, in order to isolate states giving a change of stability. Evaluation of secondary paths was only occasionally performed, even if this could be done in the present setting.

4.2 Material models

4.2.1 Mooney–Rivlin models

Simulations were performed for Mooney–Rivlin models with different values for $k=c_{2}/c_{1}$ in $\mu = 2(c_{1}+c_{2})$. Results are given in Fig. 5, as pressure-stretch curves for six values $0.18\le k \le 0.23$, and a critical sequence for a larger range.

Fig. 5

Pressure-stretch curves for Mooney–Rivlin material models with positive constitutive constants $k=c_{2}/c_{1}$, all with $\mu =2(c_{1}+c_{2})=422.5\,\text {kPa}$. Curves are for $k=0.18(0.01)0.23$ from below. Isolated critical states on equilibrium sequences are marked by ‘$+$’. Dashed line shows the evaluated critical equilibrium sequence, connecting the limit states. Subfigure b is a zoom-in of marked box in a

The critical sequence verifies that the double limit states only exist for $k\le 0.21446$. To given accuracy, the same limiting value for k was obtained with the coarser $I_{h}(1280)$ and $I_{h}(320)$ models, but the stretch at this limiting value was slightly different for the three meshes.

Negative constants For a constitutive constant $k<0$, also bifurcations appeared for the Mooney–Rivlin models [17]. The first bifurcations were well represented by the $I_{h}(5120)$ model. For $c_{1}>0, c_{2}/c_{1}=-1/2$, the limit state was found at $\lambda =1.1441$, and the two first bifurcations at $\lambda =1.1606$ and $\lambda =1.1871$, respectively, cf. Sect. 2.5.2. Equilibrium sequences obtained for a few different negative k constants are shown in Fig. 6.

Fig. 6

Pressure-stretch curves for Mooney–Rivlin material models with negative constitutive constants $k=c_{2}/c_{1}$, all with $\mu =2(c_{1}+c_{2})=422.5\,\text {kPa}$. Curves are for $k=-0.5(0.1)-0.1$ from below. Isolated critical states on equilibrium sequences before the maximum stretch are marked by ‘$+$’. Subfigure b is a zoom-in of marked box in a for the case $k=-0.2$. Numbers in b indicate multiplicity of zero eigenvalue

A magnified view on the case $k=-0.2$ is also given in Fig. 6b. The figure shows how the $\ell =5$ bifurcation was split into three distinct bifurcation states for this model, while the $\ell =6$ bifurcation was incorrectly represented. Higher order bifurcations $\ell >6$, although existing in the analytical solution, were not reached (but could be evaluated for a sequence restarted at larger stretch). The pressure-stretch relation shows how the solution deviates from the correct relation for the continuous sphere. This deviation occurs through a limit state, and original symmetry of the model is kept also on the return path after the maximum stretch state. As shown by Fig. 7, the deformation of the sphere then consists of an additional local expansion within each of the original facets of the icosahedron; no symmetry-breaking bifurcation has thus been passed.

Fig. 7

Deformation mode of the pressurized sphere, modelled with an $I_{h}(5120)$ mesh, for the final equilibrium state shown for the case $k=-0.2$ in Fig. 6a ($\lambda \approx 1.56$, $1000 p/\mu \approx 0.728$). Stars mark vertices in original icosahedron mesh. Deformations in calculated size, not magnified

4.2.2 Ogden models

Simulations were also performed with an Ogden model for different constitutive parameters. Initially, these were based on the ’well-known’ six parameters discussed above, aiming at a qualitative description of the influences from the constants $\mu _{i}, (i=1,2,3)$, but keeping the constants $\alpha _{i}$. Results are given in Fig. 8, showing also cases where $\mu _{2}=0$, $\mu _{3}=0$ or $\mu _{2}=\mu _{3}=0$.

Fig. 8

Pressure–stretch curves for Ogden material models with different constitutive constants. For all cases $\alpha _{1}=1.3$, $\alpha _{2}=5$, $\alpha _{3}=-2$. Case 1: $\mu _{1}=630, \mu _{2}=1.2, \mu _{3}=-10\,\text {kPa}$. Case 2: $\mu _{1}=630, \mu _{2}=0, \mu _{3}=-13 \,\text {kPa}$. Case 3: $\mu _{1}=630, \mu _{2}=5.2, \mu _{3}= 0\,\text {kPa}$. Case 4: $\mu _{1}=650, \mu _{2}=\mu _{3}=0\,\text {kPa}$. Isolated critical states on equilibrium sequences marked by ‘$+$’

The results in Fig. 8 show qualitatively that the two additional terms gave similar effects on the overall response when compared to Case 4 with only $\mu _{1}$ non-zero, as the incompressibility condition makes either the in-plane or the transversal stretches above 1, with the other below 1. The examples below only considered at most two terms in the Ogden formulation.

It is noted in Fig. 8 that bifurcations appeared for all cases. For Case 1, the two limit states were found at $\lambda =1.3733$ and $\lambda =4.3179$, respectively, while bifurcations appeared for $\lambda =1{.}7739$ and $\lambda =2.5383$, which agrees perfectly with the analysis in Sect. 2.5.3, and well with numerical results in [48].

One-term Ogden models Tests were then performed for a one-term Ogden model, where only the exponent $\alpha _{1}$ was varied, with $\mu _{1}=2 \mu / \alpha _{1}$. Results are given in Fig. 9, and verify that large positive and negative exponents gave monotonous responses, but that values closer to zero gave more complex responses, cf. Sect. 2.4.1. Further experiments showed that values $0< |\alpha _{1}| < 1$ gave an infinite number of bifurcation states for the continuous case, but that only a finite set of these were shown by the discretization, while $1< \alpha _{1} < 2$ gave a limited number of bifurcations. For $\alpha _{1}=1.5$, only the $\ell =1$ bifurcation was found, while $\alpha _{1}=1.3$ in Fig. 8, Case 4, gave the $\ell =1,2$ cases, and a further case with $\alpha _{1}=1.1$ was correct up to $\ell =3$ (split into one 4-fold and one 3-fold bifurcation). The $\alpha _{1}=\pm 0.5$ cases both showed the $\ell =5$ bifurcations, before the $I_{h}(5120)$ model was unable to follow the continuous solution, cf. Fig. 7.

Fig. 9

Pressure–stretch curves for 1-term Ogden material models. Variable $\alpha _{1}$, with $\mu _{1}=2\frac{\mu }{\alpha _{1}}$. Isolated critical states on equilibrium sequences are marked by ‘$+$’. Numbers on curves indicate $\alpha _{1}$. Subfigure b is a zoom-in of marked box in a

Two-term Ogden models More complex behaviors can result for cases with more than one term in the Ogden material model, and interest was focussed on two-term models.

Based on Fig. 9, parameters were chosen according to $\alpha _{1}=1.05$, $\alpha _{2}=-2$, with $\mu _{2}=-k_{\mu } \mu _{1}\, , \mu =(\mu _{1}\alpha _{1}+\mu _{2}\alpha _{2})/2$. Some results are given in Fig. 10, showing that even for a very small positive value for $k_{\mu }$ (i.e., a negative $\mu _{2}$ together with the negative $\alpha _{2}$), the response eventually regained stability. While the case $k_{\mu }=0$ (not drawn) passed through the limit pressure state $\ell =0$, and then successively up to $\ell =5$ (but no higher) for increasing stretch, a case with $k_{\mu }=10^{-5}$ passed $\ell =5$, and then successively went back through lower $\ell$ values until a stable solution was again reached at $\lambda =62.09$, from which stretch only positive eigenvalues were present. For $k_{\mu }=0.1$, only the two limit pressure states were found, and for all $k_{\mu }>0.17694$, the sphere was always stable, as seen from a critical equilibrium sequence, similar to the one in Fig. 5. An evaluation for the $\ell =1$ bifurcation showed that this 3-fold critical state only exists for $k_{\mu }\le 0.03053$.

Fig. 10

Pressure–stretch curves for 2-term Ogden material models, with $\alpha _{1}=1.05$, $\alpha _{2}=-2$ with $\mu _{2}=-k_{\mu } \mu _{1}$, always with $\mu =422.5\,\text {kPa}$. Isolated critical states on equilibrium sequences are marked by ‘$+$’. Numbers on curves indicate $k_{\mu }$. Subfigure b is a zoom-in of marked box in a

4.3 Discretization

Results above were all obtained with the $I_{h}(5120)$ model, which is considered to be an accurate representation of the continuous sphere. Even this discretization, however, has shortcomings.

The main aspects coming from the discretization of the continuous sphere into a finite number of flat linearly interpolated finite elements are shown by Fig. 6, showing how the bifurcations for $\ell \ge 3$ were distorted into either a splitting of a high order bifurcation (with many simultaneously vanishing eigenvalues) into several lower order ones, or an inability to represent a bifurcation existing for the continuous sphere. These aspects were studied for different discretizations, with a focus on the symmetry properties and the fineness of the meshes.

4.3.1 Fineness of $I_{h}$ model

Referring to Fig. 6, showing result from an $I_{h}(5120)$ model with a Mooney–Rivlin material with $k=c_{2}/c_{1}=-0.2$, icosahedron meshes of different finenesses were analysed, with respect to critical states. Results are given in Table 5, as the number of vanishing eigenvalues and the corresponding stretches $\lambda$. The four finer meshes show the same orders and splittings of the bifurcations for $\ell \le 5$, and the same failure to represent the bifurcation at $\ell =6$, where analytical results show that the critical modes should be of multiplicities $1+3+4+5$, cf. Table 3. The $I_{h}(80)$ model rather severely misrepresents the critical states for $\ell \ge 2$, even if the splittings are similar to the finer meshes for $\ell <5$.

Table 5 Critical equilibrium states isolated for different icosahedron-based meshes of pressurized sphere, modelled with a Mooney–Rivlin material model with $k=c_{2}/c_{1}=-0.2$, cf. Fig.  6

4.3.2 Symmetry properties of the mesh

The case with a two-term Ogden model for $k_{\mu }=10^{-5}$ shown in Fig. 10 was used to compare the effects of meshes with different symmetry properties. For the $I_{h}(5120)$ mesh, critical states up to $\ell =5$, and then down to $\ell =0$ were found, Fig. 11. No other meshes were able to reproduce the critical states up to order $\ell =5$, i.e., the two 11-fold bifurcations.

Not only did the models with lower symmetry fail to reach the $\ell =5$ bifurcation, but they also split the lower order critical states in different ways, cf. Sect. 3.1. Table 6 shows how the critical states for increasing $\ell$ were represented as one or more critical states of lower multiplicities.

It is noted from the table that the $\ell =4$ bifurcation was split into another sequence, $4+5$ rather than $5+4$, compared to the Mooney–Rivlin model reported in Table 5, showing that the splitting sequence order is both problem and mesh dependent. It is also noted that the cubed sphere mesh C(3072), as expected, showed a similar behavior as the octahedral $O_{h}$ mesh, even if the deviation from the purely spherical stretch took another direction, Fig. 11.

Figure 12 shows how the original symmetry of the meshes was kept during stretch, even when the results in Fig. 11 seem to indicate that the fundamental paths were left by the simulations. The subfigures show, for the icosahedral and the tetrahedral meshes, how all nodal radii of the models developed with increasing stretch. The figures verify that the meshes consisted of 30 and 102 nodal classes, respectively. The response curves in Fig. 12 are therefore primary solution sequences for the discretized meshes, and no symmetry-breaking bifurcations were introduced in the solutions. The imperfect spherical stretch is thus due to the inability of the discretizations to represent all displacement modes of the sphere.

From the figures can be noted the significantly different scales of the radial values, and also that the stretch of the sphere was outwards between the initial icosahedral vertices, while it was inwards for the tetrahedral mesh. This, however, might be different for other meshes with the same symmetry. The $T_{d}$ model simulation reported in Fig. 12b returned to an almost perfect spherical shape after a very severe deviation, where equatorial radius was less than $10\%$ of the polar for stretches around 10.

As noted above, the symmetry of a mesh can be very sensitive to disturbances. A practical consequence relates to the effects of rounding nodal coordinates. In the $I_{h}(20)$ mesh of the unit sphere, the nodal coordinates consisted of six different values (except 0 and 1), with either sign. In the simulations presented above, these values were given with machine precision. Rounding all these values to a lower number of decimal places would keep a certain regularity in nodal placement, but break the $I_{h}$ symmetry. It was by simulations verified that a rounding of all unit sphere coordinate values to six decimals before refinement was enough to destroy the correct instability behavior.

Fig. 11

Pressure–stretch curves for meshes of different symmetry properties. Isolated critical states on equilibrium sequence for the $I_{h}(5120)$ mesh are marked by ‘$+$’

Table 6 Splitting of critical states for meshes of different symmetry properties

Fig. 12

Nodal radii during stretch of sphere in two meshes of different symmetry conditions. a$I_{h}(5120)$ mesh. b$T_{d}(4096)$ mesh. Stretch measure from $u_{a}$, Normalized radii in relation to $u_{a}$. Isolated critical states on equilibrium sequence are in a marked by ‘$+$’ on the trivial radius curve

4.4 Secondary paths

The present work has focussed on the presence, isolation and identification of critical states along the primary solution sequence for the pressurized sphere, noting the difference between analytical and discretized models. Obviously, the bifurcation states will be origins for secondary branches. For bifurcations of multiplicities higher than one, several secondary paths will normally exist, and group theory can be used to provide a list of such branches [20]. As an example, the $\ell =1$ bifurcation, with the axi-symmetric ‘pear-shaped’ mode, gives a 3-dimensional critical eigenspace of zero eigenvalues, expressed by a basis of three arbitrary but orthogonal eigenvectors. While an infinite number of rotation axes exist for the continuous sphere, the discretized models will only be able to yield pear-shaped modes along certain symmetry axes of the mesh. As all $I_{h}$ meshes have 6 axes through initial icosahedron vertices, 15 axes through midpoints of the initial edges and 10 axes through initial side centers, each of these 31 symmetry axes was verified to define a secondary sequence, which could be easily followed between the bifurcations. Due to the nodal hierarchy, the three types of sequences were marginally different in their representations of the spherical mode.

The $T_{d}$ meshes similarly give four axes through a vertex and a side center, and three axes through two edge midpoints, giving a total of 7 secondary paths passing through the $\ell =1$ bifurcation, which is correctly reproduced. It is also noted that these conclusions are completely independent of the levels of refinement, and only reflect the symmetry properties of the mesh.

The higher order bifurcations lead to even more complex secondary path situations.

5 Conclusions

The paper has discussed the numerical evaluation of stability for hyper-elastic membranes, with the pressurized sphere as an example, and focussed on the dependence on the material model and the discretization of the complete geometry.

The material description has developed a general framework for hyper-elastic material models, where most common models can be introduced, the only demand being that a strain energy density can be formulated from first and second invariants of in-plane strain. The derivation shows that three fundamental material functions describe the material response for the case of uniform stretch of the sphere. From these, considering the case of infinitely small stretch, conditions on the material parameters for initial stability can be formulated. Stability conditions for the stretched equilibrium can also be expressed in these functions, for the particular material model. For common material models, the possible instability responses are thereby considerably more complex than previously found, in particular for cases where wider ranges of material parameters can be allowed within the requirements of initial stability. For instance, two-parameter Mooney–Rivlin models with one negative constitutive constant can show an infinite number of bifurcation states in the response to pressurization, whereas a two-term Ogden material model can give a response with a high but limited number of bifurcations followed by a return to stable conditions at larger stretches. The developed expressions allow a straight-forward evaluation of critical states.

For the continuous modelling of the sphere by spherical harmonics functions, an infinite series of such functions can completely represent the incremental deformations from the deformed sphere. The eigenmodes, representing either vibration or instability modes, are constructed by vector analysis from the spherical harmonics functions, introducing the fundamental material functions.

Symmetry in representation of the spherical membrane is a key aspect in discretization. The main aspects deciding what instabilities can be correctly identified by a discretized element model of the complete sphere are described through group theoretical concepts. One main conclusion is that meshes derived from a basic icosahedral geometry will give the best possibilities to represent the instabilities of a pressurized sphere, but that some limitations exist also for these.

Numerical experiments were used to verify analytical results, and in particular to show how variations in material and geometry are represented by the modelling. Performed simulations thereby accurately verified the analytical predictions of the critical sequences for the Mooney–Rivlin and Ogden material models, showing also the higher order bifurcations existing for certain sets of constitutive parameters. The numerical simulations allowed the prediction of parameter ranges where specific instabilities exist. Based on triangular flat elements on the spherical surface, simulations also showed that symmetry properties of the used mesh will affect the obtained results in a manner predicted by the group theoretical analyses. The main conclusion is that symmetry aspects of a studied problem must be carefully and very accurately considered if a full instability investigation of a structure is the aim. In particular is shown how simplified considerations of symmetries can be misleading in this context. The results also clearly show that a lack of symmetry in the mesh can not in all aspects be compensated for by a finer mesh.

Appendices

Symmetry

1.1 Group representations

A brief review of how representations naturally come out of the eigenvalue problem follows. Each transformation from the group O(3) maps the stretched sphere onto itself, but also maps any small incremental displacement to a new small incremental displacement, and this latter mapping is linear. Each element of the group is thereby associated with a linear mapping on the space of small incremental displacements. Further, two elements of the group successively applied will correspond to composition of the linear operators. To conclude, each group element g is associated with a linear operator $L_g$, and composition is preserved in that $L_{g\circ h}=L_gL_h$. This composition-preserving association between a group element and a linear operator is termed a representation of the group.

This representation is reducible in the sense that there are subspaces of the tangent space that are invariant under all of the $L_g$. One example is the one-dimensional subspace of all radial and equal displacements given by a small uniform change in radius, which is invariant under full spherical symmetry.

The infinite-dimensional full space of small incremental displacements will split into a direct sum of finite-dimensional invariant subspaces. On each such subspace of dimension n, the association of a group element g with the restriction of the linear operator $L_g$ is an irreducible representation of the group. Given a set of n basis vectors for the subspace, each linear operator will be represented by a square $n\times n$ matrix, and the basis can be taken such that the matrix is orthogonal for every operator. In such an irreducible representation, group compositions thus correspond to matrix multiplication: $\mathrm{\mathbf{M}}_{g\circ h}=\mathrm{\mathbf{M}}_g\mathrm{\mathbf{M}}_h$, with no further splitting then possible.

This splitting of the small incremental displacement space into invariant finite-dimensional subspaces and corresponding representations also splits the fully symmetric eigenproblem, as any eigenmode must be transformed into a new eigenmode with the same eigenvalue under the group operations. Thus, any invariant subspace must correspond to a single eigenvalue, which will have a multiplicity at least equal to the dimension of the subspace. In general, one can expect different subspaces to have different eigenvalues, with multiplicities precisely the dimensions of the subspaces. Knowing the irreducible representations for a group thus gives direct information about the multiplicity of eigenvalues and eigenmode shapes. Complete lists of irreducible representations are known and published for all groups considered here, cf. “Appendix C”.

1.2 Representations and eigenmodes for the spherical membrane

Since the full spherical symmetry group O(3) is the direct product of the group $\textit{SO}(3)$ of 3D rotations and the inversion group $C_i$, its representations are products of one of the representations of $\textit{SO}(3)$ with one of the two representations of $C_i$.

If first the rotation symmetry group $\textit{SO}(3)$ is considered, group representation theory shows that the representations are indexed by a non-negative integer $\ell$. The representation named²$D_\ell$ has dimension $2\ell +1$. The basis constructed from real-valued spherical harmonics introduced in Sect. 2.1 directly corresponds to these representations, since the set of $2\ell +1$ functions $Y_{\ell m}$ transforms as $D_\ell$, as (for $\ell >0$) does both the set of $\nabla ^{(S)}Y_{\ell m}$ and the set of $^*\nabla ^{(S)}Y_{\ell m}$. Thus, a full set of eigenmodes is given by

$$\begin{aligned} u&=\alpha _{0} Y_{0 0} ,&\quad \varvec{v}&=\varvec{0}&\hbox { for}\ \ell =0,\nonumber \\ u&=\alpha _{\ell _{i}} Y_{\ell m},&\quad \varvec{v}&=\beta _{\ell _{i}} (\lambda a)\nabla ^{(S)}Y_{\ell m}&\nonumber \\&+\gamma _{\ell _{i}}(\lambda a)\;^*\nabla ^{(S)}Y_{\ell m}&\hbox { for}\ \ell \ge 1 \end{aligned}$$

(49)

where $i=1,2,3$ denotes the three solutions to a physics- and $\ell$-dependent $3\times 3$ eigenvalue problem for the amplitude constants $\alpha$, $\beta$, and $\gamma$. Also, by varying m, $2\ell +1$ basis eigenmodes with the same eigenvalue exist for given $(\ell ,i)$.

Without the consideration of physics, only the mode shape corresponding to $\ell =0$ is fully determined. For higher values of $\ell$, the amplitudes given by $\alpha$, $\beta$, and $\gamma$ needs the actual physics to be determined, and will give three possibilities for each $\ell$ from a $3\times 3$ matrix eigenvalue problem.

These three can be separated into two groups of one and two, respectively, by next considering the inversion symmetry group $C_i$. Here there are two irreducible representations. In the representation named $A_g$, inversion leaves the shape unchanged, while in the representation named $A_u$, inversion causes a sign change. The spherical harmonics can be expressed as homogeneous polynomials of degree $\ell$ in the variables x, y, and z. Since inversion means changing the sign of all coordinates, it is easy to see that for even $\ell$, both $Y_{\ell m}$ and $\nabla ^{(S)}Y_{\ell m}$ are unchanged by the inversion. The $^*$ operator on the other hand will change from a rotation clockwise by a right angle to a rotation counter-clockwise. Since rotating a vector counter-clockwise by a right angle is the same as rotating the vector clockwise followed by a multiplication by $-1$, $^*\nabla ^{(S)}Y_{\ell m}$ changes sign under inversion if $\ell$ is even. For odd $\ell$, the sign changes follow the opposite pattern. This means that the eigenmodes in Eq. (49) are obtained by taking either $\gamma =0$ or $\alpha =\beta =0$.

As the modes in Eq. (2) are fully described for any $\ell$, the symmetry considerations have reduced the eigenmode problem to a set of $2\times 2$ problems for the amplitudes $\alpha _{\ell _{i}}$ and $\beta _{\ell _{i}}$ in Eq. (3), giving two possibilities $i=2,3$ for each $\ell$. Formulation and computation of the eigenvalues for the then known mode shapes requires the actual equations of motion, i.e., the physics of the problem on the sphere geometry.

1.3 Scalar spherical harmonics

The scalar spherical harmonic functions are the basis for the symmetry consideration above. The Laplace spherical harmonics functions $Y_{\ell m}$ constitute a complete set of orthogonal functions defined on the surface of a sphere. They may be organized by angular frequency, and are basis functions for representations of functions on the sphere, somewhat similar to the functions in a Fourier series. The shapes of the used functions can be roughly visualized as a two-dimensional product of trigonometric functions with crests and node lines, corresponding to a mesh with $\ell -|m|+1$ half-waves between the north and south poles, and 2|m| half-waves along the latitudes [10]. As an example of how each sperical harmonic function generates mode shapes for small incremental displacements of the sphere, we can consider the case of $\ell >0$, $m=0$, where $Y_{\ell 0}$ is independent of the longitude angle. Then the shear mode displacements are along curves of constant latitude and radius, whereas the coupled mode displacements lie in planes of constant longitude, and all displacements are axially symmetric.

1.3.1 Function and operator expressions

In the further description below, a number of differential operator expressions on the spherical harmonics functions are used. The operators are all defined on the stretched sphere. In particular, all operators can be constructed from the surface gradient $\nabla ^{(S)}$ and the quarter turn rotation operator ${}^{*}$, in combination with the surface divergence operator $\nabla ^{(S)} \bullet$. As these are homogeneous and isotropic operators on the stretched sphere, so are all operators constructed from them.

For the operator expressions used, it can first be shown that for a general scalar function d

$$\begin{aligned} \nabla ^{(S)} \bullet {}^{*}\nabla ^{(S)} d= 0 , \end{aligned}$$

(50)

and

$$\begin{aligned} \Delta ^{(S)} d= \nabla ^{(S)} \bullet \nabla ^{(S)} d . \end{aligned}$$

(51)

Further, for a general vector function $\varvec{e}$

$$\begin{aligned} {}^{*}{}^{*}\varvec{e}=-\varvec{e} , \end{aligned}$$

(52)

and

$$\begin{aligned} \Delta ^{(S)} \varvec{e}= \nabla ^{(S)} (\nabla ^{(S)} \bullet \varvec{e}) - {}^{*}\nabla ^{(S)}(\nabla ^{(S)}\bullet {}^{*}\varvec{e})+\frac{1}{(\lambda a)^{2}} \,\varvec{e} . \end{aligned}$$

(53)

The spherical harmonics functions also have the fundamental property

$$\begin{aligned} \nabla ^{(S)} \bullet \nabla ^{(S)} Y_{\ell m} = -\frac{\ell (\ell +1)}{(\lambda a)^{2}} Y_{\ell m} . \end{aligned}$$

(54)

From these basic expressions, it is straight-forward to obtain a set of relations for scalar and vector functions based on the spherical harmonics. For a scalar function

$$\begin{aligned} q=Y_{\ell m}, \end{aligned}$$

(55)

one obtains, based on Eqs. (51) and (54),

$$\begin{aligned} \Delta ^{(S)} q = \nabla ^{(S)}\bullet \nabla ^{(S)} Y_{\ell m} = -\frac{\ell (\ell +1)}{( \lambda a)^{2}}\, q \end{aligned}$$

(56)

— the operator gives a scalar multiplication for the argument.

For vectors of the format

$$\begin{aligned} \varvec{r}=\left( \lambda a\right) \nabla ^{(S)} q = \left( \lambda a\right) \nabla ^{(S)} Y_{\ell m} , \end{aligned}$$

(57)

and

$$\begin{aligned} \varvec{s}={}^{*}\varvec{r} = \left( \lambda a\right) {}^{*}\nabla ^{(S)}q = \left( \lambda a\right) {}^{*}\nabla ^{(S)} Y_{\ell m} , \end{aligned}$$

(58)

a series of expressions give the needed results. From Eqs. (52), (58), (57), (54), and (55)

$$\begin{aligned} -\nabla ^{(S)}\bullet {}^{*}\varvec{s} = \nabla ^{(S)} \bullet \varvec{r}= & {} \left( \lambda a\right) \nabla ^{(S)}\bullet \nabla ^{(S)} Y_{\ell m}\nonumber \\= & {} -\frac{\ell (\ell +1)}{( \lambda a)}\, q , \end{aligned}$$

(59)

and from Eqs. (58), (57) and (50)

$$\begin{aligned} \nabla ^{(S)} \bullet \varvec{s}=\nabla ^{(S)}\bullet {}^{*}\varvec{r}= \left( \lambda a\right) \nabla ^{(S)}\bullet {}^{*}\nabla ^{(S)} q = 0 . \end{aligned}$$

(60)

Finally, Eqs. (53), (59), (60) and (57) give

$$\begin{aligned} \Delta ^{(S)} \varvec{r}= & {} \nabla ^{(S)}(\nabla ^{(S)}\bullet \varvec{r}) -{}^{*}\nabla ^{(S)} (\nabla ^{(S)}\bullet {}^{*}\varvec{r})\nonumber \\&+\frac{1}{(\lambda a)^{2}}\varvec{r}= \frac{-\ell (\ell +1)+1}{(\lambda a)^{2}}\,\varvec{r} , \end{aligned}$$

(61)

while Eqs. (53), (59), (60) and (58) give

$$\begin{aligned} \Delta ^{(S)} \varvec{s}= & {} \nabla ^{(S)}(\nabla ^{(S)}\bullet \varvec{s}) -{}^{*}\nabla ^{(S)} (\nabla ^{(S)}\bullet {}^{*}\varvec{s})\nonumber \\&+\frac{1}{(\lambda a)^{2}}\varvec{s}= \frac{-\ell (\ell +1)+1}{(\lambda a)^{2}}\,\varvec{s} , \end{aligned}$$

(62)

— again with results which are scalar multiplications of the arguments, with the scalar dependent on the mode order $\ell$ and the stretch value $\lambda$.

Derivation of the equations of motion

This appendix derives the equations of linearized small motion around a uniformly stretched pressurized spherical membrane, using the fundamental material functions for a hyper-elastic material model.

1.1 Small displacements of a curved surface

We first review some basic notions concerning the differential geometry of surfaces. Consider a surface given by $\varvec{R}(X)$, where $X^\alpha$ ($\alpha =1,2$) is an arbitrary coordinate system for the surface. Let $\varvec{N}(X)$ be a unit normal vector to the surface. The normal direction should be consistently chosen so it varies continuously. The shape (up to rigid motions) of the surface is completely described by two tensors. The first fundamental form, or metric tensor, is

$$\begin{aligned} g_{\alpha \beta }(X)=\varvec{R}_{,\alpha }\bullet \varvec{R}_{,\beta } , \end{aligned}$$

(63)

where $_{,\alpha }$ denotes partial derivation with respect to $X^\alpha$. The second fundamental form is

$$\begin{aligned} L_{\alpha \beta }(X)=-\varvec{N}_{,\alpha }\bullet \varvec{R}_{,\beta } =\varvec{N}\bullet \varvec{R}_{,\alpha \beta }, \end{aligned}$$

(64)

where the second expression shows that $L_{\alpha \beta }$ is symmetric. While the metric deals with properties of the 2D space itself, the L tensor deals with how the space is imbedded in 3D. As with any space with a metric tensor, the metric tensor and its inverse $g^{\alpha \beta }$ can be used to raise and lower tensor indices, Christoffel symbols $\varGamma ^{\alpha }_{\beta \gamma }$ can be computed and thus the covariant derivative $_{;\alpha }$ can be defined.

Now, let us at each point X take a vector $v^\alpha (X)$ in the tangent plane of the surface and a scalar u(X), and use these to define a finite displacement of the surface in two steps. First, we follow a geodesic starting at X and with initial tangent vector v for a unit value of the affine parameter, to reach a point in the surface with coordinates $x^\alpha (X,v(X))$. For this point we move along the normal vector $\varvec{N}(x)$ with coefficient u(X) (note that this is u as a function of the original point X, not the new point x). Thus, the displaced point is

$$\begin{aligned}&\varvec{r}(X,v(X),u(X))\nonumber \\&\quad =\varvec{R}\left( x(X,v(X)))+u(X)\varvec{N}\left( x(X,v(X)\right) \right) . \end{aligned}$$

(65)

The right Cauchy–Green tensor is

$$\begin{aligned} C_{\alpha \beta }= & {} \frac{\partial }{\partial X^\alpha }\varvec{r}(X,v(X),u(X))\nonumber \\&\bullet \frac{\partial }{\partial X^\beta }\varvec{r}(X,v(X),u(X)), \end{aligned}$$

(66)

and C is needed up to second order in v and u to obtain the linearized equations of motion about a stationary solution. The result is, with terms of third and higher orders neglected,

$$\begin{aligned} C_{\alpha \beta }= & {} g_{\alpha \beta }+g_{\alpha i}v^i_{;\beta }+g_{\beta i}v^i_{;\alpha }-2L_{\alpha \beta }u\\&+\,g_{ij}v^i_{;\alpha }v^j_{;\beta }+R_{\alpha ij\beta }v^iv^j\\&-\,2\left[ L_{\alpha i}v^i_{;\beta }+L_{\beta i}v^i_{;\alpha }+L_{\alpha \beta ;i}v^i\right] u\\&+\,L_{\alpha i}L^i_\beta u^2+u_{;\alpha }u_{;\beta }, \end{aligned}$$

where $R_{\alpha ij\beta }$ is the Riemann curvature tensor, and everything is evaluated at the point X. Raising one index to $C^\alpha _\beta =g^{\alpha i}C_{i\beta }$, we can compute the two invariants

$$\begin{aligned} J_1= & {} \mathrm {Tr}(C^\alpha _\beta )/2=1+v^i_{;i}-L^i_iu\\&+g_{ij}g^{kl}v^i_{;k}v^j_{;l}/2+R_{ij}v^iv^j/2\\&-\left[ 2L^j_iv^i_{;j}+L^j_{j;i}v^i\right] u\\&+L^i_jL^j_iu^2/2+g^{ij}u_{;i}u_{;j}/2,\\ J_2= & {} \sqrt{\mathrm {Det}(C^\alpha _\beta )}=1+v^i_{;i}-L^i_iu\\&+\left[ v^i_{;i}v^j_{;j}-v^i_{;j}v^j_{;i}+R_{ij}v^iv^j\right] /2\\&-\left[ L^j_jv^i_{;i}+L^j_{j;i}v^i\right] u\\&+\left[ \left( L^i_iL^j_j-L^i_jL^j_i\right) u^2+g^{ij}u_{;i}u_{;j}\right] /2, \end{aligned}$$

where $R_{\alpha \beta }=R^i_{\;\alpha \beta i}$ is the Ricci tensor, which may alternatively be computed as $R_{\alpha \beta }=-g_{\alpha \beta }\mathrm {Det}(L^i_j)$. Alternatively, we can express $J_2$ as

$$\begin{aligned} J_2= & {} 1+v^i_{;i}-L^i_iu+\left[ v^iv^j_{;j}-v^jv^i_{;j}\right] _{;i}/2\\&-\left[ L^j_jv^i\right] _{;i}u\\&+\left[ \left( L^i_iL^j_j-L^i_jL^j_i\right) u^2+g^{ij}u_{;i}u_{;j}\right] /2 , \end{aligned}$$

where both terms involving only v are divergences.

1.2 The elastic energy for small displacements of a an unstressed membrane

Consider an elastic membrane where the undeformed reference configuration is without any tension or strain. The elastic energy per unit material volume for an isotropic material under plane stress conditions is a function $W_e(J_1,J_2)$ of $J_1$ and $J_2$. The energy density per unit material area is $tW_e$, where t is the membrane thickness. Using the definitions of the fundamental material functions

$$\begin{aligned} e(\lambda )&=t\frac{\partial W_e}{\partial J_1}(\lambda ^2,\lambda ^2) \nonumber \\ f(\lambda )&=t\frac{\partial W_e}{\partial J_2}(\lambda ^2,\lambda ^2)\nonumber \\ g(\lambda )&=t\lambda ^2\left[ \frac{\partial ^2 W_e}{\partial J_1\partial J_1}+2\frac{\partial ^2 W_e}{\partial J_1\partial J_2}\right. \end{aligned}$$

(67)

$$\begin{aligned}&\quad \left. +\frac{\partial ^2 W_e}{\partial J_2\partial J_2}\right] (\lambda ^2,\lambda ^2) , \end{aligned}$$

(68)

we have for deviations from the undeformed material (where $\lambda =1$), up to first order

$$\begin{aligned} tW_e=tW_e(1,1)+(e(1)+f(1))\left[ v^i_{;i}-L^i_iu\right] . \end{aligned}$$

(69)

Since the material is in equilibrium in the undeformed configuration, the variation of the first order terms must vanish, so $f(1)=-e(1)$. Using this, the energy can be compactly expressed to second order using the linear strain tensor

$$\begin{aligned} \epsilon _{\alpha \beta }=\left[ g_{\alpha i}v^i_{;\beta }+g_{\beta i}v^i_{;\alpha }\right] /2-L_{\alpha \beta }u \end{aligned}$$

(70)

and the deviatoric linear strain tensor

$$\begin{aligned} {\bar{\epsilon }}_{\alpha \beta }=\epsilon _{\alpha \beta }-\epsilon ^i_ig_{\alpha \beta }/2 \end{aligned}$$

(71)

which gives, to second order,

$$\begin{aligned} tW_e=tW_e(1,1)+e(1){\bar{\epsilon }}^i_j{\bar{\epsilon }}^j_i+g(1)\epsilon ^i_i\epsilon ^j_j/2. \end{aligned}$$

(72)

Thus, e(1) can be interpreted as the 2D shear modulus and g(1) as the 2D bulk modulus integrated over thickness, giving the contributions from area preserving shear deformation, and shear-free area deformations, respectively.

1.3 The elastic energy for small displacements of a uniformly stretched surface

Now we will try to relate the expressions derived for small displacements of an undeformed membrane, to the corresponding expressions for small displacements of an already deformed membrane, where stretches are different from 1. The same coordinates can still be used for the deformed membrane. We will use superscript $^{(M)}$ (for material) to denote quantities computed in the reference configuration, and superscript $^{(S)}$ (for spatial) or no superscript for the deformed configuration. The values of the Cauchy–Green tensor only depends on the coordinates, so $C^{(M)}_{\alpha \beta }=C_{\alpha \beta }$. When raising one index to form the invariants $J^{(M)}_1$ and $J^{(M)}_2$, the material inverse metric tensor $g^{(M)\alpha \beta }$ must, however, be used, and thus $J^{(M)}_1$ and $J^{(M)}_2$ are no longer close to 1.

For the special case of a surface deformed using a uniform isotropic stretch $\lambda$, the difference between material and spatial quantities is a simple scaling involving $\lambda$. For example $g^{(M)\alpha \beta }=\lambda ^2g^{(S)\alpha \beta }$, which gives

$$\begin{aligned} J_1^{(M)}=\lambda ^2J_1^{(S)},\quad J_2^{(M)}=\lambda ^2J_2^{(S)}. \end{aligned}$$

(73)

The elastic energy per unit material area is, to second order in u, v,

$$\begin{aligned} \varPhi ^{(M)}_e= & {} tW_e(J_1^{(M)},J_2^{(M)})=tW_e(\lambda ^2,\lambda ^2)\nonumber \\&+\lambda ^2\left[ e(\lambda )\left( J_1^{(S)}-1\right) +f(\lambda )\left( J_2^{(S)}-1\right) \right. \nonumber \\&\left. +g(\lambda )\left( J_1^{(S)}-1\right) ^2/2\right] , \end{aligned}$$

(74)

where in the last term we have used that $J_2^{(S)}=J_1^{(S)}$ to first order, and $J_1^{(S)}=1$ to zeroth order. If we instead compute the elastic energy per unit spatial area and ignore the constant term, we get

$$\begin{aligned} \varPhi _e= & {} e(\lambda )\left( J_1-1\right) +f(\lambda )\left( J_2-1\right) \nonumber \\&+\,g(\lambda )\left( J_1-1\right) ^2/2 . \end{aligned}$$

(75)

While we must have $e(1)=-f(1)$ for any material, so the material is in equilibrium when unstressed and unstrained, there is no reason why e and f should be equal for $\lambda \ne 1$. Thus, the first order part of the elastic energy is not zero, and some loading is required to keep the membrane in equilibrium. We will use an internal over-pressure to supply the needed loading.

1.4 Over-pressure loading on a membrane

For a closed membrane subjected to a constant over-pressure p from the inside, we can define a pressure energy $-p(V-V_0)$, where V is the enclosed volume, and $V_{0}$ a reference volume. To relate a small displacement u, v to a volume change, we note that for any v, $\varvec{r}(X,v(X),\xi )$ defines a 3D coordinate system $(X,\xi )$ for points near the surface. We can then find the volume change per unit area by integrating the Jacobi determinant of the coordinate system from $\xi =0$ to $\xi =u(X)$, to get

$$\begin{aligned} u+v^{i}_{;i}u-L^i_iu^2/2 \end{aligned}$$

(76)

to second order in v, u. The pressure energy per unit area is thus

$$\begin{aligned} \varPhi _p=-p(u+v^{i}_{;i}u-L^i_iu^2/2). \end{aligned}$$

(77)

The same expression can actually be used for both a closed membrane, and an orientable membrane with fixed boundaries, since the surface can be closed by adding suitable fixed portions.

Returning to the uniformly stretched membrane, we have the total potential energy per unit spatial area $\varPhi =\varPhi _e+\varPhi _p$ and variations of the terms linear in u, v must vanish in equilibrium when integrated over the surface. To linear order, this gives

$$\begin{aligned} \varPhi =\left[ e(\lambda )+f(\lambda )\right] (v^i_{;i}-L^i_iu)-pu. \end{aligned}$$

(78)

Now, any term which is a divergence can be converted to an integral over the boundary, and the contribution to the variation will be zero since u, v are fixed on the (possibly non-existing) boundary. Thus, terms that are divergences can be ignored. Here, the term involving $v^i_{;i}$ is of that type, since e, f are constant. Then, the u terms give for the over-pressure

$$\begin{aligned} p=-\left[ e(\lambda )+f(\lambda )\right] L^i_i. \end{aligned}$$

(79)

Since p is constant, so must $L^i_i$ (twice the mean curvature) be. We may then measure the loading using

$$\begin{aligned} \psi (\lambda )=-p(\lambda )/L^i_i=e(\lambda )+f(\lambda ), \end{aligned}$$

(80)

the constant surface tension per unit spatial length, instead of the pressure p. If f is replaced by $\psi -e$ and terms in the energy coming from e, g, and $\psi$ are collected, we get

$$\begin{aligned} \varPhi= & {} e(\lambda )\left( J_1-J_2\right) +g(\lambda )\left( J_1-1\right) ^2/2\nonumber \\&+\psi (\lambda )\left[ L^j_j\left( u+v^{i}_{;i}u-L^i_iu^2/2\right) +\left( J_2-1\right) \right] \end{aligned}$$

(81)

Ignoring terms that are pure divergences (of which the second expression for $J_2$ contains several), we conclude that

$$\begin{aligned} \varPhi= & {} e(\lambda ){\bar{\epsilon }}^i_j{\bar{\epsilon }}^j_i +g(\lambda )\epsilon ^i_i\epsilon ^j_j/2\nonumber \\&+\psi (\lambda )\left[ g^{ij}u_{;i}u_{;j}/2-L^i_jL^j_iu^2/2\right] . \end{aligned}$$

(82)

The expression for $\varPhi$ has formally the structure of small deviations of a linear, isotropic 2D material in equilibrium with 2D shear and bulk moduli $e(\lambda )$ and $g(\lambda )$, cf. Eq. (72), with an extra stiffness coming from the tension $\psi$ load, but it should be remembered that the $\psi$ contribution includes some terms from the elastic energy.

1.5 Variation of the potential energy

Contributions to the equations of motion can be obtained by computing the variations with respect to u and v of the potential energy. The covariant derivative from the variation of v can be removed by partial integration, since divergences can be ignored. Writing ${\bar{L}}^\alpha _\beta$ for the deviatoric part of L, the result is

$$\begin{aligned} -\delta (\varPhi )= & {} \delta (u)\left[ e(\lambda )2{\bar{L}}^j_i\left( v^i_{;j}-L^i_ju\right) \right. \\&\left. +\,g(\lambda )L^j_j\left( v^i_{;i}-L^i_iu\right) +\psi (\lambda )\left( L^i_jL^j_iu+g^{ij}u_{;ij}\right) \right] \\&+\,\delta (v^\alpha )\left[ e(\lambda )\left( -R_{\alpha i}v^i+g_{\alpha i}g^{jk}v^i_{;jk} -\left[ 2{\bar{L}}^i_\alpha u\right] _{;i}\right) \right. \\&\left. +\,g(\lambda )\left( v^i_{;i}-L^i_iu\right) _{;\alpha }\right] \end{aligned}$$

Finally, specializing to a sphere uniformly stretched from original radius a to radius $\lambda a$, taking the origin at the center and choosing an outwards normal, $\varvec{N}=\varvec{R}/({\lambda a})$, we get

$$\begin{aligned} L_{\alpha \beta }=-g_{\alpha \beta }/({\lambda a}) , \end{aligned}$$

(83)

and thus ${\bar{L}}^\alpha _\beta =0$. We also have

$$\begin{aligned} R_{\alpha \beta }=-g_{\alpha \beta }/({\lambda a})^2 \end{aligned}$$

(84)

whereby the variation simplifies to

$$\begin{aligned} -\delta (\varPhi )= & {} \delta (u)\left[ -2g(\lambda )\left( 2u/(\lambda a)+v^i_{;i}\right) /(\lambda a)\right. \\&\left. +\,\psi (\lambda )\left( 2u/(\lambda a)^2+g^{ij}u_{;ij}\right) \right] \\&+\,\delta (v^\alpha )\left[ e(\lambda )\left( g_{\alpha i}v^i/(\lambda a)^2+g_{\alpha i}g^{jk}v^i_{;jk}\right) \right. \\&\left. +\,\,g(\lambda )\left( 2u/(\lambda a)+v^i_{;i}\right) _{;\alpha }\right] . \end{aligned}$$

In vector notation, using $\nabla ^{(S)}$ for spatial surface gradient, $\Delta ^{(S)}$ for the spatial surface Laplacian, and $\varvec{v}$ for a vector tangent to the surface, this can be written

$$\begin{aligned} -\delta (\varPhi )= & {} \delta (u)\left[ -2g(\lambda )\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) /(\lambda a)\right. \\&\left. +\,\psi (\lambda )\left( 2u/(\lambda a)^2+\Delta ^{(S)}u\right) \right] \\&+\,\delta (\varvec{v})\bullet \left[ e(\lambda )\left( \varvec{v}/(\lambda a)^2 +\Delta ^{(S)}\varvec{v}\right) \right. \\&\left. +\,g(\lambda )\nabla ^{(S)}\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) \right] . \end{aligned}$$

1.6 Kinetic energy contribution

We assume that all kinetic energy comes from the membrane itself, not from the motion of the fluid providing the pressure. If the constant density in reference configuration is $\rho$, the kinetic energy per material unit area is

$$\begin{aligned} T^{(M)}=t\rho \left( \dot{u}^2+g^{(S)}_{ij}\dot{v}^i\dot{v}^j\right) /2. \end{aligned}$$

(85)

For the uniformly stretched membrane, the kinetic energy density per spatial unit area is

$$\begin{aligned} T=h(\lambda )\left( \dot{u}^2+g^{(S)}_{ij}\dot{v}^i\dot{v}^j\right) /2, \end{aligned}$$

(86)

using the mass density per spatial unit area $h=t\rho /\lambda ^2$. Variation, and using partial integration in time to remove the time derivative from the variation of u and v, gives

$$\begin{aligned} \delta (T)=-\delta (u)h(\lambda )\ddot{u} -\delta (v^\alpha )h(\lambda )g_{\alpha i}\ddot{v}^i , \end{aligned}$$

(87)

or, in vector notation,

$$\begin{aligned} \delta (T)=-\delta (u)h(\lambda )\ddot{u} -\delta (\varvec{v})\bullet h(\lambda )\ddot{\varvec{v}}. \end{aligned}$$

(88)

Combining the contributions to the variation from kinetic and potential energy, the equations of motion for small displacements of a uniformly stretched sphere are found as

$$\begin{aligned}&-h(\lambda ) \ddot{u} -\frac{2g(\lambda )}{\lambda a}\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) \nonumber \\&\quad +\, \psi (\lambda )\left( 2u/(\lambda a)^2+\Delta ^{(S)}u\right) =0, \nonumber \\&-\,h(\lambda ) \ddot{\varvec{v}} +e(\lambda )\left( \frac{1}{(\lambda a)^2}\varvec{v}+\Delta ^{(S)}\varvec{v}\right) \nonumber \\&\quad +\,g(\lambda )\nabla ^{(S)}\left( 2u/(\lambda a)+\nabla ^{(S)}\bullet \varvec{v}\right) =\varvec{0}. \end{aligned}$$

(89)

Using character tables to compute representation splitting caused by lowering symmetry

When symmetry is lowered by restricting to a subgroup, any irreducible representation of the supergroup is typically a reducible representation of the subgroup, i.e., it can be split into a direct sum of irreducible representations of the subgroup. For the spherical membrane, the symmetry group O(3) of the continuous model is lowered to that of a subgroup like $T_d$ by the introduction of a discretized mesh. Consequently, an irreducible representation like the 11-dimensional $D_{5u}$ of O(3) will be split into a direct sum of the irreducible representations of $T_d$: the one-dimensional $A_1$, $A_2$, the two-dimensional E, and the three-dimensional $T_1$, $T_2$. This splitting can be easily computed using published character tables for the two groups [12].

The character $\chi _\alpha$ for a representation $\alpha$ of a group is a complex valued function over the elements of the group. Specifically, if the representation $\alpha$ maps the group element g to the orthogonal matrix R(g), then

$$\begin{aligned} \chi _\alpha (g)=\mathrm {Tr}\left( R(g)\right) , \end{aligned}$$

(90)

which can be shown to be independent of which particular orthogonal matrix was used. Further, all group elements in the same conjugate class have the same value of the character. Thus, the character tables typically would be rectangular, with rows corresponding to different representations and columns to different conjugate classes of the group. Any conjugate class of a subgroup thereby corresponds to a unique conjugate class of the supergroup, but not the other way around.

The formula for computation of the splitting is given as

$$\begin{aligned} I(\alpha ,\beta )=\frac{1}{N}\sum _{g\in G}\overline{\chi _\alpha (g)}\chi _\beta (g) \end{aligned}$$

(91)

where N is the number of elements in the subgroup, $\alpha$ is a possibly reducible representation, $\beta$ an irreducible representation for the subgroup, and the overbar denotes complex conjugate. The number $I(\alpha ,\beta )$ will be a non-negative integer, denoting the number of times that $\beta$ occurs in the splitting of $\alpha$.

As an example, the number of times the representation $T_2$ occurs when splitting the representation $D_{5u}$ is computed. The representation $D_{5u}$ is reducible for $T_d$, so we will typically not find it tabulated. To compute the character values of $D_{5u}$, we note that O(3) is the direct product of the rotation group $\textit{SO}(3)$ and the inversion group $C_i$, which means that the character values of $D_{5u}$ are the products of the corresponding values of the rotation representation $D_5$ and the inversion representation $A_u$. Since $\textit{SO}(3)$ is a continuous group, the character values of its representations can not be tabulated in a finite table, but a formula can be found as

$$\begin{aligned} \chi _{D_l}(g)=\sum _{m=-l}^l\cos (m\phi ). \end{aligned}$$

(92)

Here, $\phi$ is the angle of the rotation corresponding to the element g. The representation $A_{u}$ has the character values 1 for the identity element and $-1$ for the inversion. Thus, to compute the character values of $D_{5u}$ for elements in $T_d$, the corresponding rotation angle is found, and also whether it is an inversion or not. The character values of the rotation and inversion parts are multiplied.

The conjugate classes of $T_d$ can be denoted: E (the identity element, no rotation, no inversion), $C_3$ (rotation by $\phi =2\pi /3$, no inversion, 8 different axes), $C_2$ (rotation by $\phi =\pi$, no inversion, 3 different axes), $S_4$ (rotoreflection by a quarter turn, $\phi =\pi /2$, inversion, 6 different axes), and $\sigma _d$ (reflection, $\phi =\pi$, inversion, 6 different axes), giving a total of 24 elements. Taking an element g belonging to the class $S_4$ as an example gives

$$\begin{aligned} \chi _{D_{5u}}(g)=\left( \sum _{m=-5}^5\cos (m\pi /2)\right) (-1)=-1. \end{aligned}$$

(93)

Similarly, the other conjugate classes can be computed to give the first row of Table 7.

Table 7 Character table of some representations for the tetrahedron symmetry group $T_d$

For the irreducible representations, the character tables are published in several sources. The rows for $A_1$ and $T_2$ are included in the table as examples. From this, the number of times $T_2$ occurs when $D_{5u}$ splits are easily calculated using Eq. (91) as

$$\begin{aligned} I(D_{5u},T_2)= & {} \frac{1}{24}\left[ 1\cdot 11\cdot 3+8\cdot (-1)\cdot 0\right. \nonumber \\&+\,3\cdot (-1)\cdot (-1)\nonumber \\&\left. +\,6\cdot (-1)\cdot (-1)+6\cdot 1\cdot 1\right] =2, \end{aligned}$$

(94)

showing that the splitting of $D_{5u}$ contains $T_2$ twice. Using the trivial $A_1$ row instead, gives $I(D_{5u},A_1)=0$, so $A_1$ does not occur in the splitting. Checking the other irreducible representations verifies that $D_{5u}$ is split into E, $T_1$, and $T_2$ (twice). As a small check, it can be seen that the dimensions match: $2+3+2\cdot 3=11$.