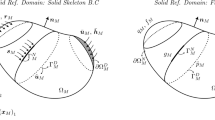Abstract
Numerical model reduction is exploited for computational homogenization of the model problem of a poroelastic medium under transient conditions. It is assumed that the displacement and pore pressure fields possess macro-scale and sub-scale (fluctuation) parts. A linearly independent reduced basis is constructed for the sub-scale pressure field using POD. The corresponding reduced basis for the displacement field is constructed in the spirit of the NTFA strategy. Evolution equations that define an apparent poro-viscoelastic macro-scale model are obtained from the continuity equation pertinent to the RVE. The present model represents an extension of models available in literature in the sense that the pressure gradient is allowed to have a non-zero macro-scale component in the nested \(\hbox {FE}^2\) setting. The numerical results show excellent agreement between the results from numerical model reduction and direct numerical simulation. It was also shown that even 3D RVEs give tractable solution times for full-fledged \(\hbox {FE}^2\) computations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A large class of natural and engineering materials are porous with a pore-fluid interacting with the solid skeleton. These materials are often micro-heterogeneous in the sense that there is a pronounced difference in the mechanical properties between the different micro-constituents, e.g. solid grains and pore fluid. Moreover, heterogeneity may occur on a much larger length scale. A typical example is porous rock which might be saturated by different pore fluids (e.g. patchy saturation models [25, 28]) or which might be composed of zones with varying material properties of the solid skeleton (e.g. double porosity models [12, 22]). In both cases, the mechanical properties, such as compressibility of the constituents and permeability of the pore space, are highly heterogeneous. The pronounced pressure gradients resulting from external loading are equilibrated via the redistribution of the contained pore fluid.
The straightforward approach is to model the problem on one single scale using Direct Numerical Simulation (DNS). However, resolving the substructural features is computationally very expensive and, therefore, some sort of homogenization strategy is preferable. When the intrinsic material properties are nonlinear and/or the fine-scale problem is inherently transient, it is necessary to resort to nested macro- and sub-scale computations (\(\hbox {FE}^2\)), whereby the sub-scale computations are carried out on a so-called Representative Volume Element (RVE)Footnote 1 in each quadrature point in the macro-scale domain, possibly within a given time step. Clearly, the purpose is to obtain macro-scale properties of engineering interest; hence, whether it is possible to avoid resolution via DNS of the fine-scale problem and accept the homogenized solution can only be assessed via some sort of goal-oriented error quantification.
However, it is widely realized that straight-forward application of the \(\hbox {FE}^2\)-strategy can be computationally intractable for a fine macro-scale mesh, particularly in 3D. Therefore, there is significant interest in reducing the cost of solving the individual RVE-problems by introducing some kind of reduced basis, here denoted Numerical Model Reduction (NMR). In particular, we note strategies that are based on the superposition of “modes” that are characteristic for the RVE-solution fields. In the case of sub-scale small strain (visco)plasticity, various attempts have been made to approximate the inelastic strain field by a reduced basis consisting of so-called “inelastic modes”. One of the early proposals is the so-called “eigendeformation-based reduced order homogenization” technique by Fish and coworkers [7, 23], which in its turn relies on the Transformation Field Analysis (TFA) that was originally proposed by Dvorak and Benveniste [4]. A similar approach, coined Nonuniform Transformation Field Analysis (NTFA), was proposed by Michel and Suquet [20, 21, 26]. Recent developments are e.g. by Fritzen and coworkers [8,9,10,11], who extended the idea further within the framework of Proper Orthogonal Decomposition (POD) and applied it to visco-elasticity and, more generally, to a subclass of Standard Dissipative Materials.
Quite importantly, however, is the obvious fact that the richness of the reduced basis will determine the accuracy of the RVE-solution, which calls for error control. Here, we consider the full FE-solution as the exact one. An example of error estimation due to model reduction, although not in a homogenization context and for a PGD-basis, is Ladeveze and Chamoin [18]. More recently, Ekre et al. [6] investigated the transport of error from the micro- to the macro-scale model in a reduced \(\hbox {FE}^2\) approach.
In recent years, several attempts have been made to establish multi-scale procedures for poroelastic media, e.g. Su et al. [27]. A recent contribution is by Khoei and Hajiabadi [17]. However, the straight-forward \(\hbox {FE}^2\)-strategy turns out, as mentioned above, to be intractable for realistic large-scale problems in 3D. Jänicke et al. [13, 15] studied the computational homogenization of heterogeneous poroelastic media under locally undrained conditions, i.e. fluid redistribution is only allowed locally whilst global fluid transport is suppressed. This “selective” homogenization approach allows to reduce the macro-scale problem to that of a single-phase viscoelastic material, whereby the “’mode coefficients” play the role of classical internal variables of the macro-scale model. More recently, this selective homogenization towards a viscoelastic macro-scale material was extended to account for Darcy-type seepage in fluid-filled fracture networks [14].
In this paper, we introduce the \(\hbox {FE}^2\) approach with Numerical Model Reduction based on the complete, i.e. non-selective, upscaling of the poroelastic fine-scale model towards a poro-viscoelastic macro-scale model. The scale transition is formulated in terms of a Variationally Consistent Homogenization scheme with weakly periodic boundary conditions on the RVE problems. Inspired by the NTFA approach, we use training computations and POD to identify a reduced basis of pore pressure modes that allows us to shift all fine-scale computations from the “online” \(\hbox {FE}^2\) solution phase towards an “offline” training phase. The resulting macro-scale model contains both the viscoelastic properties associated with local fluid redistribution on the RVE level as well as the hydro-mechanical properties of a macroscopic poroelastic medium. Therefore, it is called poro-viscoelastic. We benchmark the predictions emerging from the poro-viscoelastic NMR procedure against results from DNS in several numerical examples and demonstrate the numerical efficiency of the model in a large-scale 3D example.
Throughout this paper, meager type is used to denote scalars, whereas bold type is used to denote vectors and (higher order) tensors. Single contraction is denoted by \(\cdot \). For example, if \(\mathbf{a},\mathbf{b}\) are vectors and \(\mathbf{A}\) is a second order tensor, we have \(\mathbf{a}\cdot \mathbf{b}=a_i b_i\), \((\mathbf{A}\cdot \mathbf{b})=A_{ij}b_{j}\), where the Einstein summation convention is used.
As to homogenization in the spatial domain, volume and surface averaging of an intensive field \(\diamond \) are denoted
where the domain occupied by the RVE is \(\varOmega _{\Box }\) with boundary \(\varGamma _\Box \). The macro-scale representation of \(\diamond \) is denoted \(\bar{\diamond }\), and frequently it holds that \(\bar{\diamond }:=\left\langle \diamond \right\rangle _{\Box }\).
The paper is organized as follows: Sect. 2 gives a short review of the poroelastic fine-scale model. Section 3 is devoted to the two-scale modeling based on computational homogenization. The NMR strategy is presented in Sect. 4. Section 5 presents the numerical results for 1D, 2D and 3D settings including benchmark experiments. Finally, Sect. 6 concludes the paper with a summary and an outlook to future work.
2 Fine-scale modeling of a poroelastic medium
2.1 Preliminaries
We give a brief summary of poroelasticity under geometrically linear and quasi-static conditions. Initially introduced by Biot [1, 2], poroelasticity as a homogenized continuum model of solid-fluid mixtures with hydro-mechanical coupling can be seen as a special case of the more general class of materials described by the Theory of Porous Media (TPM) as proposed e.g. by De Boer [3] and Ehlers [5]. The primary global fields are the displacement of the solid skeleton, denoted \(\mathbf{u}\), and the intrinsic pore fluid pressure, denoted p.
2.2 Constitutive relations for the sub-scale constituents
The constitutive relations for the equilibrium stress \(\varvec{\sigma }\) and the seepage velocity \(\mathbf{w}\) become:
where \(\varvec{\varepsilon }\) is the strainFootnote 2 and \(\varvec{\zeta }\) is the pressure gradient. The material properties are as follows: \(\mathbb E\) is the fourth order elasticity modulus tensor which is defined in the simplest case of isotropy by the constant parameters G and K, which are the shear modulus and compression modulus, respectively. \(\mathbf{K}\) is the second order constant permeability tensor, defined (in the simplest case of isotropy) by the scalar permeability coefficient k. Finally, \(\alpha \) is the Biot coefficient.
We also introduce the storage function \(\varPhi \) that represents the current volume fraction of fluid
where \(\phi \) is the initial porosity of the solid phase, and \(\beta \) is the intrinsic compression compliance of the pore fluid. Note that \(\phi \) is taken as constant and independent of the deformation. As to the spatial variation of these parameters, they may be strongly heterogeneous on the fine scale.
2.3 Strong and weak format of the fine-scale problem
Restricting to quasi-statics, we thus seek the displacement \(\mathbf{u}(\mathbf{x},t): \varOmega \times \mathbb {R}^+ \rightarrow \mathbb {R}^3\) and the pore pressure \(p(\mathbf{x},t): \varOmega \times \mathbb {R}^+ \rightarrow \mathbb {R}\) that solve the system
together with the constitutive relations in (2) and (3) and the initial condition
Clearly, (4a) represents static equilibrium, whereas (4b) expresses mass conservation of the two-phase solid-fluid mixture.
The standard space-variational format corresponding to (4) reads: Find (\(\mathbf{u}(\bullet ,t),p(\bullet ,t)\)) in the appropriately defined spaces \({\mathbb {U}}\times {\mathbb {P}}\) that solve
where \(\mathbb {U}^0\) and \(\mathbb {P}^0\) are the appropriately defined test spaces.
3 Two-scale analysis based on computational homogenization
3.1 First order homogenization in the spatial domain
We replace the single-scale problem in Sect. 2 by a two-scale problem upon introducing (i) running averages in the weak format and (ii) scale separation via first-order homogenization. The first step is to replace the space-variational problem in (6) by that of finding \((\mathbf{u}(\bullet ,t),p(\bullet ,t))\in {\mathbb {U}}_{\mathrm{FE}^2}\times {\mathbb {P}}_{\mathrm{FE}^2}\) that solves
where the pertinent space-variational forms in (7) are given as
Here, (\(\mathbf{v};q\)) represent arbitrary but admissible displacement and pore pressure fields. Obviously, these space-variational forms represent running averages on square/cubic domains \(\varOmega _{\Box }\) with the side length \(L_{\Box }\) and located at each macro-scale spatial point \(\bar{\mathbf{x}}\in \varOmega \). We note that the introduced averaging results in a change of the original problem. The weak format thus serves as the basis for variationally consistent homogenization as discussed below.
Next, in order to define the two-scale solution and test spaces \({\mathbb {U}}_{\mathrm{FE}^2}, {\mathbb {V}}_{\mathrm{FE}^2}\) and \({\mathbb {P}}_{\mathrm{FE}^2}, {\mathbb {Q}}_{\mathrm{FE}^2}\) associatedFootnote 3 with \(\hbox {FE}^2\), we introduce scale separation and first-order homogenization. The standard approach is then to decompose the sub-scale fields \(\mathbf{u}\) and p into a macro-scale part, \(\mathbf{u}^{\mathrm{M}}\) and \(p^{\mathrm{M}}\), and a micro-scale or fluctuating part, \(\mathbf{u}^{\mu }\) and \(p^{\mu }\), within each RVE such that
We are now in the position to define the two-scale trial and test spaces
whereas
The trial and test spaces for the macro-scale problem are denoted \(\bar{{\mathbb {U}}}, \bar{{\mathbb {V}}}\) and for the micro-scale problem \({\mathbb {U}}^\mu _{\Box ,i}, {\mathbb {V}}^\mu _{\Box ,i}\), and \({\mathbb {P}}^\mu _{\Box ,i}, {\mathbb {Q}}^\mu _{\Box ,i}\). We introduce the notation


Hence, there exist components \((\mathbf{u}^\mu ,p^\mu )\) and corresponding spaces \(({\mathbb {U}}_{\Box ,i}^\mu ,{\mathbb {P}}^\mu _{\Box ,i})\) for each single RVE \(\varOmega _{\Box ,i}\).
We now restate the two-scale problem (7) as follows: Find  that solve
that solve


where we used the interpretation \(\delta \mathbf{u}^\mu =\delta \mathbf{u}^\mu _i\) and \(\delta p^\mu =\delta p^\mu _i\) inside \(\varOmega _{\Box ,i}\).
3.2 Macro-scale problem
We obtain the macro-scale (homogenized) problem from (13) upon choosing purely macroscopic test functions; hence \(\delta \mathbf{u}=\mathbf{u}^{\mathrm{M}}[\delta \bar{\mathbf{u}}]\) and \(\delta p=p^{\mathrm{M}}[\bar{p}]\) such that
or, more explicitly,
where we introduced the variationally consistent macro-scale (homogenized) fields
In addition, \(\bar{\mathbf{t}}^\text {p}\) and \(\bar{w}^\text {p}\) are defined as the suitably homogenized quantities on the Neumann boundary parts.
Note that, according to (15b) and (4b), the total macroscopic seepage velocity \(\bar{\mathbf{w}}\) can be computed as
Also note that the homogenized stress can be expressed in standard fashion as the surface integral
3.3 Micro-scale problem on a representative volume element
In the previous section, the macro-scale problem was defined, and it was established that the macro-scale fields in (16) depend on \((\mathbf{u},p)\) inside the pertinent \(\varOmega _\Box \). We shall now consider the local problem on a single RVE \(\varOmega _{\Box ,i}\) to determine the implicit relation \((\mathbf{u}^\mu _i,p^\mu _i)\{\bar{\mathbf{u}},\bar{p}\}\), where \(\mathbf{u}|_{\varOmega _{\Box ,i}}=\mathbf{u}^\text {M}[\bar{\mathbf{u}}]+\mathbf{u}^\mu _i\) and \(p|_{\varOmega _{\Box ,i}}=p^\text {M}[\bar{p}]+p^\mu _i\). To this end, we consider the problem in (13) for a single test function \(\delta \mathbf{u}^\mu _i\in {\mathbb {V}}_{\Box ,i}^\mu \) and \(\delta p^\mu _i\in {\mathbb {Q}}_{\Box ,i}^\mu \). For brevity, we henceforth drop index i since we now restrict to one single RVE.
The decomposition in (9) presumes that the solution \((\mathbf{u},p)\) can be uniquely decomposed into macroscopic parts \((\mathbf{u}^M,p^M)\) and fluctuations \((\mathbf{u}^\mu ,p^\mu )\). This imposes constraints on \({\mathbb {U}}_\Box ^\mu \) and \({\mathbb {P}}_\Box ^\mu \) in (13). In order to be explicit, we shall consider an expanded format of the problem. To this end, we introduce the richer spaces as follows:
where \(\text {H}^1(\bullet )\) is the Sobolev space of functions with square integrable derivatives.
In order to ensure a uniquely solvable RVE-problem, we next adopt the following additional model assumptions:
We assume that \(\mathbf{u}^{\mu }\) and \({p}^{\mu }\) are periodic, i.e.
$$\begin{aligned} \llbracket {{\mathbf{u}}^{\mu }}\rrbracket _\Box (\mathbf{x}) = \mathbf{0 }, \quad \llbracket {{p}^{\mu }}\rrbracket _\Box (\mathbf{x}) = 0 \quad \forall \delta \mathbf{x}\in \varGamma _\Box ^+, \end{aligned}$$(20)where we introduced the “difference operator” \(\llbracket {\bullet }\rrbracket _\Box (\mathbf{x}):=\bullet (\mathbf{x}) - \bullet (\mathbf{x}^-(\mathbf{x}))\); \(\mathbf{x}\in \varGamma _\Box ^+\) is an “image point” whereas \(\mathbf{x}^-(\mathbf{x})\in \varGamma ^-=\varGamma _\Box \setminus \varGamma _\Box ^+\) is the corresponding “mirror point”, see Fig. 1. Upon introducing, for the sake of brevity, the RVE-forms
$$\begin{aligned}&d^{(u)}_{\Box }(\varvec{\lambda },\mathbf{u}) := \frac{1}{|\varOmega _{\Box }|}\int _{\varGamma _\Box ^+} \varvec{\lambda }\cdot \llbracket {\mathbf{u}}\rrbracket _\Box \,\text{ d }\varGamma , \nonumber \\&d^{(p)}_{\Box }({\mu },{p}) := \frac{1}{|\varOmega _{\Box }|}\int _{\varGamma _\Box ^+} {\mu }\, [[ p ]]_\Box \,\text{ d }\varGamma , \end{aligned}$$(21)we may express the variational (weak) statementsFootnote 4 of the micro-periodicity constraints in (20) as
$$\begin{aligned} d^{(u)}_{\Box }(\delta \varvec{\lambda },\mathbf{u})&= d^{(u)}_{\Box }(\delta \varvec{\lambda },\mathbf{u}^{\mathrm{M}}[\bar{\mathbf{u}},\bar{\varvec{\varepsilon }}]), \quad \forall \delta \varvec{\lambda }\in \mathbb {T}_\Box , \end{aligned}$$(22a)$$\begin{aligned} d^{(p)}_{\Box }(\delta {\mu },p)&= d^{(p)}_{\Box }(\delta {\mu },{p}^{\mathrm{M}}[\bar{p},\bar{\varvec{{\zeta }}}]), \quad \forall \delta {\mu }\in \mathbb {P}_\Box , \end{aligned}$$(22b)whereby it is obvious that the Lagrange multiplier \(\delta \varvec{\lambda }\) in (22a) represents a field of virtual boundary tractions on \(\varGamma _\Box ^+\), whereas the Lagrange multiplier \(\delta {\mu }\) in (22b) represents a field of virtual boundary fluxes, see Remark 2 below. Here, we introduce the test spaces
$$\begin{aligned} {\mathbb {T}}_\Box = [\text {L}_2(\varGamma _\Box ^+)]^3, \quad {\mathbb {Q}}_\Box = \text {L}_2(\varGamma _\Box ^+), \end{aligned}$$(23)where \(\text {L}_2(\bullet )\) is the space of square integrable functions. Upon introducing the expressions for \(\mathbf{u}^{\mathrm{M}}\) and \({p}^{\mathrm{M}}\) from (9) on the RHS in (22a) and (22b), respectively, we obtain the explicit expressions
$$\begin{aligned} d_{\Box }^{(u)}(\delta \varvec{\lambda };\mathbf{u}^{\mathrm{M}}[\bar{\mathbf{u}},\bar{\mathbf{h}}])&= \left[ \frac{1}{|\varOmega _{\Box }|} \int _{\varGamma _{\Box }^+} \delta \varvec{\lambda }\otimes \llbracket {\mathbf{x}}\rrbracket _\Box \,\text{ d }\varGamma \right] :\bar{\mathbf{h}}, \end{aligned}$$(24a)$$\begin{aligned} d_{\Box }^{(p)}(\delta {\mu };{p}^{\mathrm{M}}[\bar{p},\bar{\varvec{{\zeta }}}])&= \left[ \frac{1}{|\varOmega _{\Box }|} \int _{\varGamma _{\Box }^+} \delta {\mu }\,\llbracket {\mathbf{x}}\rrbracket _\Box \,\text{ d }\varGamma \right] \cdot \bar{\varvec{{\zeta }}}, \end{aligned}$$(24b)where it was used that \(\int _{\varGamma _\Box }[\mathbf{x}-\bar{\mathbf{x}}]\,\text{ d }\varGamma =\mathbf{0 }\). Hence, we conclude that it is only the data \(\bar{\mathbf{h}}\) and \(\bar{\varvec{{\zeta }}}\) that will have an effect on the periodicity conditions.
We assume that \(\bar{\mathbf{u}}\) and \(\bar{p}\) physically play the role of surface-averaged quantities as follows:
$$\begin{aligned} \left\langle \left\langle \mathbf{u} \right\rangle \right\rangle _\Box = \bar{\mathbf{u}}, \quad \left\langle \left\langle p \right\rangle \right\rangle _\Box = \bar{p}, \end{aligned}$$(25)which conditions are expressed weakly as
$$\begin{aligned} \delta \bar{\varvec{\lambda }} \cdot \left\langle \left\langle \mathbf{u} \right\rangle \right\rangle _\Box&= \delta \bar{\varvec{\lambda }}\cdot \bar{\mathbf{u}} \quad \forall \delta \bar{\varvec{\lambda }}\in \mathbb {R}^3, \end{aligned}$$(26a)$$\begin{aligned} \delta \bar{\mu }\, \left\langle \left\langle p \right\rangle \right\rangle _\Box&= \delta \bar{\mu }\, \bar{p} \quad \forall \delta \bar{\mu }\in \mathbb {R}. \end{aligned}$$(26b)
The space-variational RVE-problemFootnote 5 can now be stated as follows: For a given history \(\bar{\mathbf{u}}(t)\), \(\bar{\mathbf{h}}(t)\), \(\bar{p}(t)\), \(\bar{\varvec{{\zeta }}}(t)\), find \(\mathbf{u}(\bullet ,t)\in \mathbb {U}_{\Box }\), \({p}(\bullet ,t)\in \mathbb {P}_{\Box }\), \(\varvec{\lambda }(\bullet ,t)\in \mathbb {T}_{\Box }\), \({\mu }(\bullet ,t)\in \mathbb {Q}_{\Box }\), \(\bar{\varvec{\lambda }}\in \mathbb {R}^3\), \(\bar{\mu }\in \mathbb {R}\) that solve
It is possible to identify the tractions \(\mathbf{t}\) and the flux w on the entire RVE-boundary \(\varGamma _\Box \) as follows:
In particular, it appears that the spaces \(\mathbb {T}_\Box \) and \(\mathbb {Q}_\Box \) represent “self-equilibrating” tractions and fluxes, respectively.
Remark 1
Setting \(\delta \mathbf{u}\in \mathbb {R}^3\) in (27a), we obtain the solution \(\bar{\varvec{\lambda }}=\mathbf{0 }\). Nevertheless, it is still necessary to satisfy the constraint (27e) in order to prevent Rigid Body Modes (RBM), in this case translation. However, the macro-scale stress \(\bar{\varvec{\sigma }}\) is invariant to any constant translation \(\bar{\mathbf{u}}\) within the RVE, which means that \(\bar{\mathbf{u}}\) can be prescribed to any given value, say \(\bar{\mathbf{u}}=\mathbf{0 }\). Moreover, \(\bar{\varvec{\sigma }}\) is invariant to the skew-symmetric part of \(\bar{\mathbf{h}}\) since \(\varvec{\varepsilon }[\mathbf{u}]=\bar{\varvec{\varepsilon }}+\varvec{\varepsilon }[\mathbf{u}]^\mu \); hence it is only \(\bar{\varvec{\varepsilon }}:=\bar{\mathbf{h}}^{\mathrm{sym}}\) that has to be fed to the RVE problem as data. \(\square \)
Remark 2
Setting \(\delta \varvec{\lambda }=\delta \bar{\varvec{\sigma }}\cdot \mathbf{n}\), with \(\bar{\varvec{\sigma }}\in \mathbb {R}^{3\times {3}}_{\mathrm{sym}}\), into (27c), and setting \(\delta {\mu }=\delta \bar{\mathbf{w}}\cdot \mathbf{n}\), with \(\bar{\mathbf{w}}\in \mathbb {R}^{3}\), into (27d), we obtain the conditions
In other words, the conditions that the volume-averaged strain equals \(\bar{\varvec{\varepsilon }}\), and that the volume-averaged pressure-gradient equals \(\bar{\varvec{{\zeta }}}\) are “built-in” the problem formulation. \(\square \)
Remark 3
Setting \(\delta \mathbf{u}=\dot{\mathbf{u}}\), \(\delta p=p\) and summing up (27a) and (27b), we are able to derive the relation
Moreover, taking (16)–(18) into account together with (28) and choosing \(\bar{\varvec{\lambda }}=\mathbf{0 }\), \(\bar{\mu }=-\dot{\bar{\varPhi }}\), we can derive the identity
This expression is precisely the macro-homogeneity condition; therefore, it is a “built-in” property of the problem formulation. \(\square \)
4 Numerical model reduction in space for the RVE problem
4.1 Decomposition of sub-scale fields
The standard decomposition of the sub-scale fields were given in (9). However, in order to utilize NMR for the purpose of solving the RVE problems in an efficient manner, it is convenient to introduce the alternative decompositionsFootnote 6
where the fields \((\mathbf{u}_{\mathrm{stat}},{p}_{\mathrm{stat}},\varvec{\lambda }_{\mathrm{stat}},\bar{\varvec{\lambda }}_{\mathrm{stat}},{\mu }_{\mathrm{stat}},\bar{\mu }_{\mathrm{stat}})\in \mathbb {U}_{\Box }\times \mathbb {P}_{\Box }\times \mathbb {T}_{\Box }\times \mathbb {R}^3\times \mathbb {Q}_{\Box }\times \mathbb {R}\) solve the “stationary” problem
Remark
We note that \(\mathbf{u}_{\mathrm{stat}}\ne \mathbf{u}^{\mathrm{M}}\) and \(p_{\mathrm{stat}}\ne {p}^{\mathrm{M}}\) in general; hence, \(\tilde{\mathbf{u}}^{\mu }\ne {\mathbf{u}}^{\mu }\) and \(\tilde{p}^{\mu }\ne {p}^{\mu }\). Moreover, \(\bar{\varvec{\lambda }}_{\mathrm{stat}}=\mathbf{0 }\) and \(\bar{\mu }_{\mathrm{stat}}=0\), and it is concluded that \(\bar{\varvec{\lambda }}=\tilde{\bar{\varvec{\lambda }}}^{\mu }=\mathbf{0 }\), whereas \(\bar{\mu }=\tilde{\bar{\mu }}^{\mu }\ne {0}\). Although it is possible to exclude \(\bar{\varvec{\lambda }}_{\mathrm{stat}}\) and \(\bar{\mu }_{\mathrm{stat}}\) a priori from the formulation of the sensitivity problem, these variables are retained henceforth in order to preserve symmetry of the problem formulation. \(\square \)
Since the problem in (33) is linear for each given time, t serves only as a load parameter, we may compute the solution in terms of sensitivities \((\hat{\mathbf{u}}_{ij}^{(\bar{\varepsilon })}, \hat{p}_{ij}^{(\bar{\varepsilon })}, \hat{\varvec{\lambda }}_{ij}^{(\bar{\varepsilon })}, \hat{\mu }_{ij}^{(\bar{\varepsilon })}, \hat{\bar{\varvec{\lambda }}}_{ij}^{(\bar{\varepsilon })}, \hat{\bar{\mu }}_{ij}^{(\bar{\epsilon })})\), \((\hat{\mathbf{u}}^{(\bar{p})}, \hat{p}^{(\bar{p})}, \hat{\varvec{\lambda }}^{(\bar{p})}, \hat{\mu }^{(\bar{p})}, \hat{\bar{\varvec{\lambda }}}^{(\bar{p})}, \hat{\bar{\mu }}^{(\bar{p})})\) and \((\hat{\mathbf{u}}_{i}^{(\bar{\zeta })}, \hat{p}_{i}^{(\bar{\zeta })}, \hat{\varvec{\lambda }}_{i}^{(\bar{\zeta })}, \hat{\mu }_{i}^{(\bar{\zeta })}, \hat{\bar{\varvec{\lambda }}}_{i}^{(\bar{\zeta })}, \hat{\bar{\mu }}_{i}^{(\bar{\zeta })})\) via the ansatz expansions
while noting that \(\mathbf{u}^{\mathrm{M}}\) and \({p}^{\mathrm{M}}\) can be expanded in a similar fashion as
The following set of problems are then solved “offline” as a preliminary to the model reduction. It is possible to sequentially solve for \((p_{\mathrm{stat}},{\mu }_{\mathrm{stat}},\bar{\mu }_{\mathrm{stat}})\) and \((\mathbf{u}_{\mathrm{stat}},\varvec{\lambda }_{\mathrm{stat}},\bar{\varvec{\lambda }}_{\mathrm{stat}})\), in terms of the sensitivities, from the equations (33b), (33d), (33f) and from (33a), (33c), (33e) respectively:
\(\bar{\varvec{\varepsilon }}\ne \mathbf{0 }\), \(\bar{p}=0\), \(\bar{\varvec{{\zeta }}}=\mathbf{0 }\):
Solve for sensitivity fields \((\hat{p}_{ij}^{(\bar{\varepsilon })}, \hat{\mu }_{ij}^{(\bar{\varepsilon })}), \hat{\bar{\mu }}_{ij}^{(\bar{\varepsilon })})\) from
$$\begin{aligned}&a_{\Box }^{(p)}(\hat{p}_{ij}^{(\bar{\varepsilon })};\delta {p}) + d_{\Box }^{(p)}(\hat{\mu }_{ij}^{(\bar{\varepsilon })};\delta {p}) \nonumber \\&\quad + \hat{\bar{\mu }}_{ij}^{(\bar{\varepsilon })}\left\langle \left\langle \delta p \right\rangle \right\rangle _\Box = 0 \quad \forall \delta {p}\in \mathbb {P}_{\Box }, \end{aligned}$$(36a)$$\begin{aligned}&d_{\Box }^{(p)}(\delta {\mu };\hat{\mu }_{ij}^{(\bar{\varepsilon })}) = 0 \quad \forall \delta {\mu }\in \mathbb {Q}_{\Box }, \end{aligned}$$(36b)$$\begin{aligned}&\delta \bar{\mu }\,\langle \langle \hat{p}_{ij}^{(\bar{\varepsilon })}\rangle \rangle _\Box = 0 \quad \forall \delta \bar{\mu }\in \mathbb {R}, \end{aligned}$$(36c)which has the trivial solution \(\hat{p}_{ij}^{(\bar{\varepsilon })}=0, \hat{\mu }_{ij}^{(\bar{\varepsilon })}=0, \hat{\bar{\mu }}_{ij}^{(\bar{\varepsilon })}=0\).
Solve for sensitivity fields \(( \hat{\mathbf{u}}_{ij}^{(\bar{\varepsilon })}, \hat{\varvec{\lambda }}_{ij}^{(\bar{\varepsilon })}, \hat{\bar{\varvec{\lambda }}}_{ij}^{(\bar{\varepsilon })} )\) from
$$\begin{aligned}&a_{\Box }^{(u)}(\hat{\mathbf{u}}_{ij}^{(\bar{\varepsilon })};\delta \mathbf{u}) - d_{\Box }^{(u)}(\hat{\varvec{\lambda }}_{ij}^{(\bar{\varepsilon })};\delta \mathbf{u}) \nonumber \\&\quad - \hat{\bar{\varvec{\lambda }}}_{ij}^{(\bar{\varepsilon })}\cdot \left\langle \left\langle \delta \mathbf{u} \right\rangle \right\rangle _\Box = 0 \quad \forall \delta \mathbf{u}\in \mathbb {U}_{\Box }, \end{aligned}$$(37a)$$\begin{aligned}&- d_{\Box }^{(u)}(\delta \varvec{\lambda };\hat{\mathbf{u}}_{ij}^{(\bar{\varepsilon })}) = - d_{\Box }^{(u)}(\delta \varvec{\lambda };\hat{\mathbf{u}}_{ij}^{\mathrm{M}(\bar{\varepsilon })}) \quad \forall \delta {\varvec{\lambda }}\in \mathbb {T}_{\Box }, \end{aligned}$$(37b)$$\begin{aligned}&- \delta \bar{\varvec{\lambda }}\cdot \langle \langle \hat{\mathbf{u}}_{ij}^{(\bar{\varepsilon })}\rangle \rangle _\Box = 0 \quad \forall \delta \bar{\varvec{\lambda }}\in \mathbb {R}^3. \end{aligned}$$(37c)
\(\bar{\varvec{\varepsilon }}=\mathbf{0 }\), \(\bar{p}\ne {0}\), \(\bar{\varvec{{\zeta }}}=\mathbf{0 }\):
Solve for sensitivity fields \((\hat{p}^{(\bar{p})},\hat{\mu }^{(\bar{p})},\hat{\bar{\mu }}^{(\bar{p})})\) from
$$\begin{aligned}&a_{\Box }^{(p)}(\hat{p}^{(\bar{p})};\delta {p}) + d_{\Box }^{(p)}(\hat{\mu }^{(\bar{p})};\delta {p}) \nonumber \\&\quad + \hat{\bar{\mu }}^{(\bar{p})}\left\langle \left\langle \delta {p} \right\rangle \right\rangle _\Box = 0 \quad \forall \delta {p}\in \mathbb {P}_{\Box }, \end{aligned}$$(38a)$$\begin{aligned}&d_{\Box }^{(p)}(\delta {\mu };\hat{\mu }^{(\bar{p})}) = d_{\Box }^{(p)}(\delta {\mu };\hat{p}^{\mathrm{M}(\bar{p})}) \quad \forall \delta {\mu }\in \mathbb {Q}_{\Box }, \end{aligned}$$(38b)$$\begin{aligned}&\delta \bar{\mu }\,\langle \langle \hat{p}^{(\bar{p})}\rangle \rangle _\Box = \delta \bar{\mu } \quad \forall \delta \bar{\mu }\in \mathbb {R}. \end{aligned}$$(38c)Solve for sensitivity fields \((\hat{\mathbf{u}}^{(\bar{p})}, \hat{\varvec{\lambda }}^{(\bar{p})}, \hat{\bar{\varvec{\lambda }}}^{(\bar{p})})\) from
$$\begin{aligned}&a_{\Box }^{(u)}(\hat{\mathbf{u}}^{(\bar{p})};\delta \mathbf{u}) - d_{\Box }^{(u)}(\hat{\varvec{\lambda }}^{(\bar{p})};\delta \mathbf{u}) \nonumber \\&\quad - \hat{\bar{\varvec{\lambda }}}^{(\bar{p})} \left\langle \left\langle \delta \mathbf{u} \right\rangle \right\rangle _\Box = b_{\Box }(\hat{p}^{(\bar{p})};\delta \mathbf{u}) \quad \forall \delta \mathbf{u}\in \mathbb {U}_{\Box }, \end{aligned}$$(39a)$$\begin{aligned}&- d_{\Box }^{(u)}(\delta \varvec{\lambda };\hat{\mathbf{u}}^{(\bar{p})}) = 0 \quad \forall \delta \varvec{\lambda }\in \mathbb {T}_{\Box }, \end{aligned}$$(39b)$$\begin{aligned}&- \delta \bar{\varvec{\lambda }}\cdot \langle \langle \hat{\mathbf{u}}^{(\bar{p})}\rangle \rangle _\Box = 0 \quad \forall \delta \bar{\varvec{\lambda }}\in \mathbb {R}^3. \end{aligned}$$(39c)
\(\bar{\varvec{\varepsilon }}=\mathbf{0 }\), \(\bar{p}=0\), \(\bar{\varvec{{\zeta }}}\ne \mathbf{0 }\):
Solve for sensitivity fields \((\hat{p}_{i}^{(\bar{\zeta })}, \hat{\mu }_{i}^{(\bar{\zeta })}, \hat{\bar{\mu }}_{i}^{(\bar{\zeta })})\) from
$$\begin{aligned}&a_{\Box }^{(u)}(\hat{p}_{i}^{(\bar{\zeta })};\delta {p}) + d_{\Box }^{(p)}(\hat{\mu }_{i}^{(\bar{\zeta })};\delta {p})\nonumber \\&\quad + \hat{\bar{\mu }}_{i}^{(\bar{\zeta })}\left\langle \left\langle \delta {p} \right\rangle \right\rangle _\Box = 0 \quad \forall \delta {p}\in \mathbb {P}_{\Box }, \end{aligned}$$(40a)$$\begin{aligned}&d_{\Box }^{(p)}(\delta {\mu };\hat{\mu }_{i}^{(\bar{\zeta })}) = d_{\Box }^{(p)}(\delta {\mu };\hat{p}_{i}^{\mathrm{M}(\bar{\zeta })}) \quad \forall \delta {\mu }\in \mathbb {Q}_{\Box }, \end{aligned}$$(40b)$$\begin{aligned}&\delta \bar{\mu }\,\langle \langle \hat{\bar{p}}_{i}^{(\bar{\zeta })}\rangle \rangle _\Box = 0 \quad \forall \delta \bar{\mu }\in \mathbb {R}. \end{aligned}$$(40c)Solve for sensitivity fields \((\hat{\mathbf{u}}_{i}^{(\bar{\zeta })}, \hat{\varvec{\lambda }} _{i}^{(\bar{\zeta })}, \hat{\bar{\varvec{\lambda }}}_{i}^{(\bar{\zeta })})\) from
$$\begin{aligned}&a_{\Box }^{(u)}(\hat{\mathbf{u}}_{i}^{(\bar{\zeta })};\delta \mathbf{u}) - d_{\Box }^{(u)}(\hat{\varvec{\lambda }}_{i}^{(\bar{\zeta })};\delta \mathbf{u}) \nonumber \\&\quad - \hat{\bar{\varvec{\lambda }}}_{i}^{(\bar{\zeta })} \cdot \left\langle \left\langle \delta \mathbf{u} \right\rangle \right\rangle _\Box = b_{\Box }(\hat{p}_{i}^{(\bar{\zeta })};\delta \mathbf{u}) \quad \forall \delta \mathbf{u}\in \mathbb {U}_{\Box }, \end{aligned}$$(41a)$$\begin{aligned}&- d_{\Box }^{(u)}(\delta \varvec{\lambda };\hat{\mathbf{u}}_{i}^{(\bar{\zeta })}) = 0 \quad \forall \delta \varvec{\lambda }\in \mathbb {T}_{\Box }, \end{aligned}$$(41b)$$\begin{aligned} -&\delta \bar{\varvec{\lambda }}\,\cdot \langle \langle \hat{\bar{\mathbf{u}}}_{i}^{(\bar{\zeta })}\rangle \rangle _\Box = 0 \quad \forall \delta \bar{\varvec{\lambda }}\in \mathbb {R}^3. \end{aligned}$$(41c)
4.2 Numerical model reduction based on the NTFA strategy
We first note that the fluctuation fields \(\tilde{\mathbf{u}}^{\mu }(\bullet ,t)\in \mathbb {U}_{\Box }\), \(\tilde{p}^{\mu }(\bullet ,t)\in \mathbb {P}_{\Box }\), \(\tilde{\varvec{\lambda }}^{\mu }(\bullet ,t)\in \mathbb {T}_{\Box }\), \(\tilde{\mu }^{\mu }(\bullet ,t)\in \mathbb {Q}_{\Box }\), \(\tilde{\bar{\varvec{\lambda }}}^{\mu }(\bullet ,t)\in \mathbb {R}^3\), \(\tilde{\bar{\mu }}^{\mu }(t)\in \mathbb {R}\), solve the truly transient RVE problem
Once again, \(\tilde{\bar{\varvec{\lambda }}}^{\mu }\) is kept as an unknown variable for the sake of symmetry although it is known that the solution must be \(\tilde{\bar{\varvec{\lambda }}}^{\mu }=\mathbf{0 }\).
The NMR-strategy for the solution of (42) is then outlined as follows:
Introduce the reduced RVE space \(\mathbb {P}_{\Box ,\text {R}}^0=\text {span}\{\hat{p}_a\}_{a=1}^{M_{\mathrm{R}}}\) in the spatial domain, where \(\{\hat{p}_a(\mathbf{x})\}_{a=1}^{M_{\mathrm{R}}}\) is a set of linearly independent global basis functions called “pressure modes”. The pressure modes are identified in a training phase by solving (42) with different loadings \(\dot{\mathbf{u}}_\text {stat}\) and \(\dot{p}_\text {stat}\) with a POD of extracted snapshots of \(\tilde{p}^\mu \). The “exact” solution \(\tilde{p}^{\mu }\in \mathbb {P}_{\Box }^0\) is then approximated by \(\tilde{p}^{\mu }_{\mathrm{R}}\in \mathbb {P}_{\Box ,\text {R}}^0\) as followsFootnote 7:
$$\begin{aligned} \tilde{p}^{\mu }(\mathbf{x},t) \approx \tilde{p}_{\mathrm{R}}^{\mu }(\mathbf{x},t) := \sum _{a=1}^{M_{\mathrm{R}}} \hat{p}_a(\mathbf{x})\xi _a(t) \in \mathbb {P}_{\Box ,\text {R}}^0, \end{aligned}$$(43)where \(\{\xi _a(t)\}_{a=1}^{M_{\mathrm{R}}}\) are “mode activity” parameters. For computational efficiency, \(M_{\mathrm{R}}\) should be a finite, i.e. reasonably small, number. It turns out that the parameters \(\xi _a(t)\) represent internal variables which define the viscoelastic contribution to the macro-scale model. Most importantly, however, the response of the poroelastic RVE depends on the loading in terms of the macro-scale quantities \(\{\bar{\varvec{\varepsilon }}, \bar{p}, \bar{\varvec{{\zeta }}}\}\) as well as on the parameter set \(\{\xi _a(t)\}_{a=1}^{M_{\mathrm{R}}}\).
Establish NMR-approximations for the other fluctuation fields in the spirit of NTFA, i.e. introduce the expansions
$$\begin{aligned} \tilde{\mathbf{u}}^{\mu }(\mathbf{x},t)&\approx \tilde{\mathbf{u}}_{\mathrm{R}}^{\mu }(\mathbf{x},t) := \sum _{a=1}^{M_{\mathrm{R}}} \hat{\mathbf{u}}_a(\mathbf{x})\xi _a(t) \in \mathbb {U}_{\Box ,\text {R}}^0, \end{aligned}$$(44a)$$\begin{aligned} \tilde{\varvec{\lambda }}^{\mu }(\mathbf{x},t)&\approx \tilde{\varvec{\lambda }}_{\mathrm{R}}^{\mu }(\mathbf{x},t) := \sum _{a=1}^{M_{\mathrm{R}}} \hat{\varvec{\lambda }}_a(\mathbf{x})\xi _a(t) \in \mathbb {T}_{\Box ,\text {R}}^0, \end{aligned}$$(44b)$$\begin{aligned} \tilde{\mu }^{\mu }(\mathbf{x},t)&\approx \tilde{\mu }_{\mathrm{R}}^{\mu }(\mathbf{x},t) := \sum _{a=1}^{M_{\mathrm{R}}} \hat{\mu }_a(\mathbf{x})\xi _a(t) \in \mathbb {Q}_{\Box ,\text {R}}^0, \end{aligned}$$(44c)$$\begin{aligned} \tilde{\bar{\varvec{\lambda }}}^{\mu }(t)&\approx \tilde{\bar{\varvec{\lambda }}}_{\mathrm{R}}^{\mu }(t) := \sum _{a=1}^{M_{\mathrm{R}}} \hat{\bar{\varvec{\lambda }}}_a\xi _a(t) \in \mathbb {R}^3, \end{aligned}$$(44d)$$\begin{aligned} \tilde{\bar{\mu }}^{\mu }(t)&\approx \tilde{\bar{\mu }}_{\mathrm{R}}^{\mu }(t) := \sum _{a=1}^{M_{\mathrm{R}}} \hat{\bar{\mu }}_a\xi _a(t) \in \mathbb {R}, \end{aligned}$$(44e)whereby it is noted that the same mode activity parameters are employed to represent all the fields. Now, the key property is that it is possible to determine the mode basis sets introduced in (44) in terms of the pressure basis \(\{\hat{p}_a(\mathbf{x})\}_{a=1}^{M_{\mathrm{R}}}\) which is identified in the training phase via POD. In order to do so, let us first consider the system defined by (42a), (42c), (42e) and insert the NMR-expansions for the fields \(\{\tilde{p}_{\mathrm{R}}^{\mu }, \tilde{\mathbf{u}}_{\mathrm{R}}^{\mu }, \tilde{\varvec{\lambda }}_{\mathrm{R}}^{\mu }, \tilde{\bar{\varvec{\lambda }}}_{\mathrm{R}}^{\mu }\}\). Since these equations must hold for any t, the coefficients of each mode activity parameter \(\xi _a(t)\) must vanish; hence, the problem reduces to that of finding the modes \(\hat{\mathbf{u}}_a\in \mathbb {U}_{\Box }, \hat{\varvec{\lambda }}_a\in \mathbb {T}_{\Box }, \hat{\bar{\varvec{\lambda }}}_a\in \mathbb {R}^3\) for \(a=1,2,\ldots ,M_{\mathrm{R}}\) from the system
$$\begin{aligned}&a_{\Box }^{(u)}(\hat{\mathbf{u}}_a;\delta \mathbf{u}) - d_{\Box }^{(u)}(\hat{\varvec{\lambda }}_a;\delta \mathbf{u}) \nonumber \\&\quad - \hat{\bar{\varvec{\lambda }}}_a\,\cdot \left\langle \left\langle \delta \mathbf{u} \right\rangle \right\rangle _\Box = b_{\Box }(\hat{p}_a;\delta \mathbf{u}) \quad \forall \delta \mathbf{u}\in \mathbb {U}_{\Box }, \end{aligned}$$(45a)$$\begin{aligned}&- d_{\Box }^{(u)}(\delta \varvec{\lambda };\hat{\mathbf{u}}_a) = 0 \quad \forall \delta \varvec{\lambda }\in \mathbb {T}_{\Box }, \end{aligned}$$(45b)$$\begin{aligned}&- \delta \bar{\varvec{\lambda }}\,\cdot \left\langle \left\langle \hat{\mathbf{u}}_a \right\rangle \right\rangle _\Box = 0 \quad \forall \delta \bar{\varvec{\lambda }}\in \mathbb {R}^3. \end{aligned}$$(45c)Now, since \(\mathbb {U}_{\Box ,\text {R}}\subseteq \mathbb {U}_{\Box }\) and \(\mathbb {T}_{\Box ,\text {R}}\subseteq \mathbb {T}_{\Box }\), we may choose \(\delta \mathbf{u}=\hat{\mathbf{u}}_b\) in (45a), \(\delta \varvec{\lambda }=\hat{\varvec{\lambda }}_b\) in (45b), and \(\delta \bar{\varvec{\lambda }}=\hat{\bar{\varvec{\lambda }}}_b\) in (45c) and combine the results, to give the useful (as will be shown later) relation
$$\begin{aligned} a_{\Box }^{(u)}(\hat{\mathbf{u}}_a;\hat{\mathbf{u}}_b) = b_{\Box }(\hat{p}_a;\hat{\mathbf{u}}_b), \quad a,b = 1,2,\ldots ,M_{\mathrm{R}}. \end{aligned}$$(46)As the final task, determine the values of the mode activity parameters \(\xi _a(t),\, a,b = 1,2,\ldots ,M_{\mathrm{R}}\) from (42b), (42d), (42f). Upon inserting the appropriate NMR-expansions, choosing \(\delta {p}=\hat{p}_a\) in (42b), choosing \(\delta {\mu }=\hat{\mu }_a\) in (42d) and choosing \(\delta \bar{\mu }=\hat{\bar{\mu }}_a\) in (42f), we obtain the system of equations
$$\begin{aligned}&\sum _b \left[ b_{\Box }(\hat{p}_a;\hat{\mathbf{u}}_b) + m_{\Box }(\hat{p}_a;\hat{p}_b) \right] \dot{\xi }_b \nonumber \\&\qquad + \sum _b \left[ a_{\Box }^{(p)}(\hat{p}_a;\hat{p}_b) + d_{\Box }^{(p)}(\hat{\mu }_b;\hat{p}_a) + \hat{\bar{\mu }}_b \left\langle \left\langle \hat{p}_a \right\rangle \right\rangle _\Box \right] {\xi }_b \nonumber \\&\quad = - b_{\Box }(\hat{p}_a;\dot{\mathbf{u}}_{\mathrm{stat}}) - m_{\Box }^{(p)}(\dot{p}_{\mathrm{stat}};\hat{p}_a),\nonumber \\&\quad a=1,2,\ldots ,M_{\mathrm{R}}, \end{aligned}$$(47a)$$\begin{aligned}&\sum _b d_{\Box }^{(p)}(\hat{\mu }_a;\hat{p}_b) {\xi }_b = 0, \quad a=1,2,\ldots ,M_{\mathrm{R}}, \end{aligned}$$(47b)$$\begin{aligned}&\hat{\bar{\mu }}_a \,\sum _b \left\langle \left\langle \hat{p}_b \right\rangle \right\rangle _\Box \,{\xi }_b = 0, \quad a=1,2,\ldots ,M_{\mathrm{R}}. \end{aligned}$$(47c)Noting that
- (i)
\(d_{\Box }^{(p)}(\hat{\mu }_a;\hat{p}_b)=0\) for \(a,b=1,2,\ldots ,M_{\mathrm{R}}\), which follows from (47b) and (42d) with \(\hat{\mu }_a\in {\mathbb {Q}}_\Box \),
- (ii)
\(\hat{\bar{\mu }}_a\left\langle \left\langle \hat{p}_b \right\rangle \right\rangle _\Box =0\) for \(a,b=1,2,\ldots ,M_{\mathrm{R}}\), which follows from (47c) and (42f) with \(\hat{\bar{\mu }}\in {\mathbb {R}}\), and finally,
- (iii)
the relation in (46) holds,
we may rewrite (47) as follows:
$$\begin{aligned}&\sum _b \left[ a_{\Box }^{(u)}(\hat{\mathbf{u}}_a;\hat{\mathbf{u}}_b) {+} m_{\Box }(\hat{p}_a;\hat{p}_b \right] \dot{\xi }_b {+} a_{\Box }^{(p)}(\hat{p}_a;\hat{p}_b) {\xi }_b \nonumber \\&\quad = - b_{\Box }(\hat{p}_a;\dot{{\varvec{u}}}_{\mathrm{stat}}) {-} m_{\Box }(\dot{p}_{\mathrm{stat}};\hat{p}_a),\nonumber \\&\quad a=1,2,\ldots ,M_{\mathrm{R}}. \end{aligned}$$(48)
- (i)
Remark
Since it is only the NMR-modes \(\hat{\mathbf{u}}_a\) and \(\hat{p}_a\) that occur in (48), there is no need to actually compute the basis modes \(\hat{\mathbf{u}}_a, \hat{\mu }_a\) as part of the “online” algorithm. \(\square \)
It is convenient to rewrite (48) in the abbreviated form
or, in matrix format, as
where the matrix entries are defined as
Moreover, the RHS of (49), representing the macroscopic loading, is given as
where
When (50) has been solved for \(\xi _a(t)\), we may express the pertinent macro-scale fields as
where
Finally, it is convenient to derive the spectral form of the evolution equation (50). Thus, we execute a basis shift \(\{\underline{\xi }\}\rightarrow \{\underline{\chi }=\underline{\underline{\hat{R}}}^{-1}\underline{\xi }\}\) by solving the generalized eigenvalue problem for \(\underline{\underline{\hat{S}}}\) and \(\underline{\underline{\hat{M}}}\) as presented in [14]. The matrix \(\underline{\underline{\hat{R}}}\) contains the eigenvectors of the generalized eigenvalue problem. We may write
where \(\underline{\hat{f}}^\star \) represents the sensitivity of the spectral evolution equation for \(\{\dot{\bar{\varvec{\varepsilon }}},\dot{\bar{p}},\dot{\bar{\varvec{{\zeta }}}}\}\) and the diagonal matrix \(\underline{\underline{\hat{C}}}\) contains the characteristic frequencies of the viscoelastic model. It is important to remark that the rheology of the NMR model with the spectral evolution according to equation (59) corresponds to the rheology of a generalized Maxwell–Zener model, see visualization in Fig. 2.
Generalized Maxwell rheology for the poro-viscoelastic NMR model according to the spectral evolution equation (59). \(\hat{E}_{\mathrm{stat}}\) represents the stiffness of the stationary problem
4.3 Special cases
Viscoelastic macro-scale model: An important special case of the model above is defined by the constraints \(\bar{\mu }=0\) and \(\bar{\varvec{{\zeta }}}=\mathbf{0 }\), which correspond to the situation of an “undrained” RVE, i.e the value of the storage function \(\bar{\varPhi }\) is stationary. Fluid redistribution is only possible “locally”, i.e. within the RVE. The condition \(\bar{\mu }=0\) infers that the appropriate value of \(\bar{p}=\langle \langle {p}\rangle \rangle _\Box \) is part of the solution in the sense that it is computed as post-processing when p is known. In addition, the constraint equation (27f) becomes obsolete. Altogether, these model choices give rise to the single-phase viscoelastic macro-scale model proposed in [13, 14]. The procedure may, therefore, be called “selective” homogenization. The macro-scale problem is then reduced, as compared to the coupled problem for \((\bar{\mathbf{u}},\bar{p})\) in (15), to the equilibrium problem that is pertinent to a single-phase continuum
where \(\bar{\varvec{\sigma }}\), as given in (54a), simplifies to
The fields \(\hat{\bar{\varvec{\sigma }}}_{ij}^{(\bar{\varepsilon })}\) and \(\hat{\bar{\varvec{\sigma }}}_a\) are still given in (55a) and (55d), respectively.
The corresponding NMR-reduced RVE-problem is still that in (49) with the RHS simplified as
The problem of determining the stationary solution is simplified accordingly.
Poroelastic macro-scale model: A second special case arises if the viscoelastic properties of the macro-scale model are inactive. The underlying modeling assumption is that the problem is completely described by the stationary problem (33) whilst the transient fluctuations \(\{\tilde{\mathbf{u}}^\mu , \tilde{p}^\mu , \tilde{\varvec{\lambda }}^\mu , \tilde{\mu }^\mu , \tilde{\bar{\varvec{\lambda }}}^\mu , \tilde{\bar{\mu }}^\mu \}\) are evanescent. This is the case if (i) the RVE size \(L_\Box \rightarrow 0\), i.e. the characteristic frequencies \(\hat{C}_a\rightarrow \infty \), or if (ii) the material parameters of the fine-scale model are chosen such that \(|\tilde{p}^\mu | \ll |p_\mathrm{stat}|\), i.e. \(\hat{f}_a\rightarrow 0\).
Incompressible pore fluid: The case of an incompressible pore fluid can be approximated by choosing \(\beta \rightarrow 0\). Hence, \(m_\Box (\dot{p};\delta p)\) is dropped from the transient problem (42) such that (50) can be simplified as
Hence, the poro-viscoelastic character of the macro-scale model is preserved.
4.4 Computational cost of the NMR model
To conclude this section, we address the computational cost of the NMR model. As mentioned in the previous sections, the key advantage of the method is that all computational efforts on the micro-scale can be executed as pre-computations. The computational cost for the training can be estimated as
where the first contribution to (64) refers to the \(n_{\mathrm{training}}\) transient training computations for the snapshot generation whilst the second contribution refers to the linear-elastic computations needed to determine the system matrices in (59). In the 3D case, on may choose \(n_{\mathrm{training}}=10\) (6 strain, 1 pressure, and 3 pressure gradient loading cases). The number \(n_{\mathrm{it}}\) refers to the number of iteration steps needed to solve the transient problems, \(n_S\) is the number of degrees of freedom of the RVE problem, and \(M_{\mathrm{R}}\) is the number of modes that span the reduced basis.
Once the NMR model is trained, it can be re-used to solve an arbitrary number of macroscopic initial boundary value problems on \(\varOmega \). The “online” cost of a macroscopic computation can be estimated as
where \(n_{\mathrm{M}}\) is the number of macroscopic degrees of freedom. In each Gauss point, the \(M_{\mathrm{R}}\) evolution equations need to be updated. For simplicity reasons, we assume that the number of Gauss points corresponds to \(n_{\mathrm{M}}\).
The gain in computational efficiency of the NMR model can be be quantified if the computational cost of the DNS solution is taken into account as
where \(n_{\mathrm{DNS}}\) is the number of degrees of freedom of the DNS model. Moreover, we estimate the computational cost of a conventional \(\hbox {FE}^2\) model with as nested solution of micro- and macroscopic boundary value problems as
For the sake of simplicity, we assume \(n_{\mathrm{it}}\) to be of the same order of magnitude in all three cases.
With that, the speedup from DNS to conventional \(\hbox {FE}^2\) can be estimated as
where \(\frac{n_{\mathrm{M}}}{n_{\mathrm{DNS}}}\ll 1\), \(\frac{n_{\mathrm{M}}\,n_{\mathrm{S}}}{n_{\mathrm{DNS}}}\le 1\), and \(\frac{n_{\mathrm{S}}}{n_{\mathrm{DNS}}}\ll 1\). However, the latter enters (68) only with power 1. By contrast, the speedup from DNS to NMR can be estimated as
with \(\frac{M_{\mathrm{R}}}{n_{\mathrm{S}}}\ll 1\). In particular in the 3D case, “much smaller” means in fact “several orders of magnitude smaller”.
Finally, one may quantify the gain in computational efficiency from fully-nested conventional \(\hbox {FE}^2\) to NMR by evaluating
Altogether, we conclude that the computational savings of using NMR compared with DNS and \(\hbox {FE}^2\) scale with the complexity of the problem and, thus, can be huge. In Sect. 5, we investigate computational costs in terms of examples at increasing complexity more explicitly.
5 Numerical results
In this section, we validate the proposed NMR method and demonstrate its performance in a large-scale reduced \(\hbox {FE}^2\) computation. The material parameters used to define the poroelastic fine-scale model are listed in Table 1. All simulations were carried out running the Finite Element package COMSOL Multiphysics via Matlab livelink on a standard laptop computer.
In the subsequent simulations, mechanical loads are applied by means of a linear ramp function and kept constant after \(t=t_{\mathrm{ramp}}\). Thus, we define the loading function
5.1 Consolidation of a layered poroelastic medium
a 1D RVE of the layered poroelastic medium with \(L_\Box =1\,\hbox {m}\) and \(d=0.25\,\hbox {m}\). b Example pressure modes \(\hat{p}_a^\chi \). The given numbers correspond to the mode numbers resulting from the snapshot POD. c Macroscopic consolidation experiment with \(\bar{t}^\mathrm{p}=1\texttt {e+}6\,\gamma (t)\,\hbox {Pa}\) and \(t_{\mathrm{ramp}}=1\texttt {e-}2\,\hbox {s}\)
The first numerical example aims to provide a proof of concept of the proposed poro-viscoelastic NMR procedure. For simplicity reasons, we choose a periodically layered poroelastic medium. The 1D RVE shown in Fig. 3a represents the unit cell of the layered medium with \(L_\Box =1\,\hbox {m}\) and \(d=0.25\,\hbox {m}\). Strains in the lateral directions equal zero. The material parameters are chosen according to set 1 given in Table 1. We train the poro-viscoelastic substitute medium in three transient precomputations, where we choose \(\bar{\varepsilon }=f_1\,\gamma (t)\), \(\bar{\zeta }=f_2\,\gamma (t)\,\hbox {Pa/m}\) and \(\bar{p}=f_2\,\gamma (t)\,\hbox {Pa}\) individually with \(t_{\mathrm{ramp}}=1\texttt {e-}4\,\hbox {s}\). Note that the factors \(f_1=1\texttt {e-}4\) and \(f_2=1\texttt {e+}6\) are introduced to obtain snapshots of the pore pressure with the same order of magnitude. The snapshots of the pressure field extracted from the training computations undergo a POD and result in a reduced basis that consists of 22 basis modes. The characteristic frequencies \(\hat{C}_a\) are computed as
Remark
-
We observed that it is difficult to find a reduced basis with a reasonably low approximation error if the POD includes snapshots of all loading cases (\(\bar{\varepsilon },\bar{p},\bar{\zeta }\)). The reason is that the pressure snapshots for the the loading cases (\(\bar{\varepsilon },\bar{p}\)) are strongly different from the snapshots for the \(\bar{\zeta }\) loading case. As a simple work-around, we execute two separate PODs, the first based on the snapshots from the (\(\bar{\varepsilon }\), \(\bar{p}\)) loading cases, whilst the second is based on the snapshots from the \(\bar{\zeta }\) loading case. The output of both PODs is combined to one unified reduced basis. Obviously, this procedure does not guarantee orthogonality of the reduced modes. Nevertheless, the approximation error turns out to be negligibly small as demonstrated in the subsequent validation experiments.
-
The characteristic frequencies given in (72) correspond to relaxation times of a Maxwell–Zener model. As shown subsequently, the chosen reduced basis allows for a high-fidelity approximation of the RVE properties incorporating (a) relaxation processes over many decades in time and (b) three strongly different macroscopic loading scenarios (\(\bar{\varepsilon },\bar{p},\bar{\zeta }\)). The complexity of the RVE properties explains the maybe surprisingly high number of 22 modes.
Examples of pressure modes are shown in Fig. 3b. Finally, all sensitivities and system matrices that define the poro-viscoelastic substitute medium are computed from the definitions presented in Sect. 4.
We are now in the position to utilize the poro-viscoelastic substitute model for the simulation of the macroscopic consolidation experiment shown in Fig. 3c as a reduced \(\hbox {FE}^2\) computation. For validation purposes, we also compute a DNS of the macroscopic consolidation experiment which serves as reference. The reference computation is performed with full geometrical resolution, i.e. all layers contained in the macroscopic sample are discretized. In accordance with Fig. 3, the boundary conditions are chosen as \(\bar{t}(\bar{x}=0)=\bar{t}^{\mathrm{p}}\), \(\bar{p}(\bar{x}=0)=0\) (drained boundary), \(\bar{u}(\bar{x}=10\,L_\Box )=0\), and \(\bar{w}(\bar{x}=10\,L_\Box )=0\) (undrained boundary).
Firstly, we compare the pore pressure distribution \(\bar{p}(\bar{x})\) in the macroscopic computation domain at different times during the consolidation experiment, see Fig. 4a. At \(t=1\texttt {e+}0\,\hbox {s}\), the reference computation shows pressure gradients between the layers of the fully resolved sample that are equilibrated in the course of time. Hence, at \(t=1\texttt {e+}2\,\hbox {s}\), the global pressure decay due to the drained boundary condition \(\bar{p}=0\) at \(\bar{x}=0\) becomes dominant. By construction, the reduced \(\hbox {FE}^2\) computation, using the poro-viscoelastic NMR model, is unable to resolve the fluctuations (wave-length \(L_\Box \)) of the pore pressure field at \(t=1\texttt {e+}0\,\hbox {s}\). Instead, the NMR model correctly predicts the pore pressure that is measured at the RVE boundaries. This is in line with (25)\(_2\) where we constrain the macroscopic pressure to equal the surface average of the microscopic pressure. Also, at \(t=1\texttt {e+}2\,\hbox {s}\) and \(t=1\texttt {e+}3\,\hbox {s}\), the poro-viscoelastic computation matches the reference computation with very high accuracy.
Secondly, we investigate the displacement \(\bar{u}\) measured at the surface \(\bar{x}=0\), see Fig. 4b. We observe three distinct phases of the consolidation experiment: (i) The loading phase for \(t<1\texttt {e-}4\,\hbox {s}\), (ii) the phase where the inter-layer pressure gradients are equilibrated by local redistribution of the pore fluid for \(t\in [1\texttt {e-}2,\,1\texttt {e+}1]\,\hbox {s}\) (“viscoelastic creeping”), and (iii) the phase of macroscopic drain-off due to the boundary condition \(\bar{p}=0\) at \(\bar{x}=0\) at \(t>1\texttt {e+}1\,\hbox {s}\) (“poroelastic creeping”). In all phases, the poro-viscoelastic NMR model predicts the material behavior with very high accuracy.
The macroscopic drain-off \(\bar{w}(\bar{x}=0)\) during the consolidation test as well as the change in fluid content \(\bar{\varPhi }-\left\langle \phi \right\rangle _\Box \) stored in the pore space at several evaluation points are plotted in Fig. 5. In both cases, the poro-viscoelastic NMR model is in excellent agreement with the reference computation.
5.2 Role of the RVE size
a Examples of periodic RVE realizations, \(l=0.5\,\hbox {m}\), \(|\varOmega _\Box |=\{1,\,4,\,25\}\,l^2\), with randomly distributed but equally sized circular inclusions (radius \(r=0.175\,\hbox {m}\), volume fraction \(n=0.385\)). b Macroscopic consolidation test with normal surface loading \(\bar{t}^\mathrm{p}=\bar{\mathbf{t}}^\mathrm{p}\cdot \mathbf{n}= 1\texttt {e+}6\,\hbox {Pa}\)
An important issue in computational homogenization is to decide whether the chosen volume element is large enough to be considered as sufficiently representative. In standard first-order homogenization of single-phase materials, the size of an RVE is determined mainly in terms of stochastic representativity and boundary layer effects, e.g. due to over-stiff boundary conditions, whereas computational homogenization of poroelastic media involves an additional imprinted internal length scale, namely the diffusion length.
In the subsequent study, we aim to investigate the effect of RVE size on the macroscopic poro-viscoelastic properties of the homogenized model. We consider a 2D poroelastic medium (plain strain) consisting of stiff, circular inclusions which are embedded in a softer matrix. The material parameters are chosen according to set 1 in Table 1. The RVEs are constructed such that they contain one single inclusion with radius \(r=0.175\,\hbox {m}\) per 2D volume \(l^2\). Hence, the volume fraction of the inclusions is for \(n=0.385\). The different RVE sizes, \(|\varOmega _\Box |=\{1,4,25\}\,\hbox {m}^2\), are shown in Fig. 6a. For each RVE size, we generate an ensemble of five periodic RVEs with randomly distributed inclusions. The minimal distance between the inclusions is constrained to be larger than \(0.1\,r\).
For each individual RVE, we perform training computations with a POD of the extracted snapshots and compute the properties of the corresponding poro-viscoelastic NMR model. We show the pressure modes associated with the 16 lowest characteristic frequencies in Fig. 7 for one example RVE with \(|\varOmega _\Box |=25\,l^2\). The 16 lowest characteristic frequencies associated with the poro-viscoelastic variables \(\chi _a\) are
Note that the NMR model used for the subsequent simulations contains additional pressure modes with higher characteristic frequencies. Typically, we employ 27 pressure modes for each RVE. For the sake of brevity, the higher pressure modes are omitted in Fig. 7.
Effective stress response \(\bar{\sigma }_{11}\) under the loading \(\bar{\varepsilon }_{11}(t)=1\texttt {e-}4\,\gamma (t)\), \(\bar{\varvec{{\zeta }}}=\mathbf{0 }\), \(\bar{p}=0\). a Five example RVE realizations with \(|\varOmega _\Box |=l^2\), b five example RVE realizations with \(|\varOmega _\Box |=25\,l^2\)
Effective seepage velocity \(\bar{w}_1\) under the loading \(\bar{\varvec{\varepsilon }}=\mathbf{0 }\), \(\bar{\zeta }_1(t)=1\texttt {e+}6\,\gamma (t)\,\)Pa/m, \(\bar{p}=0\). a Five example RVE realizations with \(|\varOmega _\Box |=l^2\), b five example RVE realizations with \(|\varOmega _\Box |=25\,l^2\)
Effective porosity increase \(\bar{\varPhi }-\left\langle \phi \right\rangle _\Box \) under the loading \(\bar{\varvec{\varepsilon }}=\mathbf{0 }\), \(\bar{\varvec{{\zeta }}}=\mathbf{0 }\), \(\bar{p}(t)=1\texttt {e+}6\,\gamma (t)\) Pa. a Five example RVE realizations with \(|\varOmega _\Box |=l^2\), b five example RVE realizations with \(|\varOmega _\Box |=25\,l^2\)
We now use the individually identified NMR models to predict the RVE responses to an external loading. The NMR results are validated against reference computations obtained from solving the respective RVE problems with full geometrical resolution. Examples of effective properties are plotted in Figs. 8a, 9a, and 10a for five random RVE realizations of the smallest size \(|\varOmega _\Box |=l^2\) and in Figs. 8b, 9b, and 10b for five random RVE realizations of the largest size \(|\varOmega _\Box |=25\,l^2\). The loading is applied as follows: \(\bar{\varepsilon }_{11}(t)=1\texttt {e-}4\,\gamma (t)\), \(\bar{\varvec{{\zeta }}}=\mathbf{0 }\), \(\bar{p}=0\) for Fig. 8, \(\bar{\varvec{\varepsilon }}=\mathbf{0 }\), \(\bar{\zeta }_1(t)=1\texttt {e+}6\,\gamma (t)\,\hbox {Pa/m}\), \(\bar{p}=0\) for Fig. 9, and \(\bar{\varvec{\varepsilon }}=\mathbf{0 }\), \(\bar{\varvec{{\zeta }}}=\mathbf{0 }\), \(\bar{p}(t)=1\texttt {e+}6\,\gamma (t)\,\hbox {Pa}\) for Fig. 10, \(t_\mathrm{ramp}=1\texttt {e-}4\,\hbox {s}\). All other components of the macroscopic fields are zero.
First of all, we remark that choosing a periodic RVE containing one single inclusion results in a strong scattering of the transient behavior, see Figs. 8, 9, and 10a. This might be somewhat surprising since the only difference between these RVEs with \(|\varOmega _\Box |=l^2\) is the position of the inclusion. In the case of linear elasticity, it is clear that the homogenized properties of a periodic RVE under periodic boundary conditions that contain one single inclusion do not depend on the position of the inclusion. Obviously, this is not true in the present case. The explanation for this behavior is the presence of the pressure diffusion mechanism. Since only the pore pressure fluctuation in(20)\(_2\) is periodic but not the prescribed macroscopic part \(\bar{p}^\mathrm{M}\), the position of the inclusion controls the diffusion behavior close to the RVE boundary which results in the scattering behavior as seen in Figs. 8, 9, and 10a.
The scatter is significantly reduced if we increase the RVE size. This holds, in particular, for the macroscopic stress \(\bar{\sigma }_{11}\) under the loading \(\bar{\varepsilon }_{11}(t)\), see Fig. 8, and the porosity increase \(\bar{\varPhi }-\left\langle \phi \right\rangle _\Box \) under the loading \(\bar{p}(t)\), see Fig. 10. To a lesser extent, this also holds for the effective seepage velocity \(\bar{w}_1\) under \(\bar{\zeta }_1(t)\), see Fig. 10. Moreover, for the larger RVE size we observe that the stationary state (\(t\rightarrow \infty \)) is reached much later than for the smaller RVE size. This is related to the larger diffusion length associated with a larger RVE size. We show in the subsequent experiments that, nevertheless, all RVE sizes are suitable for predicting the transient behavior. Most importantly, however, we want to highlight that all NMR predictions (lines in Figs. 8, 9, 10) are in excellent agreement with the reference computations for the chosen RVEs (dots in Figs. 8, 9, 10).
Validation of NMR predictions for the 2D consolidation test with material properties according to Table 1 (set 1). Each NMR solution is computed by averaging an ensemble of five RVEs. a Pore pressure \(\bar{p}(t)\) computed using the largest RVE size \(|\varOmega _\Box |=25\,l^2\). b Displacement \(\bar{u}_1\) observed at \(\bar{\mathbf{x}}=\mathbf{0 }\) for different RVE sizes
Validation of NMR predictions for the 2D consolidation test with material properties according to Table 1 (set 2). The NMR solution is computed by averaging an ensemble of five RVEs using the largest RVE size \(|\varOmega _\Box |=25\,l^2\). a Evolution of the pore pressure \(\bar{p}(t)\). b Displacement \(\bar{u}_1\) observed at \(\bar{\mathbf{x}}=\mathbf{0 }\)
Finally, we want to employ the identified NMR rules to execute reduced \(\hbox {FE}^2\) simulations of the macroscopic consolidation experiment shown in Fig. 6b for the two different sets of material parameters given in Table 1. For each RVE size, we execute ensemble averaging of the individual poro-viscoelastic NMR models. The ensemble averaged reduced \(\hbox {FE}^2\) computations are validated against a DNS which we use as reference solution. The reference sample for DNS is generated according to Fig. 6b. It is periodic in \(\bar{x}_2\)-direction and contains 50 stochastically distributed inclusions. The reference computation is carried out with full geometrical resolution of the inclusions. The boundary conditions on the macroscopic problem are \(\bar{\mathbf{t}}=[\bar{t}^{\mathrm{p}}, 0]^T\) at \(\bar{x}_1=0\) with the prescribed traction \(\bar{t}^{\mathrm{p}}=1\texttt {e+}6\,\gamma (t)\) and \(t_{\mathrm{ramp}}=1\texttt {e-}4\,\hbox {s}\). Moreover, \(\bar{p}=0\) at \(\bar{x}_1=0\) (drained boundary). All other boundaries undergo symmetry conditions, i.e. \(\bar{\mathbf{u}}\cdot \mathbf{n}=0\) and \(\bar{w}=0\) (undrained boundary).
The results obtained for parameter set 1 are shown in Fig. 11. As for the 1D case, we observe a pronounced fluctuation of the pore pressure field \(\bar{p}\) for \(t=1\texttt {e-}1\,\hbox {s}\) that decays rapidly over time. The associated process is local redistribution of pore fluid between the inclusions and the matrix material in their vicinity. With the passage of time, the drained boundary condition \(\bar{p}(\bar{x}_1=0)=0\) induces a macroscopic transport of pore fluid over the full length of the sample. Note that the reduced \(\hbox {FE}^2\) solution shown in Fig. 11a is computed using the largest RVE size \(|\varOmega _\Box |=25\,l^2\). The agreement with the reference computation is very good. Nevertheless, it is important to remark that a certain deviation from the reference computations is to be expected due to the fact that the reference geometry itself is stochastic.
In Fig. 11b we plot the displacement \(\bar{u}_1(\bar{\mathbf{x}}=\mathbf{0 })\). Here, we compare ensemble averages of the RVE sizes \(|\varOmega _\Box |=\{1,4,25\}\,l^2\). Whilst the displacement related to local redistribution at \(t=1\,\hbox {s}\) is not very pronounced in this example, the NMR predictions of all RVE sizes show a very good agreement with the reference computation of the transient behavior. The only systematic deviation from the reference computation is the slight underestimation of the settlement in the fully equilibrated state by the smallest RVE size.
a 3D poroelastic RVE containing 8 spherical inclusions; \(L_\Box =0.2\,\hbox {m}\), \(r=4.15\texttt {e-}2\,\hbox {m}\), \(n=0.3\). b Macroscopic inhomogeneous consolidation experiment with \(L=10\,\hbox {m}\), \(H=20\,\hbox {m}\), \(\bar{t}^{\mathrm{p}}=-1\texttt {e+}6\,\hbox {Pa}\). Data computed at point \(\mathcal{P}\,\)(6,0,-6) m will be used for RVE visualizations
The same consolidation test has been performed with parameter set 2. The pressure distribution and the settlement are plotted in Fig. 12. Because the material properties G, K, and \(\beta \) are chosen to represent a significantly softer material than in parameter set 1, the amplitude of the pressure fluctuation at \(t=1\texttt {e-}1\,\hbox {s}\) is, compared to the overall pressure level, much larger. This is also reflected in the displacement \(\bar{u}_1(\mathbf{x}=\mathbf{0 })\) where the local redistribution process at \(t=1\,\hbox {s}\) (“viscoelastic creeping”) is much more pronounced than for parameter set 1. In this case, all NMR computations have been carried out on the basis of the ensemble consisting of five RVE realizations of the largest size. Taking into account that also the reference geometry itself is stochastically disturbed, we find again a very good agreement of the reduced \(\hbox {FE}^2\) computation with the reference computation.
5.3 Consolidation experiment with inhomogeneous boundary conditions
We conclude our investigations with a 3D consolidation experiment with inhomogeneous boundary conditions. We assume a poroelastic RVE that contains 8 spherical inclusions, see Fig. 13a, and use the material parameters of set 2, see Table 1. The macroscopic problem is displayed in Fig. 13b. The loading at the top surface is applied via the prescribed traction \(\bar{\mathbf{t}}=[0, 0, \bar{t}^{\mathrm{p}}]^T\) on a rigid plate. We choose \(\bar{t}^{\mathrm{p}}=-\gamma (t)\,1\texttt {e+}6\,\hbox {Pa}\) and \(t_{\mathrm{ramp}}=1\texttt {e-}4\,\hbox {s}\). The remaining part of the top surface is traction-fee and drained (\(\bar{p}=0\)). Symmetry conditions apply to all other boundaries. Hence, \(\bar{\mathbf{u}}\cdot \mathbf{n}=0\) and \(\bar{w}=0\).
a Reduced \(\hbox {FE}^2\) computation of the macroscopic seepage \(\Vert \bar{\mathbf{w}}\Vert \) during the inhomogeneous consolidation experiment. b Microscopic seepage \(\Vert \mathbf{w}\Vert \) evaluated during \(\hbox {FE}^2\) computation in the RVE adjacent to point \(\mathcal{P}\,\)(6,0,-6) m at \(t=60\,\hbox {s}\) and at \(t=3600\,\hbox {s}\)
We follow the NMR procedure and perform training computations to identify all relevant sensitivities of the poro-viscoelastic substitute model. Examples of pressure modes are displayed in Fig. 14. Finally, we are able to execute the reduced \(\hbox {FE}^2\) computations. In Fig. 15a we display the effective seepage \(\bar{\mathbf{w}}\) in the sample at different times. The arrows represent the seepage velocity vector. In Fig. 15b, we show, as a post-processing result, the local seepage velocity \(\mathbf{w}\) as observed in an RVE adjacent to the evaluation point \(\mathcal{P}\) for the same instants of time. We see that, at \(t=60\,\hbox {s}\), the seepage is active essentially in the horizontal direction in the part of the sample which is exposed to the strong inhomogeneity of the loading. By contrast, the seepage at \(t=3600\,\hbox {s}\) is active mainly in the vertical direction towards the drained boundary. This behavior is also reflected by the streamlines in the RVE, see Fig. 15b.
It is important to remark that, for the given example, the fully resolved macroscopic geometry would contain 2,000,000 inclusions. A DNS of the sample would be far beyond typically available computing and memory resources. By contrast, the reduced \(\hbox {FE}^2\) simulation based on the poro-viscoelastic NMR approach requires only a short computation time with a low memory utilization. The computational effectiveness is discussed in more detail in the subsequent section.
5.4 Computation time
To investigate computational effectiveness, we compare the explicit computation times between DNS and NMR solutions for the previous examples. All simulations were carried out on a standard laptop computer. The computation times are reported in Table 2 for the 1D case (cf. Sect. 5.1), the 2D case (cf. Sect. 5.2) and the 3D case (cf. Sect. 5.3). The computation times are evaluated for the solution of (i) one load case on one single RVE and of (ii) the macroscopic consolidation experiments. We observe that, with increasing complexity of the problem, the NMR model becomes more and more favorable. In practice, the computational effort to solve the RVE problem by NMR does not depend on the dimensionality of the problem. The speed-up factor for solving one single 3D RVE problem is 500. With NMR, also the 3D macroscopic consolidation experiment can be solved within a few minutes, although the relaxation behavior of the RVE problem gives rise to a considerable number of evolution equations. By contrast, the DNS of the 3D consolidation test, containing 2,000,000 inclusions, exceeds the capacities of the used computer resources by far. It is, therefore, impossible to quantify the speed-up in that case. These results point to the high computational effectiveness of the proposed method.
6 Concluding remarks: outlook
To provide increased modeling capability at the computational homogenization of fine-scale poroelasticity, we have considered the situation where the pore pressure field possesses macro-scale as well as sub-scale parts. The corresponding RVE problems will become more expensive as part of the \(\hbox {FE}^2\) algorithm. Accordingly, it was expected that the NMR approach is much more efficient. Indeed, the presented numerical results show that the NMR method provides excellent agreement with the reference solution obtained from DNS for a quite small number of pressure modes. Moreover, it was shown that even 3D RVEs employed as part of the \(\hbox {FE}^2\) algorithm give tractable solution times.
As to future work, it is of significant interest to evaluate the importance of including the macro-scale viscoelastic variables, i.e. to discern when it is sufficient to assume that the RVE problem is reduced to what is coined the stationary problem. Such a reduction would mean that the macro-scale model is purely poroelastic. Another aspect that requires further investigation is the effect of the compressibility of the pore fluid on the NMR algorithm. Whilst in rock mechanics applications the bulk moduli of fluid and solid phase are usually of the same order of magnitude, the assumption of an, in practice, incompressible pore fluid is common for the description of “softer” porous media such as biological tissues or soft clay with full water saturation.
Notes
\([\bullet ]\) to denote operational arguments.
We refer to \(\hbox {FE}^2\) in a discrete sense where \(\varOmega _{\Box ,i}\) pertains to an RVE centered at the macro-scale quadrature point \(\bar{\mathbf{x}}_i\).
The concept of weakly periodic boundary conditions is discussed in more detail in [19] for first-order computational homogenization.
To simplify notation, without losing generality, we assume henceforth that the natural boundary conditions are sufficiently smooth to effect only the macro-scale problem.
Curly brackets denote implicit dependence on the argument.
Here, we consider solely the approximation involved in NMR, i.e. we completely ignore the error due to discretization in space-time.
References
Biot MA (1941) General theory of three-dimensional consolidation. J Appl Phys 12:155–164
Biot MA (1955) Theory of elasticity and consolidation for a porous anisotropic solid. J Appl Phys 26:182–185
de Boer R (2000) Theory of porous media: highlights in the historical development and current state. Springer, Berlin
Dvorak G, Benveniste Y (1992) On transformation strains and uniform fields in multiphase elastic media. Proc R Soc Lond A 437:291–310
Ehlers W (2002) Foundations of multiphasic and porous materials. In: Ehlers W, Bluhm J (eds) Porous media: theory, experiments and numerical applications. Springer, Berlin, pp 3–86
Ekre F, Larsson F, Runesson K (2019) On error controlled numerical model reduction in \(\text{ FE }^2\)-analysis of transient heat flow. Int J Numer Methods Eng 119:38–73 accepted for publication
Fish J, Yuan Z (2007) Multiscale enrichment based on partition of unity for nonperiodic fields and nonlinear problems. Comput Mech 40:249–259
Fritzen F, Böhlke T (2010) Three-dimensional finite element implementation of the nonuniform transformation field analysis. Int J Numer Methods Eng 84:803–819
Fritzen F, Böhlke T (2013) Reduced basis homogenization of viscoelastic composites. Compos Sci Technol 76:84–91
Fritzen F, Hodapp M, Leuschner M (2014) GPU accelerated computational homogenization based on a variational approach in reduced basis framework. Comput Methods Appl Mech Eng 278:186–217
Fritzen F, Leuschner M (2013) Reduced basis hybrid computational homogenization based on a mixed incremental formulation. Comput Methods Appl Mech Eng 260:143–154
Gureveich B, Brajanovski M, Galvin R, Müller T, Toms-Stewart J (2009) P-wave dispersion and attenuation in fractured and porous reservoirs: Poroelasticity approach. Geophys Prospect 57:225237
Jänicke R, Larsson F, Steeb H, Runesson K (2016) Numerical identification of a viscoelastic substitute model for heterogeneous poroelastic media by a reduced order homogenization approach. Comput Methods Appl Mech Eng 298:108–120
Jänicke R, Quintal B, Larsson F, Runesson K (2019) Identification of viscoelastic properties from numerical model reduction of pressure diffusion in fluid-saturated porous rock with fractures. Comput Mech 63:49–67
Jänicke R, Quintal B, Steeb H (2015) Numerical homogenization of mesoscopic loss in poroelastic media. Eur J Mech A Solids 49:382–395
Kanit T, Forest S, Galliet I, Mounoury V, Jeulin D (2003) Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int J Solids Struct 40:3647–3679
Khoei A, Hajiabadi M (2018) Fully coupled hydromechanical multiscale model with microdynamic effects. Int J Numer Methods Eng 115:293–327
Ladevèze P, Chamoin L (2011) On the verification of model reduction methods based on the proper generalized decomposition. Comput Methods Appl Mech Eng 200:2032–2047
Larsson F, Runesson K, Saroukhani S, Vafadari R (2011) Computational homogenization based on a weak format of micro-periodicity for RVE-problems. Comput Methods Appl Mech Eng 200:11–26
Michel JC, Suquet P (2003) Nonuniform transformation field analysis. Int J Solids Struct 40:6937–6955
Michel JC, Suquet P (2004) Computational analysis of nonlinear composite structures using the nonuniform transformation field analysis. Comput Methods Appl Mech Eng 193:5477–5502
O’Connell RJ, Budiansky B (1977) Viscoelastic properties of fluid-saturated cracked solids. J Geophys Res 82:5719–5735
Oskay C, Fish J (2007) Eigendeformation-based reduced order homogenization for failure analysis of heterogeneous materials. Comput Methods Appl Mech Eng 196:1216–1243
Ostoja-Starzewski M (2006) Material spatial randomness: from statistical to representative volume element. Probab Eng Mech 21:112–132
Quintal B, Steeb H, Frehner M, Schmalholz S (2011) Quasi-static finite element modeling of seismic attenuation and dispersion due to wave-induced fluid flow in poroelastic media. J Geophys Res 116:B01201
Roussette S, Michel JC, Suquet P (2009) Nonuniform transformation field analysis of elastic–viscoplastic composites. Compos Sci Technol 69:22–27
Su F, Larsson F, Runesson K (2011) Computational homogenization of coupled consolidation problems in micro-heterogeneous porous media. Int J Numer Methods Eng 88:1198–1218
White JE (1975) Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics 40:224–232
Acknowledgements
Open access funding provided by Chalmers University of Technology. This project is funded by the Swedish Research Council (VR) under the Grant 2017-05192. The financial support is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jänicke, R., Larsson, F. & Runesson, K. A poro-viscoelastic substitute model of fine-scale poroelasticity obtained from homogenization and numerical model reduction. Comput Mech 65, 1063–1083 (2020). https://doi.org/10.1007/s00466-019-01808-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-019-01808-x