Skip to main content
SpringerLink
Log in

An adaptive \(\hbox {FE}^2\) approach for fiber–matrix composites

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

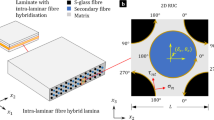
The contribution is concerned with an adaptive scheme for the finite-element square (\(\hbox {FE}^2\)) method. The \(\hbox {FE}^2\) method allows a continuous homogenization considering the current deformation state of the heterogeneous material structure. The micro-structure is represented by a representative volume element, which differs in the fiber distribution. The fiber material behavior is assumed as elasto-plastic. The non-linear response of the fiber necessitates a numerical homogenization for every load step at each integration point, which leads to an increased computational effort. An indicator for a nested \(\hbox {FE}^2\) homogenization is introduced. It takes advantage of the fact that a accompanying homogenization is only necessary in the regions of non-linear material behavior. The present work deals with an adaptive scheme for fiber–matrix composites to reduce the computational cost. Numerical examples show the capability of the proposed scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  1. Broughton JQ, Abraham FF, Bernstein N, Kaxiras E (1999) Concurrent coupling of length scales: methodology and application. Phys Rev B 60(4):2391

    Article  Google Scholar 

  2. Ibrahimbegović A, Markovič D (2003) Strong coupling methods in multi-phase and multi-scale modeling of inelastic behavior of heterogeneous structures. Comput Methods Appl Mech Eng 192(28):3089

    Article  MATH  Google Scholar 

  3. Fish J, Yuan Z (2005) Multiscale enrichment based on partition of unity. Int J Numer Methods Eng 62(10):1341

    Article  MATH  Google Scholar 

  4. Hund A, Ramm E (2007) Locality constraints within multiscale model for non-linear material behaviour. Int J Numer Methods Eng 70(13):1613

    Article  MathSciNet  MATH  Google Scholar 

  5. Ortolano J, Hernández Ortega JA, Oliver Olivella X (2013) A comparative study on homogenization strategies for multi-scale analysis of materials. Centre Internacional de Mètodes Numèrics en Enginyeria (CIMNE), Barcelona

    Google Scholar 

  6. Kanouté P, Boso D, Chaboche J, Schrefler B (2009) Multiscale methods for composites: a review. Arch Comput Methods Eng 16(1):31

    Article  MATH  Google Scholar 

  7. Voigt W (1889) Über die Beziehung zwischenden beiden Elastizitätskonstanten Isotroper Körper. Wied Ann 38(2):573

    Article  Google Scholar 

  8. Reuss A (1929) Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. Z Angew Math Mech 9(1):49

    Article  MATH  Google Scholar 

  9. Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behaviour of multiphase materials. J Mech Phys Solids 11(2):127

    Article  MathSciNet  MATH  Google Scholar 

  10. Pierard O, Friebel C, Doghri I (2004) Mean-field homogenization of multi-phase thermo-elastic composites: a general framework and its validation. Compos Sci Technol 64(10–11):1587

    Article  Google Scholar 

  11. Eshelby JD (1957) The determination of the elastic field of an ellipsoidal inclusion, and related problems. In: Proceedings of the Royal Society of London A: mathematical, physical and engineering sciences, vol 241. The Royal Society, pp 376–396

  12. Mori T, Tanaka K (1973) Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall 21(5):571

    Article  Google Scholar 

  13. Zohdi TI, Wriggers P (2008) An introduction to computational micromechanics. Springer, Berlin

    MATH  Google Scholar 

  14. Nemat-Nasser S, Hori M (2013) Micromechanics: overall properties of heterogeneous materials, vol 37. Elsevier, Amsterdam

    MATH  Google Scholar 

  15. Hill R (1963) Elastic properties of reinforced solids: some theoretical principles. J Mech Phys Solids 11(5):357

    Article  MathSciNet  MATH  Google Scholar 

  16. Gitman I, Askes H, Sluys L (2007) Representative volume: existence and size determination. Eng Fract Mech 74(16):2518

    Article  Google Scholar 

  17. Smit R, Brekelmans W, Meijer H (1998) Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput Methods Appl Mech Eng 155(1–2):181

    Article  MATH  Google Scholar 

  18. Feyel F, Chaboche JL (2000) FE\(^{2}\) multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SiC/Ti composite materials. Comput Methods Appl Mech Eng 183(3):309

    Article  MATH  Google Scholar 

  19. Miehe C, Koch A (2002) Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch Appl Mech 72(4):300. https://doi.org/10.1007/s00419-002-0212-2

    Article  MATH  Google Scholar 

  20. Gruttmann F, Wagner W (2013) A coupled two-scale shell model with applications to layered structures. Int J Numer Methods Eng 94(13):1233

    Article  MathSciNet  MATH  Google Scholar 

  21. Schröder J, Keip MA (2012) Two-scale homogenization of electromechanically coupled boundary value problems. Comput Mech 50(2):229. https://doi.org/10.1007/s00466-012-0715-9

    Article  MathSciNet  MATH  Google Scholar 

  22. Gebbeken N (1996) Zur Untersuchung des linearen Tragverhaltens von Verbundkonstruktionen mittels numerischer Methoden. Technical report 96/1, Universität der Bundeswehr München

  23. Hori M, Nemat-Nasser S (1999) On two micromechanics theories for determining micro–macro relations in heterogeneous solids. Mech Mater 31(10):667

    Article  Google Scholar 

  24. Miehe C, Schröder J, Becker M (2002) Computational homogenization analysis in finite elasticity: material and structural instabilities on the micro-and macro-scales of periodic composites and their interaction. Comput Methods Appl Mech Eng 191(44):4971

    Article  MathSciNet  MATH  Google Scholar 

  25. Saeb S, Steinmann P, Javili A (2016) Aspects of computational homogenization at finite deformations: a unifying review from Reuss’ to Voigt’s bound. Appl Mech Rev 68(5):050801

    Article  Google Scholar 

  26. Shen H, Brinson LC (2006) A numerical investigation of the effect of boundary conditions and representative volume element size for porous titanium. J Mech Mater Struct 1(7):1179

    Article  Google Scholar 

  27. Huet C (1990) Application of variational concepts to size effects in elastic heterogeneous bodies. J Mech Phys Solids 38(6):813

    Article  MathSciNet  Google Scholar 

  28. Simo JC, Hughes TJ (2006) Computational inelasticity, vol 7. Springer, Berlin

    MATH  Google Scholar 

  29. Kohlhaas B, Klinkel S (2015) An FE\(^2\) model for the analysis of shape memory alloy fiber-composites. Comput Mech 55(2):421

    Article  MathSciNet  Google Scholar 

  30. Larsson F, Runesson K (2007) RVE computations with error control and adaptivity: the power of duality. Comput Mech 39(5):647

    Article  MathSciNet  MATH  Google Scholar 

  31. Fish J, Fan R (2008) Mathematical homogenization of nonperiodic heterogeneous media subjected to large deformation transient loading. Int J Numer Methods Eng 76(7):1044

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We thank the German Research Foundation (DFG) for financial support under Grant Number KL 1345/9-1

Author information

Authors and Affiliations

  1. Lehrstuhl für Baustatik und Baudynamik, RWTH Aachen, University, Mies-van-der-Rohe-Str. 1, 52074, Aachen, Germany

    Maximilian Praster, Markus Klassen & Sven Klinkel

Authors
  1. Maximilian Praster
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Markus Klassen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sven Klinkel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maximilian Praster.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Praster, M., Klassen, M. & Klinkel, S. An adaptive \(\hbox {FE}^2\) approach for fiber–matrix composites. Comput Mech 63, 1333–1350 (2019). https://doi.org/10.1007/s00466-018-1652-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-018-1652-z

Keywords

Search

Navigation