Abstract
Surfaces of solids behave differently from the bulk due to different atomic rearrangements and processes such as oxidation or aging. Such behavior can become markedly dominant at the nanoscale due to the large ratio of surface area to bulk volume. The surface elasticity theory (Gurtin and Murdoch in Arch Ration Mech Anal 57(4):291–323, 1975) has proven to be a powerful strategy to capture the size-dependent response of nano-materials. While the surface elasticity theory is well-established to date, surface plasticity still remains elusive and poorly understood. The objective of this contribution is to establish a thermodynamically consistent surface elastoplasticity theory for finite deformations. A phenomenological isotropic plasticity model for the surface is developed based on the postulated elastoplastic multiplicative decomposition of the surface superficial deformation gradient. The non-linear governing equations and the weak forms thereof are derived. The numerical implementation is carried out using the finite element method and the consistent elastoplastic tangent of the surface contribution is derived. Finally, a series of numerical examples provide further insight into the problem and elucidate the key features of the proposed theory.








Similar content being viewed by others
Notes
The assumption of isotropy in this work is for the sake of simplicity.
The Lie derivative of a spatial surface tensor field \(\hat{\varvec{f}}(\hat{\varvec{x}}, t)\), relative to a vector field \(\hat{\varvec{v}}\) is obtained by \(\pounds _{\hat{\varvec{v}}} \hat{\varvec{f}} = \hat{\varvec{\varphi }}_* \left( \frac{\mathrm {D}}{\mathrm {D}t} \hat{\varvec{\varphi }}{}^{-1}_* (\hat{\varvec{f}})\right) \), where \(\hat{\varvec{\varphi }}_*^{-1} \) is the surface pull-back and \(\hat{\varvec{\varphi }}_* \) the surface push-forward operators.
Note that the most general set of arguments for the surface free energy contains \(\hat{\varvec{F}}_\mathrm{p}\) and \(\hat{\varvec{F}}\) in Euclidean space. Imposing the invariance under superposed rigid body motion onto the intermediate configuration results in \(\hat{\varvec{C}}_\mathrm{e}\), where \(\hat{\varvec{C}}_\mathrm{e}\) is the elastic right Cauchy–Green strain in the intermediate configuration. Imposing further invariance under superposed rigid body motion on the spatial configuration finally results in \(\hat{\varvec{b}}_\mathrm{e}\), see [59] for further details.
The spatial symmetry operator is
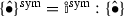 , where
, where 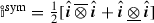 , for spatial second-order surface tensors. Its Material counterpart is defined as \(\{\hat{\bullet }\}^\mathrm {Sym} = \mathbb {I}^\mathrm {Sym}:\{\hat{\bullet }\}\), where \(\mathbb {I}^\mathrm {Sym}= \frac{1}{2}[\hat{\varvec{I}}\, {\overline{\otimes }}\,\hat{\varvec{I}} + \hat{\varvec{I}}\, {\underline{\otimes }}\,\hat{\varvec{I}}]\).
, for spatial second-order surface tensors. Its Material counterpart is defined as \(\{\hat{\bullet }\}^\mathrm {Sym} = \mathbb {I}^\mathrm {Sym}:\{\hat{\bullet }\}\), where \(\mathbb {I}^\mathrm {Sym}= \frac{1}{2}[\hat{\varvec{I}}\, {\overline{\otimes }}\,\hat{\varvec{I}} + \hat{\varvec{I}}\, {\underline{\otimes }}\,\hat{\varvec{I}}]\).Note that in Eq. (19) it is assumed that plastic spin \(\hat{\varvec{W}}_\mathrm{p}= \varvec{0}\), thus \(\hat{\varvec{L}}_\mathrm{p}\) is symmetric.
The surface trace operator for spatial second order tensor is defined as \(\widehat{\mathrm {trace}}\{\hat{\bullet }\} = \{\hat{\bullet }\}:\hat{\varvec{i}}\). In the material configuration the surface trace operator is defined correspondingly as \(\widehat{\mathrm {Trace}}\{\hat{\bullet }\} = \{\hat{\bullet }\}:\hat{\varvec{I}}\).
Note that henceforth only the classical example for metal plasticity, i.e. the von Mises-type yield criterion is considered. Thus, we only take into account the simplest plasticity model, i.e. J\(_2\) type flow theory with isotropic hardening to be developed on the surface. This is to motivate a surface elastoplasticity model and examine its computational aspects.
The term volumetric has a different meaning on the surface. A surface volumetric deformation describes a deformation that changes the area. A volumetric deformation in the bulk however changes the volume. Nonetheless, we use the same term for both the bulk and the surface for the sake of simplicity.
We mention the assumptions made for the numerical part of the current manuscript: first, the surface stress response is isotropic. Second, the plastic spin on the surface is assumed to vanish. Third, the main focus here is on metal plasticity meaning that plastic yielding is isochoric, i.e. \(\hat{J}_\mathrm{p}= 1\), which justifies the decoupling of the surface strain energy. Note that the same assumptions are also made for the bulk elastoplasticity.
Alternatively, a formulation adapting the flow rule in [62] to surface plasticity is possible.
This is the case when \(\hat{K}([\hat{F}_\mathrm{p}]_{\tau +1})\) is a non-linear function of \([\hat{F}_\mathrm{p}]_{\tau +1}\) and consequently a non-linear function of \(\Delta \gamma \) since \([\hat{F}_\mathrm{p}]_{\tau +1} = [\hat{F}_\mathrm{p}]_\tau + \sqrt{2/3}\Delta \gamma \).
In the following derivations we drop the super- and sub-index \(\mathrm{trial}\) and \({\tau +1}\) for the sake of brevity.
Due to the negligible energetic contributions of the side surfaces only the energetics of x-y surfaces are taken into account.
References
Adamson W, Gast AP (1997) Physical chemistry of surfaces. Wiley, New York
Bellet M (2001) Implementation of surface tension with wall adhesion effects in a three-dimensional finite element model for fluid flow. Commun Numer Methods Eng 17(8):563–579
Benveniste Y (2013) Models of thin interphases and the effective medium approximation in composite media with curvilinearly anisotropic coated inclusions. Int J Eng Sci 72:140–154
Benveniste Y, Miloh T (2001) Imperfect soft and stiff interfaces in two-dimensional elasticity. Mech Mater 33(6):309–323
Bottomley DJ, Ogino T (2001) Alternative to the Shuttleworth formulation of solid surface stress. Phys Rev B 63:165412
Cammarata RC (1994) Surface and interface stress effects in thin films. Prog Surf Sci 46(1):1–38
Cammarata RC (1997) Surface and interface stress effects on interfacial and nanostructured materials. Mater Sci Eng A 237(2):180–184
Chatzigeorgiou G, Javili A, Steinmann P (2013) Multiscale modelling for composites with energetic interfaces at the micro- or nanoscale. Math Mech Solids 20:1130–1145
Daher N, Maugin GA (1986) The method of virtual power in continuum mechanics application to media presenting singular surfaces and interfaces. Acta Mech 60(3–4):217–240
Davydov D, Javili A, Steinmann P (2013) On molecular statics and surface-enhanced continuum modeling of nano-structures. Comput Mater Sci 69:510–519
de Souza Neto EA, Peric D, Owen DRJ (2011) Computational methods for plasticity: theory and applications. Wiley, Chichester
dell’Isola F, Romano A (1987) On the derivation of thermomechanical balance equations for continuous systems with a nonmaterial interface. Int J Eng Sci 25:1459–1468
Dingreville R, Qu J, Cherkaoui M (2005) Surface free energy and its effect on the elastic behavior of nano-sized particles, wires and films. J Mech Phys Solids 53(8):1827–1854
Duan HL, Karihaloo BL (2007) Effective thermal conductivities of heterogeneous media containing multiple imperfectly bonded inclusions. Phys Rev B 75(6):064206
Duan HL, Wang J, Huang ZP, Karihaloo BL (2005a) Eshelby formalism for nano-inhomogeneities. Proc R Soc A Math Phys Eng Sci 461(2062):3335–3353
Duan HL, Wang J, Huang ZP, Karihaloo BL (2005b) Size-dependent effective elastic constants of solids containing nano-inhomogeneities with interface stress. J Mech Phys Solids 53(7):1574–1596
Duan HL, Wang J, Karihaloo BL (2009) Theory of elasticity at the nanoscale. Adv Appl Mech 42:1–68
Esmaeili A, Javili A, Steinmann P (2016a) A thermo-mechanical cohesive zone model accounting for mechanically energetic Kapitza interfaces. Int J Solids Struct 92–93:29–44
Esmaeili A, Javili A, Steinmann P (2016b) Coherent energetic interfaces accounting for in-plane degradation. Int J Fract 202(2):135–165
Esmaeili A, Javili A, Steinmann P (2016c) Highly-conductive energetic coherent interfaces subject to in-plane degradation. Math Mech Solids. https://doi.org/10.1177/1081286516642818
Esmaeili A, Javili A, Steinmann P (2017a) Coupled thermally general imperfect and mechanically coherent energetic interfaces subject to in-plane degradation. JoMMS 12(3):289–312
Esmaeili A, Steinmann P, Javili A (2017b) Non-coherent energetic interfaces accounting for degradation. Comput Mech 59(3):361–383
Fischer FD, Simha NK, Svoboda J (2003) Kinetics of diffusional phase transformation in multicomponent elasticplastic materials. ASME J Eng Mater Technol 125:266–276
Fischer FD, Svoboda J (2010) Stresses in hollow nanoparticles. Int J Solids Struct 47(20):2799–2805
Fischer FD, Waitz T, Vollath D, Simha NK (2008) On the role of surface energy and surface stress in phase-transforming nanoparticles. Prog Mater Sci 53(3):481–527
Fleck NA, Willis JR (2009) A mathematical basis for strain-gradient plasticity theory part I: scalar plastic multiplier. J Mech Phys Solids 57(1):161–177
Fried E, Gurtin M (2007) Thermomechanics of the interface between a body and its environment. Contin Mech Thermodyn 19(5):253–271
Fried E, Todres R (2005) Mind the gap: the shape of the free surface of a rubber-like material in proximity to a rigid contactor. J Elast 80(1–3):97–151
Gurtin ME (2008) A theory of grain boundaries that accounts automatically for grain misorientation and grain-boundary orientation. J Mech Phys Solids 56(2):640–662
Gurtin ME, Murdoch AI (1975) A continuum theory of elastic material surfaces. Arch Ration Mech Anal 57(4):291–323
Gutman EM (1995) On the thermodynamic definition of surface stress. J Phys Condens Matter 7(48):L663
Han W, Reddy BD (2013) Plasticity mathematical theory and numerical analysis. Springer, New York
Huang ZP, Sun L (2007) Size-dependent effective properties of a heterogeneous material with interface energy effect: from finite deformation theory to infinitesimal strain analysis. Acta Mech 190(1–4):151–163
Javili A, McBride A, Steinmann P (2012) Numerical modelling of thermomechanical solids with mechanically energetic (generalised) Kapitza interfaces. Comput Mater Sci 65:542–551
Javili A, McBride A, Steinmann P (2013b) Numerical modelling of thermomechanical solids with highly conductive energetic interfaces. Int J Numer Methods Eng 93(5):551–574
Javili A, McBride A, Steinmann P (2013c) Thermomechanics of solids with lower-dimensional energetics: on the importance of surface, interface, and curve structures at the nanoscale. A unifying review. Appl Mech Rev 65(1):010802
Javili A, Steinmann P (2009) A finite element framework for continua with boundary energies. Part I: the two-dimensional case. Comput Methods Appl Mech Eng 198(27–29):2198–2208
Javili A, Steinmann P (2010a) A finite element framework for continua with boundary energies. Part II: the three-dimensional case. Comput Methods Appl Mech Eng 199(9–12):755–765
Javili A, Steinmann P (2010b) On thermomechanical solids with boundary structures. Int J Solids Struct 47(24):3245–3253
Johnson WC (2000) Superficial stress and strain at coherent interfaces. Acta Mater 48:433–444
Kaptay G (2005) Classification and general derivation of interfacial forces, acting on phases, situated in the bulk, or at the interface of other phases. J Mater Sci 40:2125–2131
Kramer D, Weissmüller J (2007) A note on surface stress and surface tension and their interrelation via Shuttleworths equation and the Lippmann equation. Surf Sci 601(14):3042–3051
Leo PH, Sekerka RF (1999) The effect of surface stress on crystal–melt and crystal–crystal equilibrium. Springer, Berlin, pp 176–195
Levitas VI, Javanbakht M (2010) Surface tension and energy in multivariant martensitic transformations: phase-field theory, simulations, and model of coherent interface. Phys Rev Lett 105(16):165701
Miller RE, Shenoy VB (2000) Size-dependent elastic properties of nanosized structural elements. Nanotechnology 11:139–147
Moeckel GP (1975) Thermodynamics of an interface. Arch Ration Mech Anal 57(3):255–280
Müller P, Saúl A (2004) Elastic effects on surface physics. Surf Sci Rep 54(5):157–258
Navti SE, Ravindran K, Taylor C, Lewis R (1997) Finite element modelling of surface tension effects using a Lagrangian–Eulerian kinematic description. Comput Methods Appl Mech Eng 147:41–60
Park HS, Klein PA (2007) Surface Cauchy–Born analysis of surface stress effects on metallic nanowires. Phys Rev B 75:085408
Rusanov AI (1996) Thermodynamics of solid surfaces. Surf Sci Rep 23:173–247
Saksono PH, Perić D (2006) On finite element modelling of surface tension: variational formulation and applications—part I: quasistatic problems. Comput Mech 38(3):265–281
Saksono PH, Perić D (2006) On finite element modelling of surface tension: variational formulation and applications—part II: dynamic problems. Comput Mech 38(3):251–263
Sharma P, Ganti S (2004) Size-dependent Eshelbys tensor for embedded nano-inclusions incorporating surface/interface energies. J Appl Mech 71(5):663–671
Sharma P, Ganti S, Bhate N (2003) Effect of surfaces on the size-dependent elastic state of nano-inhomogeneities. Appl Phys Lett 82(4):535–537
Sharma P, Wheeler LT (2007) Size-dependent elastic state of ellipsoidal nano-inclusions incorporating surface/interface tension. J Appl Mech 74(3):447–454
She H, Wang B (2009) A geometrically nonlinear finite element model of nanomaterials with consideration of surface effect. Finite Elem Anal Des 45:463–467
Simha NK, Bhattacharya K (1997) Equilibrium conditions at corners and edges of an interface in a multiphase solid. Mater Sci Eng A238:32–41
Simha NK, Bhattacharya K (1998) Kinetics of phase boundaries with edges and junctions. J Mech Phys Solid 46:2323–2359
Simo JC (1988a) A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition. part I: continuum formulation. Comput Methods Appl Mech Eng 66(2):199–219
Simo JC (1988b) A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition. Part II: computational aspects. Comput Methods Appl Mech Eng 68(1):1–31
Simo JC, Hughes TJR (1998) Computational inelasticity. Springer, New York
Simo JC, Meschke G (1993) A new class of algorithms for classical plasticity extended to finite strains. Application to geomaterials. Comput Mech 11(4):253–278
Steigmann DJ, Ogden RW (1999) Elastic surface–substrate interactions. Proc R Soc Lond A Math Phys Eng Sci 455(1982):437–474
Steinmann P (2008) On boundary potential energies in deformational and configurational mechanics. J Mech Phys Solids 56(3):772–800
Steinmann P, Häsner O (2005) On material interfaces in thermomechanical solids. Arch Appl Mech 75(1):31–41
Wei G, Shouwen Y, Ganyun H (2006) Finite element characterization of the sizedependent mechanical behaviour in nanosystems. Nanotechnology 17:1118–1122
Yang F (2006) Effect of interfacial stresses on the elastic behavior of nanocomposite materials. J Appl Phys 99:054306
Yvonnet J, Mitrushchenkov A, Chambaud G, He Q-C (2011) Finite element model of ionic nanowires with size-dependent mechanical properties determined by ab initio calculations. Comput Methods Appl Mech Eng 200(5–8):614–625
Yvonnet J, Quang HL, He QC (2008) An XFEM/level set approach to modelling surface/interface effects and to computing the size-dependent effective properties of nanocomposites. Comput Mech 42:119–131
Acknowledgements
The first author gratefully acknowledges the support by the Cluster of Excellence “Engineering of Advanced Materials”.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Convergence behavior
Appendix A: Convergence behavior
In this section we present some data on the convergence behavior of the computational problem at hand. The \(L_2\) norms of the residual of few increments for some of the cases discussed in Sect. 5 are given in Table 3.
Rights and permissions
About this article
Cite this article
Esmaeili, A., Steinmann, P. & Javili, A. Surface plasticity: theory and computation. Comput Mech 62, 617–634 (2018). https://doi.org/10.1007/s00466-017-1517-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-017-1517-x




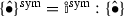 , where
, where 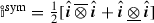 , for spatial second-order surface tensors. Its Material counterpart is defined as
, for spatial second-order surface tensors. Its Material counterpart is defined as