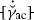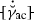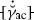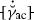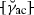Abstract
The implementation of novel material models in the microscale gives a deeper understanding of inner and intercrystalline effects of crystalline materials. For future works, this allows more precise predictions of macroscale models. Here, we present a finite gradient crystal plasticity theory which preserves the single crystal slip kinematics. However, the model is restricted to one gradient-stress, associated with the gradient of the accumulated plastic slip, in order to account for long range dislocation interactions in a physically simplified, numerically efficient approach. In order to model the interaction of dislocations with and their transfer through grain boundaries, a grain boundary yield condition is introduced. The grain boundary flow rule is evaluated at sharp interfaces using discontinuous trial functions in the finite element implementation, thereby allowing for a discontinuous distribution of the accumulated plastic slip. Simulations of crystal aggregates are performed under different loading conditions which reproduce well the size dependence of the yield strength. An analytical solution for a one-dimensional single slip supports the numerical results.












Similar content being viewed by others
Abbreviations
- \(\alpha \) :
-
Slip system index
- \(\beta \) :
-
Isotropic hardening contribution
- \(\dot{\gamma }_0\) :
-
Reference plastic slip rate
- \(\gamma _\alpha \) :
-
Plastic slip of system \(\alpha \)
- \(\dot{\gamma }_\alpha \) :
-
Plastic slip rate of system \(\alpha \)
- \(\gamma _\mathrm {ac}\) :
-
Accumulated plastic slip
- \(\breve{\gamma }_\mathrm {ac}\) :
-
Micromorphic accumulated plastic slip
-
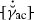 :
: -
Jump of micromorphic accumulated plastic slip rate
- \(\langle \dot{\breve{\gamma }}_{\mathrm {ac}} \rangle \) :
-
Mean value of micromorphic accumulated plastic slip rate
- \(\dot{\breve{\gamma }}_\mathrm {ac}^{+}\) :
-
Right-hand limit of micromorphic accumulated plastic slip rate
- \(\dot{\breve{\gamma }}_\mathrm {ac}^{-}\) :
-
Left-hand limit of micromorphic accumulated plastic slip rate
- \(\mathrm {\Gamma }\) :
-
Grain boundary
- \(\varTheta _{0}\) :
-
Initial hardening modulus
- \(\varTheta _{\infty }\) :
-
Asymptotic hardening modulus
- \(\varvec{\xi }\) :
-
Vector valued micromorphic stress
- \(\mathrm {\Xi }\) :
-
Micromorphic surface traction
- \(\mathrm {\Xi }^{\pm }\) :
-
Grain boundary micromorphic tractions
- \(\mathrm {\Xi }_{\mathrm {j}}\) :
-
Work conjugate micromorphic traction to
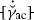
- \(\mathrm {\Xi }_{\mathrm {m}}\) :
-
Work conjugate micromorphic traction to \( \langle \dot{\breve{\gamma }}_{\mathrm {ac}} \rangle \)
- \(\mathrm {\Xi }_{\mathrm {j}}^{\mathrm {d}}\) :
-
Dissipative grain boundary micromorphic traction corresponding to
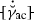
- \(\mathrm {\Xi }_{\mathrm {m}}^{\mathrm {d}}\) :
-
Dissipative grain boundary micromorphic traction corresponding to \( \langle \dot{\breve{\gamma }}_{\mathrm {ac}} \rangle \)
- \(\mathrm {\Xi }_{\mathrm {j}}^{\mathrm {e}}\) :
-
Energetic grain boundary micromorphic traction corresponding to
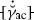
- \(\mathrm {\Xi }_{\mathrm {m}}^{\mathrm {e}}\) :
-
Energetic grain boundary micromorphic traction corresponding to \( \langle \dot{\breve{\gamma }}_{\mathrm {ac}} \rangle \)
- \(\pi \) :
-
Scalar micromorphic stress
- \(\rho _\alpha \) :
-
Dislocation density of system \(\alpha \)
- \(\varrho \) :
-
Mass density
- \(\varvec{\sigma }\) :
-
Cauchy stress
- \(\tau _\alpha \) :
-
Resolved shear stress of system \(\alpha \)
- \(\tau ^\mathrm {C}\) :
-
Critical resolved shear stress
- \(\tau ^\mathrm {C}_{0}\) :
-
Initial critical resolved yield stress
- \(\tau ^\mathrm {C}_{\infty }\) :
-
Asymptotic critical resolved yield stress
- \(\tau _\mathrm {D}\) :
-
Drag stress
- \(\varvec{\chi }\) :
-
Motion
- \(\psi \) :
-
Mass specific Helmholtz free energy
- b :
-
Absolute value of Burger’s vector
- \({\mathcal B}\) :
-
Material Body
- c :
-
Constant, dimension free parameter
- \(\varvec{ d}_\alpha \) :
-
Slip direction of system \(\alpha \)
- \(\partial {\mathcal B}_\mathrm {t}\) :
-
Neumann boundary corresponding to \( t \)
- \(\partial {\mathcal B}_\mathrm {\Xi }\) :
-
Neumann boundary corresponding to \( \mathrm {\Xi } \)
- \({\mathbb { C}}\) :
-
Forth-order elastic stiffness tensor
- \({\mathcal D}_\mathrm {tot}\) :
-
Total dissipation
- \({\mathcal D}_{\mathrm {B,red}}\) :
-
Reduced dissipation of the bulk material
- \({\mathcal D}_{\mathrm {\Gamma }}\) :
-
Dissipation of the grain boundaries
- \(\varvec{ E}_\mathrm {e}\) :
-
Elastic Green strain tensor
- \(f_\mathrm {\Gamma j}\) :
-
Grain boundary yield function related to
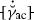
- \(f_\mathrm {\Gamma m}\) :
-
Grain boundary yield function related to \( \langle \dot{\breve{\gamma }}_{\mathrm {ac}} \rangle \)
- \(\varvec{ F}\) :
-
Deformation gradient
- \(\varvec{ F}_\mathrm {e}\) :
-
Elastic deformation gradient
- \(\varvec{ F}_\mathrm {p}\) :
-
Plastic deformation gradient
- G :
-
Shear modulus
- \(H_\chi \) :
-
Penalty factor
- J :
-
Determinant of the deformation gradient
- \(J_\mathrm {e}\) :
-
Determinant of the elastic deformation gradient
- \(k_1\) :
-
Storage coefficient
- \(k_2\) :
-
Dynamic recovery coefficient
- \(K_\mathrm {g}\) :
-
Defect energy parameter
- \(K_\mathrm {j}\) :
-
Material parameter corresponding to
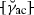
- \(K_\mathrm {m}\) :
-
Material parameter corresponding to \( \langle {\breve{\gamma }}_{\mathrm {ac}} \rangle \)
- \(\varvec{ L}\) :
-
Velocity gradient
- \(\varvec{ L}_\mathrm {p}\) :
-
Distortion rate tensor
- \(\varvec{ n}\) :
-
Outward pointing unit normal vector
- \(\varvec{ n}_\alpha \) :
-
Slip plane normal of system \(\alpha \)
- \(\varvec{ n}_{\mathrm {\Gamma }}\) :
-
Normal vector of the grain boundary
- N :
-
Number of slip systems
- \(\breve{p}\) :
-
Generalized relative stress
- \({\mathcal P}_\mathrm {ext}\) :
-
External power
- \({\mathcal P}_\mathrm {int}\) :
-
Internal power
- \(\varvec{ R}_\mathrm {e}\) :
-
Lattice rotation
- \(\varvec{ S}\) :
-
Second Piola-Kirchhoff stress
- t :
-
Time
- \(\varvec{ t}\) :
-
Surface traction
- \(\varvec{ u}\) :
-
Displacement vector
- \(\varvec{ U}_\mathrm {e}\) :
-
Lattice stretch
- \(\varvec{ v}\) :
-
Velocity vector
- \(v_\alpha \) :
-
Averaged dislocation velocity of system \(\alpha \)
- \(W_\mathrm {e}\) :
-
Elastic contribution to the free energy density
- \(W_\mathrm {g}\) :
-
Gradient contribution to the free energy density
- \(W_\mathrm {h}\) :
-
Isotropic hardening contribution to the free energy density
- \(W_\mathrm {\Gamma }\) :
-
Free energy density of the grain boundaries
- \(W_\chi \) :
-
Numerical penalty contribution to the free energy density
- \(\varvec{ x}\) :
-
Position vector of a material point in current configuration
- \(\varvec{ X}\) :
-
Position vector of a material point in reference configuration
References
Orowan E (1934) Zur Kristallplastizität. III. Z Phys 89(9):634
Polanyi M (1934) Über eine Art Gitterstörung, die einen Kristall plastisch machen könnte. Z Phys 89(9):660
Taylor GI (1934) The mechanism of plastic deformation of crystals. Part I. Theoretical. Proc R Soc Lond A Math Phys Eng Sci 145(855):362
Schmid E, Boas W (1935) Kristallplastizität, mit besonderer Berücksichtigung der Metalle. Springer, Berlin
Bishop J, Hill R (1951) A theory of the plastic distortion of a polycrystalline aggregate under combined stresses. Lond Edinb Dublin Philos Mag J Sci 42(327):414
Hill R (1966) Generalized constitutive relations for incremental deformation of metal crystals by multislip. J Mech Phys Solids 14(2):95
Armstrong R, Codd I, Douthwaite RM, Petch NJ (1962) The plastic deformation of polycrystalline aggregates. Philos Mag 7(73):45
Conrad H, Feuerstein S, Rice L (1967) Effects of grain size on the dislocation density and flow stress of niobium. Mater Sci Eng 2(3):157
Estrin Y, Tóth L, Molinari A, Bréchet Y (1998) A dislocation-based model for all hardening stages in large strain deformation. Acta Mater 46(15):5509
Kocks U, Mecking H (2003) Physics and phenomenology of strain hardening: the FCC case. Prog Mater Sci 48(3):171
Hall EO (1951) The deformation and ageing of mild steel: III discussion of results. Proc Phys Soc Sect B 64(9):747
Petch NJ (1953) The cleavage strength of polycrystals. J Iron Steel Inst 174:25
Eshelby J, Frank F, Nabarro F (1951) The equilibrium of linear arrays of dislocations. Lond Edinb Dublin Philos Mag J Sci 42(327):351
Ashby MF (1970) The deformation of plastically non-homogeneous materials. Philos Mag 21(170):399
Thompson AW, Baskes MI, Flanagan WF (1973) The dependence of polycrystal work hardening on grain size. Acta Metall 21(7):1017
Nye J (1953) Some geometrical relations in dislocated crystals. Acta Metall 1(2):153
Cermelli P, Gurtin ME (2001) On the characterization of geometrically necessary dislocations in finite plasticity. J Mech Phys Solids 49(7):1539
Aifantis E (1987) The physics of plastic deformation. Int J Plast 3:211
Forest S, Guéninchault N (2013) Inspection of free energy functions in gradient crystal plasticity. Acta Mech Sin 29(6):763
Fleck N, Muller G, Ashby M, Hutchinson J (1994) Strain gradient plasticity: theory and experiment. Acta Metall Mater 42(2):475
Gurtin ME (2000) On the plasticity of single crystals: free energy, microforces, plastic-strain gradients. J Mech Phys Solids 48(5):989
Menzel A, Steinmann P (2000) On the continuum formulation of higher gradient plasticity for single and polycrystals. J Mech Phys Solids 48(8):1777
Gurtin ME, Anand L (2005) A theory of strain-gradient plasticity for isotropic, plastically irrotational materials. Part I: small deformations. J Mech Phys Solids 53(7):1624
Ohno N, Okumura D (2007) Higher-order stress and grain size effects due to self-energy of geometrically necessary dislocations. J Mech Phys Solids 55(9):1879
Gurtin ME (2008) A finite-deformation, gradient theory of single-crystal plasticity with free energy dependent on densities of geometrically necessary dislocations. Int J Plast 24(4):702
Miehe C (2011) A multi-field incremental variational framework for gradient-extended standard dissipative solids. J Mech Phys Solids 59(4):898
Wulfinghoff S, Böhlke T (2013) Equivalent plastic strain gradient crystal plasticity-enhanced power law subroutine. GAMM Mitt 36(2):134
Bayerschen E, Stricker M, Wulfinghoff S, Weygand D, Böhlke T (2015) Equivalent plastic strain gradient plasticity with grain boundary hardening and comparison to discrete dislocation dynamics. In: Proceedings of the Royal Society of London a: mathematical, physical and engineering sciences, vol 471, p 2184
Begau C, Sutmann G, Hartmaier A (2015) Free energy function of dislocation densities by large scale atomistic simulation. arXiv:1512.02845
Jones R, Zimmerman J, Po G (2016) Comparison of dislocation density tensor fields derived from discrete dislocation dynamics and crystal plasticity simulations of torsion. arXiv:1608.04335
Bittencourt E, Needleman A, Gurtin M, Giessen E (2003) A comparison of nonlocal continuum and discrete dislocation plasticity predictions. J Mech Phys Solids 51(2):281
Forest S (2009) Micromorphic approach for gradient elasticity, viscoplasticity and damage. J Eng Mech 135:117
Eringen AC, Suhubi E (1964) Nonlinear theory of simple micro-elastic solids-I. Int J Eng Sci 2(2):189
Mindlin RD (1964) Micro-structure in linear elasticity. Arch Ration Mech Anal 16(1):51
Reddy B, Wieners C, Wohlmuth B (2012) Finite element analysis and algorithms for single-crystal strain-gradient plasticity. Int J Numer Methods Eng 90(6):784
Wulfinghoff S, Böhlke T (2012) Equivalent plastic strain gradient enhancement of single crystal plasticity: theory and numerics. In: Proceedings of the Royal Society A (The Royal Society, 2012), vol 468, pp 2682–2703
Wulfinghoff S, Bayerschen E, Böhlke T (2013) A gradient plasticity grain boundary yield theory. Int J Plast 51:33
Fredriksson P, Gudmundson P (2005) Size-dependent yield strength of thin films. Int J Plast 21(9):1834
Gurtin ME, Needleman A (2005) Boundary conditions in small-deformation, single-crystal plasticity that account for the Burgers vector. J Mech Phys Solids 53(1):1
Gurtin ME (2008) A theory of grain boundaries that accounts automatically for grain misorientation and grain-boundary orientation. J Mech Phys Solids 56(2):640
Özdemir İ, Yalçinkaya T (2014) Modeling of dislocation-grain boundary interactions in a strain gradient crystal plasticity framework. Comput Mech 54(2):255
Gottschalk D, McBride A, Reddy B, Javili A, Wriggers P, Hirschberger C (2016) Computational and theoretical aspects of a grain-boundary model that accounts for grain misorientation and grain-boundary orientation. Comput Mater Sci 111:443
Lee T, Robertson I, Birnbaum H (1990) TEM in situ deformation study of the interaction of lattice dislocations with grain boundaries in metals. Philos Mag A 62(1):131
Moës N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Methods Eng 46(1):131
Belytschko T, Moës N, Usui S, Parimi C (2001) Arbitrary discontinuities in finite elements. Int J Numer Methods Eng 50(4):993
Fries TP, Belytschko T (2010) The extended/generalized finite element method: an overview of the method and its applications. Int J Numer Methods Eng 84(3):253
Bertram A (2008) Plasticity. Springer, Berlin
Palm JH (1951) Stress-strain relations for uniform monotonic deformation under triaxial loading. Appl Sci Res 2(1):54
Bayerschen E (2017) Single-crystal gradient plasticity with an accumulated plastic slip: theory and applications. Ph.D. thesis, Karlsruhe Institute for Technologie (KIT), Karlsruhe
Cermelli P, Gurtin ME (2002) Geometrically necessary dislocations in viscoplastic single crystals and bicrystals undergoing small deformations. Int J Solids Struct 39(26):6281
Reddy BD (2011) The role of dissipation and defect energy in variational formulations of problems in strain-gradient plasticity. Part 2: single-crystal plasticity. Contin Mech Thermodyn 23(6):551
Bayerschen E, Böhlke T (2016) Power-law defect energy in a single-crystal gradient plasticity framework: a computational study. Comput Mech 58(1):13
Bayley C, Brekelmans W, Geers M (2006) A comparison of dislocation induced back stress formulations in strain gradient crystal plasticity. Int J Solids Struct 43(24):7268
Simone A, Duarte CA, Van der Giessen E (2006) A Generalized Finite Element Method for polycrystals with discontinuous grain boundaries. Int J Numer Methods Eng 67(8):1122
Osher S, Fedkiw RP (2001) Level set methods: an overview and some recent results. J Comput Phys 169(2):463
Barenblatt GI (1959) The formation of equilibrium cracks during brittle fracture: general ideas and hypotheses. J Appl Math Mech 23(3):622
Dugdale DS (1960) Yielding of steel sheets containing slits. J Mech Phys Solids 8(2):100
Gurtin ME, Anand L (2008) Nanocrystalline grain boundaries that slip and separate: a gradient theory that accounts for grain-boundary stress and conditions at a triple-junction. J Mech Phys Solids 56(1):184
Aifantis K, Soer W, Hosson JD, Willis J (2006) Interfaces within strain gradient plasticity: theory and experiments. Acta Mater 54(19):5077
Aifantis K, Ngan A (2007) Modeling dislocation-grain boundary interactions through gradient plasticity and nanoindentation. Mater Sci Eng A 459(12):251.
Yang B, Motz C, Rester M, Dehm G (2012) Yield stress influenced by the ratio of wire diameter to grain size—a competition between the effects of specimen microstructure and dimension in micro-sized polycrystalline copper wires. Philos Mag 92(25–27):3243
Acknowledgements
The support of the German Research Foundation (DFG) of the project “Process chains in sheet metal manufacturing” of the DFG Research Group 1483 is gratefully acknowledged, as well as the partial support of the DFG Research Group 1650 “Dislocation based Plasticity”.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Derivation of field equations
The application of the chain rule and Gauss’ theorem on the contributions of the virtual mechanical energy balance (cf. Eq. 13), yields

and for the micromorphic contribution

1.2 Transformation of internal power contributions
The power of the internal forces is formulated with respect to the current placement (cf. Eq. 11). A transformation of the individual contributions to the reference placement is performed.
The transformation of the contribution of the Cauchy stress \( \varvec{\sigma } \) yields
The contribution of the scalar micromorphic stress \( \pi \) is transformed
as well as the contribution of the vector valued micromorphic stress \( \varvec{\xi } \)
Finally, the transformation of the internal forces on the grain boundaries, meaning the grain boundary micromorphic tractions \( {\Xi }_{\mathrm {j}} \) and \( {\Xi }_{\mathrm {m}} \), yields

1.3 Details on the global Newton algorithm
We build the scalar product of the balance of linear momentum (cf. Eq. 15) with a trial function \( \delta \underline{w}^{u} = \underline{\underline{N}}^{u} ~\hat{\underline{w}} \) and integrate over an arbitrary volume \( {\mathcal B} \)
Hereby, the matrix of shape function gradients \( \underline{\underline{B}} \) was introduced. Furthermore, we use the micromorphic field equation, the grain boundary condition and the grain boundary yield condition (cf. Eqs. 15 and 37), and the trial function \( \delta w^{\gamma } = \underline{N}^{\gamma } ~\hat{\underline{w}} \)
where \( {\Gamma }_\mathrm {act} \) denotes the plastically active part of the grain boundaries. By using Eqs. (15) and (37) with the trial function \( \delta w^{\delta } = \underline{N}^{\delta } ~\hat{\underline{w}} \), the shape function enrichment results in an additional equation
The total derivatives of Eqs. (81)–(83) read in matrix-vector notation
The entries of the global algorithmic tangent are
1.4 Details on the convergence
In Fig. 13 the results of the convergence study are shown. The loading case as well as the material parameters were chosen in the manner of the comparison to the analytical solution with a grain rotation angle of \( \varphi _{x}=45\,\mathrm{^{\circ }} \). Hereby, the mesh discretization was varied by using 400, 600, 800, 1000 and 1200 Elements.
Rights and permissions
About this article
Cite this article
Erdle, H., Böhlke, T. A gradient crystal plasticity theory for large deformations with a discontinuous accumulated plastic slip. Comput Mech 60, 923–942 (2017). https://doi.org/10.1007/s00466-017-1447-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-017-1447-7





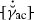 :
: