A preconditioner for the finite element computation of incompressible, nonlinear elastic deformations

Abstract

Large, incompressible elastic deformations are governed by a system of nonlinear partial differential equations. The finite element discretisation of these partial differential equations yields a system of nonlinear algebraic equations that are usually solved using Newton’s method. On each iteration of Newton’s method, a linear system must be solved. We exploit the structure of the Jacobian matrix to propose a preconditioner, comprising two steps. The first step is the solution of a relatively small, symmetric, positive definite linear system using the preconditioned conjugate gradient method. This is followed by a small number of multigrid V-cycles for a larger linear system. Through the use of exemplar elastic deformations, the preconditioner is demonstrated to facilitate the iterative solution of the linear systems arising. The number of GMRES iterations required has only a very weak dependence on the number of degrees of freedom of the linear systems.

1 Introduction

Incompressible, nonlinear elasticity has been used as a mathematical model underpinning several applications; see, for example, [1,2,3,4,5,6]. The system of partial differential equations describing this model are often solved numerically using the finite element method [7,8,9,10,11,12,13]. One step in the practical computation of the finite element approximation is the solution of a system of nonlinear algebraic equations, often containing a large number of degrees of freedom. These algebraic equations are usually solved using Newton’s method, requiring the solution of an equally large linear system of algebraic equations on each iteration of Newton’s method.

Should the number of degrees of freedom of a linear system of algebraic equations be sufficiently large, it is not feasible to solve the system using direct methods such as LU factorisation. For linear systems such as this an iterative solution method is usually employed. The choice of iterative method depends on the properties of the linear system being solved. For example, should the linear system be described by a matrix that is symmetric and positive definite, then the conjugate gradient method is an appropriate choice of iterative technique [14]. In this study we will be concerned with the linear systems that arise when using Newton’s method to compute a finite element solution of the equations governing incompressible, nonlinear elasticity. As we will see later, the matrices arising in this context do have a particular structure which we will exploit. However, they are not symmetric or positive definite, and so we may not solve these systems using the conjugate gradient method. Instead we use the Generalised Minimal RESidual (GMRES) method, the iterative method of choice for general linear systems; see, for example, [14].

Convergence of iterative schemes may often be dramatically accelerated using a preconditioner; see the review [15] and references therein. In this study we propose a preconditioner for the linear systems that arise when using Newton’s method to compute the finite element solution to the equations governing large deformation, incompressible elasticity. The key observation is that the (nonlinear) incompressibility constraint may be handled by a preconditioner in a similar way to that for the incompressibility constraint arising from Stokes equations [16,17,18,19]. Indeed, the equations governing isotropic, incompressible, small deformation (linear) elasticity are identical to Stokes equations [8]. In the limit that an elastic deformation is sufficiently small, the preconditioner proposed in this study is identical to that used for Stokes equations. The resulting preconditioner may be decomposed into two steps. The first step requires the solution of a relatively small linear system, governed by a matrix that is a mass matrix arising from the finite element method. This matrix is symmetric and positive definite, and the resulting linear system may be solved very efficiently using the preconditioned conjugate gradient method [20]. The second step is the application of a small number of multigrid cycles of a larger system; such an approach has been demonstated to be a very effective preconditioner for the GMRES iterative solver [21, 22].

We note that some authors have successfully used a nonlinear version of multigrid, rather than Newton’s method, to solve the nonlinear algebraic equations arising from discretisations of other nonlinear elliptic partial differential equations; see, for example, [23,24,25]. We shall discuss later the application of the nonlinear multigrid method to the nonlinear systems of equations arising in this study.

This paper is structured as follows. We write down the equations governing large deformation, incompressible elastic deformations in Sect. 2. We then briefly summarise a finite element method for computing the numerical solution of these equations in Sect. 3, paying particular attention to the nonlinear system of algebraic equations that arises, and the linear systems that must be solved when using Newton’s method to solve these equations. The main contribution of this study—the development of a preconditioner for these linear systems—is given Sect. 4. We then use exemplar deformations to demonstrate the use of this preconditioner in Sect. 5, before presenting our conclusions in Sect. 6.

2 The governing equations

We give only a brief summary of the governing equations in this section. For a more detailed discussion see, for example, [1]. Let $\mathbf {X}$ denote the coordinates of an undeformed, incompressible body that occupies a bounded region $\varOmega \subset \mathfrak {R}^{d}$ where d is the number of spatial dimensions. If $d=2$ we write $\mathbf {X}=\left( X_{1},X_{2}\right) ^{\top }$, and if $d=3$ we write $\mathbf {X}=\left( X_{1},X_{2},X_{3}\right) ^{\top }$; we will use the same convention for other vectors and their components. Denoting the coordinates of the deformed body by $\mathbf {x}$, the deformation gradient tensor F has entries defined by

$$\begin{aligned} F_{iM} = \frac{\partial x_{i}}{\partial X_{M}}, \qquad i,M=1,\ldots ,d, \end{aligned}$$

where we have followed the convention of writing indices associated with the undeformed body in upper case, and indices associated with the deformed body in lower case. Incompressible, elastic deformations are then governed by, for $\mathbf {X} \in \varOmega$:

$$\begin{aligned} \frac{\partial S_{Mi}}{\partial X_{M}} + \rho g_{i}= & {} 0, \qquad i=1,\ldots ,d, \end{aligned}$$

(1)

$$\begin{aligned} \det F= & {} 1, \end{aligned}$$

(2)

where S is the first Piola–Kirchhoff stress tensor, $\mathbf {g}$ is the body force per unit mass, $\rho$ is the constant density of the incompressible body, and we have used the summation convention (and will do so throughout this study). We partition the boundary into one component $\partial \varOmega _{D}$ where Dirichlet (displacement) boundary conditions are applied, and a second component $\partial \varOmega _{N}$ where Neumann (traction) boundary conditions are applied. Boundary conditions are then given by

$$\begin{aligned}&x_{i} = x_{i}^{0},&\qquad i&=1,\ldots ,d,&\qquad \mathbf {X}&\in \partial \varOmega _{D}, \end{aligned}$$

(3)

$$\begin{aligned}&S_{Mi}N_{M} = s_{i}^{0},&\qquad i&=1,\ldots ,d,&\qquad \mathbf {X}&\in \partial \varOmega _{N}, \end{aligned}$$

(4)

where $x_{i}^{0},s_{i}^{0}, i=1,\ldots ,d$, are given functions, and $\mathbf {N}$ is the outward pointing unit normal to the undeformed body.

Finally, we require a constitutive relation to specify S. We assume that the body is hyperelastic, and hence that there exists a strain energy density function W such that

$$\begin{aligned} S_{Mi} = \frac{\partial W}{\partial F_{iM}} - p \det (F) F_{Mi}^{-1}, \qquad M,i=1,\ldots ,d, \end{aligned}$$

(5)

where p is the Lagrange multiplier that is used to enforce the incompressibility constraint given by Eq. (2). We have kept the factor of $\det (F)$ in the definition of the first Piola–Kirchhoff stress tensor in Eq. (5) even though the incompressibility constraint given by Eq. (2) may be used to set $\det (F)=1$; persisting with this term will allow us to demonstrate more clearly the structure of the Jacobian matrix that arises when solving the resulting nonlinear algebraic equations using Newton’s method.

3 The finite element scheme

We will calculate a numerical solution of the governing equations using the finite element method described by Whiteley and Tavener [13]. In this section we first briefly summarise this scheme. We then write down the nonlinear algebraic system of equations that arises from this finite element discretisation. This allows us to identify the structure of the Jacobian matrix that arises when solving these nonlinear equations using Newton’s method, and hence to propose a suitable preconditioner for the solution of the linear system embedded within each Newton iteration.

3.1 Mathematical preliminaries

Defining $L_{2}(\varOmega )$ to be the space of square integrable functions on $\varOmega$, i.e.:

$$\begin{aligned} L_{2}(\varOmega ) = \left\{ v : \int _{\varOmega }v^{2}~\mathrm{d}V < \infty \right\} , \end{aligned}$$

we may define the Sobolev space $H^{1}(\varOmega )$ and some subsets of this space by

$$\begin{aligned} H^{1} (\varOmega )= & {} \bigg \{ v \in L_{2}(\varOmega ) : \frac{\partial v}{\partial X_{M}} \in L_{2}(\varOmega ), \\&M=1,\ldots ,d \bigg \}, \\ H^{1}_{E}(\varOmega )= & {} \big \{ v \in H^{1}(\varOmega ) : v~\text {satisfies Dirichlet boundary} \\&\text {conditions} \big \}, \\ H^{1}_{E_{0}}(\varOmega )= & {} \left\{ v \in H^{1}(\varOmega ) : v=0~\text {for}~\mathbf {X} \in \partial \varOmega _{D} \right\} . \end{aligned}$$

We assume that the domain $\varOmega$ has been partitioned into a mesh $\mathcal{T}^{h}$ of quadrilateral elements if the equations are posed in two dimensions, or a mesh of hexahedral elements if the equations are posed in three dimensions, and that there are no hanging nodes in the mesh. We then define $Q^{k}(\varOmega ,\mathcal{T}^{h})$ to be the set of continuous functions that are tensor product polynomials of degree k in each coordinate direction on each element when the element is mapped to the unit square (in two dimensions) or the unit cube (in three dimensions). We will require the following subspaces of $Q^{k}(\varOmega ,\mathcal{T}^{h})$:

$$\begin{aligned} Q^{k}_{E}(\varOmega ,\mathcal{T}^{h})= & {} \big \{ v \in Q^{k}(\varOmega ,\mathcal{T}^{h}) : v~\text {satisfies Dirichlet} \\&\text {boundary conditions} \big \}, \\ Q^{k}_{E_{0}}(\varOmega ,\mathcal{T}^{h})= & {} \left\{ v \in Q^{k}(\varOmega ,\mathcal{T}^{h}) : v=0~\text {for}~\mathbf {X} \in \partial \varOmega _{D} \right\} . \end{aligned}$$

3.2 The weak solution and finite element approximation

Before writing down the finite element solution we first write down the weak solution of the governing equations. Defining $\hat{\mathbf {x}}, \hat{\mathbf {v}}$ by

$$\begin{aligned} \hat{\mathbf {x}} = \begin{pmatrix} \mathbf {x} \\ p \end{pmatrix}, \qquad \hat{\mathbf {v}} = \begin{pmatrix} \mathbf {v} \\ q \end{pmatrix}, \end{aligned}$$

the weak solution of Eqs. (1) and (2), subject to the boundary conditions Eqs. (3) and (4), may be written [13]: find $\hat{\mathbf {x}} \in \left[ H_{E}^{1}(\varOmega ) \right] ^{d} \times L_{2}(\varOmega )$ such that, for all $\hat{\mathbf {v}} \in \left[ H_{E_{0}}^{1}(\varOmega ) \right] ^{d} \times L_{2}(\varOmega )$,

$$\begin{aligned} A(\hat{\mathbf {x}}, \hat{\mathbf {v}}) = L(\hat{\mathbf {v}}), \end{aligned}$$

(6)

where

$$\begin{aligned} A(\hat{\mathbf {x}}, \hat{\mathbf {v}})= & {} \int _{\varOmega } S_{Mi} \frac{\partial v_{i}}{\partial X_{M}} - q \det F~\mathrm{d}V, \end{aligned}$$

(7)

$$\begin{aligned} L(\hat{\mathbf {v}})= & {} \int _{\varOmega } \rho g_{i} v_{i} - q~\mathrm{d}V + \int _{\partial \varOmega _{N}} s_{i}^{0} v_{i}~\mathrm{d}S. \end{aligned}$$

(8)

We note that the definition of $A(\cdot ,\cdot )$ and $L(\cdot )$ in Eqs. (7) and (8) differs very slightly from that used in [13] through q being replaced by $-q$. This has the effect of multiplying the discretisation of the constraint Eq. (2) used in [13] by a factor of $-1$, and will allow us to write the Jacobian matrices arising from Newton’s method in a more convenient form.

The finite element solution follows a similar pattern to the weak solution. Defining $\hat{\mathbf {x}}^{h}, \hat{\mathbf {v}}^{h}$ by

$$\begin{aligned} \hat{\mathbf {x}}^{h} = \begin{pmatrix} \mathbf {x}^{h} \\ p^{h} \end{pmatrix}, \qquad \hat{\mathbf {v}}^{h} = \begin{pmatrix} \mathbf {v}^{h} \\ q^{h} \end{pmatrix}, \end{aligned}$$

the finite element solution of Eqs. (1) and (2), subject to the boundary conditions Eqs. (3) and (4), is given by: find $\hat{\mathbf {x}}^{h} \in \left[ Q_{E}^{k}(\varOmega ,\mathcal{T}^{h}) \right] ^{d} \times Q^{k-1}(\varOmega ,\mathcal{T}^{h})$ such that, for all $\hat{\mathbf {v}}^{h} \in \left[ Q_{E_{0}}^{k}(\varOmega ,\mathcal{T}^{h}) \right] ^{d} \times Q^{k-1}(\varOmega ,\mathcal{T}^{h})$,

$$\begin{aligned} A(\hat{\mathbf {x}}^{h}, \hat{\mathbf {v}}^{h}) = L(\hat{\mathbf {v}}^{h}), \end{aligned}$$

(9)

where k is an integer greater than or equal to 2.

3.3 Computation of the finite element solution using Newton’s method

Let $\phi _{j}(\mathbf {X})$, $j=1,2,\ldots ,N_{x}$, be a basis for the space $Q^{k}(\varOmega ,\mathcal{T}^{h})$, where k is an integer greater than or equal to 2, and let $\psi _{j}(\mathbf {X})$, $j=1,2,\ldots ,N_{p}$, be a basis for the space $Q^{k-1}(\varOmega ,\mathcal{T}^{h})$. Writing

$$\begin{aligned} x_{i}^{h}= & {} \sum _{j=1}^{N_{x}} x_{i,j}^{h} \phi _{j}(\mathbf {X}), \qquad i=1,\ldots ,d, \\ p^{h}= & {} \sum _{j=1}^{N_{p}} p_{j} \psi _{j}(\mathbf {X}), \end{aligned}$$

and substituting these expressions into Eq. (9), the finite element solution satisfies a nonlinear system of algebraic equations that we write as

$$\begin{aligned} \mathbf {R}(\mathbf {x}^{h},p^{h}) = \mathbf {0}. \end{aligned}$$

To solve this nonlinear system of algebraic equations using Newton’s method we need to compute both the residual $\mathbf {R}$ and the Jacobian matrix J arising on each Newton iteration. We now write down explicit expressions for both the residual and Jacobian in two dimensions. These expressions may easily be generalised into three dimensions.

We order the entries of $\mathbf {R}$ so that, for $k=1,2,\ldots ,N_{x}$,

$$\begin{aligned} R_{k}(\mathbf {x}^{h},p^{h})= & {} A\left( \hat{\mathbf {x}}^{h}, \begin{pmatrix} \phi _{k}^{h} \\ 0 \\ 0 \end{pmatrix} \right) - L\left( \begin{pmatrix} \phi _{k}^{h} \\ 0 \\ 0 \end{pmatrix} \right) \nonumber \\= & {} \int _{\varOmega } S_{M1} \frac{\partial \phi _{k}}{\partial X_{M}} - \rho g_{1} \phi _{k}~\mathrm{d}V\nonumber \\&- \int _{\partial \varOmega _{N}} s_{1}^{0} \phi _{k}~\mathrm{d}S, \end{aligned}$$

(10)

$$\begin{aligned} R_{k+N_{x}}(\mathbf {x}^{h},p^{h})= & {} A\left( \hat{\mathbf {x}}^{h}, \begin{pmatrix} 0 \\ \phi _{k}^{h} \\ 0 \end{pmatrix} \right) - L\left( \begin{pmatrix} 0 \\ \phi _{k}^{h} \\ 0 \end{pmatrix} \right) \nonumber \\= & {} \int _{\varOmega } S_{M2} \frac{\partial \phi _{k}}{\partial X_{M}} - \rho g_{2} \phi _{k}~\mathrm{d}V\nonumber \\&- \int _{\partial \varOmega _{N}} s_{2}^{0} \phi _{k}~\mathrm{d}S, \end{aligned}$$

(11)

and, for $k=1,2,\ldots ,N_{p}$,

$$\begin{aligned} R_{k+2N_{x}}= & {} A\left( \hat{\mathbf {x}}^{h}, \begin{pmatrix} 0 \\ 0 \\ \psi _{k}^{h} \end{pmatrix} \right) - L\left( \begin{pmatrix} 0 \\ 0 \\ \psi _{k}^{h} \end{pmatrix} \right) \nonumber \\= & {} \int _{\varOmega } \psi _{k}^{h} \left( 1 - \det (F) \right) ~\mathrm{d}V. \end{aligned}$$

(12)

The unknowns are ordered so that

$$\begin{aligned} \hat{\mathbf {x}}^{h} \!= \!\begin{pmatrix} x_{1,1}^{h}, x_{1,2}^{h},\ldots , x_{1,N_{x}}^{h}, x_{2,1}^{h},\ldots , x_{2,N_{x}}^{h}, p_{1}^{h},\ldots ,p_{N_{p}}^{h} \end{pmatrix}^{\top }. \end{aligned}$$

On using the identity

$$\begin{aligned} \frac{\partial }{\partial F_{kM}} \left( \det (F) \right) = \det (F) F^{-1}_{Mk}, \qquad k,M=1,\ldots ,d, \end{aligned}$$

we see that the Jacobian matrix J is given by

$$\begin{aligned} J= & {} \begin{pmatrix} A &{} B^{\top } \\ B &{} 0 \end{pmatrix}, \end{aligned}$$

(13)

where

$$\begin{aligned} A= & {} \begin{pmatrix} A^{11} &{} A^{12} \\ A^{21} &{} A^{22} \end{pmatrix}, \\ B= & {} \begin{pmatrix} B^{11}&B^{12} \end{pmatrix}, \end{aligned}$$

$A^{11},A^{12},A^{21},A^{22}$ are $N_{x} \times N_{x}$ matrices with entries, for $k,j=1,2,\ldots ,N_{x}$, given by

$$\begin{aligned} A^{11}_{k,j}= & {} \int _{\varOmega } \frac{\partial S_{M1}}{\partial x_{1,j}} \frac{\partial \phi _{k}}{\partial X_{M}}~\mathrm{d}V, \\ A^{12}_{k,j}= & {} \int _{\varOmega } \frac{\partial S_{M1}}{\partial x_{2,j}} \frac{\partial \phi _{k}}{\partial X_{M}}~\mathrm{d}V, \\ A^{21}_{k,j}= & {} \int _{\varOmega } \frac{\partial S_{M2}}{\partial x_{1,j}} \frac{\partial \phi _{k}}{\partial X_{M}}~\mathrm{d}V, \\ A^{22}_{k,j}= & {} \int _{\varOmega } \frac{\partial S_{M2}}{\partial x_{2,j}} \frac{\partial \phi _{k}}{\partial X_{M}}~\mathrm{d}V, \end{aligned}$$

and $B^{11},B^{12}$ are $N_{p} \times N_{x}$ matrices with entries given by, for $k=1,2,\ldots ,N_{p}$, $j=1,2,\ldots ,N_{x}$,

$$\begin{aligned} B^{11}_{k,j}= & {} - \int _{\varOmega } \psi _{k} \det (F) F^{-1}_{M1} \frac{\partial \phi _{j}}{\partial X_{M}}~\mathrm{d}V, \\ B^{12}_{k,j}= & {} - \int _{\varOmega } \psi _{k} \det (F) F^{-1}_{M2} \frac{\partial \phi _{j}}{\partial X_{M}}~\mathrm{d}V. \end{aligned}$$

Note that the expressions above for the matrices $A^{11}$, $A^{12}$, $A^{21}$, $A^{22}$ allow us to deduce that the matrix A appearing in Eq. (13) is not symmetric, and hence that J is not symmetric.

When using multigrid we are required to specify a relaxation for the linear system. The most common choice of relaxation is the Gauss–Seidel relaxation, which assumes that the matrix is diagonally dominant. However we see in Eq. (13) that the Jacobian matrix has a zero block on the diagonal, and so cannot possibly be diagonally dominant. Similar difficulties would be encountered should we attempt to use the nonlinear multigrid method to solve this system of algebraic equations. Fortunately linear systems with the structure of the Jacobian may avoid this problem by the use of a suitable preconditioner that we now describe.

4 The preconditioner

In the spirit of [26, 27] we note that the Jacobian matrix given by Eq. (13) may be factorised as

$$\begin{aligned} J = \begin{pmatrix} I &{} 0 \\ BA^{-1} &{} I \end{pmatrix} \begin{pmatrix} A &{} B^{\top } \\ 0 &{} -BA^{-1}B^{\top } \end{pmatrix}. \end{aligned}$$

(14)

Hence, if we define

$$\begin{aligned} \mathcal{P} = \begin{pmatrix} A &{} B^{\top } \\ 0 &{} -BA^{-1}B^{\top } \end{pmatrix}, \end{aligned}$$

we may write Eq. (14) as

$$\begin{aligned} J \mathcal{P}^{-1} = \begin{pmatrix} I &{} 0 \\ BA^{-1} &{} I \end{pmatrix}. \end{aligned}$$

As the matrix $J \mathcal{P}^{-1}$ has only one eigenvalue (the value 1) we may deduce that, if we were able to explicitly calculate the action of $\mathcal{P}^{-1}$ on a vector, then the GMRES method would converge in at most one iteration using $\mathcal{P}$ as a right preconditioner. Unfortunately, calculating the action of $\mathcal{P}^{-1}$ on a vector requires calculation of $A^{-1}$, which is not feasible other than for problems with very few unknowns. Instead, we construct a right preconditioner $\mathcal{P}_{h}$ that is an approximation to $\mathcal P$.

We have already noted that the equations governing small–deformation (linear) incompressible elasticity are identical to Stokes equations. For the finite element discretisation of Stokes equations, the Schur complement $BA^{-1}B^{\top }$ that appears in $\mathcal{P}$ is spectrally equivalent to the the mass matrix in the pressure space [28], i.e. the matrix M with entries given by, for $i,j=1,2,\ldots ,N_{p}$,

$$\begin{aligned} M_{ij} = \int _{\varOmega } \psi _{i}(\mathbf {X}) \psi _{j}(\mathbf {X})~\mathrm{d}V. \end{aligned}$$

We therefore define our approximate preconditioner by

$$\begin{aligned} \mathcal{P}_{h} = \begin{pmatrix} A_{h} &{} B^{\top } \\ 0 &{} -M \end{pmatrix}, \end{aligned}$$

where $A_{h}^{-1}$ is an approximation to $A^{-1}$ that will be discussed later.

To use $\mathcal{P}_{h}$ as a preconditioner in conjunction with GMRES we will require computation of the action of $\mathcal{P}_{h}^{-1}$ on a general vector. Writing

$$\begin{aligned} \hat{\mathbf {y}}_{1} = \begin{pmatrix} \mathbf {y_{1}} \\ p_{1} \end{pmatrix}, \qquad \hat{\mathbf {y}}_{2} = \begin{pmatrix} \mathbf {y_{2}} \\ p_{2} \end{pmatrix}, \end{aligned}$$

then, if the action of $\mathcal{P}_{h}^{-1}$ on a given vector $\hat{\mathbf {y}}_{1}$ may be written

$$\begin{aligned} \mathcal{P}_{h}^{-1} \hat{\mathbf {y}}_{1} = \hat{\mathbf {y}}_{2}, \end{aligned}$$

for some $\hat{\mathbf {y}}_{2}$ that is to be determined, we may write this as the linear system

$$\begin{aligned} \begin{pmatrix} A_{h} &{} B^{\top } \\ 0 &{} -M \end{pmatrix} \begin{pmatrix} \mathbf {y_{2}} \\ p_{2} \end{pmatrix} = \begin{pmatrix} \mathbf {y_{1}} \\ p_{1} \end{pmatrix}. \end{aligned}$$

An approximate solution to this linear system may be computed in two steps. First we solve (approximately) the linear system

$$\begin{aligned} M p_{2} = -p_{1}. \end{aligned}$$

(15)

The solution of this linear system may be approximated very efficiently and very accurately using the preconditioned conjugate gradient method [20]. Having approximated $p_{2}$ we then evaluate $\mathbf {y_{2}}$ from

$$\begin{aligned} A_{h} \mathbf {y_{2}} = \mathbf {y_{1}} - B^{\top } p_{2}, \end{aligned}$$

(16)

by using a small number of V-cycles of a multigrid approximation based on the matrix A. By approximating the solution of Eqs. (15) and (16) as described above, the action of $\mathcal{P}_{h}^{-1}$ on a given vector may be computed very easily.

5 Numerical experiments

We now investigate the performance of the preconditioner proposed in Sect. 4 through simulations in both two and three dimensions. One metric that may be used to indicate the size of the deformation is the magnitude of the eigenvalues of Green–Lagrange strain tensor E defined by

$$\begin{aligned} E = \frac{1}{2} \left( F^{\top } F - \mathcal{I} \right) , \end{aligned}$$

(17)

where $\mathcal{I}$ is the identity matrix. An undeformed body has all entries of E equal to zero. When E is written in terms of the displacement $\mathbf {u} = \mathbf {x}-\mathbf {X}$, one of the assumptions implicit in deriving the equations of linear elasticity is that only the linear contributions to E from $\mathbf {u}$ are required. We therefore give the maximum eigenvalue of the strain tensor in all simulations in this section to indicate why linear elasticity is not an appropriate model for these simulations.

We use a nonlinear strain energy function that has previously been used to model biological soft tissues [3, 29], given by

$$\begin{aligned} W = c_{1} \exp \left( c_{2} \left( F_{iM} F_{iM} - d \right) \right) , \end{aligned}$$

where $c_{1},c_{2}$ are positive constants. In all simulations we use the parameters $c_{1}=c_{2}=\rho =1$. We compute a finite element solution that uses a tensor product quadratic approximation to the deformed coordinates, and a tensor product linear approximation to the Lagrange multiplier p. We discretise the domain into N elements in each coordinate direction, giving a mesh of $N^{2}$ elements for simulations in two dimensions, and $N^{3}$ elements for simulations in three dimensions.

An initial guess to the solution is required when using Newton’s method to solve a system of algebraic equations. Unless otherwise stated the initial guess for the coordinates of the deformed body is the coordinates of the undeformed body, and the initial guess to the Lagrange multipler p takes the value zero at all points. For each model problem we carry out one set of simulations where solution was computed using a preconditioner where Eq. (16) was solved by defining $A_{h}^{-1}$ to be 2 multigrid V-cyles, and a second set of simulations where $A_{h}^{-1}$ was defined to be 4 multigrid V-cycles. In all cases the Newton solver was terminated when the 2-norm of the residual vector was less than $10^{-6}$.

In all simulations the first step of applying the preconditioner, i.e. the preconditioned conjugate gradient solution of Eq. (15), required only one iteration. We therefore focus on the number of GMRES iterations required on each iteration of Newton’s method, investigating both the effect of the number of degrees of freedom in the computational mesh, and the number of V-cycles used with the multigrid approximation of Eq. (16).

5.1 Simulations in two spatial dimensions

We first investigate the performance of the preconditioner using example problems in two spatial dimensions.

5.1.1 A model problem with known solution

Our first set of simulations uses a model problem described in [13], specified on the unit square $0<X,Y<1$. For constant $a>0$ we define

$$\begin{aligned} \lambda= & {} 1+aX, \\ \alpha= & {} c_{2} \left( \lambda ^{2} + \lambda ^{-2} + a^{2} Y^{2} \lambda ^{-4} -2 \right) , \end{aligned}$$

and then define the body force by

$$\begin{aligned} \mathbf {g} = - \frac{2 c_{1} c_{2} \mathrm{e}^{\alpha }}{\rho } \left( \begin{array}{l} a + \lambda \frac{\partial \alpha }{\partial X} \\ 2 \lambda ^{-3}a^{2}Y - \lambda ^{-2}aY \frac{\partial \alpha }{\partial X} + \lambda ^{-1} \frac{\partial \alpha }{\partial Y} \end{array}\right) . \end{aligned}$$

Zero displacement Dirichlet boundary conditions are applied on $X=0$, and Neumann boundary conditions are applied on the other boundaries, with $\mathbf {s}$, defined in Eq. (4), specified by

$$\begin{aligned} \mathbf {s}&= 2c_{1}c_{2} \begin{pmatrix} 0 \\ \lambda -\lambda ^{-1}\mathrm{e}^{\alpha } \end{pmatrix},&\qquad Y&=0, \\ \mathbf {s}&= 2c_{1}c_{2} \begin{pmatrix} -a \lambda ^{-2} \\ \lambda ^{-1}\mathrm{e}^{\alpha } - \lambda \end{pmatrix},&\qquad Y&=1, \\ \mathbf {s}&= 2c_{1}c_{2} \begin{pmatrix} (1+a)\mathrm{e}^{\alpha } - (1+a)^{-1} \\ -aY(1+a)^{-2}\mathrm{e}^{\alpha } \end{pmatrix},&\qquad X&=1. \end{aligned}$$

This model problem has solution

$$\begin{aligned} x= & {} X+\frac{1}{2} a X^{2}, \\ y= & {} Y(1+aX)^{-1}, \\ p= & {} 2c_{1}c_{2}. \end{aligned}$$

We carry out two sets of simulations based on this model problem: one set where $a=1$; and one set where $a=0.01$. For the set where $a=1$, the maximum eigenvalue of the strain tensor is 1.53. When $a=0.01$ the maximum eigenvalue of the strain tensor is 0.0112, and so this case models a small deformation that is governed by incompressible linear elasticity.

We begin by discussing the simulations with $a=1$. Six Newton iterations were required for the mesh where $N=8$, seven Newton iterations were required for the meshes where $N=16,32,64$, and eight Newton iterations were required for all meshes where $N=128$ or greater. The number of degrees of freedom (DOF) in the system of algebraic equations, and the maximum, minimum and average number of GMRES iterations required for each Newton iteration are given in Table 1, for both the case when 2 V-cycles of multigrid are used, and when 4 V-cycles are used. For the simulations with a low number of DOFs, increasing the number of multigrid V-cycles used in the preconditioner has very little effect on the number of GMRES iterations required. However, for the meshes with a larger number of DOFs, a preconditioner that uses 4 V-cycles of multigrid significantly reduces the number of GMRES iterations required. Most importantly, when using 4 V-cycles, we see that the number of GMRES iterations required increased by only roughly a factor of 3.5 between a mesh with 659 DOFs to a mesh with 2,364,419 unknowns.

Table 1 The number of GMRES iterations required for the computations of the model problem described in Sect. 5.1.1 with $a=1$

The number of GMRES iterations for the simulations where $a=0.01$ are given in Table 2. Three iterations of Newton’s method were required in all cases. We see the same trends in this table as in Table 1, that have been discussed earlier in this section. One further observation is that, in comparison with the results presented in Table 1, computations using $a=1$, required a significantly larger number of GMRES iterations than computations using $a=0.01$.

Table 2 The number of GMRES iterations required for the computations of the model problem described in Sect. 5.1.1 with $a=0.01$

5.1.2 Deformation under gravity in one step

The second model problem is the computation of the deformation of the unit square $0<X,Y<1$ under a body force $\mathbf {g} = (0,10)^{\top }$. Zero displacement boundary conditions are applied on the boundary $Y=0$, and zero stress boundary conditions are applied on all other boundaries. The resulting deformed body is shown in Fig. 1. The maximum eigenvalue of the strain tensor arising from this deformation is 2.39. In all of these calculations Newton’s method required seven iterations to reduce the 2-norm of the residual vector to a value less than $10^{-6}$.

Fig. 1

The deformed body resulting from the simulation described in Sect. 5.1.2 (solid line). The broken line illustrates the undeformed body

The number of degrees of freedom in the system of nonlinear equations, and the maximum, minimum, and average number of iterations of GMRES required on each Newton iteration, are shown in Table 3 for preconditioners using both 2 V-cycles and 4 V-Cycles of multigrid. We make simular observations on the performance of the preconditioner to those documented in Sect. 5.1.1 We see that, for meshes that result in a low number of DOFs, increasing the number of V-cycles from 2 to 4 has very little effect on the number of GMRES iterations required when solving the linear systems. However, for meshes that result in a larger number of DOFs we see that increasing the number of V-cycles from 2 to 4 significantly decreases the number of GMRES iterations required. Furthermore, when using 4 V-cycles, we see that the number of GMRES iterations required increased by only roughly a factor of three between a mesh with 659 DOFs to a mesh with 2,364,419 unknowns.

Table 3 The number of GMRES iterations required for the computations described in Sect. 5.1.2

5.1.3 Deformation under gravity using continuation

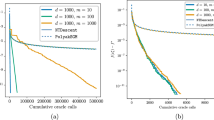
We now compute the deformation of the unit square $0<X,Y<1$ under a body force $\mathbf {g} = (0,50)^{\top }$ using continuation. That is, we sequentially compute the deformation of the body under a body force $\mathbf {g} = (0,n)^{\top }$, where $n=1,2,\ldots ,50$. For the first increment of body force we use the initial guess given in Sect. 5. On increment n, where $n=2,3,\ldots ,50$, the initial guess for both $\mathbf {x}^{h}$ and $p^{h}$ is that calculated on increment $n-1$. The average number of GMRES iterations required on each Newton iteration, as a function of continuation iteration number, is shown in Fig. 2a when 2 V-cycles are used, and in Fig. 2b when 4 V-cycles are used. As with the earlier simulations, using more V-cycles significantly reduces the number of GMRES iterations required for the simulations with a large number of degrees of freedom, but has less of an effect for smaller number of degrees of freedom. More importantly, when the number of degrees of freedom is increased from 659 to 2,364,419, the number of GMRES iterations required increases by a factor of less than 10 when 2 V-cycles are used, and a factor of less than 6 when 4 V-cycles are used. We also note that the average number of GMRES iterations increases as the body force is increased using continuation.

Fig. 2

The average number of GMRES iterations required on each continuation iteration for the simulations described in Sect. 5.1.3. a Shows the results when 2 V-cyles were used, b shows the results when 4 V-cyles were used

Fig. 3

The average number of GMRES iterations required on each continuation iteration for the simulations described in Sect. 5.1.4. a Shows the results when 2 V-cyles were used, b shows the results when 4 V-cyles were used

Fig. 4

Calculation of the deformed body using continuation, when a continuation step of 0.01 was used. A mesh of $32 \times 32$ elements was used. a The average number of GMRES iterations required on each continuation step, b the condition number of the first Jacobian matrix on each continuation step

5.1.4 The onset of buckling

We now investigate computation of the deformation of the unit square $0<X,Y<1$ under a body force $\mathbf {g} = (0,g)^{\top }$, where $g<0$. We use continuation, as described in Sect. 5.1.3, computing the deformation under a body force $\mathbf {g} = (0,-n)^{\top }$, where $n=1,2,\ldots$. Compressive deformations such as these are prone to the phenomenon known as buckling, where the solution becomes non-unique [1]. For each simulation we compute the deformation up until the value of n where solving a linear system fails. The average number of GMRES iterations required on each Newton iteration, as a function of continuation iteration number, is shown in Fig. 6a when 2 V-cycles are used, and in Fig. 6b when 4 V-cycles are used.

When Newton’s method returned a solution to the algebraic equations, similar trends were observed to the performance of the preconditioner as those described in Sect. 5.1.3. We note, however, that for these compressive simulations the continuation solution method used was capable of returning a solution only until some finite body force $\mathbf {g}$, and that this body force was critically dependent on the number of elements in the mesh. An extensive analysis of the existence and uniqueness to the solution of these discretised, nonlinear, algebraic equations is beyond the scope of this study, and so we attribute this phenomena to the concept of buckling. We do, however, focus on one individual case below in an attempt to identify some of the features of this behaviour. We use the specific case of a mesh of $32 \times 32$ elements. We again calculate the deformation under gravity using continuation. This time, however, we use a continuation step of 0.01, rather than the continuation step of 1 used in the simulations shown in Fig. 3.

Fig. 5

The deformed body resulting from the simulation described in Sect. 5.2.1 (solid line). The broken line illustrates the undeformed body

Table 4 The number of GMRES iterations required for the computations of deformation under gravity for the problem described in Sect. 5.2

Fig. 6

The average number of GMRES iterations required on each continuation iteration for the simulations described in Sect. 5.2.2. a Shows the results when 2 V-cyles were used, b shows the results when 4 V-cyles were used

Using a continuation step of 1, as shown in Fig. 3, and a mesh of $32 \times 32$ elements, we found a finite element solution for $\mathbf {g}=(0,-13)^{\top }$, but not for the next continuation step where $\mathbf {g}=(0,-14)^{\top }$. When using a continuation step of 0.01, we found a finite element solution for $\mathbf {g}=(0,-13.33)^{\top }$, but not for the next continuation step where $\mathbf {g}=(0,-13.34)^{\top }$. Using a smaller continuation step therefore did not significantly affect the body force $\mathbf {g}$ where a solution could no longer be found. In Fig. 4a we plot the average number of GMRES iterations needed on each continuation step when a continuation step of 0.01 was used. We see that this does not differ significantly to that shown in Fig. 3. In Fig. 4b we plot the condition number of the first Jacobian matrix on each continuation step. We see that the condition number has one local maximum value before the finite element method used fails. We see that the condition number then increases rapidly shortly before the finite element method fails, adding further evidence that the observed phenomenon is buckling, where the solution is not unique and the Jacobian matrix calculated using Newton’s method will be singular.

5.2 Simulations in three spatial dimensions

We now perform simulations in three spatial dimensions. We start by computing the deformation in one step, before investigating the use of continuation.

5.2.1 Deformation under gravity in one step

We calculate the deformation of the unit cube $0<X,Y,Z<1$ under a body force $\mathbf {g}=(0,0,10)^{\top }$. We apply zero displacement boundary conditions on the face $Z=0$, and zero stress boundary conditions on all other boundaries. The resulting deformation is plotted in Fig. 5. The maximum eigenvalue of the strain tensor arising from this deformation is 1.93. In all simulations we use a uniform mesh, with N elements in each coordinate direction. As with the simulations in two dimensions, for each value of N we compute the finite element solution first using a preconditioner that uses 2 V-cycles of multigrid, and then a preconditioner that uses 4 V-cycles of multigrid.

For the cases when $N=4, 8, 16$, six iterations of Newton’s method were required to reduce the norm of the residual vector to below $10^{-6}$; when $N=32$ seven iterations were required. The number of degrees of freedom, and the maximum, minimum and average number of GMRES iterations required on each Newton iteration are given in Table 4. We see qualitatively similar trends to those discussed for the computations in two dimensions in Sect. 5.1. For the computations in three dimensions we again see only a slight dependence of the number of GMRES iterations on the number of degrees of freedom of the system—the number of GMRES iterations required increased only by factor of around 2.5 as the number of DOFs increases from 2312 to 859,812. Compared to the simulations in two dimensions there appears to be less benefit in using 4 V-cycles in the preconditioner rather than 2 V-cycles.

5.2.2 Deformation under gravity using continuation

We now compute the deformation of the unit cube $0<X,Y,Z<1$ under a body force $\mathbf {g} = (0,0,50)^{\top }$ using continuation as described in Sect. 5.1.3, using 50 equal body force increments. The average number of GMRES iterations required on each Newton iteration as a function of body force increment is shown in Fig. 6a when 2 V-cycles are used, and in Fig. 6b when 4 V-cycles are used. Similar observations on the number of GMRES iterations required are made to those reported for earlier simulations. When the number of degrees of freedom is increased from 2312 to 859,812 the number of GMRES iterations required increases by a factor of slightly more than 2.

6 Discussion

In this study we first wrote down the system of nonlinear algebraic equations that arises from a finite element discretisation of the partial differential equations governing incompressible, nonlinear, elastic deformations. We have developed a preconditioner for use in conjunction with Newton’s method for solving this system of nonlinear algebraic equations. This preconditioner utilises the structure of the Jacobian matrix, and may be decomposed into two steps. First, a relatively small, symmetric, positive definite linear system must be solved using the preconditioned conjugate gradient method. For all the exemplar simulations carried out in this study this iterative technique converged after one iteration. The second step is the application of a small number of V-cycles of a multigrid approximation to a much larger linear system. Using exemplar deformations this preconditioner was demonstrated to be suitable for use with problems with a large number of degrees of freedom.