Stokes–Brinkman formulation for prediction of void formation in dual-scale fibrous reinforcements: a BEM/DR-BEM simulation

Abstract

A numerical study of voids formation in dual-scale fibrous reinforcements is presented. Flow fields in channels (Stokes) and tows (Brinkman) are solved via direct Boundary Element Method and Dual Reciprocity Boundary Element Method, respectively. The present approach uses only boundary discretization and Dual Reciprocity domain interpolation, which is advantageous in this type of moving boundary problems and leads to an accurate representation of the moving interfaces. A problem admitting analytical solution, previously solved by domain-meshing techniques, is used to assess the accuracy of the present approach, obtaining satisfactory results. Fillings of Representative Unitary Cells at constant pressure are considered to analyze the influence of capillary ratio, jump stress coefficient and two formulations (Stokes–Brinkman and Stokes–Darcy) on the filling process, void formation and void characterization. Filling times, fluid front shapes, void size and shape, time and space evolution of the saturation, are influenced by these parameters, but voids location is not.

1 Introduction

In dual-scale fibrous reinforcements used in composites processing, the permeability of the tows is several orders of magnitudes lower than the permeability of the inter-tow channels. This causes imbalances between the flow inside the tows and the flow in the channels, which can lead to the formation of voids by mechanical entrapment of air. Once these voids are formed, several phenomena can take place, among others: bubble compression, displacement, migration and splitting.

Under the assumptions that the solid phase is stationary, the fluid is Newtonian and incompressible and neglecting the inertial effects, the Navier–Stokes system of equations governing the flow inside the pores of the porous medium (microscale) reduces to the Stokes equation. By an assembled average including both phases of the porous medium (liquid and solid), the Stokes system of equations reduces to Darcy’s law, where the velocity (Darcy velocity) is linearly proportional to the pressure gradient, with proportionality constant given by the permeability, Darcy’s law was established empirically by Darcy (1856) and later derived formally by different authors using several approaches (among others see Whitaker [66]).

Considering the shearing effect between the fluid and the walls of the porous medium, Brinkman (1947) added the second-order derivatives of the velocity to the Darcy equation, resulting in the Brinkman equation. The averages implicit in the Brinkman equation can be viewed as averages over an ensemble of different scales of the porous medium that interpolate between the Stokes and Darcy equations. On small length scales, the pressure gradient balances the Laplacian of the velocity and the flow is essentially viscous, Stokes flow, while over larger length scales, the velocity is slowly varying and the pressure gradient balances the average velocity as it does in Darcy’s law (for more details see Durlofsky and Brady [9]). According to Ochoa-Tapia and Whitaker [40], Brinkman approximation can be applied when the following three length scale constrains are simultaneously satisfied: ${r_0}^2/\left( {{l_\varepsilon }{l_p}} \right) \ll 1$ , ${r_0}^2/\left( {{l_\varepsilon }{l_v}} \right) \ll 1$, ${l_f} \ll {r_0}$, where ${l_\varepsilon },\;\;{l_p},\;{l_v}$ and ${l_f}$ are the characteristic lengths associated to the porosity, pressure, velocity gradients and fluid phase, respectively, and ${r_0}$ is the characteristic length scale of the Representative Elementary Volume (REV). Krotkiewski et al.[28] reported a direct numerical simulation of the flow field in homogeneous two dimensional porous media with characteristic length $L$ and permeability $K$, concluding that the Stokes solution is dominant for $K/{L^2} \ge 10$, Darcy law is representative of the flow field if $K/{L^2} \le {10^{ - 4}}$, while for ${10^{ - 4}} \le K/{L^2} \le 10$ the Brinkman approximation should be used to account for the transition between both flow regimes, Stokes and Darcy.

The Brinkman equation includes an effective viscosity term, $\mu _{eff}$, to consider the viscous diffusion not deemed in the Darcy law. In order to explain the meaning of this term, it is necessary to consider that the volume averaging method allows describing the porous medium flow in terms of averages of the local quantities by means of the Darcy–Brinkman equation, which is given by (3) considering $\mu _{eff}=\mu$, where $\mu$ is the real fluid viscosity. This last equality is valid provided that a non-slip condition on the interfaces between the fluid and solid phases of the porous medium is considered, as done in the traditional volume-averaging method. However, the non-coincidence between $\mu _{eff}$ and $\mu$ has been demonstrated in several experimental, numerical and theoretical works, suggesting that the non-slip condition is not necessarily valid in all cases. For instance, Givler and Altobelli [17] experimentally found that $\mu _{eff}$ is 7.5 times the value of $\mu$ for high-porous open cell foams and moderate Reynolds numbers, whereas Starov and Zhdanov [70] studied the dependency of $\mu _{eff}$ on the porosity and particle size in porous media composed of equally sized spherical particles, finding that $\mu _{eff}$ can be lower or larger than $\mu$. On the other hand, the numerical flow simulations conducted by [4] in 3D regular arrays of cubes showed that $\mu _{eff}<\mu$, whereas those ones executed by [34] indicated that $\mu _{eff}>\mu$ in order to match the Brinkman equation with the numerical solutions in the boundary layer developed in the porous medium domain when it is in contact with a free-fluid domain. A very illustrative theoretical work was published by [63], where it was demonstrated that the effective viscosity, $\mu _{eff}$, is different to the fluid viscosity, $\mu$, when a slip condition at the fluid-solid interface of the porous medium is considered. Using an up-scaling procedure, a boundary-value problem to compute $\mu _{eff}$ was obtained in such work, achieving important conclusions. In general, the effective viscosity is different to the fluid viscosity, i.e, $\mu _{eff}\ne \mu$, because it is a term that ‘absorbs’ the microscale variations of the velocity gradient when a variationless velocity gradient model is used at macroscopic scale. On the other hand, as the prescribed slip coefficient at the fluid-solid interface increases, the boundary layer thickness decreases and a non-slip condition tends to be reached, in such a way that in the limit when the slip coefficient tends to infinity, $\mu _{eff}=\mu$.

In the Stokes–Brinkman approach the matching conditions at the interface channels-tows are defined in terms of the corresponding surface velocity and traction vectors. Continuity of the velocity field is always considered and two types of conditions could be employed for the tractions: continuous [39] and jump stress [40, 41]. The continuity of stress was initially implemented in [39, 48], however a jump stress matching condition was proposed later in [40] based on the non-local form of the volume-averaged momentum equation for the analysis of the region between the channel and the porous medium. By means of experiments of unidirectional flow in parallel domains, Ochoa-Tapia and Whitaker [41] found that the jump stress tensor across the interface for isotropic porous media, $\left[ {\left| {{\sigma _{ij}}{{\hat{n}}_j}} \right| } \right]$, is linearly proportional to the interface surface velocity ${u_j}$, i.e. $\left[ {\left| {{\sigma _{ij}}{n_j}} \right| } \right] = \mu {T_{ij}}{u_j}/\sqrt{K}$, where $\mu$ stands for the fluid viscosity, while the second-order tensor ${T_{ij}}$ is given by $\beta {\delta _{ij}}$, with $\beta$ as the jump stress coefficient ranging between $- 1$ and $1.47$; for more details see [23]. However, Angot [2], demonstrated mathematically that the well-posedness of the Stokes–Brinkman problem is only possible when $\beta \ge 0$. The theoretical estimation of the value of$\;\beta$ was developed in [64, 65], where it was established that $\beta$ depends on the porosity of the porous medium in the inter-region channel-tow, ${\varepsilon _{ct}}$.

The estimation of the effective viscosity term, ${\mu _{eff}}$, in the Brinkman equation is known to depend on the geometry of the porous medium and the flow itself. As suggested in the literature [23, 56, 57], an acceptable approximation for ${\mu _{eff}}$ in dual-scale fibrous reinforcements is to consider that ${\mu _{eff}} = \mu$ when the continuous stress condition is used, whereas ${\mu _{eff}} = \mu /{\varepsilon _t}$ is suitable when the jump stress condition is employed, with ${\varepsilon _t}$ as the tow porosity. In a recent work [23], focusing in the prediction of the effective saturated permeability of dual-scale reinforcements for unidirectional flow (where a value of $\beta = 0.7$ was used), it was found that the type of stress matching condition (continuity or jump) has a strong influence on the boundary layer thickness in the porous medium, but not on the effective saturated permeability, which is dependent on the pore geometry. In this point, it is relevant to mention that the study of the pore geometrical dependency of the effective permeability could be a complicated and computational expensive task, but some recent efforts have been addressed to reduce the computational cost without compromising the accuracy. For instance, a multiscale framework relating the effective permeability with some microstructural attributes extracted by X-ray tomography was proposed in [55], where several computational techniques were efficiently combined (Level Set, Graph Theory and Lattice Boltzman/Finite Element) to determine the tortuosity, porosity and homogenized effective permeability at specimen scale. The particular problem solved in [23] by FEM is also considered here for validation of the numerical technique implemented.

In the present work, simulations of fillings of RUC’s (Representative Unitary Cells) of dual-scale fibrous reinforcements are carried out using a Boundary Element/Dual Reciprocity numerical approach (BEM/DR-BEM). The flow in the channel, Stokes flow, is given by its boundary-only integral formulation, Green’s formula, and numerically treated by direct BEM, while the flow inside the tows, Brinkman flow, is given by a boundary-domain integral formulation in terms of the Stokes fundamental solutions, where the domain integral is transformed into a boundary integral using the Dual Reciprocity Boundary Element Method (DR-BEM). The present numerical approach is validated by comparison with a benchmark analytical solution used previously in the literature to assess the robustness of FEM-based numerical solutions of flow problems in dual-scale porous media [23, 58].

The developed BEM/DR-BEM numerical scheme is then used to simulate the simultaneous filling of channels and tows inside the RUC at constant pressure regime with the purpose of analyzing the influence of the stress matching conditions on the void formation at several values of the capillary ratio, ${C_{cap}} = {P_{cap,max}}/{P_{in}}$, where ${P_{cap,max}}$ and ${P_{in}}$ stand for the maximum capillary pressure and the inlet pressure, respectively. This type of filling problem has been previously considered in the literature using different formulations and numerical techniques. For instance, Gourichon et al. [19] studied the influence of the RUC porosity in the formation of voids using a Darcy–Darcy formulation and the FEM/CV conforming method. On the other hand, Schell et al. [49] studied the influence of the tow porosity, ${\varepsilon _t}$, on the final void content using the same formulation and numerical technique as in [19], while the problem of unidirectional filling of circular tows in cylindrical coordinates was analyzed in [68] using a Stokes–Brinkman formulation and the Finite Volume method, where it was studied the effect of the filling velocity, resin viscosity, inter-tow dimension and intra-tow dimension on the shape of the fluid front.

In comparison with domain-meshing numerical techniques previously used in the literature for the simulation of the filling process in dual scale fibrous reinforcements based on the Stokes–Brinkman formulation [11, 23, 50, 51, 58], two main advantages can be identified by the use of the BEM/DR-BEM approach employed in this work. Firstly, the use of BEM-based techniques does not imply any mesh discretization of the problem domain, which is not a trivial task in a domain that is continuously changing in size and shape as in the present case. Secondly, the tracking of the fluid front is directly carried out by an Euler integration of the kinematic condition at the moving interface, which assures a higher order accuracy on the prediction of the fluid front shape without the need of implementing any additional reconstruction algorithm of the moving boundaries, contrary to the case of the Volume of Fluid (VOF) [14, 15] or the Level Set Method [12, 13, 53].

Another important contribution of this work is the study of the influence of two types of stress matching conditions (continuous and jump) on the void formation. Other works have analyzed the influence of these conditions on the effective saturated permeability [23, 58], but not on the size, shape and location of the voids formed by mechanical entrapment of air. Additionally, the processes of the void formation using the Stokes–Brinkman and Stokes–Darcy formulations are compared each other, which has not been reported before to the best of our knowledge. Finally, the consideration of a flow direction-dependent capillary pressure in the tows without experimental factors and of the curvature- dependent surface traction effects for the fluid fronts in the channels are ones of the main differences between the present work and previous publications in the same field [1, 7, 49, 59].

2 Governing equations, boundary and matching conditions

In the Stokes–Brinkman formulation, the governing equations at each medium are defined as:

Mass conservation (For all domains):

$$\begin{aligned} \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\ \end{aligned}$$

(1)

Momentum for the Stokes domain (Channels flow):

$$\begin{aligned} \mathop \mu \left( {\frac{{{\partial ^2}{u_i}}}{{\partial {x_j}{x_j}}}} \right) - \frac{{\partial p}}{{\partial {x_i}}} = 0\ \end{aligned}$$

(2)

Momentum for the Brinkman domain (Porous media or tows flow):

$$\begin{aligned} \mathop {\mu _{eff}}\frac{{{\partial ^2}{u_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{{\partial p}}{{\partial {x_i}}} = \frac{\mu }{{{K_i}}}{u_i}\ \end{aligned}$$

(3)

where in the right hand side of (3) the double index notation is not considered for $i = 1,2$. Here ${u_i}$, $p$, $\mu$, ${\mu _{eff}}$ and ${K_i}$ represent the velocity vector, pressure, liquid viscosity, effective viscosity and main permeabilities, respectively.

Let us define the following non-dimensional variables for the length, velocity, time and pressure [46, 47]:

For all domains:

$$\begin{aligned} \widehat{{x_i}}= & {} {x_i}/{L^*}\ \end{aligned}$$

(4)

$$\begin{aligned} \mathop {\hat{u}_i}= & {} {u_i}/{U_{max}}\ \end{aligned}$$

(5)

$$\begin{aligned} \hat{t}= & {} t/\left( {{L^*}/{U_{max}}} \right) \ \end{aligned}$$

(6)

For the Stokes domain (Channels flow):

$$\begin{aligned} \hat{p} = \frac{p}{{\mu \cdot {U_{max}}/{L^*}}}\ \end{aligned}$$

(7)

For the Brinkman domain (Porous media or tows flow):

$$\begin{aligned} \hat{p} = \frac{p}{{{\mu _{eff}} \cdot {U_{max}}/{L^*}}}\ \end{aligned}$$

(8)

where ${L^*}$ and ${U_{max}}$ are the characteristic length and the maximum velocity of the problem, respectively. In terms of these characteristic values, the non-dimensional form of the governing Eqs. (1), (2), (3) can be written as:

$$\begin{aligned}&\frac{{\partial {{\hat{u}}_i}}}{{\partial {{\hat{x}}_i}}} = 0\ \end{aligned}$$

(9)

$$\begin{aligned}&\frac{{{\partial ^2}{{\hat{u}}_i}}}{{\partial {{\hat{x}}_j}{{\hat{x}}_j}}} - \frac{{\partial \hat{p}}}{{\partial {{\hat{x}}_i}}} = 0\ \end{aligned}$$

(10)

$$\begin{aligned}&\frac{{{\partial ^2}{{\hat{u}}_i}}}{{\partial {{\hat{x}}_j}\partial {{\hat{x}}_j}}} - \frac{{\partial \hat{p}}}{{\partial {{\hat{x}}_i}}} = \chi _i^2{\hat{u}_i}\ \end{aligned}$$

(11)

where $\chi _i^2 = 1/Da_i^* = {\left( {{L^*}} \right) ^2}\mu /\left( {{K_i}.{\mu _{eff}}} \right)$ is the inverse of the Darcian number, $Da_i^*$, in the principal direction i.

The non-dimensional matching conditions for the Stokes–Brinkman problem are as follows [2]:

• Continuity of velocities:

  $$\begin{aligned} \hat{u}_i^{\left( s \right) } = \hat{u}_i^{\left( b \right) } \end{aligned}$$

  (12)

• Normal and tangential component of the jump stress:

  $$\begin{aligned} \left( {\hat{t}_i^{\left( s \right) } + \left( {{\mu _{eff}}/\mu } \right) \hat{t}_i^{\left( b \right) }} \right) {\hat{n}_i}= & {} - \frac{{{L^*}}}{{\sqrt{{K_n}} }}{\beta _n}\hat{u}_i^{\left( s \right) }{\hat{n}_i} \end{aligned}$$

  (13)
  $$\begin{aligned} \left( {\hat{t}_i^{\left( s \right) } + \left( {{\mu _{eff}}/\mu } \right) \hat{t}_i^{\left( b \right) }} \right) {\hat{\tau }_i}= & {} - \frac{{{L^*}}}{{\sqrt{{K_\tau }} }}{\beta _\tau }\hat{u}_i^{\left( s \right) }{\hat{\tau }_i} \end{aligned}$$

  (14)

where s and b represent the Stokes and Brinkman domain, respectively, and $\hat{t}_i^{\left( s \right) } = \left( {{L^*}/\left( {\mu {U_{max}}} \right) } \right) {\sigma _{ij}}\widehat{{n_j}}$ and $\hat{t}_i^{\left( b \right) } = \left( {{L^*}/\left( {{\mu _{eff}}{U_{max}}} \right) } \right) {\sigma _{ij}}\widehat{{n_j}}$ are defined as the dimensionless traction vectors, with ${\sigma _{ij}}$ as the Cauchy stress tensor. Here ${K_n}\;$and ${K_\tau }$ are the effective permeabilities in the normal and tangential direction, respectively, with the effective permeability in any orientation, ${\phi _i}$, given by [33]:

$$\begin{aligned} \mathop {K_{eff}}\left( {{\phi _i}} \right) = \frac{{{K_1} \cdot {K_2}}}{{{K_1} \cdot \sin {^2}\left( {{\phi _i}} \right) + {K_2}\cdot \cos {^2}\left( {{\phi _i}} \right) }}\ \end{aligned}$$

(15)

where ${\phi _i}\;$is the angle between a given direction and the major axis of permeability. In the above jump stress conditions, ${\beta _n}$ and ${\beta _\tau }$ are the normal and tangential jump coefficients, which are considered equal in the present work as done in [23, 58]. Some authors consider that the minus sign of the right hand side of (13) and (14) is implicit in the stress jump coefficients, ${\beta _n}$ and ${\beta _\tau }$ [23, 58]. When a continuous surface traction at the interface is considered, the corresponding matching condition can be obtained from (13) and (14) by setting the values of ${\beta _n}$ and ${\beta _\tau }$ to zero.

In the present paper, the RUC filling is carried out at constant inlet pressure for all cases. Therefore, the non- dimensional inlet boundary conditions are as follows:

At the Stokes domain:

$$\begin{aligned} \hat{t}_1^{\left( s \right) } = - \bar{p}{L^*}/\left( {\mu {U_{max}}} \right) \widehat{n_1^{\left( s \right) }}, \hat{u}_2^{\left( s \right) } = 0 \end{aligned}$$

(16)

At the Brinkman domain:

$$\begin{aligned} \hat{t}_1^{\left( b \right) } = - \bar{p}{L^*}/\left( {{\mu _{eff}}{U_{max}}} \right) \widehat{n_1^{\left( b \right) }}, \hat{u}_2^{\left( b \right) } = 0 \end{aligned}$$

(17)

where $\bar{p}$ represents the prescribed inlet pressure. No-flux condition, ${\hat{u}_i}{\hat{n}_i} = 0,\;$and zero traction in the tangential direction, ${\hat{t}_i}{\hat{\tau }_i} = 0$, are used in boundaries where symmetry is specified.

At the fluid fronts, kinematic and dynamic boundary conditions are defined. The former condition establishes that the fluid front advances along its normal direction, while the dynamic condition accounts for the discontinuities of normal stress due to the capillary pressure, ${p_{cap}}$. Both kind of conditions are represented in (18) and (19), (20), respectively:

• Kinematic condition (For all domains):

  $$\begin{aligned} \mathop d\hat{x}_i /d\hat{t} = {\hat{u}_n}\widehat{{n_i}}\mathrm{{\;}} = \left( {{{\hat{u}}_j}.\widehat{{n_j}}} \right) \widehat{{n_i}}\ \end{aligned}$$

  (18)

• Dynamic condition (At the Stokes domain):

  $$\begin{aligned} \hat{t}_i^{\left( s \right) } = {L^*}\left( {{p_{cap}} - {p_a}} \right) /\left( {\mu {U_{max}}} \right) \widehat{{n_i}} \end{aligned}$$

  (19)

• Dynamic condition (At the Brinkman domain):

  $$\begin{aligned} \hat{t}_i^{\left( b \right) } = {L^*}\left( {{p_{cap}} - {p_a}} \right) /\left( {{\mu _{eff}}{U_{max}}} \right) \widehat{{n_i}} \end{aligned}$$

  (20)

where $\widehat{{n_i}}$, $\;{p_a}$ and ${\hat{u}_n}$ are the outwardly oriented normal vector, air pressure and dimensionless normal velocity at the fluid front, respectively. In (18), ${\hat{u}_n}$ is given by the Stokes velocity in the channel domain and by the pore velocity in the porous medium, which, in turn, is defined as the Brinkman velocity divided by the tow porosity,$\;{\varepsilon _t}$ [32, 67]. In the case of the channel flow, the capillary pressure is ${p_{cap}} = - \sigma \kappa = - \sigma \left( {\partial {{\hat{n}}_i}/\partial {x_i}} \right)$, with $\sigma$ as the surface tension and $\kappa$ as the curvature of the moving boundary. For the flow inside the porous medium, the capillary pressure can be computed using the following equation [35]:

$$\begin{aligned} \mathop {p_{cap}}= & {} 2\left( {\sigma \cdot \cos \left( \theta \right) /{R_{ec}}} \right) \ \end{aligned}$$

(21)

$$\begin{aligned} \mathop {R_{ec}}= & {} 2\left( {{A_{int,s}}/{C_{int,s}}} \right) \left( {{\varepsilon _t}/\left( {1 - {\varepsilon _t}} \right) } \right) \ \end{aligned}$$

(22)

where ${A_{int,s}}$ is the cross sectional area of the solid particles in the flow direction, ${C_{int,s}}$ is the wetted perimeter of the solid particles, $\theta$ is the contact angle and ${\varepsilon _t}$ is the tow porosity. In this work, the geometry of the porous medium is considered as a bank of aligned circular fibers and the capillary pressure in any point of the longitudinal tow (warp) depends on the angle between the normal of the fluid front and the principal axis of the fibers, $\varphi$. If the flow infiltrates the warp in parallel, $\varphi = 0$, or oblique direction, $0< \varphi < \pi /2$, ${A_{int,s}}$ and ${C_{int,s}}$ are approximated as the cross sectional area and perimeter of a truncated circular cylinder using Gauss-Kummer series for the perimeter of the resulting ellipse [5], as given by:

$$\begin{aligned} \mathop {A_{int,s}}= & {} {n_f}\pi {R^2}\sec \left( \varphi \right) \ \end{aligned}$$

(23)

$$\begin{aligned} \mathop {C_{int,s}}= & {} {n_f}\pi R\left( {1 + \sec \left( \varphi \right) } \right) \nonumber \\&\times \left( {1 + \mathop \sum \limits _{i = 1}^\infty {{\left( {\begin{array}{*{20}{c}}{1/2}\\ i\end{array}} \right) }^2}{{\left( {\frac{{\sec \left( \varphi \right) - 1}}{{\sec \left( \varphi \right) + 1}}} \right) }^{2i}}} \right) \ \end{aligned}$$

(24)

If the impregnation occurs perpendicular to the fibers, $\varphi = \pi /2$, the following equations are used:

$$\begin{aligned} \mathop {A_{int,s}}= & {} 2{n_f}{L_f}R\ \end{aligned}$$

(25)

$$\begin{aligned} \mathop {C_{int,s}}\approx & {} 2{n_f}{L_f}\ \end{aligned}$$

(26)

On the other hand, for the transverse tow (weft), it is accepted that the fluid front moves inward perpendicular to the fibers and it is used the mean capillary pressure given in [38] considering an hexagonal array of fibers:

$$\begin{aligned} \mathop {p_{cap,r}}= & {} \left( {\sigma /R} \right) .\frac{{\left[ {\sin \left( {{\alpha _{sup}} + \theta } \right) - \mathrm{{sin}}\left( {{\alpha _{inf}} + \theta } \right) } \right] }}{{\left( {\frac{{5\pi }}{6}\left( {1 + \eta } \right) - 1 - \sqrt{3} /2} \right) }} \end{aligned}$$

(27)

$$\begin{aligned} \mathop \eta= & {} d/R = \sqrt{\pi /\left( {2\sqrt{3} \left( {1 - {\varepsilon _t}} \right) } \right) } - 1\mathrm{{\;}}\;\ \end{aligned}$$

(28)

$$\begin{aligned} \mathop {\alpha _{sup}}\cong & {} \left( {\pi /2 - \theta } \right) \ \end{aligned}$$

(29)

$$\begin{aligned} \mathop {\alpha _{inf}}\cong & {} \left( {\theta - \pi /2} \right) \ \end{aligned}$$

(30)

where $R\;$ and $d$ are the fiber radius and half-distance between fibers, respectively. The model of Gebart [16] for a hexagonal array is used to calculate the permeabilities in the principal directions:

$$\begin{aligned} \mathop {K_1}= & {} 8{R^2} \cdot {\left( {1 - {V_f}} \right) ^3}\Big /\left( {c \cdot {{\left( {{V_f}} \right) }^2}} \right) \;\ \end{aligned}$$

(31)

$$\begin{aligned} \mathop {K_2}= & {} {c_1}{\left( {\sqrt{{V_{f,max}}/{V_f}} - 1} \right) ^{5/2}}{R^2}\ \end{aligned}$$

(32)

where ${V_f} = 1 - {\varepsilon _t}$ is the fiber volume fraction, while the parameters $c,{c_1}$ and ${V_{f,max}}$ are given by the following expressions:

$$\begin{aligned} \mathop c= & {} 53\ \end{aligned}$$

(33)

$$\begin{aligned} \mathop {c_1}= & {} 16/ ( {9\pi \sqrt{6} } )\ \end{aligned}$$

(34)

$$\begin{aligned} \mathop {V_{f,max}}= & {} \pi / ( {2\sqrt{3} } )\ \end{aligned}$$

(35)

3 Integral equation formulations and numerical techniques

The Stokes–Brinkman problem of this work is solved using direct BEM and DR-BEM for the channel and tows domains, respectively, with the corresponding matching and boundary conditions presented in Section 2. The integral formulation for the Stokes equation is the following:

$$\begin{aligned} \mathop {c_{ij}}\left( \xi \right) {u_j}\left( \xi \right)&= \mathop \int \limits _S^{} K_{ij}^{\left( s \right) }\left( {\xi ,y} \right) {u_j}\left( y \right) d{S_y} \nonumber \\&\quad - \mathop \int \limits _S^{} U_i^{j\left( s \right) }\left( {\xi ,y} \right) {t_j}\left( y \right) d{S_y}\ \end{aligned}$$

(36)

where ${c_{ij}} = \left( {\alpha /2\pi } \right) {\delta _{ij}}$, with $\alpha$ as the solid angle in the source point, whose value is $\alpha = \pi \;\;$for points located over a smooth contour. For points located inside the domain, ${c_{ij}} = {\delta _{ij}}$. In (36), ${u_j}$ and ${t_j}$ are the velocities and tractions in the field points, respectively.

The fundamental solutions of the integral kernels of (36) are given by:

$$\begin{aligned} \ U_i^{j\left( s \right) }\left( {\xi ,y} \right)= & {} - \frac{1}{{4\pi }}\left[ {\ln \left( {\frac{1}{r}} \right) {\delta _{ij}} + \frac{{\left( {{\xi _i} - {y_i}} \right) \left( {{\xi _j} - {y_j}} \right) }}{{{r^2}}}} \right] \ \end{aligned}$$

(37)

$$\begin{aligned} \ K_{ij}^{\left( s \right) }\left( {\xi ,y} \right)= & {} - \frac{1}{\pi }\frac{{\left( {{\xi _i} - {y_i}} \right) \left( {{\xi _j} - {y_j}} \right) \left( {{\xi _k} - {y_k}} \right) {n_k}\left( y \right) }}{{{r^4}}}\ \end{aligned}$$

(38)

$$\begin{aligned} r= & {} \left| {\xi - y} \right| \ \end{aligned}$$

(39)

where $\xi$ and $y$ are the source and field points, respectively.

On the other hand, for the anisotropic Brinkman equation, Khor et al [26] deduced fundamental solutions in the transformed Fourier space, which reduce to the isotropic fundamental solutions in the real space when ${\chi _1} = {\chi _2}$ [27, 62]. However, the transformation of these functions to the real space in the anisotropic case is not a trivial problem and to avoid these difficulties, a boundary-domain integral formulation in terms of the Stokes fundamental solutions is considered for the Brinkman equation and the resulting domain integral is transformed into a boundary integral using DR-BEM [42]. The integral formulation is as follows:

$$\begin{aligned} {c_{ij}}\left( \xi \right) {u_j}\left( \xi \right) =&\mathop \int \limits _S^{} {K_{ij}}\left( {\xi ,y} \right) {u_j}\left( y \right) d{S_y} \nonumber \\&- \mathop \int \limits _S^{} U_i^j\left( {\xi ,y} \right) {t_j}\left( y \right) d{S_y}\nonumber \\&+ \mathop \int \limits _\mathrm{{\Omega }}^{} U_i^j\left( {\xi ,y} \right) {g_j}\left( y \right) d{\mathrm{{\Omega }}_y} \end{aligned}$$

(40)

In DR-BEM, the non-homogeneous term, ${g_j}\left( y \right) =\chi _j^2{u_j}\left( y \right)$, is approximated using Radial Basis Function (RBF) interpolation given by Augmented Thin Plate Splines (ATPS). The augmented part of a generalized thin plate spline of order $n$ is a polynomial of order $n - 1$ that is added to obtain an invertible interpolation matrix [18]. In the present work, $n = 2$ and the form of the ATPS is as follows:

$$\begin{aligned} \ {f^m}\left( y \right)= & {} {r^2}\ln \left( r \right) \;for\;m = 1...,{N_B} + {N_L}\ \end{aligned}$$

(41)

$$\begin{aligned} \ {f^m}\left( y \right)= & {} 1\;\;\;\;for\;m = {N_B} + {N_L} + 1\ \end{aligned}$$

(42)

$$\begin{aligned} \ {f^m}\left( y \right)= & {} {y_1}\;\;\;for\;m = {N_B} + {N_L} + 2\ \end{aligned}$$

(43)

$$\begin{aligned} {f^m}\left( y \right)= & {} {y_2}\;\;\;for\;m = {N_B} + {N_L} + 3\ \end{aligned}$$

(44)

where ${N_B}$ is the number of boundary points, ${N_L}$ is the number of interior points and $r\left( {y,{z^m}} \right) = \left| {y - {z^m}} \right|$ is the distance between the field points, $y$, and the trial points, ${z^m}$. Accordingly, the non-homogeneous term can be expanded as follows:

$$\begin{aligned} \ {g_j}\left( y \right) = \mathop \sum \limits _{m = 1}^{{N_B} + {N_L} + 3} \alpha _l^m{\delta _{jl}}{f^m}\left( y \right) \ , \qquad j = 1,2;\;l = 1,2\ \end{aligned}$$

(45)

where $\alpha _l^m$ represent the approximation coefficients in the direction l. The ATPS represented in (41) to (44) requires the addition of orthogonality conditions, as shown in the following equation:

$$\begin{aligned} \ \mathop \sum \limits _{m = 1}^{{N_B} + {N_L}} \alpha _l^m = \mathop \sum \limits _{m = 1}^{{N_B} + {N_L}} \alpha _l^my_1^m = \mathop \sum \limits _{m = 1}^{{N_B} + {N_L}} \alpha _l^my_2^m = 0\ \end{aligned}$$

(46)

After substituting (45) into (40), the integral representation takes the following form:

$$\begin{aligned} \ {c_{ij}}\left( \xi \right) {u_j}\left( \xi \right) =&\mathop \int \limits _S^{} {K_{ij}}\left( {\xi ,y} \right) {u_j}\left( y \right) d{S_y}\nonumber \\&- \mathop \int \limits _S^{} U_i^j\left( {\xi ,y} \right) {t_j}\left( y \right) d{S_y} \nonumber \\&+ \mathop \sum \limits _{m = 1}^{{N_B} + {N_L} + 3} \alpha _l^m\mathop \int \limits _\mathrm{{\Omega }}^{} U_i^j\left( {\xi ,y} \right) {\delta _{jl}}{f^m}\left( y \right) d{\mathrm{{\Omega }}_y}\ \end{aligned}$$

(47)

The transformation of the domain integral into a boundary integral is accomplished by defining the following auxiliary Stokes field:

$$\begin{aligned}&\frac{{\partial {{\hat{u}}_j}^{\left( {ml} \right) }}}{{\partial {y_j}}} = 0 \end{aligned}$$

(48)

$$\begin{aligned}&\mathop \mu \frac{{{\partial ^2}{{\hat{u}}_j}^{\left( {ml} \right) }}}{{\partial {y_k}\partial {y_k}}} - \frac{{\partial {{\hat{p}}^{\left( {ml} \right) }}}}{{\partial {y_j}}} = {f^m}\left( y \right) {\delta _{jl}} \end{aligned}$$

(49)

with the particular solutions for the ATPS given in [10].

The substitution of the auxiliary field defined in (48) and (49) into (47) and the application of the Green’s identities in the domain integral, lead to the following boundary-only integral representation:

$$\begin{aligned} {c_{ij}}\left( \xi \right) {u_j}\left( \xi \right) =&\mathop \int \limits _S^{} {K_{ij}}\left( {\xi ,y} \right) {u_j}\left( y \right) d{S_y} \nonumber \\&- \mathop \int \limits _S^{} U_i^j\left( {\xi ,y} \right) {t_j}\left( y \right) d{S_y} \nonumber \\&+ \mathop \sum \limits _{m = 1}^{{N_B} + {N_L} + 3} \alpha _l^m\ ( {c_{ij}}\left( \xi \right) {{\hat{u}}_j}^{\left( {ml} \right) }\left( \xi \right) \nonumber \\&- \mathop \int \limits _S^{} {K_{ij}}\left( {\xi ,y} \right) {{\hat{u}}_j}^{\left( {ml} \right) }\left( y \right) d{S_y} \nonumber \\&+ \mathop \int \limits _S^{} U_i^j\left( {\xi ,y} \right) {{\hat{t}}_j}^{\left( {ml} \right) }\left( y \right) d{S_y}) \end{aligned}$$

(50)

where the coefficients $\alpha _l^m$ are given in terms of the inverse of the interpolating matrix obtained by collocation of (45) at ${N_B}$ boundary nodes and ${N_L}$ internal nodes.

The singularities arising in the kernels ${K_{ij}}$ and $U_i^j$ of (36) and (50) are dealt with the rigid body motion principle [45] and the Telles transformation [61], respectively. In these equations, the boundary and the physical variables are discretized using quadratic isoparametric interpolation. Additionally, discontinuous shape functions with a collocation factor of ${\alpha _{dis}} = 2/3$ are employed at the corners of the problem domain [69]. After the discretization of the contour and variables and the assembly of the resultant matrices, by considering the corresponding boundary and matching conditions, a linear system of equations is obtained, which is solved using singular value decomposition (SVD) to consider cases where the condition number of the global matrix is very large due to large differences on the magnitude of the problem parameters. In the DR-BEM formulation the coordinate systems of the saturated porous domains are continuously updated as the fluid front advances, in such a way that each coordinate system is located in the corresponding centroid of each saturated domain to avoid the increment of the condition number of the final system as the filling takes place.

First order Euler integration of the kinematic condition (18) is used to track the moving fronts. As an explicit time stepping-algorithm is used, the time step needs to be restricted to small values. The Courant-Friedrich-Levy (CFL) condition is used to guarantee the stability of the solution as time progresses, with the CFL constant changing as a function of the capillary ratio, ${C_{cap}}$. As ${C_{cap}}$ increases, smaller values of this constant are required, leading to shorter time intervals. Additional geometrical restrictions shall be considered to compute the time interval in order to avoid the crossing of the evolution points as the fluid front advances and to avoid the advancement of the points beyond the limits between the two regions considered (channels and bundles) or beyond the boundaries of the global domain. At a point ${x^i}$ on the moving fluid front, both the unit normal vector, ${\hat{n}^i}$, and the curvature, ${\kappa ^i}$, are computed numerically using the following fourth-order lagrangian polynomial [52]:

$$\begin{aligned} \mathop {\left( {x_{j}^{'}}\right) ^{i}}= & {} 1/6\left( {x_j^{i-2}-8x_j^{i-1}+8x_j^{i+1}-x_j^{i+2}}\right) ,\;j = 1,2\ \end{aligned}$$

(51)

$$\begin{aligned} \ {\left( {x_j^{''}} \right) ^i}= & {} \frac{{\left( { - x_j^{i - 2} + 16x_j^{i - 1} - 30x_j^i + 16x_j^{i + 1} - x_j^{i + 2}} \right) }}{3},\nonumber \\&j = 1,2 \end{aligned}$$

(52)

$$\begin{aligned} {\hat{n}^{i}}= & {} \frac{1}{{\left( {\sqrt{{{\left( {{{\left( {x_1^{'}} \right) }^i}} \right) }^2} + {{\left( {{{\left( {x_2^{'}} \right) }^i}} \right) }^2}} } \right) }} \cdot \left( {{{\left( {x_2^{'}} \right) }^i}, - {{\left( {x_1^{'}} \right) }^i}} \right) \ \end{aligned}$$

(53)

$$\begin{aligned} {\kappa ^i}= & {} \frac{{\left[ {{{\left( {x_1^{'}} \right) }^i}{{\left( {x_2^{''}} \right) }^i} - {{\left( {x_2^{'}} \right) }^i}{{\left( {x_1^{''}} \right) }^i}} \right] }}{{{{\left[ {{{\left( {{{\left( {x_1^{'}} \right) }^i}} \right) }^2} + {{\left( {{{\left( {x_2^{'}} \right) }^i}} \right) }^2}} \right] }^{3/2}}}} \end{aligned}$$

(54)

Once the meshes of the moving fronts have been reconstructed at the current time step and the normal and curvatures have been computed, the BEM/DR-BEM algorithm is used to calculate the velocity of the moving fronts and the cycle is repeated again in a quasi-static approach given the low Reynolds number of the problem. A more detailed description of the tracking technique of the fluid front can be found in a work recently published [43].

4 Results and discussion

4.1 Assessment of accuracy and convergence

To validate the proposed BEM/DR-BEM scheme for the solution of coupled Stokes–Brinkman problems a fully developed flow in two horizontal layers, porous medium and channel, is considered as shown in Fig. 1. This problem admits analytical solution and has been used by other authors to validate FEM codes [11, 23, 58]. In this problem, the inlet and outlet boundaries are subjected to pressure boundary conditions and the upper and lower ones, to symmetry boundary conditions. Both continuous and jump stress matching conditions at the interface between the two layers are considered. Equations (55) and (56) give the analytical solution for the velocity profiles (with $\phi =\mu /{\mu _{eff}}$), which is only valid provided that the boundary layer thickness of the Brinkman flow is smaller than the height of the porous medium, in such a way that the solution tends to a Darcy flow in the lower part of the porous medium domain.

$$\begin{aligned} \widehat{\mathrm{{u}}_x^s}\left( {\hat{y}} \right) =&-\left( {\hat{H}/2}\right) \cdot \left( {\hat{y} -{{\hat{y}}^2}/\hat{H}} \right) \cdot {\left( {\Delta \hat{p}/\Delta \hat{x}}\right) ^s} \nonumber \\&- \left( {\hat{H}/\left( {2{L^*}} \right) } \right) \sqrt{\phi {K_1}} /\left( {1 + \beta \sqrt{\phi }} \right) {\left( {\Delta \hat{p}/\Delta \hat{x}} \right) ^s} \nonumber \\&- \;{K_1}/\left( {{L^*}^2\left( {1 + \beta \sqrt{\phi }} \right) \phi } \right) {\left( {\Delta \hat{p}/\Delta \hat{x}} \right) ^b}\ \end{aligned}$$

(55)

$$\begin{aligned} \widehat{\mathrm{{u}}_x^b}\left( {\hat{y}}\right) =&-{K_1}/\left( {{L^*}^2\phi }\right) {\left( {\Delta \hat{p}/\Delta \hat{x}}\right) ^b} \nonumber \\&-\frac{{\left[ {\left( {\hat{H}/\left( {2{L^*}}\right) }\right) \sqrt{\phi {K_1}}{{\left( {\Delta \hat{p}/\Delta \hat{x}}\right) }^s}+{K_1}/\left( {{L^*}^2\phi }\right) {{\left( {\Delta \hat{p}/\Delta \hat{x}}\right) }^b}}\right] }}{{\left( {1 + \beta \sqrt{\phi }} \right) }}\nonumber \\&\times {e^{\left( {\sqrt{\varphi /{K_1}} \hat{y}{L^*}} \right) }} + \;{K_1}/\left( {{L^*}^2\phi } \right) {\left( {\Delta \hat{p}/\Delta \hat{x}} \right) ^b}{e^{\left( {\sqrt{\varphi /{K_1}} \hat{y}{L^*}} \right) }} \end{aligned}$$

(56)

Fig. 1

Scheme of coupled problem Stokes–Brinkman admitting analytical solution

This problem was solved by [23] using a modified Brinkman approach for the whole domain that reduces to the Stokes flow in the channel domain. In this approach, the stress jump condition is incorporated by a level-set formulation and the numerical solution is obtained by the finite element method (FEM). The authors considered the following parameters in the simulations: $H = 1~\mathrm{cm}$, $\beta = 0.7,\;\;{\mu _{eff}} = \mu /{\varepsilon _t}$ with ${\varepsilon _t} = 0.5$, and $K = {10^{ - 4}}c{m^2}$, where $K$ is the permeability of the porous medium in the flow direction. Considering a characteristic length of ${L^*} = H$ for this problem, the inverse Darcian number is ${\chi ^2} = 5.00 \times {10^3}$. Four mesh-sizes were evaluated, $h = 0.1~\mathrm{cm}$, $h = 0.05~\mathrm{cm}$, $h = 0.01~\mathrm{cm}$ and$\;h = 0.005~\mathrm{cm}$, using a uniform distribution of a regular mesh of square elements over the entire domain, with h as the length of the side of one square element, obtaining a total number of elements in each case equal to $0.1/{h^2}$. In a similar fashion, in the present case, h represents the size of one quadratic element of the contour mesh, which leads to ${N_E} = \left( {3 \times 0.1 + 2 \times 1} \right) /h$, ${N_B} = 4\left( {0.6/h + 1} \right)$ and ${N_L} = \left( {0.2/h - 1} \right) \times \left( {1/h - 1} \right)$, with ${N_E}$ as the number of boundary elements of the whole domain (Stokes and Brinkman), whereas ${N_B}$ and ${N_L}$ are the boundary and interior DR-BEM trial points in the Brinkman domain, respectively. The characteristics of the meshes for this particular case and the corresponding L$^2$ relative error norms of the BEM/DR-BEM solution are presented in Table 1, as well as the convergence rate, ${n_c}$. The L$^2$ relative error norm is defined as:

$$\begin{aligned} {L^2} = {\left( {\frac{{\mathop \sum \nolimits _{i = 1}^{{N_B} + {N_L}} {{\left( {{{\widehat{{u_x}}}_{anal}} - {{\widehat{{u_x}}}_{num}}} \right) }^2}}}{{\mathop \sum \nolimits _{i = 1}^{{N_B} + {N_L}} {{\left( {{{\widehat{{u_x}}}_{anal}}} \right) }^2}}}} \right) ^{1/2}}, \end{aligned}$$

(57)

where ${\widehat{{u_x}}_{anal}}$ and ${\widehat{{u_x}}_{num}}$ are the analytical and numerical solutions of the dimensionless horizontal velocity, respectively. The convergence rate, $n_c$, corresponds to the exponent of the power curve that fits to the data of $L^2$ relative error norm versus Element Size, i.e., ${L^2} = a.{h^{{n_c}}}$, where a is a constant and $n_c$ is the slope in a log-log plot of the $L^2$ relative error versus Element Size (see Fig. 2 with the corresponding coefficient of determination $R^2=0.988$).

Table 1 Characteristics of meshes and L$^2$ relative error norms of BEM/DR-BEM solution

According to [3], the application of the Finite Element Method (FEM) to fluid flow problems implies the use of mixed formulations where multiple field variables shall be considered, like the velocity and pressure in the case of an incompressible fluid flow. In such a cases, the discretization scheme of the domain should fulfill three conditions with the purpose to assure the solvability, stability and optimality of the FEM solution, namely, consistency, ellipticity and inf-sup condition, being the last one the most difficult to satisfy due to the choice of numerical constants to be introduced in the formulation or to the modification of the original FEM scheme in order to satisfy implicitly such a condition. The statement of the Inf-Sup condition depends on the problem being analyzed; in the case of Stokes–Darcy problems, this condition is detailed in [36]. For both Stokes and Brinkman flows, some distorted FEM meshes could not satisfy the Inf-Sup condition, resulting in spurious pressure modes (for more details see [3]). On the other hand, in the BEM/DR-BEM formulation for both flow fields, spurious pressure modes are not possible due to the unique relationship between the velocity and pressure fundamental solutions in the integral formulation of the problems. However, significant numerical errors and inaccuracy can be found by using very distorted BEM meshes, due to ill conditioning of the global matrix system and/or near singularities in the numerical integrations. Therefore, in our scheme, it is convenient to avoid a distorted mesh, i.e., a mesh having adjacent elements with very dissimilar sizes, to preserve the accuracy of the solution. As mentioned before, since the points at the fluid front are not uniformly spaced just after the fluid front advancement, we have implemented a remeshing algorithm with the purpose to obtain a balanced mesh in every time instant and avoid in this way the loss of accuracy in the solution.

The comparison of the present BEM/DR-BEM scheme with the FEM scheme of [23] is shown in Fig. 3a, b, where a semi-log plot is adopted in order to distinguish the velocities in the porous domain, which can be several orders of magnitude lower than the velocities in the channel. In the Brinkman domain, the positions of the interior trial points of the RBF interpolation are determined by an extension into the domain of the boundary mesh points, with exception of the points close to the corners. In both schemes, BEM/DR-BEM and FEM, the numerical solution converges to the analytical one, reaching a high order of accuracy when using the finer mesh, which corresponds to a value of $\ {h = 0.005~\mathrm{cm}}$, i.e., 4.000 square finite elements uniformly distributed for the FEM scheme, and, in the case of the BEM/DR-BEM scheme, 460 boundary elements distributed over the external boundary and interface between the two domains (Stokes and Brinkman), with 484 boundary and 7761 interior interpolation points in the porous domain (Brinkman), as shown in Table 1.

Fig. 2

Plot of convergence of the BEM/DR-BEM solution

Fig. 3

Velocity profiles for coupled Stokes–Brinkman problem. a BEM/DR-BEM approach. b FEM approach

Two main differences between the two results can be observed. Firstly, the BEM/DR-BEM shows high accuracy in the Stokes velocity profile, channel flow, for all mesh sizes, while the Brinkman velocity profile is over-predicted for the coarser meshes (Fig. 3a). On the other hand, the FEM scheme always predicts an accurate velocity profile in the porous medium (Brinkman), but the velocity profile in the channel (Stokes) is under-predicted for the coarser meshes (Fig. 3b). As commented in [23] the observed behavior in the FEM solution is due to the interpolation scheme used in the level-set formulation. To be more specific, it is necessary to mention that a single equivalent momentum equation for the coupled Stokes–Brinkman domain was considered in [23], which is essentially a Stokes equation modified with permeability and jump stress terms to account for the fluid flow in the porous medium and the stress matching condition in the interface, respectively. Additionally, the domain geometry was defined by a level set function, $\varPhi$, where $\varPhi =0$ at the interface, $\varPhi >0$ at the free-fluid domain and $\varPhi <0$ at the porous medium. When $\left| \varPhi \right| < {\varepsilon _{int}}$ , with $\varepsilon _{int}$ as the half thickness of the diffuse interfacial region, an interpolation function is defined to express the permeability and jump stress terms as a function of $\varPhi$ and $\varepsilon _{int}$, and the errors of such interpolation led to greater numerical errors in the Stokes velocity profile, as explained in [23]. On the other hand, the observed behavior of the numerical solution with the mesh size in the BEM/DR-BEM approach is due to the approximation error on the evaluation of the volume integral in the integral representation formula (40) used to represent the Brinkman flow. As mentioned before, in the case of the Stokes flow an exact only-boundary integral formulation is known, equation (36), requiring only the discretization of the boundary integral densities, $u_i$ and $t_i$, without any additional approximation. The discretization of the densities, $u_i$ and $t_i$, is also required in (40), as well as the corresponding approximation of the volume integral. The transformation of the domain integral appearing in (40) into the boundary integrals arising in (50) by DR-BEM approximation involves the interpolation of the non-homogeneous term, $g_j(y)$, using Augmented Thin Plate Splines (ATPS) as shown in (45). In this case, the approximation error of such interpolation, which is greater as the permeability is lower and/or the mesh is coarser, is the principal error source of the Brinkman velocity profiles. It is worth-mentioning that in the BEM /DR-BEM results no oscillations are present in points close to the interface Stokes–Brinkman for any mesh-size, contrary to the FEM scheme used in [23] where oscillations can be noticed for the coarser meshes (see details of Fig. 3a, b).

Table 2 Influence of non-dimensional parameters ${\chi ^2}$ and $\beta$ on the accuracy of the solution

To analyze the influence of the non-dimensional parameters ${\chi ^2}$ and $\beta$ on the accuracy of the solution, several simulations were performed using the data summarized in Table 2. As observed, simulations for values of ${\chi ^2} = 1 \times {10^4},\;\;{\chi ^2} = 1 \times {10^3}$, ${\chi ^2} = 1 \times {10^2}$ and ${\chi ^2} = 18$ were carried out, considering in each case three different values of the jump stress coefficient, namely, $\beta = 0,\;\;\beta = 0.5$, and $\beta = 1.0$. In all cases, the same number of boundary elements and interpolation trial points were considered, namely, 49 boundary elements, 56 boundary and 95 interior interpolation points in the porous domain (Brinkman). In Table 2 the obtained L$^2$ relative error norm for each case is also reported. As observed, the accuracy of the solution improves as the value of $\beta$ increases for ${\chi ^2} = 1 \times {10^4},\;\;{\chi ^2} = 1 \times {10^3}$ and ${\chi ^2} = 1 \times {10^2}$, however, for the case of ${\chi ^2} = 18$, this behavior is reversed. Besides, for a given value of $\beta$, a higher accuracy is found as ${\chi ^2}$ decreases, which is reasonable because in the BEM/DR-BEM scheme the approximation error of the non-homogeneous term of the Brinkman equation has a stronger influence on the results as ${\chi ^2}$ is larger.

The velocity profiles corresponding to the simulations of Table 2 and their comparison with the analytical solutions given by (55) and (56) are presented in Fig. 4a–d. The magnitude of the Stokes velocity increases as the value of $\beta$ reduces, being this effect more significant as ${\chi ^2}$ is lower (see Fig. 4d). As expected, for a constant$\;\beta$, the thickness of the boundary layer increases with the reduction of ${\chi ^2}$. On the other hand, for a constant value of ${\chi ^2}$, the boundary layer thickness increases as the value of $\beta$ reduces, being this change more notorious as ${\chi ^2}$ is smaller. Similar results to those ones shown in Fig. 4a–d were reported in [58] using a FEM approach, which means that the present scheme is consistent with previously reported results.

Fig. 4

Graphical comparison between analytical and numerical solutions for coupled Stokes–Brinkman problem. a ${\chi ^2} = 1 \times {10^4}$, b $\;{\chi ^2} = 1 \times {10^3}$, c $\;{\chi ^2} = 1 \times {10^2}$, d ${\chi ^2} = 18$

Fig. 5

Scheme of problem of simultaneous filling of a RUC

4.2 Statement of problem of void formation, simulation data and void characterization

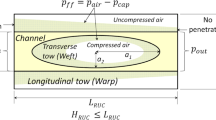
In the processing of composites materials, different sorts of RUC architectures can be examined for dual-scale fibrous reinforcements. In this section, it is considered a 2D geometry emulating a longitudinal plane of a cross ply fabric (Fig. 5). The unidirectional filling of 3D RUC’s of fabrics has been recently considered by superposition of 2D simulations at several longitudinal planes of the RUC, showing good agreement with experimental results [7]. Therefore, we can infer that the parametric study for the 2D geometry represented in the Fig. 5 can be useful to understand the influence of some factors on the void formation in cross ply fabrics.

Simulations considered in the following sections are classified into four different series. Series 1 to 3 provide different data to be used in the simulations performed with the Stokes–Brinkman formulation, while Serie 4 defines the data of the simulations run with the Stokes–Darcy formulation. The parameters of the Serie 1, which is taken as the reference case, are presented in Table 3, where the fixed parameters are prescribed and the calculated parameters are determined from the former ones. The jump stress coefficient used in the simulations of Serie 1, $\beta = 1.24$, was calculated using the model of Valdés-Parada et al. [64, 65] together with the Larson-Hidgon coefficient in the channel-tow interface, ${\gamma ^*}$ [29] :

$$\begin{aligned} \mathop \beta= & {} \frac{{2\varepsilon _{ct}^{3/2}}}{{3\sqrt{{\gamma ^*}} {{\left( {1 + {\varepsilon _{ct}}} \right) }^3}}}\ \end{aligned}$$

(58)

$$\begin{aligned} \mathop {\gamma ^*}= & {} \left( {2 \times {{10}^{ - 3}}} \right) /{\left( {1 - {\varepsilon _{ct}}} \right) ^{2/3}}\ \end{aligned}$$

(59)

Table 3 Simulation data for the reference case (Serie 1)

where the porosity of the channel-tow interface, ${\varepsilon _{ct}}$, is approximated as the porosity of the bundle, ${\varepsilon _t}$, and ${\mu _{eff}} = \mu /{\varepsilon _t}$. In Serie 2, the jump stress coefficient is changed to $\beta = 0.7$, corresponding to the approximation considered in [23], and ${\mu _{eff}} = \mu /{\varepsilon _t}$ as before. For Serie 3, the continuous stress condition is considered, i.e. $\beta = 0$, and ${\mu _{eff}} = \mu$. For the jump stress cases (Serie 1 and 2), considering a characteristic length of ${L^*} = {H_t}$, where ${H_t}$ is the tow height (see Fig. 5), the inverse Darcian numbers in the principal directions are $\chi _1^2 = 1.40 \times {10^3}$ and $\chi _2^2 = 6.80 \times {10^3}$, whereas for the continuous stress case (Serie 3), the corresponding values are $\chi _1^2 = 2.26 \times {10^3}$ and $\chi _2^2 = 1.10 \times {10^4}$. For simulations of Serie 4, a Stokes–Darcy formulation is considered and therefore the stress jump condition is not applicable. For this type of formulation, uniqueness of the solution requires continuity of surface tractions and a jump condition for the interfacial tangential velocities given by the Beavers–Joseph slip condition, for more details see (71) and (72). The slip coefficient,$\;\gamma$, of the slip condition, see (71), is usually found by mean of experiments, but when the ratio between the height of the porous medium and the square root of the permeability is very high, a good approximation for this coefficient is $\gamma = 1/\left( {{\varepsilon _t}^{1/2}} \right)$ [22]. The formulation is completed by requiring continuity of the normal component of the interfacial velocities, see (70). In Section 4.3, the results obtained using the Stokes–Darcy formulation are compared with those ones obtained with the Stokes–Brinkman formulation.

As a constant inlet pressure condition is considered in all simulations, the comparison between the pressure and capillary forces is described by the capillary ratio, ${C_{cap}} = {P_{cap,max}}/{P_{in}}$, as defined in [30], where ${P_{cap,max}}$ and ${P_{in}}$ stand for the maximum capillary pressure and inlet pressure, respectively. For Series 1, 2 and 4, three different capillary ratios are contemplated: ${C_{cap}} = 1 \times {10^{ - 2}},\;{C_{cap}} = 1 \times {10^{ - 1}}$ and ${C_{cap}} = 5 \times {10^{ - 1}}$, whereas for Serie 3 only the lower value of ${C_{cap}}$ is taking into account, i.e, ${C_{cap}} = 1 \times {10^{ - 2}}$. For each simulation the following parameters are achieved:

• Size, shape and location of voids, expressed as (see Fig. 5):

  $$\begin{aligned} Size^{*}= & {} {A_{void}}/\left( {2{A_{RUC}}} \right) \ \end{aligned}$$

  (60)
  $$\begin{aligned} \ Shape= & {} a/b\ \end{aligned}$$

  (61)
  $$\begin{aligned} \ Location= & {} {l_{void}}/\left( {2{a_1}} \right) \ \end{aligned}$$

  (62)

  where ${A_{void}}$ is the void area, ${A_{RUC}}$ is the RUC area, a and b are the semi-major and semi-minor axes of the ellipse circumscribing the void, ${a_1}$ is the semi-major axis of the weft and ${l_{void}}$ is the distance between the front edge of the weft and rear edge of the void.

• Dimensionless time, $\hat{t}$, defined by (6), and normalized time that is defined as ${t^*} = t/{t_{filling}}$, in which ${t_{filling}}$ is the total filling time of the RUC. In this work, two adjacent RUC’s are considered and the filling stops when the partial equilibrium of the bubble formed in the second RUC has been reached.

• RUC’s saturation versus Normalized time

• Compression of the voids, defined by the following compressibility ratio:

  $$\begin{aligned} \mathop \psi = \frac{{V_{void}^o - V_{void}^f}}{{V_{void}^f}}\ \end{aligned}$$

  (63)

  where $V_{void}^o$ and $V_{void}^f$ stand for the initial and final volume of the void, respectively.

The simulations of the Sects. 4.3 and 4.4 are performed with the same mesh-size used in the simulations of Fig. 4. The number of boundary elements and interpolation points changes continuously as the fluid front evolves.

4.3 Comparison between Stokes–Darcy and Stokes–Brinkman approaches

4.3.1 Description of the Stokes–Darcy approach

Two coupled domains shall be considered in the mesoscopic modeling of dual-scale fibrous reinforcements, namely, channels and tows. The modeling of the flow in the porous media (tows) can be done by the Brinkman equation, which reduces to the Darcy equation when the permeability is very low. Despite that the majority of cases of composite processing involve low permeability tows and, therefore, are prone to be modeled by the Darcy approximation, some authors prefer to use the Brinkman equation in its original form [11, 23, 58]. This is due to the possibility of imposing explicitly the matching conditions at the channel-tow interface in terms of the interfacial velocity and surface traction components, given that the Brinkman and Stokes partial differential equations are of the same order. As expected, several authors have used the Darcy equation to model the flow in the tows [24, 43, 60], but, considering that this is a first order partial differential equation, a jump matching condition on the tangential velocities at the channel-tow interface is required, which is linear proportional to the Stokes surface traction in the channel and is function of a slip coefficient, $\gamma$ (Beavers–Joseph slip condition). The value of the slip coefficient, $\gamma$, appearing in this condition is still matter of controversy. Considering that both approaches, Stokes–Brinkman and Stokes–Darcy, have been used in the literature and are consistent with the problem dealt here, the present section is devoted to compare the results of void formation obtained by both of them, namely, Serie 1 for Stokes–Brinkman and Serie 4 for Stokes–Darcy. It is important to mention that a coupled solution system is considered for both approaches, i.e., the equations of the free-fluid and porous medium domains, as well as the matching conditions, are directly included in a single solution system, which could be ill-conditioned as mentioned before. In other works, decoupling strategies have been used for the solution of Stokes–Darcy problems, such as: iterative subdomain methods [8], Lagrange multipliers [31], two-grid method [37], among others. For instance, Mu and Zhu [36], who used the Saffman matching condition for the tangential velocities (which comes from disregarding the tangential Darcy velocity in the Beavers–Joseph condition), proposed and assessed a decoupling FEM methodology based on interface approximations via temporal extrapolation for non stationary cases. This methodology allows solving two decoupled sub-problems independently by invoking conventional Stokes and Darcy solvers. After analyzing the behavior of the convergence rate and approximation errors with the time step and element size regarding a coupled strategy, it was concluded that the proposed methodology is computationally effective for this kind of problems.

In dimensionless form, the Darcy equation is as follows:

$$\begin{aligned} \mathop {\hat{u}_i} = - K_i^*\left( {\frac{{\partial {{\hat{p}}}}}{{\partial {{\hat{x}}_i}}}} \right) \ \end{aligned}$$

(64)

where $K_i^* = {K_i}/{\left( {{L^*}} \right) ^2}$ is the non-dimensional permeability in the principal direction i, $\hat{p} = p/\left( {\mu .{U_{max}}/{L^*}} \right)$ is the non-dimensional pressure, $\widehat{{x_i}} = {x_i}/{L^*}$ and ${\hat{u}_i} = {u_i}/{U_{max}}$ are the non-dimensional coordinate and non-dimensional velocity in direction i, respectively. The integral representation formula for the pressure field when the Darcy velocity (64) satisfies mass conservation (1) is given as (for more details see [6, 13, 44]):

$$\begin{aligned} \mathop c\left( \xi \right) p\left( \xi \right) =\mathop \int \limits _S^{} {p^*}\left( {\xi ,y}\right) q\left( y\right) d{S_y}-\mathop \int \limits _S^{} {q^*}\left( {\xi ,y} \right) p\left( y\right) d{S_y}\ \ \end{aligned}$$

(65)

where:

$$\begin{aligned} \ \ {p^*}\left( {\xi ,y} \right) =&- \frac{1}{{2\pi }}ln\left( {{r_e}} \right) \ \end{aligned}$$

(66)

$$\begin{aligned} \ {q^*}\left( {\xi ,y} \right) =&\frac{{{K_i}}}{{{K_e}}}\frac{{\partial {p^*}}}{{\partial {y_i}}}\left( {\xi ,y} \right) \widehat{{n_i}}\left( y \right) \nonumber \\ =&- \frac{{\left[ {\left( {{y_1} - {\xi _1}} \right) \widehat{{n_1}}\left( y \right) + \left( {{y_2} - {\xi _2}} \right) \widehat{{n_2}}\left( y \right) } \right] }}{{2\pi {{\left( {{r_e}} \right) }^2}}}\ \end{aligned}$$

(67)

$$\begin{aligned} {r_e}=&{\left[ {{{\left( {\frac{{{K_2}}}{{{K_1}}}}\right) }^{\frac{1}{2}}}{{\left( {{y_1}-{\xi _1}}\right) }^2}+{{\left( {\frac{{{K_1}}}{{{K_2}}}}\right) }^{\frac{1}{2}}}{{\left( {{y_2}-{\xi _2}}\right) }^2}}\right] ^{1/2}}\ \end{aligned}$$

(68)

$$\begin{aligned} \ {K_e} =&{\left( {{K_1}{K_2}} \right) ^{1/2}}\ \end{aligned}$$

(69)

At the channel-tow interfaces, the flow fields defined by (36) and the corresponding pressure (Stokes flow), and (64) and (65) (Darcy flow), have to satisfy the following matching conditions:

• Continuity of normal velocities:

  $$\begin{aligned} \hat{u}_i^{\left( s \right) }{\hat{n}_i} = \hat{u}_i^{\left( d \right) }{\hat{n}_i}\ \end{aligned}$$

  (70)

• Beavers–Joseph slip condition for tangential velocities:

  $$\begin{aligned} \mathop {\left( {\frac{{\partial {{\hat{u}}_i}}}{{\partial {{\hat{x}}_j}}} + \frac{{\partial {{\hat{u}}_j}}}{{\partial {{\hat{x}}_i}}}} \right) ^{\left( s \right) }}{\hat{n}_j}\widehat{{\tau _i}} = \frac{{\gamma {L^*}\left( {\hat{u}_i^{\left( d \right) } - \hat{u}_i^{\left( s \right) }} \right) \widehat{{\tau _i}}}}{{\sqrt{\left( {{K_1} + {K_2}} \right) /2} }}\ \end{aligned}$$

  (71)

• Continuity of surface tractions:

  $$\begin{aligned} \mathop {\hat{n}_i}\hat{\sigma }_{ij}^{\left( s \right) }{\hat{n}_j} = - {\hat{p}^{\left( d \right) }}\ \end{aligned}$$

  (72)

where s stands for Stokes and d stands for Darcy. Here ${\hat{n}_i}$ is the normal vector outwardly oriented from the Stokes domain, $\gamma$ is the slip coefficient, $\widehat{{\tau _i}}$ is the tangential vector, ${K_1}$ and ${K_2}$ are the main permeabilities, $\hat{\sigma }_{ij}^{\left( s \right) }$ is the dimensionless Cauchy stress tensor in the Stokes domain and ${\hat{p}^{\left( d \right) }}$ is the dimensionless pressure in the Darcy domain. In the Beavers–Joseph condition (71), the tangential Darcy velocity cannot be disregarded a priori and is approximated in terms of the interface Darcy pressure using Lagrange interpolation functions for quadratic elements,$\;{\mathrm{{L}}_j}\left( \zeta \right)$, as follows (Sum on i and j) :

$$\begin{aligned} \ u_i^{\left( d \right) }\widehat{{\tau _i}} = - \left( {{K_i}/\mu } \right) \left( {\partial \zeta /\partial {x_i}} \right) \widehat{{\tau _i}}\left( {\partial {\mathrm{{L}}_j}\left( \zeta \right) /\partial \zeta } \right) {p_j}\ \end{aligned}$$

(73)

with $\zeta \in \left[ { - 1,1} \right]$.

At the inlet of the Darcy domain, the non-dimensional boundary condition is:

$$\begin{aligned} \mathop {\hat{p}^{\left( d \right) }} = \bar{p}{L^*}/\left( {\mu {U_{max}}} \right) \ \end{aligned}$$

(74)

while, at the fluid front, the kinematic condition is given by (18) and the dynamic condition is given by:

$$\begin{aligned} \mathop {\hat{p}^{\left( d \right) }} = {L^*}\left( {{p_a} - {p_{cap}}} \right) /\left( {\mu {U_{max}}} \right) \ \end{aligned}$$

(75)

where the parameters appearing in (74) and (75) were previously defined in Section 2. The Stokes–Darcy formulation used in this work was previously validated in [43].

Fig. 6

Comparison of void formation between Stokes–Brinkman with $\beta = 1.24$ and Stokes–Darcy with $\gamma = 1.27$

4.3.2 Comparison of the RUC filling process for ${C_{cap}=1\times 10^{-2}}$

In Fig. 6, different instants of the filling process predicted by the Stokes–Darcy (S–D) and Stokes–Brinkman (S–B) approaches are compared; in each instant, the fluid front position along the channel is the same for both approaches, S–D and S–B, but different evolution times are predicted. The fluid front shapes at the first instant look very similar for both approaches (Fig. 6a vs. b), with S–D predicting a slightly greater arrival time than S–B. As expected, due to the low value of the capillary ratio considered, ${C_{cap}} = 1 \times {10^{ - 2}}$, the fluid fronts in the channel surpass the fluid front in the tow, and, after a while, the liquid completely surrounds the first weft, see Fig. 6e, f. At the instant corresponding to Fig. 6c, d, when the liquid at the channel is approximately half the way along the first weft, 6.57% of the total filling time has elapsed according to S–D, while S–B predicts a value of 5.78%. Additionally, the minimum position of the fluid front in both the warps and the weft is barely larger for the S–D simulation. When the channel fluid fronts totally surround the first weft and merge one another, the air is trapped and the void compression starts. According to Fig. 6e, f, the fluid fronts in the warps and the weft for S–D are ahead with respect to S–B, resulting in a smaller initial void (bubble) in the case of S–D. Moreover, the real arrival time to this position is longer for S–B, but the normalized time is shorter instead. This last feature is common for all the cases analyzed in Fig. 6a–h, where the normalized times of the fluid front evolution are always shorter for the S–B simulation. Figure 6g, h corresponds to the case when the fluid front in the channel is approximately at 80% of the total length of the domain; at this point of the simulation, the time in the S–D approach is 57.2% of the total evolution time, while the time in S–B is 54.7%. This is a manifestation of the reduction of the saturation rate as the fluid front progresses with respect to the initial rate, as it is confirmed later. When the channel fluid front totally surrounds the second weft another bubble is formed, undergoing a compression process until the partial equilibrium is attained (see Fig. 6i, j), as in the first bubble. In these last two figures, it can be observed that the voids predicted by the S–D simulation are smaller than those ones predicted by S–B, with the bubble of the first weft smaller than the one of the second weft for both approaches. In general, the influence of the type of approach, S–D or S–B, on the void location is not as significant as the influence on the void size and shape, for more details see Table 4

Table 4 Characterization of final voids for S–B with $\beta = 1.24$ and S–D with $\gamma = 1.27$

4.3.3 Effect of the capillary ratio on the void characterization

Let us now consider the effect of the capillary ratio on the characterization of the voids (size, shape and location) formed in the first and second weft, and the differences among these voids when they are predicted by the two formulations considered here, S–D and S–B. In our analysis three different capillary ratios are considered: ${C_{cap}} = 1 \times {10^{ - 2}},\;{C_{cap}} = 1 \times {10^{ - 1}}$ and ${C_{cap}} = 5 \times {10^{ - 1}}$; the solutions and corresponding analysis for the former capillary ratio, ${C_{cap}} = 1 \times {10^{ - 2}}$, were already discussed in the previous sub-section (Fig. 6). As it can be noticed from (21) to (30), the maximum capillary pressure in the present case is always achieved at the symmetric boundary of the warp, and it is given by:

$$\begin{aligned} \ {P_{cap,max}} = 2\mathrm{{\;}}\sigma \cos \left( \theta \right) \left( {1 - {\varepsilon _t}} \right) /\left( {R\mathrm{{\;}}{\varepsilon _t}} \right) \ \end{aligned}$$

(76)

Consequently, in all the cases considered here, where the values of $\sigma ,\mathrm{{\;}}\theta ,\mathrm{{\;}}R$ and $\mathrm{{\;}}{\varepsilon _t}$ are kept constants, the value of the maximum capillary pressure, ${P_{cap,max}}$, is always the same and therefore different values of the capillary ratio, ${C_{cap}}$, corresponds to different values of the inlet pressure given by: ${P_{in}} = {P_{cap,max}}/{C_{cap}}$.

As it was observed before in Fig. 6i (S–B) and j (S–D), for ${C_{cap}} = 1 \times {10^{ - 2}}$ the bubble of the first weft is smaller than the one of the second weft. In such case, this happens because the first bubble supports a higher pressure considering that it is closer to the inlet and consequently experiences a higher compression. The values of the compressibility ratios obtained with both formulations, S–D and S–B, are: for the bubble of the first weft, $\psi = 0.512$ (S–B) and $\psi = 0.587$ (S–D), whereas, for the second one, $\psi = 0.304$ (S–B) and $\psi = 0.332$ (S–D). Figure 7a–d show the results for the other two values of the capillary ratio (${C_{cap}} = 1 \times {10^{ - 1}}\;$and ${C_{cap}}=5\times {10^{ - 1}}$), where the flow in the channel has advanced enough to allow the formation of the bubbles in both wefts. For these two cases of ${C_{cap}}$, the bubble at the first weft is larger than the one at the second weft for both formulations, S–B and S–D, which is opposite to the case described before for ${C_{cap}} = 1 \times {10^{ - 2}}$, where the second bubble was larger than the first one. This apparent unexpected behavior is due to the larger values of the capillary ratio considered in these last two cases, ${C_{cap}} = 1 \times {10^{ - 1}}\;$and ${C_{cap}} = 5 \times {10^{ - 1}}$, in comparison with ${C_{cap}} = 1 \times {10^{ - 2}}$. From the previous analysis of the maximum capillary pressure it follows that when ${P_{cap,max}}$ is constant, as in the present cases, larger values of the capillary ratio, ${C_{cap}}$, correspond to lower values of the inlet pressure, ${P_{in}}$. At lower inlet pressure, the fluid fronts at the channel move more slowly; besides, the capillary forces always promote the weft impregnation. These two simultaneous effects result in smaller differences between the location of the fluid fronts at the channel and the location of the fluid front at the wefts before the channel fluid fronts enclose the wefts, and, consequently, in smaller initial bubbles, as ${C_{cap}}$ is higher. This consequence is in turn more pronounced at the second weft due to the slower channel flow velocities obtained there regarding the ones obtained in the first weft, given the increase of the flow resistance as the fluid front progresses; accordingly, the initial void size at the second weft will be smaller than the one at the first weft. On the other hand, at a lower inlet pressure, the bubbles are subjected to lower compression, and consequently, at larger values of the capillary ratio (${C_{cap}} = 1 \times {10^{ - 1}}$ and ${C_{cap}} = 5 \times {10^{ - 1}}$), the initial void size is very similar to the final void size for both wefts; as the initial void is smaller for the second weft, the final void is too, as can be observed in Fig. 7 for both approaches, S–B and S–D.

Fig. 7

Total fillings of RUC’s. a ${C_{cap}} = 1 \times {10^{ - 1}}$ (Stokes–Brinkman, $\beta = 1.24$), b ${C_{cap}} = 1 \times {10^{ - 1}}$ (Stokes–Darcy, $\gamma = 1.27$), c $\;{C_{cap}} = 5 \times {10^{ - 1}}$ (Stokes–Brinkman, $\beta = 1.24$), d $\;{C_{cap}} = 5 \times {10^{ - 1}}$ (Stokes–Darcy, $\gamma = 1.27$)

The results of the void characterization obtained with both formulations, S–D and S–B, are summarized in Table 4, for all values of ${C_{cap}}$ considered. As can be observed from that table, the largest voids in the first weft are obtained for ${C_{cap}} = 1 \times {10^{ - 1}}$ in both formulations and the smallest ones, for ${C_{cap}} = 5 \times {10^{ - 1}}$, with the void size corresponding to ${C_{cap}} = 1 \times {10^{ - 2}}$ in between them. On the other hand, for the second weft, the void is always smaller as ${C_{cap}}$ is higher, with no void formation, $Siz{e^*} = 0$, for ${C_{cap}} = 5 \times {10^{ - 1}}$ when using the S–B approach (see Fig. 7c), while S–D predicts the formation of a very small bubble (see Fig. 7d). Regarding the void shape, the increase of ${C_{cap}}$ generates bubbles with a higher aspect ratio for both wefts using both approaches, S–D and S–B.

Fig. 8

Saturation curves. a Comparisson Stokes–Brinkman with$\;\beta = 1.24$ versus Stokes–Darcy with$\;\gamma = 1.27$. b Stokes–Darcy for ${C_{cap}} = 1 \times {10^{ - 1}}$

4.3.4 Comparison of saturation curves

The time evolution of the saturation curves predicted by the S–D and S–B approaches for the three capillary ratios are compared in Fig. 8a, where it can be observed a similar general behavior for all curves. Figure 8b shows the saturation curve obtained with the S–D simulation for ${C_{cap}} = 1 \times {10^{ - 1}}$ in order to describe the general behavior of all cases reported in Fig. 8a. In Fig. 8b, different filling instants are highlighted using marker points, which are numerated from 0 to 5. As can be observed, the highest saturation rate, i.e., the slope of the curve, is reached at the beginning of the injection (from 0 to 1). As soon as the fluid front arrives at the first weft, point (1), the saturation rate decreases until the merging of the channel fluid fronts (from 1 to 2) due to the flow resistance exerted by the first weft. When the channel fluid fronts have surrounded the first weft and encountered one another, point (2), an increase of the saturation rate can be noticed. This rate is kept almost constant until the arrival of the fluid front to the second weft (from 2 to 3), moment from which the saturation rate progressively decreases again until the second merging of the fluid fronts (from 3 to 4) due to the resistance exerted by the second weft. In point (4), saturation rate barely increases, and from (4) to the end of simulation (5), saturation rate is essentially constant. The nearly constant saturation rate between 2 and 3 is expected since no porous obstacles are present in the channel between these points, in contrast with what happens between the points 1 to 2 and 3 to 4, where the saturation rate decreases due to the presence of the first and second weft, respectively. According to Fig. 8a, for ${C_{cap}} = 1 \times {10^{ - 2}}$ and ${C_{cap}} = 1 \times {10^{ - 1}}$, the saturation curves predicted by both approaches (S–D and S–B) are almost identical, but the final saturation is slightly higher for the S–D result (see detail in Fig. 8a). The highest differences between the saturation curves of both approaches (S–D and S–B) are observed for ${C_{cap}} = 5 \times {10^{ - 1}}$, where the capillary effects are the most relevant; in this case, the final RUC saturation is barely higher for the S–B scheme (see detail in Fig. 8a).

Fig. 9

Total fillings of RUC’s for Stokes–Brinkman with $\beta = 0.7$. a ${C_{cap}} = 1 \times {10^{ - 2}}$, b $\;{C_{cap}} = 1 \times {10^{ - 1}}$, c ${C_{cap}} = 5 \times {10^{ - 1}}$

Table 5 Influence of $\beta$ and ${C_{cap}}$ on the void size

4.4 Influence of matching conditions on the void formation for the Stokes–Brinkman approach

4.4.1 Influence of the jump stress coefficient

Let us first consider the influence of the jump stress coefficient, $\beta$, on the void formation by comparing the results obtained from Series 1 $\left( {\beta = 1.24} \right)$ and 2 $\left( {\beta = 0.70} \right)$, for the three different values of $\;{C_{cap}}$ considered here. The total fillings of the RUC for Serie 1 and the different values of $\;{C_{cap}}$ were already analyzed in the previous section and reported in Fig. 6i $( {{C_{cap}} = 1 \times {{10}^{ - 2}}})$, 7a $( {{C_{cap}} = 1 \times {{10}^{ - 1}}} )$, and 7c (${C_{cap}} = 5 \times {10^{ - 1}}$). Equivalent results for Serie 2 are shown in Fig. 9a–c, where, in the case of$\;{C_{cap}} = 1 \times {10^{ - 2}}$ (Fig. 9a), different fluid fronts with positions in the channel corresponding to the same ones reported in the first column of Fig. 6 for the Serie 1 are highlighted using arrows. As can be seen from these figures (first column of Figs. 6 and 9a), the real, dimensionless and normalized arrival times corresponding to these positions are shorter for $\beta = 0.70$ (Fig. 9a).

In Table 5, the effect of $\;{C_{cap}}$ on the void size at the first and second wefts for both values of $\beta$ ($\beta =1.24$ and $\beta =0.70$) is presented, with the smaller voids found for $\beta = 0.70$ in both wefts; the void size difference between both values of $\beta$ is less significant for ${C_{cap}} = 5 \times {10^{ - 1}}$, i.e. the larger capillary ratio examined here. Although the size of the first bubble is not a monotonic function of ${C_{cap}}$ for both values of $\beta$, with the smaller voids corresponding to ${C_{cap}} = 5 \times {10^{ - 1}}$ and the larger ones, to ${C_{cap}} = 1 \times {10^{ - 1}}$, the size of the second bubble is a decreasing monotonic function of ${C_{cap}}$, and the resulting total void size, which is the sum of the size of both bubbles, also decreases with ${C_{cap}}$. This last behavior is in agreement with results previously reported in the literature [30], where unidirectional macroscopic simulations were carried out using the software LIMS and it was found that the saturated length corresponding to the arrival of the fluid front to the end of a cavity is larger as ${C_{cap}}$ increases, which, from a mesoscopic viewpoint, can be interpreted as the reduction of the total void size with the increment of ${C_{cap}}$ for a given position along the cavity.

Fig. 10

Total filling of the RUC for the continuous-stress condition and ${C_{cap}} = 1 \times {10^{ - 2}}$

Table 6 Influence of $\beta$ and ${C_{cap}}$ on the void shape

In general, the void shapes obtained in this work are physically consistent with some experimental works. For instance, Hamidi et al. [20, 21] studied the void morphology in the Resin Transfer Molding process (RTM), observing different void shapes inside the bundles:

• Cigar-shaped bubbles with a very high aspect ratio, as those ones reported in Figs. 7c-first weft, 7d-second weft, and 9b-second weft.

• Elliptical bubbles with a lower aspect ratio than the previous ones, see for example Figs. 6i, 7a, b, 9a, b-first weft.

• Almost circular bubbles, which are less frequent, having an aspect ratio close to one, see Fig. 10

According to the results in Table 6, the void aspect ratio at the first and second wefts increases with$\;{C_{cap}}$ for both jump stress coefficients, $\beta = 0.70$ and $\beta = 1.24$. In the case of ${C_{cap}} = 1 \times {10^{ - 2}}$, the void aspect ratio does not change considerably with $\beta$ for both wefts, while for ${C_{cap}} = 1 \times {10^{ - 1}}$, a significant reduction of the aspect ratio with the increase of $\beta$ is found. On the other hand, when ${C_{cap}} = 5 \times {10^{ - 1}}$, only the first bubble is formed for both values of $\beta$ and the aspect ratio increases with $\beta$.

The obtained numerical results do not reveal a relevant influence of $\beta$ and ${C_{cap}}$ on the location of the void, which is always formed at the rear edge of the weft. This is also in agreement with the experimental results of Hamidi et al. [21], where radial injections in a circular mold were conducted, founding that the most of voids were formed at the rear edge of the tows with respect to the flow direction, both inside the tow and in the transition tow-channel. Other numerical works, [24, 25, 43, 54], have also predicted the void formation at similar locations.

In summary, it can be concluded that the process of void formation by mechanical entrapment of air is defined by a dynamic balance between the inlet and capillary pressures, which is characterized by the capillary ratio, ${C_{cap}}$. The void size and shape are also influenced by the magnitude of ${C_{cap}}$, as well as by the value of the jump stress coefficient, $\beta$. On the other hand, the void location appears to be independent on both ${C_{cap}}$ and $\beta$, since the voids are always located at the rear edge of the wefts, which is in agreement with previous numerical and experimental works.

4.4.2 Comparison of void size between continuous stress and jump stress simulations

The influence of the type of interface condition on the void formation for ${C_{cap}} = 1 \times {10^{ - 2}}$ is studied by comparing results of Serie 2 (stress jump condition, $\beta = 0.7$) and Serie 3 (continuous stress condition, $\beta = 0$). The total RUC filling for the continuous stress condition is presented in Fig. 10, where the fluid fronts having the same positions in the channel to those ones depicted in Fig. 9a are highlighted by the corresponding arrows.

The comparison between both simulations (Fig. 9a vs. Fig. 10) indicates that for the same fluid front position in the channel, the positions of the fluid fronts in the warps and wefts are more advanced in the continuous-stress case $(\beta = 0$), and consequently, the initial size of the first and second bubbles, corresponding to the instant when the channel fluid fronts completely enclose the first and second weft, respectively, is smaller in the continuous stress conditions. The initial and final void size at the first weft in the case of the jump-stress condition, Fig. 9a, is $Siz{e^*} = 1.52 \times {10^{ - 2}}$ and $Siz{e^*} = 6.57 \times {10^{ - 3}}$, respectively; on the other hand, these values for the continuous-stress condition, Fig. 10, are $Siz{e^*} = 6.30 \times {10^{ - 3}}$ and $Siz{e^*} = 2.69 \times {10^{ - 3}}$. In the case of the jump-stress condition the compressibility ratio is $\psi = 0.567$, whereas for the continuous stress this value is $\psi = 0.573$. Accordingly, the void compression does not have a relevant influence in the difference between the final void sizes for these two cases (continuous-stress and jump-stress) since the compressibility ratios are almost the same, and the main reason of this difference is the initial void size, which is smaller in the case of $\beta = 0$, leading to a smaller final void in such a case.

A similar behavior can be appreciated for the void size at the second weft, namely, the initial void is smaller in the continuous-stress case and the compressibility ratio is almost the same in both cases (continuous-stress and jump-stress); the difference between the final void sizes at the second weft for these two cases is even higher than at the first weft, with $Siz{e^*} = 8.80 \times {10^{ - 3}}$ in the case of the jump-stress condition, and $Siz{e^*} = 2.02 \times {10^{ - 4}}$ for the continuous-stress condition.

Fig. 11

Comparison of saturation curves for continuous and jump stress conditions and ${C_{cap}} = 1 \times {10^{ - 2}}$

4.4.3 Comparison of saturation curves between continuous stress and jump stress simulations

Finally, let us analyze the differences between the predicted saturation curves of both conditions, continuous stress and jump stress. Saturation curves are very important on the quantitative description of the time and space evolution of the saturated volume, and they can be very useful for the comparison of filling processes at different filling instants. The obtained saturation curves for the continuous (C-S) and jump (J-S) stress conditions are compared in Fig. 11. From this figure, it can be observed that the time evolution of the corresponding saturation curves is very similar to the one presented in Fig. 8b, with the C-S condition predicting a higher value of saturation at any normalized time, ${t^*} = t/{t_{filling}}$. In the saturation curves shown in Fig. 11, the representative filling instants reported in Fig. 8b ($i = 1,2,3,4,5$) are highlighted by the arrows. The saturation difference between the both curves (C-S and J-S conditions), defined as $ds = s_i^{cont} - s_i^{jump}$, is not the same for all filling instants . Here, $s_i^{cont}$ and $s_i^{jump}$ stand for the RUC saturation obtained with the C-S and J-S simulations, respectively. It is very important to take into account that, in this case, $ds$ is not referred to the saturation difference for a determined value of the normalized time, ${t^*}$, but to the saturation difference corresponding to any of the instants highlighted in Fig. 11, which do not necessarily correspond to the same values of ${t^*}$ in both simulations, C-S and J-S.

In the first filling instants (1), when the flow reaches the first weft, the RUC saturation is very similar for both simulations ($ds$ is very small) because it is primarily determined by the saturation of the channel, which is almost the same in both cases. During the impregnation of the first weft (from 1 to 2), $ds$ increases until the merging of the channel fluid fronts at (2), due to the higher weft saturation obtained in the C-S simulation during this period, as commented before. The change of the saturated volume of the first weft is not completely defined when the channel fluid fronts enclose it since the void undergoes a continuous compression during the filling process of the RUC until the partial equilibrium is reached. Therefore, the change of the saturated volume of the first weft from the time of merging of the fluid fronts to the time of arrival of the fluid front to the second weft (from 2 to 3) is due to the compression of the bubble. Given that during this period the filling of the channel and the warps is almost identical for the C-S and J-S simulations, the change of $ds$ is essentially determined by the compression of the bubble. Accordingly, as the compressibility ratio,$\;\psi$, of C-S and J-S is very similar for the first bubble, as mentioned before, and considering the definition of $\psi$ in (63), the change of the volume of the bubble is larger in the case of the larger initial void size, which corresponds to the J-S simulation. Therefore, the change of the saturated volume of the first weft is also larger for the J-S simulation between the time instants analyzed (from 2 to 3) and this leads to the reduction of the saturation difference, $ds$ (see Fig. 11).

In the C-S simulation, a larger infiltration at the second weft occurs between the instant of the arrival of the fluid front to this weft and the instant of merging of the channel fluid fronts to form the second bubble (from 3 to 4). During this time interval, both simulations (C-S and J-S) predict almost the same changes on the saturated volume in the channels and the warps, and the change on the saturated volume in the first weft due to the void compression is negligible in comparison with the change of the saturated volume in the second weft. These factors lead to an increment of $ds$ that is mainly determined by the change of the saturation in the second weft, which, in turn, is larger for the C-S condition as mentioned before (see Fig. 11). At the end of the simulation, the RUC saturation is $s = 0.928$ for C-S and $s = 0.904$ for J-S.

5 Conclusions

In this work, BEM techniques have been implemented for the simulation of voids formation in dual-scale fibrous reinforcements using Stokes–Darcy (S–D) and Stokes–Brinkman (S–B) mathematical formulations. The BEM solution for the S–D formulation was previously validated in [43], while a coupled Stokes–Brinkman problem with analytical solution was used here to validate the developed BEM/DR-BEM scheme (BEM for the Stokes domain and DR-BEM for the Brinkman domain), obtaining a very good accuracy. The error of the numerical solution increases with the magnitude of the inverse Darcian number, ${\chi ^2}$, for all values of the jump stress coefficient, $\beta$, considered here, and decreases with the magnitude of $\beta$ for each value of ${\chi ^2}$, except for the smallest one, ${\chi ^2} = 18,\;$where the error increases with $\beta$ (see Table 2).

The present numerical solution predicts a reduction of the Stokes velocity in the channel and of the boundary layer thickness in the porous medium with the increase of $\beta$ and ${\chi ^2}$, which is in agreement with the results in [58]. Moreover, our solution is also compared with a FEM solution previously reported in [23], finding that both approaches converge satisfactorily to the analytical solution, with larger errors in the Brinkman domain than in the Stokes domain in the present BEM/DR-BEM scheme, contrarily to the FEM scheme of [23] where the errors in the Stokes domain are greater. Conversely to the FEM solution, no numerical oscillations in the boundary layer were obtained with the present BEM/DR-BEM scheme.

The problem of void formation during the filling of two adjacent RUC’s, for three different capillary ratios, ${C_{cap}} = \left[ {1 \times {{10}^{ - 2}},1 \times {{10}^{ - 1}},5 \times {{10}^{ - 1}}} \right]$, was analyzed by using Stokes–Darcy (S–D) and Stokes–Brinkman (S–B) formulations, resulting in a similar behavior of the void size and shape with ${C_{cap}}$ for both formulations. At the first weft, the change of void size with ${C_{cap}}$ is not monotonous, with the largest voids obtained for ${C_{cap}} = 1 \times {10^{ - 1}}$, the smallest ones for ${C_{cap}} = 5 \times {10^{ - 1}}$, and the intermediate ones for ${C_{cap}} = 1 \times {10^{ - 2}}$. For the second weft, the void is smaller as ${C_{cap}}$ increases. The total void size, which is the sum of the size of both bubbles, also decreases with ${C_{cap}}$, which is in agreement with the results of [30]. On the other hand, the void aspect ratio in both wefts increases with ${C_{cap}}$.

The results of the RUC’s fillings also allow concluding that the differences between the S–D and S–B formulations depend on the capillary effects. For instance, in the particular case when the capillary effects are weak, i.e., ${C_{cap}} = 1 \times {10^{ - 2}}$, the S–D formulation predicts smaller voids and lower aspect ratios than S–B, in both wefts. On the other hand, for a same value of ${C_{cap}}$, similar saturation curves were obtained with both formulations, S–D and S–B, with exception of the case when the capillary effects are dominant, i.e., ${C_{cap}} = 5 \times {10^{ - 1}}$, where important differences between the saturation curves of both formulations were appreciated.

According to the present results, the type of matching conditions considered in the Stokes–Brinkman formulation affects the void size and shape. When using the jump stress condition (J-S), the smallest voids at both wefts were obtained for the lowest value of the jump stress coefficient, $\beta = 0.7$, for all values of ${C_{cap}}$, with the exception of the case of the second weft when ${C_{cap}} = 5 \times {10^{ - 1}}$ (when capillary effects are dominant), where no void formation was obtained for the two values of the jump stress coefficient ($\beta = 1.24\;$ and $\beta = 0.7$). Regarding the void shape, the aspect ratio always increases with ${C_{cap}}$ for each value of $\beta$ in both wefts (see Table 6). According to the BEM/DR-BEM simulations, the void location is not significantly affected by ${C_{cap}}$ and $\beta$, and is formed at the rear edge of the weft.

The general behavior of the void size and aspect ratio with ${C_{cap}}$ in both wefts, which was described above, did not change with $\beta$, as well as the decreasing behavior of the total void content with ${C_{cap}}$, which was obtained in all cases of the S–B formulation. On the other hand, for ${C_{cap}} = 1 \times {10^{ - 2}}$, the lowest void content was obtained for the continuous-stress condition (C-S), which is consistent with the larger saturation predicted by the C-S condition for all filling instants in comparison with the one predicted by J-S. Despite the saturation values differ in all filling instants, both saturations curves, C-S and J-S, showed a similar behavior.