1 Introduction

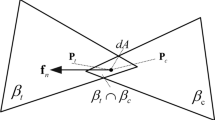
The most relevant feature in a dual-porosity model is the flow between the matrix and the fracture. Mathematically, it is described using a transfer term. This transfer term is influenced by the shape of the matrix block, flow regime [e.g., pseudo-steady state (PSS) or transient], depletion scheme of fracture pressure and physical recovery mechanism (e.g., convection or diffusion). These factors, especially the shapes of the matrix and fracture blocks, are lumped in a value that is called the shape factor. The continuities of pressures have always played a significant rule in well testing. Calculating diffusive leakage rate of brine in the case of various double-porosity parameters (Dejam et al. 2013; Dejam and Hassanzadeh 2018) and analyzing hydraulically fractured wells using semi-analytical solution (Dejam et al. 2018) are good evidence for this statement. However, despite decade-long research, it is not clear how the shape factor can be calculated. Even for the simplest geometry (rectangular cuboid matrix blocks), many different formulas have been proposed in the literature. The simplified schematic of the dual-porosity model and the transfer function is shown in Fig. 1.

Fig. 1
figure 1

Schematic of the transfer function between the matrix and the fracture

Full size image

The foundation of the dual-porosity model was laid down by Barenblatt et al. (1960) and Warren and Root (1963). They used a geometrical approach to derive the shape factors for one, two and three sets of orthogonal fractures. Warren and Root (1963) proposed an analytic solution for the single-phase radial flow in a naturally fractured reservoir and introduced the dual-porosity concept in fluid flow modeling. They ultimately used the results in well testing and gave the following definition of the shape factor for cubic matrix blocks:

$$\sigma = \frac{{4n\left( {n + 2} \right)}}{{l^{2} }}$$
(1)

Here n is the set of normal fractures and l is the characteristic length. It should be understood here that derivation of the shape factor which is described by Warren and Root (1963) in Eq. (1) is based on the assumption of the existing PSS flow in the matrix and does not utilize the pressure diffusion equation governing fluid flow within the matrix block. Therefore, the defined shape factor is not completely rigorous and is based on the PSS assumption. Kazemi et al. (1976) extended the formulation of Warren and Root (1963) for multiphase flow and numerically solved the dual-porosity system in three dimensions. They solved fluid flow in a fractured system numerically and gave the following definition for the shape factor:

$$\sigma = 4\left( {\frac{1}{{L_{{{\text{m}}x}}^{2} }} + \frac{1}{{L_{{{\text{m}}y}}^{2} }} + \frac{1}{{L_{{{\text{m}}z}}^{2} }}} \right)$$
(2)

where Lmx, Lmy and Lmz are the block lengths along the x, y and z direction, respectively.

Peaceman (1976) evaluated gas and oil transfer between the fracture and rock matrix. They obtained a shape factor of 12/L2, 14.23/L2 and 16.53/L2 for one-, two- and three-dimensional cubic matrix blocks and concluded that values of shape factors do not increase much with an increase in the number of normal sets of fractures. Thomas et al. (1983) presented an expression for the shape factor using another version of a fully implicit three-dimensional, multiphase naturally fractured simulator based on the dual-porosity approach that was validated by multiphase flow numerical simulations. They multiplied the matrix phase relative permeability values by the fracture phase saturations to include the effect of block coverage and developed a 3D, three-phase model for the shape factor by simulating the flow of fluids in a naturally fractured reservoir.

Ueda et al. (1989) used Kazemi’s model to calculate the shape factor and compared their results with fine-grid simulation results. They believed that Kazemi’s shape factor values for one- and two-dimensional matrix blocks are not suitable and need to be adjusted by a factor of 2 and 3, respectively. Coats (1989) solved the diffusivity equation to give a shape factor of 12/L2, 28.45/L2 and 49.58/L2 for one-, two- and three-dimensional cubic matrix block, respectively, for single-phase flow based on the PSS assumption.

The approximate values of shape factors for cube- and strata-shaped matrix blocks at PSS were calculated by de Swaan (1990). He found a shape factor of 60/L2 and 15/L2 for cube and strata shapes, respectively. Kazemi and Gilman (1993) updated the earlier dual-porosity simulator of Kazemi et al. (1976) by modifying the matrix–fracture transfer function that was defined by Kazemi et al. (1976) to include fracture relative permeability when fluid is flowing from the fracture to the matrix and defined another form for the matrix–fracture transfer function. Chang (1993) analytically derived the shape factor in cylindrical and spherical coordinates based on material balance and Darcy flow at PSS. The obtained results by him were exactly the values obtained by Warren and Roots’s shape factors. Zimmerman et al. (1993) developed a new dual-porosity model for single-phase fluid flow in fractured porous media. They used a nonlinear ordinary differential equation to calculate the fracture–matrix interaction term for a wide variety of matrix block boundary conditions. Their equation more accurately simulates the flux during the early and late periods of the interaction than the linear Warren–Root equation. Lim and Aziz (1995) suggested that the shape factor depends on the geometry and physics of pressure diffusion in the matrix. For the general case of an anisotropic, rectangular matrix block, they reported the following expression for the shape factor:

$$\sigma = \frac{{\uppi^{2} }}{{k_{\text{m}} }}\left( {\frac{{k_{x} }}{{L_{{{\text{m}}x}}^{2} }} + \frac{{k_{y} }}{{L_{{{\text{m}}y}}^{2} }} + \frac{{k_{z} }}{{L_{{{\text{m}}z}}^{2} }}} \right)$$
(3)

where km is the geometric average matrix permeability.

Several other studies in the area of naturally fractured reservoir simulation are devoted to analytically and numerically representing an accurate matrix–fracture transfer function (Bourbiaux et al. 1999; Coats 1989; Noetinger and Estebenet 2000; Noetinger and Estébenet 1998; Penuela et al. 2002a, b; Quintard and Whitaker 1996; Sarda et al. 2001).

Quintard and Whitaker (1996) also used the volume-averaging technique to determine the shape factor values for 1D, 2D and 3D matrix–fracture transfers in a single-phase flow. Their results were exactly the values obtained by Coats (1989). Bourbiaux et al. (1999) present different approaches to determine matrix–fracture transfer behavior. They used three methods involving either (1) local-scale flow computations, (2) the application of upscaling theory and (3) implementation of the particle random walk method to obtain the best approximate expression of the shape factor. They obtained the same expression for the shape factor, 20/a2 based on a PSS formulation of 2D matrix–fracture transfers in a single-phase fine-grid simulation where “a” is the lateral dimension of the matrix block. Noetinger and Estebenet (2000) used the continuous-time random walk technique (CTRW) to calculate the shape factor between the matrix and the fracture and compared the obtained shape factor from this technique with numerical simulation and found a good agreement.

An efficient patented solution to tackle the problem of simulating matrix–fracture exchanges with a minimum number of grid blocks is presented by Sarda et al. (2001). They developed a numerical method to calculate the matrix–fracture exchange factor from the dual-porosity concept and compared their results to other published exchange factor expressions. In their approach, matrix blocks of different volumes and shapes are associated with each fracture cell depending on the local geometry of the surrounding fractures. Their expression for the shape factors is 8/a2, 24/a2 and 48/a2 for 1D, 2D and 3D parallelepiped matrix blocks of lateral dimension a, respectively. A flow equation incorporating a time-dependent shape factor for dual-porosity modeling of the slab-shaped matrix block is derived in other studies (Penuela et al. 2002a, b). They performed a compositional simulation to verify the flow equation using the shape factor. Their numerical investigation into various matrix block sizes showed that shape factor values converge to values derived by Lim and Aziz (1995) for one set of parallel fractures. They used the analytical solution of the average pressure difference and inter-porosity flow rate for 1D flow to compute flow correction factor. Based on the flow correction factor, they obtained the following definition for shape factor:

$$\sigma = \mathop {\lim }\limits_{t \to \infty } \frac{{4F_{\text{c}} \left( t \right)}}{{L^{2} }}$$
(4)

where L is the fracture spacing, Fc is the flow correction factor, t is time and σ is the shape factor for the matrix block that is surrounded by one set of parallel fractures.

It is showed that the shape factor also depends on the way the pressure changes in the fracture. They compared several methodologies presented by these and other authors (Hassanzadeh and Pooladi-Darvish 2006; Hassanzadeh et al. 2009). Mora and Wattenbarger (2009) used numerical simulation to obtain a correct shape factor formula for various cases. They concluded that some of the most popular formulas do not seem to be correct. Hatiboglu and Babadagli (2007) studied the effect of several rocks and fluid properties such as matrix shape factor, wettability, oil viscosity and some other parameters on the rate of capillary imbibition and development of residual non-wetting phase saturation, experimentally. They used several different core samples with different shape factors to evaluate the rate of imbibition. The effect of the fracture pressure depletion regime on the shape factor for single-phase flow of a compressible fluid was investigated by Ranjbar et al. (2011). Their investigations demonstrated that the shape factor is a function of the imposed boundary conditions in the fracture and its variability with time. They used single-porosity, fine-grid, numerical simulations to verify their presented semi-analytical model for estimating the shape factor. The dependency of shape factor on the other parameters such as gas specific gravity and temperature is investigated in their study. Saboorian-Jooybari et al. (2012) developed a new time-dependent matrix–fracture shape factor to diagnose different states of the imbibition process. They obtained an analytical solution for fluid saturation distribution within a matrix block by solving capillary-diffusion equation under different boundary conditions. They used the single-porosity fine-grid simulations and the previous experimental data presented by other authors to verify their solutions and concluded that the shape factor is completely phase sensitive that is the important parameter in diagnosing different states of imbibition process. A time-dependent matrix–fracture shape factor formulation is analytically derived for two-phase flow in a three-dimensional matrix block in the imbibition process which considers both capillary and gravity forces on matrix–fracture coupling. They verified their results by a fine-grid simulation model (Saboorian-Jooybari et al. 2015). Wang et al. (2018) developed a time-dependent shape factor for single-phase flow by considering the stress sensitivity in the matrix system. They performed a fine-grid finite element numerical model to validate the accuracy of the new analytical model. Their results showed that the stress sensitivity coefficient of permeability has a great influence on the stabilized value of the matrix–fracture shape factor for a compressible formation.

The results of other methodology in obtaining the shape factor by the others are summarized in Table 1, and finally, the results of the current study were compared with the results of other authors.

Table 1 Summary of the shape factor constants σL2 found in the literature based on the solution of the diffusivity equation with constant fracture pressure
Full size table

In this study, the behavior of the shape factor between a matrix and fractures for different boundary conditions of fracture pressure for regular and irregular shaped blocks under assumptions of PSS and the transient flow regime is investigated. As most of the studies in the literature are based on single-phase flow, this study focuses on this type of flow to compare the observed trend with other studies in terms of shape factor calculation. For this purpose, we first clarified what we mean by PSS and transient approach. For both cases, several simulations were conducted in several sections. At first, the shape factor was calculated for the standard shaped blocks (symmetric and regular shapes) for a case where the fracture pressure is constant which is normally used in the literature. Then, some pressure depletion schemes were used as the fracture boundary condition on the standard shape. Finally, different boundary conditions were performed for irregular shapes.

2 Numerical model and methodology

There are a lot of debates on how to calculate shape factors in the literature. The two most commonly used equations originate from Warren and Root (1963) and Kazemi et al. (1976). In this study, several different shapes for three-dimensional matrix blocks were considered to calculate the shape factor. Different boundary conditions including (1) constant fracture pressure, (2) linearly declining fracture pressure and (3) exponentially declining fracture pressure were used in the models. The finite element method was used to generate and simulate all models. The calculated shape factors from fine-scale numerical models were compared with the known analytical and numerical values that were reported by others.

To simulate matrix–fracture drainage flow, the matrix blocks are surrounded by fractures. Then, the pressure difference between the matrix and the fracture is assigned based on the boundary conditions. Thus, the reservoir fluid will flow from the matrix into the fracture. Sufficiently large simulation time is selected for simulations until the matrix and fracture systems reach pressure equilibration. Finally, for all models, the dimensionless shape factors are plotted against dimensionless time.

A general numerical technique (finite element method) was proposed to calculate the shape factor for any arbitrary shape of the matrix block (i.e., non-orthogonal fractures) for both transient and PSS considering different boundary conditions. Using the finite element method and by defining irregular shapes, we were able to implement different pressure trends as boundary conditions. Therefore, linear and exponential forms of pressure as a function of time for the boundary conditions were implemented for different models.

2.1 Mathematical method

In this study, several standard three-dimensional models for the matrix block were constructed to simulate one-, two- and three-dimensional flow behavior between a matrix and a fracture and the simulation results were used to obtain the shape factors for irregularly shaped matrix blocks. Several different boundary conditions (fracture pressure) were performed for all mentioned models. In this section, first, we explained the governing equation and the corresponding initial and boundary conditions. The diffusivity equation for the flow in the x, y and z Cartesian coordinate is described as:

$$K_{x} \frac{{\partial^{2} P}}{{\partial x^{2} }} + K_{y} \frac{{\partial^{2} P}}{{\partial y^{2} }} + K_{z} \frac{{\partial^{2} P}}{{\partial z^{2} }} = \phi \mu c_{\text{t}} \frac{\partial P}{\partial t}$$
(5)

The model is illustrated in Fig. 2.

Fig. 2
figure 2

A simplified matrix–fracture model for three normal fracture sets

Full size image

The initial pressure is assumed uniform throughout the matrix block

$$P = P_{\text{i}} \quad {\text{when}}\;t = 0$$
(6)
$$P_{\text{f}} = P_{\text{i}} -\Delta P_{0} \quad {\text{when}}\;t = t_{0}$$
(7)

where P is the pressure, Kx, Ky, Kz are the permeability in the x, y and z directions, µ is the fluid viscosity, ct is the total compressibility, \(\phi\) is the porosity, Pf is the fracture pressure, Pi is the initial pressure of the matrix block and ∆P0 is the difference between the matrix pressure and the fracture pressure at the initial conditions (at t = 0).

The pressure and fluid flow of the matrix block at different boundary conditions are:

  • For constant fracture pressure,

    $$P = P_{\text{f}} \quad {\text{at}}\;x = 0\;{\text{and}}\;y = 0\;{\text{and}}\;z = 0$$
    (8)

  • For constant fracture pressure followed by exponentially declining pressure,

    $$P_{\text{f}} = \left( {P_{\text{i}} -\Delta P_{0} } \right)\exp \left( { - \alpha t} \right)$$
    (9)

  • For constant fracture pressure followed by linearly declining pressure,

    $$P_{\text{f}} = \left( {P_{\text{i}} -\Delta P_{0} } \right)\left( {1 - \beta t} \right)$$
    (10)

where α and β are the decline constants in the exponential and linear declining forms, respectively. Three different values of 0.0001, 0.01 and 1 were considered for the decline constant in the exponential form and a value of 0.001 in the linear form.

To express the distance, pressure and time in the dimensionless form, the following terms were used:

$${\text{Dimensionless}}\,{\text{distance}},\quad x_{\text{D}} = \frac{x}{a},\quad y_{\text{D}} = \frac{y}{b},\quad z_{\text{D}} = \frac{z}{c}$$
(11)
$${\text{Dimensionless}}\,{\text{time}},\quad t_{\text{D}} = \frac{kt}{{A\phi \mu c_{\text{t}} }}$$
(12)
$${\text{Dimensionless}}\,{\text{pressure}},\quad P_{\text{D}} = \frac{{P_{\text{i}} - P}}{{P_{\text{i}} - P_{\text{f}} }}.$$
(13)

2.2 Pseudo-steady-state (PSS) shape factor

Under the assumptions of a single-phase flow and a PSS condition in the matrix, as described by Warren and Root (1963), the transfer function between a matrix block and a fracture system is proportional to the difference between the fracture pressure and the average matrix block pressure as given by the following equation:

$$\tau = \sigma \frac{{k_{\text{m}} }}{\mu }\left( {\bar{P}_{\text{m}} - P_{\text{f}} } \right)$$
(14)

where τ is the matrix–fracture transfer function; the parameter σ has the dimensions of reciprocal of the area and is defined as a shape factor that reflects the geometry of the matrix elements and controls flow between the two porous media; km is the matrix permeability; \(\bar{P}_{\text{m}}\) is the average matrix pressure.

Equation (14) was used by Warren and Root (1963) to model the transfer function between the matrix and the fracture in a naturally fractured reservoir.

Assuming that the matrix is depleting under PSS conditions, using the compressibility equation one can write the matrix–fracture transfer function τ, that is, related to the matrix pressure by the following relationship:

$$\tau = - \phi_{\text{m}} C_{\text{m}} \left( {\frac{{\partial \bar{P}_{\text{m}} }}{\partial t}} \right)$$
(15)

where \(\phi_{\text{m}}\) is the matrix porosity and Cm is the total matrix compressibility which is equal to the summation of matrix rock and fluid compressibility.

According to Warren and Root (1963), assuming PSS behavior in the matrix, then by combining Eqs. (14) and (15) the following differential equation is obtained:

$$\sigma \frac{{k_{\text{m}} }}{\mu }\left( {\bar{P}_{\text{m}} - P_{\text{f}} } \right) = - \phi_{\text{m}} C_{\text{m}} \left( {\frac{{\partial \bar{P}_{\text{m}} }}{\partial t}} \right)$$
(16)

This leads to the definition of the single-phase shape factor:

$$\sigma = - \left( {\frac{{\partial \bar{P}_{\text{m}} }}{\partial t}} \right)\frac{1}{{\eta_{\text{m}} \left( {\bar{P}_{\text{m}} - P_{\text{f}} } \right)}}$$
(17)

where ηm is the diffusivity in a matrix block, \(\eta_{\text{m}} = {{k_{\text{m}} } \mathord{\left/ {\vphantom {{k_{\text{m}} } {(\phi \mu C_{\text{m}} )}}} \right. \kern-0pt} {(\phi \mu C_{\text{m}} )}}\).

Equation (17) was used to find the shape factor from the numerical simulation by the computational fluid dynamic (CFD) simulation. For this purpose, all parameters are known in Eq. (17) except the matrix pressure. Using the calculated pressure profile in the matrix, one can calculate σ.

2.3 Transient shape factor

The transfer function between a matrix block and a fracture system for a more general case can be described by solving the following equation:

$$\nabla^{2} P_{\text{m}} = \frac{1}{{\eta_{\text{m}} }}\left( {\frac{{\partial P_{\text{m}} }}{\partial t}} \right)$$
(18)

where Pm is the matrix block pressure and the transfer function between the matrix and the fracture is proportional to the pressure gradient at the matrix block surface as given by (Nanba 1991).

$$\tau = \frac{{A k_{\text{m}} }}{{\mu V_{\text{m}} }} \nabla P_{\text{m}}$$
(19)

where A is the fracture area or the matrix block surface area, km is the matrix permeability and Vm is the total matrix volume.

Assuming that the matrix is depleting under transient conditions, one can write the matrix–fracture transfer function τ, that is, related to the flow rate by the following relationship:

$$\tau = \frac{{Q_{\text{m}} \left( t \right)}}{{V_{\text{m}} }}$$
(20)

where Qm is the rate of the fluid transfer between the matrix and the fracture. Combining Eqs. (19) and (20) leads to the definition of the single-phase shape factor under the transient assumption:

$$\sigma = \frac{{Q_{\text{m}} \left( t \right)\mu }}{{A \left( {\bar{P}_{\text{m}} - P_{\text{f}} } \right)}}$$
(21)

In Eq. (21), the matrix pressure and the rate of fluid transfer are unknown. Therefore, for calculating the transient shape factor, one needs to know the rate (Qm) and pressure (Pm).

The obtained results for the shape factor in this study are presented in dimensionless form, which is proportional to the shape factor and characteristic length:

$$\sigma_{\text{D}} = \sigma L^{2}$$
(22)

where \(\sigma_{\text{D}}\) is the dimensionless shape factor and L is the characteristic length. For a slab-shaped matrix block, half of the matrix block thickness is considered as the characteristic length. The characteristic lengths of cylindrical and spherical matrix blocks are considered to be equal to the block radius.

2.4 Mesh independency study

To establish the accuracy of the CFD solution, three different mesh sizes were generated to predict the stabilized shape factor to determine how the mesh quality affects CFD simulation results. The predicted shape factors for one-dimensional flow under PSS for constant fracture pressure in a slab-shaped geometry for all three different mesh sizes were compared. The relative error was used to compare the simulation results for all mesh sizes [Eq. (23)].

$$E_{\text{r}} = \frac{{\left| {\sigma_{{{\text{Extra}}\,{\text{fine}}}} - \sigma_{\text{Coarser}} } \right|}}{{\sigma_{{{\text{Extra}}\,{\text{fine}}}} }} \times 100$$
(23)

where Er is the relative error and σExtra fine and σCoarser are the stabilized shape factor with the fines mesh (#1) and coarser mesh (#2 and #3), respectively. The mesh size, the number of elements and nodes, the value of the relative error and the stabilized shape factor for each grid type are shown in Table 2. It can be seen that the relative error between two consecutive grids 1 and 2 is low enough and it can be neglected, but the relative error between grids 1 and 3 is greater. Therefore, the second mesh scheme was selected as the main grid for CFD solution to keep the computational costs low.

Table 2 Mesh independency results for the stabilized shape factor
Full size table

3 Results and discussion

The rate of mass transfer from the matrix to the fracture is directly proportional to the shape factor. For modeling naturally fractured reservoirs, an accurate value of the shape factor is required for both the transient and PSS behavior and also the geometry of the matrix–fracture system.

In this section, the finite element simulation was used to generate and simulate all models. First, the simulation was conducted on regular shapes (i.e., slab, cylindrical, spherical) and then the work was extended to irregular shaped blocks. In all models, the fractured system was composed of a rock matrix surrounded by a regular or irregular system of fractures. For simple geometries, the numerical-solved values are verified with the known analytical and numerical values that were proposed by other researchers. This comparison was done to validate this numerical simulation. In the following, the values of shape factor were obtained for regular shapes with different boundary conditions and the results were presented in a dimensionless form. In this study, different boundary conditions include (1) constant fracture pressure, (2) linearly declining pressure and (3) exponentially declining pressure were investigated. The simple geometries that were used for fine-scale simulation of regular bodies are shown in Fig. 3.

Fig. 3
figure 3

Schematic representation of the problem for the slab, cylindrical and spherical blocks (Rm is the radius of cylindrical and spherical shaped matrix blocks)

Full size image

In general, there are two models to consider the matrix and fracture interaction including PSS and transient transfer. The former model ignores the pressure transient in the matrix while the latter model accounts for the pressure transient in the matrix. In this study, both PSS and transient transfer have been evaluated.

3.1 PSS shape factor, standard shaped matrix blocks

3.1.1 Constant fracture pressure

In this case, the fracture pressure at the matrix–fracture interface is constant and we are dealing with a single block. This boundary condition that is normally used in the literature is performed to validate the standard slab, cylindrical and spherical models. The significant differential pressure between the matrix and the fracture is imposed in the system. Pressures are assigned to be 5000 and 3000 psia, respectively, for the matrix and the fracture so that the reservoir fluid can flow from the matrix into the fracture till the matrix block pressure reaches equilibrium with the surrounding fracture pressure. Figure 4 shows the shape factor for different matrix block shapes of the slab (1D flow), cylindrical (2D flow) and spherical (3D flow) at constant fracture pressure, under the PSS assumption and using Eq. (17).

Fig. 4
figure 4

Dimensionless shape factor versus dimensionless time for different shapes of matrix blocks for constant fracture pressure under the PSS assumption

Full size image

Figure 4 indicates new stabilized values of 4.17, 9.7 and 16.17 for the shape factor of different matrix block shapes of the slab, cylindrical and spherical, respectively, at large dimensionless times and shows that the results are in the same range that other researchers reported (i.e., Kazemi et al. 1976; Peaceman 1976). It is shown that the matrix–fracture transfer shape factor depends on the matrix block shape and how it changes with time. All of these are derived with an assumption of PSS.

3.1.2 Variable fracture pressure

In this case, we assume that the boundary condition changes with time. For this purpose, linear and exponential depletion schemes are investigated. Figure 5 shows the results of the shape factor for linearly declining pressure. Figures 5, 6 and 7 show the results for the exponentially declining pressure scheme with different exponents. It is noted that for the exponential form, three different values of 0.0001, 0.01 and 1 are considered for the decline constant. For the linear decline, a value of 0.001 is considered (because β must be smaller than 1/t).

Fig. 5
figure 5

Dimensionless shape factor versus dimensionless time for different shapes of matrix blocks for linearly declining pressure scheme under the PSS assumption

Full size image
Fig. 6
figure 6

Dimensionless shape factor versus dimensionless time for different fracture depletion regimes for a slab shaped matrix block (1D flow) under the PSS assumption

Full size image
Fig. 7
figure 7

Dimensionless shape factor versus dimensionless time for different fracture depletion regimes for a cylindrical shaped matrix block (2D flow) under the PSS assumption

Full size image

Results show that the shape factor depends on the fracture pressure and how it changes with time. It is found that the linearly declining pressure depletion scheme leads to 4.53, 11 and 20.2 for the slab, cylindrical and spherical shapes, respectively. By comparison of Figs. 4 and 5, it can be seen that the matrix–fracture transfer shape factor depends on the matrix block shape, the pressure regime in the fracture and how it changes with time.

As shown in Figs. 6, 7 and 8, the stabilized shape factor indicated a range of 4.18–4.98, 9.74–12.1 and 16.6–22.1 by varying the decline exponent for the slab, cylindrical and spherical shapes, respectively. As it can be shown, lower values of shape factor were obtained for the fast pressure depletion (when decline exponent α is equal to 0.01 or 1), while an upper value of shape factor was obtained for low-pressure depletion (when decline exponent α is equal to 0.01).

Fig. 8
figure 8

Dimensionless shape factor versus dimensionless time for different fracture depletion regimes for a spherical shaped matrix block (3D flow) under the PSS assumption

Full size image

These figures demonstrate that the presented model can reproduce the slightly compressible fluid shape factor with acceptable accuracy.

In this section, the behavior of the shape factor for different fracture pressure depletion in different shapes of matrix blocks (i.e., slab, cylindrical and spherical) is also described.

Figures 9, 10 and 11 show the shape factor for the slab (1D flow), cylindrical (2D flow) and spherical (3D flow) shapes of the matrix blocks surrounded by fractures in different fracture depletion schemes. The shape factor for a constant fracture pressure is also shown in these figures as a comparison. As illustrated in these figures for the slab shapes, the difference between the stabilized shape factors of the different boundary conditions is low. For all shapes, the stabilized shape factor for the linearly declining fracture pressure is higher than that of the constant fracture pressure. For an exponential decline, the stabilized value of the shape factor depends on the decline exponent. The stabilized shape factor for the exponentially declining fracture with a decline exponent of 0.0001 is higher than that of the other cases. The same behavior has been reported by Chang (1993) and Hassanzadeh and Pooladi-Darvish (2006) in the case of a slightly compressible fluid. The stabilized values of the shape factor under the PSS assumption are summarized in Table 3.

Fig. 9
figure 9

Dimensionless shape factor versus dimensionless time for a slab-shaped (1D flow) matrix block subject to different boundary conditions under the PSS assumption

Full size image
Fig. 10
figure 10

Dimensionless shape factor versus dimensionless time for a cylindrical (2D flow) shaped matrix block subject to different boundary conditions under the PSS assumption

Full size image
Fig. 11
figure 11

Dimensionless shape factor versus dimensionless time for a spherical shaped matrix block (3D flow) subject to different boundary conditions under the PSS assumption

Full size image
Table 3 Shape factor constants for different geometry matrix blocks subject to different boundary conditions under the PSS assumption
Full size table

3.2 Transient shape factor, standard shaped matrix blocks

A precise value of the shape factor at the transient state is essential to consider the performance of the matrix–fracture interaction. To more precisely understand the physics of flow behavior, the shape factor was also evaluated using the transfer function (Eq. 21).

Figure 12 shows the shape factor for different slab, cylindrical and spherical shaped matrix blocks at the constant fracture pressure for transient flow.

Fig. 12
figure 12

Dimensionless shape factor versus dimensionless time for different shapes of matrix blocks for the constant fracture pressure scheme under the transient transfer assumption

Full size image

As in the previous section, the values of the shape factor for different shapes of matrix blocks under different boundary conditions were evaluated and are presented in Table 4. Generally, these values are larger compared with shape factors obtained from the PSS approach.

Table 4 Shape factor constants for different geometry matrix blocks subject to different boundary conditions under the transient transfer assumption
Full size table

The above results show that both the transient and PSS values of the single-phase shape factor depend on the geometry and how the fracture pressure changes with time.

3.3 Shape factor for 3D irregular shapes and three-dimensional flow

In this section, the work is extended to three-dimensional irregular shapes. The shapes were designed as a combination of square and triangle where there is no analytical solution to calculate the shape factor. Figure 13 shows the 3D irregular shapes of the prism- and complex shaped blocks.

Fig. 13
figure 13

Schematic representation of the problem for the prism and complex shaped blocks

Full size image

The characteristic length of the prism-shaped block is obtained as follows:

$$L = 2 \times \frac{{\sqrt {a_{1} + a_{2} + a_{3} + a_{4} + a_{5} } }}{5}$$
(24)

where a1 to a5 are the vertical distances between the center of gravity of the prism and its faces. The characteristic length was calculated to be 35.

The characteristic length of the complex shaped block was obtained based on its volume and surface. The volume and surface of the standard shapes (slab, cylindrical and spherical) and the prism shape were used to interpolate the characteristic length of the complex shaped matrix block because its measurements for complex shapes are not easy to calculate as other forms. For this purpose, we introduced three-dimensional interpolations as shown in Fig. 14, to interpolate the characteristic length of the complex shape.

Fig. 14
figure 14

Interpolated value of the characteristic length for the complex shaped matrix block

Full size image

The four blue lines shown in Fig. 14 are the characteristic length of the slab, cylindrical, spherical and prism shapes as a function of volume and surface. According to the three-dimensional interpolation results, the characteristic length for the complex shape is estimated to be 34.2 (red line in Fig. 14). The dimensionless shape factor is calculated to be 11.4 and 10.5 for the prism and complex shapes, respectively, under the PSS assumption (for constant pressure case). The obtained shape factor values for the prism and complex shaped matrix blocks are shown in Figs. 15 and 16, respectively, which are compared with the obtained value at a constant pressure scheme for fractures.

Fig. 15
figure 15

Dimensionless shape factor versus dimensionless time for the prism-shaped matrix block subject to different boundary conditions under the PSS assumption

Full size image
Fig. 16
figure 16

Dimensionless shape factor versus dimensionless time for the complex shaped matrix block subject to different boundary conditions under the PSS assumption

Full size image

The values of the shape factor for the prism and complex shapes of matrix blocks for different boundary conditions under the PSS and transient transfer assumptions are presented in Table 5.

Table 5 Shape factor constants for irregular geometry matrix blocks subject to different boundary conditions under the PSS and transient transfer assumption
Full size table

3.4 Shape factor for three-dimensional flow in regular and irregular shaped blocks

In this section, the results of the calculated shape factor for different boundary conditions of pressure of the fractures are shown. Results are for both regular and irregular shaped matrix blocks.

The regular and irregular cases to simulate three-dimensional flow in the matrix block are shown in Fig. 17.

Fig. 17
figure 17

Regular and irregular shaped matrix blocks in three-dimensional flow

Full size image

Tables 6 and 7 show stabilized shape factors in three-dimensional flow of all regular and irregular shaped matrix blocks under the PSS and transient transfer assumptions, respectively.

Table 6 Stabilized shape factors in three-dimensional flow under the PSS assumption
Full size table
Table 7 Stabilized shape factors in three-dimensional flow under the transient transfer assumption
Full size table

The results show that the shape factor is different for regular and irregular shapes and flow regimes as it is a function of time. However, having an idea about the shape and size of matrix blocks (i.e., from FMI log, geomechanical study, etc.) can help reservoir engineers to estimate a realistic range of shape factor. Both transient and PSS models can help us to determine the upper and lower limits for shape factor when the shape factor is considered as a matching parameter.

4 Comparison with existing models

As it was previously shown, when the results from different sources were compared, real differences for \(\sigma\) values were noticed. The shape factor values calculated under the PSS assumption were higher than or equal to those proposed by Kazemi et al. (1976), but less than those by Warren and Roots (1963), and Coats (1989). For 1D slab flow under the transient assumption, the shape factor obtained in this study was around 10 for the constant fracture pressure case in comparison to 12, 11.5 and 9.87 used by Quintard and Whitaker (1996), Noetinger and Estebenet (2000) and Penuela et al. (2002a, b), respectively. Figure 18 demonstrates a comparison between the presented shape factor from the new numerical model in this study with the existing ones. Figures 19 and 20 compare the stabilized values of the shape factor from the numerical solution performed in this work and other numerical/analytical studies by others for constant fracture pressure under the PSS and transient flow regimes.

Fig. 18
figure 18

Comparison of the developed shape factor model with literature models for 1D flow (slab-shaped matrix block) and slightly compressible fluid in the case of the constant fracture pressure

Full size image
Fig. 19
figure 19

Comparison of the obtained results for one-, two- and three-dimensional flow regimes under the PSS assumption for the constant fracture pressure with those from other studies (N is the number of the fracture sets)

Full size image
Fig. 20
figure 20

Comparison of the obtained results for one-, two- and three-dimensional flow regimes under the transient assumption for the constant fracture pressure with those from other studies

Full size image

5 Conclusions

  1. 1.

    In this paper, the value of the shape factor is calculated for different geometries and under transient and PSS assumptions in a systematic approach. Using fine-scale numerical simulation, it has been shown that the matrix–fracture shape factor for a single-phase flow of slightly compressible fluid illustrates a period with a decreasing value and then stabilizes to a stable value. This is true for both regular and irregular shapes.

  2. 2.

    Based on the pressure depletion regime in the fracture, the stabilized value of the shape factor varies between two limits. The upper limit is obtained for an exponentially declining fracture pressure with a decline exponent of 0.0001 which corresponds to a slow pressure depletion regime. The lower limit is derived for the constant fracture pressure boundary conditions where depletion takes place faster.

  3. 3.

    The shape factor values calculated from PSS pressure behavior for the one- and two-dimensional blocks have a good agreement with those proposed by Kazemi et al. (1976). Reasonable agreement is also found between the obtained values for the three-dimensional block and that presented by Peaceman (1976).

  4. 4.

    It has also been shown that the depletion time of a matrix block is a function of the fracture pressure depletion regimes. In the case of constant fracture pressure or exponential decline with a large exponent, the block is depleted faster than that in the linear decline and the exponential decline with a small exponent. The same behavior has been reported for a slightly compressible fluid by Chang (1993) and Hassanzadeh and Pooladi-Darvish (2006).

  5. 5.

    The shape factor is estimated and made dimensionless with characteristic length, σL2, for irregular shapes where there is no analytical solution for them. It is shown that dimensionless shape factors for irregular shapes are closer to those of the slab case. This solution facilitates accurate simulation of oil transfer between the matrix and fracture in fractured reservoirs.

Our results reveal that the shape factor is a function of time, and its value is different for regular and irregular shapes and various boundary conditions. However, the heterogeneity of the matrix is not considered in this study and different results may be obtained in this case. In addition, conducting the same investigations into multiphase flow can be considered in future work.