Towards the stabilization of the low density elements in topology optimization with large deformation

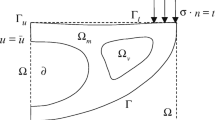
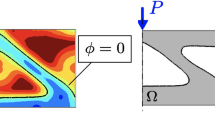
Abstract

This work addresses the treatment of lower density regions of structures undergoing large deformations during the design process by the topology optimization method (TOM) based on the finite element method. During the design process the nonlinear elastic behavior of the structure is based on exact kinematics. The material model applied in the TOM is based on the solid isotropic microstructure with penalization approach. No void elements are deleted and all internal forces of the nodes surrounding the void elements are considered during the nonlinear equilibrium solution. The distribution of design variables is solved through the method of moving asymptotes, in which the sensitivity of the objective function is obtained directly. In addition, a continuation function and a nonlinear projection function are invoked to obtain a checkerboard free and mesh independent design. 2D examples with both plane strain and plane stress conditions hypothesis are presented and compared. The problem of instability is overcome by adopting a polyconvex constitutive model in conjunction with a suggested relaxation function to stabilize the excessive distorted elements. The exact tangent stiffness matrix is used. The optimal topology results are compared to the results obtained by using the classical Saint Venant–Kirchhoff constitutive law, and strong differences are found.

Appendix

1.1 Kinematics

The following kinematical quantities are used for the description of the stress and tangent tensor. The first of them are the components of the deformation gradient ${\varvec{F}} = {\varvec{f}}_i \otimes {\varvec{e}}_i$, which represents the stretching of the fibers (Fig. 13).

Fig. 13

Deformation gradient tensor configuration

Another important kinematical variables are

$$\begin{aligned} {\varvec{g}}_1&= {\varvec{f}}_2 \times {\varvec{f}}_3, \nonumber \\ {\varvec{g}}_2&= {\varvec{f}}_3 \times {\varvec{f}}_1, \nonumber \\ {\varvec{g}}_3&= {\varvec{f}}_1 \times {\varvec{f}}_2, \end{aligned}$$

(50)

that measures the areas of fibers ${\varvec{f}}_i$, and the last equation is $J = {\varvec{f}}_{(i)} \cdot {\varvec{g}}_{(i)}$, that measures the volume changes (see Fig. 13).

1.2 Saint Venant–Kirchhoff material

The constitutive relation (10) applied to Eq. (12), gives

$$\begin{aligned} \varvec{\tau }_{i}^0 = ( \lambda \text{ I }_1 - \mu ) {\varvec{f}}_{i} + \mu ({\varvec{f}}_{j} \otimes {\varvec{f}}_j ) {\varvec{f}}_i, \end{aligned}$$

(51)

that is, the stress as a function of the strain. The component ${\varvec{f}}_3 = 1 + \gamma _{33}$ is due to the 2D assumption adopted. In what follows, we present its values and tangent operator for the PE and PS assumptions.

1.2.1 Plane strain (PE)

The PE condition $\gamma _{33} = 0$, can be applied directly to Eq. (51). The PE components of first Piola–Kirchhoff stress tensor and strain invariant are given by

$$\begin{aligned} \varvec{\tau }_{\alpha }^0 = (\varvec{\tau }_{\alpha }^{PE})^0~~~{\text{ and }}~~~\text{ I }_1 = \text{ I }_1^{PE}. \end{aligned}$$

(52)

The material tangent tensor given by its derivation is

$$\begin{aligned} \frac{\partial \varvec{\tau }_{\alpha }^{0} }{\partial \varvec{\gamma }_{\beta }} = \left( {\varvec{C}}_{\alpha \beta }^{PE} \right) ^{0} = \lambda {\varvec{f}}_{\alpha } \otimes {\varvec{f}}_{\beta } + \mu [ ({\varvec{f}}_{\alpha } \cdot {\varvec{f}}_{\beta }) {\varvec{I}} +{\varvec{f}}_{\beta } \otimes {\varvec{f}}_{\alpha }].\nonumber \\ \end{aligned}$$

(53)

1.2.2 Plane stress (PS)

As explained in Sect. 3.6, the PS condition mathematically consistent is given by the solution of the equation $\tau _{33}^0 \!=\! 0$ [15]. The PS components of first Piola–Kirchhoff stress tensor and strain invariant are given by

$$\begin{aligned} {\varvec{\tau }}_i^0&= \left( \lambda \text{ I }_1^{PE} - \mu \right) {\varvec{f}}_i + \mu \left( {\varvec{f}}_\gamma \otimes {\varvec{f}}_\gamma \right) {\varvec{f}}_i \nonumber \\&+ \lambda \tilde{\text{ I }}_1 {\varvec{f}}_i + \mu \left( {\varvec{f}}_3 \otimes {\varvec{f}}_3 \right) {\varvec{f}}_i,\\ \text{ I }_1&= \text{ I }_1^{PE} + \tilde{\text{ I }}_1.\nonumber \end{aligned}$$

(54)

The components of first Piola–Kirchhoff stress tensor from Eq. (54) can be split into two different tensors, the stress tensor from PE condition and the stress tensor of the PS effect condition $(1+\gamma {33}) {\varvec{e}}_{3}$ and are displayed bellow

$$\begin{aligned} \left( \varvec{\tau }_\alpha ^{PS} \right) ^0 = \left( \varvec{\tau }_\alpha ^{PE} \right) ^0 + \varvec{\omega }_\alpha ^0, \end{aligned}$$

(55)

where $\varvec{\omega }_\alpha ^0$ is given by

$$\begin{aligned} \varvec{\omega }_\alpha ^0 = \frac{\lambda }{2} \left( {\varvec{f}}_3 \cdot {\varvec{f}}_3 -1 \right) {\varvec{f}}_{\alpha } = \frac{\lambda }{2} \left( \left( 1 + \gamma _{33} \right) ^2 -1 \right) {\varvec{f}}_{\alpha }. \end{aligned}$$

(56)

To obtain the $\varvec{\omega }_\alpha ^0$ tensor, it is necessary to find $\gamma _{33}$, however, first, it is necessary to isolate the term $\tau _{33}^0$, by substituting Eq. (14) into Eq. (54). From $\varvec{\tau }_{3}^0$, after some algebra arises to

$$\begin{aligned} \varvec{\tau }_3^0&= \left[ {\lambda \left( {\text{ I }_1^{PE} - \frac{1}{2}} \right) - \mu } \right] \left( {1 + {\gamma _{33}}} \right) {\varvec{e}}_3 \nonumber \\&+ \left( {\frac{{\lambda + 2\mu }}{2}} \right) \left( {1 + {\gamma _{33}}} \right) ^3 {\varvec{e}}_3. \end{aligned}$$

(57)

By applying $\tau _{33}^0 = {\varvec{\tau }}_3^0 \cdot {\varvec{e}}_3$ into Eq. (57), we obtain

$$\begin{aligned} \tau _{33}^0 = \left[ {\lambda \left( {\text{ I }_1^{PE} - \frac{1}{2}} \right) - \mu } \right] \left( {1 + {\gamma _{33}}} \right) + \left( {\frac{{\lambda + 2\mu }}{2}} \right) \left( {1 + {\gamma _{33}}} \right) ^3.\nonumber \\ \end{aligned}$$

(58)

For the plane problem (2D), the stress components $\tau _{\alpha 3}^0$ and $\tau _{3\alpha }^0$ are equal to $0$, and by applying the PE condition $\tau _{33}^0=0$ into Eq. (57), $\gamma _{33}$ can be obtained

$$\begin{aligned} \gamma _{33} = \sqrt{ \frac{\lambda \left( 1 - 2 \text{ I }_1^{PE} \right) + 2 \mu }{\lambda + 2 \mu } } - 1. \end{aligned}$$

(59)

By substituting $\gamma _{33}$ from Eq. (59) into Eq. (56), the tensor $\varvec{\omega }_\alpha ^0$ for plane problem (2D) emerges as

$$\begin{aligned} \varvec{\omega }_\alpha ^0 = { - \frac{{{\lambda ^2} \text{ I }_1^{PE} }}{{\lambda + 2\mu }}{\varvec{f}}_\alpha } \end{aligned}$$

(60)

From Eqs. (53), (55), and (60), it is possible to compute the material tangent tensor for PS assumption, leading to

$$\begin{aligned} \left( {\varvec{C}}_{\alpha \beta }^{PS} \right) ^0 = \frac{{\partial \left( {\varvec{\tau }_\alpha ^{PE}}\right) ^0 }}{{\partial {\varvec{\gamma }_\beta }}} + \frac{{\partial \varvec{\omega }_\alpha ^0 }}{{\partial {\varvec{\gamma }_\beta }}} = \left( {\varvec{C}}_{\alpha \beta }^{PE} \right) ^0 + {\varvec{Q}}_{\alpha \beta }^0 \end{aligned}$$

(61)

where ${\varvec{Q}}_{\alpha \beta }^0$ is given by

$$\begin{aligned} {\varvec{Q}}_{\alpha \beta }^0 = - \frac{\lambda ^2 }{\lambda + 2 \mu } \left( {\varvec{f}}_{\alpha } \otimes {\varvec{f}}_{\beta } + \delta _{ \alpha \beta }\text{ I }_1^{PE} {\varvec{I}} \right) . \end{aligned}$$

(62)

1.3 Neo-Hookean of Simo–Ciarlet material

The constitutive relation (10) applied to Eq. (13), gives

$$\begin{aligned} \varvec{\tau }_{i}^0 = \left[ \frac{\lambda }{2} ( J^{2} -1 ) - \mu \right] \frac{{\varvec{g}}_i}{J} + \mu {\varvec{f}}_i. \end{aligned}$$

(63)

1.3.1 Plane strain (PE)

The PE condition is simply given by ${\varvec{f}}_{3} = 0$, so that the material tangent tensor is given by

$$\begin{aligned} \left( {\varvec{C}}_{\alpha \beta }^{PE} \right) ^0&= \left[ \frac{\lambda }{2} ( 1 + J^{-1} ) + \mu J^{-1} \right] {\varvec{g}}_{\alpha } \otimes {\varvec{g}}_{\beta } \nonumber \\&+ \left[ \frac{\lambda }{2} ( J - J^{-1} ) - \mu J^{-1} \right] \frac{\partial {\varvec{g}}_{\alpha }}{\partial {\varvec{f}}_{\beta }} + \delta _{\alpha \beta } \mu {\varvec{I}}. \end{aligned}$$

(64)

1.3.2 Plane stress (PS)

The solution of the PS condition obtained from Campello et al. [15] for plane problem (2D) is given by

$$\begin{aligned} \gamma _{33} = \sqrt{ \frac{2 \mu + \lambda }{ \lambda J^2 + 2 \mu }} -1, \end{aligned}$$

(65)

and the material tangent tensor is given by

$$\begin{aligned} \left( {\varvec{C}}_{\alpha \beta }^{PS} \right) ^0 = \vartheta ^{^{\prime }} {\varvec{g}}_{\alpha } \otimes {\varvec{g}}_{\beta } +\delta _{\alpha \beta } \mu {\varvec{I}} + (1 -\delta _{\alpha \beta } )~ \vartheta ~ {\varvec{e}}_3, \end{aligned}$$

(66)

where

$$\begin{aligned} \vartheta&= \left[ \frac{1}{2} \lambda ( J^{2} -1 ) - \mu \right] \frac{1}{J},\end{aligned}$$

(67)

$$\begin{aligned} \vartheta ^{^{\prime }}&= \mu \frac{(\lambda + 2 \mu )(3 \lambda J^2+ 2 \mu )}{(\lambda J^3 + 2 \mu J)^2}. \end{aligned}$$

(68)