Perfectly Packing an Equilateral Triangle by Equilateral Triangles of Sidelengths $n^{-1/2-\epsilon }$

Abstract

Equilateral triangles of sidelengths 1, $2^{-t}$, $3^{-t}$, $4^{-t},\ldots \$ can be packed perfectly into an equilateral triangle, provided that $\ 1/2<t \le 37/72$. Moreover, for t slightly greater than 1/2, squares of sidelengths 1, $2^{-t}$, $3^{-t}$, $4^{-t},\ldots \$ can be packed perfectly into a square $S_t$ in such a way that some squares have a side parallel to a diagonal of $S_t$ and the remaining squares have a side parallel to a side of $S_t$.

1 Introduction

Let $C, C_1, C_2, C_3, \ldots$ be planar convex bodies. We say that $\ C_1, C_2, \ldots$ can be packed into C if it is possible to apply translations and rotations to the sets $C_n$ so that the resulting translated and rotated bodies are contained in C and have mutually disjoint interiors. If the area of C is equal to the sum of areas of the bodies, then the packing is perfect.

There are many results concerning packings. For example, Moon and Moser showed [12] that any collection of squares whose total area does not exceed 1/2 can be packed into a square of sidelength 1. Richardson [15] proved that any collection of triangles homothetic to T, whose total area does not exceed half the area of T, can be packed in T and made the conjecture that such a result is true also for the translative packing by positive homothetic copies. This has been confirmed in [4].

In this note, we will study perfect packing.

In 1966 Moser posed the following well-known problem (see problem LM6 in [13]): Find the smallest $\varepsilon \ge 0$ such that the squares of harmonic sidelengths $\ 1/2, 1/3, 1/4, \ldots \$ can be packed into a rectangle of area $\ \frac{1}{6}\pi ^2-1+\varepsilon \$ (the sum of areas of the squares equals $\ \frac{1}{6}\pi ^2-1$).

The following upper bounds for $\varepsilon$ were obtained sequentially: $\ 1/20$ [11], 1/127 [8], 1/198 [1], and 1/1244918662 (see [14, 9], and [3]).

This packing problem can be extended. Let $S_n^t$ be a square of sidelength $n^{-t}$ for $\ n=1,2,\ldots$. If $\ t> 1/2$, then the total area of the squares is equal to $\ \sum _{n=1}^{\infty } \frac{1}{n^{2t}} = \zeta (2t)$, where $\zeta ( s)$ is the Riemann zeta function. The question is whether $\ S_1^t, S_2^t, \ldots$ (for $t>1/2$) can be packed perfectly into a rectangle. Obviously, for $t=1$, we get Moser’s original question.

Some results are known for $t < 1$. Chalcraft [2] showed that $\ S_1^t, S_2^t, S_3^t, \ldots \$ can be packed perfectly into a square for all t in the range [0.5964, 0.6]. Joós [10] checked that these squares can be packed perfectly for all t in the range $[\log _3 2, 2/3]$ ($\log _3 2 \approx 0.63$). Wästlund [17] proved that $\ S_1^t, S_2^t, S_3^t, \ldots \$ can be packed into a finite collection of squares of the same area as the sum of areas of the squares, provided that $\ 1/2< t < 2/3$. In [5] it is shown that for all t in the range $\ (1/2, 2/3]$, the squares $\ S_1^t, S_2^t, S_3^t, \ldots \$ can be packed perfectly into a single square. Recently, Tao [16] proved that for any $\ 1/2<t<1$, and any $n_0$ that is sufficiently large depending on t, the squares $\ S_{n_0}^t, S_{n_0+1}^t, \ldots$ can be packed perfectly into a square.

In this note, we will give an analog of this problem for the packing of triangles.

Let $T_n^t$ be an equilateral triangle of sidelength $n^{-t}$ for $\ n=1,2,\ldots$. The question arises whether $\ T_1^t, T_2^t, \ldots$ (for $t>1/2$) can be packed perfectly into an equilateral triangle. More precisely: whether $\ T_1^t, T_2^t, \ldots$ can be packed perfectly, for $\ 0.5 <t \le 0.761202...$ (now $1+1/2^{t} \le \sqrt{\zeta (2t)}$); whether $\ T_2^t, T_3^t, \ldots$ can be packed perfectly, provided that $\ 0.761202... < t \le \ 0.943674...$ (for such values of t the sum of sidelengths of $T_2^t$ and $T_3^t$ is smaller than $\sqrt{\zeta (2t)-1}$); whether $\ T_3^t, T_4^t, \ldots$ can be packed perfectly, provided that $\ 0.943674...<t\le 1.121936...$ (now $1/3^t +1/4^t \le \sqrt{\zeta (2t)-1-1/2^{2t}}$), etc.. It is only known [7] that $T_3^1, T_4^1, \ldots$ can be packed into an equilateral triangle of side of length $(\pi ^2/6-5/4)^{1/2}+1/270$.

In Sect. 2, we will show that equilateral triangles of sidelengths 1, $2^{-t}$, $3^{-t}$, $4^{-t},\ldots \$ can be packed perfectly into an equilateral triangle $T_t$, provided that $\ 1/2<t \le 37/72$.

In Sect. 3, we will check that if $\ 1/2<t \le 37/72$, then all packed triangles can be positive homothetic copies of $T_t$ as well as all packed triangles can be negative homothetic copies of $T_t$.

In addition, in Sect. 4, we will consider square-packing. We will prove that, for $\ 1/2<t \le (154+3\sqrt{2})/306$, squares of sidelengths 1, $2^{-t}$, $3^{-t}$, $4^{-t},\ldots \$ can be packed perfectly into a square $S_t$ in such a way that some squares have a side parallel to a diagonal of $S_t$ and the remaining squares have a side parallel to a side of $S_t$.

2 Perfect Packing

Let t be a fixed number from the interval $\ (1/2, 37/72]$ and let $T_t$ be an equilateral triangle of area $\ \frac{\sqrt{3}}{4} \zeta (2t)$.

The outline of the packing method is as follows. For each $n\ge 2$, the empty space in $T_t$, i.e., the part of $T_t$ not covered by packed triangles $\ T_1^t, \ldots , T_{n-1}^t$, will be divided into at most $3(n-1)$ trapezoids. Then, $T_n^t$ will be packed into a corner of one of these trapezoids.

Let R(l, u) be an isosceles trapezoid with legs of length l, with the measure of the base angles equal to $60^{\circ }$ and with the shorter base of length u. Clearly, the length of the longer base of R(l, u) is equal to $l+u$. If $u=0$, then R(l, 0) is an equilateral triangle.

A trapezoid R(l, u) is x-big, provided that $\ l\ge 2x$ (see Fig. 1, right).

A trapezoid R(l, u) is standard, provided that $\ u \le l$.

Obviously, each x-big trapezoid is also v-big for any $v<x$. Moreover, each standard trapezoid is x-big for sufficiently small x.

Fig. 1

Standard trapezoids R(l, u)

Proposition 1

The area of any standard trapezoid that is not x-big is smaller than $3\sqrt{3}x^2$.

Proof

The area of any standard trapezoid that is not x-big is smaller than three times the area of an equilateral triangle of sidelength 2x (see Fig. 1, left), i.e., is smaller than $3\cdot \frac{\sqrt{3}}{4} \cdot (2x)^2=3\sqrt{3}x^2$. $\square$

Lemma 2

Let R(l, u) be an x-big trapezoid. Then R(l, u) can be divided into either four or five parts: an equilateral triangle of sidelength x and at most four trapezoids which are either standard or x-big.

Proof

Let $T_i$ be the equilateral triangle of sidelength x. We divide R(l, u) into $T_i$ (denoted by“+”in Figs. 2 and 3) and four sets $A_i$, $B_i$, $C_i$, $D_i$ which are either standard trapezoids or x-big trapezoids (possibly some of them are triangles), or the empty set.

Case 1: $l\ge 4x$. The trapezoid R(l, u) is divided into: $\ T_i \cup A_i \cup B_i \cup C_i$, where $A_i=R(x,x)$, $B_i=R(l-2x,u)$ and $C_i=R(2x,l+u-3x)$. The trapezoid $A_i$ is standard. Moreover, $B_i$ and $C_i$ are x-big (see Fig. 2, left, when $l>4x$). In this case $D_i = \emptyset$.

Case 2: $3x\le l<4x$.

Subcase 2a: $u<x$. The trapezoid R(l, u) is divided into: $T_i$, two standard trapezoids $A_i=R(x,x)$, $B_i=R(l-2x,u)$ and one x-big trapezoid $C_i=R(2x,l+u-3x)$ (as in Fig. 2, left, when $3x<l\le 4x$). We take $D_i = \emptyset$.

Subcase 2b: $u\ge x$. The trapezoid R(l, u) is divided into: $T_i$, three standard trapezoids $A_i=R(x,x)$, $B_i=R(x,0)$, $C_i=R(x,l-3x)$ and one x-big trapezoid $D_i=R(l,u-x)$ (as in Fig. 2, right).

Case 3: $2x\le l<3x$.

Subcase 3a: $u<x$ and $l+u\ge 3x$. The trapezoid R(l, u) is divided into: $T_i$ and three standard trapezoids $A_i=R(x,x)$, $B_i=R(x,l+u-3x)$, and $C_i=R(l-x,u)$ as in Fig. 3, left. We take $D_i = \emptyset$.

Subcase 3b: $u<x$ and $l+u<3x$. The trapezoid R(l, u) is divided into: $T_i$ and three standard trapezoids $A_i=R(x,l+u-2x)$, $B_i=R(x,0)$, and $C_i=R(l-x,u)$ as in Fig. 3, middle. We take $D_i = \emptyset$.

Subcase 3c: $u\ge x$. The trapezoid R(l, u) is divided into: $T_i$, three standard trapezoids $A_i=B_i=R(x,0)$, $C_i=R(x,l-2x)$ and one x-big trapezoid $D_i=R(l,u-x)$ as in Fig. 3, right. $\square$

Fig. 2

Divisions of the x-big trapezoid R(l, u), when $l\ge 3x$

Fig. 3

Divisions of the x-big trapezoid R(l, u), when $2x\le l< 3x$

Since $t\le 37/72$, it follows that the sidelength of $T_t$ is greater or equal to $\sqrt{ \zeta (37/36)} >6$.

2.1 Packing Method $M_{\triangle }$

[1]:

The first triangle is packed into the lower left vertex of $T_t$. After packing $T_1^t$, the uncovered part of $T_t$ is divided into $\ A_1 \cup B_1 \cup C_1\$ as in the proof of Lemma 2 (comp. Fig. 2, left, for $u=0$). We take $\ \mathcal {R}_1 = \{ A_1, B_1, C_1\}$.

[2]:

Assume that $n>1$, that the triangles $\ T_1^t, \ldots , T_{n-1}^t$ are packed into $T_t$ and that the family $\mathcal {R}_{n-1}$ is defined. We choose one of the $n^{-t}$-big trapezoids from $\mathcal {R}_{n-1}$ in any way. Denote this trapezoid by R. We pack $T_n^t$ into R at the vertex at the longer base of R. After packing $T_n^t$, the uncovered part of R is divided into $\ A_n \cup B_n \cup C_n \cup D_n$, as in the proof of Lemma 2, and we take $\ \mathcal {R}_n = \bigl ( \mathcal {R}_{n-1}{\setminus } \{R\} \bigr ) \cup \{ A_n, B_n, C_n, D_n\}$. It is possible that $D_n=\emptyset$.

Observe that $\mathcal {R}_{n-1}$ contains at most $3(n-1)$ trapezoids with mutually disjoint interiors, for any $n\ge 2$. Each trapezoid from $\mathcal {R}_{n-1}$ is either $n^{-t}$-big or standard. It is possible that a trapezoid from $\mathcal {R}_{n-1}$ is both $n^{-t}$-big and standard.

Example 1

Figure 4 illustrates the initial stage of the packing process for $t=0.51$. The area of $T_{0.51}$ is equal to $\zeta (1.02)\sqrt{3}/4 \approx 21.9$, thus the sidelength $\sigma$ of $T_{0.51}$ is greater than 7.11. After packing $T_1^{0.51}$, the uncovered part of $T_{0.51}$ is divided into three trapezoids: $\ A_1 = R(1,1)$, $B_1=R(\sigma -2,0)$ and $C_1 = R(2, \sigma -3)$. Both trapezoids $B_1$ and $C_1$ are 2-big and therefore we have two possibilities to pack $T_2^{0.51}$. For instance, we will pack each triangle into a trapezoid of maximum leg length. After packing $T_2^{0.51}$ into $B_1$, the uncovered part of $T_{0.51}$ is partitioned into $A_1$, $C_1$, $A_2$, $B_2$ and $C_2$ ($D_2=\emptyset$).

Fig. 4

Packing method $M_{\triangle }$ for $t=0.51$

Theorem 3

For each t in the range $\ 1/2<t\le 37/72 \approx 0.5138$, the triangles $T_n^t$ can be packed perfectly into the triangle $T_t$ by the method $M_{\triangle }$.

Proof

The proof is similar to that presented in [6]. Let t be a fixed number from the interval $\ (1/2, 37/72]$. The area of $T_t$ is equal to $\ \frac{\sqrt{3}}{4} \sum _{i=1}^{\infty } \frac{1}{i^{2t}} = \frac{\sqrt{3}}{4} \zeta (2t) \ge \frac{\sqrt{3}}{4} \zeta (37/36) = \frac{\sqrt{3}}{4} \cdot 36.579\ldots$. Consequently, $T_t$ is 1-big (its leg length is greater than 2). We pack $T_1^t, T_2^t,...$ into $T_t$ by the method $M_{\triangle }$. To prove Theorem 3 it suffices to show that, for any n, there is at least one $n^{-t}$-big trapezoid in $\mathcal {R}_{n-1}$ (into which $T_n^t$ will be packed).

First, we estimate the sum of areas of trapezoids in $\mathcal {R}_{n-1}$, i.e., the area of the uncovered part of $T_t$ after packing $T_{n-1}^t$. This value is equal to the sum of areas of unpacked triangles $\ T_n^t, T_{n+1}^t, \ldots$, i.e., is equal to

$$\begin{aligned} \frac{\sqrt{3}}{4} \Bigl ( \frac{1}{n^{2t}} + \frac{1}{(n+1)^{2t}}+\ldots \Bigr )&> \frac{\sqrt{3}}{4} \cdot \int _{n}^{+\infty }\frac{1}{x^{2t}}\textrm{d}x = \frac{\sqrt{3}}{4} \cdot \frac{1}{2t-1}n^{1-2t} \\&\ge \frac{\sqrt{3}}{4} \cdot \frac{1}{2\cdot \frac{37}{72}-1}n^{1-2t}= 9\sqrt{3}n^{1-2t}. \end{aligned}$$

Assume that there is an integer n such that the triangle $T_n^t$ cannot be packed into $T_t$ by the method $M_{\triangle }$, i.e., that there is no $n^{-t}$-big trapezoid in $\mathcal {R}_{n-1}$. This means that all trapezoids in $\mathcal {R}_{n-1}$ are standard and that the length of the leg of each such trapezoid is smaller than $2n^{-t}$ (if $l\ge 2n^{-t}$, then R(l, u) is $n^{-t}$-big). By Proposition 1, the area of each such trapezoid is smaller than $3\sqrt{3}n^{-2t}$. Since there are at most $3(n-1)$ trapezoids in $\mathcal {R}_{n-1}$, it follows that the total area of trapezoids in $\mathcal {R}_{n-1}$ is smaller than $\ (3n-3) \cdot 3\sqrt{3} n^{-2t}<9\sqrt{3}n^{1-2t}$, which is a contradiction.

Consequently, $\ T_1^t, T_2^t, \ldots \$ can be packed into $T_t$. $\square$

3 Positive or Negative Copies

One side of $T_r$ is called the bottom. In our drawings, the bottom is the horizontal side of the triangle. By $T_+(l,u)$ we mean the trapezoid T(l, u) lying such that its bases are parallel to the bottom of $T_r$ and that the longer base is lower than the shortest one (see Fig. 5, left).

We call a trapezoid x-classic if it arises from rotating a trapezoid $T_+(l,u)$ by a multiple of $60^{\circ }$, where the respective T(l, u) is x-big or standard (see Fig. 5, left and right).

The image of any positive homothetic copy of $T_r$ in rotation of $60^{\circ }$ is a negative homothetic copy of $T_r$ as well as the image of any negative homothetic copy of $T_r$ in rotation of $60^{\circ }$ is a positive homothetic copy of $T_r$. The image of a triangle T(x, 0) in rotation of $180^{\circ }$ is denoted by $-T(x,0)$.

Fig. 5

Standard trapezoids T(l, u)

Lemma 4

Let R be an x-big classic trapezoid. Then R can be divided into: $T_+(x,0)$ and at most four x-classic trapezoids. Moreover, R can be divided into: $-T_+(x,0)$ and at most four x-classic trapezoids.

Proof

Let R be the x-big classic trapezoid.

Since R is the image of $T_+(l,u)$ in rotation by a multiple of $60^\circ$, it follows that R can be divided into the same shapes as $T_+(l,u)$, with possibly switching roles of $T_+(x,0)$ and $-T_+(x,0)$ (see Fig. 6). Consequently, to prove Lemma 4 it suffices to check that $T_+(l,u)$ can be divided into $T_+(x,0)$ (denoted by “+”) and at most four x-classic trapezoids as well as that $T_+(l,u)$ can be divided into $-T_+(x,0)$ (denoted by“-”in Figs. 6, 7 and 8) and at most four x-classic trapezoids.

The first option was discussed in the proof of Lemma 2. Now consider negative copies of the triangle.

Case 1: $l\ge 4x$. The trapezoid R is divided into: $-T_+(x,0)$, one standard trapezoid and two x-big trapezoids (as in Fig. 7, left; if $l\ge 4x$, then the upper trapezoid is x-big).

Case 2: $3x\le l<4x$. If $u<x$, then $T_+(l,u)$ is divided as in Fig. 7, left (now the upper trapezoid is standard). If $u\ge x$, then $T_+(l,u)$ is divided as in Fig. 7, right.

Case 3: $2x\le l<3x$. If $u<x$ and $l+u\ge 3x$, then $T_+(l,u)$ is divided as in Fig. 8, left. If $u<x$ and $l+u<3x$, then $T_+(l,u)$ is divided as in Fig 8, middle. If $u\ge x$, then $T_+(l,u)$ is divided as in Fig. 8, right. $\square$

Fig. 6

Divisions of the x-big classic trapezoid R, when $l\ge 4x$

Fig. 7

Divisions of the x-big trapezoid $T_+(l,u)$, when $l \ge 3x$

Fig. 8

Divisions of the x-big trapezoid $T_+(l,u)$, when $2x\le l< 3x$

3.1 Packing Method $M_{\triangle ^{\pm }}$

Let $\mathbb {N} = \mathbb {A} \cup \mathbb {B}$, where $\mathbb {A} \cap \mathbb {B} = \emptyset$. Since $t\le 37/72$, it follows that the sidelength of $T_t$ is greater or equal to $\sqrt{ \zeta (37/36)} >6$.

[1]:

If $1 \in \mathbb {A}$, then the first triangle is packed into $T_t$ in the place “+” described in the proof of Lemma 2 (see Fig. 2, left, if $u=0$). If $1 \in \mathbb {B}$, then the first triangle is packed in the place “-” described in the proof of Lemma 4 (see Fig. 7, left, if $l>4x$ and $u=0$). After packing $T_1^t$, the uncovered part of $T_t$ is divided into three 1-classic trapezoids as in the proof of Lemma 4. We take as $\ \mathcal {R}^{\pm }_1$ the family of these three trapezoids.

[2]:

Assume that $n>1$, that the triangles $\ T_1^t, \ldots , T_{n-1}^t$ are packed into $T_t$ and that the family $\mathcal {R^{\pm }}_{n-1}$ is defined. We choose one of the $n^{-t}$-big trapezoids from $\mathcal {R^ {\pm }}_{n-1}$ in any way. Denote this trapezoid by R. If $n \in \mathbb {A}$, then $T_n^t$ is packed in the place “+” in R; if $n \in \mathbb {B}$, then $T_n^t$ is packed in the place “-” in R (see Figs. 2, 3, 6, 7 or 8). After packing $T_n^t$, the uncovered part of R is divided into at most four $n^{-t}$-classic trapezoids as in the proof of Lemma 4. We take as $\ \mathcal {R^{\pm }}_n$ the union of the family of these trapezoids and $\mathcal {R^{\pm }}_{n-1}\setminus \{R\}$.

Fig. 9

Packing method for $t=0.51$ and $\mathbb {B}=\emptyset$

Clearly, $\mathcal {R^{\pm }}_{n-1}$ contains at most $3(n-1)$ trapezoids with mutually disjoint interiors, for any $n\ge 2$. Each trapezoid from $\mathcal {R^{\pm }}_{n-1}$ is either $n^{-t}$-big or standard.

Figure 9 illustrates the initial stage of the packing process in the case when $\mathbb {A} = \mathbb {N}$ and $\mathbb {B}=\emptyset$; note that the first twelve triangles are packed in the same places using the algorithms $M_{\triangle }$ and $M_{\triangle ^{\pm }}$. On the other hand, $\mathbb {B} = \mathbb {N}$ and $\mathbb {A}=\emptyset$ in Fig. 10.

Theorem 5

For each t in the range $\ 1/2<t\le 37/72$, the triangles $T_n^t$ can be packed perfectly into the triangle $T_t$ so that each packed triangle $T_n$ is a positive homothetic copy of $T_n^t$, provided that $n \in \mathbb {A}$ and that each packed triangle $T_n^t$ is a negative homothetic copy of $T_t$, provided that $n \in \mathbb {B}$.

Proof

We pack $T_1^t, T_2^t,...$ into $T_t$ by the method $M_{\triangle ^{\pm }}$. As in the proof of Theorem 3, the sum of areas of trapezoids in $\mathcal {R^{\pm }}_{n-1}$ is greater than $\ 9\sqrt{3}n^{1-2t}.$ If there is an integer n such that the triangle $T_n^t$ cannot be packed into $T_t$ by our method, then the total area of trapezoids in $\mathcal {R^{\pm }}_{n-1}$ is smaller than $\ (3n-3) \cdot 3\sqrt{3} n^{-2t}< 9\sqrt{3}n^{1-2t}$, which is a contradiction. $\square$

Fig. 10

Packing method for $t=0.51$ and $\mathbb {A}=\emptyset$

4 Squares

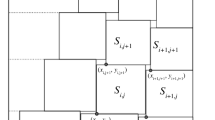
Denote by $S_t$ the square of area $\zeta (2t)$, where $\ 1/2<t\le (154+3\sqrt{2})/306\approx 0.517$. Let P(h, a) be a right trapezoid with height h and with bases of length a and $a-h$. In this section, a trapezoid P(h, a) is x-big, provided that $\ h\ge \frac{3\sqrt{2}}{2}x$. A trapezoid P(h, a) is standard, if $\ a \le \frac{3\sqrt{2}}{2}h$. A trapezoid P(h, a) is x-classic, provided that it is either standard or x-big and provided that its bases are parallel either to a side of $S_t$ or to a diagonal of $S_t$. Observe that the area of each standard trapezoid that is not x-big is smaller than $\ \bigl ( \frac{3\sqrt{2}}{2}-\frac{1}{2} \bigr ) \bigl ( \frac{3\sqrt{2}}{2} x \bigr )^2 = \frac{27\sqrt{2}-9}{4} \cdot x^2$.

Lemma 6

Let P be an x-big classic trapezoid. Then P can be divided into: a square of sidelength x with a side parallel to the bases of P and at most four x-classic trapezoids. Moreover, P can be divided into: a square of sidelength x with a diagonal parallel to the bases of P and at most five x-classic trapezoids.

Proof

Observe that P(h, a) can be divided (see Fig. 11) into a square of sidelength x with a side parallel to bases of P(h, a) and into:

Case 1::

two standard trapezoids P(x, x) and $P(x, (3\sqrt{2}/2-1)x)$ and two big trapezoids: $P(3\sqrt{2}x/2, a-x)$ and $P(h-3\sqrt{2}x/2, a- 3\sqrt{2}x/2)$, provided that $h\ge 3 \sqrt{2}x$;

Case 2::

two standard trapezoids P(x, h/2) and one big trapezoid $P(h, a-x)$, provided that $h< 3 \sqrt{2}x$ and $a-x \ge h$; clearly $h/2< 3 \sqrt{2}x/2$;

Case 3::

four standard trapezoids: $P(h-x,a-x)$, P(x, x) and two trapezoids $P(x, (a-x)/2)$, provided that $a-x<h< 3 \sqrt{2}x$ and $a>3x$; clearly $(a-x)/2< 3 \sqrt{2}x/2$ as well as $a-x<h=2(h-x)-h+2x\le 2(h-x)-3 \sqrt{2}x/2+2x<2(h-x)$;

Case 4::

two standard trapezoids: $P(h-x,a-x)$ and $P(x, a-x)$, provided that $a-x<h< 3 \sqrt{2}x$ and $a\le 3x$; clearly $a-x\le 3x-x=2x$ as well as $a-x<h<2(h-x)$.

Moreover, P(h, a) can be divided (see Fig. 12) into a square of sidelength x with a diagonal parallel to bases of P(h, a) and into:

Case 5::

two standard trapezoids P(x, x) and P(x, 2x) and two big trapezoids: $P(3\sqrt{2}x/2, a-\sqrt{2}x)$ and $P(h-3\sqrt{2}x/2, a-3\sqrt{2}x/2)$, provided that $h\ge 3 \sqrt{2}x$;

Case 6::

five standard trapezoids: $P(z,\sqrt{2}x)$, $P(h-z, h-z)$, where $z=\sqrt{2}x-(a-h)$, $P(\sqrt{2}x, \sqrt{2}x)$ and two trapezoids $P(x, (h-z)\sqrt{2}/2-x/2)$, provided that $h< 3 \sqrt{2}x$ and $z > a-h$; since $z+a-h=\sqrt{2}x$ and $z>a-h$, it follows that $z>\sqrt{2}x/2$; clearly, $\ \frac{\sqrt{2}}{2}(h-z)-\frac{1}{2}x < \frac{\sqrt{2}}{2}\Bigl (3\sqrt{2}x-\frac{\sqrt{2}}{2}x\Bigr ) - \frac{1}{2}x=2x$;

Case 7::

five standard trapezoids: $P(h-z,h-z)$, $P(a-h,\sqrt{2}x)$, $P(\sqrt{2}x, \sqrt{2}x)$ and two trapezoids $P(x, h\sqrt{2}/2-x)$, provided that $5\sqrt{2}x/2 \le h< 3 \sqrt{2}x$ and $z \le a-h< \sqrt{2}x$; clearly, $\ h \frac{\sqrt{2}}{2}-x < 3 \sqrt{2}x\cdot \frac{\sqrt{2}}{2}-x =2x$ as well as $\sqrt{2}x = z+a-h \le a-h+a-h=2(a-h)$;

Case 8::

four standard trapezoids: $P(h-z,h-z)$, $P(a-h,\sqrt{2}x)$ and two trapezoids $P(x, h\sqrt{2}/2-x/2)$, provided that $h<5\sqrt{2}x/2$ and $z \le a-h<\sqrt{2}x$; clearly, $\ h\sqrt{2}/2-x/2 < (5\sqrt{2}x/2) \cdot (\sqrt{2}/2)-x/2=2x$ as well as $\sqrt{2}x = z+a-h \le a-h+a-h=2(a-h)$;

Case 9::

one big trapezoid $P(h, a - \sqrt{2}x)$ and four standard trapezoids $P(x, (h\sqrt{2}+x)/4)$, provided that $h<3\sqrt{2}x$ and $a-h\ge \sqrt{2}x$; clearly, $\ (h\sqrt{2}+x)/4< (3\sqrt{2}x\cdot \sqrt{2}+x)/4 <\frac{3\sqrt{2}}{2}x$. $\square$

Fig. 11

Divisions of the x-big classic trapezoid P(h, a), when a side of the square is parallel to the bases of P(h, a)

Fig. 12

Divisions of the x-big classic trapezoid P(h, a), when a diagonal of the square is parallel to the bases of P(h, a)

Let $\mathbb {N} = \mathbb {A} \cup \mathbb {B}$, where $\mathbb {A} \cap \mathbb {B} = \emptyset$. Since $t\le (154+3\sqrt{2})/306$, it follows that the sidelength of $S_t$ is greater or equal to $\sqrt{ \zeta ((154+3\sqrt{2})/153)} >5.4$.

4.1 Packing Method $M_{\square }$

[1]:

The square $S_t$ is partitioned into two right isosceles triangles: $A_1$ containing the lower left vertex of $S_t$ and $B_1$ containing the upper right vertex of $S_t$. We choose one of them, say $A_1$, and pack the first square into it in the following way. If $1 \in \mathbb {A}$, then the first square is packed in the place marked in Fig. 11 (the upper left picture). If $1 \in \mathbb {B}$, then the first square is packed in the place marked in Fig. 12 (the upper left picture). After packing $S_1^t$, the uncovered part of $A_1$ is divided into four 1-classic trapezoids as in Figs. 11 and 12. We take as $\ \mathcal {P}_1$ the union of the family of these four trapezoids and $\{B_1\}$.

[2]:

Assume that $n>1$, that the squares $\ S_1^t, \ldots , S_{n-1}^t$ are packed into $S_t$ and that the family $\mathcal {S}_{n-1}$ is defined. We choose one of the $n^{-t}$-big trapezoids from $\mathcal {P}_{n-1}$ in any way. Denote this trapezoid by P. The square $S_n^t$ is packed into P in the place marked in Figs. 11 and 12. After packing $S_n^t$, the uncovered part of P is divided into at most five trapezoids. We take as $\ \mathcal {P}_n$ the union of the family of these trapezoids and $\mathcal {P}_{n-1}\setminus \{P\}$.

Figure 13 illustrates the initial stage of the square-packing process when $\mathbb {A}$ is the set of even numbers and $\mathbb {B}$ is the set of odd numbers.

Theorem 7

For each t in the range $\ 1/2<t\le (154+3\sqrt{2})/306\approx 0.517$, the squares $S_n^t$ can be packed perfectly into the square $S_t$ so that a side of each packed square $S_i$ is parallel to a side of $S_t$ for $i \in \mathbb {A}$ while a side of each packed square $S_i$ is parallel to a diagonal of $S_t$ for $i \in \mathbb {B}$.

Proof

Let t be a fixed number from the interval $\ (1/2, (154+3\sqrt{2})/306]$. We place $S_1^t, S_2^t, \ldots$ by the method $M_{\square }$. The sum of areas of trapezoids in $\mathcal {P}_{n-1}$ is greater than

$$\begin{aligned} \int _{n}^{+\infty }\frac{1}{x^{2t}}\textrm{d}x \ge \frac{1}{2\cdot \frac{154+3\sqrt{2}}{306}-1} \cdot n^{1-2t} = (27\sqrt{2}-9)n^{1-2t}. \end{aligned}$$

Assume that there is an integer n such that the square $S_n^t$ cannot be packed into $S_t$ by our method, i.e., that there is no $n^{-t}$-big trapezoid in $\mathcal {P}_{n-1}$. Since there are at most 4n trapezoids in $\mathcal {P}_{n-1}$, it follows that the total area of trapezoids in $\mathcal {P}_{n-1}$ is smaller than $\ 4n \cdot \frac{27\sqrt{2}-9}{4} \cdot n^{-2t} = (27\sqrt{2}-9)n^{1-2t}$, which is a contradiction. $\square$

Fig. 13

Square-packing method for $t=0.51$