Adjacency Graphs of Polyhedral Surfaces

Abstract

We study whether a given graph can be realized as an adjacency graph of the polygonal cells of a polyhedral surface in ${\mathbb {R}}^3$. We show that every graph is realizable as a polyhedral surface with arbitrary polygonal cells, and that this is not true if we require the cells to be convex. In particular, if the given graph contains $K_5$, $K_{5,81}$, or any nonplanar 3-tree as a subgraph, no such realization exists. On the other hand, all planar graphs, $K_{4,4}$, and $K_{3,5}$ can be realized with convex cells. The same holds for any subdivision of any graph where each edge is subdivided at least once, and, by a result from McMullen et al. (Isr. J. Math. 46(1–2), 127–144 (1983)), for any hypercube. Our results have implications on the maximum density of graphs describing polyhedral surfaces with convex cells: The realizability of hypercubes shows that the maximum number of edges over all realizable n-vertex graphs is in $\Omega (n\log n)$. From the non-realizability of $K_{5,81}$, we obtain that any realizable n-vertex graph has ${\mathcal {O}}(n^{9/5})$ edges. As such, these graphs can be considerably denser than planar graphs, but not arbitrarily dense.

1 Introduction

A polyhedral surface consists of a set of interior-disjoint polygons embedded in ${\mathbb {R}}^3$, where each edge may be shared by at most two polygons. Polyhedral surfaces have been long studied in computational geometry, and have well-established applications in for instance computer graphics [16] and geographical information science [13].

Inspired by those applications, classic work in this area often focuses on restricted cases, such as surfaces of (genus 0) polyhedra [4, 30], or x, y-monotone surfaces known as polyhedral terrains [12]. Such surfaces are, in a sense, 2-dimensional. One elegant way to capture this “essentially 2-dimensional behaviour” is to look at the adjacency graph (see below for a precise definition) of the surface: in both cases described above, this graph is planar. In fact, by Steinitz’s Theorem the adjacency graphs of surfaces of convex polyhedra are exactly the 3-connected planar graphs [47]. If we allow the surface of a polyhedron to have a boundary, then every planar graph has a representation as such a polyhedral surface [17].

Recently, applications in computational topology have intensified the study of polyhedral surfaces of non-trivial topology. In sharp contrast to the simpler case above, where the classification is completely understood, little is known about the class of adjacency graphs that describe general polyhedral surfaces. In this paper we investigate this graph class.

Our model A polyhedral surface ${\mathcal {S}} =\{S_1,\dots ,S_n\}$ is a set of n closed polygons embedded in ${\mathbb {R}}^3$ such that, for all pairwise distinct indices $i,j,k\in \{1,2,\dots ,n\}$:

• $S_i$ and $S_j$ are interior-disjoint (with respect to the 2D relative interior of the objects);

• if $S_i\cap S_j\ne \emptyset$, then $S_i\cap S_j$ is either a single corner or a complete side of both $S_i$ and $S_j$;

• if $S_i\cap S_j\cap S_k\ne \emptyset$ then it is a single corner (i.e., a side is shared by at most two polygons).

To avoid confusion with the corresponding graph elements, we consistently refer to polygon vertices as corners and to polygon edges as sides.

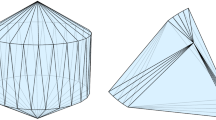
The adjacency graph of a polyhedral surface ${\mathcal {S}}$, denoted as ${\mathcal {G}} ({\mathcal {S}})$, is the graph whose vertices correspond to the polygons of ${\mathcal {S}}$ and which has an edge between two vertices if and only if the corresponding polygons of ${\mathcal {S}}$ share a side. Note that a corner–corner contact is allowed in our model but does not induce an edge in the adjacency graph. Further observe that the adjacency graph does not uniquely determine the topology of the surface. Figure 1 shows an example of a polyhedral surface and its adjacency graph. We say that a polyhedral surface ${\mathcal {S}}$  realizes a graph G if ${\mathcal {G}} ({\mathcal {S}})$ is isomorphic to G. In this case, we write ${\mathcal {G}} ({\mathcal {S}})\simeq G$.

Fig. 1

A convex-polyhedral surface ${\mathcal {S}}$ and its nonplanar 3-degenerate adjacency graph ${\mathcal {G}} ({\mathcal {S}})$

If every polygon of a polyhedral surface ${\mathcal {S}}$ is strictly convex, we call ${\mathcal {S}}$ a convex-polyhedral surface. Our paper focuses on convex-polyhedral surfaces; refer to Fig. 2 for an example of a general (nonconvex) polyhedral surface. We emphasize that we do not require that every polygon side has to be shared with another polygon.

Our work relates to two lines of research: Steinitz-type problems and contact representations.

Steinitz-type problems Steinitz’s Theorem gives a positive answer to the realizability problem for convex polyhedra. This result is typically stated in terms of the realizability of a graph as the 1-skeleton of a convex polyhedron. Our perspective comes from the dual point of view, describing the adjacencies of the faces instead of the adjacencies of the vertices.

Steinitz’s Theorem settles the problem raised in this paper for surfaces that are homeomorphic to a sphere. A slightly stronger version of Steinitz’s Theorem by Grünbaum and Barnette [8] states that every planar 3-connected graph can be realized as the 1-skeleton of a convex polyhedron with the prescribed shape of one face. Consequently, also in our model we can prescribe the shape of one polygon if the adjacency graph of the surface is planar. For other classes of polyhedra only very few partial results for their graph-theoretic characterizations are known [18, 29]. No generalization for Steinitz’s Theorem for surfaces of higher genus is known, and therefore there are also no results for the dual perspective. In higher dimensions, Richter-Gebert’s Universality Theorem implies that the realizability problem for abstract 4-polytopes is $\exists {\mathbb {R}}$-complete [42].

McMullen et al. [38] constructed a closed polyhedral surface of genus 4097—with only 4096 polygons. For the first few steps of their inductive construction; see Fig. 13. Their construction answered a question that Barnette posed in 1980; he asked whether there are polyhedra in ${\mathbb {R}}^3$ whose polygonal faces all have arbitrarily many sides. Later, Ziegler [52] gave a different construction of the family of surfaces presented by McMullen et al.

Simplicial complexes The algorithmic problem of determining whether a given k-dimensional (abstract) simplicial complex embeds in ${\mathbb {R}}^d$ is an active field of research [11, 22, 37, 39, 45, 46]. There exist at least three interesting notions of embeddability: linear, piecewise linear, and topological embeddability, which usually are not the same [37]. The case $(k,d)=(1,2)$, however, corresponds to testing graph planarity, and thus, all three notions coincide, and the problem lies in P.

While some necessary conditions for the geometric realizability of simplicial complexes are known [40, 50], the problem of recognizing the linear embeddability of k-dimensional complexes into ${\mathbb {R}}^d$ is conjectured to be NP-hard for every fixed pair (k, d) with $3\le d\le 3k+1$ [45, Conjecture 3.2.2]. Recently, Abrahamsen et al. [1] showed that deciding whether a 2-simplex (e.g., a set of triangles with prescribed edge contacts), linearly embeds in ${\mathbb {R}}^3$ is $\exists {\mathbb {R}}$-complete; this remains true even if a piecewise linear embedding is given. More generally, they showed $\exists {\mathbb {R}}$-completeness for the decision problem of linearly embedding a k-simplex in ${\mathbb {R}}^d$ for all $d\ge 3$ and $k\in \{d,d-1\}$.

Concerning piecewise-linear embeddability, determining whether a given k-complex embeds piecewise-linearly in ${\mathbb {R}}^d$ for the cases $d=3$ and $k\in \{2,3\}$ is known to be NP-hard [39] and decidable [36]. In higher dimensions, the problem is polynomial time solvable for $d\ge 4$ and $k<\nicefrac {2}{3}\cdot (d-1)$ [11], NP-hard for $d\ge 4$, $k\ge \nicefrac {2}{3}\cdot (d-1)$ and even undecidable for $d\ge 5$ and $k\in \{d,d-1\}$ [22, 46].

Contact representations A realization of a graph as a polyhedral surface can be viewed as a contact representation of this graph with polygons in ${\mathbb {R}}^3$, where a contact between two polygons is realized by sharing an entire polygon side, and each side is shared by at most two polygons. In a general contact representation of a graph, the vertices are represented by interior-disjoint geometric objects, where two objects touch if and only if the corresponding vertices are adjacent. In concrete settings, the object type (disks, lines, polygons, etc.), the type of contact, and the embedding space is specified. Numerous results concerning which graphs admit a contact representation of some type are known; we review some of them.

The well-known Andreev–Koebe–Thurston circle packing theorem [3, 35] states that every planar graph admits a contact representation by touching disks in ${\mathbb {R}}^2$. A less known but impactful generalization by Schramm [44, Theorem 8.3] guarantees that every triangulation (i.e., maximal planar graph) has a contact representation in ${\mathbb {R}}^2$ where every inner vertex corresponds to a homothetic copy of a prescribed smooth convex set; the three outer vertices correspond to prescribed smooth arcs whose union is a simple closed curve. If the prototypes and the curve are polygonal, i.e., are not smooth, then there still exists a contact representation, however, with the following shortcomings: The sets representing inner vertices may degenerate to points, which may lead to extra contacts. As observed by Gonçalves et al. [24], Schramm’s result implies that every subgraph of a 4-connected triangulation has a contact representation with aligned equilateral triangles and similarly, every inner triangulation of a 4-gon without separating 3- and 4-cycles has a hole-free contact representation with squares [20, 43].

While for the afore-mentioned existence results there are only iterative procedures that compute a series of representations converging to the desired one, there also exist a variety of shapes for which contact representations can be computed efficiently. Allowing for sides of one polygon to be contained in the side of adjacent polygons, Duncan et al. [17] showed that, in this model, every planar graph can be realized by hexagons in the plane and that hexagons are sometimes necessary. Assuming side–corner contacts, de Fraysseix et al. [15] showed that every plane graph has a triangle contact representation and how to compute one. Gansner et al. [23] presented linear-time algorithms for triangle side-contact representations for outerplanar graphs, square grid graphs, and hexagonal grid graphs. Kobourov et al. [34] showed that every 3-connected cubic planar graph admits a triangle side-contact representation whose triangles form a tiling of a triangle. For a survey of planar graphs that can be represented by dissections of a rectangle into rectangles, we refer to Felsner [20]. Moreover, there exist linear-time algorithms to compute hole-free contact representations of triangulations where each vertex is represented by an 8-sided rectilinear polygon [25, 51]. In fact, Alam et al. [2] showed that there exist contact representations where the area of the polygons can even be prescribed (however, no polynomial-time algorithm is known to compute such representations). On the negative side, Breu and Kirkpatrick [10] showed that recognizing whether a given graph admits a contact representation with unit disks is NP-hard. Later, Klemz et al. [33] showed that this statement remains true even when restricted to outerplanar graphs. Moreover, Bowen et al. [9] showed that if the unit disk contact representation is additionally required to respect a given rotation system, the recognition problem is NP-hard even when restricted to trees.

Representations with one-dimensional objects in ${\mathbb {R}}^2$ have also been studied. While every plane bipartite graph has a contact representation with horizontal and vertical segments [14], Hliněný [27] showed that recognizing segment contact graphs is an NP-complete problem even when restricted to planar graphs. Hliněný [26] also showed that recognizing curve contact graphs where no four curves meet in one point is NP-complete for planar graphs whereas the same question can be solved in polynomial time for planar triangulations.

Less is known about contact representations in higher dimensions. Every graph is the contact graph of interior-disjoint convex polytopes in ${\mathbb {R}}^3$ where contacts are shared 2-dimensional facets [49]. Hliněný and Kratochvíl [28] proved that the recognition of unit-ball contact graphs in ${\mathbb {R}}^d$ is NP-hard for $d=3$, 4, and 8. Felsner and Francis [21] showed that every planar graph has a contact representation with axis-parallel cubes in ${\mathbb {R}}^3$. For proper side contacts, Kleist and Rahman [32] proved that every subgraph of an Archimedean grid can be represented with unit cubes, and every subgraph of a d-dimensional grid can be represented with d-cubes. Evans et al. [19] showed that every graph has a contact representation where vertices are represented by convex polygons in ${\mathbb {R}}^3$ and edges by shared corners of polygons, and gave polynomial-volume representations for bipartite, 1-planar, and cubic graphs.

Contribution and organization We show that for every graph G there exists a polyhedral surface ${\mathcal {S}}$ such that G is the adjacency graph of ${\mathcal {S}}$; see Sect. 2. For convex-polyhedral surfaces, the situation is more intricate; see Sect. 3. Every planar graph can be realized by a flat convex-polyhedral surface (Proposition 3.2), i.e., a convex-polyhedral surface in ${\mathbb {R}}^2$. Some nonplanar graphs cannot be realized by convex-polyhedral surfaces in ${\mathbb {R}}^3$; in particular this holds for all supergraphs of $K_5$ (Proposition 3.4), of $K_{5,81}$ (Theorem 3.8), and of all nonplanar 3-trees (Theorem 3.13). Nevertheless, many nonplanar graphs, including $K_{4,4}$ and $K_{3,5}$, have such a realization (Propositions 3.6 and 3.7). We remark that all our positive results hold for subgraphs and subdivisions as well (Proposition 3.1). Similarly, our negative results carry over to supergraphs.

Our results have implications on the maximum density of adjacency graphs of convex-polyhedral surfaces; see Sect. 4. On the one hand, the non-realizability of $K_{5,81}$ implies that the number of edges of any realizable n-vertex graph is upperbounded by ${\mathcal {O}}(n^{9/5})$ edges. On the other hand, the realizability of hypercubes (which we derive from the above-mentioned result of McMullen et al. [38]; see Sect. 3.4) implies that there are realizable graphs with n vertices and $\Omega (n\log n)$ edges. Hence these graphs can be considerably denser than planar graphs, but not arbitrarily dense.

2 General Polyhedral Surfaces

We start with a simple positive result.

Proposition 2.1

For every graph G, there exists a polyhedral surface ${\mathcal {S}}$ such that ${\mathcal {G}} ({\mathcal {S}})\simeq G$.

Proof

We start our construction with $n=|V(G)|$ interior-disjoint rectangles such that there is a line segment s that acts as a common side of all these rectangles. We then cut away parts of each rectangle thereby turning it into a comb-shaped polygon as illustrated in Fig. 2. These polygons represent the vertices of G. For each pair $(P,P')$ of polygons that are adjacent in G, there is a subsegment $s_{PP'}$ of s such that $s_{PP'}$ is a side of both P and $P'$ that is disjoint from the remaining polygons. In particular, every polygon side is adjacent to at most two polygons. The result is a polyhedral surface whose adjacency graph is G. $\square$

Fig. 2

A realization of $K_5$ by arbitrary polygons with side contacts in ${\mathbb {R}}^3$

In our construction, the complexity of each polygon depends on the degree of the vertex it represents. If we insist on strictly convex polygons and full side contacts, this is clearly also necessary. One interesting question is how tight this dependence is.

To make this question precise, for a polyhedral surface ${\mathcal {S}}$, let $\zeta ({\mathcal {S}})$ be the total complexity of ${\mathcal {S}}$; that is, the sum of the number of vertices (or edges, which is the same) of all the polygons in ${\mathcal {S}}$. Then, for a graph G, define

$$\begin{aligned} \zeta (G) = \min _{{\mathcal {S}}: {\mathcal {G}} ({\mathcal {S}}) \simeq G}\zeta ({\mathcal {S}}) \end{aligned}$$

to be the complexity of the best possible representation of G. Proposition 2.1 implies an upper bound on $\zeta (G)$.

Corollary 2.2

Let G be a graph with $m=|E(G)|$ edges. Then $\zeta (G) \le 6m$.

Proof

Our construction for Proposition 2.1 represents a vertex of degree d by a polygon with at most $4d+2$ sides. It is not hard to improve this to exactly 3d: instead of a rectangular comb, we can use a triangular one, with triangular gaps between successive teeth. The corollary now follows from the fact that the sum of degrees is twice the number of edges in G. $\square$

For some graphs, this bound is tight; for example, the graph which consists of a single edge. However, some graphs admit much better embeddings. The lower bound on the number of sides for a vertex of degree d is exactly d. There are graphs that realize this lower bound: they are exactly the adjacency graphs of closed polyhedral surfaces. In this model, $K_7$ can be realized as the so-called Szilassi polyhedron; for an illustration, see [53]. The tetrahedron and the Szilassi polyhedron are the only two known polyhedra in which each face shares a side with every other face [53]. Which other (complete) graphs can be realized in this way remains an open problem.

3 Convex-Polyhedral Surfaces

In this section we investigate which graphs can be realized by convex-polyhedral surfaces. First of all, it is always possible to represent a subgraph or a subdivision of an adjacency graph with slight modifications of the corresponding surface: trimming the polygons allows us to represent subgraphs, while trimming and inserting chains of polygons allows subdivisions. Consequently, we obtain the following result.

Proposition 3.1

The set of adjacency graphs of convex-polyhedral surfaces in ${\mathbb {R}}^3$ is closed under taking subgraphs and subdivisions.

Proof

Obviously the set of adjacency graphs of convex-polyhedral surfaces is closed under vertex deletions. It remains to show that it is also closed under edge deletions and edge subdivisions. Consider a surface ${\mathcal {S}}$ and its adjacency graph G. We define three operations that locally change ${\mathcal {S}}$ and describe their effect on G.

Fig. 3

The three operations used in the proof of Proposition 3.1

A corner trim takes any corner v of ${\mathcal {S}}$ (which may belong to multiple polygons of ${\mathcal {S}}$) and replaces it by a set of new corners, one on each incident side, all at distance $\varepsilon$ from v for some sufficiently small $\varepsilon$; see Fig. 3, (a) and (b). Each polygon in ${\mathcal {S}}$ incident to v now uses two new copies of v instead of v; observe that the new polygons are still strictly convex. The adjacency graph of ${\mathcal {S}}$ does not change under a corner trim operation.

A side trim takes any side s of ${\mathcal {S}}$ and first performs a corner trim on both incident corners. This creates two new corners on s; we delete these two new corners from the (at most two) polygons incident to s; see Fig. 3, (a) and (c). Note that this operation still preserves strict convexity of any polygons incident to s, and that if there were two polygons that shared s, they now no longer share a side. Thus, the edge of G corresponding to s is removed.

Finally, a subdivide operation takes any side s of ${\mathcal {S}}$ that is incident to two polygons P and Q, and first performs a side trim on s. Next, we create a new polygon R as follows; for an illustration see Fig. 3, (a) and (d). Let m be the midpoint of s. We first add m to the trimmed versions of both P and Q. Now, we create two lines $\ell _P$ and $\ell _Q$ parallel to s that lie on the supporting planes of P and Q on the side of s that contains P or Q, respectively. The distance $\delta$ of these lines to s is chosen sufficiently small; in particular, we must take $\delta <\varepsilon$.

We place two new corners on the intersection of $\ell _P$ with the boundary of P and two new corners on the intersection of $\ell _Q$ with the boundary of Q. Note that the resulting points are coplanar and in convex position; our new polygon R is the convex hull of these points. If $\delta$ is chosen sufficiently small, the polygon R has a nonempty intersection with P and Q, but no other polygon of ${\mathcal {S}}$. Hence, the subdivide operation creates a new vertex in G that is adjacent to the two original endpoints of the edge that corresponds to s, and no other vertices of G. $\square$

The existence of a flat surface with the correct adjacencies follows from the Andreev–Koebe–Thurston circle packing theorem; we include a direct proof.

Proposition 3.2

For every planar graph G, there exists a flat convex-polyhedral surface ${\mathcal {S}}$ such that ${\mathcal {G}} ({\mathcal {S}})\simeq G$. Moreover, such a surface can be computed in linear time.

Proof

Let G be a planar embedded graph with at least three vertices (for at most two vertices the statement is trivially true). We use a linear time algorithm by Read [41] to find a biconnected augmentation of G on the same vertex set. For each face of the resulting graph, we now add a new vertex and connect it to all vertices of the face by adding further edges. This can be accomplished in linear time. The resulting graph $G'$ is a triangulation. Let r be one of the vertices of $G'\setminus G$.

The dual $G^\star$ of $G'$ is a cubic 3-connected planar graph. Using a linear-time algorithm by Bárány and Rote [7], we compute a planar drawing of $G^\star$ in which the boundary of each face is described by a strictly convex polygon and where the outer face is the face dual to r. Hence, the drawing is a flat convex-polyhedral surface ${\mathcal {S}}$ with ${\mathcal {G}} ({\mathcal {S}})\simeq G'-r$. By Proposition 3.1, there is also a representation of G. To compute it efficiently, observe that due to the 3-regularity of $G^*$, the side trim operation defined in the proof of Proposition 3.1 can be carried out in constant time. Moreover, the corresponding graph operation preserves the 3-regularity. Hence, it is easy to remove all unwanted adjancencies in linear time. To obtain the desired representation of G, it remains to remove the polygons corresponding to the vertices of $G'\setminus G$, which can also be done in linear time. $\square$

So for planar graphs, corner and side contacts behave similarly. For nonplanar graphs (for which the third dimension is essential), the situation is different. Here, side contacts are more restrictive.

3.1 Complete Graphs

We introduce the following notation. In a polyhedral surface ${\mathcal {S}}$ with adjacency graph G, we denote by $P_v$ the polygon in ${\mathcal {S}}$ that represents vertex v of G.

Lemma 3.3

Let ${\mathcal {S}}$ be a convex-polyhedral surface in ${\mathbb {R}}^3$ with adjacency graph G. If G contains a triangle uvw, polygons $P_v$ and $P_w$ lie in the same closed halfspace with respect to $P_u$.

Proof

Due to their convexity, each of $P_v$ and $P_w$ lie entirely in one of the closed halfspaces with respect to the supporting plane of $P_u$. Moreover, one of the halfspaces contains both $P_v$ and $P_w$; otherwise they cannot share a side and the edge vw would not be represented. (Recall that each side can be shared by at most two polygons. Thus, the side corresponding to the edge uv cannot simultaneously represent an adjacency with w.) $\square$

A graph H is subisomorphic to a graph G if G contains a subgraph $G'$ with $H \simeq G'$. Thomassen [48, p. 98] has observed the following.

Proposition 3.4

There exists no convex-polyhedral surface ${\mathcal {S}}$ in ${\mathbb {R}}^3$ such that $K_5$ is subisomorphic to ${\mathcal {G}} ({\mathcal {S}})$.

For completeness, we now prove Thomassen’s observation.

Proof

Suppose that there is a convex-polyhedral surface ${\mathcal {S}}$ with ${\mathcal {G}} ({\mathcal {S}})\simeq K_5$. By Lemma 3.3 and the fact that all vertex triples form a triangle, the surface ${\mathcal {S}}$ lies in one closed halfspace of the supporting plane of every polygon P of ${\mathcal {S}}$. In other words, ${\mathcal {S}}$ is a subcomplex of a (weakly) convex polyhedron, whose adjacency graph must be planar. This yields a contradiction to the nonplanarity of $K_5$. Together with Proposition 3.1 this implies the claim. $\square$

Evans et al. [19] showed that every bipartite graph has a contact representation by touching polygons on a polynomial-size integer grid in ${\mathbb {R}}^3$ for the case of corner contacts. As we have seen before, side contacts are less flexible. In particular, in Theorem 3.8 we show that $K_{5,81}$ cannot be represented. On the positive side, we show in the following that every (bipartite) graph that comes from subdividing each edge of an arbitrary graph (at least) once can be realized. In our construction, we place the polygons in a cylindrical fashion, which is reminiscent of the realizations created by Evans et al. However, due to the more restrictive nature of side contacts, the details of the two approaches are necessarily quite different.

Theorem 3.5

Let G be any graph, and let $G'$ be the subdivision of G in which every edge is subdivided with at least one vertex. Then there exists a convex-polyhedral surface ${\mathcal {S}}$ in ${\mathbb {R}}^3$ such that ${\mathcal {G}} ({\mathcal {S}})\simeq G'$.

Proof

Let $V(G)=\{v_1,\dots ,v_n\}$, let $E(G)=\{e_1,\dots ,e_m\}$, and let P be a strictly convex polygon with corners $p_1,\dots ,p_{2m}$ in the plane. We assume that $m\ge 2$, that $p_1$ and $p_{2m}$ lie on the x-axis, and that the rest of the polygon is a convex chain that projects vertically onto the line segment $\overline{p_1p_{2m}}$, which we call the long side of P. We call the other sides short sides. We choose P such that no short side is parallel to the long side.

Let Z be a (say, unit-radius) cylinder centered at the z-axis. For each vertex $v_i$ of G, we take a copy $P^i$ of P and place it vertically in ${\mathbb {R}}^3$ such that its long side lies on the boundary of Z; see Fig. 4(a). Each polygon $P^i$ lies inside Z on a distinct halfplane that is bounded by the z-axis. Finally, all polygons are positioned at the same height, implying that for any $j\in \{1,\dots ,2m\}$, all copies of $p_j$ lie on the same horizontal plane $h_j$ and have the same distance to the z-axis.

Fig. 4

Illustration for the proof of Theorem 3.5

Let $i\in \{1,\dots ,m\}$. Then the side $s=p_{2i-1}p_{2i}$ is a short side of P. For $k=1,2,\dots ,n$, we denote by $s^k$ and $p_i^k$ the copies of s and $p_i$ in $P^k$, respectively. We claim that, for $1\le k<\ell \le n$, the sides $s^k$ and $s^\ell$ span a convex quadrilateral that does not intersect any $P^j$ with $j\notin \{k,\ell \}$. To prove the claim, we argue as follows; see Fig. 4(b).

By the placement of $P^k$ and $P^\ell$ inside Z, the supporting lines of $s^k$ and $s^\ell$ intersect at a point z on the z-axis, implying that $s^k$ and $s^\ell$ are coplanar. Moreover, $p_{2i-1}^k$ and $p_{2i-1}^\ell$ are at the same distance from z, and the same holds for $p_{2i}^k$ and $p_{2i}^\ell$. Hence the triangle spanned by z, $p_{2i-1}^k$, and $p_{2i-1}^\ell$ is similar to the triangle spanned by z, $p_{2i}^k$, and $p_{2i}^\ell$, implying that $p_{2i-1}^kp_{2i-1}^\ell$ and $p_{2i}^kp_{2i}^\ell$ are parallel and hence span a convex quadrilateral Q (actually a trapezoid). Finally, no polygon $P^j$ with $j\notin \{k,\ell \}$ can intersect Q as any point in the interior of Q lies closer to the z-axis than any point of $P^j$ at the same z-coordinate, which proves the claim.

We use Q as the polygon for the subdivision vertex of the edge $e_i$ of G (in case $e_i$ was subdivided multiple times, we dissect Q accordingly). Let $v_a$ and $v_b$ be the endpoints of $e_i$. By our claim, Q does not intersect any $P^j$ with $j\notin \{a,b\}$. The quadrilateral Q lies in the region of Z that is bounded by the horizontal planes $h_{2i-1}$ and $h_{2i}$. Since any two such regions are vertically separated and hence disjoint, the m quadrilaterals together with the n copies of P constitute a valid representation of $G'$. $\square$

The combination of Proposition 3.4 and Theorem 3.5 rules out any Kuratowski-type characterization for adjacency graphs of convex-polyhedral surfaces. This graph class contains a subdivision of $K_5$, but it does not contain $K_5$; hence it is not minor-closed. We remark that the subdivided $K_n$ has $\left( {\begin{array}{c}n\\ 2\end{array}}\right) +n$ vertices and crossing number $\Theta (n^4)$, so it is an adjacency graph of a convex-polyhedral surface whose crossing number is quadratic in its number of vertices (and edges).

3.2 Complete Bipartite Graphs

Proposition 3.6

There exists a convex-polyhedral surface ${\mathcal {S}}$ such that ${\mathcal {G}} ({\mathcal {S}})\simeq K_{4,4}$.

Proof

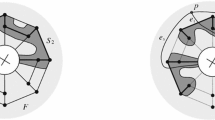
We describe how to obtain such a surface ${\mathcal {S}}$. We start with a rectangular box in ${\mathbb {R}}^3$ and stab it with two rectangles that intersect each other in the center of the box as indicated in Fig. 5(a).

Fig. 5

Construction of a convex-polyhedral surface ${\mathcal {S}}$ with ${\mathcal {G}} ({\mathcal {S}})\simeq K_{4,4}$. Subfigure (a) depicts the rectangular box and the two slanted rectangles that form the basis of the construction. The figure illustrates the situation before the intersection of the two slanted rectangles is removed by shifting a corner. Subfigure (b) illustrates the final realization. The 2-coloring of the polygons reflects the bipartition of $K_{4,4}$. Note that in the depicted projection the polygons $P_{\text {vert2}}$ and $P_{\text {vert4}}$ are shown as line-segments / very thin polygons; for a better view of these polygons, refer to Fig. 6. The orientation of the coordinate system is indicated in the bottom-left of the figure

We can now draw polygons on these eight rectangles such that each of the four vertical rectangles (representing the four vertices of one class of the bipartition of $K_{4,4}$) contains a polygon that has a side contact with a polygon on each of the four horizontal or slanted rectangles (representing the other class of the bipartition of $K_{4,4}$). To remove the intersection of the (polygons drawn on the) two slanted rectangles, we shift one corner of the original box; see Figs. 5(b) and 6. We refer to the two horizontal, the four vertical, and the two slanted polygons as $P_{\text {top}}$, $P_{\text {bot}}$, $P_{\text {vert1}}$, $P_{\text {vert2}}$, $P_{\text {vert3}}$, $P_{\text {vert4}}$, $P_{\text {diag1}}$, and $P_{\text {diag2}}$, respectively, and list the coordinates of their corners in Table 1.

Table 1 Coordinates for the polyhedral complex realizing $K_{4,4}$ as adjacency graph

With the specified coordinates, $P_{\text {diag1}}$ and $P_{\text {diag2}}$ each have a side that lies in the interior of $P_{\text {top}}$ and a side that lies in the interior of $P_{\text {bot}}$. To fix this, one needs to clip the two polygons such that they lie in the interior of the original cuboid. This can be done by intersecting them with the slab $-9.9\le z\le 9.9$. Moreover, the two polygons $P_{\text {vert1}}$ and $P_{\text {vert2}}$ (as well as $P_{\text {vert3}}$ and $P_{\text {vert4}}$) have a common side, even though they correspond to vertices in the same class of the bipartition of $K_{4,4}$. These unwanted contacts can also be removed by slightly clipping the polygons, cf. Proposition 3.1. $\square$

Fig. 6

Additional views of the realization of $K_{4,4}$

Proposition 3.7

There exists a convex-polyhedral surface ${\mathcal {S}}$ such that ${\mathcal {G}} ({\mathcal {S}})\simeq K_{3,5}$.

Proof

We call the vertices of the smaller bipartition class the gray vertices, and their polygons gray polygons. For the other class we pick a distinct color for every vertex and use the same naming-by-color convention. We start our construction with a triangular prism in which the quadrilateral faces $q_1,q_2,q_3$ are rectangles of the same size. Each of the faces $q_i$ will contain one gray polygon. All colorful polygons lie inside the prism. We call the lines resulting from the intersection of the supporting planes with the prism the colorful supporting lines. Unfolding the faces $q_1$, $q_2$, and $q_3$ into the plane yields Fig. 7, which shows the gray polygons and the colorful supporting lines. Note that the vertices of the gray polygons in the figure are actually very small edges that have the slope of the colorful supporting line on which they are placed. The colorful polygons are now already determined.

Fig. 7

Constructing a convex-polyhedral surface whose adjacency graph is isomorphic to $K_{3,5}$. The prism is unfolded into the plane. All polygon vertices are contained in the vertical grid lines

Fig. 8

Front view of the prism containing a realization of $K_{3,5}$. Lines on the back face are dashed. The thin black lines are the lines of intersection among the supporting planes of the red, yellow, and green polygons. The thick black line segments indicate which parts of the intersection lines are contained in a colorful polygon. Since the segments are disjoint, the colorful polygons are disjoint, too

It remains to check that the colorful polygons are disjoint. Figure 8 shows the prism in a view from the side where we dashed all objects on the hidden prism face. The cyan polygon $P_0$ and the blue polygon $P_4$ avoid all other colorful polygons in this projection and thus they avoid all other polygons in ${\mathbb {R}}^3$, too.

For the red polygon $P_1$, the orange polygon $P_2$ and the green polygon $P_3$, we proceed as follows to prove disjointness. Pick two of the polygons and name them $P_i$ and $P_j$. The line $\ell _{ij}$ of intersection of the supporting planes of $P_i$ and $P_j$ is determined by the two intersections of the corresponding colorful supporting lines. If the polygons intersect, they have to intersect on this line. Polygon $P_i$ intersects $\ell _{ij}$ in a segment $s_{ij}$; polygon $P_j$ intersects $\ell _{ij}$ in $s_{ji}$. Figure 8 shows, however, that $s_{ij}$ and $s_{ji}$ do not overlap in any of the three cases. (Note that $P_2$ does not intersect $\ell _{12}$ and hence $P_2$ does not intersect $P_1$ either.) We remark that our construction can be verified easily since it is grid-based in the following sense. First, note that each intersection point of the supporting plane of a colorful polygon and one of the three vertical edges of the prism has integral height in $\{0,\dots ,20\}$; see the tics in Fig. 7. Second, on each of the three vertical faces of the prism, we define a set of equally-spaced vertical lines (10 on the two front faces, 20 on the back face) such that each polygon vertex lies on the intersection of one of these lines and its supporting plane. $\square$

In contrast to Propositions 3.6 and 3.7, we can show that not every complete bipartite graph can be realized as a convex-polyhedral surface in ${\mathbb {R}}^3$.

Theorem 3.8

There exists no convex-polyhedral surface ${\mathcal {S}}$ in ${\mathbb {R}}^3$ such that $K_{5,81}$ is subisomorphic to ${\mathcal {G}} ({\mathcal {S}})$.

To prove the theorem we start with some observations about realizing complete bipartite graphs. We will consider a set R of red polygons, and a set B of blue polygons, so that each red–blue pair must have a side contact. For each $p\in R\cup B$, we denote by $p^=$ the supporting plane of p, by $p^-$ the closed half-space left of $p^=$, and by $p^+$ the closed half-space right of $p^=$ (orientations can be chosen arbitrarily). We start with a simpler setting where we have an additional constraint. We call B one-sided with respect to R if, for each blue polygon b, all red polygons lie in the same half-space with respect to b, i.e., $\forall \,b\in B:\,((\forall \,r\in R:r\subseteq b^-)\vee (\forall \,r\in R:r\subseteq b^+))$.

Lemma 3.9

Let R and B be two sets of convex polygons in ${\mathbb {R}}^3$ realizing $K_{|R|,|B|}$. If $|R|=3$ and B is one-sided with respect to R, then $|B|\le 8$.

Proof

Let $R=\{r_1,r_2,r_3\}$ and let ${\mathcal {A}}$ be the arrangement of the supporting planes of R. Assume that B is one-sided with respect to R and consider a polygon $b\in B$. For every polygon $r_i\in R$, since b is convex and shares a side with $r_i$, b is contained in $r_i^-$ or $r_i^+$. Thus, b is contained in a (closed) cell C of ${\mathcal {A}}$. Let $r_*=r_1^=\cap r_2^=\cap r_3^=$ be the intersection of the supporting planes of R.

We will first argue about the case where $r_*$ is not a point. We may assume that no two supporting planes of R coincide; otherwise, by strict convexity, two coplanar red polygons imply that all blue polygons lie in the same plane. Moreover, if $|B|\ge 2$, it follows symmetrically that all red polygons are coplanar. Hence, all polygons must lie in the same plane and the non-planarity of $K_{3,3}$ implies that $|B|\le 2$. It follows that $r_*$ is not a plane. Further, if $r_*$ is a line, then C has only two bounding planes and therefore one of the red polygons is only present as a subset of $r_*$; see Fig. 9(a). This implies that b has a side on $r_*$ and on each of the open half-planes bounding C, which is impossible. Finally, if $r_*=\emptyset$, we can apply a projective transformation such that the bounding planes of the three red polygons intersect. Therefore, we can assume that $r_*\ne \emptyset$.

It remains to consider the case where $r_*$ is a point, in which case the arrangement ${\mathcal {A}}$ defines eight (closed) cells, called octants, of the form $Q^{\alpha _0\beta _0\gamma _0}=r_1^{\alpha _0}\cap r_2^{\beta _0}\cap r_3^{\gamma _0}$, where $\alpha _0,\beta _0,\gamma _0\in \{\mathtt {+},\mathtt {-}\}$. We distinguish two subcases: either (1) no polygon in R contains the point $r_*$ (see Fig. 9(b)) or there is a red polygon whose supporting plane contains a blue polygon, or (2) $r_*$ is contained in a (single) polygon in R (see Fig. 9(c)) and there is no red polygon whose supporting plane contains a blue polygon.

Fig. 9

The three red polygons and the intersection $r_*$ of their supporting planes

Case 1: No polygon in R contains the point $r_*$ or there is a red polygon whose supporting plane contains a blue polygon. Our plan is to show that there are four octants whose union contains all blue polygons and that each of these four octants contains at most two blue polygons, which implies that the total number of blue polygons is bounded by $4\cdot 2=8$, as claimed. We start to show that there are four octants whose union contains all blue polygons. To this end, we distinguish two subcases.

Case 1.1: No polygon in R contains the point $r_*$. Since the point $r_*$ is disjoint from all red polygons, each red polygon lies on the boundary of at most six octants. More precisely, there are signs $\alpha _2,\alpha _3,\beta _1,\beta _3,\gamma _1,\gamma _2\in \{\mathtt {+},\mathtt {-}\}$ such that $r_1$ cannot intersect the two octants $Q^{\pm \beta _1\gamma _1}$, $r_2$ cannot intersect the two octants $Q^{\alpha _2{\pm }\gamma _2}$, and $r_3$ cannot intersect the two octants $Q^{\alpha _3\beta _3\pm }$. It is now easy to verify that there are at most four octants that intersect all three red polygons. For example, if $\alpha _2=\alpha _3=\beta _1=\beta _3=\gamma _1=\gamma _2={\mathtt {+}}$, then only the octants $Q^{+--}$, $Q^{-+-}$, $Q^{--+}$, and $Q^{---}$ can intersect all three red polygons. Since every blue polygon has to be contained in one of these four octants, the claim follows.

Case 1.2: There is a red polygon, say $r_1$, whose supporting plane $r_1^=$ contains a blue polygon, say $b_1$. Recall that we assume that no two supporting planes of red polygons coincide. Symmetrically, we may assume that no two supporting planes of blue polygons coincide. Hence, without loss of generality, we may assume that $r_2$ and $r_3$ intersect the interior of $b_1^+$, which, without loss of generality, coincides with $r_1^+$. Consequently, all blue polygons are contained in $r_1^+$ and, thus, they are contained in the union of the four corresponding octants.

So far, we have shown that there are four octants whose union contains all blue polygons. Now consider one octant C that contains a blue polygon (and is thus incident to all $r_i$). For the argument within this cell, we can truncate all $r_i$ to C. We claim that there can be at most two blue polygons in C. Assume towards a contradiction that we have three such polygons $b_1$, $b_2$, and $b_3$. For each $i\in \{1,2,3\}$, the polygon $b_i$ has three sides in common with $r_1,r_2,r_3$. Let $b_i'$ be the convex hull of these three sides. Consider now the set $P=\{r_1,r_2,r_3,b_1',b_2',b_3'\}$. Let $b'_i$ and $b'_j$ be two different (partial) blue polygons. Since $b^=_i$ has all (sides of) red polygons on one side, it has also the three sides defining $b'_j$ on one side. Hence, $b_j'$ is on one side of the supporting plane of $b'_i$, and this side is the same for all polygons in $P\setminus \{b'_i\}$. On the other hand, by the definition of C, every $r^=_i$ has all polygons in $P\setminus \{r_i\}$ on one common side. Thus, the polygons in P are in convex position. Consider now the convex hull ${\mathcal {H}}$ of P. We get that ${\mathcal {H}}$ is a convex polyhedron with the polygons of P embedded on its surface. We can draw the contact graph of P on that surface without crossings. Since the surface is homeomorphic to a sphere, we obtain a contradiction since the contact graph is a $K_{3,3}$ and therefore nonplanar. Thus, any octant can contain at most two blue polygons, as claimed.

Altogether, we have shown that there are four octants whose union contains all blue polygons and that each of these four octants contains at most two blue polygons, which implies that the total number of blue polygons is bounded by $4\cdot 2=8$ in Case 1.

Case 2: A red polygon contains $r_*$ and there is no red polygon whose supporting plane contains a blue polygon. Without loss of generality, $r_*\in r_1$. Similarly to Case 1.1, the polygons $r_2$ and $r_3$ both lie on the boundary of at most six octants, which implies that there are at most five octants that intersect every polygon in R. We claim that at most one polygon of B can intersect any given octant. Consider an octant Q and assume that it is intersected by two one-sided blue polygons $b_1$ and $b_2$. Note that Q is bounded by three (unbounded) faces $f_1$, $f_2$, and $f_3$ such that, for $j\in \{1,2,3\}$, the red polygon $r_j$ (truncated to Q) lies in $f_j$.

Let $\ell _{i,j}$ denote the intersection of the plane $b^=_i$ and the face $f_j$. Because there is no red polygon whose supporting plane contains a blue polygon, $\ell _{i,j}$ is not the entire face $f_j$ but a segment or a ray. Let $t_i$ be the trace formed by $\ell _{i,1},\ell _{i,2},\ell _{i,3}$. Then $t_i$ is either a triangle or the concatenation of two rays and a segment; see Fig. 10, (b) and (c). Note that the traces $t_1$ and $t_2$ intersect in at most two points.

Given two different faces $f_i$ and $f_j$ of Q, we call their intersection $f_i\cap f_j$ an axis of Q. Note that each trace intersects at least two of the three axes of Q. Hence, there is a face $f_j$ such that $\ell _{1,j}$ and $\ell _{2,j}$ have endpoints on the same axis contained in $f_j$. We complete the proof by distinguishing two subcases, depending on the intersection of $\ell _{1,j}$ and $\ell _{2,j}$.

Case 2.1: $\ell _{1,j}$ and $\ell _{2,j}$ do not intersect in the relative interior of $f_j$. See Fig. 10(d). Then one of them (say $\ell _{1,j}$) separates the other (say $\ell _{2,j}$) from $r_*$ on $f_j$. Because $r_j$ lies between $\ell _{1,j}$ and $\ell _{2,j}$, we get that $\ell _{1,j}$ separates $r_*$ from $r_j$. This is a contradiction to the fact that $b_1$ is one-sided. Thus, there are at most $1\cdot 5=5$ polygons in B in Case 2.1.

Case 2.2: $\ell _{1,j}$ and $\ell _{2,j}$ intersect in the relative interior of $f_j$. Then there is a $j'\in \{1,2,3\}\setminus \{j\}$ such that $\ell _{1,j'}$ and $\ell _{2,j'}$ have endpoints on the same axis and do not intersect; otherwise the traces intersect three times. Hence, if we replace j by $j'$, we are in Case 2.1. $\square$

Fig. 10

Illustration of Case 2 for the proof of Lemma 3.9. (a) A single octant (towards the viewer) with three truncated red polygons and a possible blue polygon within the octant that has a side contact with all three red polygons, (b) the trace of a possible blue polygon forming a triangle, (c) the trace of a possible blue polygon consisting of two rays and a segment, and (d) two traces yield at least one blue polygon that is not one-sided

With the help of Lemma 3.9 we can now prove Theorem 3.8.

Proof of Theorem 3.8

Assume that $K_{5,81}$ can be realized, and let R be a set of five red polygons. Since every $b\in B$ is adjacent to all polygons in R, b partitions R into two sets: those in $b^-$ and those in $b^+$. At least one of these subsets must have at least three elements. Arbitrarily charge b to such a set of three polygons. By Lemma 3.9, each set of three red polygons can be charged at most eight times. There are ${5\atopwithdelims ()3}=10$ sets of three red polygons. Therefore, there can be at most $8\cdot 10=80$ blue polygons; a contradiction. Together with Proposition 3.1, this implies the claim. $\square$

3.3 3-Trees

The graph class of 3-trees is recursively defined as follows: $K_4$ is a 3-tree. A graph obtained from a 3-tree G by adding a new vertex x with exactly three neighbors u, v, w that form a triangle in G is a 3-tree. We say x is stacked on the triangle uvw. It follows that for each 3-tree there exists a (not necessarily unique) construction sequence of 3-trees $G_4,G_5,\dots ,G_n$ such that $G_4\simeq K_4$, $G_n=G$, and where for $i=4,5,\dots ,n-1$ the graph $G_{i+1}$ is obtained from $G_i$ by stacking a vertex $v_{i+1}$ on some triangle of $G_i$.

By Proposition 3.2, for every planar 3-tree G there is a polyhedral surface ${\mathcal {S}}$ (even in ${\mathbb {R}}^2$) with ${\mathcal {G}} ({\mathcal {S}})\simeq G$. On the other hand, we can show that no nonplanar 3-tree has such a realization in ${\mathbb {R}}^3$. To this end, we observe that a 3-tree is nonplanar if and only if it contains the triple-stacked triangle as a subgraph. The triple-stacked triangle is the graph that consists of $K_{3,3}$ plus a cycle that connects the vertices of one part of the bipartition; see Fig. 11. We show that the triple-stacked triangle is not realizable.

Fig. 11

The unique minimal nonplanar 3-tree, which we call triple-stacked triangle

Lemma 3.10

Let uvw be a separating triangle in a plane 3-tree $G=(V,E)$. Then there exist vertices $a,b\in V$ that belong to distinct sides of uvw in G such that both $\{a,u,v,w\}$ and $\{b,u,v,w\}$ induce a $K_4$ in G.

Proof

Let $G_4,G_5,\dots ,G_n$ denote a construction sequence of $G=G_n$, and let k be the largest index in $\{4,5,\dots ,n\}$ such that uvw is nonseparating in $G_k$. Since uvw is separating in $G_{k+1}$, it follows that the vertex $v_{k+1}=a$ is stacked on uvw (say, inside uvw) to obtain $G_{k+1}$ and, hence, $\{a,u,v,w\}$ induce a $K_4$ in $G_{k+1}$ and G.

It remains to argue about the existence of the vertex b in the exterior of uvw. If uvw is one of the triangles of the original $G_4\simeq K_4$, there is nothing to show, so assume otherwise. Let j be the smallest index in $\{5,6,\dots ,n\}$ such that uvw is contained in $G_j$. It follows that one of u, v, w, say u, is the vertex $v_j$ that was stacked on some triangle xyz of $G_{j-1}$ to obtain $G_j$. Without loss of generality, we may assume that $\{v,w\}=\{y,z\}$. It follows that $x=b$ forms a $K_4$ with u, v, w in $G_j$ and G. $\square$

Lemma 3.11

A 3-tree is nonplanar if and only if it contains the triple-stacked triangle as a subgraph.

Proof

The triple-stacked triangle is nonplanar because it contains a $K_{3,3}$ (one part of the bipartition is formed by the gray vertices and the other by the colored vertices).

For the other direction, let G be a nonplanar 3-tree. Let $G_4,G_5,\dots ,G_n$ be a construction sequence of G. Let k be the smallest index in $\{4,5,\dots , n\}$ such that $G_k$ is nonplanar. By 3-connectivity, the graph $G_{k-1}$, which is planar, has a unique combinatorial embedding. Therefore, we may consider $G_{k-1}$ to be a plane graph. Let uvw be the triangle that the vertex $v_k$ was stacked on to obtain $G_k$ from $G_{k-1}$. Since $G_k$ is nonplanar, the triangle uvw is a separating triangle of $G_{k-1}$. It follows by Lemma 3.10 that $G_k$ (and, hence, G) contains the triple-stacked triangle. $\square$

Lemma 3.12

There exists no convex-polyhedral surface ${\mathcal {S}}$ in ${\mathbb {R}}^3$ such that the triple-stacked triangle is subisomorphic to ${\mathcal {G}} ({\mathcal {S}})$.

Proof

We refer to the vertices of the triple-stacked triangle as the three gray vertices and the three colored (red, green, and blue) vertices; see also Fig. 11. Given the correspondence between vertices and polygons (and their supporting planes), we also refer to the polygons (and the supporting planes) as gray and colored.

Assume that the triple-stacked triangle can be realized. Consider the arrangement of the gray supporting planes. By strict convexity, it follows that if a pair of gray polygons has the same supporting plane, then all their common neighbors lie in the same plane. This implies that all supporting planes coincide—a contradiction to the non-planarity of the triple-stacked triangle. Consequently, the gray supporting planes are pairwise distinct. (Likewise, it holds that no colored and gray supporting plane coincide.)

We now argue that all colored polygons are contained in the same closed cell of the gray arrangement. To see this, fix one gray polygon and observe, by Lemma 3.3, that all polygons are contained in the same closed half space with respect to its supporting plane.

Note that the gray plane arrangement has one of the following two combinatorics: either the three planes have a common point of intersection (cone case) or not (prism case). In the first case, the planes partition the space into eight cones, one of which contains all polygons; in the second case, the (unbounded) cell containing all polygons forms a (unbounded) prism. For a unified presentation, we transform any occurrence of the first case into the second case. To do so, we move the apex of the cone containing all polygons to the plane at infinity by a projective transformation. This turns each face of the cone into a strip that is bounded by two of the extremal rays of the cone, which we now have deformed into a prism.

Consider one of the strips, which we call S. The strip S has to contain one of the gray polygons, which we call $P_S$. We know that $P_S$ has at least five sides, one for each neighbor. Each of the two bounding lines contains a side to realize the adjacency to the other two gray polygons. We call the sides of $P_S$ that realize the adjacencies to the remaining polygons red, green, and blue, in correspondence to the vertex colors. The supporting line of the red side intersects each bounding line of S. We add a red point at each of the intersections. For the blue and green sides we proceed analogously. By convexity of $P_S$, these points are distinct. This yields a permutation of red, green, blue (see Fig. 12) on each bounding line. The permutations on the boundary of two adjacent strips coincide because the supporting lines are clearly contained in the supporting planes.

Fig. 12

The permutations of the intersections with the supporting lines of the red, green, and blue edges as in the proof of Lemma 3.12. Figures (a) and (c) illustrate possible scenarios. Figures (b) and (d) show impossible scenarios because they do not contain cells of complexity 5

Consider the line arrangement inside S given by the supporting lines of the red, green, and blue sides. Up to symmetry, Fig. 12 illustrates the different intersection patterns. To realize all contacts, the polygon $P_S$ has to lie inside a cell incident to all five lines, namely the two bounding lines and the three supporting lines. It is easy to observe that such a cell exists only if the permutation has exactly one or three inversions; see Fig. 12, (b) and (d). In particular, the number of inversions is odd.

Following the cyclic order of the bounding lines around the prism, we record three odd numbers of inversions in the permutations before coming back to the start. Since an odd number of inversions does not yield the identity, we obtain the desired contradiction. $\square$

Together, Lemmas 3.11 and 3.12 yield the following theorem.

Theorem 3.13

Let G be a 3-tree. There exists a convex-polyhedral surface ${\mathcal {S}}$ in ${\mathbb {R}}^3$ with ${\mathcal {G}} ({\mathcal {S}})\simeq G$ if and only if G is planar.

In contrast to Theorem 3.13, there are nonplanar 3-degenerate graphs that can be realized; see the example in Fig. 1.

3.4 Hypercubes

In a paper from 1983, McMullen et al. construct a polyhedron for every integer $p\ge 4$ such that all faces are convex p-gons [38, Sect. 4]. In the following, we show and illustrate how their result proves the realizability of any hypercube.

Proposition 3.14

[38] For every d-hypercube $Q_d$, $d\ge 0$, there exists a convex-polyhedral surface ${\mathcal {S}}$ in ${\mathbb {R}}^3$ with ${\mathcal {G}} ({\mathcal {S}})\simeq Q_d$ and every polygon of ${\mathcal {S}}$ is a $(d+4)$-gon.

The main building block in their construction is a polyhedral surface whose adjacency graph is a $(p-4)$-hypercube. In fact, we observed that the adjacency graph of the polyhedron they finally construct is the Cartesian product of $Q_{p-4}$ and a cycle graph $C_n$, $n\ge 3$. For the first few steps of their inductive construction; see Fig. 13.

Fig. 13

The inductive construction of McMullen et al. [38]

Recall that the d-hypercube has $2^d$ vertices. The base case for $d=0$ is given by a single 4-gon, namely by the unit square. What follows is a series of inductive steps. In every step, the value of d increases by one and the number of polygons doubles. Before explaining the step, we state the invariants of the construction. We label the corners of a polygon with $p_1,\dots ,p_k$. After every step, the orthogonal projection into the xy-plane looks like the unit square in which we have replaced the upper right corner with a convex chain as shown in Fig. 14(a). In particular $p_1$ is mapped to (0, 0), $p_2$ is mapped to (0, 1), and $p_k$ is mapped to (1, 0). For every polygon the sides $p_ip_{i+1}$ for $i\le 3\le k-2$ (non-vertical, non-horizontal in the projection) will already have two incident polygons, the four other sides $p_1p_2,p_2p_3,p_{k-1}p_k,p_kp_1$ are currently incident to only one polygon.

Fig. 14

Projection of a polygon into the xy-plane in the construction of McMullen et al. The gray rectangle depicts the unit square. Edges incident to only one polygon are drawn in blue. (a) The start configuration for $d+4=7$. (b) Cutting with the xy-plane after the shear that puts only e below the xy-plane (before glueing the reflected copy). (c) Slicing off a corner to get the initial situation for $d+4=8$ modulo a projective transformation

We explain next how to execute the inductive step. Suppose that we have a polyhedral surface where every polygon is a $(d+4)$-gon fulfilling our invariant. We apply a shear along the z-axis to assure that for every polygon the corners $p_{k-1}$ and $p_k$ have smaller z-coordinates than every corner of a polygon that is not $p_{k-1}$ or $p_k$. We then shift the whole surface such that exactly the sides $p_{k-1}p_k$ lie completely below the xy-plane; see also Fig. 13(a). These transformations do not change the projections of the polygons into the xy-plane. We then cut the surface with the xy-plane and only keep the upper part. By this we slice away one of the sides in all polygons but also add a side that lies in the xy-plane; see Fig. 14(b). Each polygon now has a side $p'_{k-1}p'_k$ that lies in the xy-plane and is disjoint from all other polygons. We now take a copy of the surface at hand and reflect it across the xy-plane. Every polygon of the original (unreflected) surfaces is now glued to its reflected copy via the common side in the xy-plane. With this step, we already have transformed the adjacency graph from a d-hypercube to a $(d+1)$-hypercube. We only need to bring the surface back into the shape required by the invariant. To do so, we cut off a corner in every polygon (see Fig. 14(c)) by slicing the whole construction with an appropriate plane orthogonal to the xy-plane; see also Fig. 13(b). This turns all $(d+4)$-gons into $(d+5)$-gons. In particular, in every polygon we cut off $p'_k$ and add two corners $p''_k$ and $p''_{k+1}$ as shown in Fig. 14(c). Finally, we apply a projective transformation to assure that the invariant holds in the end of the induction step. Such a transformation can be obtained as follows. Assume that the line connecting $p''_k$ and $p''_{k+1}$ in the xy-plane, has the form $x=ay+b$, for some parameter a and b. Then the transformation is given by

$$\begin{aligned} (x,y,z)\mapsto \frac{1}{ay+b}(x,y(a+b),z). \end{aligned}$$

It can be observed that this mapping leaves the projection of the points $p_1,p_2$ into the xy-plane for every polygon stationary. Moreover, for every polygon, the line containing $p''_k$ and $p''_{k+1}$ will be mapped to the line $x=1$ and the line containing of $p_2$ and $p_3$ will be mapped to the line $y=1$ when projected into the xy-plane. Figure 13(a)–(c) shows spatial images of this construction.

Connection to a problem of coloring adjacency graphs Thomassen [48, p. 98, Problem 2] asked whether the adjacency graph of a polyhedral surface in ${\mathbb {R}}^3$ which is homeomorphic to $S_g$ (an orientable surface of genus g) has chromatic number bounded by some absolute constant. A typical approach for proving this is to show that the graph has bounded average degree. However, Proposition 3.14 shows that the average degree is unbounded, so another approach is needed.

4 Bounds on the Density

It is an intriguing question how dense adjacency graphs of convex-polyhedral surfaces can be. In this section, we use realizability and non-realizability results from the previous sections to derive asymptotic bounds on the maximum density of such graphs, which we phrase in terms of the relation between their number of vertices and edges.

Let ${\mathcal {G}}_n$ be the class of graphs on n vertices with a realization as a convex-polyhedral surface in ${\mathbb {R}}^3$. Further, let $e_{\max }(n)=\max _{G\in {\mathcal {G}}_n}|E(G)|$ be the maximum number of edges that a graph in ${\mathcal {G}}_n$ can have.

Corollary 4.1

For any positive integer n, one has $e_{\max }(n)\in \Omega (n \log n)$ and $e_{\max }(n)\in {\mathcal {O}}(n^{9/5})$.

Proof

For the lower bound, note that by Proposition 3.14, every hypercube is the adjacency graph of a convex-polyhedral surface. As the d-dimensional hypercube has $2^d$ vertices and $2^d\cdot d/2$ edges, the bound follows.

For the upper bound, we use that, by Theorem 3.8, the adjacency graph of a convex-polyhedral surface cannot contain $K_{5,81}$ as a subgraph. It remains to apply the Kővari–Sós–Turán Theorem [31], which states that an n-vertex graph that has no $K_{s,t}$ as a subgraph can have at most ${\mathcal {O}}(n^{2-1/s})$ edges. $\square$

Before being aware of the result of McMullen et al. [38], we constructed a family of surfaces with (large, but) constant average degree. Our construction is not recursive and therefore easier to understand and visualize; for a sketch see Fig. 15, a detailed description can be found in a preprint version of this article [6, Appendix C]. Note that some polygons in our construction have polynomial degree.

Proposition 4.2

There is an unbounded family of convex-polyhedral surfaces in ${\mathbb {R}}^3$ whose adjacency graphs have average vertex degree $12-o(1)$.

Fig. 15

A family of convex-polyhedral surfaces whose adjacency graphs have average vertex degree $12-o(1)$. The main building block of our construction consists of m regular octagons arranged in a truncated square tiling, which is lifted to the paraboloid; see (b). We place m copies of this gadget in a cyclic fashion; see (a). To increase the average degree, we create ${\mathcal {O}}(m\sqrt{m})$ vertical and ${\mathcal {O}}(m)$ horizontal polygons. The vertical polygons are attached to the “outside” of the bent octagon grids (see (b)); the horizontal polygons are place in the center of our construction such that each of them touches each grid along a single polygon side (see (c)). The resulting construction contains some unwanted overlaps and intersections, which can be removed by modifying the initial grid structure slightly

5 Conclusion and Open Problems

In this paper, we have studied the class of graphs that can be realized as adjacency graphs of (convex-)polyhedral surfaces. Corollary 4.1 bounds the maximum number $e_{\max }(n)$ of edges in realizable graphs with n vertices by $\Omega (n\log n)$ and ${\mathcal {O}}(n^{9/5})$. It would be interesting to improve upon these bounds.

Question 5.1

What is the maximum number $e_{\max }(n)$ of adjacencies that a convex-polyhedral surface with n polygons can have?

We conjecture that realizability is NP-hard to decide.

Question 5.2

What is the computational complexity to decide for a given graph G whether there exists a convex-polyhedral surface ${\mathcal {S}}$ such that ${\mathcal {G}} ({\mathcal {S}})\simeq G$?

The following question is related to the previous question regarding recognition.

Question 5.3

Which structural properties are necessary or sufficient for admitting side-contact representations with convex polygons in ${\mathbb {R}}^3$?