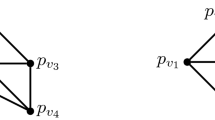Graph Reconstruction from Unlabeled Edge Lengths

Abstract

A d-dimensional framework is a pair (G, p), where $G=(V,E)$ is a graph and p is a map from V to $\mathbb {R}^d$. The length of an edge $uv\in E$ in (G, p) is the distance between p(u) and p(v). The framework is said to be globally rigid in $\mathbb {R}^d$ if every other d-dimensional framework (G, q), in which the corresponding edge lengths are the same, is congruent to (G, p). In a recent paper Gortler, Theran, and Thurston proved that if every generic framework (G, p) in $\mathbb {R}^d$ is globally rigid for some graph G on $n\ge d+2$ vertices (where $d\ge 2$), then already the set of (unlabeled) edge lengths of a generic framework (G, p), together with n, determine the framework up to congruence. In this paper we investigate the corresponding unlabeled reconstruction problem in the case when the above generic global rigidity property does not hold for the graph. We provide families of graphs G for which the set of (unlabeled) edge lengths of any generic framework (G, p) in d-space, along with the number of vertices, uniquely determine the graph, up to isomorphism. We call these graphs weakly reconstructible. We also introduce the concept of strong reconstructibility; in this case the labeling of the edges is also determined by the set of edge lengths of any generic framework. For $d=1,2$ we give a partial characterization of weak reconstructibility as well as a complete characterization of strong reconstructibility of graphs. In particular, in the low-dimensional cases we describe the family of weakly reconstructible graphs that are rigid but not redundantly rigid.

1 Introduction

Consider a graph $G=(V,E)$ and a map $p:V\rightarrow \mathbb {R}^d$. The pair (G, p) is called a d-dimensional framework. We may also say that (G, p) is a realization of G in $\mathbb {R}^d$. The length of an edge $uv\in E$ in (G, p) is defined to be the Euclidean distance between p(u) and p(v). Given a framework (G, p), a fundamental question in distance geometry is whether there exist other realizations (G, q) of G in $\mathbb {R}^d$ in which corresponding edge lengths are the same — not counting congruent realizations, which are the ones obtained by applying an isometry (say, a translation) of $\mathbb {R}^d$ to (G, p). If there are no other realizations, or equivalently, if the edge lengths of G uniquely determine all pairwise distances, then (G, p) is said to be globally rigid in $\mathbb {R}^d$. It is known that if p is generic, which means that the set of $d\,|V|$ coordinates of (G, p) is algebraically independent over the rationals, then the global rigidity of (G, p) depends only on G. Thus we may call a graph G globally rigid in $\mathbb {R}^d$ if every (or equivalently, if some) d-dimensional generic realization (G, p) of G is globally rigid.

In a recent paper Gortler, Thurston, and Theran [10] investigated the unlabeled version of the question above. In this case we are given a set of edge lengths, coming from some d-dimensional realization of a graph on n vertices, and want to decide whether this information uniquely determines the underlying graph G and the realization p, up to isomorphism and congruence, respectively. We note that several applications of the labeled as well as the unlabeled versions are mentioned in the literature, see e.g. [3, 14, 20].

However, the unlabeled question turns out to be highly non-trivial even for complete graphs, that is, even if we are given the list of all pairwise distances. This special case was first studied by Boutin and Kemper in [4]. They gave the (non-generic) two-dimensional example shown in Fig. 1, which demonstrates that in some cases even the complete list of distances may be insufficient to uniquely determine the realization of the underlying complete graph $K_n$. However, they proved that this is an exception: if $n\ge d+2$ and the distances come from a generic realization in $\mathbb {R}^d$, then the realization is unique.

Fig. 1

Two length-equivalent realizations of $K_4$ which are not congruent. We can obtain these realizations in $\mathbb {R}^2$ by putting $\ell _1 = \sqrt{10}, \ell _2 = 4, \ell _3 = 2, \ell _4 = \sqrt{2}$

The main theorem of [10] extends this result on complete graphs to all globally rigid graphs. In what follows it will be convenient to use the following notions. We say that two frameworks $(G,p)$ and $(H,q)$ are length-equivalent (under the bijection $\psi$) if there is a bijection $\psi$ between the edge sets of G and H such that for every edge e of G, the length of e in $(G,p)$ is equal to the length of $\psi (e)$ in $(H,q)$. If G and H have the same number of vertices then we say that they have the same order.

Theorem 1.1

[10, Thm. 3.4]    Let $G=(V,E)$ be globally rigid in $\mathbb {R}^d$ on at least $d+2$ vertices, where $d\ge 2$, and let $(G,p)$ be a d-dimensional generic realization of G. Suppose that $(H,q)$ is another d-dimensional framework such that G and H have the same order and $(G,p)$ is length-equivalent to $(H,q)$ under some bijection $\psi$. Then there is a graph isomorphism $\varphi :V(G)\rightarrow V(H)$ which induces $\psi$, that is, for which $\psi (uv)=\varphi (u)\,\varphi (v)$ for all $uv\in E$. In particular, G and H are isomorphic and the frameworks $(G,p)$ and $(H,q)$ are congruent after relabeling, i.e., $(G,p)$ is congruent to $(G, q\circ \varphi )$.

Note that if G is not globally rigid then we cannot expect a conclusion as strong as that of Theorem 1.1, which can be seen as a strengthening of global rigidity. In this sense the result is the best possible. Still, there is room for further investigation, as it was already pointed out in [10]: the set of edge lengths may be sufficient to uniquely reconstruct the graph G, even if the realization itself is not uniquely determined.

It turns out that if we consider frameworks as embeddings into the complex space $\mathbb {C}^d$, we arrive at a notion that is more tractable than if we restricted ourselves to real frameworks. To this end, we define the complex squared length of a vector ${\mathbf {v}} = (v_1,\dots ,v_d)\in \mathbb {C}^d$ as $\sum _{i=1}^d{v_i^2}$. Note that we do not take absolute values, and consequently this does not define a norm (or rather, the square of a norm) on $\mathbb {C}^d$. Nonetheless, using this notion of length we may extend our definition of length-equivalence to complex frameworks. This allows us to define a version of reconstructibility from unlabeled edge lengths among complex frameworks. In fact, there are at least two distinct notions that arise naturally. The definition of the first one is as follows.

Definition 1.2

Let $(G,p)$ be a generic realization of the graph G in $\mathbb {C}^d$. We say that $(G,p)$ is weakly reconstructible if whenever $(H,q)$ is a d-dimensional generic complex framework such that G and H have the same order and $(G,p)$ is length-equivalent to $(H,q)$, then H is isomorphic to G.

Consider the two one-dimensional realizations of the cycle of length four in Fig. 2. These realizations are length-equivalent under a (unique) bijection $\psi$. However, $\psi$ is not induced by a graph isomorphism. This leads us to the second definition.

Fig. 2

Length-equivalent realizations of $C_4$ where the mapping between the corresponding edges does not arise from a graph isomorphism. This shows that $C_4$ is not strongly reconstructible in $\mathbb {C}^1$

Definition 1.3

Let $(G,p)$ be a generic realization of the graph G in $\mathbb {C}^d$. We say that $(G,p)$ is strongly reconstructible if for every d-dimensional generic complex framework $(H,q)$ that is length-equivalent to $(G,p)$ under some bijection $\psi$ and has the same order, there is an isomorphism $\varphi :G \rightarrow H$ for which $\psi (uv)=\varphi (u)\,\varphi (v)$ for all $uv\in E$.

Note that, since we assume $(G,p)$ to be generic, its edge lengths are pairwise different, and hence the bijection $\psi$ is unique in the above definition.

As we shall see in Sect. 3, weak and strong reconstructibility is a generic property of a graph in the sense that if there is a generic framework (G, p) in $\mathbb {C}^d$ that is weakly (resp. strongly) reconstructible, then every generic realization of G in $\mathbb {C}^d$ is weakly (resp. strongly) reconstructible. This motivates the following definition.

Definition 1.4

A graph G is said to be (generically) weakly reconstructible (respectively (generically) strongly reconstructible) in $\mathbb {C}^d$ if every d-dimensional generic realization (G, p) of G is weakly (respectively strongly) reconstructible.

Later on, we shall define the real versions of these reconstructibility notions analogously, and our main interest is, in fact, in real frameworks, particularly as those are the ones that are most relevant to possible applications. However, as we shall see, these real versions are in some sense less well-behaved than their complex counterparts. This is partly due to the fact that, by extending our attention to complex frameworks, the problem becomes more amenable to the tools and results of algebraic geometry, many of which only hold over an algebraically closed field such as the field of complex numbers. We stress that reconstructibility in $\mathbb {C}^d$ is a stronger notion than reconstructibility in $\mathbb {R}^d$. We also note that in considering complex frameworks we are following the approach taken in [10]. In fact, the main ingredient in the proof of Theorem 1.1 is (phrased according to our terminology) the following theorem from [10].

Theorem 1.5

Let G be a graph on $n \ge d+2$ vertices, where $d \ge 2$. Suppose that G is globally rigid in $\mathbb {R}^d$. Then G is strongly reconstructible in $\mathbb {C}^d$.

Figures 2 and 3 show that the conditions on n and d in Theorem 1.5 are both necessary.

1.1 Main Results

In the next two sections we shall define and introduce the main notions and tools needed to investigate these new reconstructibility properties. In particular, we shall define rigid graphs, the rigidity matroid, and the so-called measurement variety. We shall also prove several key lemmas in these sections.

In Sect. 4 we exhibit some families of weakly reconstructible graphs in $\mathbb {C}^d$, including those not globally rigid, or even rigid. Our main contributions are in Sect. 5, where we consider the cases of $d=1$ and $d=2$ in more detail. We show that the graph isomorphism problem can be polynomially reduced to the problem of deciding whether a given graph is weakly reconstructible in one dimension (Theorem 5.9). We also introduce bridge-invariant graphs, which have the property that, roughly speaking, by replacing a non-redundant (with respect to rigidity) edge by some other non-redundant edge we always obtain the same graph. We describe the family of bridge-invariant graphs in two dimensions (Theorem 5.14). This result allows us to find all weakly reconstructible non-redundant rigid graphs in $\mathbb {C}^2$ (Theorem 5.17). We also consider strongly reconstructible graphs in one and two dimensions and provide a complete characterization of them (Theorems 5.20 and 5.22). The latter result shows that Theorem 1.5 essentially captures the complete list of strongly reconstructible graphs in $\mathbb {C}^2$. In Sect. 6 we examine some aspects of weak and strong reconstructibility in $\mathbb {R}^ d$. Finally, in Sect. 7 we discuss some open questions regarding graph reconstructibility.

Fig. 3

Two length-equivalent realizations of $K_4$ in $\mathbb {R}^3$, shown from above. The bounding triangle is kept fixed, while the edges incident to the fourth vertex (which is above the plane of the other three) are “rotated”. The edge lengths in this example may be chosen to be generic. This example shows that $K_4$ is not strongly reconstructible in $\mathbb {C}^3$, since the bijection pairing edges of the same length is not induced by a graph automorphism

2 Preliminaries

In this section we provide the definitions and results from rigidity theory and algebraic geometry that we shall use.

2.1 Graph Rigidity

2.1.1 Real Frameworks

Let $G = (V,E)$ be a graph¹ on n vertices and $d \ge 1$ some fixed integer. A d-dimensional realization of G is a pair (G, p) where $p= (p_1,\dots ,p_n)$ is a point in $\mathbb {R}^{nd}$, or equivalently, a map $p:V \rightarrow \mathbb {R}^d$. We call such a point a configuration and we say that the pair (G, p) is a framework. Two d-dimensional frameworks (G, p) and (G, q) are equivalent if $\Vert p(u) - p(v)\Vert = \Vert q(u) - q(v)\Vert$ for every edge $uv \in E$, and congruent if the same holds for every pair of vertices $u,v \in V$. Here $\Vert \,{\cdot }\,\Vert$ denotes the Euclidean norm.

Fig. 4

a Equivalent non-rigid frameworks. b Equivalent rigid, but not globally rigid frameworks

A framework is (locally) rigid if every continuous motion of the vertices which preserves the edge lengths takes it to a congruent framework, and globally rigid if every equivalent framework is congruent to it. See Fig. 4 for examples. We say that a configuration $p\in \mathbb {R}^{nd}$ is generic if its nd coordinates are algebraically independent over $\mathbb {Q}$. It is known that in any fixed dimension d, both local and global rigidity are generic properties of the underlying graph, in the sense that either every generic d-dimensional framework is locally/globally rigid or none of them are (see [1, 5, 9]). Thus, we say that a graph is rigid (respectively globally rigid) in d dimensions if every (or equivalently, if some) generic d-dimensional realization of the graph is rigid (resp. globally rigid). It follows from the definitions that globally rigid graphs are rigid. The following much stronger necessary conditions of global rigidity are due to Hendrickson [12]. We say that a graph is redundantly rigid in a given dimension if it remains rigid after deleting any edge. A graph is k-connected for some $k\ge 2$ if it has at least $k+1$ vertices and it remains connected after deleting any set of less than k vertices.

Theorem 2.1

Let G be a graph on $n \ge d+2$ vertices for some $d \ge 1$. Suppose that G is globally rigid in $\mathbb {R}^d$. Then G is $(d+1)$-connected and redundantly rigid in $\mathbb {R}^d$.

In our context it is useful to explore and understand the properties of the function mapping the realizations of a graph to the (multi-)set of their Euclidean squared edge lengths. This function is sometimes called the rigidity map, or edge function of a graph. To study the analytic and algebraic properties of this function, it is useful to regard the multi-set of edge lengths as an ordered tuple, i.e., a vector. One minor technical problem is that this order, and thus many of the concepts relying on it, is not unique. To sidestep this issue, we will always implicitly assume that there is some fixed ordering of the edges of the graph in question. In what follows the exact ordering will not be of much importance.

Let G be a graph on n vertices and m edges. We denote the aforementioned d-dimensional rigidity map by $m_{d,G}:\mathbb {R}^{nd}\rightarrow \mathbb {R}^m$, that is, for a d-dimensional realization $(G,p)$ of G, the i-th coordinate of $m_{d,G}(p)$ is $\Vert p(u) - p(v)\Vert ^2$, where uv is the i-th edge of the graph. Given a d-dimensional framework $(G,p)$, we say that $m_{d,G}(p)$ is the edge measurement sequence of $p$. Thus two frameworks $(G,p),(H,q)$ are length-equivalent if and only if there exists a bijection $\psi$ between the edge sets of G and H for which $m_{d,G}(p) = m_{d,H}(q)$, where the ordering of the edges of H is determined by the ordering of the edges of G and $\psi$.

2.1.2 The Rigidity Matroid

The rigidity matroid of a graph G is a matroid defined on the edge set of G which reflects the rigidity properties of all generic realizations of G.

Let (G, p) be a realization of a graph $G=(V,E)$ in $\mathbb {R}^d$. The rigidity matrix of the framework (G, p) is the matrix R(G, p) of size $|E|\times d\,|V|$, where, for each edge $v_iv_j\in E$, in the row corresponding to $v_iv_j$, the entries in the d columns corresponding to vertices i and j contain the d coordinates of $p(v_i)-p(v_j)$ and $p(v_j)-p(v_i)$, respectively, and the remaining entries are zeros. In other words, it is 1/2 times the Jacobian of the aforementioned rigidity map. See [28] for more details. The rigidity matrix of (G, p) defines the rigidity matroid of (G, p) on the ground set E by linear independence of rows of the rigidity matrix. Any two generic frameworks (G, p) and (G, q) have the same rigidity matroid. We call this the d-dimensional rigidity matroid ${{\mathscr {R}}}_d(G)=(E,r_d)$ of the graph G. We denote the rank of ${{\mathscr {R}}}_d(G)$ by $r_d(G)$. A graph $G=(V,E)$ is independent if $r_d(G)=|E|$ and it is a circuit if it is not independent but every proper subgraph $G'$ of G is independent. An edge e of G is a d-bridge if $r_d(G-e)=r_d(G)-1$ holds. When the dimension d is clear from the context, we shall simply write that e is a bridge.²

Gluck [8] characterized rigid graphs in terms of their rank.

Theorem 2.2

Let $G=(V,E)$ be a graph with $|V|\ge d+1$. Then G is rigid in $\mathbb {R}^d$ if and only if $r_d(G)=d\,|V|-\left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$.

Given two matroids $(S_1, {\mathscr {I}}_1)$ and $(S_2, {\mathscr {I}}_2)$, their direct sum is the matroid $(S_1 \cup S_2,{\mathscr {I}})$, where ${\mathscr {I}}=\{A \subseteq S_1\cup S_2:A\cap S_i \in {\mathscr {I}}_i\ \text {for}\ i = 1,2\}$. We say that a matroid is connected if it cannot be obtained as the direct sum of two matroids. Every matroid arises, in a unique way, as the direct sum of some connected matroids. In the case of graphic matroids, this corresponds to the decomposition of the edge set of the graph into the edge sets of its 2-connected components. For a more thorough introduction to the basic notions of matroid theory, see e.g. the book by Oxley [23]. For a detailed exposition of rigidity theory, see [16, 18, 28].

2.1.3 Complex Frameworks

Analogously to the real case, we can define a d-dimensional complex framework to be a pair $(G,p)$ where $G = (V,E)$ is a graph and $p:V\rightarrow \mathbb {C}^d$ is a complex mapping. The complex squared length of an edge $e = uv$ is

$$\begin{aligned} m_{uv}(p) = \sum _{k=1}^d (p(u)_k - p(v)_k)^2, \end{aligned}$$

where k indexes over the d dimension-coordinates. This coincides with the usual (Euclidean) squared length for real frameworks. We say, as in the real case, that two frameworks $(G,p)$ and $(G,q)$ are equivalent if $m_{uv}(p)=m_{uv}(q)$ for each edge uv, and they are congruent if the same holds for each pair of vertices $u,v \in V$. A configuration $p\in \mathbb {C}^{nd}$ is, again, generic, if the coordinates of $p$ are algebraically independent over $\mathbb {Q}$. A point $p\in \mathbb {R}^{nd}$ is generic as a real configuration precisely if it is generic as a complex one.

Using these notions one can define the analogues of rigidity and global rigidity in the complex setting. It turns out that these notions, as graph properties, coincide with their real counterpart.

Theorem 2.3

[10, 11]    Complex rigidity and global rigidity are generic properties and a graph G is rigid (respectively globally rigid) in $\mathbb {C}^d$ if and only if it is rigid (resp. globally rigid) in $\mathbb {R}^d$.

We can define the rigidity matrix R(G, p) for complex frameworks in the same way as in the real case. This, again, allows us to define the rigidity matroid of the framework. It is not difficult to show that the rigidity matroid of a generic framework in $\mathbb {C}^d$ is isomorphic to the d-dimensional rigidity matroid ${\mathscr {R}}_d(G)$. Throughout the rest of the paper we shall only consider complex frameworks, unless stated otherwise, and refer to them as frameworks.

2.2 Basic Results from Algebraic Geometry

As mentioned in the introduction, passing to the field of complex numbers allows us to use methods of algebraic geometry to analyze the set of possible edge measurements. The utility of this approach will become apparent in the next section, where we shall define the measurement variety of a graph, a complex variety which carries information about the reconstructibility properties of the graph and its realizations. In the rest of this section we introduce the relevant concepts and results from algebraic geometry.

2.2.1 The Zariski Topology

Let I be an ideal of $\mathbb {C}\,[x_1,\dots ,x_n]$, that is, a set of polynomials closed under addition and under multiplication by arbitrary polynomials, and denote by V(I) the set of points ${\mathbf {x}} \in \mathbb {C}^n$ such that $f({\mathbf {x}}) = 0$ for all $f \in I$. We say that $V \subseteq \mathbb {C}^n$ is a variety if $V = V(I)$ for some ideal I of $\mathbb {C}\,[x_1,\dots ,x_n]$. By Hilbert’s basis theorem every ideal in $\mathbb {C}\,[x_1,\dots ,x_n]$ is finitely generated, and it follows that a variety can always be written as the set of simultaneously vanishing points of a finite number of polynomials. Conversely, for any set of points $X \subseteq \mathbb {C}^n$, let I(X) denote the set of polynomials in n variables vanishing on X; this forms an ideal of $\mathbb {C}\,[x_1,\dots ,x_n]$. A variety is said to be irreducible if it is not a proper union of two subvarieties.³ For example, $\mathbb {C}^n$ itself is irreducible. Any variety can be written uniquely as the union of a finite number of irreducible varieties, called the irreducible components of the variety.

The family of varieties is closed under taking finite unions and arbitrary intersections. The empty set and $\mathbb {C}^n$ itself are easily seen to be varieties, thus varieties form the closed sets of a topology on $\mathbb {C}^n$. This is called the Zariski topology, and is a proper sub-topology of the usual Euclidean topology on $\mathbb {C}^n$. The closure of an arbitrary set $X\subseteq \mathbb {C}^n$ with respect to this topology is given by ${\overline{X}}=V(I(X))$. The product of the Zariski topologies on $\mathbb {C}^n$ and $\mathbb {C}^m$ is strictly coarser than the Zariski topology on $\mathbb {C}^{n+m}$. For example, the Zariski-closed sets of $\mathbb {C}$ are the whole set and its finite subsets. It follows that the closed sets of the product topology on $\mathbb {C}^2$ consist of a finite union of horizontal and vertical lines and points, along with $\mathbb {C}^2$ itself, while the Zariski topology contains, for example, the parabola $V(y-x^2)$. However, the closure of the product of two sets does coincide in the product topology and the Zariski topology.

Lemma 2.4

Let $U \subseteq \mathbb {C}^n, V \subseteq \mathbb {C}^m$ be arbitrary subsets. Then ${\overline{U}} \times {\overline{V}} = \overline{U \times V}$, where ${\overline{X}}$ denotes the closure of X in the respective Zariski topology.

Proof

${\overline{U}} \times {\overline{V}} \supseteq \overline{U \times V}$ follows from the fact that the left hand side is the closure in the product topology, which is coarser than the Zariski topology. For the other direction, we have to show that for any $u \in {\overline{U}}$, $v\in {\overline{V}}$, and $f \in I(U \times V) \subseteq \mathbb {C}\,[x_1,\dots ,x_n,y_1,\dots ,y_m]$ we have $f(u,v) = 0$. Notice that for any $v_0 \in V$ the polynomial $f(x,v_0) \in \mathbb {C}\,[x_1,\dots ,x_n]$ is in I(U). It follows that $f(u,v_0)=0$. Since this holds for any $v_0 \in V$, the polynomial $f(u,y) \in \mathbb {C}\,[y_1,\dots ,y_m]$ is in I(V). This implies that $f(u,v) = 0$, as desired. $\square$

2.2.2 Constructible Sets

We call a subset of $\mathbb {C}^n$ constructible if it can be obtained from varieties by taking intersections and complements finitely many times. A constructible set S is irreducible if it has an irreducible Zariski closure. We say that a variety is defined over $\mathbb {Q}$ if it can be defined by polynomials with rational coefficients. Similarly, a constructible set is said to be defined over $\mathbb {Q}$ if it can be constructed from varieties defined over $\mathbb {Q}$. It is known that in this case the closure is defined over $\mathbb {Q}$ as well. The image of a constructible set under a polynomial map is also constructible; this is Chevalley’s theorem. If the original set was defined over $\mathbb {Q}$ and the polynomial map has rational coefficients, then the image is defined over $\mathbb {Q}$ as well. Moreover, the image of an irreducible variety under a polynomial map is irreducible.

Lemma 2.5

[10, Lem. A.5]    Suppose that S is a non-empty irreducible constructible set. Then S contains a non-empty Zariski open subset U of ${\overline{S}}$. If S is defined over $\mathbb {Q}$, then U can be chosen to be defined over $\mathbb {Q}$ as well.

2.2.3 Generic Points

Let S be a constructible set, defined over $\mathbb {Q}$. A point $x \in S$ is generic if it does not satisfy any polynomial equation with rational coefficients except those in I(S). We will denote the generic points of S by ${\text {Gen}}S$.

Lemma 2.6

Let S be an irreducible constructible set defined over $\mathbb {Q}$. Then ${\text {Gen}}S$ is Zariski dense in S.

Proof

This is a consequence of [10, Lem. A.6]. $\square$

Lemma 2.7

Let V be an irreducible variety defined over $\mathbb {Q}$ and $f:V \rightarrow \mathbb {C}^m$ a polynomial map with rational coefficients. Then $f({\text {Gen}}V)={\text {Gen}}f(V)$.

Proof

This is a combination of the statements of Lemmas A.7 and A.8 from [10]. $\square$

Lemma 2.8

Let S be an irreducible constructible set defined over $\mathbb {Q}$. Then ${\text {Gen}}{\overline{S}}={\text {Gen}}S$ and, in particular, each generic point of ${\overline{S}}$ is in S.

Proof

It is clear that ${\text {Gen}}S={\text {Gen}}{\overline{S}}\cap S$, so we only need to show that ${\text {Gen}}{\overline{S}}\subseteq S$. By Lemma 2.5, S contains a non-empty open subset $U\subseteq {\overline{S}}$ that is defined over $\mathbb {Q}$. In other words, $U=\{x\in {\overline{S}}:f_1(x)\ne 0\ \text {or}\ f_2(x)\ne 0\ \text {or}\ \ldots \ \text {or}\ f_k(x)\ne 0\}$ for some polynomials $f_1,\dots ,f_k$ with rational coefficients. Since U is non-empty, $f_i\notin I({{\overline{S}}})$ for some $1\le i\le k$. It follows that generic points of ${\overline{S}}$ do not satisfy $f_i$, and thus they lie in $U \subseteq S$. $\square$

For a thorough introduction to the basic notions of algebraic geometry, see [25]. An exposition of constructible sets, including a proof of Chevalley’s theorem, can be found in [2]. The reader may also consult the appendices of [10] and [7].

3 The Measurement Variety

In this section, we define the measurement variety of a graph and examine some of its structural properties. The proof of Theorem 1.1 was obtained in [10] by exploring some properties of this variety. We shall also use it in the study of weak and strong reconstructibility.

Let G be a graph with n vertices and m edges. As before, we assume that there is some fixed ordering of the edges of G. Recall the rigidity map $m_{d,G}:\mathbb {R}^{nd}\rightarrow \mathbb {R}^m$ is defined by mapping a realization in $\mathbb {R}^d$, viewed as a point in $\mathbb {R}^{nd}$, to its edge measurement sequence. This map extends to a map from $\mathbb {C}^{nd}$ to $\mathbb {C}^m$ by mapping a realization in $\mathbb {C}^d$ to its complex edge measurement sequence. Formally, for a framework (G, p) in $\mathbb {C}^d$, let the i-th coordinate of $m_{d,G}(p)$ (which corresponds to some edge uv of G) be $m_{uv}(p)$, the squared complex edge length of uv in (G, p). It follows from Lemma 2.5 (and the two paragraphs preceding the lemma) that the image of $\mathbb {C}^{nd}$ under this polynomial map is an irreducible constructible set, defined over $\mathbb {Q}$. This leads us to the following definition.

Definition 3.1

The d-dimensional measurement variety of a graph G (on n vertices), denoted by $M_{d,G}$, is the Zariski closure of $m_{d,G}(\mathbb {C}^{nd})$.

In the next subsection we study the connection between the measurement variety and the graph reconstructibility notions defined in the introduction. The most important consequence of this connection is that both weak and strong reconstructibility in $\mathbb {C}^d$ are generic, for all d, i.e., the existence of a single reconstructible generic framework guarantees the reconstructibility of every generic framework (in a given dimension). In the rest of the section we shall consider further structural properties of the measurement variety, as well as its connection to the rigidity matroid.

3.1 Connection with Weak and Strong Reconstructibility

In what follows we shall frequently consider graphs with the same measurement variety. In this case by writing $M_{d,G} = M_{d,H}$ we mean that there is a bijection $\psi$ between the edge sets of G and H such that when using the corresponding orderings of the edges, the measurement varieties of the graphs coincide. Whenever we want to explicitly refer to this bijection, we say that $M_{d,G} = M_{d,H}$ under the edge bijection $\psi$. Moreover, if we write both $M_{d,G} = M_{d,H}$ and $m_{d,G}(p) = m_{d,H}(q)$ in the same context, we shall mean that these equalities are satisfied under the same edge bijection.

The next lemma asserts, in essence, that whether a point of the measurement variety can occur as the edge measurement sequence of a generic framework only depends on the measurement variety, and not the underlying graph. In fact, these points are precisely the generic points of the measurement variety.

Lemma 3.2

Suppose that G and H are graphs on n and $n'$ vertices respectively, such that $M_{d,G} = M_{d,H}$. Then for each generic complex d-dimensional realization $(G,p)$ there exists a generic realization $(H,q)$ that is length-equivalent to $(G,p)$.

Proof

By Lemmas 2.7 and 2.8 we have

$$\begin{aligned} m_{d,G}({\text {Gen}}\mathbb {C}^{nd})&={\text {Gen}}m_{d,G}(\mathbb {C}^{nd}) ={\text {Gen}}M_{d,G}\\&={\text {Gen}}M_{d,H}={\text {Gen}}m_{d,H}(\mathbb {C}^{n'd}) = m_{d,H}({\text {Gen}}\mathbb {C}^{n'd}), \end{aligned}$$

which immediately implies the statement. $\square$

By using this observation we can prove that weak reconstructibility is a generic property. We say that $M_{d,G}$ uniquely determines the graph G if whenever $M_{d,G} = M_{d,H}$ for some graph H with the same order as G, we have that H is isomorphic to G.

Theorem 3.3

Let G be a graph and $d \ge 1$ be fixed. The following are equivalent:

• (i) G is (generically) weakly reconstructible in $\mathbb {C}^d$.

• (ii) There exists some generic d-dimensional framework $(G,p)$ that is weakly reconstructible.

• (iii) $M_{d,G}$ uniquely determines G.

Proof

(i) $\Rightarrow$ (ii) is trivial. For (ii) $\Rightarrow$ (iii), suppose that $M_{d,G} = M_{d,H}$ for some graph H with the same order as G. By Lemma 3.2, there exists some generic realization $(H,q)$ for which $m_{d,G}(p) = m_{d,H}(q)$, that is, $(H,q)$ is length-equivalent to $(G,p)$. By the weak reconstructibility of $(G,p)$, it follows that H is isomorphic to G.

Finally, to see (iii) $\Rightarrow$ (i), take a generic d-dimensional framework $(G,p)$ and let $(H,q)$ be a length-equivalent generic framework, where H has the same order as G. Let $m_{d,G}(p) = m_{d,H}(q) = x$ denote the edge measurements of these frameworks. By Lemma 2.7, $x$, as the image of a generic configuration, is generic in $M_{d,G}$, so the only polynomials with rational coefficients that it satisfies are those that are satisfied by every element of $M_{d,G}$. But since $x\in M_{d,H}$, $x$ satisfies the (rational) polynomials defining $M_{d,H}$. It follows that $M_{d,G} \subseteq M_{d,H}$. The same argument shows that $M_{d,H} \subseteq M_{d,G}$ holds as well, so $M_{d,G} = M_{d,H}$. By our assumption this implies that G and H are isomorphic. Since p was arbitrarily chosen, this shows that G is weakly reconstructible in d dimensions. $\square$

We note that Lemma 3.2 and Theorem 3.3 are contained (either implicitly or explicitly) in [10].

Strong reconstructibility admits a similar characterization in terms of the measurement variety. Given a graph G, any permutation $\psi$ of its edge set acts on $\mathbb {C}^m$ by permuting the coordinate axes. We say that $M_{d,G}$ is invariant under $\psi$ if this action leaves it in place. The permutation $\psi$ is induced by a graph automorphism if there is an automorphism $\varphi$ of G such that for every edge $uv\in E(G)$, $\psi (uv) = \varphi (u)\,\varphi (v)$. It is clear that $M_{d,G}$ is invariant under permutations that are induced by graph automorphisms: indeed, even $m_{d,G}(\mathbb {C}^{nd})$ is invariant, so its Zariski closure must be as well. The next theorem characterizes strong reconstructibility in terms of the converse statement. In particular, it shows that, like weak reconstructibility, strong reconstructibility is a generic notion as well.

Theorem 3.4

Let G be a graph and $d \ge 1$ be fixed. The following are equivalent:

• (i) G is (generically) strongly reconstructible in $\mathbb {C}^d$.

• (ii) There exists some generic d-dimensional framework $(G,p)$ which is strongly reconstructible.

• (iii) $M_{d,G}$ uniquely determines G and whenever $M_{d,G}$ is invariant under a permutation $\psi$ of the edges of G, $\psi$ is induced by a graph automorphism.

• (iv) Whenever $M_{d,G} = M_{d,H}$ under an edge bijection $\psi$ for some graph H with the same order as G, $\psi$ is induced by a graph isomorphism.

Proof

(i) $\Rightarrow$ (ii) is again trivial. (ii) $\Rightarrow$ (iii): Since strong reconstructibility implies weak reconstructibility, $M_{d,G}$ uniquely determines G by the previous theorem. Let $\psi$ be a permutation of the edges of G under which $M_{d,G}$ is invariant. It follows that there is a d-dimensional framework (G, q) such that $m_{d,G}(p) = m_{d,G}(q)$ under the edge bijection $\psi$, and indeed, by Lemma 2.7 we can choose q to be generic. But then the strong reconstructibility of (G, p) implies that $\psi$ is induced by a graph automorphism.

(iii) $\Rightarrow$ (iv): Suppose that $M_{d,G}=M_{d,H}$. By our assumptions, it follows that there is some isomorphism $\varphi :V(G)\rightarrow V(H)$, inducing an edge bijection $\phi$. Clearly, $M_{d,H} = M_{d,G}$ under $\phi ^{-1}$. It follows that $M_{d,G}$ is invariant under the permutation $\phi ^{-1}\circ \psi$ of the edges of G, thus it is induced by some automorphism $\varphi '$ of G. Then $\psi$ is induced by the graph isomorphism $\varphi \circ \varphi '$, as desired.

(iv) $\Rightarrow$ (i): Let (G, p) be a generic d-dimensional framework and let $(H,q)$ be a length-equivalent generic framework, where H has the same order as G. Let $\psi$ denote the edge bijection between the two graphs. As in the proof of the previous theorem, from the length-equivalence of these generic frameworks (on the same number of vertices) it follows that $M_{d,G} = M_{d,H}$ under $\psi$, and thus, by our assumption, $\psi$ is induced by a graph isomorphism. $\square$

The preceding theorems show that the reconstructibility properties of a graph can be determined by considering its measurement variety. This motivates the further study of this object, both in terms of its algebraic structure and its connection with the combinatorial structure of the underlying graph. In the following subsections we investigate further graph properties which are reflected in the structure of the measurement variety.

In Sect. 6 we shall define and examine the analogues of weak and strong reconstructibility in the real setting. We shall see that, in general, the real version of weak reconstructibility is not a generic property, and thus the corresponding version of Theorem 3.3 does not hold in this case.

3.2 Basic Structure of the Measurement Variety

One of the fundamental properties of an irreducible variety V is its dimension. This number, denoted by $\dim V$, is the largest integer k for which there exists a chain

$$\begin{aligned} V=V_k \supsetneq V_{k-1} \supsetneq \ldots \supsetneq V_0 \ne \varnothing \end{aligned}$$

of irreducible subvarieties. In the case of the measurement variety, it turns out that this dimension is exactly the rank of the rigidity matroid of G.

Lemma 3.5

Let G be a graph on n vertices. Then

$$\begin{aligned} \dim M_{d,G}=r_{d}(G). \end{aligned}$$

In particular, when $n \ge d+1$ we have $\dim M_{d,G}\le nd - \left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$ and equality holds if and only if G is rigid in d dimensions.

Proof

The equality in the first part is implicit in the proof of [10, Lem. 3.3]. The second part follows from Theorem 2.2. $\square$

A consequence is the following theorem, which was already noted in [10].

Theorem 3.6

Let $(G,p)$ be a generic d-dimensional realization of the rigid graph G on n vertices and suppose that for some framework $(H,q)$, with H having the same number of edges as G and $n'\le n$ vertices, we have $m_{d,G}(p)=m_{d,H}(q)$. Then $n=n'$, H is rigid as well and $M_{d,G}=M_{d,H}$.

Proof

If $n\le d$ then G is a complete graph and the statement is easy to see. So we may suppose that $n\ge d+1$. As in the proof of Theorem 3.3, the existence of a generic point in $M_{d,G}$ that is also in $M_{d,H}$ implies $M_{d,G}\subseteq M_{d,H}$. From Lemma 3.5 and the rigidity of G we have that $\dim M_{d,G}$ is maximal among graphs on at most n vertices, and in particular $\dim M_{d,H}\le \dim M_{d,G}$. Since any strict subvariety of an irreducible variety has dimension smaller than that of the variety, we must have $M_{d,G}=M_{d,H}$. The rigidity of H and the fact that $n'=n$ must hold are immediate from Lemma 3.5. $\square$

The significance of this theorem is that for a rigid generic framework (G, p), in the definitions of weak and strong reconstructibility we can omit the condition that $(H,q)$ is generic and still arrive at the same notion. This is not true for non-rigid graphs in general: we shall illustrate this in Sect. 4. Another consequence of Lemma 3.5 is the following characterization of independent graphs.

Theorem 3.7

Let G be a graph with m edges. Then G is independent in d dimensions if and only if $M_{d,G} = \mathbb {C}^m$.

Proof

By Lemma 3.5 we have

$$\begin{aligned} \dim M_{d,G} = r_d(G) \le m = \dim \mathbb {C}^m. \end{aligned}$$

If G is independent, then equality holds, thus $M_{d,G}=\mathbb {C}^m$, since every strict subvariety of $\mathbb {C}^m$ has dimension less than m. Conversely, if G is not independent, then $\dim M_{d,G}<\dim \mathbb {C}^m$, and so the two varieties cannot be equal. $\square$

Our next aim is to show that the measurement variety of a graph determines its rigidity matroid. We will need the following observation regarding the measurement variety of subgraphs. Consider a graph $G=(V,E)$. For a subset of edges $E'\subseteq E$, let $\pi _{E'}:\mathbb {C}^m\rightarrow \mathbb {C}^{|E'|}$ denote the projection onto the axes corresponding to the edges of $E'$. We will omit the subscript when it is clear from the context. It is a basic fact of topology that for any continuous function $f:X\rightarrow Y$ between two topological spaces and for any subset $A \subseteq X$, we have $\overline{f({\overline{A}})}=\overline{f(A)}$ (see e.g. [22, Chap. 2, Thm. 18.1]). Applying this to $\pi _{E'}:\mathbb {C}^m\rightarrow \mathbb {C}^{|E'|}$ and $m_{d,G}(\mathbb {C}^{nd}) \subseteq \mathbb {C}^m$ we get the following.

Lemma 3.8

Let $G = (V,E)$ be a graph with edges $e_1,\ldots ,e_m$ and $G' = (V',E')$ a subgraph of G. Then $\overline{\pi _{E'}(M_{d,G})} = M_{d,G'}$.

We can deduce from Theorem 3.7 and Lemma 3.8 that $M_{d,G}$ fully determines the d-dimensional rigidity matroid of G: for any subgraph $G' = (V,E')$ we can decide whether $E'$ is independent or not by considering $M_{d,G'}$, which can be determined from $M_{d,G}$ by taking the closure of its projection onto some coordinate axes. This argument is made precise by the following theorem. We note that this is a straightforward generalization of [10, Lem. 5.5], which is the analogous statement in one dimension.

Theorem 3.9

Let G and H be graphs with the same number of edges and suppose that $M_{d,G} = M_{d,H}$ under some edge bijection $\psi$. Then this edge bijection defines an isomorphism between the d-dimensional rigidity matroids of G and H.

Proof

Let C be a set of edges of G, and let $C' = \psi (C)$ be the set of corresponding edges in H. By Theorem 3.7 and Lemma 3.8 we have

$$\begin{aligned} C \text { is independent }\ \Leftrightarrow \ \overline{\pi _C(M_{d,G})}=\mathbb {C}^{|C|}\&\Leftrightarrow \&\overline{\pi _{C'}(M_{d,H})}=\mathbb {C}^{|C'|}\ \\&\Leftrightarrow \&C' \text { is independent,} \end{aligned}$$

which means, by definition, that $\psi$ defines an isomorphism between the respective rigidity matroids. $\square$

In general, finding an explicit description of the defining polynomials of $M_{d,G}$ seems non-trivial. We close this subsection by showing a special case where it is feasible.⁴ We shall consider one-dimensional complex realizations of cycles. The cycle on n vertices is denoted by $C_n$. The rigidity map $m_{1,C_n}$ has a simple enough structure which allows us to describe the measurement variety in a compact form. We shall use the following observation. Let $n \ge 2$ be an integer. Define

$$\begin{aligned} f_n(x_1,\dots ,x_n) = \prod (x_1 \pm x_2 \pm \dots \pm x_n) \in \mathbb {Q}\,[x_1,\dots ,x_n]. \end{aligned}$$

Then $f_n$ is a symmetric polynomial. Moreover, if we write $f_n$ as a sum of monomials, then we can see that every variable in every term has even degree. It follows that there exists a symmetric polynomial $g_n$ with rational coefficients such that

$$\begin{aligned} f_n(x_1,\dots ,x_n) = g_n(x_1^2,\dots ,x_n^2). \end{aligned}$$

(1)

In particular, $g(a_1^2,\dots ,a_n^2)=0$ whenever $a_1 + \dots + a_n = 0$.

Theorem 3.10

$m_{1,C_n}(\mathbb {C}^{nd}) = M_{1,C_n} = V(g_n)$.

Proof

Denote the vertices of $C_n$ by $V = \{v_1,\dots ,v_n\}$ and let $E = \{e_1,\dots ,e_n\}$ be a consecutive labeling of the edges, that is, $e_i = v_iv_{i+1}$ for $i =1,\ldots ,n-1$ and $e_n = v_nv_1$. If $(C_n,p)$ is a one-dimensional realization of $C_n$ for some $p= (p_1,\dots ,p_n) \in \mathbb {C}^n$, then

$$\begin{aligned} g_n \circ m_{1,C_n}(p) = f_n(p_2-p_1,\dots ,p_n-p_{n-1},p_1-p_n) = 0, \end{aligned}$$

so $m_{1,C_n}(\mathbb {C}^{nd}) \subseteq V(g_n)$. Conversely, if $b_1,\dots ,b_n \in \mathbb {C}$ are such that $g_n(b_1,\dots ,b_n) = 0$, then taking arbitrary square roots $a_i = \sqrt{b_i}$ we have $f_n(a_1,\dots ,a_n) = 0$. By the factorization of $f_n$ this means that, by negating some of $a_i$’s, we can suppose $a_1 + \dots + a_n = 0$. Any such unsquared length measurement can be obtained by placing the vertices of $C_n$ one by one, that is, letting $p_1 = 0$ and $p_i = a_1 + \dots + a_{i-1}$ for $i = 2,\dots ,n$. $\square$

Note that $g_n$ is a symmetric polynomial, and consequently $V(g_n)=M_{1,C_n}$ is invariant under any permutation of the edge set of $C_n$. When $n\ge 4$, not all of these permutations arise from a graph automorphism; thus, using Theorem 3.4, we see again that $C_n$ is not strongly reconstructible in $\mathbb {C}^1$. On the other hand, it is weakly reconstructible in $\mathbb {C}^1$, as we shall see later on.

Theorem 3.10 shows that $M_{1,C_n}$ can be defined as the set of zeros of a single polynomial. This is not a coincidence: it is known that any irreducible variety $V\subseteq \mathbb {C}^m$ with $\dim {V} = m - 1$ can be defined by a single polynomial. Such a set is sometimes called a hypersurface. It follows from Lemma 3.5 that the measurement variety of a graph G whose edge set is a circuit in the d-dimensional rigidity matroid is a hypersurface, since we have

$$\begin{aligned} \dim M_{d,G}=r_d(G) = m - 1. \end{aligned}$$

It would be interesting to explicitly describe the measurement varieties (and their defining polynomials) of circuits in $d \ge 2$ dimensions. See [24] and references therein for more discussion about these so-called circuit polynomials.

3.3 Direct Sum Decompositions

Next we look for conditions under which the measurement variety of a graph arises as the product of the measurement varieties of some of its subgraphs $G_i$, $1\le i\le l$, where the edge sets of the $G_i$’s form a non-trivial partition of the edge set of G. In this case it will be convenient to say that $M_{d,G}$ is the direct sum of these smaller varieties and denote this by $M_{d,G}=\bigoplus _{i=1}^lM_{d,G_i}$.⁵ It is clear that $M_{d,G}$ is the direct sum of the measurement varieties of the connected components of G.

A 2-block of a graph G is a maximal 2-connected subgraph of G. Note that a single edge e is a 2-block if and only if e is a cut-edge of G.

Lemma 3.11

Let $G = (V,E)$ be a graph and let $G_1,\dots ,G_l$ be its 2-blocks. Then for any $d \ge 1$ we have $M_{d,G} = \bigoplus _{i=1}^l M_{d,G_i}$.

Proof

Consider a cut-vertex v of G and let $V'$ be the vertex set of a connected component of $G-v$. Denote by $G_1$ the subgraph of G induced by $V' + v$ and let $G_2$ be the subgraph induced by $V-V'$. Observe that for a graph H the set $m_{d,H}(\mathbb {C}^{nd})$ is not changed if we restrict the realization space by fixing the position of some vertex of H. By applying this observation to G, $G_1$, $G_2$, and v, we can deduce that, possibly after relabeling the edges, we have $m_{d,G}(\mathbb {C}^{nd}) = m_{d,G_1}(\mathbb {C}^{nd}) \oplus m_{d,G_2}(\mathbb {C}^{nd})$, and hence $M_{d,G} = M_{d,G_1} \oplus M_{d,G_2}$. The lemma follows by induction. $\square$

Note that the (edge sets of the) 2-blocks of a graph also give rise to a direct sum decomposition of ${\mathscr {R}}_d(G)$ and, as mentioned before, in the $d=1$ case this is precisely the decomposition of ${{\mathscr {R}}}_1(G)$ into connected components. In light of this, it seems plausible that there is a connection between the direct sum decomposition of the measurement variety and that of the rigidity matroid. The next statement shows that such a connection indeed exists: the edge sets corresponding to direct summands of the measurement variety also correspond to direct summands of the rigidity matroid.

Theorem 3.12

Let $G = (V,E)$ be a graph, and suppose that $M_{d,G} = M_{d,G_1} \oplus M_{d,G_2}$ for some subgraphs $G_i = (V,E_i)$ for $i = 1,2$. Then ${\mathscr {R}}_{d}(G) = {\mathscr {R}}_{d}(G_1) \oplus {\mathscr {R}}_{d}(G_2)$.

Proof

Let $C=C_1\cup C_2$ be a subset of edges with $C_i \subseteq E_i$, $i=1,2$. Then, by Theorem 3.7, C is independent precisely if $M_{d,C}=\mathbb {C}^{|C|}$. But

$$\begin{aligned} M_{d,C}&= \overline{\pi _C(M_{d,G})} = \overline{\pi _C(M_{d,G_1} \oplus M_{d,G_2})} = \overline{\pi _{C_1}(M_{d,G_1}) \oplus \pi _{C_2}(M_{d,G_2})} \\&= \overline{\pi _{C_1}(M_{d,G_1})} \oplus \overline{\pi _{C_2}(M_{d,G_2})} = M_{d,C_1} \oplus M_{d,C_2}, \end{aligned}$$

which implies that C is independent if and only if $C_1$ and $C_2$ are independent. Since this is true for any edge set C, ${\mathscr {R}}_{d}(G) = {\mathscr {R}}_{d}(G_1) \oplus {\mathscr {R}}_{d}(G_2)$ follows. $\square$

Lemma 3.11 implies that in one dimension the converse of Theorem 3.12 also holds, showing that in this case the direct sum structures of the measurement variety and the rigidity matroid coincide. It is unclear whether this remains true in higher dimensions. The next theorem shows that the converse statement holds, for all $d\ge 2$, in the special case when one of the direct summands consists of a single edge e, that is, when e is a bridge of ${{\mathscr {R}}}_d(G)$.

It is well known that if a graph G is not rigid in $\mathbb {C}^d$, then for any generic realization (G, p) in $\mathbb {C}^d$ there is an infinite number of pairwise non-congruent frameworks that are equivalent to (G, p), while if G is rigid, then there are only finitely many such frameworks. In particular, if G is rigid and $e=uv$ is a bridge of ${{\mathscr {R}}}_d(G)$, then for every generic realization $(G-e,p)$ in $\mathbb {C}^d$ there is an infinite number of frameworks equivalent to $(G-e,p)$ in which the “length” of e is different.

Theorem 3.13

Let G be a graph on n vertices with edges $e_1,\dots ,e_m$ and let $G'=G-e_m$. Then $e_m$ is a bridge of ${{\mathscr {R}}}_d(G)$ if and only if $M_{d,G} = M_{d,G'} \oplus \mathbb {C}$.

Proof

Sufficiency is implied by Theorem 3.12, so we only need to show necessity. Suppose that $e_m$ is a bridge of ${{\mathscr {R}}}_d(G)$ and let $S = m_{d,G}(\mathbb {C}^{nd})$. Note that $M_{d,G} \subseteq M_{d,G'}\oplus \mathbb {C}$ always holds, so it suffices to prove containment in the other direction. Let ${\mathbf {x}}=(x_1,\dots ,x_m) \in {\text {Gen}}S$ be a generic edge measurement sequence of G. By Lemma 2.7 this corresponds to the squared edge lengths of some complex generic realization of G. Since $e_m$ is a bridge, there is an infinite set $Y\subseteq \mathbb {C}$ such that $(x_1,\dots ,x_{m-1}) \times Y\subseteq S$. Using Lemma 2.4 and the observation that ${\overline{Y}} = \mathbb {C}$, we have

$$\begin{aligned} (x_1,\dots ,x_{m-1}) \times \mathbb {C}= \overline{(x_1,\dots ,x_{m-1}) \times Y} \subseteq {\overline{S}} = M_{d,G}. \end{aligned}$$

In fact, what we have shown is that $\pi ({\text {Gen}}S) \oplus \mathbb {C}\subseteq M_{d,G}$, where $\pi$ is the projection of $\mathbb {C}^m$ onto the first $m-1$ coordinates. Thus, we only need to show that the closure of $\pi ({\text {Gen}}S)$ is $M_{d,G'}$. This follows from Lemmas 2.6 and 3.8:

$$\begin{aligned} \overline{\pi ({\text {Gen}}S)} = \overline{\pi (\overline{{\text {Gen}}S})} = \overline{\pi (M_{d,G})} = M_{d,G'}. \end{aligned}$$

$\square$

4 Examples of Reconstructible Graphs

Some graphs are weakly reconstructible because they possess some extremal property. Trivial examples are complete graphs as well as graphs obtained by deleting an edge from a complete graph, which are obviously weakly reconstructible due to the fact that they are the only graphs, up to isomorphism, on the given number of vertices and edges.

In this section we identify two families of graphs which are weakly reconstructible because of similar, though more subtle reasons. While the structure of these graphs is highly special (both families are simple extensions of complete graphs), they provide an interesting example of using the tools and results obtained in the previous sections to prove reconstructibility, without explicitly referring to the underlying algebraic machinery. They also show that redundant rigidity, and indeed rigidity, is not a necessary condition of weak reconstructibility.

At the end of this section we shall apply some of the results of Sect. 3 to see how properties of the rigidity matroid of a graph can sometimes be used to verify weak or strong reconstructibility.

4.1 Maximally Non-Rigid and Non-Globally Rigid Graphs

We call a graph G on n vertices and m edges maximally non-globally rigid (resp. maximally non-rigid) in some fixed dimension d if it is not globally rigid (resp. not rigid) but every graph on n vertices and with more than m edges is globally rigid (resp. rigid).

Theorem 4.1

Let G be a graph on n vertices and $d \ge 2$ a fixed dimension. Suppose that G is the unique maximally non-globally rigid graph on n vertices (up to isomorphism). Then G is weakly reconstructible in $\mathbb {C}^d$.

Proof

By Theorem 3.3 it suffices to show that $M_{d,G}$ uniquely determines G. Suppose that for some graph H with the same number of vertices as G we have $M_{d,G} = M_{d,H}$. Note that H cannot be globally rigid, for otherwise Theorems 1.5 and 3.4 (or, in the case when $n \le d+1$, the fact that H must be a complete graph) would imply that G is isomorphic to H, contradicting the condition that G is not globally rigid. It follows that H is a non-globally rigid graph on n vertices and with the same number of edges as G, so by the assumption that such a graph is unique we conclude that G and H must be isomorphic. $\square$

A similar result holds for non-rigid graphs.

Theorem 4.2

Let G be a graph on n vertices and $d \ge 1$ a fixed dimension. Suppose that G is the unique maximally non-rigid graph on n vertices (up to isomorphism). Then G is weakly reconstructible in $\mathbb {C}^d$.

Proof

The proof is analogous to that of Theorem 4.1. Suppose that $M_{d,G} = M_{d,H}$ for some graph H on n vertices. Then by Theorem 3.9 the rigidity matroids of G and H are isomorphic, so in particular H cannot be rigid either. By the condition on G, this implies that G and H are isomorphic, as desired. $\square$

Next we show that for every $n\ge 2$ and $d\ge 1$ there exists a unique maximally non-globally rigid graph in d dimensions. For $2 \le n \le d+1$ this follows from the fact that in these cases the only (globally) rigid graph on n vertices is $K_n$, and hence $K_n - e$ is the unique maximally non-globally rigid graph.

It remains to consider the case when $n \ge d+2$. In the next proof we shall use the coning operation. Given a graph G and a new vertex v, the cone graph $G * v$ is obtained by adding v to the vertex set of G and connecting it to every vertex of G. The following theorem establishes a connection between rigidity properties of a graph and its cone graph.

Theorem 4.3

[6, 27]    Let $d \ge 1$ be arbitrary. Then G is rigid (respectively globally rigid) in d dimensions if and only if the cone graph $G * v$ is rigid (resp. globally rigid) in $d+1$ dimensions.

Theorem 4.4

Let H be the extension of $K_{n-1}$ by a vertex of degree d, where $d \ge 1$ and $n \ge d+2$. Then H is the unique maximally non-globally rigid graph in d dimensions on n vertices.

Proof

H is not $(d+1)$-connected, so by Theorem 2.1 it is not globally rigid. Thus we need to show that any graph G with n vertices that is not isomorphic to H and has at least $\left( {\begin{array}{c}n\\ 2\end{array}}\right) - (n - 1 - d)$ edges, is globally rigid.

We prove this by induction on n (for all d). If $n = d+2$, then G must be the complete graph $K_{d+2}$, and thus it is globally rigid. Let $n=d+3$. For $d=1$ it is easy to check that the assertion holds. Otherwise, by the condition on the number of non-edges, G must have a vertex v such that every other vertex is connected to v. By induction $G-v$ is globally rigid in $d-1$ dimensions, thus G, as the cone graph of $G-v$, is globally rigid in d dimensions. Now suppose $n > d+3$. Since G is not isomorphic to H and it has at most $n-1-d$ non-edges, every vertex must have degree at least $d+1$. Moreover, there cannot be two adjacent vertices of degree $d+1$, since this would mean that G has at least $2\cdot (n-2-d)>n-1-d$ non-edges, which is a contradiction. Let v be a vertex of G with least degree. Now v must have degree at most $n-2$, for otherwise G would be complete. By the preceding observation, every vertex in $G-v$ has degree at least $d+1$. Thus $G-v$ has at most $n-2-d$ non-edges, and hence, by the induction hypothesis, $G-v$ is globally rigid. Since v has at least $d+1$ neighbors, G contains as a subgraph the extension of $G-v$ by a vertex of degree $d+1$, an operation which is known to preserve global rigidity. It follows that G is globally rigid, as desired. $\square$

Fig. 5

The only maximally non-rigid (a) and maximally non-globally rigid (b) graph in the plane on six vertices

The situation is very similar in the case of maximally non-rigid graphs. Here, with one exception, there is only one such graph for any n and d. For $n \le d+1$ the unique maximally non-rigid graph is $K_n - e$ as we noted earlier. The next case, when $n = d+2$, is more subtle. When $d \ge 2$ and $n= d + 2$ there exist two non-isomorphic graphs that can be obtained by deleting two edges from $K_{d+2}$. Neither of these graphs have enough edges to be rigid and hence they are both maximally non-rigid. This case happens to be the only exception, as shown by the next result.

Theorem 4.5

Let H be the extension of $K_{n-1}$ by a single vertex of degree $d-1$ for some $d \ge 1$ and $n \ge d+3$. Then H is the unique maximally non-rigid graph in d dimensions on n vertices.

Proof

It is easy to see that H is not rigid. Let G be a graph on n vertices and at least $\left( {\begin{array}{c}n\\ 2\end{array}}\right) - (n-d)$ edges that is not isomorphic to H. We show that G must be rigid. If G is complete, then this is clear. Since G and H are not isomorphic, every vertex of G must have degree at least d, and it is easy to check that there can be at most three vertices of degree exactly d. Moreover, if there are three such vertices, then $n=d+3$ and G is isomorphic to $K_{d+3}$ with a triangle removed, which is known to be rigid.

So suppose that there are at most two vertices of degree d in G. Two such vertices cannot be adjacent, since this would imply that G has at least $2\cdot (n-1-d) > n-d$ non-edges, a contradiction. It follows that, by adding an edge to G that connects two non-adjacent vertices with lowest degree, we obtain a graph with at most $n-1-d$ non-edges, in which every vertex has degree at least $d+1$; but by Theorem 4.4, such a graph is globally rigid, and hence by Theorem 2.1, G must be rigid. This completes the proof. $\square$

We note that, with some exceptions in the $d=1$ case, none of the weakly reconstructible graphs presented in this section are strongly reconstructible. We sketch the proof of this in the following. First, note that in both the maximally non-rigid and the maximally non-globally rigid graphs given by Theorems 4.4 and 4.5, every edge incident to the extension vertex is a d-bridge. Let G be such a graph. If there are at least two bridges, then Theorem 3.13 implies that permuting these edges non-trivially and leaving the rest of the edges in place gives a permutation $\psi$ of the edges of G under which $M_{d,G}$ is invariant. On the other hand, it is not difficult to show that $\psi$ is not induced by a graph automorphism, so by Theorem 3.4, G is not strongly reconstructible in $\mathbb {C}^d$. A similar argument works if there is only one bridge. This is an example of a more general phenomenon: in Sect. 5.5, we shall use essentially the same argument to prove that strongly reconstructible graphs (on at least four vertices and without isolated vertices) are redundantly rigid in two dimensions.

4.2 Graph Reconstruction and the Rigidity Matroid

The following theorem is a simple but useful consequence of Theorems 3.3 and 3.9.

Theorem 4.6

Let G be a graph that is uniquely (up to isomorphism) determined by its d-dimensional rigidity matroid among graphs on the same number of vertices. Then G is weakly reconstructible in $\mathbb {C}^d$.

Proof

By Theorem 3.3 it suffices to show that $M_{d,G}$ uniquely determines G. Suppose that $M_{d,G} = M_{d,H}$ for some graph H with the same order. By Theorem 3.9 this implies that the rigidity matroids of G and H are isomorphic. By our assumption it follows that G and H are isomorphic as well, as required. $\square$

Theorem 4.6 implies that every cycle $C_n$, which is the unique circuit of ${{\mathscr {R}}}_1$ on n edges, is weakly reconstructible in $\mathbb {C}^1$.

To close this section, we show that highly vertex-connected graphs are strongly reconstructible in $\mathbb {C}^1$ and $\mathbb {C}^2$. We shall use the facts that connected graphs are rigid in $\mathbb {R}^1$ (folklore) and 6-connected graphs are rigid in $\mathbb {R}^2$ (a result of Lovász and Yemini [21]). The following results show that, at least for $d=1,2$, the rigidity matroid ${{\mathscr {R}}}_d(G)$ of a sufficiently highly connected graph G uniquely determines the underlying graph. The one-dimensional result, due to Whitney, was an important tool in [10].

Theorem 4.7

[29]    Let G be a 3-connected graph and let H be a graph with no isolated vertices. Suppose that there is a bijection $\psi$ between the edge sets of G and H, which is an isomorphism between ${{\mathscr {R}}}_1(G)$ and ${{\mathscr {R}}}_1(H)$. Then there is a graph isomorphism between G and H which induces $\psi$.

The two-dimensional analogue is due to Jordán and Kaszanitzky [17]:

Theorem 4.8

Let G be a 7-connected graph and let H be a graph with no isolated vertices. Suppose that there is a bijection $\psi$ between the edge sets of G and H, which is an isomorphism between ${{\mathscr {R}}}_2(G)$ and ${{\mathscr {R}}}_2(H)$. Then there is a graph isomorphism between G and H which induces $\psi$.

Theorem 4.9

Let G be a graph. Then:

• (i) [10] If G is 3-connected, then G is strongly reconstructible in $\mathbb {C}^1$.

• (ii) If G is 7-connected, then G is strongly reconstructible in $\mathbb {C}^2$.

Proof

In both cases G is rigid in the respective dimension, which we will denote by d. Suppose that $m_{d,G}(p) = m_{d,H}(q)$ under some edge bijection $\psi$ for some graph H on the same number of vertices and edges as G, and some generic realizations $(G,p)$ and $(H,q)$. By Theorem 3.6 we have that $M_{d,G} = M_{d,H}$ and that H is rigid, so in particular it has no isolated vertices. Then by combining Theorems 3.9, 4.7, and 4.8, we can deduce that $\psi$ is induced by a graph isomorphism, as desired. $\square$

In fact, the families of graphs of Theorem 4.9 are not only rigid but globally rigid in the respective dimension. In the case of $\mathbb {R}^1$ this follows from the fact that a graph is globally rigid in $\mathbb {R}^1$ if and only if it is 2-connected. In $\mathbb {R}^2$ 6-connectivity implies global rigidity by a theorem of Jackson and Jordán [13]. Thus Theorem 4.9 (ii) is a special case of Theorem 1.5. Theorem 4.9 (i) was also proven in [10], and, in fact, it played a key role there in the proof of Theorem 1.5.

5 Reconstructibility in Low Dimensions

In this section we examine the cases of $d=1$ and $d=2$ in more detail. In these dimensions the structure of the rigidity matroid is well understood, which turns out to be a useful tool in studying graph reconstructibility. We shall give a characterization of weakly reconstructible graphs in $\mathbb {C}^1$ that are not 2-connected. On the other hand, we will show that the problem of deciding whether a 2-connected (but not 3-connected) graph is weakly reconstructible in $\mathbb {C}^1$ is polynomially equivalent to the graph isomorphism problem. In the two-dimensional case we describe the so-called bridge invariant graphs and using this result characterize the non-redundant rigid weakly reconstructible graphs in $\mathbb {C}^2$. Finally, we shall provide a complete characterization of strongly reconstructible graphs in $\mathbb {C}^1$ and $\mathbb {C}^2$. We start with a result which holds in both one and two dimensions.

5.1 Relaxing the Condition on the Order of H

We consider the following question: is it possible to drop or weaken the assumption in our reconstructibility notions saying that the length-equivalent frameworks $(G,p)$ and $(H,q)$ must have the same order? In this context it is natural to keep the assumption that $(H,q)$ is generic, for otherwise we cannot expect positive results: any edge measurement sequence can be realized by a forest of the appropriate size (but this realization may not be generic).

In this setting, we show that if $d \le 2$ and the rigidity matroid of G in d dimensions is connected, then we can drop the condition on the order of H. It is known that the rigidity matroid of globally rigid graphs (of size at least $d+2$) is connected in dimensions $d=1,2$. Thus this result allows us to strengthen Theorems 4.9 (i) and 1.1 from [10] in one and two dimensions, respectively.

We shall need the fact that if the one-dimensional (resp. two-dimensional) rigidity matroid of a graph G (without isolated vertices) is connected, then G is rigid in $\mathbb {R}^1$ (resp. in $\mathbb {R}^2$). In $\mathbb {R}^1$ this follows from the fact that ${\mathscr {R}}_{1}(G)$ is isomorphic to the graphic matroid of G. A proof for the two-dimensional case can be found in [13, Lem. 3.1].

Theorem 5.1

Suppose that $1\le d \le 2$ and let G be a graph for which ${\mathscr {R}}_{d}(G)$ is connected. Let $(G,p)$ be a weakly reconstructible generic realization of G in $\mathbb {C}^d$ and suppose that $(G,p)$ is length-equivalent to some generic d-dimensional framework $(H,q)$ under some edge bijection $\psi$, where the order of H may be different from that of G. Then G and H are isomorphic after deleting the isolated vertices from both graphs. Furthermore, if $(G,p)$ is strongly reconstructible, then $\psi$ is induced by a graph isomorphism.

Proof

We can suppose that neither G nor H has isolated vertices by deleting any such vertex. Note that this deletion preserves the reconstructibility property of $(G,p)$. By using the argument from the proof of Theorem 3.3, we can use the equality $m_{d,G}(p) = m_{d,H}(q)$ to deduce that $M_{d,G} = M_{d,H}$, and consequently by Theorem 3.9 the d-dimensional rigidity matroids of G and H are isomorphic. In particular ${\mathscr {R}}_{d}(H)$ is connected as well. As we noted above, the fact that their rigidity matroids are connected implies that both G and H are rigid, so

$$\begin{aligned} d\,|V(G)| - \left( {\begin{array}{c}d\\ 2\end{array}}\right) = \dim M_{d,G}=\dim M_{d,H}=d\,|V(H)| - \left( {\begin{array}{c}d\\ 2\end{array}}\right) , \end{aligned}$$

and thus $|V(G)| = |V(H)|$. The claim then follows from the corresponding reconstructibility property of $(G,p)$. $\square$

The following reformulation of Theorem 5.1 will be useful later on.

Corollary 5.2

Suppose that $1\le d \le 2$ and let G be a graph for which ${\mathscr {R}}_{d}(G)$ is connected. Suppose that G is weakly (resp. strongly) reconstructible in $\mathbb {C}^d$. Then any graph $G'$ that is obtained by adding some isolated vertices to G is weakly (resp. strongly) reconstructible in $\mathbb {C}^d$.

Another consequence of Theorem 5.1 is the following result about the reconstructibility of globally rigid subgraphs in low dimensions.

Corollary 5.3

Suppose that $1 \le d \le 2$ and let (G, p) and (H, q) be generic frameworks in $\mathbb {C}^d$ that are length-equivalent under the edge bijection $\psi$. Let $G_0=(V_0,E_0)$ be a globally rigid subgraph of $G=(V,E)$ and let $H_0$ denote the subgraph of H induced by $\psi (E_0)$. Then $\psi |_{E_0}$ is induced by an isomorphism $\varphi :G_0 \rightarrow H_0$ and the frameworks $(G_0,p|_{V_0})$ and $\bigl (H_0,q|_{V(H_0)}\circ \varphi \bigr )$ are congruent.

Proof

By Theorem 1.5, $G_0$ is strongly reconstructible, and, as noted previously, ${\mathscr {R}}_d(G_0)$ is connected. Thus, Theorem 5.1 applies to $(G_0,p|_{V_0})$ and $\bigl (H_0,q|_{V(H_0)}\bigr )$, giving us that $\psi |_{E_0}$ is induced by an isomorphism $\varphi :G_0 \rightarrow H_0$. Now the length-equivalence of (G, p) and (H, q) implies that $(G_0,p|_{V_0})$ and $\bigl (H_0,q|_{V(H_0)} \circ \varphi \bigr )$ are equivalent, but since $G_0$ is globally rigid, this means that they are congruent as well. $\square$

5.2 Weak Reconstructibility in $\mathbb {C}^1$

Next, we turn our attention to the $d=1$ case. As mentioned before, the one-di mensional rigidity matroid of a graph coincides with its graphic matroid. We say that two graphs are cycle isomorphic if their graphic matroids are isomorphic.

We shall use a characterization of cycle isomorphism due to Whitney [29]. In order to describe his result, we need to introduce the following operations on graphs. The 1-sum of two graphs (or two distinct connected components of a graph) G and $G'$ along the vertices $x\in V(G)$ and $x'\in V(G')$ is the graph obtained by identifying (or “gluing”) these vertices. Vertex cutting is the reverse operation, i.e., separating the graph into two (sub)graphs along a cut-vertex. We say that a pair of subgraphs $(G_1,G_2)$ of G is a 2-separation of G if $G_1$ and $G_2$ have exactly two vertices x, y in common, and the edge sets of $G_1$ and $G_2$ form a bipartition of the edge set of G. A 2-switch operation along such a 2-separation produces a graph obtained by identifying x and y in $G_1$ with y and x, respectively, in $G_2$.

We say that the graphs G and H are 2-isomorphic if one can be reached from the other by applying a series of the 1-sum, vertex cut, and 2-switch operations. It is easy to see that 2-isomorphic graphs have isomorphic graphic matroids, since the aforementioned operations preserve (the edge sets of) cycles. Whitney showed that the converse is true as well.

Theorem 5.4

[29]    Let G and H be graphs. Then G and H are cycle isomorphic if and only if they are 2-isomorphic.

This characterization of cycle isomorphism implies the converse of Theorem 3.9 in one dimension.

Theorem 5.5

Let G and H be graphs with the same order. Then $M_{1,G} = M_{1,H}$ if and only if G and H are cycle isomorphic.

Proof

Necessity follows from Theorem 3.9. For the other direction it suffices to show, according to Theorem 5.4, that the vertex cutting, 1-sum, and 2-switch operations preserve the one-dimensional measurement variety. This follows from the fact that they preserve the edge measurements of real frameworks, since those form a Zariski-dense set in the measurement variety⁶. $\square$

In fact, the previous argument shows that the three aforementioned operations preserve the measurement variety in any dimension $d\ge 1$. Theorem 5.5 together with Theorem 3.3 imply that a graph G is weakly reconstructible in one dimension if and only if ${\mathscr {R}}_1(G)$ determines G up to isomorphism (among graphs with the same order). This immediately yields the following characterization of weak reconstructibility in $\mathbb {C}^1$. As a shorthand, we refer to the operation consisting of cutting along a cut-vertex and then taking the 1-sum of the resulting two components along some pair of vertices as the reattachment operation.

Corollary 5.6

A connected graph G is weakly reconstructible in $\mathbb {C}^1$ if and only if it is invariant under the reattachment and 2-switch operations, that is, if these operations always result in graphs isomorphic to G.

With this result in hand it seems feasible to characterize weakly reconstructible graphs in $\mathbb {C}^1$. As we have seen in Theorem 4.9, 3-connected graphs are strongly reconstructible in $\mathbb {C}^1$. On the other hand, the next theorem describes weakly reconstructible graphs that are not 2-connected. We shall need the following simple observation. Recall that a graph G is called vertex-transitive if for every pair u, v of vertices there is an automorphism of G which maps u to v.

Lemma 5.7

Let C and D be connected graphs. Then the graphs obtained as the 1-sum of C and D are pairwise isomorphic if and only if C and D are both vertex-transitive.

We shall use the fact that if G is a connected vertex-transitive graph then G is k-regular for some integer k, and the vertex-connectivity of G is strictly greater than 2k/3 (see [26]).

Theorem 5.8

Let G be a graph that is not 2-connected and has at least two edges. Then G is weakly reconstructible in $\mathbb {C}^1$ if and only if one of the following holds:

• (i) G is isomorphic to a 2-connected, weakly reconstructible graph H plus some isolated vertices.

• (ii) G is isomorphic to the 1-sum of two connected vertex-transitive graphs.

Proof

We first show necessity. Suppose first that G is not connected. Then G has at most one connected component that is not a single vertex, for otherwise we could take the 1-sum of two connected components of size at least two and add a new isolated vertex to obtain a graph $G'$ that is cycle isomorphic, but not isomorphic to G. Since G has at least two edges, it follows that it has a single connected component H with at least two edges. Now if H is not 2-connected, then cutting it at a cut-vertex and removing one of the isolated vertices of G results in a graph that contradicts the weak reconstructibility of G. Similarly, if H is not weakly reconstructible then we can replace it with a cycle isomorphic but not isomorphic graph $H'$, which, again, contradicts our assumption on G. Now suppose that G is connected but not 2-connected. Note that G must have exactly two 2-blocks, since otherwise we could obtain a graph from it with a different block-cut-vertex tree⁷ using the reattachment operation. Then Lemma 5.7 applies to the two 2-blocks.

Next, we show sufficiency. In the first case this follows from Corollary 5.2. In the second case denote the 2-blocks of G by C and D. Note that since C and D are vertex-transitive, each of them is either a single edge or is 2-connected. Thus G has exactly one cut-vertex. Then by Lemma 5.7, G is invariant under the reattachment operation. In fact, a connected vertex-transitive graph is either an edge or a cycle, or it is 3-connected. It is easy to verify that in each of these cases a 2-switch of G results in an isomorphic graph. $\square$

Thus the only case left open in the characterization of weakly reconstructible graphs in $\mathbb {C}^1$ is when the graph is 2-connected but not 3-connected. Note that these graphs are globally rigid in one dimension, and thus this is, in a sense, the case left open by Theorems 1.1 and 4.9. It turns out that this case is much harder than the others.

We shall denote the problem of deciding whether a given input graph is weakly reconstructible in $\mathbb {C}^1$ by WR-1. GI stands for the graph isomorphism problem, i.e., deciding whether two given graphs H and $H'$ are isomorphic. Similarly, GI-3 denotes the graph isomorphism problem restricted to the family of 3-connected graphs. We shall use the fact that GI is polynomially reducible GI-3, an easy consequence of the result that it is reducible to the isomorphism problem within the family of so-called k-trees. See [19] for definitions and the proof of this statement.

Theorem 5.9

GI-3 (and thus GI is polynomially reducible to WR-1.

Proof

Given two 3-connected graphs H and $H'$, and two triples of vertices $x,x_1,x_2 \in V(H)$ and $x',x'_1,x'_2 \in V(H')$, we shall construct a graph G (of size polynomial in the sizes of H and $H'$) with the following property:

This allows us to test the isomorphism of H and $H'$ using polynomially many queries to an oracle of WR-1 by simply iterating over all possible choices of $x, x_1, x_2$ and $x', x_1', x_2'$.

The construction goes as follows. First, connect $x_i$ and $x'_i$ by an edge for each $i=1,2$. Let K be a complete graph of size $|V(H)|+|V(H')|+1$ with distinct vertices y and $y'$. Remove an edge of K that is incident to y, but not to $y'$. Finally let G be the graph obtained by identifying x with y and $x'$ with $y'$. See Fig. 6.

Claim 5.10

G has property ($*$) defined above.

For a proof of this claim, see Appendix A.

Fig. 6

The graph G constructed in the proof of Theorem 5.9

5.3 Bridge Invariant Graphs

We call a rigid graph G non-redundant rigid if G has at least one bridge, that is, $G-e$ is not rigid for some edge e. Although there exist weakly reconstructible rigid graphs which are non-redundant (see Sect. 4.1), the following argument from [10, Rem. 7.4] suggests that such graphs are rare.

First we define an operation that we may perform on a rigid graph G. Suppose that G has at least $d+2$ vertices and let e be a bridge in ${{\mathscr {R}}}_d(G)$. Then there is another edge $e'$ that we can add to the flexible (i.e., non-rigid) graph $G-e$ to obtain a graph $H=G-e+e'$ which is again rigid.⁸ In this case we say that H is obtained from G by a bridge replacement operation. A graph G is called bridge invariant if every sequence of bridge replacement operations starting from G leads to a graph isomorphic to G. Notice that if H is obtained from G by a bridge replacement operation then we have $M_{d,G}=M_{d,G-e}\oplus \mathbb {C}= M_{d,H}$ by Theorem 3.13. Thus every non-redundant weakly reconstructible graph must be bridge invariant.

In this subsection we give a complete characterization of bridge invariant graphs in two dimensions. Based on this structural result we shall be able to obtain the complete list of non-redundant rigid weakly reconstructible graphs in $\mathbb {C}^2$. We shall use the following two simple combinatorial lemmas. Their proofs are given in Appendix B. A degree-2-extension of a graph G is a graph obtained from G by adding a new vertex v and two edges incident with v.

Lemma 5.11

Let G be a graph on n vertices with at least one edge. Then exactly one of the following holds:

• (i) there exist two non-isomorphic degree-2-extensions of G,

• (ii) G is isomorphic to $K_n$.

The next lemma is an analogue of Lemma 5.7.

Lemma 5.12

Let G be a graph with two connected components C, D. Then the graphs obtained from G by adding a new edge from C to D are pairwise isomorphic if and only if C and D are both vertex-transitive.

5.3.1 Bridge Invariant Graphs in the Plane

We need to recall some facts concerning generic rigidity properties of graphs in two dimensions. We say that a pair of vertices $\{u,v\}$ in a framework (G, p) is linked in (G, p) if $r_d(G + uv) = r_d(G) + 1$. From the definition it is clear that this is a generic property. A compact characterization of all linked pairs in ${\mathscr {R}}_2(G)$ can be deduced as follows. It is known that $\{u,v\}$ is linked in a generic two-dimensional framework (G, p) if and only if G has a rigid subgraph H with $\{u,v\}\subseteq V(H)$. We define a rigid component of G to be a maximal rigid subgraph of G. It is well known (see e.g. [13, Cor. 2.14]), that any two rigid components of G intersect in at most one vertex. Furthermore, for every triple of pairwise intersecting rigid components there exists a vertex that belongs to each of them. It is also known that the rigidity matroid of a graph is the direct sum of the rigidity matroids of its rigid components (see e.g. [16]).

Recall that an edge e of a rigid graph G is a bridge if and only if $G-e$ is not rigid, that is, $r_d(G-e)=r_d(G)-1$. By summarizing the above arguments we obtain the following observation about the bridge replacement operation.

Lemma 5.13

Suppose that the edge e is a bridge in the rigid graph G. Let $G'=G-e$. Then $G'+f$ is rigid for some edge $f=uv$ if and only if there is no rigid component C of $G'$ with $\{u,v\}\subseteq V(C)$.

We can now prove the main result of this subsection. Recall that the cone graph of a graph G is obtained from G by adding a new vertex v and new edges from v to every vertex of G.

Theorem 5.14

Let G be a non-redundant rigid graph in $\mathbb {R}^2$ (equivalently, in $\mathbb {C}^2$) on $n\ge 3$ vertices. Then G is bridge invariant if and only if it satisfies one of the following properties:

• (i) G is isomorphic to a degree-2-extension of $K_{n-1}$,

• (ii) G is the cone graph of a connected graph obtained from two disjoint vertex-transitive graphs on at least three vertices by adding an edge e.

Proof

We first prove sufficiency. Suppose that (i) holds. Then either G is isomorphic to $K_3$ or $K_4-e$ (in which cases every edge of G is a bridge), or G has exactly two bridges (edges incident with the degree-2 vertex). In each of these cases it is easy to see that G is bridge invariant. Next, suppose that (ii) holds. Let $H_1,H_2$ be disjoint vertex-transitive graphs and let v be the extra vertex in their cone graph. Recall that a vertex-transitive graph on at least three vertices must be 2-connected. Thus (by Theorem 4.3) the cone graph of $H_i$ is globally rigid in $\mathbb {R}^2$ for $i=1,2$. We can use this fact to deduce that the only bridge in G is e. Furthermore, if $G-e+f$ is rigid, then f is not incident with v. Hence, every bridge replacement operation corresponds to adding a new edge to the disjoint union of $H_1$ and $H_2$, and by Lemma 5.12 these result in isomorphic graphs. Thus G is bridge invariant, as desired.

Now we prove necessity. Suppose that G is a bridge invariant graph on at least three vertices. Since G is rigid, every vertex in G has degree at least two. First we consider the case when G has a vertex v of degree exactly two. Then G is a degree-2-extension of a smaller rigid graph $H=G-v$. Moreover, every degree-2-extension $H'$ of H is a rigid graph, in which the edges incident with the new degree-2 vertex are both bridges. Thus every degree-2-extension of H can be obtained by applying a sequence of bridge replacement operations starting with G. Therefore Lemma 5.11 implies that (i) holds.

In the rest of the proof we shall assume that every vertex in G has degree at least three. Our aim now is to show that (ii) holds. Fix a bridge e in G for which the order of the largest rigid component C of $G-e$ is as large as possible. The outline of the rest of the proof is as follows. First, we show that every bridge of $G-e$ is in C. Then we use this fact to show that $G-e$ must have exactly two rigid components. After this, it is not difficult to show that the common vertex of the two rigid components of $G-e$ is connected to every other vertex, and then we shall be able to use Lemma 5.12 to finish the proof.

Lemma 5.15

Every bridge of $G-e$ is in C.

Proof

Suppose, for a contradiction, that there is a bridge h of $G-e$ which is not an edge of C. Note that h is a bridge in G, too.

We claim that there is an edge wy with $w\in V(C)$, $y\notin V(C)$ which is different from h. Since G is rigid and has at least three vertices, $G-e$ is connected. Thus C is incident with at least one other rigid component of $G-e$. If it is incident with at least two rigid components or it is incident with a rigid component containing at least three vertices, then we can easily identify the required edge wy. It remains to consider the case when there is a unique rigid component incident with C, which induces a single edge h. However, in this case either there are no more rigid components in $G-e$ at all (which shows that G has a vertex of degree two, contradicting our assumption), or $G-\{e,h\}$ is disconnected. The latter case is also impossible, since a rigid graph of minimum degree at least three is 3-edge-connected (a corollary of [13, Lem. 2.6]). This completes the proof of the claim.

Let f be a new edge connecting a vertex $x\in V(C)\setminus \{w\}$ and y. Since no rigid component of $G-e$ contains the pair $\{x,y\}$, the graph $G'=G-e+f$ is rigid. So $G'$ is obtained from G by a bridge replacement operation. Note that h is a bridge in $G'$, too. Furthermore, $V(C)\cup \{y\}$ induces a rigid graph in $G'$. It follows that the largest rigid component of $G'-h$ is strictly larger than C, which shows that G and $G'$ are not isomorphic. Hence G is not bridge invariant, a contradiction. $\square$

Lemma 5.16

$G-e$ has exactly two rigid components.

Proof

Suppose to the contrary that $G-e$ has at least three rigid components. Let K be a rigid component of $G-e$. Our first observation is that there exists a rigid component L of $G-e$ not incident with K. Indeed, for otherwise, as the rigid components incident with K have no vertices in common in $V(G)-V(K)$, we have $r_2(G-e)\le 2\,|V|-3-(s-1)\le 2\,|V|-5$, where s is the number of rigid components of $G-e$, contradicting the fact that G is rigid.

The graph $G-e$ may or may not contain bridges. First we consider the case when C contains a bridge h. By the previous observation there exists a rigid component F of $G-e$ not incident with C. Let D be a rigid component incident with F. Since C contains all bridges of $G-e$, D has at least three (in fact at least four) vertices. Thus there exists some vertex x in $D-V(C)-V(F)$. Now consider two different edges that we can add to $G-e$ to make it rigid: let f be an edge from an end-vertex of h to x for which $G-e+f$ is rigid (note that at least one of the end-vertices of h must have this property), and let g be an edge from x to a vertex of $F-V(D)$. Each of these edges makes $G-e$ rigid and hence can be used in a bridge replacement operation with edge e. Note that f (resp. g) is a bridge in $G-e+f$ (resp. $G-e+g$). The key observation is that the numbers of connected components of the subgraph induced by the bridges of $G-e+f$ and that of $G-e+g$ are different. Hence these graphs are not isomorphic and G is not bridge invariant, a contradiction.

Next, consider the case when C contains no bridges, that is, when e is the only bridge in G. We claim that there is a rigid component D of $G-e$ which has a vertex d that belongs to no other rigid component of $G-e$. Let $H_1,H_2,\dots ,H_q$ denote the rigid components of $G-e$ and let $n_i=|V(H_i)|$. Since $G-e$ has no bridges, every edge of $G-e$ is in some circuit of ${{\mathscr {R}}}_2(G)$. Thus, since every circuit is rigid and has at least four vertices, we have that $n_i\ge 4$ for $1\le i\le q$. If every vertex belongs to at least two rigid components, then we have $\sum _{i=1}^q n_i \ge 2\,|V|$. Let us choose a base $B_i$ in each rigidity matroid ${{\mathscr {R}}}_2(H_i)$. Using the above inequalities we have

$$\begin{aligned} \left| \,\bigcup _{i=1}^q B_i\right| =\sum _{i=1}^q |B_i|=\sum _{i=1}^q (2n_i-3)=2\sum _{i=1}^q n_i - 3q\ge 2\,|V|+ 4q - 3q\ge 2\,|V|. \end{aligned}$$

Since ${{\mathscr {R}}}_2(G-e)$ has rank $2\,|V|-4$, this implies that $\bigcup _{i=1}^q B_i$ contains a circuit, contradicting the fact that the $B_i$’s are bases for the ${{\mathscr {R}}}_2(H_i)$’s and ${{\mathscr {R}}}_2(G-e)=\bigoplus _{i=1}^q{{\mathscr {R}}}_2(H_i)$. This proves the claim.

By the first observation of the proof there is a rigid component F of $G-e$ not incident with D. We need one more observation: there is a vertex z of F that is not incident with D. This follows from the fact that F has at least four vertices, the edges from D to F are pairwise disjoint, and three disjoint edges from D to F would make $V(D)\cup V(F)$ induce a rigid subgraph in $G-e$. Let wy be an edge leaving D and let xw be an edge in D.

Now consider two different edges that we can add to $G-e$ to make it rigid: let f be an edge from x to y, and let g be an edge from d to z. Each of these edges makes $G-e$ rigid and hence can be used in a bridge replacement operation with edge e. Note that f (resp. g) is a bridge in $G-e+f$ (resp. $G-e+g$). The key observation is that there is only one bridge in these graphs, but in one of them it belongs to a triangle (on vertices x, w, y), while in the other it does not (by the choice of d and z). Hence these graphs are not isomorphic and G is not bridge invariant, a contradiction. $\square$

Fig. 7

a The first case of Lemma 5.16. b The second case of Lemma 5.16

Thus $G-e$ has exactly two rigid components, C and D. Let w be their common vertex. Note that w is a cut-vertex in $G-e$, and that e is not incident with w in G. If w is not connected to every other vertex, then we can obtain two graphs from G by different bridge replacement operations, so that in one of them the edge connecting $C-w$ and $D-w$ belongs to a triangle, while it does not belong to a triangle in the other. Thus the numbers of triangles in the two graphs are different and hence they are not isomorphic. So we may assume that w is connected to every other vertex. There is no other vertex with this property, for otherwise one of the two components is a single edge and G has a vertex of degree two, a contradiction. So every graph obtained by a bridge replacement operation from G is the cone of a connected graph obtained from the connected graphs $C-w,D-w$ by adding an edge. Now Lemma 5.12 implies that (ii) holds. $\square$

It is easy to obtain bridge invariant graphs in $\mathbb {R}^3$ and in higher dimensions by coning the two-dimensional examples. However, not all bridge invariant graphs arise in this way. For example, the rigid graph obtained from a double banana graph (that is, the 2-sum of two $K_5$’s) by adding an edge is bridge invariant but it is not a cone: it has no vertex that is connected to every other vertex. Further examples can be obtained by taking two disjoint graphs $G_1,G_2$ so that $G_i$ is obtained from a connected vertex-transitive graph by two successive coning operations, $i=1,2$, taking the 2-sum of $G_1$ and $G_2$ along the edges that connect the pairs of coning vertices, and then adding a rigidifying edge.

5.4 Weak Reconstructibility in $\mathbb {C}^2$

Using the previous characterization of bridge-invariant graphs in the plane we can deduce the following theorem concerning non-redundant rigid graphs that are weakly reconstructible in $\mathbb {C}^2$.

Theorem 5.17

Let G be a non-redundant rigid graph in $\mathbb {R}^2$ (equivalently, in $\mathbb {C}^2$). Then G is weakly reconstructible in $\mathbb {C}^2$ if and only if G can be obtained by taking the 1-sum of two complete graphs $K_r$ and $K_s$, and then adding an edge, where $r,s\ge 2$, and if $s=3$ (resp. $r=3$) then $r=2$ (resp. $s=2$) holds.

Proof

Suppose that G is weakly reconstructible. As we observed earlier, G must be bridge invariant. Thus Theorem 5.14 implies that either G is isomorphic to a degree-2 extension of a complete graph (in which case it can be obtained by taking the 1-sum of $K_{n-1}$ and $K_2$ and then adding an edge) or G is the cone graph of a connected graph obtained from two disjoint vertex-transitive graphs K, L, on at least three vertices, by adding an edge e.

Suppose, for a contradiction, that K is not complete. Consider $G-e$ and denote its cut-vertex by v (along which the cone of K and the cone of L is merged). Note that v is connected to every other vertex. Let $H'$ be the graph obtained by taking the 1-sum of the cones of K and L along a vertex of K. Let H be a rigid graph obtained by adding an appropriate edge to $H'$. Since K is regular and non-complete, H has no vertex that is connected to every other vertex of H. Hence H is not isomorphic to G. But $M_{2,G}=M_{2,H}$ by Lemma 3.11 and Theorem 3.13, a contradiction. Thus K, L are complete graphs and hence G can be obtained by taking the 1-sum of two complete graphs $K_r$ and $K_s$, $r,s\ge 2$, and then adding an edge e. If $s=3$, say, then the edges of $K_s$ (plus e) are all bridges and then it is easy to construct a non-isomorphic graph H with $M_{2,G}=M_{2,H}$, unless $r=2$.

Conversely, suppose that $G-e = G'$ can be obtained by taking the 1-sum of two complete graphs $K_r$ and $K_s$ as in the statement. If $s=2$ or $r=2$ then G is weakly reconstructible by Theorems 4.1 and 4.4. So we may assume that $r,s\ge 4$. It is sufficient to show that $G'$ is weakly reconstructible (from the list of edge lengths obtained by removing the length of e), since any edge added to a graph isomorphic to $G'$ yields a graph isomorphic to G. Suppose that $H'$ is another graph on $r+s-1$ vertices with $M_{2,G'}=M_{2,H'}$. Since $K_r$ and $K_s$ have connected rigidity matroids, Corollary 5.2 implies that $H'$ has both of them as edge-disjoint subgraphs. But the only such graph on $r+s-1$ vertices is the 1-sum of $K_r$ and $K_s$, so $H'$ and $G'$ are indeed isomorphic. Therefore G is weakly reconstructible, too. $\square$

It is not unreasonable to expect that our methods may lead to a complete characterization of weakly reconstructible rigid graphs in $\mathbb {C}^2$. By our results above it remains to consider the redundantly rigid graphs. Furthermore, since every 3-connected and redundantly rigid graph is globally rigid in $\mathbb {R}^2$ by a result of Jackson and Jordán [13], and globally rigid graphs are strongly (and thus weakly) reconstructible by Theorem 1.5, we can restrict our attention to redundantly rigid graphs with at least one separating vertex pair. However, this case turns out to be similar to the weak reconstructibility of 2-connected, but not 3-connected graphs in $\mathbb {C}^1$. In particular, the following analogue of Theorem 5.9 holds in the 2-dimensional case. Let WR-2 denote the decision problem of recognizing graphs that are weakly reconstructible in $\mathbb {C}^2$, and let GI-6 denote the graph isomorphism problem restricted to the family of 6-connected graphs.

Theorem 5.18

GI-6 is polynomially reducible to WR-2.

The proof is based on a similar construction to the one seen in Theorem 5.9; we omit the details.

5.5 Strong Reconstructibility in $\mathbb {C}^1$ and $\mathbb {C}^2$

we consider strong reconstructibility in more detail. We show that (under some mild assumptions) a graph that is strongly reconstructible in $\mathbb {C}^d$ for some $d \ge 1$ must be 3-connected. Moreover, ${\mathscr {R}}_d(G)$ has no bridges. These results allow us to show that in $\mathbb {C}^1$ and $\mathbb {C}^2$, Theorems 4.9 (i) and 1.5 essentially characterize strongly reconstructible graphs (apart from a few exceptional cases).

Observe that any graph on at most three vertices is strongly reconstructible in $\mathbb {C}^d$ for any $d \ge 1$. This follows from the simple facts that any such graph is determined up to isomorphism by the number of its edges and vertices, and any permutation of the edges of such a graph is induced by a graph automorphism. Thus, in the rest of this subsection we shall only consider graphs on at least four vertices.

Theorem 5.19

Let G be a strongly reconstructible graph in $\mathbb {C}^d$ on at least four vertices and without isolated vertices. Then G is 3-connected.

Proof

Suppose that G is not 3-connected. If G is disconnected, then taking the 1-sum of two connected components and adding a new isolated vertex yields a non-isomorphic graph with the same measurement variety, thus G is not strongly (or indeed weakly) reconstructible.

Suppose now that G has a cut-vertex. As in the proof of Theorem 5.8, G must have exactly two 2-blocks, for otherwise we could rearrange its block-cut-vertex tree to obtain a non-isomorphic graph with the same measurement variety (here we use Lemma 3.11). Denote these blocks by C and D, so that G is the 1-sum of these graphs along the vertices v and $v'$. By size considerations, at least one of these 2-blocks, say C, must have at least three vertices. It follows that there exist two distinct neighbors u and w of v in C. Now consider the 1-sum of C and D along u and $v'$. This graph has the same measurement variety as G. However, the natural edge bijection between the two graphs (that is, the one mapping each 2-block identically to the corresponding 2-block) is not induced by a graph isomorphism, for such an isomorphism would have to map the cut-vertex (call it v) of G to u, while also mapping the edge wv to itself, a contradiction.

Finally, suppose that G has a 2-separation $(G_1,G_2)$ with common vertices u and v. As we saw in the proof of Theorem 5.5, the 2-switch operation along $(G_1,G_2)$ yields a graph $G'$ with $M_{d,G} = M_{d,G'}$. Again, the natural edge bijection between these graphs is not induced by a graph isomorphism: such an isomorphism would have to send some edge wv of $G_2$ to the edge wu of $G'$, while also sending some edge $w'v$ of $G_1$ to $w'v$ of $G'$, which is impossible.⁹$\square$

Combining Theorems 5.19 and 4.9 (i) we obtain the following characterization of strong reconstructibility in $\mathbb {C}^1$.

Theorem 5.20

Let G be a graph on at least four vertices and without isolated vertices. Then G is strongly reconstructible in $\mathbb {C}^1$ if and only if it is 3-connected.

The following theorem gives another necessary condition for strong reconstructibility in $\mathbb {C}^d$.

Theorem 5.21

Let G be a strongly reconstructible graph in $\mathbb {C}^d$ on at least $d+2$ vertices and without isolated vertices. Then ${\mathscr {R}}_d(G)$ has no bridges.

Proof

Suppose for contradiction that ${\mathscr {R}}_d(G)$ has a bridge e and let $G' = G-e$. As noted in Sect. 5.3, there is another edge f that can be added to $G'$ such that $G'' = G-e+f$ is rigid. Note that by Theorem 5.19 we have that G is 3-connected, so $G'$ is connected (indeed, 2-connected).

By Theorem 3.13 we have $M_{d,G} = M_{d,G'} \oplus \mathbb {C}= M_{d,G''}$ under the edge bijection $\psi :E(G) \rightarrow E(G'')$ that sends e to f and leaves the rest of the edges in place. Since G is strongly reconstructible in $\mathbb {C}^d$, Theorem 4.9 now implies that $\psi$ is induced by a graph isomorphism $\varphi :V(G) \rightarrow V(H)$. Now $\varphi$ is an automorphism of $G'$ that leaves every edge in place. We claim that such an automorphism must be the identity map. Indeed, for any vertex v with distinct neighbors u, w, we have that $\{v\}=\{u,v\}\cap \{w,v\}=\{\varphi (u),\varphi (v)\}\cap \{\varphi (w),\varphi (v)\}=\{\varphi (v)\}$, so $\varphi$ leaves each vertex of degree at least two in place. But in a connected graph on at least three vertices every edge has an end-vertex with degree at least two. Thus $\varphi$ leaves each edge in place and leaves at least one end-vertex of each edge in place, so it must be the identity map. But this is a contradiction, since we assumed that $\varphi$ induces $\psi$, which maps e to f. $\square$

We again recall a theorem from [13] which says that every 3-connected and redundantly rigid graph is globally rigid in $\mathbb {R}^2$, and its refined version, which says that every 3-connected graph G for which ${\mathscr {R}}_2(G)$ has no bridges is globally rigid in $\mathbb {R}^2$, see [15, Thm. 5.1]. This result, combined with Theorems 1.5, 5.19, and 5.21 gives the following characterization of strongly reconstructible graphs in $\mathbb {C}^2$.

Corollary 5.22

Let G be a graph on at least four vertices and without isolated vertices. Then G is strongly reconstructible in $\mathbb {C}^2$ if and only if it is globally rigid in $\mathbb {R}^2$.

Note that the removal of isolated vertices preserves strong reconstructibility. Thus by combining the previous theorem with Corollary 5.2 we obtain a complete description of graphs that are strongly reconstructible in $\mathbb {C}^2$: they are either isomorphic to $K_3$ or the path of length two, or they are isomorphic to some globally rigid graph, other than $K_3$, plus some (possibly zero) isolated vertices.

6 Real Reconstructibility

In this section we examine some aspects of weak and strong reconstructibility in $\mathbb {R}^d$, that is, within the family of real frameworks. To avoid confusion, throughout this section we shall refer to the weak (respectively strong) reconstructibility of a framework (G, p) in $\mathbb {C}^d$ (as defined in Definitions 1.2 and 1.3) as weak reconstructibility in $\mathbb {C}^d$ (resp. strong reconstructibility in $\mathbb {C}^d$). In contrast, we say that a framework (G, p) in $\mathbb {R}^d$ is weakly reconstructible in $\mathbb {R}^d$ if for any generic length-equivalent real framework (H, q), where H has the same order as G, we have that H is isomorphic to G. Strong reconstructibility in $\mathbb {R}^d$ is defined analogously by replacing $\mathbb {C}^d$ in Definition 1.3 by $\mathbb {R}^d$.

In the following we prove that in one dimension, weak and strong reconstructibility in $\mathbb {R}^1$ coincide with their complex counterparts. This is not true for weak reconstructibility in higher dimensions: we shall give an example showing that for $d \ge 2$, weak reconstructibility in $\mathbb {R}^d$ is not a generic property. A simple but useful observation is that in one dimension, we can obtain length-equivalent real realizations from complex ones by taking the real part of each coordinate.

Lemma 6.1

Let (G, p) and (H, q) be length-equivalent frameworks in $\mathbb {C}^1$. Then $(G, {\text {Re}}p)$ and $(H, {\text {Re}}q)$ are length-equivalent real frameworks, where ${\text {Re}}p$ is the framework obtained by taking the real part of each coordinate of p.

Proof

This follows from the fact that for a complex number z we have $2 \cdot ({{\text {Re}}z})^2 = {\text {Re}}z^2 + \Vert {z^2}\Vert$. This implies that in one dimension, the length of the real part of an edge is completely determined by its complex length. $\square$

We remark that Lemma 6.1 does not tell us whether the real frameworks obtained are generic or not, and indeed it is easy to construct examples of generic complex frameworks such that taking their real part yields non-generic frameworks. To deal with this issue, we shall need the following result, which can be seen as a real analogue of Lemma 3.2.

Theorem 6.2

Let $(G,p)$ be a generic realization in $\mathbb {R}^d$ of the rigid graph G, and suppose that the framework $(H,q)$ in $\mathbb {R}^d$ is length-equivalent to $(G,p)$, where G and H have the same order. Then $(H,q)$ is congruent to some generic realization $(H,q')$ of H.

The proof of the two-dimensional version of Theorem 6.2 can be found in [15, Cor. 3.7]: the statement there is formulated for the case $H = G$ but the proof also works for the case when H and G are different. Although Theorem 6.2 is considerably more general, the proof closely follows that of the special case, albeit with some additional technical difficulties. For completeness we give a proof in Appendix C.

Finally, we will need the following lemma concerning disconnected weakly reconstructible frameworks. The proof is a copy of the first part of the proof of Theorem 5.8.

Lemma 6.3

Let (G, p) be a generic framework in $\mathbb {R}^1$ that is weakly reconstructible in $\mathbb {R}^1$. Suppose that G is not connected. Then G is isomorphic to a 2-connected graph $G'$ with some additional isolated vertices.

Now we are in a position to prove the main theorem of this section.

Theorem 6.4

Let (G, p) be a generic framework in $\mathbb {R}^1$. Then (G, p) is weakly (respectively strongly) reconstructible in $\mathbb {R}^1$ if and only if (G, p) is weakly (resp. strongly) reconstructible in $\mathbb {C}^1$.

Proof

Sufficiency is implied by the definitions, so we shall only prove necessity. First, suppose that G is connected. Let (H, q) be a generic one-dimensional complex framework that is length-equivalent to (G, p), where G and H have the same order. By Lemma 6.1 the real framework $(H,{\text {Re}}q)$ is length-equivalent to (G, p), and since G is connected, i.e., rigid in one dimension, we can use Theorem 6.2 to obtain a generic real framework $(H,q')$ that is length-equivalent to (G, p). Since (G, p) is weakly reconstructible in $\mathbb {R}^1$, this implies that $G \cong H$, as desired. Moreover, if (G, p) is strongly reconstructible, then there is an isomorphism between G and H that induces the edge bijection between (G, p) and (H, q).

Now suppose that G is not connected. By Lemma 6.3 we obtain a 2-connected graph $G'$ by removing the isolated vertices of G. It is easy to see that if G is weakly (resp. strongly) reconstructible in $\mathbb {R}^1$, then so must be $G'$. Since $G'$ is connected, we can argue as above in the first part of the proof to deduce that $(G',p|_{V(G')})$, and consequently $G'$ itself, is weakly reconstructible (resp. strongly reconstructible) in $\mathbb {C}^1$. Since $G'$ is 2-connected, Theorem 5.1 applies, so G is weakly (resp. strongly) reconstructible in $\mathbb {C}^1$ as well. $\square$

From Theorem 6.4 it follows that weak and strong reconstructibility are both generic properties in $\mathbb {R}^1$. In two (or more) dimensions this does not hold in general, and in fact, there is a counterexample on $d+2$ vertices. For the sake of simplicity we only give full details for the $d=2$ case.

Fig. 8

a Two realizations of $K_{4} - e$ with coinciding edge measurements. b Deleting the edge xy from both frameworks yields two frameworks with non-isomorphic underlying graphs but coinciding edge measurements

Let G be the graph obtained by attaching a vertex of degree one to a triangle and denote the added edge by uv. Suppose that $(G,p)$ is a generic two-dimensional real framework such that the edge uv is longer than the sum of all the other edge lengths. It is not difficult to see that whenever $m_{d,G}(p)=m_{d,H}(q)$ for some graph H on four vertices and some two dimensional real realization $q$, we have $G \cong H$: the edge in H corresponding to uv cannot be in any cycle by length considerations, so it must be a cut-edge, and G is, up to isomorphism, the only graph on four vertices and with four edges that is not 2-edge-connected.

On the other hand, consider a generic realization in the plane of the graph obtained by deleting an edge from the complete graph $K_4$. Let z denote one of the degree two vertices with neighbors x and y. We can obtain another framework with the same edge lengths by deleting the edge zy and then rotating the edge xz so that its distance from the remaining vertex is the same as the original distance of z and y, and then replacing the zy edge with an edge between z and the remaining vertex. See Fig. 8. Note that this construction only works for suitable edge lengths, i.e., when xz and zy are not too short compared to the edges incident to the fourth vertex. By Theorem 6.2 (using the fact that $K_4 - e$ is rigid in two dimensions) we can assume that the framework constructed in this manner is generic as well. Then by deleting the edge xy we obtain generic realizations of G and $C_4$ with coinciding edge lengths, which shows that these frameworks are not weakly reconstructible. Thus G has WR as well as non-WR generic realizations in $\mathbb {R}^2$. It is not difficult to generalize this example to $d \ge 3$ dimensions by replacing G with the graph obtained by adding a vertex of degree $d-1$ to the complete graph $K_{d+1}$.

We note that G in the above example is not rigid in two dimensions. Thus it is conceivable that weak reconstructibility in $\mathbb {R}^d$ is a generic property in the case of rigid graphs. Furthermore, the genericity of strong reconstructibility in $\mathbb {R}^d$ also remains open. Note that no generic realization of the graph G in the previous example is strongly reconstructible in $\mathbb {R}^2$.

7 Conclusion and Open Problems

In this paper we studied the problem of graph reconstruction from unlabeled edge lengths, motivated by the recent work of Gortler, Thurston, and Theran [10]. The new notions and results presented here motivate numerous open problems, some of which have already been mentioned in the text. In the following we emphasize two of them.

• By Theorems 5.20 and Corollary 5.22, in $\mathbb {C}^1$ and $\mathbb {C}^2$ every strongly reconstructible graph on at least $d+2$ vertices and without isolated vertices is globally rigid. It would be interesting to see whether this holds in higher dimensions as well. A related question is whether strong reconstructibility in $\mathbb {C}^d$ implies $(d+1)$-connectedness in the $d \ge 3$ case.

• The example given at the end of Sect. 6 implies that the weak reconstructibility of a framework in $\mathbb {R}^d$ does not necessarily imply its weak reconstructibility in $\mathbb {C}^d$: indeed, it shows that some generic realization of the cycle of length four in $\mathbb {R}^2$ is weakly reconstructible in $\mathbb {R}^2$, while it is not weakly reconstructible in $\mathbb {C}^2$. It is an open question whether this implication is true for the reconstructibility of graphs, in the following sense. Suppose that for a graph G and some $d \ge 2$, every generic realization of G in $\mathbb {R}^d$ is weakly (respectively strongly) reconstructible in $\mathbb {R}^d$. Does this imply that G is weakly (resp. strongly) reconstructible in $\mathbb {C}^d$, in the sense of Definition 1.4? If the answer to this question is affirmative, we can directly use the tools and results of our paper to study real reconstructibility.

Appendices

Appendix

A GI is reducible to WR-1

We prove Claim 5.10, that is, we show that the graph G constructed in the proof of Theorem 5.9 indeed has the claimed property. First, note that by the 3-connectedness of H and $H'$, the graph G is 2-connected and the only separating pair in G is $\{x,x'\}$. It follows by Corollary 5.6 that G is weakly reconstructible in $\mathbb {C}^1$ if and only if it is invariant under the 2-switch along this separating pair. Let ${\widetilde{G}}$ denote the graph obtained by this 2-switch. We shall picture this 2-switch as “flipping” K while leaving H and $H'$ in place and name the vertices of ${\widetilde{G}}$ accordingly; in particular, in ${\widetilde{G}}$ the edge we removed from K is adjacent to $x'$, and not x.

Suppose now that there is an isomorphism $\varphi :V(H) \rightarrow V(H')$ that sends x to $x'$ and $\{x_1,x_2\}$ to $\{x_1',x_2'\}$. Then it is easy to verify that this extends to an isomorphism between G and ${\widetilde{G}}$ by sending $H'$ to H via $\varphi ^{-1}$ and leaving the vertices of K in place. Thus G is weakly reconstructible.

Conversely, suppose that there is an isomorphism $\varphi :V(G) \rightarrow V({\widetilde{G}})$. Such an isomorphism must send the unique separating pair of G to that of ${\widetilde{G}}$, and consequently (by size considerations) $\varphi |_{V(K)}$ is an automorphism of K. It follows by degree considerations that $\varphi (x) = x'$ (this was the reason for removing an edge of K).

Similarly, $\varphi$ restricted to $V(G) - V(K) + \{x,x'\}$ is an automorphism of the graph obtained by connecting H and $H'$ at $x_1x_1'$ and $x_2x_2'$. Since both H and $H'$ are 3-connected, $\{x_1x_1',x_2x_2'\}$ is the only separating edge pair of this graph. Now $\varphi (x) = x'$ implies that $\varphi$ sends V(H) to $V(H')$. Moreover, since this separating edge pair is unique, $\varphi$ leaves $\{x_1,x_2,x_1',x_2'\}$ in place. The claim follows immediately from these observations.

B Isomorphic Extensions

Proof of Lemma 5.11

It is clear that if G is a complete graph then the degree-2-extensions of G are pairwise isomorphic. In what follows, suppose that G is not complete. We shall verify that G has two non-isomorphic extensions. Let c(G) denote the number of connected components of G. If $c(G)\ge 2$ then, since G has an edge, G has a degree-2 extension with c(G) connected components as well as one with $c(G)-1$ connected components. These extensions are non-isomorphic. Thus we may assume that G is connected and $n\ge 3$.

First consider the case when G is not regular. Let $(d_1,d_2,\dots ,d_n)$ be the degree sequence of G, assuming, without loss of generality, that $d_1\ge d_2\ge \ldots \ge d_n$. Since $n\ge 3$, we must have $d_1 \ge 2$. Let $H_1$ (resp. $H_2$) be the degree-2-extensions obtained from G by adding a new vertex v and new edges $vv_1, vv_2$ (resp. $vv_{n-1},vv_n$). We claim that $H_1$ is not isomorphic to $H_2$. Indeed, if $d_1>d_2$ then the maximum degree of $H_1$ is different from that of $H_2$; if $d_1=d_2$ then the number of maximum degree vertices of $H_1$ is different from that of $H_2$.

Next suppose that G is k-regular for some $k \ge 2$. If $k=2$ then G is a cycle of length at least four. In this case G has a degree-2-extension containing a triangle as well as one with no triangles. So it remains to consider the case when $k\ge 3$. Let $H_1$ (resp. $H_2$) be a degree-2-extension of G in which the new vertex is connected to two adjacent (resp. non-adjacent) vertices of G. Now $H_1$ and $H_2$ are not isomorphic, since in $H_1$ there is a triangle containing the unique vertex of degree two, while there is no such triangle in $H_2$. This completes the proof. $\square$

Proof of Lemma 5.12

Suppose that C has at least one cut-edge. If there is a vertex v in C that is not incident with a cut-edge, then let us fix a vertex w in D and connect C and D by adding an edge from v to w and then by adding an edge from an end-vertex of a cut-edge in C to w. In these two cases the numbers of components spanned by the cut-edges in the resulting graphs are different and hence they are not isomorphic.

If every vertex of C is covered by a cut-edge then either C is an edge, in which case the statement follows easily, or C has at least two cut-edges and hence the 2-edge-connected components of C form a tree T on at least three vertices. Let $T'$ be the 2-edge-connected component tree of D. Now we may connect C and D by a new edge so that either it connects the end-vertices of two longest paths in T and $T'$ or not. In these two cases the lengths of a longest path in the tree of the 2-edge-connected components in the resulting graphs are different and hence they are not isomorphic.

The proof is complete by observing that if C and D are both 2-edge-connected then the statement is clear. $\square$

C Rigid Graphs and Quasi-Generic Configurations

For completeness, we prove Theorem 6.2. First we recall some elementary facts concerning the transcendence degree of field extensions. We restrict our definitions to the particular case of extensions of $\mathbb {Q}\subseteq \mathbb {C}$ generated by a finite number of elements. A collection of elements $\alpha _1,\dots ,\alpha _k\in \mathbb {C}$ is said to be algebraically independent over $\mathbb {Q}$ if they do not satisfy any non-zero polynomial equation with rational coefficients. Let $\mathbb {Q}\subseteq K \subseteq \mathbb {C}$ be an extension of $\mathbb {Q}$. It can be shown that cardinalities of any two maximal algebraically independent subsets of K coincide. The transcendence degree of this extension, which we shall denote by ${{\,\mathrm{tr{.}deg}\,}}_{\mathbb {Q}}(K)$, is this well-defined cardinality. If $K = \mathbb {Q}\,[\alpha _1,\dots ,\alpha _k]$, then ${{\,\mathrm{tr{.}deg}\,}}_{\mathbb {Q}}(K) \le k$. Moreover, the transcendence degree of K coincides with that of its algebraic closure ${\overline{K}} \subseteq \mathbb {C}$.

Following [15], we call a configuration $p\in \mathbb {R}^{nd}$ quasi-generic if $p$ is congruent to some generic configuration $p'\in \mathbb {R}^{nd}$. Let $G = (V,E)$ be a graph with $V = \{v_1,\dots ,v_n\}$. We say that a configuration $(G,p= (p_1,\dots ,p_n))$ is in standard position if for all $1 \le i \le d$, the first $d+1-i$ coordinates of $p_i$ are zero. We will occasionally refer to the coordinates specified in this definition as the canonical coordinates of the configuration and correspondingly to the others as the non-canonical coordinates. Every configuration can be moved into standard position by translations and rotations.

We shall also need some facts about rotations in d dimensions for $d \ge 2$. A rotation by $\theta$ radians around a $d-2$ dimensional subspace of $\mathbb {R}^d$ is a linear transformation that has matrix

$$\begin{aligned} M_{\theta } = \begin{pmatrix}\cos \theta &{}-\sin \theta \\ \sin \theta &{} \cos \theta \\ &{} &{} 1\\ &{} &{} &{} .\\ &{} &{} &{} &{} .\\ &{} &{} &{} &{} &{} .\\ &{} &{} &{} &{} &{} &{} 1 \end{pmatrix} \end{aligned}$$

in some orthonormal basis. For $1\le i<j\le d$, the rotation by $\theta$ radians defined by the i-th and j-th coordinate axes is the rotation which in the standard basis has the matrix that is obtained by swapping the first and i-th, as well as the second and j-th columns and rows of $M_{\theta }$.

The proof of Theorem 6.2 makes heavy use of a lemma, interesting in its own right, stating in effect that a configuration in standard position is quasi-generic if and only if its non-canonical coordinates are algebraically independent. In order to show this, we have to examine the interplay between algebraic independence and congruences of the Euclidean space. The case of translations is simple.

Lemma C.1

Let $v,p_1,\dots ,p_k \in \mathbb {R}^d$ be a set of points such that their coordinates are algebraically independent over $\mathbb {Q}$. Then the coordinates of $v, p_1 + v,\ldots , p_k + v$ are algebraically independent as well.

Proof

This follows immediately from the fact that, if we denote by K and L the field extensions of $\mathbb {Q}$ by the coordinates of $v,p_1,\dots ,p_k$ and $v,p_1+v,\ldots ,p_k+v$, respectively, then we have $K = L$, and so the transcendence degrees of these sets are the same. $\square$

Next, we examine how rotations affect algebraic independence.

Lemma C.2

Let $p_1,\dots ,p_k \in \mathbb {R}^d$ be a set of points for some dimension $d \ge 2$ such that their non-zero coordinates are algebraically independent over $\mathbb {Q}$, and let $\theta \in {\mathbb {R}}$ be such that $\sin \theta$ is algebraically independent from these coordinates. Suppose that T is a rotation by $\theta$ degrees around a subspace of $\mathbb {R}^d$ generated by $d-2$ coordinate axes which fixes all but one of the zero coordinates of $p_1,\dots ,p_k$. Then applying T to this set increases the number of non-zero coordinates by one, and the resulting non-zero coordinates are algebraically independent.

Proof

We can assume without loss of generality that T is determined by the last $d-2$ coordinate axes, i.e., that the image of a point $(\alpha _1,\dots ,\alpha _d)$ under T is $(\alpha _1\cos \theta -\alpha _2\sin \theta ,\alpha _1\sin \theta + \alpha _2\cos \theta ,\alpha _3,\dots ,\alpha _d)$. We can suppose that $p_1$ is the unique point which has a zero coordinate that is not fixed by T; this implies that exactly one of the first two coordinates of $p_1$ is zero, while for $p_2,\dots ,p_k$ either both or neither of the first two coordinates are zero. We suppose that $p_1 = (\alpha ,0,\ldots )$ for some $\alpha \in \mathbb {R}$; the case when $p_1=(0,\alpha ,\dots )$ is analogous. Denote by $q_i$ the image of $p_i$ under T and let K and L be the field extensions of $\mathbb {Q}$ by the coordinates of $p_1,\dots ,p_k$ and $\sin \theta$, and $q_1,\dots ,q_k$, respectively. It is sufficient to show that $K\subseteq {\overline{L}}$ holds, where ${\overline{L}} \subseteq \mathbb {C}$ is the algebraic closure of L, since the former has transcendence degree equal to the number of non-zero coordinates of $p_1,\dots ,p_k$ plus one. Since T fixes the last $d-2$ coordinates, we only have to show that the first two coordinates of $p_1,\dots ,p_k$ are each algebraic over L. We have $q_1=(q_{11}=\alpha \cos \theta ,q_{12} = \alpha \sin \theta ,\ldots )$, implying that $\alpha ^2 = q_{11}^2 + q_{12}^2$, so that $\alpha$ is algebraic over L. Then so is $\sin \theta = q_{12}/\alpha$ and $\cos \theta = q_{11}/\alpha$. For $2 \le i \le k$ we have

$$\begin{aligned} p_{i1}&= q_{i1} {{\,\mathrm{cos\,}\,}}(-\theta ) - q_{i2}{{\,\mathrm{sin\,}\,}}(-\theta )\qquad \text {and}\\ p_{i2}&= q_{i1}{{\,\mathrm{sin\,}\,}}(-\theta ) + q_{i2}{{\,\mathrm{cos\,}\,}}(-\theta ), \end{aligned}$$

so $p_{i1}$ and $p_{i2}$ are algebraic over L as well, which is what we needed to show. $\square$

Lemma C.3

Let $p\in \mathbb {R}^{nd}$ be a d-dimensional configuration in standard position. Then $p$ is quasi-generic if and only if the non-canonical coordinates of p are algebraically independent over $\mathbb {Q}$.

Proof

Suppose first that $p$ is quasi-generic and let $p'$ be a generic realization congruent to it. Let G be an arbitrary minimally rigid graph on n vertices. Let m denote the number of edges of G; note that this is the same as the number of non-canonical coordinates in $p$. Now by Theorem 3.7 we have $M_{d,G} = \mathbb {C}^m$ and so, by Lemma 2.7, $m_{d,G}(p) = m_{d,G}(p')$ is generic in $M_{d,G}=\mathbb {C}^m$, i.e., the edge lengths are algebraically independent over $\mathbb {Q}$. Every edge length of $p$ is in the field extension of $\mathbb {Q}$ by the m non-canonical coordinates of $p$. Consequently, this extension contains m algebraically independent elements, thus its transcendence degree must be m. This means that the non-canonical coordinates must be algebraically independent as well.

Conversely, suppose that the non-canonical coordinates of $p$ are algebraically independent over $\mathbb {Q}$. , they are non-zero. For the sake of convenience we suppose that $n\ge d$; this is solely to avoid notational difficulties, and does not affect the proof in any significant way. By a series of $\left( {\begin{array}{c}d\\ 2\end{array}}\right)$ rotations we can reach from $p$ a configuration $p'=(p_1',p_2',\dots ,p'_n)$, where $p'_1={\mathbf {0}}$ and $p'_2,\dots ,p'_n$ have algebraically independent coordinates. Indeed, we can apply a rotation defined by the i-th and the $j_i$-th axes for $j_i = 1,\dots ,i-1$ and $i=2,\dots ,d$. Each of these rotations fixes all but one of the zero coordinates at any point in the process, so, by Lemma C.2, if we rotate by the appropriate amount each time, we indeed maintain the algebraic independence of the non-zero coordinates. Finally, by Lemma C.1 we can apply a suitable translation to $p'$ to reach a generic configuration $p''$ that is congruent to $p$. $\square$

We are now ready to prove Theorem 6.2.

Proof of Theorem 6.2

By deleting some edges from G we can suppose that it is minimally rigid. Let n and m denote the number of vertices and edges of G, respectively. By Theorem 3.6 we have $M_{d,G} = M_{d,H}$. On the other hand, the minimal rigidity of G implies that $M_{d,G}=\mathbb {C}^m$ (see Theorem 3.7). It follows by this and Lemma 2.7 that since $p\in \mathbb {R}^{nd}$ is generic, so is $m_{d,G}(q)=m_{d,G}(p)$. Let $q'$ be a realization in standard position that is congruent to $q$. Using the same argument as in the first part of the proof of Lemma C.3, we obtain that the non-canonical coordinates of $q'$ are algebraically independent. Then, by the same lemma, $q'$, and consequently $q$, must be quasi-generic. $\square$