Globally Linked Pairs of Vertices in Generic Frameworks

Abstract

A d-dimensional framework is a pair (G, p), where $G=(V,E)$ is a graph and p is a map from V to ${\mathbb {R}}^d$. The length of an edge $xy\in E$ in (G, p) is the distance between p(x) and p(y). A vertex pair $\{u,v\}$ of G is said to be globally linked in (G, p) if the distance between p(u) and p(v) is equal to the distance between q(u) and q(v) for every d-dimensional framework (G, q) in which the corresponding edge lengths are the same as in (G, p). We call (G, p) globally rigid in ${\mathbb {R}}^d$ when each vertex pair of G is globally linked in (G, p). A pair $\{u,v\}$ of vertices of G is said to be weakly globally linked in G in ${\mathbb {R}}^d$ if there exists a generic framework (G, p) in which $\{u,v\}$ is globally linked. In this paper we first give a sufficient condition for the weak global linkedness of a vertex pair of a $(d+1)$-connected graph G in ${\mathbb {R}}^d$ and then show that for $d=2$ it is also necessary. We use this result to obtain a complete characterization of weakly globally linked pairs in graphs in ${\mathbb {R}}^2$, which gives rise to an algorithm for testing weak global linkedness in the plane in $O(|V|^2)$ time. Our methods lead to a new short proof for the characterization of globally rigid graphs in ${\mathbb {R}}^2$, and further results on weakly globally linked pairs and globally rigid graphs in the plane and in higher dimensions.

1 Introduction

A d-dimensional framework is a pair (G, p), where $G=(V,E)$ is a graph and p is a map from V to ${\mathbb {R}}^d$. We also say that (G, p) is a realization of G in ${\mathbb {R}}^d$. The length of an edge $uv\in E$ in (G, p) is $||p(u)-p(v)||$, where ||.|| denotes the Euclidean norm in ${\mathbb {R}}^d$. Two frameworks (G, p) and (G, q) are equivalent if corresponding edge lengths are the same, that is, $||p(u)-p(v)||=||q(u)-q(v)||$ holds for all pairs u, v with $uv\in E$. The frameworks (G, p) and (G, q) are congruent if $||p(u)-p(v)||=||q(u)-q(v)||$ holds for all pairs u, v with $u,v\in V$.

A d-dimensional framework (G, p) is called globally rigid if every equivalent d-dimensional framework (G, q) is congruent to (G, p). This is the same as saying that the edge lengths of (G, p) uniquely determine all the pairwise distances. It is NP-hard to test whether a given framework in ${\mathbb {R}}^d$ is globally rigid, even for $d=1$ [28]. This fundamental property of frameworks becomes more tractable if we consider generic frameworks. A framework (G, p) (and the set $\{p(v):v\in V(G)\}$) is said to be generic if the set of its d|V(G)| vertex coordinates is algebraically independent over ${\mathbb {Q}}$. It is known that in a given dimension the global rigidity of a generic framework (G, p) depends only on G: either every generic realization of G in ${\mathbb {R}}^d$ is globally rigid, or none of them are [3, 12]. Thus, we say that a graph G is globally rigid in ${\mathbb {R}}^d$ if every (or equivalently, if some) d-dimensional generic realization of G is globally rigid in ${\mathbb {R}}^d$. For $d=1,2$, combinatorial characterizations and corresponding deterministic polynomial time algorithms are known for (testing) global rigidity in ${\mathbb {R}}^d$. The case $d=1$ is a folklore result: it is not hard to see that a graph G on at least three vertices is globally rigid in ${\mathbb {R}}^1$ if and only if it is 2-connected. The necessary and sufficient conditions for $d=2$ are stated as Theorem 2.6 in the next section. The existence of such a characterization (or algorithm) for $d\ge 3$ is a major open question. For more details on globally rigid graphs and frameworks, see, e.g., [21].

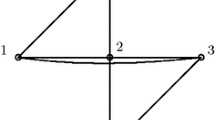
In this paper we consider a refined, local version, in which we are interested in whether the edge lengths of a framework uniquely determine the distance between a given pair of vertices, rather than all pairs of vertices. We shall need the following notions. Following [16], we say that a pair of vertices $\{u,v\}$ in a d-dimensional framework (G, p) is globally linked in (G, p) if for every equivalent d-dimensional framework (G, q) we have $||p(u)-p(v)||=||q(u)-q(v)||$. Global linkedness in ${\mathbb {R}}^d$ is not a generic property (for $d\ge 2$): a vertex pair may be globally linked in some generic d-dimensional realization of G without being globally linked in all generic realizations. See Fig. 1. We say that a pair $\{u,v\}$ is globally linked in G in ${\mathbb {R}}^d$ if it is globally linked in all generic d-dimensional frameworks (G, p). We call a pair $\{u,v\}$ weakly globally linked in G in ${\mathbb {R}}^d$ if there exists a generic d-dimensional framework (G, p) in which $\{u,v\}$ is globally linked. If $\{u,v\}$ is not weakly globally linked in G, then it is called globally loose in G. It is immediate from the definitions that G is globally rigid in ${\mathbb {R}}^d$ if and only if each vertex pair is globally linked in G in ${\mathbb {R}}^d$. As we shall see, the global rigidity of G already follows from the (seemingly weaker) condition that each vertex pair is weakly globally linked in G (see Lemma 3.2(c)).

The case $d=1$ is exceptional and well-understood. Global linkedness in ${\mathbb {R}}^1$ is a generic property: a pair $\{u,v\}$ is globally linked in G in ${\mathbb {R}}^1$ if and only if there is a cycle in G that contains both u and v. Otherwise $\{u,v\}$ is globally loose.

For $d\ge 2$ no combinatorial (or efficiently testable) characterization has previously been found for globally linked or weakly globally linked pairs in graphs in ${\mathbb {R}}^d$. These problems belong to the few major problems in combinatorial rigidity which have remained unsolved for $d=2$. The main result of this paper is a solution for the weakly globally linked pairs problem in two dimensions. We shall first give a sufficient condition for the weak global linkedness of a vertex pair of a $(d+1)$-connected graph G in ${\mathbb {R}}^d$ (Theorem 4.5) and then show that in a sense the condition is also necessary in the case of 3-connected graphs in ${\mathbb {R}}^2$ (Theorem 5.1). The general case of the two-dimensional problem is reduced to the 3-connected case by a sequence of lemmas that describe how weak global linkedness is affected by cutting a graph along a separating pair. These results lead to the main result (Theorem 5.8), which gives a characterization of weakly globally linked pairs of vertices in ${\mathbb {R}}^2$ and gives rise to an $O(|V|^2)$ algorithm for the corresponding decision problem.

Our methods and results lead to a new short proof for the sufficiency part of Theorem 2.6. We also obtain a number of other structural results on weakly globally linked pairs and globally rigid graphs in ${\mathbb {R}}^2$ and in higher dimensions.

Even though most of the known results (and conjectures) on global linkedness are concerned with globally linked pairs of graphs in ${\mathbb {R}}^2$, their characterization remains open. Globally linked pairs in two dimensions have been characterized in minimally rigid graphs [17], braced maximal outerplanar graphs [8], and in ${{{\mathcal {R}}}}_2$-connected graphs [16]. In the latter two cases global linkedness turns out to be a generic property. Hence these two results give rise to the characterization of weakly globally linked pairs, too, in the corresponding families of graphs. A few partial results in higher dimensions are also available, see [10, 19]. A conjectured characterization of globally linked pairs in ${\mathbb {R}}^2$ can be found in [16].

The rest of the paper is organized as follows. In Sect. 2 we introduce the necessary notions concerning rigid graphs and frameworks. In Sect. 3 we prove some simple but fundamental lemmas on weakly globally linked pairs in ${\mathbb {R}}^d$. Section 4 contains most of the d-dimensional results (two key geometric lemmas and a sufficient condition for weak global linkedness), and the new proof for Theorem 2.6. In Sect. 5 we state and prove our main result, a complete characterization of the weakly globally linked pairs in ${\mathbb {R}}^2$. In Sect. 6 we discuss the algorithmic aspects and collect a few concluding remarks and questions.

Fig. 1

Two pairs of equivalent generic frameworks of a graph G in ${\mathbb {R}}^2$. The vertex pair $\{u,v\}$ is globally linked in the two frameworks on the left. On the other hand, $\{u,v\}$ is not globally linked in the two frameworks on the right. Thus $\{u,v\}$ is not globally linked but is weakly globally linked in G in ${\mathbb {R}}^2$

2 Preliminaries

In this section we introduce the notions and results from the theory of (globally) rigid frameworks and graphs that we shall use.

2.1 Rigid Graphs and the Rigidity Matroid

In the structural results on global rigidity and global linkedness the notions of rigid frameworks, rigid graphs and the rigidity matroid play a key role.

Let (G, p) be a d-dimensional framework. A flexing of (G, p) is a continuous function $\pi :[0,1] \rightarrow ({\mathbb {R}}^d)^V$ such that $\pi (0)=p$ and the frameworks $(G, \pi (t))$ and (G, p) are equivalent for every $t\in [0,1]$. In other words, a flexing is a continuous motion of the vertices in ${\mathbb {R}}^d$ that preserves all the edge lengths in the framework. We say that the flexing $\pi$ is trivial if $(G, \pi (t))$ is congruent to (G, p) for every $t\in [0,1]$. The framework (G, p) is called rigid if it has no non-trivial flexing. It is known that in a given dimension the rigidity of a generic framework (G, p) depends only on G: either every generic realization of G in ${\mathbb {R}}^d$ is rigid, or none of them are [1]. Thus, we say that a graph G is rigid in ${\mathbb {R}}^d$ if every (or equivalently, if some) d-dimensional generic realization of G is rigid in ${\mathbb {R}}^d$. For $d=1,2$, combinatorial characterizations and corresponding deterministic polynomial time algorithms are known for (testing) rigidity in ${\mathbb {R}}^d$, see, e.g., [24]. The existence of such a characterization (or algorithm) for $d\ge 3$ is a major open question.

The following elementary result is well-known. For the proof of the two-dimensional case see [16, Theorem 8.1].

Proposition 2.1

Suppose that (G, p) is a rigid generic framework. Then the number of distinct congruence classes of frameworks which are equivalent to (G, p) is finite.

The rigidity matroid of a graph G is a matroid defined on the edge set of G which reflects the rigidity properties of all generic realizations of G. For a general introduction to matroid theory we refer the reader to [26].

Let (G, p) be a realization of a graph $G=(V,E)$ in ${\mathbb {R}}^d$. The rigidity matrix of the framework (G, p) is the matrix R(G, p) of size $|E|\times d|V|$, where, for each edge $uv\in E$, in the row corresponding to uv, the entries in the d columns corresponding to vertices u and v contain the d coordinates of $(p(u)-p(v))$ and $(p(v)-p(u))$, respectively, and the remaining entries are zeros. The rigidity matrix of (G, p) defines the rigidity matroid of (G, p) on the ground set E by linear independence of the rows. It is known that any pair of generic frameworks (G, p) and (G, q) have the same rigidity matroid. We call this the d-dimensional rigidity matroid $\mathcal{R}_d(G)=(E,r_d)$ of the graph G.

We denote the rank of ${{{\mathcal {R}}}}_d(G)$ by $r_d(G)$. A graph $G=(V,E)$ is ${{{\mathcal {R}}}}_d$-independent if $r_d(G)=|E|$ and it is an ${{{\mathcal {R}}}}_d$-circuit if it is not ${{{\mathcal {R}}}}_d$-independent but every proper subgraph $G'$ of G is ${{{\mathcal {R}}}}_d$-independent. We note that in the literature such graphs are sometimes called M-independent in ${\mathbb {R}}^d$ and M-circuits in ${\mathbb {R}}^d$, respectively. An edge e of G is an ${{{\mathcal {R}}}}_d$-bridge in G if $r_d(G-e)=r_d(G)-1$ holds. Equivalently, e is an $\mathcal{R}_d$-bridge in G if it is not contained in any subgraph of G that is an ${{{\mathcal {R}}}}_d$-circuit.

The following characterization of rigid graphs is due to Gluck.

Theorem 2.2

[11] Let $G=(V,E)$ be a graph with $|V|\ge d+1$. Then G is rigid in ${\mathbb {R}}^d$ if and only if $r_d(G)=d|V|-\left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$.

A graph is minimally rigid in ${\mathbb {R}}^d$ if it is rigid in ${\mathbb {R}}^d$ but $G-e$ is not rigid in ${\mathbb {R}}^d$ for every edge e of G. By Theorem 2.2, minimally rigid graphs in ${\mathbb {R}}^d$ on at least $d+1$ vertices have exactly $d|V| - \left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$ edges.

Let $G=(V,E)$ be a graph and $\{u,v\}$ be a pair of vertices of G. An induced subgraph G[X] (and the set X), for some $X\subseteq V$, is said to be (u, v)-rigid in ${\mathbb {R}}^d$ (or simply (u, v)-rigid, if d is clear from the context), if G[X] is rigid in ${\mathbb {R}}^d$ and $u,v\in X$. We say that a (u, v)-rigid subgraph G[X] is vertex-minimally (u, v)-rigid, if $G[X']$ is not (u, v)-rigid for all proper subsets $X'\subset X$. The pair $\{u,v\}$ is called linked in G in ${\mathbb {R}}^d$ if $r_d(G+uv)=r_d(G)$ holds. A graph G with at least three edges is called redundantly rigid in ${\mathbb {R}}^d$ if $G-e$ is rigid in ${\mathbb {R}}^d$ for all $e\in E(G)$.

Let ${{{\mathcal {M}}}}$ be a matroid on ground set E. We can define a relation on the pairs of elements of E by saying that $e,f\in E$ are equivalent if $e=f$ or there is a circuit C of ${{{\mathcal {M}}}}$ with $\{e,f\}\subseteq C$. This defines an equivalence relation. The equivalence classes are the connected components of $\mathcal{M}$. The matroid is connected if it has only one connected component. A graph $G=(V,E)$ is ${{{\mathcal {R}}}}_d$-connected if ${{{\mathcal {R}}}}_d(G)$ is connected. We shall use the well-known fact that if v is a vertex of degree at most d in G, then every edge incident with v is an ${{{\mathcal {R}}}}_d$-bridge in G. Hence the addition of a new vertex of degree d to a rigid graph G in ${\mathbb {R}}^d$ preserves rigidity.

The following theorem was first proved by Geiringer in 1927 and later, independently, by Laman in 1970.

Theorem 2.3

[24, 27] A graph $G=(V,E)$ is ${\mathcal {R}}_2$-independent if and only if for all subsets U of V with $|U|\ge 2$, we have $|E(U)|\le 2|U|-3$.

The following well-known statement can be deduced from Theorems 2.2 and  2.3.

Lemma 2.4

A graph $G=(V,E)$ is an ${\mathcal {R}}_2$-circuit if and only if $|E|=2|V|-2$ and $G-e$ is rigid for each $e\in E$.

It follows from Lemma 2.4 that a pair $\{u,v\}$ is linked in a graph G in ${\mathbb {R}}^2$ if and only if there exists a (u, v)-rigid subgraph of G. For more details on the 2-dimensional rigidity matroid, see [18].

2.2 Globally Rigid Graphs

The following necessary conditions for global rigidity are due to Hendrickson.

Theorem 2.5

[13] Let G be a globally rigid graph in ${\mathbb {R}}^d$ on at least $d+2$ vertices. Then G is $(d+1)$-connected and redundantly rigid in ${\mathbb {R}}^d$.

For $d=1,2$ the conditions of Theorem 2.5 together are sufficient to imply global rigidity. It is not the case for $d\ge 3$. The characterization of globally rigid graphs in ${\mathbb {R}}^2$ is as follows.

Theorem 2.6

[15] Let G be a graph on at least four vertices. Then G is globally rigid in ${\mathbb {R}}^2$ if and only if G is 3-connected and redundantly rigid in ${\mathbb {R}}^2$.

An equivalent characterization of global rigidity, in terms of the rigidity matroid of G, follows from the next lemma.

Lemma 2.7

[15, Lemma 3.1, Theorem 3.2] Let G be a graph with at least two edges. If G is $\mathcal{R}_2$-connected, then G is redundantly rigid in ${\mathbb {R}}^2$. Furthermore, if G is 3-connected and redundantly rigid in ${\mathbb {R}}^2$, then G is ${{{\mathcal {R}}}}_2$-connected.

We shall also use the following lemma.

Lemma 2.8

[22, Lemma 6.2] Let G be a rigid, but not redundantly rigid graph in ${\mathbb {R}}^2$, and suppose that all ${{{\mathcal {R}}}}_2$-bridges of G are edges of the same triangle in G. Then G is not 3-connected.

3 Properties of Weakly Globally Linked Pairs in ${\mathbb {R}}^d$

We first collect some basic properties that hold in ${\mathbb {R}}^d$ for all $d\ge 1$. The following lemma was stated for $d=2$ in [16] but the proof works for all $d\ge 1$. An edge e of a globally rigid graph H is critical if $H-e$ is not globally rigid.

Lemma 3.1

[16, Lemma 7.1] Let $G=(V,E)$ be a graph and $u,v\in V$. Suppose that $uv\notin E$, and that G has a globally rigid supergraph in ${\mathbb {R}}^d$ in which uv is a critical edge. Then $\{u,v\}$ is globally loose in G in ${\mathbb {R}}^d$.

We shall frequently use the next key lemma. For a graph $G=(V,E)$ and integer $d\ge 1$ let

$$\begin{aligned} J_d(G)=\{uv: u,v\in V, uv\notin E, \{u,v\} \ \hbox {is weakly globally linked in}\ G\ \hbox {in}\ {\mathbb {R}}^d\}. \end{aligned}$$

Lemma 3.2

Let $G=(V,E)$ be a graph and let F be a set of edges on vertex set V. Then the following hold.

• (a) If $G+J_d(G)+F$ is globally rigid in ${\mathbb {R}}^d$, then $G+F$ is globally rigid in ${\mathbb {R}}^d$.

• (b) If $G+uv$ is globally rigid in ${\mathbb {R}}^d$ for some $uv\in J_d(G)$, then G is globally rigid in ${\mathbb {R}}^d$.

• (c) G is globally rigid in ${\mathbb {R}}^d$ if and only if all pairs of vertices in G are weakly globally linked in ${\mathbb {R}}^d$.

Proof

Let us fix d and put $J=J_d(G)$.

• (a) Suppose, for a contradiction, that $G+J+F$ is globally rigid and $G+F$ is not. Then there is a (possibly empty) subset $J'\subset J$ and an edge $uv\in J-J'$ for which $G+J'+F$ is not globally rigid, but ${\bar{G}}=G+J'+F+uv$ is globally rigid. Then uv is a critical edge in ${\bar{G}}$, and hence $\{u,v\}$ is globally loose in G by Lemma 3.1, a contradiction.

• (b) If $G+uv$ is globally rigid for some $uv\in J$ then $G+J$ is globally rigid. Thus putting $F=\emptyset$ and applying (a) gives that G is globally rigid.

• (c) Necessity is obvious. If all pairs of vertices in G are weakly globally linked, then $G+J$ is a complete graph, which is globally rigid. Again, putting $F=\emptyset$ and applying (a) gives that G is globally rigid.

$\square$

The next lemma states weak global linkedness is a stronger property than linkedness.

Lemma 3.3

Let $G=(V,E)$ be a graph, $u,v\in V$. If $\{u,v\}$ is not linked in G in ${\mathbb {R}}^d$ then $\{u,v\}$ is globally loose in G in ${\mathbb {R}}^d$.

Proof

Let (G, p) be a generic d-dimensional realization of G. Since $\{u,v\}$ is not linked, there exists a non-rigid supergraph $G'$ of G for which $G'+uv$ is rigid. Then $G'$ has a non-trivial flexing. It follows from the rigidity of $G'+uv$ that during this flexing the distance between u and v is not constant. Hence, $\{u,v\}$ is not globally linked in G. $\square$

Let $H=(V,E)$ be a graph and $x,y\in V$. We use $\kappa _H(x,y)$ to denote the maximum number of pairwise internally disjoint xy-paths in H. Note that if $xy\notin E$ then, by Menger’s theorem, $\kappa _H(x,y)$ is equal to the size of a smallest set $S\subseteq V-\{x,y\}$ for which there is no xy-path in $H-S$. The following lemma is the d-dimensional version of [16, Lemma 5.6]. The proof is the same in d dimensions.

Lemma 3.4

Let $G=(V,E)$ be a graph and let $\{u,v\}$ be a non-adjacent vertex pair with $\kappa _G(u,v)\le d$. Then $\{u,v\}$ is globally loose in G in ${\mathbb {R}}^d$.

Let $G_i=(V_i,E_i)$ be a graph, $t \ge 1$ an integer, and suppose that $K_t^i$ is a complete subgraph of $G_i$ on t vertices, for $i=1,2$. Then the t-clique sum operation on $G_1,G_2$, along $K_t^1,K_t^2$, creates a new graph G by identifying the vertices of $K_t^1$ with the vertices of $K_t^2$, following some bijection between their vertex sets. The clique sum operation is a t-clique sum operation for some $t\ge 1$.

In the following lemma sufficiency follows from the simple obervation that if a vertex pair is weakly globally linked in a subgraph of G, then it is also weakly globally linked in G. Necessity follows from the fact that the clique sum operation is performed along a complete (and hence globally rigid) subgraph.

Lemma 3.5

Suppose that G is the clique sum of $G_1$ and $G_2$ and let $u,v\in V(G_1)$. Then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^d$ if and only if $\{u,v\}$ is weakly globally linked in $G_1$ in ${\mathbb {R}}^d$.

4 A Sufficient Condition for Weak Global Linkedness in ${\mathbb {R}}^d$

In this section we provide a new sufficient condition for the weak global linkedness of a pair of vertices of a $(d+1)$-connected graph in ${\mathbb {R}}^d$. An important ingredient in our proof is a geometric lemma (Lemma 4.1) presented in the next subsection. In Sect. 4.2 we prove the aforementioned sufficient condition and in Sect. 4.3 we show how it can be used to prove the sufficiency part of Theorem 2.6. In the last subsection we shall see that an appropriate converse of Lemma 4.1 is also true (Lemma 4.7). This lemma will be used in the next section where we characterize weak global linkedness in two dimensions. Roughly speaking, these two lemmas show that if a vertex pair $\{u,v\}$ belongs to a rigid subgraph H of G, then contracting some edges outside of H does not change whether $\{u,v\}$ is weakly globally linked.

4.1 The First Contraction Lemma

A basic graph operation is the contraction of a subset $V_0$ of V in the graph $G=(V,E)$. This operation, which is denoted by $G/V_0$, identifies the vertices of $V_0$ and removes the loops and parallel copies of the edges of the resulting graph that it may create. The contraction of an edge $e=xy$ is the contraction of the set $\{x,y\}$ and it is denoted by G/e.

Lemma 4.1

Let $G=(V,E)$ be a graph, $u,v\in V$, and suppose that $G[V_0]$ is a (u, v)-rigid subgraph of G. Let $e=(s_1,s_2)\in E-E(G[V_0])$ be an edge. If $\{u,v\}$ is weakly globally linked in G/e in ${\mathbb {R}}^d$, then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^d$.

Proof

We may assume that G is connected and $s_2\notin V_0$. Let s denote the vertex of G/e obtained by identifying $s_1$ and $s_2$ in G. Note that we may have $s_1\in V_0$. In this case we shall simply identify s with $s_1$ for notational convenience. Let (G/e, p) be a generic realization of G/e in which $\{u,v\}$ is globally linked. Let $(G,p_i)$ be a sequence of generic realizations of G, for which $p_i|_{V-s_1-s_2}=p|_{V-s}$, $p_i(s_1)=p(s)$, and $p_i(s_2)\rightarrow p(s)$. Suppose, for a contradiction, that $\{u,v\}$ is globally loose in G. Then $\{u,v\}$ is not globally linked in $(G,p_i)$ for all $i\ge 1$. Hence for all $i\ge 1$ there exists a realization $(G,q_i)$, equivalent to $(G,p_i)$, for which

$$\begin{aligned} ||q_i(u)-q_i(v)||\ne ||p_i(u)-p_i(v)||=||p(u)-p(v)||. \end{aligned}$$

Since $G[V_0]$ is rigid and $p|_{V_0}=p_i|_{V_0}$, it follows from Proposition 2.1 that there is an $\epsilon >0$ such that for all $i\ge 1$,

$$\begin{aligned} \big |||q_i(u)-q_i(v)||-||p(u)-p(v)||\big |\ge \epsilon . \end{aligned}$$

Since G is connected, we can translate each framework, if necessary, so that for all $i\ge 1$, $(G,q_i)$ is in the interior of a ball of radius K, centered at the origin, for some fixed positive real number K. Thus there is a convergent subsequence $q_{i_k}\rightarrow q$. Since $(s_1,s_2)\in E$, we must have $q(s_1)=q(s_2)$. By extending $q|_{V-s_1-s_2}$ with $q(s)=q(s_1)$, we obtain a realization (G/e, q) which is equivalent to (G/e, p). Furthermore, we have

$$\begin{aligned} \big |||q(u)-q(v)||-||p(u)-p(v)||\big |\ge \epsilon , \end{aligned}$$

which contradicts the fact that $\{u,v\}$ is globally linked in (G/e, p). $\square$

We obtain the following sufficient (but not necessary, see Fig. 2) condition for weak global linkedness as a corollary.

Corollary 4.2

Let $G=(V,E)$ be a graph, $u,v\in V$. Suppose that there is some $V_0\subset V$ such that $G[V_0]$ is a (u, v)-rigid subgraph of G in ${\mathbb {R}}^d$, and there is a uv-path in G that is internally disjoint from $V_0$. Then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^d$.

Fig. 2

Consider the graph on the left. The subgraph induced by the solid vertices is rigid in ${\mathbb {R}}^2$, and contracting the edges e and f results in a graph that is globally rigid in ${\mathbb {R}}^2$. Thus by Lemma 4.1, $\{u,v\}$ is weakly globally linked in ${\mathbb {R}}^2$. This shows that the sufficient condition of Corollary 4.2 is not necessary

Corollary 4.2, together with Lemma 3.2, leads to short proofs for some previous results on globally rigid graphs. We illustrate this by the following theorem.

Theorem 4.3

[4] Let $G_1$ and $G_2$ be two globally rigid graphs in ${\mathbb {R}}^d$ on at least $d+2$ vertices, with exactly $d+1$ vertices in common. Suppose that e is a common edge. Then $G=G_1\cup G_2-e$ is globally rigid in ${\mathbb {R}}^d$.

Proof

Let $e=uv$. Theorem 2.5 implies that $G_1-e$ is rigid. Since $G_2$ is $(d+1)$-connected, there is a path from u to v in G that is internally disjoint from $G_1$. Thus $\{u,v\}$ is weakly globally linked in G by Corollary 4.2. It is easy to see that $G+uv$ is globally rigid. Hence G is also globally rigid by Lemma 3.2. $\square$

By using the same proof idea we obtain a simple proof of the “rooted minor" theorem of Tanigawa [30].

4.2 The Sufficient Condition

Let $G=(V,E)$ be a graph. For $U\subseteq V$, let $N_G(U)$ denote the set of those vertices in $V-U$ that have at least one neighbour in U. For $u\in V$, let $N_G(u)=N_G(\{u\})$.

Let $\emptyset \not = X\subseteq V$ and let $V_1,V_2,\dots , V_r$ be the vertex sets of the connected components of $G-X$. The graph $\textrm{Con}(G,X)$ is obtained from G by contracting each vertex set $V_i$ into a single vertex $v_i$, $1\le i\le r$. The graph $\textrm{Clique}(G,X)$ is obtained from G by deleting the vertex sets $V_i$, $1\le i\le r$, and adding a new edge xy for all pairs $x,y\in N_G(V_i)$, $xy\notin E$, for $1\le i\le r$. See Fig. 3.

Fig. 3

An example of a graph G and the graphs $\textrm{Con}(G,X)$ and $\textrm{Clique}(G,X)$

Lemma 4.4

Let $G=(V,E)$ be a $(d+1)$-connected graph. Suppose that $G[V_0]$ is a rigid subgraph of G for some $V_0\subseteq V$. Then $\textrm{Clique}(G,V_0)$ is globally rigid in ${\mathbb {R}}^d$ if and only if $\textrm{Con}(G,V_0)$ is globally rigid in ${\mathbb {R}}^d$.

Proof

Let $E'$ be the set of those edges in $\textrm{Clique}(G,V_0)$ that are not in $G[V_0]$. Let $H=\textrm{Con}(G,V_0)+E'$. It follows from Corollary 4.2 that $\{u,v\}$ is weakly globally linked in $\textrm{Con}(G,V_0)$ for all $uv\in E'$. Hence, by Lemma 3.2, $\textrm{Con}(G,V_0)$ is globally rigid if and only if H is globally rigid. H can be obtained from $\textrm{Clique}(G,V_0)$ by adding new vertices and joining each new vertex to a clique. It follows from the $(d+1)$-connectivity of G that each of these cliques has size at least $d+1$. Thus H is globally rigid if and only if $\textrm{Clique}(G,V_0)$ is globally rigid. $\square$

We are ready to state the main result of this section.

Theorem 4.5

Let $G=(V,E)$ be a $(d+1)$-connected graph and $u,v\in V$. Suppose that $G[V_0]$ is a (u, v)-rigid subgraph of G in ${\mathbb {R}}^d$. If $\textrm{Clique}(G,V_0)$ is globally rigid in ${\mathbb {R}}^d$, then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^d$.

Proof

Suppose that $\textrm{Clique}(G,V_0)$ is globally rigid in ${\mathbb {R}}^d$. Then so is $\textrm{Con}(G,V_0)$ by Lemma 4.4. In particular, $\{u,v\}$ is weakly globally linked in $\textrm{Con}(G,V_0)$. Since $\textrm{Con}(G,V_0)$ can be obtained from G by contracting edges not induced by $V_0$, Lemma 4.1 gives that $\{u,v\}$ is weakly globally linked in G. $\square$

4.3 Globally Rigid Graphs: A New Proof

Theorem 4.5 and Lemma 3.2 lead to a new short proof of the sufficiency part of Theorem 2.6, which only uses the simple combinatorial Lemmas 2.7 and 2.8 and the fact that the global rigidity of graphs in ${\mathbb {R}}^2$ is a generic property. The original proof in [15] relies on an inductive construction of 3-connected ${{{\mathcal {R}}}}_2$-connected graphs.

Proof of sufficiency in Theorem 2.6

The proof is by induction on |V|. If $|V|=4$ then G is a complete graph on four vertices, which is globally rigid. So we may suppose that $|V|\ge 5$. First, we show that for all non-adjacent pairs u, v, there is a (u, v)-rigid proper induced subgraph G[X] of G. To see this consider two edges $e,f\in E$ incident with u and v, respectively. Since G is 3-connected and redundantly rigid, it is ${{{\mathcal {R}}}}_2$-connected by Lemma 2.7. Hence there is an ${{{\mathcal {R}}}}_2$-circuit C in G with $e,f\in E(C)$. By Lemma 2.4, $|E(C)|=2|V(C)|-2$ and $d_C(v)\ge 3$ for all $v\in V(C)$. It follows that C has at least four vertices of degree three. Thus there is a vertex $w\in V(C)$ with $w\notin \{u,v\}$ and $d_C(w)=3$. Now $X=V(C)-w$ induces the desired (u, v)-rigid subgraph.

In the rest of the proof we show that every non-adjacent vertex pair $\{u,v\}$ of G is weakly globally linked in G. The theorem will follow from this by Lemma 3.2(c). Let us fix u, v and consider a (u, v)-rigid proper induced subgraph G[X] of G. As we have shown above, such a subgraph exists. By Theorem 4.5 it suffices to show that $\textrm{Clique}(G,X)$ is globally rigid.

Let D be the vertex set of a component of $G-X$ and let H be obtained from $G-D$ by adding a new edge xy for each non-adjacent pair $x,y\in N_G(D)$. Since G can be obtained from H by attaching a graph along a complete subgraph, and removing edges, the 3-connectivity of G implies that H is 3-connected. A similar argument shows that H is rigid, and so is $H-e$ for every edge e in H not induced by $N_G(D)$. Thus if H has some $\mathcal{R}_2$-bridges, then they are all induced by $N_G(D)$. If $|N_G(D)|\ge 4$, then each edge induced by $N_G(D)$ belongs to a $K_4$ in H, so H cannot have ${{{\mathcal {R}}}}_2$-bridges at all. If $|N_G(D)|=3$, then every ${{{\mathcal {R}}}}_2$-bridge in H belongs to the same triangle, on the vertices of $N_G(D)$. But that is impossible by Lemma 2.8. Therefore H is a rigid graph with no $\mathcal{R}_2$-bridges, and hence it is redundantly rigid. By repeated applications of this argument we obtain that $\textrm{Clique}(G,X)$ is 3-connected and redundantly rigid. Since $|X|\le |V|-1$, we can now use induction to deduce that $\textrm{Clique}(G,X)$ is globally rigid. This completes the proof.

We remark that a different proof for the sufficiency part in Theorem 2.6 was also given by Tanigawa [30]. The high level ideas of his proof and the proof given in this subsection are similar. By using our notation the main lemma [30, Lemma 4.1] can be stated as follows: if v is a vertex of degree at least $d+1$ in G, $G-v$ is rigid in ${\mathbb {R}}^d$, and $\textrm{Clique}(G,V-\{v\})$ is globally rigid in ${\mathbb {R}}^d$, then G is globally rigid in ${\mathbb {R}}^d$. This statement is a special case of the “only if" direction of our Lemma 4.4.

4.4 The Second Contraction Lemma

As a corollary of Lemma 4.1, it can be deduced that if $G[V_0]$ is a (u, v)-rigid subgraph of a graph G, $V_1$ is the vertex set of a component of $G-V_0$ and $\{u,v\}$ is weakly globally linked in $G/V_1$, then $\{u,v\}$ is weakly globally linked in G. In this subsection we shall prove the converse of this statement, see Lemma 4.7 below.

We shall need some new notions and an auxiliary lemma. A configuration of a set U is a function that maps U into ${\mathbb {R}}^d$. Two configurations $p_1,p_2$ of U are said to be congruent if $||p_1(u)-p_1(v)||=||p_2(u)-p_2(v)||$ for all $u,v\in U$. Suppose that p and q are two incongruent configurations of a set U. We call a point $x\in {\mathbb {R}}^d$ (q, p)-feasible if there exists a point $y\in {\mathbb {R}}^d$ such that $||p(u)-x||=||q(u)-y||$ for all $u\in U$. We then call y a (q, p)-associate of x. Observe that if $\pi$ is an isometry of ${\mathbb {R}}^d$, then the set of (q, p)-feasible points is equal to the set of $(\pi \circ q, p)$-feasible points. The affine hull of a set $X\subseteq {\mathbb {R}}^d$ will be denoted by Aff(X).

Lemma 4.6

Let p be a configuration of a set U. Suppose that $Q=\{q_1,\dots ,q_k\}$ is a non-empty set of configurations of U such that $q_i$ is not congruent to p, for all $1\le i\le k$. Let $F_i$ be the set of $(q_i,p)$-feasible points, $1\le i\le k$. Then ${\mathbb {R}}^d-\bigcup _{i=1}^k F_i$ is a non-empty open set.

Proof

Let $S={\mathbb {R}}^d-\bigcup _{i=1}^k F_i$. We claim that $F_i$ is closed for all $1\le i\le k$, which will imply that S is open. Let $x_j\rightarrow x$ be a convergent sequence with $x_j\in F_i$, $j\in {\mathbb {N}}$, and let $y_j$ be a $(q_i,p)$-associate of $x_j$. The set $\{y_j:j\in {\mathbb {N}}\}$ is bounded. Hence there exists a convergent subsequence $y_{j_{\ell }}\rightarrow y$. Then y is a $(q_i,p)$-associate of x, which gives $x\in F_i$. This proves the claim.

In the rest of the proof we show that S is non-empty. Notice that $|U|\ge 2$ must hold. We shall prove the following stronger statement by induction on |U|: for every $a\in U$ we have

$$\begin{aligned} S\cap \text {Aff}(p(U-\{a\}))\ne \emptyset . \end{aligned}$$

(1)

First suppose that $|U|=2$, and let $U=\{a,b\}$. Then we have $||q_i(a)-q_i(b)||\ne ||p(a)-p(b)||$, since $q_i$ and p are not congruent. Thus $p(b)\in S$ and hence (1) follows.

Next suppose that $|U|\ge 3$. Let

$$\begin{aligned} Q'=\{q\in Q: p|_{U-\{a\}}\ \hbox {is not congruent to}\ q|_{U-\{a\}}\}, \end{aligned}$$

and let $Q''=Q-Q'$. By putting $F'=\bigcup _{q_i\in Q'}F_i$ and $F''=\bigcup _{q_i\in Q''}F_i$, we have $S={\mathbb {R}}^d-F'-F''$. By induction, the set $\textrm{Aff}(p(U-\{a,b\}))-F'$ is non-empty for every $b\in U-\{a\}$. Since $F'$ is closed, this implies that

$$\begin{aligned} \textrm{Aff}(p(U-\{a\}))-F'\ \hbox { is non-empty and relatively open in}\ \textrm{Aff}(p(U-\{a\})). \end{aligned}$$

(2)

We claim that for all $q_i \in Q''$ the set

$$\begin{aligned}{} & {} F_i\cap \textrm{Aff}(p(U-\{a\}))\ \hbox { is either empty or a proper affine subspace of} \nonumber \\{} & {} \textrm{Aff}(p(U-\{a\})). \end{aligned}$$

(3)

To prove the claim, let $q_i\in Q''$. By replacing $q_i$ with $\pi \circ q_i$, where $\pi$ is an appropriate isometry of ${\mathbb {R}}^d$, we may assume that $p|_{U-\{a\}}= q_i|_{U-\{a\}}$. Then it follows from the incongruency of p and $q_i$ that $p(a)\ne q_i(a)$. Suppose that $x\in \textrm{Aff}(p(U-\{a\}))$ and y is a $(q_i,p)$-associate of x. Then there exists an isometry that fixes each point of $p(U-\{a\})$ and maps x to y. This isometry fixes each point of $\textrm{Aff}(p(U-\{a\}))$, therefore, $y=x$. So the only possible $(q_i,p)$-associate of x is x itself. It follows that x is $(q_i,p)$-feasible if and only if $||x-p(a)||=||x-q_i(a)||$, that is, if x is in the bisector hyperplane H of p(a) and $q_i(a)$. Since $q_i$ and p are not congruent, we obtain $\textrm{Aff}(p(U-\{a\}))\not \subseteq H$. This proves the claim.

The lemma follows by noting that (2) and (3) yield that the set $S\cap \text {Aff}(p(U-\{a\}))=\big (\textrm{Aff}(p(U-\{a\}))-F'\big )-F''$ is non-empty, and hence (1) holds. $\square$

Lemma 4.7

Let $G=(V,E)$ be a graph, $u,v\in V$, and suppose that $G[V_0]$ is a (u, v)-rigid subgraph of G. Let $V_1$ be the vertex set of some component of $G-V_0$. Then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^d$ if and only if $\{u,v\}$ is weakly globally linked in $G/V_1$ in ${\mathbb {R}}^d$.

Proof

Since $G/V_1$ can be obtained from G by contracting edges not induced by $V_0$, the “if" direction follows by repeated applications of Lemma 4.1. To prove the “only if" direction suppose that $\{u,v\}$ is weakly globally linked in G and let (G, p) be a generic realization of G in which $\{u,v\}$ is globally linked. Let $v_1$ be the vertex of $G/V_1$ obtained by the contraction of $V_1$ in G. We shall prove that $p|_{V-V_1}$ has an extension to $(V-V_1)\cup \{v_1\}$ that is a generic realization of $G/V_1$ in which $\{u,v\}$ is globally linked. We may assume that $\{u,v\}$ is not globally linked in $(G-V_1,p|_{V-V_1})$, for otherwise we are done by choosing an arbitrary generic extension.

Let $q_1,...,q_k$ be a maximal set of pairwise incongruent configurations of $V_0$ such that, for $1\le i \le k$, there exists some realization $(G-V_1, r_i)$ equivalent to $(G-V_1, p|_{V-V_1})$ with $r_i|_{V_0} =q_i$ and $||r_i(u)-r_i(v)||\ne ||p(u)-p(v)||$. By our assumption $k\ge 1$. Since $G[V_0]$ is rigid, p is generic and $(G[V_0],q_i)$ is equivalent to $(G[V_0],p|_{V_0})$, Proposition 2.1 implies that k is finite. For $1\le i\le k$, the configurations $q_i|_{N_G(V_1)}$ and $p|_{N_G(V_1)}$ are incongruent, for otherwise $q_i$ would be extendible to a configuration $q_i'$ so that $(G,q_i')$ is equivalent to (G, p), contradicting the assumption that $\{u,v\}$ is globally linked in (G, p).

Applying Lemma 4.6 to $N_G(V_1)$, $p|_{N_G(V_1)}$ and the set $Q=\{q_1|_{N_G(V_1)},\dots , q_k|_{N_G(V_1)}\}$ gives that there is some $x=(x_1,\dots , x_d)\in {\mathbb {R}}^d$ for which x is not $(q_i|_{N_G(V_1)},p|_{N_G(V_1)})$-feasible for all $i\in \{1,\dots ,k\}$ and for which $p(V-V_1)\cup \{x\}$ is generic. We can now complete the proof of the lemma by considering the generic realization $(G/V_1,{\overline{p}})$, where ${\overline{p}}|_{V-V_1}=p|_{V-V_1}$ and ${\overline{p}}(v_1)=x$. Then $\{u,v\}$ is globally linked in $(G/V_1,{\overline{p}})$. Indeed, the existence of an equivalent realization $(G/V_1,q)$ with $||q(u)-q(v)||\ne ||{\overline{p}}(u)-{\overline{p}}(v)||$ would imply that $q|_{V_0}$ is congruent to $q_i$ for some $1\le i\le k$ and that x is $(q_i|_{N_G(V_1)},p|_{N_G(V_1)})$-feasible, contradicting the choice of x. $\square$

By using the notation of Lemma 4.7, let $e=s_1s_2\in E$ be an edge with $s_1,s_2\in V_1$. Applying the lemma to the graph G/e gives that $\{u,v\}$ is weakly globally linked in G/e if and only if it is weakly globally linked in $G/V_1$. It follows that $\{u,v\}$ is weakly globally linked in G/e if and only if it is weakly globally linked in G; cf. Lemma 4.1.

5 Weakly Globally Linked Pairs in ${\mathbb {R}}^2$

In this section we focus on the $d=2$ case. Thus, we shall occasionally write that a graph is (globally) rigid to mean that it is (globally) rigid in ${\mathbb {R}}^2$, and we may similarly omit the dimension when referring to global linkedness of vertex pairs in graphs. This section contains one of our main results, a characterization of weakly globally linked pairs in graphs.

5.1 Weakly Globally Linked Pairs in 3-Connected Graphs

We start with the special case of 3-connected graphs. By Lemma 3.3 it suffices to consider non-adjacent linked pairs $\{u,v\}$ of G, or equivalently, pairs $\{u,v\}$ for which there exists some subgraph $G_0=(V_0,E_0)$ of G with $u,v\in V_0$ such that $G_0+uv$ is an ${{{\mathcal {R}}}}_2$-circuit.

Theorem 5.1

Let $G=(V,E)$ be a 3-connected graph and $u,v\in V$ with $uv\notin E$. Suppose that $G_0=(V_0,E_0)$ is a subgraph of G with $u,v\in V_0$ such that $G_0+uv$ is an ${{{\mathcal {R}}}}_2$-circuit. Then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^2$ if and only if $\textrm{Clique}(G,V_0)$ is globally rigid in ${\mathbb {R}}^2$.

Proof

By Lemma 2.4, $G[V_0]$ is rigid, and thus sufficiency follows from Theorem 4.5. To prove the other direction suppose, for a contradiction, that $\{u,v\}$ is weakly globally linked in G but $\textrm{Clique}(G,V_0)$ is not globally rigid. Since $G_0+uv$ is redundantly rigid, so is $\textrm{Clique}(G,V_0)+uv$. The 3-connectivity of G implies that $\textrm{Clique}(G,V_0)$ is 3-connected. Thus $\textrm{Clique}(G,V_0)+uv$ is globally rigid by Theorem 2.6. Hence $\{u,v\}$ is globally loose in $\textrm{Clique}(G,V_0)$ by Lemma 3.1. As G can be obtained from $\textrm{Clique}(G,V_0)$ by clique sum operations and removing edges, Lemma 3.5 implies that $\{u,v\}$ is globally loose in G, a contradiction. $\square$

5.2 Weakly Globally Linked Pairs and 2-Separators

In this subsection we shall prove some lemmas that describe, among others, how weak global linkedness is affected when the graph is cut into two parts along a separating pair of vertices. These lemmas will enable us to reduce the question of whether a linked pair of vertices in a graph G is weakly globally linked to the case when G is 3-connected. We shall also need the following extension of [17, Corollary 5].

Lemma 5.2

Let $G=(V,E)$ be a rigid graph, $ab\in E$ an ${{{\mathcal {R}}}}_2$-bridge in G, and $u,v\in V$. Suppose that G has no (u, v)-rigid proper induced subgraph. Then the following hold.

• (a) Every generic framework $(G-ab,p)$ has a flexing that transforms it into a framework $(G-ab,q)$ such that $||p(a)-p(b)||= ||q(a)-q(b)||$ and $||p(u)-p(v)||\ne ||q(u)-q(v)||$.

• (b) The pair $\{u,v\}$ is globally loose in G.

Proof

It is clear that (a) implies (b). To prove (a) consider a minimally rigid spanning subgraph $H=(V,B)$ of G. Since ab is an $\mathcal{R}_2$-bridge, we have $ab\in B$. The graph $H+uv$ contains a unique ${{{\mathcal {R}}}}_2$-circuit C with $u,v\in V(C)$. Since G has no (u, v)-rigid proper induced subgraph, $C=H+uv$ must hold. Let $(G-ab,p)$ be a generic framework. By [17, Lemma 11] the framework $(H-ab,p)$ has a flexing $\pi$ that transforms it into a framework $(H-ab,q)$ such that $||p(a)-p(b)||= ||q(a)-q(b)||$ and $||p(u)-p(v)||\ne ||q(u)-q(v)||$. We claim that $\pi$ is a flexing of $(G-ab,p)$ as well. Consider an edge $xy\in E-B$. Since H is rigid, xy belongs to an ${{{\mathcal {R}}}}_2$-circuit $C'$ of $H+xy$. Moreover, ab is an ${{{\mathcal {R}}}}_2$-bridge in G (as well as in its subgraph $H+xy$), and hence $C'$ does not contain ab. Thus there is a rigid subgraph of $H-ab$ (namely, $C'-xy$), which contains x and y. Hence $\pi$ does not change the distance between x and y, which completes the proof. $\square$

Lemma 5.3

Let $G=(V,E)$ be a rigid graph, let $z\in V$ with $N_G(z)=\{x,y\}$, and let $u,v\in V-\{z\}$. Then $\{u,v\}$ is weakly globally linked in $G-z+xy$ if and only if $\{u,v\}$ is weakly globally linked in G.

Proof

Let $G_1=G-z+xy$. Observe that $G_1$ is isomorphic to G/zx. Since $G-z$ is rigid, we can use Lemma 4.1 to deduce that if $\{u,v\}$ is weakly globally linked in $G_1$, then $\{u,v\}$ is weakly globally linked in G. To prove the other direction suppose that $\{u,v\}$ is weakly globally linked in G. Then it is also weakly globally linked in $G+xy$. Since $G+xy$ is the clique sum of $G_1$ and a copy of $K_3$, Lemma 3.5 implies that $\{u,v\}$ is weakly globally linked in $G_1$. $\square$

A pair (a, b) of vertices of a 2-connected graph $H=(V,E)$ is called a 2-separator if $H-\{a,b\}$ is disconnected.

Lemma 5.4

Let $G=(V,E)$ be a rigid graph with $|V|\ge 4$ and (a, b) be a 2-separator in G. Let C be a connected component of $G-\{a,b\}$ and let $V_0=V(C)\cup \{a,b\}$. Suppose that $u,v\in V_0$. Then $\{u,v\}$ is weakly globally linked in G if and only if $\{u,v\}$ is weakly globally linked in $G[V_0]+ab$.

Proof

If $\{u,v\}$ is weakly globally linked in G, then it is easy to see, by using Lemma 3.5, that $\{u,v\}$ is weakly globally linked in $G[V_0]+ab$.

To prove that if $\{u,v\}$ is weakly globally linked in $G[V_0]+ab$, then $\{u,v\}$ is weakly globally linked in G, we use induction on |V|. If $|V|=4$, then we must have $G=K_4-e$ and $uv\in E$, so the statement is obvious. Suppose that $|V|\ge 5$. If there exists a (u, v)-rigid subgraph of $G[V_0]$, then, since $G[V_0]+ab$ can be obtained from G by a sequence of edge contractions, we can use Lemma 4.1 to deduce that $\{u,v\}$ is weakly globally linked in G. So in the rest of the proof we may assume that

$$\begin{aligned} G[V_0]\hbox { has no }(u,v)-\hbox {rigid subgraph.} \end{aligned}$$

(4)

In particular, $G[V_0]$ is not rigid. Hence, by the rigidity of G, it follows that $\{a,b\}$ is not linked in $G[V_0]$ and ab is an ${{{\mathcal {R}}}}_2$-bridge in $G[V_0]+ab$.

Since $\{u,v\}$ is weakly globally linked in $G[V_0]+ab$, Lemma 5.2(b) implies that there exists a (u, v)-rigid proper induced subgraph $G'=(V',E')$ of $G[V_0]+ab$. Suppose that $G'$ is vertex-minimal. By (4) we obtain $ab\in E'$ and $a,b\subset V'$. We consider three cases depending on the structure of $G[V_0]-V'$. Since $G'$ is a proper induced subgraph, we have $V_0-V'\not = \emptyset$. See Fig. 4.

Fig. 4

The case where $G[V_0]$ has no (u, v)-rigid subgraph

Case 1: $G[V_0]-V'$ has a component Z with $|V(Z)|\ge 2$.

By Lemma 4.7$\{u,v\}$ is weakly globally linked in $(G[V_0]+ab)/Z$. Since G and $G'$ are rigid, $G-V(Z)$ is also rigid, and Z has at least two neighbours in G. Hence G/Z is rigid. Thus we obtain, by induction, that $\{u,v\}$ is weakly globally linked in G/Z. By using that $G-V(Z)$ is rigid, Lemma 4.7 gives that $\{u,v\}$ is weakly globally linked in G.

Case 2: Each component of $G[V_0]-V'$ is a singleton and there exists a vertex $z\in V_0-V'$ with $d_G(z)=2$.

Let $N_G(z)=\{x,y\}$. By Lemma 5.3$\{u,v\}$ is weakly globally linked in $(G[V_0]+ab)-z+xy$. If $\{u,v\}=\{a,b\}$ and $|V_0|=3$, then $\{u,v\}$ is weakly globally linked in G by Lemma 4.1. So we may assume that $|V_0|\ge 4$, and hence (a, b) is a 2-separator of the rigid graph $G-z+xy$. Hence $\{u,v\}$ is weakly globally linked in $G-z+xy$ by induction. By using that G is rigid, Lemma 5.3 implies that $\{u,v\}$ is weakly globally linked in G.

Case 3: Each component of $G[V_0]-V'$ is a singleton and for each $z\in V_0-V'$ we have $d_G(z)\ge 3$.

We claim that for each $z\in V_0-V'$ and $x,y\in N_G(z)$ there is a rigid subgraph of $G'-ab$ which contains x and y. To see this let w be another neighbour of z, different from x, y, and let $G''$ be obtained from $G'-ab$ by adding vertex z and edges zx, zy, zw. The three edges incident with z in $G''$ cannot be ${{{\mathcal {R}}}}_2$-bridges, since it would imply, by using the rigidity of $G'$ and computing ranks, that $G''$ is (u, v)-rigid, contradicting (4). Thus there is an ${{{\mathcal {R}}}}_2$-circuit C in $G''$ containing z. Then C must contain x and y, too, and $C-z$ is a rigid subgraph of $G'-ab$ which contains x and y, as claimed.

The minimality of $G'$ implies that it has no (u, v)-rigid proper induced subgraph. Let $(G[V_0]+ab,p)$ be a generic realization. By Lemma 5.2(a) $(G'-ab,p|_{V'})$ has an equivalent realization $(G'-ab,q)$, for which $||p(u)-p(v)||\ne ||q(u)-q(v)||$, $||p(a)-p(b)||= ||q(a)-q(b)||$, and such that the distances between the linked pairs of $G'-ab$ are the same in the two realizations. Then, since each pair of neighbours of every $z\in V_0-V'$ is linked in $G'-ab$, it follows that $(G'-ab,q)$ can be extended to a realization $(G[V_0]+ab,q')$ that is equivalent to $(G[V_0]+ab,p)$. Hence $\{u,v\}$ is globally loose in $G[V_0]+ab$, a contradiction. This completes the proof. $\square$

We next extend Lemma 5.4 from rigid graphs to 2-connected graphs.

Lemma 5.5

Let $G=(V,E)$ be a 2-connected graph and $\{u,v\}$ a linked pair of vertices of G. Suppose that (a, b) is a 2-separator of G. Let C be a connected component of $G-\{a,b\}$, and let $V_0=V(C)\cup \{a,b\}$. Suppose that $u,v\in V_0$. Then $\{u,v\}$ is weakly globally linked in G if and only if $\{u,v\}$ is weakly globally linked in $G[V_0]+ab$.

Proof

If $\{u,v\}$ is weakly globally linked in G, then it follows from Lemma 3.5 that $\{u,v\}$ is weakly globally linked in $G[V_0]+ab$. To prove the “if" direction suppose that $\{u,v\}$ is weakly globally linked in $G[V_0]+ab$. Since $\{u,v\}$ is a linked pair, there is a (u, v)-rigid induced subgraph G[U] of G. If $\{a,b\}\not \subseteq U$, then U is a subset of $V_0$ and $G[V_0]+ab$ can be obtained from G by contracting edges which are not induced by U. Thus $\{u,v\}$ is weakly globally linked in G by Lemma 4.1. So we may suppose that $\{a,b\}\subseteq U$. Let $A_1,\dots , A_k$ be the components of $G-U$ contained in $V_0$, and let $B_1, \dots , B_l$ be the components of $G-U$ not contained in $V_0$. Observe that the rigidity of G[U] and the 2-connectivity of G imply that $G/A_1/\dots /A_k/B_1/\dots / B_k$ is rigid. Hence we have that

$$\begin{aligned}&\{u,v\} \text { is weakly globally linked in } G \\ \;\;\Leftrightarrow \;\;&\{u,v\} \text { is weakly globally linked in } G/A_1/\dots /A_k/B_1/\dots / B_k \\ \;\;\Leftrightarrow \;\;&\{u,v\} \text { is weakly globally linked in } G[V_0]/A_1/\dots /A_k + ab\\ \;\;\Leftrightarrow \;\;&\{u,v\} \text { is weakly globally linked in } G[V_0]+ab, \end{aligned}$$

where the first and third equivalence follows from Lemma 4.7 and the second equivalence follows from Lemma 5.4, using the rigidity of $G/A_1/\dots /A_k/B_1/\dots / B_k$. $\square$

The next lemma on the weak global linkedness of linked separating pairs follows from Lemma 5.5 by putting $\{a,b\}=\{u,v\}$. It can also be deduced from Lemma 4.1 by using that there is some component C of $G-\{u,v\}$ for which $\{u,v\}$ is linked in $G[V(C)\cup \{u,v\}]$.

Lemma 5.6

Let $G=(V,E)$ be a 2-connected graph, and $u,v\in V$ be a linked pair of vertices for which (u, v) is a 2-separator in G. Then $\{u,v\}$ is weakly globally linked in G.

We use the following operation to eliminate 2-separators. Let $G=(V,E)$ be a 2-connected graph, let (a, b) be a 2-separator in G, and let C be a connected component of $G-\{a,b\}$. We say that the graph $G[V(C)\cup \{a,b\}]+ab$ (when $ab\notin E$) or $G[V(C)\cup \{a,b\}]$ (when $ab\in E$) is obtained from G by a cleaving operation along (a, b). The graph ${\bar{G}}$ obtained from G by adding every edge ab, for which $ab\notin E$ and (a, b) is a 2-separator of G, is called the augmented graph of G.

The following lemma is easy to show by induction, using the cleaving operation.

Lemma 5.7

Let $G=(V,E)$ be a 2-connected graph and let $\{u,v\}$ be a non-adjacent vertex pair in G with $\kappa _G(u,v)\ge 3$. Then either (u, v) is a separating pair in G or there is a unique maximal 3-connected subgraph B of ${\bar{G}}$ with $\{u,v\}\subset V(B)$. In the latter case the subgraph B can be obtained from G by a sequence of cleaving operations. Furthermore, $uv\notin E(B)$, and if the pair $\{u,v\}$ is linked in G then it is also linked in B.

The subgraph B in Lemma 5.7 is called the 3-block of $\{u,v\}$ in G.

We are ready to state the main result of this section: a complete characterization of the non-adjacent weakly globally linked pairs in a graph G. By Lemma 3.3 and Lemma 3.4 we may assume that $\{u,v\}$ is linked and $\kappa _G(u,v)\ge 3$ (for otherwise $\{u,v\}$ is globally loose). By Lemma 3.5 we may also assume that G is 2-connected.

Theorem 5.8

Let $G=(V,E)$ be a 2-connected graph and let $\{u,v\}$ be a non-adjacent linked pair of vertices with $\kappa _G(u,v)\ge 3$. Then $\{u,v\}$ is weakly globally linked in G if and only if either

• (i) (u, v) is a separating pair in G, or

• (ii) $\textrm{Clique}(B,V_0)$ is globally rigid, where B is the 3-block of $\{u,v\}$ in G, and $B_0=(V_0,E_0)$ is a subgraph of B with $u,v\in V_0$ such that $B_0+uv$ is an $\mathcal{R}_2$-circuit.

Proof

The proof is by induction on the number h of vertex pairs $x,y\in V$ with $\kappa _G(x,y)=2$. If $h=0$, then $B=G$ and (ii) holds by Theorem 5.1. Suppose that $h\ge 1$ and let (a, b) be a 2-separator in G. If $\{a,b\}=\{u,v\}$ then Lemma 5.6 applies and (i) holds. Otherwise we can use Lemmas 5.5, 5.7, and induction, to complete the proof. $\square$

See Fig. 5 for an illustration of Theorem 5.8.

Fig. 5

Consider the graph G. The pair $\{u,v\}$ is linked in G, as there is a (u, v)-rigid subgraph of G, and we have $\kappa _G(u,v)=3$. B is the 3-block of $\{u,v\}$ in G. Consider the subgraph $B_0=(V_0,E_0)$ of B that is induced by the solid vertices. $B_0+uv$ is an ${{{\mathcal {R}}}}_2$-circuit. Since $\textrm{Clique}(B,V_0)$ is globally rigid, $\{u,v\}$ is weakly globally linked in G by Theorem 5.8

Further structural results on weakly globally linked pairs can be found in [20].

6 Concluding Remarks

6.1 Algorithmic Aspects

Theorem 5.8 and its proof shows that weak global linkedness of a vertex pair $\{u,v\}$ in a graph $G=(V,E)$ can be tested in $O(|V|^2)$ time, as efficient algorithms are available for each of the required subroutines. Basic graph algorithms can be used to test, in linear time, whether $\kappa _G(u,v)\ge 3$ holds and to find the maximal 2-connected block that contains u, v. After reducing the problem to the 2-connected case, the linear time algorithm of [14] can be applied to check whether (u, v) is a separating pair and (when it is not) to identify the 3-block B of $\{u,v\}$. (Note that B coincides with one of the so-called cleavage units of G.) Computing $\textrm{Clique}(G,X)$ for a given $X\subseteq V$ is also easy.

Testing whether $\{u,v\}$ is linked, and (when it is linked) finding an ${{{\mathcal {R}}}}_2$-circuit of $G+uv$ containing uv can be done in $O(|V|^2)$ time [2]. Within the same time bound, we can test whether a graph is globally rigid, see, e.g., [2, 23].

6.2 Higher Dimensions

For $d\ge 3$, a pair $\{u,v\}$ may be linked in a graph $G_0$ in ${\mathbb {R}}^d$, even if $G_0$ contains no (u, v)-rigid subgraph. Thus the following statement, suggested by D. Garamvölgyi, is an extension of Lemma 4.1.

Lemma 6.1

Let $G=(V,E)$ be a graph, $u,v\in V_0\subseteq V$, and suppose that $\{u,v\}$ is linked in $G[V_0]$ in ${\mathbb {R}}^d$. Let $e\in E-E(G[V_0])$ be an edge. If $\{u,v\}$ is weakly globally linked in G/e in ${\mathbb {R}}^d$, then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^d$.

The proof of Lemma 6.1 is essentially the same as that of Lemma 4.1; the only change required is to substitute Lemma 6.2 below for Proposition 2.1. For the definitions of the new notions appearing in the next proof, see, e.g., [21, 29].

Lemma 6.2

Let $\{u,v\}$ be a linked pair in a graph G in ${\mathbb {R}}^d$ and let (G, p) be a generic realization of G in ${\mathbb {R}}^d$. Then the set

$$\begin{aligned} \{ ||q(u) - q(v)||: (G,q) \ \hbox {is equivalent to}\ (G,p) \} \end{aligned}$$

is finite.

Proof

Suppose, for a contradiction, that there exists an infinite sequence of frameworks $(G,q_i)$, $i\ge 1$, equivalent to (G, p), in which the distances $||q_i(u) - q_i(v)||$ are pairwise different. We may assume that G is connected and $q_i(u)$ is the origin for all $i\ge 1$. Then each $(G,q_i)$ is in the interior of a ball of radius K, for some constant K. Thus, by choosing a subsequence, if necessary, we may assume that $(G,q_i)$ is convergent, with limit (G, q).

It was proved in [3] that if two frameworks are equivalent and at least one of them is generic, then their equilibrium stresses are the same.

(For a proof, see also [25, Lemma 15.24].) Thus (G, p) and (G, q) have the same equilibrium stresses. In particular, the rank of the rigidity matrix of (G, q) is equal to the maximum (generic) rank of G. This fact and the linkedness of $\{u,v\}$ imply that the ranks of the rigidity matrices of $(G+uv,q)$ and (G, q) are the same. So their kernels are the same, too. Thus every infinitesimal motion $x:V\rightarrow {\mathbb {R}}^{d}$ of (G, q) satisfies $(q(u)-q(v))^T(x(u)-x(v)) = 0$. By continuity this holds for all frameworks in a small enough neighbourhood of (G, q).

Consider the frameworks $q'_i = (q_{i+1} + q_i)/2$, which converge to q. Let $x_i = (q_{i+1} - q_i)$. The well-known averaging technique shows that for vertices $a,b\in V$,

$$\begin{aligned} (q'_i(a) - q'_i(b))^T(x_i(a)-x_i(b))= 0 \;\;\Leftrightarrow \;\; ||q_{i+1}(a)-q_{i+1}(b)||= ||q_i(a)-q_i(b)||. \end{aligned}$$

(For a proof see, e.g., [5, Theorem 13].) Hence, $x_i$ is an infinitesimal motion of $q'_i$ with $(q'_i(u) - q'_i(v))^T(x_i(u)-x_i(v))\not = 0$, for all $i\ge 1$, a contradiction. $\square$

We obtain the following corollary of Lemma 6.1.

Corollary 6.3

Let $G=(V,E)$ be a graph, $u,v\in V_0\subseteq V$, and suppose that $\{u,v\}$ is linked in $G[V_0]$ in ${\mathbb {R}}^d$. Suppose that there is a uv-path in G that is internally disjoint from $V_0$. Then $\{u,v\}$ is weakly globally linked in G in ${\mathbb {R}}^d$.

For a recent application of Corollary 6.3, see [31].

6.3 Minimally Globally Rigid Graphs

A graph $G=(V,E)$ is called minimally globally rigid in ${\mathbb {R}}^d$ if it is globally rigid in ${\mathbb {R}}^d$ and for every edge $e\in E$ the graph $G-e$ is not globally rigid in ${\mathbb {R}}^d$. Garamvölgyi and Jordán [9, Theorem 3.3] proved that if $G=(V,E)$ is minimally globally rigid in ${\mathbb {R}}^d$ and $|V|\ge d+1$, then

$$\begin{aligned} |E|\le (d+1)|V|-\left( {\begin{array}{c}d+2\\ 2\end{array}}\right) . \end{aligned}$$

Moreover, as it is noted in [9], for every globally rigid graph G in ${\mathbb {R}}^d$ on at least $d+1$ vertices, and for every minimally rigid spanning subgraph $G_0$ of G, there exists a globally rigid spanning subgraph of G that contains $G_0$ and has at most $(d+1)|V|-\left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$ edges.

The authors also conjectured that a minimally globally rigid graph in ${\mathbb {R}}^d$ is in fact ${{{\mathcal {R}}}}_{d+1}$-independent, see [9, Conjecture 4.2]. The truth of this conjecture would imply that a minimally globally rigid graph $G=(V,E)$ in ${\mathbb {R}}^d$ is not only sparse, but every subgraph of G is sparse: for each $U\subseteq V$ with $|U|\ge d+1$ we have $|E(U)|\le (d+1)|U|- \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$.

Next, we prove this upper bound in the special case when the subgraph induced by U is rigid.

Theorem 6.4

Let $G=(V,E)$ be a minimally globally rigid graph in ${\mathbb {R}}^d$. Suppose that $U\subseteq V$, $|U|\ge d+1$ and G[U] is rigid. Then $|E(U)|\le (d+1)|U|- \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$.

Proof

Let $G_0=(U,E_0)$ be a minimally rigid spanning subgraph of G[U]. Since G is globally rigid, so is $\textrm{Clique}(G,U)$. Thus, by the results of [9], there is a globally rigid spanning subgraph $G'=(U,E')$ of $\textrm{Clique}(G,U)$ that contains $G_0$ and has at most $(d+1)|U|-\left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$ edges. Suppose, for a contradiction, that there is some edge $e=uv\in E(U)-E'$. Note that $G[U]-e$ is rigid. Then $G'$ is a subgraph of $\textrm{Clique}(G-e,U)$, and hence $\{u,v\}$ is weakly globally linked in $G-e$ by Theorem 4.5. Since e is critical in G, this contradicts Lemma 3.1. It follows that G[U] is a subgraph of $G'$; therefore $|E(U)|\le |E'|\le (d+1)|U|-\left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$. $\square$

For $d=2$ we can extend Theorem 6.4 to all subsets $U\subseteq V$ with $|U|\ge d+1$, see [9, Theorem 4.7]. Here we give a short new proof of this statement.

Theorem 6.5

[9] Let $G=(V,E)$ be a minimally globally rigid graph in ${\mathbb {R}}^2$. Suppose that $U\subseteq V$ and $|U|\ge 3$. Then $|E(U)|\le 3|U|- 6$.

Proof

By Theorem 6.4 the statement is true if G[U] is rigid. Suppose that G[U] is not rigid, that is, $r_2(G[U])\le 2|U|-4$. We may assume that G[U] has no isolated vertices. It is well-known (see, e.g., [18]) that for the collection $G_i=(V_i,E_i)$, $1\le i\le k$, of the maximal rigid subgraphs of G[U] we have $\sum _{i=1}^k (2|V_i|-3)=r_2(G[U])$. For an integer $h\ge 2$ let $f(h) = 3h-6$, if $h\ge 3$, and let $f(h)=1$ otherwise. Then we have

$$\begin{aligned} |E(U)|= \sum _{i=1}^k |E_i| \le \sum _{i=1}^k f(|V_i|)\le \sum _{i=1}^k \frac{3}{2}(2|V_i|-3)=\frac{3}{2}r_2(G[U])\le 3|U|-6, \end{aligned}$$

where the first inequality follows from Theorem 6.4. $\square$

Recently, the d-dimensional version of Theorem 6.5 was proved by Garamvölgyi [6]. In that paper Garamvölgyi introduced stress-linked vertex pairs of graphs, building upon the concepts of [3, 12]. He proved that stress-linkedness in ${\mathbb {R}}^d$ implies global linkedness in ${\mathbb {R}}^d$ and conjectured that the converse is also true. He also gave a combinatorial characterization of stress-linked pairs in ${\mathbb {R}}^2$, which matches the conjectured characterization of globally linked pairs in ${\mathbb {R}}^2$ proposed in [16].