Abstract
More than 25 years ago, inspired by applications in computer graphics, Chazelle et al. studied the following question: is it possible to cut any set of n lines or other objects in \({\mathbb R}^3\) into a subquadratic number of fragments such that the resulting fragments admit a depth order? They managed to prove an \(O(n^{9/5})\) bound on the number of fragments, but only for the very special case of bipartite weavings of lines. Since then only little progress was made, until a breakthrough in 2016 by Aronov and Sharir, who showed that \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) fragments suffice for any set of lines. In a follow-up paper Aronov et al. proved an \(O(n^{3/2+\varepsilon })\) bound for triangles, but their method uses high- (albeit constant-) degree algebraic arcs to perform the cuts. Hence, the resulting pieces have curved boundaries. Thus the following natural version of the problem is still wide open: is it possible to cut any collection of n disjoint triangles in \({\mathbb R}^3\) into a subquadratic number of triangular fragments that admit a depth order? And if so, can we compute the cuts efficiently? We answer this question by presenting an algorithm that cuts any set of n disjoint triangles in \({\mathbb R}^3\) into \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\) triangular fragments that admit a depth order. The running time of our algorithm is \(O(n^{3.69})\). We also prove a refined bound that depends on the number, K, of intersections between the projections of the triangle edges onto the xy-plane: we show that \(O(n^{1+\varepsilon } + n^{1/4} K^{3/4}{{\,\mathrm{polylog}\,}}n)\) fragments suffice to obtain a depth order. This result extends to xy-monotone surface patches bounded by a constant number of bounded-degree algebraic arcs in general position, constituting the first subquadratic bound for surface patches.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let T and \(T'\) be two disjoint triangles (or other objects) in \({\mathbb R}^3\). We say that T is below \(T'\)—or, equivalently, that \(T'\) is above T—when there is a vertical line \(\ell \) intersecting both T and \(T'\) such that \(\ell \cap T\) is below \(\ell \cap T'\). We denote this relation by \(T\prec T'\). Note that two triangles may be unrelated by the \(\prec \)-relation, namely when their vertical projections onto the xy-plane are disjoint. Now let \(\mathcal {T}\) be a collection of n disjoint triangles in \({\mathbb R}^3\). A depth order on \(\mathcal {T}\) (for the vertical direction) is an ordering that is consistent with the \(\prec \)-relation, that is, an ordering \(T_1,\ldots ,T_n\) of the triangles in \(\mathcal {T}\) such that \(T_i\prec T_j\) implies \(i<j\).
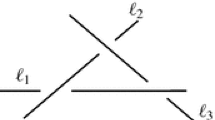
Depth orders play an important role in many applications. For example, the Painter’s Algorithm from computer graphics performs hidden-surface removal by rendering the triangles forming the objects in a scene one by one, drawing each triangle “on top of” the already drawn ones. To give a correct result the Painter’s Algorithm must handle the triangles in depth order with respect to the viewing direction. Several object-space hidden-surface removal algorithms and ray-shooting data structures need a depth order as well. Depth orders also play a role when one wants to assemble a product by putting its constituent parts one by one into place using vertical translations [26]. The problem of computing a depth order for a given set of objects has therefore received considerable attention [1, 12, 15, 16]. However, a depth order does not always exist since there can be cyclic overlap, as illustrated in Fig. 1 (i). In such cases the algorithms above simply report that no depth exists. We would then like to cut the triangles into fragments such that the resulting set of fragments is acyclic, that is, admits a depth order. This gives rise to the following problem: How many fragments are needed in the worst case to ensure that a depth order exists? And how efficiently can we compute a set of cuts resulting in a small set of fragments admitting a depth order?
The problem of bounding the worst-case number of fragments needed to remove all cycles from the depth-order relation has a long history. In the special case of lines (or line segments) one can easily get rid of all cycles using \(O(n^2)\) cuts: project the lines onto the xy-plane and cut each line at its intersection points with the other lines. (Here the cut points are removed from the fragments, so they become disjoint.) A lower bound on the worst-case number of cuts is \(\Omega (n^{3/2})\) [11]. It turned out to be amazingly hard to get any subquadratic upper bound. In 1991 Chazelle et al. [11] obtained such a bound, but only for so-called bipartite weavings; see Fig. 1 (ii). Moreover, their \(O(n^{9/5})\) bound is still far away from the \(\Omega (n^{3/2})\) lower bound. Later Aronov et al. [6] obtained a subquadratic upper bound for general sets of lines, but they only get rid of all triangular cycles—that is, cycles consisting of three lines—and their bounds are only slightly subquadratic: they use \(O(n^{2-1/69}\log ^{16/69} n)\) cuts to remove all triangular cycles. Finally, several authors studied the algorithmic problem of computing a minimum-size complete cut set—a complete cut set is a set of cuts that removes all cycles from the depth-order relation—for a set of lines (or line segments). Solan [24] and Har-Peled and Sharir [19] gave algorithms that produce a complete cut sets of size roughly \(O(n\sqrt{{{\textsc {opt}}}})\), where \({{\textsc {opt}}} \) is the minimum size of any complete cut set for the given lines. Aronov et al. [4] showed that computing a minimum-size complete cut set for a set of line segments is an np-hard problem, and they presented an algorithm that computes a complete cut set of size \(O({{\textsc {opt}}} \cdot \log {{\textsc {opt}}} \cdot \log \log {{\textsc {opt}}})\) in \(O(n^{4+2\omega } \log ^2n)=O(n^{8.764})\) time, where \(\omega <2.373\) is the exponent of the best matrix-multiplication algorithm.
Eliminating depth cycles from a set of triangles is even harder than it is for lines. The trivial bound on the number of fragments is \(O(n^3)\), which can for instance be obtained by taking a vertical cutting plane containing each triangle edge. Paterson and Yao [21] showed already in 1990 that any set of disjoint triangles admits a so-called binary space partition (BSP) of size \(O(n^2)\). This immediately implies an \(O(n^2)\) bound on the number of fragments needed to remove all cycles. Indeed, a BSP ensures that the resulting set of triangle fragments is acyclic for any direction, not just for the vertical direction. Better bounds on the size of BSPs are known for fat objects (or, more generally, low-density sets) [13] and for axis-aligned objects [2, 22, 25], but for arbitrary triangles there is an \(\Omega (n^2)\) lower bound on the worst-case size of a BSP [9]. Hence, a different approach is necessary to get a subquadratic bound on the number of fragments needed to obtain a depth order.
Very recently, using Guth’s polynomial partitioning technique [18], Aronov and Sharir [8] achieved a breakthrough by proving that any set of n lines in \({\mathbb R}^3\) can be cut into \(O(n^{3/2} {{\,\mathrm{polylog}\,}}n)\) fragments that admit a depth order. A complete cut set of size \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) can then be computed using the algorithm of Aronov et al. [4] mentioned above. Aronov and Sharir also gave a more refined bound for line segments, which depends on the number of intersections, K, between the segments in the projection. More precisely, they show that \(O(n + n^{1/2} K^{1/2}{{\,\mathrm{polylog}\,}}n)\) cuts suffice. The latter result extends to algebraic arcs [8, 23]. In a follow-up paper, Aronov et al. [7] extended the result to triangles: they show that, for any fixed \(\varepsilon >0\), any set of disjoint triangles can be cut into \(O(n^{3/2+\varepsilon })\) fragments that admit a depth order. This may seem to almost settle the problem for triangles, but the technique of Aronov et al. has a fundamental drawback:Footnote 1 it does not result in triangular fragments, since it cuts the triangles using algebraic arcs whose degree is exponential in the parameter \(\varepsilon \) appearing in the \(O(n^{3/2+\varepsilon })\) bound.
Arguably, the natural way to pose the problem for triangles is to require the fragments to be triangular as well—polygonal fragments can always be decomposed further into triangles, without increasing the number of fragments asymptotically (a consequence of Euler’s formula). Indeed, Aronov et al. state that “It is a natural open problem to determine whether a similar bound can be achieved with straight cuts [...]. Even a weaker bound, as long as it is subquadratic and generally applicable, would be of great significance.” Another open problem stated by Aronov et al. is to extend the result to surface patches:Footnote 2 “Extending the technique to curved objects (e.g., spheres or spherical patches) is also a major challenge.”
Our contribution We prove that any set \(\mathcal {T}\) of n disjoint triangles in \({\mathbb R}^3\) can be cut into \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\) triangular fragments that admit a depth order. Thus we overcome the fundamental drawback of the method of Aronov et al. although admittedly our bound is not as sharp as theirs. We also present an algorithm to perform the cuts in \(O(n^{5/2+\omega /2}\log ^2 n)=O(n^{3.69})\) time, where \(\omega <2.373\) is, as above, the exponent of the best matrix-multiplication algorithm. As a byproduct of our technique, we improve the time to compute a complete cut set of size \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) for a collection of lines: we show that a simple trick reduces the running time fromFootnote 3\(O(n^{4+2\omega }\log ^2 n)\) to \(O(n^{3+\omega }\log ^2 n)\).
We also present a more refined approach that yields a bound of \(O(n^{1+\varepsilon } + n^{1/4} K^{3/4}{{\,\mathrm{polylog}\,}}n)\) on the number of fragments, where K is the number of intersections between the triangle edges in the projection. This result extends to xy-monotone surface patches bounded by a constant number of bounded-degree algebraic arcs in general position. Thus we make progress on both open problems posed by Aronov et al.
Finally, as a minor contribution we describe a general method showing that bounds for eliminating cycles among segments in general position, carry over (up to a logarithmic factor) to segments not in general position. This is useful since dealing with degeneracies can be painful—indeed, the conference version of the paper by Aronov and Sharir [8] assumed the segments were in general position, and in the journal version such an assumption is still made for the algorithmic result. Most degeneracies can be handled by a straightforward perturbation argument, but one case—parallel segments that overlap in the projection—requires some new ideas. Being able to handle degeneracies for segments implies that our method for triangles can handle degeneracies as well.
2 Eliminating Cycles Among Triangles
Overview of the method. We first prove a proposition that gives conditions under which the existence of a depth order for a set of triangles is implied by the existence of a depth order for the triangle edges. The idea is then to take a complete cut set for the triangle edges—there is such a cut set of size \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) by the results of Aronov and Sharir—and “extend” the cuts (by taking vertical planes through the cut points) so that the conditions of the proposition are met. A straightforward extension would generate too many triangle fragments, however. Therefore our cutting procedure has two phases. In the first phase we localize the problem by partitioning space into regions such that (i) the collection of regions admits a depth order, and (ii) each region is intersected by only few triangles. (This localization is also the key to speeding up the algorithm for lines.) In the second phase we then locally extend the cuts from a complete cut set inside each region, so that the conditions of the proposition are met and we obtain an acyclic set of fragments.
Notation and terminology. Let \(\mathcal {T}\) denote the given set of disjoint non-vertical triangles, let \(\mathcal {E}\) denote the set of edges of the triangles in \(\mathcal {T}\), and let \(\mathcal {V}\) denote the set of vertices of the triangles. We assume the triangles in \(\mathcal {T}\) are closed. However, at the places where a triangle is cut it becomes open. Thus the edges of a triangle fragment that are (parts of) edges in \(\mathcal {E}\) are part of the fragment, while edges that are induced by cuts are not. We denote the vertical projection of an object o in \({\mathbb R}^3\) onto the xy-plane by \(\overline{o}\).
A proposition relating depth orders for edges to depth orders for triangles. We define a column to be a 3-dimensional region \(C_\Delta := \Delta \times (-\infty ,+\infty )\), where \(\Delta \) is an open convex polygon on the xy-plane. Our cutting procedure is based on the following proposition.
Proposition 2.1
Let \(\mathcal {T}\) be a set of disjoint triangles in \({\mathbb R}^3\), and let \(\mathcal {E}\) be the set of edges of the triangles in \(\mathcal {T}\). Let \(C_\Delta \) be a column whose interior \(\mathrm {int}(C_\Delta )\) does not contain a vertex of any triangle in \(\mathcal {T}\), and let \(\mathcal {T}_\Delta := \{ T\cap \mathrm {int}(C_\Delta ) : T\in \mathcal {T}\}\) and \(\mathcal {E}_{\Delta } := \{ e\cap \mathrm {int}(C_\Delta ) : e\in \mathcal {E}\}\). Then \(\mathcal {T}_{\Delta }\) admits a depth order if \(\mathcal {E}_{\Delta }\) admits a depth order.
Proof
For a triangle \(T_i\in \mathcal {T}\), define \(P_i := T_i \cap \mathrm {int}(C_\Delta )\). Thus \(\mathcal {T}_{\Delta } = \{ P_i : T_i\in \mathcal {T}\}\). Assume \(\mathcal {E}_{\Delta }\) admits a depth order and suppose for a contradiction that \(\mathcal {T}_{\Delta }\) does not.
Consider a cycle \(\mathcal {C}:= P_0\prec P_1\prec \cdots \prec P_{k-1}\prec P_0\) in \(\mathcal {T}_{\Delta }\). As observed by Aronov et al. [7] we can associate a (not necessarily unique) closed curve in \({\mathbb R}^3\) to \(\mathcal {C}\), as follows. For each pair \(P_i,P_{i+1}\) of consecutive polygons in \(\mathcal {C}\)—here and in the rest of the proof indices are taken modulo k—let \(b_i\in P_i\) and \(a_{i+1}\in P_{i+1}\) be points such that the segment \(b_i a_{i+1}\) is vertical. We refer to the closed polygonal curve whose ordered set of vertices is \(b_1, a_2, b_2, a_3, \ldots , a_k, b_k, a_1\) as a witness curve for \(\mathcal {C}\). We call the vertical segments \(b_i a_{i+1}\) the connections of \(\Gamma (\mathcal {C})\), and we call the segments \(a_i b_i\) the links of \(\Gamma (\mathcal {C})\). Since the connections are vertical, we have \(\overline{a_{i+1}}=\overline{b_{i}}\) and so we can write \(\overline{\Gamma (\mathcal {C})}\) as \(\overline{a_1},\overline{a_2},\ldots ,\overline{a_k},\overline{a_1}\). (Recall that \(\overline{o}\) denotes the projection of an object o onto the xy-plane.) Note that \(\overline{a_i}\in \overline{P_{i-1}}\cap \overline{P_i}\) for all i. In general, the points \(a_i\) and \(b_i\) can be chosen in many ways and so there are many possible witness curves. We will need a specific witness curve, as specified next. We say that a link \(a_i b_i\) is good if \(a_i\) and \(b_i\) lie on the same edge of their polygon \(P_i\)—this edge is also an edge in \(\mathcal {E}_{\Delta }\)—and we say that \(a_i b_i\) is bad otherwise. We now define the weight of a witness curve \(\Gamma \) to be the number of bad links in \(\Gamma \), and we define \(\Gamma (\mathcal {C})\) to be any minimum-weight witness curve for \(\mathcal {C}\).
Now consider a minimal cycle \(\mathcal {C}^*:= P_0 \prec P_1\prec \cdots \prec P_{k-1}\prec P_0\) in \(\mathcal {T}_{\Delta }\), where a cycle is minimal if any strict subset of polygons from the cycle is acyclic. We will argue that we can find a cycle in \(\mathcal {E}_{\Delta }\) consisting of edges of the polygons in \(\mathcal {C}^*\), thus contradicting that \(\mathcal {E}_{\Delta }\) admits a depth order.
Claim
All links \(a_i b_i\) of \(\Gamma (\mathcal {C}^*)\) are good.
Proof
Consider any link \(a_i b_i\). Observe that \(\overline{a_{i-1}}\) and \(\overline{a_{i+2}}\) must both lie outside \(\overline{P_i}\), otherwise \(\mathcal {C}^*\) is not minimal. Consider \(\Delta \setminus \overline{P_i}\), the complement of \(\overline{P_i}\) inside the column base \(\Delta \). The region \(\Delta \setminus \overline{P_i}\) consists of one or more connected components; it cannot be empty since then \(P_i\) cannot be part of any cycle in \(\mathcal {T}_{\Delta }\). Each connected component is separated from \(\overline{P_i}\) by a single edge of \(\overline{P_i}\), since by assumption \(T_i\) does not have a vertex inside \(C_\Delta \) and so \(\overline{P_i}\) does not have a vertex inside \(\Delta \) either. We now consider two cases, as illustrated in Fig. 2.
The two cases in the proof of Proposition 2.1. Polygon \(\overline{P_i}\) is shown in green
Case A: \(\overline{a_{i-1}}\) and \(\overline{a_{i+2}}\) lie in different components of \(\Delta \setminus \overline{P_i}\). Let \(\overline{p}\) be the point where \(\overline{a_{i-1}a_{i}}\) enters \(\overline{P_i}\). Let \(p\in P_i\) project onto \(\overline{p}\) and let e be the edge of \(P_i\) containing p. (Possibly \(\overline{p} = \overline{a_i}\).) Since \(\overline{a_{i+2}}\) lies in a different connected component of \(\Delta \setminus \overline{P_i}\) than \(\overline{a_{i-1}}\), the projection \(\overline{\Gamma (\mathcal {C}^*)}\) must cross \(\overline{e}\) a second time, at some point \(\overline{q}\). This leads to a contradiction with the minimality of \(\mathcal {C}^*\). To see this, let \(q\in \Gamma (\mathcal {C}^*)\) be a point projecting onto \(\overline{q}\) and let \(P_j\) be such that \(q\in P_j\). Then \(j\not \in \{i-1,i,i+1\}\), because \(a_{i-1}b_{i-1}\), and \(a_ib_i\), and \(a_{i+1}b_{i+1}\) are the only links of \(\Gamma (\mathcal {C}^*)\) on \(P_{i-1}\), and \(P_i\), and \(P_{i+1}\), respectively. But since \(\overline{P_i}\cap \overline{P_j}\ne \emptyset \) we have \(P_i\prec P_j\) or \(P_j\prec P_i\), and so \(j\not \in \{i-1,i,i+1\}\) contradicts that \(\mathcal {C}^*\) is minimal. Thus Case A cannot occur.
Case B: \(\overline{a_{i-1}}\) and \(\overline{a_{i+2}}\) lie in the same component of \(\Delta \setminus \overline{P_i}\). In this case \(a_i b_i\) must be a good link, because \(a_i\) and \(b_i\) must both lie on the edge e bordering the component of \(\Delta \setminus \overline{P_i}\) that contains \(\overline{a_{i-1}}\) and \(\overline{a_{i+2}}\). Indeed, if \(\overline{a_i}\) and/or \(\overline{a_{i+1}}\) would not lie on e then we can obtain a witness curve of lower weight for \(\mathcal {C}^*\), namely if we replace \(a_i\) by the point p such that \(\overline{p} = \overline{a_{i-1} a_{i}} \cap \overline{e}\) and we replace \(a_{i+1}\) by the point q such that \(\overline{q} = \overline{a_{1} a_{i+1}} \cap \overline{e}\). Note that if \(a_{i-1}=a_{i+2}\), which happens when \(\mathcal {C}^*\) consists of only three polygons, then the argument still goes through.
Thus \(a_i b_i\) is a good link, as claimed. \(\square \)
If all links \(a_i,b_i\) of \(\Gamma (\mathcal {C}^*)\) are good then \(\mathcal {C}^*\) gives a cycle in \(\mathcal {E}_{\Delta }\), contradicting that \(\mathcal {E}_{\Delta }\) admits a depth order. Hence, the assumption that \(\mathcal {T}_{\Delta }\) contains a cycle is false. \(\square \)
The cutting procedure. A naive way to apply Proposition 2.1 would be the following: compute a complete cut set X for the set \(\mathcal {E}\) of triangle edges, and take a vertical plane parallel to the yz-plane through each point in \(\mathcal {V}\cup X\). This subdivides \({\mathbb R}^3\) into columns \(C_\Delta \), where each column base \(\Delta \) is an infinite strip. These columns do not contain triangle vertices and the edge fragments inside each column are acyclic, and so the triangle fragments we obtain are acyclic. Unfortunately this straightforward approach generates too many fragments: \(\mathcal {V}\cup X\) may have size \(\Omega (n\sqrt{n})\) and each of the planes through a point in \(\mathcal {V}\cup X\) may cut \(\Omega (n)\) triangles, resulting in a total of \(\Omega (n^2\sqrt{n})\) fragments. Hence, we first subdivide space so that we do not cause too much fragmentation when we take the vertical planes through \(\mathcal {V}\cup X\). The crucial idea is to create the subdivision based on the projections of the triangle edges. This allows us to use an efficient 2-dimensional partitioning scheme resulting in cells that are intersected by only few projected triangles edges. The 2-dimensional subdivision will then be extended into \({\mathbb R}^3\), to obtain 3-dimensional regions in which we can take vertical planes through \(\mathcal {V}\cup X\) without creating too many fragments. We cannot completely ignore the triangles themselves, however, when we extend the 2-dimensional subdivision into \({\mathbb R}^3\)—otherwise we already create too many fragments in this phase. Thus we create a hierarchical 2-dimensional subdivision, and we use the hierarchy to avoid cutting the input triangles into too many fragments. Next we make these ideas precise.
Let L be a set of n lines in the plane. A (1 / r)-cutting for L is a partition \(\Xi \) of the plane into triangularFootnote 4 cells such that the interior of any cell \(\Delta \in \Xi \) intersects at most n / r lines from L. We say that a cutting \(\Xi \) c-refines a cutting \(\Xi '\), where c is some constant, if every cell \(\Delta \in \Xi \) is contained in a unique parent cell \(\Delta '\in \Xi '\), and each cell in \(\Xi '\) contains at most c cells from \(\Xi \). An efficient hierarchical (1 / r)-cutting for L, as introduced by Matoušek [20], is a sequence \(\Psi := \Xi _0,\Xi _1,\ldots ,\Xi _k\) of cuttings such that there are constants \(c,\rho \) such that the following four conditions are met:
-
(i)
\(\rho ^{k-1} < r \leqslant \rho ^k\);
-
(ii)
\(\Xi _0\) is the single cell \({\mathbb R}^2\);
-
(iii)
\(\Xi _i\) is a \((1/\rho ^i)\)-cutting for L of size \(O(\rho ^{2i})\), for all \(0\leqslant i\leqslant k\);
-
(iv)
\(\Xi _i\) is a c-refinement of \(\Xi _{i-1}\), for all \(1\leqslant i\leqslant k\).
For any set L and any parameter r with \(1\leqslant r\leqslant n\), an efficient hierarchical (1 / r)-cutting \(\Psi \) exists and can be computed in O(nr) time [10, 20]. We can view \(\Psi \) as a tree in which each node u at level i corresponds to a cell \(\Delta _u\in \Xi _i\), and a node v at level i is the child of a node u at level \(i-1\) if \(\Delta _v\subseteq \Delta _u\).
Our cutting procedure now proceeds in two steps. Recall that \(\mathcal {T}\) denotes the given set of n triangles in \({\mathbb R}^3\), and \(\mathcal {E}\) the set of 3n edges of the triangle in \(\mathcal {T}\).
-
1.
We first construct an efficient hierarchical (1 / r)-cutting \(\Psi \) for L, with \(r=n^{3/4}\), where L is the set of lines containing the edges in \(\overline{\mathcal {E}}\). Next we cut the projection \(\overline{T}\) of each triangle \(T\in \mathcal {T}\) into pieces. This is done by executing the following recursive process on \(\Psi \), starting at its root. Suppose we reach a node u of the tree. If \(\Delta _u\subseteq \overline{T}\) or u is a leaf, then \(\Delta _u\cap \overline{T}\) is one of the pieces of \(\overline{T}\). Otherwise, we recursively visit all children v of u such that \(\Delta _v\cap \overline{T} \ne \emptyset \). After cutting each projected triangle \(\overline{T}\) in this manner, we cut the original triangles \(T\in \mathcal {T}\) accordingly. Let \(\mathcal {T}_1\) denote the resulting collection of polygonal pieces.
-
2.
We extend the 2-dimensional cutting \(\Xi _k\) into \({\mathbb R}^3\) by erecting vertical walls through each of the edges in \(\Xi _k\). Thus we create a column \(C_\Delta := \Delta \times (-\infty ,\infty )\) for each cell \(\Delta \in \Xi _k\). Let \(\mathcal {K}\) be the collection of created columns. For each column \(C_{\Delta }\in \mathcal {K}\), we proceed as follows.
Let \(\mathcal {T}_1(C_{\Delta })\subseteq \mathcal {T}_1\) be the set of pieces that have an edge intersecting the interior of \(C_{\Delta }\), and let \(\mathcal {E}(C_{\Delta }) := \{ e\cap \mathrm {int}(C_{\Delta }) : e\in \mathcal {E}\}\). Note that \(\mathcal {E}(C_{\Delta })\) is the set of edges of the pieces in \(\mathcal {T}_1(C_{\Delta })\), where we only take the edges in the interior of \(C_{\Delta }\). Let \(X(C_{\Delta })\) be a complete cut set for \(\mathcal {E}(C_{\Delta })\), and let \(\mathcal {V}(C_{\Delta })\subseteq \mathcal {V}\) be the set of triangle vertices in the interior of \(C_{\Delta }\). For each point \(q\in X(C_{\Delta })\cup \mathcal {V}(C_{\Delta })\), take a plane h(q) containing q and parallel to the yz-plane, and let \(H(C_{\Delta })\) be the resulting set of planes. Cut every piece \(P\in \mathcal {T}_1(C_{\Delta })\) into fragments using the planes in \(H(C_{\Delta })\).
We denote the set of fragments generated in Step 2 inside a column \(C_{\Delta }\) by \(\mathcal {T}_2(C_{\Delta })\), and we denote the set of pieces in \(\mathcal {T}_1\) that do not have an edge crossing the interior of any column \(C_{\Delta }\in \mathcal {K}\) by \(\mathcal {T}_1^*\). Note that \(\mathcal {T}_1^{*}\) contains all pieces generated at internal nodes of \(\Psi \). Then \(\mathcal {T}_2 := \mathcal {T}_1^* \cup \bigcup _{C_{\Delta }\in \mathcal {K}} \mathcal {T}_2(C_{\Delta })\) is our final set of fragments.
Lemma 2.2
The set \(\mathcal {T}_2\) of triangle fragments resulting from the procedure above is acyclic and \(|\mathcal {T}_2| = O(n^{7/4}+ |X| \cdot n^{1/4})\), where \(X := \bigcup _{C_{\Delta }\in \mathcal {K}} X(C_{\Delta })\).
Proof
For the sake of the proof, image cutting each column \(C_\Delta \in \mathcal {K}\) into vertical prisms by slicing it with each triangle \(T\in \mathcal {T}\) that completely cuts through \(C_\Delta \). In other words, we slice \(C_\Delta \) with each triangle T such that \(\Delta \subseteq \overline{T}\). Let \(\mathcal {S}\) denote the resulting 3-dimensional subdivision. Define \(\mathcal {S}^*\) to be the set of (open) prisms in \(\mathcal {S}\), and consider the set \(\mathcal {S}^* \cup \mathcal {T}_1^{*}\).
Claim
The set \(\mathcal {S}^* \cup \mathcal {T}_1^{*}\) admits a depth order.
Proof
By construction, for any object \(o_i\in \mathcal {S}^* \cup \mathcal {T}_1^{*}\) there is a node \(u\in \Psi \) such that \(\overline{o_i} = \Delta _u\). Hence, for any two objects \(o_1,o_2\in \mathcal {S}^* \cup \mathcal {T}_1^{*}\) we have
This implies that \(\mathcal {S}^* \cup \mathcal {T}_1^{*}\) is acyclic. Indeed, suppose for a contradiction that \(\mathcal {S}^* \cup \mathcal {T}_1^{*}\) does not admit a depth order, and consider a minimal cycle \(\mathcal {C}^*:= o_1 \prec o_2\prec \cdots \prec o_{k}\prec o_1\). Obviously \(k\geqslant 3\). But then (1) implies that we can remove \(o_1\) or \(o_2\) and still have a cycle, contradicting the minimality of \(\mathcal {C}^*\). \(\square \)
For a prism \(\sigma \in \mathcal {S}\), let \(\mathcal {T}_2(\sigma )\) denote the set of fragments in \(\mathcal {T}_2\) that have an edge in the interior of \(\sigma \). The claim above implies that \(\mathcal {T}_2\) is acyclic if each set \(\mathcal {T}_2(\sigma )\) is acyclic. The latter follows if we can show that each set \(\mathcal {T}_2(C_{\Delta })\) is acyclic. To see that \(\mathcal {T}_2(C_{\Delta })\) is acyclic, note that the planes in \(H(C_{\Delta })\) partition \(C_{\Delta }\) into sub-columns that do not contain a point from \(X(C_{\Delta })\) in their interior. Hence, the set of edges of the fragments in such a sub-column is acyclic—if this were not the case, then there would be a cycle left in \(\mathcal {E}(C_{\Delta })\), contradicting that \(X(C_{\Delta })\) is a complete cut set for \(\mathcal {E}(C_{\Delta })\). Moreover, a sub-column does not contain any point from \(\mathcal {V}(C_{\Delta })\) in its interior, and so it does not contain a vertex of any fragment in its interior. We can therefore use Proposition 2.1 to conclude that within each sub-column, the fragments are acyclic. Since the fragments in each sub-column of \(C_{\Delta }\) are acyclic and the sub-columns are separated by vertical planes, \(\mathcal {T}_2(C_{\Delta })\) must be acyclic.
It remains to prove that \(|\mathcal {T}_2|=O(n^{7/4}+ |X|\cdot n^{1/4})\). We start by bounding \(|\mathcal {T}_1|\). To this end, consider a triangle \(T\in \mathcal {T}\) and let \(P\in \mathcal {T}_1\) be a piece generated for T in Step 1. Let v be the node in \(\Psi \) where P was created. Then the cell \(\Delta _u\) of the parent u of v is intersected by an edge of \(\overline{T}\). Since each node in \(\Psi \) has O(1) children and each cell \(\Delta \in \Xi _i\) intersects at most \(n/\rho ^i\) projected triangle edges, this means that
The number of additional fragments created in Step 2 can be bounded by observing that each column \(C_{\Delta }\in \mathcal {K}\) intersects at most \(n/r = O(n^{1/4})\) triangle edges, and so \(|\mathcal {T}_1(C_{\Delta })|=O(n^{1/4})\). If we now sum the number of additional fragments over all columns \(C_{\Delta }\in \mathcal {K}\) we obtain:
Hence, the total number of fragments is \(O(n^{7/4}+ |X|\cdot n^{1/4})\), which finishes the proof. \(\square \)
Lemma 2.2 leads to the following result.
Corollary 2.3
Suppose that any set of n lines has a complete cut set of size \(\gamma (n)\). Then any set \(\mathcal {T}\) of n disjoint triangles in \({\mathbb R}^3\) can be cut into \(O(n^{7/4} + \gamma (3n)\cdot n^{1/4})\) triangular fragments such that the resulting set of fragments admits a depth order.
Proof
Consider the cutting procedure described above. Define \({{\textsc {opt}}} \) to be the minimum size of a complete cut set for \(\mathcal {E}\) and, for a column \(C_{\Delta }\in \mathcal {K}\), define \({{\textsc {opt}}} _{\Delta }\) to be the minimum size of a complete cut for \(\mathcal {E}(C_{\Delta })\). Then \(\sum _{C_{\Delta }\in \mathcal {K}} {{\textsc {opt}}} _{\Delta } \leqslant {{\textsc {opt}}} \). Indeed, if \(X_{\mathrm {opt}}\) denotes a minimum-size complete cut set for \(\mathcal {E}\), then \(X_{\mathrm {opt}}\cap C_{\Delta }\) must eliminate all cycles from \(\mathcal {E}(C_{\Delta })\). Since \({{\textsc {opt}}} \leqslant \gamma (3n)\), the bound on the number of fragments generated by our cutting procedure is as claimed.
The procedure above cuts the triangles in \(\mathcal {T}\) into constant-complexity polygonal fragments, instead of into triangles: the first step results in pieces that are the intersection a triangle with a constant-complexity column, and the second step only uses cutting planes parallel to the xz-plane. In a post-processing step we can then cut these constant-complexity fragments into triangular fragments, without increasing the number of fragments asymptotically. \(\square \)
The result of Aronov and Sharir [8] thus implies that any set of n triangles can be cut into \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\) fragments such that the resulting set of fragments is acyclic.
An example showing that one sometimes needs more cuts to eliminate all cycles from \(\mathcal {T}_1(C)\) than from \(\mathcal {E}(C)\). The set \(\mathcal {T}_1(C)\) consists of the green triangle, and two red and two blue segments. (The red and blue segments can be replaced by very thin triangles.) The set \(\mathcal {E}(C)\) consists of the dark green edge of the green triangle, and the red and blue segments. Note that the configuration shown in the figure is realizable
Remark 2.4
The total number of fragments we create is \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\), while Aronov and Sharir only need \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) fragments for the case of lines. Observe that we already generate up to \(\Theta (n^{7/4})\) fragments in Step 1, since we take \(r=n^{3/4}\). To reduce the total number of fragments to \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) using our approach, we would need to set \(r:=\sqrt{n}\) in Step 1. In Step 2 we could then only use the set \(\mathcal {V}(C_{\Delta })\) to generate the vertical planes in \(H(C_{\Delta })\). This would lead to vertical columns that do not have any vertex in their interior, while only using \(O(n^{3/2})\) fragments so far. Each such sub-column \(C\subseteq C_{\Delta }\) can contain up to \(\Theta (\sqrt{n})\) triangle fragments. Hence, we cannot afford to compute a cut set X(C) for \(\mathcal {E}(C)\) and cut each triangle fragment in C with a vertical plane containing each \(q\in X(C)\). One may hope that if we can eliminate all cycles from \(\mathcal {E}(C)\) using |X(C)| cuts, then we can also eliminate all cycles from \(\mathcal {T}_1(C)\) using |X(C)| cuts. Unfortunately this is not the case, as shown in Fig. 3.
In the example, there are two cycles in \(\mathcal {T}_1(C)\): the green triangle together with the blue segments and the green triangle with the red segments. The set \(\mathcal {E}(C)\) also contains two cycles. The cycles from \(\mathcal {E}(C)\) can be eliminated by cutting the green edge at the point indicated by the arrow. However, a single cut of the green triangle cannot eliminate both cycles from \(\mathcal {T}_1(C)\). Indeed, to eliminate the blue-green cycle the cut should separate (in the projection) the parts of the blue edges projecting onto the green triangle, while to eliminate the red-green cycle the cut should separate the parts of the red edges projecting onto the green triangle—but a single cut cannot do both. The example can be generalized to sets \(\mathcal {T}_1(C)\) of arbitrary size, so that all cuts in \(\mathcal {E}(C)\) can be eliminated by a single cut, while eliminating cycles from \(\mathcal {T}_1(C)\) requires \(\Omega (|\mathcal {T}_1(C)|)\) cuts. Thus a more global reasoning is needed to improve our bound.
3 Efficient Algorithms to Compute Complete Cut Sets
The algorithm for triangles. The hierarchical cutting \(\Psi \) can be computed in \(O(nr)=O(n^{7/4})\) time [10, 20], and we can compute the set \(\mathcal {T}_1\) within the same time bound. The construction of the hierarchical cutting also gives us for each cell \(\Delta \in \Xi _k\) the projected triangle edges intersecting \(\Delta \) and, hence, the sets \(\mathcal {T}_1(C_{\Delta })\).
Next we need to compute the cut sets \(X(C_{\Delta })\). To this end we use the algorithm by Aronov et al. [4], which computes a complete cut set of size \(O({{\textsc {opt}}} _{\Delta } \cdot \log {{\textsc {opt}}} _{\Delta } \cdot \log \log {{\textsc {opt}}} _{\Delta })\), where \({{\textsc {opt}}} _{\Delta }\) is the minimum size of a complete cut set for \(\mathcal {E}(C_\Delta )\). Thus |X|, the total size of all cut sets \(X(C_\Delta )\) we compute, is bounded by
Hence, the total number of fragments we create is still \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\).
Now define \(n_\Delta := |T_1(C_\Delta )|\). Since the algorithm of Aronov et al. runs in time \(O(m^{4+2\omega }\log ^2 m)\) for m segments, the total time we spend to compute the cut sets \(X(C_{\Delta })\) is
Since \(n_{\Delta }=O(n^{1/4})\) for all \(\Delta \) and \(|\mathcal {K}| = O(n^{3/2})\), we can bound this time as follows:
Finally, for each column \(C_\Delta \) we cut all triangles in \(\mathcal {T}_1(C_\Delta )\) by the planes in \(H(C_\Delta )\) in a brute-force manner, in total time \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\).
The following theorem summarizes our main result. Note that using \(\omega <2.373\) gives a running time of \(O(n^{3.69})\).
Theorem 3.1
Any set \(\mathcal {T}\) of n disjoint non-vertical triangles in \({\mathbb R}^3\) can be cut into \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\) triangular fragments such that the resulting set of fragments admits a depth order. The time needed to compute the cuts is \(O(n^{5/2+\omega /2}\log ^2 n)\), where \(\omega <2.373\) is the exponent in the running time of the best matrix-multiplication algorithm.
Remark 3.2
The bottleneck in our algorithm is the computation of the local cut sets \(X(C_\Delta )\) inside the columns \(C_\Delta \), using the algorithm of Aronov et al. [4]. One can avoid this by computing a single global cut set for the set \(\mathcal {E}\) of triangle edges, and then distributing the cut points over the columns. Computing a global cut set of size \(O(n^{3/2+\varepsilon })\) can be done in \(O(n^{3/2+\varepsilon })\) time, by combining the method of Aronov and Sharir [8] with the recent result of Agarwal et al. [3] on computing polynomial partitions; also see the paper by Aronov et al. [5] who obtain the same time bound for cutting triangles (using curved cuts). The total running time of the algorithm then becomes \(O(n^{7/4+\varepsilon })\). However, the number of fragments increases to \(O(n^{7/4+\varepsilon })\).
The algorithm for lines. The running time we obtain in Theorem 3.1 for triangles is better than the running time obtained by Aronov and Sharir [8] to compute a complete cut set of size \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) for lines. The reason is that we apply the algorithm of Aronov et al. [4] locally, on a set of segments whose size is significantly smaller than n. We can use the same idea to speed up the computation of a complete cut set of size \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) for lines, as explained next. (But see Footnote 3.)
Let L be a set of n lines in \({\mathbb R}^3\). We project L onto the xy-plane, and compute a (1 / r)-cutting \(\Xi \) for \(\overline{L}\) of size \(O(r^2)\), with \(r:=\sqrt{n}\). We then cut each line \(\ell \in L\) at the points where its projection \(\overline{\ell }\) is cut by the cutting, that is, where \(\overline{\ell }\) crosses the boundary of a cell \(\Delta \) in \(\Xi \). Up to this point we make only \(O(nr)=O(n^{3/2})\) cuts, which does not affect the worst-case asymptotic bound on the number of cuts. Each cell \(\Delta \) of the cutting defines a column \(C_{\Delta }\), as before. Within each column, we apply the algorithm of Aronov et al. [4] to compute a cut set of size \(O({{\textsc {opt}}} _{\Delta } \cdot \log {{\textsc {opt}}} _{\Delta } \cdot \log \log {{\textsc {opt}}} _{\Delta })\), where \({{\textsc {opt}}} _{\Delta }\) is the size of an optimal cut set inside the column. In total this gives \(O({{\textsc {opt}}} \cdot \log {{\textsc {opt}}} \cdot \log \log {{\textsc {opt}}}) = O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) cuts in time \(O(n \cdot (n^{1/2})^{4+2\omega }) = O(n^{3+\omega })\).
This leads to the following result. Note that using \(\omega <2.373\) gives a running time of \(O(n^{5.38})\).
Theorem 3.3
For any set L of n disjoint lines in \({\mathbb R}^3\), we can compute in \(O(n^{3+\omega })\) time a set of \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) cut points on the lines such that the resulting set of fragments admits a depth order, where \(\omega <2.373\) is the exponent in the running time of the best matrix-multiplication algorithm.
4 A More Refined Bound and an Extension to Surface Patches
Let \(\mathcal {T}\) be a set of disjoint bounded-degree algebraic surface patches in \({\mathbb R}^3\). We assume each surface patch is xy-monotone, that is, each vertical line intersects a patch in a single point or not at all, and we assume each surface patch is bounded by a constant number of bounded-degree algebraic arcs. We refer to the arcs bounding a surface patch as the edges of the surface patch. We assume the edges are in general position as defined by Aronov and Sharir [8], except that adjacent edges of the same patch share endpoints. We will show how to cut the patches from \(\mathcal {T}\) into a collection of fragments that admits a depth order, where each fragment is bounded by a constant number of bounded-degree algebraic arcs. More precisely, an arc bounding a fragment f of a patch \(T\in \mathcal {T}\) is either (a portion of) an edge of T, or it is the intersection of T with a vertical wall through (a portion of) an edge of another patch or with a vertical wall through a line segment. The total number of fragments will depend on K, the number of intersections between the projections of the edges: for any fixed \(\varepsilon >0\), we can tune our procedure so that it generates \(O(n^{1+\varepsilon } + n^{1/4} K^{3/4} {{\,\mathrm{polylog}\,}}n)\) fragments. Trivially this implies that the same intersection-sensitive bound holds for triangles.
The extension of our procedure to obtain an intersection-sensitive bound for surface patches is fairly straightforward. First we observe that the analog of Proposition 2.1 still holds, where the base of the column can now have curved edges. In fact, the proof holds verbatim, if we allow the links of the witness cycles \(\Gamma (\mathcal {C})\) that connect points \(a_i\) and \(b_i\) on the same surface patch to be curved. Now, instead of using efficient hierarchical cuttings [10, 20] we recursively generate a sequence of cuttings using the intersection-sensitive cuttings of de Berg and Schwarzkopf [17]. This is somewhat similar to the way in which Aronov and Sharir [8] obtain an intersection-sensitive bound on the number of cuts needed to eliminate all cycles for a set of line segments in \({\mathbb R}^3\). Below we give the details.
Let \(\mathcal {E}\) denote the set of O(n) edges of the surface patches in \(\mathcal {T}\), and let \(\overline{\mathcal {E}}\) be the set of projections of the edges in \(\mathcal {E}\) onto the xy-plane. A (1 / r)-cutting for \(\overline{\mathcal {E}}\) is a subdivision of \({\mathbb R}^2\) into trapezoidal cells, such that the interior of each cell intersects at most n / r edges from \(\overline{\mathcal {E}}\). Here a trapezoidal cell is a cell bounded by at most two segments parallel to the y-axis, at most one piece of an edge in \(\overline{\mathcal {E}}\) bounding the cell from above, and at most one such piece bounding it from below. Set \(r := \min (n^{5/4}/K^{1/4},n)\). Let \(\rho \) be a sufficiently large constant, and let k be such that \(\rho ^{k-1}<r\leqslant \rho ^k\); the exact value of \(\rho \) depends on the desired value of \(\varepsilon \) in the final bound. We recursively construct a hierarchy \(\Psi := \Xi _0,\Xi _1,\ldots ,\Xi _k\) of cuttings such that \(\Xi _i\) is a \((1/\rho ^i)\)-cutting for \(\overline{\mathcal {E}}\), as follows. The initial cutting \(\Xi _0\) is the entire plane \({\mathbb R}^2\). To construct \(\Xi _i\) we take each cell \(\Delta \) of \(\Xi _{i-1}\) and we construct a \((1/\rho )\)-cutting for the set \(\overline{\mathcal {E}}_\Delta := \{ \overline{e}\cap \Delta : \overline{e}\in \overline{\mathcal {E}}\}\). De Berg and Schwarzkopf [17] have shown that there is such a cutting consisting of \(O(\rho + K_{\Delta }\rho ^2/n_\Delta ^2)\) cells, where \(n_\Delta := |\overline{\mathcal {E}}_\Delta |\) and \(K_{\Delta }\) is the number of intersections inside \(\Delta \). One can show by induction on i that for each cell \(\Delta \) in \(\Xi _{i-1}\) we haveFootnote 5\(n_\Delta \leqslant n/\rho ^{i-1}\). Hence, by combining the cuttings \(\Xi _\Delta \) over all \(\Delta \in \Xi _{i-1}\) we obtain a \((1/\rho ^i)\)-cutting \(\Xi _i\).
Let \(|\Xi _i|\) be the number of cells in \(\Xi _i\). Then \(|\Xi _0|=1\) and, for a suitable constant D—this constant depends on the degree of the edges and can be derived from the construction of de Berg and Schwarzkopf [17]—we have
Now we can proceed exactly as before. Thus we first traverse the hierarchy \(\Psi \) with each patch \(T\in \mathcal {T}\), associating T to nodes u such that \(\Delta _u\subseteq \overline{T}\) and \(\Delta _{\mathrm {parent}(u)}\not \subseteq \overline{T}\), and to the leaves that we reach. This partitions T into a number of fragments. The resulting set \(\mathcal {T}_1\) of fragments generated over all triangles \(T\in \mathcal {T}\) has total size
If we now set \(\rho := D^{1/\varepsilon }\) then \(D^k =\rho ^{k\varepsilon } = O(r^{\varepsilon })=O(n^{\varepsilon })\), and so \(|\mathcal {T}_1|=O(n^{1+\varepsilon } + Kr/n)\). We then extend the trapezoids of \(\Xi _k\) into \({\mathbb R}^3\), thus obtaining a set of columns that each intersect at most n / r surface-patch edges, take a minimum-size complete cut set \(X(C_\Delta )\) for the edges inside each column \(C_\Delta \), and generate a set \(H(C_\Delta )\) of cutting planes through the points in \(X(C_\Delta )\cup \mathcal {V}(C_\Delta )\). Here \(\mathcal {V}(C_\Delta )\) is, as before, the set of vertices of the surface patches in the interior of \(C_\Delta \). Since Aronov and Sharir [8] proved that any set of n bounded-degree algebraic arcs in general positionFootnote 6 admits a complete cut set of size \(O(n + (nK)^{1/2}{{\,\mathrm{polylog}\,}}n)\)—the constant of proportionality and the exponent of the polylogarithmic factor depend on the degree of the arcs—we have
and so the number of additional fragments created in Step 2 is bounded by
By picking \(r := \min (n^{5/4}/K^{1/4},n)\) our final bound on the number of fragments becomes \(O(n^{1+\varepsilon } + n^{1/4} K^{3/4}{{\,\mathrm{polylog}\,}}n)\). Observe that for \(K=n^2\) the bound we get is the same as in Theorem 3.1, up to the constant in the exponent of the polylogarithmic factor hidden in the \({{\,\mathrm{polylog}\,}}\)-notation.
We obtain the following theorem, where the constant of proportionality and the exponent of the polylogarithmic factor in the bound depend on the degree of the patches and their edges.
Theorem 4.1
Let \(\mathcal {T}\) be a set of n disjoint xy-monotone bounded-degree algebraic surface patches in \({\mathbb R}^3\), each bounded by a constant number of bounded-degree algebraic arcs in general position. Then for any fixed \(\varepsilon >0\) we can cut \(\mathcal {T}\) into \(O(n^{1+\varepsilon } + n^{1/4} K^{3/4}{{\,\mathrm{polylog}\,}}n)\) fragments that admit a depth order, where K is the number of intersections between the projections of the surface-patch edges. The expected time needed to compute the cuts is \(O\left( n^{1+\varepsilon } + K^{(3+\omega )/2+\varepsilon } / n^{(1+\omega )/2} \right) \), where \(\omega <2.373\) is the exponent in the running time of the best matrix-multiplication algorithm.
Proof
The bound on the number of fragments follows from the discussion above. To prove the time bound we first note that an intersection-sensitive cutting of size \(O(\rho + K_{\Delta }\rho ^2/n_\Delta ^2)\) can be computed in expected time \(O(n_\Delta \log \rho + K_\Delta \rho /n_\Delta )\) [17]. Hence, constructing the hierarchy takes expected time
The first term is the same as in equation (2) except for the extra \(\log \rho \)-factor, which is a constant, so this term is still bounded by \(O(n^{1+\varepsilon } + Kr/n)\). Since \(\rho ^{k-1}\leqslant r\), the second term is bounded by O(Kr / n), which is dominated by the first term. Thus the total expected time to compute the set \(\mathcal {T}_1\) is \(O(n^{1+\varepsilon } + Kr/n)\).
In the second stage of the algorithm we use the algorithm of Aronov et al. [4] on the set \(\mathcal {E}(C_\Delta )\) of edge fragments inside each column \(C_\Delta \in \mathcal {K}\). Aronov et al. only explicitly state their result for line segments, but it is easily checked that it works for curves as well; the fact that, for example, there can already be cyclic overlap between a pair of curves has no influence on the algorithm’s approximation factor or running time. (The crucial property still holds that cut points can be ordered linearly along a curve, and this is sufficient for the algorithm to work.) Thus the time needed to compute all cut sets \(X(C_\Delta )\) is
where \(n_\Delta \) is the number of edges inside \(C_\Delta \). Since \(n_\Delta = O(n/r)\) and \(\sum _{C_\Delta \in \mathcal {K}} n_{\Delta } = O(|\mathcal {T}_1|) = O(n^{1+\varepsilon } + Kr/n)\), computing the cut sets takes
time (for a slightly larger \(\varepsilon \) than before). Because we picked \(r := \min (n^{5/4}/K^{1/4},n)\), the time to compute the cut sets is
which dominates the time for the first stage. Finally, cutting the patches inside each column \(C_\Delta \) in a brute-force manner takes time linear in the maximum number of fragments we generate, namely \(O(n^{1+\varepsilon } + n^{1/4} K^{3/4}{{\,\mathrm{polylog}\,}}n)\). Thus the total expected time is
\(\square \)
5 Dealing with Degeneracies
In this section we present a general method to deal with degeneracies when eliminating cycles from a set of segments in \({\mathbb R}^3\), and we argue that the method for triangles presented in the main text does not need any non-degeneracy assumptions either. We do not deal with removing the non-degeneracy assumptions for the case of surface patches.
Degeneracies among segments. Let \(S=\{s_1,\ldots ,s_n\}\) be a set of disjoint segments in \({\mathbb R}^3\). (Even though we allow degeneracies, we do not allow the segments in S to intersect or touch, since then the problem is not well-defined. If the segments are defined to be relatively open, then we can also allow an endpoint of one segment to coincide with an endpoint of, or lie in the interior of, another segment.) We can assume without loss of generality that S does not contain vertical segments, since eliminating all cycles from the non-vertical segments in S also eliminates all cycles when we include the vertical segments. Consider the following non-degeneracy assumptions:
-
(i)
no endpoint of one segment projects onto any other segment;
-
(ii)
no three segments are concurrent (that is, pass through a common point) in the projection;
-
(iii)
no two segments in S are parallel.
The main difficulty in handling degeneracies arises with type (iii), in particular when there are parallel segments whose projections overlap. The problem is that a small perturbation will reduce the intersection in the projection to a single point, and cutting one of the segments at the intersection is effective for the perturbed segments but not necessarily for the original segments. Next we describe how we handle this as well as the other degeneracies.
First we slightly extend each segment in S—segments that are relatively open would be slightly shortened—to get rid of degeneracies of type (i), and we slightly translate each segment to make sure no two segments intersect in more than a single point in the projection. (The translations are not necessary, but they simplify the following description and bring out more clearly how the \(\prec \)-relations between parallel segments are treated.) Next, we slightly perturb each segment such that all degeneracies disappear and any two non-parallel segments whose projections intersect before the perturbation still do so after the perturbation. This gets rid of degeneracies of types (ii) and (iii). Let \(s'_i\) denote the segment \(s_i\) after the perturbation, and define \(S' := \{s'_1,\ldots ,s'_n\}\). The set \(S'\) has the following properties:
-
for any two non-parallel segments \(s_i,s_j\in S\) we have \(s_i\prec s_j\) if and only if \(s'_i\prec s'_j\);
-
the order of intersections along segments in the projection is preserved in the following sense: if \(\overline{s'_i}\cap \overline{s'_j}\) lies before \(\overline{s'_i}\cap \overline{s'_k}\) along \(\overline{s'_i}\) as seen from a given endpoint of \(\overline{s'_i}\), then \(\overline{s_i}\cap \overline{s_j}\) does not lie behind \(\overline{s_i}\cap \overline{s_k}\) along \(\overline{s_i}\) as seen from the corresponding endpoint of \(\overline{s_i}\);
-
if \(s_i\) and \(s_j\) are parallel then \(\overline{s'_i}\) and \(\overline{s'_j}\) do not intersect.
We will show how to obtain a complete cut set for S from a complete cut set \(X'\) for \(S'\). The cut set for S will consist of a cut set X that is derived from \(X'\) plus a set Y of \(O(n\log n)\) additional cuts, as explained next.
-
Let \(q'\in X'\) be a cut point on a segment \(s'_i\in S'\). Let \(s'_j\in S'\) be the segment such that \(\overline{s'_i}\cap \overline{s'_j}\) is the intersection point on \(\overline{s'_i}\) closest to \(\overline{q'}\), with ties broken arbitrarily. We can assume that \(s'_j\) exists, since if \(\overline{s'_i}\) does not intersect any projected segment then the cut point q is useless and can be ignored. Now we put into X the point \(q\in s_i\) such that \(\overline{q}=\overline{s_i}\cap \overline{s_j}\). (It can happen that several cut points along \(s'_i\) generate the same cut point along \(s_i\). Obviously we need to insert only one of them into X.) The crucial property of the cut point \(q\in X\) generated for \(q'\in X'\) is the following:
-
if \(\overline{q'}\) coincides with a certain intersection along \(\overline{s'_i}\) then \(\overline{q}\) coincides with the corresponding intersection along \(\overline{s_i}\);
-
if \(\overline{q'}\) separates two intersections along \(\overline{s'_i}\) then \(\overline{q}\) separates the corresponding intersections along \(\overline{s_i}\) or it coincides with at least one of them.
By treating all cut points in \(X'\) in this manner, we obtain the set X.
-
-
The set Y deals with parallel segments in S whose projections overlap. It is defined as follows. Let S(X) be the set of fragments resulting from cutting the segments in S at the cut points in X. Partition S(X) into subsets \(S_{\ell }(X)\) such that \(S_\ell (X)\) contains all fragments from S(X) projecting onto the same line \(\ell \). Consider such a subset \(S_{\ell }(X)\) and assume without loss of generality that \(\ell \) is the x-axis. Construct a segment tree [14] for the projections of the fragments in \(S_\ell (X)\). Each projected fragment \(\overline{f}\) is stored at \(O(\log |S_\ell (X)|)=O(\log n)\) nodes of the segment tree, which induces a subdivision of \(\overline{f}\) into \(O(\log n)\) intervals. We put into Y the \(O(\log n)\) points on f whose projections define these intervals. The crucial property of segment trees that we will need is the following:
-
Let \(I_v\) denote the interval corresponding to a node v. Then for any two nodes v, w we either have \(I_v\subseteq I_w\) (when v is a descendent of w), or we have \(I_v\supseteq I_w\) (when v is an ancestor of w), or otherwise the interiors of \(I_v\) and \(I_w\) are disjoint. Hence, a similar property holds for the projections of the sub-fragments resulting from cutting the fragments in \(S_\ell (X)\) as explained above.
Doing this for all fragments \(s_i\in S_\ell (X)\) and for all subsets \(S_\ell (X)\) gives us the extra cut set Y.
-
Lemma 5.1
The set \(X\cup Y\) is a complete cut set for S.
Proof
Let F denote the set of fragments resulting from cutting the segments in S at the points in \(X\cup Y\), and suppose for a contradiction that F still contains a cycle. Let \(\mathcal {C}:=f_0\prec f_1\prec \cdots \prec f_{k-1}\prec f_0\) be a minimal cycle in F, and let \(s_i\in S\) be the segment containing \(f_i\).
As explained above, the cut points in Y guarantee that for any two parallel fragments in F whose projections overlap, one is contained in the other in the projection. This implies that two consecutive fragments \(f_i,f_{i+1}\) in \(\mathcal {C}\) cannot be parallel: if they were, then \(\overline{f_i}\subseteq \overline{f_{i+1}}\) (or vice versa) which contradicts that \(\mathcal {C}\) is minimal. Hence, any two consecutive fragments are non-parallel. Now consider the witness curve \(\Gamma (\mathcal {C})\) for \(\mathcal {C}\). Since consecutive fragments in \(\mathcal {C}\) are non-parallel, \(\Gamma (\mathcal {C})\) is unique. Let \(\Gamma '\) be the corresponding curve for \(S'\), that is, \(\Gamma '\) visits the segments \(s'_0,s'_1,\ldots ,s'_{k-1},s'_0\) from \(S'\) in the given order—recall that \(f_i\subseteq s_i\) and that \(s'_i\) is the perturbed segment \(s_i\)—and it steps from \(s'_i\) to \(s'_{i+1}\) using vertical connections. Since \(X'\) is a complete cut set for \(S'\), there must be a link of \(\Gamma '\), say on segment \(s'_i\), that contains a cut point \(q'\in X'\). In other words, \(\overline{q'}\) separates \(\overline{s'_{i-1}}\cap \overline{s'_{i}}\) from \(\overline{s'_{i}}\cap \overline{s'_{i+1}}\), or it coincides with one of these points. But then the cut point \(q\in X\) corresponding to \(q'\) must separate \(\overline{s_{i-1}}\cap \overline{s_{i}}\) from \(\overline{s_{i}}\cap \overline{s_{i+1}}\) or coincide with one of these points, thus cutting the witness curve \(\Gamma (\mathcal {C})\)—a contradiction. \(\square \)
Theorem 5.2
Suppose any non-degenerate set of n disjoint segments can be cut into \(\gamma (n)\) fragments in T(n) time such that the resulting set of fragments admits a depth order. Then any set of n disjoint segments can be cut into \(O(\gamma (n)\log n)\) fragments in \(T(n)+O(n^2)\) time such that the resulting set of fragments admits a depth order.
Proof
The bound on the number of fragments immediately follows from the discussion above. The overhead term in the running time is caused by the computation of the perturbed set \(S'\), which can be done in \(O(n^2)\) time if we compute the full arrangement in the projection. \(\square \)
Degeneracies among triangles. Recall that the cuts we make on the triangles are induced by vertical planes, and that a triangle becomes open where it is cut. When a triangle is completely contained in the cutting plane, however, it is not well defined what happens. One option is to say that the triangle completely disappears; another option it to say that the triangle is not cut at all. Since vertical triangles can be ignored in the Painter’s Algorithm, we will simply assume that no triangle in \(\mathcal {T}\) is vertical. However, we can still have other degeneracies, such as edges of different triangles being parallel or triples of projected edges being concurrent. Fortunately, the fact that we do not need non-degeneracy assumptions for segments immediately implies that we can handle such cases. Indeed, degeneracies are not a problem for the hierarchical cuttings we use in Step 1 of our procedure, and in Step 2 we only assumed non-degeneracy when computing the cut set \(X(C_\Delta )\) for the edge set \(\mathcal {E}(\Delta )\)—and Theorem 5.2 implies we can get rid of the non-degeneracy assumptions in this step. Note that the \(O(n^2)\) overhead term in Theorem 5.2 is subsumed by the time needed to apply the algorithm of Aronov et al. [4].
6 Concluding Remarks
We proved that any set of n disjoint triangles in \({\mathbb R}^3\) can be cut into \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\) triangular fragments that admit a depth order, thus providing the first subquadratic bound for this important setting of the problem. We also proved a refined bound that depends on the number of intersections of the triangle edges in the projection, and generalized the result to xy-monotone surface patches. The main open problem is to tighten the gap between our bound and the \(\Omega (n^{3/2})\) lower bound on the worst-case number of fragments needed: is it possible to cut any set of triangles into roughly \(\Omega (n^{3/2})\) triangular fragments that admit a depth order, or is this only possible by using curved cuts? One would expect the former, but curved cuts seem unavoidable in the approach of Aronov et al. [7] and it seems very hard to push our approach to obtain an \(o(n^{7/4})\) bound.
Notes
Another drawback of their method, at the time of writing, was that it did not come with an efficient algorithm, because no algorithm was known for constructing the necessary polynomial partition. This has been resolved in the meantime: Aronov et al. [5] show how to construct these partitions efficiently, resulting in an algorithm with running time \(O(n^{3/2+\varepsilon })\). Also see a more general, and even more recent, result by Agarwal et al. [3] on computing polynomial partitions.
In the most recent version of their paper [7], it is stated that their method may extend to surface patches, although they leave a formal proof of this claim for further research.
The \(O(n^{4+2\omega }\log ^2 n)\) running time is obtained by applying the algorithm of Aronov et al. [4]. Applying the recent result mentioned in Footnote 1 gives a running time of \(O(n^{3/2+\varepsilon })\), but this would slightly increase the number of cuts from \(O(n^{3/2}{{\,\mathrm{polylog}\,}}n)\) to \(O(n^{3/2+\varepsilon })\). The result in Footnote 1 can also be used to speed up our algorithm for triangles to \(O(n^{7/4+\varepsilon })\), albeit at the cost of increasing the number of fragments from \(O(n^{7/4}{{\,\mathrm{polylog}\,}}n)\) to \(O(n^{7/4+\varepsilon })\); see Remark 3.2.
The cells may be unbounded, that is, we also allow wedges, half-planes, and the entire plane, as cells.
Strictly speaking this is not true, as n denotes the number of patches and not the number of edges. To avoid cluttering the notation we allow ourselves this slight abuse of notation.
We assumed the edges are in general position, but edges of the same patch may share endpoints. However, there are no endpoints in the interior of \(C_\Delta \), and so the only degeneracy that can happen is if two edges of the same patch share an endpoint that lies on the boundary of \(C_\Delta \). In this case we can slightly shorten and perturb the edges to remove this degeneracy as well.
References
Agarwal, P.K., Katz, M.J., Sharir, M.: Computing depth orders for fat objects and related problems. Comput. Geom. 5(4), 187–206 (1995)
Agarwal, P.K., Grove, E.F., Murali, T.M., Vitter, J.S.: Binary space partitions for fat rectangles. SIAM J. Comput. 29(5), 1422–1448 (2000)
Agarwal, P.K., Aronov, B., Ezra, E., Zahl, J.: An efficient algorithm for generalized polynomial partitioning and its applications. In: Proceedings of 35th International Symposium on Computational Geometry (SoCG) (2019)
Aronov, B., de Berg, M., Gray, C., Mumford, E.: Cutting cycles of rods in space: hardness and approximation. In: Proceedings of the 19th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’08), pp. 1241–1248. SIAM, Philadelphia (2008)
Aronov, B., Ezra, E., Zahl, J.: Constructive polynomial partitioning for algebraic curves in $\mathbb{R}^3$ with applications. In: Proceedings of the 30th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’19), pp. 2636–2648. SIAM, Philadelphia (2019)
Aronov, B., Koltun, V., Sharir, M.: Cutting triangular cycles of lines in space. Discrete Comput. Geom. 33(2), 231–247 (2005)
Aronov, B., Miller, E.Y., Sharir, M.: Eliminating depth cycles among triangles in three dimensions. In: Proceedings of the 28th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 2476–2494 (2017). arXiv:1607.06136
Aronov, B., Sharir, M.: Almost tight bounds for eliminating depth cycles in three dimensions. Discrete Comput. Geom. 59(3), 725–741 (2018)
Chazelle, B.: Convex partitions of polyhedra: a lower bound and worst-case optimal algorithm. SIAM J. Comput. 13(3), 488–507 (1984)
Chazelle, B.: Cutting hyperplanes for divide and conquer. Discrete Comput. Geom. 9(2), 145–158 (1993)
Chazelle, B., Edelsbrunner, H., Guibas, L.J., Pollack, R., Seidel, R., Sharir, M., Snoeyink, J.: Counting and cutting cycles of lines and rods in space. Comput. Geom. 1(6), 305–323 (1992)
de Berg, M.: Ray Shooting, Depth Orders and Hidden Surface Removal. Lecture Notes in Computer Science, vol. 703. Springer, New York (1993)
de Berg, M.: Linear size binary space partitions for uncluttered scenes. Algorithmica 28(3), 353–366 (2000)
de Berg, M., Cheong, O., van Kreveld, M., Overmars, M.: Computational Geometry: Algorithms and Applications. Springer, Berlin (2008)
de Berg, M., Gray, C.: Vertical ray shooting and computing depth orders for fat objects. SIAM J. Comput. 38(1), 257–275 (2008)
de Berg, M., Overmars, M., Schwarzkopf, O.: Computing and verifying depth orders. SIAM J. Comput. 23(2), 437–446 (1994)
de Berg, M., Schwarzkopf, O.: Cuttings and applications. Internat. J. Comput. Geom. Appl. 5(4), 343–355 (1995)
Guth, L.: Polynomial partitioning for a set of varieties. Math. Proc. Cambridge Phil. Soc. 159(3), 459–469 (2015)
Har-Peled, S., Sharir, M.: Online point location in planar arrangements and its applications. Discrete Comput. Geom. 26(1), 19–40 (2001)
Matoušek, J.: Range searching with efficient hierarchical cuttings. Discrete Comput. Geom. 10(2), 157–182 (1993)
Paterson, M.S., Yao, F.F.: Efficient binary space partitions for hidden-surface removal and solid modeling. Discrete Comput. Geom. 5(5), 485–503 (1990)
Paterson, M.S., Yao, F.F.: Optimal binary space partitions for orthogonal objects. J. Algorithms 13(1), 99–113 (1992)
Sharir, M., Zahl, J.: Cutting algebraic curves into pseudo-segments and applications. J. Comb. Theory Ser. A 150, 1–35 (2017)
Solan, A.: Cutting cycles of rods in space. In: Proceedings of the 14th Annual Symposium on Computational Geometry (SCG’98), pp. 135–142. ACM, New York (1998)
Tóth, C.D.: Binary space partitions for axis-aligned fat rectangles. SIAM J. Comput. 38(1), 429–447 (2008)
Wilson, R.H., Latombe, J.-C.: Geometric reasoning about mechanical assembly. Artif. Intell. 71(2), 371–396 (1994)
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Kenneth Clarkson
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A preliminary version of this paper was published in the 58th Annual Symposium on Foundations of Computer Science (FOCS 2017). MdB is supported by the Netherlands’ Organisation for Scientific Research (NWO) under Project No. 024.002.003.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
de Berg, M. Removing Depth-Order Cycles Among Triangles: An Algorithm Generating Triangular Fragments. Discrete Comput Geom 65, 450–469 (2021). https://doi.org/10.1007/s00454-019-00102-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-019-00102-0