Shellability and Sphericity of Finite Quasi-arc Complexes

Abstract

Quasi-triangulations of a non-orientable surface were introduced by Dupont and Palesi (J Algebr Comb 42(2):429–472, 2015). The quasi-arc complex provides an intricate description of the combinatorics of these quasi-triangulations. This is the simplicial complex where vertices correspond to quasi-arcs and maximal simplices to quasi-triangulations. We prove that when the quasi-arc complex is finite then it is shellable and, as a consequence, it is homeomorphic to a sphere.

1 Introduction

The arc complex Arc(S) of a marked orientable surface S was introduced and studied by Harer [7] whilst investigating the homology of mapping class groups of orientable surfaces. In [4, 5], Fomin, Shapiro, and Thurston found there is a strong relation between cluster algebras and these arc complexes. They showed that Arc(S) is a subcomplex of the cluster complex $\Delta (S)$ associated to the cluster algebra arising from S. Moreover, it was shown by Fomin and Zelevinsky, almost at the birth of cluster algebras, that the cluster complex of a cluster algebra has a polytopal realisation when the complex is finite, see [6]. These polytopes coming from finite type cluster algebras are known as the generalised associahedra. In particular, Arc(n-gon) is the polytope dual to the $(n-3)$-dimensional associahedron.

In [3] Dupont and Palesi consider the quasi-arc complex of unpunctured non-orientable surfaces. Imitating the approach in [5] they describe how the ‘lengths’ of quasi-arcs are related. In doing so they discover what the analogue of a cluster algebra arising from non-orientable surfaces should be. A natural question is to ask what kind of structure the quasi-arc complex has in this setting. Here, in some sense, the marked Möbius strip $M _n$ plays the role of the n-gon—being the only non-orientable surface yielding a finite quasi-arc complex.

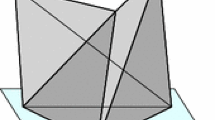
For $n \in \{1,2,3\}$ it is easy to check that the quasi-arc complex Arc$( M _n)$ of the Möbius strip is a polytope, see Fig. 2. However, in general it is difficult to find a polytopal realisation. The main tool used in the orientable case was the associated root system, which is not available here.

In this paper we prove that the finite type complexes are spherical. Our tool will be shellability.

Main Theorem (Theorem 4.44). Arc$(M_n)$ is shellable for $n \ge 1$.

Shellability stems from polytopal theory where it turned out to be the missing piece of the puzzle for obtaining the Euler–Poincaré formula. It has subsequently become a well established idea in combinatorial topology and geometry having some useful implications. For instance, Danaraj and Klee showed in [2] that every shellable pseudo-manifold is a PL-sphere. As a consequence, we obtain that the arc complex of a Möbius strip is homeomorphic to a sphere, or, in other words, that all finite quasi-arc complexes are spherical:

Corollary (Corollary 4.47). Let X be a finite quasi-arc complex. Then X is spherical.

The paper is organised as follows. In Sect. 2 we recall the work of Dupont and Palesi in [3]. Here we define the quasi-arc complex of a non-orientable surface and discuss why it is a pseudo-manifold, and when it is finite.

In Sect. 3 we firstly define shellability and recall some fundamental results. Next we restrict our attention to the n-gon and to $C_{n,0}$—the cylinder with n marked points on one boundary component, and none on the other. In the interest of introducing key ideas of the paper early on, we present a short proof that both Arc(n-gon) and Arc$(C_{n,0})$ are shellable. As a consequence, applying the result of Danaraj and Klee, we rediscover the classical fact of Harer [7] that Arc(n-gon) and Arc$(C_{n,0})$ are PL-spheres.

Section 4 is dedicated to proving the shellability of Arc$( M _n)$ and occupies the bulk of the paper.

2 Quasi-cluster Algebras

This section recalls the work of Dupont and Palesi in [3].

Let S be a compact 2-dimensional manifold with boundary $\partial S$. Fix a set M of marked points in $\partial S$. The tuple (S, M) is called a bordered surface. We wish to exclude the cases where (S, M) does not admit any triangulation. As such, we do not allow (S, M) to be a monogon, digon or triangle.

Definition 2.1

An arc is a simple curve in (S, M) connecting two (not necessarily distinct) marked points.

Definition 2.2

A closed curve in S is said to be two-sided if it admits a regular neighbourhood which is orientable. Otherwise, it is said to be one-sided.

Definition 2.3

A quasi-arc is either an arc or a simple one-sided closed curve in the interior of S. Let $A^{\otimes }(S,M)$ denote the set of quasi-arcs in (S, M) considered up to isotopy.

It is well known that a closed non-orientable surface is homeomorphic to the connected sum of k projective planes $\mathbb {R}P^2$. Such a surface is said to have (non-orientable) genus k. Recall that the projective plane is homeomorphic to a hemisphere where antipodal points on the boundary are identified. A cross-cap is a cylinder where antipodal points on one of the boundary components are identified. We represent a cross-cap as shown in Fig. 1.

Hence, a closed non-orientable surface of genus k is homeomorphic to a sphere where k open disks are removed, and have been replaced with cross-caps. More generally, a compact non-orientable surface of genus k, with boundary, is homeomorphic to a sphere where more than k open disks are removed, and k of those open disks have been replaced with cross-caps.

Fig. 1

A picture of a cross-cap together with a one-sided closed curve

Definition 2.4

Two elements in $A^{\otimes }(S,M)$ are called compatible if there exist representatives in their respective isotopy classes that do not intersect in the interior of S.

Definition 2.5

A quasi-triangulation of (S, M) is a maximal collection of mutually compatible arcs in $A^{\otimes }(S,M)$. A quasi-triangulation is called a triangulation if it consists only of arcs, i.e., there are no one-sided closed curves.

Proposition 2.6

[3, Prop. 2.4] Let T be a quasi-triangulation of (S, M). Then for any $\gamma \in T$ there exists a unique $\gamma ' \in A^{\otimes }(S,M)$ such that $\gamma \ne \gamma '$ and $\mu _{\gamma }(T) := T{\setminus } \{\gamma \} \cup \{\gamma '\}$ is a quasi-triangulation of (S, M).

Definition 2.7

$\mu _{\gamma }(T)$ is called the quasi-mutation of T in the direction $\gamma$, and $\gamma '$ is called the flip of $\gamma$ with respect to T.

The flip graph of a bordered surface (S, M) is the graph with vertices corresponding to (quasi-)triangulations and edges corresponding to flips. It is well known that the flip graph of triangulations of (S, M) is connected. Moreover, it can be seen that every one-sided closed curve, in a quasi-triangulation T, is bounded by an arc enclosing a Möbius strip with one marked point on the boundary. Therefore, if we perform a quasi-flip at each one-sided closed curve in T we arrive at a triangulation. As such, we get the following proposition.

Proposition 2.8

[3, Prop. 2.12] The flip graph of quasi-triangulations of (S, M) is connected.

Corollary 2.9

The number of quasi-arcs in a triangulation of (S, M) is an invariant of (S, M).

Definition 2.10

The quasi-arc complex Arc(S, M) is the simplicial complex on the ground set $A^{\otimes }(S,M)$ such that k-simplices correspond to sets of k mutually compatible quasi-arcs. In particular, the vertices in Arc(S, M) are the elements of $A^{\otimes }(S,M)$ and the maximum simplices are the quasi-triangulations.

Together, Corollary 2.9 and Proposition 2.6 prove the following proposition.

Proposition 2.11

Arc(S, M) is a pseudo-manifold without boundary. That is, each maximal simplex in Arc(S, M) has the same cardinality, and each simplex of co-dimension 1 is contained in precisely two maximal simplices.

Theorem 2.12

[3, Thm. 7.2] Given a non-orientable bordered surface (S, M) then Arc(S, M) is finite if and only if (S, M) is $M _n$, the Möbius strip with n marked points on the boundary.

Moreover, Arc$( M _n$) has some seemingly nice properties. Figure 2 shows that for $n \in \{1,2,3\}$ it is polytopal.

Fig. 2

The quasi-arc complexes of $\text {M}_1,\text {M}_2$ and $\text {M}_3$

3 Shellability

In this section we recall some basic facts about shellability, and introduce the fundamental ideas used throughout this chapter. These well known concepts can be found in [1, 2, 8].

3.1 Definition of Shellability and Basic Facts

Definition 3.1

An n-dimensional simplicial complex is called pure if its maximal simplices all have dimension n.

Definition 3.2

Let $\Delta$ be a finite (or countably infinite) simplicial complex. An ordering $C_1, C_2, \ldots$ of the maximal simplices of $\Delta$ is a shelling if the complex $B_k := \big ( \bigcup _{i=1}^{k-1}C_i\big ) \cap C_k$ is pure and $(\dim (C_k) -1)$-dimensional for all $k \ge 2$ (Fig. 3).

Fig. 3

The ordering of facets $F_1,F_2,F_3,F_4,F_5$ is a shelling for the left complex. However, the right complex is not shellable—the problem here is that $v \in F_1 \cap F_5$ but there is no 1-simplex which both contains the vertex v and lies in the intersection of two (distinct) facets $F_i$ and $F_j$

Definition 3.3

The simplicial join $\Delta _1 *\Delta _2$ of two simplicial complexes $\Delta _1$ and $\Delta _2$ on disjoint ground sets has its faces being sets of the form $\sigma _1 \cup \sigma _2$ where $\sigma _1 \in \Delta _1$ and $\sigma _2 \in \Delta _2$.

The following proposition is a simple and well-known result. For instance, see [8].

Proposition 3.4

The simplicial join $\Delta _1 *\Delta _2$ is shellable if and only if the simplicial complexes $\Delta _1 , \Delta _2$ are both shellable.

In particular, Proposition 3.4 tells us that the cone over a shellable complex is itself shellable.

Proposition 3.5

If $\Delta = \mathrm{{Arc}}(S,M)$ then finding a shelling for $\Delta$ is equivalent to ordering the set of triangulations $T_i$ of (S, M) so that for all k and $j<k$ there exists $i<k$ such that $T_i$ is related to $T_k$ by a mutation and $T_j \cap T_k \subseteq T_i \cap T_k$.

Proof

Note that triangulations $T_i$ of S correspond to maximal simplices in Arc(S, M) and that partial triangulations $T_i \cap T_j$ correspond to simplices of Arc(S). Note that $T_i \cap T_k$ is a $(\dim (T_k) -1)$-simplex $\textit{iff}$ $T_i$ is a mutation away from $T_k$. Furthermore, since $B_k := \big ( \bigcup _{i=1}^{k-1}T_i\big ) \cap T_k$ must be pure and $(\dim (T_k) -1)$-dimensional for all $k \ge 2$, it follows that $B_k$ is the union of $(\dim (T_k) -1)$-simplices. So we must have that for all $j<k$ there exists $i<k$ such that $T_i$ is a mutation away from $T_k$ and the partial triangulation $T_j \cap T_k$ is a face of $T_i \cap T_k$ (i.e. $T_j \cap T_k \subseteq T_i \cap T_k$). $\square$

Proposition 3.5 motivates Definition 3.6.

Definition 3.6

Given a subcollection of triangulations $\Gamma$ of a surface S call $\Gamma$ shellable if it admits an ordering of $\Gamma$ such that for all k and $j<k$ there exists $i<k$ such that $T_i$ is related to $T_k$ by a mutation and $T_j \cap T_k \subseteq T_i \cap T_k$.

Remark 3.7

Let $\Delta _{\Gamma }$ denote the induced simplicial complex of a set of triangulations $\Gamma$. Proposition 3.5 justifies the terminology of Definition 3.6 as we see $\Gamma$ is ‘shellable’ if and only if $\Delta _{\Gamma }$ is shellable.

Definition 3.8

We say two sets of triangulations $\Gamma _1$, $\Gamma _2$ are equivalent if their induced simplicial complexes are isomorphic, up to taking cones. If $\Gamma _1$ and $\Gamma _2$ are equivalent we write $\Gamma _1 \equiv \Gamma _2$.

Remark 3.9

Note that taking a cone over $\Delta _{\Gamma }$ can be thought of as disjointly adding one particular arc to every triangulation in $\Gamma$.

The following proposition is just a special case of Proposition 3.4.

Proposition 3.10

If $\Gamma _1 \equiv \Gamma _2$ then $\Gamma _1$ is shellable if and only if $\Gamma _2$ is shellable.

Notation 3.11

• $\displaystyle {{\mathrm{list}}}_{i=1}^{n} x_i$ is the ordering $x_1,x_2,\ldots , x_n$ of the set $\{x_i \,|\, 1\le i \le n\}$.

• $\displaystyle {{\mathrm{list}}}_{i\in I} x_i$ is any ordering of the set $\{x_i \,|\, i \in I\}$.

• Let $C_{n,0}$ denote the cylinder with n marked points on one boundary component and no marked points on the other. Fix an orientation on the boundary component containing marked points and cyclically label them $1, \ldots , n$. Let [i, j] denote the boundary segment $i\rightarrow j$. Note that $C_{n,0}$ arises as the partial triangulation of $M _n$ consisting of a one-sided closed curve. We choose the canonical way of defining arcs on $C_{n,0}$.

• Let $\gamma$ be an arc of $C_{n,0}$ with endpoints i, j. If $\gamma$ encloses a cylinder with boundary $[j,i]\cup {\gamma }$ then $\gamma := \langle i,j \rangle$. If $\gamma$ encloses a cylinder with boundary $[i,j]\cup {\gamma }$ then $\gamma := \langle j,i \rangle$, see Fig. 4.

Fig. 4

Notation for an arc $\gamma$ of $C_{n,0}$

The following theorem provides a very useful application of shellability.

Theorem 3.12

(Danaraj and Klee [2]) Let $\Delta$ be a simplicial complex of dimension n. If $\Delta$ is a shellable pseudo-manifold without boundary, then it is a PL n-sphere.

3.2 Shellability of Arc$(C_{n,0})$

The following proposition will help to prove the shellability of Arc$( M _n)$, and is introduced now to cement key ideas.

Proposition 3.13

Arc$(C_{n,0})$ is shellable for $n \ge 1$.

Proof

Consider the collection of triangulations $T(C_{n,0}^1) \subseteq T(C_{n,0})$ containing a loop at vertex 1. Note that by cutting along the loop we get the $(n+1)$-gon (and a copy of $C_{1,0}$) for $n \ge 2$. We will prove by induction on n that $T(C_{n,0}^1)$ is shellable. For $n=1$ the set $T(C_{1,0}^1) = T(C_{1,0})$ is trivially shellable. For $n=2$ if we cut along the loop we get the triangle and $C_{1,0}$ which are both trivially shellable, so indeed $T(C_{2,0}^1)$ is shellable by Proposition 3.4.

Let Block(i) be the set consisting of all triangulations in $T(C_{n,0}^1)$ containing the triangle with vertices (1, 1, i) for some $i\in [2,n]$, see Fig. 5.

Note that Block(i) can be equivalently viewed as the disjoint union of triangulations of the i-gon and the $(n-i+2)$-gon. Since $T(C_{k,0}^1)$ can be viewed as triangulations of the $(k+1)$-gon, then if we assume $T(C_{k,0}^1)$ is shellable for all $k < n$, Proposition 3.4 tells us that Block(i) is shellable for all i $\in [2,n]$. Let S(Block(i)) denote a shelling of Block(i).

Fig. 5

Block(i) consists of all triangulations containing this partial triangulation

Claim 3.14

The ordering $S(C_{n,0}^1) := \displaystyle {{\mathrm{list}}}_{i=n}^{2} S(\mathrm{{Block}}(i))$ is a shelling for $T(C_{n,0}^1)$.

Proof of Claim 3.14

Let S precede T in the ordering $S(C_{n,0}^1)$. Then $T \in$ Block(k) and $S \in$ Block(j) for $j \ge k$. If $j=k$ then, because S(Block(k)) is a shelling for Block(k), there exists $\gamma \in T$ such that $\mu _{\gamma }(T)$ precedes T in the ordering, and $T\cap S \subseteq T\cap \mu _{\gamma }(T)$. We may therefore assume $j > k$. In this case, the arc $\gamma = \langle k,1\rangle \in T$ is not compatible with the arc $\langle 1,j \rangle \in S$, so $\gamma \notin S$. Hence $T\cap S \subseteq T\cap \mu _{\gamma }(T)$. By Proposition 3.5 all that remains to show is that $\mu _{\gamma }(T)$ occurs before T in the ordering.

Note that we will have a triangle in T with vertices (1, k, x) where $x \in [n,k+1]$. And so $\mu _{\gamma }(T) \in$ Block(x). Since $x>k$, $\mu _{\gamma }(T)$ does precede T in the ordering. See Fig. 6. Hence $T(C_{n,0}^1)$ is shellable. $\square$

Fig. 6

As $x>k$ then $\mu _{\gamma }(T)$ precedes T in the ordering $S(C_{n,0}^1)$

Similarly we can shell $T(C_{n,0}^i)$ in the same way for all i $\in [1,n]$. Denote a shelling by $S(C_{n,0}^i)$. Combining these $S(C_{n,0}^i)$, as described in Claim 3.15 below, we get a shelling for Arc$(C_{n,0})$, which completes the proof of the lemma. $\square$

Claim 3.15

$S(\mathrm{{Arc}}(C_{n,0})) := \displaystyle {{\mathrm{list}}}_{i=1}^{n} S(C_{n,0}^i)$ is a shelling for Arc$(C_{n,0})$.

Proof

Let S precede T in the ordering $S(\mathrm{{Arc}}(C_{n,0}))$. Then $T \in S(C_{n,0}^k)$ and $S \in S(C_{n,0}^j)$ for $1 \le j \le k$. Since $S(C_{n,0}^k)$ is a shelling we may assume $j<k$. There will be a triangle in T with vertices (k, k, x) for some $x \in [1,n]\backslash \{k\}$.

If $x \in [j,k-1]$ then mutate the loop at k to give $T' \in S(C_{n,0}^x)$. $T'$ occurs before T in the ordering because $x \in [j,k-1]$. Moreover, since the loop at k cannot occur in S then $T\cap S \subseteq T\cap T'$. See Fig. 7.

Fig. 7

If $x \in [j,k-1]$ then, taking $\gamma$ to be the loop at k, we get that $T' := \mu _{\gamma }(T)$ precedes T in the ordering $S(\text {Arc} (C_{n,0}))$

If $x \in [k+1, j-1]$ then the arc $\gamma = \langle x,k \rangle$ in T is not compatible with the loop at j in S. So $T\cap S \subseteq T\cap \mu _{\gamma }(T)$. Moreover, the way we constructed the shelling $S(C_{n,0}^k)$ in Claim 3.14 means that $\mu _{\gamma }(T)$ precedes T in the ordering. See Fig. 8. $\square$

Fig. 8

If $x \in [k+1,j-1]$ then, taking $\gamma = \langle x,k\rangle$, we get that $\mu _{\gamma }(T)$ precedes T in the ordering $S(\mathrm{Arc}(C_{n,0}))$

Corollary 3.16

Arc(n-gon) is shellable for $n\ge 3$.

Proof

Follows immediately from Claim 3.14. $\square$

Applying Theorem 3.12 we rediscover the classical result of Harer [7].

Corollary 3.17

Arc($C_{n,0}\mathrm{{)}}$ and Arc(n-gon) are PL-spheres of dimension $n-2$ and $n-4$, respectively.

4 Shellability of Arc$(M_n)$

In Sect. 3 we achieved shellability of a complex by grouping facets into blocks and finding a ‘shelling order’ in terms of these blocks. The task was then simplified to finding a shelling of the blocks themselves. Here we essentially follow the same strategy twice. However, on the second iteration of the process we require a specific shelling of the blocks since in general an arbitrary shelling would not suffice.

Definition 4.1

Let $T( M _n^\circ ) \subseteq T( M _n)$ consist of all triangulations of $M _n$ (i.e., no quasi-triangulations containing a one-sided curve).

Definition 4.2

Let $\gamma$ be an arc in $T \in T( M _n^\circ )$. Call $\gamma$ a cross-cap arc (c-arc) if $M _n{\setminus }\{\gamma \}$ is orientable. (Informally, a c-arc is an arc that necessarily passes through the cross-cap). Let (i, j) denote a c-arc with endpoints i and j.

Definition 4.3

Call a triangulation $T \in T( M _n^\circ )$ a cross-cap triangulation (c-triangulation) if every arc in T is a c-arc. Let $T( M _n^\otimes ) \subseteq T( M _n^\circ )$ consist of all c-triangulations.

Definition 4.4

Let $\gamma$ be an arc in $T \in T( M _n^\circ )$ that is not a c-arc. Call $\gamma$ a bounding arc (b-arc) if the flip of $\gamma$, with respect to T, is a c-arc. Note that, unlike a c-arc, the notion of $\gamma$ being a b-arc depends on which triangulation $\gamma$ is in (Fig. 9).

4.1 Reducing the Problem to c-Triangulations

Lemma 4.5

If $T( M _n^\otimes )$ is shellable then so is $T( M _n^\circ )$.

Proof

Consider $I := \{i_1, \ldots , i_k\} \subseteq [1,n]$. Let $\Gamma _{I}^{(k)}$ consist of all triangulations $T \in T( M _n^\circ )$ such that there is a c-arc in T with endpoint j if and only if $j \in I$. Note that this condition implies the existence of an arc or boundary segment $\langle i_m,i_{m+1}\rangle$ (where $i_{k+1}:= i_1$) in every triangulation $T \in \Gamma _{I}^{(k)}$ for all m $\in [1,k]$ (Fig. 10).

By assumption $T( M _n^\otimes )$ is shellable, and by Corollary 3.16 T(m-gon) is also shellable. Hence $\Gamma _{I}^{(k)}$ is the product of shellable collections of triangulations, and so is shellable by Proposition 3.4. Denote this shelling by $S(\Gamma _{I}^{(k)})$. Below, Claim 4.6 shows how a combination of these $S(\Gamma _{I}^{(k)})$ produce a shelling for $T( M _n^\circ )$. This then completes the proof of the lemma. $\square$

Fig. 9

An example of a c-arc; a c-triangulation; and a b-arc

Fig. 10

An illustration of the type of triangulations that belong to $\Gamma _I^{(k)}$

Claim 4.6

Let Block($k) := \displaystyle {{\mathrm{list}}}_{I \in [1,n]^{(k)}}S(\Gamma _{I}^{(k)})$. Then $\displaystyle {{\mathrm{list}}}_{k=n}^{1} \mathrm{{Block}}(k)$ is a shelling for $T( M _n^\circ )$.

Proof

Let S precede T in the ordering. Then $S \in$ Block(j) and $T \in$ Block(k) where $j \ge k$. In particular, $T \in S(\Gamma _{I_1}^{(k)})$ and $S \in S(\Gamma _{I_2}^{(j)})$ for some $I_1,I_2 \in \mathcal {P}([1,n])$ where $|I_1| \le |I_2|$. Since $S(\Gamma _{I}^{(k)})$ is a shelling we may assume $I_1 \ne I_2$.

Suppose that every b-arc in T is also an arc in S. Then $I_2 \subseteq I_1$, and since $|I_1| \le |I_2|$ this implies $I_1 = I_2$. So we may assume there is at least one b-arc $\gamma \in T$ that is not an arc in S. Since $\gamma \notin S$, $T\cap S \subseteq T\cap \mu _{\gamma }(T)$. Moreover, since $\gamma$ is a b-arc, $\mu _{\gamma }(T) \in$ Block($k+1$). Hence $\mu _{\gamma }(T)$ precedes T in the ordering, see Fig. 11. $\square$

Fig. 11

Since $x \notin I_1$, and the b-arc $\gamma \in T$ flips to a c-arc with endpoint x, then $\mu _{\gamma }(T)$ precedes T in the ordering

The idea behind Lemma 4.5 is that we are decomposing $T(\text {M}^{\circ }_n)$ into blocks, and ordering these blocks. The ordering is chosen in such a way that if we manage to individually shell the blocks themselves, we will have a shelling of $T(\text {M}^{\circ }_n)$. Figure 12 shows the block structure of $T(\text {M}^{\circ }_3)$.

In particular, we realise that to shell a block it is sufficient to find a shelling of $T( M _n^\otimes )$. We will split this into two cases: n even and n odd.

Fig. 12

Block structure of $T(\text {M}^{\circ }_3)$

4.2 Shellability of $T( M _n^{\otimes })$ for Even n

In the same vein of our approach thus far, we show $T( M _n^{\otimes })$ admits a shelling by ordering smaller blocks of triangulations. In particular, these blocks will be categorised by which diagonal arcs they contain.

Definition 4.7

If a c-arc of $M _n$ is of the form $(i,\frac{n}{2}+i)$, then we call it a diagonal arc.

Let $D_{\{(1,\frac{n}{2}+1)\}}^n$ consist of all triangulations of $T( M _n^{\otimes })$ which contain the diagonal arc $(1, \frac{n}{2}+1)$ but no other diagonal arcs $(i,\frac{n}{2}+i)$ where i $\in [2,\frac{n}{2}]$. See Fig. 13.

Fig. 13

The c-triangulation on the right is not in $D_{\{(1,3)\}}^4$ because it contains two diagonal arcs

Definition 4.8

Let $T \in D_{\{(1,\frac{n}{2}+1)\}}^n$ and $\gamma$ a c-arc in T. Let $\gamma = (i,j)$ for some $i \in [1, 1+\frac{n}{2}]$ and $j \in [1+\frac{n}{2},1]$. Define the length of $\gamma$ as follows:

• If $j\ne 1$, $l(\gamma ) := j-i+1$.

• If $j=1$, $l(\gamma ):= n-i+2$.

Remark 4.9

Note that the length of a diagonal arc is $\frac{n}{2}+1$. For a triangulation $T \in D_{\{(1,\frac{n}{2}+1)\}}^n$ we shall see that, excluding the diagonal arc $(1,\frac{n}{2}+1)$, the arcs in T will have length all less than $\frac{n}{2}+1$, or all greater than $\frac{n}{2}+1$ (Fig. 14).

Fig. 14

If $i \ne 1$ or $j \ne 1$ then the number of marked points in the shaded tube equals $l(\gamma )$

Fig. 15

We shall see that each triangulation in $D_{\{(1,\frac{n}{2}+1)\}}^n$ contains either $\mathcal {X}_1^n$ or $\mathcal {X}_2^n$

Definition 4.10

Let $\mathcal {X}_1^n$ be the partial triangulation of $M _n$ consisting of the c-arcs $(1, \frac{n}{2}+1), (2,\frac{n}{2}+1), (n,\frac{n}{2}+1)$. Additionally, let $T(\mathcal {X}_1^n)$ denote the triangulations in $D_{\{(1,\frac{n}{2}+1)\}}^n$ containing $\mathcal {X}_1^n$. Similarly, let $\mathcal {X}_2^n$ be the partial triangulation of $M _n$ consisting of the c-arcs $(1, \frac{n}{2}+1), (1,\frac{n}{2}), (n,\frac{n}{2}+2)$ and let $T(\mathcal {X}_1^n)$ denote the triangulations in $D_{\{(1,\frac{n}{2}+1)\}}^n$ containing $\mathcal {X}_2^n$. See Fig. 15.

Lemma 4.11

$D_{\{(1,\frac{n}{2}+1)\}}^n = T(\mathcal {X}_1^n) \sqcup T(\mathcal {X}_2^n)$. Moreover, for any c-arc $\gamma \ne (1, \frac{n}{2}+1)$ in T we have the following:

• $l(\gamma ) < \frac{n}{2} + 1$ if $T \in T(\mathcal {X}_1^n)$.

• $l(\gamma ) > \frac{n}{2}+1$ if $T \in T(\mathcal {X}_2^n)$.

Proof

A triangulation T in $D_{\{(1,\frac{n}{2}+1)\}}^n$ will contain either the c-arc $(2,\frac{n}{2}+1)$ or the c-arc $(1,\frac{n}{2}+2)$.

Assume the c-arc $(2,\frac{n}{2}+1)$ is in T. We will show, by induction on i, the c-arc of maximal length in T with endpoint $i \in [2,\frac{n}{2}+1]$ must be the c-arc (i, x) where $x \in [\frac{n}{2}+1,\frac{n}{2}+i-1]$. Let $\gamma$ be the c-arc in T of maximal length with endpoint 2. Let j be the other endpoint of $\gamma$ and suppose for a contradiction $j \in [\frac{n}{2}+2,1]$. Since $(2,\frac{n}{2}+1) \in T$ then, as T is a c-triangulation, $(2, y) \in T$ for every y $\in [\frac{n}{2}+1,j]$. In particular $\beta := (2,\frac{n}{2}+2) \in T$—which contradicts $T \in D_{\{(1,\frac{n}{2}+1)\}}^n$. See Fig. 16.

By induction, the c-arc $\alpha$ of maximal length in T with endpoint $i-1$ is the c-arc $(i-1, x)$ where $x \in [\frac{n}{2}+1,\frac{n}{2}+i-2]$. Let $\gamma$ be the c-arc in T of maximal length with endpoint i. Let j be the other endpoint of $\gamma$ and for a contradiction suppose $j \in [\frac{n}{2}+i,1]$. But by the maximality of $\alpha$ there will be a c-arc $(i,y) \in T$ for all y $\in [x,j]$ which contradicts $\beta := (i,\frac{n}{2}+i) \notin T$—see Fig. 17. Hence $j \in [\frac{n}{2}+1,\frac{n}{2}+i-1]$ and $l(\gamma ) < \frac{n}{2} + 1$. In particular, $T \in T(\mathcal {X}_1^n)$.

Fig. 16

The base case of induction with $i = 2$

Fig. 17

We prove that if $\alpha$ is the arc of maximal length in T with endpoint $i-1$, and $l(\alpha )\le \frac{n}{2}+1$, then any arc in T with endpoint i has length less or equal to $\frac{n}{2}+1$

If we supposed $(1,\frac{n}{2}+2)$ was an arc in T, then an analogous argument shows that $T \in T(\mathcal {X}_2)$ and $l(\gamma ) > \frac{n}{2} + 1$. $\square$

The following two definitions are motivated by Lemma 4.11.

Definition 4.12

Consider a c-arc $\gamma$ in a triangulation in $T(\mathcal {X}_1^n)$. If $l(\gamma ) = \frac{n}{2}$ then call $\gamma$ a max arc.

Definition 4.13

Consider a c-arc $\gamma$ in a triangulation in $T(\mathcal {X}_2^n)$. If $l(\gamma ) = \frac{n}{2}+2$ then call $\gamma$ a min arc.

Corollary 4.14

Let $S \in T(\mathcal {X}_1^n)$ and $T \in T(\mathcal {X}_2^n)$ then $S\cap T = \{(1, \frac{n}{2}+1)\}$.

Proof

It follows from the fact that, excluding the c-arc $(1, \frac{n}{2}+1)$, the maximal length of any c-arc in $S \in T(\mathcal {X}_1^n)$ is strictly less than $\frac{n}{2}+1$, and the minimal length of any c-arc in $T \in T(\mathcal {X}_2^n)$ is strictly greater than $\frac{n}{2}+1$. $\square$

Fig. 18

The two triangulations with the c-arcs of shortest length and longest length

Corollary 4.15

The triangulation $T_{{\max }}$ in Fig. 18 is the unique triangulation in $T(\mathcal {X}_1^n)$ such that $\sum \nolimits _{\gamma \in T_{{\max }}} l(\gamma )$ is maximal. The triangulation $T_{{\min }}$ is the unique triangulation in $T(\mathcal {X}_2^n)$ such that $\sum \nolimits _{\gamma \in T_{{\max }}} l(\gamma )$ is minimal. More explicitly,

$$\begin{aligned} T_\mathrm{max}&:= \biggl \{\biggl (1, \frac{n}{2}+1\biggr )\biggr \} \cup \biggl \{\biggl (i,\frac{n}{2}+i-1\biggr )\,\big |\, i \in \biggl [2,\frac{n}{2}+1\biggr ]\biggr \} \\&\qquad \qquad \cup \biggl \{\biggl (i,\frac{n}{2}+i-2\biggr )\,\big |\, i \in \biggl [3,\frac{n}{2}+1\biggr ]\biggr \},\\ T_\mathrm{min}&:= \biggl \{\biggl (1, \frac{n}{2}+1\biggr )\biggr \} \cup \biggl \{\biggl (i,\frac{n}{2}+i+1\biggr )\,\big |\, i \in \biggl [1,\frac{n}{2}\biggr ]\biggr \}\\&\qquad \qquad \cup \biggl \{\biggl (i,\frac{n}{2}+i+2\biggr )\,\big |\, i \in \biggl [1,\frac{n}{2}-1\biggr ]\biggr \}. \end{aligned}$$

Proof

Consider the partial triangulation $P_{{\max }}$ consisting of all the maximal length c-arcs $(i,\frac{n}{2}+i-1)$ , $i\in [2,\frac{n}{2}+1]$, which can appear in a triangulation in $T(\mathcal {X}_1^n)$. $P_{{\max }}$ cuts $M _n$ into (2 triangles and) quadrilaterals bounded by the two boundary segments $[i,i+1],[\frac{n}{2}+i-1,\frac{n}{2}+i]$ and the two c-arcs $(i,\frac{n}{2}+i-1), (i+1,\frac{n}{2}+i)$, $i \in [3,\frac{n}{2}]$. Let T be a triangulation in $T(\mathcal {X}_1^n)$ containing $P_{{\max }}$. Notice that $(i,\frac{n}{2}+i) \notin T$ by definition of $D_{\{(1,\frac{n}{2}+1)\}}^n$, hence $(i+1,\frac{n}{2}+i-1) \in T$ for every $i \in [3,\frac{n}{2}+1]\}$ and so $T = T_{{\max }}$. Moreover, since $l(i+1,\frac{n}{2}+i-1) = \frac{n}{2} - 1$ then $T_{{\max }}$ is the unique triangulation in $T(\mathcal {X}_1^n)$ such that $\sum \nolimits _{\gamma \in T} l(\gamma )$ is maximal. Analogously we get the result regarding unique minimality of $T_{{\min }}$. $\square$

Consider a partial triangulation of $M _n$ consisting of the diagonal arc $(1,\frac{n}{2}+1)$ and two max arcs. Cutting along these max arcs we will be left with two regions. Let R be the region that does not contain the diagonal arc $(1,\frac{n}{2}+1)$. Note R will contain 2k marked points for some $k \in \{2,\ldots , \frac{n}{2}\}$.

Lemma 4.16

The set of c-triangulations of R such that no max arcs occur in R is equivalent to $T(\mathcal {X}_1^{2(k-1)})$.

Proof

Collapse the quadrilateral $(1,2, \frac{n}{2}+1,n)$ to a c-arc and relabel marked points as shown in Figure 19. Max arcs in R correspond to diagonal arcs in $R'$. Furthermore, up to a relabelling of vertices, triangulating $R'$ so that no diagonal arcs occur in the triangulation is precisely triangulating $\mathcal {X}_1^{2(k-1)}$ so that no diagonal arcs occur. $\square$

Fig. 19

An illustration explaining why triangulating the region between two max arcs, so that no other max arcs are present, is equivalent to $T(\mathcal {X}_1^{2k})$ for some k

Remark 4.17

Using induction we realise that Lemma 4.16 tells us that $D_{\{(1,\frac{n}{2}+1)\}}^n$ has the same flip structure as the set of all Dyck paths of length $n-2$. In particular, triangulations in $D_{\{(1,\frac{n}{2}+1)\}}^n$ correspond to Dyck paths, and arcs appearing in those triangulations correspond to nodes in the Dyck lattice. This correspondence is indicated in Fig. 20 and is best viewed in colour.

Fig. 20

$D_{\{(1,\frac{n}{2}+1)\}}^n$ and Dyck paths. See Remark 4.17 for an explanation of their connection

Definition 4.18

Let $i \in \{1,2\}$. Call an arc $\gamma$ in $T \in T(\mathcal {X}_i^n)$ $\mathcal {X}\hbox {-}{\textit{mutable}}$ if $\mu _{\gamma }(T) \in T(\mathcal {X}_i^n)$.

Definition 4.19

Let $\gamma$ be an $\mathcal {X}$-mutable arc in a triangulation $T \in D_{\{(1,\frac{n}{2}+1)\}}^n$, and let $\gamma '$ be the arc $\gamma$ mutates to. Call $\gamma$ upper-mutable if $l(\gamma ') > l(\gamma )$ and lower-mutable if $l(\gamma ') < l(\gamma )$.

Definition 4.20

Call a shelling $\mathcal {S}$ of $T(\mathcal {X}_1^n)$ $(T(\mathcal {X}_2^n))$ an upper (lower) shelling if for any triangulation $T \in \mathcal {S}$ and any upper (lower) mutable arc $\gamma$ in T, $\mu _{\gamma }(T)$ precedes T in the ordering.

Definition 4.21

Let $\mathcal {I}$ be the set of all max arcs of $D_{\{(1,\frac{n}{2}+1)\}}^n$, excluding the max arcs $\alpha _1 :=(1,\frac{n}{2}+1), \alpha _2 :=(\frac{n}{2}+1,n)$.

Lemma 4.22

If $T \in T(\mathcal {X}_1^n)$ does not contain a max arc $m \in \mathcal {I}$ then there exists an upper mutable arc $\gamma$ strictly contained between the endpoints of m, see Fig. 21.

Fig. 21

An example of an arc $\gamma$ that is strictly contained between the endpoints of m

Proof

If $n\in \{2,4\}$ then $\mathcal {I} = \emptyset$ and there is nothing to prove. So assume $n \ge 6$.

Suppose $m = (i,\frac{n}{2}+i -1)\in \mathcal {I}$ is not in the triangulation T. We will show there exists a c-arc strictly contained between the endpoints of m.

Let (i, x) be the c-arc of maximum length in T connected to i. Since $m \ne (i,x)$ then $x \in [\frac{n}{2}+1,\frac{n}{2}+i-2]$. Moreover, by maximality of (i, x), $(i+1,x) \in T$. So indeed there is a c-arc in T strictly contained between the endpoints of m, see Fig. 22.

Of the c-arcs in T that are strictly contained between the endpoints of m, let $\gamma = (j_1,j_2)$ be an arc of minimum length. We will show that $\gamma$ is upper mutable.

Fig. 22

Showing the existence of a c-arc in T contained between the endpoints of $m \notin T$

By minimality of $\gamma$ the c-arc $(j_1,j_2-1)$ is not in T. Hence the c-arc $(j_1-1,j_2)$ must be in T. Likewise the c-arc $(j_1,j_2+1)\in T$. So $\gamma$ is contained in the quadrilateral $(j_1,j_1-1,j_2,j_2+1)$. Hence mutating $\gamma$ gives $\gamma ' = (j_1-1,j_2+1)$. $l(\gamma ) < l(\gamma ')$ so $\gamma$ is indeed upper mutable, see Fig. 23. $\square$

Fig. 23

An arc $\gamma$ of minimal length in T contained between the endpoints of m will be upper mutable

Lemma 4.23

There exists an upper shelling for $T(\mathcal {X}_1^n)$. Denote this by $S(\mathcal {X}_1^n)$.

Proof

Let $\Psi _{\{\gamma _1,\ldots ,\gamma _k\}}$ be the collection of triangulations in $T(\mathcal {X}_1^n)$ containing the max arcs $\gamma _1,\ldots ,\gamma _k, \alpha _1, \alpha _2$ and no other max arcs. By Lemma 4.16 we know that $\Psi _{\{\gamma _1,\ldots ,\gamma _k\}} \equiv \prod _{i=1}^{k+1}$ T($\mathcal {X}_1^{n_i})$ where $2 \le n_i < n$.

Moreover, by induction on the trivial base case when $n=2$, and using Proposition 3.4, we get that there is an upper shelling for $\Psi _{\{\gamma _1,\ldots ,\gamma _k\}}$. Denote this shelling by $S(\Psi _{\{\gamma _1,\ldots ,\gamma _k\}})$. Merging these $S(\Psi _{\{\gamma _1,\ldots ,\gamma _k\}})$ together, as shown in Claim 4.24 below, we get an upper shelling for $T(\mathcal {X}_1^n)$, and this completes the proof of the lemma. $\square$

Claim 4.24

Let Block($k) := \displaystyle {{\mathrm{list}}}_{J \in \mathcal {I}^{(k)}}S(\Psi _J)$. Then $\displaystyle {{\mathrm{list}}}_{k=\frac{n}{2}-2}^{0} \mathrm{{Block}}(k)$ is an upper shelling for $T(\mathcal {X}_1^n)$.

Proof

Let $T,S \in T(\mathcal {X}_1^n)$ and suppose S precedes T in the proposed ordering. Then $T \in \Psi _{J_1}$ and $S \in \Psi _{J_2}$ where $J_1,J_2 \in \mathcal {P}(\mathcal {I})$ and $|J_1| \le |J_2|$. W.l.o.g. we may assume $J_1 \ne J_2$ since by induction $S(\Psi _{J_1})$ is an upper shelling.

As $|J_1| \le |J_2|$ and $J_1 \ne J_2$ there is a max arc m in S that is not in T. By Lemma 4.22 there is an upper mutable arc $\gamma$ in T strictly contained between the endpoints of m. Moreover $\gamma$ and m are not compatible so $S\cap T \subseteq \mu _{\gamma }(T)\cap T$. And $\mu _{\gamma }(T)$ precedes T in the ordering because of the upper shelling $S(\Psi _{J_1})$. $\square$

An analogous argument proves the following lemma.

Lemma 4.25

There exists a lower shelling for $T(\mathcal {X}_2^n)$. Denote this by $S(\mathcal {X}_2^n)$.

Lemma 4.26

For any $T \in T(\mathcal {X}_1^n){\setminus } \{T_{\max }\}$, $T_{\max }$ is connected to T by a sequence of lower mutations.

Proof

By Lemma 4.22 we can keep performing mutations on upper mutable arcs until we reach a triangulation containing every max arc. By Corollary 4.15 the only triangulation in $T(\mathcal {X}_1^n)$ that contains every max arc is $T_{\max }$. Hence T is connected to $T_{\max }$ by a sequence of upper mutations. Equivalently, $T_{\max }$ is connected to T by a sequence of lower mutations. $\square$

Definition 4.27

Call a c-arc $\gamma$ in a triangulation $T \in D_{\{(1,\frac{n}{2}+1)\}}^n$ special mutable if any of the following statements hold:

• $T \in T(\mathcal {X}_1^n)$ and $\gamma$ is upper mutable.

• $T \in T(\mathcal {X}_2^n)$ and $\gamma$ is lower mutable.

• $\gamma$ mutates to a diagonal c-arc.

Lemma 4.28

Let $T \in D_{\{(1,\frac{n}{2}+1)\}}^n$ and let $P_T$ be the partial triangulation of $M _n$ consisting of all the special mutable arcs in T. Then any triangulation containing $P_T$ cannot contain the diagonal c-arc $(i,\frac{n}{2}+i)$, where $i \in \{2,\ldots ,\frac{n}{2}\}$.

Proof

Assume $T \in T(\mathcal {X}_1^n)$. An analogous argument works if $T \in T(\mathcal {X}_2^n)$. We prove the lemma via induction on the upper shelling order of $T(\mathcal {X}_1^n)$.

The first triangulation in the upper shelling ordering is $T_{\max }$. The special mutable arcs in $T_{\max }$ are $(i, \frac{n}{2}+i-2)$, $i \in [3, \frac{n}{2}+1]$. However, the c-arc $(i, \frac{n}{2}+i-2)$ is not compatible with the diagonal c-arc $(i-1, \frac{n}{2}+i-1)$. And so ranging i over $3,\ldots , \frac{n}{2}+1$ proves the base inductive case.

Let $\gamma$ be a lower mutable arc in a triangulation $T \in T(\mathcal {X}_1^n)$. By Lemma 4.26, to prove the lemma it suffices to show that the special mutable arcs in $\mu _{\gamma }(T)$ prevent the same diagonal c-arcs as the special mutable arcs in T. Let $\beta _1 , \beta _2$ be the c-arcs containing $\gamma$ in a quadrilateral. See Fig. 24.

The arcs $\beta _1$ and $\beta _2$ may be special mutable in T but in $\mu _{\gamma }(T)$ they definitely won’t be. The implication of this is that $\beta _1$ and $\beta _2$ may be c-arcs in $P_T$, and prevent certain diagonal arcs, but $\beta _1,\beta _2 \notin P_{\mu _{\gamma }(T)}$ so $\mu _{\gamma }$ needs to make up this difference. Indeed, it does make up the difference as the diagonal arcs not compatible with either $\beta _1$ or $\beta _2$ are precisely the diagonal arcs not compatible with $\mu _{\gamma }$. $\square$

Fig. 24

$\beta _1$ and $\beta _2$ denote the c-arcs in T that enclose $\gamma$ in a quadrilateral

Lemma 4.29

In each c-triangulation T of $M _n$ there is at least one diagonal arc.

Proof

Let us assume, for a contradiction, that there is no diagonal arc in T. Without loss of generality, we may assume that the c-arc connected to 1, of maximum length, is $\gamma = (1,j_1)$ for some $j_1 \in [1,\frac{n}{2}]$. (Otherwise just flip the picture.)

Let $\gamma _2 = (2,j_2)$ be the c-arc of maximum length in T that is connected to 2. If $j_2 > \frac{n}{2}$ then by maximality of $\gamma _1$ there is a c-arc $(2,\frac{n}{2})$. Hence, $j_2 \in [j_1,\frac{n}{2}+1]$. Inductive reasoning shows that the c-arc connected to $j_1-1$ in T, of maximum length, is $\gamma _{j-1}=(j-1,x)$ for some $x \in [j, \frac{n}{2}+j_1-2]$. However, then by the maximality of $\gamma _{j-1}$ we must have $(j_1, \frac{n}{2}+j_1) \in T$. This gives a contradiction, and so the lemma is proved. $\square$

Lemma 4.30

$T( M _n^{\otimes })$ is shellable for even n.

Proof

Let $\mathcal {K}$ be the collection of diagonal c-arcs of $M _n$. Consider $I = \{ \gamma _1, \ldots , \gamma _k \} \subseteq \mathcal {K}$ and let $D_{I}^n$ consist of all triangulations of $T( M _n^{\otimes })$ containing every diagonal c-arc in I, but no diagonal c-arcs in $\mathcal {K}{\setminus } I$. The set of c-triangulations T(R) of a region R cut out by two diagonal c-arcs, so that no other diagonal c-arcs occur in the region, is equivalent to $D_{\{(1,\frac{m}{2}+1)\}}^m$ for some $m \in [2,n-2]$. See Fig. 25.

Choose $\displaystyle {{\mathrm{list}}}_{i=1}^2 S(\mathcal {X}_i^m)$ to be the ordering of $D_{\{(1,\frac{m}{2}+1)\}}^m$. Take the disjoint union of these orderings, over all the regions cut out by diagonal c-arcs in I, to get an ordering of $D_{I}^n$. Denote this ordering by $O(D_{I}^n)$. Below, Claim 4.31 shows that unifying these orderings produces a shelling of $T( M _n^{\otimes })$, and this completes the proof of the lemma. $\square$

Fig. 25

$T(R) \equiv T(R') = D_{\{(1,k+1)\}}^{2k}$

Claim 4.31

Let Block$(k) := \displaystyle {{\mathrm{list}}}_{I \in \mathcal {K}^{(k)}}O(D_{I}^n)$. Then $\displaystyle {{\mathrm{list}}}_{k=\frac{n}{2}}^1 \mathrm{{Block}}(k)$ is a shelling for $T( M _n^{\otimes })$.

Proof

Let $T,S \in T( M _n^{\otimes })$ and suppose S precedes T in the ordering. Then $T \in O(D_{I_1}^n)$ and $S \in O(D_{I_2}^n)$ for some $I_1,I_2 \in \mathcal {P}(\mathcal {K})$ where $|I_1| \le |I_2|$.

If there is a region R in T that contains a special mutable arc $\gamma$, such that $\gamma$ is not an arc in S, then $\mu _{\gamma }(T)$ precedes T in the ordering and $S\cap T \subseteq \mu _{\gamma }(T)\cap T$.

So suppose that for every region R of T all special mutable arcs in that region are also arcs in S. Then by Lemma 4.28, $I_2 \subseteq I_1$. Since $|I_1| \le |I_2|$ we must have $I_1 = I_2$.

If $O(D_{I}^n)$ was a shelling for $D_{I}^n$ then the proof would be finished. However, in general, it is not. To understand how we should proceed let us consider $D_{\{(1,\frac{n}{2}+1)\}}^n$.

By definition, $O(D_{\{(1,\frac{n}{2}+1)\}}^n) = \displaystyle {{\mathrm{list}}}_{i=1}^2 S(\mathcal {X}_i^n)$. Let T be the first triangulation of $S(\mathcal {X}_2)$ and let $S \in S(\mathcal {X}_1)$. Corollary 4.14 tells us that the only arc T and S share in common is the diagonal c-arc $(1,\frac{n}{2}+1)$. If $n=2$ then $O(D_{\{(1,2)\}}^2) = S,T$ is a shelling for $D_{\{(1,2)\}}^n$. However, if $n \ge 4$ then there are at least 4 arcs in S and T. Hence, $\mu _{\gamma }(T) \notin S(\mathcal {X}_1^n)$ for any arc $\gamma$ in T, since $\mu _{\gamma }(T)$ and S can share at most two arcs in common.

However, as $n \ge 4$ the first triangulation of $S(\mathcal {X}_2^n)$ contains (at least one) arc $\gamma$ that mutates to a diagonal c-arc. And so $\mu _{\gamma }(T)$ contains more diagonal c-arcs than T. Hence $\mu _{\gamma }(T)$ precedes T in the overall ordering for $T( M _n^{\otimes })$. $\square$

4.3 Shellability of $T( M _n^{\otimes })$ for Odd n

In the even case diagonal arcs were a key ingredient in the shelling of $T( M _n^{\otimes })$. We will see ’diagonal triangles’ play the same role in the odd case. For the duration of this section we fix $n = 2k+1$.

Definition 4.32

A triangle in $M _n$ comprising of two c-arcs $(i, i+k)$, $(i,i+k+1)$ and the boundary segment $(i+k,i+k+1)$ for some $i \in [1,n]$ is called a diagonal triangle (d-triangle). Additionally, call i the special vertex of the d-triangle.

Definition 4.33

Let $D_{\{(k+1,n,1)\}}^n$ denote the set of all c-triangulations of $M _n$ which contain the d-triangle $(k+1,n,1)$ but no other d-triangles. See Fig. 26.

Fig. 26

The triangulation on the right is not in $D_{\{(3,5,1)\}}^5$ because it contains three d-triangles

Definition 4.34

Let $T \in D_{\{(k+1,n,1)\}}^n$ and $\gamma$ a c-arc in T. Let $\gamma = (i,j)$ for some $i \in [1, k+1]$ and $j \in [k+1,n]$. Define the length of $\gamma$ as $l(\gamma ) := j-i+1$, see Fig. 27.

Fig. 27

‘Number of marked points in shaded tube’ $= l(\gamma )$

Lemma 4.35

The maximum length of any c-arc in $T \in D_{\{(k+1,n,1)\}}^n$ is $k+1$.

Proof

Given $T \in D_{\{(k+1,n,1)\}}^n$ we will prove by induction on $i \in [1,k+1]$ that there is no c-arc in T, with endpoint $k+i$, of length greater than $k+1$. For $i=1$ this trivially holds. Assume the statement holds true for i and let $\gamma = (x,k+i)$ and $\beta = (y,k+i+1)$ be the c-arcs in T of maximal length which have endpoints $k+i$ and $k+i+1$, respectively. Note that $x \le y$ and, by induction, we know $x \in [i,k+1]$. If $x=y=i$ then we have a d-triangle $(i,k+i,k+i+1)$ with special vertex i, which contradicts $T \in D_{\{(k+1,n,1)\}}^n$. Therefore $x\ne y$ or $x \ne i$, so indeed $l(\beta ) = k+i+2-y\le k+1$. $\square$

Lemma 4.36

$D_{\{(k+1,n,1)\}}^n \equiv T(\mathcal {X}_1^{n+1})$. As such, $T(\mathcal {X}^{n+1}_{})$ induces an upper shelling of $D_{\{(k+1,n,1)\}}^n$. Denote this upper shelling by $S(D_{\{(k+1,n,1)\}}^n)$.

Proof

For each triangulation in $D_{\{(k+1,n,1)\}}^n$ add a marked point to the d-triangle $(k+1,2k+1,1)$ and relabel the marked points. Adding the c-arc $(1,k+2)$ we get $T(\mathcal {X}_1^{n+1})$. Lemma 4.35 tells us the maximum length of an arc in $T \in D_{\{(k+1,n,1)\}}^n$ is $k+1$. And since the length of a max arc in $T(\mathcal {X}_1^{n+1})$ is also $k+1$ then $D_{\{(k+1,n,1)\}}^n \equiv T(\mathcal {X}_1^{n+1})$. See Fig. 28. $\square$

Fig. 28

An illustration explaining how $D_{\{(k+1,n,1)\}}^n$ is equivalent to $T(\mathcal {X}_1^{n+1})$

Lemma 4.37

In each c-triangulation T of $M _n$ there are an odd number of d-triangles in T. Moreover, the collection of c-triangulations of any region cut out in between d-triangles, such that no other d-triangles occur, is equivalent to $D_{\{(\frac{m+1}{2},m,1)\}}^m$ for some $m < n$.

Proof

We will show that if there are two d-triangles there must in fact be a third. Additionally we will show the collection of (legitimate) triangulations in any region cut out in between the three d-triangles is equivalent to $D_{\{(\frac{m+1}{2},m,1)\}}^m$ for some $m < n$. And applying induction on this we will have the lemma proved.

Suppose there are at least two d-triangles in a c-triangulation T. Without loss of generality we may assume the two d-triangles $(k+1,2k+1,1)$ and $(i,i+k,i+k+1)$ are in T, for some $i \in [1,k]$. See Fig. 29.

We will show there is a third d-triangle with special vertex $z \in [i+k+1,2k+1]$. Note that $(i+1,i+k+1) \notin T$ otherwise the d-triangle $(i+k+1,i,i+1) \in T$. Similarly, $(k,2k+1) \notin T$ otherwise the d-triangle $(2k+1,k+1,k) \in T$. Consequently, this implies $(i+1,x) \in T$ for some $x \in [i+k+2,2k]$, and $(k,y) \in T$ for some $y \in [i+k+2,2k]$. In turn, by induction, there is a d-triangle with special vertex $z \in [x,y]$. See Fig. 30.

What remains to prove is that each region cut out by these three d-triangles is equivalent to $D_{\{(\frac{m+1}{2},m,1)\}}^m$ for some $m < n$.

Consider the d-triangles $(k+1,2k+1,1)$ and $(i,i+k,i+k+1)$ with special vertices $k+1$ and i, respectively. Let R be the region bounded by the c-arcs $(1,k+1)$, $(i,i+k)$ and the boundary segments [1, i], $[k+1,k+i]$. Collapsing the boundary segment $[i,k+1]$ to a point and collapsing $[k+i,1]$ to a boundary segment preserves the notion of length in R. After collapsing we see that the collection of c-triangulations of R (so that no d-triangles occur) is equivalent to $D_{\{(i,2i-1,1)\}}^{2i-1}$. See Fig. 31.

Similarly the collection of c-triangulations of either of the other two regions cut out by the three d-triangles is equivalent to $D_{\{(\frac{m+1}{2},m,1)\}}^m$ for some $m < n$. This completes the proof. $\square$

Fig. 29

.

Fig. 30

By induction there is a d-triangle with its special vertex in the shaded region

Fig. 31

.

Definition 4.38

Let $T \in D_{\{(k+1,n,1)\}}^n$ and let $\gamma$ be a c-arc in T. Call $\gamma$ special mutable if it is upper mutable or $\mu _{\gamma }(T)$ contains more d-triangles than T.

Lemma 4.39

Let $T \in D_{\{(k+1,n,1)\}}^n$ and let $P_T$ be the partial triangulation of $M _n$ consisting of all special mutable arcs in T. Then for any c-triangulation of $M _n$ containing $P_T$, there are no d-triangles with special vertex $i\in [1,\dots ,n]{\setminus } \{k+1\}$.

Proof

We follow the same idea as in Lemma 4.28. Namely, we will prove the lemma by induction on the shelling order of $S(D_{\{(k+1,n,1)\}}^n)$.

Let $T_1$ be the first triangulation in the shelling. Note $\gamma _i = (i,k+i-1)$ is a special mutable c-arc in $T_1$ for every $i \in [2,k+1]$. Moreover $\gamma _i$ is not compatible with the c-arc $(i-1, k+i)$. Hence there is no d-triangle with special vertex $i-1$ or $k+i$, $i \in [2,k+1]$. This proves the base inductive case.

Let $T \in D_{\{(k+1,n,1)\}}^n$. To prove the lemma by induction it suffices to show that for any lower mutable arc $\gamma \in T$, the d-triangles incompatible with $P_T$ are precisely the d-triangles incompatible with $P_{\mu _{\gamma }(T)}$.

So let $\gamma$ be a lower mutable arc in T. Let $\beta _1, \beta _2$ be the c-arcs of the quadrilateral containing $\gamma$. See Fig. 32. Note that $\beta _1$ and $\beta _2$ could be upper mutable in T, but they will definitely not be upper mutable in $\mu _{\gamma }(T)$. Analogously to the proof of Lemma 4.28, to prove the lemma it suffices to show $\mu _{\gamma }$ is incompatible with all the d-triangles incompatible with either $\beta _1$ or $\beta _2$. This follows from the fact that a c-arc $\alpha = (x,k+y)$ of length less than k is incompatible with d-triangles with special vertex $z \in [y,x-1]\cup [k+y+1,k+x]$. See Fig. 33. $\square$

Fig. 32

$\beta _1$ and $\beta _2$ denote the c-arcs in T which enclose $\gamma$ in a quadrilateral

An analogous argument to Lemma 4.29 proves the following lemma.

Fig. 33

$\alpha$ is incompatible with d-triangles whose special vertex lies in one of the shaded regions

Lemma 4.40

In each c-triangulation T of $M _n$ there is at least one d-triangle.

Lemma 4.41

$T( M _n^{\otimes })$ is shellable for odd n.

Proof

Let $\mathcal {K}$ be the collection of d-triangles of $M _n$ that can occur in a triangulation without containing any other d-triangles. Consider $I = \{ \Delta _1, \ldots , \Delta _k \} \subseteq \mathcal {K}$ and let $D_{I}^n$ consist of all triangulations of $T( M _n^{\otimes })$ containing every d-triangle in I, and no d-triangles in $\mathcal {K}{\setminus } I$.

By Lemma 4.37, each region cut out in between the d-triangles in I is shellable. Taking the product of these shellings over all regions gives us a shelling for $D_{I}^n$. Denote this shelling by $S(D_{I}^n)$. Combining these $S(D_{I}^n)$ produces a shelling for $T( M _n^{\otimes })$, and thus completes the proof of the lemma. See Claim 4.42 below. $\square$

Claim 4.42

Let $\mathrm{{Block}}(k) := \displaystyle {{\mathrm{list}}}_{I \in \mathcal {K}^{(k)}}S(D_{I}^n)$. Then $\displaystyle {{\mathrm{list}}}_{k=\frac{n}{2}}^1 \mathrm{{Block}}(k)$ is a shelling for $T( M _n^{\otimes })$.

Proof

Let $T,S \in T( M _n^{\otimes })$ and suppose S precedes T in the ordering. Then $T \in S(D_{I_1}^n)$ and $S \in S(D_{I_2}^n)$ for some $I_1,I_2 \in \mathcal {P}(\mathcal {K})$ where $|I_1| \le |I_2|$.

If there is a region R in T that contains a special arc $\gamma$, such that $\gamma$ is not an arc in S, then $\mu _{\gamma }(T)$ precedes T in the ordering and $S\cap T \subseteq \mu _{\gamma }(T)\cap T$. So suppose that for every region R of T all special arcs in that region are also arcs in S. Then by Lemma 4.39 $I_2 \subseteq I_1$. Since $|I_1| \le |I_2|$ we must have $I_1 = I_2$. And since $S(D_{I_1}^n)$ is a shelling for $D_{I}^n$ the claim is proved. $\square$

4.4 Proof of Main Theorem

Lemma 4.43

$T( M _n^\circ )$ is shellable for $n \ge 1$.

Proof

Lemmas 4.30 and 4.41 prove $T( M _n^{\otimes })$ is shellable for all $n \ge 1$. $T( M _n^\circ )$ is therefore shellable by Lemma 4.5. $\square$

Returning to our example of $\text {M}_3$, Fig. 34 shows a shelling of $T(\text {M}^{\circ }_3)$ that we can obtain through our construction.

Fig. 34

Shelling of $T(\text {M}^{\circ }_3)$

Theorem 4.44

(Main Theorem) Arc$( M _n)$ is shellable for $n \ge 1$.

Proof

Let $\mathcal {C}$ consist of all quasi-triangulations of $M _n$ containing the one-sided closed curve. Cutting along the one-sided curve in $M _n$ we are left with the marked surface $C_{n,0}$. Therefore the induced simplicial complex of $\mathcal {C}$ is the cone over Arc$(C_{n,0})$. Arc$(C_{n,0})$ is shellable by Proposition 3.13 so Proposition 3.4 tells us $\mathcal {C}$ is also shellable. Let $S(\mathcal {C})$ denote a shelling for $\mathcal {C}$. Let $S( M _n^{\circ })$ be a shelling of $T(\text {M}^{\circ }_n)$ guaranteed by Lemma 4.43. Coupling these two shellings, as described in Claim 4.45 below, provides us with a shelling of Arc$( M _n)$, and this completes the proof of the theorem. $\square$

Claim 4.45

Let $S( M _n) := S( M _n^{\circ }), S(\mathcal {C})$. Then $S( M _n)$ is a shelling for Arc$( M _n)$.

Proof

Suppose $S,T \in S( M _n)$ and S precedes T in the ordering. Without loss of generality we may assume $S \in S( M _n^{\circ })$ and $T \in S(\mathcal {C})$. Since T contains the one-sided closed curve $\gamma$, and $\gamma \notin S$ then $S\cap T \subseteq \mu _{\gamma }(T)\cap T$. Moreover, $\mu _{\gamma }(T) \in S( M _n^{\circ })$ so precedes T in the ordering. $\square$

Remark 4.46

Recall that $\Delta _A$ denotes the induced simplicial complex of a set of (quasi) triangulations A. Since $\partial \Delta _{T( M _n^{\circ })} \cong \mathrm{{Arc}}(C_{n,0})$ and $\Delta _{\mathcal {C}} \cong Cone (\mathrm{{Arc}}(C_{n,0}))$ then Arc$( M _n)$ is the cone over the boundary of $\Delta _{T( M _n^{\circ })}$.

Corollary 4.47

Let X be a finite quasi-arc complex. Then X is spherical.

Proof

X is a finite shellable pseudo-manifold without boundary by Proposition 2.11, Theorems 2.12 and 4.44. Therefore X is spherical by Theorem 3.12. $\square$