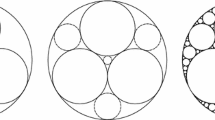
Abstract
Using transversality and a dimension reduction argument, a result of Bezdek and Kuperberg is applied to polycylinders, showing that the optimal packing density of \(\mathbb {D}^2\times \mathbb {R}^n\) equals \(\pi /\sqrt{12}\) for all natural numbers n.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Open and closed Euclidean unit n-balls will be denoted by \(\mathbb {B}^n\) and \(\mathbb {D}^n\) respectively. The closed unit interval is denoted by \(\mathbb {I}\). A general polycylinder C is a set congruent to \(\prod _{i=1}^{i=m}\lambda _i\mathbb {D}^{k_i}\) in \(\mathbb {R}^{ k_1+\dots + k_m}\), where \(\lambda _i\) is in \([0,\infty ]\). For this article, the term polycylinder refers to the special case of an infinite polycylinder over a two-dimensional disk of unit radius. A polycylinder is a set congruent to \(\mathbb {D}^2 \times \mathbb {R}^n \) in \( \mathbb {R}^{n+2}\). A polycylinder packing of \(\mathbb {R}^{n+2}\) is a family \(\mathscr {C} = \{C_i\}_{i \in I}\) of polycylinders \(C_i \subset \mathbb {R}^{n+2}\) with mutually disjoint interiors. The upper density \(\delta ^+ (\mathscr {C})\) of a packing \(\mathscr {C}\) of \(\mathbb {R}^n\) is defined to be
The upper packing density \(\delta ^+ (C)\) of an object C is the supremum of \(\delta ^+ (\mathscr {C})\) over all packings \(\mathscr {C}\) of \(\mathbb {R}^n\) by C.
This article proves the following sharp bound for the packing density of infinite polycylinders:
Theorem 1
\(\delta ^+(\mathbb {D}^2 \times \mathbb {R}^n) = \pi /\sqrt{12} \) for all natural numbers n.
Theorem 1 generalizes a result of Bezdek and Kuperberg [1] and improves on results that may be computed using a method of Fejes Tóth and Kuperberg [3], cf. [2, 5]; it gives some of the first sharp upper bounds for packing density in high dimensions.
2 Transversality
This section introduces the required transversality arguments from affine geometry. A d-flat is a d-dimensional affine subspace of \(\mathbb {R}^n\). The parallel dimension \(\mathrm{dim}_\parallel \{F,\dots , G\}\) of a collection of flats \(\{F, \dots , G\}\) is the dimension of their maximal parallel sub-flats. The notion of parallel dimension can be interpreted in several ways, allowing a modest abuse of notation.
-
For a collection of flats \(\{F, \dots , G\}\), consider their tangent cones at infinity \(\{F_\infty , \dots , G_\infty \}\). The parallel dimension of \(\{F, \dots , G\}\) is the dimension of the intersection of these tangent cones. This may be viewed as the limit of a rescaling process \(\mathbb {R}^n \rightarrow r\mathbb {R}^n\) as r tends to 0, leaving only the scale-invariant information.
-
For a collection of flats \(\{F, \dots , G\}\), consider each flat as a system of linear equations. The corresponding homogeneous equations determine a collection of linear subspaces \(\{F_\infty , \dots , G_\infty \}\). The parallel dimension is the dimension of their intersection \(F_\infty \,\cap \dots \cap \, G_\infty \).
Two disjoint d-flats are parallel if their parallel dimension is d, that is, if every line in one is parallel to a line in the other.
Lemma 1
A pair of disjoint n-flats in \(\mathbb {R}^{n+k}\) with \(n\ge k\), has parallel dimension strictly greater than \(n-k.\)
Proof
Let F and G be such a pair. By homogeneity of \(\mathbb {R}^{n+k}\), let \(F=F_\infty .\) As \(F_\infty \) and G are disjoint, G contains a non-trivial vector \(\mathbf{v}\) such that \(G = G_\infty +\mathbf{v}\) and \(\mathbf{v}\) is not in \(F_\infty + G_\infty .\) It follows that
Count dimensions to find \(n+k > n +n - \mathrm{dim}_\parallel (F_\infty ,G_\infty ).\) \(\square \)
Corollary 1
A pair of disjoint n-flats in \(\mathbb {R}^{n+2}\) has parallel dimension at least \(n-1\).
3 Dimension Reduction
3.1 Pairwise Foliations
The core \(a_i\) of a polycylinder \(C_i\) congruent to \(\mathbb {D}^2 \times \mathbb {R}^n\) in \(\mathbb {R}^{n+2}\) is the distinguished n-flat defining \(C_i\) as the set of points at most distance 1 from \(a_i\). In a packing \(\mathscr {C}\) of \(\mathbb {R}^{n+2}\) by polycylinders, Corollary 1 shows that, for every pair of polycylinders \(C_i\) and \(C_j\), one can choose parallel \((n-1)\)-dimensional subflats \(b_i \subset a_i\) and \(b_j \subset a_j\) and define a product foliation
with \(\mathbb {R}^3\) leaves that are orthogonal to \(b_i\) and to \(b_j\). Given a point x in \(a_i\), there is a distinguished \(\mathbb {R}^3\) leaf \(F_x^{b_i,b_j}\) that contains the point x. The foliation \(\mathscr {F}^{b_i,b_j}\) restricts to foliations of \(C_i\) and \(C_j\) with right-circular-cylinder leaves.
3.2 The Dirichlet Slice
In a packing \(\mathscr {C}\) of \(\mathbb {R}^{n+2}\) by polycylinders, the Dirichlet cell \(D_i\) associated with a polycylinder \(C_i\) is the set of points in \(\mathbb {R}^{n+2}\) which lie no further from \(C_i\) than from any other polycylinder in \(\mathscr {C}\). The Dirichlet cells of a packing partition \(\mathbb {R}^{n+2},\) as \(C_i \subset D_i\) for all polycylinders \(C_i\). To bound the density \(\delta ^+(\mathscr {C})\), it is enough to fix an i in I and consider the density of \(C_i\) in \(D_i\).
Consider the following slicing of the Dirichlet cell \(D_i\). Given a fixed polycylinder \(C_i\) in a packing \(\mathscr {C}\) of \(\mathbb {R}^{n+2}\) by polycylinders and a point x on the core \(a_i\), the plane \(p_x\) is the 2-flat orthogonal to \(a_i\) and containing the point x. The Dirichlet slice \(d_x\) is the intersection of \(D_i\) and \(p_x.\)
Note that \(p_x\) is a sub-flat of \(F_x^{b_i,b_j}\) for all j in I.
3.3 Bezdek–Kuperberg Bound
For any point x on the core \(a_i\) of a polycylinder \(C_i\), the results of Bezdek and Kuperberg [1] apply to the Dirichlet slice \(d_x\).
Lemma 2
A Dirichlet slice is convex and, if bounded, a parabola-sided polygon.
Proof
Construct the Dirichlet slice \(d_x\) as an intersection. Define \(d^j\) to be the set of points in \(p_x\) which lie no further from \(C_i\) than from \(C_j\). Then the Dirichlet slice \(d_x\) is realized as
Each arc of the boundary of \(d_x\) in \(p_x\) is given by an arc of the boundary of some \(d^j\) in \(p_x.\) The boundary of \(d^j\) in \(p_x\) is the set of points in \(p_x\) equidistant from \(C_i\) and \(C_j.\) Since the foliation \(\mathscr {F}^{b_i,b_j}\) is a product foliation, the arc of the boundary of \(d^j\) in \(p_x\) is also the set of points in \(p_x\) equidistant from the leaf \(C_i \cap F_x^{b_i,b_j}\) of \(\mathscr {F}^{b_i,b_j}|_{C_i}\) and the leaf \(C_j \cap F_x^{b_i,b_j}\) of \(\mathscr {F}^{b_i,b_j}|_{C_j}\). This reduces the analysis to the case of a pair of cylinders in \(\mathbb {R}^3.\) From [1], it follows that \(d^j\) is convex and the boundary of \(d_j\) in \(p_x\) is a parabola; the intersection of such sets \(d^j\) in \(p_x\) is convex, and a parabola-sided polygon if bounded. \(\square \)
Let \(S_x(r)\) be the circle of radius r in \(p_x\) centered at x.
Lemma 3
The vertices of \(d_x\) are not closer to \(S_x(1)\) than the vertices of a regular hexagon circumscribed about \(S_x(1).\)
Proof
A vertex of \(d_x\) occurs where three or more polycylinders are equidistant, so the vertex is the center of a \((n+2)\)-ball B tangent to three polycylinders. Thus B is tangent to three disjoint unit \((n+2)\)-balls \(B_1\), \(B_2\), \(B_3\). By projecting into the affine hull of the centers of \(B_1\), \(B_2\), \(B_3\), it is immediate that the radius of B is no less than \(2/\sqrt{3} -1.\) \(\square \)
Lemma 4
Let y and z be points on the circle \(S_x(2/\sqrt{3})\). If each of y and z is equidistant from \(C_i\) and \(C_j\), then the angle yxz is smaller than or equal to \(2\arccos (\sqrt{3} -1) = 85.8828\dots ^\circ .\)
Proof
Following [1, 4], the existence of a supporting hyperplane of \(C_i\) that separates \({{\mathrm{int}}}(C_i)\) from \({{\mathrm{int}}}(C_j)\) suffices. \(\square \)
In [1], it is shown that planar objects satisfying Lemmas 2, 3 and 4 have area no less than \(\sqrt{12}.\) As the bound holds for all Dirichlet slices, it follows that \(\delta ^+(\mathbb {D}^2\times \mathbb {R}^n) \le \pi /\sqrt{12}\) in \(\mathbb {R}^{n+2}.\) The product of the dense disk packing in the plane with \(\mathbb {R}^n\) gives a polycylinder packing in \(\mathbb {R}^{n+2}\) that achieves this density. Combining this with the result of Thue [6] for \(n=0\) and the result of Bezdek and Kuperberg [1] for \(n=1\), Theorem 1 follows.
References
Bezdek, A., Kuperberg, W.: Maximum density space packing with congruent circular cylinders of infinite length. Mathematika 37(1), 74–80 (1990)
Blichfeldt, H.F.: The minimum value of quadratic forms, and the closest packing of spheres. Math. Ann. 101(1), 605–608 (1929)
Tóth, G.F., Kuperberg, W.: Blichfeldt’s density bound revisited. Math. Ann. 295(1), 721–727 (1993)
Kusner, W.: Upper bounds on packing density for circular cylinders with high aspect ratio. Discrete Comput. Geom. 51(4), 964–978 (2014)
Rankin, R.A.: On the closest packing of spheres in n dimensions. Ann. Math. 48, 228–229 (1947)
Thue, A.: On the densest packing of congruent circles in the plane. Skr. Vidensk-Selsk, Christiania 1, 3–9 (1910)
Acknowledgments
Thanks to Thomas Hales, Włodzimierz Kuperberg and Robert Kusner. The author was supported by Austrian Science Fund (FWF) Project 5503 and National Science Foundation (NSF) Grant No. 1104102.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: János Pach
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kusner, W. On the Densest Packing of Polycylinders in Any Dimension. Discrete Comput Geom 55, 638–641 (2016). https://doi.org/10.1007/s00454-016-9766-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-016-9766-6