Abstract
We establish an isoperimetric inequality with constraint by \(n\)-dimensional lattices. We prove that, among all sets which consist of lattice translations of a given rectangular parallelepiped, a cube is the best shape to minimize the ratio involving its perimeter and volume as long as the cube is realizable by the lattice. For its proof a solvability of finite difference Poisson–Neumann problems is verified. Our approach to the isoperimetric inequality is based on the technique used in a proof of the Aleksandrov–Bakelman–Pucci maximum principle, which was originally proposed by Cabré (Butll Soc Catalana Mat 15:7–27, 2000) to prove the classical isoperimetric inequality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The classical isoperimetric inequality asserts that for any bounded \(E \subset \mathbf {R}^n\) we have

where \(|E|\) and \(|\partial E|\) denote, respectively, the volume of \(E\) and the perimeter of \(E\), and \(\mathbf {B}_r:=\{ x \in \mathbf {R}^n \ | \ |x|<r \}\) is a ball. This inequality says that among all sets a ball is the best shape to minimize the ratio given as the left-hand side of (1.1). Topics related to the classical isoperimetric problem or arguments on its generalization can be found in the book [5] and the survey paper [22]. See also the recent book [27] for connections with Sobolev inequalities and optimal transport.
In this paper we are concerned with the case where \(E\) is a collection of rectangular parallelepipeds with a common shape. To describe the situation more precisely we first define a weighted lattice. For each \(i \in \{ 1,\dots ,n \}\) we fix a positive constant \(h_i>0\) as a step size in the direction of \(x_i\). Then the resulting lattice is
Consider a subset \(\varOmega \subset h\mathbf {Z}^n\). We define \(\overline{\varOmega }\), the closure of \(\varOmega \), as
where \(\{ e_i \}_{i=1}^n \subset \mathbf {R}^n\) is the standard orthogonal basis of \(\mathbf {R}^n\), e.g., \(e_1=(1,0,\dots ,0)\). Note that \(\overline{\varOmega }\) is not a closure in \(\mathbf {R}^n\). We also set \(\partial \varOmega :=\overline{\varOmega } \setminus \varOmega \), the boundary of \(\varOmega \). (See the left of Fig. 1.)
When \(\varOmega =\{ P_i \}_{i=1}^3 \subset h\mathbf {Z}^2\), its closure and boundary are given as \(\overline{\varOmega }=\{ P_i \}_{i=1}^3 \cup \{ S_i \}_{i=1}^7\) and \(\partial \varOmega =\{ S_i \}_{i=1}^7\), respectively, as in the left figure. The right figure shows the definition of \(E[\varOmega ]\)
Given a bounded \(\varOmega \subset h\mathbf {Z}^n\), we define the volume of \(\varOmega \) and the perimeter of \(\varOmega \) as, respectively,
with
where \(h^n:=h_1 \times \dots \times h_n\) and \(\# A\) stands for the number of elements of a set \(A\). The number \(\omega _i\) counts the edges that are parallel to the \(x_i\)-direction and are connecting points of \(\varOmega \) with points of \(\partial \varOmega \). For example, when \(\varOmega \subset h\mathbf {Z}^2\) is given as in Fig. 1, we have \(\omega _1=\omega _2=4\). Our definitions of the volume and the perimeter are natural in that if we let
for a given \(\varOmega \subset h\mathbf {Z}^n\) (see the right of Fig. 1), we then have \(\mathrm {Vol}(\varOmega )=\mathcal {L}^n(E)\), the \(n\)-dimensional Lebesgue measure of \(E\), and \(\mathrm {Per}(\varOmega )=\mathcal {H}^{n-1}(\partial E)\), the \((n-1)\)-dimensional Hausdorff measure of \(\partial E\) (the boundary of \(E\) in \(\mathbf {R}^n\)). We say \(\varOmega \subset h \mathbf {Z}^n\) is connected if for all \(x,y \in \varOmega \) there exist \(m \in \{ 1,2, \dots \}\) and \(z_1, \dots , z_m \in \varOmega \) such that \(z_1 \in \overline{\{ x \}}\), \(z_{k+1} \in \overline{\{ z_k \}} \ (k=1,\dots ,m-1)\) and \(y \in \overline{\{ z_m \}}\).
We denote by \(\mathbf {Q}_r\) and \(\bar{\mathbf {Q}}_r\), respectively, the open and closed cube in \(\mathbf {R}^n\) centered at \(0\) with side-length \(2r>0\), i.e., \(\mathbf {Q}_r:=(-r,r)^n \subset \mathbf {R}^n\) and \(\bar{\mathbf {Q}}_r:=[-r,r]^n \subset \mathbf {R}^n\). Let \(\bar{\mathbf {Q}}_r(a):=a+\bar{\mathbf {Q}}_r\) for \(a \in \mathbf {R}^n\). The volume and perimeter of \(\mathbf {Q}_r\) are, respectively, \(|\mathbf {Q}_r|=(2r)^n\) and \(|\partial \mathbf {Q}_r|=2n (2r)^{n-1}\). We are now in a position to state our main result.
Theorem 1.1
(Discrete Isoperimetric Inequality) For any nonempty, bounded and connected \(\varOmega \subset h\mathbf {Z}^n\) we have

Moreover, the equality in (1.3) holds if and only if \(E[\varOmega ]\) is a cube, i.e., \(E[\varOmega ]=\bar{\mathbf {Q}}_r(a)\) for some \(r>0\) and \(a \in \mathbf {R}^n\).
The isoperimetric constant for the cube is \(|\partial \mathbf {Q}_1|^n / |\mathbf {Q}_1|^{n-1}=(2n)^n\). Although (1.3) can be regarded as a “continuous” isoperimetric inequality if we identify \(\varOmega \) with \(E[\varOmega ]\) in (1.2), we call (1.3) a “discrete” isoperimetric inequality since our approach to Theorem 1.1 uses numerical techniques which study functions defined on the lattice \(h\mathbf {Z}^n\). Note that our result is different from the classical one in that the minimizer of the left-hand side of (1.3) is a cube. This is a consequence of the constraint by square lattices; see Example 2.4. We also remark that the equality in (1.3) does not necessarily hold; consider the two dimensional case where \(h_1=1\) and \(h_2=\sqrt{2}\).
Isoperimetric problems on discrete spaces are studied by many authors. The paper [1] gives a survey, and in the recent book [13, Chapter 8] isoperimetric problems are studied on graphs (networks). Various results including discrete Sobolev inequalities on finite graphs are also found in [9]. Isoperimetric problems concerning lattices are discussed in several previous works; however, their settings and problems are different from ours. The authors of [2, 15] study planar convex subsets and lattice points lying in them. In [4] isoperimetric inequalities for lattice-periodic sets are derived. The reader is also referred to its related work [3, 14, 24]. Properties of planar subsets with constraint by a triangular lattice are discussed in [11].
For the proof of our discrete isoperimetric inequality we employ the idea by Cabré. As an application of the technique used in a proof of the Aleksandrov–Bakelman–Pucci (ABP for short) maximum principle, Cabré pointed out in [8] (and the original paper [7] in Catalan) that the ABP method gives a simple proof of the classical isoperimetric inequality (1.1).
The ABP maximum principle ([12, Theorem 9.1], [6, Theorem 3.2]) is a pointwise estimate for solutions of elliptic partial differential equations. In a typical case the principle asserts that if \(u\) is a (sub)solution of the equation \(F(\nabla ^2 u)=f(x)\) in \(E \subset \mathbf {R}^n\), where \(F\) is a possibly nonlinear elliptic operator and \(\nabla ^2 u\) denotes the Hessian of \(u\), then we have

Here \(C>0\), \(\Vert f \Vert _{L^n(\Gamma )}=(\int _{\Gamma } |f(x)|^n dx)^{1/n}\) and \(\Gamma \) is an upper contact set of \(u\) which is defined as the set of points in \(E\) where the graph of \(u\) has a tangent plane that lies above \(u\) in \(E\). Discrete versions of the ABP estimate are also established in a series of studies by Kuo and Trudinger; see [16, 21] for linear equations, [17] for nonlinear operators, [18, 20] for parabolic cases and [19, 20] for general meshes.
Unfortunately, the result in [8] does not cover subsets having corners such as (1.2) since domains \(E\) in [8] is assumed to be smooth in order to solve Neumann problems on \(E\). To be more precise, the author of [8] takes a function \(u\) which solves the Poisson–Neumann problem
and proves (1.1) by studying the \(n\)-dimensional Lebesgue measure of \(\nabla u (\Gamma )\), the image of the upper contact set of \(u\) under the gradient of \(u\). Here \(\nu \) is the outward unit normal vector to \(\partial E\). In this paper we solve a finite difference version of (1.4) instead of the continuous equation. Considering such discrete equations and their discrete solutions enables us to deal with non-smooth domains.
Our proof is similar to that in [8] except that the minimizers are not balls but cubes and that a superdifferential of \(u\), which is the set of all slopes of hyperplanes touching \(u\) from above, is used instead of the gradient of \(u\) ([16]). However, there are some extra difficulties in our case. One is a solvability of the discrete Poisson–Neumann problem. Such problems are discussed in the previous work [23, 25, 26, 28], but domains are restricted to rectangles [23, 26, 28] or their collections [25]. For the proof of our discrete isoperimetric inequality, fortunately, it is enough to require \(u\) to be a subsolution of the Poisson equation in (1.4) and to satisfy the Neumann condition in (1.4) with some direction \(\nu \). For this reason we are able to construct such solutions on general subsets of \(h\mathbf {Z}^n\). Another difficulty is to study a necessary and sufficient condition which leads to the equality in (1.3). This is not discussed in [8].
This paper is organized as follows. In Sect. 2 we give a proof of the discrete isoperimetric inequality. Since we use a discrete solution of the Poisson–Neumann problem in the proof, we show the existence of such solutions in Sect. 3. In Sect. 4 we present two results on maximum principles; one is an ABP maximum principle shown by a similar method to the isoperimetric inequality, and the other is a strong maximum principle which is used in Sect. 3.
2 A Proof of the Discrete Isoperimetric Inequality
Throughout this paper we always assume
We first introduce a notion of superdifferentials and upper contact sets, and then study their properties. Let \(u: \overline{\varOmega } \rightarrow \mathbf {R}\). We denote by \(\partial ^+ u(z)\) a superdifferential of \(u\) on \(\varOmega \) at \(z \in \varOmega \), which is given as

where \(\langle \cdot , \cdot \rangle \) stands for the Euclidean inner product in \(\mathbf {R}^n\). It is easy to see that \(\partial ^+ u(z)\) is a closed set in \(\mathbf {R}^n\). We next define \(\Gamma [u]\), an upper contact set of \(u\) on \(\varOmega \), as

For \(x \in \varOmega \) and \(i \in \{1, \dots , n \}\) we define discrete differential operators as follows:
Lemma 2.1
Let \(u: \overline{\varOmega } \rightarrow \mathbf {R}\). For all \(z \in \Gamma [u]\) we have  for every \(i \in \{ 1, \dots ,n \}\) and
for every \(i \in \{ 1, \dots ,n \}\) and
Proof
Let \(p=(p_1, \dots , p_n) \in \partial ^+ u(z)\). From the definition of the superdifferential it follows that  for all \(x \in \overline{\varOmega }\). In particular, taking \(x=z \pm h_i e_i \in \overline{\varOmega }\), we have
for all \(x \in \overline{\varOmega }\). In particular, taking \(x=z \pm h_i e_i \in \overline{\varOmega }\), we have

that is,

This implies  and (2.1). \(\square \)
and (2.1). \(\square \)
Remark 2.2
Since  at \(z \in \Gamma [u]\) by Lemma 2.1, we see that
at \(z \in \Gamma [u]\) by Lemma 2.1, we see that  for all \(i \in \{ 1,\dots ,n \}\).
for all \(i \in \{ 1,\dots ,n \}\).
In the proof of the classical isoperimetric inequality proposed by Cabré [7, 8], solutions of the Poisson–Neumann problem (1.4) are studied, and actually the proof still works for a subsolution \(u\) of (1.4), i.e.,  in \(E\) and \(\partial u / \partial \nu =-1\) on \(\partial E\). Similarly to this classical case, for the proof of Theorem 1.1 we consider the discrete version of (1.4) on \(\varOmega \), which is
in \(E\) and \(\partial u / \partial \nu =-1\) on \(\partial E\). Similarly to this classical case, for the proof of Theorem 1.1 we consider the discrete version of (1.4) on \(\varOmega \), which is

We denote the problem (2.2) with (2.3) by (DPN). The meaning of solutions of (DPN) is given as follows. We say \(u: \overline{\varOmega } \rightarrow \mathbf {R}\) is a discrete solution of (DPN) if
-
(a)
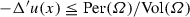 for all \(x \in \varOmega \);
for all \(x \in \varOmega \); -
(b)
For all \(x \in \partial \varOmega \) there exist some \(i \in \{ 1, \dots , n \}\) and \(\sigma \in \{ -1,1 \}\) such that \(x+\sigma h_i e_i \in \varOmega \) and
$$\begin{aligned} \frac{u(x)-u(x+\sigma h_i e_i)}{h_i}=-1. \end{aligned}$$
The condition (b) requires that the outward normal derivative of \(u\) be \(-1\) for some direction \(\nu =\pm e_i\). This boundary condition is also explained by saying that \(\delta ^+_i u(x)=1\) or \(\delta ^-_i u(x)=-1\) for all \(x \in \partial \varOmega \). We will prove the existence of discrete solutions of (DPN) in the next section (Proposition 3.2).
Proof of Theorem 1.1
1. Let \(u: \overline{\varOmega } \rightarrow \mathbf {R}\) be a discrete solution of (DPN) and let \(\Gamma [u]\) be the upper contact set of \(u\) on \(\varOmega \).
We claim
Let \(p \in \mathbf {Q}_1\). We take a maximum point \(\hat{x} \in \overline{\varOmega }\) of \(u(x)-\langle p, x \rangle \) over \(\overline{\varOmega }\). To show (2.4) it is enough to prove that \(\hat{x} \in \varOmega \) since we then have \(\hat{x} \in \Gamma [u]\) and \(p \in \partial ^+ u(\hat{x})\). Suppose by contradiction that \(\hat{x} \in \partial \varOmega \). Take any \(i \in \{ 1, \dots , n \}\) and \(\sigma \in \{ -1,1 \}\) such that \(y:=\hat{x}+\sigma h_i e_i \in \varOmega \). Since \(u(x)-\langle p, x \rangle \) attains its maximum at \(\hat{x}\) and since \(p\) lies in the open cube \(\mathbf{Q}_1\), we compute

This implies that \(u\) does not satisfy the boundary condition (2.3) at \(\hat{x} \in \partial \varOmega \), a contradiction. Therefore (2.4) follows. We also remark that (2.4) guarantees \(\Gamma [u]\) is nonempty.
2. By (2.4) we see

Also, for each \(z \in \Gamma [u]\) Lemma 2.1 implies

We next apply the arithmetic–geometric mean inequality to obtain

Consequently, combining (2.5)–(2.7) yields

Since \(n=|\partial \mathbf {Q}_1|/|\mathbf {Q}_1|\), it follows that

3. We next assume that the equality in (1.3) holds. In view of Step 2, we then have \(\Gamma [u]=\varOmega \) by (2.8) and

by (2.5), (2.6) and (2.7), respectively. Here we have derived (2.11) from the equality case of the arithmetic–geometric mean inequality. We claim
One inclusion is known by (2.1). Also, both the sets in (2.12) are closed and have the same measure by (2.10). Thus they have to be the same set. For the same reason it follows from (2.4) and (2.9) that
4. Let \(x,y \in \varOmega \) be such that \(y=x+h_i e_i\) for some \(i \in \{ 1, \dots ,n \}\). Then we show \(\mu (x)=\mu (y)\) and
with \(\mu _0:=\mu (x)\), where \(\mu (\cdot )\) is the function in (2.11). Without loss of generality we may assume \(x=0\), \(y=h_1 e_1\) and \(u(x)=0\). We then notice that \(u(y)=h_1 \delta ^+_1 u(0)\). Fix \(i \in \{ 2,\dots , n \}\) and set \(p^{\pm }:=\delta ^+_1 u(0)e_1 + \delta ^{\pm }_i u(0)e_i\). Because of (2.12) we see that \(p^{\pm }\) belong to \(\partial ^+ u(0)\). Since \(x=0 \in \Gamma [u]\), we observe that  for all \(z \in \overline{\varOmega }\). In particular, letting \(z=h_1 e_1 \pm h_i e_i\), we deduce
for all \(z \in \overline{\varOmega }\). In particular, letting \(z=h_1 e_1 \pm h_i e_i\), we deduce  , i.e.,
, i.e.,  and
and  . Changing the role of \(x\) and \(y\) we also have
. Changing the role of \(x\) and \(y\) we also have  and
and  . Thus
. Thus
for all \(i \in \{ 2,\dots , n \}\). By (2.11) these equalities imply \(\mu (x)=\mu (y)\), and then \(\delta ^{\pm }_1 u(y)\) are computed as
Namely, we have \([\delta ^-_1 u(y),\delta ^+_1 u(y)] =[\delta ^-_1 u(x),\delta ^+_1 u(x)]+h_1 \mu _0\), which together with (2.15) shows (2.14).
5. By translation we may let \(0 \in \varOmega \). Set \(R:=[-h_1/2,h_1/2] \times \dots \times [-h_n/2,h_n/2]\) and in view of (2.11) and (2.12) there exists \(z \in \mathbf {R}^n\) such that \(\partial ^+ u(0)=z+\mu R\) with \(\mu :=\mu (0)\). Since \(\varOmega \) is now connected, as a consequence of Step 4 we see \(\mu (x) \equiv \mu \) and \(\partial ^+ u(x)=\partial ^+ u(0)+\mu x =z+\mu x +\mu R\) for all \(x \in \varOmega \). Therefore (2.13) implies
Finally, from translation and rescaling it follows that
which is the desired conclusion. \(\square \)
Remark 2.3
If a nonempty and bounded subset \(\varOmega ' \subset h\mathbf {Z}^n\) is not connected, then we have the strict inequality
This is shown by docking one connected component with another one. To be more precise, translating two connected components \(\varOmega _1\) and \(\varOmega _2\), we are able to construct one connected set whose volume is equal to that of \(\varOmega _1 \cup \varOmega _2\) and whose perimeter is strictly less than that of \(\varOmega _1 \cup \varOmega _2\). Iterating this procedure, we finally obtain a connected set \(\varOmega \) such that \(\mathrm {Vol}(\varOmega ')=\mathrm {Vol}(\varOmega )\) and \(\mathrm {Per}(\varOmega ')>\mathrm {Per}(\varOmega )\). These relations and Theorem 1.1 imply (2.16).
Example 2.4
In the planar case (\(n=2\)) it is easily seen that round-shaped subsets are not optimal. Let \(h_1=h_2=1\) for simplicity, and consider \(\varOmega \subset \mathbf {Z}^2\) which is nonempty, bounded and connected. We choose \(R=\{ a,a+1, \dots ,a+M-1 \} \times \{ b,b+1, \dots ,b+N-1 \} \subset \mathbf {Z}^2\) as the minimal rectangle such that \(\varOmega \subset R\). Obviously, \(\mathrm {Vol}(\varOmega )<\mathrm {Vol}(R)\) if \(\varOmega \ne R\). We next consider their perimeters. Since \(\varOmega \) is connected, for each \(x \in \{ a,a+1, \dots ,a+M-1 \}\) there exist \((x,y_-), (x,y_+) \in \varOmega \) such that \((x,y_- -1), (x,y_+ +1) \not \in \varOmega \). This implies  . Similarly, we obtain
. Similarly, we obtain  , and therefore
, and therefore  . We thus conclude that \(\mathrm {Per}(\varOmega )^2/\mathrm {Vol}(\varOmega )>\mathrm {Per}(R)^2/\mathrm {Vol}(R)\), i.e., \(\varOmega \) is not optimal. Moreover, we see that, among all rectangles \(R=\{ a,a+1, \dots ,a+M-1 \} \times \{ b,b+1, \dots ,b+N-1 \}\), a square is the best shape since
. We thus conclude that \(\mathrm {Per}(\varOmega )^2/\mathrm {Vol}(\varOmega )>\mathrm {Per}(R)^2/\mathrm {Vol}(R)\), i.e., \(\varOmega \) is not optimal. Moreover, we see that, among all rectangles \(R=\{ a,a+1, \dots ,a+M-1 \} \times \{ b,b+1, \dots ,b+N-1 \}\), a square is the best shape since

by the arithmetic–geometric mean inequality. Therefore, in the planar case Theorem 1.1 is easily shown. However, the above argument is not valid for  since the inequalities
since the inequalities  do not necessarily hold.
do not necessarily hold.
On the contrary, if we define a volume and a perimeter of \(\varOmega \) as \(\# \varOmega \) and \(\# (\partial \varOmega )\), respectively, then it is easily seen that a cube is not an optimal shape. In the article [10] the author asserts that if \(\varOmega \) has a minimal \(\# \partial \varOmega \), then \(\varOmega \) is roughly diamond-shaped. In the present paper, however, we do not discuss the problem concerning the functional \((\# (\partial \varOmega ))^n/(\# \varOmega )^{n-1}\).
3 An Existence Result for the Poisson–Neumann Problem
We shall prove the solvability of (DPN), the Poisson equation with the Neumann boundary condition which appeared in the proof of the discrete isoperimetric inequality. Before starting the proof, using a simple example, we explain how to construct the solutions.
Example 3.1
Consider \(\varOmega \subset h\mathbf {Z}^2\) which consists of three points \(P_1\), \(P_2\) and \(P_3\) in the left lattice of Fig. 2. We also denote by \(S_1, \dots , S_7\) all points on \(\partial \varOmega \) as in the same figure. In order to determine values of \(u\) on \(\overline{\varOmega }\) we solve a system of linear equations of the matrix form \(L \vec {a}=\vec {b}\) which corresponds to the finite difference equation (DPN). However, if we require \(u\) to satisfy the Neumann condition (2.3) at \(S_1\) toward both adjacent points \(P_1\) and \(P_3\), the linear system may not be solvable since the number of the unknowns is less than that of equations; in the present example there are 10 and 11, respectively. Thus it might seem natural to remove one of the equations by imposing the Neumann condition at \(S_1\) toward only one of the points \(P_1\) and \(P_3\). We are now allowed to do this since such a solution is still a discrete solution of (DPN) according to our definition. Then the number of equations decreases to 10, but, unfortunately, it becomes difficult to study the linear system since the new matrix \(L\) is not symmetric. In addition, we do not know a priori how to choose the adjacent point toward which the Neumann condition is satisfied.
To avoid these situations we regard \(S_1\) as two different points \(S_{1,1}\) and \(S_{1,2}\) which are connected to \(P_1\) and \(P_3\), respectively, and consider a modified system with new unknowns \(u(S_{1,1})\) and \(u(S_{1,2})\) instead of \(u(S_1)\); see the right lattice in Fig. 2. Then the number of the unknowns in our example becomes 11. Thanks to this increase of the unknowns, it turns out that the modified linear system admits at least one solution \((u(P_1),u(P_2),u(P_3),u(S_{1,1}),u(S_{1,2}),u(S_2), \dots , u(S_7))\). (In the notation of the proof below we write \(u(S_{1,1})=\beta (1,1) \) and \(u(S_{1,2})=\beta (1,2)\).) In the process of proving the solvability we find that the right-hand side of (2.2) should be \(\mathrm {Per}(\varOmega )/\mathrm {Vol}(\varOmega )\). Also, for its proof we employ the strong maximum principle for the discrete Laplace equation.
The remaining problem is how to define \(u(S_1)\). We define \(u(S_1)\) as the maximum of \(u(S_{1,1})\) and \(u(S_{1,2})\), so that, if  , we have
, we have  since
since  and \(\{u(S_1)-u(P_1)\}/h_2=-1\) since \(u(S_1)=u(S_{1,1})\). In this way we obtain a solution of (DPN).
and \(\{u(S_1)-u(P_1)\}/h_2=-1\) since \(u(S_1)=u(S_{1,1})\). In this way we obtain a solution of (DPN).
Discrete solutions of (DPN) are not unique as well as the continuous case since adding a constant gives another solution. Accordingly, the resulting coefficient matrix of a linear system which corresponds to (DPN) is not invertible even if the number of unknown is increased. Thus an existence of discrete solutions is established by determining the kernel of the matrix. It turns out that the kernel is a straight line which is spanned by a vector \((1,1,\dots ,1)\).
Proposition 3.2
The problem \((\mathrm {DPN})\) admits at least one discrete solution.
Proof
1. We first introduce notations. Let \(\varOmega = \{ P_1,\dots , P_M \}\) and \(\partial \varOmega = \{ S_1,\dots , S_{N_0} \}\), where \(M:=\# \varOmega \) and \(N_0:= \# (\partial \varOmega )\). For each \(i \in \{ 1,\dots ,M \}\) we define subsets \(\mathcal {M}(i) \subset \{ 1,\dots ,M \}\) and \(\mathcal {N}(i) \subset \{ 1,\dots ,N_0 \}\) so that \(\overline{\{ P_i \}} \setminus \{ P_i \}=\{ P_j \}_{j \in \mathcal {M}(i)} \cup \{ S_j \}_{j \in \mathcal {N}(i)}\). We also set \(s_i:=\# (\overline{\{ S_i \}} \cap \varOmega )\) for \(i \in \{ 1,\dots ,N_0 \}\), which stands for the number of points of \(\varOmega \) adjacent to \(S_i\), and \(N:=\sum _{j=1}^{N_0}s_j\). Next, for \(i \in \{ 1,\dots ,N_0 \}\) we define a map \(n_i: \{ 1,\dots , s_i \} \rightarrow \{ 1,\dots , M \}\) such that \(n_i(1)<n_i(2)<\cdots \) and \(\overline{\{S_i \}} \cap \varOmega = \{ P_{n_i(j)} \}_{j=1}^{s_i}\). We denote by \(n_i^{-1}\) the inverse map of \(n_i\); that is, \(P_j\) is the \(n^{-1}_i(j)\)-th point of \((P_{n_i(1)},\dots ,P_{n_i(s_i)})\) if \(P_j \in \overline{\{S_i \}} \cap \varOmega \). (We illustrate the definitions of the above notations by referring to Fig. 2. When \(\varOmega \subset h\mathbf {Z}^2\) is given as in Fig. 2, we have \(M=3\), \(N_0=7\), \(\mathcal {M}(1)=\{ 2 \}\), \(\mathcal {M}(2)=\{ 1,3 \}\), \(\mathcal {M}(3)=\{ 2 \}\), \(\mathcal {N}(1)=\{ 1,2,3 \}\), \(\mathcal {N}(2)=\{ 4,5 \}\), \(\mathcal {N}(3)=\{ 1,6,7 \}\), \(s_1=2\), \(s_2=\dots =s_7=1\), \(N=8\), \(n_1(1)=1\), \(n_1(2)=3\), \(n_2(1)=n_3(1)=1\), \(n_4(1)=n_5(1)=2\), \(n_6(1)=n_7(1)=3\).)
For \(x,y \in \overline{\varOmega }\) such that \(y=x+\sigma h_i e_i\) with \(\sigma =\pm 1\) and \(i\in \{ 1, \dots , n \}\) we set \(h(x,y):=h_i\). Obviously, we then have \(h(x,y)=h(y,x)\). We denote by \(E(i,j)\) the \((M+N) \times (M+N)\) matrix with 1 in the \((i,j)\) entry and 0 elsewhere. Given a vector
where \({}^t \vec {v}\) means the transpose of a vector \(\vec {v}\), we define \(u=u[\vec {a}]: \overline{\varOmega } \rightarrow \mathbf {R}\) as

2. We consider the following system of linear equations
where \(\vec {a} \in \mathbf {R}^{M+N}\) is the unknown vector and \(\vec {b}=(b_k)_{k=1}^{M+N} \in \mathbf {R}^{M+N}\) is given as
Here \(s_0=0\). Also, the \((M+N) \times (M+N)\) matrix \(L\) is defined by
where \(I_M\) is the identity matrix of dimension \(M\) and \(\theta :=2\sum _{i=1}^n (1/h_i^2)\). (See Example 3.4, where we will give a small sized matrix \(L\) along the example of Fig. 2.) By definition \(L\) is symmetric. To check the symmetricity we first take \(i \in \{ 1,\dots ,M \}\) and \(j \in \mathcal {M}(i)\). Then the \((i,j)\) entry of \(L\) is \(-1/h(P_i,P_j)^2\). Since \(j \in \mathcal {M}(i)\), we see \(P_j \in \overline{\{ P_i \}}\). Thus \(P_i \in \overline{\{ P_j \}}\) and this implies \(i \in \mathcal {M}(j)\). As a result, it follows that the \((j,i)\) entry of \(L\) is \(-1/h(P_j,P_i)^2\). We next let \(i \in \{ 1,\dots ,M \}\) and \(j \in \mathcal {N}(i)\), so that the \((i,M+\sum _{l=0}^{j-1} s_l+n_j^{-1}(i))\) entry of \(L\) is \(-1/h(P_i,S_j)^2\). In this case we have \(S_j \in \overline{\{P_i \}}\), and so \(P_i \in \overline{\{S_j \}}\). By the definition of \(n_j\) it follows that \(n_j(t)=i\) for some \(t \in \{ 1,\dots , s_j \}\), i.e., \(t=n_j^{-1}(i)\). Since \((M+\sum _{l=0}^{j-1} s_l+n_j^{-1}(i),i)=(M+\sum _{l=0}^{j-1} s_l+t,n_j(t))\), we conclude that the \((M+\sum _{l=0}^{j-1} s_l+n_j^{-1}(i),i)\) entry of \(L\) is \(-1/h(S_j,P_{n_j(t)})^2=-1/h(S_j,P_i)^2\). Hence the symmetricity of \(L\) is proved.
3. We claim that if \(\vec {a} \in \mathbf {R}^{M+N}\) is a solution of (3.2), then \(u=u[\vec {a}]\) is a discrete solution of (DPN). Let \(x \in \varOmega \), i.e., \(x=P_i\) for some \(i\). Without loss of generality we may assume \(x=P_1\). Since \(\vec {a}\) satisfies (3.2), comparing the first coordinates of both the sides in (3.2), we observe

We next let \(x \in \partial \varOmega \). Again we may assume \(x=S_1\). We also let  . Then the (\(M+j_0\))-th coordinates in (3.2) implies
. Then the (\(M+j_0\))-th coordinates in (3.2) implies
that is,
Consequently, we see that \(u\) is a discrete solution of (DPN) in our sense.
4. We shall show that (3.2) is solvable. For this purpose, we first assert that \(\mathrm {Ker} L =\mathbf {R} \vec {\xi }\), where \(\mathrm {Ker} L\) is the kernel of \(L\) and
By the definition of \(L\) we see that the sum of each row of \(L\) is zero. This implies \(\mathrm {Ker} L \supset \mathbf {R} \vec {\xi }\). We next let \(\vec {a} \in \mathrm {Ker} L\), i.e., \(L\vec {a}=0\). We represent each component of \(\vec {a}\) as in (3.1). Now, by the same argument as in Step 3 we see that \(u=u[\vec {a}]\) is a discrete solution of

where the notion of a discrete solution of (3.3) with (3.4) is the same as that of (DPN). We take a maximum point \(z \in \overline{\varOmega }\) of \(u\) over \(\overline{\varOmega }\). If \(z \in \partial \varOmega \), there exists some \(y\in \overline{\{ z \}} \cap \varOmega \) such that \(u(y)=u(z)\) since \(u\) satisfies the Neumann boundary condition (3.4) at \(z\). Thus \(u\) attains its maximum at some point in \(\varOmega \). Since \(\varOmega \) is now bounded and connected, the strong maximum principle for the Laplace equation (Corollary 4.5) ensures that \(u\) must be some constant \(c \in \mathbf {R}\) on \(\overline{\varOmega }\). From this it follows that \(\alpha (1)=\dots =\alpha (M)=c\). Also, since \(L \vec {a}=0\), we have \(\beta (i,j)=\alpha (n_i(j))\) for all \(i \in \{ 1,\dots , N_0 \}\) and \(j \in \{ 1,\dots , s_i \}\). As a result, we see \(\vec {a}=c\vec {\xi }\in \mathbf {R}\vec {\xi }\). We thus conclude that \(\mathrm {Ker} L =\mathbf {R} \vec {\xi }\).
5. Since \(L\) is symmetric and \(\mathrm {Ker} L =\mathbf {R} \vec {\xi }\), we see that \((\mathrm {Im} L)^{\perp }=\mathbf {R} \vec {\xi }\), where \((\mathrm {Im} L)^{\perp }\) stands for the orthogonal complement of \(\mathrm {Im} L\), the image of \(L\). Thus, for \(\vec {b}' \in \mathbf {R}^{M+N}\) it follows that \(\vec {b}' \in \mathrm {Im} L\) if and only if \(\langle \vec {\xi }, \vec {b}' \rangle =0\). Noting that \(-1/h_i\) appears \(\omega _i\) times in a sequence \(\{ b_k \}_{k=M+1}^{M+N}\) for each \(i \in \{ 1, \dots , n \}\), we compute
Consequently \(\vec {b} \in \mathrm {Im} L\), and therefore the problem (3.2) has at least one solution \(\vec {a} \in \mathbf {R}^{M+N}\). Hence by Step 3 the corresponding \(u=u[\vec {a}]\) solves (DPN). \(\square \)
Remark 3.3
We have actually proved that \(u\), which we constructed as a subsolution, is a solution of (2.2) in \(\varOmega \setminus \overline{\partial \varOmega }\). Namely, we have \(-\Delta 'u(x)=\mathrm {Per}(\varOmega )/\mathrm {Vol}(\varOmega )\) for all \(x \in \varOmega \setminus \overline{\partial \varOmega }\). This is clear from the construction of \(u\).
Example 3.4
We revisit Example 3.1 and consider \(\varOmega \) given in Fig. 2. Let us solve the system (3.2). For simplicity we assume \(h_1=h_2=:h>0\). In the notation used in the proof of Proposition 3.2, the unknown vector \(\vec {a}\) is given as

Here \(\alpha (i)\) (\(i=1,2,3\)) represents the value of \(u(P_i)\). Also, \(\beta (1,j)\) (\(j=1,2\)) and \(\beta (k,1)\) (\(k=2,3,\dots ,7\)) represent the values of \(u(S_{1,j})\) and \(u(S_k)\), respectively. Since \(\mathrm {Vol}(\varOmega )=3h^2\) and \(\mathrm {Per}(\varOmega )=8h\) in this example, we see

and the coefficient matrix \(L\) is

The rest entries in \(L\) are zeros. A direct computation shows that \(\vec {a_0}\) given as

is a particular solution of (3.2). Since the kernel of \(L\) is known, we conclude that the general solution of (3.2) is \(\vec {a}=\vec {a_0}+c \ {}^t (1, \dots ,1)\) with \(c \in \mathbf {R}\).
4 Maximum Principles
In this section we present a few results on maximum principles for elliptic difference equations. The first one is an ABP maximum principle. The result is more or less known ([16, 17, 21]) and technique for the proof is essentially same as them, but we present it here in order to show how the proof of the isoperimetric inequality is related to that of the ABP maximum principle. We next prove a strong maximum principle. The strong maximum principle for the Laplace equation, which was used in Step 4 of the proof of Proposition 3.2, is well known in the literature. In this paper we study a wider class of elliptic equations and give a necessary and sufficient condition for the strong maximum principle. As far as the author knows, such general statement is new.
4.1 An ABP Maximum Principle
We consider the second order fully nonlinear elliptic equations of the form
where \(F:\mathbf {R}^n \rightarrow \mathbf {R}\) and \(f:\varOmega \rightarrow \mathbf {R}\) are given functions such that \(F(0,\dots ,0)=0\). Let \(\vec {\delta }^2 u(x):=(\delta ^2_1 u(x), \dots , \delta ^2_n u(x))\). We say \(u: \overline{\varOmega } \rightarrow \mathbf {R}\) is a discrete subsolution of (4.1) if  for all \(x \in \varOmega \). As an ellipticity condition on \(F\) for our ABP estimate, we use the following:
for all \(x \in \varOmega \). As an ellipticity condition on \(F\) for our ABP estimate, we use the following:
-
(F1)
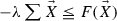 for all \(\vec {X}\in \mathbf {R}^n\) with
for all \(\vec {X}\in \mathbf {R}^n\) with 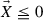 .
.
Here \(\lambda >0\). Also, \(\sum \vec {X}:=\sum _{i=1}^n X_i\) for \(\vec {X}=(X_1,\dots ,X_n) \in \mathbf {R}^n\) and the inequality  means that
means that  for every \(i \in \{1,\dots ,n\}\). For \(K \subset h\mathbf {Z}^n\) and \(g:K \rightarrow \mathbf {R}\) the \(n\)-norm of \(g\) over \(K\) is given as \(\Vert g \Vert _{\ell ^n(K)}:=\left( \sum _{x \in K}h^n |g(x)|^n \right) ^{1/n}\). We also set \(\mathrm {diam}(\varOmega ):=\max _{x\in \varOmega , y\in \partial \varOmega }|x-y|\) and \(|\mathbf {B}_r|:=\mathcal {L}^n (\mathbf {B}_r)\).
for every \(i \in \{1,\dots ,n\}\). For \(K \subset h\mathbf {Z}^n\) and \(g:K \rightarrow \mathbf {R}\) the \(n\)-norm of \(g\) over \(K\) is given as \(\Vert g \Vert _{\ell ^n(K)}:=\left( \sum _{x \in K}h^n |g(x)|^n \right) ^{1/n}\). We also set \(\mathrm {diam}(\varOmega ):=\max _{x\in \varOmega , y\in \partial \varOmega }|x-y|\) and \(|\mathbf {B}_r|:=\mathcal {L}^n (\mathbf {B}_r)\).
Theorem 4.1
(ABP Maximum Principle) Assume (F1). Let \(u: \overline{\varOmega } \rightarrow \mathbf {R}\) be a discrete subsolution of (4.1). Then the estimate

holds, where \(C_A=C_A (\lambda ,n)\) is given as \(C_A=(\lambda n |\mathbf {B}_1|^{1/n})^{-1}\).
A crucial estimate to prove Theorem 4.1 is
Proposition 4.2
For all \(u: \overline{\varOmega } \rightarrow \mathbf {R}\) we have

Proof
1. We first prove \(\mathbf {B}_d \subset \bigcup _{z \in \Gamma [u]} \partial ^+ u(z)\), where \(d\) is a constant given as \(d=(\max _{\overline{\varOmega }}u-\max _{\partial \varOmega }u)/\mathrm {diam}(\varOmega )\). If \(d=0\), the assertion is obvious. We assume \(d>0\), i.e., \(u(\hat{x})= \max _{\overline{\varOmega }}u>\max _{\partial \varOmega }u\) for some \(\hat{x} \in \varOmega \). Let \(p \in \mathbf {B}_d\) and set \(\phi (x):= \langle p, x-\hat{x} \rangle \). We take a maximum point \(z\) of \(u-\phi \) over \(\overline{\varOmega }\). Then we have \(z \in \varOmega \). Indeed, for all \(x \in \partial \varOmega \) we observe

Thus \(z \in \varOmega \), and so we conclude that \(z \in \Gamma [u]\) and \(p \in \partial ^+ u(z)\).
2. By Step 1 the estimate (2.5) with \(\mathbf {B}_d\) instead of \(\mathbf {Q}_1\) holds. Thus the same argument as in the proof of Theorem 1.1 yields

Applying \(|\mathbf {B}_d|=d^n |\mathbf {B}_1|\) to the above inequality, we obtain (4.3) by the choice of \(d\). \(\square \)
Proof of Theorem 4.1
By Remark 2.2 we have  for \(z \in \Gamma [u]\), and therefore the condition (F1) yields
for \(z \in \Gamma [u]\), and therefore the condition (F1) yields  . Since \(u\) is a discrete subsolution of (4.1), we also have
. Since \(u\) is a discrete subsolution of (4.1), we also have  . Applying these two inequalities to (4.3), we obtain (4.2). \(\square \)
. Applying these two inequalities to (4.3), we obtain (4.2). \(\square \)
4.2 A Strong Maximum Principle
We study homogeneous equations of the form
From the ABP maximum principle (4.2) we learn that all discrete subsolutions \(u\) of (4.4) satisfy

if (F1) holds. This is the so-called weak maximum principle. Our aim in this subsection is to prove that a certain weaker condition on \(F\) actually leads to the strong maximum principle and conversely the weaker condition is necessary for it. Here the rigorous meaning of the strong maximum principle is
-
(SMP)
If \(u : \overline{\varOmega } \rightarrow \mathbf {R}\) is a discrete subsolution of (4.4) such that \(\max _{\overline{\varOmega }} u =\max _{\varOmega } u\), then \(u\) must be constant on \(\overline{\varOmega }\).
Following the classical theory of partial differential equations, we consider bounded and connected subsets \(\varOmega \subset h\mathbf {Z}^n\) for (SMP). It turns out that the strong maximum principle holds if and only if \(F\) satisfies the following weak ellipticity condition (F2). It is easily seen that (F1) implies (F2).
-
(F2)
If \(\vec {X}\in \mathbf {R}^n\),
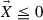 and
and 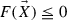 , then \(\vec {X}\) must be zero, i.e., \(\vec {X} \equiv 0\).
, then \(\vec {X}\) must be zero, i.e., \(\vec {X} \equiv 0\).
Theorem 4.3
(Strong Maximum Principle) The two conditions (SMP) and (F2) are equivalent.
To show this theorem we first study discrete quadratic functions. They will be used when we prove that (SMP) implies (F2).
Example 4.4
Let \((A_1, \dots , A_n) \in \mathbf {R}^n\). We define a quadratic function \(q : h \mathbf {Z}^n \rightarrow \mathbf {R}\) as
Then \(\delta ^2_i q\) is a constant for each \(i \in \{1,\dots ,n \}\). Indeed, we observe
for all \(x=(h_1 x_1, \dots ,h_n x_n) \in h \mathbf {Z}^n\).
Proof of Theorem 4.3
1. We first assume (F2). Let \(u : \overline{\varOmega } \rightarrow \mathbf {R}\) is a discrete subsolution of (4.4) such that \(u(\hat{x})=\max _{\overline{\varOmega }} u\) for some \(\hat{x} \in \varOmega \). This maximality implies that for each \(i \in \{ 1, \dots ,n\}\)

Thus  . Since \(u\) is a discrete subsolution, we also have
. Since \(u\) is a discrete subsolution, we also have  . It now follows from (F2) that \(\vec {\delta }^2 u (\hat{x}) \equiv 0\), and hence we see that \(u(\hat{x})=u(\hat{x}\pm h_i e_i)\) for all \(i\). We next apply the above argument with the new central point \(\hat{x}\pm h_i e_i\) if the point is in \(\varOmega \). Iterating this procedure, we finally conclude that \(u \equiv u(\hat{x})\) on \(\overline{\varOmega }\) since \(\varOmega \) is now connected.
. It now follows from (F2) that \(\vec {\delta }^2 u (\hat{x}) \equiv 0\), and hence we see that \(u(\hat{x})=u(\hat{x}\pm h_i e_i)\) for all \(i\). We next apply the above argument with the new central point \(\hat{x}\pm h_i e_i\) if the point is in \(\varOmega \). Iterating this procedure, we finally conclude that \(u \equiv u(\hat{x})\) on \(\overline{\varOmega }\) since \(\varOmega \) is now connected.
2. We next assume (SMP). Take any \(\vec {X}=(X_1,\dots , X_n)\in \mathbf {R}^n\) such that  and
and  . We may assume \(0 \in \varOmega \). Now, we take the quadratic function \(q\) in Example 4.4 with
. We may assume \(0 \in \varOmega \). Now, we take the quadratic function \(q\) in Example 4.4 with  . By the calculation in Example 4.4 we then have \(\delta ^2_i q(x)=X_i\) for all \(i\), i.e., \(\vec {\delta }^2 q(x)=\vec {X}\). Thus
. By the calculation in Example 4.4 we then have \(\delta ^2_i q(x)=X_i\) for all \(i\), i.e., \(\vec {\delta }^2 q(x)=\vec {X}\). Thus  , which means that \(q\) is a discrete subsolution of (4.4). Next, we deduce from the nonpositivity of each \(A_i\) that \(q\) attains its maximum over \(\overline{\varOmega }\) at \(0 \in \varOmega \). Therefore (SMP) ensures that \(q \equiv q(0)=0\) on \(\overline{\varOmega }\), which implies that \(A_i=0\) for all \(i \in \{ 1, \dots ,n \}\). Consequently, we find \(\vec {X} \equiv 0\). \(\square \)
, which means that \(q\) is a discrete subsolution of (4.4). Next, we deduce from the nonpositivity of each \(A_i\) that \(q\) attains its maximum over \(\overline{\varOmega }\) at \(0 \in \varOmega \). Therefore (SMP) ensures that \(q \equiv q(0)=0\) on \(\overline{\varOmega }\), which implies that \(A_i=0\) for all \(i \in \{ 1, \dots ,n \}\). Consequently, we find \(\vec {X} \equiv 0\). \(\square \)
A simple example of \(F\) satisfying (F2) is \(F(\vec {X})=-\sum \vec {X}\), and then (4.4) represents the Laplace equation for \(u\). We therefore have
Corollary 4.5
Let \(u : \overline{\varOmega } \rightarrow \mathbf {R}\). If  for all \(x \in \varOmega \) and \(\max _{\overline{\varOmega }} u =\max _{\varOmega } u\), then \(u\) is constant on \(\overline{\varOmega }\).
for all \(x \in \varOmega \) and \(\max _{\overline{\varOmega }} u =\max _{\varOmega } u\), then \(u\) is constant on \(\overline{\varOmega }\).
5 Concluding Remark
The extension of the result presented in this paper to general lattices rather than rectangular lattices is an interesting open problem. However, in such a case we must address the following issues in a consistent way:
-
(1)
definitions of a volume and a perimeter;
-
(2)
a definition of a discrete Laplace operator \(\Delta '\);
-
(3)
an optimal estimate for \(\mathcal {L}^n (\partial ^+ u(z))\) by \(-\Delta 'u(z)\), where \(z\) is a point of the upper contact set of \(u\);
-
(4)
solvability of the Poisson–Neumann problem \(-\Delta 'u=\mathrm {Per}/\mathrm {Vol}\), \(\partial u/\partial \nu =-1\).
One of possible definitions of \(\Delta '\) is the definition appearing in the finite volume method in numerical analysis which is related to the Voronoi diagram for the set of points. Since the idea of the Voronoi diagram will also be needed when we derive an inclusion relation of the type (2.4), such definition seems to be natural. However, it seems non-trivial to complete the proof. We hope the ABP method presented in the present paper could be extended in the future.
References
Bezrukov, S.L.: Isoperimetric problems in discrete spaces. Extremal problems for finite sets. Bolyai Soc. Math. Stud. 3, 59–91 (1994)
Block, H.D.: Discrete isoperimetric-type inequalities. Proc. Am. Math. Soc. 8, 860–862 (1957)
Bokowski, J., Hadwiger, H., Wills, J.M.: Eine Ungleichung zwischen Volumen, Oberfläche und Gitterpunktanzahl konvexer Körper im \(n\)-dimensionalen euklidischen Raum. Math. Z. 127, 363–364 (1972)
Brass, P.: Isoperimetric inequalities for densities of lattice-periodic sets. Monatsh. Math. 127, 177–181 (1999)
Burago, Y.D., Zalgaller, V.A.: Geometric Inequalities. Grundlehren der Mathematischen Wissenschaften. Springer Series in Soviet Mathematics, vol. 285. Springer, Berlin (1988)
Caffarelli, L.A., Cabré, X.: Fully Nonlinear Elliptic Equations. American Mathematical Society Colloquium Publications, vol. 43. American Mathematical Society, Providence, RI (1995)
Cabré, X.: Partial differential equations, geometry and stochastic control. Butll. Soc. Catalana Mat. 15, 7–27 (2000)
Cabré, X.: Elliptic PDE’s in probability and geometry: symmetry and regularity of solutions. Discrete Contin. Dyn. Syst. 20, 425–457 (2008)
Chung, F.: Discrete isoperimetric inequalities. Surv. Differ. Geom. IX, 53–82 (2004)
Daykin, D.E.: An isoperimetric problem on a lattice. Math. Mag. 46, 217–219 (1973)
Duarte, J.A.M.S.: An approach to the isoperimetric problem on some lattices. Nuovo Cimento B 11(54), 508–516 (1979)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Reprint of the 1998th edn. Classics in Mathematics. Springer, Berlin (2001)
Grady, L.J., Polimeni, J.R.: Discrete Calculus. Applied Analysis on Graphs for Computational Science. Springer, London (2010)
Hadwiger, H.: Gitterperiodische Punktmengen und Isoperimetrie. Monatsh. Math. 76, 410–418 (1972)
Hillock, P.W., Scott, P.R.: Inequalities for lattice constrained planar convex sets. J. Inequal. Pure Appl. Math. 3(2–23), 1–10 (2002)
Kuo, H.-J., Trudinger, N.S.: Linear elliptic difference inequalities with random coefficients. Math. Comput. 55, 37–53 (1990)
Kuo, H.-J., Trudinger, N.S.: Discrete methods for fully nonlinear elliptic equations. SIAM J. Numer. Anal. 29, 123–135 (1992)
Kuo, H.-J., Trudinger, N.S.: On the discrete maximum principle for parabolic difference operators. RAIRO Modélisation. Math. Anal. Numér. 27, 719–737 (1993)
Kuo, H.-J., Trudinger, N.S.: Positive difference operators on general meshes. Duke Math. J. 83, 415–433 (1996)
Kuo, H.-J., Trudinger, N.S.: Evolving monotone difference operators on general space–time meshes. Duke Math. J. 91, 587–607 (1998)
Kuo, H.-J., Trudinger, N. S.: A note on the discrete Aleksandrov–Bakelman maximum principle. In: Proceedings of 1999 International Conference on Nonlinear Analysis (Taipei), Taiwanese J. Math. 4, pp. 55–64 (2000)
Osserman, R.: The isoperimetric inequality. Bull. Am. Math. Soc. 84, 1182–1238 (1978)
Rosser, J.B.: Finite-difference solution of Poisson’s equation in rectangles of arbitrary proportions. Z. Angew. Math. Phys. 28, 186–196 (1977)
Schnell, U., Wills, J.M.: Two isoperimetric inequalities with lattice constraints. Monatsh. Math. 112, 227–233 (1991)
Schumann, U., Benner, J.: Direct solution of the discretized Poisson–Neumann problem on a domain composed of rectangles. J. Comput. Phys. 46, 1–14 (1982)
Schumann, U., Sweet, R.A.: A direct method for the solution of Poisson’s equation with Neumann boundary conditions on a staggered grid of arbitrary size. J. Comput. Phys. 20, 171–182 (1976)
Villani, C.: Optimal Transport: Old and New. Grundlehren der Mathematischen Wissenschaften, vol. 338. Springer, Berlin (2009)
Zhuang, Y., Sun, X.-H.: A high-order fast direct solver for singular Poisson equations. J. Comput. Phys. 171, 79–94 (2001)
Acknowledgments
The author is grateful to Professor Xavier Cabré for letting him know a proof of the classical isoperimetric inequality by the ABP method in a school “New Trends in Nonlinear PDEs” held at Centro di Ricerca Matematica Ennio De Giorgi during 18–22 June 2012. The author next sends his gratitude to Dr. Takahito Kashiwabara for many helpful discussions on maximum principles. The author thanks the anonymous referees for their careful reading of the original manuscript and valuable comments. The work of the author was supported by Grant-in-aid for Scientific Research of JSPS Fellows No. 23-4365 and No. 26-30001.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hamamuki, N. A Discrete Isoperimetric Inequality on Lattices. Discrete Comput Geom 52, 221–239 (2014). https://doi.org/10.1007/s00454-014-9617-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-014-9617-2
Keywords
- Discrete isoperimetric inequality
- Finite difference method
- Poisson–Neumann problem
- Aleksandrov–Bakelman–Pucci maximum principle




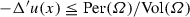 for all
for all 
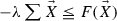 for all
for all 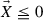 .
.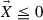 and
and 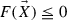 , then
, then