Perfect Graphs and Guarding Rectilinear Art Galleries

Abstract

In this paper we introduce a new method based on perfect graphs that can be used to prove bounds on the number of guards necessary to guard a rectilinear art gallery in terms of the number of vertices, area and perimeter, respectively. Using this method, we prove that a polyomino with perimeter $l\ge 6$ can be guarded by at most $\lfloor \tfrac{l}{6}\rfloor$ guards. Moreover, we give a new proof for the rectilinear art gallery theorem, stating that any rectilinear art gallery with $n$ vertices can be guarded by at most $\lfloor \frac{n}{4}\rfloor$ guards. Finally, we give a new proof that at most $\lfloor \tfrac{m+1}{3}\rfloor$ guards are necessary to guard an $m$-polyomino, even if the polyomino contains holes.

1 Introduction

A well known problem in computational geometry is the art gallery problem that was posed by Victor Klee in 1973. The task is to position a minimum number of point guards (sometimes called watchmen) in a polygon such that they can together see every point of the polygon. Chvátal [2] proved that $\lfloor \tfrac{n}{3}\rfloor$ guards are always sufficient where $n$ is the number of vertices of the polygon. Later, a simpler proof was found by Fisk [3].

A special case is the rectilinear (or orthogonal) art gallery problem, where the edges of the polygon are either horizontal or vertical. Kahn et al. [8] first showed that $\lfloor \tfrac{n}{4}\rfloor$ guards are sufficient in this case. Alternative proofs of this result were found by Győri [5], Lubiw [10] and O’Rourke [11].

In this paper we introduce a new method based on perfect graphs that can be used to bound the number of guards necessary to guard rectilinear art galleries in terms of vertices and to guard polyominoes in terms of area and perimeter, respectively. A polyomino is the union of a finite number of lattice squares. Unless otherwise stated the polyominoes and art galleries considered in this paper do not contain holes.

The bounds in terms of vertices and area are already known. One new result of our paper is the following theorem.

Theorem 1

The minimum number of guards necessary to guard a polyomino is at most $\max \left\{ 1, \left\lfloor \tfrac{l}{6} \right\rfloor \right\}$ where $l$ denotes the perimeter of the polyomino.

This variant of the art gallery problem was proposed by Jäger [7], who originally conjectured the statement of Theorem 1.

Section 3 contains a new proof of the rectilinear art gallery theorem based on properties of perfect graphs, which are recalled in Sect. 2. Section 4 contains the proof of Theorem 1. Section 5 gives a new proof for the recent area bound of Bield et al. [1] for guarding polyominoes.

2 Preliminaries

In this section we introduce the idea of our method based on maximal rectangles within an art gallery and their connection to guards and perfect graphs.

Let $\mathcal {R}$ be the set of all maximal axis-parallel rectangles that are inside the gallery. A rectangle $R$ is maximal if it is inside the gallery and there is no other rectangle $R^{\prime }\ne R$ inside the gallery with $R\subset R^{\prime }$.

We have to specify which points inside a gallery can be seen from a point $v\in \mathbb {R}^2$. In the original setting a point $v$ covers (or sees) a point $w$ if the line segment $vw$ is part of the gallery. An alternative model of visibility is the so called $r$-visibility. Two points $v$ and $w$ are $r$ -visible if the minimum axis-parallel rectangle containing $v$ and $w$ is completely inside the gallery. Note that $r$-visibility implies visibility.

An $r$ -star is a polygon $P$ such that there exists a point $v$ with $P\!=\!\{w\!\mid \!v\;\text {and}\;w\;\text {are} r\text {-visible}\}$. Note that this implies that $P$ is the union of all maximal rectangles $R\in \mathcal {R}$ such that $v\in R$. One method to find an upper bound on the number of guards is to find a set of $r$-stars covering the gallery.

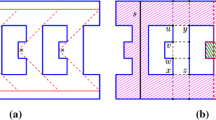
Our approach is slightly different. Instead of looking for a minimum number of guards that cover the gallery we want to find a minimum number of guards $\tau (\mathcal {R})$ such that each maximal rectangle $R\in \mathcal {R}$ contains at least one of them. Such a set of guards or points is a transversal of $\mathcal {R}$ and $\tau (\mathcal {R})$ is the transversal number of $\mathcal {R}$. It is obvious that such a set of guards covers the gallery. There are galleries such that $\tau (\mathcal {R})$ is greater than the minimum number of $r$-stars necessary to cover the gallery (see Fig. 1). Nevertheless, transversals yield upper bounds for the number of guards necessary to guard a gallery.

Fig. 1

A gallery where the transversal number $\tau (\mathcal {R})$ is 3 (a), but where 2 $r$-stars are sufficient to cover the gallery (b)

To bound $\tau (\mathcal {R})$ from above we investigate the intersection graph of $\mathcal {R}$ with vertex set $\mathcal {R}$ and edges between pairs of rectangles with nonempty intersection. A clique cover of a graph $G$ is a set of cliques $C_1,\ldots ,C_k$ in $G$ such that every vertex $v\in V(G)$ lies in at least one of these cliques. For a guard $p$ let $\mathcal {R}_p\subseteq \mathcal {R}$ be the set of maximal rectangles that contain $p$. Since all rectangles in $\mathcal {R}_p$ have $p$ in common, they form a clique in the intersection graph $G_{\mathcal {R}}$. On the other hand, consider a clique $C\subseteq \mathcal {R}$ in $G_{\mathcal {R}}$, that is, any pair of rectangles $R,R^{\prime }\in C$ has a non-empty intersection. By Helly’s theorem [6] there exists a point $q$ that is contained in all rectangles in $C$. We conclude that every transversal of $\mathcal {R}$ corresponds to a clique cover of $G_{\mathcal {R}}$ of the same size and vice versa. Due to this fact we denote the minimum size of a clique cover of a graph $G$ by $\tau (G)$.

Next we prove that in the case of rectilinear galleries $\tau (G_{\mathcal {R}})$ equals the maximum size of an independent set of $G_{\mathcal {R}}$. In order to do this, we introduce some notation and known results from graph theory. For a graph $G$ let a vertex coloring of $G$ be a function $c:V(G)\rightarrow \mathbb {N}$ such that no two adjacent vertices receive the same color, that is, $c(v)\ne c(w)$ for all $\{v,w\}\in E(G)$. The chromatic number $\chi (G)$ is the smallest number of colors needed to color the vertices of $G$. The vertices of the same color form an independent set in $G$. Thus a coloring of $G$ with $k$ colors is equivalent to a partitioning of $V(G)$ into $k$ independent sets.

The clique number $\omega (G)$ of $G$ is the number of vertices in a maximum clique in $G$. Since every vertex in a clique receives a different color, we have $\chi (G)\ge \omega (G)$. A graph $G$ is perfect if for every induced subgraph $G'$ of $G$, the clique number equals the chromatic number, that is, $\omega (G')=\chi (G')$.

We denote the maximum size of an independent set in a graph $G$ by $\alpha (G)$. It is easy to see that every clique in $G$ corresponds to an independent set in the complement $\bar{G}$ of $G$ and every vertex coloring of a graph $G$ corresponds to a clique cover in $\bar{G}$. Thus

$$\begin{aligned} \alpha (G)=\omega (\bar{G})\le \chi (\bar{G})= \tau (G). \end{aligned}$$

(1)

By the Weak Perfect Graph Theorem [9], the complement of a perfect graph is itself perfect. This immediately implies that for a perfect graph $G$ the equation

$$\begin{aligned} \alpha (G)=\tau (G) \end{aligned}$$

(2)

holds.

Now we consider again the set $\mathcal {R}$ of maximal rectangles and its intersection graph $G_{\mathcal {R}}$. Shearer [13] proved the following lemma.

Lemma 2

(Shearer [13]) The intersection graph of maximal rectangles in a rectilinear polygon without holes is perfect.

By (2), we obtain $\alpha (G_{\mathcal {R}})= \tau (G_{\mathcal {R}})$, that is, the minimum size of a clique cover equals the maximum size of an independent set in $G_{\mathcal {R}}$. A maximum independent set in $G_{\mathcal {R}}$ corresponds to a set of pairwise disjoint rectangles $\mathcal {P}\subseteq \mathcal {R}$ (also called a packing of $\mathcal {R}$) of maximum size.

Proposition 3

Let $\mathcal {R}$ be the set of maximal rectangles in a rectilinear gallery $M$. The maximum size of a packing of $\mathcal {R}$ is an upper bound for the number of guards necessary to cover $M$.

Note that the number of maximum rectangles inside a gallery $M$ is polynomially bounded in the number of vertices of $M$. Thus the intersection graph $G$ of maximal rectangles in $M$ has polynomial size. Grötschel et al. [4] described a polynomial time algorithm to compute a minimum size vertex coloring in perfect graphs. Applying this algorithm on $\bar{G}$ we get a clique covering $\mathcal {C}$ of $G$ of size $\alpha (G)$ which is equal to $\tau (G)$ by Proposition 2. Finally, we can place for every clique $C$ of $\mathcal {C}$ a guard in the non-empty intersection of the rectangles in $C$. In summary, there exists a polynomial time algorithm to compute the positions of $\tau (G)$ guards covering the gallery.

3 The Rectilinear Art Gallery Theorem

A well known result is the following rectilinear art gallery theorem stated and first proved by Kahn et al. [8].

Theorem 4

(Kahn et al. [8]) A rectilinear art gallery with $n$ vertices can be guarded by $\lfloor \tfrac{n}{4}\rfloor$ guards.

Many alternative proofs of Theorem 4 and stronger versions of the theorem (in which the galleries might contain holes and the guards have to be placed on vertices) are known; see for example Győri [5], Lubiw [10] and O’Rourke [11].

Our method yields a new proof of the theorem using packings of maximal rectangles.

Proof

By Proposition 3 the minimum number of guards that are sufficient to guard the gallery is bounded by the maximum size a set $\mathcal {P}$ of pairwise disjoint maximal rectangles that are inside the gallery. To complete the proof we show that every maximal rectangle contains at least $4$ vertices of the gallery.

Let $R\in \mathcal {P}$ and $(a,b)\in \mathbb {R}^2$ be the lower left corner of $R$. Let $\{ (a,y)\mid b' \le y \le b'' \}$ be the bottommost wall segment that is part of the left side of $R$ and let $\{ (x,b)\mid a' \le x \le a''\}$ be the leftmost wall segment that is part of the lower side of $R$. Due to the maximality of $R$ such segments with $b'<b''$ and $a'<a''$ exist. If $(a,b')=(a',b)= (a,b)$ then $(a,b)$ is a vertex of the gallery. Otherwise, at least one of $(a,b')$ and $(a',b)$ is distinct from $(a,b)$ and is thus a vertex of the gallery. By analogous arguments for the other three corners of $R$ we obtain that each rectangle $R\in \mathcal {P}$ contains at least $4$ vertices of the gallery.

As the rectangles in $\mathcal {P}$ are pairwise disjoint, no vertex is in more than one of them and hence $|\mathcal {P}|\le \lfloor \tfrac{n}{4}\rfloor$. $\square$

4 Bounding the Number of Guards in Terms of the Perimeter

In this section we prove Theorem 1 using the concept of maximum rectangle packings. To this end consider a polyomino $M$, which might contain holes.

In order to give a bound in terms of the perimeter $l$ of $M$, we split up the boundary of $M$ into segments of length $1$, where a segment is a set $\{(x,b)| a< x <a+1\}$ or $\{(a,y)| b< y <b+1\}$ for some $a,b\in \mathbb {Z}$. As all vertices have integral coordinates, either all points or none of the points of a segment belongs to the boundary of the polygon. A wall segment is a segment that is part of the boundary. Let $W$ be the set of all wall segments. Hence the perimeter $l$ of $M$ is equal to $|W|$.

Now let $\mathcal {P}\subseteq \mathcal {R}$ be a maximum size packing. If $l=4$, then $|\mathcal {P}| =1$. Our goal is to show $|\mathcal {P}|\le \frac{l}{6}$ for $l\ge 6$. Removing $\cup _{R\in \mathcal {P}} R$ from $M$ separates the polyomino into disjoint connected regions. Let $\mathcal {Q}$ be the set of the closures of the maximal connected regions of $M{\setminus } \cup _{R\in \mathcal {P}} R$.

Consider the bipartite graph $G$ with vertex set $\mathcal {P}\cup \mathcal {Q}$ and edge set $E$ where the edges $E$ are the pairs of regions $\{R,Q\},\;R\in \mathcal {P}, Q\in \mathcal {Q}$, that intersect (see Fig. 2). Note that such regions $\mathcal {Q}$ and such a graph $G$ can be constructed for any rectilinear gallery and not only for polyominoes. For $v\in V(G)$, we denote by $d_G(v)=|\{w\in V(G)|\{v,w\}\in E(G)\}|$ the degree of $v$ in $G$.

Fig. 2

a A polyomino with a maximum number of disjoint maximal rectangles. b The corresponding bipartite graph $G$

Using this bipartite graph we count the number of wall segments that are contained in each region in $V(G)$. First we consider the maximal rectangles.

Lemma 5

Each maximal rectangle in a polyomino contains at least 4 wall segments.

Proof

A maximal rectangle contains a wall segment in each direction. Otherwise, we can enlarge the rectangle in a direction that does not contain such a segment which is a contradiction to its maximality. $\square$

If one guard is sufficient to cover the gallery, Theorem 1 holds. Thus we assume that we need at least $2$ guards. By Proposition 3, we have $|\mathcal {P}|\ge 2$. In addition, note that each wall segment belongs to exactly one region of $\mathcal {P}\cup \mathcal {Q}$.

Lemma 6

If $\mathcal {Q}$ and $G$ are defined as above, then each region $Q\in \mathcal {Q}$ contains at least $d_{G}(Q)$ wall segments.

Proof

Let $Q\in \mathcal {Q},\;d=d_{G}(Q)$ and let $p$ be a point on the border of $Q$. We traverse the border of $Q$ counterclockwise, starting at $p$, until we reach $p$ again. During this traversal we pass the borders of the $d$ rectangles $R_{1},\ldots , R_{d}$ (in this order) that are adjacent to $Q$, that is, $\{Q, R_{j}\}\in E(G)$ and hence $Q\cap R_{j}\ne \emptyset$. For simplicity let $R_{d+1}=R_1$. Since any two consecutive rectangles $R_{j}$ and $R_{j+1}$ are disjoint, there is at least one wall segment on the path between these rectangles and these wall segments are in $Q$ due to its maximality. We conclude that there are at least $d$ wall segments in $Q$. $\square$

Lemma 7

If $\mathcal {P}$ and $G$ are defined as above and if $R\in \mathcal {P}$ is a vertex of degree $1$ in $G$, then there are at least $5$ wall segments in $R$.

Proof

First observe that $R$ contains at least two squares as otherwise it is not maximal. Say the northern and the southern edge of $R$ have length at least 2, that is, they contain at least two segments. By Lemma 5, there are $4$ wall segments on the border of $R$, one in each direction. Note that $R$ has only one neighbor in $G$. Hence either all segments of the northern edge or all segments of the southern edge of $R$ are wall segments. Thus this edge contains at least 2 wall segments. $\square$

Now we give a lower bound for the number of wall segments in terms of $|\mathcal {P}|$.

Lemma 8

A polyomino (with possible holes) with a maximum size packing $\mathcal {P}$ of maximal rectangles contains at least $6|\mathcal {P}|$ wall segments.

Proof

Let $G$ and $\mathcal {Q}$ be defined as above and denote by $\sigma :\mathcal {P}\cup \mathcal {Q}\rightarrow \mathbb {N}$ the number of wall segments contained in each region. As $G$ is bipartite, each edge is incident to one vertex of $\mathcal {Q}$ and we obtain

$$\begin{aligned} \textstyle {\sum \limits _{v\in \mathcal {Q}}} d_G(v) = |E(G)|. \end{aligned}$$

(3)

Let $L$ be the set of all rectangles in $\mathcal {P}$ that have degree $1$ in $G$. Then every rectangle in $L$ is incident to one edge of $G$ and every rectangle of $\mathcal {P}{\setminus } L$ is incident to at least two edges of $G$. Since all these edges are disjoint we conclude

$$\begin{aligned} |E(G)|\ge 2|\mathcal {P}| - |L|. \end{aligned}$$

(4)

Therefore the number of wall segments satisfies

$$\begin{aligned} \textstyle {\sum \limits _{v\in \mathcal {P}\cup \mathcal {Q}}} \sigma (v)&= \textstyle {\sum \limits _{v\in \mathcal {P}}} \sigma (v) + \textstyle {\sum \limits _{v\in \mathcal {Q}}} \sigma (v) \\&\ge \textstyle {\sum \limits _{v\in \mathcal {P}}}\sigma (v) + \textstyle {\sum \limits _{v\in \mathcal {Q}}} d_G(v)\quad (\text {Lemma 6}) \\&= \textstyle {\sum \limits _{v\in \mathcal {P}}} \sigma (v) + |E(G)|\quad (\text {by (3))} \\&\ge 5|L| + 4(|\mathcal {P}|-|L|) + |E(G)|\quad (\text {Lemmas 5 and 7)} \\&\ge 5|L| + 4(|\mathcal {P}|-|L|) + 2|\mathcal {P}| - |L|\quad (\text {by (4))}\\&= 6|\mathcal {P}|. \end{aligned}$$

$\square$

Theorem 1 now immediately follows from Lemma 8 and Proposition 3. Figure 3 shows the well known “comb” example, proving that the bound of Theorem 1 is tight.

Fig. 3

A gallery where $\frac{l}{6}$ guards are necessary

Note that Lemma 8 is true for packings of maximal rectangles in any polyomino, even if the polyomino contains holes. We were not able to prove that the packing number is also an upper bound for the number of guards necessary to guard a gallery with holes. However, we feel that this is still true in the general case.

Conjecture 9

In any rectilinear gallery which might contain holes the maximum size of a packing of maximal rectangles is an upper bound on the number of guards required to guard the gallery.

If this conjecture is true, then by the above observations Theorem 1 is also true for polyominoes with holes. Note that in rectilinear polygons with holes the intersection graph of the maximal rectangles is not necessarily perfect. However, this is no contradiction to our conjecture.

Figure 4 shows a gallery with one hole in which the intersection graph of the maximal rectangles is not perfect because it contains an induced cycle of length 5. Nevertheless, there is a packing of size 3, which is the minimum number of guards necessary to guard the gallery.

Fig. 4

A gallery with one hole in which the intersection graph of the maximal rectangles is not perfect

5 Guarding $m$-Polyominoes

A polyomino that is the union of $m$ squares is called an $m$-polyomino. Note that an $m$-polyomino and can have holes. Recently Biedl et al. [1] proved the following bound in terms of the area of a polyomino:

Theorem 10

(Biedl et al. [1]) At most $\lfloor \tfrac{m+1}{3}\rfloor$ guards are necessary to guard an $m$-polyomino.

In this section we show that our bound on the number of guards in terms of the perimeter implies this bound in terms of the area.

First consider the case that the gallery does not contain a hole. Let $\mathcal {P}, \mathcal {Q}$ and $G$ be defined as above. Again, we assume that $|\mathcal {P}|\ge 2$. Let $a(P)$ be the area of a polygon $P\in \mathcal {P}\cup \mathcal {Q}$.

Lemma 11

For all $R\in \mathcal {P}$ and $Q\in \mathcal {Q}$ we have $a(R)\ge 2$ and $a(Q)\ge d_G(Q)-1$.

Proof

Observe that every maximal rectangle contains at least two unit squares, that is, $a(R)\ge 2$ for all $R\in \mathcal {P}$. By Lemma 6, each region $Q\in \mathcal {Q}$ contains at least $d_G(Q)$ wall segments. Moreover, it contains at least $d_G(Q)$ segments in its boundary that are not wall segments, one for each neighbor of $Q$ in $G$. Thus the perimeter of $Q$ is at least $2 d_G(Q)$. The area of a connected polyomino with perimeter $2k$ is at least $k-1$. As $Q$ itself is a connected polyomino the claim follows directly. $\square$

The graph $G$ is connected and thus

$$\begin{aligned} |E(G)| \ge |V(G)| -1 = |\mathcal {Q}| + |\mathcal {\mathcal {P}}| -1. \end{aligned}$$

(5)

We conclude using Lemma 11

$$\begin{aligned} m= \textstyle {\sum \limits _{R\in \mathcal {P}}}a(R) + \textstyle {\sum \limits _{Q\in \mathcal {Q}}} a(Q)&\ge 2|\mathcal {P}| + \textstyle {\sum \limits _{Q\in \mathcal {Q}}} (d_G(Q) -1) \quad (\text {Lemma 11)}\\&\ge 2|\mathcal {P}| - |\mathcal {Q}| + |E(G)| \quad (\text {by (3))}\\&\ge 3|\mathcal {P}| -1. \qquad \qquad \qquad \quad (\text {by (5))} \end{aligned}$$

By Proposition 3, $|\mathcal {P}|$ is an upper bound for the number of guards necessary to guard the gallery. This proves Lemma 10 in the case that the gallery has no holes.

If there are holes we add additional walls to make the gallery hole-free. This can be done by connecting holes to other holes or to the exterior with new walls (see e.g. [12]) such that the interior of the gallery is a connected region with no hole. For an example see Fig. 5a, b. By this procedure we increase the number of walls and more guards might be necessary, but the area of the gallery does not change.

Fig. 5

The transformation for the proof of Theorem 10 for polyominoes with holes. a Original polyomino with holes. b The new gallery $M$ after inserting additional walls. c The gallery $M'$. d $M'$ with packing $\mathcal {P}'$ of maximal rectangles. e The corresponding maximal rectangles in the gallery $M$

Denote by $M$ the new gallery and let $\mathring{M}$ be the interior of $M$, that is, all points of $M$ that are not on a wall. We “shrink” the gallery by setting

$$\begin{aligned} M^{\prime }=\big \{(x,y)\in \mathbb {R}^2|\max _{p\notin \mathring{M}} ||p-(x,y)||_1 \ge \varepsilon \big \} \end{aligned}$$

for a fixed $\varepsilon >0$ (Fig. 5c). The new $M'$ does not contain any holes and there exists an obvious one-to-one correspondence between the maximum rectangles in $M$ and $M'$. Let $\mathcal {P}'$ be a maximal packing of maximum rectangles in $M'$ and define $\mathcal {Q}'$ and $G'$ as above (Fig. 5d). Let $\mathcal {P}$ and $\mathcal {Q}$ be the sets we obtain by replacing the regions in $\mathcal {P}'$ and $\mathcal {Q}'$ by their corresponding regions in $M$ and let $G$ be the corresponding graph with vertex set $\mathcal {P}\cup \mathcal {Q}$ (Fig. 5e). Some of the rectangles in $\mathcal {P}$ might share the same walls and vertices of $M$, but the interiors of the regions $\mathcal {P}\cup \mathcal {Q}$ are pairwise disjoint. Hence, we apply Lemma 5 and the method for hole-free polyominoes on $\mathcal {P}, \mathcal {Q}$ and $G$. We conclude that at most $\lfloor \tfrac{m+1}{3}\rfloor$ guards are sufficient to guard $M$ and thus $\lfloor \tfrac{m+1}{3}\rfloor$ guards are also sufficient to guard the original polyomino with holes. This proves Lemma 10 in the general case.