On Packing $\mathbb {R}^3$ with Thin Tori

Abstract

We show that $\mathbb {R}^3$ can be packed at a density of $0.222\ldots$ with tori whose minor radius goes to zero. Furthermore, we show that the same torus arrangement yields an asymptotically optimal number of pairwise-linked tori.

1 Introduction and Main Result

Geometric packing problems in $\mathbb {R}^3$ received huge attention over many decades (see [1, 3, 10–13, 15, 16, 20–22, 27] for books on packings). Still, the sphere is the only body which does not tile $\mathbb {R}^3$ and for which we know the exact packing density [17]. For other bodies such as platonic solids [5, 23] and ellipsoids [2, 9], dense packing constructions are known, but no proof of optimality exists and a vast amount of related questions remain open (see the books [4] and [8]).

On the other hand, there is only a very limited amount of the literature studying packings involving non-convex objects, such as the work of Jiao et al. [19, 24, 25]. We would thus like to extend this line of research by considering packings with the possibly simplest non-convex shape, the torus. Note that although Conway and Hopcroft showed in [6] that using the axiom of choice it is possible to fill $\mathbb {R}^3$ with unit circles, the problem addressed here is of different types, since we are dealing with solid bodies and not with one-dimensional curve.

Throughout this note we refer to a torus with major radius 1 and minor radius going to zero as a thin torus.

Theorem 1

$\mathbb {R}^3$ can be packed with thin tori at a density of $0.222\ldots$.

Theorem 2

It is possible to pairwise link $\varTheta (1/s^2)$ many tori of major radius $1$ and minor radius $s < 1/3$ and this is asymptotically optimal.

2 Proof of Theorem 1

Given a torus lying in a plane $H$ and a point $p$ on its surface, there are three different types of non-trivial circles through $p$. One can draw a circle through $p$ which lies in a plane parallel to the plane $H$ and one can draw a circle through $p$ in the plane perpendicular to $H$. A third type of circles is obtained by cutting the torus open at $p$ along a plane which is bitangential to the torus and then draw two circles on the surface of the torus along the cut as shown in Fig. 1a. These circles have a radius which corresponds to the major radius of the torus and were first observed by Yvon Villarceau thus they are called Villarceau circles [26]. Most prominently, Villarceau circles appear in topology, when the Hopf fibration [18] of a 3-sphere is stereographically projected into $\mathbb {R}^3$.

In order for the torus arrangement to pack $\mathbb {R}^3$ with positive density, it is necessary that some tori are linked. This holds, since the volume of the bounding box of a torus with minor radius $s$ is $\varTheta (s)$, while the volume of the torus is $\varTheta (s^{2})$. Thus, for $s \rightarrow 0$, the packing density of an arrangement of unlinked thin tori goes to 0. Therefore, it is not a priori clear that a packing of thin tori with positive density exists.

Fig. 1

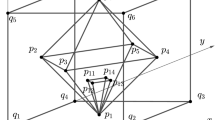
a An illustration [14] of a bitangential plane and its two Villarceau circles through $p$. b A family of Villarceau circles obtained by rotating the bitangential cutting plane in discrete steps around the $z$-axis

Throughout this note we denote by $T(R, r)$ a torus of major radius $R$ and minor radius $r$. The basic idea of the torus arrangement is to first pack $\mathbb {R}^3$ with an auxiliary lattice packing of fat tori $T_\mathrm{{F}} = T(1, r)$ for some constant $r$. All such tori are placed parallel to the $xy$-plane and are centered at points of the lattice, generated by the vectors

$$\begin{aligned} \Bigg (\begin{array}{c} 2+\sqrt{3}r \\ 0 \\ r \\ \end{array}\Bigg ),\quad \Bigg (\begin{array}{c} 1+r \\ \sqrt{3}(1+r) \\ 0\\ \end{array}\Bigg ),\quad \Bigg (\begin{array}{c} 0 \\ 0 \\ 2r \\ \end{array}\Bigg ). \end{aligned}$$

Since the parallelepiped of this lattice has volume $2\sqrt{3} \, \big ( 2+\sqrt{3}r \big ) \left( 1+r \right) r$, the lattice packing of $\mathbb {R}^3$ with $T_\mathrm{{F}}$ tori has a density of

$$\begin{aligned} \delta _L(r) = \frac{\pi ^2r}{\sqrt{3} \big ( 2+\sqrt{3}r \big ) \big ( 1+r \big ) }. \end{aligned}$$

(1)

Fig. 2

A vertical cut through $T_\mathrm{{F}}$, the nested sequence of $T_k$ tori and a schematic representation of the $T(1, s)$ tori through one point on each $T_k$

Inside every $T_\mathrm{{F}}$ torus we build a second auxiliary structure by forming a nested sequence of concentric tori $T_{\lfloor \frac{r - s}{2s} \rfloor } , \ldots , T_1$ centered at lattice points, with $T_k = T(1,2ks)$. Here, $s$ denotes the minor radius of the thin tori which we will ultimately use to pack $\mathbb {R}^3$. Next, a $2s$ neighborhood of the surface of each $T_k$ torus gets packed with thin $T(1, s)$ tori as illustrated in Fig. 2. For this we construct a family of Villarceau circles by rotating the bitangential cutting plane of $T_k$ in discrete steps around the $z$-axis in such a way that the smallest distance between any two Villarceau circles is at least $2s$ (see Fig. 2). Note that we only chose one of the two resulting Villarceau circles associated with each cutting plane. Replacing every Villarceau circle by a $T(1, s)$ torus yields a packing of the $2s$ neighborhood of the surface of $T_k$. Denoting by $V_k$ the volume of the union of all $T(1, s)$ tori on $T_k$, we obtain a total volume of

$$\begin{aligned} V = \textstyle \sum \limits ^{\lfloor \frac{r-s}{2s} \rfloor }_{k=1} V_k \end{aligned}$$

for the nested arrangement of thin tori inside $T_\mathrm{{F}}$ and thus a packing density of $\delta _T(r) = V/(2\pi ^2r^2)$ with respect to $T_\mathrm{{F}}$. Therefore, the packing density of the $T(1, s)$ torus arrangement with respect to $\mathbb {R}^3$ is $\delta (r) = \delta _T(r) \delta _L(r)$.

The remaining part of this section is used to calculate the volume $V$.

Lemma 1

Given a torus $T(R, r)$ lying in the $xy$-plane and two Villarceau circles $c_0,c_1$ lying in the bitangential planes $H_0, H_1$, respectively. In order for the minimum distance between $c_0$ and $c_1$ to be at least $d$, an angular distance between $H_0$ and $H_1$ of $\psi = \arcsin \frac{dR}{r(R-r)}$ around the $z$-axis suffices, given $r \le R-d$.

Proof

A Villarceau circle of a torus $T(R,r)$ centered at the origin and lying in the $xy$-plane can be parameterized (see [7]) as

$$\begin{aligned} \mathbf {c}(\psi , t) = \Bigg ( \begin{array}{c@{\quad }c@{\quad }c} \cos \psi &{} \sin \psi &{} 0 \\ -\sin \psi &{} \cos \psi &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \Bigg ) \Bigg ( \begin{array}{c} \sqrt{R^2-r^2} \cos t \\ r+R \sin t\\ r \cos t \end{array} \Bigg ). \end{aligned}$$

Here $\psi$ denotes the rotation angle of the bitangential cutting plane around the $z$-axis and $t$ defines the location on the Villarceau circle. At $\psi = 0$, the derivatives of $\mathbf {c}$ are

$$\begin{aligned} \frac{ \partial \mathbf {c}}{\partial t} =\Bigg ( \begin{array}{c} -\sqrt{R^2-r^2} \sin t\\ R \cos t \\ -r \sin t \end{array} \Bigg ) \end{aligned}$$

and

$$\begin{aligned} \frac{ \partial \mathbf {c}}{\partial \psi } = \Bigg ( \begin{array}{c} r + R \sin t \\ -\sqrt{R^2-r^2} \cos t \\ 0 \end{array} \Bigg ). \end{aligned}$$

The closest distance between the circle $c_0 =\mathbf {c}(0,t)$ and a circle $c_1$ rotated around the $z$-axis appears on $c_0$, when $\frac{ \partial \mathbf {c}}{\partial \psi }$ assumes the smallest value in the direction perpendicular to $\frac{ \partial \mathbf {c}}{\partial t }$, i.e., at the point where

$$\begin{aligned} \big | \frac{ \partial \mathbf {c}}{\partial \psi } \big |\sin \gamma \end{aligned}$$

attains its minimum, with $\gamma$ denoting the angle between $\frac{ \partial \mathbf {c}}{\partial t }$ and $\frac{ \partial \mathbf {c}}{\partial \psi }$.

Since

$$\begin{aligned} \sin \gamma = \sqrt{1- \Bigg (\frac{ \frac{ \partial \mathbf {c}}{\partial \psi }\cdot \frac{ \partial \mathbf {c}}{\partial t }}{\big | \frac{ \partial \mathbf {c}}{\partial \psi }\big |\big | \frac{ \partial \mathbf {c}}{\partial t }\big |}\Bigg )^2} \end{aligned}$$

we want to minimize

$$\begin{aligned} \sqrt{\big |\frac{ \partial \mathbf {c}}{\partial \psi } \big |^2 - \Bigg (\frac{\frac{ \partial \mathbf {c}}{\partial \psi } \cdot \frac{ \partial \mathbf {c}}{\partial t }}{\big | \frac{ \partial \mathbf {c}}{\partial t}\big |}\Bigg )^2}, \end{aligned}$$

which simplifies to

$$\begin{aligned} \frac{r}{R}\sqrt{{ \big ( 2\,rR\sin \big ( t \big ) +{r}^{2}+{R}^{2}+ (\big ( \sin \big ( t \big ) \big ) ^{2} -1){r}^{2} \big ) }} \end{aligned}$$

and attains its minimum at $t =-\arcsin {R/r}$. Since $r < R$, the minimum occurs when $\sin t = -1$. If we denote this point $(0,r-R,0)$ by $q$, its minimum distance to the cutting plane $H_1$ provides a lower bound for the minimum distance $d$ between $c_0$ and $c_1$. Since the normal unit vector of $H_1$ is $\mathbf {n_1} = (r/R\cos \psi , -r/R\sin \psi , \sqrt{1-r^2/R^2})$,

$$\begin{aligned} d \ge \mathbf {n_1} \cdot q = \frac{r(R-r)}{R}\sin \psi . \end{aligned}$$

Thus, an angular distance between $H_0$ and $H_1$ around the $z$-axis of at least

$$\begin{aligned} \psi = \arcsin \frac{dR}{r(R-r)} \end{aligned}$$

results in a minimum distance of at least $d$ between $c_0$ and $c_1$. $\square$

It follows from Lemma 1 that the $2s$ neighborhood of the surface of a $T_k$ torus can be packed with $\big \lfloor \frac{2\pi }{\arcsin \frac{1}{k(1-2ks)}} \big \rfloor$ many $T(1, s)$ tori. Using the fact that $11x/7 \ge \arcsin x$ for $0 \le x \le 1$, the volume of the union of these tori is

$$\begin{aligned} V_k \ge 2\pi ^2 s^2 \big \lfloor \frac{14}{11}\pi k(1-2ks) \big \rfloor . \end{aligned}$$

For $s \rightarrow 0$, the volume of the union of all $T(1, s)$ tori inside one $T_\mathrm{{F}}$ torus becomes

$$\begin{aligned} \overline{V} = \lim _{s \rightarrow 0} \textstyle \sum \limits ^{\lfloor \frac{r-s}{2s} \rfloor }_{k=1} V_k \ge \frac{7}{66}{\pi }^{3}\,{r}^{2} \big ( 3-2\,r\big ), \end{aligned}$$

and thus the packing density $\delta _T(r)$ with respect to $T_\mathrm{{F}}$ is

$$\begin{aligned} \delta _T(r) = \frac{7}{132}\pi (3-2r). \end{aligned}$$

(2)

Combining Eqs. (1) and (2), the packing density of the thin tori with respect to $\mathbb {R}^3$ evaluates to

$$\begin{aligned} \delta (r)= \delta _L(r) \delta _T(r) = {\frac{7{\pi }^{3}r \big ( 3-2\,r \big ) }{ 132\sqrt{3} \big ( 2 + \sqrt{3}r \big )\big (1+r\big )}} \end{aligned}$$

which, at $r = 0.441\ldots$, obtains the maximum value of $0.222\ldots$.

3 Proof of Theorem 2

In order to prove Theorem 2, we show that in the nested torus construction of the previous section all thin tori are pairwise linked. Let $c_0$ and $c_1$ be two Villarceau circles on two nested (auxiliary) unit tori $T_0$ and $T_1$ with minor radius $r_0$ and $r_1$, respectively, and assume $r_0 < r_1$. We prove the claim by showing that $c_1$ and $T_0$ are linked, which, since Villarceau circles are fully contained in the surface of a torus, is equivalent to showing that $c_1$ is linked with the unit circle $c$ defining the axis of revolution of $T_0$. Furthermore, wlog we may assume that the cutting plane defining $c_1$ is unrotated (around the $z$-axis), since otherwise we may just rotate the whole coordinate system around the $z$-axis. It thus follows that $c_1$ intersects the $y$-axis at distances $-1 + r_1$ and $1 + r_1$. In order to show that $c_1$ and $c$ are linked, it suffices to note that $y$-axis intersects $c$ inside the interval $(-1 + r_1,1 + r_1)$ exactly once, namely at $1$. Since all Villarceau circles on the same torus are linked (see [7]), the claim follows.

We set the minor radius $r$ of $T_\mathrm{{F}}$, defined in the previous section, equal to $1$, i.e., $T_\mathrm{{F}}$ becomes a Horn torus and we note that the outermost torus of the nested structure inside $T_\mathrm{{F}}$ has minor radius $1-s$. As argued in the previous section, the number of pairwise-linked tori of minor radius $s$ in the nested construction is

$$\begin{aligned} \textstyle \sum \limits ^{\lfloor \frac{1-s}{2s} \rfloor }_{k=1}\big \lfloor \frac{14}{11}\pi k(1-2ks) \big \rfloor , \end{aligned}$$

which is lower bounded by

$$\begin{aligned} {\frac{1}{132}}\,{\frac{ ( 3\,s-1) \big ( -7\,\pi -21\, \pi \,s+66\,s+28\,\pi \,{s}^{2} \big ) }{{s}^{2}}} . \end{aligned}$$

(3)

It is easy to see that expression (3) is contained in $\varOmega (1/s^2)$ for $s \in (0,1/3)$. On the other hand, a simple area argument shows that at most $O(1/s^2)$ tori of major radius 1 and minor radius $s$ can be linked with a single such torus, thus implying that the construction is asymptotically optimal. Obviously, the construction is also asymptotically optimal for linking many tori with one single torus.