Holding Circles and Fixing Frames

Abstract

A circle $C$ holds a convex body $K \subset \mathbb {R}^3$ if $K$ can’t be moved far away from its position without intersecting $C$. One of our results says that there is a convex body $K \subset \mathbb {R}^3$ such that the set of radii of all circles holding $K$ has infinitely many components. Another result says that the circle is unique in the sense that every frame different from the circle holds a convex body $K$ (actually a tetrahedron) so that every nontrivial rigid motion of $K$ intersects the frame.

1 Circles Holding Convex Bodies

Can a circle hold a convex body? Yes, it can. Not every convex body, but many, most of them: it is proved in [8] that those convex bodies which cannot be held by a circle form a nowhere dense family.

What does this holding mean, mathematically?

Let $K\subset {\mathbb R^3}$ be a convex body with interior int $K\ne \emptyset$. Consider the space $\mathcal C$ of all circles in ${\mathbb R^3}$ disjoint from int$K$, equipped with the Pompeiu–Hausdorff metric, and ${\mathcal C}(r)$ the set of all circles in $\mathcal C$ of fixed radius $r>0$.

We say that a circle holds $K$ if it belongs to a bounded component of ${\mathcal C}(r)$ for some $r$.

We say that a holding circle $C$ fixes $K$ if the only possible movement of $C$ in $\mathcal C$ is a rotation which keeps $C$ fixed.

The midpoints of the edges of a hamiltonian cycle in the 1-skeleton of a regular tetrahedron are the vertices of a square. The circle circumscribed to that square fixes the tetrahedron, and many circles slightly larger than but close to it hold it. Assuming the tetrahedron $T$ has edge-length 1, it can be held by circles of diameter in the interval $[1/\sqrt{2}, 0.896\ldots [$, a result of Itoh et al. [4]. There are three circles of diameter $1/\sqrt{2}$, each of which fixes $T$. And $T$ can pass through circles of diameter at least $0.896\ldots$ Remark that the (circular) section of the circumscribed cylinder of $T$ (this is the infinite circular cylinder of smallest section surrounding int$T$) has diameter 1.

The set $H(K)$ of all diameters of circles holding $K$ is called the holding range of $K$. Put

$$\begin{aligned} d_h(K) = \inf H(K), \quad d^h(K)=\sup H(K). \end{aligned}$$

Further, let $d_p(K)$ be the lower bound of all diameters of circles through which $K$ can pass, and let $d_c(K)$ denote the diameter of the (normal) section of the circumscribed cylinder.

It seems quite reasonable to think that in general there exist circles of diameter $d_h(K)$ fixing $K$, and

$$\begin{aligned} d^h = d_p < d_c, \end{aligned}$$

as in the case of the regular tetrahedron.

However, in fact the situation is often different. Generally true are only the trivial inequalities directly derived from the definitions.

The number $d_p(K)$ is, for various $K$, rather independent of $d_h(K)$ and $d^h(K)$. It can be smaller than $d_h(K)$, larger than $d^h(K)$, or in between.

While, indeed, for most convex bodies $K, d_p(K)<d_c(K)$ (this was proved by the second author [9]), there are still lots of them for which equality holds.

Fruchard [3] proved that, while $d_h(K)$ can be less than the width $w(K)$ of $K$, we always have $d_h(K)/w(K) > 2/3.$ He also showed [3] that $d^h(K)/d_c(K)$ can be arbitrarily small (which comes close to our Theorem 3).

The set $H(K)$ of all diameters of circles holding $K$, the holding range of $K$, may be disconnected. Maehara [7] showed that the holding range of the regular icosahedron has two components. He also constructed an octahedron whose holding range has three components, and asked whether the number of components can be arbitrarily large [7].

Theorem 1

There are convex bodies $K$ such that $H(K)$ has arbitrarily many components.

The proof will be clear after reading the proof of Theorem 2.

Let $\overline{ab}$ denote the line through $a,b\in {\mathbb R^3}$, let $ab$ denote the line-segment from $a$ to $b$, and let $]ab[$ denote $ab$ deprived of its endpoints. The convex hull, interior, and boundary of $S\subset {\mathbb R^3}$ are denoted by $\mathrm{conv}S, \mathrm{int}S$, and $\partial S$ respectively. If $a_1,\ldots , a_k\in {\mathbb R^3},$ we also write $a_1a_2\ldots a_k$ for the convex hull of the set $\{a_1,\ldots ,a_k\}.$

Theorem 2

There are convex bodies $K$ for which $H(K)$ has infinitely many components.

Proof

Let $\Delta _0, \Delta _1, \Delta _2,\ldots$ be consecutive half-lines in the plane $x\mathbf{0}y$, starting at $\mathbf 0$, such that their angles $\angle \Delta _i\Delta _j$ satisfy

• (1) $\angle \Delta _0\Delta _1= \pi /24,$

• (2) $\angle \Delta _i\Delta _{i+1}=\pi /2^{i+2} \ \ (i=1,2,\ldots )$.

Let $a_1$ be a point on the trisector of the angle $\Delta _1\Delta _2$ closer to $\Delta _1$, and consider the orthogonal projections $b_1, b_2$ of $a_1$ onto $\Delta _1, \Delta _2$, respectively. Let $a_0$ be the intersection of the line $\overline{a_1b_1}$ with $\Delta _0$, and $a_2$ the intersection of $\overline{a_1b_2}$ with the trisector of the angle $\Delta _2\Delta _3$ closer to $\Delta _2$ (see Fig. 1).

Fig. 1

The construction for Theorem 2

The obvious iteration leads to the sequences $\{a_n\}_{n=1}^\infty$ and $\{b_n\}_{n=1}^\infty$, both convergent to the same point $a$ on the half-line $\Delta$, limit of $\{\Delta _n\}_{n=1}^\infty$. $\angle \Delta _0\Delta =(\pi /4)+(\pi /24).$ It follows from the construction that $a_{i+1}<b_i <a_i$.

Finally, let $c$ be the point of coordinates $(0,0,{\varepsilon })$ for a small ${\varepsilon }>0$.

We define our convex body

$$\begin{aligned} K= \mathrm{conv}\{a_0,a_1,a_2,\ldots ,a,c,-c\}. \end{aligned}$$

Each circle on which $\mathbf{0}$ and $b_i$ are diametrally opposite, and whose plane makes an angle of $\pi /4$ with $x\mathbf{0}y$, holds $K\ \ (i=1,2,\ldots ).$ Close to it there are circles of diameters in $[\Vert b_i\Vert , \Vert a_i\Vert [$ holding $K$. Circles with diameter in $[\Vert a_{i+1}\Vert , \Vert b_i\Vert [$ do not hold $K$.

The circles with centres close to $\mathbf 0$ which hold $K$ have diameter close to $2{\varepsilon }$, smaller than $\Vert a\Vert$. Thus, $[\Vert b_i\Vert , \Vert a_i\Vert [$ are connected components of $H(K)$ for all $i\ge 1.$

This proves the theorem. $\square$

Theorem 3

There are convex bodies K with $d^h(K)/d_p(K)$ as small as wished.

Proof

Choose $a, b \ne \mathbf{0}$ in the plane $x\mathbf{0}y$ such that $\pi /2 < \angle \mathbf{0}ab < \pi$, and take $c=(0, 0, {\varepsilon }),$ for small ${\varepsilon }>0$ and set $c'=-c$. Then

$$\begin{aligned} K = \mathrm{conv}\{a, b, c, c'\} \end{aligned}$$

is an appropriate convex body. Indeed, all circles holding $K$ have centres close to $\mathbf 0$, and $d^h(K)=2{\varepsilon }$. On the other hand, $d_p(K)$ equals the minimal value $v$ of the diameter of the circle circumscribed to $axx'$, where $x, x'$ are running on $bc$, respectively $bc'$, and $v$ is larger than the height, $h$, of the triangle $\mathbf{0}ab$ at $a$. Thus, $d^h(K)/d_p(K)<{\varepsilon }/h$ can be made arbitrarily small. $\square$

Theorem 4

• (a) There are convex bodies K with $d_c(K)/d_h(K)$ as small as wished.

• (b) There are convex bodies admitting holding circles, but admitting no fixing circle.

Proof

Let ${\varepsilon }>0$ be small, and $C_i$ be the circles

$$\begin{aligned} y^2 + z^2 = 4{\varepsilon }^2 \end{aligned}$$

in the plane $x=i$. Consider the segment $\sigma$ connecting the points $(3,0,{\varepsilon })$ and $(3,0,-{\varepsilon })$, and the segment $\tau$ connecting $(0,{\varepsilon },0)$ and $0,-{\varepsilon },0)$. The convex body

$$\begin{aligned} K = \mathrm{conv}(\tau \cup \sigma \cup C_1\cup C_2) \end{aligned}$$

obviously has $d_h(K)=3$ and $d_p(K)=d_c(K)=4{\varepsilon }$.

This $K$ has holding circles, but no fixing circles. $\square$

We saw in the preceding example that a convex body $K$ with holding circles may have no fixing circle, but the holding circles of minimal diameter allow only rotations of $K$.

A holding circle $C$ fixes $K$ up to rotations, if the only possible movements of $K$ are rotations fixing the sphere circumscribed to $C$. The natural question arises, whether the existence of holding circles yields the existence of fixing circles up to rotations.

Theorem 5

There are convex bodies admitting holding circles but admitting no fixing circle up to rotations.

Fig. 2

The construction for Theorem 5

Proof

Let $abcda'b'c'd'$ be a box (a parallelepiped with all angles right), with centre $\mathbf{0}$, opposite faces $abcd$ and $a'b'c'd'$, long edges $bc, da, b'c', d'a'$, and very short edges $aa', bb', cc', dd'$ (see Fig. 2). Let $C$ be the circle circumscribed to $abb'a'$. Choose $u$ in the plane $\Pi$ of $C$, outside of $C$ but close to $C$, such that $\Vert u-a\Vert =\Vert u-b\Vert >\Vert u-a'\Vert .$ Set $u^{\prime }=-u$ and consider

$$\begin{aligned} K' = \mathrm{conv}\{a,b,c,d,a',b',c',d',u,u'\} \end{aligned}$$

and the ball $B$ of centre $\mathbf{0}$ and radius $\Vert u\Vert$.

Let $\mathcal H$ be the family of all closed half-spaces containing $K'$ and bounded by the planes of all faces of $K'$ except $abb'ua'$ and $c'd'du'c$. Then

$$\begin{aligned} K = B\cap \bigcap _{H\in {\mathcal H}}H \end{aligned}$$

is a suitable convex body. This can be seen as follows.

Let $Z$ be the bounded cylinder $\partial \mathrm{conv}(C\cup -C)$. Let $a''$ be the intersection of $Z$ with $uc'$.

Obviously, all planes parallel to $\Pi$ and separating $a''$ from $-a''$ meet $Z$ along circles, of diameter $d_h(K) = \mathrm{diam}C$, which hold but do not fix $K$.

The spherical parts of $\partial K$ prohibit the existence of other components of $H(K)$. Thus, no circle fixes $K$. $\square$

2 Frames Fixing Convex Bodies

A frame is a planar closed convex curve. The notions of holding or fixing can be easily generalized from the circle to any frame.

We noticed that a circle cannot fix any convex body $K$ in the sense that $K$ doesn’t move at all; so, we allowed rotation in the definition for the circle. Is only the circle in this situation? No, Maehara, Tokushige and the first author [1] showed that no triangle can hold any convex body, and a fortiori it cannot fix it. A more detailed analysis follows.

A fixed plane $P \subset {\mathbb R^3}$ and a convex compact set $F\subset P$, whose boundary $\partial F$ is our frame, are given. We always assume that $\mathrm{int}F$ is nonempty. A rigid motion is a continuous map $M: {\mathbb R^3}\times [0,1] \rightarrow {\mathbb R^3}$ with $M(\cdot ,0)=I$ (the identity) such that $M_t=M(\cdot ,t)$ is a congruence of ${\mathbb R^3}$ for all $t \in [0,1]$. So a rigid motion $M_t$ is a homotopy (with congruences) between the identity $I$ and $M_1$. Given a convex body $K\subset {\mathbb R^3}$, the rigid motion $M_t$ moves $K$ through $F$ if $(M_tK)\cap P \subset F$ for all $t \in [0,1]$. This definition models the case when $F$ is a hole in the wall $P$ and one wants to move $K$ through the hole, and also, when one wants to see that $K$ is stuck in the hole.

Thus, the frame $\partial F$ holds $K$ if no rigid motion $M_t$ that moves $K$ through $F$ satisfies $M_1K \cap P=\emptyset$. The frame fixes $K$ if every rigid motion moving $K$ through $F$ satisfies $M_tP=P$ for all $t\in [0,1]$. If $F$ fixes $K$ then, of course, it holds $K$ as well. The following result is known.

Theorem 6

[1]. Every frame that is not a triangle fixes some tetrahedron.

In the definition of fixing we did not require that $M_t$ equal the identity because, for instance, even if a circle fixes some convex body $K$, there is a rigid motion $M_t$ (the one that rotates the disk around its centre) with $(M_tK)\cap P \subset F$ for all $t \in [0,1]$ which is not the identity. We are going to show that the circle is, essentially, the only exception. We need one more definition: We say that a convex body $K\subset {\mathbb R^3}$ is fixed without motion by the frame $\partial F$ if every rigid motion $M_t$ of $K$ through $F$ satisfies $M_t=I$ for all $t$.

Theorem 7

If $F$ is neither a triangle nor a circular disk, then some tetrahedron $T \subset {\mathbb R^3}$ is fixed without motion by $F$.

Some preparations are needed before the proof. Let $f:F\times F \rightarrow {\mathbb R}$ be the Euclidean distance function, that is, $f(x,y)=\Vert x-y\Vert$, restricted to $F$.

The proof uses the following two ingredients of the proof of Theorem 6.

Lemma 1

Assume that $f$ has a local maximum at $(a, b)$, that $]ab[ \subset \mathrm{int}F$, and that $c,d \in \partial F$ are on opposite sides of $\overline{ab}$. Then there is a tetrahedron $T$ that is fixed by $\partial F$ and satisfies $T \cap P=abcd$.

Although such a $T$ need not be unique, the proof of the lemma constructs it explicitly. We will denote it by $T=T(a,b;c,d)$.

Lemma 2

Assume $ab$ is a diameter of $F, ab\subset \partial F$, and the function $f_a(x)=f(a,x)$ is non-decreasing as $x$ moves from $a$ to $b$ on $\partial F\setminus ab$. Then $F$ fixes a tetrahedron $T$ without motion.

Proof of Theorem 7

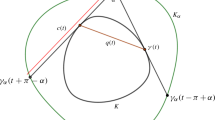
Assume first that $F$ has a diameter $ab$ such that $]ab[\subset \mathrm{int}F$. Let $I_a$ be an arc on $\partial F$ containing $a$ and maximal with respect to the property that for every $x \in I_a$ there is $y \in F$ such that $xy$ is a diameter of $F$. Of course, $I_a$ may consist of a single point (namely $a$) and may coincide with $\partial F$, in which case $F$ is of constant width. The arc $I_b$ is defined analogously.

Case 1 When $I_a=\{a\}$. Choose $c,d \in \partial F\setminus ab$ from opposite sides of $ab$. As $(a,b)$ is a local maximum of $f$, Lemma 1 applies and the tetrahedron $T(a,b;c,d)$ is fixed by $\partial F$. Now let $M_t$ be a continuous rigid motion with $M_0=I$ and $(M_tT)\cap P\subset F$ for all $t \in [0,1]$. Then $M_tP=P$ and $M_ta=a$ for all $t$, as $M_t$ maps a diameter of $F$ to another diameter. Then $M_t$ is a rotation with centre $a$, and it follows easily that $M_t=I$ for all $t$ (see Fig. 3 left).

Case 2 When neither $I_a$ nor $I_b$ is a single point or the whole $\partial F$. Then $I_a$, resp. $I_b$, is an arc from $a_1$ to $a_2$, resp. $b_1, b_2$, on $\partial F$. We choose the notation so that $a_1,a_2,b_1,b_2$ are in this order on $\partial F$. It is easy to see that $a_1b_1$ and $a_2b_2$ are diameters of $F$. Thus, Lemma 1 applies again and gives a tetrahedron $T(a_1,b_1;a_2,b_2)$ which is fixed by $F$. Any rigid motion $M_t$ (as in the definition of fixing) would move the endpoints of $a_1b_1$ or $a_2b_2$ outside $I_a$ or $I_b$. Thus $M_t$ must be identity (see Fig. 3 right).

Fig. 3

Case 1 and 2 of Theorem 7

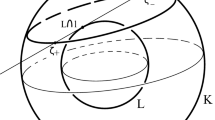
Case 3 When $I_a=I_b=\partial F$, i.e. $F$ is of constant width, then for every $x \in \partial F$ there is $y \in \partial F$ such that $xy$ is a diameter of $F$. Let $B$ be the unique smallest area Euclidean disk containing $F$; assume its centre is $\mathbf{0}$. Set $H=\partial F \cap \partial B$. It is well known that $H$ is nonempty and $\mathbf{0}\in \mathrm{conv}H$. If $H$ contains a pair of antipodal points then $F$ and $B$ coincide. Then $F$ would be a circular disk, which is excluded by the hypothesis of the theorem.

So $H$ contains no antipodal pair of points. Then there are points $a,b,c \in H$ with $\mathbf{0}\in abc$. Let $aa^*, bb^*, cc^*$ be diameters of $F$.

Assume that the diameter $aa^*$ does not separate the points $b$ and $c$, meaning that they are on the same side of the diameter $aa^*$. Let $I(a,b)$ (resp. $I(a,c)$) be the arc on $\partial F$ between $a$ and $b$ not containing $c$ (and between $a$ and $c$ not containing $b$). Thus, $a^*$ lies in $I(a,b)$ or $I(a,c)$. It lies on $I(a,c)$, say. As any two diameters have a common point, $bb^*$ and $aa^*$ intersect, implying that $b^* \in I(a,c)$. Hence, $a$ and $c$ are separated by $bb^*$.

We showed that either $aa^*$ separates $b$ and $c$ or $bb^*$ separates $a$ and $c$. For simpler writing, we assume that $bb^*$ separates $a$ and $c$. Now Lemma 1 applies since $(b,b^*)$ is a local maximum of $f$ and $a,c$ are on opposite sides of $bb^*$. Thus, the tetrahedron $T(b,b^*;a,c)$ is fixed by $F$.

Assume there is a continuous rigid motion $M_t$, as in the definition. Then $M_t(abc)\subset F \subset B$. The triangles $abc$ and $M_t(abc)$ are congruent, so $B$ is the minimal area disk containing $M_t(abc)$. Then $M_tB=B$ and consequently $M_t$ is a rotation with centre $\mathbf{0}$.

Let $J_a,J_b,J_c \subset H$ be maximal arcs containing $a,b,c$, respectively. If any of these arcs is a single point, then $M_t=I$. So assume none of them is a single point, and write $a_1,a_2$ resp. $b_1,b_2$ and $c_1,c_2$ for the endpoints of $J_a,J_b,J_c$, so that the points $a_1,a_2,b_1,b_2,c_1,c_2$ come in this order on $\partial F$, see Fig. 4. Lemma 1 gives the tetrahedron $T(b,b^*;a_2,c_1)$. Now let $N_t$ be the rigid motion with $N_0=I$ and $(N_tT)\cap P\subset F$. As we have seen before, $N_t$ is a rotation with center $\mathbf{0}$. But if $N_t\ne I$ then either $N_ta_2$ moves outside $J_a$ or $N_tc_1$ moves outside $J_c$, which is impossible. This finishes Case 3 and, further, all cases when a diameter of $F$ does not lie on its boundary.

Now let $ab\subset \partial F$ be a diameter of $F$. If $f_a(x)$ is non-decreasing (in the sense of Lemma 2), then this lemma guarantees the existence of a tetrahedron $T$ that is fixed by $F$ without motion. Assume now that $f_a(\cdot )$ has a local maximum at $c \in \partial F\setminus ab$.

Case 4 When $]ac[ \subset \partial F$. Then, as it is easy to check, $(c,b)$ is a local maximum of $f$. Note that $]cb[ \subset \mathrm{int}F$, as otherwise $F$ is a triangle. Choose a point $d$ from the arc connecting $c,b$ and not containing $a$. Lemma 1 applies and gives a tetrahedron $T(b,c;a,d)$ fixed by $\partial F$. It is clear that this fixing is without motion: the triangle $abc$ has only one congruent copy contained in $F$, namely $abc$.

Case 5 When $]ac[ \subset \mathrm{int}F$. Choose $d$ from the arc connecting $a,c$ on $\partial F$ which is not containing $b$. Lemma 1 applies again: $(a,c)$ is a local maximum of $f$ and $b,d$ are on opposite sides of $ac$. The tetrahedron $T=T(a,c;b,d)$ is fixed by $\partial F$. If this fixing goes with a rigid motion $M_t$ then $M_t(ab)$ is a diameter of $F$. As any two diameters of $F$ intersect, and the diameter $ab$ lies on the boundary of $F$, $M_ta=a$ or $M_tb=b$ holds for every $t \in [0,1]$, and $M_t$ is a rotation with centre $a$ or $b$. It follows again that $M_t=I$. $\square$

Fig. 4

Case 3 of Theorem 7

A frame $\partial F$ fixes tightly a convex body $K$, if it fixes it and lies on its boundary. Note that this does not imply that the frame fixes $K$ without motion: let $K$ be the convex hull of the union of the regular tetrahedron $abcd$ with the smallest disk $D$ circumscribed to the square with vertices $(a+b)/2,(a+c)/2,(d+b)/2,(d+c)/2$. The frame $\partial D$ fixes $K$ (it even fixes the regular tetrahedron) but not without motion. The following theorem gives a positive answer to Problem 2 from [1].

Theorem 8

Every tetrahedron is tightly fixed by some frame.

Proof

Let $a,b,c,d$ be the vertices of $T$, and $ab$ be the longest edge of $T$ (or one of the longest ones). We distinguish two cases.

Case 1 The angle between the faces $abc$ and $abd$ of $T$ is at least $\pi /2$.

Case 2 The angle between the faces $abc$ and $abd$ of $T$ is less than $\pi /2$.

Case 1 is simpler. The shortest distance between the lines $\overline{ab}$ and $\overline{cd}$ is reached on a line-segment $xy$ with $x \in ab$ and $y \in cd$, as one can easily check (this is the point where we need the large angle). Consider the circular cylinder with radius $\rho$ whose axis is the line $\overline{xy}$. For small $\rho >0$ this cylinder is disjoint from the broken path through $a,c,b,d,a$. So there is a smallest $\rho >0$ when they have a common point, say $u$. So $u$ is (one of) the point(s) on the broken path which is closest to the segment $xy$ (ties broken arbitrarily). It is clear that $u$ does not coincide with either of the points $a,b,c,d$. We can assume without loss of generality that $u\in ac$. Let $P$ be the plane spanned by $x,y,u$. $P$ intersects $T$ in a quadrilateral $Q=T \cap P$ with vertices $x,y,u,v$ where $v\in bd$. We claim that, as a frame, $\partial Q$ fixes $T$.

Fact. $(x,y)$ is a strict local maximum of the distance function $f: Q\times Q \rightarrow {\mathbb R}$. (This is trivial.)

Assume that $M_t$ is a rigid motion of ${\mathbb R^3}$ with $P \cap M_tT \subset Q$ for all $t \in [0,t_0]$ where $t_0>0$. The Fact implies that $M_t(xy)=xy$. Consequently, $M_t$ is a rotation around the line $\overline{xy}$. It follows that $M_t(xyu)$ is not contained in $xyu$ unless $M_t$ is the identity, as $M_tu \in ac$, and every point of $ac$, including $M_tu$, is farther from $xy$ than $u$. It follows that $M_tQ$ cannot be contained in $Q$ unless $M_t$ is the identity (see Fig. 5 left).

In Case 2 choose a plane $P$ parallel with $ab$, perpendicular to $abc$, and close to $ab$. (How close will be clear later.) Let $P$ intersect the edges $ac,ad,bd,bc$ respectively in points $x,y,z,v$. (The existence of $y,z$ follows from the assumption that the angle is smaller than $\pi /2$.) We show that the frame $\partial Q$, with $Q=xyzv$, fixes $T$ (see Fig. 5 right). Note that $Q$ is a trapezoid contained in the triangle ${\Delta }^*$ with vertices $a^*b^*d^*$ (where $a^*,b^*,d^*$ are the projections of $a,b,d$ onto $P$), and that the angles of $Q$ at $z$ and $y$ are obtuse.

Fig. 5

Case 1 and 2 of Theorem 8

Suppose again that a rigid motion $M_t$ of ${\mathbb R^3}$ moves $T$, with $P\cap M_tT \subset Q$ for all $t \in [0,t_0]$.

Set $Q_t=x_ty_tz_tv_t=M_t^{-1}P \cap T$. Thus, $Q_t$ fits into $Q$. Let $Q^t=x^ty^tz^tv^t$ be the orthogonal projection of $Q_t$ onto the plane $P$. By Kovalyov’s result in [6], (see also Kós and Törőcsik [5] or Debrunner and Mani-Levitska [2]), $Q^t$ also fits into $Q$. Then $Q^t$ fits into the triangle ${\Delta }^*$, since $Q \subset a^*b^*d^*$.

Note that, given ${\varepsilon }>0$, we can choose the plane $P$ so close to $ab$ that $|x-a|,|v-a|,|y-b|,|z-b|<{\varepsilon }$, which implies that $|x-a^*|,|v-a^*|,|y-b^*|,|z-b^*|<{\varepsilon }$. Further, given any ${\delta }>0$, for all small enough $t>0$ the angles of $Q_t$ at $z_t$ and $v_t$ are obtuse, and $|x-x_t|,|y-y_t|,|z-z_t|,|v-v_t|<{\delta }$.

Fact. If ${\varepsilon },{\delta }>0$ are small enough, then $Q^t$ fits into $a^*b^*d^*$ in a unique way, that is, there is a unique congruent copy of $Q^t$ contained in $a^*b^*d^*$, namely $Q^t$.

The proof is a direct 2-dimesional argument in the plane $P$. As $x_t,y_t,z_t,v_t$ resp. are on edges $ac,bd,bc,ad$ of $T$, their projections $x^t,y^t,z^t,v^t$ resp. are on edges $a^*d^*,b^*d^*,b^*c^*,a^*d^*$ of ${\Delta }^*$.

Take a congruent copy of $Q^t$ contained in $a^*b^*d^*, Q^1$ say, with vertices $x^1,y^1,z^1,v^1$. Apply a parallel translation to $Q^1$ towards $a^*b^*$ by a translation orthogonal to $a^*b^*$ as long as the translated copy of $Q^1$ lies in ${\Delta }^*$. Let $Q^2$ be the final position of $Q^1$ in this translation, with vertices $x^2,y^2,z^2,v^2$. Then either $x^2 \in a^*b^*$ or $v^2 \in a^*b^*$ because $a^*b^*$ is the longest edge of ${\Delta }^*$ and $Q^t$ is very close to $[a^*,b^*]$ when ${\varepsilon }$ and $t$ are small enough.

By symmetry we can assume $x^2 \in a^*b^*$. Now rotate $Q^2$ around its vertex $x^2$ so that $v^2$ moves towards $a^*b^*$ as long as the rotated copy of $Q^2$ is contained in ${\Delta }^*$. So we stop when $v^2$ reaches $a^*b^*$ or $z^2$ reaches $b^*d^*$ or when $y^2$ reaches $d^*a^*$, whichever happens first. As the angles of $Q^2$ at vertices $z^2$ and $y^2$ are obtuse, the points $z^2$ resp. $y^2$ move away from the edges $b^*d^*$ and $d^*a^*$ during the rotation. So we stop when $v^2$ reaches $a^*b^*$. Let $Q^3$ be the final position of $Q^2$ during this rotation, its vertices are $x^3,y^3,z^3,y^3$.

It follows that $Q^3 \subset {\Delta }^*$ and $x^3,v^3 \in a^*b^*$. Also, $Q^t \subset {\Delta }^*$ and $x^t,v^t \in a^*b^*$ (for small enough $t$). But $Q^3$ is congruent to $Q^t$, and their vertices are on the same edges of ${\Delta }^*$. So they coincide. Then there was no rotation, and there was no translation, so $Q^1=Q^2=Q^3=Q^t$.$\square$

The Fact shows that $Q^t$ fits into $Q$ in a unique way as well. Then $z^t=z$ because $z^t$ resp. $z$ is the unique common point of $Q^t$ and $Q$ with $[b^*d^*]$. Then $z_t=z^t=z$. Similarly $y_t=y^t=y$, implying that $M_t$ is a rotation around the axis $\overline{zy}$.

Finally, $P$ is perpendicular to $abc$, so the width of $T\cap M_t^{-1}P$ is larger than that of $xyuv$, unless $M_t$ is the identity.