Sample-Based Distance-Approximation for Subsequence-Freeness

Abstract

In this work, we study the problem of approximating the distance to subsequence-freeness in the sample-based distribution-free model. For a given subsequence (word) $w = w_1 \ldots w_k$, a sequence (text) $T = t_1 \ldots t_n$ is said to contain w if there exist indices $1 \le i_1< \cdots < i_k \le n$ such that $t_{i_{j}} = w_j$ for every $1 \le j \le k$. Otherwise, T is w-free. Ron and Rosin (ACM Trans Comput Theory 14(4):1–31, 2022) showed that the number of samples both necessary and sufficient for one-sided error testing of subsequence-freeness in the sample-based distribution-free model is $\Theta (k/\epsilon )$. Denoting by $\Delta (T,w,p)$ the distance of T to w-freeness under a distribution $p:[n]\rightarrow [0,1]$, we are interested in obtaining an estimate $\widehat{\Delta }$, such that $|\widehat{\Delta }- \Delta (T,w,p)| \le \delta$ with probability at least 2/3, for a given error parameter $\delta$. Our main result is a sample-based distribution-free algorithm whose sample complexity is $\tilde{O}(k^2/\delta ^2)$. We first present an algorithm that works when the underlying distribution p is uniform, and then show how it can be modified to work for any (unknown) distribution p. We also show that a quadratic dependence on $1/\delta$ is necessary.

1 Introduction

Distance approximation algorithms, as defined in [31], are sublinear algorithms that approximate (with constant success probability) the distance of objects from satisfying a prespecified property $\mathcal {P}$. Distance approximation (and the closely related notion of tolerant testing) is a natural extension of property testing [21, 34], where the goal is to distinguish between objects that satisfy a property $\mathcal {P}$ and those that are far from satisfying the property.¹ Indeed, while in some cases a (standard) property testing algorithm suffices, in others, actually approximating the distance to the property in question is more desirable.

In this work, we consider the property of subsequence-freeness. For a given subsequence (word) $w_1 \dots w_k$ over some alphabet $\Sigma$, a sequence (text) $T = t_1 \dots t_n$ over $\Sigma$ is said to be w-free if there do not exist indices $1 \le j_1< \dots < j_k \le n$ such that $t_{j_i} = w_i$ for every $i \in [k]$.²

In most previous works on property testing and distance approximation, the algorithm is allowed query access to the object, and distance to satisfying the property in question, $\mathcal {P}$, is defined as the minimum Hamming distance to an object that satisfies $\mathcal {P}$, normalized by the size of the object. However, there are applications in which we need to deal with the more challenging setting in which only sampling access to the object is available, and furthermore, the samples are not necessarily uniformly distributed, so that the distance measure should be defined with respect to the underlying distribution.

In this work, we consider the sample-based model in which the algorithm is only given a random sample from the object. In particular, when the object is a sequence $T = t_1 \dots t_n$, each element in the sample is a pair $(j,t_j)$. We study both the case in which the underlying distribution according to which each index j is selected (independently) is the uniform distribution over [n], and the more general case in which the underlying distribution is some arbitrary unknown $p:[n] \rightarrow [0,1]$. We refer to the former as the uniform sample-based model, and to the latter as the distribution-free sample-based model. The distance (to satisfying the property) is determined by the underlying distribution. Namely, it is the minimum total weight according to p of indices j such that $t_j$ must be modified so as to make the sequence w-free. Hence, in the uniform sample-based model, the distance measure is simply the Hamming distance normalized by n.

The related problem of testing the property of subsequence-freeness in the distribution-free sample-based model was studied by Ron and Rosin [33]. They showed that the sample-complexity of one-sided error testing of subsequence-freeness in this model is $\Theta (k/\epsilon )$ (where $\epsilon$ is the given distance parameter). A natural question is whether we can design a sublinear algorithm, with small sample complexity, that actually approximates the distance of a text T to w-freeness. It is worth noting that, in general, tolerant testing (and hence distance-approximation) for a property may be much harder than testing the property (see e.g., [3, 13, 19, 22, 32]). We also empahsize that we consider a general alphabet $\Sigma$, rather than the special case of a binary alphabet $\Sigma = \{0,1\}$. Hence, we cannot simply reduce the problem of (tolerant) testing of subsequence-freeness to (agnostic) learning of the corresponding function class (when viewing T as a function from [n] to $\Sigma$), as can be done when $\Sigma = \{0,1\}$.

1.1 Our Results

For a text T of length n and a distribution p over [n], represented as a vector $p = (p_1,\dots ,p_n)$, we say that a sample is selected from T according to p, if for each sample point $(j,t_j)$, j is selected independently from [n] according to p. When p is the uniform distribution, then we say that the sample is selected uniformly from T. For a word w, we use $\Delta (T,w,p)$ to denote the distance of T from w-freeness under the distribution p. That is, $\Delta (T,w)$ is the minimum, taken over all texts $T' = t'_1,\dots ,t'_n$ that are w-free, of $\sum _{j: t_j \ne t'_j} p_j$. When p is the uniform distribution, then we use the shorthand $\Delta (T,w)$. Let $\delta \in (0,1)$ denote the error parameter given to the algorithm. Our main theorem is stated next.

Theorem 1.1

There exists a sample-based distribution-free distance-approximation algorithm for subsequence-freeness, that, for any subsequence w of length k, takes a sample of size $O\left( \frac{k^2}{\delta ^2}\cdot \log \left( \frac{k}{\delta }\right) \right)$ from T, distributed according to an unknown distribution p, and outputs an estimate $\widehat{\Delta }$ such that $|\widehat{\Delta }- \Delta (T,w,p)| \le \delta$ with probability at least $\frac{2}{3}$.³ The running time of the algorithm is $O\left( \frac{k^2}{\delta ^2}\cdot \log ^2\left( \frac{k}{\delta }\right) \right)$.

As we discuss in detail in Sect. 1.2, we prove Theorem 1.1 by first presenting an algorithm for the case in which p is the uniform distribution, and then show how to build on this algorithm so as to obtain the more general result stated in Theorem 1.1.

We also address the question of how tight is our upper bound. We show (using a fairly simple argument) that the quadratic dependence on $1/\delta$ is indeed necessary, even when p is the uniform distribution. To be precise, denoting by $k_d$ the number of distinct symbols in w, we give a lower bound of $\Omega (1/(k_d\delta ^2))$ under the uniform distribution (that holds for every w with $k_d$ distinct symbols, sufficiently large n and sufficiently small $\delta$—for a precise statement, see Theorem 4.1).

1.2 A High-Level Discussion of Our Algorithms

Our starting point is a structural characterization of the distance to w-freeness under the uniform distribution, which is proved in [33, Sec. 3.1].⁴ In order to state their characterization, we introduce the notion of copies of w in T, and more specifically, role-disjoint copies.

Definition 1.1

A copy of $w = w_1\dots w_k$ in $T = t_1\dots t_n$ is a sequence of indices $(j_1,\dots ,j_k)$ such that $1\le j_1< \dots < j_k \le n$ and $t_{j_1}\dots t_{j_k} = w$. A copy is represented as an array C of size k where $C[i] = j_i$.

We say that two copies C and $C'$ of w in T are role-disjoint if $C[i] \ne C'[i]$ for every $i \in [k]$ (though it is possible that $C[i] = C'[i']$ for $i \ne i'$). A set of copies is role-disjoint if every pair of copies in the set are role-disjoint.

Observe that in the special case where the symbols of w are all different from each other, a set of copies is role-disjoint simply if it consists of disjoint copies. Ron and Rosin prove [33, Theorem 3.4 $+$ Claim 3.1] that $\Delta (T,w)$ equals the maximum number of role-disjoint copies of w in T, divided by n.

Note that the analysis of the sample complexity of one-sided error sample-based testing of subsequence-freeness translates to bounding the size of the sample that is sufficient and necessary for ensuring that the sample contains evidence that T is not w-free when $\Delta (T,w)>\epsilon$. Here evidence is in the form of a copy of w in the sample, so that the testing algorithm simply checks whether such a copy exists. On the other hand, the question of distance-approximation has a more algorithmic flavor, as it is not determined by the problem what must be done by the algorithm given a sample.

Focusing first on the uniform case, Ron and Rosin used their characterization (more precisely, the direction by which if $\Delta (T,w) > \epsilon$, then T contains more than $\epsilon n$ role-disjoint copies of w), to prove that a sample of size $\Theta (k/\epsilon )$ contains at least one copy of w with probability at least 2/3. In this work, we go further by designing an algorithm that actually approximates the number of role-disjoint copies of w in T (and hence approximates $\Delta (T,w)$), given a uniformly selected sample from T. It is worth noting that the probability of obtaining a copy in the sample might be quite different for texts that have exactly the same number of role-disjoint copies of w (and hence the same distance to being w-free).⁵

In the next subsection we discuss the aforementioned algorithm (for the uniform case), and in the following one address the distribution-free case. As can be seen from this discussion, while we rely on structural results presented in [33], the main focus and contribution of our work is in designing and analyzing new sublinear sample-based approximation algorithms that exploit these results.

1.2.1 The Uniform Case

Let $R(T,w)$ denote the number of role-disjoint copies of w in T. In a nutshell, the algorithm works by computing estimates of the numbers of occurrences of symbols of w in a relatively small number of prefixes of T, and using them to derive an estimate of $R(T,w)$. The more precise description of the algorithm and its analysis are based on several combinatorial claims that we present and which we discuss shortly next.

Let $R_i^j(T,w)$ denote the number of role-disjoint copies of the length-i prefix of w, $w_1\dots w_i$, in the length-j prefix of T, $t_1\dots t_j$, and let $N_i^j(T,w)$ denote the number of occurrences of the symbol $w_i$ in $t_1\dots t_j$. In our first combinatorial claim, we show that for every $i\in [k]$ and $j\in [n]$, the value of $R_i^j(T,w)$ can be expressed in terms of the values of $N_i^{j'}(T,w)$ for $j' \in [j]$ (in particular, $N_i^j(T,w)$) and the values of $R_{i-1}^{j'-1}(T,w)$ for $j' \in [j]$. In other words, we establish a recursive expression which implies that if we know what are $R_{i-1}^{j'-1}(T,w)$ and $N_i^{j'}(T,w)$ for every $j' \in [j]$, then we can compute $R_i^j(T,w)$ (and as an end result, compute $R(T,w) = R_k^n(T,w)$).

In our second combinatorial claim we show that if we only want an approximation of $R(T,w)$, then it suffices to define (also in a recursive manner) a measure that depends on the values of $N_i^{j}(T,w)$ for every $i\in [k]$ but only for a relatively small number of choices of j, which are evenly spaced. To be precise, each such j belongs to the set $J = \left\{ r\cdot \gamma n\right\} _{r=1}^{1/\gamma }$ for $\gamma = \Theta (\delta /k)$. We prove that since each interval of integers⁶$[(r-1)\gamma n+1,r\gamma n]$ is of size $\gamma n$ for this choice of $\gamma$, we can ensure that the aforementioned measure (which uses only $j\in J$) approximates $R(T,w)$ to within $O(\delta n)$.

We then prove that if we replace each $N_i^{j}(T,w)$ for these choices of j (and for every $i\in [k]$) by a sufficiently good estimate, then we incur a bounded error in the approximation of $R(T,w)$. Finally, such estimates are obtained using (uniform) sampling, with a sample of size $\tilde{O}(k^2/\delta ^2)$.

1.2.2 The Distribution-Free Case

In [33, Sec. 4] it is shown that, given a word w, a text T and a distribution p, it is possible to define a word $\widetilde{w}$ and a text $\widetilde{T}$ for which the following holds. First, $\Delta (T,w,p)$ is closely related to $\Delta (\widetilde{T},\widetilde{w})$. Second, the probability of observing a copy of w in a sample selected from T according to p is closely related to the probability of observing a copy of $\widetilde{w}$ in a sample selected uniformly from $\widetilde{T}$.

We use the first relation stated above (i.e., between $\Delta (T,w,p)$ and $\Delta (\widetilde{T},\widetilde{w})$). However, since we are interested in distance-approximation rather than one-sided error testing, the second relation stated above (between the probability of observing a copy of w in T and that of observing a copy of $\widetilde{w}$ in $\widetilde{T}$) is not sufficient for our needs, and we need to take a different (once again, more algorithmic) path, as we explain shortly next.

Ideally, we would have liked to sample uniformly from $\widetilde{T}$, and then run the algorithm discussed in the previous subsection using this sample (and $\widetilde{w}$). However, we only have sampling access to T according to the underlying distribution p, and we do not have direct sampling access to uniform samples from $\widetilde{T}$. Furthermore, since $\widetilde{T}$ is defined based on (the unknown) p, it is not clear how to determine the aforementioned subset of (evenly spaced) indices J.

For the sake of clarity, we continue the current exposition while making two assumptions. The first is that the distribution p is such that there exists a value $\beta$, such that $p_j/\beta$ is an integer for every $j\in [n]$ (the value of $\beta$ need not be known). The second is that in w there are no two consecutive symbols that are the same. Under these assumptions, $\widetilde{T}= t_1^{p_1/\beta } \dots t_n^{p_n/\beta }$, $\widetilde{w}= w$, and $\Delta (\widetilde{T},\widetilde{w}) = \Delta (T,w,p)$ (where $t_j^x$ for an integer x is the subsequence that consists of x repetitions of $t_j$).

Our algorithm for the distribution-free case (working under the aforementioned assumptions), starts by taking a sample distributed according to p and using it to select a (relatively small) subset of indices in [n]. Denoting these indices by $b_0,b_1,\dots ,b_\ell$, where $b_0=0< b_1< \dots< b_{\ell -1} < b_\ell =n$, we would have liked to ensure that the weight according to p of each interval $[b_{u-1}+1,b_u]$ is approximately the same (as is the case when considering the intervals defined by the subset J in the uniform case). To be precise, we would have liked each interval to have relatively small weight, while the total number of intervals is not too large. However, since it is possible that for some single index $j\in [n]$, the probability $p_j$ is large, we also allow intervals with large weight, where these intervals consist of a single index (and there are few of them).

The algorithm next takes an additional sample, to approximate, for each $i\in [k]$ and $u\in [\ell ]$, the weight, according to p, of the occurrences of the symbol $w_i$ in the length-$b_u$ prefix of T. Observe that prefixes of T correspond to prefixes of $\widetilde{T}$. Furthermore, the weight according to p of occurrences of symbols in such prefixes, translates to numbers of occurrences of symbols in the corresponding prefixes in $\widetilde{T}$, normalized by the length of $\widetilde{T}$. The algorithm then uses these approximations to obtain an estimate of $\Delta (\widetilde{T},\widetilde{w})$.

We note that some pairs of consecutive prefixes in $\widetilde{T}$ might be far apart, as opposed to what we had in the algorithm for the uniform case described in Sect. 1.2.1. However, this is always due to single-index intervals in T (for j such that $p_j$ is large). Each such interval corresponds to a consecutive subsequence in $\widetilde{T}$ with repetitions of the same symbol, and we show that no additional error is incurred because of such intervals.

1.3 Related Results

As we have previously mentioned, the work most closely related to ours is that of Ron and Rosin on distribution-free sample-based testing of subsequence-freeness [33]. For other related results on property testing (e.g., testing other properties of sequences, sample-based testing of other types of properties and distribution-free testing (possibly with queries)), see the introduction of [33], and in particular Sect. 1.4.⁷ For another line of work, on sublinear approximation of the longest increasing subsequence, see [29] and references within. Here we shortly discuss related results on distance approximation / tolerant testing.

As already noted, distance approximation and tolerant testing were first formally defined in [31], and were shown to be significantly harder for some properties in [3, 13, 19, 22, 32]. Almost all previous results are query-based, and where the distance measure is with respect to the uniform distribution. These include [1, 7, 11, 17, 18, 20, 23, 25, 27, 28, 30]. Kopparty and Saraf [26] present results for query-based tolerant testing of linearity under several families of distributions. Berman, Raskhodnikova and Yaroslavtsev [5] give tolerant (query based) $L_p$-testing algorithms for monotonicity. Berman, Murzbulatov and Raskhodnikova [4] give a sample-based distance-approximation algorithms for image properties that work under the uniform distribution.

Canonne et al. [12] study the property of k-monotonicity of Boolean functions over various posets. A Boolean function over a finite poset domain D is k-monotone if it alternates between the values 0 and 1 at most k times on any ascending chain in D. For the special case of $D = [n]$, the property of k-monotonicity is equivalent to being free of w of length $k+2$ where $w_1 \in \{0,1\}$ and $w_i = 1 - w_{i-1}$ for every $i \in [2,k+2]$. One of the results in [12] implies an upper bound of $\widetilde{O}\left( \frac{k}{\delta ^3}\right)$ on the sample complexity of distance-approximation for k-monotonicity of functions $f:[n] \rightarrow \{0,1\}$ under the uniform distribution (and hence for w-freeness when w is a binary subsequence of a specific form). This result generalizes to k-monotonicity in higher dimensions (at an exponential cost in the dimension d).

Blum and Hu [9] study distance-approximation for k-interval (Boolean) functions over the line in the distribution-free active setting. In this setting, an algorithm gets an unlabeled sample from the domain of the function, and asks queries on a subset of sample points. Focusing on the sample complexity, they show that for any underlying distribution p on the line, a sample of size $\widetilde{O}\left( \frac{k}{\delta ^2}\right)$ is sufficient for approximating the distance to being a k-interval function up to an additive error of $\delta$. This implies a sample-based distribution-free distance-approximation algorithm with the same sample complexity for the special case of being free of the same pair of w’s described in the previous paragraph, replacing $k+2$ by $k+1$.

Blais, Ferreira Pinto Jr. and Harms [8] introduce a variant of the VC-dimension and use it to prove lower and upper bounds on the sample complexity of distribution-free testing for a variety of properties. In particular, one of their results implies that the linear dependence on k in the result of [9] is essentially optimal.

Finally, we mention that our procedure in the distribution-free case for constructing “almost-equal-weight” intervals by sampling is somewhat reminiscent of techniques used in other contexts of testing when dealing with non-uniform distributions [6, 10, 24].

1.4 Further Research

The main open problem left by this work is closing the gap between the upper and lower bounds that we give, and in particular understanding the precise dependence on k, or possibly other parameters determined by w (such as $k_d$). One step in this direction can be found in the Master Thesis of the first author [14].

1.5 Organization

In Sect. 2, we present our algorithm for distance-approximation under the uniform distribution. The algorithm for the distribution-free case appears in Sect. 3. In Sect. 4 we prove our lower bound. In the appendix we provide Chernoff bounds and a few proofs of technical claims.

2 Distance Approximation Under the Uniform Distribution

In this section, we establish Theorem 1.1 for the case in which p is the uniform distribution over [n]. Namely, we design and analyze a sample-based distance approximation algorithm for the case in which the underlying distribution is uniform, whose sample complexity is $O\left( \frac{k^2}{\delta ^2}\cdot \log \left( \frac{k}{\delta }\right) \right)$. As mentioned in the introduction, Ron and Rosin showed [33, Thm. 3.4] that $\Delta (T,w)$ (the distance of T from w-freeness under the uniform distribution), equals the number of role-disjoint copies of w in T, divided by $n = |T|$ (where role-disjoint copies are as defined in the introduction—see Definition 1.1 in Sect. 1.2).

We start with some central notations (some already appeared in the introduction).

Definition 2.1

For $T = t_1,\dots ,t_n$, we let $T[j] = t_j$ for every $j\in [n]$. For every $i\in [k]$ and $j\in [n]$, let $N_i^{j}(T,w)$ denote the number of occurrences of the symbol $w_i$ in the length j prefix of T, $T[1,j]=T[1]\dots T[j]$.⁸ Let $R_{i}^{j}(T,w)$ denote the number of role-disjoint copies of the subsequence $w_1\dots w_i$ in T[1, j].

Observe that $R(T,w)$ (the total number of role-disjoint copies of w in T) equals $R_k^n(T,w)$, and that $R_{1}^{j}(T,w)$ equals $N_{1}^{j}(T,w)$ for every $j\in [n]$. Also note that $R_i^j(T,w)\le R_{i-1}^j(T,w)$ for every $i\in [k]$ such that $i>1$ and every $j\in [n]$. The reason is that for each set of role-disjoint copies of the subsequence $w_1\dots w_i$ in T[1, j], the prefixes of length $i-1$ of these copies are role disjoint copies of $w_1\dots w_{i-1}$ in T[1, j].

Since, as noted above, $\Delta (T,w) = R(T,w)/n$, we would like to estimate $R(T,w)$. More precisely, given $\delta >0$ we would like to obtain an estimate $\widehat{R}$, such that: $\left| \widehat{R} - R(T,w) \right| \le \delta n$. To this end, we first establish two combinatorial claims. The first claim shows that the value of each $R_i^j(T,w)$ can be expressed in terms of the values of $N_i^{j'}(T,w)$ for $j' \in [j]$ (in particular, $N_i^j(T,w)$) and the values of $R_{i-1}^{j'-1}(T,w)$ for $j' \in [j]$. In other words, if we know what are $R_{i-1}^{j'-1}(T,w)$ and $N_i^{j'}(T,w)$ for every $j' \in [j]$, then we can compute $R_i^j(T,w)$.

Claim 2.1

For every $i \in \{2,\dots ,k\}$ and $j\in [n]$,

$$\begin{aligned} R_{i}^{j}(T,w) = N_i^{j}(T,w) - \max _{ j' \in [j]}\left\{ N_i^{j'}(T,w) - R_{i-1}^{j'-1}(T,w) \right\} \;. \end{aligned}$$

(2.1)

Clearly, $R_{i}^{j}(T,w) \le N_i^{j}(T,w)$ (for every $i \in \{2,\dots ,k\}$ and $j\in [n]$), since each role-disjoint copy of $w_1\dots w_i$ in T[1, j] must end with a distinct occurrence of $w_i$ in T[1, j]. Claim 2.1 states by exactly how much is $R_{i}^{j}(T,w)$ smaller than $N_i^{j}(T,w)$. The expression $\max _{ j' \in [j]}\left\{ N_i^{j'}(T,w) - R_{i-1}^{j'-1}(T,w) \right\}$ accounts for the number of occurrences of $w_i$ in T[1, j] that cannot be used in role-disjoint copies of $w_1\dots w_i$ in T[1, j].

Proof

For simplicity (in terms of notation), we prove the claim for the case that $i=k$ and $j=n$. The proof for general $i\in \{2,\dots ,k\}$ and $j\in [n]$ is essentially the same up to renaming of indices. Since T and w are fixed throughout the proof, we use the shorthand $N_i^j$ for $N_i^j(T,w)$ and $R_i^j$ for $R_i^j(T,w)$.

For the sake of the analysis, we start by describing a simple greedy procedure, that constructs a set of role-disjoint copies of w in T. It follows from [33, Claim 3.5] and a simple inductive argument, that the size of this set, denoted R, is maximum. That is, $R= R_{k}^{n}$ (for details see Appendix B).

Every copy $C_m$, for $m\in [R]$ is an array of size k whose values are monotonically increasing, where for every $i\in [k]$ we have that $C_m[i] \in [n]$, and $T[C_m[i]] = w_{i}$. Furthermore, for every $i\in [k]$ the indices $C_1[i],\dots ,C_{R}[i]$ are distinct. For every $m = 1,\dots ,R$ and $i = 1,\dots ,k$, the procedure scans T, starting from $T[C_m[i-1]+1]$ (where we define $C_m[0]$ to be 0) and ending at T[n] until it finds the first index j such that $T[j]=w_{i}$ and $j \notin \{C_1[i],\dots ,C_{m-1}[i]\}$. It then sets $C_m[i]=j$. For $i>1$ we say in such a case that the procedure matches j to the partial copy $C_m[1],\dots ,C_m[i-1]$.

For each $i \in [k]$, let $G_i$ denote the subset of indices in [n] that correspond to occurrences of $w_i$ in T. That is, $G_i = \{j\in [n] \,:\, T[j]=w_i\}$. We also define two (complementary) subsets of $G_i$. The first, $G_i^+$, consists of those indices $j \in G_i$ for which there exists a “greedy copy” (i.e., a copy of w found by the greedy algorithm), whose i-th symbol occurs in index j of T. The second, $G_i^-$, consists of those indices in $G_i$ for which there is no such greedy copy. That is, $G_i^+ = \{j \in G_i \,:\,\exists m, C_m[i] = j\}$ and $G_i^- = \{j \in G_i \,:\,\not \exists m, C_m[i]=j\}$ (recall that $C_m[i]$ denotes the i-th index in the m-th greedy copy).

Observe that $\left| G_i\right| = N_{i}^{n}$, $\left| G_i^+\right| = R_{i}^{n}$ and $\left| G_i\right| = \left| G_i^+\right| + \left| G_i^-\right|$. To complete the proof, we will show that $\left| G_i^-\right| = \max _{j\in [n]}\left\{ N_i^{j} - R_{i-1}^{j-1} \right\}$.

Let $j^*$ be an index j that maximizes $\left\{ N_i^{j} - R_{i-1}^{j-1} \right\}$. In the interval $[j^*]$ we have $N_i^{j^*}$ occurrences of $w_i$, and in the interval $[j^{*}-1]$ we only have $R_{i-1}^{j^*-1}$ role-disjoint copies of $w_1\dots w_{i-1}$. This implies that in the interval $[j^{*}]$ there are at least $N_i^{j^*} - R_{i-1}^{j^*-1}$ occurrences of $w_i$ that cannot be the i-th index of any greedy copy, and so we have

$$\begin{aligned} \left| G_i^-\right| \ge N_i^{j^*} - R_{i-1}^{j^*-1} = \max _{j\in [n]}\left\{ N_i^{j} - R_{i-1}^{j-1} \right\} \;. \end{aligned}$$

(2.2)

On the other hand, denote by $j^{**}$ the largest index in $G_i^-$. Since each index $j \in [j^{**}]$ such that $T[j]=w_i$ is either the i-th element of some copy or is not the i-th element of any copy, $N_i^{j^{**}} = R_{i}^{j^{**}-1} + \left| G_i^-\right|$. We claim that $R_{i}^{j^{**}-1} = R_{i-1}^{j^{**}-1}$. As noted following Definition 2.1, $R_{i}^{j^{**}-1} \le R_{i-1}^{j^{**}-1}$, and hence it remains to verify that $R_{i}^{j^{**}-1}$ is not strictly smaller than $R_{i-1}^{j^{**}-1}$. Assume, contrary to this claim, that $R_{i}^{j^{**}-1} < R_{i-1}^{j^{**}-1}$. But then, the index $j^{**}$, which belongs to $G_i$, would have to be the i-th element of a greedy copy, in contradiction to the fact that $j^{**} \in G_i^-$. Hence,

$$\begin{aligned} \left| G_i^-\right| = N_i^{j^{**}} - R_{i-1}^{j^{**}-1} \le \max _{j\in [n]}\left\{ N_i^{j} - R_{i-1}^{j-1} \right\} \;. \end{aligned}$$

(2.3)

In conclusion,

$$\begin{aligned} \left| G_i^-\right| = \max _{j\in [n]}\left\{ N_i^{j} - R_{i-1}^{j-1} \right\} \;, \end{aligned}$$

(2.4)

and the claim follows. $\square$

In order to state our next combinatorial claim, we first introduce one more definition, which will play a central role in obtaining an estimate for $R(T,w)$ (the number of role-disjoint copies of w in T).

Definition 2.2

For $\ell \le n$, let $\mathcal {N}$ be a $k\times \ell$ matrix of non-negative numbers, where we use $\mathcal {N}_i^r$ to denote $\mathcal {N}[i][r]$. For every $r\in [\ell ]$, let $M_1^r(\mathcal {N}) = \mathcal {N}_1^r$, and for every $i \in \{2,\dots ,k\}$, let

$$\begin{aligned} M_i^r(\mathcal {N}) {\mathop {=}\limits ^\textrm{def}}\mathcal {N}_i^r - \max _{r'\in [r]} \left\{ \mathcal {N}_i^{r'} - M_{i-1}^{r'}(\mathcal {N})\right\} \;. \end{aligned}$$

(2.5)

When $i=k$ and $r=\ell$, we use the shorthand $M(\mathcal {N})$ for $M_k^\ell (\mathcal {N})$.

Consider letting $\ell = n$, and determining the $k\times n$ matrix $\mathcal {N}$ in Definition 2.2 by setting $\mathcal {N}[i][r] = N_i^r(T,w)$ (the number of occurrences of $w_i$ in T[1, r]) for each $i \in [k]$ and $r\in [n]$. Then the recursive definition of $M_i^r(\mathcal {N})$ in Eq. (2.5) for this setting of $\mathcal {N}$, almost coincides with Eq. (2.1) in Claim 2.1 for $R_i^r(T,w)$ (the number of role-disjoint copies of $w_1\dots w_i$ in T[1, r]). Indeed, if the maximum on the right hand side of Eq. (2.5) would be over $\mathcal {N}_i^{r'} - M_{i-1}^{r'-1}(\mathcal {N})$ rather than over $\mathcal {N}_i^{r'} - M_{i-1}^{r'}(\mathcal {N})$, then we would get that $M_i^r(\mathcal {N})$ equals $R_i^r(T,w)$ for every $i \in [k]$ and $r\in [n]$, and in particular $M(\mathcal {N})$ would equal $R(T,w)$.

In our second combinatorial claim, we show that for an appropriate choice of a matrix $\mathcal {N}$, whose entries are only a subset of all values in $\left\{ N_i^j(T,w)\right\} _{i\in [k]}^{j\in [n]}$, we can bound the difference between $M(\mathcal {N})$ and $R(T,w)$. We later apply sampling to obtain an estimated version of $\mathcal {N}$ and use this estimated version to obtain an estimate of $R(T,w)$ by combining Claim 2.2 and Definition 2.2.

Claim 2.2

Let $J = \left\{ j_0,j_1, \dots , j_{\ell }\right\}$ be a set of indices satisfying $j_0=0< j_1< j_2<\dots < j_\ell =n$. Let $\mathcal {N}= \mathcal {N}(J,T,w)$ be the matrix whose entries are $\mathcal {N}_i^r = N_i^{j_r}(T,w)$, for every $i \in [k]$ and $r \in [\ell ]$. Then we have

$$\begin{aligned} \left| M(\mathcal {N}) - R(T,w)\right| \le (k-1)\cdot \max _{\tau \in [\ell ]}\left\{ j_{\tau } - j_{\tau -1}\right\} . \end{aligned}$$

Proof

Recall that $M(\mathcal {N}) = M_{k}^{\ell }(\mathcal {N})$ and $R(T,w) = R_{k}^{j_{\ell }}(T,w)$. We shall prove that for every $i \in [k]$ and for every $r\in [\ell ]$, $\left| M_{i}^{r}(\mathcal {N}) - R_{i}^{j_{r}}(T,w)\right| \le (i-1)\cdot \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\}$. We prove this by induction on i.

For $i=1$ and every $r\in [\ell ]$,

$$\begin{aligned} \left| M_{1}^r(\mathcal {N}) - R_{1}^{j_r}(T,w)\right|= & {} \left| N_1^{j_r}(T,w) - N_1^{j_r}(T,w) \right| \nonumber \\= & {} 0 \le (1-1) \cdot \max _{\tau \in [1]}\left\{ j_{\tau } - j_{\tau -1}\right\} , \end{aligned}$$

(2.6)

where the first equality follows from the setting of $\mathcal {N}$ and the definitions of $M_1^r(\mathcal {N})$ and $R_1^{j_r}(T,w)$.

For the induction step, we assume the claim holds for $i-1 \ge 1$ (and every $r\in [\ell ]$) and prove it for i. We have,

$$\begin{aligned}{} & {} M_{i}^{r}(\mathcal {N}) - R_{i}^{j_r}(T,w) \nonumber \\{} & {} \quad = N_i^{j_r}(T,w) - \max _{b \in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} - R_{i}^{j_r}(T,w) \end{aligned}$$

(2.7)

$$\begin{aligned}{} & {} \quad = \max _{j \in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} - \max _{b\in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} ,\qquad \quad \end{aligned}$$

(2.8)

where Eq. (2.7) follows from the setting of $\mathcal {N}$ and the definition of $M_{i}^{r}(\mathcal {N})$, and Eq. (2.8) is implied by Claim 2.1. Denote by $j^*$ an index $j \in [j_r]$ that maximizes the first max term and let $b^*$ be the largest index such that $j_{b^*} \le j^*$. We have:

$$\begin{aligned}{} & {} \max _{ j\in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} - \max _{b \in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} \nonumber \\{} & {} \quad \le N_i^{j^*}(T,w) - R_{i-1}^{j^*-1}(T,w) - N_i^{j_{b^*}}(T,w) + M_{i-1}^{b^*}(\mathcal {N}) \nonumber \\{} & {} \quad = N_i^{j^*}(T,w) + R_{i-1}^{j_{b^*}}(T,w) - R_{i-1}^{j_{b^*}}(T,w) - R_{i-1}^{j^*-1}(T,w) \nonumber \\{} & {} \qquad - N_i^{j_{b^*}}(T.w) + M_{i-1}^{b^*}(\mathcal {N}) \nonumber \\{} & {} \quad {=} \left( M_{i-1}^{b^*}(\mathcal {N}) - R_{i-1}^{j_{b^*}}(T,w)\right) + \left( N_i^{j^*}(T,w) - N_i^{j_{b^*}}(T,w) \right) \nonumber \\{} & {} \qquad +\left( R_{i-1}^{j_{b^*}}(T,w) - R_{i-1}^{j^*-1}(T,w)\right) \nonumber \\{} & {} \quad \le (i-2) \max _{\tau \in [{b^*}]}\left\{ j_{\tau } - j_{\tau -1}\right\} + \left( j^{*} - j_{b^{*}}\right) +\left( j_{b^{*}} - (j^{*}-1)\right) \end{aligned}$$

(2.9)

$$\begin{aligned}{} & {} \quad {\le } (i-2) \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} + 1 \nonumber \\{} & {} \quad \le (i-2) \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} + \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} \nonumber \\{} & {} \quad = (i-1)\max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} , \end{aligned}$$

(2.10)

where in Eq. (2.9) we used the induction hypothesis. By combining Eqs. (2.8) and (2.10), we get that

$$\begin{aligned} M_{i}^{r}(\mathcal {N}) - R_{i}^{j_r}(T,w) \le (i-1)\max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} \;. \end{aligned}$$

(2.11)

Similarly to Eq. (2.8),

$$\begin{aligned} R_{i}^{j_r}(T,w) - M_{i}^{r}(\mathcal {N})= & {} \max _{b\in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} \nonumber \\{} & {} - \max _{j\in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} . \end{aligned}$$

(2.12)

Let $b^{**}$ be the index $b\in [r]$ that maximizes the first max term. We have

$$\begin{aligned}{} & {} \max _{b \in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} - \max _{ j \in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} \nonumber \\{} & {} \quad \le N_i^{j_{b^{**}}}(T,w) - M_{i-1}^{{b^{**}}}(\mathcal {N}) - N_i^{j_{b^{**}}}(T,w) + R_{i-1}^{j_{b^{**}}-1}(T,w) \nonumber \\{} & {} \quad {=} R_{i-1}^{j_{b^{**}}}(T,w) - M_{i-1}^{b^{**}}(\mathcal {N}) \;\le \; \left| R_{i-1}^{j_{b^{**}}}(T,w) - M_{i-1}^{b^{**}}(\mathcal {N})\right| \nonumber \\{} & {} \quad \le (i-2) \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} \;\le \; (i-1) \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} . \end{aligned}$$

(2.13)

Hence (combining Eqs. (2.12) and (2.13)),⁹

$$\begin{aligned} R_{i}^{j_r}(T,w) - M_{i}^{r}(\mathcal {N}) \le (i-1) \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} \;. \end{aligned}$$

(2.14)

Together, Eqs. (2.11) and (2.14) give us that

$$\begin{aligned} \left| M_{i}^{r}(\mathcal {N}) - R_{i}^{j_r}(T,w)\right| \le (i-1) \max _{\tau \in [r]}\left\{ j_{\tau } - j_{\tau -1}\right\} \;, \end{aligned}$$

(2.15)

and the proof is completed. $\square$

In our next claim, we bound the difference between $M(\mathcal {A})$ and $M(\mathcal {D})$ for any two matrices $\mathcal {A}$ and $\mathcal {D}$ (with dimensions $k\times \ell$), given a bound on the $L_\infty$ distance between them. We later apply this claim with $\mathcal {D}= \mathcal {N}$ for $\mathcal {N}$ as defined in Claim 2.2, and $\mathcal {A}$ being a matrix that contains estimates of $N_{i}^{j_r}(T,w)$. We discuss how to obtain such a matrix $\mathcal {A}$ in Claim 2.4.

Claim 2.3

Let $\gamma \in (0,1)$, and let $\mathcal {A}$ and $\mathcal {D}$ be two $k\times \ell$ matrices. If for every $i \in [k]$ and $r \in [\ell ]$,

$$\begin{aligned} \left| \mathcal {A}_{i}^{r} - \mathcal {D}_{i}^{r} \right| \le \gamma n\;, \end{aligned}$$

then

$$\begin{aligned} \left| M(\mathcal {A}) - M(\mathcal {D})\right| \le (2k-1)\gamma n\;. \end{aligned}$$

Proof

We prove that, given the premise of the claim, for every $t \in [k]$ and for every $r\in [\ell ]$, $\left| M_t^r(\mathcal {A}) - M_t^r(\mathcal {D})\right| \le (2t-1)\gamma n$. We prove this by induction on t.

For $t = 1$ and every $r\in [\ell ]$, we have

$$\begin{aligned} \left| M_1^r(\mathcal {A}) - M_1^r(\mathcal {D}) \right| \;=\; \left| \mathcal {A}_{1}^{r} - \mathcal {D}_1^r \right| \;\le \; \gamma n \;. \end{aligned}$$

(2.16)

Now assume the claim is true for $t-1 \ge 1$ and for every $r \in [\ell ]$, and we prove it for t. For any $r \in [\ell ]$, by the definition of $M_t^r(\cdot )$,

$$\begin{aligned}{} & {} \left| M_{t}^{r}(\mathcal {A}) - M_{t}^{r}(\mathcal {D})\right| \nonumber \\{} & {} \quad =\left| \mathcal {A}_t^{r} - \max _{r' \in [r]}\left\{ \mathcal {A}_t^{r'} - M_{t-1}^{r'}(\mathcal {A})\right\} - \mathcal {D}_t^{r} + \max _{r'' \in [r]}\left\{ \mathcal {D}_t^{r''} - M_{t-1}^{r''}(\mathcal {D})\right\} \right| \nonumber \\{} & {} \quad \le \gamma n + \left| \max _{r'' \in [r]}\left\{ \mathcal {D}_t^{r''} - M_{t-1}^{r''}(\mathcal {D})\right\} - \max _{r' \in [r]}\left\{ \mathcal {A}_t^{r'} - M_{t-1}^{r'}(\mathcal {A})\right\} \right| , \end{aligned}$$

(2.17)

where in the last inequality we used the premise of the claim.

Assume that the first max term in Eq. (2.17) is at least as large as the second (the case that the second term is larger than the first is handled analogously), and let $r^*$ be the index that maximizes the first max term.

Then,

$$\begin{aligned}{} & {} \left| \max _{r'' \in [r]}\left\{ \mathcal {D}_t^{r''} - M_{t-1}^{r''}(\mathcal {D})\right\} - \max _{r' \in [r]}\left\{ \mathcal {A}_t^{r'} - M_{t-1}^{r'}(\mathcal {A})\right\} \right| \nonumber \\{} & {} \quad \le \left| \left( \mathcal {D}_t^{r^*} - \mathcal {A}_t^{r^*}\right) + \left( M_{t-1}^{r^*}(\mathcal {A}) - M_{t-1}^{r^*}(\mathcal {D})\right) \right| \nonumber \\{} & {} \quad \le \left| \mathcal {D}_t^{r^*} - \mathcal {A}_t^{r^*}\right| + \left| M_{t-1}^{r^*}(\mathcal {A}) - M_{t-1}^{r^*}(\mathcal {D})\right| \nonumber \\{} & {} \quad \le \gamma n + (2t-3) \gamma n = (2t-2) \gamma n , \end{aligned}$$

(2.18)

where we used the premise of the claim once again, and the induction hypothesis. The claim follows by combining Eqs. (2.17) with (2.18). $\square$

The next claim states that we can obtain good estimates for all values in $\left\{ N_{i}^{j_r}(T,w)\right\} _{i\in [k]}^{r\in [\ell ]}$ (with a sufficiently large sample). Its proof is deferred to Appendix B (the probabilistic analysis is simple and standard, and the running time analysis is technical).

Claim 2.4

For any $\gamma \in (0,1)$ and $J = \{j_1,\dots ,j_\ell \}$ (such that $1 \le j_1< \dots < j_\ell =n$), by taking a sample of size $s = O\left( \frac{\log (k\cdot \ell )}{\gamma ^2}\cdot \right)$ from T, we can obtain, with probability at least 2/3, estimates $\left\{ \widehat{\mathcal {N}}_i^r\right\} _{i\in [k]}^{r\in [\ell ]}$, such that

$$\begin{aligned} \left| \widehat{\mathcal {N}}_{i}^{r} - N_{i}^{j_r}(T,w) \right| \le \gamma n\;, \end{aligned}$$

(2.19)

for every $i\in [k]$ and $r\in [\ell ]$. Furthermore, the $k\cdot \ell$ estimates $\left\{ \widehat{\mathcal {N}}_i^r\right\} _{i\in [k]}^{r\in [\ell ]}$ can be obtained in time $O(k\cdot (\log k+ \ell ) + s\cdot (\log k + \log \ell ))$.

Before stating and proving our main theorem for distance approximation under the uniform distribution, we establish one more claim regarding the computation of $M(\cdot )$.

Claim 2.5

For $\ell \le n$, let $\mathcal {N}$ be a $k\times \ell$ matrix of non-negative numbers. Then $M(\mathcal {N})$ can be computed in time $O(k\cdot \ell )$.

Proof

Considering Definition 2.2, we first set $M_1^r(\mathcal {N})$ to $\mathcal {N}_1^r$ for each $r \in [\ell ]$ (taking time $O(\ell )$). For $i=2$ to k, we compute $M_i^r(\mathcal {N})$ for every $r\in [\ell ]$ using Eq. (2.5) in Definition 2.2, so that when $i=k$ and $r = \ell$ we get $M(\mathcal {N}) = M_k^\ell (\mathcal {N})$. At first glance it seems that, according to Eq. (2.5), computing each $M_i^r(\mathcal {N})$ (given $M_{i-1}^{r'}(\mathcal {N})$ for all $r'\le r$) takes time linear in r (since we need to compute a maximum over r values). This would give a total running time of $O(k\ell ^2)$.

However, it is actually possible to compute $M_i^r(\mathcal {N})$ for any $i>1$ and all $r \in [\ell ]$ (given $M_{i-1}^r(\mathcal {N})$ for all $r\in [\ell ]$), in time $O(\ell )$. To verify this, let $X_i^r(\mathcal {N}) = \max _{r'\le r}\{\mathcal {N}_i^{r'} - M_i^{r'}(\mathcal {N})\}$, so that $M_i^r(\mathcal {N}) = \mathcal {N}_i^r - X_i^r(\mathcal {N})$. Observe that for any $r>1$, we have that $X_i^r(\mathcal {N}) = \max \{X_i^{r-1}(\mathcal {N}),\mathcal {N}_i^r - M_i^r(\mathcal {N})\}$. Therefore, for any $i>1$, we can compute $M_i^1(\mathcal {N}),\dots ,M_i^\ell (\mathcal {N})$ one after the other, in time $O(\ell )$, giving a total running time of $O(k\cdot \ell )$ to compute $M(\mathcal {N}) = M_k^\ell (\mathcal {N})$. $\square$

Theorem 2.1

There exists a sample-based distance-approximation algorithm for subsequence-freeness under the uniform distribution, that, for any subsequence w of length k, takes a sample of size $O\left( \frac{k^2}{\delta ^2}\cdot \log \left( \frac{k}{\delta }\right) \right)$ and outputs an estimate $\widehat{\Delta }$ such that $|\widehat{\Delta }- \Delta (T,w)| \le \delta$ with probability at least 2/3.¹⁰ The running time of the algorithm is $O\left( \frac{k^2}{\delta ^2}\cdot \log ^2\left( \frac{k}{\delta }\right) \right)$.

Proof

The algorithm performs the following steps.

• 1. Set $\gamma = \delta /(3k)$ and $J=\left\{ r\cdot \gamma n\right\} _{r=1}^\ell$ for $\ell = 1/\gamma$.

• 2. Apply Claim 2.4 with the above setting of $\gamma$ and J to obtain the estimates $\left\{ \widehat{\mathcal {N}}_i^r\right\}$ for every $i\in [k]$ and $r\in [\ell ]$. Let $\widehat{\mathcal {N}}$ be the $k\times \ell$ matrix defined by $\widehat{\mathcal {N}}[i][r] = \widehat{\mathcal {N}}_i^r$.

• 3. Compute $M(\widehat{\mathcal {N}})$ following Definition 2.2 (as described in the proof of Claim 2.5).

• 4. Output $\widehat{\Delta }= M(\widehat{\mathcal {N}})/n$.

The sample complexity of the algorithm follows from Claim 2.4, and the running time from Claim 2.4 and Claim 2.5, together with the setting of $\gamma$ and $\ell$.

It remains to verify that $\widehat{\Delta }$ is as stated in the theorem. By Claim 2.4, with probability at least 2/3, every estimate $\widehat{\mathcal {N}}_i^r$ satisfies Eq. (2.19). We henceforth condition on this event.

If we take $\mathcal {A}= \widehat{\mathcal {N}}$ and ${\mathcal {D}} = \mathcal {N}$ for $\mathcal {N}$ as defined in Claim 2.2, then the premise of Claim 2.3 holds. We can therefore apply Claim 2.3, and get that $\left| M(\widehat{\mathcal {N}}) - M(\mathcal {N})\right| \le (2k-1)\gamma n$. By Claim 2.2 and the definition of J, $\Big |M(\mathcal {N}) - R(T,w)\Big | \le (k-1) \gamma n$. Hence, by the triangle inequality,

$$\begin{aligned} \left| M(\widehat{\mathcal {N}}) - R(T,w) \right|\le & {} {\left| M(\widehat{\mathcal {N}}) - M(\mathcal {N})\right| + \Big |M(\mathcal {N}) - R(T,w)\Big | } \end{aligned}$$

(2.20)

$$\begin{aligned}\le & {} (2k-1)\gamma n + (k-1) \gamma n \;\;=\;\; (3k-2) \gamma n \;\;\le \;\; \delta n.\nonumber \\ \end{aligned}$$

(2.21)

Since $\widehat{\Delta }= M(\widehat{\mathcal {N}})/n$ and $R(T,w)/n = \Delta (T,w)$, the theorem follows. $\square$

3 Distribution-Free Distance Approximation

As noted in the introduction, our algorithm for approximating the distance from subsequence-freeness under a general distribution p works by reducing the problem to approximating the distance from subsequence-freeness under the uniform distribution. However, we won’t be able to use the algorithm presented in Sect. 2 as is. There are two main obstacles, explained shortly next. In the reduction, given a word w and access to samples from a text T, distributed according to p, we define a word $\widetilde{w}$ and a text $\widetilde{T}$ such that if we can obtain a good approximation of $\Delta (\widetilde{T},\widetilde{w})$ then we get a good approximation of $\Delta (T,w,p)$. (Recall that $\Delta (T,w,p)$ denotes the distance of T from being w-free under the distribution p.) However, first, we don’t actually have direct access to uniformly distributed samples from $\widetilde{T}$, and second, we cannot work with a set J of indices that induce equally sized intervals (of a bounded size), as we did in Sect. 2.

We address these challenges (as well as precisely define $\widetilde{T}$ and $\widetilde{w}$) in several stages. We start, in Sects. 3.1 and 3.2, by using sampling according to p, in order to construct intervals in T that have certain properties (with sufficiently high probability). The role of these intervals will become clear in the subsections that follow.

3.1 Interval Construction and Classification

We begin this subsection by defining intervals of integers in [n] that are determined by p (which is unknown to the algorithm). We then construct intervals by sampling from p, where the latter intervals are in a sense approximations of the former (this will be formalized subsequently). Each constructed interval will be classified as either “heavy” or “light”, depending on its (approximated) weight according to p. Ideally, we would have liked all intervals to be light, but not too light, so that their number won’t be too large (as was the case when we worked under the uniform distribution and simply defined intervals of equal size). However, for a general distribution p we might have single indices $j \in [n]$ for which $p_j$ is large, and hence we also need to allow heavy intervals (each consisting of a single index). We shall make use of the following two definitions.

Definition 3.1

For any two integers $j_1 \le j_2$, let $[j_1,j_2]$ denote the interval of integers $\{j_1,{j_1+1},\dots ,j_2\}$. For every $j_1, j_2 \in [n]$, define

$$\begin{aligned} \textrm{wt}_p([j_1,j_2]) {\mathop {=}\limits ^\textrm{def}}\sum _{j=j_1}^{j_2}p_j \end{aligned}$$

to be the weight of the interval $[j_1,j_2]$ according to p. We use the shorthand $\textrm{wt}_p(j)$ for $\textrm{wt}_p([j,j])$.

Definition 3.2

Let S be a multiset of size s, with elements from [n]. For every $j \in [n]$, let $N_S(j)$ be the number of elements in S that equal j. For every $j_1, j_2 \in [n]$, define

$$\begin{aligned} \textrm{wt}_{S}([j_1,j_2]) {\mathop {=}\limits ^\textrm{def}}\frac{1}{s}\sum _{j=j_1}^{j_2}N_S(j) \end{aligned}$$

to be the estimated weight of the interval $[j_1,j_2]$ according to S. We use the shorthand $\textrm{wt}_S(j)$ for $\textrm{wt}_S([j,j])$.

In the next definition, and the remainder of this section, we use

$$\begin{aligned} z \;= \; \frac{100 k}{\delta }\;. \end{aligned}$$

(3.1)

We next define the aforementioned set of intervals, based on p. Roughly speaking, we try to make the intervals as equally weighted as possible, keeping in mind that some indices might have a large weight, so we assign each to an interval of its own.

Definition 3.3

Define a sequence of indices in the following iterative manner. Let $h_0=0$ and for $\ell = 1,2,\dots$, as long as $h_{\ell -1} < n$, let $h_\ell$ be defined as follows. If $\textrm{wt}_{p}(h_{\ell -1}+1) > \frac{1}{8z}$, then $h_\ell = h_{\ell -1}+1$. Otherwise, let $h_\ell$ be the maximum index $h'_\ell \in [h_{\ell -1}+1,n]$ such that $\textrm{wt}_{p}([h_{\ell -1}+1,h_{\ell }']) \le \frac{1}{4z}$ and for every $h''_\ell \in [h_{\ell -1}+1,h'_\ell ]$, $\textrm{wt}_{p}(h''_\ell ) \le \frac{1}{8z}$. Let L be such that $h_L = n$.

Based on the indices $\{h_\ell \}_{\ell =0}^L$ defined above, for every $\ell \in [L]$, let $H_\ell = [h_{\ell -1}+1,h_\ell ]$ and let $\mathcal {H} = \left\{ H_\ell \right\} _{\ell =1}^{L}$. We partition $\mathcal {H}$ into three subsets as follows. Let $\mathcal {H}_{sin}$ be the subset of all $H \in \mathcal {H}$ such that $|H| = 1$ and $\textrm{wt}_p(H) > \frac{1}{8z}$. Let $\mathcal {H}_{med}$ be the set of all $H \in \mathcal {H}$ such that $|H| \ne 1$ and $\frac{1}{8z} \le \textrm{wt}_p(H) \le \frac{1}{4z}$. Let $\mathcal {H}_{sml}$ be the set of all $H \in \mathcal {H}$ such that $\textrm{wt}_p(H) < \frac{1}{8z}$.

Observe that since $\textrm{wt}_p(T) = 1$, we have that $|\mathcal {H}_{sin}\cup \mathcal {H}_{med}| \le 8z$. In addition, we claim that $|\mathcal {H}_{sml}| \le 8z + 1$. To verify this, consider any pair of intervals $H',H'' \in \mathcal {H}_{sml}$, where $H' = [h_{\ell (H')-1}+1,h_{\ell (H')}]$, $H'' = [h_{\ell (H'')-1}+1,h_{\ell (H'')}]$, and $\ell (H') < \ell (H'')$. Given the process by which the indices $\{h_\ell \}_{\ell =0}^L$ are selected and the definition of $\mathcal {H}_{sml}$ and $\mathcal {H}_{sin}$, there has to be at least one $H \in \mathcal {H}_{sin}$ between $H'$ and $H''$ (i.e., $H = [h_{\ell (H)-1}+1,h_{\ell (H)}]$ where $\ell (H')< \ell (H) < \ell (H'')$).

By its definition, $\mathcal {H}$ is determined by p. We next construct a set of intervals $\mathcal {B}$ based on sampling according to p (in a similar, but not identical, fashion to Definition 3.3). Consider a sample $S_1$ of size $s_1$ selected from [n] according to p (with repetitions), where $s_1$ will be set subsequently.

Definition 3.4

Given a sample $S_1$ (multiset of elements in [n]) of size $s_1$, determine a sequence of indices in the following iterative manner. Let $b_0=0$ and for $u = 1,2,\dots$, as long as $b_{u-1} < n$, let $b_u$ be defined as follows. If $\textrm{wt}_{S_1}(b_{u-1}+1) > 1/z$, then $b_u = b_{u-1}+1$. Otherwise, let $b_u$ be the maximum index $b'_u \in [b_{u-1}+1,n]$ such that $\textrm{wt}_{S_1}([b_{u-1}+1,b_{u}']) \le \frac{1}{z}$. Let y be such that $b_{y} = n$.

Based on the indices $\{b_u\}_{u=0}^{y}$ defined above, for every $u \in [y]$, let $B_u = [b_{u-1}+1,b_u]$, and let $\mathcal {B} = \left\{ B_u\right\} _{u=1}^{y}$. For every $u \in [y]$, if $\textrm{wt}_{S_1}(B_{u}) > \frac{1}{z}$, then we say that $B_u$ is heavy, otherwise it is light.

Observe that each heavy interval consists of a single element and that $y = O(z) = O(k/\delta )$.

In order to relate between $\mathcal {H}$ and $\mathcal {B}$, we introduce the following event, based on the sample $S_1$.

Definition 3.5

Denote by $E_1$ the event where

$$\begin{aligned} \forall H \in \mathcal {H}_{sin}\cup \mathcal {H}_{med}, \;\; \textrm{wt}_{S_1}(H) \ge \frac{1}{2}\textrm{wt}_{p}(H) \;. \end{aligned}$$

Claim 3.1

If the size of the sample $S_1$ is $s_1 \ge 100 z \log (40z)$ then

$$\begin{aligned} \textrm{Pr}\left[ E_1\right] \ge \frac{4}{5}\;, \end{aligned}$$

where the probability is over the choice of $S_1$.

Proof

Recall that $\textrm{wt}_p(H) \ge \frac{1}{8z}$ for every $H \in \mathcal {H}_{sin}\cup \mathcal {H}_{med}$. Using the multiplicative Chernoff bound (see Theorem A.1) we get that for every $H \in \mathcal {H}_{sin}\cup \mathcal {H}_{med}$,

$$\begin{aligned} \textrm{Pr}\left[ \textrm{wt}_{S_1}(H)< \frac{1}{2}\textrm{wt}_{p}(H)\right]< \exp \left( -\frac{1}{12} \textrm{wt}_{p}(H) s_1\right) < \frac{1}{40z}\;. \end{aligned}$$

(3.2)

Using a union bound over all $H \in \mathcal {H}_{med}\cup \mathcal {H}_{sml}$ (recall that by the discussion following Definition 3.3, $|\mathcal {H}_{sin}\cup \mathcal {H}_{med}| \le 8z$), we get

$$\begin{aligned} \textrm{Pr}[E_1] \ge 1 - 8z \cdot \frac{1}{40z} \ge \frac{4}{5}\;, \end{aligned}$$

(3.3)

and the claim is established. $\square$

Claim 3.2

Conditioned on the event $E_1$, for every $u \in [y]$ such that $B_u$ is light, $\textrm{wt}_{p}(B_u) < \frac{5}{z}$.

Proof

Consider an interval $B_u$ that is light. Let $\mathcal {H}(B_u) = \{H\in \mathcal {H}\,:\,H\subseteq B_u\}$, and $\mathcal {H}'(B_u) = \{H\in \mathcal {H}{\setminus } \mathcal {H}(B_u) \,:\,H\cap B_u\ne \emptyset \}$, so that

$$\begin{aligned} \bigcup _{H\in \mathcal {H}(B_u)} H \subseteq \; B_u \; \subseteq \bigcup _{H\in \mathcal {H}(B_u)\cup \mathcal {H}'(B_u)} H \;. \end{aligned}$$

(3.4)

Observe that $|\mathcal {H}'(B_u)| \le 2$ (because $B_u$ is an interval) and that for each $H \in \mathcal {H}'(B_u)$ we have that $H \in \mathcal {H}_{med}\cup \mathcal {H}_{sml}$ (because for every $H \in \mathcal {H}_{sin}$ it holds that $|H|=1$ implying that either $H \subseteq B_u$ or $H\cap B_u = \emptyset$). Let $\mathcal {H}_{sin}(B_u) = \mathcal {H}(B_u)\cap \mathcal {H}_{sin}$, and define $\mathcal {H}_{med}(B_u)$ and $\mathcal {H}_{sml}(B_u)$ analogously.

Conditioned on $E_1$ (Definition 3.5), we have that $\textrm{wt}_{S_1}(H) \ge \frac{1}{2}\textrm{wt}_p(H)$ for every $H \in \mathcal {H}_{sin}$, and since $\textrm{wt}_p(H) \ge \frac{1}{8z}$ for every $H \in \mathcal {H}_{sin}$, we get that $\textrm{wt}_{S_1}(H) \ge \frac{1}{16z}$ for every $H \in \mathcal {H}_{sin}(B_u)$. Since $B_u$ is light, $\textrm{wt}_{S_1}(B_u) \le \frac{1}{z}$, implying that $|\mathcal {H}_{sin}(B_u)| \le 16$. As mentioned before, there has to be at least one interval $H \in \mathcal {H}_{sin}$ between any pair of intervals $H', H'' \in \mathcal {H}_{sml}$, implying that $|\mathcal {H}_{sml}(B_u)| \le |\mathcal {H}_{sin}(B_u)| + 2 \le 18$. Therefore (recalling that $\textrm{wt}_p(H) \le \frac{1}{4z}$ for every $H \in \mathcal {H}_{med}$ and $\textrm{wt}_p(H) \le \frac{1}{8z}$ for every $H \in \mathcal {H}_{sml})$,

$$\begin{aligned} \textrm{wt}_p(B_u)&\le \sum _{H \in \mathcal {H}(B_u)} \textrm{wt}_p(H) + \sum _{H \in \mathcal {H}'(B_u)} \textrm{wt}_p(H) \end{aligned}$$

(3.5)

$$\begin{aligned}&= \sum _{H \in \mathcal {H}_{sin}(B_u) \cup \mathcal {H}_{med}(B_u)} \textrm{wt}_p(H) + \sum _{H\in \mathcal {H}_{sml}(B_u)} \textrm{wt}_p(H) + \sum _{H \in \mathcal {H}'(B_u)} \textrm{wt}_p(H) \end{aligned}$$

(3.6)

$$\begin{aligned}&\le 2\sum _{H \in \mathcal {H}_{sin}(B_u)\cup \mathcal {H}_{med}(B_u)} \textrm{wt}_{S_1}(H) + |\mathcal {H}_{sml}(B_u)|\cdot \frac{1}{8z} + 2\cdot \frac{1}{4z} \end{aligned}$$

(3.7)

$$\begin{aligned}&\le 2\textrm{wt}_{S_1}(B_u) + \frac{18}{8z} + \frac{1}{2z} \end{aligned}$$

(3.8)

$$\begin{aligned}&\le \frac{2}{z} + \frac{11}{4z} < \frac{5}{z}\;, \end{aligned}$$

(3.9)

and the claim follows. $\square$

3.2 Estimation of Symbol Density and Weight of Intervals

In this subsection we estimate the weight, according to p, of every interval $[b_u]$ for $u \in [y]$, as well as its symbol density, focusing on symbols that occur in w. Note that $[b_u]$ is the union of the intervals $B_1,\dots ,B_u$. We first introduce some notations.

Definition 3.6

For any word $w^{*}$, text $T^{*}$, $i \in [|w^{*}|]$ and $j\in [|T^{*}|]$, let $I_{i}^{j}(T^{*},w^{*}) = 1$ if $T^{*}[j] = w^{*}_i$ and 0 otherwise.

Definition 3.7

Let $w^{*}$ be a word of length $k^*$, $T^*$ a text of length $n^*$, $p^*$ a distribution over $[n^*]$, and $b^*_0 = 0< b^*_1< \dots < b^*_{y^*} = n$ a sequence of indices. For each $i \in [k^*]$ and $u \in [y^*]$, define the following density measure:

$$\begin{aligned} \xi _{i}^{u}\left( T^*,w^*,p^*,\{b^*_r\}_{r=1}^{y^*} \right) = \sum _{j \in [b^*_u]} I_i^j(T^*,w^*) p^*_j\;. \end{aligned}$$

(3.10)

Namely, $\xi _{i}^{u}\left( T^*,w^*,p^*,\{b^*_r\}_{r=1}^{y^*} \right)$ is the weight, according to $p^*$, of those indices in the interval $[b^*_u]$, where $w^*_i$ appears in $T^*$ (i.e., $j\in [b^*_u]$ such that $T^*[j] = w^*_i$).

When $T^*=T$, $w^*=w$, $p^*=p$, and $\{b^*_r\}_{r=1}^{y^*} = \{b_r\}_{r=1}^y$ are as determined in Definition 3.4 (based on a sample $S_1$ selected according to p), we shall use the shorthand

$$\begin{aligned} \xi _{i}^{u} = \xi _{i}^{u}\left( T,w,p,\{b_r\}_{r=1}^{y} \right) \;, \end{aligned}$$

(3.11)

for the “original” density measure. We later apply the definition of the density measure $\xi _i^u(\cdot ,\cdot ,\cdot ,\cdot )$ to other texts, words, distributions and sequence of indices (endpoints of intervals).

Definition 3.8

Let $S_2$ be a sample of size $s_2$ of pairs $(j,t_j)$ with repetitions. For $\{b_r\}_{r=1}^y$ as determined in Definition 3.4, and for each $i \in [k]$ and $u \in [y]$, define the estimator:

$$\begin{aligned} \breve{\xi }_{i}^{u} = \frac{1}{s_2} \sum _{j \in [b_u]}I_i^j(T,w) N_{S_2}(j)\;. \end{aligned}$$

(3.12)

Namely, $\breve{\xi }_{i}^{u}$ is the fraction of sampled indices j in $S_2$ that fall in the interval $[b_u]$, and for which $T[j]=w_i$. Thus, for $S_2$ selected according to p, $\breve{\xi }_{i}^{u}$ is an empirical estimate of $\xi _i^u$.

Definition 3.9

The event $E_2$ (based on a sample $S_2$) is defined as follows. For every $i \in [k]$ and $u \in [y]$,

$$\begin{aligned} \left| \breve{\xi }_{i}^{u} - \xi _{i}^{u} \right| \le \frac{1}{z} \;, \end{aligned}$$

(3.13)

and for every $u \in [y]$,

$$\begin{aligned} \big |\textrm{wt}_{S_2}([b_u]) - \textrm{wt}_p([b_u]) \big | \le \frac{1}{z}\;. \end{aligned}$$

(3.14)

Claim 3.3

If the size of the sample $S_2$ is $s_2 \ge z^2 \log \left( 40k y \right)$, then

$$\begin{aligned} \textrm{Pr}\left[ E_2\right] \ge \frac{9}{10}\;, \end{aligned}$$

where the probability is over the choice of $S_2$.

Proof

Using the additive Chernoff bound (see Theorem A.1) along with the fact that $\mathbb {E}\left[ \frac{N_{S_2}(j)}{s_2}I_i^j(T,w)\right] = I_i^j(T,w) p_j$, yields the following.

$$\begin{aligned} \textrm{Pr}\left[ \left| \breve{\xi }_{i}^{u} - \xi _{i}^{u} \right|> \frac{1}{z} \right]&= \textrm{Pr}\left[ \left| \frac{1}{s_2} \sum _{j \in [b_u] }I_i^j(T,w) N_{S_2}(j) - \sum _{j \in [b_u] }I_i^j(T,w) p_j \right| > \frac{1}{z} \right] \end{aligned}$$

(3.15)

$$\begin{aligned}&< 2 \exp (-2 \frac{1}{z^2} s_2) \le \frac{1}{20 k y}\;. \end{aligned}$$

(3.16)

By applying a union bound over all $i \in [k]$ and $u \in [y]$, we get that with probability of at least $\frac{19}{20}$, $\left| \breve{\xi }_{i}^{u} - \xi _{i}^{u} \right| \le \frac{1}{z}$. Another use of the additive Chernoff bound along with the fact that $\mathbb {E}\left[ \frac{N_{S_2}(j)}{s_2}\right] = p_j$ gives us that

$$\begin{aligned}&\textrm{Pr}\left[ \big |\textrm{wt}_{S_2}([b_u]) - \textrm{wt}_p([b_u]) \big |> \frac{1}{z} \right] = \textrm{Pr}\left[ \left| \frac{1}{s_2} \sum _{j \in [b_u] } N_{S_2}(j) - \sum _{j \in [b_u] } p_j \right| > \frac{1}{z} \right] \end{aligned}$$

(3.17)

$$\begin{aligned}&\quad < 2 \exp (-2 \frac{1}{z^2} s_2) \le \frac{1}{20y}\;. \end{aligned}$$

(3.18)

Again using a union bound over all $u \in [y]$, we get that with probability of at least $\frac{19}{20}$ we have $\left| \textrm{wt}_{S_2}([b_u]) - \textrm{wt}_p([b_u]) \right| \le \frac{1}{z}$. One last use of the union bound gives us that $\textrm{Pr}\left[ E_2\right] \ge \frac{9}{10}$ $\square$

3.3 Reducing from Distribution-Free to Uniform

In this subsection we give the details for the aforementioned reduction from the distribution-free case to the uniform case, using the intervals and estimators that were defined in the previous subsections. We start by providing three definitions, taken from [33], which will be used in the reduction. The first two definitions are for the notion of splitting (variants of this notion were also used in previous works, e.g., [15]).

Definition 3.10

For a text $T = t_1 \dots t_n$, a text $\widetilde{T}$ is said to be a splitting of T if $\widetilde{T}= t_1^{\alpha _1} \dots t_n^{\alpha _n}$ for some $\alpha _1 \dots \alpha _n \in \mathbb {N}^{+}$. We denote by $\phi$ the splitting map, which maps each (index of a) symbol of $\widetilde{T}$ to its origin in T. Formally, $\phi : [|\widetilde{T}|] \rightarrow [n]$ is defined as follows. For every $\ell \in [|\widetilde{T}|] = [\sum _{i=1}^{n} \alpha _i]$, let $\phi (\ell )$ be the unique $i \in [n]$ that satisfies $\sum _{r=1}^{i-1}\alpha _r < \ell {\le } \sum _{r=1}^{i}\alpha _r$.

Note that by this definition, $\phi$ is a non-decreasing surjective map, satisfying $\widetilde{T}[\ell ] = T[\phi (\ell )]$ for every $\ell \in [|\widetilde{T}|]$. For a set $S \subseteq [|\widetilde{T}|]$ we let $\phi (S) = \left\{ \phi (\ell ): \ell \in S \right\}$. With a slight abuse of notation, for any $i \in [n]$ we use $\phi ^{-1}(i)$ to denote the set $\left\{ \ell \in [|\widetilde{T}|]: \phi (\ell ) = i\right\}$, and for a set $S \subseteq [n]$ we let $\phi ^{-1}(S) = \left\{ \ell \in [|\widetilde{T}|]: \phi (\ell ) \in S \right\}$

Definition 3.11

For a text $T = t_1 \dots t_n$ and a corresponding probability distribution $p = (p_1, \dots , p_n)$, a splitting of (T, p) is a text $\widetilde{T}$ along with a corresponding probability distribution $\hat{p} = (\hat{p}_1, \dots , \hat{p}_{|\widetilde{T}|})$, such that $\widetilde{T}$ is a splitting of T and $\sum _{\ell \in \phi ^{-1}(i)} \hat{p}_{\ell } = p_i$ for every $i \in [n]$.

The third definition is of a set of words, where no two consecutive symbols are the same.

Definition 3.12

Let $\mathcal {W}_c = \left\{ w \,:\, w_{j+1} \ne w_j, \forall j \in [k-1] \right\} \;$.

3.3.1 A Basis for Reducing from Distribution-Free to Uniform

Let $\widetilde{w}$ be a word of length $\widetilde{k}$ and $\widetilde{T}$ a text of length $\widetilde{n}$. In this subsection we establish a claim, which gives sufficient conditions on a (normalized version) of an estimation matrix $\widehat{\mathcal {N}}$, under which it can be used to obtain an estimate of $\Delta (\widetilde{T},\widetilde{w})$ with a small additive error.

We first state a claim that is similar to Claim 2.2, with a small, but important difference, that takes into account intervals in $\widetilde{T}$ (determined by a set of indices J) that consist of repetitions of a single symbol. Since its proof is very similar to the proof of Claim 2.2, it is deferred to Appendix B. Recall that $R(\widetilde{T},\widetilde{w})$ denotes the number of role-disjoint copies of $\widetilde{w}$ in $\widetilde{T}$ and that $M(\cdot )$ was defined in Definition 2.2. We remind the reader that $M(\cdot )$ is defined via a recursive formula in a manner similar to what is shown in Claim 2.1 holds for $R(\cdot )$. As in the proof of Claim 2.2, this similarity allows us to bound the difference between $M(\mathcal {N})$ and $R(\widetilde{T},\widetilde{w})$ for an appropriate choice of $\mathcal {N}$.

Claim 3.4

Let $J = \left\{ j_0,j_1, \dots , j_{\ell }\right\}$ be a set of indices satisfying $j_0=0< j_1< j_2<\dots < j_\ell =\widetilde{n}$. Let $\mathcal {N}$ be the matrix whose entries are $\mathcal {N}_i^r = N_i^{j_r}(\widetilde{T},\widetilde{w})$ for every $i \in [\widetilde{k}]$ and $r \in [\ell ]$. Let $J' = \{r\in [\ell ]\,:\,\widetilde{T}[j_{r-1}+1]=\dots =\widetilde{T}[j_r]\}$. Then

$$\begin{aligned} \left| M(\mathcal {N}) - R(\widetilde{T},\widetilde{w})\right| \le (\widetilde{k}-1)\cdot \max _{r \in [\ell ]\setminus J'}\left\{ (j_{r} - j_{r-1})\right\} . \end{aligned}$$

The following observation can be easily proved by induction.

Observation 3.5

Let $\widehat{\mathcal {N}}$ be a matrix of size $\widetilde{k}\times \ell$. Then

$$\begin{aligned} \frac{1}{\widetilde{n}}M(\widehat{\mathcal {N}}) = M\left( \frac{\widehat{\mathcal {N}}}{\widetilde{n}}\right) \;. \end{aligned}$$

(3.19)

The next claim will serve as the basis for our reduction from the general, distribution-free case, to the uniform case.

Claim 3.6

Let $\widehat{\mathcal {N}}$ be a $\widetilde{k}\times \ell$ matrix, $J = \left\{ j_0,j_1, j_2, \dots , j_{\ell }\right\}$ be a set of indices satisfying $j_0=0< j_1< j_2<\dots < j_\ell =\widetilde{n}$ and let $c_1$ and $c_2$ be constants. Suppose that the following conditions are satisfied.

• 1. For every $r \in [\ell ]$, if $j_r - j_{r - 1} > c_1 \cdot \frac{\delta \widetilde{n}}{\widetilde{k}}$, then $\widetilde{T}[j_{r-1}+1]=\dots =\widetilde{T}[j_{r}]$.

• 2. For every $i \in [\widetilde{k}]$ and $r\in [\ell ]$, $\left| \widehat{\mathcal {N}}_{i}^{r} - N_{i}^{j_r}(\widetilde{T},\widetilde{w}) \right| \le c_2 \cdot \frac{\delta \widetilde{n}}{\widetilde{k}}$.

Then,

$$\begin{aligned} \left| M\left( \frac{\widehat{\mathcal {N}}}{\widetilde{n}}\right) - \Delta (\widetilde{T},\widetilde{w})\right| \le (c_1 + 2c_2) \delta \;. \end{aligned}$$

Proof

Let $\mathcal {N}$ be the matrix whose entries are $\mathcal {N}_i^r = N_i^{j_r}(\widetilde{T},\widetilde{w})$ for every $i \in [\widetilde{k}]$ and $r \in [\ell ]$. We use Claim 3.4 and Item 1 in the premise of the current claim to obtain that $\left| M(\mathcal {N}) - R(\widetilde{T},\widetilde{w})\right| \le c_1 \delta \widetilde{n}$. We also use Claim 2.3 and Item 2 in the premise of the current claim to obtain that $\left| M(\widehat{\mathcal {N}}) - M(\mathcal {N})\right| \le 2 c_2 \delta \widetilde{n}$. Combining these bounds we get that $\left| M(\widehat{\mathcal {N}}) - R(\widetilde{T},\widetilde{w})\right| \le (c_1+2c_2) \delta \widetilde{n}$. The claim follows by applying Observation 3.5 along with the fact that $\frac{R(\widetilde{T},\widetilde{w})}{\widetilde{n}} = \Delta (\widetilde{T},\widetilde{w})$. $\square$

3.3.2 Establishing the Reduction for $w\in \mathcal {W}_c$ and Quantized p

For ease of readability, we begin by addressing the special case in which $w \in \mathcal {W}_c$ (recall Definition 3.12) and where there exists $\beta \in (0,1)$ such that $p_j/\beta$ is an integer for every $j \in [n]$. We later show how to deal with the general case, where we rely on techniques from [33] and introduce some new ones that are needed for implementing our algorithm.

For the case considered in this subsection, let $\widetilde{T}= t_{1}^{\alpha _1}\dots t_{n}^{\alpha _{n}}$ where $\alpha _j = \frac{p_{j}}{\beta }$ for every $j \in [n]$, so that $|\widetilde{T}|=\frac{1}{\beta }$. Define $\widetilde{p}$ by $\widetilde{p}_j = \beta$ for every $j \in$, so that $\widetilde{p}$ is the uniform distribution over $[|\widetilde{T}|]$. Since $p_j = \beta \cdot \alpha _j$, for every $j \in [n]$, we get that $(\widetilde{T},\widetilde{p})$ is a splitting of (T, p) (recall Definition 3.11), and hence by [33, Clm. 4.4] (using the assumption that $w\in \mathcal {W}_c$),

$$\begin{aligned} \Delta (\widetilde{T},w,\widetilde{p}) = \Delta (T,w,p)\;. \end{aligned}$$

(3.20)

Denote $\widetilde{n}= |\widetilde{T}|$. We begin by defining a set of intervals of $[\widetilde{n}]$, where $\{b_0,\dots ,b_y\}$ and $\mathcal {B} = \{B_1,\dots ,B_y\}$ are as defined in Sect. 3.1, and $\phi$ is as in Definition 3.11.

Definition 3.13

Let $\widetilde{b}_0 = 0$, and for every $u \in [y]$, let $\widetilde{b}_u = \max \left\{ h \in [\widetilde{n}]: \phi (h) = b_u\right\}$. For every $u \in [y]$, let $\widetilde{B}_u = [\widetilde{b}_{u-1}+1,\widetilde{b}_u]$, and define $\mathcal {\widetilde{B}} = \left\{ \widetilde{B}_u\right\} _{u=1}^{y}\;$.

Thus, there is a one-to-one correspondence between the intervals in $\mathcal {\widetilde{B}}$ and the intervals in $\mathcal {B}$, where the former are “splitted versions” of the latter, so that, in particular, $\textrm{wt}_{\widetilde{p}}(\widetilde{B}_u) = \textrm{wt}_{p}(B_u)$ for every $u\in [y]$.

For every $i \in [k]$ and $u \in [y]$, we use the shorthand

$$\begin{aligned} {\widetilde{\xi }}_{i}^{u} = {\xi _i^u\left( \widetilde{T},w,\widetilde{p},\{\widetilde{b}_r\}_{r=1}^y\right) \,} \end{aligned}$$

(3.21)

where $\xi _u^i(\cdot ,\cdot ,\cdot ,\cdot )$ is as in Definition 3.7. Therefore, the “splitted” density measure, $\widetilde{\xi }_{i}^{u}$, is the weight, according to $\widetilde{p}$, of those indices in the interval $[\widetilde{b}_u]$, where $w_i$ appears in $\widetilde{T}$ (i.e., $j\in [\widetilde{b}_u]$ such that $\widetilde{T}[j] = w_i$). Since $\widetilde{p}$ is the uniform distribution over $[\widetilde{n}]$,

$$\begin{aligned} \widetilde{\xi }_{i}^{u} = \frac{1}{\widetilde{n}}N_{i}^{b_u}(\widetilde{T},w)\;. \end{aligned}$$

(3.22)

For the next claim recall that $\xi _i^u$ is a shorthand for $\xi _i^u\left( T,w,p,\{b_r\}_{r=1}^y\right)$.

Claim 3.7

For every $i \in [k]$ and $u \in [y]$,

$$\begin{aligned} \widetilde{\xi }_{i}^{u} = \xi _{i}^{u}\;. \end{aligned}$$

Proof

$$\begin{aligned} \xi _{i}^{u}&= \sum _{j \in [b_u]}I_{i}^{j}(T,w) p_j = \sum _{j \in [b_u]}I_{i}^{j}(T,w) \sum _{\tilde{j} \in \phi ^{-1}(j)}\widetilde{p}_{\tilde{j}} \end{aligned}$$

(3.23)

$$\begin{aligned}&= \sum _{j \in [b_u]} \sum _{\tilde{j} \in \phi ^{-1}(j)} I_{i}^{j}(T,w) \widetilde{p}_{\tilde{j}} = \sum _{j \in [b_u]} \sum _{\tilde{j} \in \phi ^{-1}(j)} I_{i}^{\tilde{j}}(\widetilde{T},w) \widetilde{p}_{\tilde{j}} \nonumber \\&= \sum _{\tilde{j} \in \widetilde{b}_u} I_{i}^{\tilde{j}}(\widetilde{T},w) \widetilde{p}_{\tilde{j}} = {\widetilde{\xi }}_{i}^{u}\;, \end{aligned}$$

(3.24)

and the claim is established. $\square$

We can now state and prove the following lemma.

Lemma 3.8

Let w be a word of length k in $\mathcal {W}_c$, T a text of length n, and p a distribution over [n] for which there exists $\beta \in (0,1)$ such that $p_j/\beta$ is an integer for every $j\in [n]$. There exists an algorithm that, given a parameter $\delta \in (0,1)$, takes a sample of size $\Theta \left( \frac{k^2}{\delta ^2}\cdot \log \left( \frac{k}{\delta }\right) \right)$ from T, distributed according to p, and outputs an estimate $\widehat{\Delta }$ such that $|\widehat{\Delta }- \Delta (T,w,p)| \le \delta$ with probability at least 2/3. The running time of the algorithm is $O\left( \frac{k^2}{\delta ^2}\cdot \log ^2\left( \frac{k}{\delta }\right) \right)$.

Proof

The algorithm performs the following steps.

• 1. Take a sample $S_1$ of size $s_1 = 100 z \log (40z)$ and construct a set of intervals $\mathcal {B}$ as defined in Definition 3.4.

• 2. Take an additional sample, $S_2$, of size $s_2 = z^2 \log (40 k y)$, and use it to determine an estimation matrix $\widehat{\xi }$ of size $k \times y$ by setting $\widehat{\xi }[i][u] = \breve{\xi }_{i}^{u}$ for every $i \in [k]$ and $u \in [y]$, where $\breve{\xi }_{i}^{u}$ is as defined in Definition 3.8.

• 3. Compute $M(\widehat{\xi })$ following Definition 2.2 (as described in the proof of Claim 2.5) and output $\widehat{\Delta }= M(\widehat{\xi })$.

Since $z = O(k/\delta )$ and $y = O(z)$ (the upper bound $y \le s_1$ would also suffice for our purposes), the total sample complexity of the algorithm is as stated in the lemma. We next verify that the running time is also as stated in the lemma. First note that Step 1 takes time $O(s_1\log s_1)$. This holds because the sequence $b_0,\dots ,b_y$, which determines the set of intervals $\mathcal {B}$, can be constructed by first sorting the sample indices, and then making a single pass over the sorted sample. Similarly to what is shown in the proof of Claim 2.4, Step 2 takes time $O(k\cdot (\log k+ y) + s_2\cdot (\log k + \log y))$. By Claim 2.5, Step 3 times time $O(k\cdot y)$. Summing over all steps we get the stated upper bound on the running time.

We would next like to apply Claim 3.6 in order to show that $|\widehat{\Delta }- \Delta (\widetilde{T},w)| \le \delta$ with probability of at least $\frac{2}{3}$. By the setting of $s_1$, applying Claim 3.1 gives us that with probability at least $\frac{4}{5}$, the event $E_1$, as defined in Definition 3.5, holds. By the setting of $s_2$, applying Claim 3.3 gives us that with probability at least $\frac{9}{10}$, the event $E_2$, as defined in Definition 3.9, holds. We henceforth condition on both events (where they hold together with probability at least 7/10).

In order to apply Claim 3.6, we set $\widetilde{w}= w$, $J = \left\{ \widetilde{b}_0,\widetilde{b}_1,\dots ,\widetilde{b}_y\right\}$ (recall Definition 3.13) and $\widehat{\mathcal {N}}= \widetilde{n}\cdot \widehat{\xi }$, for $\widehat{\xi }$ as defined above. Also, we set $c_1 = \frac{1}{2}$ and $c_2 = \frac{1}{4}$. We next show that both items in the premise of the claim are satisfied.

To show that Item 1 is satisfied, we first note that since $\widetilde{p}$ is uniform, then for every $u \in [y]$, $\textrm{wt}_{\widetilde{p}}(b_u) = \frac{\widetilde{b}_{u} - \widetilde{b}_{u-1}}{\widetilde{n}}$. We use the consequence of Claim 3.2 (recall that we condition on $E_1$) by which for every u such that $\frac{\widetilde{b}_{u} - \widetilde{b}_{u-1}}{\widetilde{n}} \ge \frac{5}{z}$, $B_u$ is heavy (since for every $u \in [y]$, $\textrm{wt}_{\widetilde{p}}(\widetilde{B}_u) = \textrm{wt}_{p}(B_u)$). By Definition 3.4 this implies that $B_u$ contains only one index, and so $\widetilde{T}[\widetilde{b}_{u-1}+1] = \dots = \widetilde{T}[\widetilde{b}_{u}]$. By the definition of z (Eq. (3.1)) and the setting of $c_1$, the item is satisfied.

To show that Item 2 is satisfied, we use the definition of $E_2$ (Definition 3.9, Eq. (3.13)) together with Claim 3.7, which give us $|\widehat{\xi }_{i}^{u} - \widetilde{\xi }_{i}^{u}| \le \frac{1}{z}$ for every $i \in [k]$ and $u \in [y]$. By Eq. (3.22), the definition of z and the setting of $c_2$, we get that the item is satisfied.

After applying Claim 3.6 we get that $|\widehat{\Delta }- \Delta (\widetilde{T},w)| \le ( c_1 + 2c_2)\delta$, which by the setting of $c_1$ and $c_2$ is at most $\delta$. Since $\widetilde{p}$ is the uniform distribution, $\Delta (\widetilde{T},w) = \Delta (\widetilde{T},w,\widetilde{p})$ and since $\Delta (\widetilde{T},w,\widetilde{p}) = \Delta (T,w,p)$ (by Eq. (3.20)), the lemma follows. $\square$

In the next subsections we turn to the general case where we do not necessarily have that $w \in \mathcal {W}_c$ or that there exists a value $\beta$ such that for every $j \in [n]$, $p_j/\beta$ is an integer. In this general case we need to take some extra steps until we can perform a splitting. Beginning with performing a reduction to a slightly different distribution, then performing a reduction to $w \in \mathcal {W}_c$. While this follows [33], for the sake of our algorithm, along the way we need to show how to define the estimation matrix $\widehat{\xi }$ ($= \widehat{\mathcal {N}}/\widetilde{n}$) and the corresponding set of indices J so that we can apply Claim 3.6, similarly to what was shown in the proof of Lemma 3.8.

3.4 Quantized Distribution

Let $\eta = c_{\eta }\frac{1}{n z}$, where $c_{\eta } = {\frac{1}{2}}$. We define $\ddot{p} {:[n] \rightarrow [0,1]}$ by “rounding” $p_j$ for every $j \in [n]$ to its nearest larger integer multiple of $\eta$. Namely, $\ddot{p}_j = \big \lceil {\frac{p_j}{\eta }}\big \rceil \eta$, for every $j \in [n]$. By this definition,

$$\begin{aligned} L_1(\ddot{p},p) = \sum _{j=1}^{n}|\ddot{p}_j-p_j| \le \eta n = \frac{c_{\eta }}{z}\;. \end{aligned}$$

(3.25)

We define $\dot{p}$ to be a normalized version of $\ddot{p}$. That is, letting $\zeta = \frac{1}{\sum _{j=1}^{n}\ddot{p}_j}$, we set $\dot{p}_j = \zeta \ddot{p}_j$, for every $j \in [n]$, and note that $\zeta \le 1$. Observe that

$$\begin{aligned} L_1(\dot{p},\ddot{p}) = \sum _{j=1}^{n}|\zeta \ddot{p}_j-\ddot{p}_j| = \frac{|\zeta -1|}{\zeta } = \frac{1}{\zeta } - 1\;. \end{aligned}$$

(3.26)

Also observe that $\frac{1}{\zeta } = \sum _{j=1}^{n}(p_j+(\ddot{p}_j-p_j)) = 1 + \sum _{j=1}^{n}(\ddot{p}_j - p_j)$. Therefore,

$$\begin{aligned} L_1(\dot{p},\ddot{p}) = \frac{1}{\zeta } - 1 = \sum _{j=1}^{n}(\ddot{p}_j - p_j) \le \sum _{j=1}^{n}|\ddot{p}_j - p_j| = L_1(p,\ddot{p})\;. \end{aligned}$$

(3.27)

Using the triangle inequality we get that

$$\begin{aligned} L_1(p,\dot{p}) \le L_1(p,\ddot{p}) + L_1(\ddot{p},\dot{p}) \le 2 L_1(p,\ddot{p}) \le 2 \frac{c_{\eta }}{z}\;. \end{aligned}$$

(3.28)

By [33, Clm. 4.1] we have that

$$\begin{aligned} |\Delta (T,w,p) - \Delta (T,w,\dot{p})| \le L_1(p,\dot{p})\;. \end{aligned}$$

(3.29)

Finally, note that for every $j \in [n]$, $\dot{p}_j$ is an integer multiple of $\zeta \eta$, as $\dot{p}_j = \zeta \eta \big \lceil {\frac{p_j}{\eta }}\big \rceil$.

Recalling Definition 3.7 for $\xi _i^u(\cdot ,\cdot ,\cdot ,\cdot )$, for every $i\in [k]$ and $u\in [y]$, we use the shorthand

$$\begin{aligned} \dot{\xi }_{i}^{u} = \xi _i^u\left( T,w,\dot{p}_j,\{b_r\}_{r=1}^y\right) \;, \end{aligned}$$

(3.30)

for the “quantized” density measure. Once again recall that $\xi _i^u$ is a shorthand for $\xi _i^u\left( T,w,p,\{b_r\}_{r=1}^y\right)$ (the “original” density measure).

Claim 3.9

For every $i \in [k]$ and $u \in [y]$,

$$\begin{aligned} \left| \dot{\xi }_{i}^{u} - \xi _{i}^{u}\right| \le \sum _{j \in [b_u] }|\dot{p}_j-p_j|\;, \end{aligned}$$

(3.31)

and for every $u \in [y]$,

$$\begin{aligned} |\textrm{wt}_{\dot{p}}([b_u]) - \textrm{wt}_{p}([b_u])| \le \sum _{j \in [b_u]}|\dot{p}_j-p_j|\;. \end{aligned}$$

(3.32)

Proof

Recall that by Definition 3.6, $I_{i}^{j}(T,w) = 1$ if $T[j] = w_i$ and 0 otherwise. Equation (3.31) follows by using the triangle inequality along with the fact that $I_{i}^{j}(T,w) \le 1$ for every $i \in [k]$ and $j \in [n]$. and hence,

$$\begin{aligned} \left| \dot{\xi }_{i}^{u} - \xi _{i}^{u}\right| = \left| \sum _{j \in [b_u] } I_{i}^{j}(T,w)(\dot{p}_j - p_j) \right| \le \sum _{j \in [b_u] } \left| \dot{p}_j-p_j\right| \;. \end{aligned}$$

(3.33)

Equation (3.32) follows by the triangle inequality:

$$\begin{aligned} |\textrm{wt}_{\dot{p}}([b_u]) - \textrm{wt}_{p}([b_u])| = \left| \sum _{j \in [b_u]}\dot{p}_j - p_j \right| \le \sum _{j \in [b_u]}|\dot{p}_j-p_j| \;, \end{aligned}$$

(3.34)

and the claim is established. $\square$

3.5 Handling $w \notin \mathcal {W}_c$

We would have liked to consider a splitting (recall Definition 3.11) of $(T,\dot{p})$ for $\dot{p}$ as defined in Sect. 3.4, and then use the relationship between the distance from w-freeness before and after the splitting. However, we only know this connection between the distances in the case of $w \in \mathcal {W}_c$. Hence, we shall apply a reduction from a general w to $w \in \mathcal {W}_c$, as was done in [33], in their proof of Lemma 4.8. Without loss of generality, assume 0 is a symbol that does not appear in $w=w_1\dots w_k$ or $T= t_1\dots t_n$. Let $w' = w_1 0 w_2 0\dots w_{k-1} 0 w_k 0$, $T' = t_1 0 t_2 0\dots t_n 0$ and $p' = (\dot{p}_1/2,\dot{p}_1/2,\dots ,\dot{p}_n/2,\dot{p}_n/2)$. Note that $w'$ is in $\mathcal {W}_c$. By [33, Clm. 4.6],

$$\begin{aligned} \Delta (T',w',p') = \frac{1}{2} \Delta (T,w,\dot{p})\;. \end{aligned}$$

(3.35)

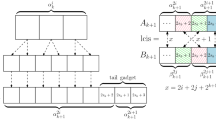
Here too we define a set of intervals, this time of ${[|T'|] =} [2n]$, given an indication whether corresponding intervals of [n] are heavy or light. The precise way the setting of the end-points of these intervals is determined, is described in Algorithm 1, but first we explain the underlying idea. Let $\mathcal {B}$ be a set of (disjoint and consecutive) intervals of [n], where each interval is either heavy or light, and each heavy interval contains a single element. We define a set of intervals $\mathcal {B}'$ of [2n] as follows. For each interval $B = [x,y]$ in $\mathcal {B}$, if B is light, then we have an interval $B' = [2x-1,2y]$ in $\mathcal {B}'$, and if B is heavy, so that $y=x$, then we have two single-element intervals, $B' = [2x-1,2x-1]$ and and $B'' = [2x,2x]$. Observe that by the definition of $T'$ (which is based on T), in the first case, $T'[B'] = T'[2x-1,2y] = t_x 0 t_{x+1} 0 \dots t_y 0$, and in the second case, $T'[B'] = T'[2x-1,2x-1] = t_x$, and $T'[B''] = T'[2x,2x] = 0$. This ensures that if an interval B in $\mathcal {B}$ is heavy, so that it contains a single element, the two corresponding interval, $B'$ and $B''$, in $\mathcal {B}'$ each contains a single element as well. This will play a role when we perform a splitting of $(T',p')$ and want to apply Claim 3.6.

Definition 3.14

Let $b'_0 = 0$. Define $y'$, $\left\{ b'_u\right\} _{u=1}^{y'}$ and the function $f: [y'] \rightarrow [y]$ using Algorithm 1. For every $u \in [y']$, let $B'_u = [b'_{u-1}+1,b'_u]$, and define $\mathcal {B}' = \left\{ B'_u\right\} _{u=1}^{y'}\;$.

We make two simple observations following Algorithm 1. The first relates between weights of intervals according to $p'$ and weights of corresponding intervals according to $\dot{p}$.

Observation 3.10

For every $u \in [y']$, if $B_{f(u)}$ is light, then $\textrm{wt}_{p'}(B'_u) = \textrm{wt}_{\dot{p}}(B_{f(u)})$, and if $B_{f(u)}$ is heavy, then $\textrm{wt}_{p'}(B'_u) = \frac{1}{2}\textrm{wt}_{\dot{p}}(B_{f(u)})$ and $B'_u$ is a single-element interval.

Recalling Definition 3.7 for $\xi _i^u(\cdot ,\cdot ,\cdot ,\cdot )$, for every $i \in [2k]$ and $u \in [y']$, we use the shorthand

$$\begin{aligned} {\xi '_i}^{u} = \xi _i^u\left( T',w',p'_j,\{b'_r\}_{r=1}^{y'}\right) \;, \end{aligned}$$

(3.36)

for the “separated” density measure (where we use the term “separated” since symbols in w and T are separated by 0s in $w'$ and $T'$, respectively).

The second observation relates between the above separated density measures and the corresponding quantizied ones.

Observation 3.11

For every $u \in [y']$ and for every $i \in [2k]$ such that $2 \not | \;i$ (meaning $w'_i \ne 0$),

$$\begin{aligned} {\xi '_{i}}^{u} = \frac{1}{2}\dot{\xi }_{\frac{i+1}{2}}^{f(u)}, \end{aligned}$$

(3.37)

whereas if $2 \mid i$ (meaning $w'_i = 0$),

$$\begin{aligned} {\xi '_{i}}^{u} = \frac{1}{2} {\left\{ \begin{array}{ll} \textrm{wt}_{\dot{p}}\left( [b_{f(u)}]\right) &{} \text {if } B_{f(u)} \text {is light} \\ \textrm{wt}_{\dot{p}}\left( [b_{f(u)}]\right) &{} \text {if } B_{f(u)} \text {is heavy and } T'[b'_{u}] = 0 \\ \textrm{wt}_{\dot{p}}\left( [b_{f(u)-1}]\right) &{} \text {if } B_{f(u)} \text {is heavy and } T'[b'_{u}] \ne 0. \end{array}\right. } \end{aligned}$$

(3.38)

3.6 Uniform Distribution via Splitting

Recall that $\eta$ and $\zeta$ were defined at the beginning of Sect. 3.4, whereas $T' = t'_1 \dots t'_{2n}$ and $p':[2n]\rightarrow [0,1]$ were defined in Sect. 3.5. Let $\widetilde{T}= {t'}_{1}^{\alpha _1}\dots {t'}_{2n}^{\alpha _{2n}}$ where $\alpha _j = \big \lceil {\frac{p_{j}}{\eta }} \big \rceil$ for every $j \in [2n]$. Define the distribution $\widetilde{p}$ by $\widetilde{p}_j = \frac{1}{2} \zeta \eta$ for every $j \in [|\widetilde{T}|]$, so that $\widetilde{p}$ is the uniform distribution over $[|\widetilde{T}|]$. Since $p'_j = \frac{1}{2} \zeta \eta \cdot \alpha _j = \sum _{\tilde{j} \in \phi ^{-1}(j)}\widetilde{p}_{\tilde{j}}$, for every $j \in [2n]$, we get that $(\widetilde{T},\widetilde{p})$ is a splitting of $(T',p')$ (recall Definition 3.11).

We make another use of [33, Thm. 4.4], by which splitting preserves the distance from w-freeness, to establish that

$$\begin{aligned} \Delta (\widetilde{T},w',\widetilde{p}) = \Delta (T',w',p')\;. \end{aligned}$$

(3.39)

Denote $\widetilde{n}= |\widetilde{T}| = \frac{2}{\zeta \eta }$. We next define a set of intervals of $[\widetilde{n}]$.

Definition 3.15

Let $\widetilde{b}_0 = 0$, and for every $u \in [y']$, let $\widetilde{b}_u = \max \left\{ h \in [\widetilde{n}]: \phi (h) = b'_u\right\}$. For every $u \in [y']$ let $\widetilde{B}_u = [\widetilde{b}_{u-1}+1,\widetilde{b}_u]$, and define $\widetilde{\mathcal {B}} = \left\{ \widetilde{B}_u\right\} _{u=1}^{y'}\;$.

Here we use the shorthand

$$\begin{aligned} \widetilde{\xi }_{i}^{u} = \xi _i^u\left( \widetilde{T},w',\widetilde{p},\{\widetilde{b}_r\}_{r=1}^{y'}\right) \;, \end{aligned}$$

(3.40)

and note that (since $\widetilde{p}$ is the uniform distribution over $[\widetilde{n}]$),

$$\begin{aligned} \widetilde{\xi }_{i}^{u} = \frac{1}{\widetilde{n}}N_{i}^{\widetilde{b}_u}(\widetilde{T},w')\;. \end{aligned}$$

(3.41)

The proof of the next claim is almost identical to the proof of Claim 3.7, and is hence omitted.

Claim 3.12

For every $i \in [2k]$ and $u \in [y']$, $\widetilde{\xi }_{i}^{u} = {\xi '_{i}}^{u}$.

For the last claim in this subsection, recall that the event $E_1$ was defined in Definition 3.5 (based on a sample of indices from [n]).

Claim 3.13

Conditioned on the event $E_1$, for every $u \in [y']$, if $B_{f(u)}$ is light, then $\textrm{wt}_{\widetilde{p}}(\widetilde{B}_{u}) < \frac{5}{z} + \frac{{2}c_{\eta }}{z}$.

Proof

Consider any $u \in [y']$ such that $B_{f(u)}$ is light. Conditioned on the event $E_1$, the consequence of Claim 3.2 holds and so $\textrm{wt}_p(B_{f(u)}) < \frac{5}{z}$. By Observation 3.10, if $B_{f(u)}$ is light, then $\textrm{wt}_{p'}(B'_{u}) = \textrm{wt}_{\dot{p}}(B_{f(u)})$, so that $\textrm{wt}_{p'}(B'_{u}) - \textrm{wt}_p(B_{f(u)}) =\textrm{wt}_{\dot{p}}(B_{f(u)}) -\textrm{wt}_p(B_{f(u)})$, which is upper bounded by $L_1(\dot{p},p)$. By the definition of $\widetilde{p}$ and $\widetilde{B}_u$, $\textrm{wt}_{\widetilde{p}}(\widetilde{B}_{u}) = \textrm{wt}_{p'}(B'_{u})$ and by Eq. (3.28), $L_1(\dot{p},p) \le \frac{2c_{\eta }}{z}$. Combining the above,

$$\begin{aligned} \textrm{wt}_{\widetilde{p}}(\widetilde{B}_{u})= & {} \textrm{wt}_{p'}(B'_{u}) = \textrm{wt}_{\dot{p}}(B_{f(u)}) =\textrm{wt}_p(B_{f(u)}) + \textrm{wt}_{\dot{p}}(B_{f(u)}) - \textrm{wt}_p(B_{f(u)}) \nonumber \\< & {} \frac{5}{z} + \frac{2c_{\eta }}{z}, \end{aligned}$$

(3.42)

and the claim follows. $\square$

3.7 Estimators for the Distribution-Free Case

In this subsection we define estimators for the weights of intervals of $\widetilde{n}= |\widetilde{T}|$ according to $\widetilde{p}$. As there are several cases, it will be useful to introduce the following notations. For every $i \in [2k]$ and $u \in [y']$, let x(u, i) take the following values:

• $x(u,i)=1$ if $2 \not | \;i$ (so that $w_i \ne 0$),

• $x(u,i)=2$ if $2 \mid i$ and $B_{f(u)}$ is light,

• $x(u,i)=2$ (also) if $2 \mid i$ and $B_{f(u)}$ is heavy and $T'[b'_{u}] = 0$,

• $x(u,i)=3$ if $2 \mid i$ and $B_{f(u)}$ is heavy and $T'[b'_{u}] \ne 0$.

Define the following estimator. For every $i \in [2k]$ and $u \in [y']$,

$$\begin{aligned} \widehat{\xi }_{i}^{u} = \frac{1}{2} {\left\{ \begin{array}{ll} \breve{\xi }_{\frac{i+1}{2}}^{f(u)} &{} \text {if } x(u,i) = 1 \\ \textrm{wt}_{S_2}\left( [b_{f(u)}]\right) &{} \text {if } x(u,i) = 2 \\ \textrm{wt}_{S_2}\left( [b_{f(u-1)}]\right) &{} \text {if } x(u,i) = 3\;, \\ \end{array}\right. } \end{aligned}$$

(3.43)

where $\breve{\xi }_{i'}^{u'}$ is the “original” estimator defined in Definition 3.8.

For the next claim, recall that the event $E_2$ was defined in Definition 3.9.

Claim 3.14

Conditioned on the event $E_2$, for every $i \in [2k]$ and $u \in [y']$,

$$\begin{aligned} \left| \widehat{\xi }_{i}^{u} - \widetilde{\xi }_{i}^{u}\right| \le \frac{c_{\eta }}{z} + \frac{1}{2z}. \end{aligned}$$

(3.44)

Proof

Using Claim 3.12 (for the first equality below), Eq. (3.43) and Observation 3.11 (for the second equality), the triangle inequality and Claim 3.9 (for the final step), we get that for every $i \in [2k]$ and $u \in [y']$,

$$\begin{aligned} \left| \widehat{\xi }_{i}^{u} - \widetilde{\xi }_{i}^{u}\right|= & {} {\left| \widehat{\xi }_{i}^{u} - {\xi '}_{i}^{u}\right| } \\= & {} { \frac{1}{2} {\left\{ \begin{array}{ll} \left| \breve{\xi }_{{\frac{i+1}{2}}}^{f(u)} - \dot{\xi }_{\frac{i+1}{2}}^{f(u)}\right| &{} \text {if } x(u,i) = 1 \\ \left| \textrm{wt}_{S_2}\left( [b_{f(u)}]\right) - \textrm{wt}_{\dot{p}}\left( [b_{f(u)}]\right) \right| &{} \text {if } x(u,i) = 2 \\ \left| \textrm{wt}_{S_2}\left( [b_{f(u-1)}]\right) - \textrm{wt}_{\dot{p}}\left( [b_{f(u-1)}]\right) \right| &{} \text {if } x(u,i) = 3 . \end{array}\right. } } \\\le & {} \frac{1}{2} {\left\{ \begin{array}{ll} \left| \breve{\xi }_{{\frac{i+1}{2}}}^{f(u)} - \xi _{\frac{i+1}{2}}^{f(u)}\right| &{} \text {if } x(u,i) = 1 \\ \left| \textrm{wt}_{S_2}\left( [b_{f(u)}]\right) - \textrm{wt}_p\left( [b_{f(u)}]\right) \right| &{} \text {if } x(u,i) = 2 \\ \left| \textrm{wt}_{S_2}\left( [b_{f(u-1)}]\right) - \textrm{wt}_p\left( [b_{f(u-1)}]\right) \right| &{} \text {if } x(u,i) = 3 \end{array}\right. } \\{} & {} + \frac{1}{2} \sum _{{j \in [b_{f(u)}]}}\left| \dot{p}_j - p_j\right| . \end{aligned}$$

Using Eq. (3.28) and since we conditioned on $E_2$ we get the desired inequality. $\square$

We prove another claim to establish a connection between $\Delta (\widetilde{T},w',\widetilde{p})$ and $\Delta (T,w,p)$.

Claim 3.15

$$\begin{aligned} |2\Delta (\widetilde{T},w',\widetilde{p}) - \Delta (T,w,p)| \le L_1(p,\dot{p}) \;. \end{aligned}$$

(3.45)

Proof

The claim follows by combining Eqs. (3.29), (3.35) and (3.39). $\square$

3.8 Wrapping Things Up in the General Case

We can now restate and prove the main theorem of this section (as it appeared in the introduction).

Theorem 1.1

There exists a sample-based distribution-free distance-approximation algorithm for subsequence-freeness, that, for any subsequence w of length k, takes a sample of size $O\left( \frac{k^2}{\delta ^2}\cdot \log \left( \frac{k}{\delta }\right) \right)$ from T, distributed according to an unknown distribution p, and outputs an estimate $\widehat{\Delta }$ such that $|\widehat{\Delta }- \Delta (T,w,p)| \le \delta$ with probability at least $\frac{2}{3}$.¹¹ The running time of the algorithm is $O\left( \frac{k^2}{\delta ^2}\cdot \log ^2\left( \frac{k}{\delta }\right) \right)$.

The proof of Theorem 1.1 is similar to the proof of Lemma 3.8, but there are several important differences, and for the sake of completeness it is given in full detail.

Proof

The algorithm performs the following steps.

• 1. Take a sample $S_1$ of size $s_1 = 100 z \log (40z)$ and construct a set of intervals $\mathcal {B}$ as defined in Definition 3.4. For each interval in $\mathcal {B}$, determine whether it is heavy or light (as stated in the definition).

• 2. Take an additional sample, $S_2$, of size $s_2 = z^2 \log (40 k y)$. Compute $\textrm{wt}_{S_2}([b_u])$ for every $u \in [y]$ according to Definition 3.2, and define a matrix $\breve{\xi }$ of size $k \times y$ as follows. For every $i \in [k]$ and $u \in [y]$, set $\breve{\xi }[i][u] = \breve{\xi }_{i}^{u}$, where $\breve{\xi }_{i}^{u}$ is as defined in Definition 3.8 (based on $\mathcal {B}$ and the sample $S_2$).

• 3. Set $w' = w_1 0 w_2 0 \dots w_k 0$ and let $\mathcal {B}'$ be the set of $y'$ intervals as defined in Definition 3.14, using Algorithm 1. Recall that the algorithm also determines the function $f:[y']\rightarrow [y]$.

• 4. Define a matrix $\widehat{\xi }$ of size $2k \times y'$ as follows. For every $i \in [2k]$ and $u \in [y']$, set $\widehat{\xi }[i][u] = \widehat{\xi }_{i}^{u}$, where $\widehat{\xi }_{i}^{u}$ is as defined in Eq. (3.43).

• 5. Compute $M(\widehat{\xi })$ following Definition 2.2 (as described in the proof of Claim 2.5), and output $\widehat{\Delta }= 2 M(\widehat{\xi })$.

Since $z = O(k/\delta )$ and $y = O(z)$ (the upper bound $y \le s_1$ would also suffice for our purposes), the total sample complexity of the algorithm is as stated in the theorem. We next verify that the running time is also as stated in the Theorem. As in the proof of Lemma 3.8, Step 1 takes time $O(s_1\log s_1)$, and Step 2 takes time $O(k\cdot (\log k+ y) + s_2\cdot (\log k + \log y))$. Step 3 takes time O(y), and Step 4 takes time $O(k\cdot y)$. By Claim 2.5, Step 5 times time $O(k\cdot y)$. Summing over all steps we get the stated upper bound on the running time.

We would next like to apply Claim 3.6 in order to show that $|\widehat{\Delta }- \Delta (T,w,p)| \le \delta$ with probability of at least $\frac{2}{3}$. By the setting of $s_1$, applying Claim 3.1 gives us that with probability at least $\frac{4}{5}$, the event $E_1$, as defined in Definition 3.5, holds. By the setting of $s_2$, applying Claim 3.3 gives us that with probability at least $\frac{9}{10}$ the event $E_2$, as defined in Definition 3.9, holds. We henceforth condition on both events (where they hold together with probability at least 7/10).

In order to apply Claim 3.6, we set $\widetilde{w}= w'$, $J = \left\{ \widetilde{b}_0,\widetilde{b}_1,\dots ,\widetilde{b}_{y'}\right\}$ (recall Definition 3.15) and $\widehat{\mathcal {N}}= \widetilde{n}\widehat{\xi }$, for $\widehat{\xi }$ as defined above. We also set $c_1 = \frac{1}{8}$ and $c_2 = \frac{1}{8}$, and recall that $z = \frac{100k}{\delta }$ (Eq. (3.1)) and $c_{\eta }=\frac{1}{2}$ (as set in the beginning of Sect. 3.4). We next show that all the items in the premise of Claim 3.6 are satisfied.

To show that Item 1 is satisfied, we first note that the following is true for every $u \in [y']$. Since $\widetilde{p}$ is the uniform distribution over $[\widetilde{n}]$, $\frac{\widetilde{b}_{u} - \widetilde{b}_{u-1}}{\widetilde{n}} = \textrm{wt}_{\widetilde{p}}(\widetilde{\mathcal {B}}_{u})$. Therefore, if $\frac{\widetilde{b}_{u} - \widetilde{b}_{u-1}}{\widetilde{n}} {> c_1\cdot \frac{\delta }{\tilde{k}}} = \frac{25}{4}\cdot \frac{1}{z}$, then $\textrm{wt}_{\widetilde{p}}(\widetilde{\mathcal {B}}_{u}) > \frac{25}{4}\cdot \frac{1}{z}$, which by the setting of $c_{\eta }$ is greater than $(5 + 2c_{\eta })\cdot \frac{1}{z}$. By Claim 3.13 (recall we condition on $E_1$), we get that $\mathcal {B}_{f(u)}$ is heavy. This in turn means that $\mathcal {B}'_{u}$ contains only one index, which implies that $\widetilde{T}[\widetilde{b}_{u-1}+1] = \dots = \widetilde{T}[\widetilde{b}_{u}]$. Hence, the first item is satisfied.

To show that Item 2 is satisfied, we use Claim 3.14, which gives us that $\left| \widehat{\xi }_{i}^{u} - \widetilde{\xi }_{i}^{u}\right| \le \frac{c_{\eta }}{z} + \frac{1}{2z}$ for every $i \in [2k]$ and $u \in [y']$. By the setting of $c_2$ along with Eq. (3.41) and the definitions of z and $c_{\eta }$ we get that this item is satisfied as well.

After applying Claim 3.6 we get that $|\widehat{\Delta }- 2\Delta (\widetilde{T},w')| \le 2(c_1 \delta + 2c_2 \delta )$, which by the setting of $c_1$ and $c_2$ is at most $\frac{3 \delta }{4}$. Since $\widetilde{p}$ is the uniform distribution, $\Delta (\widetilde{T},w') = \Delta (\widetilde{T},w',\widetilde{p})$. Using Claim 3.15 and Eq. (3.28) we get $|2\Delta (\widetilde{T},w',\widetilde{p}) - \Delta (T,w,p)| \le 2 \frac{c_{\eta }}{z}$, which by the definition of z and $c_{\eta }$ is at most $\frac{\delta }{4}$, so the claim follows. $\square$

4 A Lower Bound for Distance Approximation

In this section we give a lower bound for the number of samples required to perform distance-approximation from w-freeness of a text T. The lower bound holds when the underlying distribution is the uniform distribution.

Theorem 4.1

Let $k_d$ be the number of distinct symbols in w. Any distance-approximation algorithm for w-freeness under the uniform distribution must take a sample of size $\Omega (\frac{1}{k_d\delta ^2})$, conditioned on $\delta \le \frac{1}{300 k_d}$ and $n > \max \left\{ \frac{8k}{\delta }, \frac{200}{k_d\delta ^2}\right\}$.

Note that if $\delta \ge 1/k_d$, then the algorithm can simply output 0. This is true since the number of role disjoint copies of w in T is at most the number of occurrences of the symbol in w that is least frequent in T. This number is upper bounded by $\frac{n}{k_d}$, and so the distance from w-freeness is at most $\frac{1}{k_d}$. In this case no sampling is needed, so only the trivial lower bound holds. The proof will deal with the case of $\delta \in (0,\frac{1}{300 k_d}]$.

Proof

The proof is based on the difficulty of distinguishing between an unbiased coin and a coin with a small bias. Precise details follow.

Let $V = \left\{ v_1,\dots ,v_{k_d}\right\}$ be the set of distinct symbols in w, and let 0 be a symbol that does not belong to V. We define two distributions over texts, $\mathcal {T}_1$ and $\mathcal {T}_2$ as follows. For each $\tau \in [\frac{n}{k_d}]$ and $\rho \in [0,1]$, let $\lambda _{\rho }^{\tau }$ be a random variable that equals 0 with probability $\rho$ and equals $v_1$ with probability $1-\rho$. Let $\delta ' = 3 k_d\delta$ and consider the following two distributions over texts

$$\begin{aligned} \mathcal {T}_1&= \left[ \lambda _{\frac{1}{2}}^1,v_2,v_3,\dots ,v_{k_d},\lambda _{\frac{1}{2}}^2,v_2,v_3,\dots ,v_{k_d},\dots \dots ,\lambda _{\frac{1}{2}}^{n/k_d},v_2,v_3,\dots ,v_{k_d}\right] \;, \end{aligned}$$

(4.1)

$$\begin{aligned} \mathcal {T}_2&= \left[ \lambda _{\frac{1}{2}+\delta '}^1,v_2,v_3,\dots ,v_{k_d},\lambda _{\frac{1}{2}+\delta '}^2,v_2,v_3,\dots ,v_{k_d},\dots \dots ,\lambda _{\frac{1}{2}+\delta '}^{n/k_d},v_2,v_3,\dots ,v_{k_d}\right] \;. \end{aligned}$$

(4.2)

Namely, the supports of both distributions contain texts that consist of $n/k_d$ blocks of size $k_d$ each. For $i\in \{2,\dots ,k_d\}$, the i-th symbol in each block is $v_i$. The distributions differ only in the way the first symbol in each block is selected. In $\mathcal {T}_1$ it is 0 with probability 1/2 and $v_1$ with probability 1/2, while in $\mathcal {T}_2$ it is 0 with probability $1/2 + \delta ' = 1/2 + 3 \delta k_d$, and $v_1$ with probability $1/2 - \delta '$.

For $b\in \{1,2\}$, consider selecting a text $T_b$ according to $\mathcal {T}_b$ (denoted by $T_b \sim \mathcal {T}_b$), and let $O_b$ be the number of occurrences of $v_1$ in the text (so that $O_b$ is a random variable). Observe that $\mathbb {E}[O_1] = \frac{n}{2k_d}$ and $\mathbb {E}[O_2] = \frac{n}{2k_d} - 3\delta n$. By applying the additive Chernoff bound (Theorem A.1) and using the premise of the theorem regarding n,

$$\begin{aligned} \textrm{Pr}_{T_1\sim \mathcal {T}_1}\left[ O_1 < \mathbb {E}[O_1] - \delta n/8 \right] \le \exp (-2 (k_d\delta /8)^2 \cdot n/k_d) \le \frac{1}{100}\;, \end{aligned}$$

(4.3)

and

$$\begin{aligned} \textrm{Pr}_{T_2\sim \mathcal {T}_2} \left[ O_2 < \mathbb {E}[O_2] + \delta n/8 \right] \le \exp (-2 (k_d\delta /8)^2 \cdot n/k_d) \le \frac{1}{100}\;. \end{aligned}$$

(4.4)

For $b\in \{1,2\}$ let $R_b = R(T_b,w)$ (recall that $R(T_b,w)$ denotes the number of disjoint copies of w in $T_b$, and note that $R_b$ is a random variable). Observe that $R_1 \ge O_1 - k+1$, and $R_2 \le O_2$.

Hence, by Eq. (4.3), if we select $T_1$ according to $\mathcal {T}_1$ and use the premise that $n > \frac{8k}{\delta }$, then $R(T_1,w) \ge \frac{n}{2k_d} - \frac{1}{8}\delta n - k + 1 \ge \frac{n}{2k_d} - \frac{2}{8}\delta n$ with probability at least 99/100, and by Eq. (4.4), if we select $T_2$ according to $\mathcal {T}_2$, then $R(T_2,w) \le \frac{n}{2k_d} - 3\delta n + \frac{1}{8}\delta n = \frac{n}{2k_d} - \frac{23}{8}\delta n$ with probability at least 99/100.

Assume, contrary to the claim, that we have a sample-based distance-approximation algorithm for subsequence-freeness that takes a sample of size $Q(k_d,\delta ) = 1/(ck_d\delta ^2)$, for some sufficiently large constant c, and outputs an estimate of the distance to w-freeness that has additive error at most $\delta$, with probability at least 2/3. Consider running the algorithm on either $T_1 \sim \mathcal {T}_1$ or $T_2 \sim \mathcal {T}_2$. Let L denote the number of times that the sample landed on an index of the form $j = \ell \cdot k_d+1$ for an integer $\ell$. By Markov’s inequality, the probability that $L > 10\cdot Q(k_d,\delta )/k_d= 10/(ck_d^2 \delta ^2)$ is at most 1/10.

By the above, if we run the algorithm on $T_1 \sim \mathcal {T}_1$, then with probability at least $2/3 - 1/100 - 1/10$ the algorithm outputs an estimate $\widehat{\Delta }\ge \frac{n}{2 k_d} - \frac{10}{8}$ while $L \le 10/(ck_d^2 \delta ^2)$. Similarly, if we run it on $T_2 \sim \mathcal {T}_2$, then with probability at least $2/3 - 1/100 - 1/10$ the algorithm outputs an estimate $\widehat{\Delta }\le \frac{n}{2 k_d} - \frac{15}{8}$ while $L \le 10/(ck_d^2 \delta ^2)$. (In both cases the probability is taken over the selection of $T_b\sim \mathcal {T}_b$, the sample that the algorithm gets, and possibly additional internal randomness of the algorithm.) Based on the definitions of $\mathcal {T}_1$ and $\mathcal {T}_2$, this implies that it is possible to distinguish between an unbiased coin and a coin with bias $3 k_d\delta$ with probability at least $2/3 - 1/100 - 1/10 > \frac{8}{15}$, using a sample of size $\frac{1}{c' k_d^2 \delta ^2}$ in contradiction to the result of Bar-Yosef [2, Thm. 8] (applied with $m=2$, $\epsilon = 3 k_d\delta$. Since we have $\delta < \frac{1}{300 k_d}$, then $\epsilon < \frac{1}{96}$, as the cited theorem requires). $\square$

Appendices

Chernoff Bounds

Theorem A.1

Let $\chi _1,\dots ,\chi _m$ be m independent random variables where $\chi _i \in [0,1]$ for every $1\le i \le m$. Let $p {\mathop {=}\limits ^\textrm{def}}\frac{1}{m}\sum _i \mathbb {E}[\chi _i]$. Then, for every $\gamma \in (0,1]$, the following bounds hold:

• (Additive Form)

  $$\begin{aligned}{} & {} \textrm{Pr}\left[ \frac{1}{m}\sum _{i=1}^{m} \chi _i > p + \gamma \right] < \exp \left( -2\gamma ^2 m\right) \end{aligned}$$

  (A.1)
  $$\begin{aligned}{} & {} \textrm{Pr}\left[ \frac{1}{m}\sum _{i=1}^{m} \chi _i< p - \gamma \right] < \exp \left( -2\gamma ^2 m\right) \end{aligned}$$

  (A.2)

• (Multiplicative Form)

  $$\begin{aligned}{} & {} \textrm{Pr}\left[ \frac{1}{m}\sum _{i=1}^{m} \chi _i > (1 + \gamma ) p \right] < \exp \left( -\gamma ^2 p m/3\right) \end{aligned}$$

  (A.3)
  $$\begin{aligned}{} & {} \textrm{Pr}\left[ \frac{1}{m}\sum _{i=1}^{m} \chi _i< (1 - \gamma ) p \right] < \exp \left( -\gamma ^2 p m/2\right) \end{aligned}$$

  (A.4)

Missing Proofs

Claim B.1

The greedy algorithm described as a part of the proof of Claim 2.1 finds a maximum-size set of role-disjoint copies of w in T.

Proof

We start by introducing the notion of ordered role-disjoint copies. According to [33, Definition 3.8], two role-disjoint copies $C=(i_1,\dots ,i_k)$ and $C'=(i'_1,\dots ,i'_k)$ of w in T are ordered and $C'$ succeeds C, if $i'_j>i_j$ for every $j \in [k]$. A sequence $(C_1,\dots ,C_m)$ of role-disjoint copies of w in T is a sequence of ordered role-disjoint copies if for every $r \in [m-1]$ we have it that $C_{r+1}$ succeeds $C_r$.

By [33, Claim 3.5], for every set of role-disjoint copies of w in T, there exists a sequence of ordered role-disjoint copies of w in T with the same size. Since the greedy algorithm described in the proof of Claim 2.1 finds a sequence of ordered role-disjoint copies of w in T, it remains to show that there is no other longer (larger) sequence of ordered role-disjoint copies of w of T.

Denote by $\mathcal {C}= (C_1,\dots ,C_{|\mathcal {C}|})$ the sequence of ordered role-disjoint copies of w in T that is found by the greedy algorithm. Assume, contrary to the claim that there is a longer sequence, $\widetilde{\mathcal {C}}= (\widetilde{C}_1,\dots ,\widetilde{C}_{|\widetilde{\mathcal {C}}|})$ of ordered role-disjoint copies of w in T. In what follows we show, by induction on m and i, that $C_m[i] \le \widetilde{C}_m[i]$ for every pair $(m,i)\in [|\mathcal {C}|]\times [k]$, which will imply a contradiction to the counter assumption.

For every $m \in [|\mathcal {C}|]$ and for $i=1$, by the definition of the greedy algorithm, $C_{m}[1]$ is the index of the mth occurrence of $w_1$ in T. Since $\widetilde{\mathcal {C}}$ is ordered, so that $\widetilde{C}_1[1]< \widetilde{C}_2[1]< \dots < \widetilde{C}_{m}[1]$, we have that $\widetilde{C}_{m}[1]$ is the index of occurrence number $m' \ge m$ of $w_1$ in T. Hence $C_m[1] \le \widetilde{C}_m[1]$ for every $m \in [|\mathcal {C}|]$.

In order to prove the claim for (m, i) where $i> 1$, we assume by induction that it holds for $(m,i-1)$ and for $(m-1,i)$, where for the sake of the argument (so that $C_{m-1}$ and $\widetilde{C}_{m-1}$ are defined also for $m=1$) we define $C_0[i] = \widetilde{C}_0[i] = -k+i$. By the induction hypothesis, $C_m[i-1] \le \widetilde{C}_m[i-1]$ and $C_{m-1}[i] < \widetilde{C}_{m-1}[i]$. Because indices of a copy are always strictly increasing, $\widetilde{C}_m[i-1] < \widetilde{C}_m[i]$, and since $\widetilde{\mathcal {C}}$ is ordered, $\widetilde{C}_{m-1}[i] < \widetilde{C}_m[i]$. Therefore, $C_m[i-1] < \widetilde{C}_m[i]$ and $C_{m-1}[i] < \widetilde{C}_m[i]$. By the definition of the algorithm, $C_m[i]$ is the index of the first occurrence of $w_i$ following $C_m[i-1]$ that is larger than $C_{m-1}[i]$. Since $T[\widetilde{C}_m[i]]=w_i$ we get that $C_m[i] \le \widetilde{C}_m[i]$, as claimed.

Finally, by the counter assumption, $|\widetilde{\mathcal {C}}| > |\mathcal {C}|$. By what we have shown above, this implies that $C_{m}[i] < \widetilde{C}_{|C|+1}[i]$ for every $m \in [|C|]$, and $i \in [k]$. But this contradicts the fact that the algorithm did not find any role-disjoint copy after $C_{|\mathcal {C}|}$. $\square$

Proof of Claim 2.4

Let $s = \frac{\log (6k\cdot \ell )}{2\gamma ^2}$. We take s samples from [n] selected uniformly, independently at random (allowing repetitions). Denote the q-th sampled index by $\rho _q$. For every $i \in [k]$, $r \in [\ell ]$ and $q \in [s]$, define the random variables $\chi _q^{i,r}$ to equal 1 if and only if $\rho _q \in [j_r]$ and $T[\rho _q]=w_i$, Otherwise $\chi _q^{i,r} = 0$.

For every $i \in [k]$ and $r \in [\ell ]$, set

$$\begin{aligned} \widehat{\mathcal {N}}_{i}^{r} = \frac{n}{s}\sum _{q=1}^{s}\chi _q^{i,r} \;, \end{aligned}$$

(B.1)

and notice that

$$\begin{aligned} \mathbb {E}\left[ \chi _q^{i,j}\right] = \frac{N_{i}^{j_r}(T,w)}{n}\;. \end{aligned}$$

(B.2)

By the additive Chernoff bound (see Theorem A.1) and the setting of s, we get

$$\begin{aligned} \textrm{Pr}\left[ \left| \widehat{\mathcal {N}}_{i}^{r} - N_{i}^{j_r}(T,w) \right|> \gamma n\right]= & {} \textrm{Pr}\left[ \left| \frac{n}{s}\sum _{q=1}^{s}\chi _q^{i,r} - N_{i}^{j_r}(T,w) \right|> \gamma n\right] \nonumber \\= & {} \textrm{Pr}\left[ \left| \frac{1}{s}\sum _{q=1}^{s}\chi _q^{i,r} - \frac{N_{i}^{j_r}(T,w)}{n} \right| > \gamma \right] \nonumber \\< & {} 2 \exp \left( -2 \gamma ^2 s\right) = \frac{1}{3 k\cdot \ell }. \end{aligned}$$

(B.3)

Applying the union bound over all pairs $(i,r) \in [k]\times [\ell ]$ we get that with probability at least $\frac{2}{3}$, for every $i \in [k]$ and $r\in [\ell ]$,

$$\begin{aligned} \left| \widehat{\mathcal {N}}_{i}^{r}- N_{i}^{j_r}(T,w) \right| \le \gamma n \;, \end{aligned}$$

(B.4)

as required. Computing the estimates can be done as follows.

• 1. Perform a preprocessing step that depends only on w. Let $k'$ be the number of distinct symbols in w. We may assume that there is some total order over these symbols (and in general, the symbols in $\Sigma$). Create an array W of size $k'$ where entry number d in W contains the d-th distinct symbol in w in sorted order and a pointer to a sorted list of the indices in w where this symbol appears.

• 2. Initialize each $\widehat{\mathcal {N}}_{i}^{r}$ to 0.

• 3. Make a single pass over the sample, and for each sample point $(j,t_j)$, let r(j) be the minimum r for which $j \le j_r$ and let $i(t_j)$ be the minimum i such that $w_i = t_j$. Increase $\widehat{\mathcal {N}}_{i(t_j)}^{r(j)}$ by $\frac{n}{s}$.

• 4. For $r = 2$ to $\ell$, increase $\widehat{\mathcal {N}}_i^r$ by $\widehat{\mathcal {N}}_i^{r-1}$ for every $i\in k$.

• 5. For $i=2$ to k, let $i'$ be the minimum index for which $w_i = w_{i'}$. If $i\ne i'$, then set $\widehat{\mathcal {N}}_i^r = \widehat{\mathcal {N}}_{i'}^r$ for every $r\in [\ell ]$.

The first step takes time $O(k\log k)$. The second step takes time $O(k\cdot \ell )$. The third step takes time $O(s\cdot (\log \ell + \log k))$ (using J and W to find r(j) and $i(t_j)$, respectively, for each sample point $(j,t_j)$). The fourth and fifth steps take time $O(k\cdot \ell )$. $\square$

Proof of Claim 3.4

For the sake of simplicity, we use T and w instead of $\widetilde{T}$ and $\widetilde{w}$, respectively. Recall that $M(\mathcal {N}) = M_{k}^{\ell }(\mathcal {N})$ and $R(T,w) = R_{k}^{j_{\ell }}(T,w)$. We shall prove that for every $i \in [k]$ and for every $r\in [\ell ]$, $\left| M_{i}^{r}(\mathcal {N}) - R_{i}^{j_{r}}(T,w)\right| \le (i-1)\cdot \max _{\tau \in [r] {\setminus } J' }\left\{ j_{\tau } - j_{\tau -1}\right\}$. We prove this by induction on i.

For $i=1$ and every $r\in [\ell ]$:

$$\begin{aligned} \left| M_{1}^r(\mathcal {N}) - R_{1}^{j_r}(T,w)\right|= & {} \left| N_1^{j_r}(T,w) - N_1^{j_r}(T,w) \right| \nonumber \\ {}= & {} 0 \le (1-1) \cdot \max _{\tau \in [1] \setminus J'}\left\{ j_{\tau } - j_{\tau -1}\right\} , \end{aligned}$$

(B.5)

where the first equality follows from the setting of $\mathcal {N}$ and the definitions of $M_1^r(\mathcal {N})$ and $R_1^{j_r}(T,w)$.

For the induction step, we assume the claim holds for $i-1 \ge 1$ (and every $r\in [\ell ]$) and prove it for i. We have,

$$\begin{aligned}{} & {} M_{i}^{r}(\mathcal {N}) - R_{i}^{j_r}(T,w)\nonumber \\{} & {} \quad = N_i^{j_r}(T,w)- \max _{b \in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} - R_{i}^{j_r}(T,w) \end{aligned}$$

(B.6)

$$\begin{aligned}{} & {} \quad = \max _{j \in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} - \max _{b\in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} ,\qquad \quad \end{aligned}$$

(B.7)

where Eq. (B.6) follows from the setting of $\mathcal {N}$ and the definition of $M_{i}^{r}(\mathcal {N})$, and Eq. (B.7) is implied by Claim 2.1. Denote by $j^*$ an index $j \in [j_r]$ that maximizes the first max term and let $b^*$ be the smallest index such that $j_{b^*} \ge j^*$. We have:

$$\begin{aligned}{} & {} \max _{ j\in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} - \max _{b \in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} \nonumber \\{} & {} \quad \le N_i^{j^*}(T,w) - R_{i-1}^{j^*-1}(T,w) - N_i^{j_{b^*}}(T,w) + M_{i-1}^{b^*}(\mathcal {N}) \nonumber \\{} & {} \quad = N_i^{j^*}(T,w) + R_{i-1}^{j_{b^*}}(T,w) - R_{i-1}^{j_{b^*}}(T,w) - R_{i-1}^{j^*-1}(T,w) \nonumber \\{} & {} \qquad - N_i^{j_{b^*}}(T.w) + M_{i-1}^{b^*}(\mathcal {N}) \nonumber \\{} & {} \quad \le \left( M_{i-1}^{b^*}(\mathcal {N}) - R_{i-1}^{j_{b^*}}(T,w)\right) + \left( N_i^{j^*}(T,w) - N_i^{j_{b^*}}(T,w) \right) \nonumber \\{} & {} \qquad +\left( R_{i-1}^{j_{b^*}}(T,w) - R_{i-1}^{j^*-1}(T,w)\right) \nonumber \\{} & {} \quad \le (i-2) \max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} \nonumber \\{} & {} \qquad + {\left\{ \begin{array}{ll} 0 &{} \text {, if } T[j_a^*] = \dots = T[j_b^*]] \\ \max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} &{} \text {otherwise}\\ \end{array}\right. } \nonumber \\{} & {} \quad \le (i-1)\max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} , \end{aligned}$$

(B.8)

Where in the third inequality we used the induction assumption and the fact that if we don’t have $T[j_{b^*}] = \dots = T[j^*]]$, then $\left( N_i^{j^*}(T,w) - N_i^{j_{b^*}}(T,w) \right) +\left( R_{i-1}^{j_{b^*}}(T,w) - R_{i-1}^{j^{*}-1}(T,w)\right) \le (j_{b^*} - j^* + 1) \le \max _{\tau \in [r] {\setminus } J' }\left\{ j_{\tau } - j_{\tau -1}\right\}$.

By combining Eqs. (B.7) and (B.8), we get that

$$\begin{aligned} M_{i}^{r}(\mathcal {N}) - R_{i}^{j_r}(T,w) \le (i-1)\max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} \;. \end{aligned}$$

(B.9)

Similarly to Eq. (B.7):

$$\begin{aligned} R_{i}^{j_r}(T,w) - M_{i}^{r}(\mathcal {N}) = \max _{b\in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} - \max _{j\in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} . \nonumber \\ \end{aligned}$$

(B.10)

Let $b^{**}$ be the index $b\in [r]$ that maximizes the first max term. We have:

$$\begin{aligned}{} & {} \max _{b \in [r]}\left\{ N_i^{j_b}(T,w) - M_{i-1}^{b}(\mathcal {N}) \right\} - \max _{ j \in [j_r]}\left\{ N_i^{j}(T,w) - R_{i-1}^{j-1}(T,w) \right\} \nonumber \\{} & {} \quad \le N_i^{j_{b^{**}}}(T,w) - M_{i-1}^{{b^{**}}}(\mathcal {N}) - N_i^{j_{b^{**}}}(T,w) + R_{i-1}^{j_{b^{**}}-1}(T,w) \nonumber \\{} & {} \quad \le R_{i-1}^{j_{b^{**}}}(T,w) - M_{i-1}^{b^{**}}(\mathcal {N}) \nonumber \\{} & {} \quad \le \left| R_{i-1}^{j_{b^{**}}}(T,w) - M_{i-1}^{b^{**}}(\mathcal {N})\right| \nonumber \\{} & {} \quad \le (i-2)\max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} \le (i-1)\max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} . \end{aligned}$$

(B.11)

Hence (combining Eqs. (B.10) and (B.11)),¹²

$$\begin{aligned} R_{i}^{j_r}(T,w) - M_{i}^{r}(\mathcal {N}) \le (i-1)\max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} \; \end{aligned}$$

(B.12)

Together, Eqs. (B.9) and (B.12) give us that

$$\begin{aligned} \left| M_{i}^{r}(\mathcal {N}) - R_{i}^{j_r}(T,w)\right| \le (i-1)\max _{\tau \in [r] \setminus J' }\left\{ j_{\tau } - j_{\tau -1}\right\} \;, \end{aligned}$$

(B.13)

and the proof is completed. $\square$