Runtime Analysis of Competitive Co-evolutionary Algorithms for Maximin Optimisation of a Bilinear Function

Abstract

Co-evolutionary algorithms have a wide range of applications, such as in hardware design, evolution of strategies for board games, and patching software bugs. However, these algorithms are poorly understood and applications are often limited by pathological behaviour, such as loss of gradient, relative over-generalisation, and mediocre objective stasis. It is an open challenge to develop a theory that can predict when co-evolutionary algorithms find solutions efficiently and reliable. This paper provides a first step in developing runtime analysis for population-based competitive co-evolutionary algorithms. We provide a mathematical framework for describing and reasoning about the performance of co-evolutionary processes. To illustrate the framework, we introduce a population-based co-evolutionary algorithm called PDCoEA, and prove that it obtains a solution to a bilinear maximin optimisation problem in expected polynomial time. Finally, we describe settings where PDCoEA needs exponential time with overwhelmingly high probability to obtain a solution.

1 Introduction

Many real-world optimisation problems feature a strategic aspect, where the solution quality depends on the actions of other—potentially adversarial—players. There is a need for adversarial optimisation algorithms that operate under realistic assumptions. Departing from a traditional game theoretic setting, we assume two classes of players, choosing strategies from “strategy spaces” ${\mathcal {X}}$ and ${\mathcal {Y}}$ respectively. The objectives of the players are to maximise their individual “payoffs” as given by payoff functions $f,g:{\mathcal {X}}\times {\mathcal {Y}}\rightarrow {\mathbb {R}}$.

A fundamental algorithmic assumption is that there is insufficient computational resources available to exhaustively explore the strategy spaces ${\mathcal {X}}$ and ${\mathcal {Y}}$. In a typical real world scenario, a strategy could consist of making n binary decisions. This leads to exponentially large and discrete strategy spaces ${\mathcal {X}}={\mathcal {Y}}=\{0,1\}^n$. Furthermore, we can assume that the players do not have access to or the capability to understand the payoff functions. However, it is reasonable to assume that players can make repeated queries to the payoff function [13]. Together, these assumptions render many existing approaches impractical, e.g., Lemke–Howson, best response dynamics, mathematical programming, or gradient descent-ascent.

Co-evolutionary algorithms (CoEAs) (see [28] for a survey) could have a potential in adversarial optimisation, partly because they make less strict assumptions than the classical methods. Two populations are co-evolved (say one in $\mathcal {X}$, the other in $\mathcal {Y}$), where individuals are selected for reproduction if they interact successfully with individuals in the opposite population (e.g. as determined by the payoff functions f, g). The hoped for outcome is that an artificial “arms race” emerges between the populations, leading to increasingly sophisticated solutions. In fact, the literature describe several successful applications, including design of sorting networks [16], software patching [2], and problems arising in cyber security [26].

It is common to separate co-evolution into co-operative and competitive co-evolution. Co-operative co-evolution is attractive when the problem domain allows a natural division into sub-components. For example, the design of a robot can be separated into its morphology and its control [27]. A cooperative co-evolutionary algorithm works by evolving separate “species”, where each species is responsible for optimising one sub-component of the overall solution. To evaluate the fitness of a sub-component, it is combined with sub-components from the other species to form a complete solution. Ideally, there will be a selective pressure for the species to cooperate, so that they together produce good overall designs [29].

The behaviour of CoEAs can be abstruse, where pathological population behaviour such as loss of gradient, focusing on the wrong things, and relativism [30] prevent effective applications. It has been a long-standing open problem to develop a theory that can explain and predict the performance of co-evolutionary algorithms (see e.g. Section 4.2.2 in [28]), notably runtime analysis. Runtime analysis of EAs [10] has provided mathematically rigorous statements about the runtime distribution of evolutionary algorithms, notably how the distribution depends on characteristics of the fitness landscape and the parameter settings of the algorithm. Following from the publication of the conference version of this paper, several other results on the runtime of competitive co-evolutionary algorithms have appeared considering variants of the Bilinear game introduced in Sect. 4. Hevia, Lehre and Lin analysed the runtime of Randomised Local Search CoEA (RLS-PD) on Bilinear [12]. Hevia and Lehre analysed the runtime of $(1,\lambda )$ CoEA on a lattice variant of Bilinear [15].

The only rigorous runtime analysis of co-evolution the author is aware of focuses on co-operative co-evolution. In a pioneer study, Jansen and Wiegand considered the common assumption that co-operative co-evolution allows a speedup for separable problems [17]. They compared rigorously the runtime of the co-operative co-evolutionary (1+1) Evolutionary Algorithm (CC (1+1) EA) with the classical (1+1) EA. Both algorithms follow the same template: They keep the single best solution seen so far, and iteratively produce new candidate solution by “mutating” the best solution. However, the algorithms use different mutation operators. The CC (1+1) EA restricts mutation to the bit-positions within one out of k blocks in each iteration. The choice of the current block alternates deterministically in each iteration, such that in k iterations, every block has been active once. The main conclusion from their analysis is that problem separability is not a sufficient criterion to determine whether the CC (1+1) EA performs better than the (1+1) EA. In particular, there are separable problems where the (1+1) EA outperforms the CC (1+1) EA, and there are inseparable problems where the converse holds. What the authors find is that CC (1+1) EA is advantageous when the problem separability matches the partitioning in the algorithm, and there is a benefit from increased mutation rates allowed by the CC (1+1) EA.

Much work remains to develop runtime analysis of co-evolution. Co-operative co-evolution can be seen as a particular approach to traditional optimisation, where the goal is to maximise a given objective function. In contrast, competitive co-evolutionary algorithms are employed for a wide range of solution concepts [14]. It is unclear to what degree results about co-operative CoEAs can provide insights about competitive CoEAs. Finally, the existing runtime analysis considers the CC (1+1) EA which does not have a population. However, it is particularly important to study co-evolutionary population dynamics to understand the pathologies of existing CoEAs.

This paper makes the following contributions: Sect. 2 introduces a generic mathematical framework to describe a large class of co-evolutionary processes and defines a notion of “runtime” in the context of generic co-evolutionary processes. We then discuss how the population-dynamics of these processes can be described by a stochastic process. Section 3 presents an analytical tool (a co-evolutionary level-based theorem) which can be used to derive upper bounds on the expected runtime of co-evolutionary algorithms. Section 4 specialises the problem setting to maximin-optimisation, and introduces a theoretical benchmark problem Bilinear. Section 5 introduces the algorithm PDCoEA which is a particular co-evolutionary process tailored to maximin-optimisation. We then analyse the runtime of PDCoEA on Bilinear using the level-based theorem, showing that there are settings where the algorithm obtains a solution in polynomial time. Since the publication of the conference version of this paper, the PDCoEA has been applied to a cyber-security domain [21]. In Sect. 6, we demonstrate that the PDCoEA possesses an “error threshold”, i.e., a mutation rate above which the runtime is exponential for any problem. Finally, the appendix contains some technical results which have been relocated from the main text to increase readability.

1.1 Preliminaries

For any natural number $n\in {\mathbb {N}}$, we define $[n]:=\{1,2,\ldots , n\}$ and $[0..n]:=\{0\}\cup [n]$. For a filtration $(\mathscr {F}_{t})_{t\in {\mathbb {N}}}$ and a random variable X we use the shorthand notation $\mathbb {E}_t\left[ X\right] := \mathbb {E}\left[ X\mid \mathscr {F}_{t}\right]$. A random variable X is said to stochastically dominate a random variable Y, denoted $X\succeq Y$, if and only if $\Pr \left( Y\le z\right) \ge \Pr \left( X\le z\right)$ for all $z\in {\mathbb {R}}$. The Hamming distance between two bitstrings x and y is denoted H(x, y). For any bitstring $z\in \{0,1\}^n$, $\Vert z\Vert :=\sum _{i=1}^n z_i$, denotes the number of 1-bits in z.

2 Co-evolutionary Algorithms

This section describes in mathematical terms a broad class of co-evolutionary processes (Algorithm 1), along with a definition of their runtime for a given solution concept. The definition takes inspiration from level-processes (see Algorithm 1 in [4]) used to describe non-elitist evolutionary algorithms.

Algorithm 1

Co-evolutionary Process

We assume that in each generation, the algorithm has two¹ populations $P\in \mathcal {X} ^\lambda$ and $Q\in \mathcal {Y} ^\lambda$ which we sometimes will refer to as the “predators” and the “prey”. Note that these terms are adopted only to connect the algorithm with their biological inspiration without imposing further conditions. In particular, we do not assume that predators or prey have particular roles, such as one population taking an active role and the other population taking a passive role. We posit that in each generation, the populations interact $\lambda$ times, where each interaction produces in a stochastic fashion one new predator $x\in \mathcal {X}$ and one new prey $y\in \mathcal {Y}$. The interaction is modelled as a probability distribution ${\mathcal {D}}(P,Q)$ over $\mathcal {X} \times \mathcal {Y}$ that depends on the current populations. For a given instance of the framework, the operator ${\mathcal {D}}$ encapsulates all aspects that take place in producing new offspring, such as pairing of individuals, selection, mutation, crossover, etc. (See Sect. 5 for a particular instance of ${\mathcal {D}}$).

As is customary in the theory of evolutionary computation, the definition of the algorithm does not state any termination criterion. The justification for this omission is that the choice of termination criterion does not impact the definition of runtime we will use.

Notice that the predator and the prey produced through one interaction are not necessarily independent random variables. However, each of the $\lambda$ interactions in one generation are independent and identically distributed random variables.

We will restrict ourselves to solution concepts that can be characterised as finding a given target subset ${\mathcal {S}}\subseteq \mathcal {X} \times \mathcal {Y}$. This captures for example maximin optimisation or finding pure Nash equilibria. Within this context, the goal of Algorithm 1 is now to obtain populations $P_t$ and $Q_t$ such that their product intersects with the target set ${\mathcal {S}}$. We then define the runtime of an algorithm A as the number of interactions before the target subset has been found.

Definition 1

(Runtime) For any instance ${\mathcal {A}}$ of Algorithm 1 and subset ${\mathcal {S}}\subseteq \mathcal {X} \times \mathcal {Y}$, define $T_{{\mathcal {A}},{\mathcal {S}}}:= \min \{t\lambda \in {\mathbb {N}}\mid (P_t\times Q_t)\cap {\mathcal {S}}\ne \emptyset \}.$

We follow the convention in analysis of population-based EAs that the granularity of the runtime is in generations, i.e., multiples of $\lambda$. The definition overestimates the number of interactions before a solution is found by at most $\lambda -1$.

2.1 Tracking the Algorithm State

We will now discuss how the state of Algorithm 1 can be captured with a stochastic process. To determine the trajectory of a co-evolutionary algorithm, it is insufficient, naturally, to track only one of the populations, as the dynamics of the algorithm is determined by the relationship between the two populations.

Given the definition of runtime, it will be natural to describe the state of the algorithm via the Cartesian product $P_t\times Q_t$. In particular, for subsets $A\subset \mathcal {X}$ and $B\subset Y$, we will study the drift of the stochastic process $Z_t:= \vert (P_t\times Q_t)\cap (A\times B) \vert$.

Naturally, the predator x and the prey y sampled in line 3 of Algorithm 1 are not necessarily independent random variables. However, a predator x sampled in interaction $i_1$ is probabilistically independent of any prey sampled in an interaction $i_2\ne i_1$. In order to not have to explicitly take these dependencies into account later in the paper, we now characterise properties of the distribution of $Z_t$ in Lemma 1.

Lemma 1

Given subsets $A\subset {\mathcal {X}}, B\subset {\mathcal {Y}}$, assume that for any $\delta >0$ and $\gamma \in (0,1)$, the sample $(x,y)\sim {\mathcal {D}}(P_t,Q_t)$ satisfies

$$\begin{aligned} \Pr \left( x\in A\right) \Pr \left( y\in B\right) \ge (1+\delta )\gamma , \end{aligned}$$

and $P_t$ and $Q_t$ are adapted to a filtration $(\mathscr {F}_{t})_{t\in {\mathbb {N}}}$. Then the random variable $Z_{t+1}:=\vert (P_{t+1}\times Q_{t+1}) \cap (A\times B)\vert$ satisfies

• (1) $\mathbb {E}\left[ Z_{t+1}\mid \mathscr {F}_{t}\right] \ge \lambda (\lambda -1)(1+\delta )\gamma$.

• (2) $\mathbb {E}\left[ e^{-\eta Z_{t+1}}\mid \mathscr {F}_{t}\right] \le e^{-\eta \lambda (\gamma \lambda -1)}$ for $0<\eta \le (1-(1+\delta )^{-1/2})/\lambda$

• (3) $\Pr \left( Z_{t+1}< \lambda (\gamma \lambda -1)\mid \mathscr {F}_{t} \right) \le e^{-\delta _1\gamma \lambda \left( 1-\sqrt{\frac{1+\delta _1}{1+\delta }}\right) }$ for $\delta _1\in (0,\delta )$.

Proof

In generation $t+1$, the algorithm samples independently and identically $\lambda$ pairs $(P_{t+1}(i),Q_{t+1}(i))_{i\in [\lambda ]}$ from distribution ${\mathcal {D}}(P_t,Q_t)$. For all $i\in [\lambda ]$, define the random variables $X'_{i}:= \mathbb {1}_{\{P_{t+1}(i)\in A\}}$ and $Y'_{i}:= \mathbb {1}_{\{Q_{t+1}(i)\in B\}}$. Then since the algorithm samples each pair $(P_{t+1}(i),Q_{t+1}(i))$ independently, and by the assumption of the lemma, there exists $p,q\in (0,1]$ such that $X':=\sum _{i=1}^\lambda X'_i\sim {{\,\textrm{Bin}\,}}(\lambda ,p)$, and $Y':=\sum _{i=1}^\lambda Y'_i\sim {{\,\textrm{Bin}\,}}(\lambda ,q)$, where $pq\ge \gamma (1+\delta )$. By these definitions, it follows that $Z_{t+1}=X'Y'$.

Note that $X'$ and $Y'$ are not necessarily independent random variables because $X'_i$ and $Y'_i$ are not necessarily independent. However, by defining two independent binomial random variables $X\sim {{\,\textrm{Bin}\,}}(\lambda ,p)$, and $Y\sim {{\,\textrm{Bin}\,}}(\lambda ,q)$, we readily have the stochastic dominance relation

$$\begin{aligned} Z_{t+1} = X'Y'&= \left( \sum _{i=1}^\lambda X'_i\right) \left( \sum _{j=1}^\lambda Y'_j\right) \end{aligned}$$

(1)

$$\begin{aligned}&= \left( \sum _{i=1}^\lambda X_i\right) \left( \sum _{j\ne i} Y_j\right) + \sum _{i=1}^\lambda X'_iY'_i \end{aligned}$$

(2)

$$\begin{aligned}&= XY - \sum _{i=1}^\lambda X_iY_i + \sum _{i=1}^\lambda X'_iY'_i \end{aligned}$$

(3)

$$\begin{aligned}&\succeq XY - \sum _{i=1}^\lambda X_iY_i. \end{aligned}$$

(4)

The first statement of the lemma is now obtained by exploiting (4), Lemma 27 in the appendix, and the independence between X and Y

$$\begin{aligned} \mathbb {E}_t\left[ Z_{t+1}\right]&\ge \mathbb {E}\left[ XY-\sum _{i=1}^\lambda X_iY_i\right] = \mathbb {E}\left[ X\right] \mathbb {E}\left[ Y\right] -\sum _{i=1}^\lambda \mathbb {E}\left[ X_i\right] \mathbb {E}\left[ Y_i\right] \\&= p\lambda q\lambda - \lambda p q = pq\lambda (\lambda -1) \ge (1+\delta )\gamma \lambda (\lambda -1). \end{aligned}$$

For the second statement, we apply Lemma 18 wrt X, Y, and the parameters $\sigma :=\sqrt{1+\delta }-1$ and $z:=\gamma$. By the assumption on p and q, we have $pq \ge (1+\delta )\gamma = (1+\sigma )^2z,$ furthermore the constraint on parameter $\eta$ gives

$$\begin{aligned} \eta&\le \frac{1}{\lambda }\left( 1-\frac{1}{\sqrt{1+\delta }}\right) = \frac{\sqrt{1+\delta }-1}{\lambda \sqrt{1+\delta }} = \frac{\sigma }{(1+\sigma )\lambda }. \end{aligned}$$

The assumptions of Lemma 18 are satisfied, and we obtain from (4)

$$\begin{aligned} \mathbb {E}_t\left[ e^{-\eta Z_{t+1}}\right]&\le \mathbb {E}\left[ \exp \left( -\eta XY+\eta \sum _{i=1}^\lambda X_iY_i\right) \right] \\&< e^{\eta \lambda }\cdot \mathbb {E}\left[ e^{-\eta XY}\right] < e^{\eta \lambda }\cdot e^{-\eta \gamma \lambda ^2} = e^{-\eta \lambda (\gamma \lambda -1)}. \end{aligned}$$

Given the second statement, the third statement will be proved by a standard Chernoff-type argument. Define $\delta _2>0$ such that $(1+\delta _1)(1+\delta _2)=1+\delta$. For

$$\begin{aligned} \eta := \frac{1}{\lambda }\left( 1-\frac{1}{\sqrt{1+\delta _2}}\right) = \frac{1}{\lambda }\left( 1-\sqrt{\frac{1+\delta _1}{1+\delta }}\right) \end{aligned}$$

and $a:=\lambda (\gamma \lambda -1)$, it follows by Markov’s inequality

$$\begin{aligned} \Pr {}_t\left( Z_{t+1}\le a\right)&= \Pr {}_t\left( e^{-\eta Z_{t+1}}\ge e^{-\eta a}\right) \le e^{\eta a}\cdot \mathbb {E}_t\left[ e^{-\eta Z_{t+1}}\right] \\&\le e^{\eta a}\cdot \exp \left( -\eta \lambda (\gamma (1+\delta _1)\lambda -1)\right) \\&= e^{\eta a - \eta a-\eta \gamma \lambda ^2\delta _1} = e^{-\eta \gamma \lambda ^2\delta _1}\\&= \exp \left( -\delta _1\left( 1-\sqrt{\frac{1+\delta _1}{1+\delta }}\right) \gamma \lambda \right) , \end{aligned}$$

where the last inequality applies statement 2. $\square$

The next lemma is a variant of Lemma 1, and will be used to compute the probability of producing individuals in “new” parts of the product space $\mathcal {X} \times \mathcal {Y}$ (see condition (G1) of Theorem 3).

Lemma 2

For $A\subset {\mathcal {X}}$ and $B\subset {\mathcal {Y}}$ define

$$\begin{aligned} r:=\Pr \left( (P_{t+1}\times Q_{t+1})\cap (A\times B)\ne \emptyset \right) . \end{aligned}$$

If for $(x,y)\sim \mathcal {D}(P_t,Q_t)$, it holds $\Pr \left( x\in A\right) \Pr \left( y\in B\right) \ge z,$ then

$$\begin{aligned} \frac{1}{r} < \frac{3}{z(\lambda -1)}+1. \end{aligned}$$

Proof

Define $p:= \Pr \left( x\in A\right) , q:=\Pr \left( y\in B\right)$ and $\lambda ':=\lambda -1$. Then by the definition of r and Lemma 25

$$\begin{aligned} r&\ge \Pr \left( \exists k\ne \ell : P_{t+1}(k)=u\wedge Q_{t+1}(\ell )=v \right) \\&\ge (1-(1-p)^\lambda )(1-(1-q)^{\lambda '}) > \left( \frac{\lambda 'p}{1+\lambda 'p}\right) \left( \frac{\lambda 'q}{1+\lambda 'q}\right) \\&\ge \frac{\lambda '^2z}{1+\lambda '(p+q)+\lambda '^2z} \ge \frac{\lambda '^2z}{1+2\lambda '+\lambda '^2z}. \end{aligned}$$

Finally,

$$\begin{aligned} \frac{1}{r} \le \frac{2}{z\lambda '}+\frac{1}{z\lambda '^2}+1 < \frac{3}{z\lambda '}+1=\frac{3}{z(\lambda -1)}+1. \end{aligned}$$

$\square$

3 A Level-Based Theorem for Co-evolutionary Processes

This section provides a generic tool (Theorem 3), a level-based theorem for co-evolution, for deriving upper bounds on the expected runtime of Algorithm 1. Since this theorem can be seen as a generalisation of the original level-based theorem for classical evolutionary algorithms introduced in [4], we will start by briefly discussing the original theorem. Informally, it assumes a population-based process where the next population $P_{t+1}\in {\mathcal {X}}^\lambda$ is obtained by sampling independently $\lambda$ times from a distribution ${\mathcal {D}}(P_t)$ that depends on the current population $P_t\in {\mathcal {X}}^\lambda$. The theorem provides an upper bound on the expected number of generations until the current population contains an individual in a target set $A_{\ge m}\subset {\mathcal {X}}$, given that the following three informally-described conditions hold. Condition (G1): If a fraction $\gamma _0$ of the population belongs to a “current level” (i.e., a subset) $A_{\ge j} \subset {\mathcal {X}}$, then the distribution ${\mathcal {D}}(P_t)$ should assign a non-zero probability $z_j>0$ of sampling individuals in the “next level” $A_{\ge j+1}$. Condition (G2): If already a $\gamma$-fraction of the population belongs to the next level $A_{\ge j+1}$ for $\gamma \in (0,\gamma _0)$, then the distribution ${\mathcal {D}}(P_t)$ should assign a probability at least $\gamma (1+\delta )$ to the next level. Condition (G3) is a requirement on the population size $\lambda$. Together, conditions (G1) and (G2) ensure that the process “discovers” and multiplies on next levels, thus evolving towards the target set. Due to its generality, the classical level-based theorem and variations of it have found numerous applications, e.g., in runtime analysis of genetic algorithms [5], estimation of distribution algorithms [22], evolutionary algorithms applied to uncertain optimisation [8], and evolutionary algorithms in multi-modal optimisation [6, 7].

We now present the new theorem, a level-based theorem for co-evolution, which is one of the main contributions of this paper. The theorem states four conditions (G1), (G2a), (G2b), and (G3) which when satisfied imply an upper bound on the runtime of the algorithm. To apply the theorem, it is necessary to provide a sequence $(A_j\times B_j)_{j\in [m]}$ of subsets of $\mathcal {X} \times \mathcal {Y}$ called levels, where $A_1\times B_1=\mathcal {X} \times \mathcal {Y},$ and where $A_m\times B_m$ is the target set. It is recommended that this sequence overlaps to some degree with the trajectory of the algorithm. The “current level” j corresponds to the latest level occupied by at least a $\gamma _0$-fraction of the pairs in $P_t\times Q_t$. Condition (G1) states that the probability of producing a pair in the next level is strictly positive. Condition (G2a) states that the proportion of pairs in the next level should increase at least by a multiplicative factor $1+\delta$. The theorem applies for any positive parameter $\delta$, and does not assume that $\delta$ is a constant with respect to m. Condition (G2a) implies that the fraction of pairs in the current level should not decrease below $\gamma _0$. Finally, Condition (G3) states a requirement in terms of the population size.

In order to make the “current level” of the populations well defined, we need to ensure that for all populations $P\in {\mathcal {X}}^\lambda$ and $Q\in {\mathcal {Y}}^\lambda$, there exists at least one level $j\in [m]$ such that $\vert (P\times Q)\cap (A_j\times B_j)\vert \ge \gamma _0\lambda ^2$. This is ensured by defining the initial level $A_1\times B_1:={\mathcal {X}}\times {\mathcal {Y}}$.

Notice that the notion of “level” here is more general than in the classical level-based theorem [4], in that they do not need to form a partition of the search space.

Theorem 3

Given subsets $A_j\subseteq {\mathcal {X}}$, $B_j\subseteq {\mathcal {Y}}$ for $j\in [m]$ where $A_1:={\mathcal {X}}$ and $B_1:={\mathcal {Y}}$, define $T:= \min \{t\lambda \mid (P_t\times Q_t)\cap (A_{m}\times B_m)\ne \emptyset \}$, where for all $t\in {\mathbb {N}}$, $P_t\in {\mathcal {X}}^\lambda$ and $Q_t\in {\mathcal {Y}}^\lambda$ are the populations of Algorithm 1 in generation t. If there exist $z_1,\dots ,z_{m-1},\delta \in (0,1]$, and $\gamma _0 \in (0,1)$ such that for any populations $P\in {\mathcal {X}}^\lambda$ and $Q\in {\mathcal {Y}}^\lambda$ with so-called “current level” $j:=\max \{i\in [m]\mid \vert (P\times Q)\cap (A_i\times B_i)\vert \ge \gamma _0\lambda ^2\}$

• (G1) if $j\in [m-1]$ and $(x,y)\sim {\mathcal {D}}(P, Q)$ then

  $$\begin{aligned} \displaystyle \Pr \left( x\in A_{j+1}\right) \Pr \left( y\in B_{j+1}\right) \ge z_j, \end{aligned}$$

• (G2a) for all $\gamma \in (0,\gamma _0)$, if $j\in [m-2]$ and $\vert (P\times Q) \cap (A_{j+1}\times B_{j+1})\vert \ge \gamma \lambda ^2$, then for $(x,y)\sim {\mathcal {D}}(P, Q)$,

  $$\begin{aligned} \Pr \left( x\in A_{j+1}\right) \Pr \left( y\in B_{j+1}\right) \ge (1+\delta )\gamma ,\end{aligned}$$

• (G2b) if $j\in [m-1]$ and $(x,y)\sim {\mathcal {D}}(P, Q)$, then

  $$\begin{aligned} \Pr \left( x\in A_{j}\right) \Pr \left( y\in B_{j}\right) \ge (1+\delta )\gamma _0,\end{aligned}$$

• (G3) and the population size $\lambda \in {\mathbb {N}}$ satisfies for $z_*:=\min _{i\in [m-1]} z_i$ and any constant $\upsilon >0$

  $$\begin{aligned} \lambda \ge 2\left( \frac{1}{\gamma _0\delta ^2}\right) ^{1+\upsilon }\ln \left( \frac{m}{z_*}\right) , \end{aligned}$$

then for any constant $c''>1$, and sufficiently large $\lambda$,

$$\begin{aligned} \mathbb {E}\left[ T\right] \le \frac{c''\lambda }{\delta }\left( m\lambda ^2+ 16\sum _{i=1}^{m-1}\frac{1}{z_i}\right) . \end{aligned}$$

(5)

The proof of Theorem 3 uses drift analysis, and follows closely the proof of the original level-based theorem [4], however there are some notable differences, particularly in the assumptions about the underlying stochastic process and the choice of the “level functions”. For ease of comparison, we have kept the proof identical to the classical proof where possible. We first recall the notion of a level-function which is used to glue together two distance functions in the drift analysis.

Definition 2

([4]) For any $\lambda ,m\in {\mathbb {N}}\setminus \{0\}$, a function $g:[0..\lambda ^2]\times [m]\rightarrow {\mathbb {R}}$ is called a level function if the following three conditions hold

• 1. $\forall x\in [0..\lambda ^2], \forall y\in [m-1], g(x,y) \ge g(x,y+1)$,

• 2. $\forall x\in \cup [0..\lambda ^2-1], \forall y\in [m], g(x,y)\ge g(x+1,y)$, and

• 3. $\forall y\in [m-1], g(\lambda ^2,y)\ge g(0,y+1)$.

It follows directly from the definition that the set of level functions is closed under addition. More precisely, for any pair of level functions $g,h:[0..\lambda ^2]\times [m]\rightarrow {\mathbb {R}}$, the function $f(x,y):=g(x,y)+h(x,y)$ is also a level function. The proof of Theorem 3 defines one process $(Y_t)_{t\in {\mathbb {N}}}\in [m]$ which informally corresponds to the “current level” of the process in generation t, and a sequence of m processes $(X^{(1)}_t)_{t\in {\mathbb {N}}},\ldots ,(X^{(m)}_t)_{t\in {\mathbb {N}}}$, $j\in [m]$, where informally $X^{(j)}_t$ refers to the number of individuals above level j in generation t. Thus, $X^{(Y_{t})}_t$ corresponds to the number of individuals above the current level in generation t. A level-function g and the following lemma will be used to define a global distance function used in the drift analysis.

Lemma 4

([4]) If $Y_{t+1}\ge Y_t,$ then for any level function g

$$\begin{aligned} g\left( X^{(Y_{t+1}+1)}_{t+1},Y_{t+1}\right) \le g\left( X^{(Y_t+1)}_{t+1},Y_t\right) . \end{aligned}$$

Proof

The statement is trivially true when $Y_t=Y_{t+1}$. On the other hand, if $Y_{t+1}\ge Y_t+1$, then the conditions in Definition 2 imply

$$\begin{aligned} g\left( X^{(Y_{t+1}+1)}_{t+1},Y_{t+1}\right)&\le g\left( 0,Y_{t+1}\right) \le g\left( 0,Y_{t}+1\right) \\&\le g\left( \lambda ^2,Y_{t}\right) \le g\left( X^{(Y_t+1)}_{t+1},Y_t\right) . \end{aligned}$$

$\square$

We now proceed with the proof of the level-based theorem for co-evolutionary processes.

Proof of Theorem 3

We apply Theorem 26 (the additive drift theorem) with respect to the parameter $a=0$ and the process $Z_t:= g\left( X_{t}^{(Y_t+1)},Y_t\right) ,$ where g is a level-function, and $(Y_t)_{t\in {\mathbb {N}}}$ and $(X^{(j)}_t)_{t\in {\mathbb {N}}}$ for $j\in [m]$ are stochastic processes, which will be defined later. $({\mathscr {F}}_t)_{t\in {\mathbb {N}}}$ is the filtration induced by the populations $(P_t)_{t\in {\mathbb {N}}}$ and $(Q_t)_{t\in {\mathbb {N}}}$.

We will assume w.l.o.g. that condition (G2a) is also satisfied for $j=m-1$, for the following reason. Given Algorithm 1 with a certain mapping $\mathcal {D}$, consider Algorithm 1 with a modified mapping $\mathcal {D}'(P,Q)$: If $(P\times Q)\cap (A_{m}\times B_m)=\emptyset$, then $\mathcal {D}'(P,Q)=\mathcal {D}(P,Q)$; otherwise $\mathcal {D}'(P,Q)$ assigns probability mass 1 to some pair (x, y) of $P\times Q$ that is in $A_{m}$, e.g., to the first one among such elements. Note that $\mathcal {D}'$ meets conditions (G1), (G2a), and (G2b). Moreover, (G2a) hold for $j=m-1$. For the sequence of populations $P'_0,P'_1,\dots$ and $Q'_0,Q'_1,\dots$ of Algorithm 1 with mapping $\mathcal {D}'$, we can put ${T':= \min \{\lambda t \mid (P'_t\times Q'_t)\cap (A_{m}\times B_m) \ne \emptyset \}}$. Executions of the original algorithm and the modified one before generation $T'/\lambda$ are identical. On generation $T'/\lambda$ both algorithms place elements of $A_{m}$ into the populations for the first time. Thus, $T'$ and T are equal in every realisation and their expectations are equal.

For any level $j\in [m]$ and time $t\ge 0$, let the random variable $X_t^{(j)}:= \vert (P_t\times Q_t) \cap (A_j\times B_j) \vert$ denote the number of pairs in level $A_{j}\times B_j$ at time t. As mentioned above, the current level $Y_t$ of the algorithm at time t is defined as

$$\begin{aligned} Y_t&:= \max \left\{ j\in [m] \;\mid \; X_t^{(j)} \ge \gamma _0\lambda ^2 \right\} . \end{aligned}$$

Note that $(X^{(j)}_t)_{t\in {\mathbb {N}}}$ and $(Y_t)_{t\in {\mathbb {N}}}$ are adapted to the filtration $({\mathscr {F}}_t)_{t\in {\mathbb {N}}}$ because they are defined in terms of the populations $(P_t)_{t\in {\mathbb {N}}}$ and $(Q_t)_{t\in {\mathbb {N}}}$.

When $Y_t <m$, there exists a unique $\gamma \in [0,\gamma _0)$ such that

$$\begin{aligned} X_t^{(Y_t+1)}&= \vert (P_t\times Q_t)\cap (A_{Y_t+1}\times B_{Y_t+1})\vert = \gamma \lambda ^2, \text { and} \end{aligned}$$

(6)

$$\begin{aligned} X_t^{(Y_t)}&= \vert (P_t\times Q_t)\cap (A_{Y_t}\times B_{Y_t})\vert \ge \gamma _0\lambda ^2. \end{aligned}$$

(7)

Finally, we define the process $(Z_t)_{t\in {\mathbb {N}}}$ as $Z_t:=0$ if $Y_t=m$, and otherwise, if $Y_t<m$, we let

$$\begin{aligned} Z_t:=g\left( X_{t}^{(Y_t+1)},Y_t\right) , \end{aligned}$$

where for all $k\in [\lambda ^2]$, and for all $j\in [m-1]$, $g(k,j):=g_1(k,j)+g_2(k,j)$ and

$$\begin{aligned} g_1(k,j)&:= \frac{\eta }{1+\eta }\cdot ((m-j)\lambda ^2-k)\\ g_2(k,j)&:= \varphi \cdot \left( \frac{e^{-\eta k}}{q_{j} } + \sum ^{m-1}_{i=j+1} \frac{1}{q_i}\right) , \end{aligned}$$

where $\eta \in (3\delta /(11\lambda ),\delta /(2\lambda ))$ and $\varphi \in (0,1)$ are parameters which will be specified later, and for $j\in [m-1]$, $q_j:= \lambda z_j/(4+\lambda z_j).$

Both functions have partial derivatives $\frac{\partial g_i}{\partial k}<0$ and $\frac{\partial g_i}{\partial j}<0$, hence they satisfy properties 1 and 2 of Definition 2. They also satisfy property 3 because for all $j\in [m-1]$

$$\begin{aligned} g_1(\lambda ^2,j)&= \frac{\eta }{1+\eta }((m-j)\lambda ^2-\lambda ^2) = g_1(0,j+1)\\ g_2(\lambda ^2,j)&> \sum ^{m-1}_{i=j+1} \frac{\varphi }{q_i} = g_2(0,j+1). \end{aligned}$$

Therefore $g_1$ and $g_2$ are level functions, and thus also their linear combination g is a level function.

Due to properties 1 and 2 of level functions (see Definition 2), it holds for all $k\in [0..\lambda ^2]$ and $j\in [m-1]$

$$\begin{aligned} 0\le g(k,j)\le g(0,1)&= \frac{\eta (m-1)\lambda ^2}{1+\eta } +\varphi \cdot \left( \frac{1}{q_{1} } + \sum ^{m-1}_{i=2} \frac{1}{q_i}\right) \end{aligned}$$

(8)

$$\begin{aligned}&< \frac{\eta m\lambda ^2}{1+\eta } +\sum _{i=1}^{m-1} \frac{\varphi }{q_i} \end{aligned}$$

(9)

$$\begin{aligned}&< \frac{\eta m\lambda ^2}{1+\eta }+ \varphi \sum _{i=1}^{m-1}\frac{4+\lambda z_i}{\lambda z_i} \end{aligned}$$

(10)

using $\eta >0$

$$\begin{aligned}&< m\left( \eta \lambda ^2+ \frac{4\varphi }{\lambda z_*}+\varphi \right) \end{aligned}$$

(11)

using $\varphi ,z_*\in (0,1)$ and $\lambda >11\eta /(3\delta )$

$$\begin{aligned}&< \frac{m}{z_*}\left( 2\eta \lambda ^2+ \frac{44\eta }{3\delta }\right) \end{aligned}$$

(12)

assuming $\lambda >44/3$ and using $\lambda ^2>\lambda \delta ^{-2(1+\upsilon )}>44/(3\delta )$

$$\begin{aligned}&< \frac{3\eta \lambda ^2m}{z_*}. \end{aligned}$$

(13)

Hence, we have $0\le Z_t<g(0,1)<\infty$ for all $t\in {\mathbb {N}}$ which implies that condition 2 of the drift theorem is satisfied.

The drift of the process at time t is $\mathbb {E}_t\left[ \Delta _{t+1}\right]$, where

$$\begin{aligned} \Delta _{t+1}&:= g\left( X_t^{(Y_t+1)},Y_t\right) -g\left( X_{t+1}^{(Y_{t+1}+1)},Y_{t+1}\right) . \end{aligned}$$

We bound the drift by the law of total probability as

$$\begin{aligned} \mathbb {E}_t\left[ \Delta _{t+1}\right]&= (1-\Pr {}_t\left( Y_{t+1}<Y_t\right) )\mathbb {E}_t\left[ \Delta _{t+1} \mid Y_{t+1}\ge Y_t\right] \nonumber \\&\quad \; + \Pr {}_t\left( Y_{t+1}<Y_t\right) \mathbb {E}_t\left[ \Delta _{t+1} \mid Y_{t+1}< Y_t\right] . \end{aligned}$$

(14)

The event $Y_{t+1}< Y_t$ holds if and only if $X_{t+1}^{(Y_t)}<\gamma _0\lambda ^2$, which by Lemma 1 statement 3 for $\gamma :=\gamma _0+1/\lambda$ and a parameter $\delta _1\in (0,\delta )$ to be chosen later, and conditions (G2b) and (G3), is upper bounded by

$$\begin{aligned} \Pr {}_t\left( Y_{t+1}<Y_t\right)&= \Pr {}_t\left( X_{t+1}^{(Y_t)}<\gamma _0\lambda ^2\right) \end{aligned}$$

(15)

$$\begin{aligned}&= \Pr {}_t\left( X_{t+1}^{(Y_t)}<\lambda (\gamma \lambda -1)\right) \end{aligned}$$

(16)

$$\begin{aligned}&< \exp \left( -\delta _1\gamma \lambda \left( 1-\sqrt{\frac{1+\delta _1}{1+\delta }}\right) \right) \end{aligned}$$

(17)

by Lemma 28 and $\gamma <\gamma _0$

$$\begin{aligned}&< \exp \left( -\delta _1\gamma _0\lambda \left( \frac{3\delta -4\delta _1}{11}\right) \right) \end{aligned}$$

(18)

to minimise the expression, we choose $\delta _1:=(3/8)\delta$

$$\begin{aligned}&= \exp \left( -\frac{9}{16}\delta ^2\gamma _0\lambda \right) . \end{aligned}$$

(19)

Given the low probability of the event $Y_{t+1}<Y_t$, it suffices to use the pessimistic bound (13)

$$\begin{aligned} \mathbb {E}_t\left[ \Delta _{t+1} \mid Y_{t+1}<Y_t\right]&\ge -g(0,1) \end{aligned}$$

(20)

If $Y_{t+1}\ge Y_t$, we can apply Lemma 4

$$\begin{aligned}&\mathbb {E}_t\left[ \Delta _{t+1} \mid Y_{t+1}\ge Y_t\right] \ge \mathbb {E}_t\left[ g\left( X^{(Y_t+1)}_{t},Y_t\right) - g\left( X^{(Y_t+1)}_{t+1},Y_{t}\right) \mid Y_{t+1}\ge Y_t\right] . \end{aligned}$$

If $X_{t}^{(Y_t+1)}=0$, then $X_{t}^{(Y_t+1)}\le X_{t+1}^{(Y_t+1)}$ and

$$\begin{aligned} \mathbb {E}_t\left[ g_1\left( X_t^{(Y_t+1)},Y_t\right) - g_1\left( X_{t+1}^{(Y_t+1)},Y_t\right) \mid Y_{t+1}\ge Y_t\right] \ge 0, \end{aligned}$$

because the function $g_1$ satisfies property 2 in Definition 2. Furthermore, we have the lower bound

$$\begin{aligned} \mathbb {E}_t\left[ g_2\left( X_t^{(Y_t+1)},Y_t\right) -g_2\left( X_{t+1}^{(Y_t+1)},Y_t\right) \mid Y_{t+1}\ge Y_t\right] \\ > \Pr {}_t\left( X_{t+1}^{(Y_t+1)}\ge 1\right) \left( g_2\left( 0,Y_t\right) -g_2\left( 1,Y_t\right) \right) \ge \frac{\eta \varphi }{1+\eta }. \end{aligned}$$

where the last inequality follows because

$$\begin{aligned} \Pr {}_t\left( X_{t+1}^{(Y_t+1)}\ge 1\right)&= \Pr {}_t\left( (P_{t+1}\times Q_{t+1})\cap (A_{Y_t+1}\times B_{Y_t+1})\ne \emptyset \right) \\&\ge q_{Y_t}, \end{aligned}$$

due to condition (G1) and Lemma 2, and

$$\begin{aligned} g_2\left( 0,Y_t\right) -g_2\left( 1,Y_t\right) = (\varphi /q_{Y_t})(1-e^{-\eta }) \ge \frac{\varphi \eta }{(1+\eta )q_{Y_t}} \end{aligned}$$

In the other case, where $X_t^{(Y_t+1)}=\gamma \lambda ^2\ge 1$, Lemma 1 and condition (G2a) imply for $\varphi :=\delta (1-\delta ')$ for an arbitrary constant $\delta '\in (0,1)$,

$$\begin{aligned} \mathbb {E}_t\left[ g_1\left( X_t^{(Y_t+1)},Y_t\right) -g_1\left( X_{t+1}^{(Y_t+1)},Y_t\right) \mid Y_{t+1} \ge Y_{t}\right] \nonumber \\ = \frac{\eta }{1+\eta }\mathbb {E}_t\left[ X_{t+1}^{(Y_t+1)}\mid Y_{t+1} \ge Y_{t}\right] -\frac{\eta }{1+\eta } X_t^{(Y_t+1)}\nonumber \\ \ge \frac{\eta }{1+\eta }(\lambda (\lambda -1)(1+\delta )\gamma -\gamma \lambda ^2) > \frac{\eta }{1+\eta }\delta (1-\delta ')=\frac{\eta \varphi }{1+\eta }, \end{aligned}$$

(21)

where the last inequality is obtained by choosing the minimal value $\gamma =1/\lambda ^2$. For the function $g_2$, we get

$$\begin{aligned} \mathbb {E}_t\left[ g_2\left( X_t^{(Y_t+1)},Y_t\right) -g_2\left( X_{t+1}^{(Y_t+1)},Y_t\right) \mid Y_{t+1} \ge Y_{t}\right] = \\ \frac{\varphi }{q_{Y_t}} \left( e^{-\eta X_t^{(Y_t+1)}} - \mathbb {E}_t\left[ e^{-\eta X_{t+1}^{(Y_t+1)}}\right] \right) >0, \end{aligned}$$

where the last inequality is due to statement 2 of Lemma 1 for the parameter

$$\begin{aligned} \eta := \frac{1}{\lambda }\left( 1-\frac{1}{\sqrt{1+\delta }}\right) . \end{aligned}$$

By Lemma 28 for $\delta _1=0$, this parameter satisfies

$$\begin{aligned} \frac{3\delta }{11\lambda }<\eta< \frac{\delta }{2\lambda } < \frac{1}{\lambda }. \end{aligned}$$

(22)

Taking into account all cases, we have

$$\begin{aligned} \mathbb {E}_t\left[ \Delta _{t+1} \mid Y_{t+1}\ge Y_t \right] \ge \frac{\eta \varphi }{1+\eta }. \end{aligned}$$

(23)

We now have bounds for all the quantities in (14) with (19), (20), and (23). Before bounding the overall drift $\mathbb {E}_t\left[ \Delta _{t+1}\right]$, we remark that the requirement on the population size imposed by condition (G3) implies that for any constants $\upsilon >0$ and $C>0$, and sufficiently large $\lambda$,

$$\begin{aligned} \frac{\lambda }{16C\ln \lambda }> \lambda ^{\frac{1}{1+\upsilon }}> \frac{1}{\delta ^2\gamma _0}, \end{aligned}$$

which implies that

$$\begin{aligned} C\ln \lambda < \frac{\lambda \delta ^2\gamma _0}{16}. \end{aligned}$$

(24)

The overall drift is now bounded by

$$\begin{aligned} \mathbb {E}_t\left[ \Delta _{t+1}\right]&= (1 - \Pr {}_t\left( Y_{t+1}<Y_t\right) )\mathbb {E}_t\left[ \Delta _{t+1} \mid Y_{t+1}\ge Y_t\right] \end{aligned}$$

(25)

$$\begin{aligned}&\quad + \Pr {}_t\left( Y_{t+1}<Y_t\right) \mathbb {E}_t\left[ \Delta _{t+1} \mid Y_{t+1}< Y_t\right] \end{aligned}$$

(26)

$$\begin{aligned}&\ge \frac{\eta \varphi }{1+\eta } - \exp \left( -\frac{9}{16}\delta ^2\gamma _0\lambda \right) \left( \frac{3m\eta \lambda ^2}{z_*}+\frac{\eta \varphi }{1+\eta }\right) \end{aligned}$$

(27)

$$\begin{aligned}&= \frac{\eta \varphi }{1+\eta } - \exp \left( -\frac{9}{16}\delta ^2\gamma _0\lambda +C\ln \lambda \right) \left( \frac{3m\eta \lambda ^{2-C}}{z_*} +\frac{\eta \varphi }{(1+\eta )\lambda ^C}\right) \end{aligned}$$

(28)

by (24)

$$\begin{aligned}&> \frac{\eta \varphi }{1+\eta } - \exp \left( -\frac{1}{2}\delta ^2\gamma _0\lambda \right) \left( \frac{3m\eta \lambda ^{2-C}}{z_*} +\frac{\eta \varphi }{(1+\eta )\lambda ^C}\right) \end{aligned}$$

(29)

by condition (G3)

$$\begin{aligned}&> \frac{\eta \varphi }{1+\eta } -(\frac{z_*}{m}) \left( \frac{3m\eta \lambda ^{2-C}}{z_*} +\frac{\eta \varphi }{\left( 1+\eta \right) \lambda ^C}\right) \end{aligned}$$

(30)

choosing $C=3$

$$\begin{aligned}&= \frac{\eta \varphi }{1+\eta } - \frac{3\eta }{\lambda } -\frac{\eta \varphi }{(1+\eta )\lambda ^3m} \end{aligned}$$

(31)

by condition (G3), $\sqrt{\lambda }>1/\delta$

$$\begin{aligned}&> \frac{\eta \varphi }{1+\eta } - \frac{3\eta \delta }{\sqrt{\lambda }} -\frac{\eta \varphi }{(1+\eta )\lambda ^3m} \end{aligned}$$

(32)

finally, by noting that $1+\eta <1+1/\lambda$ from Eq. (22) and that $\varphi =\delta (1-\delta ')$ for a constant $\delta '\in (0,1)$ mean that for any constant $\rho \in (0,1)$, for sufficiently large $\lambda$

$$\begin{aligned}&> \frac{\eta \varphi (1-\rho ) }{1+\eta }. \end{aligned}$$

(33)

We now verify condition 3 of Theorem 26, i.e., that T has finite expectation. Let $p_*:=\min \{(1+\delta )(1/\lambda ^2), z_*\}>0$, and note by conditions (G1) and (G2a) that the current level increases by at least one with probability $\Pr {}_t\left( Y_{t+1}>Y_t\right) \ge (p_*)^{\gamma _0\lambda }$. Due to the definition of the modified process $D'$, if $Y_t=m$, then $Y_{t+1}=m$. Hence, the probability of reaching $Y_t=m$ is lower bounded by the probability of the event that the current level increases in all of at most m consecutive generations, i.e., $\Pr {}_t\left( Y_{t+m} =m\right) \ge (p_*)^{\gamma _0\lambda m}>0$. It follows that $\mathbb {E}\left[ T\right] <\infty$.

By Theorem 26, the upper bound on g(0, 1) in (10) and the lower bound on the drift in Eq. (33) and the definition of T,

$$\begin{aligned} \mathbb {E}\left[ T\right]&\le \frac{\lambda (1+\eta )g(0,1)}{\eta \varphi (1-\rho )}\\&< \frac{\lambda (1+\eta )}{\eta \varphi (1-\rho )}\left( \frac{\eta m\lambda ^2}{1+\eta }+\varphi \sum _{i=1}^{m-1}\frac{4+\lambda z_i}{\lambda z_i}\right) \\&< \frac{\lambda }{(1-\rho )}\left( \frac{m\lambda ^2}{\varphi }+\frac{1+\eta }{\eta }\sum _{i=1}^{m-1}\left( \frac{4}{\lambda z_i}+1\right) \right) \end{aligned}$$

using Eq. (22) and $\varphi :=\delta (1-\delta ')$

$$\begin{aligned}&< \frac{\lambda }{(1-\rho )}\left( \frac{m\lambda ^2}{\delta (1-\delta ')}+\left( \frac{11\lambda }{3\delta }+1\right) \sum _{i=1}^{m-1}\left( \frac{4}{\lambda z_i}+1\right) \right) \end{aligned}$$

noting that $1<1/\delta \le \lambda /(3\delta )$ for $\lambda \ge 3$

$$\begin{aligned}&< \frac{\lambda }{(1-\rho )}\left( \frac{m\lambda ^2}{\delta (1-\delta ')}+\left( \frac{4\lambda }{\delta }\right) \sum _{i=1}^{m-1}\left( \frac{4}{\lambda z_i}+1\right) \right) \\&= \frac{\lambda }{(1-\rho )}\left( \frac{m\lambda ^2}{\delta (1-\delta ')}+\frac{4\lambda (m-1)}{\delta }+\left( \frac{16}{\delta }\right) \sum _{i=1}^{m-1}\frac{1}{z_i}\right) \end{aligned}$$

since $\delta '$ is a constant with respect to $\lambda$, for large $\lambda$, this is upper bounded by

$$\begin{aligned}&< \frac{\lambda }{(1-\rho )\delta }\left( \frac{m\lambda ^2}{(1-\delta ')^2}+16\sum _{i=1}^{m-1}\frac{1}{z_i}\right) \end{aligned}$$

for any constant $c''>1$, we can choose the constants $\rho$ and $\delta '$ such that $c''>(1-\rho )^{-1}(1-\delta ')^{-2}$

$$\begin{aligned}&< \frac{c''\lambda }{\delta }\left( m\lambda ^2+16\sum _{i=1}^{m-1}\frac{1}{z_i}\right) . \end{aligned}$$

$\square$

4 Maximin Optimisation of Bilinear Functions

4.1 Maximin Optimisation Problems

This section introduces maximin-optimisation problems which is an important domain for competitive co-evolutionary algorithms [1, 18, 23]. We will then describe a class of maximin-optimisation problems called Bilinear.

It is a common scenario in real-world optimisation that the quality of candidate solutions depend on the actions taken by some adversary. Formally, we can assume that there exists a function

$$\begin{aligned} g:{\mathcal {X}}\times {\mathcal {Y}}\rightarrow {\mathbb {R}}, \end{aligned}$$

where g(x, y) represents the “quality” of solution x when the adversary takes action y.

A cautious approach to such a scenario is to search for the candidate solution which maximises the objective, assuming that the adversary takes the least favourable action for that solution. Formally, this corresponds to the maximin optimisation problem, i.e., to maximise the function

$$\begin{aligned} f(x) := \min _{y\in {\mathcal {Y}}} g(x,y). \end{aligned}$$

(34)

It is desirable to design good algorithms for such problems because they have important applications in economics, computer science, machine learning (GANs), and other disciplines.

However, maximin-optimisation problems are computationally challenging because to accurately evaluate the function f(x), it is necessary to solve a minimisation problem. Rather than evaluating f directly, the common approach is to simultaneously maximise g(x, y) with respect to x, while minimising g(x, y) with respect to y. For example, if the gradient of g is available, it is popular to do gradient ascent-gradient descent.

Following conventions in theory of evolutionary computation [11], we will assume that an algorithm has oracle access to the function g. This means that the algorithm can evaluate the function g(x, y) for any selected pair of arguments $(x,y)\in \mathcal {X} \times \mathcal {Y}$, however it does not have access to any other information about g, including its definition or the derivative. Furthermore, we will assume that $\mathcal {X} =\mathcal {Y} =\{0,1\}^n$, i.e., the set of bitstrings of length n. While other spaces could be considered, this choice aligns well with existing runtime analyses of evolutionary algorithms in discrete domains [10, 31]. To develop a co-evolutionary algorithm for maximin-optimisation, we will rely on the following dominance relation on the set of pairs ${\mathcal {X}}\times {\mathcal {Y}}$.

Definition 3

Given a function $g:{\mathcal {X}}\times {\mathcal {Y}}\rightarrow {\mathbb {R}}$ and two pairs $(x_1,y_1),(x_2,y_2)\in {\mathcal {X}}\times {\mathcal {Y}}$, we say that $(x_1,y_1)$ dominates $(x_2,y_2)$ wrt g, denoted $(x_1,y_1)\succeq _g (x_2,y_2),$ if and only if

$$\begin{aligned} g(x_1,y_2) \ge g(x_1,y_1) \ge g(x_2,y_1). \end{aligned}$$

4.2 The Bilinear Problem

In order to develop appropriate analytical tools to analyse the runtime of evolutionary algorithms, it is necessary to start the analysis with simple and well-understood problems [31]. We therefore define a simple class of a maximin-optimisation problems that has a particular clear structure. The maximin function is defined for two parameters $\alpha ,\beta \in [0,1]$ by

$$\begin{aligned} {{\textsc {Bilinear}}}(x,y)&:= \Vert y\Vert (\Vert x\Vert -\beta n)-\alpha n \Vert x\Vert , \end{aligned}$$

(35)

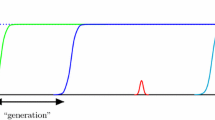
where we recall that for any bitstring $z\in \{0,1\}^n$, $\Vert z\Vert :=\sum _{i=1}^n z_i$ denotes the number of 1-bits in z. The function is illustrated in Fig. 1 (left). Extended to the real domain, it is clear that the function is concave-convex, because $f(x)=g(x,y)$ is concave (linear) for all y, and $h(y)=g(x,y)$ is convex (linear) for all x. The gradient of the function is $\nabla g = (\Vert y\Vert - \alpha n,\Vert x\Vert - \beta n)$. Clearly, we have $\nabla g=0$ when $\Vert x\Vert =\beta n$ and $\Vert y\Vert =\alpha n$.

Fig. 1

Left: Bilinear for $\alpha =0.4$ and $\beta =0.6$. Right: Dominance relationships in Bilinear

Assuming that the prey (in $\mathcal {Y}$) always responds with an optimal decision for every $x\in X$, the predator is faced with the unimodal function f below which has maximum when $\Vert x\Vert =\beta n$.

$$\begin{aligned} f(x) := \min _{y\in \{0,1\}^n} g(x,y) = {\left\{ \begin{array}{ll} \Vert x\Vert (1-\alpha n)-\beta n&{} \text {if } \Vert x\Vert \le \beta n\\ -\alpha n\Vert x\Vert &{} \text {if } \Vert x\Vert > \beta n. \end{array}\right. } \end{aligned}$$

The special case where $\alpha =0$ and $\beta =1$ gives $f(x) = \text {OneMax} (x)-n$, i.e., the function f is essentially equivalent to OneMax, one of the most studied objective functions in runtime analysis of evolutionary algorithms [10].

We now characterise the dominated solutions wrt Bilinear.

Lemma 5

Let $g:=$ Bilinear. For all pairs $(x_1,y_1),(x_2,y_2)\in {\mathcal {X}}\times {\mathcal {Y}}$, $(x_1,y_1)\succeq _g (x_2,y_2)$ if and only if

$$\begin{aligned} \Vert y_2\Vert (\Vert x_1\Vert -\beta n)\; \ge \; \Vert y_1\Vert (\Vert x_1\Vert -\beta n)&\quad \wedge \\ \Vert x_1\Vert (\Vert y_1\Vert -\alpha n)\; \ge \; \Vert x_2\Vert (\Vert y_1\Vert -\alpha n)&. \end{aligned}$$

Proof

The proof follows from the definition of $\succeq _g$ and g:

$$\begin{aligned}&g(x_1,y_2)\ge g(x_1,y_1)\\ \Longleftrightarrow \quad&\Vert x_1\Vert \Vert y_2\Vert -\alpha n\Vert x_1\Vert -\beta n\Vert y_2\Vert \ge \Vert x_1\Vert \Vert y_1\Vert -\alpha n\Vert x_1\Vert -\beta n\Vert y_1\Vert \\ \Longleftrightarrow \quad&\Vert y_2\Vert (\Vert x_1\Vert -\beta n)\ge \Vert y_1\Vert (\Vert x_1\Vert -\beta n). \end{aligned}$$

The second part follows analogously from $g(x_1,y_1)\ge g(x_2,y_1)$. $\square$

Figure 1 (right) illustrates Lemma 5, where the x-axis and y-axis correspond to the number of 1-bits in the predator x, respectively the number of 1-bits in the prey y. The figure contains four pairs, where the shaded area corresponds to the parts dominated by that pair: The pair $(x_1,y_1)$ dominates $(x_2,y_2)$, the pair $(x_2,y_2)$ dominates $(x_3,y_3)$, the pair $(x_3,y_3)$ dominates $(x_4,y_4)$, and the pair $(x_4,y_4)$ dominates $(x_1,y_1)$. This illustrates that the dominance-relation is intransitive. Lemma 6 states this and other properties of $\succeq _g$.

Lemma 6

The relation $\succeq _g$ is reflexive, antisymmetric, and intransitive for $g=$ Bilinear.

Proof

Reflexivity follows directly from the definition. Assume that $(x_1,y_1)\succeq _g (x_2,y_2)$ and $(x_1,y_1)\ne (x_2,y_2)$. Then, either $g(x_1,y_2)>g(x_1,y_2),$ or $g(x_1,y_1)>g(x_2,y_1)$, or both. Hence, $(x_2,y_2)\not \succeq _g (x_1,y_1)$, which proves that the relation is antisymmetric.

To prove intransitivity, it can be shown for any $\varepsilon >0,$ that $p_1\succeq _g p_2\succeq _g p_3\succeq _g p_2 \succeq _g p_1$ where

$$\begin{aligned} p_1&= (\beta +\varepsilon , \alpha -2\varepsilon )&p_2&= (\beta -2\varepsilon , \alpha -\varepsilon ) \\ p_3&= (\beta -\varepsilon , \alpha +2\varepsilon )&p_4&= (\beta +2\varepsilon , \alpha +\varepsilon ). \end{aligned}$$

$\square$

We will frequently use the following simple lemma, which follows from the dominance relation and the definition of Bilinear.

Lemma 7

For Bilinear, and any pairs of populations $P\in {\mathcal {X}}^\lambda , Q\in {\mathcal {Y}}^\lambda$, consider two samples $(x_1,y_1),(x_2,y_2)\sim {{\,\textrm{Unif}\,}}(P\times Q)$. Then the following conditional probabilities hold.

$$\begin{aligned} \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid y_1\le y_2\wedge x_1>\beta n\wedge x_2>\beta n\right)&\ge 1/2\\ \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid y_1\ge y_2\wedge x_1<\beta n\wedge x_2<\beta n\right)&\ge 1/2\\ \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid x_1\ge x_2\wedge y_1>\alpha n\wedge y_2>\alpha n\right)&\ge 1/2\\ \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid x_1\le x_2\wedge y_1<\alpha n\wedge y_2<\alpha n\right)&\ge 1/2. \end{aligned}$$

Proof

All the statements can be proved analogously, so we only show the first statement. If $y_1\le y_2$ and $x_1>\beta n$, $x_2>\beta n$, then by Lemma 5, $(x_1,y_1)\succeq (x_2,y_2)$ if and only if $x_1\le x_2$.

Since $x_1$ and $x_2$ are independent samples from the same (conditional) distribution, it follows that

$$\begin{aligned} 1&\ge \Pr \left( x_1>x_2\right) + \Pr \left( x_1<x_2\right) = 2\Pr \left( x_1>x_2\right) \end{aligned}$$

(36)

Hence, we get $\Pr \left( x_1\le x_2\right) = 1-\Pr \left( x_1>x_2\right) \ge 1-1/2 = 1/2$. $\square$

5 A Co-evolutionary Algorithm for Maximin Optimisation

We now introduce a co-evolutionary algorithm for maximin optimisation (see Algorithm 2).

The predator and prey populations of size $\lambda$ each are initialised uniformly at random in lines 1–3. Lines 6–17 describe how each pair of predator and prey are produced, first by selecting a predator–prey pair from the population, then applying mutation. In particular, the algorithm selects uniformly at random two predators $x_1,x_2$ and two prey $y_1,y_2$ in lines 7–8. The first pair $(x_1,y_1)$ is selected if it dominates the second pair $(x_2,y_2)$, otherwise the second pair is selected. The selected predator and prey are mutated by standard bitwise mutation in lines 14–15, i.e., each bit flips independently with probability $\chi /n$ (see Section C3.2.1 in [3]). The algorithm is a special case of the co-evolutionary framework in Sect. 2, where line 3 in Algorithm 1 corresponds to lines 6–17 in Algorithm 2.

Algorithm 2

Pairwise Dominance CoEA (PDCoEA)

Fig. 2

Partitioning of search space $\mathcal {X} \times \mathcal {Y}$ of Bilinear

Next, we will analyse the runtime of PDCoEA on Bilinear using Theorem 3. For an arbitrary $\varepsilon \ge 1/n$ (not necessarily constant), we will restrict the analysis to the case where $\alpha - \varepsilon > 4/5$, and $\beta < \varepsilon$. Our goal is to estimate the time until the algorithm reaches within an $\varepsilon$-factor of the maximin-optimal point $(\beta n,\alpha n)$. We note that our analysis does not extend to the general case of arbitrary $\alpha$ and $\beta$, or $\varepsilon =0$ (exact optimisation). This is a limitation of the analysis, and not of the algorithm. Our own empirical investigations show that PDCoEA with appropriate parameters finds the exact maximin-optimal point of Bilinear for any value of $\alpha$ and $\beta$.

In this setting, the behaviour of the algorithm can be described intuitively as follows. The population dynamics will have two distinct phases. In Phase 1, most prey have less than $\alpha n$ 1-bits, while most predators have more than $\beta n$ 1-bits. During this phase, predators and prey will decrease the number of 1-bits. In Phase 2, a sufficient number of predators have less than $\beta n$ 1-bits, and the number of 1-bits in the prey-population will start to increase. The population will then reach the $\varepsilon$-approximation described above.

From this intuition, we will now define a suitable sequence of levels. We will start by dividing the space $\mathcal {X} \times \mathcal {Y}$ into different regions, as shown in Fig. 2. Again, the x-axis corresponds to the number of 1-bits in the predator, while the y-axis corresponds to the number of 1-bits in the prey.

For any $k\in [0,(1-\beta )n]$, we partition $\mathcal {X}$ into three sets

$$\begin{aligned} R_0&:= \left\{ x\in \mathcal {X} \mid 0 \le \Vert x\Vert < \beta n\right\} \end{aligned}$$

(37)

$$\begin{aligned} R_1(k)&:= \left\{ x\in \mathcal {X} \mid \beta n \le \Vert x\Vert < n - k \right\} , \text { and } \end{aligned}$$

(38)

$$\begin{aligned} R_2(k)&:= \left\{ x\in \mathcal {X} \mid n-k \le \Vert x\Vert \le n \right\} . \end{aligned}$$

(39)

Similarly, for any $\ell \in [0,\alpha n)$, we partition $\mathcal {Y}$ into three sets

$$\begin{aligned} S_0&:= \left\{ y\in \mathcal {Y} \mid \alpha n \le \Vert y\Vert \le n\right\} \end{aligned}$$

(40)

$$\begin{aligned} S_1(\ell )&:= \left\{ y\in \mathcal {Y} \mid \ell \le \Vert y\Vert < \alpha n \right\} , \text { and} \end{aligned}$$

(41)

$$\begin{aligned} S_2(\ell )&:= \left\{ y\in \mathcal {Y} \mid 0 \le \Vert y\Vert < \ell \right\} . \end{aligned}$$

(42)

For ease of notation, when the parameters k and $\ell$ are clear from the context, we will simply refer to these sets as $R_0,R_1,R_2, S_0,S_1$, and $S_2$. Given two populations P and Q, and $C\subseteq \mathcal {X} \times \mathcal {Y}$, define

$$\begin{aligned} p(C)&:= \Pr _{(x,y)\sim {{\,\textrm{Unif}\,}}(P\times Q)}\left( (x,y)\in C \right) \\ p_{\text {sel}}({C})&:= \Pr _{(x,y)\sim \texttt {select} (P\times Q)}\left( (x,y)\in C \right) . \end{aligned}$$

In the context of subsets of $\mathcal {X} \times \mathcal {Y}$, the set $R_i$ refers to $R_i\times \mathcal {Y}$, and $S_i$ refers to $\mathcal {X} \times S_i$. With the above definitions, we will introduce the following quantities which depend on k and $\ell$:

$$\begin{aligned} p_0&:= p(R_0)&p(k)&:= p(R_1(k))&q_0&:= p(S_0)&q(\ell )&:= p(S_1(\ell )) \end{aligned}$$

During Phase 1, the typical behaviour is that only a small minority of the individuals in the Q-population belong to region $S_0$. In this phase, the algorithm “progresses” by decreasing the number of 1-bits in the P-population. In this phase, the number of 1-bits will decrease in the Q-population, however it will not be necessary to analyse this in detail. To capture this, we define the levels for Phase 1 for $j\in [0..(1-\beta )n]$ as $A^{(1)}_j:= R_0\cup R_1(j)$ and $B^{(1)}_j:= S_2((\alpha -\varepsilon ) n).$

During Phase 2, the typical behaviour is that there is a sufficiently large number of P-individuals in region $R_0$, and the algorithm progresses by increasing the number of 1-bits in the Q-population. The number of 1-bits in the P-population will decrease or stay at 0. To capture this, we define the levels for Phase 2 for $j\in [0,(\alpha -\varepsilon )n]$ $A^{(2)}_j:= R_0$ and $B^{(2)}_j:= S_1(j).$

The overall sequence of levels used for Theorem 3 becomes

$$\begin{aligned} (A_0^{(1)}\times B_0^{(1)}), \ldots , (A^{(1)}_{(1-\beta )n},B^{(1)}_{(1-\beta )n}), (A_0^{(2)}\times B_0^{(2)}), \ldots , (A^{(2)}_{(\alpha -\varepsilon )n},B^{(2)}_{(\alpha -\varepsilon )n}), \end{aligned}$$

The notion of “current level” from Theorem 3 together with the level-structure can be exploited to infer properties about the populations, as the following lemma demonstrates.

Lemma 8

If the current level is $A^{(1)}_j\times B^{(1)}_j$, then $p_0<\gamma _0/(1-q_0)$.

Proof

Assume by contradiction that $p_0(1-q_0)\ge \gamma _0$. Note that by (42), it holds $S_2(0) = \emptyset .$ Therefore, $1-q(0)-q_0=0$ and $q(0)=1-q_0$. By the definitions of the levels in Phase 2 and (41),

$$\begin{aligned} \left| (P\times Q)\cap (A^{(2)}_0\times B_0^{(2)})\right|&= \left| (P\times Q)\cap (R_0\times S_1(0))\right| \\&= p_0 q(0) \lambda ^2 = p_0 (1-q_0)\lambda ^2 \ge \gamma _0\lambda ^2, \end{aligned}$$

implying that the current level must be level $A^{(2)}_0\times B_0^{(2)}$ or a higher level in Phase 2, contradicting the assumption of the lemma. $\square$

5.1 Ensuring Condition (G2) During Phase 1

The purpose of this section is to provide the building blocks necessary to establish conditions (G2a) and (G2b) during Phase 1. The progress of the population during this phase will be jeopardised if there are too many Q-individuals in $S_0$. We will employ the negative drift theorem for populations [19] to prove that it is unlikely that Q-individuals will drift via region $S_1$ to region $S_0$. This theorem applies to algorithms that can be described on the form of Algorithm 3 which makes few assumptions about the selection step. The Q-population in Algorithm 2 is a special case of Algorithm 3.

Algorithm 3

Population Selection-Variation Algorithm [19]

We now state the negative drift theorem for populations.

Theorem 9

( [19]) Given Algorithm 3 on $\mathcal {Y} =\{0,1\}^n$ with population size $\lambda \in {{\,\textrm{poly}\,}}(n)$, and transition matrix $p_\textrm{mut}$ corresponding to flipping each bit independently with probability $\chi /n$. Let a(n) and b(n) be positive integers s.t. $b(n)\le n/\chi$ and $d(n):=b(n)-a(n)=\omega (\ln n)$. For an $x^*\in \{0,1\}^n$, let T(n) be the smallest $t\ge 0$, s.t. $\min _{j\in [\lambda ]}H(P_t(j), x^*)\le a(n)$. Let $S_t(i):= \sum _{j=1}^\lambda [I_t(j)=i]$. If there are constants $\alpha _0\ge 1$ and $\delta >0$ such that

• (1) $\mathbb {E}\left[ S_t(i)\mid a(n)<H(P_t(i),x^*)<b(n)\right] \le \alpha _0$ for all $i\in [\lambda ]$

• (2) $\psi := \ln (\alpha _0)/\chi + \delta < 1$, and

• (3) $\frac{b(n)}{n} < \min \left\{ \frac{1}{5}, \frac{1}{2}-\frac{1}{2}\sqrt{\psi (2-\psi )}\right\}$,

then $\Pr \left( T(n)\le e^{cd(n)}\right) \le e^{-\Omega (d(n))}$ for some constant $c>0$.

To apply this theorem, the first step is to estimate the reproductive rate [19] of Q-individuals in $S_0\cup S_1$.

Lemma 10

If there exist $\delta _1,\delta _2\in (0,1)$ such that $q+q_0\le 1-\delta _1$, $p_0<\sqrt{2(1-\delta _2)}-1$, and $p_0q=0$, then $p_{\text {sel}}({S_0\cup S_1})/p(S_0\cup S_1) < 1-\delta _1\delta _2.$

Proof

The conditions of Lemma 24 are satisfied, hence

$$\begin{aligned} p_{\text {sel}}({S_0\cup S_1})&= 1-p_{\text {sel}}({S_2})\\&\le 1 - (1+\delta _2(q_0+q))p(S_2)\\&= 1 - (1+\delta _2(q_0+q))(1-q-q_0)\\&= (q_0+q)(1-(1-q-q_0)\delta _2)\\&\le (q_0+q)(1-\delta _1\delta _2)\\&= p(S_0\cup S_1)(1-\delta _1\delta _2). \end{aligned}$$

$\square$

Lemma 11

If $p_0=0$ and $q_0+q\le 1/3$, then no Q-individual in $Q\cap (S_0\cup S_1)$ has reproductive rate higher than 1.

Proof

Consider any individual $z\in Q\cap (S_0\cup S_1)$. The probability of selecting this individual in a given iteration is less than

$$\begin{aligned} \Pr \left( y_1=z\wedge y_2\in S_0\cup S_1\right) \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid y_1=z\wedge y_2\in S_0\cup S_1\right) \\ + \Pr \left( y_2=z\wedge y_1\in S_0\cup S_1\right) \Pr \left( (x_1,y_1)\not \succeq (x_2,y_2)\mid y_2=z\wedge y_1\in S_0\cup S_1\right) \\ + \Pr \left( y_2=z\wedge y_1\in S_2\right) \Pr \left( (x_1,y_1)\not \succeq (x_2,y_2)\mid y_2=z\wedge y_1\in S_2\right) \\ \le \frac{2}{\lambda }(q_0+q)+(1-q-q_0)/(2\lambda ) = \frac{1}{2\lambda }\left( 1+3(q+q_0)\right) \le \frac{1}{\lambda }. \end{aligned}$$

Hence, within one generation of $\lambda$ iterations, the expected number of times this individual is selected is at most 1. $\square$

We now have the necessary ingredients to prove the required condition about the number of Q-individuals in $S_0$.

Lemma 12

Assume that $\lambda \in {{\,\textrm{poly}\,}}(n),$ and for two constants $\alpha ,\varepsilon \in (0,1)$ with $\alpha -\varepsilon \ge 4/5$, the mutation rate is $\chi \le 1/(1-\alpha +\varepsilon ).$ Let T be as defined in Theorem 15. For any $\tau \le e^{cn}$ where c is a sufficiently small constant, define $\tau _*:=\min \{ T/\lambda -1, \tau \}$, then

$$\begin{aligned} \Pr \left( \bigvee _{t=0}^{\tau _*} (Q_t\cap S_0) \ne \emptyset \right) \le \tau e^{-\Omega (n)}+\tau e^{-\Omega (\lambda )}. \end{aligned}$$

Proof

Each individual in the initial population $Q_0$ is sampled uniformly at random, with $n/2 \le (\alpha -\varepsilon ) n/(1+3/5)$ expected number of 1-bits. Hence, by a Chernoff bound [24] and a union bound, the probability that the initial population $Q_0$ intersects with $S_0\cup S_1$ is no more than $\lambda e^{-\Omega (n)}=e^{-\Omega (n)}$.

We divide the remaining $t-1$ generations into a random number of phases, where each phase lasts until $p_0>0$, and we assume that the phase begins with $q_0=0$.

If a phase begins with $p_0>0$, then the phase lasts one generation. Furthermore, it must hold that $q((\alpha -\varepsilon )n)=0$, otherwise the product $P_t\times Q_t$ contains a pair in $R_0\times S_1((\alpha -\varepsilon )n)$, i.e., an $\varepsilon$-approximate solution has been found, which contradicts that $t<T/\lambda$. If $q((\alpha -\varepsilon )n)=0$, then all Q-individuals belong to region $S_2$. In order to obtain any Q-individual in region $S_0$, it is necessary that at least one of $\lambda$ individuals mutates at least $\varepsilon n$ 0-bits, an event which holds with probability at most $\lambda \cdot {n\atopwithdelims ()\varepsilon n}\left( \frac{\chi }{n}\right) ^{\varepsilon n} \le \lambda e^{-\Omega (n)} = e^{-\Omega (n)}.$

If a phase begins with $p_0=0$, then we will apply Theorem 9 to show that it is unlikely that any Q-individual will reach $S_0$ within $e^{cn}$ generations, or the phase ends. We use the parameter $x^*:=1^n$, $a(n):=(1-\alpha )n$, and $b(n):=(1-\alpha +\varepsilon )n<n/\chi$. Hence, $d(n):=b(n)-a(n)=\varepsilon n=\omega (\ln (n))$.

We first bound the reproductive rate of Q-individuals in $S_1$. For any generation t, if $q_0+q<(1-\delta _2)$, then by Lemma 10, and a Chernoff bound, $\vert Q_{t+1}\cap S_0\cup S_1\vert \le (q_0+q)\lambda$ with probability $1-e^{-\Omega (\lambda )}$. By a union bound, this holds with probability $1-te^{-\Omega (\lambda )}$ within the next t generations. Hence, by Lemma 11, the reproductive rate of any Q-individual within $S_0\cup S_1$ is at most $\alpha _0:=1$, and condition 1 of Theorem 9 is satisfied. Furthermore, $\psi := \ln (\alpha _0)/\chi +\delta = \delta ' < 1$ for any $\delta '\in (0,1)$ and $\chi >0$, hence condition 2 is satisfied. Finally, condition 3 is satisfied as long as $\delta '$ is chosen sufficiently small. It follows by Theorem 9 that the probability that a Q-individual in $S_0$ is produced within a phase of length at most $\tau <e^{cn}$ is $e^{-\Omega (n)}$.

The lemma now follows by taking a union bound over the at most $\tau$ phases. $\square$

We can now proceed to analyse Phase 1, assuming that $q_0=0$. For a lower bound and to simplify calculations, we pessimistically assume that the following event occurs with probability 0

$$\begin{aligned} (x_1,y_1)\in (R_1\times (S_1\cup S_2))\;\wedge \; (x_2,y_2)\in (R_2\times S_0). \end{aligned}$$

We will see that the main effort in applying Theorem 3 is to prove that conditions (G2a) and (G2b) are satisfied. The following lemma will be useful in this regard for phase 1. Consistent with the assumptions of phase 1, the lemma assumes an upper bound on the number of predators in region $R_0$ and prey in region $S_0$, and no predator–prey pairs in region $R_0\times S_1$. Under these assumptions, the lemma implies that the number of pairs in region $(R_0\cup R_1)\times S_2$ will increase.

Lemma 13

If there exist $\rho ,\psi \in (0,1)$ such that

• (1) $p_0\le \sqrt{2(1-\rho )}-1$

• (2) $q_0\le \sqrt{2(1-\rho )}-1$

• (3) $p_0q=0$

then if $(p_0+p)(1-q-q_0) \le \psi$, it holds that

$$\begin{aligned} \varphi :=\frac{p_{\text {sel}}({R_0\cup R_1})}{p(R_0\cup R_1)}\cdot \frac{p_{\text {sel}}({S_2})}{p(S_2)} \ge 1+\rho (1-\sqrt{\psi }), \end{aligned}$$

otherwise, if $(p_0+p)(1-q-q_0) \ge \psi$, then $p_{\text {sel}}({R_0\cup R_1})p_{\text {sel}}({S_2}) \ge \psi .$

Proof

Given the assumptions, Lemma 23 and Lemma 24 imply

$$\begin{aligned} \varphi \ge (1+\rho (1-p-p_0))(1+\rho (q+q_0))\ge 1. \end{aligned}$$

(43)

For the first statement, we consider two cases:

Case 1: If $p_0+p<\sqrt{\psi }$, then by (43) and $q_0+q\ge 0$, it follows $\varphi \ge (1+\rho (1-\sqrt{\psi }))\cdot 1.$

Case 2: If $p_0+p\ge \sqrt{\psi }$, then by assumption $(1-q-q_0)\le \sqrt{\psi }$. By (43) and $1-p-p_0\ge 0$, it follows that $\varphi \ge 1\cdot (1+\rho (1-\sqrt{\psi })).$

For the second statement, (43) implies

$$\begin{aligned} p_{\text {sel}}({R_0\cup R_1})p_{\text {sel}}({S_2})&= \varphi p(R_0\cup R_1)p(S_2)\\&= \varphi (p_0+p)(1-q-q_0) \ge 1\cdot \psi . \end{aligned}$$

$\square$

5.2 Ensuring Condition (G2) During Phase 2

We now proceed to analyse Phase 2.

Corollary 14

For any $\delta _2\in (0,1),$ if $q_0\in [0,\delta _2/1200)$, $p_0q<1-\delta _2$, and $p_0\in (1/3,1]$, then for $\delta _2':= \min \{\delta _2/20-8q_0,1/10-12q_0,\frac{\delta _2}{300}(40-\delta _2(17-\delta _2))\}$, it holds

$$\begin{aligned} \frac{p_{\text {sel}}({R_0})}{p(R_0)} \frac{p_{\text {sel}}({S_1})}{p(S_1)} > 1+\delta _2'. \end{aligned}$$

(44)

Proof

We distinguish between two cases with respect to the value of $p_0$.

If $p_0\in (1/3,1-\delta _2/10)$, then we apply Lemma 19. The conditions of Lemma 19 hold for the parameter $\delta _1:=\delta _2/10$, and the statement follows for

$$\begin{aligned} \delta _2'=\delta _1'&= \min \{\delta _1/2-8q_0,1/10-12q_0\}\\&= \min \{\delta _2/20-8q_0,1/10-12q_0\}. \end{aligned}$$

If $p_0\in [1-\delta _2/10,1]$, then we apply Lemma 20 for $\rho =\delta _2$, which implies that the statement holds for

$$\begin{aligned} \delta _2'=\frac{\delta _2}{300}(40-\delta _2(17-\delta _2)). \end{aligned}$$

(45)

$\square$

5.3 Main Result

We now obtain the main result: Algorithm 2 can efficiently locate an $\varepsilon$-approximate solution to an instance of Bilinear.

Theorem 15

Assume that $2000\ln (n)\le \lambda \in {{\,\textrm{poly}\,}}(n)$ and $\chi =\frac{1}{2}\ln \left( \frac{42}{41(1+\delta )}\right)$ for any constant $\delta \in (0,1/41)$. Let $\alpha ,\beta ,\varepsilon \in (0,1)$ be three constants where $\alpha -\varepsilon \ge 4/5$. Define $T:= \min \{\lambda t\mid (P_t\times Q_t) \cap (R_0\times S_1((\alpha -\varepsilon ))n)\}$ where $P_t$ and $Q_t$ are the populations of Algorithm 2 applied to Bilinear $_{\alpha ,\beta }$. Then for all $r\in {{\,\textrm{poly}\,}}(n)$ and any constant $c''>1$, it holds

$$\begin{aligned} \Pr \left( T>\frac{2rc''\lambda }{\delta }\left( \lambda ^2n +\frac{23n}{\chi }\ln \left( \frac{1}{\beta (1-\alpha +\varepsilon )}\right) \right) \right) \le (1/r)(1+o(1)). \end{aligned}$$

Proof

Note that $0< \chi< 1 < 1/(1-\alpha +\varepsilon ).$

The proof will refer to four parameters $\rho ,\delta ,\delta _3,\gamma _0\in (0,1)$, which will be defined later, but which we for now assume satisfy the following four constraints

$$\begin{aligned} 1/3< \gamma _0&\le \sqrt{2(1-\rho )}-1 < 1/2 \end{aligned}$$

(46)

$$\begin{aligned} 1+\delta&\le (1+\rho (1-\sqrt{\gamma _0(1+\delta _3)}))e^{-2\chi }(1-o(1)) \end{aligned}$$

(47)

$$\begin{aligned} 1+\delta&\le (1+\delta _3)e^{-2\chi }(1-o(1)) \end{aligned}$$

(48)

$$\begin{aligned} 1+\delta&\le (1+1/40)e^{-2\chi }(1-o(1)). \end{aligned}$$

(49)

For some $\tau \in {{\,\textrm{poly}\,}}(n)$ to be defined later, let $\tau _*:=\min \{ T/\lambda -1, \tau \}$. We will condition on the event that $q_0=0$ holds for the first $\tau _*$ generations, and consider the run a failure otherwise. By Lemma 12, the probability of such a failure is no more than $\tau e^{-\Omega (\lambda )}+\tau e^{-\Omega (n)}=e^{-\Omega (\lambda )}+e^{-\Omega (n)}$, assuming that the constraint $\lambda \ge c\log (n)$ holds for a sufficiently large constant c.

We apply Theorem 3 with $m=m_1+m_2$ levels, with $m_1=(1-\beta )n+1$ levels during phase 1, and $m_2=(\alpha -\varepsilon )n+1$ levels during phase 2, where the levels

$$\begin{aligned} \left( A_0^{(1)}\times B_0^{(1)}\right) , \ldots , \left( A^{(1)}_{(1-\beta )n},B^{(1)}_{(1-\beta )n}\right) , \left( A_0^{(2)}\times B_0^{(2)}\right) , \ldots , \left( A^{(2)}_{(\alpha -\varepsilon )n},B^{(2)}_{(\alpha -\varepsilon )n}\right) , \end{aligned}$$

are as defined in Sect. 5. Hence, in overall the total number of levels is $m\le 2(n+1)$.

We now prove conditions (G1), (G2a), and (G2b) separately for Phase 1 and Phase 2.

Phase 1: Assume that the current level belongs to phase 1 for any $j\in [0,(1-\beta )n]$. To prove that condition (G2a) holds, we will now show that the conditions of Lemma 13 are satisfied for the parameter $\psi :=\gamma _0$. By Lemma 8, we have $p_0<\gamma _0/(1-q_0)=\gamma _0 \le \sqrt{2(1-\rho )}-1$, hence condition 1 is satisfied. Condition 2 is satisfied by the assumption on $q_0=0$. By the definition of the level, $(p_0+p)(1-q-q_0)<\gamma _0=\psi$. Finally, for condition 3, we pessimistically assume that $p_0q=0$, otherwise the algorithm has already found an $\varepsilon$-approximate solution to the problem. All three conditions of Lemma 13 are satisfied. To produce an individual in $A_{j+1}^{(1)}$, it suffices to select and individual in $A_{j+1}^{(1)}$ and not mutate any of the bits, and analogously to produce an individual in $B_{j+1}^{(1)}$. In overall, for a sample $(x,y)\sim {\mathcal {D}}(P,Q)$, this gives

$$\begin{aligned}&\Pr \left( x\in A_{j+1}^{(1)}\right) \Pr \left( y\in B_{j+1}^{(1)}\right) \end{aligned}$$

(50)

$$\begin{aligned}&\ge p_{\text {sel}}({A_{j+1}^{(1)}})p_{\text {sel}}({B_{j+1}^{(1)}})\left( 1-\frac{\chi }{n}\right) ^{2n} \end{aligned}$$

(51)

$$\begin{aligned}&\ge (1+\rho (1-\sqrt{\gamma _0}))p(A_{j+1}^{(1)})p(B_{j+1}^{(1)})e^{-2\chi }(1-o(1)) \end{aligned}$$

(52)

$$\begin{aligned}&> \left( 1+\rho (1-\sqrt{\gamma _0(1+\delta _3)})\right) p(A_{j+1}^{(1)})p(B_{j+1}^{(1)})e^{-2\chi }(1-o(1)) \end{aligned}$$

(53)

$$\begin{aligned}&\ge \gamma (1+\delta ), \end{aligned}$$

(54)

where the last inequality follows from assumption (47). Condition (G2a) of the level-based theorem is therefore satisfied for Phase 1.

We now prove condition (G2b). Assume that $\gamma _0\le p_{\text {sel}}({A_{j}^{(1)}})p_{\text {sel}}({B_{j}^{(1)}})$. To produce an individual in $A_{j}^{(1)}$, it suffices to select an individual in $A_{j}^{(1)}$ and not mutate any of the bits, and analogously for $B_{j}^{(1)}$. For a sample $(x,y)\sim {\mathcal {D}}(P,Q)$, we therefore have

$$\begin{aligned} \Pr \left( x\in A_{j}^{(1)}\right) \Pr \left( y\in B_{j}^{(1)}\right)&\ge p_{\text {sel}}({A_{j}^{(1)}})p_{\text {sel}}({B_{j}^{(1)}})\left( 1-\frac{\chi }{n}\right) ^{2n}. \end{aligned}$$

(55)

To lower bound the expression in (55), we apply Lemma 13 again, this time with parameter $\psi :=\gamma _0(1+\delta _3)$. We distinguish between two cases.

In the case where $\gamma _0\le p(A_{j}^{(1)})p(B_{j}^{(1)})\le \gamma _0(1+\delta _3)$, the first statement of Lemma 13 gives

$$\begin{aligned} p_{\text {sel}}({A_{j}^{(1)}})p_{\text {sel}}({B_{j}^{(1)}})\left( 1-\frac{\chi }{n}\right) ^{2n}&\ge \gamma _0(1+\rho (1-\sqrt{\psi })e^{-2\chi }(1-o(1))\\&= \gamma _0(1+\rho (1-\sqrt{\gamma _0(1+\delta _3)})e^{-2\chi }(1-o(1))\\&\ge \gamma _0(1+\delta ), \end{aligned}$$

where the last inequality follows from assumption (47). In the case where $p(A_{j}^{(1)})p(B_{j}^{(1)})\ge \gamma _0(1+\delta _3)$, the second statement of Lemma 13 gives

$$\begin{aligned} p_{\text {sel}}({A_{j}^{(1)}})p_{\text {sel}}({B_{j}^{(1)}})\left( 1-\frac{\chi }{n}\right) ^{2n}&\ge \gamma _0(1+\delta _3)e^{-2\chi }(1-o(1))\\&\ge \gamma _0(1+\delta ), \end{aligned}$$

where the last inequality follows from assumption (48). In both cases, it follows that

$$\begin{aligned} \Pr \left( x\in A_{j}^{(1)}\right) \Pr \left( y\in B_{j}^{(1)}\right) \ge \gamma _0(1+\delta ), \end{aligned}$$

which proves that Condition (G2b) is satisfied in phase 1.

We now consider condition (G1). Assume that $p(A_j^{(1)}\times B_j^{(1)})=(p_0+p)(1-q-q_0)\ge \gamma _0$ and $(x,y)\sim {\mathcal {D}}(P,Q)$. Then, a P-individual can be obtained in $A_{j+1}^{(1)}$ by selecting an individual in $A_j^{(1)}$. By definition, the selected individual has in the worst case $n-j$ 1-bits, and it suffices to flip any of these bits and no other bits, an event which occurs with probability at least

$$\begin{aligned} \Pr \left( x\in A_{j+1}^{(1)}\right)&\ge p_{\text {sel}}({A_j^{(1)}})\frac{(n-j)\chi }{n}\left( 1-\frac{\chi }{n}\right) ^{n-1}\\&\ge p_{\text {sel}}({A_j^{(1)}})\cdot \frac{(n-j)\chi }{ne^{\chi }} (1-o(1)). \end{aligned}$$

A Q-individual can be obtained in $B_{j+1}^{(1)}$ by selecting an individual in $B_{j+1}^{(1)}$ and not mutate any bits. This event occurs with probability at least

$$\begin{aligned} \Pr \left( y\in B_{j+1}^{(1)}\right)&\ge p_{\text {sel}}({B_j^{(1)}})\left( 1-\frac{\chi }{n}\right) ^{n} \ge \frac{\gamma _0(1-o(1))}{p_{\text {sel}}({A_j^{(1)}})e^{\chi }} \end{aligned}$$

Hence, for a sample $(x,y)\sim {\mathcal {D}}(P,Q)$, we obtain by (55),

$$\begin{aligned} \Pr \left( x\in A_{j+1}^{(1)}\right) \Pr \left( y\in B_{j+1}^{(1)}\right) \ge \frac{(n-j)\gamma _0\chi }{ne^{2\chi }} (1-o(1)) =:z^{(1)}_j. \end{aligned}$$

(56)

hence condition (G1) is satisfied.

Phase 2: The analysis is analogous for this phase. To prove (G2a), assume that the current level belongs to phase 2 for any $j\in [0,(\alpha -\varepsilon )n]$. By the definitions of the levels in this phase and the assumptions of (G2a), we must have

$$\begin{aligned} p_0q(j+1)=\gamma<\gamma _0<1/2, \end{aligned}$$

(57)

and $p_0 q(j)\ge \gamma _0$, thus $p_0\ge \gamma _0> 1/3$ where the last inequality follows from our choice of $\gamma _0$. Together with the assumption $q_0=0$, Corollary 14 gives for $\delta _2:=1/2$ and

$$\begin{aligned} \delta _2'&:=\min \{\delta _2/20-8q_0,1/10-12q_0,\frac{\delta _2}{300}(40-\delta _2(17-\delta _2))\} = \frac{1}{40}. \end{aligned}$$

we get the lower bound

$$\begin{aligned} \Pr \left( x\in A_{j+1}^{(2)}\right) \Pr \left( y\in B_{j+1}^{(2)}\right)&\ge p_{\text {sel}}({A_{j+1}^{(2)}})p_{\text {sel}}({B_{j+1}^{(2)}})\left( 1-\frac{\chi }{n}\right) ^{2n} \end{aligned}$$

(58)

$$\begin{aligned}&\ge (1+\delta _2')p(A_{j+1}^{(1)})p(B_{j+1}^{(1)})e^{-2\chi }(1-o(1)) \end{aligned}$$

(59)

$$\begin{aligned}&\ge (1+\delta )\gamma , \end{aligned}$$

(60)

where the last inequality follows from assumption (49).

Condition (G2b) can be proved analogously to Phase 1. Again, we have

$$\begin{aligned} \Pr \left( x\in A_{j}^{(2)}\right) \Pr \left( y\in B_{j}^{(2)}\right)&\ge p_{\text {sel}}({A_{j}^{(2)}})p_{\text {sel}}({B_{j}^{(2)}})\left( 1-\frac{\chi }{n}\right) ^{2n}. \end{aligned}$$

(61)

In the case where $p_{\text {sel}}({A_{j}^{(2)}})p_{\text {sel}}({B_{j}^{(2)}})=p_0(j)q<1-\delta _2$ for $\delta _2=9/20$, Corollary 14 for $\delta '_2=\min (1/90,\delta _2/40)=1/90$ gives as above

$$\begin{aligned} p_{\text {sel}}({A_{j}^{(2)}})p_{\text {sel}}({B_{j}^{(2)}})\left( 1-\frac{\chi }{n}\right) ^{2n}&\ge \gamma _0(1+\delta '_2)e^{-2\chi }(1-o(1))\\&\ge \gamma _0(1+\delta ). \end{aligned}$$

In the case where $p_{\text {sel}}({A_{j}^{(2)}})p_{\text {sel}}({B_{j}^{(2)}})=p_0(j)q\ge 1-\delta _2$, we get

$$\begin{aligned} p_{\text {sel}}({A_{j}^{(2)}})p_{\text {sel}}({B_{j}^{(2)}})\left( 1-\frac{\chi }{n}\right) ^{2n}&\ge (1-\delta _2)e^{-2\chi }(1-o(1))\\&= (1/2)(1+1/10)e^{-2\chi }(1-o(1))\\&> \gamma _0(1+\delta '_2)e^{-2\chi }(1-o(1))\\&\ge \gamma _0(1+\delta ). \end{aligned}$$

Therefore, condition (G2b) also holds in Phase 2.

To prove condition (G1), we proceed as for Phase 1 and observe that to produce an individual in $A_{j+1}^{(2)}$, it suffices to select a P-individual in $A_{j}^{(2)}$ and not mutate any of the bits. To produce an individual in $B_{j+1}^{(2)}$, it suffices to select a Q-individual in $B_{j}^{(2)}$ and flip one of the at least $n-j$ number of 0-bits. Similarly to in (56), we obtain

$$\begin{aligned} \Pr \left( x\in A_{j+1}^{(2)}\right) \Pr \left( y\in B_{j+1}^{(2)}\right)&\ge \frac{(n-j)\gamma _0\chi }{ne^{2\chi }} (1-o(1)) =: z^{(2)}_j. \end{aligned}$$

hence condition (G1) will be satisfied during phase 2.

Condition (G3) is satisfied as long as $\lambda \ge 2\left( \frac{1}{\gamma _0\rho ^2}\right) ^{1+\upsilon }\ln (m/z_*)$.

All the conditions are satisfied, and assuming that $q_0=0$, it follows that the expected time to reach an $\varepsilon$-approximation of Bilinear is for any constant $c''>1$ no more than

$$\begin{aligned} \mathbb {E}\left[ T\right]&\le \frac{c''\lambda }{\delta }\left( \lambda ^2m+16\sum _{i=1}^{m-1}\frac{1}{z_i}\right) \end{aligned}$$

(62)

$$\begin{aligned}&\le \frac{2c''\lambda }{\delta }\left( \lambda ^2(n+1)+8\sum _{i=1}^{m_1-1}\frac{1}{z^{(1)}_i}+8\sum _{i=1}^{m_2-1}\frac{1}{z^{(2)}_i}\right) \end{aligned}$$

(63)

$$\begin{aligned}&\le \frac{2c''\lambda }{\delta }\left( \lambda ^2(n+1) +\frac{8e^{2\chi }n(1+o(1))}{\gamma _0\chi }\left( \sum _{i=1}^{m_1-1} \frac{1}{n-i} + \sum _{i=1}^{m_2-1} \frac{1}{n-i} \right) \right) \end{aligned}$$

(64)

$$\begin{aligned}&\le \frac{2c''\lambda }{\delta }\left( \lambda ^2(n+1) +\frac{8e^{2\chi }n(1+o(1))}{\gamma _0\chi }\left( 2\sum _{i=1}^{n-1}\frac{1}{i} -\sum _{i=1}^{\beta n} \frac{1}{i} -\sum _{i=1}^{(1-\alpha +\varepsilon )n} \frac{1}{i} \right) \right) \end{aligned}$$

(65)

$$\begin{aligned}&\le \frac{2c''\lambda }{\delta }\left( \lambda ^2(n+1) +\frac{8e^{2\chi }n(1+o(1))}{\gamma _0\chi }\ln \left( \frac{1}{\beta (1-\alpha +\varepsilon )}\right) \right) . \end{aligned}$$

(66)

We now choose the parameters $\rho ,\delta ,\delta _3,\gamma _0\in (0,1)$, where numerical maximisation of $\delta$ subject to the constraints, give approximate solutions $\gamma _0=9/25$, $\delta _3=1/40$, $\rho =47/625$, and choosing

$$\begin{aligned} \delta := \left( 1+\frac{1}{41}\right) e^{-2\chi }-1\le \left( 1+\frac{1}{40}\right) e^{-2\chi }(1-o(1))-1 , \end{aligned}$$

(67)

thus assumption (49) is satisfied. Furthermore, numerical evaluation show that the choices of $\delta _3,\rho ,$ and $\gamma _0$ give

$$\begin{aligned} \rho (1-\sqrt{\gamma _0(1+\delta _3)})> \frac{29}{1000} > \delta _3, \end{aligned}$$

thus assumptions (48) and (47) follow from assumption (49). Finally, assumption (46) is also satisfied because

$$\begin{aligned} \frac{1}{3}<\gamma _0=\frac{9}{25} = \sqrt{2(1-\rho )}-1 < \frac{1}{2}. \end{aligned}$$

Note that condition (G3) is satisfied since for a sufficiently small constant $\upsilon >0$,

$$\begin{aligned} \lambda&\ge 2000\ln (n)\\&\ge 2\left( \frac{1}{\gamma _0\rho ^2}\right) ^{1+\upsilon }\ln (n^2)(1+o(1))\\&\ge 2\left( \frac{1}{\gamma _0\rho ^2}\right) ^{1+\upsilon }\ln \left( \frac{2n^2e^{2\chi }}{\gamma _0\chi }\right) \\&\ge 2\left( \frac{1}{\gamma _0\rho ^2}\right) ^{1+\upsilon }\ln (m/z_*) \end{aligned}$$

Inserting these parameter choices into (66) gives

$$\begin{aligned} \mathbb {E}\left[ T\right]&\le \frac{2c''\lambda }{\delta }\left( \lambda ^2n +\frac{200e^{2\chi }n}{9\chi }\ln \left( \frac{1}{\beta (1-\alpha +\varepsilon )}\right) \right) (1+o(1))\\&= \frac{2c''\lambda }{\delta }\left( \lambda ^2n +\frac{42}{41(1+\delta )}\frac{200n}{9\chi }\ln \left( \frac{1}{\beta (1-\alpha +\varepsilon )}\right) \right) (1+o(1))\\&< \frac{2c''\lambda }{\delta }\left( \lambda ^2n +\frac{23n}{\chi }\ln \left( \frac{1}{\beta (1-\alpha +\varepsilon )}\right) \right) (1+o(1)) := \tau . \end{aligned}$$

By Markov’s inequality, the probability that a solution has not been obtained in $r\tau$ time is less than 1/r. Hence, in overall, taking into account all failure events, we obtain

$$\begin{aligned} \Pr \left( T>r\tau \right) \le 1/r + e^{-\Omega (n)} + e^{-\Omega (\lambda )}\le (1/r)(1+o(1)). \end{aligned}$$

Since the statement holds for all choices of the constant $c''>1$, it also holds for

$$\begin{aligned} \tau ':=\frac{2c''\lambda }{\delta }\left( \lambda ^2n +\frac{23n}{\chi }\ln \left( \frac{1}{\beta (1-\alpha +\varepsilon )}\right) \right) \end{aligned}$$

(i.e., $\tau$ without the extra factor $1+o(1)$), giving the final result

$$\begin{aligned} \Pr \left( T>r\tau '\right) \le 1/r + e^{-\Omega (n)} + e^{-\Omega (\lambda )}\le (1/r)(1+o(1)). \end{aligned}$$

$\square$

6 A Co-evolutionary Error Threshold

The previous section presented a scenario where Algorithm 2 obtains an approximate solution efficiently. We now present a general scenario where the algorithm is inefficient. In particular, we show that there exists a critical mutation rate above which the algorithm fails on any problem, as long as the problem does not have too many global optima (Theorem 16). The critical mutation rate is called the “error threshold” of the algorithm [19, 25]. As far as the author is aware, this is the first time an error threshold has been identified in co-evolution. The proof of Theorem 16 uses the so-called negative drift theorem for populations (Theorem 9) [19].

Theorem 16

There exists a constant $c>0$ such that the following holds. If A and B are subsets of $\{0,1\}^n$ with $\min \{ \vert A\vert , \vert B\vert \}\le e^{cn}$, and Algorithm 2 is executed with population size $\lambda \in {{\,\textrm{poly}\,}}(n)$ and constant mutation rate $\chi >\ln (2)/(1-2\delta )$ for any constant $\delta \in (0,1/2)$, then there exists a constant $c'$ such that $\Pr \left( T_{A\times B}<e^{c'n}\right) = e^{-\Omega (n)}$.

Proof

Without loss of generality, assume that $\vert B\vert \le \vert A\vert$. For a lower bound on $T_{A\times B}$, it suffices to compute a lower bound on the time until the Q-population contains an element in B.

For any $y\in B,$ we will apply Theorem 9 to bound $T_{y}:=\min \{ t\mid H(Q_t,y)\le 0 \}$, i.e., the time until the Q population contains y. Define $a(n):=0$ and $b(n):=n\min \{1/5,1/2-(1/2)\sqrt{1-\delta ^2},1/\chi \}$. Since $\delta$ is a constant, it follows that $d(n)=b(n)-a(n)=\omega (\ln n)$. Furthermore, by definition, $b(n)\le n/\chi$.

We now show that condition 1 of Theorem 9 holds for $\alpha _0:=2$. For any individual $u\in \mathcal {Y}$, the probability that the individual is selected in lines 7–12 is at most $1-\Pr \left( y_1\ne u\wedge y_2\ne u\right) = 1-(1-1/\lambda )^2 = (1/\lambda )(2-1/\lambda ).$ Thus within the $\lambda$ iterations, individual u is selected less than 2 times in expectation. This proves condition 1.

Condition 2 is satisfied because by the assumption on the mutation rate, $\psi :=\ln (\alpha _0)/\chi +\delta \le 1-\delta <1$. Finally, condition 3 trivially holds because $b(n)\le n/5$ and $1/2-\sqrt{\psi (2-\psi )}/2 \le 1/2-\sqrt{1-\delta ^2}/2 \le b(n)/n.$

All conditions are satisfied, and Theorem 9 imply that for some constant $c'$, $\Pr \left( T_{y^*}<e^{c'n}\right) =e^{-\Omega (n)}.$ Taking a union bound over all elements in B, we get for sufficiently small c

$$\begin{aligned} \Pr \left( T_{A\times B}<e^{c'n}\right)&\le \Pr \left( T_{B\times {\mathcal {Y}}}<e^{c'n}\right) \\&\le \sum _{y\in B}\Pr \left( T_{y}<e^{c'n}\right) \\&\le e^{cn}\cdot e^{-\Omega (n)} = e^{-\Omega (n)}. \end{aligned}$$

$\square$

7 Conclusion

Co-evolutionary algorithms have gained wide-spread interest, with a number of exciting applications. However, their population dynamics tend to be significantly more complex than in standard evolutionary algorithms. A number of pathological behaviours are reported in the literature, preventing the potential of these algorithms. There has been a long-standing goal to develop a rigorous theory for co-evolution which can explain when they are efficient. A major obstacle for such a theory is to reason about the complex interactions that occur between multiple populations.

This paper provides the first step in developing runtime analysis for population-based, competitive co-evolutionary algorithms. A generic mathematical framework covering a wide range of CoEAs is presented, along with an analytical tool to derive upper bounds on their expected runtimes. To illustrate the approach, we define a new co-evolutionary algorithm PDCoEA and analyse its runtime on a bilinear maximin-optimisation problem Bilinear. For some problem instances, the algorithm obtains a solution within arbitrary constant approximation ratio to the optimum within polynomial time $O(r\lambda ^3n)$ with probability $1-(1/r)(1+o(1))$ for all $r\in {{\,\textrm{poly}\,}}(n)$, assuming population size $\lambda \in \Omega (\log n)\cap {{\,\textrm{poly}\,}}(n)$ and sufficiently small (but constant) mutation rate. Additionally, we present a setting where PDCoEA is inefficient. In particular, if the mutation rate is too high, the algorithm needs with overwhelmingly high probability exponential time to reach any fixed solution. This constitutes a co-evolutionary “error threshold”.

Future work should consider broader classes of problems, as well as other co-evolutionary algorithms.

Technical Results

Lemma 17

(Lemma 18 in [20]) If $Z\sim {{\,\textrm{Bin}\,}}(\lambda ,r)$ with $r\ge \alpha (1+\delta )$, then for any $\kappa \in (0,\delta ]$, $\mathbb {E}\left[ e^{-\kappa Z}\right] \le e^{-\kappa \alpha \lambda }$.

Lemma 18

Consider any pair of independent binomial random variables $X\sim {{\,\textrm{Bin}\,}}(\lambda ,p)$ and $Y\sim {{\,\textrm{Bin}\,}}(\lambda ,q)$, where $pq\ge (1+\sigma )^2z,$ $p,q,z\in (0,1)$ and $\sigma >0$. Then $\mathbb {E}\left[ e^{-\eta XY}\right] \le e^{-\eta z\lambda ^2}$ for all $\eta$ where $0<\eta \le \frac{\sigma }{(1+\sigma )\lambda }$.

Proof

The proof applies Lemma 17 twice.

First, we apply Lemma 17 for the parameters $Z:=X$, $\alpha :=(z/q)(1+\sigma )$ and $\kappa :=\eta Y$. The assumptions of the lemma then imply $p\ge \frac{z(1+\sigma )^2}{q} = \alpha (1+\sigma )$ and $\kappa \le \frac{\sigma Y}{(1+\sigma )\lambda } \le \sigma$, i.e., the conditions of Lemma 17 are satisfied. This then gives

$$\begin{aligned} \mathbb {E}\left[ e^{-\eta XY}\mid Y\right]&= \mathbb {E}\left[ e^{-\kappa X}\mid Y\right] \le e^{-\kappa \alpha \lambda } = \exp \left( -\frac{\eta z}{q}(1+\sigma )\lambda Y\right) . \end{aligned}$$

(68)

Secondly, we apply Lemma 17 for the parameters $Z:=Y$, $\alpha :=q/(1+\sigma )$ and $\kappa :=\frac{z\eta }{q}(1+\sigma )\lambda$. We have $q = \alpha (1+\sigma )$, and by the assumption on $\eta$ and the fact that $1\ge q\ge z>0$, it follows that

$$\begin{aligned} \kappa \le \frac{\sigma }{(1+\sigma )\lambda }\frac{z}{q}(1+\sigma )\lambda \le \sigma . \end{aligned}$$

The conditions of Lemma 17 are satisfied, giving

$$\begin{aligned} \mathbb {E}\left[ \exp \left( -\frac{\eta z}{q}(1+\sigma )\lambda Y\right) \right]&= \mathbb {E}\left[ e^{-\kappa Y}\right] \le e^{-\kappa \alpha \lambda } \end{aligned}$$

(69)

$$\begin{aligned}&= \exp \left( -\frac{z\eta }{q}(1+\sigma )\lambda \frac{q}{1+\sigma }\lambda \right) = e^{-\eta z\lambda ^2}. \end{aligned}$$

(70)

By (68), (70), and the tower property of the expectation, it follows that

$$\begin{aligned} \mathbb {E}\left[ e^{-\eta XY}\right] =\mathbb {E}\left[ \mathbb {E}\left[ e^{-\eta XY}\right] \mid Y\right] < e^{-\eta z\lambda ^2}. \end{aligned}$$

$\square$

Lemma 19

For any $\delta _1\in (0,1)$, if $1/3<p_0<1-\delta _1$,

then for $\delta _1':=\min \{\delta _1/2-8q_0,1/10-12q_0\}$, it holds

$$\begin{aligned} \varphi :=\frac{p_{\text {sel}}({R_0})}{p(R_0)} \frac{p_{\text {sel}}({S_1})}{p(S_1)} > 1+\delta _1'. \end{aligned}$$

Proof

By Lemma 21 and Lemma 22

$$\begin{aligned} \varphi&> \left( \frac{3}{2}(2-p_0)p_0(1-q)+q-4q_0\right) \times \frac{1}{2}\left( (1-q_0)(3+q_0)-p_0(1-q_0(2+q_0))\right) \\&> \frac{1}{4}\left( 3(2-p_0)p_0(1-q)+2q-8q_0\right) \times \left( 3-q_0(2+q_0)-p_0+p_0q_0(2+q_0\right) \\&> \frac{1}{4}\left( 3(2-p_0)p_0+q(2-3(2-p_0)p_0)-8q_0\right) \times \left( 3-p_0-4q_0\right) \end{aligned}$$

Considering the variable q independently, we distinguish between two cases.

Case 1: $2<3(2-p_0)p_0$. In this case, the expression is minimised for $q=1$, giving

$$\begin{aligned} \varphi&> \frac{1}{4}\left( 2-8q_0\right) \left( 3-p_0-4q_0\right) \\&> \frac{1}{4}\left( 2-8q_0\right) \left( 2+\delta _1-4q_0\right) \\&> \frac{1}{4}\left( 2(2+\delta _1)-8q_0-(2+\delta _1)8q_0\right) \\&> 1+\delta _1/2-8q_0. \end{aligned}$$

Case 2: $2\ge 3(2-p_0)p_0$. In this case, the expression is minimised for $q=0$, giving

$$\begin{aligned} \varphi&> \frac{1}{4}\left( 3(2-p_0)p_0-8q_0\right) \left( 3-p_0-4q_0\right) \\&> \frac{3}{4}(2-p_0)p_0(3-p_0)-\frac{q_0}{4}\left( 4\cdot 3(2-p_0)p_0+8(3-p_0)\right) \\&> \frac{3}{4}(2-p_0)p_0(3-p_0)-12q_0 \end{aligned}$$

Note that the function $f(x):=(2-x)(3-x)x$ has derivative $f'(x)<0$ for $(5-\sqrt{7})/2<x<1$ and $f'(x)>0$ if $1/3<x<(5-\sqrt{7})/2$. Hence, to determine the minimum of the expression, it suffices to evaluate f at the extremal values $x=1/3$ and $x=1$, where $f(1/3)=40/27$ and $f(1)=2$. Hence, in case 2, we lower bound $\varphi$ by $\varphi > \frac{3}{4}\cdot \frac{40}{27}-12q_0 = \frac{10}{9}-12q_0.$ $\square$

Lemma 20

For any $\rho \in (0,1)$, if $p_0q<1-\rho$, $p_0\ge 1-\rho /10$ and $q_0<\rho /90$ then

$$\begin{aligned} \frac{p_{\text {sel}}({R_0})}{p(R_0)} \frac{p_{\text {sel}}({S_1})}{p(S_1)} > 1+\frac{\rho }{300}(40-\rho (17-\rho )). \end{aligned}$$

Proof

Note first that the assumptions imply

$$\begin{aligned} 3p_0q_0 < \rho /30. \end{aligned}$$

(71)

When $p_0$ is sufficiently large, it suffices to only consider the cases where both $x_1$ and $x_2$ are selected in $R_0$. More precisely, conditional on the event $x_1\in R_0\wedge x_2\in R_0$, the probability of selecting an element in $S_1$ is

$$\begin{aligned} p_{\text {sel}}({S_1\mid x_1\in R_0\wedge x_2\in R_0})&\ge \Pr \left( y_1\in S_1\wedge y_2\in S_1\right) \\&\quad + \Pr \left( y_1\in S_1\wedge y_2\in S_2\right) /2\\&\quad + \Pr \left( y_1\in S_2\wedge y_2\in S_1\right) \\&= q^2 + q(1-q-q_0)/2 + (1-q-q_0)q\\&= \frac{q}{2}(3-q-3q_0). \end{aligned}$$

Hence, the unconditional probability of selecting a pair in $S_1$ is

$$\begin{aligned} p_{\text {sel}}({S_1})&> \frac{p_0^2q}{2}\left( 3-q-3q_0\right) \\&> \frac{p_0q}{2}\left( 3(1-\rho /10)-(1-\rho )-3p_0q_0\right) \end{aligned}$$

using (71)

$$\begin{aligned}&> \frac{p_0q}{2}\left( 2+\rho -\rho (3/10)-\rho /30\right) \\&= p_0q\left( 1+\rho /3\right) . \end{aligned}$$

Using that $p(S_1)=q,$ and $p_{\text {sel}}({R_0})\ge p_0^2$, we get

$$\begin{aligned} \frac{p_{\text {sel}}({R_0})}{p(R_0)} \frac{p_{\text {sel}}({S_1})}{p(S_1)}&\ge \frac{p_0^2}{p_0}\frac{p_{\text {sel}}({S_1})}{p(S_1)}\\&> (1-\rho /10)^2\left( 1+\rho /3\right) \\&= 1+\frac{\rho }{300}(40-\rho (17-\rho )). \end{aligned}$$

$\square$

Lemma 21

$$\begin{aligned} \varphi := \frac{p_{\text {sel}}({R_0})}{p(R_0)} \ge \frac{1}{2}\left( (3+q_0)(1-q_0)-p_0(1-q_0(2+q_0))\right) \end{aligned}$$

Proof

Using Lemma 7, we get

$$\begin{aligned} p_{\text {sel}}({R_0})&= \Pr \left( x_1\in R_0\wedge x_2\in R_0\right) + \\&\quad + \Pr \left( x_1\in R_0 \wedge x_2\not \in R_0\right) \\&\quad \quad \times \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid x_1\in R_0 \wedge x_2\not \in R_0\right) \\&\quad + \Pr \left( x_1\not \in R_0 \wedge x_2\in R_0\right) \\&\quad \quad \times (1-\Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid x_1\not \in R_0 \wedge x_2\in R_0\right) )\\&\ge \Pr \left( x_1\in R_0\wedge x_2\in R_0\right) + \\&\quad + \Pr \left( (x_1,y_1)\in R_0\times S_1\cup S_2\wedge (x_1,y_1)\in R_1\cup R_2\times S_1\cup S_2\right) /2\\&\quad + \Pr \left( x_1\not \in R_0 \wedge x_2\in R_0\right) (1-\Pr \left( y_1\in S_0\wedge y_2\in S_0\right) )\\&\quad \ge p_0^2+p_0(1-p_0)(1-q_0)^2/2+p_0(1-p_0)(1-q_0^2) \end{aligned}$$

Recalling that $p(R_0)=p_0$, we get

$$\begin{aligned} \varphi&\ge p_0+(1-p_0)(1-q_0)^2/2+(1-p_0)(1-q_0^2)\\&= \frac{1}{2}\left( (3+q_0)(1-q_0)-p_0(1-q_0(2+q_0))\right) \end{aligned}$$

$\square$

Lemma 22

$$\begin{aligned} \varphi := \frac{p_{\text {sel}}({S_1})}{p(S_1)} > \frac{3}{2}(2-p_0)p_0(1-q)+q-4q_0. \end{aligned}$$

Proof

Using Lemma 7, we get

$$\begin{aligned} p_{\text {sel}}({S_1})&= \Pr \left( y_1\in S_1\wedge y_2\in S_1\right) + \\&\quad + \Pr \left( y_1\in S_1 \wedge y_2\not \in S_1\right) \\&\quad \quad \times \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid y_1\in S_1 \wedge y_2\not \in S_1\right) \\&\quad + \Pr \left( y_1\not \in S_1 \wedge y_2\in S_1\right) \\&\quad \quad \times (1-\Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid y_1\not \in S_1 \wedge y_2\in S_1\right) )\\&\ge \Pr \left( y_1\in S_1\wedge y_2\in S_1\right) + \\&\quad + \Pr \left( (x_1,y_1)\in R_0\times S_1 \wedge (x_2,y_2)\in R_0\times S_2\right) /2\\&\quad + \Pr \left( (x_1,y_1)\in R_0\times S_1 \wedge (x_2,y_2)\in R_1\cup R_2\times S_2\right) \\&\quad + \Pr \left( (x_1,y_1)\in R_1\times S_1 \wedge (x_2,y_2)\in R_1\times S_0\right) /2\\&\quad + \Pr \left( (x_1,y_1)\in R_1\times S_1 \wedge (x_2,y_2)\in R_2\times S_0\right) \\&\quad + \Pr \left( (x_1,y_1)\in R_2\times S_1 \wedge (x_2,y_2)\in R_2\times S_0\right) /2\\&\quad + \Pr \left( y_2\in S_1\right) \\&\quad \quad \times (1-\Pr \left( y_1\in S_1\right) \\&\quad \quad \quad -\Pr \left( (x_1,y_1)\in R_0\times S_0 \wedge x_2\in R_0\right) \\&\quad \quad \quad -\Pr \left( (x_1,y_1)\in R_1\times S_2 \wedge x_2\in R_1\cup R_2\right) \\&\quad \quad \quad -\Pr \left( (x_1,y_1)\in R_2\times S_2 \wedge x_2\in R_2\right) )\\&\ge q^2+qp_0(1-q-q_0)(p_0/2+1-p_0)+\\&\quad + qpq_0(p/2+1-p-p_0)+q(1-p-p_0)^2q_0/2\\&\quad + q(1-q-p_0^2q_0\\&\quad \quad -(1-q-q_0)(p(1-p_0)+(1-p-p_0)^2) \end{aligned}$$

Recalling that $p(S_1)=q$ and noting that $(4-p_0)p_0<4$, it follows that

$$\begin{aligned} \varphi&> \frac{3}{2}(2-p_0)p_0(1-q)+q\\&\quad + q_0\left( \frac{3}{2}-(4-p_0)p_0\right) +p(1-q-q_0)(1-p-p_0)\\&> \frac{3}{2}(2-p_0)p_0(1-q)+q-4q_0. \end{aligned}$$

$\square$

Lemma 23

If there exists $\rho >0$ such that

• (1) $q_0\le \sqrt{2(1-\rho )}-1$

then

$$\begin{aligned} \varphi :=\frac{p_{\text {sel}}({R_0\cup R_1})}{p(R_0\cup R_1)}>1+\rho (1-p-p_0). \end{aligned}$$

Proof

Using Lemma 7, we get

$$\begin{aligned} p_{\text {sel}}({R_0\cup R_1})&= \Pr \left( x_1\in R_0\cup R_1\wedge x_2\in R_0\cup R_1\right) + \\&\quad + \Pr \left( x_1\in R_0\cup R_1 \wedge x_2\not \in R_0\cup R_1\right) \\&\quad \quad \times \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid x_1\in R_0\cup R_1 \wedge x_2\not \in R_0\cup R_1\right) \\&\quad + \Pr \left( x_1\not \in R_0\cup R_1 \wedge x_2\in R_0\cup R_1\right) \\&\quad \quad \times (1-\Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid x_1\not \in R_0\cup R_1 \wedge x_2\in R_0\cup R_1\right) )\\&\ge \Pr \left( x_1\in R_0\cup R_1\wedge x_2\in R_0\cup R_1\right) + \\&\quad + \Pr \left( (x_1,y_1)\in R_0\cup R_1\times S_0\cup S_1 \wedge (x_2,y_2)\in R_2\times S_0\cup S_1\right) /2\\&\quad + \Pr \left( x_2\in R_0\cup R_1\right) \\&\quad \quad \times (1-\Pr \left( y_2\in S_0\wedge (x_1,y_1)\in R_2\times S_0\right) -\Pr \left( x_1\in R_0\cup R_1\right) )\\&\ge (p_0+p)^2+(p_0+p)(1-q_0)^2(1-p-p_0)/2+\\&\quad + (p_0+p)(1-(p_0+p)-q_0^2(1-p-p_0)) \end{aligned}$$

Recalling that $p(R_0\cup R_1)=p_0+p$, and the assumption of the lemma, it follows that

$$\begin{aligned} \varphi&\ge 1+(1-p-p_0)((1-q_0)^2/2-q_0)\\&= 1+(1-p-p_0)(1/2-q_0(1-q_0/2))\\&\ge 1+(1-p-p_0)(1/2-(1-2\rho )/2)\\&= 1 + \rho (1-p-p_0). \end{aligned}$$

$\square$

Lemma 24

If there exist $\rho >0$ such that

• (1) $p_0 q = 0$.

• (2) $p_0<\sqrt{2(1-\rho )}-1$

then

$$\begin{aligned} \varphi :=\frac{p_{\text {sel}}({S_2})}{p(S_2)} \ge 1+\rho (q_0+q). \end{aligned}$$

Proof

Using Lemma 7, we get

$$\begin{aligned} p_{\text {sel}}({S_2})&= \Pr \left( y_1\in S_2\wedge y_2\in S_2\right) + \\&\quad + \Pr \left( y_1\in S_2 \wedge y_2\not \in S_2\right) \\&\quad \quad \times \Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid y_1\in S_2 \wedge y_2\not \in S_2\right) \\&\quad + \Pr \left( y_1\not \in S_2 \wedge y_2\in S_2\right) \\&\quad \quad \times (1-\Pr \left( (x_1,y_1)\succeq (x_2,y_2)\mid y_1\not \in S_2 \wedge y_2\in S_2\right) )\\&\ge \Pr \left( y_1\in S_2\wedge y_2\in S_2\right) + \\&\quad + \Pr \left( (x_1,y_1)\in R_1\cup R_2\times S_2 \wedge (x_2,y_2)\in R_1\cup R_2\times S_0\cup S_1\right) /2\\&\quad + \Pr \left( y_2\in S_2\right) \\&\quad \quad \times (1-\Pr \left( (x_1,y_1)\in R_0\times S_1\right) \\&\quad \quad \quad -\Pr \left( (x_1,y_1)\in R_0\times S_0\wedge y_2\in S_2\right) -\Pr \left( y_1\in S_2\right) )\\&= (1-q-q_0)^2 \\&\quad + (1-q-q_0)(1-p_0)^2(q_0+q)/2 \\&\quad + (1-q-q_0)(1-p_0q-p_0^2q_0-(1-q-q_0)) \end{aligned}$$

From $p(S_2)=1-q-q_0$ and the assumptions of the lemma,

$$\begin{aligned} \varphi&\ge 1 + (1-p_0)^2(q_0+q)/2 -p_0q-p_0^2q_0\\&= 1 + (q_0+q)/2 - p_0q_0(1+p_0/2)\\&\ge 1 + (q_0+q)/2 - q_0(1/2-\rho )\\&\ge 1 + (q_0+q)\rho . \end{aligned}$$

$\square$

Lemma 25

([8]) For $n\in {\mathbb {N}}$ and $x\ge 0$, we have $1-(1-x)^n\ge 1-e^{-xn}\ge \frac{xn}{1+xn}$

Theorem 26

(Additive drift theorem [4]) Let $(Z_t)_{t\in {\mathbb {N}}}$ be a discrete-time stochastic process in $[0,\infty )$ adapted to any filtration $(\mathscr {F}_{t})_{t\in {\mathbb {N}}}$. Define $T_a:= \min \{t\in {\mathbb {N}} \mid Z_t \le a\}$ for any $a\ge 0$. For some $\varepsilon >0$ and constant $0<b<\infty$, define the conditions

• (1.1) $\mathbb {E}\left[ Z_{t+1} - Z_{t} + \varepsilon \;; t<T_{a} \mid \mathscr {F}_{t}\right] \le 0$ for all $t\in {\mathbb {N}}$,

• (1.2) $\mathbb {E}\left[ Z_{t+1} - Z_{t} + \varepsilon \;; t<T_{a} \mid \mathscr {F}_{t}\right] \ge 0$ for all $t\in {\mathbb {N}}$,

• (2) $Z_t<b$ for all $t\in {\mathbb {N}}$, and

• (3) $\mathbb {E}\left[ T_a \right] < \infty$.

If (1.1), (2), and (3) hold, then $\mathbb {E}\left[ T_a \mid \mathscr {F}_{0}\right] \le Z_0 / \varepsilon$.

If 1.2), 2), and 3) hold, then $\mathbb {E}\left[ T_a \mid \mathscr {F}_{0}\right] \ge (Z_0 - a) / \varepsilon$.

Lemma 27

(Corollary 1.8.3 in [9]) If $X\succeq Y$, then $\mathbb {E}\left[ X\right] \ge \mathbb {E}\left[ Y\right]$.

Lemma 28

For all $\delta \in (0,1)$ and $\delta _1\in [0,\delta )$

$$\begin{aligned} \frac{3\delta -4\delta _1}{11}<1-\sqrt{\frac{1+\delta _1}{1+\delta }}<\frac{4\delta -3\delta _1}{8}. \end{aligned}$$

Proof

By taking the first two terms of the Maclaurin series of $\sqrt{1+x}$ for any $x\in (0,1)$, we first obtain

$$\begin{aligned} \sqrt{1+x}&> 1+\frac{x}{2}-\frac{x^2}{8} > 1+\frac{3x}{8}, \end{aligned}$$

(72)

where the last inequality uses the assumption $x\in (0,1)$. Similarly, taking only the first term in the Maclaurin series, we obtain

$$\begin{aligned} \sqrt{1+x} < 1 + \frac{x}{2} \end{aligned}$$

(73)

Hence, using $\delta \in (0,1)$ we obtain

$$\begin{aligned} \frac{3\delta -4\delta _1}{11}&< \frac{3\delta -4\delta _1}{8+3\delta } = \frac{8+3\delta -8-4\delta _1}{8+3\delta } = 1-\frac{1+\frac{\delta _1}{2}}{1+\frac{3\delta }{8}} < 1-\frac{\sqrt{1+\delta _1}}{\sqrt{1+\delta }}. \end{aligned}$$

where the last inequality applies (72) for $x=\delta$ and (73) for $x=\delta _1$.

Analogously, the lower bound (73) for $x=\delta$, the upper bound (72) for $x=\delta _1$, and the assumption $\delta \in (0,1)$ give

$$\begin{aligned} 1-\frac{\sqrt{1+\delta _1}}{\sqrt{1+\delta }}&< 1-\frac{1+\frac{3\delta _1}{8}}{1+\frac{\delta }{2}} = \frac{2+\delta }{2+\delta }-\frac{2+\frac{3\delta _1}{4}}{2+\delta } = \frac{\delta -\frac{3\delta _1}{4}}{2+\delta } < \frac{4\delta -3\delta _1}{8}. \end{aligned}$$

$\square$