On the Parameterized Intractability of Determinant Maximization

Abstract

In the Determinant Maximization problem, given an $n \times n$ positive semi-definite matrix ${\textbf {A}}$ in $\mathbb {Q}^{n \times n}$ and an integer k, we are required to find a $k \times k$ principal submatrix of ${\textbf {A}}$ having the maximum determinant. This problem is known to be NP-hard and further proven to be W[1]-hard with respect to k by Koutis (Inf Process Lett 100:8–13, 2006); i.e., a $f(k)n^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$-time algorithm is unlikely to exist for any computable function f. However, there is still room to explore its parameterized complexity in the restricted case, in the hope of overcoming the general-case parameterized intractability. In this study, we rule out the fixed-parameter tractability of Determinant Maximization even if an input matrix is extremely sparse or low rank, or an approximate solution is acceptable. We first prove that Determinant Maximization is NP-hard and W[1]-hard even if an input matrix is an arrowhead matrix; i.e., the underlying graph formed by nonzero entries is a star, implying that the structural sparsity is not helpful. By contrast, Determinant Maximization is known to be solvable in polynomial time on tridiagonal matrices (Al-Thani and Lee, in: LAGOS, 2021). Thereafter, we demonstrate the W[1]-hardness with respect to the rank r of an input matrix. Our result is stronger than Koutis’ result in the sense that any $k \times k$ principal submatrix is singular whenever $k > r$. We finally give evidence that it is W[1]-hard to approximate Determinant Maximization parameterized by k within a factor of $2^{-c\sqrt{k}}$ for some universal constant $c > 0$. Our hardness result is conditional on the Parameterized Inapproximability Hypothesis posed by Lokshtanov et al. (in: SODA, 2020), which asserts that a gap version of Binary Constraint Satisfaction Problem is W[1]-hard. To complement this result, we develop an $\varepsilon$-additive approximation algorithm that runs in $\varepsilon ^{-r^2} \cdot r^{{{\,\mathrm{\mathcal {O}}\,}}(r^3)} \cdot n^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$ time for the rank r of an input matrix, provided that the diagonal entries are bounded.

1 Introduction

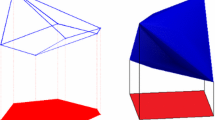
Background. We study the following Determinant Maximization problem: Given an $n \times n$ positive semi-definite matrix ${\textbf {A}}$ in $\mathbb {Q}^{n \times n}$ and an integer k in [n] denoting the solution size, find a $k \times k$ principal submatrix of ${\textbf {A}}$ having the maximum determinant; namely, maximize $\det ({\textbf {A}} _{S})$ subject to $S \in {[n] \atopwithdelims ()k}$. One motivating example for this problem is a subset selection task. Suppose we are given n items (e.g., images or products) associated with feature vectors $\textbf{v}_1, \ldots , \textbf{v}_n$ and required to select a “diverse” set of k items among them. We can measure the diversity of a set S of k items using the principal minor $\det ({\textbf {A}} _S)$ of the Gram matrix ${\textbf {A}}$ defined by feature vectors such that $A_{i,j} \triangleq \langle \textbf{v}_i, \textbf{v}_j \rangle$ for all $i, j \in [n]$, resulting in Determinant Maximization. This formulation is justified by the fact that $\det ({\textbf {A}} _S)$ is equal to the squared volume of the parallelepiped spanned by $\{\textbf{v}_i: i \in S\}$; that is, a pair of vectors at a large angle is regarded as more diverse. See Fig. 1 for an example of Determinant Maximization and its volume interpretation. In artificial intelligence and machine learning communities, Determinant Maximization is also known as MAP inference on a determinantal point process [8, 32], and has found many applications over the past decade, including tweet timeline generation [44], object detection [30], change-point detection [45], document summarization [10, 28], YouTube video recommendation [43], and active learning [7]. See the survey of Kulesza and Taskar [29] for further details. Though Determinant Maximization is known to be NP-hard to solve exactly [26], we can achieve an $\textrm{e}^{-k}$-factor approximation in polynomial time [37], which is nearly optimal because a $2^{-ck}$-factor approximation for some constant $c > 0$ is impossible unless P  $=$ NP [13, 16, 27].

Fig. 1

Example of Determinant Maximization with $n=4$ and $k=3$

Having known a nearly tight hardness-of-approximation result in the polynomial-time regime, we resort to parameterized algorithms [15, 18, 20]. We say that a problem is fixed-parameter tractable (FPT) with respect to a parameter $k \in \mathbb {N}$ if it can be solved in $f(k) \vert {\mathcal {I}}\vert ^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$ time for some computable function f and instance size $\vert {\mathcal {I}}\vert$. One very natural parameter is the solution size k, which is expected to be small in practice. By enumerating all $k \times k$ principal submatrices, we can solve Determinant Maximization in $n^{k + {{\,\mathrm{\mathcal {O}}\,}}(1)}$ time; i.e., it belongs to the class XP. Because FPT  $\subsetneq$ XP [18], it is even more desirable if an FPT algorithm exists. Unfortunately, Koutis [27] has already proven that Determinant Maximization is W[1]-hard with respect to k, which in fact follows from the reduction due to Ko et al. [26]. Therefore, under the widely-believed assumption that FPT  $\ne$ W[1], an FPT algorithm for Determinant Maximization does not exist.

However, there is still room to explore the parameterized complexity of Determinant Maximization in the restricted case, in the hope of circumventing the general-case parameterized intractability. Here, we describe three possible scenarios. One can first assume an input matrix ${\textbf {A}}$ to be sparse. Of particular interest is the structural sparsity of the symmetrized graph of ${\textbf {A}}$ [11, 14] defined as the underlying graph formed by nonzero entries of ${\textbf {A}}$, encouraged by numerous FPT algorithms for NP-hard graph-theoretic problems parameterized by the treewidth [15, 21]. For example, in change-point detection applications, Zhang and Ou [45] observed a small-bandwidth matrix and developed an efficient heuristic for Determinant Maximization. In addition, one may adopt a strong parameter. The rank of an input matrix ${\textbf {A}}$ is such a natural candidate. We often assume that ${\textbf {A}}$ is low-rank in applications; for instance, the feature vectors $\textbf{v}_i$ are inherently low-dimensional [9] or the largest possible subset is significantly smaller than the ground set size n. Since any $k \times k$ principal submatrix of ${\textbf {A}}$ is singular whenever $k > {{\,\textrm{rank}\,}}({\textbf {A}} )$, we can ensure that $k \leqslant {{\,\textrm{rank}\,}}({\textbf {A}} )$; namely, parameterization by ${{\,\textrm{rank}\,}}({\textbf {A}} )$ is considered stronger than that by k. Intriguingly, the partition function of product determinantal point processes is FPT with respect to rank while $\#$ P-hard in general [41]. The last possibility to be considered is FPT-approximability. Albeit W[1]-hardness of Determinant Maximization with parameter k, it could be possible to obtain an approximate solution in FPT time. It has been demonstrated that several W[1]-hard problems can be approximated in FPT time, such as Partial Vertex Cover and Minimum k -Median [23] (refer to the survey of Marx [35] and Feldmann et al. [19]). One may thus envision the existence of a $1/\rho (k)$-factor FPT-approximation algorithm for Determinant Maximization for a small function $\rho$. Alas, we refute the above possibilities under a plausible assumption in parameterized complexity.

Fig. 2

Structure of arrowhead matrices, where “$*$” denotes nonzero entries

Fig. 3

Structure of tridiagonal matrices, where “$*$” denotes nonzero entries

Our Results. We improve the W[1]-hardness of Determinant Maximization due to Koutis [27] by showing that it is still W[1]-hard even if an input matrix is extremely sparse or low rank, or an approximate solution is acceptable, along with some tractable cases.

We first prove that Determinant Maximization is NP-hard and W[1]-hard with respect to k even if the input matrix ${\textbf {A}}$ is an arrowhead matrix (Theorem 3.1). An arrowhead matrix is a square matrix that can include nonzero entries only in the first row, the first column, or the diagonal; i.e., its symmetrized graph is a star (cf. Fig. 2). Our hardness result implies that the “structural sparsity” of input matrices is not helpful; in particular, it follows from Theorem 3.1 that this problem is NP-hard even if the treewidth, pathwidth, and vertex cover number of the symmetrized graph are all 1. The proof is based on a parameterized reduction from k -Sum, which is a parameterized version of Subset Sum known to be W[1]-complete [1, 17], and involves a structural feature of the determinant of arrowhead matrices. On the other hand, Determinant Maximization is known to be solvable in polynomial time on tridiagonal matrices [2], whose symmetrized graph is a path graph (cf. Fig. 3). Though an extended abstract of this paper appearing in ISAAC’22 includes a polynomial-time algorithm on tridiagonal matrices, Lee pointed out to us that Al-Thani and Lee already proved the polynomial-time solvability on tridiagonal matrices in LAGOS’21 [2] and on spiders of bounded legs [3]. We thus omitted the proof for tridiagonal matrices from this article.

Thereafter, we demonstrate that Determinant Maximization is W[1]-hard when parameterized by the rank of an input matrix (Corollary 4.3). In fact, we obtain the stronger result that it is W[1]-hard to determine whether an input set of n d-dimensional vectors includes k pairwise orthogonal vectors when parameterized by d (Theorem 4.2). Unlike the proof of Theorem 3.1, we are allowed to construct only a f(k)-dimensional vector in a parameterized reduction. Therefore, we reduce from a different W[1]-complete problem called Grid Tiling due to Marx [34, 36]. In Grid Tiling, we are given $k^2$ nonempty sets of integer pairs arranged in a $k \times k$ grid, and the task is to select $k^2$ integer pairs such that the vertical and horizontal neighbors agree respectively in the first and second coordinates (see Problem 4.4 for the precise definition). Grid Tiling is favorable for our purpose because the constraint consists of simple equalities, and each cell is adjacent to (at most) four cells. To express the consistency between adjacent cells using only a f(k)-dimensional vector, we exploit Pythagorean triples. It is essential in Theorem 4.2 that the input vectors can include both positive and negative entries in a sense that we can find k d-dimensional nonnegative vectors that are pairwise orthogonal in FPT time with respect to d (Observation 4.6).

Our final contribution is to give evidence that it is W[1]-hard to determine whether the optimal value of Determinant Maximization is equal to 1 or at most $2^{-c\sqrt{k}}$ for some universal constant $c > 0$; namely, Determinant Maximization is FPT-inapproximable within a factor of $2^{-c\sqrt{k}}$ (Theorem 5.1). Our result is conditional on the Parameterized Inapproximability Hypothesis (PIH), which is a conjecture posed by Lokshtanov et al. [31] asserting that a gap version of Binary Constraint Satisfaction Problem is W[1]-hard when parameterized by the number of variables. PIH can be thought of as a parameterized analogue of the PCP theorem [4, 5]; e.g., Lokshtanov et al. [31] show that assuming PIH and FPT  $\ne$ W[1], Directed Odd Cycle Transversal does not admit a $(1-\varepsilon )$-factor FPT-approximation algorithm for some $\varepsilon > 0$. The proof of Theorem 5.1 involves FPT-inapproximability of Grid Tiling under PIH, which is reminiscent of Marx’s work [34] and might be of some independent interest. Because we cannot achieve an exponential gap by simply reusing the parameterized reduction from Grid Tiling of the second hardness result (as inferred from Observation 5.11 below), we apply a gadget invented by Çivril and Magdon-Ismail [13] to construct an ${{\,\mathrm{\mathcal {O}}\,}}(k^2 n^2)$-dimensional vector for each integer pair of a Grid Tiling instance. We further show that the same kind of hardness result does not hold when parameterized by the rank r of an input matrix. Specifically, we develop an $\varepsilon$-additive approximation algorithm that runs in $\varepsilon ^{-r^2} \cdot r^{{{\,\mathrm{\mathcal {O}}\,}}(r^3)} \cdot n^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$ time for any $\varepsilon > 0$, provided that the diagonal entries are bounded (Observation 5.11).

More Related Work. Determinant Maximization is not only applied in artificial intelligence and machine learning but also in computational geometry [22] and discrepancy theory; refer to Nikolov [37] and references therein. On the negative side, Ko et al. [26] prove that Determinant Maximization is NP-hard, and Koutis [27] proves that it is further W[1]-hard. NP-hardness of approximating Determinant Maximization has been investigated in [13, 16, 27, 40]. On the algorithmic side, a greedy algorithm achieves an approximation factor of 1/k! [12]. Subsequently, Nikolov [37] gives an $\textrm{e}^{-k}$-factor approximation algorithm; partition constraints [38] and matroid constraints [33] are also studied. Several $\#$ P-hard computation problems over matrices including permanents [11, 14], hyperdeterminants [11], and partition functions of product determinantal point processes [41] are efficiently computable if the treewidth of the symmetrized graph or the matrix rank is bounded.

2 Preliminaries

Notations and Definitions. For two integers $m,n \in \mathbb {N}$ with $m \leqslant n$, let $[n] \triangleq \{1, 2, \ldots , n\}$ and $[m\mathrel {..}n] \triangleq \{m,m+1,\ldots , n-1,n\}$. For a finite set S and an integer k, we write ${S \atopwithdelims ()k}$ for the family of all size-k subsets of S. For a statement P, $[\![P]\!]$ is 1 if P is true, and 0 otherwise. The base of logarithms is 2. Matrices and vectors are written in bold letters, and scalars are unbold. The Euclidean norm is denoted $\Vert \cdot \Vert$; i.e., $\Vert \textbf{v}\Vert \triangleq \sqrt{\sum _{i \in [d]}(v(i))^2}$ for a vector $\textbf{v} \in \mathbb {R}^{d}$. We use $\langle \cdot , \cdot \rangle$ for the standard inner product; i.e., $\langle \textbf{v}, \textbf{w} \rangle \triangleq \sum _{i \in [d]} v(i) \cdot w(i)$ for two vectors $\textbf{v}, \textbf{w} \in \mathbb {R}^{d}$. For an $n \times n$ matrix ${\textbf {A}}$ and an index set $S \subseteq [n]$, we use ${\textbf {A}} _S$ to denote the principal submatrix of ${\textbf {A}}$ whose rows and columns are indexed by S. For an $m \times n$ matrix ${\textbf {A}}$, the spectral norm $\Vert {\textbf {A}} \Vert _2$ is defined as the square root of the maximum eigenvalue of ${\textbf {A}} ^\top {\textbf {A}}$ and the max norm is defined as $\Vert {\textbf {A}} \Vert _{\max } \triangleq \max _{i,j} \vert {A_{i,j}}\vert$. It is well-known that $\Vert {\textbf {A}} \Vert _{\max } \leqslant \Vert {\textbf {A}} \Vert _2 \leqslant \sqrt{mn} \cdot \Vert {\textbf {A}} \Vert _{\max }$. The symmetrized graph [11, 14] of an $n \times n$ matrix ${\textbf {A}}$ is defined as an undirected graph G that has each integer of [n] as a vertex and an edge $(i,j) \in {[n] \atopwithdelims ()2}$ if $A_{i,j} \ne 0$ or $A_{j,i} \ne 0$; i.e., $G = ([n], \{ (i,j): A_{i,j} \ne 0 \})$. For a matrix ${\textbf {A}} \in \mathbb {R}^{n \times n}$, its determinant is defined as follows:

$$\begin{aligned} \det ({\textbf {A}} ) \triangleq \sum _{\sigma \in {\mathfrak {S}}_n} {{\,\textrm{sgn}\,}}(\sigma ) \prod _{i \in [n]} A_{i,\sigma (i)}, \end{aligned}$$

(2.1)

where ${\mathfrak {S}}_n$ denotes the symmetric group on [n], and ${{\,\textrm{sgn}\,}}(\sigma )$ denotes the sign of a permutation $\sigma$. We define $\det ({\textbf {A}} _{\emptyset }) \triangleq 1$. For a collection ${\textbf {V}} = \{\textbf{v}_1, \ldots , \textbf{v}_n\}$ of n vectors in $\mathbb {R}^{d}$, the volume of the parallelepiped spanned by ${\textbf {V}}$ is defined as follows:

$$\begin{aligned} {{\,\textrm{vol}\,}}({\textbf {V}} ) \triangleq \Vert \textbf{v}_1\Vert \cdot \prod _{2 \leqslant i \leqslant n} {{\,\textrm{d}\,}}(\textbf{v}_i, \{\textbf{v}_1, \ldots , \textbf{v}_{i-1}\}). \end{aligned}$$

(2.2)

Here, ${{\,\textrm{d}\,}}(\textbf{v}, {\textbf {P}} )$ denotes the distance of $\textbf{v}$ to the subspace spanned by ${\textbf {P}}$; i.e., ${{\,\textrm{d}\,}}(\textbf{v}, {\textbf {P}} ) \triangleq \Vert \textbf{v} - {{\,\textrm{proj}\,}}_{{\textbf {P}} }(\textbf{v}) \Vert ,$ where ${{\,\textrm{proj}\,}}_{{\textbf {P}} }(\cdot )$ is an operator of orthogonal projection onto the subspace spanned by ${\textbf {P}}$. We define ${{\,\textrm{vol}\,}}(\emptyset ) \triangleq 1$ for the sake of consistency to the determinant of an empty matrix (i.e., $\det ([\;]) = 1 = {{\,\textrm{vol}\,}}^2(\emptyset )$). Note that any symmetric positive semi-definite matrix is a Gram matrix. Then, if ${\textbf {A}}$ is the Gram matrix defined as $A_{i,j} \triangleq \langle \textbf{v}_i, \textbf{v}_j \rangle$ for all $i,j \in [n]$, we have a simple relation between the principal minor and the volume of the parallelepiped that

$$\begin{aligned} \det ({\textbf {A}} _S) = {{\,\textrm{vol}\,}}^2(\{\textbf{v}_i : i \in S\}) \end{aligned}$$

(2.3)

for every $S \subseteq [n]$; see [12] for the proof. We formally define the Determinant Maximization problem as follows,¹

Problem 2.1

Given a positive semi-definite matrix ${\textbf {A}}$ in $\mathbb {Q}^{n \times n}$ and a positive integer $k \in [n]$, Determinant Maximization asks to find a set $S \in {[n] \atopwithdelims ()k}$ such that the determinant $\det ({\textbf {A}} _S)$ of a $k \times k$ principal submatrix is maximized. The optimal value is denoted ${{\,\textrm{maxdet}\,}}({\textbf {A}} ,k) \triangleq \max _{S \in {[n] \atopwithdelims ()k}} \det ({\textbf {A}} _S)$.

Due to the equivalence between squared volume and determinant in Eq. 2.3, Determinant Maximization is equivalent to the following problem of volume maximization: Given a collection of n vectors in $\mathbb {Q}^d$ and a positive integer $k \in [n]$, we are required to find k vectors such that the volume of the parallelepiped spanned by them is maximized. We shall use the problem definition based on the determinant and the volume interchangeably.

Parameterized Complexity. Given a parameterized problem $\Pi$ consisting of a pair $\langle \mathcal {I}, k \rangle$ of instance $\mathcal {I}$ and parameter $k \in \mathbb {N}$, we say that $\Pi$ is fixed-parameter tractable (FPT) with respect to k if it is solvable in $f(k) \vert {\mathcal {I}}\vert ^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$ time for some computable function f, and slice-wise polynomial (XP) if it is solvable in $\vert {\mathcal {I}}\vert ^{f(k)}$ time; it holds that FPT  $\subsetneq$ XP [18]. The value of parameter k may be independent of the instance size $\vert {\mathcal {I}}\vert$ and may be given by some computable function $k = k(\mathcal {I})$ on instance $\mathcal {I}$ (e.g., the rank of an input matrix). Our objective is to prove that a problem (i.e., Determinant Maximization) is unlikely to admit an FPT algorithm under plausible assumptions in parameterized complexity. The central notion for this purpose is a parameterized reduction, which is used to demonstrate that a problem of interest is hard for a particular class of parameterized problems that is believed to be a superclass of FPT. We say that a parameterized problem $\Pi _1$ is parameterized reducible to another parameterized problem $\Pi _2$ if (i) an instance $\mathcal {I}_1$ with parameter $k_1$ for $\Pi _1$ can be transformed into an instance $\mathcal {I}_2$ with parameter $k_2$ for $\Pi _2$ in FPT time and (ii) the value of $k_2$ only depends on the value of $k_1$. Note that a parameterized reduction may not be a polynomial-time reduction and vice versa. W[1] is a class of parameterized problems that are parameterized reducible to k -Clique, and it is known that FPT  $\subseteq$ W[1]  $\subseteq$ XP. This class is often regarded as a parameterized counterpart to NP of classical complexity; in particular, the conjecture FPT  $\ne$ W[1] is a widely-believed assumption in parameterized complexity [18, 20]. Thus, the existence of a parameterized reduction from a W[1]-complete problem to a problem $\Pi$ is a strong evidence that $\Pi$ is not in FPT. In Determinant Maximization, a simple brute-force search algorithm that examines all ${[n] \atopwithdelims ()k}$ subsets of size k runs in $n^{k+{{\,\mathrm{\mathcal {O}}\,}}(1)}$ time; hence, this problem belongs to XP. On the other hand, it is proven to be W[1]-hard [27].

3 W[1]-Hardness and NP-Hardness on Arrowhead Matrices

We first prove the W[1]-hardness with respect to k and NP-hardness on arrowhead matrices. A square matrix ${\textbf {A}}$ in $\mathbb {R}^{[0 \mathrel {..}n] \times [0 \mathrel {..}n]}$ is an arrowhead matrix if $A_{i,j} = 0$ for all $i, j \in [n]$ with $i \ne j$. In the language of graph theory, ${\textbf {A}}$ is arrowhead if its symmetrized graph is a star $K_{1,n}$. See Fig. 2 for the structure of arrowhead matrices.

Theorem 3.1

Determinant Maximization on arrowhead matrices is NP-hard and W[1]-hard when parameterized by k.

The proof of Theorem 3.1 requires a reduction from k -Sum, a natural parameterized version of the NP-complete Subset Sum problem, whose membership of W[1] and W[1]-hardness was proven by Abboud et al. [1] and Downey and Fellows [17], respectively.

Problem 3.2

(k -Sum due to Abboud et al. [1]) Given n integers $x_1, \ldots , x_n \in [0\mathrel {..}n^{2k}]$, a target integer $t \in [0 \mathrel {..}n^{2k}]$, and a positive integer $k \in [n]$, we are required to decide if there exists a size-k set $S \in {[n] \atopwithdelims ()k}$ such that $\sum _{i \in S} x_i = t.$

Here, we introduce a slightly-modified version of k -Sum such that the input numbers are rational and their sum is normalized to 1, without affecting its computational complexity.

Problem 3.3

( k -Sum modified from [1]) Given n rational numbers $x_1, \ldots , x_n$ in $(0,1) \cap \mathbb {Q}_+$, a target rational number t in $(0,1) \cap \mathbb {Q}_+$, and a positive integer $k \in [n]$ such that $x_i$’s are integer multiples of some rational number at least $\frac{1}{n^{2k+1}}$ and $\sum _{i \in [n]} x_i = 1$, k -Sum asks to decide if there exists a set $S \in {[n] \atopwithdelims ()k}$ such that $\sum _{i \in S} x_i = t.$

Hereafter, for any set $S \subseteq [0\mathrel {..}n]$ including 0, we denote $S_{-0} \triangleq S \setminus \{0\}$.

3.1 Reduction from k -Sum and Proof of Theorem 3.1

In this subsection, we give a parameterized, polynomial-time reduction from k -Sum. We first use an explicit formula of the determinant of arrowhead matrices.

Lemma 3.4

Let ${\textbf {A}}$ be an arrowhead matrix in $\mathbb {R}^{[0\mathrel {..}n] \times [0 \mathrel {..}n]}$ such that $A_{i,i} \ne 0$ for all $i \in [n]$. Then, for any set $S \subseteq [0 \mathrel {..}n]$, it holds that

$$\begin{aligned} \det ({\textbf {A}} _S) = {\left\{ \begin{array}{ll} \prod _{i \in S_{-0}} A_{i,i} \cdot \left( A_{0,0} - \sum _{i \in S_{-0}} \frac{A_{0,i} \cdot A_{i,0}}{A_{i,i}} \right) &{} \text {if } 0 \in S, \\ \prod _{i \in S} A_{i,i} &{} \text {if } 0 \not \in S. \end{array}\right. } \end{aligned}$$

(3.1)

Proof

The case of $0 \not \in S$ is evident because ${\textbf {A}} _S$ is diagonal. Showing the case of $S \triangleq [0 \mathrel {..}n]$ suffices to complete the proof. Here, we enumerate permutations $\sigma \in {\mathfrak {S}}_{S}$ such that $A_{i,\sigma (i)}$ is possibly nonzero for all $i \in S$ by the case analysis of $\sigma (0)$.

Case 1:

If $\sigma (0) = 0$: we must have $\sigma (i) = i$ for all $i \in [n]$ and ${{\,\textrm{sgn}\,}}(\sigma ) = +1$.

Case 2:

If $\sigma (0) = i$ for $i \ne 0$: we must have $\sigma (i) = 0$, and thus, it holds that $\sigma (j) = j$ for all $j \in S {\setminus } \{i\}$ and ${{\,\textrm{sgn}\,}}(\sigma ) = -1$.

Expanding $\det ({\textbf {A}} _S)$, we derive

$$\begin{aligned} \begin{aligned} \det ({\textbf {A}} _S)&= \sum _{\sigma \in {\mathfrak {S}}_{S}} {{\,\textrm{sgn}\,}}(\sigma ) \prod _{i \in S} A_{i,\sigma (i)} \\&= \prod _{i \in S} A_{i,i} - \sum _{i \in [n]} A_{0,i} \cdot A_{i,0} \prod _{j \in [n] \setminus \{i\}} A_{j,j} \\&= \prod _{i \in S_{-0}} A_{i,i} \cdot \left( A_{0,0} - \sum _{i \in S_{-0}} \frac{A_{0,i} \cdot A_{i,0}}{A_{i,i}} \right) , \end{aligned} \end{aligned}$$

(3.2)

completing the proof. $\square$

Lemma 3.4 shows us a way to express the product of $\exp \left( \sum _{i \in S_{-0}} x_i\right)$ and $1 - C \cdot \sum _{i \in S_{-0}} x_i$ for some constant C, which is a key step in proving Theorem 3.1. Specifically, given n rational numbers $x_1, \ldots , x_n$ and a target rational number t as a k -Sum instance, we construct $n+1$ 2n-dimensional vectors $\textbf{v}_0, \ldots , \textbf{v}_n$ in $\mathbb {R}_+^{2n}$, each entry of which is defined as follows:

$$\begin{aligned} v_0(j) = {\left\{ \begin{array}{ll} \gamma \cdot \sqrt{x_j} &{} \text {if } j \leqslant n, \\ 0 &{} \text {otherwise}, \end{array}\right. } v_i(j) = {\left\{ \begin{array}{ll} \sqrt{\alpha \cdot \textrm{e}^{x_i}} &{} \text {if } j = i, \\ \sqrt{\beta \cdot \textrm{e}^{x_i}} &{} \text {if } j = i+n, \\ 0 &{} \text {otherwise}, \end{array}\right. } \text { for all } i \in [n], \end{aligned}$$

(3.3)

where $\alpha$, $\beta$, and $\gamma$ are parameters, whose values are positive and will be determined later. We calculate the principal minor of the Gram matrix defined by $\textbf{v}_0, \ldots , \textbf{v}_n$ as follows.

Lemma 3.5

Let ${\textbf {A}}$ be the Gram matrix defined by $n+1$ vectors $\textbf{v}_0, \ldots , \textbf{v}_n$ that are constructed from an instance of k -Sum by Eq. 3.3. Then, ${\textbf {A}}$ is an arrowhead matrix, and for any set $S \subseteq [0 \mathrel {..}n]$, it holds that

$$\begin{aligned} \begin{aligned} \det ({{\textbf {A}}}_S) = {\left\{ \begin{array}{ll} \displaystyle (\alpha + \beta )^{\vert {S}\vert -1} \cdot \gamma ^2 \cdot \exp \left( \sum _{i \in S_{-0}}x_i\right) \cdot \left( 1- \frac{\alpha }{\alpha +\beta } \sum _{i \in S_{-0}} x_i\right) &{}{} \text{ if } 0 \in S, \\ \displaystyle (\alpha + \beta )^{\vert {S}\vert } \cdot \exp \left( \sum _{i \in S} x_i\right) &{}{} \text{ if } 0 \not \in S. \end{array}\right. } \end{aligned} \end{aligned}$$

(3.4)

Moreover, if we regard the principal minor $\det ({\textbf {A}} _S)$ in the case of $0 \in S$ as a function in $X \triangleq \sum _{i \in S_{-0}} x_i$, it is maximized when $X = \frac{\beta }{\alpha }$.

Proof

Observe first that the inner product between each pair of the vectors (i.e., each entry of ${\textbf {A}}$) is calculated as follows:

$$\begin{aligned} \begin{aligned} \langle \textbf{v}_0, \textbf{v}_0 \rangle&= A_{0,0} = \gamma ^2 \sum _{i \in [n]} x_i = \gamma ^2, \\ \langle \textbf{v}_0, \textbf{v}_i \rangle&= A_{0,i} = A_{i,0} = \gamma \cdot \sqrt{\alpha \cdot x_i \cdot \textrm{e}^{x_i}}&\text { for all } i \in [n], \\ \langle \textbf{v}_i, \textbf{v}_i \rangle&= A_{i,i} = (\alpha + \beta ) \cdot \textrm{e}^{x_i}&\text { for all } i \in [n], \\ \langle \textbf{v}_i, \textbf{v}_j \rangle&= A_{i,j} = 0&\text { for all } i \ne j \in [n]. \end{aligned} \end{aligned}$$

(3.5)

Thus, ${\textbf {A}}$ is an arrowhead matrix. According to Lemma 3.4, for any set $S \subseteq [0 \mathrel {..}n]$ including 0, we have

$$\begin{aligned} \begin{aligned} \det ({\textbf {A}} _S)&= \prod _{i \in S_{-0}} A_{i,i} \cdot \left( A_{0,0} - \sum _{i \in S_{-0}} \frac{A_{0,i} \cdot A_{i,0}}{A_{i,i}} \right) \\&= \left( \prod _{i \in S_{-0}} (\alpha + \beta ) \cdot \textrm{e}^{x_i}\right) \cdot \left( \gamma ^2 - \sum _{i \in S_{-0}} \frac{\gamma ^2 \cdot \alpha \cdot x_i \cdot \textrm{e}^{x_i}}{(\alpha + \beta ) \cdot \textrm{e}^{x_i}} \right) \\&= (\alpha + \beta )^{\vert {S}\vert -1} \cdot \gamma ^2 \cdot \exp \left( \sum _{i \in S_{-0}} x_i\right) \cdot \left( 1-\frac{\alpha }{\alpha + \beta } \sum _{i \in S_{-0}}x_i\right) . \end{aligned} \end{aligned}$$

(3.6)

On the other hand, if $0 \not \in S$, we have

$$\begin{aligned} \det ({\textbf {A}} _S) = \prod _{i \in S} A_{i,i} = (\alpha + \beta )^{\vert {S}\vert } \cdot \exp \left( \sum _{i \in S} x_i\right) . \end{aligned}$$

(3.7)

Setting the derivative of Eq. 3.6 by a variable $X \triangleq \sum _{i \in S} x_i$ equal to 0, we obtain

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial X} \left\{ (\alpha + \beta )^{\vert {S}\vert -1} \cdot \gamma ^2 \cdot \textrm{e}^X \cdot \left( 1-\frac{\alpha }{\alpha + \beta } X\right) \right\} = 0 \\ \implies&\textrm{e}^X \left( 1-\frac{\alpha }{\alpha + \beta } X\right) + \textrm{e}^X \left( -\frac{\alpha }{\alpha + \beta }\right) = \textrm{e}^X \cdot \frac{\beta - \alpha X}{\alpha + \beta } = 0 \\ \implies&X = \frac{\beta }{\alpha }. \end{aligned} \end{aligned}$$

(3.8)

This completes the proof. $\square$

We now determine the values of $\alpha$, $\beta$, and $\gamma$. Since Lemma 3.5 demonstrates that the principal minor for S including 0 is maximized when $\sum _{i \in S_{-0}} x_i = \frac{\beta }{\alpha }$, we fix $\alpha \triangleq 1$ and $\beta \triangleq t$. We define $\delta \triangleq \frac{1}{n^{2k+1}}$, denoting a lower bound on the minimum possible absolute difference between any sum of $x_i$’s; i.e., $\vert {\sum _{i \in S}x_i - \sum _{i \in T}x_i}\vert \geqslant \delta$ for any $S, T \subseteq [n]$ whenever $\sum _{i \in S}x_i \ne \sum _{i \in T}x_i$. For the correctness of the value of $\delta$, refer to the definition of Problem 3.3. We finally fix the value of $\gamma$ as $\gamma \triangleq 5$, so that

$$\begin{aligned} (1+t)^2 \cdot \textrm{e}^{1-t} \cdot \frac{1}{\textrm{e}^{-\delta } \cdot (1+\delta )} \leqslant 2^2 \cdot \textrm{e}\cdot \frac{1}{\textrm{e}^{-\frac{1}{2}} \cdot 1} < 25 = \gamma ^2. \end{aligned}$$

(3.9)

The above inequality ensures that $\det ({\textbf {A}} _S)$ is “sufficiently” small whenever $0 \not \in S$, as validated in the following lemma.

Lemma 3.6

Let ${\textbf {A}}$ be the Gram matrix defined by $n+1$ vectors constructed according to Eq. 3.3, where $\alpha =1$, $\beta =t$, and $\gamma =5$. Define $\textsf{OPT}\triangleq (1+t)^{k-1} \cdot \gamma ^2 \cdot \textrm{e}^t$. Then, for any set $S \in {[0\mathrel {..}n] \atopwithdelims ()k+1}$,

$$\begin{aligned} \begin{aligned} \det ({{\textbf {A}}}_S) \text{ is } {\left\{ \begin{array}{ll} \text{ equal } \text{ to } \textsf{OPT}&{}{} \quad \text{ if } 0 \in S \text{ and } \sum _{i \in S_{-0}}x_i = t, \\ \text{ at } \text{ most } \textrm{e}^{-\delta } (1+\delta ) \cdot \textsf{OPT}&{}{} \quad \text{ otherwise, } \end{array}\right. } \end{aligned} \end{aligned}$$

(3.10)

where $\delta = \frac{1}{n^{2k+1}}$. In particular, ${{\,\textrm{maxdet}\,}}({\textbf {A}} ,k+1)$ is $\textsf{OPT}$ if k -Sum has a solution, and is at most $\textrm{e}^{-\delta } (1+\delta ) \cdot \textsf{OPT}< \textsf{OPT}$ otherwise.

Proof

For any set $S \in {[0 \mathrel {..}n] \atopwithdelims ()k+1}$ such that $0 \in S$ and $\sum _{i \in S_{-0}} x_i = t$ (i.e., k -Sum has a solution), Lemma 3.5 derives that

$$\begin{aligned} \det ({\textbf {A}} _S) = (\alpha + \beta )^k \cdot \gamma ^2 \cdot \exp (t) \cdot \left( 1-\frac{\alpha }{\alpha + \beta } \cdot t\right) = \textsf{OPT}, \end{aligned}$$

(3.11)

which is the maximum possible principal minor under $0 \in S$. For any set $S \in {[n] \atopwithdelims ()k+1}$ excluding 0, by definition of $\gamma$ and Eq. 3.9, we obtain

$$\begin{aligned} \begin{aligned} \det ({\textbf {A}} _S)&= (1+t)^{k+1} \cdot \exp \left( \sum _{i \in S_{-0}}x_i\right) \\&\leqslant (1+t)^{k+1} \cdot \textrm{e}\cdot \left\{ \gamma ^2 \cdot \underbrace{\frac{1}{(1+t)^2} \cdot \textrm{e}^{t-1} \cdot \textrm{e}^{-\delta } \cdot (1+\delta )}_{\geqslant \gamma ^{-2}} \right\} \\&= \textrm{e}^{-\delta }(1+\delta ) \cdot \underbrace{(1+t)^{k-1} \cdot \textrm{e}^t \cdot \gamma ^2}_{= \textsf{OPT}} \\&= \textrm{e}^{-\delta } (1+\delta ) \cdot \textsf{OPT}. \end{aligned} \end{aligned}$$

(3.12)

We now bound $\det ({\textbf {A}} _S)$ for any set $S \in {[0 \mathrel {..}n] \atopwithdelims ()k+1}$ such that $0 \in S$ and $\sum _{i \in S_{-0}} x_i \ne t$. Consider first that $\sum _{i \in S_{-0}} x_i$ is greater than t; i.e., $\sum _{i \in S_{-0}} x_i = t + \Delta$ for some $\Delta > 0$. By Lemma 3.5, we have

$$\begin{aligned} \begin{aligned} \det ({\textbf {A}} _S)&= (1+t)^k \cdot \gamma ^2 \cdot \exp (t+\Delta ) \cdot \left( 1-\frac{t+\Delta }{1+t}\right) \\&= \textrm{e}^{\Delta } (1-\Delta ) \cdot \textsf{OPT}\leqslant \textrm{e}^{-\delta } (1-\delta ) \cdot \textsf{OPT}, \end{aligned} \end{aligned}$$

(3.13)

where we used the fact that $\Delta \geqslant \delta$ by definition of $\delta$ and $\textrm{e}^{\Delta } (1-\Delta )$ is a decreasing function for $\Delta > 0$. Consider then that $\sum _{i \in S_{-0}} x_i = t - \Delta$ for some $\Delta > 0$, which yields that

$$\begin{aligned} \begin{aligned} \det ({\textbf {A}} _S)&= (1+t)^k \cdot \gamma ^2 \cdot \exp (t-\Delta ) \cdot \left( 1-\frac{t-\Delta }{1+t}\right) \\&= \textrm{e}^{-\Delta } (1+\Delta ) \cdot \textsf{OPT}\leqslant \textrm{e}^{-\delta } (1+\delta ) \cdot \textsf{OPT}, \end{aligned} \end{aligned}$$

(3.14)

where we used the fact that $\Delta \geqslant \delta$ and $\textrm{e}^{-\Delta } (1+\Delta )$ is a decreasing function for $\Delta > 0$. By combining Eqs. 3.12–3.14, if $S\in {[0 \mathrel {..}n] \atopwithdelims ()k+1}$ satisfies that $0 \not \in S$ or $\sum _{i \in S_{-0}} x_i \ne t$, its principal minor is bounded as follows:

$$\begin{aligned} \det ({\textbf {A}} _S) \leqslant \max \Bigl \{ \textrm{e}^{-\delta } (1+\delta ), \textrm{e}^{\delta } (1-\delta ) \Bigr \} \cdot \textsf{OPT}= \textrm{e}^{-\delta }(1+\delta ) \cdot \textsf{OPT}. \end{aligned}$$

(3.15)

Observing that $\textrm{e}^{-\delta }(1+\delta ) < 1$ for any $\delta > 0$ accomplishes the proof. $\square$

We complete our reduction by approximating the Gram matrix ${\textbf {A}}$ of $n+1$ vectors defined in Eq. 3.3 by a rational matrix ${\textbf {B}}$ whose maximum determinant maintains sufficient information to solve k -Sum.

Lemma 3.7

Let ${\textbf {B}}$ be the Gram matrix in $\mathbb {Q}^{(n+1) \times (n+1)}$ defined by $n+1$ vectors $\textbf{w}_0, \ldots , \textbf{w}_n$ in $\mathbb {Q}^{2n}$, each entry of which is a $(1 \pm \varepsilon )$-factor approximation to the corresponding entry of $n+1$ vectors $\textbf{v}_0, \ldots , \textbf{v}_n$ defined by Eq. 3.3, where $\varepsilon = 2^{-{{\,\mathrm{\mathcal {O}}\,}}(k \log (nk))}$. Then,

(3.16)

Moreover, we can calculate ${\textbf {B}}$ in polynomial time.

The crux of its proof is to approximate ${\textbf {A}}$ within a factor of $\varepsilon = 2^{-{{\,\mathrm{\mathcal {O}}\,}}(k \log (nk))}$. To this end, we use the following lemma.

Lemma 3.8

(cf. [6], page 107) For two complex-valued $n \times n$ matrices ${\textbf {A}}$ and ${\textbf {B}}$, the absolute difference in the determinant of ${\textbf {A}}$ and ${\textbf {B}}$ is bounded from above by

$$\begin{aligned} \vert {\det ({\textbf {A}} ) - \det ({\textbf {B}} )}\vert \leqslant n \cdot \max \{\Vert {\textbf {A}} \Vert _2, \Vert {\textbf {B}} \Vert _2\}^{n-1} \cdot \Vert {\textbf {A}} - {\textbf {B}} \Vert _2. \end{aligned}$$

(3.17)

Proof of Lemma 3.7

Let n rational numbers $x_1, \ldots , x_n$, a target rational number t, and a positive integer k be an instance of k -Sum. Suppose we are given the Gram matrix ${\textbf {A}}$ defined by $n+1$ vectors $\textbf{v}_0, \ldots , \textbf{v}_n$ constructed according to Eq. 3.3 and the rational Gram matrix ${\textbf {B}}$ defined by $n+1$ rational vectors $\textbf{w}_0, \ldots , \textbf{w}_n$, each entry of which is a $(1\pm \varepsilon )$-factor approximation to the corresponding entry of $\textbf{v}_i$’s. If the absolute difference between ${\textbf {A}} _S$ and ${\textbf {B}} _S$ is at most $\frac{1}{3}( \textsf{OPT}- \textrm{e}^{-\delta }(1+\delta ) \cdot \textsf{OPT})$ for every $S \in {[0 \mathrel {..}n] \atopwithdelims ()k+1}$, we can use Lemma 3.6 to ensure that

$$\begin{aligned} \det ({\textbf {B}} _S)&\geqslant \left( \frac{2}{3} + \frac{1}{3} \textrm{e}^{-\delta }(1+\delta )\right) \cdot \textsf{OPT}\; \text { if } 0 \in S \text { and } \sum _{i \in S_{-0}}x_i = t, \end{aligned}$$

(3.18)

$$\begin{aligned} \det ({\textbf {B}} _S)&\leqslant \left( \frac{1}{3} + \frac{2}{3} \textrm{e}^{-\delta }(1+\delta )\right) \cdot \textsf{OPT}\; \text { otherwise}. \end{aligned}$$

(3.19)

In particular, we can use either the optimal value or solution for Determinant Maximization defined by $({\textbf {B}} ,k+1)$ to determine whether k -Sum has a solution.

We demonstrate that this is the case if $\varepsilon = 2^{-{{\,\mathrm{\mathcal {O}}\,}}(k \log (nk))}$. Owing to the nonnegativity of $\textbf{v}_i$’s and $\textbf{w}_i$’s, we have $(1-\varepsilon ) v_i(e) \leqslant w_i(e) \leqslant (1+\varepsilon ) v_i(e)$ for every $i \in [0 \mathrel {..}n]$ and $e \in [2n]$, implying that:

$$\begin{aligned} \begin{aligned}&(1-\varepsilon )^2 \cdot v_i(e) v_j(e) \leqslant w_i(e)w_j(e) \leqslant (1+\varepsilon )^2 \cdot v_i(e) v_j(e) \\&\implies (1-\varepsilon )^2 \cdot \underbrace{\langle \textbf{v}_i, \textbf{v}_j \rangle }_{=A_{i,j}} \leqslant \underbrace{\langle \textbf{w}_i, \textbf{w}_j \rangle }_{=B_{i,j}} \leqslant (1+\varepsilon )^2 \cdot \underbrace{\langle \textbf{v}_i, \textbf{v}_j \rangle }_{=A_{i,j}}. \end{aligned} \end{aligned}$$

(3.20)

Because it holds that $(1+\varepsilon )^2 \leqslant 1+3\varepsilon$ and $(1-\varepsilon )^2 \geqslant 1-3\varepsilon$ for any $\varepsilon \in (0,\frac{1}{3})$, there exists a number $\rho _{i,j} \in [1-3\varepsilon , 1+3\varepsilon ]$ such that $B_{i,j} = \rho _{i,j} \cdot A_{i,j}$ for each $i,j \in [0 \mathrel {..}n]$. By applying Lemma 3.8, we can bound the absolute difference between the determinant of ${\textbf {A}} _S$ and ${\textbf {B}} _S$ for any set $S \in {[0\mathrel {..}n] \atopwithdelims ()k+1}$ as:

$$\begin{aligned} \vert {\det ({\textbf {A}} _S) - \det ({\textbf {B}} _S)}\vert \leqslant (k+1) \cdot \max \{ \Vert {\textbf {A}} _S\Vert _2, \Vert {\textbf {B}} _S\Vert _2 \}^k \cdot \Vert {\textbf {A}} _S - {\textbf {B}} _S\Vert _2. \end{aligned}$$

(3.21)

Each term in the above inequality can be bounded as follows:

$$\begin{aligned}&\Vert {\textbf {A}} _S\Vert _2 \leqslant (k+1) \cdot \Vert {\textbf {A}} _S\Vert _{\max } \leqslant (k+1) \cdot \Vert {\textbf {A}} \Vert _{\max }, \end{aligned}$$

(3.22)

$$\begin{aligned}&\begin{aligned}\Vert {{\textbf {B}}}_S\Vert _2&\leqslant (k+1) \cdot \Vert {{\textbf {B}}}_S\Vert _{\max } \\ {}&\leqslant (k+1) \cdot \Vert {{\textbf {A}}} \Vert _{\max } \cdot \max _{i,j} \vert {\rho _{i,j}}\vert \\ {}&\leqslant (k+1) (1+3\varepsilon ) \cdot \Vert {{\textbf {A}}} \Vert _{\max }, \end{aligned} \end{aligned}$$

(3.23)

$$\begin{aligned}&\begin{aligned}\Vert {{\textbf {A}}}_S - {{\textbf {B}}}_S\Vert _2&\leqslant (k+1) \cdot \Vert {{\textbf {A}}}_S - {{\textbf {B}}}_S\Vert _{\max } \\ {}&\leqslant (k+1) \cdot \max _{i,j \in S} \vert {A_{i,j} - \rho _{i,j}A_{i,j}}\vert \\ {}&\leqslant (k+1) 3\varepsilon \cdot \Vert {{\textbf {A}}} \Vert _{\max }. \end{aligned} \end{aligned}$$

(3.24)

Here, $\Vert {\textbf {A}} \Vert _{\max }$ is bounded using its definition (see the beginning of the proof of Lemma 3.5):

$$\begin{aligned} \begin{aligned} \Vert {\textbf {A}} \Vert _{\max }&= \max \left\{ \max _{i \in [n]} \; (1+t) \cdot \textrm{e}^{x_i}, \gamma ^2, \max _{i \in [n]} \; \gamma \sqrt{\alpha \cdot x_i \cdot \textrm{e}^{x_i}} \right\} \\&\leqslant \max \Bigl \{ 2 \textrm{e}, 25, 5 \sqrt{\textrm{e}} \Bigr \} = 25. \end{aligned} \end{aligned}$$

(3.25)

Putting it all together, we get

$$\begin{aligned} \begin{aligned} \vert {\det ({\textbf {A}} _S) - \det ({\textbf {B}} _S)}\vert&\leqslant (k+1) \cdot \{ (k+1) \cdot 25 \cdot (1+3\varepsilon ) \}^k \cdot (k+1) \cdot 25 \cdot 3\varepsilon \\&= (k+1)^{k+2} \cdot 25^{k+1} \cdot (1+3\varepsilon )^k \cdot 3\varepsilon . \end{aligned} \end{aligned}$$

(3.26)

Therefore, for the absolute difference of the determinant between ${\textbf {A}} _S$ and ${\textbf {B}} _S$ to be less than $\frac{1}{3}(1 - \textrm{e}^{-\delta }(1+\delta )) \cdot \textsf{OPT}$, the value of $\varepsilon$ should be less than

$$\begin{aligned} \varepsilon < \Bigl \{ (k+1)^{k+2} \cdot 25^{k+1} \cdot (1+3\varepsilon )^k \cdot 3 \Bigr \}^{-1} \cdot \frac{1}{3} (1-\textrm{e}^{-\delta } (1+\delta ))\cdot \textsf{OPT}. \end{aligned}$$

(3.27)

Observe that each term in Eq. 3.27 can be bounded as follows:

$$\begin{aligned} \Bigl \{ (k+1)^{k+2} \cdot 25^{k+1} \cdot (1+3\varepsilon )^k \cdot 3 \Bigr \}^{-1}&> (100000k)^{-k} \;\text { for all } k \geqslant 1 \text { if } \varepsilon \leqslant 1, \end{aligned}$$

(3.28)

$$\begin{aligned} 1-\textrm{e}^{-\delta }(1+\delta )&\geqslant \frac{\delta ^2}{2} - \frac{\delta ^3}{3}> 0 \;\text { for any } \delta > 0, \end{aligned}$$

(3.29)

$$\begin{aligned} \textsf{OPT}&\geqslant 1. \end{aligned}$$

(3.30)

Consequently, we can set the value of $\varepsilon$ so as to satisfy Eq. 3.27; thus, Eqs. 3.18 and 3.19:

$$\begin{aligned} \varepsilon \triangleq (100000k)^{-k} \cdot \left( \frac{\delta ^2}{2} - \frac{\delta ^3}{3} \right) = 2^{-{{\,\mathrm{\mathcal {O}}\,}}(k \log (nk))}. \end{aligned}$$

(3.31)

We finally claim that each entry of $\textbf{w}_i$’s can be computed in polynomial time. Because of the definition of $\textbf{v}_i$’s in Eq. 3.3, it suffices to compute a $(1\pm \frac{\varepsilon }{2})$-approximate value of $\exp (x)$ and $\sqrt{x}$ for a rational number x in polynomial time in the input size and $\log \varepsilon ^{-1} = {{\,\mathrm{\mathcal {O}}\,}}(k \log (nk))$, completing the proof.²$\square$

What remains to be done is to prove Theorem 3.1 using Lemma 3.7.

Proof of Theorem 3.1

Our parameterized reduction is as follows. Given n rational numbers $x_1, \ldots , x_n \in (0,1) \cap \mathbb {Q}$, a target rational number $t \in (0,1) \cap \mathbb {Q}$, and a positive integer $k \in [n]$ as an instance of k -Sum, we construct $n+1$ rational vectors $\textbf{w}_0, \ldots , \textbf{w}_n$ in $\mathbb {Q}_+^{2n}$, each of which is an entry-wise $(1 \pm \varepsilon )$-factor approximation to $\textbf{v}_0, \ldots , \textbf{v}_n$ defined by Eq. 3.3, where $\varepsilon = 2^{-{{\,\mathrm{\mathcal {O}}\,}}(k \log (nk))}$. This construction requires polynomial time owing to Lemma 3.7. Thereafter, we compute the Gram matrix ${\textbf {B}}$ in $\mathbb {Q}^{(n+1) \times (n+1)}$ defined by $\textbf{w}_0, \ldots , \textbf{w}_n$. Consider Determinant Maximization defined by $({\textbf {B}} ,k+1)$ with parameter $k+1$. According to Lemma 3.7, the maximum principal minor ${{\,\textrm{maxdet}\,}}({\textbf {B}} ,k+1)$ is at least $(\frac{2}{3} + \frac{1}{3}\textrm{e}^{-\delta }(1+\delta )) \cdot \textsf{OPT}$ if and only if k -Sum has a solution. Moreover, if this is the case, the optimal solution $S^*$ for Determinant Maximization satisfies that $\sum _{i \in S^*_{-0}} x_i = t$. The above discussion ensures the correctness of the parameterized reduction from k -Sum to Determinant Maximization, finishing the proof. $\square$

3.2 Note on Polynomial-Time Solvability for Tridiagonal Matrices and Spiders of Bounded Legs [2, 3]

Here, we mention some tractable cases of Determinant Maximization due to Al-Thani and Lee [2, 3]. Recall that a tridiagonal matrix is a square matrix ${\textbf {A}}$ such that $A_{i,j} = 0$ whenever $\vert {i-j}\vert \geqslant 2$; i.e., its symmetrized graph is a path graph (and thus a linear forest). A graph is called a spider if it is a tree having at most one vertex of degree greater than 2, and its leafs are called legs.

Observation 3.9

(Al-Thani and Lee [2, 3]) Determinant Maximization can be solved in polynomial time if an input matrix is a tridiagonal matrix, or its symmetrized graph is a spider with a constant number of legs.

4 W[1]-Hardness With Respect to Rank

We then prove the W[1]-hardness of Determinant Maximization when parameterized by the rank of an input matrix. In fact, we obtain the stronger hardness result on the problem of finding a set of pairwise orthogonal rational vectors, which is formally stated below.

Problem 4.1

Given n d-dimensional vectors $\textbf{v}_1, \ldots , \textbf{v}_n$ in $\mathbb {Q}^d$ and a positive integer $k \in [n]$, we are required to decide if there exists a set of k vectors that is pairwise orthogonal, i.e., a set $S \in {[n] \atopwithdelims ()k}$ such that $\langle \textbf{v}_i, \textbf{v}_j \rangle = 0$ for all $i \ne j \in S$.

Theorem 4.2

Problem 4.1 is W[1]-hard when parameterized by the dimension d of the input vectors. Moreover, the same hardness result holds even if every vector has the same Euclidean norm.

The following is immediate from Theorem 4.2.

Corollary 4.3

Determinant Maximization is W[1]-hard when parameterized by the rank of an input matrix.

Proof

Let ${\textbf {A}}$ be the Gram matrix defined by any n d-dimensional vectors $\textbf{v}_1, \ldots , \textbf{v}_n \in \mathbb {Q}^d$ having the same Euclidean norm, say, $c \in \mathbb {Q}_+$. Consider Determinant Maximization defined by $({\textbf {A}} , k)$. For any $S \in {[n] \atopwithdelims ()k}$, the principal minor $\det ({\textbf {A}} _S)$ is equal to $c^{2k}$ if the set of k vectors $\{\textbf{v}_i: i \in S\}$ is pairwise orthogonal and is strictly less than $c^{2k}$ otherwise. Observing that ${{\,\textrm{rank}\,}}({\textbf {A}} ) \leqslant d$ completes the proof. $\square$

Unlike the proof of Theorem 3.1, f(k) -dimensional vectors can only be used in a parameterized reduction. The key tool to bypass this difficulty is Grid Tiling introduced in the next subsection.

4.1 Grid Tiling and Pythagorean Triples

We first define Grid Tiling due to Marx [34].

Table 1 Example of Grid Tiling with $k=3$ and $n=4$

Problem 4.4

(Grid Tiling due to Marx [34]) For two integers n and k, given a collection $\mathcal {S}$ of $k^2$ nonempty sets $S_{i,j} \subseteq [n]^2$ for each $i,j \in [k]$, Grid Tiling asks to find an assignment $\sigma :[k]^2 \rightarrow [n]^2$ with $\sigma (i,j) \in S_{i,j}$ such that

• (1) Vertical neighbors agree in the first coordinate; i.e., if $\sigma (i,j) = (x,y)$ and $\sigma (i,(j+1) \bmod k) = (x',y')$, then $x = x'$, and

• (2) Horizontal neighbors agree in the second coordinate; i.e., if $\sigma (i,j) = (x,y)$ and $\sigma ((i+1) \bmod k,j) = (x',y')$, then $y = y'$,

where we define $(k+1) \bmod k \triangleq 1$, and hereafter omit the symbol $\text {mod}$ for modulo operator. Each pair $(i,j) \in [k]^2$ will be referred to as a cell.

See also Table 1 for an example. Grid Tiling parameterized by k is proven to be W[1]-hard by Marx [34, 36]. We say that two cells $(i_1,j_1)$ and $(i_2,j_2)$ are adjacent if the Manhattan distance between them is 1. Let $\mathcal {I}$ be the set of all pairs of two adjacent cells; i.e.,

$$\begin{aligned} \mathcal {I}\triangleq \Bigl \{ (i_1,j_1,i_2,j_2) \in [k]^4 : \vert {i_1-i_2}\vert + \vert {j_1-j_2}\vert = 1 \Bigr \}. \end{aligned}$$

(4.1)

Note that $\vert {\mathcal {I}}\vert = 2k^2$. Grid Tiling has the two useful properties that (i) the constraint to be satisfied is the equality on the first and second coordinates, which is pretty simple, and (ii) there are only $k^2$ cells and each cell is adjacent to (at most) four cells. To represent the consistency between adjacent cells using only f(k)-dimensional vectors, we use a rational point $(\frac{a}{c}, \frac{b}{c})$ on the unit circle generated from a Pythagorean triple (a, b, c). A Pythagorean triple is a triple of three positive integers (a, b, c) such that $a^2 + b^2 = c^2$; e.g., $(a,b,c) = (3,4,5)$. It is further said to be primitive if (a, b, c) are coprime; i.e., $\gcd (a,b) = \gcd (b,c) = \gcd (c,a) = 1$. We assume for a while that we have n primitive Pythagorean triples, denoted $(a_1, b_1, c_1), \ldots , (a_n, b_n, c_n)$.

4.2 Reduction from Grid Tiling and Proof of Theorem 4.2

We are now ready to describe a parameterized reduction from Grid Tiling to Problem 4.1. Given an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling, we define a rational vector for each $(x,y) \in S_{i,j}$, whose dimension is bounded by some function in k. Each vector consists of $\vert {\mathcal {I}}\vert = 2k^2$ blocks (indexed by an element of $\mathcal {I}$), each of which is two dimensional and is either a rational point on the unit circle or the origin $\text {O}$. Hence, each vector is of dimension $2\vert {\mathcal {I}}\vert = 4k^2$. Let $\textbf{v}^{(i,j)}_{x,y}$ denote the vector for an element $(x,y) \in S_{i,j}$ of cell $(i,j) \in [k]^2$, let $\textbf{v}^{(i,j)}_{x,y}(i_1,j_1,i_2,j_2)$ denote the block of $\textbf{v}^{(i,j)}_{x,y}$ corresponding to each pair of adjacent cells $(i_1,j_1,i_2,j_2) \in \mathcal {I}$. Each block is defined as follows:

$$\begin{aligned} \textbf{v}^{(i,j)}_{x,y}(e) \triangleq {\left\{ \begin{array}{ll} \left[ -\frac{b_x}{c_x}, \frac{a_x}{c_x}\right] &{} \text {if } e = (i,j-1,i,j), \\ \left[ \frac{a_x}{c_x}, \frac{b_x}{c_x}\right] &{} \text {if } e = (i,j,i,j+1), \\ \left[ -\frac{b_y}{c_y}, \frac{a_y}{c_y}\right] &{} \text {if } e = (i-1,j,i,j), \\ \left[ \frac{a_y}{c_y}, \frac{b_y}{c_y}\right] &{} \text {if } e = (i,j,i+1,j), \\ {[}0,0] &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(4.2)

Because each vector contains exactly four points on the unit circle, its squared norm is equal to 4. We denote by ${\textbf {V}} ^{(i,j)}$ the set of vectors corresponding to the elements of $S_{i,j}$; i.e., $\displaystyle {\textbf {V}} ^{(i,j)} \triangleq \{ \textbf{v}^{(i,j)}_{x,y}: (x,y) \in S_{i,j} \}.$ We now define an instance $({\textbf {V}} , K)$ of Problem 4.1 as ${\textbf {V}} \triangleq \bigcup _{i,j \in [k]} {\textbf {V}} ^{(i,j)} \text { and } K \triangleq k^2.$ Note that ${\textbf {V}}$ consists of $N \triangleq \sum _{i,j \in [k]}\vert {S_{i,j}}\vert$ vectors. We prove that the existence of a set of pairwise orthogonal $k^2$ vectors yields the answer of Grid Tiling. The key property of the above construction is that $\left[ -\frac{b_x}{c_x}, \frac{a_x}{c_x}\right]$ and $\left[ \frac{a_{x'}}{c_{x'}}, \frac{b_{x'}}{c_{x'}}\right]$ are orthogonal if and only if $x = x'$.

Lemma 4.5

Let ${\textbf {V}}$ be the set of vectors constructed from an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling according to Eq. 4.2. Then, Grid Tiling has a solution if and only if Problem 4.1 has a solution.

Proof

We first prove the only-if direction. Suppose the Grid Tiling instance $\mathcal {S}$ has a solution denoted $\sigma :[k]^2 \rightarrow [n]^2$. We show that the set ${\textbf {S}} \triangleq \{\textbf{v}^{(i,j)}_{x,y}: i,j \in [k], (x,y) = \sigma (i,j) \}$ of $k^2$ vectors is pairwise orthogonal. Observe easily that any two vectors corresponding to nonadjacent cells are orthogonal. We then verify the orthogonality of two vectors corresponding to vertically adjacent cells (i, j) and $(i,j+1)$ for any $i,j \in [k]$. Calculating the inner product between $\textbf{v}^{(i,j)}_{x,y}$ and $\textbf{v}^{(i,j+1)}_{x,y'}$ in ${\textbf {S}}$, where $(x,y) = \sigma (i,j)$ and $(x,y') = \sigma (i,j+1)$ for some $x,y,y' \in [n]$ by assumption, we obtain that

$$\begin{aligned} \left\langle \textbf{v}^{(i,j)}_{x,y}, \textbf{v}^{(i,j+1)}_{x,y'} \right\rangle = \left\langle \left[ \frac{a_x}{c_x}, \frac{b_x}{c_x}\right] , \left[ -\frac{b_x}{c_x}, \frac{a_x}{c_x}\right] \right\rangle = \frac{a_x b_x - a_x b_x}{c_x^2} = 0. \end{aligned}$$

(4.3)

Similarly, for two horizontally adjacent cells (i, j) and $(i+1,j)$, we derive that $\langle \textbf{v}^{(i,j)}_{x,y}, \textbf{v}^{(i+1,j)}_{x',y} \rangle = 0$, where $(x,y) = \sigma (i,j)$ and $(x',y) = \sigma (i+1,j)$ for some $x,x',y \in [n]$ by assumption. This accomplishes the proof for the only-if direction.

We then prove the if direction. Suppose ${\textbf {S}}$ is a set of $k^2$ vectors from ${\textbf {V}}$ that is pairwise orthogonal. Observe first that ${\textbf {S}}$ must include exactly one vector from each ${\textbf {V}} ^{(i,j)}$, because otherwise it includes a pair of vectors $\textbf{v}^{(i,j)}_{x,y}$ and $\textbf{v}^{(i,j)}_{x',y'}$ for some distinct $(x,y) \ne (x',y') \in S_{i,j}$, which is nonorthogonal. Indeed, their inner product is

$$\begin{aligned} \left\langle \textbf{v}^{(i,j)}_{x,y}, \textbf{v}^{(i,j)}_{x',y'} \right\rangle = 2 \cdot \frac{a_xa_{x'}+b_xb_{x'}}{c_xc_{x'}} + 2 \cdot \frac{a_ya_{y'}+b_yb_{y'}}{c_yc_{y'}} > 0. \end{aligned}$$

(4.4)

We can thus define the unique assignment $\sigma (i,j) \triangleq (x,y) \in S_{i,j}$ such that $\textbf{v}^{(i,j)}_{x,y} \in \textbf{S}$ for each cell $(i,j) \in [k]^2$. We show that $\sigma$ is a solution of Grid Tiling. Calculating the inner product between $\textbf{v}^{(i,j)}_{x,y}$ and $\textbf{v}^{(i,j+1)}_{x',y'}$ for two vertically adjacent cells (i, j) and $(i,j+1)$, where $(x,y) = \sigma (i,j)$ and $(x',y') = \sigma (i,j+1)$, we have

$$\begin{aligned} \left\langle \textbf{v}^{(i,j)}_{x,y}, \textbf{v}^{(i,j+1)}_{x',y'} \right\rangle = \frac{a_{x'} b_x - a_x b_{x'}}{c_x c_{x'}} = 0, \end{aligned}$$

(4.5)

i.e., it must hold that $a_{x'} b_x = a_x b_{x'}$ as $c_x c_{x'} > 0$. Since $a_x$ and $b_x$ are coprime, $a_{x'}$ must divide $a_x$ and $b_{x'}$ must divide $b_x$; since $a_{x'}$ and $b_{x'}$ are coprime, $a_x$ must divide $a_{x'}$ and $b_x$ must divide $b_{x'}$, implying that $a_x = a_{x'}$ and $b_x = b_{x'}$. Consequently, $x = x'$; i.e., the vertical neighbors agree in the first coordinate. Similarly, for two horizontally adjacent cells (i, j) and $(i+1,j)$, we can show that $a_y = a_{y'}$ and $b_y = b_{y'}$, where $(x,y) = \sigma (i,j)$ and $(x',y') = \sigma (i+1,j)$, and thus $y=y'$; i.e., the horizontal neighbors agree in the second coordinate. This accomplishes the proof for the if direction. $\square$

Proof of Theorem 4.2

Our parameterized reduction is as follows. Given an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling, we first generate n primitive Pythagorean triples $(a_1, b_1, c_1), \ldots , (a_n, b_n, c_n)$. This can be done efficiently by simply letting $(a_x,b_x,c_x) \triangleq (2x+1, 2x^2+2x, 2x^2+2x+1)$ for all $x \in [n]$. We then construct a set ${\textbf {V}}$ of N $4k^2$-dimensional rational vectors from $\mathcal {S}$ according to Eq. 4.2 in polynomial time, where $N \triangleq \sum _{i,j \in [k]}\vert {S_{i,j}}\vert$. According to Lemma 4.5, $\mathcal {S}$ has a solution of Grid Tiling if and only if there exists a set of $k^2$ pairwise orthogonal vectors in ${\textbf {V}}$. Since Grid Tiling is W[1]-hard with respect to k, Problem 4.1 is also W[1]-hard when parameterized by dimension $d (= 4k^2)$. Note that every vector is of squared norm 4, completing the proof. $\square$

4.3 Problem 4.1 on Nonnegative Vectors is FPT

We note that Problem 4.1 is FPT with respect to the dimension if the input vectors are nonnegative. Briefly speaking, Problem 4.1 on nonnegative vectors is equivalent to Set Packing parameterized by the size of the universe, which is easily shown to be FPT.

Observation 4.6

Problem 4.1 is FPT with respect to the dimension if every input vector is entry-wise nonnegative.

Proof

Let $\textbf{v}_1, \ldots , \textbf{v}_n$ be n d-dimensional nonnegative vectors in $\mathbb {Q}_+^d$ and $k \in [n]$ a positive integer. Without loss of generality, we can assume that $k \leqslant d$ because otherwise, there is always no solution. For each vector $\textbf{v}_i$, we denote by ${{\,\textrm{nz}\,}}(\textbf{v}_i)$ the set of coordinates of positive entries; i.e., ${{\,\textrm{nz}\,}}(\textbf{v}_i) \triangleq \{e \in [d]: v_i(e) > 0\}$. Then, the vector set $\{\textbf{v}_i: i \in S\}$ for any $S \subseteq [n]$ is pairwise orthogonal if and only if ${{\,\textrm{nz}\,}}(\textbf{v}_i) \cap {{\,\textrm{nz}\,}}(\textbf{v}_j) = \emptyset$ for every $i \ne j \in S$; i.e., the problem of interest is Set Packing in which we want to find k pairwise disjoint sets from the family $\mathcal {F}\triangleq \{ {{\,\textrm{nz}\,}}(\textbf{v}_i): i \in [n] \}$. Observing that $\vert {\mathcal {F}}\vert \leqslant 2^d$ because duplicates (i.e., ${{\,\textrm{nz}\,}}(\textbf{v}_i) = {{\,\textrm{nz}\,}}(\textbf{v}_j)$ for some $i \ne j$) are discarded, there are at most ${\vert {\mathcal {F}}\vert \atopwithdelims ()k} \leqslant 2^{dk}$ possible subsets of size k. Hence, we construct $\mathcal {F}$ in ${{\,\mathrm{\mathcal {O}}\,}}(nd)$ time and perform an exhaustive search in time $2^{dk} \cdot d^{{{\,\mathrm{\mathcal {O}}\,}}(1)} \leqslant 2^{d^2} \cdot d^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$, completing the proof. $\square$

5 W[1]-Hardness of Approximation

Our final result is FPT-inapproximability of Determinant Maximization as stated below.

Theorem 5.1

Under the Parameterized Inapproximability Hypothesis, it is W[1]-hard to approximate Determinant Maximization within a factor of $2^{-c\sqrt{k}}$ for some universal constant $c > 0$ when parameterized by the number k of vectors to be selected. Moreover, the same hardness result holds even if the diagonal entries of an input matrix are restricted to 1.

Since the above result relies on the Parameterized Inapproximability Hypothesis, Sect. 5.1 begins with its formal definition.

5.1 Inapproximability of Grid Tiling Under Parameterized Inapproximability Hypothesis

We first introduce Binary Constraint Satisfaction Problem, for which the Parameterized Inapproximability Hypothesis asserts FPT-inapproximability. For two integers n and k, we are given a set $V \triangleq [k]$ of k variables, an alphabet $\Sigma \triangleq [n]$ of size n, and a set of constraints $\mathcal {C}= (C_{i,j})_{i,j \in V}$ such that $C_{i,j} \subseteq \Sigma ^2$.³ Each variable $i \in V$ may take a value from $\Sigma$. Each constraint $C_{i,j}$ specifies the pairs of values that variables i and j can take simultaneously, and it is said to be satisfied by an assignment $\psi :V \rightarrow \Sigma$ of values to the variables if $(\psi (i), \psi (j)) \in C_{i,j}$. For example, for a graph $G = (V,E)$, define $C_{i,j} \triangleq \{(1,2),(2,1),(2,3),(3,2),(3,1),(1,3)\}$ for all edge (i, j) of G. Then, any assignment $\psi :V \rightarrow [3]$ is a 3-coloring of G if and only if $\psi$ satisfies all constraints simultaneously.

Problem 5.2

Given a set V of k variables, an alphabet set $\Sigma$ of size n, and a set of constraints $\mathcal {C}= (C_{i,j})_{i,j \in V}$, Binary Constraint Satisfaction Problem (BCSP) asks to find an assignment $\psi :V \rightarrow \Sigma$ that satisfies the maximum fraction of constraints.

It is well known that BCSP parameterized by the number k of variables is W[1]-complete from a standard parameterized reduction from k -Clique. Lokshtanov et al. [31] posed a conjecture asserting that a constant-factor gap version of BCSP is also W[1]-hard.

Hypothesis 5.3

(Parameterized Inapproximability Hypothesis (PIH) [31]) There exists some universal constant $\varepsilon \in (0,1)$ such that it is W[1]-hard to distinguish between BCSP instances that are promised to either be satisfiable, or have a property that every assignment violates at least $\varepsilon$-fraction of the constraints.

Here, we prove that an optimization version of Grid Tiling is FPT-inapproximable assuming PIH. Given an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling and an assignment $\sigma :[k]^2 \rightarrow [n]^2$, $\sigma (i,j)$ and $\sigma (i',j')$ for a pair of adjacent cells $(i,j,i',j') \in \mathcal {I}$ are said to be consistent if they agree on the first coordinate when $i=i'$ or on the second coordinate when $j=j'$, and inconsistent otherwise. The consistency of $\sigma$, denoted ${{\,\textrm{cons}\,}}(\sigma )$, is defined as the number of pairs of adjacent cells that are consistent; namely,

$$\begin{aligned} {{\,\textrm{cons}\,}}(\sigma ) \triangleq \sum _{(i_1,j_1,i_2,j_2) \in \mathcal {I}} \Bigl [\!\!\Bigl [ \sigma (i_1,j_1) \text { and } \sigma (i_2,j_2) \text { are consistent} \Bigr ]\!\!\Bigr ]. \end{aligned}$$

(5.1)

The inconsistency of $\sigma$ is defined as the number of inconsistent pairs of adjacent cells. The optimization version of Grid Tiling asks to find an assignment $\sigma$ such that ${{\,\textrm{cons}\,}}(\sigma )$ is maximized.⁴ Note that the maximum possible consistency is $\vert {\mathcal {I}}\vert = 2k^2$. We will use ${{\,\textrm{opt}\,}}(\mathcal {S})$ to denote the optimal consistency among all possible assignments. We now demonstrate that Grid Tiling is FPT-inapproximable in an additive sense under PIH, whose proof is reminiscent of [34].

Lemma 5.4

Under PIH, there exists some universal constant $\delta \in (0,1)$ such that it is W[1]-hard to distinguish Grid Tiling instances between the following cases:

• Completeness: the optimal consistency is $2k^2$.

• Soundness: the optimal consistency is at most $2k^2 - \delta k$.

Proof

We show a gap-preserving parameterized reduction from BCSP to Grid Tiling. Given an instance of BCSP $(V,\Sigma , \mathcal {C}=(C_{i,j})_{i,j\in V})$, where $V = [k]$ and $\Sigma = [n]$, we define $\mathcal {S}$ to be a collection of $k^2$ nonempty subsets $S_{i,j} \subseteq [n]^2$ such that $S_{i,i} \triangleq [n]^2$ for all $i \in [k]$ and $S_{i,j} \triangleq C_{i,j} \subseteq [n]^2$ for all $i \ne j \in [k]$. Suppose first there exists a satisfying assignment $\psi :V \rightarrow \Sigma$ for the BCSP instance; i.e., $(\psi (i), \psi (j)) \in C_{i,j}$ for all $i \ne j \in V$. Constructing another assignment $\sigma :[k]^2 \rightarrow [n]^2$ for Grid Tiling defined by $\mathcal {S}$ such that $\sigma (i,j) \triangleq (\psi (i), \psi (j)) \in S_{i,j}$ for each $i,j \in [k]$, we have ${{\,\textrm{cons}\,}}(\sigma ) = 2k^2$, proving the completeness part.

Suppose then we are given an assignment $\sigma :[k]^2 \rightarrow [n]^2$ for Grid Tiling whose inconsistency is at most $\delta k$ for some $\delta \in (0,1)$. Define a subset $A \subseteq [n]$ as follows:

$$\begin{aligned} \begin{aligned} A \triangleq [k] \setminus \Bigl (&\Bigl \{ i\in [k] : \exists j \in [k] \text { s.t. } \sigma (i,j) \text { and } \sigma (i,j+1) \text { are inconsistent} \Bigr \} \cup \\&\Bigl \{ j\in [k] : \exists i \in [k] \text { s.t. } \sigma (i,j) \text { and } \sigma (i+1,j) \text { are inconsistent} \Bigr \} \Bigr ). \end{aligned} \end{aligned}$$

(5.2)

It follows from the definition that $\vert {A}\vert \geqslant (1-\delta ) k$ and the restriction of $\sigma$ on $A^2$ is of zero inconsistency. Thus, if we define an assignment $\psi : V \rightarrow \Sigma$ for BCSP as

$$\begin{aligned} \psi (i) \triangleq z \text { such that } \sigma (i,i) = (z,z) \text { for each } i \in V, \end{aligned}$$

(5.3)

then it holds that $(\psi (i), \psi (j)) \in S_{i,j} = C_{i,j}$ for all $i \ne j \in A$. The fraction of constraints in the BCSP instance satisfied by $\psi$ is then at least

$$\begin{aligned} \begin{aligned} \frac{{\vert {A}\vert \atopwithdelims ()2}}{{k \atopwithdelims ()2}}&= \frac{(k-\delta k)(k-\delta k-1)}{2}\frac{2}{k(k-1)} \\&= (1-\delta )\left( 1- \frac{\delta k}{k-1}\right) \\&\geqslant (1-\delta )\left( 1- \frac{3}{2}\delta \right)&\text { (for } k \geqslant 3 \text {)} \\&\geqslant \left( 1-\frac{3}{2}\delta \right) ^2 \\&\geqslant 1-3\delta . \end{aligned} \end{aligned}$$

(5.4)

Consequently, if the optimal consistency ${{\,\textrm{opt}\,}}(\mathcal {S})$ is at least $2k^2 - \delta k$ for some $\delta \in (0,1)$, then the maximum fraction of satisfiable constraints of BCSP instance must be at least $1-3\delta$, which completes (the contraposition of) the soundness part. Under PIH, it is W[1]-hard to decide if the optimal consistency of a Grid Tiling instance is equal to $2k^2$ or less than $2k^2 - \delta k$, where $\delta \triangleq \frac{\varepsilon }{3}$ and $\varepsilon \in (0,1)$ is a constant appearing in Hypothesis 5.3. $\square$

It should be noted that we may not be able to significantly improve the additive term ${{\,\mathrm{\mathcal {O}}\,}}(k)$ owing to a polynomial-time $\varepsilon k^2$-additive approximation algorithm for any constant $\varepsilon > 0$:

Observation 5.5

Given an instance of Grid Tiling and an error tolerance parameter $\varepsilon > 0$, we can find an assignment whose consistency is at least ${{\,\textrm{opt}\,}}(\mathcal {S}) - \varepsilon k^2$ in $\varepsilon ^2 k^2 n^{{{\,\mathrm{\mathcal {O}}\,}}(1/\varepsilon ^2)}$ time.

Proof

Given an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling and $\varepsilon > 0$, if $\varepsilon k < 4$, we can use a brute-force search algorithm to find an optimal assignment in time $n^{{{\,\mathrm{\mathcal {O}}\,}}(k^2)} = n^{{{\,\mathrm{\mathcal {O}}\,}}(1/\varepsilon ^2)}$. Hereafter, we safely assume that $\varepsilon k \geqslant 4$. Defining $\displaystyle \ell \triangleq \left\lfloor \frac{\varepsilon k}{2} - 1\right\rfloor$ and , we observe that

(5.5)

We partition $k^2$ cells of $\mathcal {S}$ into $\ell ^2$ blocks, denoted $\{P_{\hat{\imath }, \hat{\jmath }}\}_{\hat{\imath }, \hat{\jmath }\in [\ell ]}$, each of which is of size at most $B^2$ and defined as follows:

$$\begin{aligned} P_{\hat{\imath },\hat{\jmath }}&\triangleq \Bigl [B(\hat{\imath }-1)+1 \mathrel {..}\min \{B\hat{\imath }, k\}\Bigr ] \times \Bigl [B(\hat{\jmath }-1)+1 \mathrel {..}\min \{B\hat{\jmath }, k\}\Bigr ]\nonumber \\&\qquad \text { for all } \hat{\imath }, \hat{\jmath }\in [\ell ]. \end{aligned}$$

(5.6)

Consider for each $\hat{\imath },\hat{\jmath }\in [\ell ]$, a variant of Grid Tiling denoted by $\mathcal {S}_{\hat{\imath },\hat{\jmath }} \triangleq \{ S_{i,j}: (i,j) \in P_{\hat{\imath },\hat{\jmath }} \}$, which requires maximizing the number of consistent pairs of adjacent cells of $P_{\hat{\imath },\hat{\jmath }}$ in $\mathcal {I}$, where $\mathcal {I}$ is defined in Eq. 4.1. Because each instance $\mathcal {S}_{\hat{\imath },\hat{\jmath }}$ contains at most $B^2$ cells, we can solve this variant exactly by exhaustive search in $n^{B^2 + {{\,\mathrm{\mathcal {O}}\,}}(1)}$ time. Denote by $\sigma _{\hat{\imath },\hat{\jmath }} :P_{\hat{\imath },\hat{\jmath }} \rightarrow [n]^2$ the obtained partial assignment on $P_{\hat{\imath }, \hat{\jmath }}$. Concatenating all $\sigma _{\hat{\imath },\hat{\jmath }}$’s, we can construct an assignment $\sigma :[k]^2 \rightarrow [n]^2$ to the original Grid Tiling instance $\mathcal {S}$. Because each partial assignment $\sigma _{\hat{\imath },\hat{\jmath }}$ is optimal on $\mathcal {S}_{\hat{\imath },\hat{\jmath }}$, the number of consistent pairs of adjacent cells within the same block is at least ${{\,\textrm{opt}\,}}(\mathcal {S})$. By contrast, the number of (possibly inconsistent) pairs of adjacent cells across different blocks is $2 k \ell$. Accordingly, the consistency of $\sigma$ is ${{\,\textrm{cons}\,}}(\sigma ) \geqslant {{\,\textrm{opt}\,}}(\mathcal {S}) - 2 k \ell \geqslant {{\,\textrm{opt}\,}}(\mathcal {S}) - \varepsilon k^2$. Note that the entire time complexity is bounded by $\ell ^2 \cdot n^{B^2 + {{\,\mathrm{\mathcal {O}}\,}}(1)} = \varepsilon ^2 k^2 n^{{{\,\mathrm{\mathcal {O}}\,}}(1/\varepsilon ^2)}$ completing the proof. $\square$

Our technical result is a gap-preserving parameterized reduction from Grid Tiling to Determinant Maximization, whose proof is presented in the subsequent subsection.

Lemma 5.6

There is a polynomial-time, parameterized reduction from an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling to an instance $({\textbf {A}} ,k^2)$ of Determinant Maximization such that all diagonal entries of ${\textbf {A}}$ are 1 and the following conditions are satisfied:

• Completeness: If ${{\,\textrm{opt}\,}}(\mathcal {S}) = 2k^2$, then ${{\,\textrm{maxdet}\,}}({\textbf {A}} ,k^2) = 1$.

• Soundness: If ${{\,\textrm{opt}\,}}(\mathcal {S}) \leqslant 2k^2 - \delta k$ for some $\delta > 0$, then ${{\,\textrm{maxdet}\,}}({\textbf {A}} ,k^2) \leqslant 0.999^{\delta k}$.

Using Lemma 5.6, we can prove Theorem 5.1.

Proof of Theorem 5.1

Our gap-preserving parameterized reduction is as follows. Given an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling, we construct an instance $({\textbf {A}} \in \mathbb {Q}^{N \times N}, K \triangleq k^2)$ of Determinant Maximization in polynomial time according to Lemma 5.6, where $N \triangleq \sum _{i,j \in [k]}\vert {S_{i,j}}\vert$. The diagonal entries of ${\textbf {A}}$ are 1 by definition. Since K is a function only in k, this is a parameterized reduction. According to Lemma 5.4 and 5.6, it is W[1]-hard to determine whether ${{\,\textrm{maxdet}\,}}({\textbf {V}} ,K) = 1$ or ${{\,\textrm{maxdet}\,}}({\textbf {V}} ,K) \leqslant 0.999^{\delta k}$ under PIH, where $\delta \in (0,1)$ is a constant appearing Lemma 5.4. In particular, Determinant Maximization is W[1]-hard to approximate within a factor better than $0.999^{\delta k} = 2^{-c\sqrt{K}}$ when parameterized by K, where $c \in (0,1)$ is some universal constant. This completes the proof. $\square$

5.2 Gap-Preserving Reduction from Grid Tiling and Proof of Lemma 5.6

To prove Lemma 5.6, we describe a gap-preserving parameterized reduction from Grid Tiling to Determinant Maximization. Before going into its details, we introduce a convenient gadget due to Çivril and Magdon-Ismail [13].

Lemma 5.7

(Çivril and Magdon-Ismail [13], Lemma 13) For any positive even integer $\ell$, we can construct a set of $2^{\ell }$ rational vectors ${\textbf {B}} ^{(\ell )} = \{\textbf{b}_1, \ldots , \textbf{b}_{2^{\ell }}\}$ of dimension $2^{\ell +1}$ in ${{\,\mathrm{\mathcal {O}}\,}}(4^{\ell })$ time such that the following conditions are satisfied:

• Each entry of vectors is either 0 or $2^{-\frac{\ell }{2}}$; $\Vert \textbf{b}_i\Vert = 1$ for all $i \in [2^{\ell }]$.

• $\langle \textbf{b}_i, \textbf{b}_j \rangle = \frac{1}{2}$ for all $i, j\in [2^\ell ]$ with $i \ne j$.

• $\langle \textbf{b}_i, \overline{\textbf{b}_j} \rangle = \frac{1}{2}$ for all $i,j \in [2^\ell ]$ with $i \ne j$, where $\overline{\textbf{b}_j} \triangleq 2^{-\frac{\ell }{2}} \cdot \textbf{1} - \textbf{b}_j$.

By definition of ${\textbf {B}} ^{(\ell )}$, we further have the following:

$$\begin{aligned} \langle \textbf{b}_i, \overline{\textbf{b}_i} \rangle&= 2^{-\frac{\ell }{2}} \langle \textbf{1}, \textbf{b}_i \rangle - \langle \textbf{b}_i, \textbf{b}_i \rangle = 0, \end{aligned}$$

(5.7)

$$\begin{aligned} \langle \overline{\textbf{b}_i}, \overline{\textbf{b}_j} \rangle&= \langle 2^{-\frac{\ell }{2}} \textbf{1} - \textbf{b}_i, 2^{-\frac{\ell }{2}} \textbf{1} - \textbf{b}_j \rangle \nonumber \\&= 2^{-\ell } \langle \textbf{1}, \textbf{1} \rangle - 2^{-\frac{\ell }{2}} \langle \textbf{1}, \textbf{b}_i + \textbf{b}_j \rangle + \langle \textbf{b}_i, \textbf{b}_j \rangle \nonumber \\&= \langle \textbf{b}_i, \textbf{b}_j \rangle . \end{aligned}$$

(5.8)

Our reduction strategy is very similar to that of Theorem 4.2. Given an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling, we construct a rational vector $\textbf{v}_{x,y}^{(i,j)}$ for each element $(x,y) \in S_{i,j}$ of cell $(i,j) \in [k]^2$. Each vector consists of $\vert {\mathcal {I}}\vert = 2k^2$ blocks indexed by $\mathcal {I}$, each of which is either a vector in the set ${\textbf {B}} ^{(2\lceil \log n \rceil )}$ or the zero vector $\textbf{0}$. Hence, the dimension of the vectors is $2k^2 \cdot 2^{2\lceil \log n \rceil +1} = {{\,\mathrm{\mathcal {O}}\,}}(k^2 n^2)$. Let $\textbf{v}_{x,y}^{(i,j)}(i_1,j_1,i_2,j_2)$ denote the block of $\textbf{v}_{x,y}^{(i,j)}$ corresponding to a pair of adjacent cells $(i_1,j_1,i_2,j_2) \in \mathcal {I}$. Each block is subsequently defined as follows:

$$\begin{aligned} \textbf{v}^{(i,j)}_{x,y}(e) \triangleq {\left\{ \begin{array}{ll} \overline{\textbf{b}_x} &{} \text {if } e = (i,j-1,i,j), \\ \textbf{b}_x &{} \text {if } e = (i,j,i,j+1), \\ \overline{\textbf{b}_y} &{} \text {if } e = (i-1,j,i,j), \\ \textbf{b}_y &{} \text {if } e = (i,j,i+1,j), \\ \textbf{0} &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(5.9)

Hereafter, two vectors $\textbf{v}^{(i,j)}_{x,y}$ and $\textbf{v}^{(i',j')}_{x',y'}$ are said to be adjacent if (i, j) and $(i',j')$ are adjacent, and two adjacent vectors are said to be consistent if (x, y) and $(x',y')$ are consistent (i.e., $x=x'$ whenever $i=i'$ and $y=y'$ whenever $j=j'$) and inconsistent otherwise. Since each vector contains exactly four vectors chosen from ${\textbf {B}} ^{(2 \lceil \log n \rceil )}$, its squared norm is equal to 4. In addition, $\textbf{v}^{(i,j)}_{x,y}$ and $\textbf{v}^{(i',j')}_{x',y'}$ are orthogonal whenever (i, j) and $(i',j')$ are not identical or adjacent. Observe further that if two cells are adjacent, the inner product of two vectors in ${\textbf {V}}$ is calculated as follows:

$$\begin{aligned}&\left\langle \textbf{v}^{(i,j)}_{x,y}, \textbf{v}^{(i,j+1)}_{x',y'} \right\rangle = \langle \textbf{b}_x, \overline{\textbf{b}_{x'}} \rangle ={\left\{ \begin{array}{ll} 0 &{} \quad \text {if they are consistent (i.e., } x = x'\mathrm{)}, \\ \frac{1}{2} &{} \quad \text {otherwise (i.e., } x \ne x'\text {)}, \end{array}\right. } \end{aligned}$$

(5.10)

$$\begin{aligned}&\begin{aligned} \left\langle {\textbf {v}}^{(i,j)}_{x,y}, {\textbf {v}}^{(i+1,j)}_{x',y'} \right\rangle&= \langle {\textbf {b}}_y, \overline{{\textbf {b}}_{y'}} \rangle = {\left\{ \begin{array}{ll} 0 &{}\quad {} \text{ if } \text{ they } \text{ are } \text{ consistent } \text{(i.e., } y = y'\text {)}, \\ \frac{1}{2} &{}\quad {} \text{ otherwise } \text{(i.e., } y \ne y'\text{) }. \end{array}\right. } \end{aligned} \end{aligned}$$

(5.11)

On the other hand, the inner product of two vectors in the same cell is as follows:

$$\begin{aligned} \begin{aligned} \left\langle \textbf{v}^{(i,j)}_{x,y}, \textbf{v}^{(i,j)}_{x',y'} \right\rangle&= 2 \cdot \langle \textbf{b}_x, \textbf{b}_{x'} \rangle + 2 \cdot \langle \textbf{b}_y, \textbf{b}_{y'} \rangle \\&= {\left\{ \begin{array}{ll} 4 &{} \text {if } x=x' \text { and } y=y', \\ 3 &{} \text {if } x=x' \text { xor } y=y',\\ 2 &{} \text {if } x \ne x' \text { and } y \ne y'. \end{array}\right. } \end{aligned} \end{aligned}$$

(5.12)

We denote by ${\textbf {V}} ^{(i,j)}$ the set of vectors corresponding to the elements of $S_{i,j}$; i.e., ${\textbf {V}} ^{(i,j)} \triangleq \{ \textbf{v}^{(i,j)}_{x,y}: (x,y) \in S_{i,j} \}$ for each $i,j \in [k]$. We now define an instance $({\textbf {V}} , K)$ of Determinant Maximization as ${\textbf {V}} \triangleq \bigcup _{i,j \in [k]} {\textbf {V}} ^{(i,j)} \text { and } K \triangleq k^2.$ Note that ${\textbf {V}}$ contains $N \triangleq \sum _{i,j \in [k] }\vert {S_{i,j}}\vert$ vectors.

We now proceed to the proof of (the soundness argument of) Lemma 5.6. Let ${\textbf {S}}$ be a set of $k^2$ vectors from ${\textbf {V}}$. Define ${\textbf {S}} ^{(i,j)} \triangleq {\textbf {V}} ^{(i,j)} \cap {\textbf {S}} = \{ \textbf{v}^{(i,j)}_{x,y} \in {\textbf {S}} : (x,y) \in S_{i,j} \}$ for each $i,j\in [k]^2$. Denote by ${{\,\textrm{cov}\,}}({\textbf {S}} )$ the number of cells $(i,j) \in [k]^2$ such that ${\textbf {S}}$ includes $\textbf{v}^{(i,j)}_{x,y}$ for some (x, y); i.e., ${{\,\textrm{cov}\,}}({\textbf {S}} ) \triangleq \{ (i,j) \in [k]^2: {\textbf {S}} ^{(i,j)} \ne \emptyset \},$ and we also define ${{\,\textrm{dup}\,}}({\textbf {S}} ) \triangleq \{ (i,j) \in [k]^2: {\textbf {S}} ^{(i,j)} = \emptyset \}.$ It follows from the definition that ${{\,\textrm{cov}\,}}({\textbf {S}} ) + {{\,\textrm{dup}\,}}({\textbf {S}} ) = k^2$ and ${{\,\textrm{dup}\,}}({\textbf {S}} )$ counts the total number of “duplicate” vectors in the same cell. We first present an upper bound on the volume of ${\textbf {S}}$ in terms of ${{\,\textrm{dup}\,}}({\textbf {S}} )$, implying that we cannot select many duplicate vectors from the same cell.

Lemma 5.8

If ${{\,\textrm{dup}\,}}({\textbf {S}} ) \leqslant \frac{k^2}{2}$, then it holds that

$$\begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {S}} ) \leqslant 4^{k^2} \cdot \left( \frac{3}{4}\right) ^{{{\,\textrm{dup}\,}}({\textbf {S}} )}. \end{aligned}$$

(5.13)

Proof

We first introduce Fischer’s inequality. Suppose ${\textbf {A}}$ and ${\textbf {B}}$ are respectively $m \times m$ and $n \times n$ positive semi-definite matrices, and ${\textbf {C}}$ is an $m \times n$ matrix. Then, it holds that $\det \left( \bigg [\begin{array}{ll} {\textbf {A}} &{} {\textbf {C}} \\ {\textbf {C}} ^\top &{} {\textbf {B}} \end{array}\bigg ]\right) \leqslant \det ({\textbf {A}} ) \cdot \det ({\textbf {B}} ).$ As a corollary, we have the volume version of Fischer’s inequality stating that for any two sets of vectors ${\textbf {P}} , {\textbf {Q}}$,

$$\begin{aligned} {{\,\textrm{vol}\,}}({\textbf {P}} \uplus {\textbf {Q}} ) \leqslant {{\,\textrm{vol}\,}}({\textbf {P}} ) \cdot {{\,\textrm{vol}\,}}({\textbf {Q}} ). \end{aligned}$$

(5.14)

Because we have

$$\begin{aligned} {{\,\textrm{vol}\,}}({\textbf {S}} ) \leqslant \prod _{i,j \in [k]} {{\,\textrm{vol}\,}}({\textbf {S}} ^{(i,j)}) \end{aligned}$$

(5.15)

by Fischer’s inequality in Eq. 5.14, we consider bounding ${{\,\textrm{vol}\,}}({\textbf {S}} ^{(i,j)})$ from above for each $i,j \in [k]$. We will show the following:

$$\begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {S}} ^{(i,j)}) = {\left\{ \begin{array}{ll} 1 &{} \text {if } {\textbf {S}} ^{(i,j)} = \emptyset , \\ 4 \cdot 3^{\vert {{\textbf {S}} ^{(i,j)}}\vert -1} &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(5.16)

Suppose ${\textbf {S}} ^{(i,j)} = \{\textbf{v}_1, \ldots , \textbf{v}_m\}$ for $m \triangleq \vert {{\textbf {S}} ^{(i,j)}}\vert$. By the definition of volume in Eq. 2.2, we have

$$\begin{aligned} \begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {S}} ^{(i,j)})&= \Vert \textbf{v}_1\Vert ^2 \cdot \prod _{2 \leqslant i \leqslant m} \Bigl \Vert \textbf{v}_i - {{\,\textrm{proj}\,}}_{\{\textbf{v}_1, \ldots , \textbf{v}_{i-1}\}}(\textbf{v}_i) \Bigr \Vert ^2 \\&\leqslant 4 \cdot \prod _{2 \leqslant i \leqslant m} \Bigl \Vert \textbf{v}_i - {{\,\textrm{proj}\,}}_{\{\textbf{v}_1\}}(\textbf{v}_i) \Bigr \Vert ^2. \end{aligned} \end{aligned}$$

(5.17)

Because the projection of each $\textbf{v}_i$ with $i \ne 1$ onto $\textbf{v}_1$ is calculated as

$$\begin{aligned} {{\,\textrm{proj}\,}}_{\{\textbf{v}_1\}}(\textbf{v}_i) = \frac{\langle \textbf{v}_1, \textbf{v}_i \rangle }{\Vert \textbf{v}_1\Vert ^2} \textbf{v}_1 = \frac{\langle \textbf{v}_1, \textbf{v}_i \rangle }{4} \textbf{v}_1, \end{aligned}$$

(5.18)

we obtain

$$\begin{aligned} \begin{aligned} \Bigl \Vert \textbf{v}_i - {{\,\textrm{proj}\,}}_{\{\textbf{v}_1\}}(\textbf{v}_i)\Bigr \Vert ^2&= \Vert \textbf{v}_i\Vert ^2 + \left\| \frac{\langle \textbf{v}_1, \textbf{v}_i \rangle }{4} \textbf{v}_1 \right\| ^2 - 2 \cdot \left\langle \textbf{v}_i, \frac{\langle \textbf{v}_1, \textbf{v}_i \rangle }{4} \textbf{v}_1 \right\rangle \\&= 4 + \frac{\langle \textbf{v}_1, \textbf{v}_i \rangle ^2}{16} \cdot 4 - \frac{\langle \textbf{v}_1, \textbf{v}_i \rangle ^2}{2} \\&= 4 - \frac{1}{4} \cdot \langle \textbf{v}_1, \textbf{v}_i \rangle ^2. \end{aligned} \end{aligned}$$

(5.19)

By Eq. 5.12, $\langle \textbf{v}_1, \textbf{v}_i \rangle$ with $i \ne 1$ is either 2 or 3; hence, it holds that $\Bigl \Vert \textbf{v}_i - {{\,\textrm{proj}\,}}_{\{\textbf{v}_1\}}(\textbf{v}_i)\Bigr \Vert ^2 \leqslant 3$, ensuring Eq. 5.16 as desired. Consequently, we get

$$\begin{aligned} \begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {S}} ) \leqslant \prod _{i,j \in [k]} {{\,\textrm{vol}\,}}^2({\textbf {S}} ^{(i,j)}) \leqslant \prod _{i,j \in [k]: {\textbf {S}} ^{(i,j)} \ne \emptyset } 4 \cdot 3^{\vert {{\textbf {S}} ^{(i,j)}}\vert - 1} \\ = \left( \frac{4}{3}\right) ^{{{\,\textrm{cov}\,}}({\textbf {S}} )} \cdot \prod _{i,j \in [k]} 3^{\vert {{\textbf {S}} ^{(i,j)}}\vert } = 4^{k^2} \cdot \left( \frac{3}{4}\right) ^{{{\,\textrm{dup}\,}}({\textbf {S}} )}, \end{aligned} \end{aligned}$$

(5.20)

completing the proof. $\square$

We then present another upper bound on the volume of ${\textbf {S}}$ in terms of the inconsistency of a partial solution of Grid Tiling constructed from the selected vectors. For a set ${\textbf {S}}$ of $k^2$ vectors from ${\textbf {V}}$, a partial assignment $\sigma _{{\textbf {S}} } :[k]^2 \rightarrow [n]^2 \cup \{\bigstar \}$ for Grid Tiling is defined as

$$\begin{aligned} \sigma _{{\textbf {S}} }(i,j) \triangleq {\left\{ \begin{array}{ll} \text {any } (x,y) \text { s.t.~} \textbf{v}^{(i,j)}_{x,y} \in {\textbf {S}} ^{(i,j)} &{} \text {if such } (x,y) \text { exists}, \\ \bigstar &{} \text {otherwise (i.e., } {\textbf {S}} ^{(i,j)} = \emptyset \text {)}, \end{array}\right. } \end{aligned}$$

(5.21)

where the symbol “$\bigstar$” means undefined and the choice of (x, y) is arbitrary. The inconsistency of a partial assignment $\sigma _{{\textbf {S}} }$ is defined as

$$\begin{aligned} \sum _{(i_1,j_1,i_2,j_2) \in \mathcal {I}} \left[ \!\!\left[ \begin{gathered} \sigma (i_1,j_1) \ne \bigstar \text {; } \sigma (i_2,j_2) \ne \bigstar \text {;} \\ \sigma (i_1,j_1)\text { and }\sigma (i_2,j_2)\text { are inconsistent} \end{gathered} \right] \!\!\right] . \end{aligned}$$

(5.22)

Note that the sum of the consistency and inconsistency of $\sigma _{{\textbf {S}} }$ is no longer necessarily $2k^2$. Using $\sigma _{{\textbf {S}} }$, we define a partition $({\textbf {P}} , {\textbf {Q}} )$ of ${\textbf {S}}$ as ${\textbf {P}} \triangleq \{ \textbf{v}^{(i,j)}_{x,y} \in {\textbf {S}} : i,j \in [k], \sigma _{{\textbf {S}} }(i,j) = (x,y) \}$ and ${\textbf {Q}} \triangleq {\textbf {S}} \setminus {\textbf {P}}$. We further prepare an arbitrary ordering $\prec$ over $[k]^2$; e.g., $(i,j) \prec (i',j')$ if $i<i'$, or $i=i'$ and $j<j'$. We abuse the notation by writing $\textbf{v}^{(i,j)}_{x,y} \prec \textbf{v}^{(i',j')}_{x',y'}$ for any two vectors of ${\textbf {V}}$ whenever $(i,j) \prec (i',j')$. Define now ${\textbf {P}} _{\prec \textbf{v}} \triangleq \{ \textbf{u} \in {\textbf {P}} : \textbf{u} \prec \textbf{v} \}.$ The following lemma states that the squared volume of $k^2$ vectors exponentially decays in the minimum possible inconsistency among all assignments of $\mathcal {S}$.

Lemma 5.9

Suppose ${{\,\textrm{opt}\,}}(\mathcal {S}) \leqslant 2k^2 - \delta k$ for some $\delta > 0$ and ${{\,\textrm{cov}\,}}({\textbf {S}} ) \geqslant k^2 - \gamma k$ for some $\gamma > 0$. If $\delta k - 4 \gamma k$ is positive, then it holds that

$$\begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {S}} ) \leqslant 4^{k^2} \cdot \left( \frac{63}{64}\right) ^{\frac{\delta - 4 \gamma }{4} k}. \end{aligned}$$

(5.23)

The proof of Lemma 5.9 involves the following claim.

Claim 5.10

Suppose the same conditions as in Lemma 5.9 are satisfied. Then, the inconsistency of $\sigma _{{\textbf {S}} }$ is at least $\delta k - 4\gamma k$. Moreover, the number of vectors $\textbf{v}$ in ${\textbf {P}}$ such that $\textbf{v}$ is inconsistent with some adjacent vector of ${\textbf {P}} _{\prec \textbf{v}}$ is at least $\frac{\delta k - 4\gamma k}{4}$.

Proof

Assuming that the inconsistency of $\sigma _{{\textbf {S}} }$ is less than $\delta k - 4 \gamma k$, we can construct a (complete) assignment $\sigma :[k]^2 \rightarrow [n]^2$ from $\sigma _{{\textbf {S}} }$ by filling in undefined values (i.e., “$\bigstar$”) with an arbitrary integer pair in the corresponding cell. The inconsistency of $\sigma$ is clearly less than $\delta k$, which is a contradiction. $\square$

On the other hand, assume that there are only less than $\frac{\delta k - 4\gamma k}{4}$ vectors $\textbf{v}$ in ${\textbf {P}}$ that are inconsistent with some adjacent vector of ${\textbf {P}} _{\prec \textbf{v}}$. Then, the inconsistency of $\sigma _{{\textbf {S}} }$ must be less than $\frac{\delta k - 4\gamma k}{4} \cdot 4$,⁵ which is a contradiction.

Proof of Lemma 5.9

By applying Eq. 5.14, we have ${{\,\textrm{vol}\,}}^2({\textbf {S}} ) \leqslant {{\,\textrm{vol}\,}}^2({\textbf {P}} ) \cdot {{\,\textrm{vol}\,}}^2({\textbf {Q}} )$. Observe easily that

$$\begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {Q}} ) \leqslant 4^{\vert {{\textbf {Q}} }\vert } \text { and } {{\,\textrm{vol}\,}}^2({\textbf {P}} ) = \prod _{\textbf{v} \in {\textbf {P}} } {{\,\textrm{d}\,}}^2(\textbf{v}, {\textbf {P}} _{\prec \textbf{v}}). \end{aligned}$$

(5.24)

Thereafter, we bound ${{\,\textrm{d}\,}}^2(\textbf{v}, {\textbf {P}} _{\prec \textbf{v}})$ for each $\textbf{v} \in {\textbf {P}}$ using the following case analysis:

Case 1:

$\textbf{v}$ is consistent with all adjacent vectors in ${\textbf {P}} _{\prec \textbf{v}}$: because $\langle \textbf{u}, \textbf{v} \rangle = 0$ for all $\textbf{u} \in {\textbf {P}} _{\prec \textbf{v}}$, we have ${{\,\textrm{proj}\,}}_{{\textbf {P}} _{\prec \textbf{v}}}(\textbf{v}) = \textbf{0}$, implying that

$$\begin{aligned} {{\,\textrm{d}\,}}^2(\textbf{v}, {\textbf {P}} _{\prec \textbf{v}}) = \Bigl \Vert \textbf{v} - {{\,\textrm{proj}\,}}_{{\textbf {P}} _{\prec \textbf{v}}}(\textbf{v})\Bigr \Vert ^2 = \Vert \textbf{v}\Vert ^2 = 4. \end{aligned}$$

(5.25)

Case 2:

There exists a vector $\textbf{u}$ in ${\textbf {P}} _{\prec \textbf{v}}$ that is inconsistent with $\textbf{v}$: because $\langle \textbf{u}, \textbf{v} \rangle = \frac{1}{2}$ by Eqs. 5.10 and 5.11, the projection of $\textbf{v}$ on $\textbf{u}$ is equal to

$$\begin{aligned} {{\,\textrm{proj}\,}}_{\{\textbf{u}\}}(\textbf{v}) = \frac{\langle \textbf{u}, \textbf{v} \rangle }{\Vert \textbf{u}\Vert ^2} \cdot \textbf{u} = \frac{1}{8} \cdot \textbf{u}. \end{aligned}$$

(5.26)

Therefore, we have

$$\begin{aligned} \begin{aligned} {{\,\textrm{d}\,}}^2(\textbf{v}, {\textbf {P}} _{\prec \textbf{v}})&\leqslant {{\,\textrm{d}\,}}^2(\textbf{v}, \{\textbf{u}\}) = \Bigl \Vert \textbf{v} - {{\,\textrm{proj}\,}}_{\{\textbf{u}\}}(\textbf{v}) \Bigr \Vert ^2 \\&= \Vert \textbf{v}\Vert ^2 + \left\| \frac{1}{8} \cdot \textbf{u}\right\| ^2 - 2 \cdot \frac{1}{8} \langle \textbf{u}, \textbf{v} \rangle \\&= 4 + \frac{4}{64} - 2 \cdot \frac{1}{16} = \frac{63}{16}. \end{aligned} \end{aligned}$$

(5.27)

As illustrated in Lemma 5.10, at least $\frac{\delta - 4 \gamma }{4}k$ vectors of ${\textbf {P}}$ fall into the latter case; it thus turns out that

$$\begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {P}} ) = \prod _{\textbf{v} \in {\textbf {P}} } {{\,\textrm{d}\,}}^2(\textbf{v}, {\textbf {P}} _{\prec \textbf{v}}) \leqslant 4^{\vert {{\textbf {P}} }\vert - \frac{\delta - 4 \gamma }{4}k} \cdot \left( \frac{63}{16}\right) ^{\frac{\delta - 4 \gamma }{4}k} = 4^{\vert {{\textbf {P}} }\vert } \cdot \left( \frac{63}{64}\right) ^{\frac{\delta - 4 \gamma }{4}k}. \end{aligned}$$

(5.28)

Consequently, the squared volume of ${\textbf {S}}$ can be bounded as

$$\begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {S}} ) \leqslant 4^{\vert {{\textbf {P}} }\vert + \vert {{\textbf {Q}} }\vert } \cdot \left( \frac{63}{64}\right) ^{\frac{\delta - 4 \gamma }{4}k} = 4^{k^2} \cdot \left( \frac{63}{64}\right) ^{\frac{\delta - 4 \gamma }{4}k}, \end{aligned}$$

(5.29)

which completes the proof. $\square$

Using Lemmas 5.8 and 5.9, we can easily conclude the proof of Lemma 5.6 as follows.

Proof of Lemma 5.6

Observe that the reduction described in Sect. 5.2 is a parameterized reduction as it requires polynomial time and an instance $\mathcal {S}= (S_{i,j})_{i,j \in [k]}$ of Grid Tiling is transformed into an instance $({\textbf {V}} , k^2)$ of Determinant Maximization. In addition, the construction of ${\textbf {B}} ^{(2\lceil \log n \rceil )}$ completes in time ${{\,\mathrm{\mathcal {O}}\,}}(4^{2 \lceil \log n \rceil }) = {{\,\mathrm{\mathcal {O}}\,}}(n^4)$ by Lemma 5.7.

We now prove the correctness of the reduction. Let us begin with the completeness argument. Suppose ${{\,\textrm{opt}\,}}(\mathcal {S}) = 2k^2$; i.e., there is an assignment $\sigma$ of consistency $2k^2$. Then, $k^2$ vectors in the set ${\textbf {S}} \triangleq \{ \textbf{v}^{(i,j)}_{\sigma (i,j)}: i,j \in [k] \}$ are orthogonal to each other, implying that ${{\,\textrm{vol}\,}}^2({\textbf {S}} ) = 4^{k^2}$. On the other hand, because every vector of ${\textbf {V}}$ is of squared norm 4, the maximum possible squared volume among $k^2$ vectors in ${\textbf {V}}$ is $4^{k^2}$; namely, ${{\,\textrm{maxdet}\,}}({\textbf {V}} ,k^2) = 4^{k^2}$.

We then prove the soundness argument. Suppose ${{\,\textrm{opt}\,}}(\mathcal {S}) \leqslant 2k^2 - \delta k$ for some constant $\delta > 0$. Then, for any set $\mathcal {S}$ of $k^2$ vectors from ${\textbf {V}}$ such that ${{\,\textrm{dup}\,}}({\textbf {S}} ) > \frac{\log 0.999^{-1}}{\log (\frac{3}{4})^{-1}} \cdot \delta k,$ we have that by Lemma 5.8, ${{\,\textrm{vol}\,}}^2({\textbf {S}} ) < 4^{k^2} \cdot 0.999^{\delta k}.$ It is thus sufficient to consider the case that

$$\begin{aligned} {{\,\textrm{dup}\,}}({\textbf {S}} ) \leqslant \frac{\log 0.999^{-1}}{\log (\frac{3}{4})^{-1}} \cdot \delta k \approx 0.0035 \cdot \delta . \end{aligned}$$

(5.30)

In particular, it suffices to assume that ${{\,\textrm{dup}\,}}({\textbf {S}} ) \leqslant \gamma k$ for some $\gamma \in (0, \frac{\delta }{4})$. Simple calculation using Lemmas 5.8 and 5.9 derives that

$$\begin{aligned} \begin{aligned} {{\,\textrm{vol}\,}}^2({\textbf {S}} )&\leqslant \min \left\{ 4^{k^2} \cdot \left( \frac{3}{4}\right) ^{\gamma k}, 4^{k^2} \cdot \left( \frac{63}{64}\right) ^{\frac{\delta - 4\gamma }{4}k} \right\} \\&\leqslant 4^{k^2} \cdot \min \left\{ \left( \frac{63}{64}\right) ^{\gamma k}, \left( \frac{63}{64}\right) ^{\frac{\delta - 4\gamma }{4}k} \right\} \\&\leqslant 4^{k^2} \cdot \left( \frac{63}{64}\right) ^{\displaystyle \underbrace{\min \left\{ \gamma , \frac{\delta - 4\gamma }{4}\right\} }_{\heartsuit } \cdot k } \\&\leqslant 4^{k^2} \cdot \left( \frac{63}{64}\right) ^{\frac{\delta }{8} k} \leqslant 4^{k^2} \cdot 0.999^{\delta k}, \end{aligned} \end{aligned}$$

(5.31)

where the second-to-last inequality is due to the fact that $\heartsuit$ is maximized when $\gamma = \frac{\delta - 4 \gamma }{4}$; i.e., $\gamma = \frac{\delta }{8} > 0$.

Because the diagonal entries of the Gram matrix ${\textbf {A}}$ defined by the vectors of ${\textbf {V}}$ are 4, we can construct another instance of Determinant Maximization as $(\widetilde{{\textbf {A}} }, k^2)$, where $\widetilde{{\textbf {A}} } \triangleq \frac{1}{4}{\textbf {A}}$. Observe finally that the diagonal entries of $\widetilde{{\textbf {A}} }$ are 1 and $\det (\widetilde{{\textbf {A}} }_S) = 4^{-\vert {S}\vert } \cdot \det ({\textbf {A}} _S)$ for any S, which completes the proof. $\square$

5.3 $\varepsilon$-Additive FPT-Approximation Parameterized by Rank

Here, we develop an $\varepsilon$-additive FPT-approximation algorithm parameterized by the rank of an input matrix ${\textbf {A}}$, provided that ${\textbf {A}}$ is the Gram matrix of vectors of infinity norm at most 1. Our algorithm complements Lemma 5.6 in a sense that we can solve the promise problem in FPT time with respect to ${{\,\textrm{rank}\,}}({\textbf {A}} )$. The proof uses the standard rounding technique.

Observation 5.11

Let $\textbf{v}_1, \ldots , \textbf{v}_n$ be n d-dimensional vectors in $\mathbb {Q}^d$ such that $\Vert \textbf{v}_i\Vert _{\infty } \leqslant 1$ for all $i \in [n]$, ${\textbf {A}}$ the Gram matrix defined by the vectors, $k \in [d]$ a positive integer, and $\varepsilon > 0$ an error tolerance parameter. Then, we can compute an approximate solution $S \in {[n] \atopwithdelims ()k}$ to Determinant Maximization in $\varepsilon ^{-d^2} \cdot d^{{{\,\mathrm{\mathcal {O}}\,}}(d^3)} \cdot n^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$ time such that $\det ({\textbf {A}} _S) \geqslant {{\,\textrm{maxdet}\,}}({\textbf {A}} ,k) - \varepsilon$.

Proof

Let $\textbf{v}_1, \ldots , \textbf{v}_n$ be n d-dimensional vectors in $\mathbb {Q}^d$ such that $\Vert \textbf{v}_i\Vert _{\infty } \leqslant 1$ for all $i \in [n]$, and ${\textbf {A}}$ be the Gram matrix in $\mathbb {Q}^{n \times n}$ defined by them; i.e., $A_{i,j} = \langle \textbf{v}_i, \textbf{v}_j \rangle$ for all $i,j \in [n]$. We introduce a parameter $\Delta > 0$, which is a reciprocal of some positive integer. The value of $\Delta$ is determined later based on d, k, and $\varepsilon$. We then define the set $I_{\Delta }$ of rational numbers equally spaced on the interval $[-1,1]$ as follows:

$$\begin{aligned} I_{\Delta } \triangleq \Bigl \{-1, -1 + \Delta , \ldots , -2\Delta , -\Delta , 0, \Delta , 2\Delta , \ldots , 1-\Delta , 1\Bigr \}. \end{aligned}$$

(5.32)

Subsequently, we construct n d-dimensional vectors $\textbf{w}_1, \ldots , \textbf{w}_n$ from $\textbf{v}_1, \ldots , \textbf{v}_n$ as follows: for each $i \in [n]$ and $e \in [d]$, $w_i(e)$ is defined to be a number of $I_\Delta$ closest to $v_i(e)$. Observe that $\vert {v_i(e) - w_i(e)}\vert \leqslant \Delta$ and $\Vert \textbf{w}_i\Vert _\infty \leqslant 1$. Let ${\textbf {B}} \in \mathbb {Q}^{n \times n}$ be the Gram matrix defined by $\textbf{w}_1, \ldots , \textbf{w}_n$. The absolute difference of the determinant between ${\textbf {A}}$ and ${\textbf {B}}$ is bounded as shown below, whose proof is based on the application of Lemma 3.8. $\square$

Claim

For n d-dimensional vectors $\textbf{v}_1, \ldots , \textbf{v}_n$ such that $\Vert \textbf{v}_i\Vert _{\infty } \leqslant 1$ for all $i \in [n]$ and n d-dimensional vectors $\textbf{w}_1, \ldots , \textbf{w}_n$ constructed from $\textbf{v}_i$’s and $\Delta$ according to the procedure described above, let ${\textbf {A}}$ and ${\textbf {B}}$ be the Gram matrices defined respectively by $\textbf{v}_i$’s and $\textbf{w}_i$’s. Then, for any set $S \in {[n] \atopwithdelims ()k}$ for $k \leqslant d$, it holds that,

$$\begin{aligned} \vert {\det ({\textbf {A}} _S) - \det ({\textbf {B}} _S)}\vert \leqslant 3 \cdot d^{2d+1} \cdot \Delta . \end{aligned}$$

(5.33)

Moreover, the number of distinct vectors in the set $\{ \textbf{w}_1, \ldots , \textbf{w}_n \}$ is at most $(\frac{2}{\Delta } + 1)^d$.

Proof

To apply Lemma 3.8, we first bound the matrix norm of ${\textbf {A}}$, ${\textbf {B}}$, and ${\textbf {A}} -{\textbf {B}}$. The max norm of ${\textbf {A}}$ and ${\textbf {B}}$ can be bounded as follows:

$$\begin{aligned} \Vert {\textbf {A}} \Vert _{\max }&= \max _{i,j} \vert {A_{i,j}}\vert \leqslant \max _{i,j} \left\{ \sum _{e \in [d]} \vert {v_i(e) \cdot v_j(e)}\vert \right\} \leqslant d, \end{aligned}$$

(5.34)

$$\begin{aligned} \Vert {\textbf {B}} \Vert _{\max }&= \max _{i,j} \vert {B_{i,j}}\vert \leqslant \max _{i,j} \left\{ \sum _{e \in [d]} \vert {w_i(e) \cdot w_j(e)}\vert \right\} \leqslant d, \end{aligned}$$

(5.35)

where we used the fact that $\Vert \textbf{v}_i\Vert _{\infty } \leqslant 1$ and $\Vert \textbf{w}_i\Vert _{\infty } \leqslant 1$. For each $i \in [n]$ and $e \in [d]$, let $w_i(e) = v_i(e) + \Delta _{i,e}$ for some $\vert {\Delta _{i,e}}\vert \leqslant \Delta$. We then bound the absolute difference between $v_i(e) \cdot v_j(e)$ and $w_i(e) \cdot w_j(e)$ for each $i,j \in [n]$ and $e \in [d]$ as

$$\begin{aligned} \begin{aligned}&\vert {v_i(e) \cdot v_j(e) - w_i(e) \cdot w_j(e)}\vert \\&= \vert { v_i(e)\cdot v_j(e) - (v_i(e)+\Delta _{i,e})\cdot (v_j(e)+\Delta _{j,e}) }\vert \\&= \vert {\Delta _{i,e} \cdot v_j(e) + \Delta _{j,e} \cdot v_i(e) + \Delta _{i,e} \cdot \Delta _{j,e}}\vert \\&\leqslant 2\Delta + \Delta ^2 \leqslant 3 \Delta , \end{aligned} \end{aligned}$$

(5.36)

where we used the fact that $\Delta _{i,e} \leqslant \Delta \leqslant 1$. Consequently, the max norm of the difference between ${\textbf {A}}$ and ${\textbf {B}}$ can be bounded as

$$\begin{aligned} \begin{aligned} \Vert {\textbf {A}} -{\textbf {B}} \Vert _{\max }&= \max _{i,j} \vert {A_{i,j} - B_{i,j}}\vert \\&= \max _{i,j} \vert { \langle \textbf{v}_i, \textbf{v}_j \rangle - \langle \textbf{w}_i, \textbf{w}_j \rangle }\vert \\&\leqslant \sum _{e \in [d]} \vert {v_i(e) \cdot v_j(e) - w_i(e)\cdot w_j(e)}\vert \\&\leqslant 3d \Delta . \end{aligned} \end{aligned}$$

(5.37)

Calculation using Lemma 3.8 derives that for any set $S \in {[n] \atopwithdelims ()k}$ for $k \leqslant d$,

$$\begin{aligned} \begin{aligned}&\vert {\det ({\textbf {A}} _S) - \det ({\textbf {B}} _S)}\vert \\&\leqslant k \cdot \max \{ \Vert {\textbf {A}} _S\Vert _2, \Vert {\textbf {B}} _S\Vert _2 \}^{k-1} \cdot \Vert {\textbf {A}} _S - {\textbf {B}} _S\Vert _2 \\&\leqslant k \cdot \max \{ k \cdot \Vert {\textbf {A}} \Vert _{\max }, k \cdot \Vert {\textbf {B}} \Vert _{\max } \}^{k-1} \cdot k \cdot \Vert {\textbf {A}} - {\textbf {B}} \Vert _{\max } \\&\leqslant k \cdot (kd)^{k-1} \cdot k \cdot 3d \Delta \\&\leqslant 3 \cdot d^{2d+1} \cdot \Delta . \end{aligned} \end{aligned}$$

(5.38)

Since every vector $\textbf{w}_i$ is in $I_{\Delta }^d$, the number of distinct vectors in the set $\{\textbf{w}_1, \ldots , \textbf{w}_n\}$ is bounded by $\vert {I_{\Delta }^d}\vert = (\frac{2}{\Delta } + 1)^d$, completing the proof. $\square$

Our parameterized algorithm works as follows. Given the Gram matrix ${\textbf {A}} \in \mathbb {Q}^{n \times n}$ of n d-dimensional rational vectors $\textbf{v}_1, \ldots , \textbf{v}_n \in \mathbb {Q}^d$ and an error tolerance parameter $\varepsilon > 0$, we set the value of $\Delta$ as

$$\begin{aligned} \Delta \triangleq \frac{\lfloor \varepsilon ^{-1} \rfloor ^{-1}}{6 \cdot d^{2d+1}} = \varepsilon \cdot d^{{{\,\mathrm{\mathcal {O}}\,}}(d)}. \end{aligned}$$

(5.39)

Since $1/\Delta$ is a positive integer by definition, $I_{\Delta }$ is defined; we construct n d-dimensional rational vectors ${\textbf {W}} \triangleq \{\textbf{w}_1, \ldots , \textbf{w}_n\}$ in $\mathbb {Q}^d$ according to the procedure described above and the Gram matrix ${\textbf {B}} \in \mathbb {Q}^{n \times n}$ defined by ${\textbf {W}}$. We claim that Determinant Maximization on ${\textbf {B}}$ can be solved exactly in FPT time with respect to $\varepsilon ^{-1}$ and d. Observe that if ${\textbf {W}}$ includes at most $k-1$ distinct vectors, we can return an arbitrary set $S \in {[n] \atopwithdelims ()k}$ whose principal minor is always $\det ({\textbf {B}} _S) = 0$; therefore, we can safely consider the case $\vert {{\textbf {W}} }\vert \geqslant k$ only. According to the claim above, it holds that $\vert {{\textbf {W}} }\vert \leqslant (\frac{2}{\Delta } + 1)^d$. We can thus enumerate the set of k distinct vectors in ${\textbf {W}}$ in time

$$\begin{aligned} {(\frac{2}{\Delta } + 1)^d \atopwithdelims ()k} \leqslant \left( \frac{2}{\Delta } + 1\right) ^{dk} \leqslant \left( \frac{1}{\varepsilon }\right) ^{d^2} \cdot d^{{{\,\mathrm{\mathcal {O}}\,}}(d^3)}. \end{aligned}$$

(5.40)

Calculating the principal minor in ${{\,\mathrm{\mathcal {O}}\,}}(k^3)$ time for each Gram matrix defined by k distinct vectors, we can find the one, denoted $S_B^*$, having the maximum principal minor and return $S_B^*$ as a solution. The overall time complexity is bounded by $(1/\varepsilon )^{d^2} \cdot d^{{{\,\mathrm{\mathcal {O}}\,}}(d^3)} \cdot {{\,\mathrm{\mathcal {O}}\,}}(k^3) \cdot n^{{{\,\mathrm{\mathcal {O}}\,}}(1)} = \varepsilon ^{-d^2} \cdot d^{{{\,\mathrm{\mathcal {O}}\,}}(d^3)} \cdot n^{{{\,\mathrm{\mathcal {O}}\,}}(1)}$. We finally prove an approximation guarantee of $S_B^*$. Let $S^*$ be the optimal solution for Determinant Maximization on ${\textbf {A}}$; i.e., $S^* \triangleq {{\,\textrm{argmax}\,}}_{S \in {[n] \atopwithdelims ()k}} \det ({\textbf {A}} _S)$. By the claim above, we have for any set $S \in {[n] \atopwithdelims ()k}$,

$$\begin{aligned} \vert {\det ({\textbf {A}} _S) - \det ({\textbf {B}} _S)}\vert \leqslant 3\cdot d^{2d+1}\cdot \Delta \leqslant 3 \cdot d^{2d+1} \cdot \frac{\varepsilon }{6 \cdot d^{2d+1}} = \frac{\varepsilon }{2}. \end{aligned}$$

(5.41)

In particular, it holds that

$$\begin{aligned} \begin{aligned} \det ({\textbf {A}} _{S_B^*})&\geqslant \det ({\textbf {B}} _{S_B^*}) - \frac{\varepsilon }{2}&(\text {by Eq.} (5.41)) \\&\geqslant \det ({\textbf {B}} _{S^*}) - \frac{\varepsilon }{2}&\text {(by optimality of } S_B^* \text {)} \\&\geqslant \det ({\textbf {A}} _{S^*}) - \varepsilon .&\text {(by Eq.} (5.41)) \end{aligned} \end{aligned}$$

(5.42)

This completes the proof. $\square$

6 Open Problems

We investigated the W[1]-hardness of Determinant Maximization in the three restricted cases, improving upon the result due to Koutis [27]. Our parameterized hardness results leave a few natural open problems: For what kinds of sparse matrices is Determinant Maximization FPT? Is there a $(1-\varepsilon )$-factor (rather than “additive”) FPT-approximation algorithm with respect to the matrix rank? Quantitative lower bounds can be also proved; e.g., due to the lower bound of k -Sum [42], Determinant Maximization on tridiagonal matrices cannot be solved in $n^{o(k)}$ time, unless Exponential Time Hypothesis [24, 25] fails.