1 Introduction

An informative labeling scheme is an elegant formalization of the idea that identifiers of nodes in a network can be chosen to carry some additional information. Peleg [33] defined such a scheme for a function f defined on subsets of nodes to consist of two components: an encoder and a decoder. First, the encoder is given a description of the whole graph G and assigns a binary string to each of its nodes. The string assigned to a node is called its label. Second, the decoder is given the labels assigned to a subset of nodes W and needs to calculate f(W). This must be done without any information about the graph except for the given labels and the fact that G belongs to a specific family \({\mathscr {G}}\). The main goal is to make the labels as short as possible, that is, to minimize the maximum length of a label assigned to a node in G. A particularly clean example of a function f that one might want to consider in this model is adjacency. Kannan et al. [25] observed that an adjacency labeling scheme is related (in fact, equivalent) to a so-called vertex-induced universal graph, a purely combinatorial object that has been considered already in the 60s [32]. By now, we have a rich body of work concerning not only adjacency labeling [3, 4, 8,9,10, 13, 34], but also flow and connectivity labeling [22, 26, 28], Steiner tree labeling [33] and, most relevant to this paper, distance labeling.

Distance labeling. A distance labeling scheme is an assignment of labels, that is, binary strings, to all nodes of a graph G, so that the distance \(\delta _{G}(u,v)\) between any two nodes u, v can be computed from their labels. Unless specified otherwise, we consider unweighted graphs, so \(\delta _{G}(u,v)\) is the smallest number of edges on a path between u and v. The main goal is to make the labels as short as possible, that is, to minimize the maximum length of a label. The secondary goal is to optimize the query time, that is, the time necessary to compute \(\delta _{G}(u,v)\) given the labels of u and v. Distance labeling for general unweighted undirected graphs on n nodes was first considered by Graham and Pollak [21], who obtained labels consisting of \(O(n)\) bits. The decoding time was subsequently improved to \(O(\log \log n)\) by Gavoille et al. [17], then to \(O(\log ^{*}n)\) by Weimann and Peleg [35], and finally Alstrup et al. [6] obtained \(O(1)\) decoding time with labels of length \(\frac{\log 3}{2}n+o(n)\).Footnote 1 It is known that, for every labeling scheme, some labels must consist of at least \(\frac{n}{2}\) bits [25, 32], so achieving sublinear bounds is not possible in the general case.

Better schemes for distance labeling are known for restricted classes of graphs. As a prime example, trees admit a distance labeling scheme with labels of length \(\frac{1}{4}\log ^{2}n+o(\log ^{2}n)\) bits [16], and this is known to be tight up to lower-order terms [7]. In fact, any sparse graph admits a sublinear distance labeling scheme [5] (see also [18] for a somewhat simpler construction). However, the best known upper bound is still rather far away from the best known lower bound of \(\varOmega (\sqrt{n})\) [17], and recently Kosowski et al. [29] showed that, for a natural class of schemes based on storing the distances to a carefully chosen set of hubs, the best achievable hub-label size and distance-label size in sparse graphs may be \(\varTheta (n/2^{(\log n)^{c}})\) for some \(0< c < 1\).

Planar graphs. An important subclass of sparse graphs are planar graphs, for which Gavoille et al. [17] constructed a scheme with labels of length \(O(\sqrt{n}\log n)\). They also proved that in any such scheme some label must consist of \(\varOmega (n^{1/3})\) bits. In fact, their upper bound of \(O(\sqrt{n}\log n)\) bits is also valid for weighted planar graphs, under a natural assumption that the weights are bounded by a polynomial in n. The lower bound is based on designing a family of grid-like graphs on \(k \times k\) nodes and each edge being of length \(O(k)\). The family consists of \(2^{\varTheta (k^{2})}\) graphs and admits the following property: the pairwise distances of \(O(k)\) nodes on the boundaries uniquely determine the graph. This construction immediately implies that, for weighted planar graphs, there must be a node with label consisting of \(\varOmega (\sqrt{n})\) bits. However, for unweighted planar graphs, this only implies a lower bound of \(\varOmega (n^{1/3})\), as one needs to replace an edge of length \(\ell \) with \(\ell \) edges, thus increasing the size of the graph to \(k^{3}\). Abboud and Dahlgaard [1] extended this construction to show that, in fact, for graphs with the length of each edge bounded by a polynomial in n, there must be a node with label consisting of \(\varOmega (\sqrt{n}\log n)\) bits. Interestingly, they were able to use essentially the same construction to establish a strong conditional lower bound for dynamic planar graph algorithms. Unfortunately, there has been no progress in improving the construction for unweighted planar graphs.

Abboud et al. [2] provided a reasonable explanation for the lack of progress on improving the unweighted grid-like construction. They showed that for any unweighted planar graph G with k distinguished nodes, there is an encoding consisting of \(\tilde{O}(\min \{k^{2},\sqrt{k\cdot n}\})\) bits that allows calculating the distance between any pair of distinguished nodes. This implies that the approach based on fixing a family \({\mathscr {G}}\) of unweighted planar graphs, with each graph containing k distinguished nodes such that their pairwise distance uniquely determine \(G\in {\mathscr {G}}\), cannot result in a higher lower bound than \(\tilde{O}(\min \{k^{2},\sqrt{k\cdot n}\})/k=\tilde{O}(n^{1/3})\). This indicates that we should seek a significantly different proof technique or a better upper bound. Determining the complexity of distance labeling in unweighted planar graphs remains to be a major open problem in this area.

Our contribution. We present an improved upper bound for distance labeling of unweighted planar graphs on n nodes. We design a distance labeling scheme with labels consisting of \(O(\sqrt{n})\) bits. While this might be seen as “only” a logarithmic improvement, it provides a separation for distance labeling between unweighted and weighted planar graphs. Furthermore, we believe that lack of any progress on resolving the complexity of distance labeling in unweighted planar graphs in the last 16 years makes any asymptotic decrease desirable. Our method easily extends to undirected planar graphs with edges of length from [1, W], allowing us to decrease the label length from \(O(\sqrt{n}\log (nW))\) to \(O(\sqrt{n}\log W)\), and (unweighted) undirected graphs with genus g, decreasing the label length from \(O(\sqrt{ng}\log n)\) to \(O(\sqrt{ng}\log g)\) for graphs of genus at most g. Decoding time in our construction for planar unweighted graphs is \(O(\sqrt{n})\) (as in the previously known scheme of Gavoille et al. [17]), but we augment it with a mechanism that computes the distance in polylogarithmic time, however at the expense of increasing the label length to \(O(\sqrt{n\log n})\). Table 1 summarizes the current state of knowledge concerning this problem.

Table 1 Summary of known results concerning distance labeling of planar (and related) graphs on n nodes
Full size table

Techniques and roadmap. As in the previous scheme of Gavoille et al. [17], we apply a recursive separator decomposition. This scheme is presented in detail in Sect. 2. Our improvement is based on the following observation: if each separator is, in fact, a cycle, then we can shave off a factor of \(\log n\) by appropriately encoding the stored distances. For a triangulated graph, one can indeed always find a balanced cycle separator, but our graph does not have to be triangulated. In some applications, the solution to this problem is to simply triangulate with edges of sufficiently large length (as to not change the distance), but we need to keep the graph unweighted. In Sect. 3, we overcome this difficulty by designing a novel method of replacing each face of the original graph G with an appropriately chosen gadget to obtain a new unweighted graph \(G'\) with every face of length at most 4. The crucial property is that, for any two nodes that exist in both G and \(G'\), their distance in \(G'\) is at least the logarithm of their distance in G. So, while inserting the gadgets may decrease the distances, we are able to control this decrease. We believe that this might be of independent interest. To facilitate efficient decoding, in Sect. 5 we build on the distance oracle of Gawrychowski et al. [19]. This requires some tweaks in their point location structure to make it smaller at the expense of increasing the query time (but still keeping it polylogarithmic) and adjusting our scheme to balance the lengths of different parts of the label.

Computational model. When discussing the decoding time we assume the Word RAM model with words of length \(\log n\). A label of length \(\ell \) is packed in \(\lceil \ell /\log n\rceil \) words, and the decoder computing the distance between u and v can access in constant time any word from their labels. Standard arithmetic and Boolean operations on words are assumed to take constant time.

2 Previous Scheme

We briefly recap the scheme of Gavoille et al. [17]. Their construction is based on the notion of separators, that is, sets of nodes which can be removed from the graph so that every remaining connected component consists of at most \(\frac{2}{3}n\) nodes. By the classical result of Lipton and Tarjan [30] any planar graph on n nodes has such a separator consisting of \(O(\sqrt{n})\) nodes. Now the whole construction for a connected graph G proceeds as follows: find a separator S of G, and let \(G_1,G_2,\ldots \) be the connected components of \(G \setminus S\). The label of \(v \in G_i\) in G, denoted \(\ell _G(v)\), is composed of i, recursively constructed \(\ell _{G_i}(v)\), and the distances from v to every \(u\in S\) in G, denoted \(\delta _{G}(v,u)\), written down in the same order for every \(v\in G\). A label of \(v\in S\) consists of only the distances \(\delta _{G}(v,u)\) for all \(u\in S\) (also written down in the same order).

The space complexity of the whole scheme is dominated by the space required to store |S| distances, each consisting of \(\log n\) bits, resulting in \(O(\sqrt{n}\log n)\) bits in total. The bound of \(O(\sqrt{n})\) on the size of a separator is asymptotically tight. However, the total length of the label of \(v\in G\) (in bits) depends not on the size of the separator, but on the number of bits necessary to encode the distances from v to the nodes of the separator. If one can write \(S=(u_{1},u_{2},\ldots ,u_{|S|})\), where every \(u_{i}\) and \(u_{i+1}\) are adjacent (we implicitly assume \(u_{|S|+1}=u+1\)), then \(|\delta _{G}(v,u_{i})-\delta _{G}(v,u_{i+1})|\le 1\), for every \(i=1,2,\ldots ,|S|-1\), and consequently writing down \(\delta _{G}(v,u_{1})\) explicitly and then storing all the differences \(\delta _{G}(v,u_{i})-\delta _{G}(v,u_{i+1})\) takes only \(O(\sqrt{n})\) bits in total. It is known that if the graph is triangulated, there always exists a simple cycle separator [31], so for such graphs labels of length \(O(\sqrt{n})\) are enough. We show that, in fact, for any planar graph it is possible to select a separator so that the obtained sequence of differences is compressible. This is done by inserting some gadgets into every face of the graph.

3 Improved Scheme

We use the notion of weighted separators, as introduced in [31]. Consider a planar graph, where every node has a non-negative weight and all these weights sum up to 1. Then a set of nodes is a weighted separator if after removing these nodes the total weight of every remaining connected component is at most \(\frac{2}{3}\). We have the following well-known theorem (the result is in fact more general and allows assigning weights also to edges and faces, but this is not needed in our application):

Lemma 1

([31]) For every planar graph on n nodes having assigned non-negative weights summing up to 1, either there exists a node that is a weighted separator or there exists a simple cycle of length at most \(2\sqrt{2\lfloor d/2 \rfloor n}\) which is a weighted separator, where d is the maximum face size.

We will use the above tool to show our main technical lemma.

Lemma 2

Any planar graph G has a separator S, such that

$$\begin{aligned} \sum _{i=1}^{|S|-1} \left( 1+\log \delta _{G}(u_i,u_{i+1})\right) = O(\sqrt{n}) \end{aligned}$$

for some ordering \(u_{1},u_{2}\ldots ,u_{|S|}\) of all nodes of S.

Before proving the lemma, we first describe a family of subdivided cycles. A subdivided cycle on \(s\ge 3\) nodes, denoted \(D_s\), consists of a cycle \(C_s=(v_1,\ldots ,v_s)\) and possibly some auxiliary nodes. \(D_3\) and \(D_4\) are simply \(C_3\) and \(C_4\), respectively. For \(s>4\), we add \(\lceil \frac{s}{2} \rceil \) auxiliary nodes \(u_1,\ldots ,u_{\lceil \frac{s}{2} \rceil }\), and connect every \(v_i\) with \(u_{\lceil \frac{i}{2} \rceil }\). To complete the construction, we recursively build \(D_{\lceil \frac{s}{2} \rceil }\) and identify its cycle with \((u_1,\ldots ,u_{\lceil \frac{s}{2} \rceil })\). (An example of such a subdivided cycle on 10 nodes is shown in Fig. 1.) We have the following property.

Lemma 3

For any distinct \(u,v \in C_s\), \(\delta _{D_s}(u,v) \ge 1 + \log \delta _{C_s}(u,v)\).

Fig. 1
figure 1

A face of size 10 is transformed by replacing \(C_{10}\) with \(D_{10}\) containing 8 new auxiliary nodes

Full size image

Proof

We apply induction on s. It is easy to check that the lemma holds when \(s \le 4\), so we assume \(s \ge 5\). Let us denote \(\delta _{D_{s}}(u,v)=d'\) and \(\delta _{C_{s}}(u,v)=d\). We proceed with another induction on \(d'\). When \(d'=1\) then u and v must be neighbors on \(C_{s}\), so \(d=1\) and the claim holds. When \(d=1\) then \(d'=1\) (because we always have \(d'\le d\)) and the claim also holds. Now assume \(d',d \ge 2\) and consider a shortest path connecting u and v in \(D_{s}\). If it consists of only auxiliary nodes except for the endpoints u and v, then we consider the immediate neighbors of u and v on the path, denoted \(u'\) and \(v'\), respectively. As \(u'\) and \(v'\) are auxiliary nodes, they both must belong to the cycle \(C_{\lceil \frac{s}{2} \rceil }\) of \(D_{\lceil \frac{s}{2} \rceil }\), as no other auxiliary nodes are neighbours of non-auxiliary nodes. Next, we analyze the distance between \(u'\) and \(v'\) on \(C_{\lceil \frac{s}{2} \rceil }\). Every node of \(C_{\lceil \frac{s}{2} \rceil }\) is connected to at most two nodes of \(C_{s}\). Consequently, if there are t nodes strictly between \(u'\) and \(v'\) on \(C_{\lceil \frac{s}{2} \rceil }\), then there are at most \(2t+2\) nodes strictly between u and v on \(C_{s}\). Thus, the distance between \(u'\) and \(v'\) on \(C_{\lceil \frac{s}{2} \rceil }\) must be at least \(\lfloor \frac{d}{2} \rfloor \), as otherwise the distance between u and v on \(C_{s}\) would be at most \(2(\lfloor \frac{d}{2} \rfloor -2)+3<d\). This allows us to apply the inductive assumption applied with smaller \(\lceil \frac{s}{2} \rceil < s\) (and using \(d\ge 2\)):

$$\begin{aligned} d' \ge 2 + 1 + \log \lfloor d/2 \rfloor = 1 + \log (4\lfloor d/2 \rfloor ) > 1+\log d. \end{aligned}$$

Otherwise, let w be an intermediate node of the path that belongs to the cycle \(C_{s}\). Let \(\delta _{D_{s}}(u,w)=d_{0}'\) and \(\delta _{C_{s}}(u,w)=d_{0}\) and \(\delta _{D_{s}}(w,v)=d_{1}'\) and \(\delta _{C_{s}}(w,v)=d_{1}\). Because w is an intermediate node, we can apply the inductive assumption with the same s but smaller \(d'_{0},d'_{1}<d'\) to obtain \(d_{0}' \ge 1+\log d_{0}\) and \(d_{1}' \ge 1+\log d_{1}\). Then:

$$\begin{aligned} d'&= d'_{0}+d'_{1} \\&\ge 1 + \log d_{0} + 1 + \log d_{1}{} & {} \text {by the inductive assumption} \\&= 1 + \log (2d_{0}d_{1}) \\&\ge 1 + \log (d_{0}+d_{1}){} & {} 2xy\ge x+y\text { for any }x,y\ge 1 \\&\ge 1 + \log d{} & {} \text {by the triangle inequality} \end{aligned}$$

as required. \(\square \)

of Lemma 2

Let \(G'\) be the graph constructed from G by replacing every face (including the external face) with a subdivided cycle of appropriate size. More precisely, let \((v_{1},v_{2},\ldots ,v_{s})\) be a boundary walk of a face of G. Note that nodes \(v_{i}\) are not necessarily distinct. We create a subdivided cycle \(D_{s}\) and identify its cycle \(C_{s}\) with \((v_{1},v_{2},\ldots ,v_{s})\). Clearly \(G'\) is also planar and each of its faces is either a triangle or a square. Since any subdivided cycle has at most twice as many auxiliary nodes as cycle nodes and the lengths of all boundary walks sum up to twice the number of edges, which is at most \(3n-6\) (as G is planar, and without losing the generality simple), \(G'\) contains at most \(n' = n+4\cdot (3n-6) < 13n\) nodes.

We assign weights to nodes of \(G'\) so that every node also appearing in G has weight 1 and every new node has weight 0. By Lemma 1 either there exists a single node s that is a weighted separator or there exists a weighted simple cycle separator \(S'\) in \(G'\) of size at most \(2\sqrt{52 n}\). In the former case, s is also a weighted separator in G and there is nothing to prove. In the latter case, let \(S=S' \cap G\) be a separator in G. Because \(S'\) is a simple cycle separator, \(S=(u_{1},u_{2},\ldots ,u_{c})\), and \(u_{i}\) and \(u_{i+1}\) are incident to the same face f of G. The boundary walk of f, consisting of \(s_{i}\) nodes, has been identified with the cycle \(C_{s_{i}}\) of a copy of the subdivided cycle \(D_{s_{i}}\) such that \(S'\) connects \(u_{i}\) and \(u_{i+1}\) either directly or by visiting some auxiliary nodes of the copy of \(D_{s_{i}}\), for every \(i=1,2,\ldots ,c\) (we assume \(u_{c+1}=u_{1}\)). In either case, \(S'\) connects \(u_{i}\) and \(u_{i+1}\) with a path from \(v_{i}\) to \(v'_{i}\) in the copy of \(D_{s_{i}}\), thus:

$$\begin{aligned} \sum _i \delta _{D_{s_{i}}}(v_i,v'_{i}) \le |S'| = O(\sqrt{n}). \end{aligned}$$

By Lemma 3, \(\delta _{D_{s_{i}}}(v_i,v'_{i}) \ge 1+\log \delta _{C_{s_{i}}}(v_i,v'_{i})\), so altogether:

$$\begin{aligned} \sum _i (1+\log \delta _{G}(u_i,u_{i+1})) \le \sum _i (1+\log \delta _{C_{s_{i}}}(v_i,v'_{i})) = O(\sqrt{n}) \end{aligned}$$

as required. \(\square \)

While not relevant in this section, later we will need to verify that \(G'\) obtained from G in the proof of Lemma 2 is biconnected.

Lemma 4

If \(n\ge 4\) then \(G'\) is biconnected.

Proof

It is straightforward to verify that removing an auxiliary node cannot disconnect the graph. Consider a node u of G, and let \(v_{0},v_{1},\ldots ,v_{d-1}\) be its neighbors arranged in a clockwise order. We claim that \(v_{i}\) and \(v_{(i+1)\bmod d}\) are still connected in \(G'\) after removing u from \(G'\). Consider the face containing \(v_{i},u,v_{(i+1)\bmod d}\) as a part of the boundary walk. If the boundary walk is of size at least 5 then the artificial nodes guarantee the connectivity. When the boundary walk contains just one occurrence of u then the non-auxiliary nodes guarantee the connectivity after removing the only occurrence of u. The only remaining case is that the boundary walk is \(u,v_{i},u,v_{(i+1)\bmod d}\), but then there are no other edges in G and \(n\le 3\). \(\square \)

Now we proceed to the main result of this section:

Theorem 1

Any planar graph on n nodes admits a distance labeling scheme of length \(O(\sqrt{n})\).

Proof

We proceed as in the previously known scheme of size \(O(\sqrt{n}\log n)\), except that in every step we apply our Lemma 2. In more detail, to construct the label of every node \(v\in G\) we proceed as follows. First, we find a separator \(S=(u_{1},u_{2}\ldots ,u_{c})\) using Lemma 2. We have \(\sum _{i} (1+\log \delta _{G}(u_{i},u_{i+1})) = O(\sqrt{n})\), so in particular \(c=O(\sqrt{n})\) and \(\sum _{i=2}^{c}\log \delta _{G}(u_{i-1},u_{i}) = O(\sqrt{n})\). For every \(v\in G\) we encode its distances to all nodes of the separator as follows. We use the Elias \(\gamma \) code [14], which gives a prefix-free encoding of a number x using \(2\lceil \log x\rceil +1\) bits. Formally, this encoding assigns a bitstring \(\textsf{code}(x)\) to every number x. For every x, the length of \(\textsf{code}(x)\) is at most \(2\lceil \log x\rceil +1\). Additionally, for every \(x\ne y\), \(\textsf{code}(x)\) is not a prefix of \(\textsf{code}(y)\) (nor vice versa). We first encode \(\delta _{G}(v,u_1)\) using the Elias \(\gamma \) code. Then we encode the differences \(\delta _{G}(v,u_{i})-\delta _{G}(v,u_{i-1})\), for all \(i=2,\ldots ,c\), also using the Elias \(\gamma \) code and an extra bit to denote the sign. All encodings are concatenated, and by the prefix-free property given the concatenation we can recover all the distances. The total length of the concatenation is:

$$\begin{aligned} O(\sqrt{n}+\sum _{i=2}^{c}\log |\delta _{G}(v,u_{i})-\delta _{G}(v,u_{i-1})|). \end{aligned}$$

Consequently, by \(|\delta _{G}(v,u_{i})-\delta _{G}(v,u_{i-1})|\le \delta _{G}(u_{i-1},u_{i})\) and the properties of our separator the encoding takes \(O(\sqrt{n})\) bits. Second, for every node we store the name of its connected component of \(G\setminus S\) in \(O(\log n)\subseteq O(\sqrt{n})\) bits. Third, we recurse on every connected component of \(G\setminus S\) and append the obtained labels to the current labels. To calculate \(\delta _{G}(u,v)\), we first compute \(d=\min _{w\in S} (\delta _{G}(u,w)+\delta _{G}(w,v))\), extracting \(\delta _{G}(u,w)\) from the label of u and \(\delta _{G}(w,v)=\delta _{G}(v,w)\) from the label of v. Then, if u and v belong to the same connected component of \(G\setminus S\), we proceed recursively there and return the minimum of d and the recursively found distance in the connected component. The correctness is clear: either a shortest path between u and v is fully within one of the connected components, or it visits some \(w\in S\), and in such case we can recover \(\delta _{G}(u,w)+\delta _{G}(w,v)\) from the stored distances. The final size of every label is \(O(\sqrt{n}+\sqrt{\frac{2}{3}n}+\ldots )=O(\sqrt{n})\) bits. \(\square \)

4 Simple Extensions

In this section, we describe two simple extensions of Theorem 1. First, consider a planar graph G with edges of length from [1, W], for some \(W\ge 2\). Applying the scheme of Gavoille et al. [17] results in labels consisting of \(\varTheta (\sqrt{n}\log (nW))\) bits for this case, as on the topmost level of the recursion we need to store \(\varTheta (\sqrt{n})\) distances bounded by nW. We improve this to \(O(\sqrt{n}\log W)\).

Theorem 2

Any planar graph on n nodes with edges of length from [1, W], for \(W\ge 2\), admits a distance labeling scheme of length \(O(\sqrt{n}\log W)\).

Proof

We proceed as in proof of Theorem 1. On every level of the recursion, we find the separator S by considering an unweighted planar graph \(G_{1}\) obtained from G by disregarding the length of every edge. However, the encoded distances are computed in the original G. On the topmost level of the recursion, the total length of all these encoded distances is bounded by

$$\begin{aligned}&O(\sqrt{n}+\log (nW)+\sum _{i=2}^{c}\log \delta _{G}(u_{i-1},u_{i})) \\&\quad = O(\sqrt{n}+\log W+\sum _{i=2}^{c}\log (W\cdot \delta _{G_{1}}(u_{i-1},u_{i})))\\&\quad =O(\sqrt{n}+c\log W+\sum _{i=2}^{c}\log \delta _{G_{1}}(u_{i-1},u_{i})). \end{aligned}$$

which, by the choice of S in \(G_{1}\), this is \(O(\sqrt{n}\log W)\). Summing this over all levels of the recursion, we obtain the theorem. \(\square \)

The second extension concerns bounded-genus (unweighted) graphs. For a genus g graph on n nodes, Gavoille et al. [17] showed how to construct labels consisting of \(O(\sqrt{ng}\log n)\) bits. We improve this to \(O(\sqrt{ng}\log g)\).

Theorem 3

Any genus-g planar graph on n nodes admits a distance labeling scheme of length \(O(\sqrt{ng}\log g)\).

Proof

Let G be such a genus-g graph on n nodes, and consider its 2-cell embedding in a surface of genus g. Then, every face of G is homeomorphic to an open disc. We can assume that G is simple, that is, every face is incident to at least three edges, and so the number of edges is \(O(n+g)\). We obtain \(G'\) by inserting a copy of the subdivided cycle inside every face of G as in the proof of Lemma 2 while increasing the number of nodes to \(O(n+g)\) (by the bound on the number of faces of \(G'\)). Then, we apply the theorem of Hutchinson [23] to find a short non-contractible cycle. A non-contractible cycle is either separating and deleting it divides the graph into two graphs of strictly smaller genus, or non-separating and deleting it decreases the genus by at least one. The theorem states that, for any triangulated graph on n nodes, we can find such a cycle of length \(O(\sqrt{n/g}\log g)\). We cannot apply this directly, as our graph might have faces of size four. So, we temporarily triangulate \(G'\) to obtain \(G''\), apply the theorem on \(G''\) to find a short non-contractible cycle \(C''\), and then translate it to a walk \(C'\) in \(G'\) by routing along the faces, which increases its length only by a constant factor, so \(|C'|=O(\sqrt{(n+g)/g}\log g)\). Finally, we consider \(C=C'\cap G\). We can encode the distances from any \(v\in G\) to all nodes of C as described in the proof of Theorem 1 in \(O(\sqrt{(n+g)/g}\log g)\) bits. This encoding becomes part of the label of every node \(v\in G\) and allows us to compute the distance if there exists a shortest path visiting a node of C. If \(C''\) was a separating cycle then removing C from G separates it into two graphs \(G_{1},G_{2}\) with smaller genus. We recursively construct the label of every node of \(G_{1}\) and \(G_{2}\). The label of every node of C consists only of the encoding of the distances to all nodes of C. The label of every node of \(G\setminus C\) additionally contains its label in the corresponding \(G_{1}\) or \(G_{2}\), together with a single bit denoting whether the node belongs to \(G_{1}\) or \(G_{2}\). If \(C''\) was not separating then removing C from G decreases the genus. We repeat the reasoning on \(G\setminus C\), and obtain the label of every node of C and \(G{\setminus } C\) similarly as in the previous case, except that now there is no need for the single bit denoting whether the node belongs to \(G_{1}\) or \(G_{2}\). In the recursion, when \(g=0\) we obtain a planar graph and apply Theorem 1. To bound the overall length of a label obtained through this recursive construction, we notice that every node participates in at most one smaller instance of the same problem until it becomes either a part of the separator (and does not participate further) or a planar graph (when we apply Theorem 1). Each step of this process appends \(O(\sqrt{(n+g)/g}\log g)\) bits to the label, and then possibly we add \(O(\sqrt{n})\) bits in the last step. The overall length of a label is thus \(O(\sqrt{(n+g)g}\log g)\). If \(g\le n\) then this is already \(O(\sqrt{ng}\log g)\) as desired, and otherwise we can switch to an \(O(n)\)-bit distance labeling scheme for general unweighted graphs [6]. \(\square \)

5 Efficient Decoding

The drawback of the scheme from Theorem 1 is its high decoding time. Computing \(\delta _{G}(u,v)\) given \(\ell _{G}(u)\) and \(\ell _{G}(v)\) is done as follows. First, we iterate over \(w\in S\) and consider \(\delta _{G}(u,w)+\delta _{G}(v,w)\) as a possible distance, extracting \(\delta _{G}(u,w)\) from \(\ell _{G}(u)\) and \(\delta _{G}(v,w)\) from \(\ell _{G}(v)\). Then, we check if u and v belong to the same component \(G_{i}\), and if so recurse on \(\ell _{G_{i}}(u)\) and \(\ell _{G_{i}}(v)\). Even assuming that extracting any \(\delta _{G}(u,w)\) takes constant time, it is not clear how to avoid iterating over all \(w\in S\), so we cannot hope for anything faster than \(O(\sqrt{n})\). In this section we show how to overcome this difficulty by applying the machinery of Voronoi diagrams on planar graphs, introduced for computing the diameter of a planar graph in subquadratic time by Cabello [11]. Our method roughly follows the approach of Gawrychowski et al. [19] (also see [12]), but we need to make sure that the information can be distributed among the labels, and carefully adjust the parameters of the whole construction. We start with presenting the necessary definitions and tools.

r-divisions. A region R of G is an edge-induced subgraph of G. An r-division of G is a collection of regions such that each edge of G is in at least one region, there are \(O(n/r)\) regions, each region has at most r nodes and \(O(\sqrt{r})\) boundary nodes that belong to more than one region. We work with a fixed planar embedding of G, and all of its subgraphs, in particular the regions, inherit this embedding. A hole of a region R is a face that is not a face of G. An r-division with few holes has the additional property that each edge belonging to two regions is on a hole in each of them, and each region has \(O(1)\) holes.

Lemma 5

([27]) For a constant s, there is a linear-time algorithm that, for any biconnected triangulated planar embedded graph G and any \(r\ge s\), outputs an r-division of G with few holes.

The above theorem additionally guarantees that each region is connected and its boundary nodes are exactly the nodes incident to its holes.

Voronoi diagrams. Following the description in [19], let S be the nodes (called sites) incident to the external face h of an internally triangulated planar graph G. Note that while our goal is to consider unweighted graphs, Voronoi diagrams can be defined for weighted graphs, and indeed this is how we are going to use them. This allows us to perturb the weights to ensure that all shortest paths are unique, see e.g. [15]. In our case, we need to additionally verify that the perturbed weights are not too large, but the standard argument based on the Isolation Lemma shows that \(O(\log n)\) additional bits of accuracy are enough to this end.

Fig. 2
figure 2

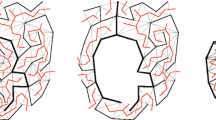
An example of Voronoi diagram with 4 sites (denoted with different colours) based on [19]), top left: \(\textsf{VD}(S,\omega )\), top right: \(\textsf{VD}_{0}\), bottom left: \(\textsf{VD}_{1}\), bottom right: \(\textsf{VD}^{*}(S,\omega )\)

Full size image

Each site \(u\in S\) has a weight \(\omega (u)\), defined as the distance from some node v of the larger graph to u, and the distance between a site \(u\in S\) and a node v, denoted by d(u, v), is defined as \(\omega (u)+\delta _{G}(u,v)\). The (additively) weighted Voronoi diagram of \((S,\omega )\) within G, denoted \(\textsf{VD}(S,\omega )\), is a partition of the nodes of G into pairwise disjoint sets, one set \(\textsf{Vor}(u)\) for every \(u\in S\). \(\textsf{Vor}(u)\) is called the cell of u and contains all nodes of G that are closer to u than any other site \(u'\). The standard perturbation as described above allows us to assume that this is well defined, that is, for every node v there is only one site u for which \(\omega (u)+\delta _{G}(u,v)\) achieves the minimum. We work with a dual representation of \(\textsf{VD}(S,\omega )\), denoted by \(\textsf{VD}^{*}(S,\omega )\), defined as follows. Let \(G^{*}\) be the dual of G, and \(\textsf{VD}_{0}\) is the subgraph of \(G^{*}\) containing the duals of all edges (u, v) of G such that u and v belong to different cells. Then, let \(\textsf{VD}_{1}\) be obtained from \(\textsf{VD}_{0}\) by contracting edges incident to vertices of degree 2 one-by-one as long as possible. A vertex of \(\textsf{VD}_{1}\) is called a Voronoi vertex, and is dual to a face f such that the nodes incident to f belong to at least three Voronoi cells. In particular, \(h^{*}\) is a Voronoi vertex. Finally, \(\textsf{VD}^{*}(S,\omega )\) is obtained from \(\textsf{VD}_{1}\) by replacing \(h^{*}\) by multiple copies, one for each incident edge. See Fig. 2 for an example. The complexity of \(\textsf{VD}^{*}(S,\omega )\) is \(O(|S|)\) and, assuming that every node belongs to its cell is a tree. This assumption is not necessarily true in the general case, as we could have \(\omega (s_{i})>\omega (s_{j})+\delta _{G}(s_{j},s_{i})\) for some different sites \(s_{i},s_{j}\). However, in our case the weighs \(\omega (s_{i})\) will be actually distances from the same node u in a larger graph, and hence before the perturbation we will necessarily have \(\omega (s_{i})\le \omega (s_{j})+\delta _{G}(s_{j},s_{i})\). Therefore, assuming that we perturb the weight of every edge by adding a strictly positive value, we will indeed guarantee that \(s_{i}\in \textsf{Vor}(s_{i})\). We will also assume that the graph is biconnected, so that the boundary walk of the external face is simple.

Point location. The main technical contribution of [19] is a point location structure for \(\textsf{VD}(S,\omega )\) that, given a node v, finds its cell in \(O(\log |S|)\) time, assuming constant-time access to certain primitives. We briefly describe the required primitives and then the high-level idea of this structure, but the reader is strongly advised to consult the original description.

For any site u, let \(T_{u}\) be the shortest path tree rooted at u. Additionally, for each face f other than h we add an artificial node \(v_{f}\) whose embedding coincides with the embedding of \(f^{*}\). In \(T_{u}\), \(v_{f}\) is a leaf connected with a zero-length edge to the node \(y_{f}\) incident to f that is closest to u. For any site u and node v, we might need to have access to the following information:

  1. 1.

    d(u, v),

  2. 2.

    for any face f, is v on the path in in \(T_{u}\) from u to \(v_{f}\), or left/rightFootnote 2 of this path.

If the goal is to build a global structure of size \(O(n^{1.5})\), such queries can be supported by storing, for every site u separately, the pre- and postorder number of every node in \(T_{u}\) (in particular, for v and \(v_{f}\)), together with the value of d(u, v) for every node v. In our case this is not possible, and we will explicitly describe which queries are required and how implement them.

Let \(s_{1},s_{2},\ldots ,s_{|S|}\) be the boundary walk of the external face containing every site. Recall that \(\textsf{VD}^{*}(S,\omega )\) is a tree with no vertices of degree 2. A centroid decomposition of such a tree T on n nodes is recursively defined as follows: we find a centroid \(u\in T\) such that removing u from T and replacing it with copies, one for each edge incident to u, results in a set of trees, each with at most \((n+1)/2\) edges, and repeat the reasoning on each of these trees. The construction terminates when the tree has no nodes of degree 3 or more (i.e. it consists of a single edge by the assumption of no degree-2 vertices). The point location structure consists of a centroid decomposition of \(\textsf{VD}^{*}(S,\omega )\).

In the query, the centroid decomposition of \(\textsf{VD}^{*}(S,\omega )\) is traversed starting from the root. In every step, we consider a centroid \(f^{*}\) of the current connected subtree \(T^{*}\) of \(\textsf{VD}^{*}(S,\omega )\). Removing \(f^{*}\) partitions \(T^{*}\) into \(T_{0}^{*}\), \(T_{1}^{*}\) and \(T_{2}^{*}\). Assuming that the graph is triangulated, there are three nodes \(y_{0},y_{1},y_{2}\) incident to f, where \(y_{i}\in \textsf{Vor}(s_{i_{j}})\). Let \(e_{j}^{*}\) be the edge of \(\textsf{VD}^{*}(S,\omega )\) incident to \(f^{*}\) that is on the boundary of the cells of \(s_{i_{j}}\) and \(s_{i_{j+1}}\), and let \(T_{j}^{*}\) contain \(e_{j}^{*}\). Finally, let \(p_{j}\) be the shortest path from site \(s_{j}\) to \(y_{i}\). We first need to find site \(s_{i_{j}}\) such that v is closer to site \(s_{i_{j}}\) than to sites \(s_{i_{j-1}}\) and \(s_{i_{j+1}}\). Next, we need to determine if v is to the left/right of \(p_{i_{j}}\). The first possibility is that the sought site s such that \(v\in \textsf{Vor}(s)\) is in fact \(s_{i_{j}}\). Otherwise, depending on whether v is to the left/right of \(p_{i_{j}}\), we recurse on \(T_{j+1}^{*}\) or \(T_{j}^{*}\), respectively. The depth of the recursion is of course \(O(\log |S|)\).

As explained in [19, Lemma 5], the invariant of the traversal is that all the boundary edges of the sought \(\textsf{Vor}(s)\) are contained in the current \(T^{*}\). This implies that the number of remaining possible sites s is bounded by the number of edges of \(T^{*}\). Further, let k be the depth of the current vertex in the centroid decomposition. We claim that all remaining possible sites s constitute \(O(k)\) contiguous segments in the natural cyclic order around h. This is proven by induction on k. Assume that the claim holds for the previous vertex at depth \(k-1\), and consider the next step. As described above, we recurse on either \(T_{j+1}^{*}\) or \(T_{j}^{*}\), for concreteness assume the latter case. We eliminate from further consideration all sites s such that not all boundary edges of \(\textsf{Vor}(s)\) are contained in \(T_{j}^{*}\). All such sites are between \(s_{i_{0}}\) and \(s_{i_{1}}\) in the natural cyclic order around h (note that some of these sites might have been already eliminated). Thus, at depth k the eliminated sites constitute at most k contiguous segments in the natural cyclic order around h, and the claim follows.

Bitvectors. Recall that in the proof of Theorem 1 we stored the differences \(\delta _{G}(v,u_{i})-\delta _{G}(v,u_{i-1})\), for \(i=2,3,\ldots ,c\), by concatenating their Elias \(\gamma \) encodings. Now we need to compute any prefix sum \(\delta _{G}(v,u_{i})-\delta _{G}(v,u_{1})\) in constant time. We will augment the concatenation of all Elias \(\gamma \) encodings with some small extra information and a rank structure allowing us to access the appropriate position in constant time. We first recall the interface of a rank/select structure.

Lemma 6

([24]) A bitvector B[1..n] can be augmented with o(n) extra bits so that the following queries can be answered in constant time: \(\textsf{rank}_{b}(i)\) that returns \(|\{j\le i: B[j]=b \}|\) for \(b\in \{0,1\}\) and \(\textsf{select}_{b}(i)\) that returns the position of the i-th occurrence of \(b\in \{0,1\}\) in B[1..n].

This allows us to implement the following mechanism.

Lemma 7

For any \(\epsilon >0\), given any sequence of integers \(\varDelta _{1},\varDelta _{2},\ldots ,\varDelta _{s}\), such that \(\sum _{i=1}^{j}\varDelta _{i}\in [-n,n]\) for every j, we can construct a structure consisting of \(O(n^{\epsilon }+\sum _{i=1}^{s}(1+\log \varDelta _{i}))\) bits that returns \(\sum _{i=1}^{j}\varDelta _{i}\), for any j, in constant time.

Proof

We start with concatenating the Elias \(\gamma \) encodings of all numbers \(\varDelta _{i}\) to obtain a bitvector \(E[1..\ell ]\), where \(\ell =O(\sum _{i=1}^{s}(1+\log \varDelta _{i}))\). Additionally, we construct a bitvector \(B[1..\ell ]\) in which we mark with a 1 the starting position of the encoding of every \(\varDelta _{i}\), and apply Lemma 6 on B. We partition the numbers into \(O(\ell /\log n)\) contiguous subsequences (called groups) with the following property: either the group consists of a single number, or the Elias \(\gamma \) encodings of the numbers in the group consist of at most \(\frac{\epsilon }{2} \log n\) bits in total. To see that such a partition exists, first designate every number with the Elias \(\gamma \) encoding consisting of more than \(\frac{\epsilon }{4}\log n\) bits to be in a separate group, there are no more than \(O(\ell /\log n)\) such numbers. To partition the remaining numbers, apply the following reasoning: a sequence of numbers \(\varDelta _{x},\varDelta _{x+1},\ldots ,\varDelta _{y}\) such that the Elias \(\gamma \) encoding of each number consists of at most \(\frac{\epsilon }{4}\log n\) bits can be greedily partitioned into a number of groups with the total length of the Elias \(\gamma \) encodings in each group belonging to \([\frac{\epsilon }{4}\log n,\frac{\epsilon }{2}\log n]\), and possibly one group with the total length less than \(\frac{\epsilon }{4}\log n\).

We create another bitvector \(C[1..\ell ]\) in which we mark with a 1 the starting position of the encoding of the first number in every group, and apply Lemma 6 on C. Additionally, we store a precomputed table for every possible group consisting of numbers with the total length of the Elias \(\gamma \) encodings not exceeding \(\frac{\epsilon }{2}\log n\). A description of such a group consists of at most \(\frac{\epsilon }{2}\log n\) bits, and can be represented with two numbers: the length \(\ell \) and an \(\ell \)-bit number. The table is first indexed by \(\ell \in \{0,\ldots ,\frac{\epsilon }{2}\log n\}\) and then a number from \(\{0,2^{\frac{\epsilon }{2}\log n}-1\}\) corresponding to a possible group. For each such group, the table stores the prefix sums of all its prefixes in an array of at most \(\frac{\epsilon }{2}\log n\) numbers consisting of \(\log n\) bits each. This allows us to retrieve the prefix sum of any prefix in constant time, assuming that we have \(\ell \) and the \(\ell \)-bit number corresponding to the concatenated Elias \(\gamma \) encodings. The table is stored in \(O(\frac{\epsilon }{2}\log n \cdot n^{\epsilon /2}\cdot \frac{\epsilon }{2}\log ^{2} n)=O(n^{\epsilon })\) bits.

Finally, we store the binary encoding of every \(\sum _{i=1}^{j}\varDelta _{i}\) such that \(\varDelta _{j}\) is the last number of its group. Each encoding consists of \(1+\log n\) bits, and the encodings are concatenated one after another using \(O(\ell /\log n)(1+\log n) = O(\ell )\) bits in total. This finishes the description of the structure.

To compute \(\sum _{i=1}^{j}\varDelta _{i}\), we first use rank/select queries on \(B[1..\ell ]\) and \(C[1..\ell ]\) to determine which group contains \(\varDelta _{j}\), and the offset of \(\varDelta _{j}\) in its group. In more detail, we first use a select query on \(B[1..\ell ]\) to determine the starting position of the encoding of \(\varDelta _{j}\). Next, we use a rank query on \(C[1..\ell ]\) to determine its group, and with another select query on \(C[1..\ell ]\) we determine the starting position of the encoding of the first number in that group. Finally, a rank query on \(B[1..\ell ]\) allows us to translate the starting position to the index of the first number in the group, and consequently the offset of \(\varDelta _{j}\) in its group. Then, if \(\varDelta _{j}\) is the last number in its group, we return the precomputed partial sum. Otherwise, we retrieve the precomputed prefix sum \(\sum _{i=1}^{j'}\varDelta _{i}\), where \(\varDelta _{j'}\) is the last number in the previous group. This needs to be increased by the appropriate prefix sum of the group of \(\varDelta _{j}\), which can be retrieved from the precomputed table in constant time. \(\square \)

Having gathered all the technical ingredients, we are now ready to describe a modification of the proof of Theorem 1 that allows us to guarantee polylogarithmic decoding time. We first describe the high-level idea, then highlight two technical difficulties and proceed with a detailed description.

We would like to apply reasoning from the proof of Theorem 1 to find a balanced Jordan curve separator \(S=(u_{1},u_{2},\ldots ,u_{c})\) in G with the property that the distances in G from a node u to all nodes in S can be encoded in \(O(\sqrt{n})\) bits. S partitions G into the external part \(G_{ext}\) and the internal part \(G_{int}\), and we want to augment the labels with enough information so that, given \(\ell _{G}(v)\) and \(\ell _{G}(v')\), we can compute \(\delta _{G}(v,v')\) in polylogarithmic time if there is a shortest path from v to \(v'\) that visits some node of S (this is always the case when \(v\in G_{int}\) and \(v'\in G_{ext}\)). By repeating the reasoning on \(G_{ext}\) and \(G_{int}\) recursively, this allows us to compute any \(\delta _{G}(v,v')\). The natural idea would be to proceed as follows when constructing the label \(\ell _{G}(v)\). First, define a Voronoi diagram of \(G_{int}\) by setting the weight of each node \(u_{i}\) to be \(\delta _{G}(v,u_{i})\). Then, store its point location structure that allows us to efficiently minimize \(\delta _{G}(v,u_{i})+\delta _{G_{ext}}(u_{i},v')\) (which is equal to the sought \(\delta _{G}(v,v')\)). However, this takes too much space, as the point location structure is a tree on \(c=\varTheta (\sqrt{n})\) nodes, and it appears that we need to store in \(\ell _{G}(v)\) a constant number of integers consisting of \(\log n\) bits for each node of this tree. To overcome this, one might try to store only the top part of the centroid decomposition corresponding to subtrees of sufficiently large size, say \(\log n\). Then we can afford to store a description of this top part in \(\ell _{G}(v)\), and it can be used to either find the nearest site, or narrow down the set of remaining sites to \(O(\log n)\). However, this still requires some information about \(v'\), and in particular we need its position in every \(T_{u_{i}}\) (there is no clear way of how to restrict the number of sites \(u_{i}\) for which such information needs to be stored, as \(v'\) is oblivious to v, and different nodes v might need to access different sites when traversing their top parts of the centroid decomposition). Therefore, we need a more complex approach that adds \(O(\sqrt{n\log n})\) bits to every label.

The modified construction proceeds as follows. \(G'\) is biconnected but not necessarily triangulated, as there might be faces of length 4. We triangulate \(G'\) to obtain \(G''\), and then apply Lemma 5 to obtain an r-division, with some r that will be chosen at the end as to optimise the overall size of the labels. By the properties of an r-division, there are \(O(n/r)\) regions. Each region R contains \(O(\sqrt{r})\) boundary nodes incident to \(O(1)\) holes. The boundary walk \((u_{1},u_{2},\ldots ,u_{c})\) of every hole h of R is a (not necessarily simple) cycle in \(G''\), and by the construction of \(G''\) we can find a walk \((u'_{1},u'_{2},\ldots ,u'_{c'})\) in \(G'\) that contains \((u_{1},u_{2},\ldots ,u_{c})\) as a subsequence, and \(c'=O(c)=O(\sqrt{r})\). The r-division of \(G''\) naturally induces an r-division of \(G'\), and we will refer to \((u'_{1},u'_{2},\ldots ,u'_{c'})\) as a boundary walk of h. Note that because we have defined the r-division by applying Lemma 5 to \(G''\), some nodes \(u'_{i}\) might not belong to R, and we do not guarantee that all nodes incident to a hole are boundary nodes.

The label of every node v of G consists of two asymmetric parts. Let h be a hole of a region R, and \((u'_{1},u'_{2},\ldots ,u'_{c'})\) a boundary walk of h, where \(c'=O(\sqrt{r})\). Furthermore, let \((u''_{1},u''_{2},\ldots ,u''_{c''})\) be a subsequence of \((u'_{1},u'_{2},\ldots ,u'_{c'})\) consisting of the nodes of G. By the reasoning from the proof of Theorem 1, we have \(\sum _{i}(1+\log \delta _{G}(u''_{i},u''_{i-1}))=O(\sqrt{r})\). The first part of the label of v in G encodes \(\delta _{G}(v,u''_{1})\) in \(O(\log n)\) bits, and then the differences \(\delta _{G}(v,u''_{i})-\delta _{G}(v,u''_{i-1})\) using Lemma 7. This takes \(O(\log n + \sqrt{r})\) bits for every hole by setting \(\epsilon < 1/2\), so \(O(n/\sqrt{r})\) bits in total for all R and h. If \(v'\) is a boundary node of R incident to a hole h then we store the identity of R and h in the label of \(v'\) (there could be multiple such pairs R and h, we choose any of them), together with the position of any occurrence of \(v'\) in \((u''_{1},u''_{2},\ldots ,u''_{c''})\). This is already enough to determine \(\delta _{G}(v,v')\) in constant time for any boundary node \(v'\). Otherwise, \(v'\) belongs to exactly one region R, and either v is not a boundary node and belongs to the same region R or a shortest path from v to \(v'\) goes through one of the boundary nodes of R. To take the former case into the account, we consider the connected components of the subgraph of G consisting of the non-boundary nodes of R. Each such node stores the identity of its component in \(O(\log n)\) bits, so that we can verify if v and \(v'\) belong to the same connected component and recurse there if so (that is, the whole construction is repeated on every connected component, and the resulting label is a concatenation of the labels defined in the subsequent steps of the recursion). To deal with the latter case, we need to show how to find the shortest path in G from v to \(v'\) that first goes from v to a boundary node u of R and then goes to \(v'\) without visiting any other boundary node (note that this might happen even when v and \(v'\) belong to the same connected component). We focus on this in the remaining part of the description.

Consider a region R and its hole h. We make h the external face, triangulate the non-external faces, and make the weight of every edge that does not belong to G infinite to obtain a weighted graph \(R'\) (we also perturb the weights of all edges in \(R'\) to make the shortest paths unique). Let \(u_{1},u_{2},\ldots \) be the boundary nodes of R incident to h. We construct the Voronoi diagram of the obtained weighted graph \(R'\) with sites \(u_{1},u_{2},\ldots \), setting the weight of every \(u_{i}\) to be its distance from v in G. Storing the centroid decomposition of this Voronoi diagram would take \(O(\sqrt{r})\) words, which is too much. Instead, we store its top part obtained by stopping as soon as the size of the current subtree is less than B, for some \(B=\mathop {\textrm{polylog} {\,(}}n)\) that will be chosen at the end as to optimise the overall size of the labels (while keeping the query time polylogarithmic). The size of this top part is \(O(\sqrt{r}/B)\) by the following lemma.

Lemma 8

Consider the centroid decomposition of a bounded-degree tree T and a parameter b. The decomposition contains \(O(|T|/b)\) subtrees of size less than b obtained by choosing a centroid in a subtree of size at least b.

Proof

The decomposition can be naturally interpreted as a tree \({\mathscr {T}}\), with every node corresponding to a subtree obtained during the process. The leaves of \({\mathscr {T}}\) correspond to single edges of T, and internal nodes of \({\mathscr {T}}\) correspond to larger subtrees. The weight w(u) of \(u\in {\mathscr {T}}\) is the number of leaves in its subtree (equal to the size of the corresponding subtree of T), and for each child v we have \(w(v)\le (w(u)+1)/2\). Because the degree of T is bounded by a constant, it is enough to count \(u\in {\mathscr {T}}\) such that \(w(u) \ge b\); we call such nodes heavy. There are clearly at most \((|T|+1)/b\) heavy nodes with no heavy children, as their subtrees are disjoint. This also bounds the number of heavy nodes with more than one heavy child. It remains to bound the number of heavy nodes u with exactly one heavy child v. However, such u must have some non-heavy children \(v_{1},v_{2},...\) of total weight at least \(b-1\), as \(w(v) \le (w(u)+1)/2\) and \(b\le w(v)\) so \(b-1 \le w(u)-w(v)\) and \(w(u)-w(v)=w(v_{1})+w(v_{2})+\ldots \). so there are no more than \(|T|/(b-1)\) such nodes u. Overall, this is \(O(|T|/b)\) as claimed. \(\square \)

For each leaf in the top part of the decomposition, we store \(O(\log n)\) contiguous segments of the sites that might be relevant.Footnote 3 This takes \(O(\sqrt{r}/B\cdot \log ^{2}n)\) bits. For every non-leaf, we have a centroid \(f^{*}\) used for deciding where to descend. We store the weights \(\omega (s_{i_{j}})\) of the three relevant sites, and the preorder number of every \(y_{j}\) in its corresponding shortest path tree \(T_{s_{j}}\). This takes \(O(\sqrt{r}/B\cdot \log n)\) bits. Summed over all regions R and holes h, this is \(O(n/(\sqrt{r}B)\log ^{2}n)\) bits per node.

To use the centroid decomposition, we need to store enough information in the label of \(v'\) as to be able to compute any \(\delta _{R'}(u_{i},v')\) in constant time. Recall that for a non-boundary node \(v'\) we have exactly one relevant R and a constant number of Voronoi diagrams corresponding to the holes of R. Therefore, because there are only \(O(\sqrt{r})\) sites in every Voronoi diagram, we can afford to store every \(\delta _{R'}(u_{i},v')\) in binary using \(O(\sqrt{r}\log n)\) bits overall. Additionally, \(v'\) stores its preorder number in the shortest path tree rooted at every \(T_{u_{i}}\), this also takes \(O(\sqrt{r}\log n)\) bits.

To compute \(\delta _{G}(v,v')\), we consider every hole h of the unique region R containing \(v'\). We first navigate through the stored top part of the centroid decomposition. In every step, we need to first determine the closest site \(s_{i_{j}}\). This is possible as we know every weight \(\omega (s_{i_{j}})\) and distance \(\delta _{R'}(s_{i_{j}},v')\). Next, we decide where to descend by checking if \(v'\) is to left/right of the path \(p_{s_{j}}\), this is possible using the stored preorder numbers of v and \(y_{j}\) in \(T_{s_{j}}\). After reaching a leaf in the top part of the centroid decomposition, we simply consider the remaining at most B possible sites one-by-one. In this last step, we use the distances in the whole G, that is, \(\delta _{G}(v,s_{i_{j}})\) and \(\delta _{G}(v',s_{i_{j}})\). Overall, this takes \(O(\log n)\) to traverse the top part, and then \(O(B)\) for a leaf. Finally, if v and \(v'\) belong to the same connected component we recurse there. Overall, the decoding time is \(O(B\cdot \log n)\). The total length of every label is:

$$\begin{aligned} O(n/\sqrt{r}+n/(\sqrt{r}B)\log ^{2}n+O(\sqrt{r}\log n) \end{aligned}$$

which is minimized by choosing \(r=n/\log n\) and then \(B=\log ^{2}n\) to obtain the final theorem.

Theorem 4

Any planar graph on n nodes admits a distance labeling scheme of length \(O(\sqrt{n\log n})\) with \(O(\log ^{3}n)\) decoding time.