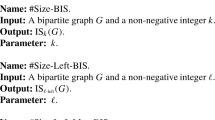Parameterised Counting in Logspace

Abstract

Logarithmic space-bounded complexity classes such as $\textbf{L}$ and $\textbf{NL}$ play a central role in space-bounded computation. The study of counting versions of these complexity classes have lead to several interesting insights into the structure of computational problems such as computing the determinant and counting paths in directed acyclic graphs. Though parameterised complexity theory was initiated roughly three decades ago by Downey and Fellows, a satisfactory study of parameterised logarithmic space-bounded computation was developed only in the last decade by Elberfeld, Stockhusen and Tantau (IPEC 2013, Algorithmica 2015). In this paper, we introduce a new framework for parameterised counting in logspace, inspired by the parameterised space-bounded models developed by Elberfeld, Stockhusen and Tantau. They defined the operators $\textbf{para}_{\textbf{W}}$ and $\textbf{para}_\beta$ for parameterised space complexity classes by allowing bounded nondeterminism with multiple-read and read-once access, respectively. Using these operators, they characterised the parameterised complexity of natural problems on graphs. In the spirit of the operators $\textbf{para}_{\textbf{W}}$ and $\textbf{para}_\beta$ by Stockhusen and Tantau, we introduce variants based on tail-nondeterminism, $\textbf{para}_{{\textbf{W}}[1]}$ and $\textbf{para}_{\beta {\textbf{tail}}}$. Then, we consider counting versions of all four operators and apply them to the class $\textbf{L}$. We obtain several natural complete problems for the resulting classes: counting of paths in digraphs, counting first-order models for formulas, and counting graph homomorphisms. Furthermore, we show that the complexity of a parameterised variant of the determinant function for (0, 1)-matrices is $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$-hard and can be written as the difference of two functions in $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$. These problems exhibit the richness of the introduced counting classes. Our results further indicate interesting structural characteristics of these classes. For example, we show that the closure of $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$ under parameterised logspace parsimonious reductions coincides with $\#\textbf{para}_\beta \textbf{L}$. In other words, in the setting of read-once access to nondeterministic bits, tail-nondeterminism coincides with unbounded nondeterminism modulo parameterised reductions. Initiating the study of closure properties of these parameterised logspace counting classes, we show that all introduced classes are closed under addition and multiplication, and those without tail-nondeterminism are closed under parameterised logspace parsimonious reductions. Finally, we want to emphasise the significance of this topic by providing a promising outlook highlighting several open problems and directions for further research.

1 Introduction

Parameterised complexity theory, introduced by Downey and Fellows [1], takes a two-dimensional view on the computational complexity of problems and has revolutionised the algorithmic world. Two-dimensional here refers to the fact that the complexity of a parameterised problem is analysed with respect to the input size n and a parameter k associated with the given input as two independent quantities. The notion of fixed-parameter tractability is the proposed notion of efficient computation. A parameterised problem is fixed-parameter tractable (fpt, or in the class $\textbf{FPT}$) if there are a computable function f and a deterministic algorithm deciding it in time $f(k)\cdot n^{O(1)}$ time for any input of length n with parameter k. The primary notion of intractability in this setting is captured by the -hierarchy.

Since its inception, the focus of parameterised complexity theory has been to identify parameterisations of $\textbf{NP}$-hard problems that allow for efficient parameterised algorithms, and to address structural aspects of the classes in the -hierarchy and related complexity classes [2]. This led to the development of machine-based and logical characterisations of parameterised complexity classes (see the book by Flum and Grohe [2] for more details). While the structure of classes in hierarchies such as the -hierarchy and the related -hierarchy is well understood, a parameterised view of parallel and space-bounded computation lacked attention.

In 2013, Elberfeld et al. [3, 4] focused on parameterised space complexity classes and initiated the study of parameterised circuit complexity classes. In fact, they introduced parameterised analogues of deterministic and nondeterministic logarithmic space-bounded classes. The machine-based characterisation of (the class of problems that are fpt-reducible to a certain weighted circuit satisfiability question), and the type of access to nondeterministic choices (multi-read or read-once) led to two different variants of parameterised logspace (para-logspace), namely, $\textbf{para}_{\textbf{W}}\textbf{L}$ and $\textbf{para}_\beta \textbf{L}$. Elberfeld et al. [4] obtained several natural complete problems for these classes, such as parameterised variants of reachability in graphs.

Bannach, Stockhusen and Tantau [5] further studied parameterised parallel algorithms. They used colour coding techniques [6] to obtain efficient parameterised parallel algorithms for several natural problems. A year later, Chen and Flum [7] proved parameterised lower bounds for $\mathbf {AC^{0}}$ by adapting circuit lower bound techniques.

Apart from decision problems, counting problems have found a prominent place in complexity theory. Valiant [8] introduced the notion of counting complexity classes that capture natural counting problems such as counting the number of perfect matchings in a graph, or counting the number of satisfying assignments of a CNF formula. Informally, $\#\textbf{P}$ (resp., $\#\textbf{L}$) consists of all functions $F:\{0,1\}^*\rightarrow \mathbb {N}$ such that there is a nondeterministic Turing machine (NTM) running in polynomial time (resp., logarithmic space) in the input length whose number of accepting paths on every input $x\in \{0,1\}^*$ is equal to F(x). Valiant’s theory of $\#\textbf{P}$-completeness led to several structural insights into complexity classes around $\textbf{NP}$ and interactive proof systems, as well as to the seminal result of Toda [9].

While exact counting problems in $\#\textbf{P}$ stayed in the focus of research for long, the study of the determinant by Damm [10], Vinay [11], and Toda [12] established that the complexity of computing the determinant of an integer matrix characterises the class $\#\textbf{L}$ up to a closure under subtraction. Allender and Ogihara [13] analysed the structure of complexity classes based on $\#\textbf{L}$. The importance of counting classes based on logspace-bounded Turing machines (TMs) was further established by Allender, Beals and Ogihara [14]. They characterised the complexity of testing feasibility of linear equations by a class which is based on $\#\textbf{L}$. Beigel and Fu [15] then showed that small depth circuits built with oracle access to $\#\textbf{L}$ functions lead to a hierarchy of classes which can be seen as the logspace version of the counting hierarchy. In a remarkable result, Ogihara [16] showed that this hierarchy collapses to the first level. Further down the complexity hierarchy, Caussinus et al. [17] introduced counting versions of $\mathbf {NC^{1}}$ based on various characterisations of $\mathbf {NC^{1}}$. The counting and probabilistic analogues of $\mathbf {NC^{1}}$ exhibit properties similar to their logspace counterparts [18]. Moreover, counting and gap variants of the class $\mathbf {AC^{0}}$ were defined by Agrawal et al. [19].

The theory of parameterised counting classes was pioneered by Flum and Grohe [20] as well as McCartin [21]. The class is the counting analogue of and consists of all parameterised counting problems that reduce to the problem of counting k-cliques in a graph. Flum and Grohe [20] proved that counting cycles of length k is complete for . Curticapean [22] further showed that counting matchings with k edges in a graph is also complete for . These results led to several remarkable completeness results and new techniques (see, e.g., the works of Curticapean [23, 24], Curticapean, Dell and Marx [25], Jerrum and Meeks [26], Brand and Roth [27], as well as recent advances [28, 29]).

Motivation Given the rich structure of logspace-bounded counting complexity classes, studying parameterised variants of these classes is the next logical step to obtain a finer classification of counting problems.

A theory of para-logspace counting did not exist before. We wanted to overcome this defect to understand further the landscape of counting problems with decision versions in para-logspace-based classes. Our new framework allows us to classify many of these problems more precisely. In this article, we define counting classes inspired by the parameterised space complexity classes introduced by Elberfeld et al. [3, 4].

In the realm of space-bounded computation, different manners in which nondeterministic bits are accessed lead to different complexity classes. For example, the standard definition of $\textbf{NL}$ implicitly gives the corresponding NTMs only read-once access to their nondeterministic bits [30]: nondeterminism is given only in the form of choices between different transitions. This means that nondeterministic bits are not re-accessible by the machine later in the computation. When instead using an auxiliary read-only tape for these bits and allowing for multiple passes on it, one obtains the class $\textbf{NP}$. This is due to the fact that ${\textbf {SAT}}$ is $\textbf{NP}$-complete with respect to logspace many-one reductions [30], and that one can evaluate a CNF formula in deterministic logspace even when the assignment is given on a read-only tape. However, polynomial time-bounded NTMs still characterise $\textbf{NP}$ even when the machine is allowed to do only one pass on the nondeterministic bits as they can simply store all nondeterministic bits on the work-tape. In consequence, it is very natural to investigate whether the distinction between read-once and unrestricted access to nondeterministic bits leads to new insights in our setting.

With parameterisation as a means for a finer classification, Stockhusen and Tantau [3] defined nondeterministic logarithmic space-bounded computation based on how (unrestricted or read-once) the nondeterministic bits are accessed. Based on this distinction, they defined two operators: $\textbf{para}_{\textbf{W}}$ (unrestricted) and $\textbf{para}_\beta$ (read-once). Their study led to many compelling natural problems that characterise the power of logspace-bounded nondeterministic computations in the parameterised setting. Thereby, a rich structure of computational power based on the restrictions on the number of reads of the nondeterministic bits was exhibited.

In this article, we additionally differentiate based on when—unrestricted or in the tail of the computation—the nondeterministic bits are accessed. Intuitively, tail-nondeterminism means that all nondeterministic bits are read at the end of the computation, and k-boundedness limits the number of these nondeterministic bits to $f(k)\cdot \log |x|$ many for all inputs (x, k). The concept of tail-nondeterminism allowed to capture the parameterised complexity class —via tail-nondeterministic, k-bounded machines—and thereby relates to many interesting problems such as searching for cliques [2, Thm. 6.1], independent sets [2, Cor. 6.2], homomorphisms [2, Ex. 6.4], and evaluating conjunctive queries [2, Ex. 6.9]. Contrarily, the complexity class is characterised via at most $f(k)\cdot \log n$ nondeterministic steps that can occur anytime during the computation [31]. In this way, the restriction to tail-nondeterminism makes the difference between and , the two most prominent nondeterministic classes in the parameterised world. This motivates our study of the impact of tail-nondeterminism in the setting of our comparatively small classes, leading to the new operators $\textbf{para}_{{\textbf{W}}[1]}$ and $\textbf{para}_{\beta {\textbf{tail}}}$.

Studying counting complexity often improves the understanding of related classical problems and classes (e.g., Toda’s theorem [9]). With regard to space-bounded complexity, there are several characterisations of logspace-bounded counting classes in terms of natural problems. For example, counting paths in directed graphs is complete for $\#\textbf{L}$, and checking if an integer matrix is singular or not is complete for the class $\mathbf {C_=} \textbf{L}$ (see Allender et al. [14]). Testing if a system of linear equations is feasible or not can be done in $\textbf{L}$ with queries to any complete language for $\mathbf {C_=} \textbf{L}$.

Moreover, two hierarchies built over counting classes for logarithmic space collapse either to the first level [16] or to the second level [14]. Apart from this, the separation of various counting classes defined in terms of logarithmic space computations remains widely open. For example, it is not known whether the class $\mathbf {C_=} \textbf{L}$ is closed under complementation.

We consider different parameterised variants of the logspace-bounded counting class $\#\textbf{L}$ to give a new perspective on its fine structure.

Results We introduce counting variants of parameterised space-bounded computation. More precisely, we define natural counting counterparts for the parameterised logspace complexity classes defined by Stockhusen and Tantau [3]. By also considering tail-nondeterminism in the setting of the resulting classes, we obtain four different variants of parameterised logspace counting classes, namely, $\#\textbf{para}_{\textbf{W}}\textbf{L}, \#\textbf{para}_\beta \textbf{L}, \#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$, and $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$. We show that $\#\textbf{para}_{\textbf{W}}\textbf{L}$ and $\#\textbf{para}_\beta \textbf{L}$ are closed under para-logspace parsimonious reductions and that all four of our new classes are closed under addition and multiplication.

Furthermore, we develop a complexity theory in the setting of parameterised space-bounded counting by obtaining natural complete problems for the new classes. We introduce variants of the problem of counting walks of parameter-bounded length that are complete for the classes $\#\textbf{para}_\beta \textbf{L}$ (Theorems 14, 15 and 18) and $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$ (Theorem 16). Since the same problem is shown to be complete for both $\#\textbf{para}_\beta \textbf{L}$ and $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$, we get the somewhat surprising result that the closure of $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$ under para-logspace parsimonious reductions coincides with $\#\textbf{para}_\beta \textbf{L}$ (Corollary 17). Also, we show that a parameterised version of the problem of counting homomorphisms from coloured path structures to arbitrary structures is complete for $\#\textbf{para}_\beta \textbf{L}$ with respect to para-logspace parsimonious reductions (Theorem 26).

Afterwards, we study variants of the problem of counting satisfying assignments to free first-order variables in a quantifier-free $\textrm{FO}$-formula. We identify complete problems for the classes $\#\textbf{para}_\beta \textbf{L}$ and $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ in this context. More specifically, counting satisfying assignments to free first-order variables in a quantifier-free formula with relation symbols of bounded arity and the syntactical locality of the variables in the formula being restricted ($p\text{- }\#\textrm{MC}({\varSigma }_{0}^{r\text {-local}})_a$) is shown to be complete for the classes $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$ and $\#\textbf{para}_\beta \textbf{L}$ with respect to para-logspace parsimonious reductions (Theorem 21). When there is no restriction on the locality of the variables, counting the number of satisfying assignments to free first-order variables in a quantifier-free formula of bounded arity in a given structure ($p\text{- }\#\textrm{MC}({\varSigma }_0)_a$) is complete for $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ with respect to para-logspace parsimonious reductions (Theorem 22).

Finally, we consider a parameterised variant of the determinant function ($p\text{- }\textrm{det}$) introduced by Chauhan and Rao [32]. By adapting the arguments of Mahajan and Vinay [33], we show that $p\text{- }\textrm{det}$ on (0, 1)-matrices can be expressed as the difference of two functions in $\#\textbf{para}_\beta \textbf{L}$, and is $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$-hard with respect to para-logspace many-one reductions (Theorem 31).

Figure 1 shows a class diagram including the complete problems we identified.

Fig. 1

Diagram of studied classes with list of complete problems, assuming pair-wise difference between classes

Main Techniques Our primary contribution is laying the foundations for the study of parameterised logspace-bounded counting complexity classes. The completeness results in Theorems 15 and 22 required a quantised normal form for k-bounded nondeterministic Turing Machines (NTMs) (Lemma 9). This normal form quantises the nondeterministic steps of a k-bounded NTM into chunks of $\log n$-many steps such that the total number of accepting paths remains the same. We believe that the normal form given in Lemma 9 will be useful in the structural study of parameterised counting classes.

The study of $p\text{- }\textrm{det}$ involved definitions of so-called parameterised clow sequences generalising the classical notion [33]. Besides, a careful assignment of signs to clow sequences was necessary for our complexity analysis of $p\text{- }\textrm{det}$.

Related Results Dalmau and Johnson [34] investigated the complexity of counting homomorphisms and provided generalisations of results by Grohe [35] to the counting setting. Chen and Müller [36] studied the parameterised complexity of evaluating conjunctive queries, a problem closely related to the homomorphism problem. In both cases, a classification of the complexity of the respective problem was obtained based on the structure of the input. A similar classification in our setting could give new insights into the complexity of the homomorphism problem (Open Problem 3). The behaviour of our classes with respect to reductions is similar to the one observed for by Bottesch [37, 38]. For sub-graph problems a good survey paper exists by Meeks [39]. Parameterised approximation counting is a related branch of research [40,41,42,43,44,45]. Counting answers to conjunctive queries has been studied by Chen, Durand and Mengel [46, 47].

Outline In Sect. 2, we introduce the considered machine model, as well as needed foundations of parameterised complexity theory and logic. Section 3 presents structural results regarding our introduced notions in the parameterised counting context. Afterwards, in Sect. 4, our main results on counting walks, FO-assignments, homomorphisms as well as regarding the determinant are shown. Finally, we conclude in Sect. 5.

Prior Work This is an extended version of the conference publication [48]. A major difference to the conference version is incorporating the full proof details of all results.

Compared to the conference version, we made the definition of configurations and related notions more precise. Furthermore, we corrected inaccuracies in different proofs of the paper, some of which resulted from imprecisions in the definitions of configurations and related notions which have been made accurate, now. Unfortunately, two results could not be salvaged and are now open for further research: Namely, the graph-based problems we claimed to be complete for $\textbf{para}_{\textbf{W}}\textbf{L}$ do not seem to be contained in that class. While one could further restrict these problems to arrive at promise problems complete for the class, these do not seem to be natural problems anymore. Consequently, we removed these two problems from this version of the paper.

2 Preliminaries

In this section, we describe the computational models and complexity classes that are relevant to parameterised complexity theory. We use standard notions and notations from parameterised complexity theory [1, 2], as well as from graph theory [49]. As we are working with problems that deal with functions (see Sect. 3), we will use a fraktur alphabet letter ${\mathfrak {G}}$ for a graph to avoid confusions with a function G whenever both appear simultaneously. Finally, without loss of generality, we only consider binary inputs for our computation models.

Turing Machines (TMs) with Random Access to the Input We consider an intermediate model between TMs and Random Access Machines (RAMs) on words. Particularly, we make use of TMs that have random access to the input tape and can query relations in input structures in constant time. This can be achieved with two additional tapes of logarithmic size (in the input length), called the random access tape and the relation query tape. On the former, the machine can write the index of an input position to get the value of the respective bit of the input. On the relation query tape, the machine can write a tuple t of the input structure together with a relation identifier R to get the bit stating whether t is in the relation specified by R. Note that our model achieves linear speed-up for accessing the input compared to the standard TM model. (This is further justified by Remark 7.) For convenience, in the following, whenever we speak about TMs we mean the TM model with random access to the input.

Nondeterministic Turing Machines (NTMs) are a generalisation of TMs where multiple transitions from a given configuration are allowed. This can be formalised by allowing the transition to be a relation rather than a function. An NTM N accepts a given input x if there is a valid sequence of configurations starting from the initial configuration that terminate in an accepting configuration. (See, e.g., [30] for more details.)

Denote by $\textbf{SPACETIME}(s,t)$ ($\textbf{NSPACETIME}(s,t)$) with $s,t:\mathbb {N}\rightarrow \mathbb {N}$ the class of languages that are accepted by (nondeterministic) TMs with space-bound O(s) and time-bound O(t). A ${\mathcal {C}}$-machine for ${\mathcal {C}}=\textbf{SPACETIME}(s,t)$ (${\mathcal {C}}=\textbf{NSPACETIME}(s,t)$) is a (nondeterministic) TM that is O(s) space-bounded and O(t) time-bounded.

Sometimes, it is helpful to view NTMs as TMs with an additional tape, called the (nondeterministic) choice tape which is typically read-only. Let M be a deterministic TM with a choice tape.

The language accepted by M, L(M) is defined as

$$\begin{aligned} \left\{ x \in \{0,1\}^* \,\big |\, \begin{array}{l} \exists y\in \{0,1\}^*\text { s.t. }\, M \text { accepts } x \text { when}\\ \text {the choice tape is initialised with } y \end{array} \right\} . \end{aligned}$$

Notice that in this framework the machine M may have two-way or one-way access to the choice tape. The power of computation varies depending on the type of access allowed to the choice tape. Furthermore, in a space-bounded computation, the choice tape must be read-only and hence the space occupied by the choice tape is not counted for space bounds. Note that TMs with a read-once choice tape can be simulated by NTMs with the similar resource bounds. In fact, an NTM can guess the bits in the choice tape first and then simulate the machine in a deterministic fashion. Conversely, TMs with read-once choice tape can simulate NTMs as well:

Proposition 1

(Folklore) Let N be a t time-bounded and s space-bounded NTM accepting a language L. Then, there is an O(t) time-bounded and O(s) space-bounded TM M with choice tape such that $L = L(M)$. Furthermore, M has read-once access to the choice tape.

Proof sketch

Let $\delta _N$ be the transition relation of N. Without loss of generality, assume that for any state p and tape symbol a, $|\{q~|~ \delta ((p,a),q)\}| \in \{0,1,2\}$. That is, there will be at most two next configurations from any given configuration. Let M be the machine that runs N on its input x. At every step, if the current state p is such that $|\{q~|~ \delta ((p,a),q)\}| =2$, then M reads the bit on the choice tape under the current head position, chooses the next state of N based on the value read. Further, M moves the head of the choice tape to one position right. If $|\{q~|~ \delta ((p,a),q)\}| =1$, then M does the simulation without reading from the choice tape. M accepts if and only if N accepts. From the simulation, we have $L(N) = L(M)$. The simulation of N by M can be done in time O(t) and space O(s). (Here we have assumed that M is a multi-tape TM and can have more tapes compared to N.) Finally, note that M moves the head of the choice tape only in the rightward direction, and hence M is read-once on the choice tape. $\square$

From the above, we can treat NTMs as TMs with a choice tape. In this paper, we regard nondeterministic TMs as deterministic ones with a choice tape.

Before we proceed to the definition of parameterised complexity classes, a clarification on the choice of the model is due. Note that RAMs and NRAMs are often appropriate in the parameterised setting as exhibited by several authors (see, e.g., the textbook of Flum and Grohe [2]). They allow to define bounded nondeterminism quite naturally. On the other hand, in the classical setting, branching programs (BPs) are one of the fundamental models that represent space-bounded computation, in particular logarithmic space. Since BPs inherently use bit access, this relationship suggests the use of a bit access model.

Consequently, we consider a hybrid computational model: Turing machines with random access to the input. While the computational power of this model is the same as that of Turing machines and RAMs, it seems to be a natural choice to guarantee a certain robustness, allowing for desirable characterisations of our classes.

Parameterised Complexity Classes Let $\textbf{FPT}$ denote the class of parameterised problems that can be decided by a deterministic TM running in time $f(k)\cdot p(|x|)$ for any input (x, k), where f is a computable function and p is a polynomial. Similarly, let $\textbf{XP}$ be the class obtained by allowing time $|x|^{f(k)}$ instead. Furthermore, naturally lift the notion of $\textbf{SPACETIME}(\cdot ,\cdot )$/$\textbf{NSPACETIME}(\cdot ,\cdot )$ to parameterised problems.

Two central classes in parameterised complexity theory are and which were originally defined via special types of circuit satisfiability [2]. Flum, Chen and Grohe [50] obtained a characterisation of these two classes using the following notion of k-bounded NTMs.

Definition 2

(k-bounded NTMs) An NTM M, working on inputs of the form (x, k) with $x \in \{0,1\}^*, k \in \mathbb {N}$, is said to be k-bounded if for all inputs (x, k) it reads at most $f(k)\cdot \log |x|$ bits from the choice tape on input (x, k), where f is a computable function.

Note that it is irrelevant how k is encoded as the parametric value appears only in the function f.

Here, we will work with the following characterisation of . The characterisation for needs another concept that will be defined on the next page.

Proposition 3

([2, 50]) is the set of all parameterised problems that are accepted by some k-bounded $\textbf{FPT}$-machine with a choice tape.

Now, we recall three complexity theoretic operators that define parameterised complexity classes from an arbitrary classical complexity class, namely $\textbf{para}, \textbf{para}_{\textbf{W}}$ and $\textbf{para}_\beta$, following the notation of Stockhusen [51].

Definition 4

([52]) Let ${\mathcal {C}}$ be any complexity class. Then $\textbf{para}{\mathcal {C}}$ is the class of all parameterised problems $P \subseteq \{0,1\}^* \times \mathbb {N}$ for which there is a computable function ${\pi }:\mathbb {N} \rightarrow \{0,1\}^*$ and a language $L \in {\mathcal {C}}$ with $L \subseteq \{0,1\}^* \times \{0,1\}^*$ such that for all $x \in \{0,1\}^*$, $k \in \mathbb {N}$: $(x,k) \in P \Leftrightarrow (x, {\pi }(k)) \in L.$

A $\textbf{para}{\mathcal {C}}$-machine for ${\mathcal {C}}=\textbf{SPACETIME}(s,t)$ (${\mathcal {C}}=\textbf{NSPACETIME}(s,t)$) is a (nondeterministic) TM, working on inputs of the form (x, k), that is $O(s(|x|+f(k)))$ space-bounded and $O(t(|x|+f(k)))$ time-bounded where f is a computable function. Notice that $\textbf{para}\textbf{P}= \textbf{FPT}$ is the standard precomputation characterisation of $\textbf{FPT}$ and even more, $\textbf{FPT}$ can equivalently be defined with either running times of the form $O(f(k) \cdot \text {poly}(|x|))$ or $O(f(k) + \text {poly}(|x|))$ for some computable function f [52]. Now, consider the class $\textbf{para}\textbf{L}$, which can be seen as the parameterised version of $\textbf{L}$. By the above definiton, it is the class of parameterised problems decidable in space $O(f(k) + \log |x|)$ for some computable function f. Here, changing the definition to allow space $O(f(k) \cdot \log |x|)$ instead would likely change the class and not even yield a subclass of $\textbf{FPT}$, as such computations may take time $O(|x|^{f(k)})$, only showing membership in $\textbf{XP}$. This further indicates that $\textbf{para}\textbf{L}$ is the right way to define parameterised logspace.

The class $\textbf{XP}$ and the -hierarchy [2] capture intractability of parameterised problems. Though the -hierarchy was defined using the weighted satisfiability of formulas with bounded weft, which is the number of alternations between gates of high fan-in, Flum and Grohe [52] characterised central classes in this context using bounded nondeterminism. Stockhusen and Tantau [3, 51] considered space-bounded and circuit-based parallel complexity classes with bounded nondeterminism.

The following definition is a more formal version of the one given by Stockhusen and Tantau [3, Def. 2.1]. They use $\text {para}\exists ^{\leftrightarrow }_{f\log }{\mathcal {C}}$ instead of $\textbf{para}_{\textbf{W}}{\mathcal {C}}$ for a complexity class ${\mathcal {C}}$.

Definition 5

Let ${\mathcal {C}}=\textbf{SPACETIME}(s,t)$ for some $s,t:{\mathbb {N}}\rightarrow {\mathbb {N}}$. Then, $\textbf{para}_{\textbf{W}}{\mathcal {C}}$ is the class of all parameterised problems Q that are accepted by some k-bounded $\textbf{para}{\mathcal {C}}$-machine with a choice tape.

For example, $\textbf{para}_{\textbf{W}}\textbf{L}$ denotes the parameterised version of $\textbf{NL}$ with k-bounded nondeterminism. One can also restrict this model by only giving one-way access to the nondeterministic tape. The following definition is a more formal version of the one of Stockhusen and Tantau [3, Def. 2.1] who use the symbol $\text {para}\exists ^{\rightarrow }_{f\log }$ instead.

Definition 6

Let ${\mathcal {C}}=\textbf{SPACETIME}(s,t)$ for some $s,t:{\mathbb {N}}\rightarrow {\mathbb {N}}$. Then $\textbf{para}_\beta {\mathcal {C}}$ denotes the class of all parameterised problems Q that can be accepted by a k-bounded $\textbf{para}{\mathcal {C}}$-machine with a choice tape with one-way read access to the choice tape.

As there is only read-once access to the nondeterministic bits, $\textbf{para}_\beta {\mathcal {C}}$ can be equivalently defined via nondeterministic transitions and without using a choice tape.

Another notion studied in parameterised complexity is tail-nondeterminism. A k-bounded machine M is tail-nondeterministic if there exists a computable function g such that on all inputs (x, k), after its first nondeterministic step, M makes at most $g(k)\cdot \log |x|$ further steps in the computation. The value of this concept is evidenced by the machine characterisation of  (Chen et al. [50]). We hope to get new insights by transferring this concept to space-bounded computation. In consequence, we introduce the tail-nondeterministic versions of $\textbf{para}_{\textbf{W}}{\mathcal {C}}$ and $\textbf{para}_\beta {\mathcal {C}}$, which are denoted by $\textbf{para}_{{\textbf{W}}[1]}{\mathcal {C}}$ and $\textbf{para}_{\beta {\textbf{tail}}}{\mathcal {C}}$.

Note that the restriction of the above classes to k-boundedness is crucial in the context of logarithmic space. If we drop this restriction, the machines are able to access $2^{f(k)+\log |x|}$, i.e., fpt-many nondeterministic bits. Regarding multiple-read access, this allows for solving SAT in logarithmic space (with constant parameterisation). That is, the class would contain a $\textbf{para}\textbf{NP}$-complete problem. For read-once access, we expect a similar result for $\textbf{para}\textbf{NL}$. When adding tail-nondeterminism, k-boundedness is always implicitly given.

Configurations Let M be a TM with choice tape. A configuration of M on an input (x, k), is the snapshot of M at some point during the computation on M on input (x, k). Disregarding the input query tape and relation query tape for the moment, a configuration more formally is a tuple $(p,\gamma , h_1,h_2, h_3)\in Q\times {\varSigma }^*\times \mathbb {N}\times \mathbb {N}\times \mathbb {N}$, where p is the state, $\gamma$ is the content of the work tapes, $h_1$ is the head position on the work tape, $h_2$ is the head position on the input tape and $h_3$ is the head position on the choice tape. In the case of machines with multiple work tapes, the notion of a configuration can be modified accordingly by adding for each of them both the content and the head position to the configuration. Input query tape and relation query tape are treated in the same way as a usual work tape. For an s space-bounded machine, a configuration is of size O(s). Note that we do not store the contents of input and choice tapes in a configuration.

A configuration C is said to be nondeterministic if the next configuration is dependent on the content of the choice tape at the current head position.

Remark 7

Note that it is important to have random access to the input tape in the case of tail-nondeterminism. Without random access to input bits and input relations, a TM cannot even make reasonable queries to the input in time $g(k)\cdot \log (n)$.

Logic We assume basic familiarity with first-order logic (FO). A vocabulary is a finite ordered set of relation symbols and constants. Each relation symbol ${\textsf{R}}$ has an associated arity $\textrm{arity}({\textsf{R}})\in {\mathbb {N}}$. Let $\tau$ be a vocabulary. A $\tau$-structure $\textbf{A}$ consists of a nonempty finite set $\textrm{dom}(\textbf{A})$ (its universe), and an interpretation ${\textsf{R}}^{\textbf{A}}\subseteq \textrm{dom}(\textbf{A})^{\textrm{arity}({\textsf{R}})}$ for every relation symbol ${\textsf{R}}\in \tau$. Syntax and semantics are defined as usual (see, e.g., the textbook of Ebbinghaus et al. [53]).

Let $\textbf{A}$ be a structure with universe A. We denote by $|\textbf{A}|$ the size of a binary encoding of $\textbf{A}$, i.e., the number of bits required to represent the universe and relations as lists of tuples. For example, if ${\textsf{R}}$ is a relation symbol of arity 3, then ${\textsf{R}}^\textbf{A}$ is represented as a subset of $A^3$, i.e., a set of triples over A. This requires $O(|{\textsf{R}}^{\textbf{A}}|\cdot \textrm{arity}({\textsf{R}}))\cdot \log |A|)$ bits to represent the relation ${\textsf{R}}^{\textbf{A}}$, assuming $\log |A|$ bits to represent an element in A. As analysed by Flum et al. [54, Sect. 2.3], this means that $|\textbf{A}|\in {\varTheta }((|A|+|\tau |+\sum _{{\textsf{R}}\in \tau } |{\textsf{R}}^{\textbf{A}}|\cdot \textrm{arity}({\textsf{R}}))\cdot \log |A|)$.

Recall the following important classes of $\textrm{FO}$-formulas. A formula is in prenex normal form if it begins with a quantifier prefix followed by a quantifier-free formula. Moreover, ${\varSigma }_i$ (for $i \in \mathbb {N}$) refers to the fragment of $\textrm{FO}$ containing all formulas in prenex normal form with i quantifier blocks alternating between existential and universal quantifiers and the outermost quantifier being existential.

Counting Problems A counting problem is a function of the form $f:{\varSigma }^* \rightarrow \mathbb {N}$, where ${\varSigma }$ is a finite alphabet. The counting class $\#\textbf{P}$ is characterised by the set of all functions that can be expressed as the number of accepting paths in a nondeterministic polynomial time-bounded Turing Machine. Valiant [8] developed the theory of counting problems by showing that counting the number of perfect matchings in a graph is complete for $\#\textbf{P}$.

For any counting problem $f:{\varSigma }^*\rightarrow \mathbb {N}$, the associated decision problem is the problem of deciding $f(x) >0$ or not. For example, the associated decision problem for $\#\textrm{SAT}$ is the well known problem of $\textrm{SAT}$. For further details, we refer the reader to an excellent book on counting problems by Jerrum [55].

3 Parameterised Counting in Logarithmic Space

A good survey article on counting problems in parameterised complexity is by Curticapean [56]. Now, we define the counting counterparts based on the parameterised classes defined using bounded nondeterminism. A parameterised function is a function $F:\{0,1\}^* \times \mathbb {N} \rightarrow \mathbb {N}$. For an input (x, k) of F with $x \in \{0,1\}^*$, $k \in \mathbb {N}$, we call k the parameter of that input. If ${\mathcal {C}}$ is a complexity class and a parameterised function F belongs to ${\mathcal {C}}$, we say that F is ${\mathcal {C}}$-computable. Let M be an NTM. We denote by $\#\textrm{acc}_M(x)$ the number of words y such that M on input x with the choice tape initialised with y accepts and reads y completely during its computation. When transforming a Turing machine with a choice tape into a standard nondeterministic Turing machine, this notion coincides with the number of accepting computation paths of M on input x.

Definition 8

Let ${\mathcal {C}}=\textbf{SPACETIME}(s,t)$ for some $s,t:{\mathbb {N}}\rightarrow {\mathbb {N}}$. Then a parameterised function F is in $\#\textbf{para}_{\textbf{W}}{\mathcal {C}}$ if there is a k-bounded nondeterministic $\textbf{para}{\mathcal {C}}$-machine M such that for all inputs (x, k), we have that $\#\textrm{acc}_M(x,k)=F(x,k)$. Furthermore, F is in

• $\#\textbf{para}_\beta {\mathcal {C}}$ if there is such an M with read-once access to its nondeterministic bits,

• $\#\textbf{para}_{{\textbf{W}}[1]}{\mathcal {C}}$ if there is such an M that is tail-nondeterministic, and

• $\#\textbf{para}_{\beta {\textbf{tail}}}{\mathcal {C}}$ if there is such an M with read-once access to its nondeterministic bits that is tail-nondeterministic.

By definition, we get $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L} \subseteq {\mathcal {C}}\subseteq \#\textbf{para}_{\textbf{W}}\textbf{L}$ for ${\mathcal {C}}\in \{\#\textbf{para}_\beta \textbf{L},\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L} \}$.

The following lemma shows that $\textbf{para}\textbf{L}$-machines can be normalised in a specific way. This normalisation will play a major role in Sect. 4.

Lemma 9

For any k-bounded nondeterministic $\textbf{para}\textbf{L}$-machine M there exists a k-bounded nondeterministic $\textbf{para}\textbf{L}$-machine $M'$ with $\#\textrm{acc}_M(x,k) = \#\textrm{acc}_{M'}(x,k)$ for all inputs (x, k) such that $M'$ has the following properties:

• 1. $M'$ has a unique accepting configuration,

• 2. on any input (x, k), every computation path of $M'$ accesses exactly $g(k)\cdot \log |x|$ nondeterministic bits (for some computable function g), and $M'$ counts on an extra tape (tape $S$) the number of nondeterministic steps, and

• 3. $M'$ has an extra tape (tape $C$) on which it remembers previous nondeterministic bits, resetting the tape after every $\log |x|$-many nondeterministic steps.

Additionally, if M has read-once access to its nondeterministic bits, or is tail-nondeterministic, or both, then $M'$ also has these properties.

Proof

We construct the machine $M'$ with the three desired properties and the same number of accepting computation paths as M step by step, ensuring that the properties from previous steps are preserved.

First, note that without loss of generality M can be assumed to have a single accepting state. We can modify M so that upon reaching an accepting state, it erases everything in the work tape and moves the head positions of every tape to the left end marker. This ensures that M has a unique accepting configuration, which is property (1). This does not alter the number of accepting paths of M on any input.

To ensure (2), we construct a new machine N that behaves as M but additionally maintains a counter on tape $S$ for the number of nondeterministic bits that have already been accessed: Every time a new nondeterministic bit is accessed, the counter is incremented. If M halts with the counter being less than $g(k)\cdot \log |x|$, then the modified machine N keeps making nondeterministic choices until the count is $g(k)\cdot \log |x|$. As the machine has multiple read access to nondeterministic bits, it is not clear when exactly new bits are accessed. This can be handled using two additional counters: One stores the index of the rightmost position on the choice tape that has already been accessed and one stores the current head position on the choice tape. As we use at most $g(k) \cdot \log |x|$ nondeterministic bits, these counters can be stored by a $\textbf{para}\textbf{L}$-machine. We define N to accept if and only if M accepts and all of the additional nondeterministic bits guessed by N have the value 0. Note that N does not use any additional space except for maintaining and updating the counter. For all $(x,k) \in \{0,1\}^* \times \mathbb {N}$, the machine N accesses exactly $g(k)\cdot \log |x|$ nondeterministic bits on all computation paths and $\#\textrm{acc}_M(x,k) = \#\textrm{acc}_N(x,k)$. Also, N still has property (1), since the tape S has the same content and head position for all accepting configurations and the remaining part of accepting configurations does not change compared to M.

Finally, to ensure (3), we modify N from the previous step to obtain $M'$ as follows. The new machine $M'$ has an additional tape (tape $C$) on which it initially marks exactly $\log |x|$ cells, placing the head on the left-most cell afterwards. Whenever N reads a nondeterministic bit, $M'$ copies the nondeterministic bit to tape $C$ (that is, $M'$ copies the bit to tape $C$ and moves the head position to the right). If the current head position in tape $C$ is on the right-most marked cell, then $M'$ erases the content of tape $C$ in the marked cells and copies the nondeterministic bit currently being read to the first marked cell on tape $C$. Finally, $M'$ accepts if and only if N accepts. Since this modification does not introduce new nondeterministic steps, the number of accepting computation paths of $M'$ on any input is the same as that of N and the modification preserves property (2). To re-establish property (1), whenever we would reach an accepting configuration, we first clear tape C and then accept. $\square$

The following result follows from a simple simulation of nondeterministic machines by deterministic ones. Let $\textbf{F}\textbf{FPT}$ be the class of functions computable by $\textbf{FPT}$-machines with output.

Theorem 10

$\#\textbf{para}_\beta \textbf{L} \subseteq \textbf{F}\textbf{FPT}$.

Proof

Let $F\in \#\textbf{para}_\beta \textbf{L}$ via the machine M with space-bound $g(k) + c\log n$ for some constant $c>0$. For an input (x, k), let ${\mathfrak {G}}(x,k)=(V(x,k),E(x,k))$ be the configuration graph of M on (x, k). Since $|V(x,k)| = 2^{O(g(k) + c \log |x|)}$, ${\mathfrak {G}}$ can be constructed in $\textbf{FPT}$ time given the input (x, k). Now, $\#\textrm{acc}_M(x,k)$ is equal to the number of paths from the starting configuration s(x, k) of M on input (x, k) to the unique accepting configuration $C_\textrm{acc}$ (by virtue of Lemma 9). Note that computing $\#\textrm{acc}_M(x,k)$ can be done by counting the number of paths from the initial configuration to the accepting configuration in ${\mathfrak {G}}(x,k)$. This can be done via a simple dynamic programming algorithm (in the fashion of matrix multiplication) computing the number of paths from the initial configuration to a given configuration in a dynamic fashion. Let $C_0$ be the initial configuration. Initialise $L(C_0) =1$ and $L(C) =0$ for every other configuration C in ${\mathfrak {G}}(x,k)$. At every iteration, update the value of L(C) for every configuration C based on the values of all configurations that have an edge to C. For every C, after $|{\mathfrak {G}}(x,k)|$ many iterations, L(C) will the the number of paths from $C_0$ to C. Since $|{\mathfrak {G}}(x,k)|$ is fpt, this can be implemented in fpt time. $\square$

Using the notion of oracle machines (see, e.g., [57]), we define Turing, metric, and parsimonious reductions computable in $\textbf{para}\textbf{L}$. In the space-bounded setting, we need to assume that the oracle tape is write-once. Further, the answer to an oracle query is written on a read-once tape.

With the above assumptions, the oracle tape is always exempted from space restrictions which is often the case in the context of logspace Turing reductions [58]. A study on the effect of changing this assumption might be interesting.

Definition 11

(Reducibilities) Let $F, F' :\{0,1\}^* \times \mathbb {N} \rightarrow \mathbb {N}$ be two functions.

• 1. F is para-logspace Turing reducible to $F'$, $F \le ^{\textrm{plog}}_TF'$, if there is a $\textbf{para}\textbf{L}$ oracle TM M that computes F with oracle $F'$ and the parameter of any oracle query of M is bounded by a computable function in the parameter.

• 2. F is para-logspace metrically reducible to $F'$, $F \le ^{\textrm{plog}}_{\textrm{met}}F'$, if there is such an M that uses only one oracle query.

• 3. F is para-logspace parsimoniously reducible to $F'$, $F \le ^{\textrm{plog}}_{\textrm{pars}}F'$, if there is such an M that returns the answer of the first oracle query.

For any reducibility relation $\preccurlyeq$ and any complexity class ${\mathcal {C}}$, $[{\mathcal {C}}]^\preccurlyeq :=\{\,A\mid \exists C\in {\mathcal {C}}\text { such that\ }A\preccurlyeq C \,\}$ is the $\preccurlyeq$-closure of ${\mathcal {C}}$.

Next, we show that both new classes that are not restricted to tail-nondeterminism are closed under $\le ^{\textrm{plog}}_{\textrm{pars}}$.

Lemma 12

The classes $\#\textbf{para}_{\textbf{W}}\textbf{L}$ and $\#\textbf{para}_\beta \textbf{L}$ are closed under $\le ^{\textrm{plog}}_{\textrm{pars}}$.

Proof

We start with $\#\textbf{para}_{\textbf{W}}\textbf{L}$. Let $F,{F'}:\{0,1\}^*\times {\mathbb {N}}\rightarrow {\mathbb {N}}$ and $F'\in \#\textbf{para}_{\textbf{W}}\textbf{L}$ via the k-bounded, $s_{F'}$ space-bounded NTM $M_{F'}$. Furthermore, let $F\le ^{\textrm{plog}}_{\textrm{pars}}{F'}$ via the $\textbf{para}\textbf{L}$ oracle TM M. Let $\sigma :\{0,1\}^*\times \mathbb {N}\rightarrow \{0,1\}^*$ and $h:\{0,1\}^*\times \mathbb {N}\rightarrow \mathbb {N}$ such that the machine M on input (x, k) uses the only oracle query $(\sigma (x,k),h(x,k))$.

Let $M_\sigma$, $M_h$ with space-bounds $s_\sigma$, $s_h$ be the machines computing $\sigma$, h. To show that $F\in \#\textbf{para}_{\textbf{W}}\textbf{L}$, we construct a new k-bounded nondeterministic $\textbf{para}\textbf{L}$-machine $M_F$ as follows.

On input (x, k), the machine $M_F$ simulates $M_{F'}$ on $(\sigma (x,k),h(x,k))$ using $M_\sigma$ and $M_h$. Initially, h(x, k) is computed using $M_h$ and the value is stored. Then, whenever $M_{F'}$ reads the i-th input symbol, $M_F$ runs $M_\sigma$ on (x, k) until it outputs the i-th symbol and uses it as the next input symbol. For this, note that $|{\sigma }(x,k)|$ is fpt-bounded. Afterwards, $M_F$ continues the simulation of $M_{F'}$. On (x, k) the number of accepting paths of $M_F$ is exactly the number of accepting paths of $M_{F'}$ on $(\sigma (x,k),h(x,k))$, which is equal to ${F'}(\sigma (x,k),h(x,k))=F(x,k)$ as required. The space required by $M_F$ is bounded by the sum of the following: The space required to compute and store h(x, k), the space used by $M_{F'}$ on input $({\sigma }(x,k), h(x,k))$, the space used by $M_{{\sigma }}$ on input (x, k), and bookkeeping. Regarding bookkeeping, we need an index counter for $M_{F'}$’s input head position. Formally, the space is bounded by

$$\begin{aligned} s_h(x,k) + |h(x,k)| + s_{F'}(|\sigma (x,k)|,h(x,k)) + s_\sigma (|x|,k) + s_\text {bk}(|x|,k), \end{aligned}$$

where $s_\text {bk}(|x|,k)$ is the space required for bookkeeping. This sum is in $O(\log |x|+f(k))$.

The number of nondeterministic bits required by $M_F$ is the same as $M_{F'}$ on input $(\sigma (x,k),h(x,k))$. Consequently, the computation of $M_F$ is still k-bounded as the number of nondeterministic bits is bounded by

$$\begin{aligned} f'(h(x,k))\cdot \log |\sigma (x,k)|\le f''(k)\cdot \log |x|, \end{aligned}$$

where $f',f''$ are computable functions. This is due to $|\sigma (x,k)|$ being fpt-bounded and h(x, k) being bounded by a computable function in k.

We continue with $\#\textbf{para}_\beta \textbf{L}$. The proof is analogous but $M_{F'}$ has read-once access to its nondeterministic bits. Note that the only time $M_F$ accesses nondeterministic bits is when $M_{F'}$ accesses its nondeterministic bits. Moreover, the order in which nondeterministic bits are accessed is preserved. Consequently, $M_F$ has read-once access to its nondeterministic bits. $\square$

It is not clear whether the classes restricted to tail-nondeterminisnm share this closure property. In Corollary 16, we will show that in case of read-once access and tail-nondeterminisnm, taking the closure under para-logspace parsimonious reductions is as powerful as lifting the restriction to tail-nondeterminism, i.e. $[\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L} ]^{\le ^{\textrm{plog}}_{\textrm{pars}}} = \#\textbf{para}_\beta \textbf{L}$. Open Problem 2 on page 44 asks what class corresponds to the corresponding closure of $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$.

Another important question is whether classes are closed under certain arithmetic operations. We show that all newly introduced classes are closed under addition and multiplication.

Theorem 13

For any , the class $\#\textbf{para}_o\textbf{L}$ is closed under addition and multiplication.

Proof

Let C be any class $\#\textbf{para}_o\textbf{L}$, where . Let $F_1, F_2$ be in C via the NTMs $M_1$ and $M_2$, respectively. Let h be a computable function such that $M_1$ and $M_2$ both are $O(\log |x| + h(k))$ space-bounded. We start by showing that the above classes are closed under addition. We first consider $\#\textbf{para}_{\textbf{W}}\textbf{L}$ and $\#\textbf{para}_\beta \textbf{L}$. The argument is similar for both of the classes. We give details for $\#\textbf{para}_{\textbf{W}}\textbf{L}$. We construct a new machine M as follows: M nondeterministically chooses whether to simulate the machine $M_1$ or the machine $M_2$ on the given input using a single additional nondeterministic bit. By construction we have $\#\textrm{acc}_M(x,k) = \#\textrm{acc}_{M_1}(x,k) + \#\textrm{acc}_{M_2}(x,k) = F_1(x,k) + F_2(x,k)$. Also, M is $O(\log |x| + h(k))$ space-bounded and k-bounded, since apart from the initial step choosing which machine to run, it behaves exactly like either $M_1$ or $M_2$.

We conclude that the class $\#\textbf{para}_{\textbf{W}}\textbf{L}$ is closed under addition. The same argument works for $C=\textbf{para}_\beta \textbf{L}$, as read-once access to nondeterministic bits is preserved by the construction.

For $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ and $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$, we modify M as follows: M first simulates the deterministic parts up until the first nondeterministic step of both machines $M_1$ and $M_2$. That is M first runs $M_1$ until the first nondeterminstic step is reached. Say $C_1$ is the corresponding configuration. Store $C_1$, and now simulate $M_2$ until the fist nondeterminstic step. Let $C_2$ be the corresponding configuration. We then nondeterministically choose $a \in \{0,1\}$. If $a=1$, then continue with the simulation of $M_1$ starting at $C_1$, discard the configuration $C_2$. If $a=0$, then continue with simulation of $M_2$ starting at $C_2$ and discard $C_1$. Accept if and only if the simulated machine accepts. This ensures that M is tail-nondeterministic if $M_1$ and $M_2$ are tail-nondeterministic. Also, read-once access to nondeterministic bits is still preserved. Further, M accepts an input if and only if either $M_1$ accepts it or $M_2$ accepts it. Further, the number of accepting path of M is equal to the sum of the number of accepting paths of $M_1$ and $M_2$. Total space requirement of M is bounded by the sum of the spaces used by $M_1$ and $M_2$.

We now show that the above classes are closed under multiplication, starting again with $\#\textbf{para}_{\textbf{W}}\textbf{L}$ and $\#\textbf{para}_\beta \textbf{L}$. We construct a new machine $M'$. On input (x, k), $M'$ first simulates $M_1$ on input (x, k). Whenever, $M_1$ needs a nondeterministic bit, M gets it from its choice tape, moving the head direction as done by $M_1$. Additionally, we keep two counters ($c_1$ and $c_2$) to keep track of the position on the choice tape. Initially, $c_1 = c_2=1$, indicating that the head is at the first bit on the choice tape. The first counter ($c_1$) is incremented if $M_1$ moves the head on the choice tape to the right, and is decremented if the $M_1$ moves the choice tape head to the left. Whenever $M_1$ moves the choice tape head to the right, we increment $c_2$ if $c_1 = c_2$. If $M_1$ accepts, then $M'$ simulates $M_2$ on (x, k) such that the start of the choice tape head is at position $c_2$. The machine $M'$ never lets $M_2$ move the choice tape head to the left of position $c_2$. ($M'$ will reject if $M_2$ ever tries to do so.) Finally, $M'$ accepts if and only if $M_2$ accepts. Note that we use the counters $c_1$ and $c_2$ to ensure that simulations of $M_1$ and $M_2$ are done on disjoint sets of nondeterministic choices. This is needed especially for $\#\textbf{para}_{\textbf{W}}\textbf{L}$. When $M_1$ and $M_2$ both have read-once access to nondeterministic choices, we do not need to use the counters $c_1$ and $c_2$.

Since $M_1$ and $M_2$ are k-bounded, $M'$ is also k-bounded. The space used by $M'$ is at most the maximum of that of $M_1$ and $M_2$. By construction we have $\#\textrm{acc}_{M'}(x,k)= \#\textrm{acc}_{M_1}(x, k)\cdot \#\textrm{acc}_{M_2}(x,k) = F(x,k) \cdot F'(x, k)$. Accordingly, the class $C = \#\textbf{para}_{\textbf{W}}\textbf{L}$ is closed under multiplication. Additionally, if $M_1$ and $M_2$ only have read-once access to the nondeterministic bits, so has the new machine $M'$. We conclude that $\#\textbf{para}_\beta \textbf{L}$ is closed under multiplication.

We now cover the case of $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ and $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$. Here, $M_1$ and $M_2$ are tail-nondeterministic. We modify the constructed machine $M'$ similar to what was done to show that these classes are closed under addition. $M'$ first simulates the deterministic parts up until the first nondeterministic configuration of both machines $M_1$ and $M_2$. Then $M'$ simulates $M_1$ starting from the first nondeterministic configuration. If $M_1$ accepts, $M'$ simulates $M_2$ starting from the first nondeterministic configuration and accepts if and only if $M_2$ accepts. As both $M_1$ and $M_2$ are tail-nondeterministic, the number of steps of $M_1$ and $M_2$ starting from their first nondeterministic configuration is k-bounded. Furthermore, the machine $M'$ does not perform any nondeterministic steps until it starts simulating $M_1$ from configuration $C_1$. This ensures that $M'$ is tail-nondeterministic.

Formally, let $C_1$ be the first nondeterministic configuration of $M_1$ on input (x, k) and $C_2$ be the first nondeterministic configuration of $M_2$ on (x, k). The new machine $M'$ runs $M_1$ on (x, k) until the configuration $C_1$ is reached. Then $M'$ stores the configuration $C_1$ and runs $M_2$ on (x, k) until the configuration $C_2$ is reached. Storing $C_2$ in a separate tape, $M'$ now proceeds with the nondeterministic computation of $M_1$ starting with the configuration $C_1$. For every accepting configuration of $M_1$, the machine $M'$ starts the computation of $M_2$ from configuration $C_2$ accepting on all paths where $M_2$ does. Further, when $M_1$ and $M_2$ have two-way access to the nondeterministic bits (that is in the case of $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$), we need two counters $c_1$ and $c_2$ as done in the case of $\#\textbf{para}_{\textbf{W}}\textbf{L}$.

By construction, we have $\#\textrm{acc}_{M'}(x,k)= \#\textrm{acc}_{M_1}(x, k)\cdot \#\textrm{acc}_{M_2}(x,k) = F(x,k) \cdot F'(x, k)$ and $M'$ is tail-nondeterministic. Moreover, it can again be seen that read-once access to nondeterministic bits is preserved by the construction. $\square$

Closure properties of counting classes under various operations are studied a lot in the literature. Apart from addition and multiplication, operations of decrement (i.e., max of $n-1$ and 0), and monus have received wide attention in the literature. There are several results in the literature concerning closure of counting classes under the monus operation (see, e.g., [59, 60]). We believe that knowing the closure properties of the parameterised counting classes introduced in this article under the monus operation might be interesting in its own right:

Open Problem 1

Which of the classes are closed under monus, that is, $\max \{F-G,0\}$?

4 Complete Problems

In this section, we study complete problems for the previously defined classes. The complete problems are related to counting walks in directed graphs, model-checking for $\textrm{FO}$ formulas, and counting homomorphisms between $\textrm{FO}$-structures, as well as a parameterised version of the determinant.

4.1 Counting Walks

We start with parameterised variants of counting walks in directed graphs, which will be shown to be complete for the introduced classes.

Theorem 14

For every $b > 2$, $\mathrm {p\text{- }}\#\textrm{LOG}\textrm{REACH}_b$ is $\#\textbf{para}_\beta \textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$-reductions.

Proof

We start with the proof idea. For the upper bound, guess a path of length exactly a. The number of nondeterministic bits is bounded by $O(k\cdot \log |V|)$ since successors can be referenced by numbers in $\{0,\dots ,b-1\}$.

For the lower bound, using Lemma 9, construct the configuration graph ${\mathfrak {G}}$ restricted to nondeterministic configurations and the unique accepting configuration $C_\textrm{acc}$, where the edge relation expresses whether a configuration is reachable with exactly one nondeterministic, but an arbitrary number of deterministic steps. Accepting computations of the machine correspond to paths from the first nondeterministic configuration to $C_\textrm{acc}$ of length $f(k)\cdot \log |{\mathfrak {G}}|$ in ${\mathfrak {G}}$.

Now we turn to the details of the proof.

Algorithm 1 shows membership. The algorithm first checks the constraint on a. Then it starts from vertex s and guesses an arbitrary path of length exactly a, using the fact that the out-degree of all vertices is bounded by b to limit the number of nondeterministic bits needed for this task. More precisely, we choose a natural ordering depending on the encoding of vertices and use this to reference successors of the current node by numbers $0,\dots ,b-1$. The needed number of nondeterministic bits is $a \cdot \log (b) \in O(k \cdot \log |V|)$. Furthermore, at any point of time, the encoding of at most two vertices as well as one number bounded by a constant are stored, so the algorithm uses logarithmic space.

Regarding the lower bound, let $F \in \#\textbf{para}_\beta \textbf{L}$ via the machine M. Using Lemma 9, we can assume that M has a unique accepting configuration $C_\textrm{acc}$ and there is a computable function f such that for any input (x, k) all accepting computation paths of M on input (x, k) use exactly $f(k) \cdot \log |x|$ nondeterministic bits. Let (x, k) be an input of M. Consider the graph ${\mathfrak {G}}(x,k) = (V(x,k),E(x,k))$ where V(x, k) is the set containing all nondeterministic configurations of M on input (x, k) as well as $C_\textrm{acc}$ and E(x, k) contains an edge $(C,C')$ if and only if $C'$ is reached from C using exactly one nondeterministic step and any number of deterministic steps in the computation of M on input (x, k). Now the number of accepting computation paths of M on input (x, k) is exactly the number of paths of length $f(k) \cdot \log |x|$ from the first nondeterministic configuration s(x, k) reached in the computation of M on input (x, k) to the unique accepting configuration in ${\mathfrak {G}}$. To ensure that the length of accepting paths is bounded by $f(k)\cdot \log |{\mathfrak {G}}|$, we further assume, without loss of generality, that $|V(x,k)| \ge |x|$. This can be ensured as follows: In the beginning of the computation, guess $\lceil \log |x|\rceil$ nondeterministic bits. If all these bits are 0, continue with the original computation of M. Otherwise, reject. This results in $2^{\lceil \log |x|\rceil } \ge |x|$ additional nondeterministic configurations. Note that no (directed) cycle is reachable from the initial configuration in the configuration graph of M on any input. For that reason, no cycle is reachable from s(x, k) in ${\mathfrak {G}}$ and hence every s-t-walk in ${\mathfrak {G}}$ is an s-t-path. We now have for all (x, k) that

$$\begin{aligned} F(x,k)&= \#\textrm{acc}_M(x,k)\\&= \mathrm {p\text{- }}\#\textrm{LOG}\textrm{REACH}_b(({\mathfrak {G}}(x,k), s(x,k), t, f(k) \cdot \log |x|),f(k)). \end{aligned}$$

The output ${\mathfrak {G}}(x,k)$ needs to be on a write-once tape. We note that the adjacency within ${\mathfrak {G}}(x,k)$ can be computed from (x, k) in parameterised logspace. That is, given two nodes $C,C' \in V(x,k)$, we can decide whether $(C,C') \in E(x,k)$ or not in parameterised logspace. We run the machine M starting from C as long as M uses at most one nondeterministc choice. This essentially means exploring two paths in the computation of M starting from the configuration C. This can be done by storing at most three configurations at any point of time. If $C_1$ is the first nondeterministic configuration reached starting from C, we store $C_1$ and explore the subsequent configurations originating from $C_1$ with the nondeterministic choice as 0 until we reach a nondeterministic configuration. Then abandon this path and restart with $C_1$ with nondeterministic choice as 1 and proceed until a nondeterministic configuration is reached. During this, check if the configuration reached at any point is the same as $C'$. If yes, then output the edge $(C,C')$. We repeat this for every pair $(C,C')$ of vertices in V(x, k).

In the above, the reduction outputs an edge list representation of ${\mathfrak {G}}(x,k)$ on a write-once tape. The argument can be extended to the case when an adjacency matrix representation is needed.

Furthermore, the new parameter is bounded by a computable function in the old parameter. Accordingly, the construction yields a para-logspace parsimonious reduction. $\square$

In the above problem, the out-degree b could also be taken as part of the parameter instead of being fixed, maintaining $\#\textbf{para}_\beta \textbf{L}$-completeness. Hardness immediately transfers, while membership can be shown with essentially the same algorithm. Let n be the input length, and k+b be the parameter. The required space is still in para-logspace, as the algorithm still only needs to store two vertices and one number between 1 and b at any point. The number of nondeterministic bits used is in $O(k \log n \log b)$ as $\log b$ nondeterministic bits are needed in each of the $k \log n$ iterations, which is clearly k-bounded.

Now consider the problem $\mathrm {p\text{- }}\#\textrm{REACH}$, defined as follows.

In contrast to the previous problem, nodes can here have unbounded out-degree, but we count walks of length k instead of length $a \le k \cdot \log |x|$. Note that the analogue problem for counting paths is -complete [20]. However, we will see now that the problem for walks is $\#\textbf{para}_\beta \textbf{L}$-complete.

Theorem 15

$\mathrm {p\text{- }}\#\textrm{REACH}$ is $\#\textbf{para}_\beta \textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$.

Proof

For membership, we modify Algorithm 1. As the length of the path is exactly k, lines 1–3 are omitted and the loop in line 5 now runs for $1 \le i < k$. In lines 6–11, instead of guessing the index of a successor, we directly guess any vertex $v_2$ and reject, if it is not a successor of $v_1$. As a successor is only guessed less than k times, the new algorithm is still k-bounded.

Regarding hardness, let $F \in \#\textbf{para}_\beta \textbf{L}$ via the machine M. Without loss of generality, M is in the normal form from Lemma 9. Let f be the computable function such that M on any input (x, k) uses exactly $f(k) \cdot \log |x|$ nondeterministic bits. Also, assume without loss of generality that the accepting configuration of M is deterministic. Fix an input (x, k). We reduce the problem of counting the accepting computation paths of M on input (x, k) to the problem of counting walks in a modified version of the configuration graph of M on input (x, k). The difference to the hardness proof of Theorem 14 is that edges now encode computations comprised of $\log |x|$-many nondeterministic steps. More precisely, define ${\mathfrak {G}}= (V,E)$ and $s,t \in V$ as follows: V consists of all nondeterministic configurations of M on input (x, k) and the (unique) accepting configuration $C_\textrm{acc}$ of M. For $C' \ne C_\textrm{acc}$, $(C,C') \in E$ if and only if configuration $C'$ is reachable from C in exactly $\log |x|$-many nondeterministic steps (and any number of deterministic steps) in the computation of M on input (x, k). Furthermore, $(C, C_\textrm{acc}) \in E$ if and only if $C_\textrm{acc}$ is reachable from C using exactly one nondeterministic step and any number of deterministic steps, i.e. no additional nondeterministic configurations appear. Finally, s is the first nondeterministic configuration reached in the computation of M on input (x, k) and $t = C_\textrm{acc}$.

Since all accepting computation paths in the configuration graph of M on input (x, k) use exactly $f(k) \cdot \log |x|$ nondeterministic bits, the change made compared to the reduction used for Theorem 14 does not change the number of paths and we can simply count paths of length exactly f(k) in the new graph. By the above we have

$$\begin{aligned} F(x,k)&= \#\textrm{acc}_M(x,k)\\&= \mathrm {p\text{- }}\#\textrm{REACH}(({\mathfrak {G}}, s(x,k), t), f(k)). \end{aligned}$$

Note that this equality crucially depends on the machine storing the last $\log |x|$ nondeterministic bits on the extra tape which can be assumed thanks to Lemma 9.

The set E can still be computed by a $\textbf{para}\textbf{L}$-machine: To check whether an edge $(C,C')$ is present, we simply loop over all values for the next $\log |x|$ nondeterministic bits and verify whether the corresponding sequence of configurations starting from C is a path ending in $C'$ in the configuration graph of M on input (x, k). Consequently, the construction yields a para-logspace parsimonious reduction. $\square$

As the length of paths that are counted in $\mathrm {p\text{- }}\#\textrm{REACH}$ is k, the runtime of the whole algorithm used to prove membership in the previous theorem is actually bounded by $k \cdot \log |x|$ on input (x, k). This means that the computation is tail-nondeterministic. Also, it may be noted that query access to the input is necessary to ensure tail-nondeterminism. Apart from Theorem 16 we need this assumptions in Theorems 21 and 14.

Theorem 16

$\mathrm {p\text{- }}\#\textrm{REACH}$ is $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$.

Proof

This almost immediately follows from the proof of Theorem 15. For membership, first observe that finding the j-th successor is not a problem thanks to the RAM access. Furthermore, the runtime of the modified algorithm described in that proof is bounded by $O(k \cdot \log n)$, and hence the algorithm is already tail-nondeterministic. For hardness, it suffices that the problem is $\#\textbf{para}_\beta \textbf{L}$-hard and $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L} \subseteq \#\textbf{para}_\beta \textbf{L}$. $\square$

The previous results together with the fact that $\#\textbf{para}_\beta \textbf{L}$ is closed under $\le ^{\textrm{plog}}_{\textrm{pars}}$ yield the following surprising collapse (a similar behaviour was observed by Bottesch [37, 38]).

Corollary 17

$[\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L} ]^{\le ^{\textrm{plog}}_{\textrm{pars}}} = \#\textbf{para}_\beta \textbf{L}$.

We continue with another variant of $\mathrm {p\text{- }}\#\textrm{LOG}\textrm{REACH}_b$, namely $\mathrm {p\text{- }}\#\textrm{LOG}\textrm{WALK}_b$. Here, all walks of length a are counted, if $a \le k \cdot \log |x|$ (and s, t are not part of the input).

Theorem 18

$\mathrm {p\text{- }}\#\textrm{LOG}\textrm{WALK}_b$ is $\#\textbf{para}_\beta \textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_T$.

Proof

For membership, we use Algorithm 1 but nondeterministically guess nodes $s,t\in V$.

For hardness, let $F\in \#\textbf{para}_\beta \textbf{L}$ via the machine M. Without loss of generality assume that M is in the normal form from Lemma 9 and that f is a computable function such that on input (x, k), M uses exactly $f(k) \cdot \log |x|$ nondeterministic bits.

Similarly as in the proof of Theorem 14, let ${\mathfrak {G}}(x,k)=(V(x,k),E(x,k))$ be the modified configuration graph where edges represent one nondeterministic step and an arbitrary number of deterministic steps. Furthermore, we extend ${\mathfrak {G}}(x,k)$ by adding a path of fresh vertices $v_1,\dots ,v_{\log |x|}$ with $(v_i,v_{i+1})\in E(x)$ for $1\le i<\log |x|$. The reason for this construction lies in possible “bad” paths that start in some configuration that is not reachable from the starting configuration, but end in the unique accepting configuration. Such paths are depicted in Fig. 2.

Fig. 2

Construction of ${\mathfrak {G}}(x)$ in the proof of Theorem 18. The black chains of unnamed vertices depict possibly occurring “bad” configuration sequences in the configuration graph that should not be considered as they are unreachable from the initial configuration

Furthermore, without loss of generality we assume $|V(x,k)| \ge |x|$.

Now, any path in ${\mathfrak {G}}(x,k)$ going from $v_1$ to the initial configuration s(x, k) and then to the accepting configuration t is of length $\ell (x,k) :=(f(k)+1)\cdot \log |x|$. Notice, that the number of such $v_1$-t-paths is equivalent to the number of accepting paths of M on input x.

Next, consider the graph ${\mathfrak {G}}'(x,k)$ obtained from ${\mathfrak {G}}(x,k)$ by removing the edge $(v_1, v_2)$. This ensures that in ${\mathfrak {G}}'(x,k)$, among paths of length $\ell (x,k)$, exactly the “good” accepting paths are missing compared to ${\mathfrak {G}}(x,k)$. Consequently, the number of accepting computation paths $\#\textrm{acc}_M(x,k)$ is exactly the difference between the number of paths of length $\ell (x,k)$ in ${\mathfrak {G}}(x,k)$ and in ${\mathfrak {G}}'(x,k)$:

$$\begin{aligned} \#\textrm{acc}_M(x,k)&= \mathrm {p\text{- }}\#\textrm{LOG}\textrm{WALK}_b({\mathfrak {G}}(x,k), \ell (x,k), f(k)+1) \\&\quad -\mathrm {p\text{- }}\#\textrm{LOG}\textrm{WALK}_b({\mathfrak {G}}'(x,k), \ell (x,k), f(k)+1). \end{aligned}$$

These numbers of paths cannot be stored on the worktape as they are only bounded by $2^{\ell (x,k)} = 2^{(f(k)+1) \cdot \log |x|}$. Hence, for a $\le ^{\textrm{plog}}_T$-reduction, we need to compute the difference bit by bit by querying both oracles for each bit and only storing the carry bit and a counter for the current position in the output. As the output only has $O((f(k)+1) \cdot \log |x|)$ many bits, this is possible in para-logspace. $\square$

Remark 19

Though the completeness in Theorem 18 is stated for Turing reductions, the reduction does not use the full power of Turing reductions. In fact, we need only a difference of the results of two queries. Such a reduction is studied in the literature and is known as a subtractive reduction [61]. Due to the technicalities involved in extending the notion of subtractive reductions to the parameterised logspace setting, we have stated the completeness for Turing reductions.

Furthermore, one might think that a simple layering of the graph might be enough to make the reduction parsimonious instead of Turing. However, this does not work, for the target problem counts all walks of given length, not only s-t-walks. However, we need to extract the number of s-t-paths in the configuration graph. It is not clear how layering helps here. Even with layering, $p\text{- }\#\text {LOGWALK}_{\text {b}}$ will count the number of walks from the first layer to the last layer. We will still need two queries.

It may be noted that the decision versions of the problems $\mathrm {p\text{- }}\#\textrm{REACH}$ and $\mathrm {p\text{- }}\#\textrm{LOG}\textrm{REACH}_b$ are complete for the respective decision complexity classes. Stockhusen [51] presents path variants of these problems and proves completeness for those problems. However, Stockhusen considers paths of length at most k, where as our variants seek paths of length exactly k. We do not know if the counting versions of the path related problems in [51] are contained in the corresponding counting classes. It will be interesting to see if the counting versions of parameterised path problems in [51] characterise the corresponding counting classes as well.

4.2 Counting FO-Assignments

Let $\mathcal {F}$ be a class of first-order formulas. The problem of counting satisfying assignments to free $\textrm{FO}$-variables in $\mathcal {F}$-formulas, $p\text{- }\#\textrm{MC}(\mathcal {F})$, is defined as follows.

Here, ${\varphi }(\textbf{A})$ is the set of satisfying assignments of ${\varphi }$ in $\textbf{A}$:

$$\begin{aligned} {\varphi }(\textbf{A}) = \{\,(a_1,\ldots , a_n) \in \textrm{dom}(\textbf{A})^n \mid {\textbf{A}}\models \varphi (a_1,\ldots , a_n)\,\}. \end{aligned}$$

We investigate parameterisations of variants of this problem and in this way obtain complete problems for some of our new complexity classes in the setting of first-order model-checking.

Denote by $p\text{- }\#\textrm{MC}(\mathcal {F})_a$ the variant where for all relations the arity is at most $a\in {\mathbb {N}}$. Furthermore, we consider a fragment of $\textrm{FO}$ obtained by restricting the occurrence of variables in the syntactic tree of a formula in a purely syntactic manner. Formally, the syntax tree of a quantifier-free $\textrm{FO}$-formula $\varphi$ is a tree with edge-ordering whose leaves are labelled by atoms of $\varphi$ and whose inner vertices are labelled by Boolean connectives. We now introduce a purely syntactical notion of locality. Note that the definition for the ${\varSigma }_i$-classes can be found at page 18 in the subsection on ‘Logic’ within the preliminaries.

Definition 20

Let $r \in \mathbb {N}$ and ${\varphi }$ be a quantifier-free $\textrm{FO}$-formula. Let ${\theta }_1, \dots , {\theta }_m$ be the atoms of ${\varphi }$ in the order of their occurrence in the standard encoding of ${\varphi }$ as a string. We say that ${\varphi }$ is r-local if for any ${\theta }_i$, ${\theta }_j$ that involve the same variable, we have $|i-j| \le r$.

We define ${\varSigma }_{0}^{r\text {-local}} :=\{\,\varphi \in {\varSigma }_0\mid \varphi \text { is r-local}\,\}.$

Using this syntactic notion of locality, we obtain a complete problem for our classes with read-once access to nondeterministic bits in the setting of first-order model-checking. The following proofs will utilise the straightforward model-counting algorithm for ${\varSigma }_0$-formulae of bounded arity, see Algorithm 2.

Theorem 21

For $a\ge 2,r\ge 1$, $\mathrm {p\text{- }}\#\textrm{MC}({\varSigma }_{0}^{r\text {-local}})_a$ is $\#\textbf{para}_\beta \textbf{L}$-complete and $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$.

Proof

Let us start with a proof idea. Regarding membership, Algorithm 2 can be used with a slight modification. Note that the whole running time of the algorithm is bounded by $f(|\varphi |)\cdot \log |\textbf{A}|$ for some computable function f and thereby the procedure is tail-nondeterministic. Furthermore, we need to ensure that any assignment to a free variable, which is stored globally, is removed when the variable cannot occur anymore due to r-locality. After removing an assignment, the space can be reused for further assignments in the computation. For this, note that the algorithm visits the atoms in the order of their occurrence in the standard encoding of ${\varphi }$ as a string. Hence, r-locality ensures that the number of assignments that need to be stored at any point is bounded sufficiently.

Regarding the lower bound, we reduce from $\mathrm {p\text{- }}\#\textrm{REACH}$ and use the formula

$$\begin{aligned} {\varphi }_k(x_1, \dots , x_k) :=(x_1 = {\textsf{s}}) {\wedge }{\textsf{E}}(x_1, x_2) {\wedge }{\textsf{E}}(x_2, x_3) \wedge \dots \wedge {\textsf{E}}(x_{k-1}, x_k) {\wedge }x_k = {\textsf{t}} \end{aligned}$$

expressing that a tuple of vertices $(v_1, \dots , v_k)$ is an ${\textsf{s}}^{\textbf{A}}$-${\textsf{t}}^{\textbf{A}}$-walk in an $({\textsf{E}},{\textsf{s}},{\textsf{t}})$-structure $\textbf{A}$.

Now, we are ready to present the proof details. We show both completeness results by showing membership in $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$ and hardness for $\#\textbf{para}_\beta \textbf{L}$.

For membership, let ${\varphi }\in {{\varSigma }_{0}^{r\text {-local}}}$ be a formula over some vocabulary ${\sigma }$ of bounded arity, $\textbf{A}$ be a ${\sigma }$-structure and $k \in \mathbb {N}$. Without loss of generality, $|{\varphi }| \le k$, since we can immediately reject otherwise. Now Algorithm 2 can be used to count the satisfying assignments of ${\varphi }$ in $\mathcal {A}$. Here, the assignments for variables are guessed nondeterministically whenever a variable first occurs and are stored globally. The only parts of the algorithm that depend on the structure $\mathcal {A}$ are the stored assignments as well as the tuples written to the relation query tape. Hence, the space needed for book-keeping of the recursion is bounded by a computable function in $|{\varphi }| \le k$. As ${\varphi }$ has bounded arity, the tuples written to the relation query tape are of size $O(\log n)$. Also, the total number of nondeterministic bits used by the algorithm is k-bounded, as there are at most $|{\varphi }| \le k$ variables and each gets an assignment of $O(\log n)$ bits.

Leaving the algorithm unchanged means that we also need $O(k \log n)$ bits to store all assignments. To avoid this, we use the fact that ${\varphi }$ is r-local and has bounded arity. We store any assignment $x_i \mapsto a$ as the pair (i, a) followed by the delimiter $\#$. By r-locality, we can then remove any assignment after evaluating r more atoms and reuse the space. For this, after reaching an atom, we check for all assignments that are currently stored how many atoms occur in ${\varphi }$ before the first occurrence of that variable and the current atom. If this number exceeds r, the assignment can be removed. This means that at any point during the computation, we store an assignment only for the variables that occurred in the previous r atoms, that is, for at most $a\cdot r$ variables.

Finally, we need to argue that the algorithm is tail-nondeterministic. This is trivial, as the running time of the whole algorithm is k-bounded. For this, observe that the size of the recursion tree of the algorithm is bounded by a computable function in the parameter. Furthermore, the running time for connectives is constant, while the running time for atoms is bounded by the time needed to search for a constant number of assignments as well as writing a tuple on the relation query tape. As the space needed by all assignments is in $O(\log n)$ and the tuples written to the relation query tape are of bounded arity, both operations can be done in time $O(\log n)$. This means that the running time of the algorithm is k-bounded and, consequently, it is tail-nondeterministic.

To show hardness, we reduce from $\mathrm {p\text{- }}\#\textrm{REACH}$, which is $\#\textbf{para}_\beta \textbf{L}$-complete by Theorem 15. Define the vocabulary ${\sigma }:=({\textsf{E}},{\textsf{s}},{\textsf{t}})$. Fix an input $(({\mathfrak {G}}= (V,E), s,t), k)$ of $\mathrm {p\text{- }}\#\textrm{REACH}$. The formula

$$\begin{aligned} {\varphi }_k(x_1, \dots , x_k) :=(x_1 = {\textsf{s}}) {\wedge }{\textsf{E}}(x_1, x_2) {\wedge }{\textsf{E}}(x_2, x_3) \wedge \dots \wedge {\textsf{E}}(x_{k-1}, x_k) {\wedge }x_k = {\textsf{t}} \end{aligned}$$

expresses that a tuple of vertices $(v_1, \dots , v_k)$ is an ${\textsf{s}}^{\textbf{A}}$-${\textsf{t}}^{\textbf{A}}$-walk in the input structure $\textbf{A}$. We define the ${\sigma }$-structure $\textbf{G}$ as (V, E, s, t). By construction, the number of satisfying assignments of ${\varphi }$ in structure $\textbf{G}$ is exactly the number of s-t-paths of length k in ${\mathfrak {G}}$. Also, $|{\varphi }|$ is bounded by k. As a result, the mapping $(({\mathfrak {G}}, \textsf {s}, \textsf {t}), k) \mapsto (({\varphi }_k, \textbf{G}), |{\varphi }|)$ is the desired reduction. $\square$

We will now consider the more general problem $p\text{- }\#\textrm{MC}({\varSigma }_0)_a$ for $a \in {\mathbb {N}}$ and show that it is complete for tail-nondeterministic para-logspace with multiple-read access to nondeterministic bits. Note that the decision version of $p\text{- }\#\textrm{MC}({\varSigma }_0)_a$ asks whether there is an assignment to the free variables satisfying the formula. Hence, the free variables can be viewed as existentially quantified and the problem is equivalent to parameterised model-checking for ${\varSigma }_1$-sentences. This problem has received wide attention in the literature [2, Chapter 7.4]. We prove:

Theorem 22

For $a \ge 3$, $p\text{- }\#\textrm{MC}({\varSigma }_0)_a$ is $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$ reductions.

Proof

Membership in $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ again follows from a modified version of Algorithm 2. Here, the modification consists of using the contents of the choice tape as assignments to the free variables. The number of nondeterministic bits needed is still in $O(k \cdot \log n)$, where k is the parameter and n is the input length. As we have multiple-read access to the choice tape, we do not need to store the assignments on a work tape. Instead, we copy them to the relation query tape directly from the choice tape whenever needed. This means that the considerations for space and running time given in the proof of Theorem 21 mostly still apply. The only difference comes from the time needed to access an assignment. To access the assignment to a single variable, we at most need to go over the whole relevant part of the choice tape once and copying a word of length $O(\log n)$, needing time at most $O(k \log n)$ in total. As there are at most $|{\varphi }| \le k$ occurrences of variables in the formula, accessing the correct assignments and copying them to the relation query tape needs time at most $O(k^2 \log n)$ in total. In total, this still results in a k-bounded running time, meaning that the algorithm is still tail-nondeterministic.

Regarding hardness, let $F\in \#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ via the NTM M. Without loss of generality, assume that M is in the normal form from Lemma 9. Furthermore, let f be a computable function such that M is $O(\log |x|+f(k))$ space-bounded and M uses exactly $f(k)\cdot \log |x|$ nondeterministic bits on any input (x, k). Fix an input (x, k). The idea for the reduction is to construct from (x, k) the configuration graph of M on input (x, k) as a first-order structure $\textbf{A}$ together with a formula ${\varphi }(\overline{b})$. The formula ${\varphi }$ expresses that M accepts (x, k), if the choice tape contains the binary word encoded by $\overline{b}$.

A naive approach would now be to use a relation ${\textsf{R}}$ with the following interpretation. Let $(C, C', \overline{b}) \in {\textsf{R}}^{\textbf{A}}$, if $C'$ is reached from C in the computation of M, when the choice tape contains the binary word encoded by $\overline{b}$. The problem is that this would lead to the size of $\textbf{A}$ not being fpt-bounded. Hence, we instead construct ${\textsf{R}}^{\textbf{A}}$ in such a way that $(C, C', a) \in {\textsf{R}}^{\textbf{A}}$, if $C'$ is reached from C using exactly $\log |x|$ nondeterministic and any number of deterministic steps in the computation of M, when the nondeterministic bits accessed by M in these steps are exactly the bits of a. As a now only needs to encode $\log |x|$ bits, the resulting structure is fpt-bounded.

As it is not clear in advance which bits of $\overline{b}$ are used at what point of the computation, we need an additional tuple $\overline{a}$ of free variables encoding the actual nondeterministic bits encountered in the computation. Moreover, we need additional relation symbols ${\textsf{S}}_0, \dots , {\textsf{S}}_{f(k)-1}$ specifying whether the bits of $\overline{a}$ actually encode the nondeterministic bits encountered by the computation of M starting from a given configuration, when the choice tape contains the binary word encoded by $\overline{b}$.

This is done by letting $(C, a, b) \in {\textsf{S}}_j^{\textbf{A}}$, if the bits of a being the actual next $\log |x|$ nondeterministic bits accessed by M starting from configuration C is consistent with b encoding the content of the j-th block of length $\log |x|$ on the choice tape. More precisely: Consider the next $\log |x|$ nondeterministic configurations reached by M starting from C, when the bits of a are the bits read from the choice tape in these steps. Let $\textrm{pos}_1, \dots , \textrm{pos}_{\log |x|}$ be the indices of the cells of the choice tape accessed in those configurations in the order they are reached. Now $(C, a, b) \in {\textsf{S}}_j^{\textbf{A}}$ means that for all i, if $\textrm{pos}_i$ lies in the j-th block of length $\log |x|$ on the choice tape, i.e. $\lfloor \textrm{pos}_i / \log |x|\rfloor = j$, then the i-th bit of a is exactly the corresponding bit on the choice tape as given by b, i.e. the i-th bit of a equals the $(\textrm{pos}_i \mathop {\textrm{MOD}} \log |x|)$-th bit of b. In this construction, both $\overline{a}$ and $\overline{b}$ are tuples of arity f(k) and each element encodes a binary word with $\log |x|$ bits.

Finally, we need the constants ${\textsf{C}}_0$ and ${\textsf{C}}_{\text {acc}}$ for the first nondeterministic configuration of M on input (x, k) and the unique accepting configuration, respectively. This results in the vocabulary ${\sigma }= ({\textsf{R}}^3, {\textsf{S}}_0^3, \dots , {\textsf{S}}_{f(k)-1}^3; {\textsf{C}}_0, {\textsf{C}}_{\text {acc}})$.

Given the above construction of $\textbf{A}$ and ${\sigma }$, we can now define ${\varphi }$ as follows:

$$\begin{aligned} {\varphi }(\overline{b}, \overline{a}, \overline{x}) :=x_0 = {\textsf{C}}_0 {\wedge }x_{f(k)} = {\textsf{C}}_{\text {acc}}{\wedge }\bigwedge _{i=0}^{f(k)-1} \Big ( {\textsf{R}}(x_i, x_{i+1}, a_i) {\wedge }\!\!\bigwedge _{j=0}^{f(k)-1}\!\! {\textsf{S}}_j(x_i, a_i, b_j) \Big ), \end{aligned}$$

where $\overline{b} = (b_0, \dots , b_{f(k)-1})$, $\overline{a} = (a_0, \dots , a_{f(k)-1})$, and $\overline{x} = (x_0, \dots , x_{f(k)})$. On a high level, ${\varphi }$ expresses that ${\textsf{C}}_{\textrm{acc}}$ is reached from ${\textsf{C}}_0$ within f(k) batches of $\log |x|$ steps each, when the choice tape contais the binary word encoded by $\overline{b}$. This is done as follows: The tuple $\overline{x}$ encodes a sequence of configurations starting from the first nondeterministic configuration and ending in the unique accepting configuration. Using ${\textsf{R}}$, ${\varphi }$ expresses that configuration $x_{i+1}$ is reached from $x_i$ in exactly $\log |x|$ nondeterministic steps and any number of deterministic steps in the computation of M, provided that $a_i$ encodes the nondeterministic bits that are accessed in these steps. Using the relations ${\textsf{S}}_j$, the formula further expresses that $a_i$ encodes the actual nondeterministic bits accessed within the i-th batch, when $\overline{b}$ encodes the content of the choice tape. For correctness, also note that, if ${\varphi }$ is satisfiable, the assignments to both $\overline{a}$ and $\overline{x}$ are uniquely determined by the assignment to $\overline{b}$. $\square$

Having seen in Corollary 17 that $[\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L} ]^{\le ^{\textrm{plog}}_{\textrm{pars}}} = \#\textbf{para}_\beta \textbf{L}$, we want to conclude this subsection with the question of whether the $\le ^{\textrm{plog}}_{\textrm{pars}}$-closure of $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ also coincides with some known class.

Open Problem 2

Is the class $[\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L} ]^{\le ^{\textrm{plog}}_{\textrm{pars}}}$ equivalent to some known class?

4.3 Counting Homomorphisms

This subsection is devoted to the study of the problem of counting homomorphisms between two structures in the parameterised setting. Typically, the size of the universe of the first structure is considered as the parameter. The complexity of counting homomorphisms has been intensively investigated for almost two decades [34,35,36, 62].

Definition 23

(Homomorphism) Let $\textbf{A}$ and $\textbf{B}$ be structures over some vocabulary $\tau$ with universes A and B, respectively. A function $h:A\rightarrow B$ is a homomorphism from $\textbf{A}$ to $\textbf{B}$ if for all ${\textsf{R}}\in \tau$ and for all tuples $(a_1,\dots , a_{\textrm{arity}({\textsf{R}})})\in {\textsf{R}}^{\textbf{A}}$, we have $(h(a_1),\dots ,h(a_{\textrm{arity}({\textsf{R}})})) \in {\textsf{R}}^{\textbf{B}}$.

A bijective homomorphism h between two structures $\textbf{A},\textbf{B}$ such that the inverse of h is also a homomorphism is called an isomorphism. If there is an isomorphism between $\textbf{A}$ and $\textbf{B}$, then $\textbf{A}$ is said to be isomorphic to $\textbf{B}$.

Definition 24

Let $\textbf{A}$ be a structure with universe A. We denote by $\textbf{A}\!^*$ the extension of $\textbf{A}$ by a fresh unary relation symbol ${\textsf{C}}_a$ interpreted as ${\textsf{C}}_a^{\textbf{A}}=\{a\}$ for each $a\in \textrm{dom}(\textbf{A})$. For a class of structures $\mathcal {A}$, we analogously denote the class $\{\,\textbf{A}\!^*\mid \textbf{A}\in \mathcal {A}\,\}$ by $\mathcal {A}^*$.

Define $\mathrm {p\text{- }}\#\textrm{Hom}(\mathcal {A})$ as the following problem. Given a pair of structures $(\textbf{A},\textbf{B})$ where $\textbf{A}\in \mathcal {A}$, and parameter k, output the number of homomorphisms from $\textbf{A}$ to $\textbf{B}$, if $|\textrm{dom}(\textbf{A})| \le k$, and 0 otherwise.

Notice that $\textbf{B}$ can be any structure.

For $n \ge 2$, let $P_n$ be the canonical undirected path of length n, that is, the $({\textsf{E}})$-structure with universe $\{1, \dots , n\}$ and ${\textsf{E}}^{P_n} = \{\,(i,i+1),(i+1,i)\mid 1 \le i < n\,\}$. Let $\mathcal {P}$ be the class of structures isomorphic to some $P_n$. We next want to show that $\mathrm {p\text{- }}\#\textrm{Hom}(\mathcal {P}^*)$ is $\#\textbf{para}_\beta \textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$. For this, we will reduce to $\mathrm {p\text{- }}\#\textrm{REACH}$ for membership, and from a normalised, coloured variant of $\mathrm {p\text{- }}\#\textrm{REACH}$ for hardness. We begin by introducing said variant and showing that it is still $\#\textbf{para}_\beta \textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$. Here, a colouring function $\ell :V\rightarrow \{1,\dots ,m\}$ for some $m \in \mathbb {N}$ is given as an additional part of the input.

Lemma 25

$\mathrm {p\text{- }}\#\textrm{REACH}^*$ is $\#\textbf{para}_\beta \textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$.

Proof sketch

The proof is very similar to that of Theorem 15. For membership, the algorithm additionally needs to check in each step of the path whether the guessed successor is consistent with the labeling.

Regarding hardness, we outline the main difference and the process of labeling the vertices. Let $F\in \#\textbf{para}_\beta \textbf{L}$ via a k-bounded $\log$-space NTM M which has read-once access to nondeterministic bits. Consider an input (x, k) and let ${\mathfrak {G}}=(V,E)$ be the configuration graph of M on input (x, k) as defined in the proof of Theorem 15. For a nondeterministic configuration $C\in V$, let $\ell (C)$ be the number represented in tape S in the configuration C. Now it is not hard to see that $F(x,k) = \mathrm {p\text{- }}\#\textrm{REACH}^*({\mathfrak {G}},s,t,\ell )$, where s is the first nondeterministic configuration reachable from the initial configuration of M on (x, k) and t is the unique accepting configuration of M. $\square$

Theorem 26

$\mathrm {p\text{- }}\#\textrm{Hom}(\mathcal {P}^*)$ is $\#\textbf{para}_\beta \textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$.

Proof

Fig. 3

Example for the membership proof of Theorem 26

Regarding membership, we will show $\mathrm {p\text{- }}\#\textrm{Hom}(\mathcal {P}^*)\le ^{\textrm{plog}}_{\textrm{pars}}\mathrm {p\text{- }}\#\textrm{REACH}$, where the latter is in $\#\textbf{para}_\beta \textbf{L}$ by Theorem 15. The proof idea is visualised in Fig. 3 with an example. Consider an arbitrary input $((\textbf{A},\textbf{B}), k)$ to $\mathrm {p\text{- }}\#\textrm{Hom}(\mathcal {P}^*)$ with $\textrm{FO}$-structures $\textbf{A}, \textbf{B}$ and $k \in \mathbb {N}$. By definition of the problem we have $\textbf{A}\in \mathcal {P}^*$. Let $A = \textrm{dom}(\textbf{A}), B = \textrm{dom}(\textbf{B})$. We assume that $\textbf{A}$ and $\textbf{B}$ have the same underlying vocabulary ${\sigma }$ and $|A| \le k$, since the remaining cases can easily be handled. Let ${\textsf{E}}$ be the edge relation symbol in ${\sigma }$. Furthermore, let $A=\{a_1,\dots ,a_{n}\}$ with $n\in \mathbb {N}$ be the universe of $\textbf{A}$ such that $(a_i,a_{i+1})\in {\textsf{E}}^{\textbf{A}}$ and let B be the universe of $\textbf{B}$.

Now, define the directed graph ${\mathfrak {G}}=(B\cup \{s,t\},E')$ with $s,t\notin B$ and

$$\begin{aligned} E':=&\{\,(s,x)\mid x\in {\textsf{C}}_{a_1}^{\textbf{B}}\,\}\cup \\&\{\,(x,y)\in {\textsf{E}}^{\textbf{B}}\mid \exists 1\le i\le n: x\in {\textsf{C}}_{a_i}^{\textbf{B}}, y\in {\textsf{C}}_{a_{i+1}}^{\textbf{B}} \,\}\cup \\&\{\,(x,t)\mid x\in {\textsf{C}}_{a_n}^{\textbf{B}}\,\}. \end{aligned}$$

The reduction is given by the mapping $((\textbf{A}, \textbf{B}), k) \mapsto (({\mathfrak {G}}, s, t), |A|+2)$.

We show correctness by giving a 1-1-correspondence between homomorphisms from $\textbf{A}$ to $\textbf{B}$ and s-t-walks in ${\mathfrak {G}}$ of length $|A|+2$. This correspondence is given by the following mapping. Let h be a homomorphism from $\textbf{A}$ to $\textbf{B}$. This homomorphism is bijectively mapped to an s-t-path as follows. The homomorphism yields a sequence $(h(a_1),\dots ,h(a_n))$ with $h(a_i)\in {\textsf{C}}_{a_i}^{\textbf{B}}$, $(h(a_i),h(a_{i+1}))\in {\textsf{E}}^{\textbf{B}}$ for $1\le i<n$. From this, we obtain the s-t-path $(s,h(a_1),\dots ,h(a_n),t)$ in ${\mathfrak {G}}$.

Regarding injectivity, let $h\ne h'$ be two different homomorphisms from $\textbf{A}$ to $\textbf{B}$. As a result, there exists an $1\le i< n$ such that $h(a_i)\ne h'(a_i)$. Consequently, $(s,h(a_1),\dots ,h(a_n),t)\ne (s,h'(a_1),\dots ,h'(a_n),t)$.

Regarding surjectivity, let $(s,v_1,\dots ,v_n,t)$ be an s-t-path in ${\mathfrak {G}}$. Now, $(s,v_1)$, $(v_i,v_{i+1})$, $(v_n,t)\in E'$ for all $1\le i<n$. By construction of $E'$, this means $v_i\in {\textsf{C}}_{a_i}^{\textbf{B}}$ for $1\le i\le n$ and $(v_i,v_{i+1})\in {\textsf{E}}^{\textbf{B}}$ for $1\le i<n$. Consequently, the function h with $h(a_i) = v_i$ for all i is a homomorphism from $\textbf{A}$ to $\textbf{B}$ as well as a preimage of $(s, v_1, \dots , v_n, t)$ under the given mapping.

The reduction can be computed by a $\textbf{para}\textbf{L}$-machine as follows. The vertex set of the graph is just the universe B extended by two new vertices. Store the sequence $a_1,\dots ,a_n$. To compute $E'$, the machine identifies all vertices $x\in {\textsf{C}}_{a_1}^{\textbf{B}}$ and prints for each the edge (s, x); similarly for all edges (x, t) with $x\in {\textsf{C}}_{a_n}^{\textbf{B}}$. Then, for each edge $(x,y)\in {\textsf{E}}^{\textbf{B}}$, we find and store the index i such that $x\in {\textsf{C}}_{a_i}^{\textbf{B}}$ and check whether $y\in {\textsf{C}}_{a_{i+1}}^{\textbf{B}}$ is true. The machine only queries relations of $\textbf{B}$ for individual tuples which can be achieved with binary counters.

For hardness, we show $\mathrm {p\text{- }}\#\textrm{REACH}^*\le ^{\textrm{plog}}_{\textrm{pars}}\mathrm {p\text{- }}\#\textrm{Hom}(\mathcal {P}^*)$. Given a directed graph ${\mathfrak {G}}=(V,E)$, $s,t\in V$, $k\in \mathbb {N}$, $\ell :V\rightarrow \{1,\dots ,k\}$, we define two structures $\textbf{A},\textbf{B}$ as follows. Let the universe of $\textbf{A}$ be defined as $\{1,\dots ,k\}$, ${\textsf{E}}^{\textbf{A}}:=\{\,(i,i+1),(i+1,i)\mid 1\le i<k\,\}$, and ${\textsf{C}}_{i}^{\textbf{A}}:=\{i\}$ for $1\le i\le k$. Define the universe of $\textbf{B}$ as V, ${\textsf{E}}^{\textbf{B}}:=\{\,(u,v),(v,u)\mid (u,v)\in E \text { and } \ell (v) = \ell (u) + 1\,\}$, and ${\textsf{C}}_i^{\textbf{B}}:=\{\,u\mid \ell (u)=i\,\}$.

Regarding correctness, the function that maps each s-t-path $\pi =(s=v_1,\dots ,v_k=t)$ to the homomorphism $h_\pi$ with $h_\pi (i)=v_i$ for all $1\le i\le k$ is a bijective mapping between colour-respecting s-t-paths $\pi$ in ${\mathfrak {G}}$ and homomorphisms $h_\pi$ from $\textbf{A}$ to $\textbf{B}$. The mapping is injective due to the fact that each node in the path contributes to the construction of the homomorphism. The mapping is surjective as for each homomorphism h the path $(h(1),\dots ,h(k))$ is a colour-respecting s-t-path in ${\mathfrak {G}}$ and a preimage of h.

We now argue that the above reduction can be computed in $\textbf{para}\textbf{L}$. The structure $\textbf{A}$ only depends on the parameter. The universe of structure $\textbf{B}$ is a copy. The relation ${\textsf{E}}^{\textbf{B}}$ is the symmetric closure of E (i.e., for every $(u,v) \in E$, ${\textsf{E}}^{\textbf{B}}$ contains both (u, v) and (v, u)) with the additional condition that edges have to be consistent with the labeling function $\ell$. The relations ${\textsf{C}}_i^{\textbf{B}}$ require a $\log |V|$-counter to check for each $u\in V$ whether $\ell (u)=i$. This completes the proof. $\square$

Open Problem 3

Is there a natural class of structures $\mathcal {A}$ such that $\mathrm {p\text{- }}\#\textrm{Hom}(\mathcal {A})$ is $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$-complete with respect to $\le ^{\textrm{plog}}_{\textrm{pars}}$?

4.4 The Parameterised Complexity of the Determinant

In this section, we consider a parameterised variant of the determinant function introduced by Chauhan and Rao [32]. For $n>0$ let $\mathcal {S}_n$ denote the set of all permutations of $\{1,\ldots , n\}$. For each $k\le n$, we define the subset $\mathcal {S}_{n,k}$ of $\mathcal {S}_n$ containing all permutations with exactly k non-fixpoints:

$$\begin{aligned} \mathcal {S}_{n,k} = \{\,\pi \,|\, \pi \in S_n, |\{\,i:\,\pi (i) \ne i\,\}| = k\,\}. \end{aligned}$$

We define the parameterised determinant function of an $n\times n$ square matrix $A = (a_{i,j})_{1 \le i,j \le n}$ as

$$\begin{aligned} p\text{- }\textrm{det}(A,k) = \sum _{\pi \in S_{n,k}} \textrm{sign}(\pi ) \prod _{i: \pi (i) \ne i} a_{i,\pi (i)}. \end{aligned}$$

Remark 27

The reader might wonder why the product in the above definition is over i such that $\pi (i)\ne i$. The original idea in the definition was to have $p\text{- }\textrm{det}$ as a polynomial function of degree bounded by the parameter, so that it will be of use in the development of parameterised algebraic complexity theory. The two notions are equivalent if we ensure that diagonal entries are all 1’s, i.e., the underlying graph has a self-loop at every vertex.

In the following, we will assume that A is a matrix with entries from $\{0,1\}$. Using an interpolation argument, it can be shown that $p\text{- }\textrm{det}$ is in $\textbf{F}\textbf{P}$ when k is part of the input and thereby in $\textbf{F}\textbf{FPT}$ [32]. In fact, the same interpolation argument can be used to show that $p\text{- }\textrm{det}$ is in ${\textbf{Gap}\textbf{L}}$ (the class of functions f(x) such that for some $\textbf{NL}$-machine, f(x) is the number of accepting minus the number of rejecting paths). However, this does not give a space efficient algorithm for $p\text{- }\textrm{det}$ in the sense of parameterised classes. The $\textbf{Gap}\textbf{L}$ algorithm may require a large number of nondeterministic steps and accordingly is not k-bounded. We show that the space efficient algorithm for the determinant given by Mahajan and Vinay [33] can be adapted to the parameterised setting, proving that $p\text{- }\textrm{det}$ can be written as the difference of two $\#\textbf{para}_\beta \textbf{L}$ functions. Recall the notion of a clow sequence introduced by Mahajan and Vinay [33].

Definition 28

(Clow) Let ${\mathfrak {G}}=(V,E)$ be a directed graph with $V = \{1,\ldots , n\}$ for some $n \in \mathbb {N}$. A clow in ${\mathfrak {G}}$ is a walk $C= (w_1,\ldots , w_{r-1}, w_r = w_1)$ where $w_1$ is the minimal vertex among $w_1, \dots , w_{r-1}$ with respect to the natural ordering of V and $w_1 \ne w_j$ for all $1< j < r$. Node $w_1$ is called the head of C, denoted by $\textrm{head}(C)$.

Definition 29

(Clow sequence) A clow sequence of a graph ${\mathfrak {G}}=(\{1,\dots ,n\},E)$ is a sequence ${W} = (C_1,\ldots , C_\ell )$ such that $C_i$ is a clow of ${\mathfrak {G}}$ for $1 \le i \le \ell$ and

• the heads of the sequence are in ascending order, that is, $\textrm{head}(C_1)<\cdots < \textrm{head}(C_\ell )$, and

• the total number of edges (including multiplicities), that is, $|C_1|+\dots +|C_\ell |$, is exactly n, where |C| denotes the number of edges in the clow C.

For a clow sequence W of some graph ${\mathfrak {G}}=(\{1,\dots ,n\}, E)$ consisting of r clows the sign of W, $\textrm{sign}(W)$, is defined as $(-1)^{n+r}$. Note that, if the clow sequence is a cycle cover $\sigma$, then $(-1)^{n+r}$ is equal to the sign of the permutation represented by $\sigma$ (that is, $(-1)^{\#\text {inversions in }\sigma }$). Mahajan and Vinay came up with this sign-function to derive their formula for the determinant.

For an $(n\times n)$-matrix A, ${\mathfrak {G}}_A$ is the weighted directed graph with vertex set $\{1, \dots , n\}$ and weighted adjacency matrix A. For a clow (sequence) W, $\textrm{weight}(W)$ is the product of weights of the edges (clows) in w. For any ${\mathfrak {G}}$ as above, $\mathcal {W}_{{\mathfrak {G}}}$ is the set of all clow sequences of ${\mathfrak {G}}$. Mahajan and Vinay proved that $\det (A) = \sum _{W\in {\mathcal {W}_{{\mathfrak {G}}_A}}} \textrm{sign}(W)\cdot \textrm{weight}(W)$ [33].

We adapt these notions to the parameterised setting. First observe that for a permutation $\sigma \in S_{n,k}$, we have that $\textrm{sign}(\sigma ) = (-1)^{n+r}$, where r is the number of cycles in the permutation. However, the number of cycles in $\sigma$ is $n-k+r'$, where $r'$ is the number of cycles of length at least two in $\sigma$, the rest being fixed points, i.e., self loops. Accordingly, we have $\textrm{sign}(\sigma ) = (-1)^{2n-k+r'}$. Adapting the definition of a clow sequence, for $k \ge 0$, define a k-clow sequence to be a clow sequence where the total number of edges (including multiplicity) in the sequence is exactly k, every clow has at least two edges, and no self loop edge of the form (i, i) occurs in any of the clows. For any graph ${\mathfrak {G}}$ with vertex set $\{1,\dots ,n\}$ for $n \in \mathbb {N}$, ${\mathcal {W}}_{{\mathfrak {G}},k}$ is the set of all k-clow sequences of ${\mathfrak {G}}$. For a k-clow sequence $W \in {\mathcal {W}}_{{\mathfrak {G}},k}$, $\textrm{sign}(W)$ is $(-1)^{2n-k+r'}$, where $r'$ is the number of clows in W. Mahajan and Vinay showed that the signed sum of the weights of all clow sequences is equal to the determinant [33, Theorem 1]. At the outset, this is a bit surprising, since the determinant is equal to the signed sum of weights of cycle covers, whereas there are clow sequences that are not cycle covers. Mahajan and Vinay observed that every clow sequence that is not a cycle cover can be associated with a unique clow sequence of opposite sign, and thereby all such clow sequences cancel out [33]. We observe a parameterised version of the above result [33, Theorem 1].

Lemma 30

$p\text{- }\textrm{det}(A,k) = \sum _{W \in \mathcal{W}_{{\mathfrak {G}}_A,k}}\textrm{sign}(W)\cdot \textrm{weight}(W)$, for a (0, 1)-matrix A, $k \in \mathbb {N}$.

Proof

The statement essentially follows from the arguments of Mahajan and Vinay [33, Theorem 1]. The reader is referred to the original article for a full construction. Their proof involves defining an involution $\eta$ (i.e., $\eta$ is a bijection whose inverse is itself) on the set of clow sequences such that $\eta$ is the identity on the set of all cycle covers (i.e., $\eta (C) = C$ for any cycle cover C) and for any clow sequence W that is not a cycle cover, we have $\textrm{sign}(W) = -\textrm{sign}(\eta (W))$.

We briefly describe the involution $\eta$ given by Mahajan and Vinay [33]. For a clow sequence ${W} =(W_1,\ldots ,W_r)$, the clow sequence $\eta ({ W})$ is obtained from W as follows. Let $i \in \{1, \dots , r\}$ be the smallest index such that clows $W_{i+1}, \ldots , W_r$ are vertex disjoint simple cycles. Traverse the clow $W_i$ starting from the head until we reach some vertex v such that either v is in some $W_j$ for $i+1 \le j\le r$ or v completes a simple cycle within $W_i$. In the former case, we merge the simple cycle $W_j$ with the clow $W_i$ and remove $W_j$ from the sequence to get the clow sequence $\eta (W)$. In the latter case, we split the clow $W_i$ at the vertex v to get a new clow $W_i'$ and a simple cycle $C'$. Then $\eta (W)$ is the clow sequence obtained by replacing $W_i$ by the new clow $W_i'$ and inserting the cycle $C'$ into the resulting clow sequence. The remaining clows in W are kept untouched.

We now give a brief justification for why ${\eta }$ is self-inverse and consequently an involution, which was proven by Mahajan and Vinay [33, Theorem 1]. Restricted to cycle covers, ${\eta }$ is the identity function and hence clearly self-inverse. Otherwise, the operations applied in the two cases of the construction of ${\eta }$ are opposite to each other: In the first case a simple cycle is merged into another clow in the sequence, while in the second case a clow in the sequence is split by extracting a simple cycle from it. Showing that ${\eta }$ is indeed an involution now boils down to verifying the following: Whenever ${\eta }(W)$ is obtained from W by merging two clows, another application of ${\eta }$ will reverse that operation by splitting the merged clow. Whenever ${\eta }(W)$ is obtained from W by splitting a clow, another application of ${\eta }$ will reverse that operation by merging the two parts of the split clow.

We note that the involution $\eta$ described above does not require that the clow sequence W has exactly n edges. In particular, $\eta (W)$ is well defined even when $W \in \mathcal{W}_{{\mathfrak {G}},k}$ for some graph ${\mathfrak {G}}$. Furthermore, for $W \in \mathcal{W}_{{\mathfrak {G}},k}$ we have $\eta (W) \in \mathcal{W}_{{\mathfrak {G}},k}$ and $\textrm{sign}(W) = -\textrm{sign}(\eta (W))$, since $\eta (W)$ has the same number of edges as W and in case that W is not a cycle cover either has one clow more than W or one clow less than W. Combining with the argument that $\eta$ is indeed an involution, and that $p\text{- }\textrm{det}(A,k)$ is the alternating sum of weights of cycle covers with exactly k non-self-loop edges, we get:

$$\begin{aligned} p\text{- }\textrm{det}(A,k) = \sum _{W \in \mathcal{W}_{{\mathfrak {G}}_A, k}}\textrm{sign}(W)\cdot \textrm{weight}(W). \end{aligned}$$

This concludes the proof. $\square$

Using this characterisation, the upper bound in the following theorem can be obtained. For hardness a reduction from $\mathrm {p\text{- }}\#\textrm{REACH}$ suffices.

Theorem 31

The problem $p\text{- }\textrm{det}$ for (0, 1)-matrices can be written as the difference of two functions in $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$, and is $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$-hard with respect to $\le ^{\textrm{plog}}_{\textrm{met}}$.

Proof

We prove this using a parameterised version of the algorithm given by Mahajan and Vinay [33, Thm. 2]. Let A be the adjacency matrix of a directed graph ${\mathfrak {G}}$. We construct two k-bounded nondeterministic $\textbf{para}\textbf{L}$-machines $M_0$ and $M_1$ that have read-once access to their nondeterministic bits such that $p\text{- }\textrm{det}(A,k) = \#\textrm{acc}_{M_0}(A,k) -\#\textrm{acc}_{M_1}(A,k).$

Both $M_0$ and $M_1$ behave exactly the same except for the last step, where their answer is flipped. More precisely, both machines nondeterministically guess a k-clow sequence, and $M_0$ accepts if the guessed clow sequence has a positive sign while $M_1$ accepts if the guessed clow sequence has a negative sign. Then, it follows from Lemma 30 that $p\text{- }\textrm{det}(A,k) =\#\textrm{acc}_{M_0}(A,k) -\#\textrm{acc}_{M_1}(A,k).$

Now, we describe the process of guessing nondeterministic bits. The process is the same for both $M_0$ and $M_1$. We need the following variables throughout the process: curr-head, curr-vertex, parity, count, ccount. The variable curr-head contains the head of the clow currently being constructed, while parity holds the sign of the partial clow sequence constructed so far and is initialised to $(-1)^{2n-k}$. In fact, for a partial clow sequence $\mathcal{W}$, its sign is defined as $(-1)^{2n-k+r'}$, where $r'$ is the number of clows in $\mathcal{W}$. Note that we have choosen $(-1)^{2n-k}$ as the initial value of parity because we are going to compute the sign of a clow sequence W as $(-1)^{2n-k+r'}$, where $r'$ is the number of clows in W with at least two edges. The variable count keeps track of the total number of edges used in the partial clow sequence constructed so far and ccount keeps track of the number of edges in the current clow. The machines $M_0$ and $M_1$ are described in Algorithm 3.

Note that the guess $a=0$ in step 5 leads to expansion of the current clow with addition of a newly guessed edge. The guess $a=1$ in step 5 leads to completion of the current clow by chosing the back edge to the head (step 10, only the existence of such an edge needs to be checked), and guessing the head for a new clow. Since the parity of the number of clows changes for the case when $a=1$, we flip the parity (step 16). Note that the algorithm reaches step 20 if and only if the nondeterministic choices correspond to a clow sequence with exactly k edges. Hence, for $b \in \{0,1\}$ the machine $M_b$ accepts on all nondeterministic paths where the guessed k-clow sequence has sign $(-1)^b$ which completes the correctness proof.

Since both $M_0$ and $M_1$ guess exactly k vertices, they are k-bounded. Also, only curr-vertex and curr-head need to be stored at any point of time, consequently the machines only need read-once access to nondeterministic bits. Finally, the machines use $O(\log |A| + \log k)$ space and are tail-deterministic, taking only $O(k\cdot \log |A|)$ steps after the first nondeterministic step.

For hardness we give a reduction from $\mathrm {p\text{- }}\#\textrm{REACH}$. Note that, even when the input graph is a directed acyclic graph (i.e., a DAG), $\mathrm {p\text{- }}\#\textrm{REACH}$ remains $\#\textbf{para}_{\beta {\textbf{tail}}}\textbf{L}$ hard. Let ${\mathfrak {G}},s,t$ be an instance of $\mathrm {p\text{- }}\#\textrm{REACH}$, where ${\mathfrak {G}}$ is a DAG. Let ${\mathfrak {G}}'$ be the graph obtained by adding the “back edge” (t, s) to ${\mathfrak {G}}$. Note that the set of all s-t paths in ${\mathfrak {G}}$ is in bijective correspondence with the set of cycles in ${\mathfrak {G}}'$. This correspondence is given by mapping any s-t path to the cycle obtained by adding the edge (t, s) to that path. As each cycle in ${\mathfrak {G}}'$ contains the edge (t, s), this means that there is also a bijection between the set of s-t paths in ${\mathfrak {G}}$ of length k and the set of clow sequences consisting of one simple cycle and containing $k+1$ edges in ${\mathfrak {G}}'$. More precisely: Let $A'$ be the adjacency matrix of ${\mathfrak {G}}'$. Then $p\text{- }\textrm{det}(A',k+1) = (-1)^{2n-k}\cdot R$ where R is the number of s-t paths in ${\mathfrak {G}}$. As a result, R can be retrieved from $p\text{- }\textrm{det}(A',k)$ in deterministic logspace. This completes the proof. $\square$

5 Conclusions and Outlook

We developed foundations for the study of parameterised space complexity of counting problems. Our results show interesting characterisations for classes defined in terms of k-bounded para-logspace NTMs. We believe that our results will lead to further research of parameterised logspace counting complexity. Notice that the studied walk problems in Sect. 4.1 can be considered restricted to DAGs yielding the same completeness results.

Comparing our newly introduced classes to the -hierarchy (which is defined in terms of weighted satisfiability problems for circuits of so-called bounded weft), one might ponder whether there is an alternative definition of our classes in terms of such circuit satisfiability problems. While we did not explore weighted satisfiability in this article, the closely related problem $p\text{- }\textrm{MC}({\varSigma }_0)_a$ sheds some light on this. Theorem 22 shows that $p\text{- }\textrm{MC}({\varSigma }_0)_a$ is complete for $\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ (in fact, we show this for their counting versions) under $\le ^{\textrm{plog}}_{m}$-reductions. However, if we take $\textbf{FPT}$-reductions, $p\text{- }\textrm{MC}({\varSigma }_0)_a$ is complete for . Interestingly, this phenomenon is more general as witnessed by the following observation whose proof has been pointed out by an anonymous reviewer.

Observation 32

.

In other words, any problem that is $\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$-complete under $\le ^{\textrm{plog}}_{m}$-reductions is complete for under FPT reductions. To see that this is true, take a ${\textbf {para}}_{{{\textbf {W}}}[1]}{} {\textbf {L}}$-complete problem A under $\le ^{\text {plog}}_{\text {pars}}$-reductions. Now, it suffices that the -complete problem p-$\textrm{CLIQUE}$ $\textbf{FPT}$-reduces to A. Since p-$\textrm{CLIQUE}$ is in $\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ and since A is complete for this class under $\le ^{\textrm{plog}}_{\textrm{pars}}$-reductions, we know p-$\textrm{CLIQUE}$ $\le ^{\textrm{plog}}_{\textrm{pars}}$-reduces to A. But, then p-$\textrm{CLIQUE}$ also $\textbf{FPT}$-reduces to A. Notice that this connection is in line with the even stronger statement from the classical setting that $[\exists \textbf{AC}^0]^{\le ^\textbf{P}_m}=\textbf{NP}$.

One might also ask the question whether $\textbf{para}_{\textbf{W}}\textbf{L}$ is contained in $\textbf{FPT}$. This is unlikely based on the view expressed above. For example, $p\text{- }\textrm{MC}({\varSigma }_0)$ is complete for both $\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ and , albeit under two different reductions. As a result, $\textbf{para}_{\textbf{W}}\textbf{L} \subseteq \textbf{FPT}$ would imply that $p\text{- }\textrm{MC}({\varSigma }_0)\in \textbf{FPT}$ and, accordingly, as $\textbf{FPT}$ is closed under $\textbf{FPT}$-reductions.

We close with interesting tasks for further research:

• Study further closure properties of the new classes (e.g., Open Problem 1).

• Find a characterisation of the $\le ^{\textrm{plog}}_{\textrm{pars}}$-closure of $\#\textbf{para}_{{\textbf{W}}[1]}\textbf{L}$ (Open Problem 2).

• Identify a natural class of structures for which the homomorphism problem is $\#\textbf{para}_{\textbf{W}}\textbf{L}$-complete (Open Problem 3).

• Establish a broader spectrum of complete problems for the classes $\textbf{para}_\beta \textbf{L}$ and $\textbf{para}_{\textbf{W}}\textbf{L}$, e.g., in the realm of satisfiability questions.

• Identify further characterisations of the introduced classes, e.g., in the vein of descriptive complexity, which could highlight their robustness.

• Study gap classes [63] based on our classes. This might help improving Theorem 31 and, more generally, the understanding of the complexity of $p\text{- }\textrm{det}$.

• Investigate relations to branching programs. The characterisation of classes in terms of branching programs only seems to hold for classes with non-tail-nondeterminism. More precisely, one can easily obtain a characterisation of non-tail-nondeterministic classes in the non-uniform setting. Uniform characterisations of the tail-nondeterministic classes in terms of branching programs remains an open question.

• There are recent techniques in the area of counting complexity that might help in further strengthening some of the hardness results, namely, inclusion–exclusion or polynomial interpolation [56] or the graph-motif-parameter framework by Curticapean, Dell and Marx [25]. It seems that inclusion–exclusion can be used to yield a para-logspace Turing reduction in the context of counting homomorphisms. Also, counting answers to an FO-formula without existential quantifiers could yield a para-logspace reduction that is used as a linear combination of homomorphism counts, again. Yet, the concrete details have to be worked out.