Abstract
Computing small kernels for the hitting set problem is a well-studied computational problem where we are given a hypergraph with n vertices and m hyperedges, each of size d for some small constant d, and a parameter k. The task is to compute a new hypergraph, called a kernel, whose size is polynomial with respect to the parameter k and which has a size-k hitting set if, and only if, the original hypergraph has one. State-of-the-art algorithms compute kernels of size \(k^d\) (which is a polynomial as d is a constant), and they do so in time \(m\cdot 2^d {\text {poly}}(d)\) for a small polynomial \({\text {poly}}(d)\) (which is linear in the hypergraph size for d fixed). We generalize this task to the dynamic setting where hyperedges may continuously be added or deleted and one constantly has to keep track of a size-\(k^d\) kernel. This paper presents a deterministic solution with worst-case time \(3^d {\text {poly}}(d)\) for updating the kernel upon inserts and time \(5^d {\text {poly}}(d)\) for updates upon deletions. These bounds nearly match the time \(2^d {\text {poly}}(d)\) needed by the best static algorithm per hyperedge. Let us stress that for constant d our algorithm maintains a hitting set kernel with constant, deterministic, worst-case update time that is independent of n, m, and the parameter k. As a consequence, we also get a deterministic dynamic algorithm for keeping track of size-k hitting sets in d-hypergraphs with update times O(1) and query times \(O(c^k)\) where \(c = d - 1 + O(1/d)\) equals the best base known for the static setting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The hitting set problem is a fundamental combinatorial problem that asks, given a hypergraph, whether there is a small vertex subset that intersects (“hits”) each hyperedge. Many interesting problems reduce to it. A dominating set of a graph is just a hitting set in the hypergraph that for every vertex v contains a hyperedge consisting of the closed neighborhood of v. For any fixed graph H, the question of whether we can delete k vertices from a graph G in order to make G an H-free graph can be reduced to the hitting set problem for the hypergraph to which each occurrence of H in G contributes one hyperedge – and this problem in turn generalizes problems such as triangle-deletion and cluster-vertex-deletion [1]. The hitting set problem also finds applications in the area of descriptive complexity, as a fragment of first-order logic can be reduced to it [2].
The hitting set problem is  -complete [3] and its parameterized version \(\mathrm {p}_{k}\text {-}{{\textsc {hitting}}\text {-}{\textsc {set}}}\) is
-complete [3] and its parameterized version \(\mathrm {p}_{k}\text {-}{{\textsc {hitting}}\text {-}{\textsc {set}}}\) is  -complete [4]. However, if we restrict the size of hyperedges to at most some constant d, the resulting problem \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) lies in
-complete [4]. However, if we restrict the size of hyperedges to at most some constant d, the resulting problem \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) lies in  [5] and even has polynomial kernels. In particular, \(d=2\) is the vertex cover problem, which is still
[5] and even has polynomial kernels. In particular, \(d=2\) is the vertex cover problem, which is still  -complete, but one of the best-investigated parameterized problems. Already the jump from \(d=2\) to \(d=3\) turns out to be nontrivial in this setting. In detail, the inputs for our algorithms are a hypergraph \(H = (V,E)\) and an upper bound k for the size of a hitting set X wanted (a set for which \(e \cap X \ne \emptyset \) holds for all \(e \in E\)). We think of the numbers \(n = \vert V\vert \) and \(m = \vert E\vert \) as large numbers, of k as a (relatively small) parameter, and of \(d = {\text {max}}_{e \in E}\vert e\vert \) as a small constant (already the cases \(d=3\) and \(d=4\) are of high interest).
-complete, but one of the best-investigated parameterized problems. Already the jump from \(d=2\) to \(d=3\) turns out to be nontrivial in this setting. In detail, the inputs for our algorithms are a hypergraph \(H = (V,E)\) and an upper bound k for the size of a hitting set X wanted (a set for which \(e \cap X \ne \emptyset \) holds for all \(e \in E\)). We think of the numbers \(n = \vert V\vert \) and \(m = \vert E\vert \) as large numbers, of k as a (relatively small) parameter, and of \(d = {\text {max}}_{e \in E}\vert e\vert \) as a small constant (already the cases \(d=3\) and \(d=4\) are of high interest).
Parameterized algorithms for the hitting set problem proceed in two steps: First, the input (H, k) is kernelized, which means that we quickly compute a (small) new hypergraph K such that H has a size-k hitting set iff K has one. Afterwards the problem is solved on K using an expensive algorithm based on search trees or iterative compression. The currently best algorithm for computing a kernel with respect to the number of kernel edges is due to Fafianie and Kratsch [6], see also [7, 8] for some recent developments. The cited algorithm outputs a kernel of size \(k^d\) (meaning that K has at most \(k^d\) hyperedges) in time \(m\cdot 2^d {\text {poly}}(d)\) (meaning that time \(2^d {\text {poly}}(d)\) is needed on average per hyperedge of H). The best algorithms for solving the hitting set problem on the computed kernel K run in time \(O(c^k)\), where the exact value of \(c = d - 1 + O(1/d)\) is a subject of ongoing research [9, Section 6] and [10,11,12,13,14]. In summary, on input (H, k) one can solve the hitting set problem in time \(O(2^d{\text {poly}}(d) \cdot m + c^k)\).
Our objective in this paper is to transfer (only) the first part of solving the hitting set problem (namely the computation of the kernel K) into the dynamic setting. Instead of a single hypergraph H being given at the beginning, there is a sequence \(H_0,H_1,H_2,H_3,\dots \) of hypergraphs each of which differs from the previous one by a single edge being either added or deleted. One continuously has to keep track of hitting set kernels \(K_0,K_1,K_2,K_3,\dots \) for the current \(H_i\) (including moments when \(H_i\) has no size-k hitting set). Our aim is to compute the updated kernel \(K_{i+1}\) from \(K_i\) in constant time based solely on the knowledge which edge was added to or deleted from \(H_i\) in order to obtain \(H_{i+1}\).
Doing the necessary bookkeeping to dynamically manage a hitting set kernel is not easy. As an example, consider two hypergraphs H and \(\tilde{H}\) with disjoint vertex sets, were H is a clear no-instance (like a matching of size \(k+1\)) while \(\tilde{H}\) is a hard, borderline case that can only be reduced to a relatively large kernel \(\tilde{K}\). A dynamic kernel algorithm that works on \(H \mathbin {\dot{\cup }} \tilde{H}\) must be able to cope with the situation that we first add all the edges of H (at which point a natural kernel would be a trivial size-1 no-instance K), followed by all the edges of \(\tilde{H}\) (which even underlines the fakt that the trivial no-instance K is a correct kernel for the ever-larger hypergraph), followed by a deletion of the edges from H. At some point during these deletions, a dynamic kernel algorithm must switch from the constant-size K to the large kernel \(\tilde{K}\). Previous work from the literature [15] shows that it is already tricky to achieve this switch in time polynomial in the size of kernels K and \(\tilde{K}\). The challenge we address is to do the updates in constant worst-case time, which forces our dynamic algorithm to spread the necessary changes over time while neither resorting to amortization nor to randomization.
Note that we only give a dynamic algorithm for keeping the kernel up-to-date with constant update times – we make no claims concerning the time needed to actually compute a hitting set for the current kernel \(K_i\) (and, thus, for the current \(H_i\)). Phrased in terms of dynamic complexity theory, there are two different problems for which we present algorithms with differing update times (the time needed for updating internal data structures) and query times (the time needed to construct an output upon request): For the first problem of (just) computing hitting set kernels K for inputs H, we present a dynamic algorithm with constant update time and zero query time (since the current kernel \(K_i\) is explicitly stored in memory as an adjacency matrix at all times). For the second problem of computing size-k hitting sets X for inputs H, our dynamic algorithm also has constant update time (to keep track of kernels \(K_i\)), but has a query time of \(c^k\) (to compute \(X_i\) from \(K_i\), i. e., a hitting set for \(H_i\)). Since in both cases our update times are constant and since it is not hard to see that one cannot improve the query times beyond the time needed by the fastest static algorithm, these bounds are optimal.
Main Result: A Fully Dynamic Hitting Set Kernel In the fully dynamic case where edges may be inserted and deleted over time, the hypergraph may repeatedly switch between having and not having a size-k hitting set. This turns out to be a big obstacle for updating a kernel in just a few steps. Dynamic kernels have already been constructed by Alman, Mnich, and Williams [15]. They present a \(\mathrm {p}_{k}\text {-}{\textsc {vertex}\text {-}\textsc {cover}}\) kernel with O(k) worst-case update time and O(1) amortized update time. For the \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) they achieve a kernel of size \((d-1)!k(k+1)^{d-1}\) with update time \((d!)^d\cdot k^{O(d^2)}\).
In this paper, for each fixed number d we present a fully dynamic algorithm that maintains a \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) kernel of size \(O(k^d)\) with constant updates.
Theorem 1
For every \(d \ge 2\) there is a deterministic, fully dynamic kernel algorithm for the problem \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) that maintains at most \(\sum _{i=0}^d k^i \le (k+1)^d\) hyperedges in the kernel, has worst-case insertion time \(3^d {\text {poly}}(d)\), and worst-case deletion time \(5^d {\text {poly}}(d)\). As d is a constant, the algorithm performs both insertions and deletions in time that is constant and independent of the input and parameter k.
Corollary 1
There is a fully dynamic algorithm for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) with update time O(1) and query time \(O(c^k)\), where \(c = d - 1 + O(1/d)\).
In order to achieve update times independent of k, this paper makes three major improvements on the general sunflower approach [1]. First, relevant objects are handled hierarchically. This allows an inductive construction and an analysis that improves the bounds on the kernel size as well as the update time. Second, we replace the notion of strong edges (see [15]) by needed edges to be defined later. Whenever a flower is formed, the replacement of its petals can be handled much more easily this way. Finally, the use of b-flowers (see also [6]) instead of generalized sunflowers [15] decreases the size of the kernel.
Our kernel is a full kernel [16]: It preserves all size-k solution. Therefore, we can use the kernel for counting and enumeration problems; and we can use it as approximate solution. The kernel size is optimal insofar as \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) has no kernel of size \(O(k^{d-\epsilon })\) unless  [17]. Note that if we feed the hyperedges of a static hypergraph to our algorithm one-at-a-time, we compute a static kernel in time \(3^d{\text {poly}}(d) \cdot m\). Since the currently best algorithms [6, 7, 18] run in time \(2^d{\text {poly}}(d) \cdot m\), our algorithm is not far from the best static runtime: the difference just lies in the constant factor \(3^d\) versus \(2^d\).
[17]. Note that if we feed the hyperedges of a static hypergraph to our algorithm one-at-a-time, we compute a static kernel in time \(3^d{\text {poly}}(d) \cdot m\). Since the currently best algorithms [6, 7, 18] run in time \(2^d{\text {poly}}(d) \cdot m\), our algorithm is not far from the best static runtime: the difference just lies in the constant factor \(3^d\) versus \(2^d\).
Extension to Set Packing: Our hitting set kernelization can be adapted for \(\mathrm {p}_{k}\text {-}{\textsc {matching}}\) and the more general \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {set}\text {-}\textsc {packing}}\): The input (H, k) is as before, but the question is whether there is a packing \(P \subseteq E\) with \(\vert P\vert \ge k\) (that is, \(e \cap f = \emptyset \) for any two different \(e,f \in P\)).
Theorem 2
For every \(d\ge 2\) there is a deterministic, fully dynamic kernel algorithm for the problem \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {set}\text {-}\textsc {packing}}\) that maintains at most \(\sum _{i=0}^d (d(k-1))^i \le d^dk^d\) hyperedges in the kernel, has worst-case insertion time \(3^d {\text {poly}}(d)\), and worst-case deletion time \(5^d {\text {poly}}(d)\).
Related Work A sequence of improved upper bounds on the kernel size for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) is due to Flum and Grohe [5], van Bevern [18], and Fafianie and Kratsch [6]. Damaschke studied full kernels for the problem, which are kernels that contain all small solutions [16]. There are also optimized algorithms for specific values of d. For instance the algorithm by Buss and Goldsmith [19] for \(d=2\), or by Niedermeier and Rossmanith [12] and Abu-Khzam [1] for \(d=3\).
Dynamic algorithms can be used in a variety of monitoring applications such as maintaining a minimum spanning tree [20] or connected components [21]. There is also a recent trend in studying dynamic approximation algorithms, for instance for vertex-cover [22]. Algorithms that maintain a solution for a dynamically changing input can also be studied using descriptive complexity, as suggested by Patnaik and Immerman [23]. A recent break-through result in this area is that reachability is contained in  [24].
[24].
Iwata and Oka [25] were the first to combine kernelization and dynamic algorithms by studying a dynamic quadratic kernel for \(\mathrm {p}_{k}\text {-}{\textsc {vertex}\text {-}\textsc {cover}}\). Their dynamic kernel algorithm requires \(O(k^2)\) update time and works in a promise model where at all times it is guaranteed that there actually is a size-k vertex cover in the input graph. Alman, Mnich, and Williams extended this line of research by studying dynamic parameterized algorithms for a broad range of problems [15]. Among others, they provided a \(\mathrm {p}_{k}\text {-}{\textsc {vertex}\text {-}\textsc {cover}}\) kernel with O(k) worst-case update time and O(1) amortized update time that works in the fully dynamic model. Their generalization to a fully dynamic algorithm for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) with a slightly larger kernel size and noninstant update time has already been mentioned above. Recent advances in dynamic FPT-algorithms were achieved by a dynamic data structure that maintains an optimum-height elimination forest for a graph of bounded treedepth [26].
Organization of This Paper: After a short introduction to dynamic algorithms, data structures, and parameterized complexity in Sect. 2, we first illustrate the algorithm for the special case of \(\mathrm {p}_{k}\text {-}{\textsc {vertex}\text {-}\textsc {cover}}\) in Sect. 3. Then, in Sect. 4, we generalize the algorithm to \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\). In Sect. 5 we argue that with slight modifications, the same algorithm can be used to maintain a polynomial kernel for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {set}\text {-}\textsc {packing}}\).
2 A Framework for Parametrized Dynamic Algorithms
Our aim is to dynamically maintain kernels with minimal update time. To formalize this, let us begin with the definition of kernels and then explain properties of dynamic kernels. Since we are interested in constant update times, some remarks on standard data structures will also be of interest.
Parameterized Hypergraph Problems and Kernels: A d-hypergraph is a pair \(H = (V,E)\) consisting of a set V of vertices and a set E of hyperedges with \(e \subseteq V\) and \(\vert e\vert \le d\) for all \(e \in E\). Let \(n = \vert V\vert \) and \(m = \vert E\vert \). The degree of v is \(\deg _H(v) = \bigl \vert \bigl \{\,e \in E \mid v \in e\,\bigr \}\bigr \vert \). A uniform d-hypergraph has \(\vert e\vert =d\) for all \(e \in E\), e. g., a graph is a uniform 2-hypergraph. We use \(\left( {\begin{array}{c}V\\ d\end{array}}\right) \) to denote the set \(\{\,e \subseteq V \mid \vert e\vert = d\,\}\) of all size-d hyperedges and let \(\smash {\left( {\begin{array}{c}V\\ \le d\end{array}}\right) } = \{\,e \subseteq V \mid \vert e\vert \le d\,\}\). Parameterized hypergraph problems are sets \(Q \subseteq \Sigma ^* \times \mathbb N\), where instances \((H,k) \in \Sigma ^* \times \mathbb N\) consist of a hypergraph H and a parameter k. The \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) and \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {set}\text {-}\textsc {packing}}\) problems from the introduction are examples. Note that in both cases k is the parameter while d is fixed; the special cases for \(d=2\) are exactly \(\mathrm {p}_{k}\text {-}{\textsc {vertex}\text {-}\textsc {cover}}\) and \(\mathrm {p}_{k}\text {-}{\textsc {matching}}\). A parameterized problem is in  if the question \((H,k)\in Q\) can be decided in time \(f(k) \cdot (\vert V\vert +\vert E\vert )^c\) for some computable function f and constant c. It is known that
if the question \((H,k)\in Q\) can be decided in time \(f(k) \cdot (\vert V\vert +\vert E\vert )^c\) for some computable function f and constant c. It is known that  holds iff kernels can be computed for Q in polynomial time [27]. Kernels of polynomial size are of special interest: For a polynomial \(\sigma \), a \(\sigma \)-kernel for an instance \((H,k) \in \Sigma ^* \times \mathbb N\) of a problem Q is another instance \((H',k') \in \Sigma ^* \times \mathbb N\) with \(\vert H'\vert \le \sigma (k)\), \(k' \le \sigma (k)\), and \((H,k) \in Q \Leftrightarrow (H',k') \in Q\). Kernel algorithms normally ensure \(k'\le k\) and we always have \(k'=k\). Polynomial kernels for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) can be computed in polynomial time; our objective is to maintain such kernels in a dynamic setting.
holds iff kernels can be computed for Q in polynomial time [27]. Kernels of polynomial size are of special interest: For a polynomial \(\sigma \), a \(\sigma \)-kernel for an instance \((H,k) \in \Sigma ^* \times \mathbb N\) of a problem Q is another instance \((H',k') \in \Sigma ^* \times \mathbb N\) with \(\vert H'\vert \le \sigma (k)\), \(k' \le \sigma (k)\), and \((H,k) \in Q \Leftrightarrow (H',k') \in Q\). Kernel algorithms normally ensure \(k'\le k\) and we always have \(k'=k\). Polynomial kernels for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) can be computed in polynomial time; our objective is to maintain such kernels in a dynamic setting.
Dynamic Hypergraphs and Dynamic Kernels: One might consider several properties of hypergraphs that change in a dynamic way. We consider as fixed and immutable the bound d on the hyperedge sizes, the vertex set V, and also the parameter k. That means only the most specific one, the hyperedge set E, will change dynamically. We assume that initially it is the empty set:
Definition 1
(Dynamic Hypergraphs) A dynamic hypergraph consists of a fixed vertex set \(V=\{v_1, \dots , v_n\}\) and a sequence \(o_1, o_2, o_3, \dots \) of update operations, where each \(o_j\) is either \({\textit{insert}}(e_j)\) or \({\textit{delete}}(e_j)\) for a hyperedge \(e_j \subseteq V\).
A dynamic hypergraph defines a sequence of hypergraphs \(H_0,H_1,\ldots \) with \(H_0 = (V, \emptyset )\), \(H_j = (V, E(H_{j-1}) \cup \{e_j\})\) for \(o_j = {\textit{insert}}(e_j)\), and finally with \(H_j =(V, E(H_{j-1}) \setminus \{e_j\})\) for \(o_j = {\textit{delete}}(e_j)\). For convenience (and without loss of generality) we assume only missing hyperedges are inserted and only existing ones deleted. A dynamic hypergraph algorithm gets the update sequence of a dynamic hypergraph as input and has to output a sequence of solutions, one for each \(H_i\). Crucially, the solution for \(H_i\) must be generated before the next operation \(o_{i+1}\) is read. While after each update we could solve the problem from scratch for \(H_i\), we may do better by taking into account that the difference between \(H_{i-1}\) and \(H_i\) is small. With the help of an internal auxiliary data structure \(A_i\) that the algorithm updates alongside the graphs, one might be able to solve the original problem faster after each update. The problem we wish to solve dynamically is to compute for each \(H_i\) a kernel \(K_i\) (as opposed to the problem of solving the parameterized problem Q itself).
Definition 2
(Dynamic Kernel Algorithm) Let Q be a parameterized problem and \(\sigma :\mathbb {N}\rightarrow \mathbb {N}\) be a bound. A dynamic kernel algorithm  for Q with kernel size \(\sigma (k)\) has three methods:
for Q with kernel size \(\sigma (k)\) has three methods:
-
1.
 gets the size n of V and the parameter k as inputs, neither of which will change during a run of the algorithm, and must initialize an auxiliary data structure \(A_0\) and a kernel \(K_0\) for \((H_0,k)\) and Q and \(\sigma \) (observe that \(H_0 = (V,\emptyset )\) holds).
gets the size n of V and the parameter k as inputs, neither of which will change during a run of the algorithm, and must initialize an auxiliary data structure \(A_0\) and a kernel \(K_0\) for \((H_0,k)\) and Q and \(\sigma \) (observe that \(H_0 = (V,\emptyset )\) holds). -
2.
 gets a hyperedge e to be added to \(H_{i-1}\) and must update \(A_{i-1}\) and \(K_{i-1}\) to \(A_i\) and \(K_i\) with, again, \(K_i\) being a kernel for \((H_i,k)\) and Q and \(\sigma \).
gets a hyperedge e to be added to \(H_{i-1}\) and must update \(A_{i-1}\) and \(K_{i-1}\) to \(A_i\) and \(K_i\) with, again, \(K_i\) being a kernel for \((H_i,k)\) and Q and \(\sigma \). -
3.
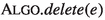 removes an edge instead of adding it.
removes an edge instead of adding it.
One could also require that only the data structure \(A_i\) is updated in each step, while a kernel \(K_i\) would only be needed to be computed upon a query request. This would allow to differentiate between update times and query times for computing kernels. By requiring that the kernel \(K_i\) is explicitly computed at each step alongside \(A_i\), our definition implies a query time of zero for computing \(K_i\). However, solving the query \((H_i,k) \in ^? Q\) using \(K_i\) may take exponential time in k. Concerning the update times, an efficient dynamic kernel algorithm should of course compute \(A_i\) and \(K_i\) faster than a static kernelization that processes \(H_i\) completely. The best one could hope for is constant time for the initialization and per update, even independent of the parameter k – and this is exactly what we achieve in this paper.
Data Structures for Dynamic Algorithms: The \(A_i\) rely on data structures such as objects and arrays. We additionally use a novel data structure called relevance list, which are ordinary lists equipped with a relevance bound \(\rho \in \mathbb N\): the first \(\rho \) elements are said to be relevant, while the others are irrelevant. This data structure supports insertion and deletion, querying the relevance status of an element, and querying the last relevant element – each in O(1) time. For concrete implementations and an analysis, see the appendix.
3 Dynamic Vertex Cover with Constant Update Time
In order to better explain the ideas behind our dynamic kernel algorithm, we first tackle the case \(d=2\) in this section and show how we can maintain kernels of size \(O(k^2)\) for the vertex cover problem with update time O(1). The idea is based on a well-known static kernel: Buss [19] noticed that in order to cover all edges of a graph \(G = (V,E)\) with k vertices, we must pick any vertex with more than k neighbors (let us call such vertices heavy). If there are more than \(k^2\) edges after all heavy vertices have been picked and removed, no vertex cover of size k is possible, since each light vertex can cover at most k edges (light vertices being all but the heavy ones).
To turn this idea into a dynamic kernel, let us first consider only insertions. Initially, new edges can simply be added to the kernel; but at some point a vertex v “becomes heavy.” In the static setting one would remove v from the graph and decrease the parameter by 1. In the dynamic setting, however, removing v with its adjacent edges would take time O(k) rather than O(1). Instead, we leave v in the graph, but do not add further edges containing v to the kernel once v becomes heavy. We call the first \(k+1\) edges relevant for the vertex and the rest irrelevant. By putting the relevant edges of a heavy vertex in the kernel, we ensure that this vertex still must be chosen for any vertex cover. By leaving out the irrelevant edges, we ensure a kernel size of at most \(O(k^2)\). More precisely, if the kernel size now threatens to exceed \(k^2 + k + 1\), then any additional edges will be irrelevant for the kernel since the already inserted edges already form a proof that no size-k vertex cover exists.
Being relevant for a vertex is a “local” property: For an edge \(e= \{u,v\}\), the vertex u may consider e to be relevant, while v may consider it to be irrelevant. An edge only “makes it to the kernel” when it is relevant for both endpoints – then it will be called needed. It is not obvious that this is how the case of a “disagreement” should be resolved and that this is the right notion of “needed edges” – but Lemma 3 shows that it leads to a correct kernel.
A Dynamic Vertex Cover Kernel Algorithm: We turn the sketched ideas into a formal algorithm in the sense of Definition 2. The initialization sets up the auxiliary data structures for a hypergraph with n vertices and a parameter k: One relevance list \(L_v\) with relevance bound \(k+1\) per vertex v (to keep track of the edges that are relevant for v) and one relevance list L (to keep track of the edges that are relevant for the kernel). The code violates the requirement that the initialization procedures should run in constant time, but a trick [28] for ensuring this will be discussed in the general hitting set case.

The insert operation adds an edge e to the relevance lists of both endpoints of e. Furthermore, it also adds e to L if it is needed, which meant “relevant for both sides”.

The delete operation for an edge e is more complex: When \(e = \{u,v\}\) is removed from the lists \(L_u\), \(L_v\), and L, formerly irrelevant edges may suddenly become relevant from the point of view of these three lists and, thus, possibly also needed. Fortunately, we know which edge \(e'\) may suddenly have become relevant for a list: After the removal of e, the edge \(e'\) that is now the last relevant edge stored in the list is the (only) one that may have become relevant – and relevance lists keep track of the last relevant element.

Correctness and Kernel Size: The relevant edges in L clearly have some properties that we would expect of a kernel: First, there are at most \(k^2 + k + 1\) of them (for the simple reason that L caps the number of relevant edges in line 4) – which is exactly the size that a kernel should have. Second, it is also easy to see from the code of the algorithm that all operations run in time O(1). Two lemmas make these observations precise, where R(L) denotes the set of relevant edges in a list L and E(L) denotes all edges in L; and where we say that a dynamic algorithm maintains an invariant if that invariant holds for its auxiliary data structure right after the \({\textit{init}}\) method has been called and after every call to \({\textit{insert}}\) and \({\textit{delete}}\).
Lemma 1
\({ \textsc {DynKernelVC}}\) maintains the invariant \(\vert R(L)\vert \le k^2 + k + 1\).
Proof of Lemma 1
The relevance list L is setup in line 4 to have the claimed number of relevant elements at most.
Lemma 2
\({ \textsc {DynKernelVC}}.{\textit{insert}}\) and \({ \textsc {DynKernelVC}}.{\textit{delete}}\) run in time O(1).
Proof of Lemma 2
The codes itself clearly only need time O(1) and call only operations on relevance lists, all of which run in constant time.
The crucial, much less obvious property of the algorithm is stated in the next lemma, whose proof contains a non-trivial recursive analysis showing that irrelevant edges must already be covered by relevant edges inserted earlier.
Lemma 3
\({ \textsc {DynKernelVC}}\) maintains the invariant that (V, R(L)) and the current graph (V, E) have the same size-k vertex covers.
Proof of Lemma 3
One direction is trivial since \(R(L) \subseteq E\). For the other direction, consider a size-k vertex cover X of R(L), that is, a set X with \(\vert X\vert = k\) and \(X \cap e \ne \emptyset \) for all \(e \in R(L)\). We need to show that \(X \cap e\ne \emptyset \) holds for all \(e \in E\). We distinguish three cases: \(e \in R(L)\), \(e \in E(L) - R(L)\), and \(e \in E - E(L)\).
Case 1: The edge is in L and is relevant. The first case is trivial: If \(e \in R(L)\), then by assumption we have \(X \cap e \ne \emptyset \) as claimed.
Case 2: The edge is in L, but is irrelevant. For the second case, we need an observation:
Claim 1
The degree of vertices in (V, R(L)) is at most \(k+1\).
Proof
Consider any \(v \in V\). All edges in R(L) that contain v must be relevant edges with respect to \(L_v\) since the function \({\textit{check if needed}}\) only allows such edges to enter L. However, the \({\textit{init}}\) method sets \(L_v\) to contain at most \(k+1\) relevant edges.
Using this observation, we see that the second case (\(e \in E(L) - R(L)\)) cannot happen: L can only have an irrelevant edge if there are already \(k^2+k+1\) relevant edges in R(L). However, by the claim, each of the k many \(x \in X\) covers at most \(k+1\) edges in R(L), implying that X covers at most \(k(k+1) = k^2 + k\) edges of R(L). In particular, contrary to the assumption, one edge of R(L) is not covered by X.
Case 3: The edge is not even in L. For the third case, let \(e \in E - E(L)\), that is, let \(e = \{u,v\}\) be an edge that “did not make it into the L list.” This can only happen because it was irrelevant for \(L_u\) or \(L_v\) (or both).
Recall that when e is irrelevant for a list \(L_u\), this means that u has more than \(k+1\) adjacent edges in E and, hence, u must be present in any vertex cover of \(G= (V,E)\). If all the relevant edges of u are also present in R(L), then u has exactly \(k+1\) neighbors in the graph (V, R(L)) and, in particular, its vertex cover X must include u. Unfortunately, it may happen that even though a vertex u has some irrelevant adjacent edges in E, not all relevant edges of \(L_u\) make it into L: After all, the other endpoint v of an edge \(e = \{u,v\}\) may also have irrelevant adjacent edges and e may happen to be one of them. We can now try to apply the same argument to v; but may again find yet another edge \(e'\) and another vertex w that causes v to have a degree less than \(k+1\) in R(L). Fortunately, it turns out that after a finite number of steps, we arrive at a vertex that must be present in X. Furthermore, starting from this vertex, we can track back to show that eventually we must have \(u \in X\). The details are as follows.
Claim 2
There is an ordering \(u_1,\dots ,u_q\) of the vertices of degree at least \(k+1\) in E such that for each \(i \in \{1,\dots ,q\}\) there are at least \(k+1 - (i-1)\) edges in R(L) of the form \(\{u_i,v\}\) with \(v \notin \{u_1,\dots ,u_{i-1}\}\).
Proof
In the current graph G, each edge e has a time \(t_e\) when it entered the graph and these times define a total order on the edges in E. For each vertex v, let l(v) be the last relevant edge of \(L_v\), that is, the edge returned by \(L_v.{\textit{last relevant}}\). Order the vertices of degree at least \(k+1\) in E according to the following rule: For \(i < j\) we must have that \(t_{l(u_i)} \le t_{l(u_j)}\) (if two vertices \(u_i\) and \(u_j\) happen to have the same last relevant edge, they can be ordered arbitrarily).
Consider any \(u_i\). Then all edges from \(u_i\) to any vertex \(v \notin \{u_1,\dots ,u_{i-1}\}\) are relevant for \(L_v\) since the last relevant edge of \(L_v\) is an edge that came later than the edge \(\{u_i,v\}\) and, hence, \(\{u_i,v\}\) is relevant for \(L_v\). However, this means that the only edges of \(R(L_{u_i})\) that do not get passed to L can be those of the form \(\{u_i,u_j\}\) for some \(j \in \{1,\dots , i-1\}\). Clearly, since \(L_{u_i}\) has \(k+1\) relevant edges and only \(i-1\) do not get passed, we get the claim.
We can use this claim to show \(\{u_1,\dots ,u_q\} \subseteq X\): We show by induction on i that \(\{u_1,\dots , u_i\} \subseteq X\) holds. The case \(i=0\) is trivial. For the inductive step from \(i-1\) to i, consider \(u_i\). By the claim, there are \(k+1 - (i-1)\) edges in R(L) from \(u_i\) to vertices \(v \notin \{u_1,\dots ,u_{i-1}\}\). Since by the induction hypothesis we have \(\{u_1,\dots ,u_{i-1}\} \subseteq X\), if we do not have \(u_i \in X\), then the set \(X - \{u_1,\dots ,u_{i-1}\}\) must contain enough vertices to cover the \((k+1) - (i-1)\) edges between \(u_i\) and vertices not in \(\{u_1,\dots ,u_{i-1}\}\). However, \(\vert X - \{u_1,\dots ,u_{i-1}\}\vert \le k-(i-1)\) and, thus, this is impossible.
This concludes the third case: If \(e \in E - E(L)\), then one or both elements of e must be one of the \(u_i\) – and we just saw that all of them are in X. Hence, \(X \cap e \ne \emptyset \).
Put together, we get the following special case of Theorem 1:
Theorem 3
 is a dynamic kernel algorithm for \(\mathrm {p}_{k}\text {-}{\textsc {vertex}\text {-}\textsc {cover}}\) with update time O(1) and kernel size \(k^2 + k + 1\).
is a dynamic kernel algorithm for \(\mathrm {p}_{k}\text {-}{\textsc {vertex}\text {-}\textsc {cover}}\) with update time O(1) and kernel size \(k^2 + k + 1\).
Proof of Theorem 3
Lemmas 1, 2, and 3 together state that at all times during a run of the algorithm \({ \textsc {DynKernelVC}}\) the graph (V, R(L)) has at most \(k^2 + k + 1\) edges and has the same size-k vertex covers as the current graph. Thus, (V, R(L)) is almost a kernel except that R(L) is actually a linked list of edges (with potentially large vertex identifiers).
However, we can simultaneously keep track of an adjacency matrix of a graph K with the vertex set \(V_K = \{1,\dots ,2(k^2+k+1)\}\) and with an edge set \(E_K\) that is always isomorphic to R(L), that is, \(E_K \sim R(L)\). In particular, K has a size-k hitting set if, and only if, G has one.
The update times are constant. The time needed for  can be made constant with the already mentioned trick [28], see Lemma 16.
can be made constant with the already mentioned trick [28], see Lemma 16.
4 Dynamic Hitting Set Kernels
The hitting set problem is a generalization of vertex-cover to hypergraphs. However, allowing larger hyperedges introduces considerable complications into the algorithmic machinery. Nevertheless, we still seek and prove an update time that is constant. More precisely, it is independent of \(n=\vert V\vert \), \(m=\vert E\vert \), and the parameter k, while it does depend on d (in fact even exponentially). Such an exponential dependency on d seems unavoidable, since a direct consequence of our dynamic algorithm is a static algorithm with running time \( 3^d {\text {poly}}(d)\cdot m\), and the currently best static algorithm runs in time \(2^d {\text {poly}}(d) \cdot m\).
The first core idea of our algorithm concerns a replacement notion for the “heavy vertices” from the previous section. Sunflowers [29] are usually a stand-in (see [5, Section 9.1] and [8, 30]), but they are hard to find and especially hard to manage dynamically. Instead, we use an idea first proposed by Fafianie and Kratsch [6], but adapted to our dynamic setting: a generalizations of sunflowers, which we call b-flowers for different parameters \(b \in \mathbb N\) that will be easier to keep track of dynamically.
The second core idea is to recursively reduce each case d to the case \(d-1\): For a fixed \(d > 2\), we compute a set of hyperedges relevant for the kernel (the set R(L), but now called \(R(L^d[\emptyset ])\) in the more general case), but additionally we dynamically keep track of an instance for \(\mathrm {p}_{k}\text {-}{({ d}-1)\text {-}\textsc {hitting}\text {-}\textsc {set}}\) and merge the dynamic kernel for this instance (which we get from the recursion) with the list of hyperedges relevant for the kernel.
4.1 From High-Degree Vertices in Graphs to Flowers in Hypergraphs
A sunflower in a d-hypergraph \(H=(V,E)\) is a collection of hyperedges \(S\subseteq E\) such that there is a set \(c\subseteq V\), called the core, with \(x\cap y=c\) for all distinct pairs \(x,y\in S\). For example, the edges adjacent to a heavy vertex v form a (large) sunflower with core \(\{v\}\). In general, any size-k hitting set has to intersect with the core of a sunflower if it has more than k edges – which means that replacing large sunflowers by their cores is a reduction rule for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\). This rule yields a kernel since the Sunflower Lemma [29] states that every d-hypergraph with more than \(k^{d}\cdot d!\) hyperedges contains a sunflower of size \(k+1\).
Unfortunately, it is not easy to find sunflowers for larger d in the first place, let alone to keep track of them in a dynamic setting with constant update times. Rather than trying to find all sunflowers, we use a more general concept called b-flowers. We remark that we introduce this notation here to illustrate the general idea of the algorithm, but we will only need the definition later in Lemma 10 to prove the kernel properties.
Definition 3
For a hypergraph \(H = (V,E)\) and \(b \in \mathbb N\), a b-flower with core c is a set \(F \subseteq E\) such that \(c \subseteq e\) for all \(e \in F\) and \(\deg _{(V,F)}(v) \le b\) for all \(v \in V - c\).
Note that a 1-flower is exactly a sunflower and, thus, b-flowers are in fact a generalization of sunflowers, see Fig. 1 for an example.
A hypergraph \(H=(\{a,b,c,d,e,f,g\},E)\) in which each hyperedge \(e\in E\) is drawn as a line and contains all vertices it “touches”. The three red edges form a 1-flower (a sunflower) with core \(\{a,b\}\). The hyperedges \(\bigl \{\{a,c\}, \{a,d\}, \{a,g\}, \{a,b,e\}\bigr \}\) also form a 1-flower, now with with core \(\{a\}\), but if we add the hyperedges \(\{a,b,f\}\) and \(\{a,c,d\}\), we no longer have a 1-flower – but still a 2-flower with core \(\{a\}\). All edges together form a 3-flower with core \(\{a\}\)
The following property of b-flowers is essential for our dynamic kernelization strategy (it implies that we can replace large flowers by their cores):
Lemma 4
Let F be a b-flower with core c in H and X a size-k hitting set of H. If \(\vert F\vert > b\cdot k\), then \(X \cap c \ne \emptyset \) (“X must hit c”).
Proof of Lemma 4
If we had \(X \cap c = \emptyset \), then each \(v \in X\) could hit at most b hyperedges in F since \(\deg _{(V,F)}(v) \le b\). Then F can contain at most \(b\cdot \vert X\vert \) hyperedges, contradicting \(\vert F\vert > b\cdot k\).
4.2 Dynamic Hitting Set Kernels: A Recursive Approach
As previously mentioned, the core idea behind our main algorithm is to recursively reduce the case d to \(d-1\). To better explain this idea, we illustrate how the (already covered) case \(d=2\) can be reduced to \(d=1\) and how this in turn can be reduced to \(d=0\). Following this, we present the complete recursive algorithm, prove its correctness, and analyze its runtime.
Recall that \({ \textsc {DynKernelVC}}\) adds up to \(k+1\) edges per vertex v into the kernel R(L) to ensure that v “gets hit.” In the recursive hitting set scenario we ensure this differently: When we notice that v is “forced” into all hitting sets, we add a new hyperedge \(\{v\}\) to an internal 1-hypergraph used exclusively to keep track of the forced vertices (clearly the only way to hit \(\{v\}\) is to include v in the hitting set). When, later on after a deletion, we notice that a singleton hyperedge is no longer forced, we remove it from the internal 1-hypergraph once more. Since we have to ensure that not too many new hyperedges make it into the final kernel, we keep track of a dynamic kernel of the internal 1-hypergraph (using a dynamic kernel algorithm for \(d=1\)) and then join this kernel with R(L).
Using a hypergraph to track the forced vertices allows us to change the relevance bounds of the algorithm: For the lists \(L_v\) these were \(k+1\), but since we explicitly “force” \(\{v\}\) into the solution by generating a new hyperedge, it is enough to set the bound to k. Similarly, the bound for the original list L was set to \(k^2+k+1\) since this constitutes a proof that no size-k vertex cover exists. In the new setting with the relevance bound for \(L_v\) lowered to k, we can also lower the relevance bound for L to \(k^2\): All vertices \(v\in V\) have a degree of at most k in R(L) and, thus, k vertices can hit at most \(k^2\) hyperedges. If L contains more elements, we consider the (unhittable) empty hyperedge as forced and add it to the 1-hypergraph.
In order to dynamically keep track of a kernel for the internal 1-hypergraph, we proceed similarly: We simply put all its hyperedges (which have size 1 or 0) in a list (called \(L^1[\emptyset ]\) in the algorithm). If the number of hyperedges in this list exceeds k, we immediately know that no hitting set of size k exists; and we “recursively remember this” by inserting the empty set into yet another internal 0-hypergraph – this is the recursive call to \(d=0\).
Managing Needed and Forced Hyperedges: In the general setting (now for arbitrary d), we need a uniform way to keep track of lists like the \(L_v\) and L for the many different internal hypergraphs. We do this using arrays \(L^i\) for \(i \in \{0,\dots ,d\}\) with domains \(\left( {\begin{array}{c}V\\ \le i\end{array}}\right) \), one for each i-hypergraph, where each \(L^i[s]\) stores a relevance list. The list \(L^i[s]\) has relevance bound \(k^{i-\vert s\vert }\) and we only stores edges \(e \in \left( {\begin{array}{c}V\\ \le i\end{array}}\right) \) with \(e \supseteq s\) in it.
The idea behind this construction is as follows. For \(d=2\) the list \(L^2[\{v\}]\) represents the list \(L_v\) of  and \(L^2[\emptyset ]\) represents the list L. The lists \(L^2[\{u,v\}]\) are new and will only store a single element and are only added to simplify the code: When an edge \(e = \{u,v\}\) is inserted into the 2-hypergraph, we add it to \(L^2[e]\), but more importantly also to \(L^2[\{u\}]\) and \(L^2[\{v\}]\). If it is relevant for both lists, we call it needed and add it also to \(L^2[\emptyset ]\). If \(L^2[s]\) contains an irrelevant edge, then s is forced, and we insert it into \(L^1[s]\). For \(L^1\), the array that manages the internal 1-hypergraph, we have similar rules for being needed and forced. An example of how this works is shown in Fig. 2. The next two definitions generalize the idea of needed and forced hyperedges to arbitrary d and lie at the heart of our algorithm. The earlier rules for \(d=2\) are easily seen to be special cases:
and \(L^2[\emptyset ]\) represents the list L. The lists \(L^2[\{u,v\}]\) are new and will only store a single element and are only added to simplify the code: When an edge \(e = \{u,v\}\) is inserted into the 2-hypergraph, we add it to \(L^2[e]\), but more importantly also to \(L^2[\{u\}]\) and \(L^2[\{v\}]\). If it is relevant for both lists, we call it needed and add it also to \(L^2[\emptyset ]\). If \(L^2[s]\) contains an irrelevant edge, then s is forced, and we insert it into \(L^1[s]\). For \(L^1\), the array that manages the internal 1-hypergraph, we have similar rules for being needed and forced. An example of how this works is shown in Fig. 2. The next two definitions generalize the idea of needed and forced hyperedges to arbitrary d and lie at the heart of our algorithm. The earlier rules for \(d=2\) are easily seen to be special cases:
Definition 4
(Needed Hyperedges and the Need Invariant) A hyperedge e is needed in a list \(L^i[s]\) with \(s \subsetneq e\) if \(e \in R(L^i[t])\) holds for all \(t\subseteq e\) with \(s \subsetneq t\). A dynamic algorithm maintains the Need Invariant if for all \(e \in \left( {\begin{array}{c}V\\ \le d\end{array}}\right) \), all \(s \subsetneq e\), and for all \(i \in \{0,\dots ,d\}\) the list \(L^i[s]\) contains e iff e is needed in it.
Definition 5
(Forced Hyperedges and the Force Invariant) A set of vertices s is forced by \(L^i[s]\) into \(L^{i-1}[s]\) or just forced by \(L^i[s]\) if \(L^i[s]\) has an irrelevant hyperedge. A dynamic algorithm maintains the Force Invariant if for all \(i \in \{1,\dots ,d\}\) and all \(s \in \left( {\begin{array}{c}V\\ <i\end{array}}\right) \), the list \(L^{i-1}[s]\) contains s iff s is forced by \(L^i[s]\).
The data stored in the lists \(L^2\), \(L^1\), and \(L^0\) for \(k=3\) and a dynamic 2-hypergraph with 16 (orange) vertices created with 19 edge insertions (numbers indicate insertion times; there are no deletions in this example). Normal edges are shown as straight lines, singleton edges \(\{v\}\) as circles around v, and the empty set as an empty circle. In \(L^2\), the members of \(L^2[\emptyset ]\) are drawn in black. They are all relevant for both endpoints and thus needed in \(L^2[\emptyset ]\). The red edges are not relevant for one of the endpoints and thus neither needed in nor added to \(L^2[\emptyset ]\). Among the black edges, only the first \(k^2 = 9\) are relevant, the rest (dotted) are irrelevant. In \(L^1\), we store the “forced s” that \(L^2\) forces into \(L^1\) at the indicated timestamps: each time, it is the first time an irrelevant edge e is inserted into \(L^2[s]\). After the first three s (two singletons at timestamps 6 and 10 and then the empty set at timestamp 13) got inserted into \(L^1[\emptyset ]\), further edges are irrelevant and trigger the insertion of the empty set into \(L^0[\emptyset ]\)
We will show in Lemmas 9 and 12 that the union \(K = \bigcup _{i=0}^d R(L^i[\emptyset ])\) is the sought kernel: Each \(R(L^i[\emptyset ])\) contains (only) those hyperedges e that have not already been taken care of by having forced a subset s of e into the internal \((i-1)\)-hypergraph.
In the following, we develop code that ensures that the Need Invariant and the Force Invariant hold at all times. We will show that this is the case both for an insert operation and also for delete operations. Then we show that the invariants imply that \(K = \bigcup _{i=0}^d R(L^i[\emptyset ])\) is a kernel for the hitting set problem. Finally, we analyze the runtimes.
Initializiation The initialization creates the arrays \(L^i\) and the relevance lists.

The construct  allocates a new array with domain D and then immediately set the value of each entry \(s \in D\) to f(s). (So, in our case, each \(L^i[s]\) will be a new, empty relevance list with relevance bound \(k^{i-\vert s\vert }\).) The important point is that both allocation and pre-filling can be done in constant time using the standard trick to work with uninitialized memory [28].
allocates a new array with domain D and then immediately set the value of each entry \(s \in D\) to f(s). (So, in our case, each \(L^i[s]\) will be a new, empty relevance list with relevance bound \(k^{i-\vert s\vert }\).) The important point is that both allocation and pre-filling can be done in constant time using the standard trick to work with uninitialized memory [28].
Independently of the time needed for the allocation, observe that the amount of memory we allocate is about \(O(n^d)\) – which is already too much in almost any practical setting for \(d =3\), see [31, Chapter 5] for a discussion of experimental findings. However, we will only use a very small fraction of the allocated memory: The only lists \(L^i[s]\) that are non-empty at any point during a run of the algorithms are those where \(s \subseteq e \in E\) holds. This means that we actually only need space \(O(2^d \vert E\vert )\) to manage the non-empty lists if we use hash tables. Of course, this entails a typically non-constant overhead per access for managing the hash tables, which is why our analysis is only for the wasteful implementation above. For a clever way around this problem in the static setting, see [8].
Lemma 5
The Need and Force Invariant hold after the \({\textit{init}}\) method has been called.
Proof of Lemma 5
All lists are empty after the initialization.
Insertions We view insertions as a special case of “forcing an edge,” namely as forcing it into the lists of \(L^d\). Adding an edge e to a list \(L^i[e]\) can, of course, change the set of relevant edges in \(L^i[e]\), which means that e may also be needed in lists \(L^i[s]\) for \(s \subsetneq e\). It is the job of the method \({\textit{fix needs downward}}\) to add e to the necessary lists.

The method \({\textit{fix needs downward}}\) is more complex than necessary here, but we will need the extra flexibility for the delete method later on: For two sets of vertices s and p with \(s \supseteq p\) and a fixed number i, let us say that the Need Invariant holds for s above p if for all \(s' \supseteq p\) we have \(s \in E(L^i[s'])\) iff s is needed for \(L^i[s']\). Let us say that the Need Invariant holds for s below \(s'\) if for all \(s' \subseteq p\) we have \(s \in E(L^i[s'])\) iff s is needed for \(L^i[s']\). In the context of the insert operation, \({\textit{fix needs downward}}\) always gets called with \(s = p\), meaning that in the following lemma the premise (“the Need Invariant holds for s above p”) is trivially true.
Lemma 6
Let s and p with \(s \supseteq p\) be sets of vertices and let i be fixed. Suppose the Need Invariant holds for s above p. Then after the call \({\textit{fix needs downward}}(s,p,i)\) the Need Invariant will also hold for \(s'\) below p.
Proof of Lemma 6
We need to show that the code ensures for all \(s' \subseteq p\) that if s is needed in \(L^i[s']\), it gets inserted. It is the job of line 22 to test whether such an insertion is necessary. The line tests whether \(\forall v \in p-s' :s \in R(L^i[s' \cup \{v\}])\) holds. By Definition 4 of needed hyperedges, what we are supposed to test is whether for all \(t \subseteq s\) with \(s'\subsetneq t\) we have \(s \in R(L^i[t])\). Observe that the property of being needed is “upward closed”: if s is needed in \(L^i[p]\), it is also needed in all \(L^i[s^*]\) with \(p \subseteq s^* \subseteq s\). This implies that by processing the hyperedges \(s'\) in descending order of size (line 20), s will be needed for \(L^i[s']\) iff s is needed for all the hyperedges \(t = s' \cup \{v\}\) that are one element larger than s. This is exactly what we test.
Lemma 7
The Need and Force Invariant are maintained by the \({\textit{insert}}\) method.
Proof of Lemma 7
For the Need Invariant, observe that whenever the \({\textit{fix force}}\) method adds an edge s to \(L^i[s]\) in line 12, it calls \({\textit{fix needs}}(s,s,i)\). By Lemma 6, this ensures that s is inserted exactly into those \(L^i[s']\) for \(s' \subseteq s\) where it is needed. For the Force Invariant, observe that we only add elements to lists of \(L^i\), which means that they can only become forced – they cannot lose this status through an addition of an edge. However, after any insertion of s into any list of \(L^i\) (in lines 12 and 23) we immediately call \({\textit{fix forced}}\), which inserts s into \(L^{i-1}[s]\) if s is forced.
Deletions: The delete operation has to delete an edge e from all places where it might have been inserted to, which is just from all lists \(L^d[s]\) for \(s \subseteq e\). However, removing e from such a list can have two side-effects: First, it can cause \(L^d[s]\) to lose its last irrelevant element, changing the status of s from “forced” to “not forced” and we need to “unforce” it (remove it from \(L^{d-1}[s]\)), which may recursively entail new deletions. Furthermore, removing e from \(L^d[s]\) may make a previous irrelevant hyperedge (the first irrelevant hyperedge of \(L^d[s]\)) relevant. Then one has to fix the needs for this hyperedge once more, which may entail new inserts and forcings, but no new deletions (see Table 2).

Lemma 8
The Need and Force Invariant are maintained by the \({\textit{delete}}\) method.
Proof of Lemma 8
Proving the Need and Force Invariants for the delete operation is trickier than for the insert operation since a delete can, internally, trigger insert operations – namely in line 44. For this reason, we prove by induction on i that the Need and Force Invariants still hold for all elements in all \(L^j[s']\) for \(j\le i\), \(s'\subseteq s\) after a call to \({\textit{delete}}(s,i)\). For \(i=0\) this is trivial since the only possible s is \(\emptyset \) and the loop only considers \(s' = \emptyset \), deletes it from \(L^0[\emptyset ]\), and does nothing else.
For the inductive step, first consider the Need Invariant on s. The loop removes s from \(L^i[s]\) and also from all \(L^i[s']\) (the loop from line 36 executes a remove operation for each \(s' \subseteq s\) in the next line). This ensures the Need Invariant on s. Next, observe that removing a hyperedge from a list \(L^i[s']\) can only reduce the number of irrelevant hyperedge, meaning that \(s'\) can only change its status from forced to unforced. If this happens, as tested in line 38, we recursively remove \(s'\) from \(L^{i-1}[s']\). By the induction hypothesis, this will maintain the Need and Force Invariants on all the \(L^j\) for \(j < i\).
While we have now correctly accounted for the needed and the forced status of s and its subsets \(s' \subseteq s\), the removal of an edge s from a list \(L^i[s']\) can have a second side-effect, besides (possibly) unforcing \(s'\): It can also make a previously irrelevant hyperedge relevant. This happens when, firstly, s used to be a relevant hyperedge in \(L^i[s']\) and, secondly, there was a (first) irrelevant hyperedge f in \(L^i[s]\). In this case, the mechanics of relevance lists automatically change the relevance status of f from irrelevant to relevant. Note that at most one edge is deleted from \(L^i[s']\) during a call of \({\textit{delete}}(s,i)\), namely s, and hence at most one hyperedge f can become relevant per list \(L^i[s']\). Note that more than one hyperedge can be deleted from the same list \(L^{i-1}[s']\) by recursive calls during a single call of \({\textit{delete}}(s,i)\) – but by the induction hypothesis the Need and Force Invariants are maintained by the calls \({\textit{delete}}(s',i-1)\).
When a hyperedge f becomes relevant in a list \(L^i[s']\), this may change the need status of f in sets \(s'' \subsetneq s\): Previously, we had \(f \notin R(L^i[s'])\) and, hence, \(f \notin R(L^i[s''])\) for all \(s'' \subsetneq s'\). Now, however, f might be needed in some of the lists \(L^i[s'']\) “further down.” To address this, we call \({\textit{fix needs}}(f,s',i)\) in line 44, which will ensure that the Need Invariant of f is fixed below \(s'\) (see Lemma 6) provided the Need Invariant did hold for f above \(s'\). However this was the case: the very fact that \(f \in E(L^i[s'])\) used to hold shows that f was already relevant and present everywhere above \(s'\) (otherwise, f would not have made it into \(L^i[s']\)). Since we do not know whether f was needed before, a sanity check is in order to prevent edges from being inserted multiple times.
Crucially, observe that both the Need Invariant and the Force Invariant now hold for all hyperedges whose relevance status may have changed, namely s (as shown earlier) and all f in line 43. No other hyperedges in \(L^i\) change their relevance status (and for \(L^j\) with \(j<i\) the invariants hold by the inductive assumption).
Kernel: As stated earlier, the kernel maintained by  is the set \(K = \bigcup _{i=0}^d R(L^i[\emptyset ])\). (K is given only indirectly via d linked lists, but one can do the same transformations as in the proof of Theorem 3 to obtain a compact matrix representation.)
is the set \(K = \bigcup _{i=0}^d R(L^i[\emptyset ])\). (K is given only indirectly via d linked lists, but one can do the same transformations as in the proof of Theorem 3 to obtain a compact matrix representation.)
Correctness: We have already established that the algorithm maintains the Need Invariant and the Force Invariant. Our objective is now to show that  does maintain a kernel at all times. We start with the size:
does maintain a kernel at all times. We start with the size:
Lemma 9
 maintains the invariant \(\vert K\vert \le k^d + k^{d-1} + \cdots + k + 1\).
maintains the invariant \(\vert K\vert \le k^d + k^{d-1} + \cdots + k + 1\).
Proof of Lemma 9
The \({\textit{init}}\)-method installs a relevance bound of \(k^i\) for \(L^i[\emptyset ]\) for all \(i\in \{0,\dots ,d\}\).
Lemma 12 shows the crucial property that the current K has a hitting set of size k iff the current hypergraph does. The proof hinges on the following two lemmas on “flower properties”:
Lemma 10
 maintains the invariant that for all \(i \in \{0,\dots ,d\}\) and all \(s \in \left( {\begin{array}{c}V\\ \le i-1\end{array}}\right) \), the set \(E(L^i[s])\) is a \(k^{i-\vert s\vert -1}\)-flower with core s.
maintains the invariant that for all \(i \in \{0,\dots ,d\}\) and all \(s \in \left( {\begin{array}{c}V\\ \le i-1\end{array}}\right) \), the set \(E(L^i[s])\) is a \(k^{i-\vert s\vert -1}\)-flower with core s.
Proof of Lemma 10
First, for all \(e \in E(L^i[s])\) we have \(s \subseteq e\) since in all places in the \({\textit{insert}}\)-method where we append an edge e to a list \(L^i[s]\), we have \(s \subseteq e\) (in line 12 we have \(e=s\) and in line 23 we have \(s \subsetneq e\) by line 20). Second, consider a vertex \(v \in V - s\). We have to show that \(\deg _{(V,E(L^i[s]))}(v) \le k^{i-\vert s\vert -1}\) (recall Definition 3) or, spelled out, that v lies in at most \(k^{i-\vert s\vert -1}\) hyperedges \(e \in E(L^i[s])\). By the Need Invariant, all \(e \in E(L^i[s])\) are needed. In particular, for \(t = s \cup \{v\}\) Definition 4 tells us \(e \in R(L^i[t])\). Therefore, we have \(\{\,e\in E(L^i[s])\mid v\in e\,\} \subseteq R(L^i[s \cup \{v\}])\) and the latter set has a maximum size of \(k^{i-\vert s\cup \{v\}\vert } = k^{i-\vert s\vert -1}\) due to the relevance bound installed in line 5.
Lemma 11
 maintains the invariant that for all \(X \in \smash {\left( {\begin{array}{c}V\\ \le k\end{array}}\right) }\) and for all \(i \in \{1,\dots ,d\}\) and all \(s \in \left( {\begin{array}{c}V\\ \le i\end{array}}\right) \), if s is forced into \(L^{i-1}\) and if X hits all elements of \(E(L^i[s])\), then X hits s.
maintains the invariant that for all \(X \in \smash {\left( {\begin{array}{c}V\\ \le k\end{array}}\right) }\) and for all \(i \in \{1,\dots ,d\}\) and all \(s \in \left( {\begin{array}{c}V\\ \le i\end{array}}\right) \), if s is forced into \(L^{i-1}\) and if X hits all elements of \(E(L^i[s])\), then X hits s.
Proof of Lemma 11
By Definition 5, “being forced into \(L^{i-1}\)” means that \(L^i[s]\) has an irrelevant edge. In particular, \(\vert E(L^i[s])\vert > k^{i-\vert s\vert }\). By Lemma 10, \(E(L^i[s])\) is a \(k^{i-\vert s\vert -1}\)-flower with core s. By Lemma 4, since \(\vert E(L^i[s])\vert > k^{i-\vert s\vert } = k \cdot k^{i-\vert s\vert -1}\), we know that X hits s, as claimed.
Lemma 12
 maintains the invariant that H and K have the same size-k hitting sets.
maintains the invariant that H and K have the same size-k hitting sets.
Proof of Lemma 12
For the first direction, let X be a size-k hitting set of \(H = (V,E)\). For \(i =d\), \(i=d-1\), ..., \(i=1\), and \(i=0\) we show inductively that all lists \(L^i[s]\) for all \(s \in \left( {\begin{array}{c}V\\ \le i\end{array}}\right) \) only contain hyperedges that are hit by X. For \(i=d\) the claim is trivial since the lists \(L^d[s]\) contain only edges from E, all of which are hit by X by assumption. Now assume that the claim holds for i and consider any \(s \in L^{i-1}[s']\) for some \(s' \in \left( {\begin{array}{c}V\\ \le i-1\end{array}}\right) \). By the Need Invariant, this can only happen if \(s \in L^{i-1}[s]\) holds. By the Force Invariant, this means that s is forced by \(L^i[s]\). By Lemma 11, this means that X hits s. Since X hits all hyperedges in all lists, it also hits all hyperedges in the kernel, which is just a union of such lists.
For the second direction, let X be a size-k hitting set of K. Let \(e \in \left( {\begin{array}{c}V\\ \le d\end{array}}\right) \) be an arbitrary hyperedge (not necessarily in E). We show by induction on i that if \(e \in E(L^i[e])\), then e gets hit by X. This will show that X hits all of H: The \({\textit{insert}}\)-method ensures that for all \(e \in E\) we have \(e \in E(L^d[e])\) and, hence, they all get hit by X.
The case \(i=0\) is trivial since we can only have \(e \in L^0[e]\) for \(e = \emptyset \) and \(L^0[\emptyset ]\) is part of the kernel K and all its elements get hit by assumption (actually, \(\emptyset \in K\) means that the assumption that X hits the kernel is never satisfied; the implication is true anyway). Next, consider a larger i and a hyperedge \(e \in E(L^i[e])\).
First assume that \(e \in E(L^i[s]) - R(L^i[s])\) holds for some \(s \subseteq e\). Then s is forced by \(L^i[s]\) since it contains an irrelevant edge (e). By the Force Invariant, we know that \(s \in L^{i-1}[s]\) and, by the inductive assumption, that X hits s. Since \(s \subseteq e\), X hits e as claimed.
Second assume that \(e \notin E(L^i[s]) - R(L^i[s])\) holds for all \(s \subseteq e\). Suppose there is an \(s\subseteq e\) with \(e \notin E(L^i[s])\). Then there is also an s that is inclusion-maximal, meaning that for all \(t \subseteq e\) with \(s \subsetneq t\) we have \(e \in E(L^i[t])\) and hence also \(e \in R(L^i[t])\) since \(e \notin E(L^i[t]) - R(L^i[t])\). However, by definition, this means that e is needed in \(L^i[s]\) and, hence, \(e \in E(L^i[s])\) contrary to the assumption. In particular, we now know that for \(s=\emptyset \) we have \(e \in E(L^i[s])\) and, thus, also \(e \in R(L^i[s]) = R(L^i[\emptyset ]) \subseteq K\). Since X hits all of K, it also hits e, as claimed.
Run-Time Analysis: It remains to bound the run-times of the insert and delete operations.
Lemma 13
 runs in time \(3^d {\text {poly}}(d)\).
runs in time \(3^d {\text {poly}}(d)\).
Proof of Lemma 13
The call  will result in at least one call of \({\textit{insert}}(s,i)\): The initial call is for \(s=e\) and \(i=d\), but the method \({\textit{fix force}}\) may cause further calls for different values. However, observe that all subsequently triggered calls have the property \(s \subsetneq e\) and \(i < d\). Furthermore, observe that \({\textit{insert}}(s,i)\) returns immediately if s has already been inserted. We will establish a time bound \(t_{\mathrm {insert}}(\vert s\vert ,i)\) on the total time needed by a call of \({\textit{insert}}(s,i)\) and a time bound
will result in at least one call of \({\textit{insert}}(s,i)\): The initial call is for \(s=e\) and \(i=d\), but the method \({\textit{fix force}}\) may cause further calls for different values. However, observe that all subsequently triggered calls have the property \(s \subsetneq e\) and \(i < d\). Furthermore, observe that \({\textit{insert}}(s,i)\) returns immediately if s has already been inserted. We will establish a time bound \(t_{\mathrm {insert}}(\vert s\vert ,i)\) on the total time needed by a call of \({\textit{insert}}(s,i)\) and a time bound  where we do not count the time needed by the recursive calls (made to \({\textit{insert}}\) in line 28), that is, for a “stripped” version of the method where no recursive calls are made. We can later account for the missing calls by summing up over all calls that could possibly be made (but we count each only once, as we just observed that subsequent calls for the same parameters return immediately). In a similar fashion, let us try to establish time bounds \(t_{\mathrm {fix}}(\vert s'\vert ,i)\) and
where we do not count the time needed by the recursive calls (made to \({\textit{insert}}\) in line 28), that is, for a “stripped” version of the method where no recursive calls are made. We can later account for the missing calls by summing up over all calls that could possibly be made (but we count each only once, as we just observed that subsequent calls for the same parameters return immediately). In a similar fashion, let us try to establish time bounds \(t_{\mathrm {fix}}(\vert s'\vert ,i)\) and  on the time needed (including or excluding the time needed by calls to \({\textit{insert}}\)) by a call to the method \({\textit{fix needs downward}}(s,s',i)\) (note that, indeed, these times are largely independent of s and its size – it is the size of \(s'\) that matters).
on the time needed (including or excluding the time needed by calls to \({\textit{insert}}\)) by a call to the method \({\textit{fix needs downward}}(s,s',i)\) (note that, indeed, these times are largely independent of s and its size – it is the size of \(s'\) that matters).
The starred versions are easy to bound: We have  as we call \({\textit{fix needs downward}}\) for \(s' = s\). We have
as we call \({\textit{fix needs downward}}\) for \(s' = s\). We have  since the run-time is clearly dominated by the loop in line 20, which iterates over all subsets \(s''\) of \(s'\). For each of these \(2^{\vert s'\vert }\) many sets, we run a test in line 22 that needs time \(O(\vert s'\vert )\), yielding a total run-time of
since the run-time is clearly dominated by the loop in line 20, which iterates over all subsets \(s''\) of \(s'\). For each of these \(2^{\vert s'\vert }\) many sets, we run a test in line 22 that needs time \(O(\vert s'\vert )\), yielding a total run-time of  . For the unstarred version we get:
. For the unstarred version we get:

Pluggin in the bound \(2^c {\text {poly}}(c)\) for \(t^*_{\mathrm {insert}}(c,j)\), we get that everything following the binomial can be bounded by \((d-c)2^c {\text {poly}}(c)=2^c {\text {poly}}'(c)\). This means that the main sum we need to bound is \(\sum _{c=0}^{\vert s\vert -1} \left( {\begin{array}{c}\vert s\vert \\ c\end{array}}\right) 2^c \le \sum _{c=0}^{\vert s\vert } \left( {\begin{array}{c}\vert s\vert \\ c\end{array}}\right) 2^c\). The latter is equal to \(3^{\vert s\vert }\), which yields the claim.
Lemma 14
 runs in time \(5^d {\text {poly}}(d)\).
runs in time \(5^d {\text {poly}}(d)\).
Proof of Lemma 14
Similarly to the analysis of the \({\textit{insert}}\) method, let \(t_{\mathrm {delete}}(\vert s\vert ,i)\) denote the run-time needed by \({\textit{delete}}(s,i)\) and let \(t^*_{\mathrm {delete}}(\vert s\vert ,i)\) the time to delete excluding the time needed by the recursive calls made to \({\textit{delete}}(s',i-1)\) inside this method. In other words, we do not count the (huge) time actually needed in line 39, where a recursive call is made, and will once more later on account for this time by summing over all \(t_{\mathrm {delete}}(\vert s\vert ,i)\); but \(t^*_{\mathrm {delete}}(\vert s\vert ,i)\) will include the run-time needed for the second loop, starting at line 42, where we (possibly) fix the Need Invariant for many f (this loop does not involve any recursive calls to the \({\textit{delete}}\) method). Note that – as in the insertion case – if there are multiple calls of \({\textit{delete}}(s,i)\) for the same s and i, we only need to count one of them since all subsequent ones return immediately (and could be suppressed).
A call to \({\textit{delete}}(s,i)\) clearly spends at most time \(2^{\vert s\vert } {\text {poly}}\vert s\vert \) in the first loop (starting on line 36) if we ignore the recursive calls. For the second loop, we iterate over all \(s' \subseteq s\) and for each of them we call \({\textit{fix needs downwards}}(f,s',i)\):

With the bound of \(3^{\vert s'\vert } {\text {poly}}\vert s'\vert \) established in the proof of Lemma 13 for \(t_{\mathrm {fix}}(\vert s'\vert ,i)\), we can focus on bounding \(\sum _{s' \subseteq s} 3^{\vert s'\vert } = \sum _{c=0}^{\vert s\vert } \left( {\begin{array}{c}\vert s\vert \\ c\end{array}}\right) 3^c\) and this is equal to \(4^{\vert s\vert }\). Therefore, we have \(t^*_{\mathrm {delete}}(\vert s\vert ,i) = 4^{\vert s\vert } {\text {poly}}\vert s\vert \). We can now bound the total run-time of the delete method by summing over all recursive calls:

Plugging in \(4^{\vert s'\vert } {\text {poly}}\vert s'\vert \) for \(t^*_{\mathrm {delete}}(\vert s'\vert ,j)\) we get that the crucial sum is
yielding \(t_{\mathrm {delete}}(\vert s\vert ,i) = 5^{\vert s\vert } {\text {poly}}\vert s\vert \) as claimed.
Proof of Theorem 1
5 Dynamic Set Packing Kernels
Like the static kernel [1], the dynamic kernel algorithm we have developed in the previous section also works, after a slight modification, for the set packing problem, which is the “dual” of the hitting set problem: Instead of trying to “cover” all hyperedges using as few vertices as possible, we must now “pack” as many hyperedges as possible. These superficially quite different problems allow similar kernelization algorithms because correctness of the dynamic hitting set kernel algorithm hinges on Lemma 4, which states that every size-k hitting set X must hit the core of any b-flower F with \(\vert F\vert > b\cdot k\). It leads to the central idea behind the complex management of the lists \(L^i[s]\): The lists \(L^i[s]\) were all b-flowers for different values of b by construction and the moment one of them gets larger than \(b\cdot k\), we stop adding hyperedges to its relevant part and instead “switch over to the core s” by adding s to \(L^{i-1}[s]\). It turns out that a similar lemma also holds for set packings:
Lemma 15
Let F be a b-flower with core c in a d-hypergraph \(H = (V,E)\) and let \(\vert F\vert > b\cdot d\cdot (k-1)\). If \(E \cup \{c\}\) has a packing of size k, so does E.
Proof of Lemma 15
Let P be the size-k packing of \(E \cup \{c\}\). If \(c \notin P\), we are done, so assume \(c \in P\). For each \(p \in P - \{c\}\), consider the hyperedges in \(e \in F\) with \(p \cap e \ne \emptyset \). Since p has at most d elements v and since each v lies in at most b different hyperedges of the b-flower F, we conclude that p intersects with at most \(d \cdot b\) hyperedges in F. However, this means that the \((k-1)\) different \(p \notin P - \{c\}\) can intersect with at most \((k-1)\cdot b\cdot d\) hyperedges in F. In particular, there is a hyperedge \(f \in F\) with \(f \cap p =\emptyset \) for all \(p \in P - \{c\}\). Since \(F \subseteq E\), we get that \(P - \{c\} \cup \{f\}\) is a packing of E of size k.
Keeping this lemma in mind, suppose we modify the relevance bounds of the lists \(L^i[s]\) as follows: Instead of setting them to \(k^{i-\vert s\vert }\), we set them to \((d(k-1))^{i-\vert s\vert }\). Then all lists are b-flowers for a value of b such that whenever more than \(b \cdot d(k-1)\) hyperedges are in \(L^i[s]\), the set s gets forced into \(L^{i-1}[s]\). Lemma 15 now essentially tells us that instead of considering the flower \(E(L^i[s])\), it suffices to consider the core s. Thus, simply by replacing line 5 inside the \({\textit{init}}\) method as follows, we get a dynamic kernel algorithm for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {set}\text {-}\textsc {packing}}\):

Proof of Theorem 2
We have to show that there is an algorithm  that is a dynamic kernel algorithm for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {set}\text {-}\textsc {packing}}\) with at most \(\sum _{i=0}^d (d(k-1))^i\) hyperedges in the kernel, insertion time \(3^d{\text {poly}}(d)\), and deletion time \(5^d{\text {poly}}(d)\). For this, we mainly need to show that an analogue of Lemma 12 holds, which stated that
that is a dynamic kernel algorithm for \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {set}\text {-}\textsc {packing}}\) with at most \(\sum _{i=0}^d (d(k-1))^i\) hyperedges in the kernel, insertion time \(3^d{\text {poly}}(d)\), and deletion time \(5^d{\text {poly}}(d)\). For this, we mainly need to show that an analogue of Lemma 12 holds, which stated that  maintains the invariant that H and K have the same size-k hitting sets. We now have to show for \(H = (V,E)\):
maintains the invariant that H and K have the same size-k hitting sets. We now have to show for \(H = (V,E)\):
Claim 3
 maintains the invariant that E has a size-k packing if, and only if, K does.
maintains the invariant that E has a size-k packing if, and only if, K does.
Proof
We start with an observation: For every hyperedge \(e \in E\) there is a subset \(s \subseteq e\) with \(s \in K\). To see this, for a given e consider the smallest i such that there is an \(s \subseteq e\) with \(s \in E(L^i[s'])\) for some \(s' \subseteq s\) (such an i, s, and \(s'\) must exist, since at least for \(s = s' = e\) and \(i=d\) we have the property \(s \in E(L^i[s'])\)). If we have \(s\in R(L^i[\emptyset ])\), we have \(s \in K\) as claimed. Otherwise, there must be an inclusion-maximal \(t \subseteq s'\) such that \(s \in E(L^i[t]) - R(L^i[t])\) (as we have \(s \notin R(L^i[\emptyset ])\), but \(s \in E(L^i[s'])\)). But, then, t would be forced into \(L^{i-1}[t]\) and hence \(t \in E(L^{i-1}[t])\) would hold, violating the minimality of i.
We now prove the claim by proving two directions. The first direction is easy: Consider a packing P of E. By the above observations, for every \(p \in P\) there is a set \(s_p \in K\) with \(s_p \subseteq p\). Then \(\{s_p \mid p \in P\}\) is a packing of size k in K.
For the second direction, let P be a packing of K of size k. For some number \(i \in \{0,\dots ,d\}\) let \(A_i = \bigcup _{s \in \left( {\begin{array}{c}V\\ \le i\end{array}}\right) } E(L^i[s])\) be the set of all hyperedges “mentioned in \(L^i[s]\) for some s” and let \(B_i = \bigcup _{j=i}^d A_j\) be the “hyperedges mentioned in some \(L^d[s]\), \(L^{d-1}[s]\), ..., \(L^i[s]\) for some s.” Observe that \(K \subseteq B_0\) and that \(E = A_d = B_d\) (since \(e \in L^d[e]\) holds for all \(e \in E\) and no edges \(e \notin E\) make it into any \(L^d[s]\)). Since P is a packing of \(K \subseteq B_0\), we know that \(B_0\) has a size-k packing. We show by induction on i that all \(B_i\) have a size-k packing and, hence, in particular \(B_d = E\) as claimed.
For the inductive step, let \(B_{i-1}\) have a size-k packing and let P be one of these with the minimum number of elements that do not already lie in \(B_i\) (that is, which lie only in \(A_{i-1}\)). If the number is zero, P is already a size-k packing of \(B_i\); so let \(p \in P - B_i\). By the force property, a hyperedge p can lie in \(A_{i-1}\) only because it was forced, that is, because \(L^i[s]\) has an irrelevant hyperedge. This means that \(E(L^i[s]) \subseteq B_i\) is a \((d(k-1))^{i-\vert s\vert -1}\)-flower (by Lemma 10 where we clearly just have to replace k by \(d(k-1)\)). Since \(\vert E(L^i[s])\vert \) is larger than the relevance bound of \((d(k-1))^{i-\vert s\vert }\), Lemma 15 tells us that there is a set \(f\in E(L^i[s])\) such that \(P - \{p\} \cup \{f\}\) is also a packing of \(B_i\). Since \(f \in B_i\), this violates the assumed minimality of P. Thus, P must be a size-k packing of \(B_i\).
Clearly, the analysis of the kernel size and of the runtimes is identical to the hitting set case, yielding the claim.
6 Conclusion
We introduced a fully dynamic algorithm that maintains a \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) kernel of size \(\sum _{i=0}^d k^i \le (k+1)^d\) with update time \(5^d {\text {poly}}(d)\) – which is a constant, deterministic, worst-case bound – and zero query time. Since \(\mathrm {p}_{k}\text {-}{{ d}\text {-}\textsc {hitting}\text {-}\textsc {set}}\) has no kernel of size \(O(k^{d-\epsilon })\) unless  [17], and since the currently best static algorithm requires time \(\vert E\vert \cdot 2^d {\text {poly}}(d)\) [18], this paper essentially settles the dynamic complexity of computing hitting set kernels. While it seems possible that the update time can be bounded even tighter with an amortized analysis, we remark that this could, at best, yield an improvement from the already constant worst-case time \(5^d {\text {poly}}(d)\) to an amortized time of \(2^d {\text {poly}}(d)\).
[17], and since the currently best static algorithm requires time \(\vert E\vert \cdot 2^d {\text {poly}}(d)\) [18], this paper essentially settles the dynamic complexity of computing hitting set kernels. While it seems possible that the update time can be bounded even tighter with an amortized analysis, we remark that this could, at best, yield an improvement from the already constant worst-case time \(5^d {\text {poly}}(d)\) to an amortized time of \(2^d {\text {poly}}(d)\).
Our algorithm has the useful property that any size-k hitting set of a kernel is a size-k hitting set of the input graph. Therefore, we can also dynamically provide the following “gap” approximation with constant query time: Given a dynamic hypergraph H and a number k, at any time the algorithm either correctly concludes that there is no size-k hitting set, or provides a hitting set of size at most \(\sum _{i=0}^d k^i\). With a query time that is linear with respect to the kernel size, we can also greedily obtain a solution of size dk, which gives a simple d-approximation. A “real” dynamic approximation algorithm, however, should combine the concept of \(\alpha \)-approximate pre-processing algorithms [32, 33] with dynamic updates of the hypergraph. This seems manageable if we allow only edge insertions, but a solution for the general case is not obvious to us.
References
Abu-Khzam, F.N.: A Kernelization Algorithm for d-Hitting Set. Journal of Computer and System Sciences 76(7), 524–531 (2010). https://doi.org/10.1016/j.jcss.2009.09.002
Chen, Y., Flum, J., Huang, X.: Slicewise Definability in First-Order Logic with Bounded Quantifier Rank. In: Proceedings of the 26th EACSL Annual Conference on Computer Science Logic, CSL 2017, August 20–24, 2017, Stockholm, Sweden, pp. 19–11916 (2017). https://doi.org/10.4230/LIPIcs.CSL.2017.19
Karp, R.M.: Reducibility Among Combinatorial Problems. In: Proceedings of a Symposium on the Complexity of Computer Computations, Held March 20–22, 1972, at the IBM Thomas J. Watson Research Center, Yorktown Heights, New York, USA, pp. 85–103 (1972). https://doi.org/10.1007/978-1-4684-2001-2_9
Downey, R.G., Fellows, M.R.: Fundamentals of Parameterized Complexity. Texts in Computer Science. Springer, Berlin Heidelberg (2013). https://doi.org/10.1007/978-1-4471-5559-1
Flum, J., Grohe, M.: Parameterized Complexity Theory. Texts in Theoretical Computer Science. Springer, Berlin Heidelberg (2006). https://doi.org/10.1007/3-540-29953-X
Fafianie, S., Kratsch, S.: A shortcut to (sun)flowers: Kernels in logarithmic space or linear time. In: Proceedings of the 40th International Symposium on Mathematical Foundations of Computer Science, MFCS 2015, Milan, Italy, August 24–28, 2015. Lecture Notes in Computer Science, vol. 9235, pp. 299–310. Springer, Milan (2015). https://doi.org/10.1007/978-3-662-48054-0_25
Bannach, M., Skambath, M., Tantau, T.: Kernelizing the hitting set problem in linear sequential and constant parallel time. In: 17th Scandinavian Symposium and Workshops on Algorithm Theory, SWAT 2020, June 22–24, 2020, Tórshavn, Faroe Islands, pp. 9–1916 (2020). https://doi.org/10.4230/LIPIcs.SWAT.2020.9
van Bevern, R., Smirnov, P.V.: Optimal-size problem kernels for d-hitting set in linear time and space. Information Processing Letters 163(105998) (2020). https://doi.org/10.1016/j.ipl.2020.105998
Wahlström, M.: Algorithms, measures and upper bounds for satisfiability and related problems. PhD thesis, Linköping University, Sweden (2007)
Fernau, H.: A top-down approach to search-trees: Improved algorithmics for 3-hitting set. Algorithmica 57(1), 97–118 (2010). https://doi.org/10.1007/s00453-008-9199-6
Fomin, F.V., Gaspers, S., Kratsch, D., Liedloff, M., Saurabh, S.: Iterative compression and exact algorithms. Theor. Comput. Sci. 411(7–9), 1045–1053 (2010). https://doi.org/10.1016/j.tcs.2009.11.012
Niedermeier, R., Rossmanith, P.: An Efficient Fixed-Parameter Algorithm for 3-Hitting Set. Journal of Discrete Algorithms 1(1), 89–102 (2003). https://doi.org/10.1016/S1570-8667(03)00009-1
van Bevern, R., Smirnov, P.V.: Optimal-size problem kernels for d-hitting set in linear time and space. Information Processing Letters 163, 105998 (2020). https://doi.org/10.1016/j.ipl.2020.105998
van Bevern, R., Kirilin, A.M., Skachkov, D.A., Smirnov, P.V., Tsidulko, O.Y.: Serial and parallel kernelization of multiple hitting set parameterized by the dilworth number, implemented on the GPU. CoRR abs/2109.06042 (2021) 2109.06042
Alman, J., Mnich, M., Vassilevska Williams, V.: Dynamic parameterized problems and algorithms. ACM Trans. Algorithms 16(4), 1–46 (2020). https://doi.org/10.1145/3395037
Damaschke, P.: Parameterized Enumeration, Transversals, and Imperfect Phylogeny Reconstruction. Theoretical Computer Science 351(3), 337–350 (2006). https://doi.org/10.1016/j.tcs.2005.10.004
Dell, H., van Melkebeek, D.: Satisfiability Allows No Nontrivial Sparsification Unless the Polynomial-Time Hierarchy Collapses. Journal of the ACM 61(4), 23–12327 (2014). https://doi.org/10.1145/2629620
van Bevern, R.: Towards Optimal and Expressive Kernelization for \(d\)-Hitting Set. Algorithmica 70(1), 129–147 (2014). https://doi.org/10.1007/s00453-013-9774-3
Buss, J.F., Goldsmith, J.: Nondeterminism Within P. SIAM Journal on Computing 22(3), 560–572 (1993). https://doi.org/10.1137/0222038
Henzinger, M., King, V.: Maintaining Minimum Spanning Forests in Dynamic Graphs. SIAM Journal on Computing 31(2), 364–374 (2001). https://doi.org/10.1137/S0097539797327209
Holm, J., de Lichtenberg, K., Thorup, M.: Poly-Logarithmic Deterministic Fully-Dynamic Algorithms for Connectivity, Minimum Spanning Tree, 2-Edge, and Biconnectivity. Journal of the ACM 48(4), 723–760 (2001). https://doi.org/10.1145/502090.502095
Bhattacharya, S., Henzinger, M., Italiano, G.F.: Deterministic Fully Dynamic Data Structures for Vertex Cover and Matching. In: Proceedings of the 26th ACM-SIAM Symposium on Discrete Algorithms, SODA 2015, San Diego, CA, USA, January 4–6, 2015, pp. 785–804 (2015). https://doi.org/10.1137/1.9781611973730.54
Patnaik, S., Immerman, N.: DynFO: A Parallel, Dynamic Complexity Class. Journal of Computer and System Sciences 55(2), 199–209 (1997). https://doi.org/10.1006/jcss.1997.1520
Datta, S., Kulkarni, R., Mukherjee, A., Schwentick, T., Zeume, T.: Reachability Is in DynFO. Journal of the ACM 65(5), 33–13324 (2018). https://doi.org/10.1145/3212685
Iwata, Y., Oka, K.: Fast Dynamic Graph Algorithms for Parameterized Problems. In: Proceedings of the 14th Scandinavian Symposium and Workshop on Algorithm Theory, SWAT 2014, Copenhagen, Denmark, July 2–4, 2014, pp. 241–252 (2014). https://doi.org/10.1007/978-3-319-08404-6_21
Chen, J., Czerwinski, W., Disser, Y., Feldmann, A.E., Hermelin, D., Nadara, W., Pilipczuk, M., Pilipczuk, M., Sorge, M., Wróblewski, B., Zych-Pawlewicz, A.: Efficient fully dynamic elimination forests with applications to detecting long paths and cycles. In: Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, Virtual Conference, January 10–13, 2021, pp. 796–809. SIAM, Virtual Conference (2021). https://doi.org/10.1137/1.9781611976465.50
Downey, R.G., Fellows, M.R., Stege, U.: Parameterized complexity: A framework for systematically confronting computational intractability. In: Graham, R.L., Kratochvíl, J., Nesetril, J., Roberts, F.S. (eds.) Contemporary Trends in Discrete Mathematics: From DIMACS and DIMATIA to the Future, Proceedings of a DIMACS Workshop, Stirín Castle, Czech Republic, May 19–25, 1997. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 49, pp. 49–99. DIMACS/AMS, Stirín Castle (1997). https://doi.org/10.1090/dimacs/049/04
Mehlhorn, K.: Data Structures and Algorithms 1: Sorting and Searching. EATCS Monographs on Theoretical Computer Science. Springer, Berlin Heidelberg (1984)
Erdős, P., Rado, R.: Intersection Theorems for Systems of Sets. Journal of the London Mathematical Society 1(1), 85–90 (1960)
Bannach, M., Tantau, T.: Computing Hitting Set Kernels By AC\(^0\)-Circuits. Theory Comput. Syst. 64(3), 374–399 (2020). https://doi.org/10.1007/s00224-019-09941-z
van Bevern, R.: Fixed-Parameter Linear-Time Algorithms for NP-hard Graph and Hypergraph Problems Arising in Industrial Applications. Foundations of Computing, vol. 1. Universitätsverlag der TU Berlin, Berlin (2014). https://doi.org/10.14279/depositonce-4131
Fellows, M.R., Kulik, A., Rosamond, F.A., Shachnai, H.: Parameterized approximation via fidelity preserving transformations. J. Comput. Syst. Sci. 93, 30–40 (2018). https://doi.org/10.1016/j.jcss.2017.11.001
Lokshtanov, D., Panolan, F., Ramanujan, M.S., Saurabh, S.: Lossy kernelization. In: Hatami, H., McKenzie, P., King, V. (eds.) Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2017, Montreal, QC, Canada, June 19–23, 2017, pp. 224–237. ACM, Montreal (2017). https://doi.org/10.1145/3055399.3055456
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A Appendix: Implementation Details of Data Structures
Appendix A Appendix: Implementation Details of Data Structures
The dynamic kernel algorithms that we present in this paper internally employ different standard dynamic data structures like linked lists or small arrays that allow update operations in time O(1). In the following, for completeness, we sketch how these basic data structures can be implemented so that all basic operations work in constant time.
Objects: We will often store and treat mathematical entities like edges or sequences as objects in the sense of object-oriented programming. As is customary, they are just blocks of memory storing the object’s current attributes and the object can be referenced with a pointer to the start of the memory block. For an object X we write \(X.{\textit{attribute}}\) for the current value of an attribute.
Arrays: By arrays we refer to the usual notion of arrays that store a value for each index number from an immutable domain \(D = \{1,\dots , r\}\). We write A[i] for the value stored at position \(i \in D\), write \(A[i] \leftarrow v\) to indicate that we store the value v (typically an object or a number) at the ith position in A and we write \(A[i] = \bot \) to indicate that nothing is stored at an address i. In order to allocate a new array, we write  , whose semantics is the following:
, whose semantics is the following:

Of course, implemented this way, while the allocation of an uninitialized memory block in line 1 will take constant time on a normal operating system, filling the array with initial values in the for-loop will take time \(O(\vert D\vert t_f)\), where \(t_f\) is the time needed to compute f. However, a trick [28] allows us to perform this initialization in constant time:
Lemma 16
Let the time needed to allocate an uninitialized array of size \(\vert D\vert \) (so the initial content can be random) be constant and let \(t_f\) be the time needed to compute the function f. Then  can be implemented in such a way that it runs in time O(1) and such that it subsequently takes extra time at most \(O(t_f)\) each time an element A[i] is accessed for the first time.
can be implemented in such a way that it runs in time O(1) and such that it subsequently takes extra time at most \(O(t_f)\) each time an element A[i] is accessed for the first time.
In particular, if \(t_f\) is constant (as is the case in our paper, where this is the time needed to initialize an empty relevance list), the creation of the array takes only constant time and only a constant time overhead is incurred for later accesses.
Proof
We only sketch the proof. The idea is from [28, Section III.8.1]: Alongside A, in constant time we allocate two further uninitialized arrays B and C of the same size \(\vert D\vert \) as A, which hold integer values (indices), and we setup a counter c:

The idea is that we use B, C and c to keep track of which elements of A have been already accessed. When we notice later on that A[i] is accessed for the first time, we set \(A[i] \leftarrow f(i)\) before proceeding.
We keep track of which elements of A have been accessed (ever) using the following invariant: The ith element of A will have been accessed if, and only if, \(C[B[i]] = i\) and \(1 \le B[i] \le c\). Initially, the invariant is trivially fulfilled as \(c = 0\) and no element of A has been accessed.
Clearly, when A[i] is about to be accessed, we can easily check whether the invariant holds for a given i in constant time. Now suppose we notice that A[i] is accessed for the first time (as \(B[i] \notin \{1,\dots , c\}\) or \(C[B[i]] \ne i\)). In this case, we first increase c by 1, so \(c \leftarrow c + 1\), and then set \(B[i] \leftarrow c\) and set \(C[c] \leftarrow i\). Note that this ensures that the invariant is now satisfied for A[i] and, also, still satisfied for all other A[j] for \(j \ne i\).
For convenience, we also allow domains D that are not sets of numbers, but whose elements can easily be mapped to numbers. For instance, we would also allow the domain \(D = \left( {\begin{array}{c}V\\ 2\end{array}}\right) \) of undirected edges since we can easily map D to \(\bigl \{1,\dots ,\left( {\begin{array}{c}n\\ 2\end{array}}\right) \bigr \}\). We can then write \(G[e] \leftarrow v\) to store a value v for an edge \(e = \{u,v\}\). Clearly, for hypergraphs this can be generalized to \(D = \left( {\begin{array}{c}V\\ \le d\end{array}}\right) \) for fixed constants d since this D, too, can easily be mapped to elements of \(\bigl \{1,\dots ,\sum _{i=0}^d \left( {\begin{array}{c}n\\ i\end{array}}\right) \bigr \}\). By storing arrays as tables of size \(O(\vert D\vert )\), reading from and writing to an array can be done in time O(1) for any reasonable machine model. Unfortunately, this model of storing values is not very memory-efficient when \(A[i] = \bot \) holds for most i and, therefore, it is better to store A as a hash table. In practice, hash tables also allow us to read and write in time O(1). For this paper, we just assume that in whatever way arrays are really implemented, reading and writing from arrays can be done in time O(1).
Maps: Maps (also known as associative arrays) are similar to arrays, but may be indexed by keys k, which can be arbitrary objects, and not just by numbers from a small domain. We still write M[k] for the value v stored at the key k (and \(M[k] = \bot \) if nothing is stored) and write \(M[k] \leftarrow v\) to indicate that we store the value v for the key k, possibly replacing any previous value stored for k. Implementing maps is normally much trickier than implementing arrays, but we will only need and use maps that store values for a constant number of keys. In this case, even if we implement accesses using just a linear search in a normal array, all reading and writing can be done in time O(1).
Lists: We will use the standard data structure of doubly-linked lists a lot, which we will just refer to as lists. We consider lists L to be objects that store pointers to the first and last cell of the list. Each cell stores pointers to the next and the previous cell in the list plus a pointer to an object, called the payload of the cell. For a list L, we write \(L.{\textit{append}}(x)\) to indicate that a new cell c gets created with x as its payload and then c is added to the list at the end (and the last and, possibly, first cells stored in L are updated appropriately).
Quite less standard, when creating a cell c for a list L, we also store the cell c in x: We assume that x has an attribute \({\textit{lists}}\) that is a map and we execute \(x.{\textit{lists}}[L] \leftarrow c\). In other words, inside x, we store a back-pointer to the cell c. This allows us to perform the operation \(L.{\textit{delete}}(x)\) without being given the cell c: We first lookup the cell c that has x as its payload in the map \(x.{\textit{lists}}\) and can then easily remove the cell from the doubly-linked list in constant time. Storing back-pointers in objects allows us to remove elements in time O(1) provided that (i) no element is added more than once to a list (this will always be the case) and (ii) each element is added only to a constant number of lists (this will also always be the case).
Relevance Lists: The next data structure is more specific to the needs of the present paper: relevance lists. These are normal lists with a parameter \(\rho \in \mathbb {N}\) in which the first \(\rho \) elements are “more relevant” than later elements (with respect to the order of the elements inside the list). Once a relevance list L for a bound \(\rho \) has been allocated by the call  , we wish the following to hold for its elements: If there are only \(\rho \) or less elements in L, all of them are relevant; but if there are more, all elements after the \(\rho \)th element are irrelevant. The operations we wish to support (in time O(1)) in addition to the normal list operations \({\textit{append}}\) and \({\textit{delete}}\) are \(L.{\textit{is relevant}}(x)\), which should return whether x is one of the first \(\rho \) elements in L, and \(L.{\textit{last relevant}}\), which should return the last relevant element of the list, respectively. For convenience, we will also use \(L.{\textit{first irrelevant}}\), which is the successor of \(L.{\textit{last relevant}}\) (and thus \(\bot \) if there are no irrelevant elements), and \(L.{\textit{has irrelevant elements}}\), which just checks whether \(L.{\textit{last relevant}}\) has a successor.
, we wish the following to hold for its elements: If there are only \(\rho \) or less elements in L, all of them are relevant; but if there are more, all elements after the \(\rho \)th element are irrelevant. The operations we wish to support (in time O(1)) in addition to the normal list operations \({\textit{append}}\) and \({\textit{delete}}\) are \(L.{\textit{is relevant}}(x)\), which should return whether x is one of the first \(\rho \) elements in L, and \(L.{\textit{last relevant}}\), which should return the last relevant element of the list, respectively. For convenience, we will also use \(L.{\textit{first irrelevant}}\), which is the successor of \(L.{\textit{last relevant}}\) (and thus \(\bot \) if there are no irrelevant elements), and \(L.{\textit{has irrelevant elements}}\), which just checks whether \(L.{\textit{last relevant}}\) has a successor.
Note that it is not immediately clear how the two additional operations of relevance list can be implemented in time O(1): The relevance status of an element can change when far-away elements get added or deleted. The following lemma shows how this can be achieved:
Lemma 17
A relevance list can be implemented such that the two methods \(L.{\textit{is relevant}}(x)\) and \(L.{\textit{last relevant}}\) run in time O(1).
Proof of Lemma 17
A relevance list object L stores the immutable bound \(\rho \) as an attribute. It also stores the length of the list using an additional attribute (just increment or decrement it as needed). To keep track of which elements x are relevant with respect to L and which one is the last of them, we use two kinds of “trackers”: First, we store one bit of information in each element x as follows. In x we have, in addition to the map attribute \({\textit{lists}}\) mentioned earlier, another attribute \({\textit{relevances}}\). It is also a map and we set \(x.{\textit{relevances}}[L] \leftarrow true \) for relevant x and set \(x.{\textit{relevances}}[L] \leftarrow false \) otherwise. Clearly, if we can keep these values up-to-date, we can implement \(L.{\textit{is relevant}}(x)\) simply as returning \(x.{\textit{relevances}}[L]\). Second, in L we store a pointer to the last relevant element in an attribute \({\textit{last relevant}}\). Once more, if we can keep this pointer up-to-date, we can trivially access it in time O(1).
To keep the introduced trackers up to date, first consider the operation \(L.{\textit{append}}(x)\): Before we insert x, we check whether the length of L is at most \(\rho -1\). If so, after x has been appended, it is flagged as relevant (\(x.{\textit{relevances}}[L] \leftarrow true \)) and \(L.{\textit{last relevant}} \leftarrow x\); and otherwise it is flagged as irrelevant and \(L.{\textit{last relevant}}\) is not changed. Next, consider the operation \(L.{\textit{delete}}(x)\). If x is not relevant (\(x.{\textit{relevances}}[L] = false \)), we can simply delete it. However, if x is relevant, deleting x will make the first irrelevant element (if it exists) relevant: before deleting x, if \(L.{\textit{last relevant}}\) has a successor s, we set \(L.{\textit{last relevant}} \leftarrow s\) and \(s.{\textit{relevances}}[L] \leftarrow true \). As a special case, if x happens to be the last relevant element and has no successor, set \(L.{\textit{last relevant}}\) to the predecessor of x.
Note that all operations needed to keep the trackers up-to-date can be implemented to run in time O(1), yielding the claim.
Dense Adjacency Matrices: The final data structure that we introduce addresses a specific subtlety of kernelizations: In our algorithms, we keep track of linked lists of hyperedges \(e \in \left( {\begin{array}{c}V\\ \le d\end{array}}\right) \) that, collectively, form a kernel. However, a kernel should be a mathematical object whose encoding only depends on the parameter k – while encoding the lists takes something like \(O(k^d d \log n)\) bits since we need \(O(\log n)\) bits to encode a vertex number and the lists are “scattered around in memory.” Furthermore, the whole idea behind kernelizations is, of course, that we wish to perform further computations on the kernel once it has been determined. Thus, we should not insist on constant update times in our algorithms while then allowing time \(O(k^d)\) to transform lists into something “usable” when we actually use the kernel to find a solution. Fortunately, it turns out that we can keep track of a “real” kernel in the form of a dense adjacency matrix with only constant extra time per update. For simplicity, we only describe the case of graphs, the generalization to hypergraphs is straightforward.
For a set E of edges, let \(\bigcup E = \{ x \mid \exists e \in E:x \in e\}\) denote the set of all vertices mentioned in any edge of E. For two graphs \(G_1 = (V_1,E_1)\) and \(G_2 = (V_2,E_2)\) let us write \(G_1 \sim G_2\) if \(G_1\) and \(G_2\) are isomorphic. For two edge sets \(E_1\) and \(E_2\), let us write \(E_1 \sim E_2\) if \((\bigcup E_1, E_1) \sim (\bigcup E_2,E_2)\) (so vertices that are not involved in any edges are ignored).
Our objective is the following: Suppose we already have a dynamic algorithm that keeps track of a set F of edges for the vertex set V (in our dynamic vertex cover kernel algorithm we have \(F = R(L)\); in the dynamic hitting set kernel algorithm we have \(F = \bigcup _{i=0}^d R(L^i[\emptyset ])\)) and suppose that we have a bound \(\rho \) such that \(\vert F\vert \le \rho \) always holds. In the following lemma we show that we can then dynamically manage the adjacency matrix of a graph \(K = (V_K,E_K)\) with the fixed vertex set \(V_K = \{1,\dots ,2\rho \}\) such that we always have \(E_K \sim F\) with only constant additional update times. (In the statement of the lemma, by “gets a dynamically changing set as input” we mean that whenever an edge e is added to F, the method \({\textit{insert}}(e)\) of the algorithm gets called, and whenever e is removed from F, a call of \({\textit{delete}}(e)\) is triggered.)
Lemma 18
There is an algorithm \({ \textsc {DynamicDenseAdjacencyMatrix}}\) that takes as input a dynamically changing edge set F over the vertex set V and a bound \(\rho \) with \(\vert F\vert \le \rho \), and keeps track of the adjacency matrix of \(K = (V_K,E_K)\) with the fixed vertex set \(V_K = \{1,\dots ,2\rho \}\) such that we have \(E_K \sim F\). The update times are O(1).
Proof of Lemma 18
The algorithm starts by setting up the following auxiliary data structures:
-
1.
An adjacency matrix of Boolean entries storing \(E_K \subseteq \left( {\begin{array}{c}V_K\\ 2\end{array}}\right) \), indicating which edges are present in K,
-
2.
a mapping I that stores for each vertex of \(\bigcup F\) to which vertex in \(V_K\) it corresponds (and \(I(x) = \bot \) for \(x \notin \bigcup F\)),
-
3.
an array D that stores for each \(v \in V_K\) the degree of v in K, and
-
4.
a list Z of zero degree vertex intervals in K. Each element of the list is a pair (a, b) of numbers from \(V_K\) that stands for the interval [a, b]. The semantics is that the union of the intervals should be exactly the set of vertices in \(V_K\) that have degree 0 in K. Clearly, we can initialize the Z with the single interval \([1,2\rho ]\) to ensure that this holds at the beginning.
Translated to code, we get:

Let us now see how these auxiliary data structures allow us to keep track of \(E_K\) such that \(E_K \sim F\) holds when edges enter or leave F. Suppose \(e = \{u,v\}\) is about to enter F and this triggered a call of the following \({\textit{insert}}(e)\) method, which should now update the matrix \(E_K\). First, we test whether \(u \notin \bigcup F\) holds (by testing whether \(I[u] = \bot \) holds). In this case, consider the first interval [a, b] in Z (such an interval must exist since there will never be more than \(2\rho \) vertices in \(\bigcup F\) by assumption and, hence, there is always a vertex of degree 0 in K when a new vertex is about to enter \(\bigcup F\)). If \(a=b\), remove this interval from Z, otherwise replace it by \([a+1,b]\). We think of this as “allocating” a and will store in I that u gets mapped to a. Next, if \(v \notin \bigcup F\) holds, we allocate a vertex from \(V_K\) for it. Then both u and v have corresponding vertices in \(V_K\) and we store an edge between them in \(E_K\) and adjust the values in D accordingly:

Observe that after the above steps and after e has been added to F, we have \(E_K \sim F\) and all auxiliary data structures hold the proper values.
Now suppose \(e = \{u,v\}\) is about to be deleted from F. The code for this case is simple:

Once more, \(E_K \sim F\) holds after the updates and all auxiliary data structures have also been updated correctly.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bannach, M., Heinrich, Z., Reischuk, R. et al. Dynamic Kernels for Hitting Sets and Set Packing. Algorithmica 84, 3459–3488 (2022). https://doi.org/10.1007/s00453-022-00986-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-022-00986-0





 gets the size n of V and the parameter k as inputs, neither of which will change during a run of the algorithm, and must initialize an auxiliary data structure
gets the size n of V and the parameter k as inputs, neither of which will change during a run of the algorithm, and must initialize an auxiliary data structure  gets a hyperedge e to be added to
gets a hyperedge e to be added to 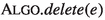 removes an edge instead of adding it.
removes an edge instead of adding it.
