Succinct Encoding of Binary Strings Representing Triangulations

Fuentes-Sepúlveda, José; Seco, Diego; Viaña, Raquel

doi:10.1007/s00453-021-00861-4

Succinct Encoding of Binary Strings Representing Triangulations

Open access
Published: 09 August 2021

Volume 83, pages 3432–3468, (2021)
Cite this article

Download PDF

You have full access to this open access article

Algorithmica Aims and scope Submit manuscript

Succinct Encoding of Binary Strings Representing Triangulations

Download PDF

973 Accesses
1 Citation
Explore all metrics

This article has been updated

Abstract

We consider the problem of designing a succinct data structure for representing the connectivity of planar triangulations. The main result is a new succinct encoding achieving the information-theory optimal bound of 3.24 bits per vertex, while allowing efficient navigation. Our representation is based on the bijection of Poulalhon and Schaeffer (Algorithmica, 46(3):505–527, 2006) that defines a mapping between planar triangulations and a special class of spanning trees, called PS-trees. The proposed solution differs from previous approaches in that operations in planar triangulations are reduced to operations in particular parentheses sequences encoding PS-trees. Existing methods to handle balanced parentheses sequences have to be combined and extended to operate on such specific sequences, essentially for retrieving matching elements. The new encoding supports extracting the d neighbors of a query vertex in O(d) time and testing adjacency between two vertices in O(1) time. Additionally, we provide an implementation of our proposed data structure. In the experimental evaluation, our representation reaches up to 7.35 bits per vertex, improving the space usage of state-of-the-art implementations for planar embeddings.

Implementing the Topological Model Succinctly

I/O-Efficient Path Traversal in Succinct Planar Graphs

Article 17 December 2015

Dynamic Compact Planar Embeddings

1 Introduction

Consider the set of unlabeled and connected finite planar graphs, where neither loops nor multiple edges are allowed, that admit planar embeddings in which each face has three and only three incident edges. One such planar embedding provides, for any vertex, a cyclic ordering of the edges it is incident with. This ordering determines a finite number of equivalence classes, each of which is called a triangulation. A triangulation is said to be rooted if an edge is distinguished and directed. All triangulations appearing in this work are considered to be rooted.

Poulalhon and Schaeffer [37] provided an optimal compression scheme for triangulations. Their algorithm enriches a particular vertex spanning tree (VST) of the triangulation with two leaves per node, obtaining what we call a PS-tree. Each leaf corresponds to an edge of the triangulation which does not belong to the VST. The PS-tree uniquely associated to a triangulation with n vertices is represented by a binary string S of size 4n, created by performing a left-to-right depth-first-search traversal of the PS-tree. Taking as the binary elements of S opening and closing parentheses symbols, an opening parenthesis symbol, ‘(’, is assigned to each down step along VST edges, and a closing parenthesis symbol, ‘)’, is assigned to both leaves and up steps along the VST edges. As string S has n symbols of type ‘(’ and 3n symbols of type ‘)’, the encoding space is further reduced to 3.24 bits per vertex. Such information-theory optimal encoding is suitable for storage or network transmission. However, once the encoding process has been performed, the triangulation is not accessible any more until the whole encoding is sequentially decoded. In this work, local access is provided at the expense of extra o(n) space. This functionality allows managing string S in main memory while navigation queries are supported.

The problem under study in this paper has also been treated by Castelli Aleardi et al. [2]. In their work, the authors make use of the succinct representation paradigm: triangulations are hierarchically decomposed into tiny and small triangulations, formalizing the catalog-tiny-small framework. Their proposal requires an extra storage of o(n) bits, and supports adjacency queries between vertices and faces in constant time. The technique presented in this work completely differs from such approach, avoiding the management of the exhaustive catalog of all tiny triangulations, the only common point being the use of the Poulalhon and Schaeffer bijection [37].

The new proposal makes use of a special parenthesis sequence, which comes from a depth-first-search traversal on the contour of the PS-tree uniquely associated to the triangulation. It does not correspond to a standard balanced parenthesis sequence of equal number of ‘)’ and ‘(’ symbols because, besides the balanced binary sequence of the VST, where ‘(’ represent down steps and ‘)’ up steps during the left-to-right depth-first-search traversal of the tree, there are interleaved ‘)’ symbols corresponding to traversed leaves. Hence, previous results to manage standard balanced binary sequences with operators such as matching cannot be directly applied. On the other side, techniques for dealing with general sequences are not efficient. By exploiting the particular structure of sequence S, a new technique to handle it has been developed in this paper. The new representation is the first string based encoding requiring the information theoretically optimal space of 3.24 bits per vertex plus an o(n) term which allows testing adjacency between two vertices in O(1) time and extracting the d neighbors of a query vertex in O(d) time. In previous work based on parentheses encodings, these operations were allowed at the cost of increasing storage space [16, 17].

Our contribution in this paper is twofold:

1.
We complement the bijection of Poulalhon and Schaeffer, allowing efficient navigation of the triangulation, while the triangulation is encoded in $3.24n+o(n)$ bits, with n the number of vertices of the triangulation. To support efficient navigation, additional compact data structures of o(n) bits are added. From the two major approaches in the area of succinct representations of triangulations we have previously described, namely catalog-based representations and string-based representations, this paper offers an alternative approach to the former one and contributes to the latter.
2.
We provide an experimental evaluation of our proposal. We measure the space usage and the query time for several datasets. In practice, our structure reaches up to 7.35 bits per vertex, improving the space usage of the current best result of Ferres et al. [21].

The rest of the paper is organized as follows. In Sect. 2 we discuss the state-of-the-art of the succinct representations of planar graphs and triangulations. In Sect. 3, the necessary background for our contribution is presented. In Sect. 4 we describe our succinct encoding, and in Sect. 5, procedures to check if two vertices are adjacent and to retrieve the list of neighbors of a vertex are shown. In Sect. 6, we present an implementation of our proposal. Finally, in Sect. 7 some conclusions are given.

2 Related Work

In 1962, Tutte’s enumerative work [41] showed that the minimum number of bits to encode a triangulation is $\lg \left( \frac{256}{27}\right) \approx 3.245$ bits per vertex.^{Footnote 1} Turán [40] proposed a simple and elegant representation for any planar graph in 4 bits per edge (asymptotically 12n bits, where n is the number of vertices). Since then, decades of research were devoted to obtain a space-optimal data structure for both planar maps and triangulations (see [34, Chapter 9]).

Jacobson [32] started in 1989 a stream of research by posing the problem of encoding a graph as shortly as possible while allowing to answer queries. He proposes a compact representation for plane graphs with n vertices requiring O(n) bits that supports basic operations such as searching and adjacency testing in O(1) time in the RAM model ($O(\lg n)$ time in the bit probe model). The result is based in decomposing plane graphs into k-page embeddings, and encoding them as sequences of one type of parenthesis. Following the same decomposition for planar graphs, Munro and Raman [33] provided another encoding requiring $2m+8n+o(m+n)$ bits, where m is the number of edges, providing analogous query support. Geary et al. [24] presented a simpler parenthesis representation which supports the operations required by the algorithms in [32, 33], such as retrieving the parenthesis matching a given one, is proposed. Its space bound has a smaller o(n) term.

The technique used by Chuang et al. [17] is conceptually different, as graphs are encoded as sequences of several types of parentheses, achieving a space requirement of $2m+(5+1/k)n+o(m+n)$ bits, for some constant $k>0$, with the same query support. Following the same line of work, Chiang et al. [16] gave a representation for simple planar graphs using in $2m+2n+o(n)$ bits, allowing adjacency and degree queries in constant time. Yamanaka and Nakano [42] further reduced the space cost for planar triangulations to $2m+o(m)$ bits with the same support for queries.

Besides proposing the first succinct representation for labeled graphs, Barbay et al. [8] presented a succinct representation for unlabeled planar triangulations using $2m\lg 6+o(m)$ bits, which also supports rank and select operations of edges in counterclockwise order. A succinct encoding of arbitrary graphs with adjacency, neighborhood and degree queries in constant time based in the encoding of its adjacency matrix was presented by Farzan and Munro [20]. The space required for the encoding is a factor of $1+\epsilon$ away from the minimum for any arbitrarily small constant $\epsilon >0$.

Blandford et al. [10] introduced a representation for separable graphs. It supports adjacency and degree queries in constant time, and neighborhood queries in time linear in the output size, but their representation requires O(n) bits. Blelloch and Farzan [12] presented a succinct representation for separable graphs which supports the same queries, all in constant time. Their encoding scheme partitions the graph into smaller subgraphs recursively until their size is small enough to be catalogued and listed into a look-up table.

He et al. [30] proposed the first optimal encoding for triangulations, without query support. Castelli Aleardi et al. [4, 6] proposed a hierarchical decomposition for triangulations into sub-triangulations of small and tiny size, small enough to be handled by the use of table-lookup and local pointers, reaching 4.35 bits per vertex. Their results were improved latter [2] to obtain an optimal representation for 3-connected planar graphs and triangulations, while supporting adjacency queries between vertices and faces in constant time. Poulalhon and Schaeffer [37] proposed an optimal encoding for triangulations based on Schnyder woods [39]. We will describe their work in more detail later, since our representation is built upon theirs.

Some practical results have been proposed, providing a tradeoff between space and time performances. Gurung et al. [27] proposed a data structure which experimentally requires on average either 1.08 references per triangle or optionally 26.2 bits per triangle. It has linear space and time complexity, while supporting constant-time adjacency queries. The same authors [28] gave an alternative presentation which uses in average 12 bits per vertex, and supports standard traversal operations in constant time. In the branch of separable graphs, Blandford et al. [10, 11] provided experimental results for static and dynamic planar graphs. Castelli Aleardi et al. [1, 3, 5, 14] showed practical compact data structures for triangulations and meshes. Turán’s non-optimal encoding for planar graphs was enriched by Ferres et al. [21] with a sublinear number of bits allowing neighbors retrieval in constant time per neighbor, and adjacency test in O(f(m))-time for any given function $f(m)\in \omega (1)$. The encoding is based in the representation of both a vertex spanning tree of the graph and the complementary spanning tree of the dual of the graph. Additionally, Ferres et al. proposed a PRAM EREW algorithm to construct their encoding in $O(\lg ^2m\lg ^*m)$ time using O(m) processors. Their algorithm can also be adapted to work in the PRAM arbitrary CRCW model in $O(\lg ^2m)$ time using $O(m/\lg m)$ processors, or in $O(\lg m)$ time using $O(m^3)$ processors.

3 Background

In this section we review previous results on which this article is based, namely the encoding of triangulations given by Poulalhon and Schaeffer [37], the results given by Geary et al. [24] to encode balanced binary strings and the result of Raman et al. [38] to encode bit-strings in optimal space.

3.1 PS-Tree of a Triangulation

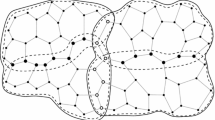
Let $\mathcal {T}$ be a triangulation with oriented root edge $(u_2,u_1)$. By convention, we consider that the root edge has the infinite face on its right. The rest of faces are said to be finite. Let $u_3$ be the third vertex of $\mathcal {T}$ incident with the infinite face. A linear time algorithm is given in [37] to construct uniquely from $\mathcal {T}$ a vertex spanning tree. It is based on a minimal Schnyder wood of $\mathcal {T}$ [13, 39], and it satisfies that each vertex (except the root vertex, its only child and its only grandchild) has two leaves. From now on, such spanning tree is referred to as the PS-tree of $\mathcal {T}$. From such tree, triangulation $\mathcal {T}$ can be reconstructed [37]. In Fig. 1a, b, both a triangulation and its PS-tree are shown.

Adapting the terminology of [37], inner nodes are vertices of degree at least 2, and leaves are vertices of degree 1 (with the only exception of the root vertex $u_1$, which has degree 1 but is an inner node). Inner edges are edges connecting two inner nodes, and stems are edges connecting an inner node to a leaf. By merging leaves to inner nodes, triangular faces are created. Let $u_i$, $u_j$, $u_k$ be inner nodes, and l be a leaf, such that $u_i$, $u_j$, $u_k$ and l are found in this order when the infinite face is traversed in counterclockwise order. The triple $\big ((u_i,u_j),(u_j,u_k),(u_k,l)\big )$ is called an admissible triple. The local closure of such an admissible triple consists in merging leaf l with inner node $u_i$ to create a bounded face of degree 3. Stem $(u_k,l)$ then becomes inner edge $(u_k,u_i)$. The recursive application of local closure to all available admissible triples builds the original triangulation. Provided there are several admissible triples, the order of application of local closure is irrelevant. In Fig. 1c, several admissible triples are shown. Dashed lines indicate those stems which become inner edges when the local closure of the corresponding admissible triples is performed. In Fig. 1d, the next step of local closure is shown.

The triangulation $\mathcal {T}$ can be encoded in a binary string S by performing a linear time left-to-right depth-first-search of its PS-tree. For the sake of clarity we will build string S with opening parentheses instead of 1’s and closing parentheses instead of 0’s. Whenever an inner edge is found the first time, a ‘(’ symbol is added to S. Re-visited inner edges and stems are represented by ‘)’ symbols in S. Taking into account that in a triangulation with n vertices there are $n-1$ inner edges and $2n-5$ stems, the length of string S is $4n-7$ plus an extra ‘( )’ pair enclosing the whole sequence (Fig. 1e). From now on, by balanced binary strings we refer to strings formed by matching ‘( )’ pairs, an by balanced-quadruple string we refer to the string S whose construction we have just explained and where, besides each ‘(’ and its matching ‘)’, there are some other ‘)’ symbols. Since the string S has $n-1$ 1-bits and $3n-5$ 0-bits, it can be encoded into $nH_0(S)+o(n)\approx 3.24n+o(n)$ bits using a compressed bit-string, such as the representation of Raman et al. [38]. In the expression, $H_0(S)$ corresponds to the zeroth-order empirical entropy of S.

To reconstruct the triangulation from string S, the exhaustive recursive application of local closure to all admissible triples has to be performed.

3.2 Encoding of Balanced Binary Strings

Given a balanced binary string of length 2n, Geary et al. [24] introduced a representation which supports the following operations in O(1) time:

find 1 (p) returns the position of the 1 that matches a given 0 in position p.
find 0 (p) returns the position of the 0 that matches a given 1 in position p.
enclose (p) finds the 1 of the matching pair that most tightly encloses the element in position p.

Proposition 1

(Geary et al. [24, Theorem 6]). A balanced binary string of 2n elements can be represented using $2n+O\left( \frac{n\lg \lg n}{\lg n} \right)$ bits so that the operations find1, find0 and enclose can be supported in O(1) time.

To implement these operations, the given string is divided into blocks of size $B=\Theta (\lg n)$, and a set of $O\left( \frac{n}{B}\right)$ elements are identified as pioneers. Considering only those elements which have their matchings in a block different to the block they belong to, a 1 that is a pioneer indicates that its matching 0 is in a different block than the matching of the first 1 to its left.

A bit-vector V of the same length as original string (2n) with 1’s at the positions of pioneer elements is created. The positions of the sequence of pioneer elements are stored in o(n) bits using a data structure called a Nearest Neighbor Dictionary (NND). This NND encoding V supports the following operations in O(1) time:

rank $_1(i,V)$: returns the number of 1’s up to the i-th element (included) in V.
select $_1(i,V)$: returns the position of the i-th 1 in V.
pred (i, V): returns the position of the first 1 to the left of the i-th element in V. It returns i if the i-th element is a 1.
succ (i, V): returns the position of the first 1 to the right of the i-th element in V. It returns i if the i-th element is a 1.

A bit-vector W of length |W| is said to be uniformly sparsed if it satisfies the following two properties: (i) the number of 1 elements in W is $O\left( \frac{|W|}{\lg |W|}\right)$, (ii) the number of 0 elements between any two 1’s is at most $O\left( \lg ^c |W|\right)$ for some constant $c\ge 1$. A simplified NND, called SNND, is proposed by Geary et al. [24] for uniformly sparsed sets. This SNND requires four arrays of $O\left( \frac{|W|\lg \lg |W|}{\lg |W|}\right)$ bits each and three tables of $O\left( |W|^{2/3}\right)$ bits each. In the next lemma some properties of the SNND structure are given.

Lemma 1

(Geary et al. [24, Section 2.3]). Given a uniformly sparsed bit-vector W, a SNND representing it supports operations rank $_1(i,W)$ and select $_1(i,W)$ in O(1) time. The SNND can be constructed from W in $O\left( \frac{|W|}{\lg |W|}\right)$ time using additional $O\left( \frac{|W|\lg \lg |W|}{\lg |W|}\right)$ bits of workspace.

The substring considering only pioneers is itself a balanced substring of length $O\left( \frac{n}{\lg n}\right)$. By applying a recursive process on such substring, a new set of $O\left( \frac{n}{\lg ^2 n}\right)$ pioneers appear. For each of them, the pre-computed answers for each required operation find1, find0, or enclose, are stored in a table.

Based on the previous operations acting on balanced strings and some others that will be developed to handle the balanced-quadruple binary string encoding a triangulation, more complex operators to navigate through the triangulation will be developed. They must provide tools to transform operations on the triangulations on operations on the balanced-quadruple binary string encoding it, for example finding the two endpoints of any edge in the triangulation.

3.3 Compact Representation of Bit-strings

Given a bit-string S of length n, Raman et al. [38] introduced a succinct representation of S using $nH_0(S)+o(n)$ bits of space which supports rank/select operations in constant time. The first term of the space complexity corresponds to the zeroth-order empirical entropy S, and the second term corresponds to some lookup tables to support the efficient decoding of the bit-string. We will apply this data structure to a bit-string with, roughly, 25% of 1-bits. In this way, we take advantage of the $H_0(S)$ term in the space complexity.

In their data structure, Raman et al. divide S into blocks of size b. The block $S_i$ is represented by a class $c_i$ and an offset $o_i$, where $c_i$ corresponds to the number of 1-bits in $S_i$, and $o_i$ is an index to identify which block is $S_i$ among all the blocks of the same class $c_i$. Thus, the bit-string S is represented by two arrays $C[1..\lceil \frac{n}{b}\rceil ]$ and $O[1..\lceil \frac{n}{b}\rceil ]$, storing the class and the offset of each block. Given the class and the offset of a block, it is possible to recover the whole block of size b in O(1) time, using a lookup table of o(n) bits. This is particularly useful to our encoding of triangulations, since we use lookup tables that are indexed by blocks of size b.

4 Our Proposal

Our representation is built upon the bijection of Poulalhon and Schaeffer [37] to represent a triangulation $\mathcal {T}$ as bit string S. We represent S in optimal space using the compressed bit-vector of Raman et al. [38]. In this section we discuss some primitives acting on string S which will be used to implement navigational operations on the triangulation $\mathcal {T}$. To justify the necessity of such primitives, let us focus on the problem of retrieving the neighbours of a vertex in a triangulation $\mathcal {T}$. A procedure to obtain them, which will be thoroughly studied in Section 5, consists in performing a counterclockwise traversal around the query vertex to reach the ordered set of neighbouring vertices. Let us consider as the first neighbour to be reached the vertex of the triangulation which is the parent of the query vertex in the PS-tree. For obtaining such vertex we will take into account that each vertex of triangulation $\mathcal {T}$, except root vertex $u_1$, is uniquely associated to an inner edge connecting the vertex to its ancestor in the PS-tree, and is encoded in S by a pair of symbols, a ‘(’ and a ‘)’, which are said to be matching. By considering an extra ‘( )’ pair enclosing the whole encoding sequence, vertex $u_1$ also satisfies this property. Let us assume that the vertices of the triangulation $\mathcal {T}$ are stored in an array as they are found the first time when the left-to-right depth-first-search traversal of the PS-tree is performed. In the triangulation of Fig. 1, the ordered sequence of vertices stored in the array of vertices would be $u_1$, $u_2$,$\ldots$,$u_{10}$. Then, vertex $u_i$ corresponds to the i-th ‘(’ symbol in S, and the problem of obtaining the parent of vertex $u_i$ in the PS-tree consists in retrieving in S the ‘(’ element of the pair of matching parentheses enclosing the i-th ‘(’ symbol in S. If such element is the j-th ‘(’ symbol in S, the parent of $u_i$ in the PS-tree will be vertex $u_j$.

Once we have sketched how the navigational operations on triangulation $\mathcal {T}$ can be translated into operations on string S encoding $\mathcal {T}$, we remark that an inner edge is represented in the binary string S by a ‘( )’ matching pair, whereas a stem is encoded in S by just one ‘)’. Hence, each ‘)’ in binary string S represents either an inner edge or a stem. For the sake of clarity, from now on we will denote by ‘)’ the closing parentheses in S corresponding to inner edges, and by ‘ ]’ the closing parentheses in S associated to stems. However, we must always keep in mind that both symbols ‘)’ and ‘ ]’ represent ‘)’ elements in S. According to this criterion, string S encoding the triangulation of Fig. 1 is denoted by:

$$\begin{aligned} (\,(\,(\,(\, (\,(\,]\,]\, (\,]\,]\,)\,(\,]\,(\,]\,]\,(\,]\,]\,)\,)\,]\,)\,)\,]\,]\,)\,]\,]\,)\,]\,)\,)\,), \end{aligned}$$

as we can observe in Fig. 1f.

We give next some basic properties of PS-trees and their encoding sequences, which will be useful all over this section to build the required primitives acting on S. The proof is left to the reader.

Lemma 2

Let S be a binary string encoding triangulation $\mathcal {T}$. Then,

1.
S can be built in linear time by performing a depth-first-search traversal of the PS-tree of $\mathcal {T}$. The PS-tree is obtained by computing the minimal Schnyder wood decomposition of the triangulation $\mathcal {T}$, which can also be done in linear time [37, Section 4.1].
2.
A left-to-right depth-first-search traversal of the PS-tree of $\mathcal {T}$ reaches, between the two occurrences of an inner edge connecting a vertex $u_i$, with $i> 3$, to its ancestor in the PS-tree, the two stems incident with $u_i$. That is, between a ‘(’ and its matching ‘)’ in S, their two associated ‘ ]’ symbols are located.
3.
Each element of S, except its first three and its last four elements, belongs to a ‘( ] ] )’ quadruple. The elements of each ‘( ] ] )’ quadruple do not necessarily appear consecutive. Moreover, all substrings nested in a quadruple, i.e., explicitly strings x, y and z in a string ‘$\,(\,x\,]\,y\,]\,z\,)$’, where the shown parenthesis form a quadruple, correspond to the empty string or to a balanced-quadruple string.
4.
Given a stem of the PS-tree, represented in S by a ‘ ]’ symbol, the ‘(’ of the ‘( ] ] )’ quadruple containing it corresponds to an inner node of the PS-tree the stem is incident with.

Taking into account the properties established in this lemma, the following primitives acting on S, as well as some others whose meaning will be explained later on, will be studied in this section:

Given an element p of S which is either a ‘(’ or a ‘)’ representing an inner edge, retrieve its matching element.
Given an element of S, retrieve its enclosing ‘( )’ pair.
Given a ‘(’ of S, retrieve the two elements of type ‘ ]’ of its associated ‘( ] ] )’ quadruple.

The rest of the section is organized as follows. In Sect. 4.1 we show how to find in S the two occurrences of an inner edge, and how to perform some other required operations in S. In Sect. 4.2 we give a proposal to retrieve the two inner nodes connected by a stem. A procedure to find the stem edges incident at a vertex is given in Sect. 4.3. In Sect. 4.4 the storage space required by the proposal is given.

4.1 Detecting in S the Two Occurrences of an Inner Edge

To perform operations on S in constant time, some of its elements deserve special consideration. We will be as faithful as possible to original notation of Jacobson [32] for retrieving matching elements, and its subsequent extensions [24, 33], in terms of blocks, pioneers, etc., to designate such elements. Assume S is divided into blocks of fixed size, and let p be an element of type either ‘(’ or ‘)’ encoding an inner edge. With an abuse of notation, we will call indistinctly to both element p and its position in S. The element matching p will be denoted $\mu (p)$, and the block in which p lies b(p). We will say that p is far$^{()}$ if $b(p)\not = b(\mu (p))$. A block will be called near$^{()}$ if it has not any p that is far$^{()}$. We note that in Fig. 2 there is not any near$^{( )}$ block. Moreover, all elements encoding inner edges are far$^{( )}$ elements.

With the next definition we distinguish those ‘(’ that indicate a change in the block in which its matching ‘)’ lies, when traversing S from left to right (see Fig. 2). That is, all ‘(’ which are between any two such distinguished ‘(’ have their matching ‘)’ in the same block. Some ‘)’ will be distinguished in a similar way, when S is traversed from right to left.

Definition 1

Consider string S corresponding to a PS-tree as defined above.

(a)
Let p be a ‘(’ of S such that p is far$^{( )}$. We say that p is a pioneer $^{(}$ if either p is the first element of S or
$$\begin{aligned} b(\mu (p))\not = b(\mu (l)), \end{aligned}$$
where l is the first far$^{( )}$ element of type ‘(’ to the left of p.
(b)
Let q be a ‘)’ of S such that q is far$^{( )}$. We say that q is a pioneer$^{)}$ if either q is the last element of S or
$$\begin{aligned} b(\mu (q))\not = b(\mu (r)), \end{aligned}$$
where r is the first far$^{( )}$ element of type ‘)’ to the right of q.

The reason why pioneer$^{(}$ elements are relevant is given in the next proposition, where we prove that the matching of any ‘(’ in S can be retrieved from the matching of its previous pioneer$^{(}$. Similarly, pioneer$^{)}$ elements are relevant to compute the ‘(’ that matches a given ‘)’. For the sake of conciseness, only the procedure of finding the ‘)’ matching a given ‘(’ is detailed in this section, the case of retrieving the ‘(’ matching a given ‘)’ being analogous.

Proposition 2

Let S be a binary string encoding triangulation $\mathcal {T}$, p be a ‘(’ in S such that p is a far$^{( )}$ element that is not a pioneer$^{(}$, and $p^*$ be the first pioneer$^{(}$ to the left of p. Then,

$$\begin{aligned} \mu (p)=\mu (p^*)-(3N_1-N_0)-4M_1-3, \end{aligned}$$

(1)

where $N_1$ is the number of ‘(’ between p and $p^*$, $N_0$ is the number of ‘)’ and ‘ ] ’ between p and $p^*$, and $M_1$ is the number of ‘(’ between $\mu (p)$ and $\mu (p^*)$. In all this counting, all endpoints p, $p^*$, $\mu (p)$ and $\mu (p^*)$, are excluded.

Proof

Build the graph whose nodes are the elements of S, and whose edges join matching ‘( )’ pairs (see Fig. 2). The substring of S formed by each ‘(’ and its matching ‘)’ is balanced. Thus, the edges of such a graph can be drawn without any crossing, and all far$^{( )}$ elements between p and $p^*$ have their matchings between $\mu (p)$ and $\mu (p^*)$. As stated in Lemma 2, the construction of string S from a PS-tree implies that, for each ‘(’ in S, its two associated ‘ ] ’ symbols must be placed before its matching ‘)’. Quantity $3N_1-N_0$ counts three times each ‘(’ between p and $p^*$ and subtracts the number of ‘)’ and ‘ ] ’ between such positions, reminding the reader that ‘)’ and ‘ ] ’ are all ‘)’ in binary string S. That is, for every quadruple ‘ ( ] ] ) ’ placed between p and $p^*$, such quantity is 0. If, on the contrary, all elements of such quadruple are not between p and $p^*$, it means that the remaining ‘ ] ’ and ‘)’ have to be placed between $\mu (p)$ and $\mu (p^*)$. Therefore, starting at the position of $\mu (p^*)$ and moving towards the left as many positions as the number of such ‘ ] ’ and ‘)’, the position of $\mu (p)$ will be reached. In this process, every ‘ ( ] ] ) ’ quadruple between $\mu (p)$ and $\mu (p^*)$ must be skipped, which is taken into account by the $4M_1$ term in (1). $\square$

The matching of a pioneer$^{(}$ element needs not be a pioneer$^{)}$, and the same holds for the matching of a pioneer$^{)}$. As an example, we observe in Fig. 2 that the last ‘(’ in the first block of S is a pioneer$^{(}$ element, whereas its matching ‘)’ is not a pioneer$^{)}$. Also, the matching of the pioneer$^{)}$ placed in first position in the fifth block of S has a matching ‘(’ which is not a pioneer$^{(}$. In the following definition the set of pioneer$^{(}$ and pioneer$^{)}$ elements is expanded to obtain a family of pioneers which is a balanced substring of S. Besides, to achieve that each block has at least a pioneer element and that the substring continues being balanced, the first and last element of each near$^{( )}$ block are also added to such family.

Definition 2

We call pseudo pioneer family^{( )} of S, and denote it $P{\,}^{\left( \,\right) }$, to the set of the following elements of S:

1.
Every pioneer$^{(}$ and its matching
2.
Every pioneer$^{)}$ and its matching
3.
The first and last element of each near$^{( )}$ block.

With this definition, for each near$^{( )}$ block its first and its last element are added to the set of pioneer$^{(}$ and pioneer$^{)}$ elements. And for any other block, the leftmost ‘(’ element that is far$^{( )}$, if existing, is also added, as well as the rightmost ‘)’ element that is far$^{( )}$, provided such element exists. The elements of $P{\,}^{\left( \,\right) }$ in string S of Fig. 2 have been depicted surrounded by a square in Fig. 3. In the next proposition a bound for the size of $P{\,}^{\left( \,\right) }$, as well as a possible encoding for the positions of its elements in S, are given.

Proposition 3

Let S be a binary string encoding triangulation $\mathcal {T}$, and let $P{\,}^{\left( \,\right) }$ be the pseudo pioneer family^{( )} of S. Then,

(a)
The size of $P{\,}^{\left( \,\right) }$ is at most $4\beta -6$, where $\beta$ is the number of blocks.
(b)
Assuming blocks of size^{Footnote 2}$\frac{\lg (4n)}{8}$, bit-vector V encoding the positions of $P{\,}^{\left( \,\right) }$ can be represented by a SNND.

Proof

(a) The proof of Jacobson [32] to provide an upper bound for the number of pioneer elements in a balanced string will be straightforwardly adapted to our balanced-quadruple string. The graph whose nodes represent the blocks of S, and whose edges join each block containing a pioneer$^{(}$, resp. pioneer$^{)}$, with the block containing its matching ‘)’, resp. ‘(’, is a simple outerplanar graph, thus having at most $2\beta -3$ edges, which is the number of edges of a maximal outerplanar graph with $\beta$ nodes. Thus, the number of elements satisfying item 1 and item 2 of Definition 2 is at most $4\beta -6$. In case some near$^{( )}$ block in S exists, it corresponds to an isolated node of the outerplanar graph, and as each vertex of a maximal outerplanar graph has at least degree 2, it follows that for each such block the bound of edges decreases by at least two. On the other side, each near$^{( )}$ block adds exactly two elements at $P{\,}^{\left( \,\right) }$. We conclude that the upper bound of $4\beta -6$ remains valid although near$^{( )}$ blocks exist. (b) A bit-vector V of the same length as S will be created. An element of V will be a 1 when the element of S in the same position belongs to $P{\,}^{\left( \,\right) }$. For V to be encoded by a SNND we must prove that V is a uniformly sparsed set: (i) For a binary string of size 4n and a block size $\frac{\lg (4n)}{8}$, we have $\beta =\frac{32n}{\lg (4n)}$. Thus, according to (a) the number of 1-bits is at most $\frac{128n}{\lg (4n)}$. (ii) In each near$^{( )}$ block the first and last elements belong to P$^{()}$. For any other block, at least one far$^{( )}$ element exists. Hence, at least one of the elements in the block belongs to P$^{()}$. Therefore, the number of 0-bits between any two consecutive 1-bits in V is at most $\frac{\lg (4n)}{4}$. $\square$

Now, a recursive procedure will be applied to $P{\,}^{\left( \,\right) }$, with the only difference that $P{\,}^{\left( \,\right) }$ is a balanced string, whereas S is not. All available techniques for dealing with balanced strings [24] can be applied to $P{\,}^{\left( \,\right) }$. In particular, consider $P{\,}^{\left( \,\right) }$ fictitiously divided into blocks of the same length as the blocks of S. A SNND will be created to encode the pseudo pioneer family of $P{\,}^{\left( \,\right) }$. As explained in Sect. 3.2, the number of pioneer$^{(}$ elements in $P{\,}^{\left( \,\right) }$ will be $O\left( \frac{n}{\lg ^2 n}\right)$. For each element $p^{**}$ in $P{\,}^{\left( \,\right) }$ that is a pioneer$^{(}$, its matching element in S, $\mu (p^{**})$, is explicitly stored. Thus, the SNND’s of V and the pseudo pioneer family of $P{\,}^{\left( \,\right) }$, together with some tables, allow to obtain in S the matching ‘)’ of a pioneer$^{(}$ $p^*$ in O(1) time.

Once $\mu (p^*)$ is known, to obtain $\mu (p)$ by table lookup, some more definitions are given. We refer the reader to Fig. 4. At any position p of a block, we define the net-left-excess(p) as three times the number of ‘(’ minus the number of ‘)’, associated to both ‘)’ and ‘ ] ’ symbols, from the left end of the block up to p, including p. Similarly, we define the net-right-excess(p) as the number of ‘)’, associated to both ‘)’ and ‘ ] ’ symbols, minus three times the number of ‘(’ from the right end of the block up to p included. The following proposition shows how the information required to retrieve $\mu (p)$ can be found from such excess information.

Proposition 4

Let p be a ‘(’ of S such that p is a far$^{( )}$ element, and let $p^*$ be the first element to its left that is a far$^{( )}$ element of $P{\,}^{\left( \,\right) }$, which will be possibly coincident with p. Then, the position of $\mu (p)$ is the leftmost position of a ‘)’ in $b(\mu (p^*))$ whose net-right-excess is:

$$\begin{aligned} \text {net-right-excess}(\mu (p^*))+\text {net-left-excess}(p) -\text {net-left-excess}(p^*) \end{aligned}$$

(2)

Proof

We begin by observing that both p and $p^*$ belong to the same block. First we compute the net-right-excess of $\mu (p)$. According to the definition, it is the net-right-excess of $\mu (p^*)$ plus the number of ‘)’ between $\mu (p^*)$ and $\mu (p)$ minus three times the number of ‘(’ between $\mu (p)$ and $\mu (p^*)$. In both cases, $\mu (p)$ is included and $\mu (p^*)$ is excluded. Each ‘(’ between $\mu (p)$ and $\mu (p^*)$ must have each of its associated ‘ ] ] ) ’ elements before $\mu (p^*)$, and hence the net-right-excess of $\mu (p)$ does not depend on the number of ‘(’ between $\mu (p)$ and $\mu (p^*)$. The net-right-excess of $\mu (p)$ is therefore obtained from the net right excess of $\mu (p^*)$ by adding one for each ‘)’ or ‘ ] ’ between $\mu (p)$ and $\mu (p^*)$ whose corresponding ‘(’ is between p and $p^*$, and that quantity is net-left-excess(p)-net-left-excess$(p^*)$. Second, we claim that a ‘)’ in $b(\mu (p))$ to the left of $\mu (p)$ with its same net-right-excess cannot exist: each ‘)’, representing ‘)’ or ‘ ] ’, to the left of $\mu (p)$ adds up one to the net-right-excess. Due to the construction of string S, a ‘(’ to the left of $\mu (p)$ would substract three to the net-right-excess. Hence, it cannot exist unless each element of its associated ‘ ( ] ] ) ’ triple is placed between such ‘(’ and $\mu (p)$. Hence the only elements in $b(\mu (p))$ to the left of $\mu (p)$ with its same net-right-excess can be ‘(’. $\square$

Both quantities, net-right-excess and net-left-excess, will be stored for each position of the block. Storing also, for each block, the leftmost position in the block with net-right-excess i, where for a block size B we have $-3B\le i\le B$ (the table stores 0 if there is not any element in the block with net right excess i), the matching of p is retrieved in O(1) time.

Unlike what happens with the algorithm to compute the matching of an element, which was not applicable from previous work, operation enclose for balanced binary strings (see Proposition 1) to retrieve the tightest pair of matching ‘(’ and ‘)’ enclosing any given element of the string can be straightforwardly applied to our case by using the recursive structure we already have. For each pioneer$^{(}$ $p^{**}$ in $P{\,}^{\left( \,\right) }$, the element in S enclosing $p^{**}$ is explicitly stored. From this information, the SNND of V, the pseudo pioneer family of $P{\,}^{\left( \,\right) }$, and the inclusion of enclosing information in the tables, the ‘(’ enclosing any pioneer$^{(}$ $p^*$ in S is obtained in O(1) time. Using the recursive structure, and also in constant time, the ‘(’ enclosing any element p of S can be found.

Next, we study two operations to be performed on S that will be useful later. The first one requires the use of a structure similar to the representation we have developed here. The second one makes use of the structure developed in this section and some more tables for transforming a portion of binary string S into its corresponding ternary portion.

4.1.1 Retrieving the Two ‘ ] ’ Associated to a ‘ (’

Given a ‘(’ of S, we are now interested in finding the positions in S of the two ‘ ] ’ of its ‘ ( ] ] ) ’ associated quadruple. We can apply an idea similar to what we have done up to now, just considering a different SNND. In order not to be repetitive we will only outline the procedure, illustrated in Fig. 5.

Let p be a ‘(’ of S, l be the leftmost ‘ ] ’ associated to p, and r be the rightmost ‘ ] ’ associated to p. We say p is far$^{\,(\,\,]\,]\,}$ if r is not in b(p). Let us assume that p is far$^{\,(\,\,]\,]\,}$, and let q be the first far$^{\,(\,\,]\,]\,}$ element of type ‘(’ to the left of p in S. We say that p is a pioneer $^{\,(\,\,]\,]\,}$ if l is in a block different than the leftmost of the two ‘ ] ’ associated to q. Pioneer family $P^{\,(\,\,]\,]\,}$ is formed by:

The quadruples ‘ ( ] ] ) ’ corresponding to each ‘(’ that is a pioneer$^{\,(\,\,]\,]\,}$.
The third ‘(’ of S, and its only associated ‘ ] ’.
Provided a block does not contain any element indicated in the two previous items, the quadruple ‘ ( ] ] ) ’ corresponding to the first ‘(’ of the block. It can be easily proved that such ‘(’ always exists.

Then, a bit-vector V is built with 1 at the positions of elements in $P^{\,(\,\,]\,]\,}$.

By defining:

$$N=\text {net-left-excess}(p)+\text {net-right-excess}(l^*)-\text {net-left-excess}(p^*),$$

we have that l is the leftmost ‘)’ in $b(l^*)$ whose net-right-excess is $N-2$, and r is the leftmost ‘)’ in $b(l^*)$ whose net-right-excess is $N-1$. In a recursive level the ‘(’ that are far$^{\,(\,\,]\,]\,}$ elements of $P^{\,(\,\,]\,]\,}$ and the ‘(’ that are pioneer$^{\,(\,\,]\,]\,}$ elements of $P^{\,(\,\,]\,]\,}$ are considered. For the latter, their associated ‘ ] ’ are explicitly stored. With this newly created SNND and the corresponding lookup tables, the ‘ ] ’ associated to a ‘(’ can be retrieved in O(1) time.

4.1.2 Passing from Binary to Ternary Strings

Taking into account how string S has been constructed from the PS-tree, ensuring that its substring containing all ‘(’ and their matching ‘)’ is balanced, and that between a ‘(’ and its matching ‘)’ their two associated ‘ ] ’ must be placed, the ternary sequence corresponding to S can be built from S by a linear inspection of S. We propose here a more efficient procedure when only a portion of S has to be turned into a ternary sequence of ‘(’, ‘)’ and ‘ ] ’.

Let us assume we are interested in obtaining the ternary sequence of any portion of a block of S between a ‘(’ element p of S and its previous pioneer$^{(}$ element $p^*$. Let us consider a double size block starting from the left with the portion of S between $p^*$ and p, both included, completed with as many ‘(’ as necessary to reach the size of the blocks in S. Then, the portion of S between $\mu (p)$ and $\mu (p^*)$, both included, is added, completed with as many ‘)’ to its left as necessary until the size of the block is reached. The part of such double size block excluding the ‘(’ and ‘)’ between p and $\mu (p)$ (both excluded) is called the portion of interest. In Fig. 6a, the elements not belonging to the portion of interest have been represented by $\star$ symbols. In such figure we observe how applying the simple rules of the construction of S, for example a ‘)’ after a ‘(’ is always a ‘ ] ’ symbol, all ‘)’ in the portion of interest which correspond to ‘ ] ’ can be found. In general, the ‘ ] ’ symbols of any portion of S between two far$^{( )}$ elements whose known matching elements belong to the same block are uniquely determined by taking into account that S is formed by nested sequences of ‘ ( ] ] ) ’ quadruples, and the corresponding binary and ternary blocks can be stored in a table. With this lookup table procedure, the portion of interest can be turned into a ternary string of ‘(’, ‘)’ and ‘ ] ’ elements in O(1) time.

A similar process is performed when the part of S between a ‘)’ element and the first pioneer$^{)}$ element to its right has to be turned into a ternary portion.

Next, the main problem considered in this section is retaken. We extend the problem studied here to stem edges, that is, finding the two vertices of the triangulation that are the endpoints of a stem edge.

4.2 Retrieving the Two Inner Nodes Linked to a Stem

Given triangulation $\mathcal {T}$ represented by binary string S, an edge of $\mathcal {T}$ corresponding to a stem is represented in S by a ‘)’, and denoted by ‘ ] ’. Consider the problem of retrieving the two endpoints of a stem. One of its endpoints is easily obtained, as the inner node of the PS-tree it is incident with corresponds to the ‘(’ of the ‘ ( ] ] ) ’ quadruple containing it. Hence it can be retrieved by simply computing the ‘( )’ pair enclosing ‘ ] ’. It will be called the first endpoint of e. For an example, we refer again to Fig. 1. Consider the edge of $\mathcal {T}$ joining inner nodes $u_5$ and $u_{10}$. Such edge is represented in string S by the 4-th symbol of type ‘ ] ’, starting from the end. As we observe in Fig. 2, the ‘(’ of the ‘( )’ pair enclosing such symbol is the 5-th symbol of type ‘(’, which corresponds to $u_5$.

A naive algorithm to detect the other endpoint of a stem ‘ ] ’, called its second endpoint, consists in considering the positions previous to ‘ ] ’ in S, and retrieving as many admissible triples as necessary until the two edges previous to it in the counterclockwise traversal of the infinite face are both inner edges. Continuing with the previous example, let us now consider Fig. 7, where stem called $s_3$ corresponds to a symbol ‘ ] ’ belonging to the portion of S shown in the figure. To retrieve the second endpoint of stem $s_3$ emanating from $u_5$, the two previous inner edges in the counterclockwise traversal of the infinite face must be retrieved. Such edges are ($u_{10},u_8$) and ($u_8,u_5$). In the original encoding both of them were stems. Hence, two local closure operations must be performed, transforming them into two inner edges, before local closure creating edge ($u_{10},u_5$) is done. In general, the retrieval of the two previous inner edges to create an admissible triple following this sequential approach takes O(n) time. Next, a technique is developed to obtain the second endpoint of a stem in O(1) time.

Let us consider an outerplanar representation of triangulation $\mathcal {T}$, as the one given by Turán in [40]. Every time a vertex of $\mathcal {T}$ is reached in the left-to-right depth-first-search traversal of the PS-tree, an occurrence of such vertex is put on a circle with its number of occurrence indicated by a superscript (see Fig. 8). This way, each inner edge in the PS-tree appears twice as an edge on the outer face of such outerplanar representation. Each stem is drawn by a diagonal connecting two vertices in the circle. From the planarity of $\mathcal {T}$ it follows that the diagonals are non-intersecting.

A graph, called the ]-graph of $\mathcal {T}$, is created from this outerplanar representation of the triangulation. A traversal of the cyclic sequence of edges bounding the infinite face in the outerplanar graph will be performed. It starts at edge $(u_1^{(1)}, u_2^{(1)})$, on the side of the edge adjacent at a finite face of the outerplanar graph, as shown by dashed arrows in Fig. 8. Once this first edge has been traversed, a counterclockwise turn around $u_2^{(1)}$ is performed until next edge $(u_2^{(1)},u_3^{(1)})$ is reached. The traversal continues until the first vertex $u_1^{(1)}$ is again found. This process is equivalent to performing a left-to-right depth-first-search traversal of the PS-tree (see [40]). On the basis of such traversal, the ]-graph will be defined (see Fig. 9). The nodes of the ]-graph are created by adding a ‘(’, resp. a ‘)’, every time the first, resp. second, traversal of an inner edge is found, and a ‘ ] ’ symbol whenever a stem is reached. Hence, the nodes of the ]-graph are the elements of string S. The edges of the ]-graph are uniquely associated to the diagonals of the outerplanar graph. In particular, a diagonal of the outerplanar graph joining vertices $u_i^{(j)}$ (from which a stem emanates) and $u_k^{(l)}$ will be represented in the ]-graph by an edge connecting the ‘ ] ’ node to the node $(u_k^{(l)},u_m^{(n)})$, which can be either a ‘(’ or a ‘)’. This way, the two incident nodes of each edge are a source node, corresponding to either a ‘(’ or a ‘)’ symbol, and a destination node always being a ‘ ] ’ symbol. The source node and the destination node are said to be adjacent.

Let us now see how to encode the ]-graph from string S. Given a ‘ ] ’ element in S, we call its matching element to the either ‘(’ or ‘)’ adjacent to it in the ]-graph. We remark that each ‘ ] ’ of S has exactly one matching element, as can be observed in Fig. 9, where the element matching each ‘ ] ’ of S is shown. A ‘ ] ’ element is said to be far$^{\,]}$ if its matching element lies not inside its own block. A block is said to be a near$^{\,]}$ block if it does not contain any node adjacent to a node of a different block. A far$^{\,]}$ is a pioneer$^{\,]}$ if either it is the first ‘ ] ’ in S or its matching element is in a different block than that of the far$^{\,]}$ previous to it in S when traversing S from left to right.

The next proposition gives a necessary and sufficient condition for a ‘( ’ or ‘)’ of S representing an inner edge to be adjacent to a ‘ ] ’ of the ]-graph.

Proposition 5

Let p be either a ‘( ’ or a ‘)’ representing an inner edge in S. Then, p is adjacent at some ‘ ] ’ in the ]-graph if and only if the first element to the right of p in S is not a ‘ ] ’.

Proof

Let p be either a ‘( ’ or a ‘)’ in the ]-graph. Provided p is joined by an arc of the ]-graph to some ‘ ] ’, such ‘ ] ’ must be to the right of p (see Fig. 10a). We distinguish two cases: (1) If the element next to p in S were a ‘ ] ’, the ‘( ’ or ‘)’ matching such ‘ ] ’ would be placed to the left of p, and the planarity condition of the ]-graph would not be satisfied. (2) Consider p corresponds to edge $(u_i^{(j)},u_k^{(l)})$ in the ]-graph. Let us now assume p is not followed by a ‘ ] ’ in S. If p were not adjacent at some ‘ ] ’, then there would not exist any edge in the ]-graph with source node $u_i^{(j)}$, and this in turn would imply that in the PS-tree there would be three or more inner edges traversed consecutively in the left-to-right depth-first-search traversal of the PS-tree. Hence, a non-triangular face would exist (see Fig. 10 (b)). $\square$

As a corollary, in a block with two or more elements containing no ‘ ] ’ element, some ‘( ’ or ‘)’ must exist which is joined by an arc of the ]-graph to a ‘ ] ’ in a different block, otherwise there would be two or more consecutive ‘(’ or ‘)’ without any ‘ ] ’ adjacent at any of them, what would imply the existence of a non triangular face. Hence, in each near$^{\,]}$ block some ‘ ] ’ element must exist, what makes possible the following definition. It introduces some more elements required to navigate efficiently on the ]-graph.

Definition 3

We call pseudo pioneer family$^{\,]}$ of S, and denote it $P^{\,]}$, to the set of the following elements in S:

1.
Each pioneer$^{\,]}$ element and its matching.
2.
The leftmost far$^{\,]}$ in each block, if existing, and its matching.
3.
The first ‘ ] ’ element of each near$^{\,]}$ block.

In the next proposition, a bound for the size of $P^{\,]}$ is given. Also, it is shown that such family can be encoded by a SNND. The proof of this proposition is similar to the proof of Proposition 3 and is left to the reader.

Proposition 6

Let S be a binary string encoding triangulation $\mathcal {T}$, and let $P^{\,]}$ be the pseudo pioneer family$^{\,]}$ of S. Then,

(a) The size of $P^{\,]}$ is at most $4\beta -6$, where $\beta$ is the number of blocks.

(b) Assuming blocks of size $\frac{\lg (4n)}{8}$, bit-vector W keeping the positions of the elements in $P^{\,]}$ can be encoded by a SNND.

Let us now show how to find the matching of a far$^{\,]}$ element $q^*$ of $P^{\,]}$. To retrieve the either ‘( ’ or ‘)’ matching $q^*$, instead of storing $P^{\,]}$ a modification consisting in a ternary string represented by $P^{{^*}^{\,]}}$ will be stored, as illustrated in Fig. 9b. It is created from string $P^{\,]}$ by replacing each ‘)’ which does not correspond to a ‘ ] ’ symbol by a ‘(’. Provided any element of $P^{\,]}$ that is not a ‘ ] ’ is incident in the ]-graph at d elements of type ‘ ] ’, with $d> 1$, then $d-1$ elements denoted ‘ ( $^*$ ’ will be placed after the corresponding ‘(’. On this ternary string, only operations rank$_($ and select $_($ have to be supported [9, 26]. These operators allow the position of $q^*$ in $P^{{^*}^{\,]}}$ to be known . By fictitiously identifying symbols ‘ ( $^*$ ’ and ‘(’ a balanced binary sequence is obtained. On this balanced sequence, the procedure explained in the previous section to operate on $P{\,}^{\left( \,\right) }$ is valid, and according to it the either ‘( ’ or ‘)’ matching $q^*$ can be retrieved in O(1) time. Operations rank$_($ and select$_($ on $P^{{^*}^{\,]}}$ allow to obtain the position of the element matching $q^*$ in $P^{\,]}$. Then, the position of $q^*$ in S is also known.

Next, let us explain how to retrieve the matching of an element q of type ‘ ] ’. First, the ternary block q belongs to is obtained as explained in Sect. 4.1.2. Provided the matching of q lies inside its own block, such matching is retrieved by lookup table. Let us assume that, on the contrary, q is a far$^{\,]}$ element. Let $q^*$ be the far$^{\,]}$ element of $P^{\,]}$ previous to q in block b(p). If $q^*$ does not exist, it means that q is the first far$^{\,]}$ in its block. Hence q is a pioneer$^{\,]}$, and we have explained how to retrieve its matching in the previous paragraph. In case $q^*$ exists, two cases are distinguished. First, provided $q^*$ is either a ‘(’ or a ‘)’, the ‘ ] ’ adjacent at $q^*$ in the ]-graph must be a ‘ ] ’ to the right of q (see Fig. 11a). Due to the planarity of the ]-graph, element $\mu (q)$ must be placed between $q^*$ and q. Hence q is not a far$^{\,]}$ element. Second, if $q^*$ is a ‘ ] ’, according to Definition 3 we have $b(\mu (q))=b(\mu (q^*))$, as illustrated in Fig. 11b. Then, let us consider the portions of interest of the ternary blocks corresponding to b(q) and $b(\mu (q))$, that is, the part of $b(\mu (q^*))$ to the left of $\mu (q^*)$ and the part of $b(q^*)$ to the right of $q^*$. From these two portions of ternary blocks, knowing that the last element of the first block, $\mu (q^*)$, matches the first element of the second block, the rest of elements in the first block matching each ‘ ] ’ between $p^*$ and p are uniquely determined, and can be stored in a table. From the previous reasoning, the next result follows.

Proposition 7

Let S be the encoding string of a given triangulation. The second endpoint of any stem can be retrieved from S in O(1) time.

4.3 Retrieving the ‘ ] ’ of the ]-graph Adjacent at a ‘(’ or a ‘)’

The problem we focus on now is finding all the ‘ ] ’ adjacent in the ]-graph at a given ‘(’ or a ‘)’ of S. This operation will be crucial in the next section to obtain the neighbors of the vertex represented in S by a ‘(’ and its matching ‘)’.

Let p be either a ‘(’ or a ‘)’ of S. First, the ‘ ] ’ adjacent at p in the block b(p) in which p lies can be retrieved by table lookup on the corresponding ternary block. In the ]-graph shown in Fig. 12 we observe that there is not any ‘ ] ’ in b(p) whose matching element is p.

Second, by assuming p is adjacent at some ‘ ] ’ in another block, two cases must be considered for retrieving them:

(i)
p belongs to $P^{\,]}$ (see Fig. 12 (a)). Pseudo-balanced pioneer family $P^{*~]}$ allows obtaining the far$^{\,]}$ elements of $P^{\,]}$ adjacent at p. Let $~]_1,~]_2,\ldots ,~]_k$ be such elements, ordered from left to right. All ‘ ] ’ adjacent at p to the right of $~]_k$ must be in $b(~]_k)$, and can be retrieved from the ternary blocks b(p) and $b(~]_k)$. Due to the planarity of the ]-graph, an element in $b(~]_k)$ to the left of $~]_k$ that is adjacent at p cannot exist. Similarly, for the rest of $~]_i$, with $1\le i <k$, any ‘ ] ’ adjacent at p between the first element of the block $b(~]_i)$ and $~]_i$ cannot exist. Between $~]_i$ and either $~]_{i+1}$ in $b(~]_i)$, if it exists, or the end of $b(~]_i)$, all the ‘ ] ’ adjacent at p can be retrieved by lookup table. To retrieve the ‘ ] ’ adjacent at p to the left of $~]_1$, let us consider the ‘(’ or ‘)’ of $P^{\,]}$ to the right of p in b(p). Let us call it $p^*_{post}$. If such element does not exist it implies that $~]_1$ is the leftmost ‘ ] ’ adjacent at p. Provided $p^*_{post}$ exists, by considering the ternary portions of S between p and $p^*_{post}$ and between the rightmost ‘ ] ’ adjacent at $p^*_{post}$ and the last position of the block such ‘ ] ’ belongs to, the ‘ ] ’ adjacent at p previous to $~]_1$, if existing, are retrieved.
(ii)
Provided p does not belong to $P{\,}^{\left( \,\right) }$ (see Fig. 12b), let $p^*_{post}$ be the ‘(’ or ‘)’ posterior to p in $P^{\,]}$. Then, the leftmost ‘ ] ’ adjacent at $p^*_{post}$ is obtained, and as all the ‘ ] ’ adjacent at p are placed in $b(p^*_{post})$, they can be retrieved by lookup table.

The next result follows from the previously explained process.

Proposition 8

Given a ‘(’ or a ‘)’ in S, each of the ‘ ] ’ it is adjacent at can be retrieved, from left to right, in O(1) time.

4.4 Storage Requirements

The pioneer families $P{\,}^{\left( \,\right) }$, $P^{\,(\,\,]\,]\,}$ and $P^{\,]}$ can be encoded using the SNND structure, storing four arrays of $O\left( \frac{n\lg \lg n}{\lg n}\right)$ bits and three tables of $O\left( n^{\frac{2}{3}}\right)$ bits each [24].

According to Proposition 3, the size of pioneer family $P{\,}^{\left( \,\right) }$ is $|P^{()}|\le \frac{128n}{\lg (4n)}$. Balanced binary string $P{\,}^{\left( \,\right) }$ is explicitly stored, which requires at most $\frac{128n}{\lg (4n)}=O(\frac{n}{\lg n})$ bits. For the balanced sequence of $|P{\,}^{\left( \,\right) }|$ elements, a new pioneer family $P_2{\,}^{\left( \,\right) }$ of size $|P_2{\,}^{\left( \,\right) }|\le 32\frac{|P{\,}^{\left( \,\right) }|}{\lg (|P{\,}^{\left( \,\right) }|)}=O\left( \frac{n}{\lg ^2 n}\right)$ is stored. For each element $p^{**}$ in $P_2{\,}^{\left( \,\right) }$, the values of both its matching and enclosing element are explicitly stored, what requires $2|P_2{\,}^{\left( \,\right) }|\lg (|P_2{\,}^{\left( \,\right) }|)=O(\frac{n}{\lg n})$ bits. The same space bound is valid for $P^{\,(\,\,]\,]\,}$.

The upper bound for the size of $P^{\,]}$ given in Proposition 6 is also valid for $P^{*~]}$. This is justified since in the counting of such proposition, for each edge joining an element of $P^{\,]}$ and its matching, its two nodes are considered. Thus the size of pseudo-balanced ternary string $P^{*~]}$ satisfies $\left| P^{*~]}\right| \le \frac{128n}{\lg (4n)}$. The simplest approach, which uses 2 bits per ternary element, requires thus $\frac{256n}{\lg (4n)}$ bits for the storage of $P^{*~]}$. Operators rank$_1$ and select$_1$ acting on $P^{*~]}$ are required, involving an amount of space of o(n) bits, using the compressed rank/select structure of Barbay et al. [9].

Some lookup tables are needed for the efficient navigation on the pioneer families:

To find the matching elements inside a block of length $\frac{\lg (4n)}{8}$, all the possible combinations are stored, spending $\root 8 \of {4n}~\frac{\lg (4n)}{8}\lg \left( \frac{\lg (4n)}{8}\right) =o(n)$ bits. This matching information must be stored considering two possible cases: first, that the block belongs to a balanced binary sequence, and second that the block belongs to balanced-quadruple string S. Similar tables can be built and stored for other information such as enclosing or for keeping the net left and right excess in each position.
Also, relevant positions in a block can be stored. For example, the leftmost position in a block with net-right-excess i, where $-3\frac{\lg (4n)}{8}\le i \le \frac{\lg (4n)}{8}$, if existing, or 0 otherwise, can be stored in a lookup table of $\root 8 \of {4n}~\frac{\lg (4n)}{2}\lg \left( \frac{\lg (4n)}{8}\right) =o(n)$ bits.
To obtain the required double size ternary blocks from the corresponding double size binary blocks, another table has to be created. A double size binary block is $\frac{\lg (4n)}{4}$ bits long. A simple representation of a ternary block of the same length requires 2 bits per element, that is, $\frac{\lg (4n)}{2}$ bits. Hence, a bit-string of size $\frac{3\lg (4n)}{4}$ is required to store a double size binary block together with its corresponding ternary block. The number of different strings of such length is $\root 4 \of {\lg (4n)^3}$.
From two ternary blocks such that the last element of the first block, either a ‘(’ or a ‘)’, matches the first element of the second block, a ‘ ] ’, the position of the element in the first block matching each ‘ ] ’ in the second block is stored (and 0 is stored in case the matching of a ‘ ] ’ in the second block is also in the second block). In this case, $\sqrt{4n}~\frac{\lg (4n)}{8}\lg \left( \frac{\lg (4n)}{8}\right) =o(n)$ bits are required.

Finally, the bit-string S is stored in optimal space using the compressed bit-vector of Raman et al. [38], spending $(4n-5)H_0(S)+o(n) \approx 3.24n+o(n)$ bits, for a block of size $\frac{\lg (4n)}{8}$.

The main results obtained in this section are summarized in the next theorem.

Theorem 1

Let S be the encoding string of a given triangulation with n vertices. An encoding of S requiring $3.24n+o(n)$ bits exists such that the following operations can be performed in O(1) time:

Given an element p of S which is either a ‘(’ or a ‘)’ representing an inner edge, retrieve its matching element.
Given an element of S, retrieve its enclosing ‘( )’ pair.
Given a ‘(’ of S, retrieve the two ‘ ] ’ of its associated ‘ ( ] ] ) ’ quadruple.
Given a ‘ ] ’ of S, retrieve its adjacent either ‘(’ or ‘)’ in the ]-graph.
Given an element p of S which is either a ‘(’ or a ‘)’ representing an inner edge, retrieve each of its adjacent ‘ ] ’ in the ]-graph from left to right.

5 Answering Queries on the Triangulation

Let us consider that the vertices of the triangulation are stored in an array in the order given by the left-to-right depth-first-search traversal of the PS-tree, namely $u_1,u_2,\ldots ,u_n$. Retrieving the ‘(’ associated to the i-th reached vertex is equivalent to obtain the i-th ‘(’ in S. This is common operation for binary strings, that as we have previously seen is usually denoted select$_((S, i)$. Another frequent operation, denoted rank$_((S, i)$, consists in counting the number of ‘(’ up to position i in S. Both operations have been thoroughly studied in the literature [29, 31, 36], and their combination allows us to answer the queries posed in this section.

5.1 Neighborhood Retrieval

Let $u_i$, with $1\le i \le n$, be the query vertex whose neighborhood, i.e. the set of its adjacent vertices in the triangulation, has to be retrieved. For $i>1$, vertex $u_i$ is uniquely associated to inner edge $(u_{_{parent}},u_i)$, where $u_{_{parent}}$ is the parent of $u_i$ in the PS-tree, and is therefore represented in string S by the i-th symbol of type ‘(’. Let $p_i$ be the i-th symbol of type ‘(’ in S. The first neighbor of $u_i$ in the triangulation to be found is $u_{_{parent}}$. It is obtained by retrieving the ‘(’ of the ‘( )’ pair enclosing $p_i$. Provided such ‘(’ is the j-th symbol of type ‘(’ in S, with $j < i$, we have $u_{_{parent}}=u_j$.

For vertex $u_1$, we remind the reader that string S is formed by a binary encoding of the PS-tree plus an extra ‘( )’ pair enclosing the whole sequence. Thus, $u_1$ is represented by the first ‘(’ in S. As $u_2$ is always a neighbor of $u_1$, we consider $u_2$ plays from now on the role of $u_{_{parent}}$ for $u_1$, in the sense of being the departure edge to retrieve the neighbors of $u_1$ ($u_3$ could have been chosen indistinctly).

Once $u_{_{parent}}$ has been reached, a recursive process starts which performs a 360$^{\circ }$ counterclockwise turn from edge $(u_i,u_{_{parent}})$ around $u_i$ until the ‘)’ matching $p_i$ is reached. We denote by $u_n$ the next counterclockwise neighbor of $u_i$ to be found when such turn is performed. To retrieve it, some element $p_j$ in S has to be analyzed. In the first step, when finding the first counterclockwise neighbor after $u_{_{parent}}$, $p_j$ is the first element to the right of $p_i$ in S. Such element can be either a ‘(’ or a ‘)’:

(a)
$p_j$ is a ‘)’ which corresponds to a ‘ ] ’. Let us note that in case of being computing the first counterclockwise neighbor of $u_i$ after $u_{_{parent}}$ we have that $p_j$ is a ‘)’ immediately after $p_i$, which is a ‘(’, and hence $p_j$ must correspond to a ‘ ] ’ symbol. In general, as $p_j$ corresponds to a ‘ ] ’, edge $(u_i,u_j)$ corresponds to a stem edge, which is represented in the PS-tree by a leaf incident at $u_i$ (see Fig. 13a). Next counterclockwise neighbor is thus $u_n=u_j$, and it can be obtained as shown in Proposition 7. Then, the element to be analyzed next will be the first element to the right of $p_j$ in S.
(b)
$p_j$ is a ‘(’. In this case two situations are distinguished:
1. (b.1)
  Element $p_k$ next to $p_j$ in S is a ‘)’. Again we have a ‘)’ placed in S immediately after a ‘(’, and hence $p_k$ must correspond to a ‘ ] ’ symbol. According to Proposition 5, there is not any ‘ ] ’ adjacent at $p_j$ in the ]-graph. Therefore, $(u_i,u_j)$ corresponds to an inner edge and next counterclockwise neighbor $u_n$ is $u_j$ (see Fig. 13b.1). In this situation, the index of $u_n$ in the array of vertices will be the number of ‘(’ before $p_j$ in S. Then, the element of S to be analyzed next will be the ‘)’ matching $p_j$.
2. (b.2)
  Element $p_k$ next to $p_j$ in S is a ‘(’. Proposition 5 ensures that some stem exists whose second endpoint is $u_i$ (see Fig. 13 (b.2)). The ‘ ] ’ adjacent at $p_i$ in the ]-graph can be computed as stated in Proposition 8. The set of second endpoints of the stems in counterclockwise order immediately previous to $u_j$ must be found. The counterclockwise neighbor of $u_i$ immediately after them is $u_j$. Finally, the element to be analyzed next is the ‘)’ matching $p_j$.
(c)
$p_j$ is a ‘)’ which does not correspond to a ‘ ] ’. In this case two situations are also distinguished:
1. (c.1)
  Element $p_k$ next to $p_j$ is a ‘ ] ’. We are in the same situation as (b.1).
2. (c.2)
  Element $p_k$ next to $p_j$ is either a ‘(’ or a ‘)’. In this case we are in the same situation as (b.2).

This procedure is repeated, advancing along string S until $p_i$ is reached.

As all the involved operations can be performed in constant time, retrieving the neighbors of vertex $u_i$ from S in counterclockwise order is performed in time linear in the degree of $u_i$.

We note that navigation in clockwise direction can be performed with an straightforward adaptation of the procedure.

5.2 Adjacency Testing

Let $u_i$ and $u_j$ be two vertices of the triangulation. Let us explain how to know in O(1) time whether they are adjacent or not. A two step process is performed.

First, we will check if one of them is parent of the other one in the PS-tree. Let us assume that the index of $u_i$ is smaller than the index of $u_j$, that is, $u_i$ is traversed previously to $u_j$ in the left-to-right depth-first-search traversal of the PS-tree. By computing the parent of $u_j$ in such tree, as explained in Sect. 5.1, we will know whether $u_i$ is the parent of $u_j$ or not.

Second, provided $u_i$ is not the parent of $u_j$, it must be checked if there exists some stem in the PS-tree joining them. Let us take the two stems whose first endpoint is $u_i$, obtained as explained in Sect. 4.1.1. For each of the two stems, in Sect. 4.2 we have shown how its second endpoint can be retrieved in O(1) time. Thus, it must only be checked whether any such second endpoints is coincident with $u_j$. If this is not the case, we will consider the two stems whose first endpoint is $u_j$, and check if for some of them its second endpoint is $u_i$.

The next theorem states the results obtained in this section.

Theorem 2

A triangulation of n vertices can be represented using $3.24n+o(n)$ bits so that the operations to obtain each neighbor of a vertex in counterclockwise direction or to check if two vertices are adjacent are supported in O(1) time.

6 Implementation

As a proof a concept, in this section we present an implementation of our proposed solution. Even though our approach is based on pioneers, previous studies on succinct representations of trees have shown that solutions based on Range Min-Max trees (RmMTs) [35] have a better practical behavior compared to solutions based on pioneers [7]. For that reason, we adapted our solution to use RmMTs, in order to provide a faster implementation. A drawback of using RmMTs is that we must represent the three symbols ‘(’, ‘)’ and ‘]’ of S, converting the sequence S in a ternary sequence, hence increasing the space of the structure. Nevertheless, as we will see in the experimental results, even with the space increment, our implementation overcomes state-of-the-art implementations. Originally, RmMTs were designed to navigate a tree represented as a balanced parentheses sequence, where an open/close parenthesis is represented by a 1/0 bit. Similar to our solution for triangulations, an excess value is computed for the balanced parentheses sequence as the number of open parentheses minus the number of closing parentheses from a left-to-right traversal of the sequence. Then, the parentheses sequence is logically divided into blocks of length w. An RmMT is a complete tree where the minimum, maximum and rightmost excess values of each block are stored in its leaves. For an internal node v of the RmMT, the minimum and maximum excess values of the leaves of the subtree rooted at v are stored. Given a position i of the balanced parentheses sequence, we can find the closest position to the left (and also to the right) of i with excess e in $O(\lg \frac{n}{w})$ time, where n is the length of the sequence. To do that, an up/down traversal of the RmMT is performed to locate the block containing the answer, using the minimum/maximum excess values stored in the tree during the traversal. The final answer is obtained using lookup tables. Theoretically, the time complexities can be reduced to O(1). For interested readers, we refer to Navarro and Sadakane [35] for more details.

Our implementation consists of the following components:

Bit-string $S_1[1..4n-5]$, with $S_1[i]=1$ if the i-th symbol during the traversal of the PS-tree is a ‘(’, and $S_1[i]=0$, otherwhise. Notice that $S_1$ corresponds to the string S described in previous sections.
Bit-string $S_2[1..4n-5]$, with $S_2[i]=1$ if the i-th symbol during the traversal of the PS-tree is a ‘)’, and $S_2[i]=0$, otherwhise.
Support for the rank operation over $S_1$ and $S_2$.
An RmMT, called RmMT$_\mathrm{left}$, over the net-left-excess described in Sect. 4.1, storing the minimum (m) and maximum (M) excess of each block. See, for example, the RmMT of Fig. 14a.
An RmMT over a new excess, called ]-excess, defined as a right-to-left traversal of S, adding 1 for each ‘]’ and subtracting 1 for each ‘(’ or ‘)’. We start the traversal at the rightmost ‘]’ of S, assigning to it an excess of 2. In each node of this RmMT we not only store the minimum (m) and maximum (M) excess, but also the minimum excess occurring in a position with a ‘]’ symbol ($m_]$). We use $m_]$ excess to implement the retrieval of the neighborhood of a vertex. For instance, see Fig. 14b. We call it RmMT$_{[}$.

With those components, we can compute the net-left-excess and ]-excess at a given position i in constant time, as follows:

$$\begin{aligned} \text {net-left-excess}(i)&= 4\times \texttt {rank}_1(i,S_1) - i\\ \text {]-excess}(i)&= 2\times \texttt {rank}_1(i-1,S_1) + 2\times \texttt {rank}_1(i-1,S_2) - i \end{aligned}$$

For instance, in Fig. 14a, if we want to find the corresponding 0 matching the 1 at position 13 of S, which has net-left-excess $e=19$, we need to find the leftmost position $j>13$ with net-left-excess $e'=e-3=16$. For that, we first check if the answer is in the same block using lookup tables. Since the answer is not there, we check the right sibling with $m=19$ and $M=22$. Then, we go up until the right child of the root. Such node has $m=5$ and $M=19$, which means that the answer is in the subtree below it. We go down following the leftmost path, until reaching the node with $m=15$ and $M=19$. Finally, we check the block associated to such node using lookup tables until obtaining the answer. Similarly, if we want to find the first (alt. second) ‘ ] ’ symbol of S[13], we repeat the process with $e'=e-1=18$ (alt. $e'=e-2=17$).

Each bit-string $S_1$ and $S_2$ can be stored in $(4n-5)H_0(S_1)+o(n)$ bits using the compressed bit-vector of Raman et al. [38], where $H_0(S_1)$ corresponds to the zeroth-order empirical entropy of $S_1$. In this case, since both $S_1$ and $S_2$ have n 1-bit and $3n-5$ 0-bit, $H_0(S_1)\approx \frac{1}{4}\lg 4 + \frac{3}{4}\lg \frac{4}{3}\approx 3.24$. The compressed bit-vector of Raman et al. also supports rank operations in constant time. Each excess value stored in the RmMTs uses $O(\lg n)$ bits. The RmMT for net-left-excess can be stored in two arrays of length $2\lceil \frac{4n-5}{w}\rceil -1$, one array for the m values and one for M values. Similarly, the RmMT for ]-excess can be stored in three arrays of length $2\lceil \frac{4n-5}{w}\rceil -1$, for the m, M, and $m_]$ values. Thus, the final space of our implementation is bounded by $8nH_0(S_1)+O(\frac{n}{w}\lg n)\approx 6.49n+O(\frac{n}{w}\lg n)$ bits. In our experiments, we tested several values of w in order to reduce the final size of the structure.

6.1 Experimental Setup

For the implementation of our proposal, we use the library SDSL [25], a C++ library for the implementation of succinct data structures.^{Footnote 3} In our implementation, the block size of the compressed bit-vectors of Raman et al. was set to 63, and each entry of the RmMTs was stored using $\lceil \lg e_{\max }\rceil$ bits, where $e_{max}$ corresponds to the maximum excess value of each RmMT.^{Footnote 4} We compared against the representation of Ferres et al. [21], Pemb, the most space-efficient implementation in the state-of-the-art, designed for the succinct representation of planar embeddings. Besides, we reviewed the implementation of Castelli Aleardi and Devillers [5] for triangle meshes. Their implementation uses about 100 bits per vertex, which is up to 6 times more space than the space needed by Pemb, and therefore out of the scope of our work. We compiled our solution and the baseline with GCC 6.3 and optimization flag -O3. The experiments ran on a machine with two Intel® Xeon® Silver 4110 Processors with 16 physical cores clocked at 2.1GHz, with per-core L1 and L2 caches of 32KB and 1MB respectively, a per-processor L3 cache of 11MB and 252GB of DDR3 RAM memory (126GB per NUMA node). Running time was measured with the functions in <time.h>. We report the median running time of 30 repetitions. We tested the block sizes $b=\{63, 126, 252, 504, 1008\}$.

We performed experiments with several triangulations, varying the number of vertices. Table 1 shows a summary of the datasets. Each triangulation was obtained by generating random points (x, y) with the function rnorm of R.^{Footnote 5}. The only exception is the dataset wc, which corresponds to the coordinates of 2, 243, 467 unique cities in the world.^{Footnote 6} From those points, we obtained a Delaunay Triangulation using Triangle, a software for the generation of meshes and triangulations.^{Footnote 7} Then, we generated maximal triangulations from the Delaunay triangulations with the Boost Library [18], using the function make_maximal_planar.^{Footnote 8} Finally, we compute the mininal Schnyder woods of the triangulations using the function minimal_schnyder_wood.^{Footnote 9} We measured the running time of the two queries explained in Sect. 5. For adjacency testing, we tested two different sets of edges with 10,000 edges each set. The first set corresponds to random edges that are present in the triangulations, called real edges, and the second set corresponds to random edges that does not exist in the triangulations, called non edges. For the recovery of the neighborhood of a vertex, we tested 10,000 random vertices of each triangulation.

Table 1 Datasets used in our experiments

Full size table

6.2 Experimental Results

The results of our experiments are shown in Figs. 15 and 16. Figure 15 shows the space usage of the succinct representation of each triangulation. For each triangulation, the space of each component, $S_1$, $S_2$, RmMT$_{left}$ and RmMT$_{[}$, is reported, varying the block size. As expected, the size of RmMT$_{left}$ and RmMT$_{[}$ depend directly on the block size, while bit-strings $S_1$ and $S_2$ are independent on it. Figure 16 provides a space-time trade-off of our strucuture compare to Pemb. We only report the results for the datasets tri1M and wc, since the results for the other datasets are similar. For all tested block sizes, our structure uses less space than Pemb, reaching up to 7.35 bits per vertex for tri1M and 7.56 bits per vertex for wc, which corresponds to an improvement of a 56% and 54% over the space usage of Pemb, respectively. In Figs. 16a and c we show the running time of the adjacency test of the two set of edges, real edges and non edges. The set non-edges exhibit a worse running time compared to real-edges, since to conclude that two vertices are not neighbors, more operations must be performed. For both sets, the running time increases proportionally with the block size. A similar situation occurs in Figs. 16b and d, for the retrieval of the neighborhood of a vertex. For a block size of 1008, our data structure uses less than half of the space used by Pemb, at the cost of being up to two orders of magnitude slower. However, our data structure offers some other interesting trade-offs. For example, for a block size of 126, it is one order of magnitude slower than Pemb, while retaining a significant reduction in the space usage of up to 40%. In scenarios where the available main memory has a reduced size, our proposed data structure may still fit in, while Pemb must access to the next level of the memory hierarchy, the disk. In such situations, our proposal is expected to be more time efficient than Pemb.

7 Conclusions

The main contribution of this work is a theoretical new approach to the succinct encoding of triangulations by handling a special type of binary string. Two graphs are created whose nodes are the elements of such string, one of them encoding the edges of a particular vertex spanning tree of the triangulation, and the other one encoding the non-tree edges. They allow to establish a method to navigate efficiently on the original triangulation by translating operations on the triangulations to operations on such graphs. The data structures encoding both graphs are not new, being slight variations of the ones that have been previously developed by Geary et al. [24]. The total storage cost of maintaining such structures remains the same than in the aforementioned paper, $O\left( \frac{n\lg \lg n}{\lg n}\right)$. The cost of storing tables could be reduced or even eliminated at the expense of increasing computation time. Additionally, we provide an implementation of our proposal based on range min-max trees [35]. In practice, our succinct encoding reduces significatively the space usage of the state-of-the-art implementations for planar embeddings, obtaining reductions of up to 56% at the cost of being two orders of magnitude slower for query time. Our implementation also provides a trade-off, which allow us to improve the query time (being just one order of magnitude slower) while still obtaining a important space saving of 40%.

The underlaying strategy throughout this paper is rather general, and can be easily adapted to deal with other classes of graphs. For the case of planar triangulations with boundaries and quadrangulations, Castelli Aleardi et al. [15] modify the encoding defined by Poulalhon and Schaeffer [37] to handle these graphs. As the proposal we have given is also based in the encoding given by Poulalhon and Schaeffer, the techniques developed in our work could be subsequently modified to encode such classes of graphs. In particular, for the case of planar triangulations with a boundary, Castelli Aleardi et al. define a tree which represents the triangulation, encoding such tree by a string similarly to the bijection of Poulalhon and Schaeffer. Each non-boundary vertex carries two stems, and the boundary, with k vertices, carries in total $k + 2$ stems. For planar quadrangulations with no boundary, the bijection of Poulalhon and Schaeffer is straighforward applied, and a spanning tree with one stem per inner node is created. In the case of bipartite planar quadrangulations with a boundary, the technique is similar to that of the triangulations.

Fusy et al. [23] considered tree-based bijections for 3-connected planar graphs. The proposed encoding is based on an orientation associated to the minimal Schnyder wood of a 3-connected planar map. Local closure operations are similar to the ones described by Poulalhon and Schaeffer, but the bijection between the map and the considered tree on which local closure operations are performed is different. Irreducible triangulations and quadrangulations are also encoded by Fusy [22]. A bijection between ternary trees and irreducible triangulations and a closure operation yield to an optimal encoding of 4-connected triangulations. In these cases, a modification of the encoding involving a different type of binary string is required.

Despré et al. [19] generalized the method given by Poulalhon and Schaeffer for the torus. The proposed encoding is asymptotically optimal, requiring 3.2451n+o(n) bits. It is shown that any toroidal triangulation with n vertices can be encoded by a plane rooted tree with n vertices where each vertex has exactly two stems. Such tree is encoded by a binary string of 4n-2 bits, of which $n-1$ elements that are 1 and $3n-1$ elements that are 0, exactly as occurs in the case we have studied. Hence, the work developed in this paper is also applicable to the toroidal case.

From the practical side, an interesting future work is the reduction of the space usage of our implementation. Currently, our implementation uses 2.3 times more space than the optimal, since we store two bit-strings, $S_1$ and $S_2$. Theoretically, $S_1$ plus some additional lookup tables are enough to support the navigational operations. Another interesting future work is an implementation based on pioneers. Even when range min-max trees have shown a better practical behavior than pioneers for succinct trees, it is still open a similar study in the context of succinct triangulations.

Change history

04 November 2021
The original online version of this article was revised: Open Access funding note “Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature”.

Notes

All logarithms appearing in this paper are in base 2.
Floors and ceilings will be ignored for the sake of clarity.
The implementation is available at https://github.com/jfuentess/sdsl-lite.
In the SDSL library, this can be done with the function bit_compress().
The rnorm function generates random numbers with normal distribution given a mean and a standard deviation. In our case, the x and y components were generated using mean 0 and standard deviation 10000. For more information about the rnorm function, visit https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Normal.html
The dataset containing the coordinates was created by MaxMind, available from https://www.maxmind.com/en/free-world-cities-database. The original dataset contains 3, 173, 959 cities, but some of them have the same coordinates. We selected the 2, 243, 467 cities with unique coordinates to build our dataset wc.
Available at http://www.cs.cmu.edu/~quake/triangle.html. Our triangulations were generated using the options -cezCBVPNE.
For more details of the function make_maximal_planar, please visit http://www.boost.org/doc/libs/1_49_0/libs/graph/doc/make_maximal_planar.html.
For more details of the function minimal_schnyder_wood, please visit http://doc.sagemath.org/html/en/reference/graphs/sage/graphs/schnyder.html.

References

Aleardi, L.C., Devillers, O., Rossignac, J.: ESQ: editable squad representation for triangle meshes. In: Conference on Graphics, Patterns and Images (SIBGRAPI), pp. 110–117 (2012)
Castelli Aleardi, L., Devillers, O., Schaeffer, G.: Succinct representations of planar maps. Theoret. Comput. Sci. 408(2), 174–187 (2008)
Article MathSciNet Google Scholar
Aleardi, L.C., Devillers, O., Mebarki, A.: Catalog-based representation of 2D triangulations. Int. J. Comput. Geom. Appl. 21(04), 393–402 (2011)
Article MathSciNet Google Scholar
Aleardi, L.C., Devillers, O., Schaeffer, G.: Succinct representation of triangulations with a boundary. In: Algorithms and Data Structures (WADS). Springer, Waterloo, Canada, pp. 134–145 (2005)
Aleardi, L.C., Devillers, O.: Array-based compact data structures for triangulations: Practical solutions with theoretical guarantees. J. Comput. Geom. 9(1), 247–289 (2018)
MathSciNet MATH Google Scholar
Aleardi, L.C., Devillers, O., Schaeffer G.: Dynamic updates of succinct triangulations. In: Canadian Conference on Computational Geometry (CCCG), pp. 134–137 (2005)
Arroyuelo, D., Cánovas R., Navarro, G., Sadakane, K.: Succinct trees in practice. In: Algorithm Engineering & Expermiments (ALENEX). Philadelphia, PA, USA, pages 84–97 (2010). Society for Industrial and Applied Mathematics
Barbay, J., Aleardi, L.C., He, M., Munro, J.I.: Succinct representation of labeled graphs. In: International Symposium on Algorithms and Computation (ISAAC). Berlin, Heidelberg, pp. 316–328 (2007). Springer Berlin Heidelberg
Barbay, J., Claude, F., Gagie, T., Navarro, G., Nekrich, Y.: Alphabet partitioning for compressed rank/select and applications. In: International Symposium on Algorithms and Computation (ISAAC). Berlin, Heidelberg, pp. 315–326 (2010)
Blandford, D.K., Blelloch, G.E., Kash, I.A.: Compact representations of separable graphs. In: Symposium on Discrete Algorithms (SODA). Philadelphia, PA, USA, pp. 679–688 (2003). Society for Industrial and Applied Mathematics
Blandford, D.K., Blelloch, G.E., Kash, I.A.: An experimental analysis of a compact graph representation. In: ALENEX/ANALC. SIAM, pp. 49–61 (2004)
Blelloch, G.E., Farzan, A.: Succinct representations of separable graphs. In: Combinatorial Pattern Matching (CPM). Springer, New York, NY, USA, pp. 138–150 (2010)
Brehm, E.: 3-orientations and schnyder 3-tree-decompositions, construction and order structure. Diploma thesis, Freie Universität Berlin (2000)
Aleardi, L.C., Devillers, O.: Explicit array-based compact data structures for triangulations. In: International Symposium on Algorithms and Computation (ISAAC). Berlin, Heidelberg, pp. 312–322 (2011)
Aleardi, L.C., Fusy, E., Lewiner, T.: Optimal encoding of triangular and quadrangular meshes with fixed topology. In: Canadian Conference on Computational Geometry (CCCG). Winnipeg, Canada (2010)
Chiang, Y.T., Lin, C.C., Lu, H.I.: Orderly spanning trees with applications to graph encoding and graph drawing. In: Symposium on Discrete Algorithms (SODA). Philadelphia, PA, USA, pp. 506–515 (2001). Society for Industrial and Applied Mathematics
Chuang, R.C.N., Garg, A., He, X., Kao, M.Y., Lu, H.I.: Compact encodings of planar graphs via canonical orderings and multiple parentheses. In: Automata, Languages and Programming (ICALP). Berlin, Heidelberg, pp. 118–129 (1998)
Dawes, B., Abrahams, D.: Boost: C++ libraries. http://www.boost.org/. Last accessed: August 06 2019
Despré, V., Gonçalves, D., Lévêque, B.: Encoding toroidal triangulations. Discrete Comput. Geom. 57(3), 507–544 (2017)
Article MathSciNet Google Scholar
Farzan, A., Munro, J.I.: Succinct encoding of arbitrary graphs. Theoret. Comput. Sci. 513, 38–52 (2013)
Article MathSciNet Google Scholar
Ferres, L., Fuentes-Sepulveda, J., Gagie, T., He, M., Navarro, G.: Fast and compact planar embeddings. Computat. Geom. 89, 101630 (2020)
Article MathSciNet Google Scholar
Éric, F.: Transversal structures on triangulations: a combinatorial study and straight-line drawings. Discrete Math. 309(7), 1870–1894 (2009)
Article MathSciNet Google Scholar
Fusy, É., Schaeffer, G., Poulalhon, D.: Dissections, orientations, and trees with applications to optimal mesh encoding and random sampling. ACM Trans. Algorithms 4(2), 1–48 (2008)
Article MathSciNet Google Scholar
Geary, R.F., Rahman, N., Raman, R., Raman, V.: A simple optimal representation for balanced parentheses. Theor. Comput. Sci. 368(3), 231–246 (2006)
Article MathSciNet Google Scholar
Gog, S., Beller, T., Moffat, A., Petri, M.: From theory to practice: plug and play with succinct data structures. In: Symposium on Experimenal Algorithms (SEA). Springer, pp. 326–337 (2014)
Golynski, A., Munro, J.I., Rao S.S.: Rank/select operations on large alphabets: a tool for text indexing. In: Symposium on Discrete Algorithm (SODA). Philadelphia, PA, USA, pp. 368–373 (2006) Society for Industrial and Applied Mathematics
Gurung, T., Luffel, M., Lindstrom, P., Rossignac, J.: LR: Compact connectivity representation for triangle meshes. ACM Trans. Graph. 30(4), 67:1-67:8 (2011)
Article Google Scholar
Gurung, T., Luffel, M., Lindstrom, P., Rossignac, J.: Zipper: a compact connectivity data structure for triangle meshes. Computer-Aided Des. 45(2), 262–269 (2013)
Article Google Scholar
He, M., Munro, J.I.: Succinct representations of dynamic strings. In: String Processing and Information Retrieval (SPIRE). Springer, Los Cabos, Mexico, pp. 334–346 (2010)
He, X., Kao, M., Lu, H.: A fast general methodology for information-theoretically optimal encodings of graphs. SIAM J. Comput. 30(3), 838–846 (2000)
Article MathSciNet Google Scholar
Jacobson, G.: Succinct static data structures. PhD thesis, School of computer science, Carnegie Mellon University, Pittsburgh, PA, USA (1988)
Jacobson, G.: Space-efficient static trees and graphs. In: Symposium on Foundations of Computer Science (FOCS), pp. 549–554 (1989)
Munro, J., Raman, V.: Succinct representation of balanced parentheses and static trees. SIAM J. Comput. 31(3), 762–776 (2001)
Article MathSciNet Google Scholar
Navarro, G.: Compact Data Structures: A Practical Approach. Cambridge University Press, Cambridge (2016)
Book Google Scholar
Navarro, G., Sadakane, K.: Fully functional static and dynamic succinct trees. ACM Trans. Algorithms 10(3), 16:1-16:39 (2014)
Article MathSciNet Google Scholar
Patrascu, M.: Succincter. In: Symposium on Foundations of Computer Science (FOCS), pp. 305–313 (2008)
Poulalhon, D., Schaeffer, G.: Optimal coding and sampling of triangulations. Algorithmica 46(3), 505–527 (2006)
Article MathSciNet Google Scholar
Raman, R., Raman, V., Satti, S.R.: Succinct indexable dictionaries with applications to encoding k-ary trees, prefix sums and multisets. ACM Trans. Algorithms 3(4), 43-es (2007)
Article MathSciNet Google Scholar
Schnyder, W.: Embedding planar graphs on the grid. In: Symposium on Discrete Algorithms (SODA). Philadelphia, PA, USA, pp. 138–148 (1990). Society for Industrial and Applied Mathematics
György, T.: On the succinct representation of graphs. Discrete Appl. Math. 8(3), 289–294 (1984)
Article MathSciNet Google Scholar
Tutte, W.T.: A census of planar triangulations. Can. J. Math. 14, 21–38 (1962)
Article MathSciNet Google Scholar
Yamanaka, K., Nakano, S.I.: A compact encoding of plane triangulations with efficient query supports. Inf. Process. Lett. 110(18), 803–809 (2010)
Article MathSciNet Google Scholar

Download references

Funding

Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.

Author information

Authors and Affiliations

Department of Computer Science, Universidad de Concepción, Concepción, Chile
José Fuentes-Sepúlveda & Diego Seco
Millennium Institute for Foundational Research on Data (IMFD), Santiago, Chile
Diego Seco
Departamento de Física y Matemáticas, Universidad de Alcalá, 28871, Alcalá de Henares, Madrid, Spain
Raquel Viaña

Authors

José Fuentes-Sepúlveda
View author publications
You can also search for this author in PubMed Google Scholar
Diego Seco
View author publications
You can also search for this author in PubMed Google Scholar
Raquel Viaña
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Raquel Viaña.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported in part by National Agency for Research and Development (ANID)—Millennium Science Initiative Program—Code ICN17_002, and ANID—PAI under Grant 77190038, Fondecyt Postdoctoral under grant 3170534 and Basal Funds FB0001 (José Fuentes-Sepúlveda) and through Fondecyt Regular under Grant 1170497 (Diego Seco). This research has also been supported by Spanish Research Grant PGC2018-096321-B-I00 from the Spanish Ministerio de Ciencia, Innovación y Universidades. The author Raquel Viaña is a member of the Research Group asynacs (Ref.CT-CE2019/683) of Universidad de Alcalá.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this article

Cite this article

Fuentes-Sepúlveda, J., Seco, D. & Viaña, R. Succinct Encoding of Binary Strings Representing Triangulations. Algorithmica 83, 3432–3468 (2021). https://doi.org/10.1007/s00453-021-00861-4

Download citation

Received: 03 September 2019
Accepted: 18 July 2021
Published: 09 August 2021
Issue Date: November 2021
DOI: https://doi.org/10.1007/s00453-021-00861-4

Keywords

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

Succinct Encoding of Binary Strings Representing Triangulations

Abstract

Similar content being viewed by others

Implementing the Topological Model Succinctly

I/O-Efficient Path Traversal in Succinct Planar Graphs

Dynamic Compact Planar Embeddings

1 Introduction

2 Related Work

3 Background

3.1 PS-Tree of a Triangulation

3.2 Encoding of Balanced Binary Strings

Proposition 1

Lemma 1

3.3 Compact Representation of Bit-strings

4 Our Proposal

Lemma 2

4.1 Detecting in S the Two Occurrences of an Inner Edge

Definition 1

Proposition 2

Proof

Definition 2

Proposition 3

Proof

Proposition 4

Proof

4.1.1 Retrieving the Two ‘ ] ’ Associated to a ‘ (’

4.1.2 Passing from Binary to Ternary Strings

4.2 Retrieving the Two Inner Nodes Linked to a Stem

Proposition 5

Proof

Definition 3

Proposition 6

Proposition 7

4.3 Retrieving the ‘ ] ’ of the ]-graph Adjacent at a ‘(’ or a ‘)’

Proposition 8

4.4 Storage Requirements

Theorem 1

5 Answering Queries on the Triangulation

5.1 Neighborhood Retrieval

5.2 Adjacency Testing

Theorem 2

6 Implementation

6.1 Experimental Setup

6.2 Experimental Results

7 Conclusions

Change history

04 November 2021

Notes

References

Funding

Author information

Authors and Affiliations

Corresponding author

Additional information

Publisher's Note

Rights and permissions

About this article

Cite this article

Share this article

Keywords

Search

Navigation