A New Algorithm for the $^K$DMDGP Subclass of Distance Geometry Problems with Exact Distances

Abstract

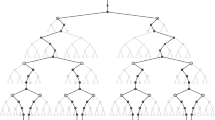
The fundamental inverse problem in distance geometry is the one of finding positions from inter-point distances. The Discretizable Molecular Distance Geometry Problem (DMDGP) is a subclass of the Distance Geometry Problem (DGP) whose search space can be discretized and represented by a binary tree, which can be explored by a Branch-and-Prune (BP) algorithm. It turns out that this combinatorial search space possesses many interesting symmetry properties that were studied in the last decade. In this paper, we present a new algorithm for this subclass of the DGP, which exploits DMDGP symmetries more effectively than its predecessors. Computational results show that the speedup, with respect to the classic BP algorithm, is considerable for sparse DMDGP instances related to protein conformation.

Appendix: Proof of Lemma 2

Proof

Since $x(s')$ from Eq. (4) involves only partial reflections, in view of Property 3 in Remark 2, $x(s') \in \hat{X}$, i.e $\Vert x_u(s') - x_w(s') \Vert = d_{uw}, \forall \{u,w\} \in E_D$.

It remains to show that $x(s')$ does not violate distance constraints associated to pruning edges in $P^{ij}$. Since the reflections are applied to positions $x_{\ell }$ such that $\ell \ge i+K+1$, pruning edges $\{u,w\} \in P^{ij}$ with $u<w\le i+K$ are not affected. Thus, assume that $i+K+1 \le w \le n$. If $u \le i$, then for $\ell = i+K+1,\dots ,w$ there exists $\{u,w\}$ such that $u+K+1 \le \ell \le w$, which implies that $v_{i+K+1},\dots ,v_{w} \not \in S^{ij}$, meaning that the first symmetry vertex $v_{\ell }$ in $S^{ij}$ is such that $\ell \ge w+1$. Thus, according to (2) and (4), partial reflections are not applied to $x_{i+K+1},\dots ,x_{w}$, i.e $x_{\ell }(s') = x_{\ell }(s)$, for $\ell =i+K+1,\dots ,w$ and $\Vert x_u(s') - x_w(s') \Vert = d_{uw}$ holds. Otherwise, for $u \ge i+1$, we have that $v_{u+K+1},\dots ,v_w \not \in S^{ij}$, and from (4) and (2), positions $x_{\ell },\dots ,x_{u+K+1},\dots ,x_w$ are updated by reflections $R_{x}^{\ell }(x_{\ell }), \dots , R_{x}^{\ell }(x_{u+K+1}), \dots , R_{x}^{\ell }(x_w)$, for $i+K+1 \le \ell \le u+K$ such that $v_{\ell } \in S^{ij}$. Since either $u \le \ell - 1$, i.e $x_u$ is in the hyperplane associated to $v_{\ell }$, or $u \ge \ell$, i.e. $x_u$ comes after this hyperplane, in view of Remark 2, Property 2, these reflections are such that $\Vert x_u(s') - x_v(s') \Vert = d_{uw}$. $\square$