Abstract
This article shows how to construct an overlay network of constant degree and diameter \(O(\log n)\) in \(O(\log n)\) time starting from an arbitrary weakly connected graph. We assume a synchronous communication network in which nodes can send messages to nodes they know the identifier of, and new connections can be established by sending node identifiers. Suppose the initial network’s graph is weakly connected and has constant degree. In that case, our algorithm constructs the desired topology with each node sending and receiving only \(O(\log n)\) messages in each round in \(O(\log n)\) time w.h.p., which beats the currently best \(O(\log ^{3/2} n)\) time algorithm of Götte et al. (International colloquium on structural information and communication complexity (SIROCCO), Springer, 2019). Since the problem cannot be solved faster than by using pointer jumping for \(O(\log n)\) rounds (which would even require each node to communicate \(\Omega (n)\) bits), our algorithm is asymptotically optimal. We achieve this speedup by using short random walks to repeatedly establish random connections between the nodes that quickly reduce the conductance of the graph using an observation of Kwok and Lau (Approximation, randomization, and combinatorial optimization. Algorithms and techniques (APPROX/RANDOM 2014), Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2014). Additionally, we show how our algorithm can be used to efficiently solve graph problems in hybrid networks (Augustine et al. in Proceedings of the fourteenth annual ACM-SIAM symposium on discrete algorithms, SIAM, 2020). Motivated by the idea that nodes possess two different modes of communication, we assume that communication of the initial edges is unrestricted, whereas only polylogarithmically many messages can be sent over edges that have been established throughout an algorithm’s execution. For an (undirected) graph G with arbitrary degree, we show how to compute connected components, a spanning tree, and biconnected components in \(O(\log n)\) time w.h.p. Furthermore, we show how to compute an MIS in \(O(\log d + \log \log n)\) time w.h.p., where d is the initial degree of G.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many modern distributed systems (especially those which operate via the internet) are not concerned with the physical infrastructure of the underlying network. Instead, these large-scale distributed systems form logical networks that are often referred to as overlay networks or peer-to-peer networks. In these networks, nodes are considered as connected if they know each other’s IP addresses. Examples include overlay networks like Chord [55], Pastry [51], and skip graphs [3]. This work considers the fundamental problem of constructing an overlay network of low diameter as fast as possible from an arbitrary initial state. Note that \(O(\log n)\) is the obvious lower bound for the problem: If the nodes initially form a line, it takes \(O(\log n)\) rounds for the two endpoints to learn each other, even if every node could introduce all of its neighbors to each other in each round.
To the best of our knowledge, the first overlay construction algorithm with polylogarithmic time and communication complexity that can handle (almost) arbitrary initial states has been proposed by Angluin et al. [2]. The authors assume a weakly connected graph of initial degree d. If in each round, each node can send and receive at most d messages, and new edges can be established by sending node identifiers, their algorithm transforms the graph into a binary search tree of depth \(O(\log n)\) in \(O(d+\log ^2 n)\) time, w.h.p.Footnote 1 A low-depth tree can easily be transformed into many other topologies, and fundamental problems such as sorting or routing can be easily solved from such a structure.
This idea has sparked a line of research investigating how quickly such overlays can be constructed. Table 1 provides an overview of the works that can be compared with our result. For example, [4] gives an \(O(\log n)\) time algorithm for initial graphs with outdegree 1. If the initial degree is d and nodes can send and receive \(O(d\log n)\) messages, there is a deterministic \(O(\log ^2 n)\) time algorithm [30]. Very recently, this has been improved to \(O(\log ^{3/2} n)\), w.h.p. [31]. However, to the best of our knowledge, there is no \(O(\log n)\)-time algorithm that can construct a well-defined overlay with logarithmic communication for any topology. This article finally closes the gap and presents the first algorithm that achieves these bounds, w.h.p.
All of the previous algorithms (i.e., [2, 4, 28, 30, 31]) essentially employ the same high-level approach of [2] to alternatingly group and merge so-called supernodes (i.e., sets of nodes that act in coordination) until only a single supernode remains. However, these supernodes need to be consolidated after being grouped with adjacent supernodes to distinguish internal from external edges. This consolidation step makes it difficult to improve the runtime further using this approach. This work presents a radically different approach, arguably simpler than existing solutions. Instead of arranging the nodes into supernodes (and paying a price of complexity and runtime for their maintenance), we establish random connections between the nodes by performing short constant length random walks. Each node starts a small number of short random walks, connects itself with the respective endpoints, and drops all other connections. Then, it repeats the procedure on the newly obtained graph.
The approach is based on classical overlay maintenance algorithms for unstructured networks such as, for example, [41] or [29] as well as practical libraries for overlays like JXTA [48]. Note that our analysis significantly differs from [41] and [29] as we do not assume that nodes arrive one after the other. Instead, we assume an arbitrary initial graph with possibly small conductance. Using novel techniques by Kwok and Lau [39] combined with elementary probabilistic arguments, we show that short random walks incrementally reduce the conductance of the graph. Once the conductance is constant, the graph’s diameter must be \(O(\log n)\). Note that such a graph can easily be transformed into many other overlay networks, such as a sorted ring, e.g., by performing a BFS and applying the algorithm of Aspnes and Wu [4] to the BFS tree or by using the techniques by Gmyr et al. [30]
1.1 Related work
The research on overlay construction is not limited to the examples in the introduction. Since practical overlay networks are often characterized by dynamic changes coming from churn or adversarial behavior, many papers aim to reach and maintain a valid topology of the network in the presence of faults. These works can be roughly categorized into two areas. On the one hand, there are so-called self-stabilizing overlay networks, which try to detect invalid configurations locally and recover the system into a stable state (see, e.g., [21] for a comprehensive survey). However, since most of these solutions focus on a very general context (such as asynchronous message passing and arbitrary corrupted memory), only a few algorithms provably achieve polylogarithmic runtimes [14, 35], and most have no bounds on the communication complexity. On the other hand, there are overlay construction algorithms that use only polylogarithmic communication per node and proceed in synchronous rounds. We have algorithms maintaining an overlay topology under randomized or adversarial errors in this category. These works focus on quickly reconfiguring the network to distribute the load evenly (under churn) or to reach an unpredictable topology (in the presence of an adversary) [9, 10, 18, 32]. However, a common assumption is that the overlay starts in some well-defined initial state. Gilbert et al. [28] combine the fast overlay construction with adversarial churn. They present a construction algorithm that tolerates adversarial churn as long as the network remains connected, and there eventually is a period of length \(\Omega (\log n^2)\) where no churn happens. The exact length of this period depends on the goal topology. Further, there is a paper by Augustine et al. [6] that considers \(\widetilde{O}(d)\)-timeFootnote 2 algorithms for so-called graph realization problems. They aim to construct graphs of any given degree distributions as fast as possible. They assume, however, that the network starts as a line, which makes the construction of the graphs considered in this work considerably more straightforward.
One of the main difficulties in designing algorithms to construct overlay networks quickly lies in the node’s limited communication capabilities in a broader context. Therefore, our algorithm further touches on a fundamental question in designing efficient algorithms for overlay networks: How can we exploit the fact that we can (theoretically) communicate with every node in the system but are restricted to sending and receiving \(O(\log n)\) messages? Recently, the impact of this restriction has been studied in the so-called Node-Capacitated Clique (NCC) model [7], in which the nodes are connected as a clique and can send and receive at most \(O(\log n)\) messages in each round. The authors present \(\widetilde{O}(a)\) algorithms, where a is the arboricityFootnote 3 of G for local problems such as MIS, matching, or coloring, a \(\widetilde{O}(D+a)\) algorithm for BFS tree, and a \(\widetilde{O}(1)\) algorithm for the minimum spanning tree (MST) problem. Robinson [50] investigates the information the nodes need to learn to solve graph problems and derives a lower bound for constructing spanners in the NCC. Interestingly, his result implies that spanners with constant stretch require polynomial time in the NCC and are much harder to compute than MSTs. As pointed out in [20], the NCC can simulate PRAM algorithms efficiently under certain limitations. If the input graph’s degree is polylogarithmic, for example, we easily obtain polylogarithmic time algorithms for (minimum) spanning forests [17, 34, 49]. Notably, Liu et al. [43] recently proposed an \(O(\log D + \log \log _{m/n} n)\) time algorithm for computing connected components in the CRCW PRAM model, which would also likely solve overlay construction. Assadi et al. [5] achieve a comparable result in the MPC model (that uses \(O(n^{\delta })\) communication per node) with a runtime logarithmic in the input graph’s spectral expansion. Note that, however, the NCC, the MPC model, and PRAMs are arguably more powerful than the overlay network model considered in this article since nodes can reach any other node (or, in the case of PRAMs, processors can contact arbitrary memory cells), which rules out a naive simulation that would have \(\Omega (\log n)\) overhead if we aim for a runtime of \(O(\log n)\). Also, if the degree is unbounded (our assumption for the hybrid model), simulating PRAM algorithms, which typically have work \(\Theta (m)\), becomes completely infeasible. Furthermore, since many PRAM algorithms are very complicated, it is highly unclear whether their techniques can be applied to our model. Last, there is a hybrid network model by Augustine et al. [8] that combines global (overlay) communication with classical distributed models such as \(\textsf{CONGEST}\) or \(\textsf{LOCAL}\). Here, in a single round, each node can communicate with all its neighbors in a communication graph G, and in addition, can send and receive a limited amount of messages from each node in the system. So far, most research for hybrid networks focussed on shortest-path problems [8, 20, 38]. For example, in general graphs, APSP can be solved exactly and optimally (up to polylogarithmic factors) in \(\widetilde{O}(\sqrt{n})\) time, and SSSP can be computed in \(\widetilde{O}\left( \min \left\{ n^{2/5}, \sqrt{D}\right\} \right) \) time exactly. Whereas even an \(\Omega (\sqrt{n})\) approximation for APSP takes time \(\widetilde{O}(\sqrt{n})\), a constant approximation of SSSP can be computed in \(\widetilde{O}(n^\varepsilon )\) time [8, 38]. Note that these algorithms require very high (local) communication. If the initial graph is very sparse, then SSSP can be solved in (small) polylogarithmic time and with limited local communication, exploiting the power of the NCC [20].
1.2 Our contribution
The main goal of this article is to construct a well-formed tree, which is a rooted tree of degree \(O(\log n)\) and diameter \(O(\log n)\) that contains all nodes of G. We chose this structure because any well-behaved overlays of logarithmic degree and diameter (e.g., butterfly networks, path graphs, sorted rings, trees, regular expanders, De Bruijn Graphs, etc.) can be constructed in \(O(\log n)\) rounds, w.h.p., starting from a well-formed tree. Distributed algorithms can use these overlays for common tasks like aggregation, routing, or sampling in logarithmic time. We present an algorithm that constructs such a tree in \(O(\log {n})\) time, w.h.p., in the P2P-\(\textsf{CONGEST}\) model. In addition to their initial neighborhood, we only assume that all nodes know an approximation of \(\log {n}\), i.e., a very loose polynomial upper bound on n, the number of nodes. All nodes must know the same approximation as we use it to synchronize between the different stages of the algorithm. More precisely, all know a common value \(L \in \Theta (\log {n})\) that affects the runtime. Further, all nodes must know a common value \(\Lambda \in \Omega (\log n)\) that controls how many overlay edges the nodes create, which in turn affects the algorithm’s success probability. We believe that the common knowledge of these variables is a realistic assumption, as a node may simply use the length of its identifier as an approximation for \(\log {n}\). Our main result is the following:
Theorem 1.1
(Main theorem) Let \(G = (V, E)\) be a weakly connected directed graph with degree O(d) and assume each node knows a runtime bound \(L \in \Theta (\log n)\) and security parameter \(\Lambda \in \Omega (\log n)\). There is a randomized algorithm in the P2P-\(\textsf{CONGEST}\) model that with probability \(1-e^{-\Theta (\Lambda )}\)
-
1.
constructs a well-formed tree \(T_G = (V,T_V)\) in O(L) rounds, and
-
2.
lets each node send at most \(O(d\Lambda )\) messages per round.
Note that for \(L,\Lambda \in \Theta (\log n)\), the algorithm completes in \(O(\log n)\) time and sends \(O(d\log n)\) messages, w.h.p. We present the promised algorithm in Sect. 3. Note that we can use techniques from [30] or [4] to further refine our constructions and to reduce the degree of the well-formed tree to O(1). However, since the main focus of our algorithm is the novel idea of using random walks, we omit further details here and refer the reader to [30] and [4].
Our result comes with various applications and implications for several distributed computation problems. First, we point out the following immediate implications that simply follow from the fact that any initial overlay topology can be turned into a well-formed overlay in \(O(\log n)\) time.
-
1.
Every monitoring problem presented in [30] where the goal is to observe the properties of the input graph can be solved in \(O(\log n)\) time, w.h.p., instead of \(O(\log ^2 n)\) deterministically. These problems include monitoring the graph’s node and edge count, its bipartiteness, and the approximate (and even exact) weight of an MST.
-
2.
For the churn-resistant overlays from [6, 9, 10, 18, 32], the common assumption is that the graph starts in a well-initialized overlay. This assumption can be dropped.
-
3.
For most algorithms presented for the NCC (and hybrid networks that model the global network by the NCC) [7, 8, 20], the rather strong assumption that all node identifiers are known may be dropped. Instead, suppose the initial knowledge graph has degree \(O(\log n)\). In that case, we can construct a butterfly network in \(O(\log n)\) time, which suffices for most primitives to work (note that all presented algorithms have a runtime of \(\Omega (\log n)\) anyway).
In Sect. 4, we then give further applications of the algorithm for the hybrid model. For an (undirected) graph G with arbitrary degree, we show how to compute connected components (cf. Sect. 4.1), a maximal independent set (cf. Sect. 4.2), a spanning tree (cf. Sect. 4.3), and biconnected components (cf. Sect. 4.4). As already pointed out, all of the following algorithms can be performed in the hybrid network model of Augustine et al. [8], which provides a variety of novel contributions for these networks. The local capacity of each edge is O(1), which corresponds to the classic \(\textsf{CONGEST}\) model. For each algorithm, we give a bound on the required global capacity. Note that our algorithms may likely be optimized to require a smaller global capacity using more sophisticated techniques. We remark that all of the following algorithms can be adapted to achieve the same runtimes in the NCC\(_0\) model if the initial degree is constant. In the following, we briefly summarize the results.
1.2.1 Connected components
As a first application of our algorithm, in Sect. 4.1, we show how to establish a well-formed tree on each connected component of G (if G is not connected initially).
Theorem 1.2
Let \(G = (V, E)\) be a directed graph. Further, all components have a (known) size of \(O(n')\). There is a randomized algorithm that constructs a well-formed tree on each connected component of (the undirected version of) G in \(O(\log {n'})\) rounds, w.h.p., in the hybrid model. The algorithm requires global capacity \(O(\log ^2 n)\), w.h.p.
If the graph is connected, i.e., there is exactly one component with n nodes, this theorem simply translates Theorem 1.1 to the hybrid model. Note that in the hybrid model, a node \(v \in V\) can no longer create \(O(d(v)\log n)\) overlay edges, which was possible in the \(\textsc {P2P}-\textsf{CONGEST} \) model. Thus, high degree nodes cannot simply simulate the algorithm from before. The section, therefore, presents an adaption of our main algorithm that circumvents some problems introduced by the potentially high node degrees. Here, we first need to transform the graph into a sparse spanner using the efficient spanner construction of Miller et al. [46], later refined by Elkin and Neiman [19]. In their algorithm, each node \(v \in V\) draws an exponential random variable \(\delta _u\) and broadcasts it to all nodes in the graphFootnote 4. Let \(u^*_v\) be the node that maximizes \(\delta _{u^*_v} - \textsf{dist}(u^*_v,v) \) where \(\textsf{dist}(u^*_v,v) \) is the hop distance between \(u^*_v\) and v. Then, v joins the cluster of \(u^*_v\) by storing its identifier and adding the first edge over which it received the broadcast from \(u^*_v\) to the spanner. Finally, the nodes share the identifier of their cluster with their neighbors and add edges between the clusters to obtain a connected graph. It is known that the resulting subgraph of G has very few edges as each node has only a few neighbors in different clusters. This follows from the fundamental properties of the exponential distribution.
We show that if the size of each connected component in graph G is bounded by \(n'\), it suffices to observe variables \(\delta _v\) that are conditioned on being smaller than \(4\log {n'}\), i.e., truncated exponential random variables. With this small change, we speed up the algorithm to \(O(\log {n'})\) while still producing a sparse subgraph with fewer edges. This graph can then be rearranged into a connected \(O(\log n)\)-degree network, allowing us to apply our main algorithm of Theorem 1.1 with parameters \(L \in O(\log {n'})\) and \(\Lambda \in O(\log {n})\). Note that the message complexity per node is still logarithmic in n, the size of the original graph, and not in \(n'\).
1.2.2 Maximal independent set (MIS)
In the MIS problem, we ask for a set \(S \subseteq V\) such that (1) no two nodes in S are adjacent in the initial graph G and (2) every node \(v \in V \setminus S\) has a neighbor in S. We present an efficient MIS algorithm that combines the shattering technique [12, 23] with our overlay construction algorithm to solve the MIS problem in almost \(O(\log d)\) time, w.h.p. This technique shatters the graph into small components of undecided nodes in \(O(\log d)\) time, w.h.p. We then compute a well-formed tree of depth \(O(\log {d}+\log \log n)\) in all these small components. This takes \(O(\log {d}+\log \log n)\) rounds w.h.p. using the algorithm of Theorem 1.2. In each component, we can now independently compute MIS solutions using \(O(\log {n})\) parallel executions of the \(\textsf{CONGEST}\) algorithm by Metivier et al. [47]. As we will see, at least one of these executions must finish after \(O(\log d +\log \log n)\) round w.h.p, so the nodes only need to agree on a solution. The problem is that the nodes cannot locally check which executions have finished. However, we can use our well-formed tree to broadcast information on the executions to all nodes in the component in \(O(\log {d}+\log \log n)\) time. This leads to an \(O(\log d + \log \log n)\) time algorithm, where d is the initial graph’s degree. In Sect. 4.2, we provide the necessary details omitted in this overview and show that:
Theorem 1.3
Let \(G = (V, E)\) be a weakly connected directed graph. There is a randomized algorithm that computes an MIS of G in \(O(\log d + \log \log n)\) rounds, w.h.p., in the hybrid model. The algorithm requires global capacity \(O(\log ^2 n)\), w.h.p.
1.2.3 Spanning trees
A spanning tree \((V, E_S)\) is a subgraph of G with \(n-1\) edges that connects all its nodes. In Sect. 4.3, we compute a (not necessarily minimum) spanning tree of the initial graph G. We show how to obtain this spanning tree by unwinding the random walks over which the additional edges to make up our well-formed tree have been established. More precisely, for each edge (v, w) used by our algorithm, the identifier of w must have somehow been sent to v along some random walk \((v_1 = w, \dots , v_\ell = v)\). Given that (v, w) is part of spanning tree, we show how replace (v, w) by some edge \((v_i,v_{i+1})\). Through recursively applying this trick, we show that:
Theorem 1.4
Let \(G = (V, E)\) be a weakly connected directed graph. There is a randomized algorithm that constructs a spanning tree of (the undirected version of) G in \(O(\log n)\) rounds, w.h.p., in the hybrid model. The algorithm requires global capacity \(O(\log ^2 n)\), w.h.p.
We remark that it is unclear whether our algorithm also helps compute a minimum spanning tree, which is easily possible with earlier overlay construction algorithms. It seems that in order to do so, we would need different techniques.
1.2.4 Biconnected components
We call an undirected graph H biconnected if every two nodes \(u,v \in V\) are connected by two directed node-disjoint paths. Intuitively, biconnected graphs are guaranteed to remain connected even if a single node fails. Our goal is to find the biconnected components of G, which are the maximal biconnected subgraphs of G. Note that cut vertices,i.e., nodes whose removal increases the number of connected components, are contained in multiple biconnected components. In Sect. 4.4, we show how to apply the PRAM algorithm of Tarjan and Vishkin [56] to compute the biconnected components of a graph to the hybrid model. The algorithm relies on a spanning tree computation, which allows us to use Theorem 1.4 to achieve a runtime of \(O(\log n)\), w.h.p.
Theorem 1.5
Let \(G = (V, E)\) be a weakly connected directed graph. There is a randomized algorithm that computes the biconnected components of (the undirected version of) G in \(O(\log n)\) rounds, w.h.p., in the hybrid model. Furthermore, the algorithm computes whether G is biconnected and, if not, determines its cut nodes and bridge edges. The algorithm requires global capacity \(O(\log ^5 n)\), w.h.p.
2 Mathematical preliminaries
Before we formally define the problems considered in this article, we first review some basic concepts from graph theory, probability theory, and in particular, the analysis of random walks.
2.1 Basic terms from graph theory
We begin with some general terms that will be used throughout this article. Recall that \(G = (V,E)\) is a directed graph with \(n := \vert V\vert \) nodes and \(m := \vert E\vert \) edges. A node’s outdegree denotes the number of outgoing edges, i.e., the number of identifiers it stores. Analogously, its indegree denotes the number of incoming edges, i.e., the number of nodes that store its identifier. A node’s degree is the sum of its in- and outdegree, and the graph’s degree is the maximum degree of any node, which we denote by d. We say that a graph is weakly connected if there is a (not necessarily directed) path between all pairs of nodes. For a node pair \(v,w \in V\), we let \(\textsf{dist}(v,w)\) we let be the length of a shortest path between v and w in the undirected version of G, i.e., the minimum number of hops to get from v to w. A graph’s diameter is the length of the longest shortest path in G. Last, for a graph G we define \(G^{\ell } := (V,E_{\ell })\) to be the \(\ell \)-walk graph of G, i.e., \(G^\ell \) is the multigraph where each edge \((v,w) \in E_{\ell }\) corresponds to an \(\ell \)-step walk in G. Note that a walk can visit the same edge more than once, so \(G^{\ell }\) must be a multigraph. For a subset \(S \subseteq V\), we denote \(\overline{S} := V \setminus S\). We define the cut \(c(S,\overline{S})\) as the set of all edges \((v,w) \in V\) with \(v \in S\) and \(w \in \overline{S}\). We define the number edges that cross a cut \(c(S,\overline{S})\) as \(O_S:=\vert c(S,\overline{S})\vert \).
2.2 Probability theory and combinatorics
In this section, we establish well-known bounds and tail estimates from probability theory and useful facts from combinatorics that help us analyze certain random events in our algorithms. The first bound is Markov’s inequality, which estimates the probability of a random variable reaching a certain value based on its expectation. It holds:
Lemma 2.1
(Markov’s inequality) Let X be a non-negative random variable and \(a>0\), then it holds:
While this inequality applies to various variables, it is not very precise. For more precise bounds, we heavily use the well-known Chernoff bound, another standard tool for analyzing distributed algorithms. In particular, we will use the following version:
Lemma 2.2
(Chernoff bound) Let \(X = \sum _{i=1}^n X_i\) for independent distributed random variables \(X_i \in \{0,1\}\) and \(\mathbb {E}(X) \le \mu _H\) and \(\delta \ge 1\).
Similarly, for \(\mathbb {E}(X) \ge \mu _L\) and \(0 \le \delta \le 1\) we have
Further, we use the union bound that helps us to bound the probability for many correlated events as long as all these events have a very small probability of happening. It holds:
Lemma 2.3
(Union bound) Let \(\mathcal {B} := B_1, \dots , B_m\) be a set of m (possibly dependent) events. Then, the probability any of the events in \(\mathcal {B}\) happens can be bounded as follows:
This bound is tremendously helpful when dealing with a polynomial number of bad events, say \(n^{c}\) many, that do not happen with high probability, say \(1-n^{c'}\) for some tunable constant \(c'\). If we choose this constant \(c'\) big enough, the union bound trivially implies that the probability of any bad event happening is \({n^{-c''}}\) for a constant \(c'' := c'-c\). Thus, if we can show that a specific event holds for a single node w.h.p., the union bound implies that it holds for all nodes w.h.p. However, if the number of events in question is superpolynomial, i.e., bigger than \(n^c\) for any constant c, the union bound alone is not enough to show that these events do not happen w.h.p. In this work, we need to make some statements about events that correlate to all possible subsets of nodes of a random graph. Since there are exponentially many of these subsets, we need to apply the union bound more carefully. Indeed, we can show the following technical lemma:
Lemma 2.4
(Cut-based union bound) Let \(G := (V,E)\) be a (multi-)graph with n nodes and m edges and let \(\mathcal {B} := \{\mathcal {B}_S \mid S \subseteq V \wedge \vert S\vert \le n/2\}\) a set of bad events.
Suppose that the following three properties hold:
-
1.
G has at most \(m \in O(n^{c_1})\) edges for some constant \(c_1>1\).
-
2.
For each \(\mathcal {B}_S\) it holds \({\textbf{Pr}\left[ \mathcal {B}_S\right] } \le e^{-c_2 O_S}\) for some constant \(c_2>0\).
-
3.
The minimum cut of G is at least \(\Lambda := 4\frac{c_1}{c_2}c_3\log n\) edges for some tunable constant \(c_3>1\).
Then, the probability any of the events in \(\mathcal {B}\) happens can be bounded by:
In other words, w.h.p. no event from \(\mathcal {B}\) occurs.
Proof
The core of this lemma is a celebrated result of Karger [36] that bounds the number of cuts (and therefore the number of subsets \(S \subset V\) with \(\vert S\vert \le n/2\) as one side of each cut must have fewer than n/2 nodes) with at most \(\alpha \Lambda \) outgoing edges by \(O(n^{2\alpha })\). More precisely, it holds:
Theorem 2.1
(Theorem 3.3 in [36], simplified) Let G be an undirected, unweighted (multi-)graph and let \(\Lambda >1\) be the size of a minimum cut in G. For an even parameter \(\alpha \ge 1\), the number of cuts with at most \(\alpha \Lambda \) edges is bounded by \(n^{2\alpha } \).
Thus, if the probability of a bad event for a set S exponentially depends on \(O_S\) (and not some constant c), a careful application of the union bound will give us the desired result. The idea behind the proof is to divide all subsets into groups based on the number of their outgoing edges. Then, we use Karger’s Theorem to bound the number of sets in a group and use the union bound for each group individually.
More precisely, let \(\textsf{Pow}(V)\) denote all possible subsets of V. Then, we define \(\mathcal {S}_\alpha \in \textsf{Pow}(V)\) to be the set of all sets that have a cut of size \(c \in [\alpha \Lambda ,2\alpha \Lambda )\). Using this definition, we can show that the following holds by using the union bound and regrouping the sum:
Note that the upper limit \(\frac{m}{\Lambda }\) of the outermost sum is derived from the fact that at most m edges may cross any cut in the graph. Further note that that for each \(\alpha > 1\) it holds that \(\mathcal {S}_{\alpha } \subset \{S \subset V \mid O_S \le 2\alpha \Lambda \}\) by definition and therefore \(\vert \mathcal {S}_{\alpha }\vert \le \vert \{S \subset V \mid O_S \le 2\alpha \Lambda \}\vert \) Now we can apply Theorem 2.1 and see that
Here, inequality (8) followed from Theorem 2.1, everything else from the definition of \(S_{\alpha }\) and \(\mathcal {B}_S\). Finally, our specific choice of \(\Lambda \ge 4\frac{c_1}{c_2}c_3\log n\) comes into play. Plugging it into the exponent of our bound, we get:
To complete the proof, we need to bound \(\frac{m}{\Lambda }\). Per definition, it holds that \(m \le n^{c_1}\). Back in the formula, we get
This proves the lemma. \(\square \)
2.3 Random walks on regular graphs
Finally, we observe the behavior of (short) random walks on regular graphs and establish useful definitions and results. Starting with the most basic definition, a random walk on a graph \(G := (V, E)\) is a stochastic process \(\left( v_i \right) _{i \in \mathbb {N}}\) that starts at some node \(v_0 \in V\) and in each step moves to some neighbor of the current node. If G is \(\Delta \)-regular, the probability of moving from v to its neighbor w is  . Here, e(u, w) denotes the number of edges between u and w as G is a multigraph. We say that a \(\Delta \)-regular graph G (and the corresponding walk on its nodes) is lazy if each node has at least \(\frac{\Delta }{2}\) self-loops (and therefore a random walk stays at its current node with probability at least
. Here, e(u, w) denotes the number of edges between u and w as G is a multigraph. We say that a \(\Delta \)-regular graph G (and the corresponding walk on its nodes) is lazy if each node has at least \(\frac{\Delta }{2}\) self-loops (and therefore a random walk stays at its current node with probability at least  in each step). For \(v,w \in V\) let \(X^\ell _v(w, G)\) be the indicator for the event that an \(\ell \)-step random walk in G which started in v ends in w. Analogously, let \(X^1_v(w, G^\ell )\) be the indicator that a 1-step random walk in \(G^\ell \) which started in v ends in w. If we consider a fixed node v that is clear from the context, we may drop the subscript and write \(X^1(w, G^\ell )\) instead. Further, let \(P_\ell (v,w)\) be the exact number of walks of length \(\ell \) between v and w in G. Note that it holds \(P_1(v,w) = e(v,w)\). Given these definitions, the probability to move from v to w in \(G^\ell \) is given by the following lemma:
in each step). For \(v,w \in V\) let \(X^\ell _v(w, G)\) be the indicator for the event that an \(\ell \)-step random walk in G which started in v ends in w. Analogously, let \(X^1_v(w, G^\ell )\) be the indicator that a 1-step random walk in \(G^\ell \) which started in v ends in w. If we consider a fixed node v that is clear from the context, we may drop the subscript and write \(X^1(w, G^\ell )\) instead. Further, let \(P_\ell (v,w)\) be the exact number of walks of length \(\ell \) between v and w in G. Note that it holds \(P_1(v,w) = e(v,w)\). Given these definitions, the probability to move from v to w in \(G^\ell \) is given by the following lemma:
Lemma 2.5
Let G be a \(\Delta \)-regular graph and \(G^\ell \) its \(\ell \)-walk graph for some \(\ell > 1\) , then it holds:
Proof
The statement can be proved via an induction over \(\ell \), the length of the walk. For the base case, we need to show that 1-step random walk in G is equivalent to picking an outgoing edge in \(G^1 := G\) uniformly at random. This follows trivially from the definition of a random walk. Now suppose that performing an \((\ell -1)\)-step random walk in G is equivalent to performing a 1-step walk in \(G^{\ell -1}\). Consider a node \(w \in V\) and let \(N_w\) denote its neighbors in G and witself. By the law of total probability, it holds:
Using the induction hypothesis we we can substitute \({\textbf{Pr}\left[ X^{\ell -1}(u,G) = 1\right] }\) for \({\textbf{Pr}\left[ X^{1}(u,G^{\ell -1}) = 1\right] }\) and get:
Recall that G is a multigraph, and there can be more than one edge between each u and w and e(u, w) denote the number of edges between u and w for every \(u \in N_w\). Since we defined that \(w \in N_w\), the value e(w, w) counts w’s self-loops. Since G is \(\Delta \)-regular, the probability that a random walk at node u moves to w is exactly \(\frac{e(u,w)}{\Delta }\). Back in the formula, we get:
Finally, note that \(\sum _{u \in N_w} {P_{\ell -1}(v,u)}\cdot {e(u,w)}\) counts all paths of length exactly \(\ell \) from v to w in G. This follows because each path \(P := (e_1, \ldots , e_\ell )\) from u to w can be decomposed into a path \(P' := (e_1, \ldots , e_{\ell -1})\) of length \(\ell -1\) to some neighbor of w (or w itself) and the final edge (or self-loop) \(e_\ell \). Thus, it follows that:
This was to be shown.
\(\square \)
In other words, the multigraph \(G^\ell \) is \(\Delta ^\ell \)-regular and has edge (v, w) for every walk of length \(\ell \) between v and w.
Our analysis will heavily rely on the conductance of the communication graph. The conductance of set \(S \subset V\) is the ratio of its outgoing edges and all its edges. The conductance \(\Phi _{G}\) of a graph G is the minimal conductance of every subset that contains less than n/2 nodes. Formally, the conductance is defined as follows:
Definition 1
(Conductance) Let \(G := (V,E)\) be a connected \(\Delta \)-regular graph and \(S \subset V\) with \(\vert S\vert \le \frac{\vert V\vert }{2}\) be any subset of G with at most half its nodes. Then, the conductance \(\Phi _{G}(S) \in (0,1)\) of S is
We further need the notion of small-set conductance, which is a natural generalization of conductance. Instead of denoting the minimum conductance of all sets smaller than n/2, small-set conductance only considers sets of size \(\frac{\delta \vert V\vert }{2}\) for any \(\delta \in (0,1]\). Analogous to the conductance, it is defined as follows:
Definition 2
(Small-set conductance) Let \(G := (V,E)\) be a connected \(\Delta \)-regular graph and \(S \subset V\) with \(\vert S\vert \le \frac{\delta \vert V\vert }{2}\) be any subset of G. The small-set conductance \(\Phi _{\delta }\) of G is
We further need two well-known facts about the conductance. First, we see that we can relate the minimum conductance of a \(\Delta \)-regular graph to its minimum cut. It holds:
Lemma 2.6
(Minimum conductance) Let \(G := (V,E)\) be any \(\Delta \)-regular connected graph with minimum cut \(\Lambda \ge 1\). Then for all \(\delta \in (0,1]\) it holds:
Proof
Consider the set S with \(\vert S\vert \le \frac{\delta n}{2}\) that minimizes \(\Phi (S')\) among all sets \(\vert S'\vert \le \frac{\delta }{2}n\). Then, it holds by the definition \(\Phi _\delta (G)\), S and \(\Lambda \) that:
\(\square \)
Second, we show that a constant conductance implies a logarithmic diameter if the graph is regular. It holds:
Lemma 2.7
(High conductance implies low diameter) Let \(G := (V,E)\) be any lazy bi-directed \(\Delta \)-regular graph with conductance \(\Phi \), then the diameter of G is at most \(O(\Phi ^{-2}\log n)\).
Proof
We will prove this lemma by analyzing the distribution of random walks on G. Let \(v,w \in V\) be two nodes of G and let \(\ell >0\) be an integer. We denote \(p^{\ell }(v,w)\in [0,1]\) as the probability that an \(\ell \)-step random walk that starts in v, ends in w. Note that \(p^{\ell }(v,w)>0\) implies that there must exist path of length \(\ell \) from v to w. Following this argument, if it holds \(p^{\ell }(v,w)>0\) for all pairs \(v,w \in V\), then the graph’s diameter must be smaller or equal to \(\ell \). Thus, in the following, we will show that for \(\ell \in \Omega (\Phi _G^{-2}\log {n})\) we have \(p^{\ell }(v,w)>0\) for all pairs of nodes. First, we note that a sharp upper bound on the probabilities also implies a lower bound.
Claim 1
Let \(v \in V\) be a node with \(p^{\ell }(v,w) \le \frac{1}{n}+\frac{1}{n^2}\) for all \(w \in V\). Then, it holds
Proof
As each random walk must end some node \(w \in V\), we have:
Together with our upper bound of \(\frac{1}{n}+\frac{1}{n^2}\), we can now derive the following lower bound
\(\square \)
Thus, a low enough maximal probability implies a positive lower bound. Our next goal is to find such a precise upper bound. We will use well-known concepts from the analysis of Markov chains to do this. We define \(\pi := \left( \pi _v\right) _{v \in V}\) as the stationary distribution of a random walk on G. For any \(\Delta \)-regular graph, it holds:
For a connected, bidirected, non-bipartite graph, the distribution of possible endpoints of a random walk converges towards its stationary distribution. For a fixed \(\ell \), we define the relative pointwise distance as:
This definition describes how far the distribution is from the stationary distribution after \(\ell \) steps. Given this definition, it is easy to see that the following claim holds:
Claim 2
Suppose that \(\rho _G(\ell ) < \frac{1}{n}\), then it holds for all \(v,w \in V\) that
Proof
For contradiction, assume that the statement is false. Then, there is a pair \(v',w' \in V\) with
for some \(c>1\). Further, it must hold that
This is the desired contradiction. \(\square \)
Thus, we will determine an upper bound for \(\rho _G(\ell )\) in the remainder. In an influential article, Jerrum and Sinclair proved that relative pointwise distance after \(\ell \) steps is closely tied to the graph’s conductance. In particular, they showed that:
Lemma 2.8
(Theorem 3.4 in [54], simplified) Let G be lazy, regular, and connected. Further, let \(\pi \) be its stationary distribution of a random walk. Then for any node \(v \in V\), the relative pointwise distance satisfies
With \(\pi ^* := \max _{v \in V}\{\pi _v\}\)
In the original lemma, the underlying Markov chain must be ergodic, i.e., every state is reachable from every other state, and time-reversible, i.e., it holds \(p^\ell (v,w) = p^\ell (w,v)\). The first property is implied by the fact that the graph is connected, so every node is reachable. The latter follows from the facts that the graph is bi-directed and regular, so it holds \(p_1(v,w) = \frac{e(v,w)}{\Delta } = \frac{e(w,v)}{\Delta } = p_1(w,v)\). Further, note that for our graph, we have \(\pi ^* := \frac{1}{n}\). Plugging this and \(\ell := 4\Phi ^{-2}\log {n}\) in the formula, we get:
Here, inequality (57) follows from the well-known fact that  for any \(x>1.5\), which clearly holds as \(\Phi _G^2 < 1\). Thus, following Claims 1 and 2, all probabilities are strictly positive after \(\ell \) steps of the random walk and the diameter must be smaller \(\ell \). \(\square \)
for any \(x>1.5\), which clearly holds as \(\Phi _G^2 < 1\). Thus, following Claims 1 and 2, all probabilities are strictly positive after \(\ell \) steps of the random walk and the diameter must be smaller \(\ell \). \(\square \)
For our analysis, it will be crucial to observe the (small-set) conductance of \(G^\ell \) for a constant \(\ell \). However, the standard Cheeger inequality (see, e.g., [53] for an overview) that is most commonly used to bound a graph’s conductance with the help of the graph’s eigenvalues does not help us in deriving a meaningful lower bound for \(\Phi _{G^\ell }\). In particular, it only states that \(\Phi _{G^\ell } = \Theta (\ell \Phi _{G}^{2})\). Thus, it only provides a useful bound if \(\ell = \Omega (\Phi _{G}^{-1})\), which is too big for our purposes, as \(\Omega (\Phi _{G}^{-1})\) is only constant if \(\Phi _{G}\) is constant. More recent Cheeger inequalities shown in [42] relate the conductance of smaller subsets to higher eigenvalues of the random walk matrix. At first glance, this seems helpful, as one could use these to show that at least the small sets start to be more densely connected and then, inductively, continue the argument. Still, even with this approach, constant length walks are out of the question as these new Cheeger inequalities introduce an additional tight \(O(\log n)\) factor in the approximation for these small sets. Thus, the random walks would need to be of length \(\Omega (\log n)\), which is still too much to achieve our bounds. Instead, we use the following result by Kwok and Lau [39], which states that \(\Phi _{G^\ell }\) improves even for constant values of \(\ell \). Given this bound, we can show that benign graphs increase their (expected) conductance from iteration to iteration. In the following, we prove Lemma 2.9 by outlining the proofs of Theorem 1 and 3 in [39]. It holds that:
Lemma 2.9
(Conductance of \(G^\ell \), based on Theorem 1 and 3 in [39]) Let \(G = (V,E)\) be any connected \(\Delta \)-regular lazy graph with conductance \(\Phi _{G}\) and let \(G^\ell \) be its \(\ell \)-walk graph. For a set \(S \subset G\) define \(\Phi _{G^\ell }(S)\) as the conductance of S in \(G^\ell \). Then, it holds:
Further, if \(\vert S\vert \le \delta n\) for any \(\delta \in (0,\frac{1}{2}]\), we have
Proof
Before we go into the details, we need another batch of definitions from the study of random walks and Markov chains. Let \(G:=(V,E)\) be a \(\Delta \)-regular, lazy graph and let \(A_G \in \mathbb {R}^{n \times n}\) the stochastic random walk matrix of G. Each entry \(A_G(v,w)\) in the matrix has the value \(\frac{e(v,w)}{\Delta }\) where e(v, w) denotes the number of edges between v and w (or self-loops if \(v=w\)). Likewise \(A^\ell _G\) is the random walk matrix of \(G^\ell \) where each entry has value \(\frac{P_\ell (v,w)}{\Delta ^\ell }\). Note that both \(A_G\) and \(A^\ell _G\) are doubly-stochastic, meaning that their rows and columns sum up to 1. For these types of weighted matrices, Kwok and Lau define the expansion \(\varphi (S)\) of a subset \(S \subset V\) as follows:
For regular graphs (and only those), this value is equal to the conductance \(\Phi _{G}(S)\) of S, which we observed before. The following elementary calculation can verify this claim:
Therefore, the claim that Kwok and Lau make for the expansion also holds for the conductance of regular graphsFootnote 5. The proof in [39] is based on the function \(C^{(\ell )}(\vert S\vert )\) introduced by Lovász and Simonovits [44]. Consider a set \(S \subset V\), then Lovasz and Simonovits define the following curve that bounds the distribution of random walk probabilities for the nodes of S.
Here, the vector \(p_S\) is the so-called characteristic vector of S with \(p_i = \frac{1}{\vert S\vert }\) for each \(v_i \in S\) and 0 otherwise. Further, the term \((A^{\ell } p)_i\) denotes the \(i^{th}\) value of the vector \(A^{\ell } p_S\). Lovász and Simonovits used this curve to analyze the mixing time of Markov chains. Kwok and Lau now noticed that it also holds that:
Lemma 2.10
(Lemma 6 in [39]) It holds:
Based on this observation, they deduce that a bound for \(1-C^{(\ell )}(S)\) doubles as a bound for \(\Phi _{G^\ell }\). In particular, they can show the following bounds for \(C^{(\ell )}(\vert S\vert )\):
Lemma 2.11
(Lemma 7 in [39]) It holds
We refer the interested reader to Lemma 7 of [39] for the full proof with all necessary details. For the next step, we need the following well-known inequality:
Lemma 2.12
For any \(t>1\) and \(z \le \frac{1}{2}\), it holds:
Now assume that G does not already have a constant conductance of \(\Phi (G) = \frac{1}{2}\). Plugging this assumption and the two insights by Kwok and Lau together, we get
The last inequality follows from the fact that \(\sqrt{\ell }\Phi _{G}\) is at most \(\frac{1}{2}\). The second part of the theorem can be derived similarly. Again, we observe an auxiliary lemma by Kwok and Lau and see:
Lemma 2.13
(Lemma 10 in [39]) Let S be set of size at most \(\delta n\) with \(\delta \in [0,\frac{1}{4})\). Then, it holds:
Proof
Analogously to the previous case, we get for \(\Phi _{2\delta }(G) \le \frac{1}{4}\) that
In the last inequality, we used Lemma 2.12 with \(z=2\Phi _{2\delta }(G)\). \(\square \)
Finally, these two lower bounds are too loose for graphs (and subsets) that already have good conductance. Instead we require that \(\Phi _{G^\ell }(S)\) is at least as big as \(\Phi _{G}(S)\). Note that this is not necessarily the case for all graphs. Instead, we must use the fact that our graphs are lazy. We show this in the following lemma:
Lemma 2.14
Let \(G := (V,E)\) be any connected \(\Delta \)-regular lazy graph with conductance \(\Phi _{G}\) and let \(G^\ell \) be its \(\ell \)-walk graph. For a set \(S \subset G\) define \(\Phi _{G^\ell }(S)\) the conductance of S in \(G^\ell \). Then, it holds:
Proof
Our technical argument is based on the following recursive relation between \(C^{(\ell +1)}\) and \(C^{(\ell )}\), which was (in part) already shown in [44]: \(\square \)
Lemma 2.15
(Lemma 1.4 in [44]) It holds
Here, we use the abbreviation \(\hat{\vert S\vert } := \max \{\vert S\vert , n-\vert S\vert \}\). The remainder of the proof is based on two claims. First, we claim that \(C^{(\ell )}(\vert S\vert )\) is monotonically increasing in \(\ell \).
Claim 3
It holds \(C^{(\ell )}(\vert S\vert ) \le C^{(\ell -1)}(\vert S\vert )\)
Proof
This fact was already remarked in [44] based on an alternative formulation. However, given that \(C^{(\ell )}\) is concave, it holds that for all values \(\gamma , \beta \ge 0\) with \(\gamma \le \beta \) that
And thus, together with Lemma 2.15, we get:
Here, we chose \(\beta =2\Phi _{G}\) and \(\gamma =0\) and applied Eq. 81. This proves the first claim. \(\square \)
Second, we claim that \(C^{(1))}(\vert S\vert )\) is equal to \(1-\Phi _{G}(S)\) as long as the graph we observe is lazy.
Claim 4
It holds \(C^{(1)}(\vert S\vert ) = 1-\Phi _{G}(S)\)
Proof
For this claim (which was not explicitly shown in [39], but implied in [44]) we observe
and find the assignment of the \(\delta \)’s that maximizes the sum. Lovasz and Simonovits already remarked that it is maximized by setting \(\delta _i=1\) for all \(v_i \in S\). However, we prove it here since there is no explicit lemma or proof to point to in [44]. First, we show that all entries \((A_Gp_S)_i\) for nodes \(v_i \in S\) are least \(\frac{1}{2\vert S\vert }\) and all entries \((A_Gp_S)_{i'}\) for nodes \(v_{i'} \not \in S\) are at most \(\frac{1}{2\vert S\vert }\). We begin with the nodes in S. Given that G is \(\Delta \)-regular and lazy, we have for all \(v_i \in S\) that
Here, \({p_S}_i = \frac{1}{\vert S\vert }\) follows because \(v_i \in S\) per definition. The inequality \(A_G(v_i,v_i) \ge \frac{1}{2}\) follows from the fact that A is lazy and each node has a self-loop with probability \(\frac{1}{2}\). As a result, the entry \((A_Gp_S)_i\) for \(v_i \in S\) has at least a value of \(\frac{1}{2\vert S\vert }\), even if it has no neighbors in S. On the other hand, we have for all nodes \(v_{i'} \not \in S\) that
This follows from excluding all entries \(p_j\) with \(v_j \not \in S\). Note that for these values, it holds \(p_j=0\). Further, Since A is \(\Delta \)-regular and lazy, each node \(v_{i'} \not \in S\) has at most \(\frac{\Delta }{2}\) edges to nodes in S.
Thus, the corresponding value \((A_Gp_S)_i\) of any \(v_i \in S\) is at least as big as value \((A_Gp_S)_{i'}\) of \(v_{i'} \not \in S\). By a simple greedy argument, we now see that \(\sum _{i=1}^n \delta _i (A^{\ell } p_S)_i\) is maximized by picking \(\delta _i = 1\) for all nodes in S: To illustrate this, suppose that there is a choice of the \(\delta \)’s such that \(\sum _{i=1}^n \delta _i (A_Gp_s)_i\) is maximized and it holds \(\delta _i < 1\) for some \(v_i \in S\). Since no \(\delta \) can be bigger than 1 and the \(\sum _{i = 1}^n \delta _i = \vert S\vert \) there must be a \(v_{i'} \not \in S\) with \(\delta _{i'}>0\). Since \((A_Gp_S)_i \ge (A_Gp_S)_{i'}\) decreasing \(\delta _{i'}\) and increasing \(\delta _{i}\) does not decrease the sum. Thus, choosing \(\delta _i=1\) for all \(v_i \in S\) must maximize the term \(\sum _{i=1}^n \delta _i (A_Gp_s)_i\). This yields:
Here, the value \({O_S}\) denotes the edges leaving S. Given that the graph is \(\Delta \)-regular, the term \(\Delta \vert S\vert -{O_S}\) counts all edges in S. This was to be shown. \(\square \)
If we combine our two claims, the lemma follows. \(\square \)
Thus, \(\Phi _{G^\ell }(S)\) is at least as big as \(\Phi _{G}(S)\). Together with the previous lemmas, this proves Lemma 2.9. \(\square \)
3 The overlay construction algorithm
In this section, we present our algorithm to construct a well-formed tree in \(O(\log n)\) time, w.h.p., and give the proof to establish the correctness of Theorem 1.1. To the best of our knowledge, our approach is different from all previous algorithms for our problem [3, 4, 30, 31] in that it does not use any form of clustering to contract large portions of the graph into supernodes. On a high level, our algorithm progresses through \(O(\log n)\) iterations, where the next graph is obtained by establishing random edges on the current graph. More precisely, each node of a graph simply starts a few random walks of constant length and connects itself with the respective endpoints. The next graph only contains the newly established edges. We will show that after \(O(\log n)\) iterations of this simple procedure, we reach a graph with diameter \(O(\log n)\). One can easily verify that this strategy does not trivially work on any graph, as the graph’s degree distributions and other properties significantly impact the distribution of random walks. However, as it turns out, we only need to ensure that the initial graph has some nice properties to obtain well-behaved random walks. More precisely, throughout our algorithm, we maintain that the graph is benign, which we define as follows.
Definition 3
(Benign graphs) Let \(G:= (V, E)\) be a simple undirected graph and \(\Lambda \in \Omega (\log n)\) and \(\Delta \ge 64\Lambda \) be two values (with big enough constants hidden by the \(\Omega \)-Notation). Then, we call G benign if and only if it has the following three properties:
-
1.
(G is \(\Delta \)-regular) Every node \(v \in V\) has exactly \(\Delta \) in- and outgoing edges (which may be self-loops).
-
2.
(G is lazy) Every node \(v \in V\) has at least
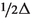 self-loops.
self-loops. -
3.
(G has a \(\Lambda \)-sized minimum cut) Every cut \(c(S,\overline{S})\) with \(S \subset V\) has at least \(\Lambda \) edges.
The properties of benign graphs are carefully chosen to be as weak as possible while still ensuring the correct execution of our algorithm. A degree of \(\Delta \in \Omega (\log n)\) is necessary to keep the graph connected. If we only had a constant degree, a standard result from random graphs implies that, w.h.p., there would be nodes disconnected from the graph when sampling new neighbors. If the graphs were not lazy, many theorems from the analysis of Markov chains would not hold as the graph could be bipartite, which would greatly complicate the analysis. This assumption only slows down random walks by a factor of 2. Lastly, the \(\Lambda \)-sized cut ensures that the graph becomes more densely connected in each iteration, w.h.p. In fact, with constant-sized cuts, we cannot easily ensure this property when using random walks of constant length.
3.1 Algorithm description
We will now describe the algorithm in more detail. Recall that throughout this section, we will assume the P2P-\(\textsf{CONGEST}\) model. Further, we assume that the initial graph has maximum degree d and is connected. Given these preconditions, the algorithm has four input parameters \(\ell ,\Delta ,\Lambda \), and L known to all nodes. Recall that \(L \in \Theta (\log n)\) is an upper bound on \(\log n\) and determines the runtime. The value \(\ell \in \Omega (1)\) denotes the length of the random walks, \(\Delta \in O(\log n)\) is the desired degree, and \(\Lambda \in O(\log n)\) denotes the (approximate) size of the minimum cut. All of these parameters are tunable and the hidden constants need to be chosen big enough for the algorithm to succeed, w.h.p. In particular, the value of \(\Lambda \) will determine the success probability. We discuss this in more detail in the analysis.
Our algorithm consists of three stages. In the first stage, we ensure that the initial graph is benign by adding additional edges to each node. In the second stage, which is the main part of the algorithm, we continuously increase the graph’s conductance to random walks while assuring that it stays benign. Finally, in the last stage, we exploit the graph’s logarithmic diameter to construct a well-formed tree in \(O(\log n)\) time. This phase primarily uses techniques from [3, 4, 30, 31]. We now describe each phase in more detail.
Stage 1: Initialization
Before the first iteration, we need to prepare the initial communication graph to comply with parameters \(\Delta \) and \(\Lambda \), i.e., we must turn it into a benign graph. W.l.o.g., we can assume that G is a simple bidirected graph. Otherwise, all of its multi-edges can be merged into a single edge, and all directed edges \((v,w) \in E\) can be bi-directed by sending v’s identifier to w. Next, we deal with the graph’s regularity. Arguably, the easiest way to make a graph of maximum degree d regular is adding \(d-d(v)\) self-loops to each node \(v \in V\), so all nodes have the same degree. However, this is not possible in general, as in our model, each node can only send and receive \(O(d(v)\log {n})\) messages per round, which might be lower than d. Thus, we need another approach. For this, we need the concept of virtual nodes \(V'\), which are simulated by the nodes of graph G. A virtual node \(v' \in V'\) is simulated by \(v \in V\) and has its own virtual identifier of size \(O(\log {n})\). This virtual identifier consists of the original node’s identifier combined with a locally unique identifier. For the simulation, any message intended for \(v'\) will first be sent to v (using v’s identifier) and then locally passed to \(v'\). Given this concept, we show that the node in graph \(G:= (V, E)\) can simulate a graph \(G':= (V', E')\) with \(\vert V'\vert = 2\vert E\vert \) that only consists of virtual nodes and edges between them. We construct \(V'\) through the following process:
-
1.
First, For each edge \(\{v,w\} \in E\) both v and w create and simulate virtual nodes \(v'\) and \(w'\) and add them to \(V'\).
-
2.
Second, v and w connect the virtual nodes \(v'\) and \(w'\) via an edge \(\{v',w'\}\) by exchanging the respective identifiers. This ensures that for each edges \((v,w) \in E\), there is an edge \((v',w') \in E'\).
-
3.
Finally, all virtual nodes of a real node v are connected in a cycle. For this, v first sorts its virtual nodes in an arbitrary order \( v'_1, \dots , v'_{d(v)}\). Then, it adds bidirected edges between \(v_1\) and \(v_{d(v)}\) and every consecutive pair of nodes in the order.
The resulting graph \(G'\) is connected and each node \(v' \in V'\) has at most 3 edges. To be precise, it has exactly one edge to another virtual node \(w' \in V'\) simulated by \(v \ne w \in V\) and at most two connections to the predecessor and successor in the cycle of virtual nodes simulated by v. Further, each original node simulates exactly d(v) virtual nodes, so as long as each virtual node receives at most \(O(\log n)\) messages (which is the case in our algorithm), this is possible in our model. Later, we will show how to revert the simulation and obtain a well-formed tree for the original node set V.
Given that the graph is regular, we need to increase its degree and minimal cut. Since the input graph has a maximum degree of 3, this is quite simple as we can assume \(6\Lambda \le \Delta \) by choosing \(\Delta \) big enough. Given this assumption, the graph can be turned benign in 2 steps:
-
1.
First, all edges are copied \(\Lambda \) times to obtain the desired minimum cut. After this step, each node has at least \(\Lambda \) edges to other nodes and at least \(\Lambda \) edges cross each cut.
-
2.
Then, each node adds self-loops until its degree is \(\Delta \) and each node has \(\frac{\Delta }{2}\) self-loops. As we chose \(6\Lambda \le \Delta \), this is always possible.
Thus, the resulting graph is benign. Further, note that the resulting graph is a multi-graph while G is a simple graph.
Stage 2: Construction of a Low Diameter Overlay
Let now \(G_0 = (V', E_0)\) be the resulting benign graph. The algorithm proceeds in iterations \(1, \dots , L\). In each iteration, a new communication graph \(G_i = (V', E_i)\) is created through sampling \(\frac{\Delta }{8}\) new neighbors via random walks of length \(\ell \). Each node \(v \in V'\) creates \(\frac{\Delta }{8}\) messages containing its own identifier, which we call tokens. Each token is randomly forwarded for \(\ell \) rounds in \(G_i\). More precisely, each node that receives a token picks one of its incident edges in \(G_i\) uniformly at random and sends the token to the corresponding node.Footnote 6 This happens independently for each token. If v receives less than \(\frac{3}{8}\Delta \) tokens after \(\ell \) steps, it sends its identifier back to all the tokens’ origins to create a bidirected edge. Otherwise, it picks \(\frac{3}{8}\Delta \) tokens at random (without replacement)Footnote 7. Since the origin’s identifier is stored in the token, both cases can be handled in one communication round. Finally, each node adds self-loops until its degree is \(\Delta \) again. The whole procedure is given in Fig. 1 as the method CreateExpander(\(G_0,\ell ,\Delta ,\Lambda ,L\)). The subroutine MakeBenign(\(G_0,\ell ,\Delta ,\Lambda \)) add edges and self-loops to make the graph comply with Definition 3 (i.e., it implements the first stage). Our main observation is that after \(L = O(\log n)\) iterations, the resulting graph \(G_L\) has constant conductance, w.h.p., which implies that its diameter is \(O(\log n)\). Furthermore, the degree of \(G_L\) is \(O(\Delta )\) by construction. Finally, if we add any virtual nodes in the first stage, we can now merge them back into a single node (with all connections of all its virtual nodes). For this, we simply transform each edge \((v',w') \in E_L\) between two virtual nodes \(v',w'\) to an edge (v, w) between two original nodes \(v,w \in V\). This produces a graph with the same degree distribution as G and can only decrease the diameter further. We denote this graph as \( G'_L\).
Stage 3: Finalization
To obtain a well-formed tree \(T_G\), perform a BFS on \( G'_L\) starting from the node with the lowest identifier. Since a node cannot locally check whether it has the lowest identifier, the implementation of this step is slightly more complex. The algorithm proceeds for \(L \in O(\log n)\) rounds. In the first round, every node creates a token message that contains its identifier. Then, it sends the token to all its neighbors. For all remaining rounds \(1, \ldots , L\), every node that receives one or more tokens only forwards the token with the lowest identifier to all its neighbors and drops all others. Since the graph’s diameter is \(O(\log n)\), all nodes must have received the lowest identifier at least once after these \(L \in O(\log n)\) rounds. Finally, each node v marks the edge (v, w) over which it first received the token with the lowest identifier. Ties can be broken arbitrarily. If the node itself has the smallest identifier, it does not mark any edge. All marked edges then constitute a tree T with degree \(O(\Delta )\) and diameter \(O(\log n)\). Note that this process requires \(O(\Delta )\) messages per node and round, as each node sends at most one token to all its neighbors per round. To transform this tree T into a well-formed tree, we perform the merging step of the algorithm of [30, Theorem 2]. This deterministic subroutine transforms any tree of degree \(O(\Delta )\) into a well-formed tree of degree \(O(\log n)\) in \(O(\log n)\) rounds.
To make this article self-contained, we sketch the approach of [30, Theorem 2] in the remainder. The algorithm first transforms T into a constant-degree child-sibling tree [4], in which each node arranges its children as a path and only keeps an edge to one of them. For each inner node \(w \in V\) let \(w_1, \dots , w_{d^{+}(w)}\) denote its children in T sorted by increasing identifier. Now v only keeps the child with the lowest identifier and delegates the others as follows: Each \(w_i \in N(w)\) with \(i>1\) changes its parent to be its predecessor \(w_{i-1}\) on the path and stores its successor \(w_{i+1}\) as a sibling (if it exists). In the resulting tree, each node stores at most three identifiers: a parent and possibly a sibling and a child. Since we can interpret the sibling of a node as a second child, we obtain a binary tree. This transformation takes O(1) rounds and requires \(O(\Delta )\) communication as each node needs to send two identifiers to its children.
Note that the tree’s diameter has now been increased by a factor of \(O(\Delta )\). Based on this binary tree, we construct a ring of virtual nodes using the so-called Euler tour technique (see, e.g., [20, 30, 56]). Consider the depth-first traversal of the tree that visits the children of each node in order of increasing identifier. A node occurs at most three times in this traversal. Let each node act as a distinct virtual node for each such occurrence and let \(k\le 3n\) be the number of virtual nodes. More specifically, every node v executes the following steps:
-
1.
v creates virtual nodes \(v^{0}, \dots , v^{d(v)-1}\) where \(v^i\) has the virtual identifier \(id(v^i) := v \circ i\). Intuitively, the node \(v^0\) corresponds to the traversal visiting v from its parent. Analogously, each \(v^{i}\) is the visit from child \(w_i\).
-
2.
v sends the identifier of \(v^0\) and \(v^{d(v)-1}\) to its parent. Note that \(v^0\) and \(v^{d(w)-1}\) may be the same virtual node if v has no children.
-
3.
Let \(w_{i}^0\) and \(w_{i}^{d(w)-1}\) be the identifier received from \(w_i\), i.e., the \(i^{th}\) child of v. Then v sets \(w_{i}^0\) as the successor of \(v^{i-1}\) and \(w_{i}^{d(w)-1}\) as the predecessor of \(v^i\). In other words, \(v^{i-1}\) and \(v^i\) are connected to the first and last virtual node of \(w_i\).
-
4.
Finally, each virtual node introduces itself to its predecessor and successor.
Therefore, the nodes can connect their virtual nodes into a ring in O(1) rounds by sending at most two messages per edge in each round. Next, we use the Pointer jumping technique (see, e.g., [20, 30, 56]) to quickly add chords (i.e., shortcut edges) to the ring. To be precise, the virtual nodes execute the following protocol for \(L \in O(\log n)\) rounds:
-
1.
Let \(l_0\) and \(r_0\) be the predecessor and successor of v in the ring. In the first round of pointer jumping, v sends \(l_0\) to \(r_0\) and vice versa.
-
2.
In round \(t>0\), each node receives an identifier \(l_{t-1}\) and \(r_{t-1}\) sent in the previous round. It sets \(l_{t}\) to the identifier received from \(l_{t-1}\) and \(r_t\) to the identifier received from \(r_{t-1}\). Finally, it sends \(l_t\) to \(r_t\) and vice versa.
A simple induction reveals that the distance between these neighbors (w.r.t the ring) doubles from round to round (until the distance exceeds the number of virtual nodes k). Based on this observation, it is not hard to show that after the L rounds, the graph’s diameter has reduced to \(O(\log n)\) while the degree has grown to \(O(\log n)\). A final BFS from the node of the lowest identifier then yields our desired well-formed tree \(T_G\), which concludes the algorithm.
With further techniques that exploit the structure of the chords, the degree can be reduced to 6. For details, we refer to [30, Theorem 2]. Another possibility to achieve a constant degree is the algorithm by Aspnes and Wu [4]. This algorithm requires a graph of outdegree 1—which simply is a by-product of the BFS—and requires \(O(W+\log n)\) time, w.h.p. The term W denotes the length of the node identifiers, which is also \(O(\log n)\) in our case. Although the algorithm is simple, elegant, and has the desired runtime, we do not use it as a black box as it would lead to problems with some applications. We need to create a well-formed tree for subgraphs with \(n' < n\) nodes for some of the applications and require that the runtime is logarithmic in \(n'\) and not n. Without additional analysis, the algorithm by Aspnes and Wu would still take \(O(\log n)\) time, w.h.p., whereas the approach sketched above always finishes in \(O(\log {n'})\) time.
3.2 Analysis of CreateExpander
The main challenge of our analysis is to show that after \(L \in O(\log n)\) iterations, the final graph \(G_{L}\) has a diameter of \(O(\log n)\). We will conduct an induction over the graphs \(G_1, \ldots , G_L\) to show this. Our main insight is that—given the communication graph is benign—we can use short random walks of constant length to iteratively increase the graph’s conductance until we reach a graph of low diameter. In the following, we will abuse notation and refer to the virtual nodes \(V'\) used in this stage of the algorithm as V. We show the following:
Lemma 3.1
Let \(G_0 := (V,E_0)\) a benign (multi-)graph with n nodes and \(O(n^3)\) edges. Let \(L:=3\log n\) and \(\Lambda := 6400\lambda \log n\) for some tunable \(\lambda >1\). Then, it holds:
Intuitively, this makes sense as the conductance is a graph property that measures how well-connected a graph is, and—since the random walks monotonically converge to the uniform distribution—the newly sampled edges can only increase the graph’s connectivity. Our formal proof is structured into four steps: First, we show that w.h.p. each node receives and sends at most \(O(\Delta )\) messages in each round. Thus, no messages are dropped during the execution of the algorithm. With this technicality out of the way, we show that the conductance of \(G_{i+1}\) increases by a factor of \(\Omega (\sqrt{\ell })\) w.h.p. if \(G_i\) is benign. Furthermore, we show that each \(G_{i+1}\) is benign if \(G_i\) is benign. Finally, we use the union bound to tie these facts together and prove Theorem 1.1.
3.2.1 Bounding the communication complexity
Before we go into the proof’s more intricate details, let us first prove that all messages are successfully sent during the algorithm’s execution. Remember that we assume the nodes have a communication capacity of \(O(\log n)\). Thus, a node can only send and receive \(O(\log n)\) messages as excess messages are dropped arbitrarily. To prove that no message is dropped, we must show that no node receives more than \(O(\log n)\) random walk tokens in a single step. However, this is a well-known fact about the distribution of random walks:
Lemma 3.2
(Also shown in [16, 18, 52]) For a node \(v \in V\) and an integer t, let X(v, t) be the random variable that denotes the number of tokens at node v in round t. Then, it holds \({\textbf{Pr}\left[ X(v,t) \ge \frac{3\Delta }{8}\right] } \le e^{-\frac{\Delta }{12}}\).
The lemma follows from the fact that each node receives \(\frac{\Delta }{8}\) tokens in expectation, given that all neighbors received \(\frac{\Delta }{8}\) tokens in the previous round. This holds because \(G_i\) is regular. Since all nodes start with \(\frac{\Delta }{8}\) tokens, the lemma follows inductively. Since all walks are independent, a simple application of the Chernoff bound with \(\delta =2\) (cf. Lemma 2.2) yields the result as
Note that this Lemma also directly implies that, w.h.p., all random walks create an edge as every possible endpoint receives less than \(\frac{3\Delta }{8}\) token and therefore replies to all of them. For our concrete value of \(\Delta \) it holds:
Lemma 3.3
Let \(\Delta \ge \Lambda := 6400 \lambda \log n\) for some tunable parameter \(\lambda > 1\). Then, for any round t it holds with probability at least \(1-{n^{-8\lambda }}\) that every node holds fewer than \(\frac{3}{8}\Delta \) tokens.
Proof
This follows directly from Lemma 3.2. Denote X(v, t) the number of tokens that node \(v \in V\) receives after t steps. Consider the event that node v receives more than \(\frac{3}{8}\Delta \) tokens. Recall that the probability for this event is
Now we use that \(\Delta \) is at least as big as \(\Lambda := 6400\lambda \log n\). Plugging this into the formula yields:
Finally, let \(\mathcal {B}\) the event that any node receives more than \(\frac{3}{8}\Delta \) tokens. By the union bound, we see
\(\square \)
Therefore, all nodes receive less than \(\frac{3\Delta }{8}\) tokens each round and the algorithm stays within the congestion bounds of our model with probability \(1-{n^{-8\lambda }}\). Since all iterations take \(\ell \cdot L \in O(\log n)\) rounds in total, the union bound implies that no node receives too many messages in any round, w.h.p.
3.2.2 Bounding the conductance of \(G_i\)
In this section, we show that the graph’s conductance is increasing by a factor \(\Omega (\sqrt{\ell })\) from \(G_i\) to \(G_{i+1}\) w.h.p. if \(G_i\) is benign. More formally, we show the following:
Lemma 3.4
Let \(\lambda > 0\) be a parameter and let \(G_i\) and \(G_{i+1}\) be the graphs created in iteration i and \(i+1\), respectively. Finally, assume that \(G_i\) is benign with a minimum cut of at least \(\Lambda \ge 6400 \lambda \log n\) and degree \(\Delta > 64\Lambda \). Then, it holds with probability at least \(1-n^{-7\lambda }\) that
In particular, for any \(\ell \ge (2 \cdot 640)^2\), it holds
Our first observation is the fact that random walks of length \(\ell \) are distributed according to 1-step walks in \(G_i^{\ell }\). In particular, if we consider a subset \(S \subset V\) and pick a node \(v \in S\) uniformly at random, then \(\Phi _{G_i^\ell }(S)\) denotes the probability that a random walk started at v ends outside of the subset after \(\ell \) steps.
Lemma 3.5
Let G be a \(\Delta \)-regular graph and \(S \subset V\) be a any subset of nodes with \(\vert S\vert \le \frac{n}{2}\) and suppose each node in S starts \(\frac{\Delta }{8}\) random walks. Let \(\mathcal {Y}_S\) count the \(\ell \)-step random walks that start at some node in \(v \in S\) and end at some node \(w \in V \setminus S\). Then, it holds:
Proof
First, we observe that we can express \(\mathcal {Y}_S\) as the sum of binary random variables for each walk. For each \(v_i \in S\) let \(Y_i^1, \dots , Y_i^{d}\) be indicator variables that denote if a token started by \(v_i\) ended in \(\overline{S} := V\setminus S\) after \(\ell \) steps. Given this definition, we see that
Recall that an \(\ell \)-step random walk in \(G_i\) corresponds to a 1-step random walk in \(G^\ell _i\). This means that for each of its \(\frac{\Delta }{8}\) tokens node \(v_j\) picks one of its outgoing edges in \(G^\ell _i\) uniformly at random and sends the token along this edge (which corresponds to an \(\ell \)-step walk). For ease of notation, let \(O^\ell _j\) be the number of edges of node \(v_j \in S\) in \(G^\ell _i\) where the other endpoint is not in S, i.e.,
Now consider the \(k^{th}\) random walk started at \(v_j\) and observe \(Y_j^k\). Note that it holds:
Here, Eq. (116) follows from Lemma 2.5. Let \({O}^\ell _S\) be the number of all outgoing edges from the whole set S in \(G_i^{\ell }\). It holds that \(O^\ell _S := \sum _{v_j \in S} {O}^\ell _j\). Recall that the definition of \(\Phi _{G_i^\ell }\) is the ratio of edges leading out of S and all edges with at least one endpoint in S. Given that \(G_i^{\ell }\) is a \(\Delta ^{\ell }\)-regular graph, a simple calculation yields:
In the last line , we used that \(\Phi _{G_i^\ell }(S) := \frac{O^\ell _S}{\vert S\vert \Delta ^{\ell }}\) per definition as \({O}^\ell _S\) counts the edges with an endpoint outside of S and \(\vert S\vert \Delta ^\ell \) counts the total number edges with an endpoint in S as \(G_i^{\ell }\) is a \(\Delta ^{\ell }\)-regular graph. This proves the lemma. \(\square \)
Therefore, a lower bound on \(\Phi _{G_i^\ell }\) gives us a lower bound on the expected number of tokens that leave any set S. Thus, as long as \(G_i\) is regular and lazy, we have a suitable lower bound for \(\Phi _{G_i^\ell }\) with Lemma 2.9. In fact, given that the random walks are independent, we can even show the following:
Lemma 3.6
Let \(S \subset V\) be set of nodes with \(O_S\) outgoing edges, then it holds:
Proof
This follows from the Chernoff bound and the fact that the random walks are independent. Recall that for each set S, the number of outgoing edges \(\mathcal {Y}_S := \sum ^{s}_{i=1} \sum _{k=1}^{\Delta /8} Y_i^k\) in \(G_{i+1}\) is determined by a series independent binary variables. Thus, by the Chernoff bound, it holds that
By choosing  , we get
, we get
Therefore, it remains to show that our claim that \(\mathbb {E}[\mathcal {Y}] \ge \frac{O_S}{8}\) holds, and we are done. By Lemma 3.5 we have for all set with \(O_S\) outgoing edges that
This proves the lemma. \(\square \)
Recall that we need to show that every subset \(S \subset V\) with \(\vert S\vert \le n/2\) has a conductance of \(O(\sqrt{\ell }\Phi _{G_i})\) in \(G_{i+1}\) in order to prove that \(\Phi _{G_{i+1}} = \Omega (\sqrt{\ell }\Phi _{G_i})\). In the following, we want to prove that for every set S, there are at least \(\Theta (\sqrt{\ell }\Phi _{G_i})\) tokens that start at some node \(v \in S\) and end at some node \(w \in \overline{S}\) after \(\ell \) steps w.h.p. These tokens are counted by the random variable \(\mathcal {Y}_S\), which we analyzed above. In particular, given that a set S has \(O_S\) outgoing edges, the value of \(\mathcal {Y}_S\) is concentrated around its expectation with probability \(e^{-\Omega (O_S)}\). Thus, we can apply Lemma 2.4 and show that—for a big enough \(\Lambda \)—all sets have many tokens that escape.
Lemma 3.7
Let \(G_i\) be a benign graph with \(\Lambda \ge 6400\lambda \log n\). Then, it holds
Proof
For a set \(S \subset V\) we define \(\mathcal {B}_S\) to be the event that S has bad conductance, i.e., it holds that \(\mathcal {Y}_S\)—the number of tokens that leave S—is smaller than \(\min \left\{ \frac{\Delta \vert S\vert }{32},\frac{\Delta \vert S\vert }{640}\sqrt{\ell }\Phi _G \right\} \). We let \(\mathcal {B}_1 = \bigcup _{S \subset V} \mathcal {B}_S\) be the event that there exists a set S with bad conductance, i.e., there is any \(\mathcal {B}_S\) that is true. By Lemma 3.6, we know that the probability of \(\mathcal {B}_S\) exponentially depends on \(O_S\). Thus, we want to use Lemma 2.4 to that no \(\mathcal {B}_S\) occurs w.h.p. Therefore, we must show that the three conditions mentioned in the lemma are fulfilled. The first and third property follow directly from the definition of benign graphs, as the graph is polynomial in size and has a logarithmic minimum cut with a tunable constant. For the concrete constants, it holds:
-
1.
G has at most \(m \in O(n^{c_1})\) edges for some constant \(c_1>1\): Recall that we limited ourselves to simple initial graphs with \(O(n^2)\) edges and copied each edge \(O(\Lambda )\) times. Since \(\Lambda \in o(n)\), we have strictly less than \(n^{3}\) edges. Thus, we have \(c_1 := 3\).
-
2.
For each \(\mathcal {B}_S\) it holds \({\textbf{Pr}\left[ \mathcal {B}_S\right] } \le e^{-c_2 O_S}\) for some constant \(c_2>0\): By Lemma 3.6 a bad event \(\mathcal {B}_S\) for a set \(S \subseteq V\) happens with probability at most \(e^{-\frac{O_S}{64}}\). Thus, we have \(c_2 := \frac{1}{64}\).
-
3.
The minimum cut of G is at least \(\Lambda := 4\frac{c_1}{c_2}c_3\log n\) edges for some tunable variable \(c_3>1\): Since \(G_i\) is benign, it holds \(\Lambda \ge 6400\lambda \log n > \left( 4\cdot 3\cdot 64 \right) 8\lambda \log n\) for a constant \(\lambda \). Thus, we have \(c_3 := 8\lambda \). Note that \(\lambda \) is tunable as it can be chosen as high as we want by constructing a sufficiently large minimum cut in \(G_0\) by creating copies of each initial edge.
Given that all three conditions are fulfilled with constants \(c_1=3\),\(c_2=\frac{1}{64}\), and \(c_3 = 8\lambda \), Lemma 2.4 implies that it holds:
This was to be shown. \(\square \)
With this insight, we can now formally prove Lemma 3.4:
Proof of Lemma 3.4
First, we note that if no set \(S \subset V\) with \(\vert S\vert \le n/2\) has less than \(\min \left\{ \frac{\Delta \vert S\vert }{32},\frac{\Delta \vert S\vert }{640}\sqrt{\ell }\Phi _{G_i}\right\} \) tokens that end outside of S and all tokens are used to create an edge, then the resulting conductance of \(G_{i+1}\) must also be at least \(\min \left\{ \frac{1}{32},\frac{1}{640}\sqrt{\ell }\Phi _{G_i}\right\} \) and the lemma follows. This can easily be verified by observing the algorithm: We note that by construction, the degree can never be higher than \(\Delta \). Recall that every node creates its edges for \(G_{i+1}\) based on the tokens it received. If any node receives fewer than \(\Delta \) tokens, it creates self-loops to reach a degree of \(\Delta \). Excess edges are dropped arbitrarily to ensure a degree of at most \(\Delta \). Thus, each set S maintains \(\Delta \vert S\vert \) edges in total, as each node will always have \(\Delta \) edges regardless of how many tokens it receives. Further, we let \(O^{(i+1)}_S\) be the number of edges that leave S in \(G_{i+1}\). Two sets of edges determine the value of \(O^{(i+1)}_S\):
-
1.
The edges that are created by nodes outside S. These are based on tokens they received from nodes in S. We denote these edges by \(\widetilde{\mathcal {Y}}_S\).
-
2.
The edges that are created by nodes in S. These are based on tokens they received from nodes outside. We do not make any statements about these edges and ignore them for the remainder of the proof.
For easier notation, let \(\overline{\mathcal {B}_1}\) be the event that each set \(S \subset V\) has \(\min \left\{ \frac{\Delta \vert S\vert }{32},\frac{\Delta \vert S\vert }{640}\sqrt{\ell }\Phi _{G_i}\right\} \) tokens that end outside of the set. Moreover, let \({\mathcal {B}_1}\) be the event that this is not the case. Further, let \(\overline{\mathcal {B}_2}\) be the event that all these tokens are used to create an edge. Again, let \(\overline{\mathcal {B}_2}\) denote the complementary event. Note that the event \(\overline{B}_2\) directly implies that \(\widetilde{\mathcal {Y}}_S = {\mathcal {Y}}_S\). Given these facts and definitions, we can use Lemma 3.5 from above and see that the events \(\overline{\mathcal {B}_1}\) and \(\overline{\mathcal {B}_2}\) imply that the conductance of each set is bigger or equal to \(\min \left\{ \frac{1}{32},\frac{\sqrt{\ell }\Phi _{G_i}}{640}\right\} \). If they both occur simultaneously, it holds for each set \(S \subset V\):
Since this implication holds for all sets \(S \subset V\), we get:
Therefore, it holds that
This proves the lemma. \(\square \)
3.2.3 Ensuring that each G_i is benign
Since all the arguments from before only hold if \(G_i\) is benign, we must make sure that each graph in \(\mathcal {G}:= G_1, \ldots , G_L\) is indeed benign. As before, we prove this step by step and show that \(G_{i+1}\) is benign given that \(G_i\) is benign.
Lemma 3.8
Let \(G_i\) and \(G_{i+1}\) be the graphs created in iteration i and \(i+1\), respectively, and assume that \(G_i\) is benign. Then with probability at least \(1-n^{-8\lambda }\) the graph \(G_{i+1}\) is also benign
Proof
We will show that each \(G_{i+1}\) is a \(\Delta \)-regular, lazy graph with a \(\Lambda \)-sized cut. Note that the last property also ensures that \(G_{i+1}\) is connected. The first property follows directly from observing the algorithm: Recall that every node creates its edges for \(G_{i+1}\) based on the tokens it received. If any node receives fewer than \(\Delta \) tokens, it creates self-loops to reach a degree of \(\Delta \). Excess edges are dropped arbitrarily to ensure a degree of at most \(\Delta \). By a similar argument, we can easily see that \(G_{i+1}\) lazy. For this, recall that a node connects to endpoints of all its \(\frac{\Delta }{8}\) tokens and additionally to the origins of all (but at most \(\frac{3\Delta }{8}\)) tokens it received. Thus, in the worst case, it creates at most \(\frac{\Delta }{8}+\frac{3\Delta }{8} = \frac{\Delta }{2}\) edges. Therefore, it creates at least \(\frac{\Delta }{2}\)—and therefore enough—self-loops. The third property—the \(\Lambda \)-sized minimum cut—is perhaps the most difficult to show. However, at a closer look, the proof is almost identical to the proof of Lemma 3.4. In particular, we show that all cuts that are close to the minimum cut will (in expectation and w.h.p.) increase in size in each iteration and never fall below \(\Lambda \). The idea behind the proof uses the fact that [39] (and therefore Lemma 2.9) gives us a stronger bound on the expected growth of the subset than just the conductance. This observation is enough to show that all sets that have close to \(\Lambda \) outgoing connections will slightly increase the number of outgoing connections for a big enough \(\ell \). In particular, it holds:
Lemma 3.9
Suppose that \(\ell \ge \left( 2 \cdot 640\right) ^2\). Then, for any set \(S \subseteq V\) with \(\vert S\vert \le \frac{n}{2}\) and \(O_S\) outgoing edges, it holds:
Proof
By Lemma 3.6 we have that
Thus, it remains to show that for all sets \(S \subseteq V\), it holds:
Consider a set of size \(\vert S\vert := \delta _s n\). For this set, it holds:
This follows because \(\Phi _{\delta _s}(G_i^\ell ) \le \Phi _{G_i^\ell }(S)\) per definition. Due to Lemma 2.9, we know that we can bound this as follows:
Case 1: \(\delta _s \ge \frac{1}{4}\) It holds:
Case 2: \(\delta _s \le \frac{1}{4}\) It holds:
The factor of 2 that appears in the denominator in the second line results from a subtle detail in Lemma 2.9. Since we observe a set of size \(\delta _s n\), we must consider \(\Phi _{2\delta _s}\). Since we always consider sets of size at most \(\frac{n}{4}\), this is always well-defined.
Putting these bounds back into the formula gives us (for a set of any size):
Now, choosing \(\ell > (2 \cdot 640)^2\) yields:
We need to again distinguish between two cases:
Case 1 : \(\frac{1}{4} \le \frac{1}{16}\frac{\Lambda }{\Delta \vert S\vert }\) In this case, we have:
Here, we used that \(\Delta \ge 64\Lambda \) as \(G_i\) is benign.
Case 2 : \(\frac{1}{4} > \frac{1}{16}\frac{\Lambda }{\Delta \vert S\vert }\) In this case, we have:
This proves that \(\mathbb {E}[\mathcal {Y}_S] \le 2 \Lambda \) and therefore the lemma. \(\square \)
We can round up the proof with the same trick as before. Again, we must show that every cut has a value of at \(\Lambda \) and use Karger’s bound together with Lemma 3.9 to show that no cut has a worse value, w.h.p.
Lemma 3.10
Let \(G_i\) be a benign graph with \(\Lambda \ge 6400\lambda \log n\). Then, it holds
Proof
The proof is completely analogous to the proof of Lemma 3.7 down to the constants. For each set S with \(\vert S\vert \le n/2\), we observe the event \(\mathcal {B}_S\) that \(\mathcal {Y}_S\) is smaller than \(\Lambda \). Just as in Lemma 3.7, the graph \(G_i\) has at most \(n^3\) edges, the event \(\mathcal {B}_S\) has probability at most \(e^{-\frac{O_S}{64}}\), and the minimum cut is of size \(6400\lambda \log n\). Thus, Lemma 2.4 yields this lemma. \(\square \)
Finally, recall that each token creates an edge with probability \(1-n^{-8\lambda }\) by Lemma 3.6 and at least \(\Lambda \) tokens leave each set with prob. \(1-n^{-8\lambda }\) by Lemma 3.10. By the union bound, both these events hold with prob. at least \(1-n^{-7\lambda }\). This implies that each cut in \(G_{i+1}\) has at least size \(\Lambda \) w.h.p. and therefore proves Lemma 3.8
\(\square \)
3.2.4 Finalizing the proof
To round up the analysis, we only need to prove Lemma 3.1 and show that after \(O(\log n)\) iterations, the graph has constant conductance. Based on our insights, we can conclude that if \(\Delta ,\ell \), and \(\Lambda \) are big enough and \(G_i\) is benign, then \(G_{i+1}\) is benign and has at least twice its conductance w.h.p. (if it was not already constant). To be precise, assume that \(G_i\) is benign and let \(\ell := (2\cdot 640)^2\) and \(\Lambda \ge 6400\lambda \log n\). Then, it holds that with probability \(1-n^{-7\lambda }\) that
-
1.
\(G_{i+1}\) has conductance at least \(2\Phi _{G_i}\) (if \(\Phi \) was not already constant) by Lemma 3.4, and
-
2.
\(G_{i+1}\) is benign by Lemma 3.8.
For an easier notion, let \(\mathcal {Z}_{i+1}\) be a random variable that takes the value of \(G_{i+1} \)’s conductance if \(G_{i+1}\) benign and 0 otherwise. For any value \(\varphi > (0,\frac{1}{32})\), it holds that:
Here, the first inequality follows from the law of total expectation and the last follows from Lemmas 3.4 and 3.8 as well as the union bound. Given that after every iteration the graph’s conductance increases by a factor of 2 w.h.p, Inequality (160) implies the following:
If we inductively apply this argument L times, we get:
By choosing \(L := 3\log n\), we obtain:
Since the minimal conductance of any benign graph is \(O(n^{-3})\) by Lemma 2.6, it follows:
Therefore, the graph, w.h.p., has a constant conductance after \(O(\log n)\) iterations. This takes \(O(\log n)\) rounds, since each iteration lasts only \(\ell \in O(1)\) rounds. Finally, a constant conductance implies a logarithmic diameter by Lemma 2.7. This concludes the analysis.
4 Applications and implications
Several connectivity problems (Connected Components, Spanning Tree, Biconnectivity) and Maximum Independent Set can be solved faster using our approach as a subroutine. Note that all of the following algorithms can be performed in the hybrid network model of Augustine et al. [8] with local \(\textsf{CONGEST}\) edges. For each algorithm, we give a bound on the required global capacity. Note that our algorithms can very likely be optimized to require a much smaller global capacity by using more sophisticated techniques, i.e., we did not aim to optimize logarithmic factors here.
4.1 Connected components
This section shows how our algorithm can be extended to find connected components in an arbitrary graph G. In particular, for each connected component C of G, we want to establish a well-formed tree of overlay edges that contains all nodes of C. The main result of this section is the following theorem:
Theorem 1.2
Let \(G = (V, E)\) be a directed graph. Further, all components have a (known) size of \(O(n')\). There is a randomized algorithm that constructs a well-formed tree on each connected component of (the undirected version of) G in \(O(\log {n'})\) rounds, w.h.p., in the hybrid model. The algorithm requires global capacity \(O(\log ^2 n)\), w.h.p.
Note that the main difficulty preventing us from applying Theorem 1.1 directly on each component is that we now assume the initial graph’s degree is unbounded. Therefore, the main contribution of this section is a preprocessing algorithm that transforms any connected subgraph of G into a graph of bounded degree \(O(\log n)\). Then, we execute the algorithm of Theorem 1.1 to create a well-formed tree for each component. By Theorem 1.1, this takes \(O(\log {n'})\) time, w.h.p., for parameters \(L \in O(\log {n'})\) and \(\Lambda \in O(\log n)\). Therefore, we only need to prove the following lemma.
Lemma 4.1
Let \(G = (V, E)\) be a directed graph in which each component contains at most m nodes. There exists a randomized algorithm that transforms G into a directed graph \(H := (V, E_H)\) that has degree \(O(\log n)\) and in which two nodes lie in the same component if and only if they lie in the same component in G. The algorithm takes \(O(\log {n'})\) rounds w.h.p., in the \(\textsf{CONGEST}\) model.
The algorithm will be executed in parallel on all connected components of the graph G. In the remainder, we will w.l.o.g. focus on a single connected component C and its implied subgraph \(G_C := (V_C, E_C)\). In particular, we present an algorithm that creates a bounded degree graph \(H(G_C)\)for the nodes of \(G_C\), so our main algorithm can transform it into a well-formed tree in \(O(\log {n'})\) time. Since there is no communication between components and we run the algorithm independently for each component, focusing on a single component is enough to prove the lemma.
The algorithm’s main idea is to first eliminate most edges by constructing a sparse spanner. Then, in a second step, we let all remaining nodes of high degree delegate their edges to nodes of lower degree. This roughly means that each node introduces its neighbor to each other in a way that preserves the connectivity but massively reduces its own degree (if it is higher than \(\omega (\log {n})\)) while only slightly increasing the neighbors’ degrees. If every node of a high degree has sufficiently many neighbors of a low degree, the overall degree becomes small enough for our algorithm to handle. Here, we use the fact that most modern spanner construction algorithms create spanners with exactly this property. To be precise, the spanners have a low arboricity. The arboricity of a graph is the minimum number of forests it can be partitioned into. As we will see, this property implies that we will have relatively few nodes of high degree, and all these nodes have many neighbors of low degree, which is exactly what we are aiming for.
Note that well-known spanner constructions take \(O(\log n)\) time, so a more careful analysis is required to show that we can construct such a graph in \(O(\log {n'})\) time, i.e., logarithmic in the size of the biggest connected component. Further, we remark that—although we use the term spanner—we are not interested in the approximation of shortest paths but only in the sparsification of the initial graph.
In the following, we present the two steps of our preprocessing algorithm, the spanner construction and the delegation of edges in detail.
Step 1: Create a Sparse Spanner \(S(G_C)\).
In the first step, we will construct a spanner \(S(G_C):= (V_C, S(E_C))\) of \(G_C\) to reduce the number of edges to \(O(n\log n)\) and its arboricity to \(O(\log n)\). In particular, we note that \(S(G_C)\) is a subgraph of G, so every edge in \(S(G_C)\) is a local edge in our hybrid model. We will adapt spanner construction algorithms based on exponential start time clustering [57]. For the most part, we will follow the idea of Miller et al.’s spanner construction [46]. However, we will use some of the insights by Elkin and Neiman [19] and technical details from Haeupler and Li [33], who present a similar algorithm explicitly tailored to the \(\textsf{CONGEST}\) model. Note that Haupler and Li use the geometric distribution, but this does not make too much of a difference.
Conceptually, our algorithm can be subdivided into two phases. First, we construct clusters of nodes. Each cluster is a subset of nodes that is internally connected via a spanning tree. Then, in the second phase, we add additional edges to connect the clusters.
Our algorithm does the same as Haeupler and Li’s algorithm but uses a slightly different mechanism to construct the clusters. We begin with the description of clustering phase where each node joins some cluster. By joining a cluster, we mean that a node \(v \in V\) either declares itself the head of a cluster or picks a neighbor \(p(w) \in N_v\), such that the edge (v, p(w)) is the next edge of a path to the head of the cluster. In the latter case, we will refer to p(w) as the predecessor of v. The clusters are constructed as follows.
-
1.
In the beginning, each node v independently draws a random value \(r_v\) from the exponential distribution with parameter
 . Values larger than \(4\log {n'}\) are redrawn until \(r_v \le 4\log {n'}\), i.e., we draw exponentially distributed variables conditioned on being smaller than \(4\log {n'}\).
. Values larger than \(4\log {n'}\) are redrawn until \(r_v \le 4\log {n'}\), i.e., we draw exponentially distributed variables conditioned on being smaller than \(4\log {n'}\). -
2.
If a node v did not receive any message until round \(4\log {n'}-\lceil r_v \rceil \), it creates the message \((r_v,v,0)\) that contains its random value \(r_v\), its identifier, and a hop counter. Finally, node v delivers this message to itself together with all other messages received in this round.
-
3.
Once a node v receives one or more messages of the form \((r_u,u,x_{u})\) with \(u \in V\), it joins a cluster. Let \({u^*}\) be node that maximizes the term \(r_{u^*}-x_{u^*}\) among all received values. Then, v joins the cluster of \(u^*\). If \(u^*=v\), it declares itself the cluster head. Otherwise, v joins \(u^*\)’s cluster. For this, it stores the identifier of \(u^*\) and the identifier of the neighbor p(v) from which it received the message \((r_{u^*},u^*,x_{u^*})\). In other words, we declare node p(v) to be its predecessor. If v received the message simultaneously from more than one neighbor, it picks the one with the smallest identifier as its predecessor. In the end, v sends \((r_{u^*},u^*,x_{u^*}+1)\), i.e., the same message with an increased hop counter, to all its neighbors.
After each node joins a cluster, all nodes add the edge to their predecessor to the spanner (if they have one). By adding an edge to w to the spanner, we mean that a node v locally marks w as a neighbor in the spanner and sends a message to w, so w also locally marks v as a neighbor in the spanner. Thus, the edges are always bi-directed and we only add edges that are present in the initial graph \(G_C\). The latter is very important for our construction, as we will require local communication on these edges later on.
However, the subgraph implied by the edges added during this phase is not necessarily connected. These edges only connect a node with its predecessor in its cluster. As we will see, these edges imply a spanning tree rooted in the node’s respective cluster head, but there are no paths to nodes in other clusters. Thus, in the second part, we add edges between the clusters to the spanner to ensure it is connected. To simplify notation, we refer to all clusters that contain at least one neighbor of a node as its neighboring clusters. We create the edges between clusters in the following way. First, all nodes send the identifier of their cluster head to all their neighbors to inform them about their neighboring clusters. This way, each node can determine all its neighboring clusters and which of its neighbors are in which neighboring clusters. Second, all nodes add an edge to exactly one node of each neighboring cluster. To be precise, suppose that \(v \in V\) is in the cluster of some node \(u^*_v \in V\) and a neighbor \(w \in N_v\) is in the cluster of some node \(u^*_v \ne u^*_w \in V\). Then, after receiving the identifier \(u^*_w\) from w, node v adds an edge w to the spanner. If more than one neighbor is in this cluster, node v again picks the neighbor with the smallest identifier and only adds the edge to this neighbor to the spanner. As a result, it is also possible that that w perhaps adds another edge to another member of v’s cluster. However, the number of edges each individual node adds is bounded by the number of their neighboring clusters. This concludes the construction of the spanner and the first phase of our preprocessing algorithm.
It is fairly straightforward to see that this step takes \(O(\log {n'})\) communication rounds. For the clustering phase, note that a node \(v \in V\) joins a cluster at the latest in round \(4\log {n'}-\lceil r_v \rceil \) when it creates its own message. Thus, after \(4\log {n'}+1\) steps, all nodes joined a cluster due to our choice of the \(r_v\)’s. Therefore, the runtime of the first phase is only \(O(\log {n'})\). In the second phase, all nodes only exchange two messages with their neighbors in \(S(G_C)\), so its runtime is O(1). Since all nodes know the same estimate of \(O(\log {n'})\), the phases can be synchronized via round counters. Thus, it remains to show that the subgraph created by our procedure is indeed connected and there are few edges between the clusters. We show that it holds:
Lemma 4.2
The algorithm above creates a connected subgraph \(S(G_C)\) of \(G_C\) in \(O(\log {n'})\) rounds where each node has at most \(O(\log n)\) neighboring clusters w.h.p.
We present the proof in Sect. 4.1.1.
The key difference—besides the use of the exponential distribution—between our algorithm and the construction by Haeupler and Li is that we broadcast the values for only \(O(\log {n'})\) and not \(O(\log n)\) rounds, and redraw \(r_v\)’s that are larger than \(O(\log {n'})\). Therefore, our algorithm creates slightly different spanners but allows us to reuse some analytical results from Elkin and Neiman. Finally, we want to remark that Elkin and Neiman only described the algorithm differently without the concept of clusters. However, the end result is basically the same as we will see in our analysis.
Step 2: Transform \(S(G_C)\) into a bounded degree graph \(H(G_C)\).
Now we will construct a bounded degree graph \(H(G_C)\) from \(S(G_C)\). Note that \(H(G_C)\)—in contrast to \(S(G_C)\)—is not a subgraph of \(G_C\) and contains additional edges. Although \(S(G_C)\) has few edges in total, there can still be high-degree nodes. Our goal is for high-degree nodes to redirect their edges to other nodes to balance the degrees. This technique is conceptually similar to constructing a child-sibling tree as in [4] and [30].
-
1.
In the first step, we add an orientation to the edges similar to the Nash-Williams Forest Decomposition, which is often utilized in algorithms for sparse graphs [7, 11]. This procedure adds an orientation to each edge \(\{v,w\}\) such that it is either oriented towards v or w. We will slightly abuse notation and refer to all edges oriented towards a node \(v \in V\) as its incoming edge and all others as \(outgoing \) edges. Note that we will still require bidirectional communication between v and w. It is well known that any graph of arboricity a has an orientation where each node has at most O(a) outgoing edges [7, 11]. However, instead of directly bounding our spanner’s arboricity and using standard techniques to create the orientation, we take a slightly different path. Given the clustering from the previous step, a sufficiently good orientation can be constructed in a single round. Every node \(v \in V\) declares all edges it added during spanner construction as outgoing edges. Recall that this includes the edge to the predecessor and an edge to one node of each neighboring cluster. The nodes inform their neighbors about the orientation by sending a message containing their identifier. Recall that we have not used our nodes’ global communication capabilities to compute the spanner’s edges. Each node simply marked a set of edges in the initial graph using only local communication. Since the corresponding edges must also have existed in the initial graph, we can again use local communication on these edges. Note that each node has at most one predecessor by construction and at most \(O(\log {n})\) neighboring clusters w.h.p. by Lemma 4.2. Therefore, it has at most \(O(\log {n})\) outgoing edges. However, it can have up to n incoming edges as it can be the predecessor of many nodes.
-
2.
Next, we delegate all incoming edges away and create line-like connections between all incoming nodes. For the construction, consider a node \(v \in V\) and let \(w_1, \dots , w_k\) be all nodes with \((w_i,v) \in S(E_C)\), i.e, the incoming edges of v. W.l.o.g., assume that \(w_1, \dots , w_k\) are ordered by increasing identifier. Then, for each \(i>1\), v sends the identifier of \(w_{i}\) to \(w_{i-1}\) and vice versa.
One can easily verify that each node has at most one incoming edge left (i.e., the edge from \(w_1\) to v) and received at most two edges for each outgoing edge (i.e., the edges to \(w_{i-1}\) and \(w_{i-1}\)). Thus, the resulting graph \(H(G_C)\) has a degree of \(O(\log n)\) as needed. Further, this part of the algorithm only requires O(1) of communication between neighboring nodes.
4.1.1 Proof of Lemma 4.2
In the following, we will show that the resulting graph \(S(G_C)\) is connected and each node has at most \(O(\log n)\) neighboring clusters, w.h.p. First, we show that the connectivity follows directly from our construction of the clusters. We begin with the connections within a cluster. Intuitively, the path along the predecessors leads to the head of the cluster. For completeness, we formally show the following claim:
Claim 5
Suppose that \(v \in V\) joined the cluster of \(u^* \in V\), then there is a bi-directed path from v to \(u^*\) in \(S(G_C)\).
Proof
Recall that a node \(w \in V\) joins \(u^*\)’s cluster by receiving a message of the form \((r_{u^*},u^*,x_{u^*})\). Here, \(x_{u^*}\) is the hop counter that is increased each time the message is forwarded. For each node \(w \in V\) that is in \(u^*\)’s cluster, we can therefore define \(x^w_{u^*} \ge 0\) as the value of the hop counter when it joins the clusterFootnote 8.
Equipped with this definition, we can now prove the lemma via an induction over all possible values of \(x^v_{u^*}\). For the start of the induction, suppose that \(x^v_{u^*} = 0\). Note that \(x_{u^*}^v = 0\) can only hold if \(v=u^*\). Recall that the message \((r_{u^*},u^*,x_{u^*})\) that lets nodes join the cluster originates at \(u^*\) with a hop counter of 0. The hop counter is increased every round, so \(u^*\) is the only node that can ever receive \((r_{u^*},u^*,0)\). Thus, for \(x_{u^*}^v = 0\), it must hold \(v=u^*\) and there is a trivial path contained in the spanner as a node has a path to itself.
Now we get to the induction step. Assume that \(x^v_{u^*} = i\) and for all nodes \(w \in V\) with \(x_{u^*}^w = i-1\) there is a path to \(u^*\) in the spanner. We claim that one of these nodes must be v’s predecessor p(v). First, we observe that node p(v) must be part of \(u^*\)’s cluster as each node only forwards the message of the cluster it joined. Therefore, the value \(x_{u^*}^{p(v)}\) is well-defined. According to the algorithm, p(v) joins the cluster when it receives \((r_{u^*},u^*,x_{u^*}^{p(v)})\) and then fowards \((r_{u^*},u^*,x_{u^*}^{p(v)}+1)\) to v. Upon receiving this message, v joins the cluster. This implies that for v and its predecessor p(v), it holds \(x_{u^*}^v = x_{u^*}^{p(v)}+1\). Therefore, we have \(x_{u^*}^{p(v)} = i-1\) as we assumed \(x_{u^*}^v=i\). Finally, v adds a bi-directed edge to p(v) and p(v) has a bi-directed path to \(u^*\) per induction hypothesis, so the lemma follows. \(\square \)
Note that this lemma directly implies that the spanner is connected. Consider an edge \((v,w) \in E_C\). If both nodes are in the same cluster of some node \(u^*\), the lemma certifies that for both nodes, there is a bi-directed path to \(u^*\) connecting them. Otherwise, there are two possibilities if the nodes are in different clusters. Either v directly adds the edge (v, w) to the spanner, or it adds another edge \((v,w')\) where \(w' \in N_v\) is in the same cluster as w. In the latter case, there must be a path from w to \(w'\) by the same argument as before, as they are in the same cluster. Thus, for each edge \((v,w) \in E\), there is a path that connects v and w in \(S(G_C)\).
Next, we consider the number of neighboring clusters, which is a bit more involved. Before we go into the details of the analysis, we first introduce some helpful definitions. First, recall that we denote the distance, i.e., the number of hops on the shortest path between two nodes v and w in \(G_C\), as \(\textsf{dist}(v,w) \). As we only consider unweighted graphs, all distances are integer and we have \(\textsf{dist}(v,v):=0\) and \(\textsf{dist}(v,w) \ge 1\) for any \(w\ne v\). Further, for all nodes \(u \in V\), we define the value
We denote m(v) to the maximum among these values and \(u^*_v \in V\) as the node that drew the respective variable. In other words, it holds:
These values will be integral to our analysis as we will see \(u^*_v\) is indeed the node that takes v into its cluster. Equipped with these definitions, we show the following.
Lemma 4.3
Fix a node \(v \in V\) and let \(u^*_v\) be the node that maximizes m(v). Then, v receives the message \((u^*_v,r_{u^*_v},\textsf{dist}(v,u^*_v))\) in round \(\left( 4\log {n'}-\lceil r_{u^*_v}\rceil \right) +\textsf{dist}(v,u^*_v) \) and joins the cluster of \(u^*\).
Proof
For this proof, we will drop the subscript from \(u^*_v\) and simply write \(u^*\) if clear from the context. Note that \(\left( 4\log {n'}-\lceil r_{u^*}\rceil \right) +\textsf{dist}(v,u^*) \) is the earliest round in which the message can possibly be received by node v as the message is started in round \(\left( 4\log {n'}-\lceil r_{u^*}\rceil \right) \) and takes (at least) \(\textsf{dist}(v,u^*) \) steps to reach v. First, we show that v cannot receive another message in an earlier round.
Claim 6
v will not receive any message before round \(\big (4\log {n'}-\lceil r_{u^*}\rceil \big )+\textsf{dist}(v,u^*) \).
Proof
We begin the proof by noting that \(u^*\) minimizes \(\left( 4\log {n'} - r_u\right) + \textsf{dist}(v,u) \) among all nodes of V. This can be shown through an elementary calculation. We start with:
To simplify the term, we subtract \(4\log {n'}\). Then, we get:
Let \(U \subset V\) be the set of nodes whose messages reach v first (note that several such messages may be received in the same round from different neighbors of v). Denote the round in which v first receives something as t. For all nodes \(u\in U\), it holds:
We argue that \(u^*\) must be contained in U. For contradiction, suppose that the value would be received in a later round, i.e., it holds:
Now, note that for all values \(u \in U\), it holds that \(\lceil r_u\rceil - r_u < 1\). Therefore, we have:
By combining these two observations, we see that \(u^*\) would not be the node with minimal value as any node in U has a smaller one. This is a contradiction as we defined \(u^*\) to be minimal. \(\square \)
We will see that our lemma holds if all nodes on a shortest path from \(u^*\) join the cluster of \(u^*\) and forward the message. In particular, we claim the following
Claim 7
Let \(l := \textsf{dist}(u^*,v) \) and let \(P = (w_0 := u^*, \dots , w_l:= v)\) be any shortest path from \(u^*\) to v. For \(0 \le i \le l\), it holds that \(w_i\) joins the cluster of \(u^*\) in round \(\left( 4\log {n'}- \lceil r_{u^*} \rceil \right) + i\).
Proof
For contradiction, assume that \(w_i \in P\) is the first node that does not join the cluster. As all nodes \(w_0, \ldots , w_{i-1}\) until this point joined the cluster of \(u^*\), it holds that \(w_{i-1}\) must have sent the message \((r_{u*},u^*,i)\) in round \(\left( 4\log {n'}- \lceil r_{u^*} \rceil \right) + (i-1)\). Therefore, \(w_i\) must have joined another cluster in or before this round. As \(w_i\) cannot have received a message in an earlier round due to Claim 6, \(w_i\) must decide for another cluster in round \(\left( 4\log {n'}- \lceil r_{u^*} \rceil \right) + i\). More specifically, there is a vertex \(z \in V\), such that \(w_i\) receives \((r_z,z,x_z)\) and it holds:
As \(x_z\) increases on every hop from z to \(w_i\), it is lower bounded by \(\textsf{dist}(z,w) \). This implies that:
However, this has implications for the value \(m_z(v)\). Using our observations, we see that it holds:
Here, inequality (187) follows from the triangle inequality, inequality (189) follows from inequality (186), and equality (190) holds because \(w_i\) is on the shortest path from \(u^*\) to v. This is a contradiction as m(v) must be bigger or equal to \(m_z(v)\) per definition. Therefore, \(u^*\) must the node which minimizes \((r_{u^*}-x_{u^*})\) among all values received by \(w_i\). Thus, \(w_i\) would not have joined another cluster and must have forwarded \(u^*\)’s message. \(\square \)
Finally, as \(v := w_l\) and \(l:= \textsf{dist}(u^*,v) \), the lemma follows. \(\square \)
Next, we observe neighboring clusters of a node v and show that they are bounded by \(O(\log n)\) w.h.p. Suppose that \(v \in V\) has a neighbor \(w \in V\) that joined another cluster. Then, there must a node \(u^*_v \ne u^*_w \in V\) that maximizes \(r_{u^*_w}-\textsf{dist}(u^*_w,w) \). Since v and w are neighbors, the value \(r_{u^*_w}\) cannot be much bigger than \(r_{u^*_v}\) because otherwise, the corresponding message would reach v much earlier and it would join a different cluster. Following this intuition, we show that the following holds:
Lemma 4.4
. Let \(v, w \in V\) be two neighboring nodes in different clusters. Then it holds \(m(v) \le m(w)+1\)
Proof
Note that it holds
due to the triangle inequality and the fact that v and w are neighbors. This implies that:
Using inequality (192), we see that:
This proves the statement. \(\square \)
Therefore, the number of neighboring clusters of any node \(v \in V\) is upper bounded by the number of values \(m_{u'}:= r_{u} - \textsf{dist}(u,v) \) which are close to m(v). Elkin and Neimann analyzed this random value for the case that the random variables are drawn according to the exponential distribution without truncation. Note that their lemma is itself based on an observation by Miller et al. [46]. They show the following:
Lemma 4.5
(Lemma 1 in [19]) Let \(d_1\le \ldots \le d_{m}\) be arbitrary values and let \(\delta _1,\dots ,\delta _{m}\) be independent random variables sampled from the exponential distribution with parameter \(\beta \). Define the random variables \(M=\max _i\{\delta _i-d_i\}\) and \(I=\{i~:~\delta _i-d_i\ge M-1\}\). Then for any \(1\le t\le m\),
Although we draw the variables differently, their bound will be a very good approximation for our algorithm. Now we can show the following lemma:
Lemma 4.6
Every node has at most \(O(\log n)\) neighboring clusters, w.h.p.
Proof
For a node \(v \in V\) let \(X_v\) denote the number of its neighboring clusters. It holds:
Further, let \(\delta _1, \ldots , \delta _{n'}\) be a series of independent, exponentially distributed random variables with parameter \(\beta \). Define \(\hat{m}(v) = \max _{u \in V}\{\delta _i - \textsf{dist}(u,w) \}\) and consider the variable
Note that \(\hat{X}_v\) can be analyzed using Lemma 4.5 by choosing the shortest path distances to v as the \(d_i\)’s and \(\hat{m}(v)\) as M. Finally, let \(\mathcal {Z}\) be the event that all variables \(\delta _1, \ldots , \delta _m\) are smaller than \(4\log {n'}\). Then, it holds:
Given these definitions, we want to show that there are constants \(c, c'>0\), such that it holds:
By the law of total probability, it holds:
Note that the term in the nominator removed the condition that the variables are smaller than \(4\log {n'}\). Thus, it can be bounded with Lemma 4.5. By choosing  and \(t = c_1 \log n\) with \(c_1 := e^{-\frac{1}{2}} \cdot c_2+1\), we see that:
and \(t = c_1 \log n\) with \(c_1 := e^{-\frac{1}{2}} \cdot c_2+1\), we see that:
The last inequality followed from the fact that \((1-1/x)^x \le e^{-1}\) for any \(x>0\). On the other hand, we have the following:
The last inequality follows from the union bound. Finally, we use that each \(\delta _i\) is exponentially distributed with parameter  . It holds:
. It holds:
Note that we can assume \({n'}\ge 2\) as a component with one node has no edges. Plugging our two insights together, we get the following:
Thus, by a union bound, every node has at most \(c_1\log n\) neighboring clusters with probability at least \(1-n^{-c_3}\) with \(c_3 = c_2-2\). This proves the Eq. (200) for \(c_1 \ge c_3\cdot e^{-\frac{1}{2}}+3\) and therefore the lemma. \(\square \)
4.2 Maximal independent set
This section describes our Maximal Independent Set (MIS) algorithm. The MIS is defined as follows:
Definition 4
(Maximal Independent Set (MIS)) Let \(G:= (V, E)\) be an undirected graph, then \(S \subseteq V\) is an MIS if and only if it fulfills the two following properties:
-
1.
No two nodes in S are adjacent in the initial graph G.
-
2.
Every node \(v \in V \setminus S\) has a neighbor in S.
By a result of Kuhn et al. [37], there are graphs of degree d in which computing the MIS takes \(\Omega \left( {\frac{\log d}{\log \log d}}\right) \) rounds, even in the \(\textsf{LOCAL}\) model. In models in which the communication is not limited to the neighbors of a node (which roughly corresponds to our notion of global communication), the runtime is often exponentially better. For example, both in the congested clique and the MPC model [13, 15, 25, 26] one can achieve runtimes of \(O(\log \log n)\) or even \(O(\log \log d)\) which beats this lower bound. However, these models allow for communication primitives beyond our model’s capabilities. Thus, these extreme improvements are still out of reach. Nevertheless, we can show a little improvement compared to the \(\textsf{LOCAL}\) model where bounds are also of the form \(O(\log d + \text {polylog}({\log n}))\) [27]. More precisely, we prove the following theorem:
Theorem 1.3
Let \(G = (V, E)\) be a weakly connected directed graph. There is a randomized algorithm that computes an MIS of G in \(O(\log d + \log \log n)\) rounds, w.h.p., in the hybrid model. The algorithm requires global capacity \(O(\log ^2 n)\), w.h.p.
Before we go into the details of our algorithm, we take a short detour and recap some known techniques used in MIS algorithms. Many state-of-the-art MIS algorithms employ the so-called shattering technique [12, 23], which conceptually works in two stagesFootnote 9:
-
1.
First, there is the so-called shattering stage, where the problem is solved for most nodes using a local strategy. As a result of this stage, each node knows—with probability \(1-o(1/d)\)—whether it is in the MIS itself or has a neighbor in the MIS and, therefore, cannot be in the MIS. We say that these nodes have decided as the state of these nodes will not change for the remainder of the algorithm. Likewise, we refer to all other nodes as undecided nodes.
-
2.
In the second stage, we solve the problem for all remaining undecided nodes. These undecided nodes only need to communicate with their undecided neighbors as all other nodes know whether they are in the MIS or not. Note that the probability of \(1-o(d)\) implies that each undecided node has less than one undecided neighbor in expectation. By a Galton-Watson argument, the graph G is, therefore, shattered into small isolated subgraphs \(G_1, \dots , G_k\) of undecided nodes after the first stage. Two undecided nodes are part of the same subgraph \(G_i\) if there is a path of undecided nodes between them. In the second stage, the MIS is solved on these subgraphs where we can exploit that the subgraphs \(G_1, \dots , G_k\) are far smaller than G.
The first phase can be implemented in (nearly) optimal \(O(\log d)\) time due to a brilliant result by Ghaffari [23, 24]. It holds:
Lemma 4.7
(Based on Lemmas 4.2 in [23] and 2.1 in [24]) Let c be a large enough constant and \(G:= (V, E)\) be a simple undirected graph. There is a distributed MIS algorithm \(\mathcal {A}\) with following properties:
-
1.
Let B be the set of nodes remaining undecided after \(O(c \log d )\) rounds of \(\mathcal {A}\). Then, with probability at least \(1-n^{-c}\), all connected components of G[B], the subgraph of G induced by nodes in B, have each at most \(O(d^4\log _d(n))\) nodes.
-
2.
Each message only consists of 1 bit.
Given this result, the crux of many modern MIS algorithms lies in their implementation of the second phase. In the \(\textsf{LOCAL}\) and \(\textsf{CONGEST}\) model, we can use deterministic algorithms to obtain sublogarithmic runtimes. Note that we need to be very careful when we execute randomized algorithms in this phase if the probability of failure only depends on the number of nodes. Since the number of nodes \(n'\) in each component is much smaller than n, a bound of \(1-o(n'^{-c})\) does not imply that the algorithm succeeds w.h.p. In models with massive global communication, all remaining nodes and edges of a component can be gathered at a single node using the global communication and then solved locally. This, of course, requires this node to receive a huge amount of messages in a single round. Because of this high message load, this approach cannot be used directly in our model. However, we can do something similar that requires far fewer messages while still coming close to the \(\Omega \left( {\frac{\log d}{\log \log d}}\right) \) bound for \(\textsf{LOCAL}\). This emphasizes that even a small amount of non-local communication is as strong as unbounded local communication.
Next, we consider the \(\textsf{CONGEST}\) model. Here, the MIS problem can be solved in \(O(\log n)\) time—in expectation and w.h.p.—due to a celebrated algorithm by Luby [45] and Alon et al. [1]. The idea behind the algorithms is quite simple: Each node picks a random rank in [0, 1], which is sent to all neighbors. Then, all local minima join the MIS and inform their neighbors about it. All remaining nodes, i.e., nodes that did not join the set and had no neighbor that joined the set, repeat this process until every node has decided. Later, Métivier et al. [47] provided a simpler analysis and showed that sending a single bit per round and edge is sufficient. For our algorithm, we take a closer look at the fact that Métivier et al.’s algorithm has an expected runtime of \(O(\log n)\). In particular, it holds that in every round, in expectation, half of all edges disappear due to nodes deciding (see [47] or the appendix of [23] for a comprehensive proof). Thus, if we execute it on a subgraph with \({n'}^2\) edges, it finishes after \(O(\log {n'})\) rounds in expectation. That means, by Markov’s inequality, with at least constant probability, the algorithm only takes \(O(\log {n'})\) rounds. In fact, Métivier et al. even prove the following more precise statement:
Lemma 4.8
(Theorem 3 in [47]) There is a randomized distributed algorithm for arbitrary simple graphs \(G:=(V,E)\) with n nodes in the \(\textsf{CONGEST}\) model that:
-
1.
finishes in \(O(\log n)\) time with probability \(1-o(n^{-1})\), and
-
2.
each message contains only 1 bit.
The lemma implies a success probability of \(1-\frac{1}{m}\) if we run the algorithm on a graph of m nodes. Therefore, if we execute it \(O(\log n)\) times independently in parallel, there must be at least one execution that finishes within \(O(\log {n'})\) rounds, w.h.p.
Now we go back to the shattering technique and consider the undecided nodes after the shattering stage. Instead of reporting all edges to an observer that solves the problem locally for each subgraph of undecided nodes, we execute Metevier et al.’s algorithm \(O(\log n)\) times in parallel and report which executions finished. Once there is one execution in which all nodes are finished, we signal the nodes to stop via broadcast and let them agree on the outcome of one execution. To do so efficiently, we execute the algorithm of Theorem 1.2 on each component of undecided nodes. Note that this requires far fewer messages per node than aggregating all edges at a node and still achieves a sublogarithmic runtime.
More precisely, our algorithm to solve the MIS problem operates in the following three steps of length \(O(\log d + \log \log n)\) each. To synchronize these steps, we need to assume that, in addition to an approximation of \(\log \log n\), the nodes also know an approximation of \(\log d\).
Step 1: Shatter the Graph into Small Components.
First, we run Ghaffari’s shattering algorithm from [23] for \(O(\log d)\) rounds. Note that Ghaffari’s algorithm can seamlessly be implemented in the \(\textsf{CONGEST}\) model as it only sends 1-bit messages. After executing it for \(O(\log d)\) rounds, each knows with probability \(1-o(d^{-1})\) whether it is in the MIS. Thus, w.h.p, the graph is shattered into isolated, undecided components \(G_1, \dots , G_k\) of size at most \(O(d^4\log _{d} n)\)). Obviously, the nodes can use the local edges to determine which neighbors are in the same component. The remainder of our algorithm will run on each of these \(G_i\)’s in parallel.
Step 2: Construct an Overlay for each Component.
Next, we establish a well-formed tree \(S_i\) on each \(G_i\) using the algorithm of Theorem 1.2. Since each component has size \(O(d^4\log _{d} n)\), the construction takes \(O(\log (d^4\log _{d} n)) = O(\log d + \log \log n)\) time, w.h.p., by Theorem 1.2. Further, the resulting trees \(S_1, \dots , S_k\) also have a height of only \(O(\log d + \log \log n)\). However, the message complexity is still \(O(d+\log ^2 n)\).
Step 3: Execute Métivier et al.’s Algorithm in Parallel.
Using the well-formed tree from the previous step, we can (deterministically) compute aggregate functions on each \(G_i\) in \(O(\log d + \log \log n)\) time. Given this powerful tool, we construct an MIS for each \( G_i\) as follows:
-
1.
On each \(G_i\), we run the MIS algorithm of Métivier et al. independently \(c_1\log n\) times in parallel for \(\tau _{c_2} := c_2\left( \log \Delta +\log \log n\right) \) rounds. Here, \(c_1\) and \(c_2\) are some tunable constants, but \(c_2\) is chosen such that \(\tau _{c_2}\) is bigger than the diameter of \(S_i\). By Theorem 1.2, such a minimal \(c_2\) can always be found. Since each execution needs messages of size 1, all messages sent by all executions can be sent in one round of the \(\textsf{CONGEST}\) model. More precisely, in each round \(r \in [0,\tau _{c_2}]\), a node simply sends the random bit string \(M^{r}(w) := \left( m_1^{r}(w), \ldots , m_{c_1\log n}^{r}(w)\right) \) of length \(c_1\log n\) to its neighbor w. Here, the value \(m_j^{r}(w) \in \{0,1\}\) is the 1-bit message that is sent by execution j to w in round r.
-
2.
After \(\tau _{c_2}\) rounds, each node checks in which executions it has decided, i.e., itself or one of its neighbors joined the MIS. It creates the bit string \(F^{(0)}_v := (f_1, \ldots , f_{c_1\log n})\), where \(f_j = 1\) if and only if the node v has decided in execution j and \(f_j = 0\) otherwise. Again, since there are at most \(O(\log n)\) executions, the information on which executions have finished can be fitted into \(O(\log n)\) bits and therefore be sent as a single message.
-
3.
We then use \(S_i\) to aggregate all executions where all nodes have decided. To be precise, we need to compute the logical AND of all \(F_v\) for all \(v \in G_i\). Recall that this operation returns 1 if all its inputs are 1 and 0 otherwise. The algorithm to do this is trivial: For \(\tau _{c_2}\) rounds, each node sends its current value of \(F_v\) to all its neighbors and computes the logical AND of all values it received (including its own). More precisely, in round \(r>0\) the current value \(F^{(r)}_v\) is computed as follows:
$$\begin{aligned} F^{(r)}_v := \bigotimes _{w \in N_{S_i}(v) \cup \{v\}} F^{(r-1)}_w \end{aligned}$$(211)Here, the set \(N_{S_i}(v)\) contains all of v’s neighbors in \(S_i\) and \(\otimes \) denotes the logical AND. One can easily verify that for a big enough \(c_2\), all nodes know all finished execution after \(\tau _{c_2}\) rounds. Note that the bits of a finished execution will never be flipped to 0 as all of them are 1. Therefore, we must show that all bits of all non-finished executions are 0, i.e., the value \(f_j\) for an execution j will be set to 0 in every node if there is at least one node, say v, that did not decide. A simple induction yields that after r rounds, each node in the distance r to v sets its \(f_i\)-value to 0. Since the diameter of \(S_i\) is smaller than \(\tau _{c_2}\), all nodes know if at least one node in a given execution did not decide.
-
4.
Finally, the nodes adopt the result of an execution that has finished (if there is one). If several executions are finished, the execution with the smallest index is chosen.
Since the correctness of the first two steps follows directly from Lemmas 4.7 and Theorem 1.2, we focus only on the last stage. In particular, we need to show that there are constants \(c_1\) and \(c_2\) such that in all components, there is at least one execution that finishes in \(\tau _{c_2}\) time. For a given component \(G_i\) and execution j, let \(X_j \in \{0,1\}\) be the random variable that all nodes have decided after \(\tau _{c_2}\) rounds. Note that each undecided component must have at least 2 nodes: Seeking contradiction, let there be a component consisting of a single node v. If all of v’s neighbors have decided and no neighbor joined the MIS, then v can join the MIS. Otherwise, if there is one neighbor in the MIS, then v has decided per definition as it cannot join the MIS. Combining this fact with Lemma 4.8, we have that:
Since all executions are independent, the probability that none of the \(c_1\log n\) executions finishes after \(\tau _{c_2}\) rounds is:
Now recall that there are at most n undecided components. Therefore—by the union bound—all components have at least one finished execution. Thus, all nodes have decided at the end of stage 3 w.h.p. Since the time and message bounds follow directly from the algorithms we used as a black box, this proves Theorem 1.3
4.3 Spanning trees
We will now show how the algorithm of Theorem 1.2 can be used to construct a spanning tree of the (undirected version of the) initial graph G. For simplicity, we assume that this graph is connected; our algorithm can easily be extended to also compute spanning forests of unconnected graphs by running it in each connected component. We show the following theorem:
Theorem 1.4
Let \(G = (V, E)\) be a weakly connected directed graph. There is a randomized algorithm that computes an MIS of G in \(O(\log d + \log \log n)\) rounds, w.h.p., in the hybrid model. The algorithm requires global capacity \(O(\log ^2 n)\), w.h.p.
Our algorithm will heavily rely on node labelings, i.e., we assign a short label l(v) to each node \(v \in V\) that can be compared with other labels. If a node \(v \in V\) has edge \(\{v,w\} \in E\) to some node w with \(l(w)<l(v)\), we call this a critical edge. Our goal is to exploit the following simple fact:
Lemma 4.9
(Ordering implies spanning tree) Let \(G := (V, E)\) be an undirected graph and \(l(v_0), \ldots , l(v_n)\) be an ordered labeling of the nodes. Further, let \(E_S\) be a set of edges. Suppose it holds that
-
1.
There is exactly one node \(v'\) with \(l{(v')} < l(v)\) for all \(v \in V \setminus \{v'\}\), and
-
2.
all other nodes \(v \in V \setminus \{v'\}\) have a critical edge.
Then, if each \(v \in V \setminus \{v'\}\) adds a critical edge to \(E_S\), the resulting graph \((V, E_S)\) is a spanning tree of G.
Proof
Since each node (except \(v'\)) adds at most one edge, the resulting graph can have at most \(n-1\) edges and is either a tree or a forest. Therefore, it remains to show that it is connected and, therefore, a tree. However, this follows because each node must have a path to \(v'\). Otherwise, there either would be a node v with \(l(v)>l({v'})\) that did not add an edge, or there are two nodes with minimal labels. Both options contradict one of the two conditions; thus, our claim follows. \(\square \)
Our goal is to find such a labeling. Our strategy roughly works as follows: Note that the algorithm of Theorem 1.2 constructs a graph \(G_{L}\) that results from \(L \in O(\log n)\) evolutions of the graph \(G_0\) that resulted from Lemma 4.1. Therefore, it has diameter \(O(\log n)\) and degree \(O(\log ^2 n)\), w.h.p. We will use this graph as the starting point for our construction, not the final well-formed tree (i.e., we skip the last step where we reduce the degree). First, we construct a spanning tree \(S_{L}\) of \(G_{L}\) by performing a BFS from the node with the lowest identifier and then compute an ordering on \(S_{L}\). Our idea is to iteratively replace all the edges of \(S_{L}\) by edges of \(G_{{L}-1}\), replace these edges by edges of \(G_{{L}-2}\), and so on until we reach a graph that contains only edges of \(G_0\). In every step of the recursion, we also carefully update the ordering and preserve the conditions mentioned in Lemma 4.9, such that the final ordering implies a spanning tree in G.
More precisely, our algorithm executes the following steps.
Step 1: Create a Locally Checkable Ordering.
Let \(v_0\) be the node with the lowest identifier. We first perform a BFS in \(G_L\) from \(v_0\) and create our initial (BFS-)tree \(S_L\). Each node \(v \in V \setminus \{v_0\}\) stores the round in which the broadcast reached it, i.e., its distance to \(v_0\), as its label. Note that there can be nodes with equal labels. However, it holds that
-
1.
the root \(v_0\) is the only node with label \(l_{v_0} = 0\), and
-
2.
all nodes have a parent with a lower label (as the broadcast reached them in the previous round).
Therefore, we have a labeling as required by Lemma 4.9.
Step 2: Recursively Replace Edges.
Next, we want to replace all edges of \(S_{L}\) with edges of \(G_0\) in a recursive fashion. In each step of the recursion, each node maintains a label l(v) such that each node v with \(l(v) \ne l({v_0})\) has at least one critical edge and the root stays unique. Since all nodes initially know their hop distance to the root, this condition is trivially fulfilled for \(S_L\). Now we get to the recursive replacement: Suppose we are in the \(i^{th}\) step of the recursion, i.e., we want to construct \(S_{L-(i+1)}\) from \(S_{L-i}\). Let the edge \((v,w) \in S_{L-i}\) be the result of a random walk \((v, v_1, \ldots , v_{\ell -1}, w)\) in our main algorithm. We assume for the moment that v knows all nodes of the walk and can communicate with them. Then we perform the following steps:
-
1.
v sends the label \(\left( l(v) \circ j\right) \) to each \(v_j\) on the walk. Here, \(\circ \) denotes the concatenation operator for two bit strings.
-
2.
\(v_j\) then picks the minimum of all its received labels as its new label and informs all its neighbors in \(G_{L-(i+1)}\) about it.
-
3.
The root \(v_0\) sets its label to \(l({v_0}) = l({v_0}) \circ 0\) (which obviously remains the unique minimal label).
Finally, each node except the root picks a critical edge \((v,w')\) with \(l({w'}) \le l(v)\) and adds it to \(S_{L-(i+1)}\).
To prove that this indeed is a spanning tree, we must show that the conditions from above still hold: Since there is only one root with the minimal label by construction, we must only show that all other nodes have a critical edge. In particular, if v is not the root, there must be a neighbor with a smaller label. Let now \(l'_v := l({x}) \circ j\) the minimal label that was assigned to v, i.e., v is the \(j^{th}\) node on some walk from x to y in \(G_{L-(i+1)}\). Consider the following cases:
-
If \(v = x\), then v assigned a label to itself, so the prefix of the new label is its old label l(v). However, since v has a parent p(v) in \(S_{L-i}\), it must have received a label \(l'_{p(v)}\) with prefix l(p(v)) from p(v). Since (v, p(v)) was a critical edge by construction, it holds \(l({p(v)}) < l({v})\), i.e., the label \(l'({p(v)})\) sent by p(v) is strictly smaller than \(l'({v})\). Thus, v did not pick the minimum label, which is a contradiction.
-
Otherwise, if \(x \ne v\), there must be a predecessor in the walk that is a neighbor of v in \(G_{L-(i+1)}\). This predecessor can only get a label smaller or equal to \(l({x}) \circ j-1\) which therefore is smaller than v’s new label \(l'({v})\).
Thus, each \(v \in V\) has a neighbor that has a critical edge or is the root (which has the unique minimal label). By Lemma 4.9, we can construct \(S_{L-(i+1)}\) in one step by picking a critical edge.
As mentioned, our algorithm requires that the two endpoints of every edge e need to know the nodes that the corresponding walk traversed (i.e., the nodes that make up e) while sending no more than \(O(\log ^3 n)\) messages. To implement this, we slightly adapt our main algorithm to add the identifier of each traversed node to each token. Further, when creating an edge all of these identifiers are sent back to the node that started the token (i.e., we sample the whole walk instead of just the endpoint). Note that as the token traverses \(\ell \in O(1)\) nodes, the size of each token stays (asymptotically) the same. Thus, the endpoints of each edge e of \(S_{L-i}\) can inform the endpoints of all edges of \(G_{L-(i+1)}\) that make up e. Recall that a node needs to send at most \(\ell \) labels for each edge, resulting in at most \(O(\ell \log ^2 n)\) labels. The size of a label grows by an additive O(1) bits for each recursion as we always add a constant number to the label. So, after \(L \in O(\log n)\) recursions, the label size is still \(O(\log n)\) and therefore, a global capacity of \(O(\log ^2 n)\) suffices. Finally, since each recursion step takes O(1) rounds, we finish after \(L \in O(\log n)\) rounds.
Step 3: Replace Spanner Edges.
Recall that an edge \(\{u,w\}\) in \(S_0\) may not exist in G, i.e., if it resulted from a redirection of an edge \(\{u,v\}\) in \(G_0\) in the algorithm of Sect. 4.1, where u and w were incoming nodes of v. So \(S_0\) may not be a spanning tree of G. Now, as before, we can simply model each edge \(\{u,w\}\) that does not exist in G as the result of the walk that crossed \(\{u,v\}\) and then \(\{v,w\}\) in G. This is not a random walk, but that is immaterial. Node u computes the new labels exactly as before and sends them to v and w. Each node v can be part of O(d(v)) walks. However, since we can now use the local \(\textsf{CONGEST}\) edges, a node v can send and receive a new label to and from all its neighbors in one round. Given the labels, we can construct the tree as before.
We conclude Theorem 1.4.
4.4 Biconnected components
In this section, we present an adaptation of Tarjan and Vishkin’s biconnectivity algorithm [56] to compute the biconnected components of G in \(O(\log n)\) time, proving the following theorem.
Theorem 1.5
Let \(G = (V, E)\) be a weakly connected directed graph. There is a randomized algorithm that computes the biconnected components of (the undirected version of) G in \(O(\log n)\) rounds, w.h.p., in the hybrid model. Furthermore, the algorithm computes whether G is biconnected and, if not, determines its cut nodes and bridge edges. The algorithm requires global capacity \(O(\log ^5 n)\), w.h.p.
The algorithm constructs a helper graph \(G'=(E, E')\) with the edges of G as nodes and with an edge set \(E'\) chosen such that any two edges of G are connected in \(G'\) if and only if they lie on a cycle in G. Therefore, the nodes of each connected component of \(G'\) are edges of the same biconnected component in G. If there is only one component in \(G'\), then G is biconnected.
On a high level, the algorithm can be divided into five steps. In Step 1, we construct a rooted spanning tree T of G and enumerate the nodes from 1 to n, assigning each node v a label l(v), according to the order in which they are visited in a depth-first traversal of T. Let D(v) be the set of descendants of v in T (including v). The goal of Step 2 is to compute \(nd(v) := \vert D(v)\vert \) as well as \(high(v) := \max \{l(u) \mid u \in D^+(v)\}\) and \(low(v) := \min \{l(u) \mid u \in D^+(v)\}\), where \(D^+(v) := D(v) \cup \{u \in V \mid \{u,w\} \in E\setminus T, w \in D(v)\}\) is the union of v’s descendants and its descendants’ neighbors in the undirected version of G. Using these values, in Step 3, the nodes construct the subgraph \(G''\) of \(G'\) that only contains the nodes that correspond to edges of T (i.e., it does not include nodes for the non-tree edges of \(G-T\)). The nodes simulate \(G''\) in a way that allows them to perform Theorem 1.2 without any overhead to establish a well-formed tree on each connected component of \(G''\) in Step 4. Finally, in Step 5, the components of \(G''\) are extended by nodes corresponding to non-tree edges to obtain the full biconnected components of G.
In the remainder of this section, we describe how the five steps can be implemented in the hybrid model in \(O(\log n)\) time using Theorem 1.1 together with the results of [7] and [20]. The correctness of Theorem 1.5 then follows directly from [56, Theorem 1].
Step 1: Construct T.
T is computed using Theorem 1.4 in \(O(\log n)\) time, w.h.p. The tree can be rooted using the algorithm of [20, Lemma 4], which arranges the nodes of T as an overlay ring corresponding to a depth-first traversal of T and performs pointer jumping on that ring. As a by-product, we can easily enumerate the nodes in the order they are visited in the depth-first traversal, whereby each node obtains its label.
Step 2: Compute Subtree Aggregates.
To retrieve the value nd(v) for each node \(v \in V\), the nodes perform the algorithm of [20, Lemma 6] on T: If each node u stores a value \(p_u\), then the algorithm computes the sum of all values that lie in each of v’s adjacent subtrees (i.e., the components into which G decomposes if v gets removed) deterministically in \(O(\log n)\) time; we obtain nd(v) by setting \(p_u = 1\) for each \(u \in V\). However, to compute high(v) and low(v), for each node \(v \in V\), the nodes need to compute maxima and minima. Therefore, we need the following lemma, which is a generalization of [20, Lemma 6].Footnote 10
The directed edges are tree edges, and the undirected edge is a non-tree edge. Left: The first rule adds an edge between the two parent edges of v and w. Center: The second rule connects all nodes on the two paths from v to w to their lowest common ancestor. Right: The edge \(\{v,w\}\) is connected to the component using the third rule
Lemma 4.10
Let \(T=(V, E)\) be a tree and assume that each node \(v\in V\) stores some value \(p_v\). Let f be a distributive aggregate function. The goal of each node v is to compute the value \(f(\{p_w \mid w \in C_u\})\) for each of its neighbors u in H, where \(C_u\) is the connected component C of the subtree \(T'\) of T induced by \(V\setminus \{v\}\) that contains u. The problem can be solved in \(O(\log n)\) time, w.h.p.
Proof
As described before, we enumerate the nodes of T from 1 to n by assigning them a label l(v) according to the order in which they are visited in a depth-first traversal of T (starting at the node s with the smallest identifier). Furthermore, we construct a list L as an overlay in ascending order of their label and root T towards s. This can be done in \(O(\log n)\) time using techniques of [20]. Afterward, the nodes perform pointer jumping on L to create shortcut edges \(E_S\) for \(O(\log n)\) rounds, which decreases the diameter of L to \(O(\log n)\). Additionally, the endpoints i, j of a shortcut edge \(\{i,j\} \in E_S\) learn the weight \(w(\{i,j\}) := f(\{p_k \mid k \in V, l(i) \le l(k) \le l(j)\})\). Now consider some node \(v \in V\). First, we show how v can compute \(f(\{p_u \mid u \in D(v)\})\), i.e., the aggregate of all values in v’s subtree. Note that this value is exactly \(f(\{p_k \mid k \in V, l(v) \le l(k) \le l(w)\})\), where w is the node for which \(l(w) = l(v) + \vert D(v)\vert - 1\) (i.e., the node in v’s subtree with largest label). Note that this value is the aggregate of all values on the segment between v and w on L. To obtain this value, v only needs to learn the weights of at most \(O(\log n)\) shortcut edges on that segment. More formally, there is a path \(P = (v = v_1, v_2, \ldots , v_t = w)\) on L such that \(l(v_{k+1}) = l(v_k) + 2^{\lfloor \log (l(w) - l(v_k)) \rfloor }\) for all \(k < t\). Obviously, \(t = O(\log n)\), and there is a shortcut edge between any two consecutive nodes on that path. To learn the weights of all these shortcut edges, v needs to contact all \(v_k\).
However, since many nodes may want to contact the same node, we cannot send request messages directly, even if each node knows all node identifiers. Instead, we make use of techniques of [7] to construct multicast trees towards each nodeFootnote 11. Since each node needs to contact \(O(\log n)\) nodes, it participates in constructing \(O(\log n)\) multicast trees. Further, each node \(u\in V\) is the root of at most \(O(\log n)\) multicast trees (one for each of its adjacent shortcut edges). When u multicasts the weight of a shortcut edge in the respective multicast tree, all nodes that participated in constructing that tree will be informed. Plugging the parameters \(L = O(n \log n)\) (which is the total number of requests) and \(l = \hat{l} = O(\log n)\) (which is the number of weights each node wants to learn) into [7, Theorem 2.3] and [7, Theorem 2.4], we get that each node learns all weights in \(O(\log n)\) time, w.h.p.Footnote 12
After having learned the weights of all edges on P, v can easily compute \(f(\{p_u \mid u \in D(v)\})\). By sending this value to its parent in T (over a local edge), each node learns the aggregate of the subtree of each of its children. It remains to compute \(f(\{p_u \mid V \setminus D(v)\})\), i.e. the aggregate of all non-descendants of v. Note that since the descendants of v form a connected segment from v to w in L, these non-descendants form exactly two segments on L: one from s to v (excluding v) and one from w to the last node of L (excluding w). Using the same strategy as before, v can compute the aggregate of all these values by learning the weight of \(O(\log n)\) shortcut edges. \(\square \)
Step 3: Construct \(G''\).
Recall that \(G''\) is the subgraph of \(G'\) induced only by the nodes corresponding to edges of T. In order to simulate \(G''\), we let each node v of G act on behalf of the node of \(G''\) that corresponds to v’s parent edge. That is, when simulating an algorithm on \(G''\), v is responsible for all messages the node corresponding to v’s parent edge is supposed to communicate. We now need to connect all nodes corresponding to edges on a common simple cycle in G. Tarjan and Vishkin showed that it suffices to consider the simple cycles consisting of a non-tree edge and the unique shortest path between its adjacent nodes [56]. To do this, they propose the following rules:
-
1.
If (v, u) and (w, x) are edges in the rooted tree T (directed from child to parent), and \(\{v,w\}\) is an edge in \(G-T\) such as that v is no descendant of w and w is no descendant of v in T (i.e., v and w lie in different subtrees), add \(\{\{u,v\},\{x,w\}\}\) to \(G''\).
-
2.
If (w, v) and (v, u) are edges in T and some edge of G connects a descendant of w with a non-descendant of v, add \(\{\{u,v\},\{v,w\}\}\) to \(G''\).
Roughly speaking, for each non-tree edge \(\{v,w\}\) that connects two different subtrees of T, the first rule connects the parent edges of v and w, whereas the second rule connects all edges of T that lie on the two paths from v to w to their lowest common ancestor. An illustration of these rules can be found in the left and center image of Fig. 2.
As Tarjan and Vishkin point out, each node v can determine each connection of its parent edge that is formed according to the first rule by comparing \(l(v) + nd(v)\) with the label l(u) of each of its neighbors u in G; if \(l(v) + nd(v) \le l(u)\), then the two parent edges of v are connected in \(G''\). For the second rule, each node v, \(l(v) \ne 1\) with child w connects its parent edge with the parent edge of w if \(low(w) < v\) or \(high(w) \ge v + nd(v)\).
Step 4: Compute Connected Components of \(G''\).
To compute the connected components of \(G''\), we execute the algorithm of Theorem 1.2 on \(G''\). Note that every two nodes that are connected in \(G''\) are simulated by adjacent nodes in G; therefore, the local communication in \(G''\) can be carried out using the local edges of G. Furthermore, since each node of G simulates at most one node of \(G''\), the global communication can also be simulated with the same communication capacity as in Theorem 1.2. After \(O(\log n)\) rounds, w.h.p., we have established a well-formed tree on each connected component of \(G''\).
Step 5: Extend \(G''\) to \(G'\).
Finally, we incorporate the non-tree edges into the connected components of \(G''\) using the following rule of Tarjan and Vishkin.
-
3.
If (w, u) is an edge of T and \(\{v,w\}\) is an edge in \(G-T\), such that \(l(v)<l(w)\), add \(\{\{u,w\},\{v,w\}\}\) to \(G''\).
An example can be found in the right image of Fig. 2. Note that this only extends the connected components of \(G''\) by single nodes (i.e., it does not merge components of \(G''\)). Therefore, we know the biconnected component of each edge of G. Specifically, if there is only one biconnected component in \(G'\) (which can easily be determined by counting the number of nodes that act as the root of a well-formed tree in \(G''\)), we can determine whether G is biconnected. Furthermore, we can determine the cut nodes and bridge edges in G. We conclude Theorem 1.5.
5 Concluding remarks and future work
In this article, we answered the longstanding open question of whether an overlay network can be transformed into a graph of diameter \(O(\log n)\) in \(O(\log n)\) time with polylogarithmic communication. We present several applications for our algorithm and thereby show that it can speed up solutions for various other distributed problems. Whereas our solution is asymptotically time-optimal, our communication bounds may improve. If the initial degree is d, then our nodes need to communicate \(\Theta (d + \log ^2 n)\) many messages. However, there might be an algorithm that only requires a communication capacity of \(\Theta (d+\log n)\). Eradicating the additional \(\log n\) factor from our algorithm seems non-trivial and poses an exciting goal. Furthermore, we believe that—due to its simplicity—our algorithm can also be extended to construct expanders under (randomized) churn. Last, since our algorithm runtime is strongly tied to the initial graph’s conductance, it may also be used to speed up distributed algorithms for property testing (see [22, 40] for examples) in hybrid networks.
Notes
An event holds with high probability (w.h.p.) if it holds with probability at least \(1 - 1/n^c\) for an arbitrary but fixed constant \(c > 0\).
\(\widetilde{O}(\cdot )\) hides polylogarithmic factors
The arboricity of a graph is the minimum number of forests its edges can be partitioned into.
We describe the concrete implementation of this broadcast in Sect. 4.1 and assume that it is possible for the moment.
Indeed, they explicitly mention that for non-regular graph one could define a escape probability for which their claims would hold and which could be used instead of the conductance in our proofs. Nevertheless, since we only observe regular graphs, we use the notion of conductance to avoid introducing more concepts.
We will show that each node only sends and receives at most \(O(\Delta )\) tokens in each round, w.h.p.
We will see, however, that this case does not occur w.h.p.
Later on, we will see that it actually holds \(x^w_{u^*} = \textsf{dist}(u^*,w) \), but this is immaterial for this proof.
Note that the faster algorithms are more intricate and use more preprocessing stages to reduce degrees, but still rely on this scheme in the end.
Note that a naive PRAM simulation in a butterfly introduces an additional factor of (at least) \(\Theta (\log n)\) to the runtime, which we cannot afford. Furthermore, this result may be of independent interest for hybrid networks.
[7, Theorem 2.4] actually restricts each node to multicasting at most one multicast message. However, the theorem can easily be extended to allow multiple messages without increasing the runtime. The authors in [7] assume a global capacity of \(O(\log n)\). Since we assume a global capacity of \(\Omega {\log ^2{n}}\), each node can execute the algorithm \(O(\log n)\) times in parallel with the same complexity. Thus, we can build \(O(\log {n})\) multicast trees per node in time \(O(\log {n})\).
References
Alon, N., Babai, L., Itai, A.: A fast and simple randomized parallel algorithm for the maximal independent set problem. J. Algorithms 7(4), 567–583 (1986)
Angluin, D., Aspnes, J., Chen, J., Wu, Y., Yin, Y.: Fast construction of overlay networks. In: Proceeding of the 17th Annual ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), pp. 145–154 (2005)
Aspnes, J., Shah, G.: Skip graphs. In: Proceeding of the 14th ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 384–393 (2003)
Aspnes, J., Wu, Y.: O(logn)-time overlay network construction from graphs with out-degree 1. In: Tovar, E., Tsigas, P., Fouchal, H. (eds.) Proceedings of the 11th International Conference on Principles of Distributed Systems (OPODIS), volume 4878 of Lecture Notes in Computer Science, pp. 286–300. Springer (2007)
Assadi, S., Sun, X., Weinstein, O.: Massively parallel algorithms for finding well-connected components in sparse graphs. In: Robinson, P., Ellen, F. (eds.) Proceedings of the 2019ACM Symposium on Principles of Distributed Computing (PODC), pp. 461–470. ACM (2019)
Augustine, J., Choudhary, K., Cohen, A., Peleg, D., Sivasubramaniam, S., Sourav, S.: Distributed graph realizations . In: 2020 IEEE International Parallel and Distributed Processing Symposium (IPDPS), New Orleans, LA, USA, May 18–22, 2020, pp. 158–167. IEEE (2020)
Augustine, J., Ghaffari, M., Gmyr, R., Hinnenthal, K., Kuhn, F., Li, J., Scheideler, C.: Distributed computation in node-capacitated networks. In: Proceedings of the 31st Annual ACM Symposium on Parallelism in Algorithms and Architectures (SPAA) (2019)
Augustine, J., Hinnenthal, K., Kuhn, F., Scheideler, C., Schneider, P.: Shortest paths in a hybrid network model. In: Proceedings of the Fourteenth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1280–1299. SIAM (2020)
Augustine, J., Pandurangan, G., Robinson, P., Roche, S.T., Upfal, E.: Enabling robust and efficient distributed computation in dynamic peer-to-peer networks. In: Proceedings of 56th IEEE Annual Symposium on Foundations of Computer Science (FOCS), pp. 350–369 (2015)
Augustine, J., Sivasubramaniam, S.: Spartan: a framework for sparse robust addressable networks. In: Proceedings of the 32nd IEEE International Parallel and Distributed Processing Symposium (IPDPS), pp. 1060–1069 (2018)
Barenboim, L., Elkin, M.: Sublogarithmic distributed MIS algorithm for sparse graphs using Nash–Williams decomposition. Distrib. Comput. 22(5–6), 363–379 (2010)
Barenboim, L., Elkin, M., Pettie, S., Schneider, J.: The locality of distributed symmetry breaking. J. ACM 63(3), 20:1-20:45 (2016)
Behnezhad, S., Brandt, S., Derakhshan, M., Fischer, M., Hajiaghayi, T.M., Karp, R.M., Uitto, J.: Massively parallel computation of matching and MIS in sparse graphs. In: Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, pp. 481–490 (2019)
Berns, A., Ghosh, S., Pemmaraju, S.V.: Building self-stabilizing overlay networks with the transitive closure framework. Theor. Comput. Sci. 512, 2–14 (2013)
Brandt, S., Fischer, M., Uitto, J.: Breaking the linear-memory barrier in MPC: fast MIS on trees with strongly sublinear memory. In: International Colloquium on Structural Information and Communication Complexity, pp. 124–138. Springer (2019)
Censor-Hillel, K., Fischer, E., Schwartzman, G., Vasudev, Y.: Fast distributed algorithms for testing graph properties. Distrib. Comput. 32(1), 41–57 (2019)
Chong, K.W.A., Han, Y., Lam, T.W.: Concurrent threads and optimal parallel minimum spanning trees algorithm. J. ACM 48, 297–323 (2001)
Drees, M., Gmyr, R., Scheideler, C.: Churn- and dos-resistant overlay networks based on network reconfiguration. In: Proceedings of the 28th ACM Symposium on Parallelism in Algorithms and Architectures (SPAA)
Elkin, M., Neiman, O.: Efficient algorithms for constructing very sparse spanners and emulators. ACM Trans. Algorithms (TALG) 15(1), 1–29 (2018)
Feldmann, M., Hinnenthal, K., Scheideler, C.: Fast hybrid network algorithms for shortest paths in sparse graphs. In: Proceedings of the 24th International Conference on Principles of Distributed Systems (OPODIS), pp. 31:1–31:16 (2020)
Feldmann, M., Scheideler, C., Schmid, S.: Survey on algorithms for self-stabilizing overlay networks. ACM Comput. Surv. 53(4) (2020)
Fichtenberger, H., Vasudev, Y.: A two-sided error distributed property tester for conductance. In: 43rd International Symposium on Mathematical Foundations of Computer Science (MFCS 2018). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2018)
Ghaffari, M.: An improved distributed algorithm for maximal independent set. In: Proceedings of the 27th Annual ACM-SIAM Symposium on Discrete algorithms (SODA), pp. 270–277. SIAM (2016)
Ghaffari, M.: Distributed maximal independent set using small messages. In: Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA ’19, pp. 805–820. Society for Industrial and Applied Mathematics (2019)
Ghaffari, M., Gouleakis, T., Konrad, C., Mitrović, S., Rubinfeld, R.: Improved massively parallel computation algorithms for MIS, matching, and vertex cover. In: Proceedings of the 2018 ACM Symposium on Principles of Distributed Computing, pp. 129–138 (2018)
Ghaffari, M., Grunau, C., Jin, C.: Improved MPC algorithms for MIS, matching, and coloring on trees and beyond. In: Attiya, H. (ed.) 34th International Symposium on Distributed Computing (DISC 2020), volume 179 of Leibniz International Proceedings in Informatics (LIPIcs), pp. 34:1–34:18. Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Dagstuhl, Germany (2020)
Ghaffari, M., Grunau, C., Rozhon, V.: Improved deterministic network decomposition. In: Dániel, M. (ed.) Proceedings of the 2021 ACM-SIAM Symposium on Discrete Algorithms, SODA 2021, Virtual Conference, January 10–13, pp. 2904–2923. SIAM (2021)
Gilbert, S., Pandurangan, G., Robinson, P., Trehan, A.: Dconstructor: Efficient and robust network construction with polylogarithmic overhead. In: Proceedings of ACM Symposium on Principles of Distributed Computing (PODC), pp. 438–447. ACM (2020)
Gkantsidis, C., Mihail, M., Saberi, A.: Random walks in peer-to-peer networks. In: Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM). IEEE (2004)
Gmyr, R., Hinnenthal, K., Scheideler, C., Sohler, C.: Distributed Monitoring of Network Properties: The Power of Hybrid Networks. In: Proceedings of the 44th International Colloquium on Automata, Languages, and Programming (ICALP), pp. 137:1–137:15 (2017)
Götte, T., Hinnenthal, K., Scheideler, C.: Faster construction of overlay networks. In: International Colloquium on Structural Information and Communication Complexity (SIROCCO), pp. 262–276. Springer (2019)
Götte, T., Vijayalakshmi, V.R., Scheideler, C.: Always be two steps ahead of your enemy. In: Proceedings of the 33rd IEEE International Parallel and Distributed Processing Symposium (IPDPS) (2019)
Haeupler, B., Li, J.: Faster distributed shortest path approximations via shortcuts. In: Schmid, U, Widder, J. (eds.) 32nd International Symposium on Distributed Computing, DISC 2018, New Orleans, LA, USA, October 15–19, 2018, volume 121 of LIPIcs, pp. 33:1–33:14. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2018)
Halperin, S., Zwick, U.: Optimal randomized EREW PRAM algorithms for finding spanning forests. J. Algorithms 39(1), 1–46 (2001)
Jacob, R., Richa, A.W., Scheideler, C., Schmid, S., Täubig, H.: Skip+: a self-stabilizing skip graph. J. ACM 61(6), 36:1-36:26 (2014)
Karger, D.R.: Minimum cuts in near-linear time. J. ACM (JACM) 47(1), 46–76 (2000)
Kuhn, F., Moscibroda, T., Wattenhofer, R.: What cannot be computed locally! In: Proceedings of the Twenty-Third Annual ACM Symposium on Principles of Distributed Computing, pp. 300–309 (2004)
Kuhn, F., Schneider, P.: Computing shortest paths and diameter in the hybrid network model. In: Proceedings of the 39th Annual ACM Symposium on Principles of Distributed Computing (PODC), pp. 109–118. ACM (2020)
Kwok, T.C., Lau, L.C.: Lower bounds on expansions of graph powers. In: Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques (APPROX/RANDOM 2014). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2014)
Łącki, Jakub, Mitrović, Slobodan, Onak, Krzysztof, Sankowski, Piotr: Walking randomly, massively, and efficiently. In Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing, 364–377 (2020)
Law, C., Siu, K.-Y.: Distributed construction of random expander networks. In: Proceedings IEEE INFOCOM 2003, The 22nd Annual Joint Conference of the IEEE Computer and Communications Societies, San Franciso, CA, USA, March 30–April 3, 2003, pp. 2133–2143. IEEE Computer Society (2003)
Lee, J.R., Gharan, S.O., Trevisan, L.: Multiway spectral partitioning and higher-order Cheeger inequalities. J. ACM (JACM) 61(6), 1–30 (2014)
Liu, S.C., Tarjan, R.E., Zhong, P.: Connected components on a PRAM in log diameter time. In: Scheideler, C., Spear, M. (eds.) Proceedings of the 32nd ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), Virtual Event, USA, July 15–17, 2020, pp. 359–369. ACM (2020)
Lovász, L., Simonovits, M.: The mixing rate of Markov chains, an isoperimetric inequality, and computing the volume. In: Proceedings of 31st Annual Symposium on Foundations of Computer Science (FOCS), pp. 346–354. IEEE (1990)
Luby, M.: A simple parallel algorithm for the maximal independent set problem. SIAM J. Comput. 15(4), 1036–1053 (1986)
Miller, G.L., Peng, R. , Vladu, A., Xu, S.C.: Improved parallel algorithms for spanners and hopsets. In: Proceedings of the 27th ACM symposium on Parallelism in Algorithms and Architectures (SPAA), pp. 192–201 (2015)
Métivier, Y., Robson, J.M., Nasser, S.-D., Zemmari, A.: An optimal bit complexity randomized distributed MIS algorithm. In: International Colloquium on Structural Information and Communication Complexity (SIROCCO), pp. 323–337. Springer (2009)
Oaks, S., Gong, L.: Jxta in a Nutshell. O’Reilly & Associates Inc, USA (2002)
Pettie, S., Ramachandran, V.: A randomized time-work optimal parallel algorithm for finding a minimum spanning forest. SIAM J. Comput. 31, 1879–1895 (2002)
Robinson, P.: Being fast means being chatty: the local information cost of graph spanners. In: Proceedings of the 15th ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 2105–2120 (2021)
Rowstron, A.I.T., Druschel, P.: Pastry: scalable, decentralized object location, and routing for large-scale peer-to-peer systems. In: Proceedings of IFIP/ACM International Conference on Distributed Systems Platforms (Middleware), pp. 329–350 (2001)
Sarma, A.D., Molla, A.R., Pandurangan, G., Upfal, E.: Fast distributed pagerank computation. In: International Conference on Distributed Computing and Networking, pp. 11–26. Springer (2013)
Sinclair, A.: Algorithms for Random Generation and Counting: A Markov chain approach. Springer, New York (2012)
Sinclair, A., Jerrum, M.: Approximate counting, uniform generation and rapidly mixing Markov chains. Inf. Comput. 82(1), 93–133 (1989)
Stoica, I., Morris, R.T., Karger, D.R., Kaashoek, M.F., Balakrishnan, H.: Chord: a scalable peer-to-peer lookup service for internet applications. In: Proceedings of the 2018 Conference of the ACM Special Interest Group on Data Communication (SIGCOMM), pp. 149–160 (2001)
Tarjan, R.E., Vishkin, U.: An efficient parallel biconnectivity algorithm. SIAM J. Comput. 14(4), 862–874 (1985)
Xu, S.C.: Exponential Start Time Clustering and its Applications in Spectral Graphy Theory. PhD thesis, Carnegie Mellon University, Pittsburgh, August 2017. CMU CS Tech Report CMU-CS-17-120
Acknowledgements
This work was partially supported by the German Research Foundation (DFG) within the Collaborative Research Centre On-The-Fly Computing (GZ: SFB 901/3) under the project number 160364472.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Götte, T., Hinnenthal, K., Scheideler, C. et al. Time-optimal construction of overlay networks. Distrib. Comput. 36, 313–347 (2023). https://doi.org/10.1007/s00446-023-00442-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00446-023-00442-4




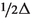 self-loops.
self-loops.
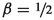 . Values larger than
. Values larger than 