Quantifying uncertainty in probabilistic volcanic ash hazard forecasts, with an application to weather pattern based wind field sampling

Abstract

Probabilistic forecasting of volcanic ash dispersion involves simulating an ensemble of realistic event scenarios to estimate the probability of a particular hazard threshold being exceeded. Although the number of samples that make up the ensemble, how they are chosen, and the desired threshold all set the uncertainty of (or confidence in) the estimated exceedance probability, current practice does not quantify and communicate the uncertainty in ensemble predictions. In this study, we use standard statistical methods to estimate the variance in probabilistic ensembles and use this measure of uncertainty to assess different sampling strategies for the wind field, using the example of volcanic ash transport from a representative explosive eruption in Iceland. For stochastic (random) sampling of the wind field, we show how the variance is reduced with increasing ensemble size and how the variance depends on the desired hazard threshold and the proximity of a target site to the volcanic source. We demonstrate how estimated variances can be used to compare different ensemble designs, by comparing stochastic forecasts with forecasts obtained from a stratified sampling approach using a set of 29 Northern European weather regimes, known as Grosswetterlagen (GWL). Sampling wind fields from within the GWL regimes reduces the number of samples needed to achieve the same variance as compared to conventional stochastic sampling. Our results show that uncertainty in volcanic ash dispersion forecasts can be straightforwardly calculated and communicated, and highlight the need for the volcanic ash forecasting community and operational end-users to jointly choose acceptable levels of variance for ash forecasts in the future.

Introduction

A key consideration in forecasting the spatial extent and intensity of future natural hazard events is accounting for the variability in environmental conditions that influence them. This is commonly investigated using a probabilistic approach, which involves simulating sufficiently many realistic event scenarios, where environmental conditions are sampled from a distribution of sufficient duration, to incorporate much of the likely variability (Bonadonna , 2006; Jenkins et al. , 2012). The simulation results are then aggregated to estimate the probability of exceeding a given threshold, or the threshold exceeded at a given probability (Rougier , 2013). In the volcanological literature, there is no commonly applied principle that informs the number of simulations that is ‘sufficient’ to characterise the variability of environmental conditions, so choices are often made on a pragmatic basis (Bonadonna et al. , 2005; Jenkins et al. , 2012; Jenkins et al. , 2015; Harvey et al. , 2020; Zidikheri and Lucas , 2021). Furthermore, these predictions are often stated without a confidence bound on the prediction, which is critical given that the use of simulations to determine hazard probabilities is an exercise in statistical estimation (Rougier , 2013). In this paper, we explore the relationship between sample size, uncertainty, and sampling strategies in probabilistic assessments of volcanic ash dispersion.

Atmospheric dispersion of volcanic ash is driven by wind fields and atmospheric turbulence; dispersion models are forced using measured or interpolated wind fields (typically reported as means at regular intervals), and turbulence is parameterised within the models. Given a historical record of wind fields, a convenient approach is to sample the wind fields stochastically by randomly selecting the start date in this record (Bonadonna et al. , 2005; Jenkins et al. , 2012). If the eruption source parameters are held constant to solely investigate the influence of the environmental forcing, then this is termed the ‘One Eruption Scenario’ (Bonadonna , 2006). The stochastic approach assumes that, with enough randomly selected samples, the variability in the natural occurrence of different wind directions and velocities will be reproduced in the wind field data used and that there are no underlying trends in the wind behaviour which evolve over the long term (i.e. the dataset is stationary). Stochastic sampling is widely used in probabilistic assessments of volcanic ash dispersion (e.g. Connor et al. 2001; Bonadonna et al. 2005; Bonadonna 2006; Macedonio et al. 2008; Jenkins et al. 2012, 2015; Biass et al. 2016). These studies vary widely in the number of individual simulations that are used to construct the ensemble, for example from 73 (Macedonio et al. , 2008) to 19,200 (Jenkins et al. , 2015), and primarily limitations on computational resources or time are the justifications given for the choice of ensemble size. Quantifying the uncertainty associated with the choice of sample size is crucial to appropriately balance the trade-off between accuracy and computation.

In this paper, we introduce the use of standard statistical measures to compare results from ensembles of different sizes. The use of stochastic simulations to create probabilistic ash dispersion forecasts is guided by the idea that a larger number of simulations will better reflect the range of environmental conditions that control dispersion. To be concrete, we consider estimation of the expectation of some output of the simulator, i.e. the average of that output over all possible inputs. A natural estimator for this quantity is the sample mean, i.e. the average of that output over a finite number of randomly sampled inputs, requiring that number of simulator runs. The sample mean of only a few outputs is typically quite variable, in the sense that it may be quite different to the true mean, and one way to quantify this variability is through the variance of the sample mean: the expected squared deviation of the sample mean from the true mean. In fact, the variance of the sample mean is inversely proportional to the sample size itself, so running more simulations will decrease the variance of the estimator.

A typical aim of stochastic simulation is to make a prediction together with some quantification of the associated uncertainty, and in some cases, it is necessary for the uncertainty to be below some prescribed level (Rougier , 2013). A standard way to accomplish the former is to construct confidence intervals, which depend explicitly on the variance of the estimator, and the former can be addressed by drawing sufficiently many samples such that the variance is below the prescribed level. Presenting the results of a stochastic method without an assessment of the uncertainty in them provides incomplete information to end-users, as previously emphasised for the estimation of exceedance probabilities for natural hazards generally (Rougier , 2013) and for ash dispersion ensembles in particular (Marzocchi et al. , 2015). Looking forward, guidance for future operational probabilistic forecasts of airborne volcanic ash concentration in the atmosphere requires their results to be stated with associated confidence intervals or variance estimates (ICAO , 2017; WMO-IUGG , 2019).

The use of stochastic sampling of wind fields for volcanic ash dispersion assumes that the wind fields are stationary in time, and so the historical record for wind fields provides an appropriate distribution for wind fields at an unspecified future date. There is, however, an underlying structure to the wind fields over shorter-term intervals because they occur as a result of large-scale weather systems. This structure allows daily conditions to be identified as belonging to one of a set of weather patterns; for example, the weather systems over northern Europe have been classified into a set of 29 synoptic (1000 km scale) weather regimes, named Grosswetterlagen (James , 2007). Grouping wind fields into regimes allows an alternative stratified sampling approach to be taken (Cochran , 1977): sample forcing data from within individual weather regimes, then weight each resulting set of simulations by the frequency of occurrence of that pattern. The potential benefits of this approach are to reduce the number of simulations needed to reproduce the variability of the natural wind fields, because the number of patterns is smaller than the number of individual different states of the wind field. Stratified sampling approaches are widely used to achieve reductions in variance in other applications (e.g. Hens and Tiwari 2012; D’Amato et al. 2012; Da Silva Fonseca Junior et al. 2015).

In this paper, we will demonstrate the use of variance computations to compare ensemble predictions of volcanic ash dispersion and explore the potential of stratified sampling using weather regimes to reduce the variance in those predictions. We use a dataset of simulations made using the dynamic ash dispersion model FALL3D (Folch et al. , 2009), to assess potential ash impacts to northwestern Europe from a representative eruption of an Icelandic volcano. The paper is set out as follows: we first introduce the statistical background that quantifies the relationship between the number of samples, the estimates of exceedance probabilities, and the variance of these estimates. We then present the data and methods used, and in the “Results” section, we present results comparing the variances of ensembles of different sizes and demonstrate that stratified sampling of weather regimes reduces the number of samples needed to achieve a desired variance. In the “Discussion” section, we discuss the benefits of quantifying and presenting measures of uncertainty, and of employing a stratified sampling approach, in probabilistic assessment of volcanic ash dispersion.

Statistical background

This section presents the background, principles, and definitions of stochastic sampling in the context of volcanic ash hazard assessment. We introduce the widely used method for estimating the exceedance probability of an ash concentration threshold and demonstrate the calculation of its variance for use in the construction of confidence intervals before proceeding to illustrate the relationship between such probabilities and their variances. We show that the number of samples required for exceedance probability estimates is intrinsically linked to the magnitude of the probability itself and, hence, the threshold of interest. Furthermore, the desire to attain some level of confidence in the estimate suggests the need for some minimum number of simulations, indicating the existence of a relationship between the threshold of interest, the variance of its exceedance probability estimate, and the computational resources required for accurate estimation.

An ensemble is constructed by carrying out a number of simulations whose inputs are sampled stochastically from some distribution which is assumed to be representative of the real world. The outputs returned by the simulator are aggregated to construct the resulting probabilistic assessment of the eruption scenario. Deterministic simulators such as FALL3D (Folch et al. , 2009) simulate the dispersion and transportation of ash over time given wind field data and eruption source conditions. Since no additional stochasticity is introduced by such a simulator, by keeping the volcanological inputs constant across simulations and drawing wind fields from historical data, we arrive at an ensemble of simulations whose variability is dependent only upon the wind field data. Provided that the historical record is representative of the long-term variability in wind fields, the ensemble should encapsulate the variability of likely real-world outcomes of the eruption scenario.

Drawing such wind field data from a historical dataset consists of choosing a date from the historical record and providing the corresponding wind field data to the simulator. We can therefore view the simulator output as the application of a function to some randomly chosen start date.

Stochastic sampling for exceedance probability estimation

Denoting the set of possible start dates by $\mathcal {Z}$, we view the start date provided to the simulator as a random variable Z which is drawn uniformly at random (i.e. with equal probability) from $\mathcal {Z}$. In the One Eruption Scenario, since the volcanological inputs remain fixed, we then view the output of the (deterministic) simulator as the result of applying some function $\phi$ to the realised value z of Z, $\phi (z)$. The exceedance probability of an ash concentration threshold c $\mu$g m$^{-3}$, is defined as the probability that, at the location of interest, the maximum ash concentration that persists for more than some specified period of time (e.g. 24 h) is greater than c $\mu$g m$^{-3}$. Mathematically, we can view this maximum concentration as the result of applying a second function $\psi$ to the output of the simulator, which we represent by $\psi \circ \phi \, (z)$, where $\circ$ denotes the composition of functions.

The random variable $X = \mathbbm {1} \left\{ \psi \circ \phi \, (Z) \ge c \right\}$, where $\mathbbm {1}$ denotes the indicator function, then represents the event of exceedance. X has a Bernoulli distribution with success parameter p, which depends implicitly on $\psi$, $\phi$, and c: X takes value 1 with probability p and value 0 with probability $1-p$. The expectation of X is $\mathbb {E}_{}\!\left[ X\right] =p$, and its variance (its expected squared deviation from its mean) is $\textrm{Var}_{}\!\left( X\right) = \mathbb {E}_{}\!\left[ (X-\mathbb {E}_{}\!\left[ X\right] )^2\right] = p \, (1-p)$. The exceedance probability is precisely p, and we aim to estimate this value with a high degree of confidence.

Typically, a probabilistic ash hazard assessment will estimate the exceedance probability of an impact threshold via a simple Monte Carlo approach, which we hereby refer to as the stochastic sampling approach. Given some specified number of samples n, we sample $Z_1, \dots , Z_n$ independently and uniformly from the set $\mathcal {Z}$ and transform these into independent Bernoulli samples $X_1, \dots , X_n$, where $X_i:=\mathbbm {1}\left\{ \psi \circ \phi \, (Z_i) \ge c \right\}$ for $i \in \{1, \dots , n\}$. We estimate p intuitively by the sample mean of $X_1, \dots , X_n$,

$$\begin{aligned} p_{\text {simple}}^n := \frac{1}{n} \sum _{i=1}^n X_i, \end{aligned}$$

(1)

where the superscript n indicates the estimate is computed from n samples and the subscript that a simple Monte Carlo approach is used. This provides an unbiased estimate of p, meaning that the expected value of $p_{\text {simple}}^n$ is p. Its variance is given by

$$\begin{aligned} \textrm{Var}_{}\!\left( p_{\text {simple}}^n\right) = \frac{1}{n^{2}} \sum _{i=1}^n \textrm{Var}_{}\!\left( X_i\right) = \frac{1}{n} p (1-p), \end{aligned}$$

(2)

which we can estimate by replacing p with its estimate $p_{\text {simple}}^n$; the estimate will tend towards the true value of the variance as n increases. We proceed to describe how to use this variance estimate to obtain an approximate confidence interval for p.

Confidence intervals

Given data $\textbf{X}:= \left( X_1, \dots , X_n \right)$, a confidence interval (CI) for a parameter is a random interval $\left[ L(\textbf{X}), U(\textbf{X}) \right]$, where the endpoints $L(\textbf{X})$ and $U(\textbf{X})$ of the interval are themselves random variables. A CI should be constructed to have a high probability of containing the true value of that parameter. The size $U(\textbf{X}) - L(\textbf{X})$ of the interval therefore indicates how much uncertainty there is in the value of the parameter. More specifically, for a general parameter $\theta$ associated with the distribution of X, a $100(1-\alpha )\%$ confidence interval for $\theta$ is an interval $\left[ L(\textbf{X}), U(\textbf{X}) \right]$ such that the true value of $\theta$ lies within the interval with probability at least $1-\alpha$ (DeGroot and Schervish , 2012):

$$\begin{aligned} \mathbb {P}\!\left( L(\textbf{X}) \le \theta \le U(\textbf{X}) \right) \ge 1-\alpha , \end{aligned}$$

(3)

where $\alpha \in (0, 1)$ is typically small. We call the probability that $\theta$ lies between $L(\textbf{X})$ and $U(\textbf{X})$ the coverage of the CI.

Given data $\textbf{x}$, we can compute the endpoints $L(\textbf{x})$ and $U(\textbf{x})$ of a real, observed CI. We construct an asymptotically exact CI for a parameter through the notion of asymptotic normality, which we define formally in Appendix B. The important result to note is that we can construct approximate CIs based on the standard normal distribution given an asymptotically normal estimator. In particular, the sample mean $\hat{\mu }_n = \frac{1}{n} \sum _{i=1}^n X_i$ is an asymptotically normal estimator for the expected value of X, $\mu = \mathbb {E}[X]$, and an accompanying estimator for its variance $\sigma ^2 = \textrm{Var}_{}\!\left( X\right)$ is $\hat{\sigma }_n^2 = \frac{1}{n} \sum _{i=1}^n \left( X_i - \hat{\mu }_n \right) ^2$, so an approximate $100(1-\alpha )\%$ CI for $\mu$ is

$$\begin{aligned} \hat{\mu }_n \pm z_{\alpha /2} \sqrt{\frac{\sum _{i=1}^n \left( X_i - \hat{\mu }_n \right) ^2}{n} }. \end{aligned}$$

(4)

where $z_{\alpha /2}:= \Phi ^{-1} \left( 1 - \alpha /2 \right)$ and $\Phi ^{-1}$ is the inverse cumulative distribution function of a standard normal random variable. A traditional choice of confidence level is $\alpha =0.05$ so that $z_{\alpha /2} = 1.96$, giving a 95% CI. Furthermore, since Eq. 1 is simply the sample mean of a $\textrm{Bernoulli}\!\left( p\right)$ random variable, an approximate $100(1-\alpha )\%$ CI for the exceedance probability p is given by

$$\begin{aligned} p_{\text {simple}}^n \pm z_{\alpha /2} \sqrt{\frac{p_{\text {simple}}^n (1-p_{\text {simple}}^n)}{n}}. \end{aligned}$$

(5)

When probabilities are small and we want to capture and convey the risk of a set of hazardous events, it is often beneficial to view these probabilities on a logarithmic scale. In particular, we want to visualise estimates of probabilities of differing magnitudes, and our confidence in these estimates, on the same scale. In Appendix B, we show that an approximate $100(1-\alpha )\%$ CI for $\log p$ which is centred about $\log \left( p_{\text {simple}}^n\right)$ is given by

$$\begin{aligned} \log \left( p_{\text {simple}}^n \right) \pm z_{\alpha /2} \sqrt{\frac{1-p_{\text {simple}}^n}{np_{\text {simple}}^n}}. \end{aligned}$$

(6)

Relationship between threshold and variance

When carrying out a probabilistic hazard assessment, we are usually interested in a set of several impact thresholds rather than a single value. It is clear that the exceedance probability associated with a high ash concentration threshold will be lower than that of a smaller threshold. We would therefore expect more simulations to be required in order to observe at least one exceedance event in our ensemble as the threshold increases. In this section, we demonstrate how to choose our ensemble size such that the lowest exceedance probability of interest can be estimated with some desired level of confidence.

For estimating the value of some p, we must consider a minimal sample size n for which a sensible CI is achievable. Suppose we have an ensemble of size 1000 and the true value of the exceedance probability p for some threshold of interest is $10^{-4}$. Then, the closest possible estimates we might obtain for p using Eq. 1 are either 0 or $10^{-3}$. The former arises by observing no exceedances in the ensemble and the latter by observing a single exceedance in 1000 samples, providing us with an estimate which is 10 times greater than the truth. Furthermore, approximate 95% CI for p would then be either (0, 0) or $(-9.6 \times 10^{-4}, \, 2.96 \times 10^{-3})$, respectively.

A natural way to examine the relationship between the ensemble size n and exceedance probability p is to consider the expectation of the number of exceedances $Y_n:= \sum _{i=1}^n X_i$:

$$\begin{aligned} \mathbb {E}_{}\!\left[ Y_n\right] = \mathbb {E}_{}\!\left[ \sum _{i=1}^{n} X_i\right] = \sum _{i=1}^{n} \mathbb {E}_{}\!\left[ X_i\right] = np. \end{aligned}$$

(7)

In order to have $\mathbb {E}_{}\!\left[ Y_n\right] \ge 1$, we must set $n \ge 1/p$. As such, if we have some prior belief on p for the highest threshold of interest, we can use this relationship to set the number of samples. If $p=10^{-4}$, then at least 10,000 samples are needed in order to expect to observe at least one exceedance.

A single exceedance event does not provide us with much confidence in our estimate, however. Having a higher degree of confidence in our estimate corresponds to reducing our variance such that our CIs centred about this estimate are smaller. Guidance exists for choosing n such that the CI has a desired width, such as Liu and Bailey (2002). We note that for estimates of small Bernoulli probabilities p, the associated variances $p \, (1-p) / n$ are also small, but for small n, these variances are large when compared with the value of p itself. It should therefore be beneficial to consider a measure of the variance in relation to the probability itself rather than the variance in isolation. We introduce the relative variance of the estimate as the ratio of the variance of the estimate and its squared expectation. For Bernoulli probabilities, this provides a natural measure of the variability in relation to the scale of the probability itself:

$$\begin{aligned} \textrm{Var}_{}\!\left( \frac{p_{\text {simple}}^n}{p}\right) = \frac{\textrm{Var}_{}\!\left( p_{\text {simple}}^n\right) }{p^2} = \frac{1-p}{np}. \end{aligned}$$

(8)

We can choose n such that the relative variance is less than some $\varepsilon \in (0,1)$, giving $n > (1-p) / \varepsilon p$. Given some domain knowledge of the exceedance probability for our highest threshold of interest, we can then decide on a suitable number of simulations such that the relative variance of our estimate is constrained. Notice that in Eq. 6, the term within the square root is an estimate of Eq. 8. Thus, choosing n such that the relative variance is restricted directly reduces the width of the CI for $\log p$.

Fig. 1

European sites chosen for testing and the volcanic source (red triangle) in Iceland

We proceed to describe an approach for further reducing the variance of our exceedance probability estimates through a straightforward adaptation to stochastic sampling referred to as stratification.

Data and methods

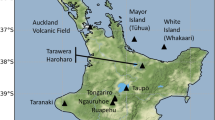
We compare and contrast probabilistic tephra hazard across Europe, and at a number of key locations (Fig. 1 and Table 1), to investigate how, where, and why hazard differs between approaches using stochastic and targeted sampling of meteorological conditions. Tephra from a hypothetical Volcanic Explosivity Index (VEI; Newhall and Self 1982 4 eruption from Iceland is simulated. This is one of the most prominent sources of tephra for northern Europe because of the frequency of Icelandic eruptions and the predominance of westerly winds in the region (Crosweller et al. , 2012). Key locations were chosen for analysis here (Fig. 1 and Table 1) because they have record of Icelandic tephra deposits (Swindles et al. , 2011) and to cover a range of bearings and distances.

Table 1 Distance and bearing (degrees from north) of the European sites in Fig. 1, relative to the volcanic source in Iceland

Volcanic source and ash dispersion modelling

We simulated volcanic ash dispersion from Iceland to northern Europe using the open-source dynamic three-dimensional advection–diffusion FALL3D model version 7.0 (Folch et al. , 2009). In this application, we provided hourly reanalysis meteorological data as input to calculate ash transport; the model interpolates to hourly outputs of three-dimensional (latitude, longitude, and altitude) ash concentration and ground ash thickness. We simulated 4 days (96 h) of ash transport starting from the onset of an 8 h eruption—this was found to be sufficiently long to capture long-range ash transport and deposition.

We chose volcanic source conditions to be representative of a VEI 4 size eruption as follows. The plume height was chosen based on empirical fits of observed plume heights to erupted volume (Jenkins et al. , 2007). Ash within the plume was assumed to follow a Suzuki distribution (Suzuki , 1983), with parameters such that more ash is released beyond the convective thrust region and in the upper portion of the plume (Table 2). Eruptions were considered to last for 8 h to represent a large silicic eruption (Mastin et al. , 2009). The erupted total particle sizes follow a Gaussian distribution with ten size classes between 1 and 10 $\phi$ (0.9 $\mu$ and 0.5 mm), with a mean of 2.5 $\phi$ (0.18 mm) and standard deviation of 4.5 $\phi$ (0.04 mm), following those derived by Folch et al. (2012) for the 2010 Eyjafjallajökull eruption in Iceland. Particle densities of 1500 $\text {kg m}^{-3}$ and 2500 $\text {kg m}^{-3}$, consistent with intermediate magma compositions, are associated with coarse (1 $\phi$) and fine (6 $\phi$) particles, respectively. The commonly used Ganser model (Ganser , 1993) is used within the model to calculate the terminal settling velocities of the near spherical particles through the atmosphere. The mass flow rate of the eruption (in $\text {kg s}^{-1}$) is calculated within FALL3D using an empirical fit between mass flow rate and plume height due to Mastin et al. (2009), assuming a magma density of 2500 $\text {kg m}^{-3}$. Parameters used in the dispersion modelling are summarised in Table 2.

Table 2 Overview of FALL3D model inputs for a VEI 4 eruption

For this study, we used a ‘One Eruption Scenario’ approach (Bonadonna , 2006) and compiled a dataset of 6000 simulation results using these initial conditions with meteorological forcing data sampled from 6-hourly mean data from the ECMWF ERA-5 dataset, where start dates were randomly selected between January 1997 and December 2005.

Meteorological data

The vast majority of large-scale weather variability can be classified into a manageable number of synoptic patterns or regimes. A weather regime is any configuration of the weather that tends to remain relatively constant for a period of a few days to weeks (James , 2006); they may be classified manually or using an objective classification system. Weather regimes have been classified for the UK (Jones et al. 1993, $n=8$), Europe and the north-east Atlantic (James 2006, $n=29$), the Western US (Robertson and Ghil 1999, $n=6$), the Northern Hemisphere (Barnston and Livezey 1987, $n=13$), South America Solman and Menendez 2003, $n=5$), and New Zealand (Kidson 2000, $n=2$, across four broad types), among others. The scale over which regimes are categorised therefore varies significantly from the relatively small island of the UK to a whole hemisphere. For an Icelandic eruption, we have used the Grosswetterlagen regimes described in the following section.

Grosswetterlagen system

Fig. 2

Duration distributions for each of the 29 GWL regimes. Boxplots show the minimum, 25th percentile, median, 75th percentile, and maximum durations recognised for each regime across the 1997 to 2005 ECMWF ERA-40 reanalysis dataset. Regimes are ordered from most frequently observed (WZ) to least (SEZ), and the daily frequencies between 1997 and 2005 are shown by the black dots

The widely used Grosswetterlagen (GWL) series of synoptic weather regimes is the only classification system currently in use that can capture both large-scale and local weather regime characteristics (James , 2006). The GWL system was developed by Baur et al. (1944) and is now maintained by the German weather service (DWD , 2015). More recently, James (2007) produced an objective method for classification that can be used with either the ECMWF ERA-5 or NCEP/NCAR reanalysis data, providing GWL classifications from 1948 to present. We obtained a dataset of GWL regimes assigned for every daily ECMWF ERA-5 reanalysis record between January 1997 and December 2005 (Parker, Pers. Comm., 2014). The ECMWF ERA-5 reanalysis catalogue contains global meteorological records at a spatial resolution of 0.25$^{\circ }$, approximately 28 km at the equator, for 137 hybrid sigma-pressure levels, related to altitudes up to more than 80 km above sea level (dataset available here).

GWL regimes typically last 4 days in duration, although some regimes (WZ, SWZ, NEA, SEZ) are as short as 3 days and some (WZ, WA, BM, NWZ, SWA, HNA, HNFZ) as long as a week or more (Fig. 2). Descriptions for each GWL regime are provided in Appendix A. Westerly regimes are the most prevalent, although a zonal ridge of high pressure across Central Europe (BM), similar to the weather patterns that dispersed ash towards mainland Europe during the Eyjafjallajökull crisis in 2010, has a relatively high probability of occurrence.

In our analysis, meteorological inputs are chosen randomly from the ECMWF catalogue between 1997 and 2005 and provided to the simulator as 96 h of reanalysis data (Table 2). As GWL patterns last 4 days on average, it is likely that a 4-day period chosen at random from the catalogue will contain a transition between GWL regimes. In order to simplify the process of stratified sampling (which we introduce in the following section) via GWL regimes and to ensure that the resultant number of strata (groupings of the data) is not excessively large, we classify each 4-day period as belonging to the GWL classification of the first day, regardless of any transition between regimes occurring during that period.

Stratification for variance reduction

GWL regimes represent a partitioning of the whole set of daily wind fields into a smaller number (29) of groups with distinctive properties. Given that this grouping is possible, we make use of a statistical sampling technique called stratification to reduce the variance of an estimate of an expectation (Cochran , 1977). In our case, each GWL regime constitutes a separate stratum, and samples can be drawn independently from each stratum to form estimates which are then combined to obtain an unbiased estimate of the expectation whose variance is lower than that of the comparable stochastic sampling estimate.

Given that we can assign an individual GWL regime to each start date in the ECMWF ERA-5 reanalysis record, we can determine the probability of occurrence of an individual regime or its weighting within the distribution. More formally, for the 29 GWL regimes, we divide the set of start dates $\mathcal {Z}$ into $J=29$ disjoint regions $\mathcal {Z}_1, \dots , \mathcal {Z}_J$, according to the GWL classification for that date. Then, the following 96 h of meteorological data provided to the simulator is regarded as belonging to that GWL classification. We then refer to $\mathcal {Z}_j$ as the jth stratum. If the random variable Z is drawn uniformly at random from $\mathcal {Z}$, the probability that Z was drawn from stratum $j \in \left\{ 1, \dots , J \right\}$ is the weight of stratum j, denoted by

$$\begin{aligned} w_j := \mathbb {P}\!\left( Z \in \mathcal {Z}_j\right) , \end{aligned}$$

(9)

where the sum of these probabilities is one: $\sum _{j=1}^{J} w_j = 1$.

The key to stratification is the fact that the population mean is the weighted sum of stratum means (Cochran , 1977),

$$\begin{aligned} p&= \sum _{j=1}^J \mathbb {P}\left( {Z \in \mathcal {Z}_j}\right) \mathbb {P}\left( {X=1}\left| {Z \in \mathcal {Z}_j}\right. \right) \end{aligned}$$

(10)

$$\begin{aligned}&= \sum _{j=1}^J w_j p_j, \end{aligned}$$

(11)

where, for each $j \in \{1,\ldots ,J\}$, $p_j$ is the exceedance probability associated with stratum j:

$$\begin{aligned} p_j := \mathbb {P}\left( {X=1}\left| {Z \in \mathcal {Z}_j}\right. \right) . \end{aligned}$$

(12)

Stratified sampling estimates

To carry out a stratified sampling procedure, we must know the weights $w_1, \dots , w_J$ and be able to sample directly from each stratum. In our case, we have access to the ECMWF ERA-5 catalogue from 1997 to 2005 alongside the GWL classification for each date in the catalogue. We can therefore calculate the weights using the relative frequencies of occurrence of each GWL regime and sample uniformly from each stratum by choosing a start date for the simulation from the set of dates with the corresponding weather classification. For each stratum $j \in \left\{ 1, \dots , J \right\}$, we sample $n_j$ start dates $Z_{j,1}, \dots , Z_{j, n_j}$ independently and uniformly at random from stratum j and consequently obtain $n_j$ independent Bernoulli samples $X_{j,1}, \dots , X_{j, n_j}$, where $X_{j, i}:= \mathbbm {1} \left\{ \psi \circ \phi \, (Z_{j,i}) \ge c\right\}$ for $i \in \{1, \dots , n_j\}$. We estimate $p_{j}$ by the jth stratum sample mean:

$$\begin{aligned} p_j^n := \frac{1}{n_{j}} \sum _{i=1}^{n_{j}} X_{j,i}, \end{aligned}$$

(13)

which is an unbiased estimator of $p_j$ with variance $p_j (1-p_j) / n_j$. The stratified sampling estimate of p is the weighted sum of the estimates of $p_j$:

$$\begin{aligned} p_{\text {strat}}^n := \sum _{j=1}^J w_j p_j^n. \end{aligned}$$

(14)

This is unbiased with variance given by

$$\begin{aligned} \textrm{Var}_{}\!\left( p_{\text {strat}}^n\right) = \sum _{j=1}^J \frac{w_j^2}{n_j} p_j (1-p_j), \end{aligned}$$

(15)

which we can estimate by replacing $p_j$ with $p_j^n$.

Proportional stratum allocation

Proportional allocation (Cochran , 1977) is a straightforward way to assign the values $n_1,\ldots ,n_J$. For some positive m, let $n_j = \lceil m w_j \rceil$, i.e. the smallest integer greater than or equal to $m w_j$. The total number of samples is $n = \sum ^J_{j=1} n_j \le m + J$.

The estimator is very similar to the standard Monte Carlo estimator Eq. 1, except that the number of samples in each region $\mathcal {Z}_j$ is deterministic rather than random. We obtain the variance bound

$$\begin{aligned} \textrm{Var}_{}\!\left( p_{\text {strat}}^n\right) \le \frac{1}{m} \sum _{j=1}^J w_j p_j (1-p_j), \end{aligned}$$

(16)

with equality if $n=m$. To compare stratified sampling with regular stochastic sampling, it is helpful to decompose the variance of $X \sim \textrm{Bernoulli}\!\left( p\right)$ into within- and between-stratum variances as follows:

$$\begin{aligned} p (1-p) = \sum _{j=1}^J w_j p_j (1-p_j) + \sum _{j=1}^J w_j (p_j - p)^2. \end{aligned}$$

(17)

By comparing Eq. 16 with Eq. 2, stratification is likely to be beneficial if the within-stratum variances are dominated by the between-stratum variance, since the between-stratum variance is not present in Eq. 2. That is, if samples drawn from the same stratum are typically similar to each other, and samples from different strata are typically distinct. An intuitive explanation for this phenomenon is that by using the precise stratum weights in Eq. 14, one source of uncertainty about p is removed and variability arises only from the variability of estimates of the stratum probabilities $p_j$.

In our results, we illustrate that proportional allocation allows us to obtain low-variance estimates of exceedance probabilities for a range of thresholds. The results indicate that stratified sampling allows us to achieve results comparable to stochastic sampling from fewer samples, thus reducing the amount of computational resources required to obtain high-precision estimates of exceedance probabilities.

In Appendix C, we describe an optimum stratum allocation which will always reduce the variance of the estimate, where the stratum sample sizes are allocated proportionally to the weights and stratum variances if these values are known. We describe also a variant of stratified sampling referred to as post-stratification (Jagers et al. , 1985), whereby the variance of an estimate can be reduced post-hoc if samples have already been drawn according to random sampling, and illustrate an example application of this method.

Results

In this section, we present the results of our analysis. We first present results related to simple Monte Carlo sampling of ensemble members, for common ash dispersion metrics as well as exceedance probabilities, and proceed to compare the results for exceedance probabilities with those obtained via stratified sampling of GWL regimes.

Relationship between sample size and confidence for ash dispersion metrics

Fig. 3

The variation of mean ash thickness estimates with ensemble size for simulations of a VEI 4 eruption from Iceland. Ensemble size increases from left to right, and each column shows ash thickness maps for the estimated maximum thickness (‘maximum thickness estimate’) and the lower and upper limits of the 95% CI for the maximum thickness (‘lower 95% limit’ and ‘upper 95% limit’, respectively). Note the logarithmic colour scale for thickness in cm. The ‘95% CI width’ maps indicate the size of the CI, which is the difference in logarithm thickness values between the upper and lower limits. Ash thickness is computed from ash deposition using the particle densities given in Table 2

Fig. 4

a Ground-level ash concentration estimates over time at Edinburgh, smoothed over a 24-h window, shown for different ensemble sizes. Full lines and shaded regions represent the sample means and 95% CIs, respectively, obtained using the specified number of samples. Dashed lines show the mean obtained from the whole set of 6000 samples. b Cumulative estimate (sample mean) of the peak concentration at Edinburgh, against ensemble size, with 95% CIs. c Cumulative estimate of the time from eruption onset at which the peak ground-level ash concentration is attained, against ensemble size, with 95% CIs

Volcanic ash dispersion simulations are typically used to predict ash thickness deposits, and more recently estimates of airborne or ground-level ash concentration have become important for impacts to aviation and infrastructure (Biass et al. , 2014; Capponi et al. , 2022; Harvey et al. , 2020). In this context, probabilistic simulation will allow us to estimate the expected value of these quantities via the sample mean and compute an approximate CI using Eq. 4.

Figure 3 maps the estimated mean ash thickness from a VEI 4 eruption from Iceland, together with 95% CIs, for three ensembles of increasing sample size. Each FALL3D simulation took 3 h to complete on average, run in parallel on a high-performance computing cluster. The mean thickness is the cumulative value of ash thickness per unit area after the duration of the simulation, divided by the number of hours (96 h here); we estimate thicknesses in excess of 1 cm proximally to less than 0.1 mm distally. The thickness is shown on a logarithmic colour scale to visualise the orders-of-magnitude difference in deposition over very long transport distances; the CI width colour scale is the difference in logarithm thickness between the upper and lower limits of the 95% CI, and we use it here to illustrate relative differences in confidence between different ensemble sizes.

The variation of mean ash thickness decreases with increasing ensemble size—this can be seen from both the CI limit maps and most easily from the CI width maps. For the smallest ensemble (50 samples), there are orders of magnitude difference in mean ash thickness across northern Europe between the upper and lower limits of the CI, but this difference is significantly reduced if ensemble size is increased to 500 samples. For this largest ensemble, there is only a very small difference between the upper and lower ends of the CI, except in the most distal locations (thousands of kilometres from the source). The variation in ash thickness is generally lowest at proximal locations and increases with distance from the source; in proximal locations, ash deposition is dominated by larger particle sizes whose dispersion is less affected by wind field variations because of their higher terminal fall velocities and thus lower residence times in the atmosphere.

In Fig. 4a, we show plots of the variation in estimated ground-level ash concentration at some location as a function of time for ensembles of increasing size. Here, the ash concentration is smoothed over a 24-h window, so that the concentration at x hours from the eruption onset is the average from time x to $x+24$. This is an important measure for assessing ash impacts to human health, visibility, and infrastructure using filters such as generators and air conditioning systems (Jenkins et al. , 2015). On each sub-figure, the mean for the whole set of 6000 samples provides a visual guide as to how closely the means for different sample sizes match the mean of the whole set, which is our closest estimate of the ‘true’ value.

Fig. 5

The variation of exceedance probability estimates with ensemble size for simulations of a VEI 4 eruption from Iceland. The probability of the ground-level ash concentration exceeding 500 $\mu$g m$^{-3}$ for 24 h or more is estimated at each point for increasing ensemble size (left to right). Each column shows maps of exceedance probability estimates (‘exceedance probability estimate’) and the lower and upper limits of the 95% confidence interval for the probability estimate (‘lower 95% limit’ and ‘upper 95% limit’, respectively). The ‘width of 95% CI’ maps illustrate the size of the confidence interval or the difference between the upper and lower limits, and the accompanying curves (bottom row) illustrate these widths as a function of the exceedance probability itself

Fig. 6

a Exceedance probability estimates against threshold for each location in Table 1, with shaded regions indicating 95% confidence intervals. b Exceedance probability estimates against threshold on a logarithmic scale for the same locations, with 95% confidence intervals

The location of interest in Fig. 4 is Edinburgh, 1270 km from the volcanic source. Results using an ensemble of 10 samples (Fig. 4a) show poor agreement with the results of the whole sample set, with the peak mean concentration occurring at 64 h from the eruption onset, compared to the ‘true’ peak at 20 h. If only a very small sample size is used, it is unlikely that the ensemble will adequately reproduce the dominant trend of ash transport to the UK by northwesterly winds. This particular ensemble is formed of simulations that have resulted in a longer arrival time compared to the mean of the full set of 6000 samples. If a different set of 10 samples were chosen, it is highly likely that the mean of the concentration values at each time, and hence the arrival times, would be significantly different. With a larger ensemble (50–100 samples), the peak timing is closer to that of the whole sample size, and the confidence intervals include the whole sample mean, but span a large range. Ensembles with greater than 1000 samples show good agreement with the ‘true’ variation and have progressively narrower confidence intervals. We emphasise that each sub-figure is obtained by averaging a set of concentration values and that a different set of the same size would result in a slightly different trajectory, but these differences become smaller as the ensemble size increases.

Figures 4b and c provide cumulative estimates for the peak concentration and the time at which the peak occurs, along with 95% CIs, to illustrate how these CIs shrink with linearly increasing sample size. Note that the mean of the peak concentration is not the same as the peak of the mean concentration (and similarly for peak times), so these estimates do not match the peaks in Fig. 4a.

Relationship between sample size and confidence for exceedance probabilities

For volcanic ash impact studies, the results of stochastic simulations are typically presented using exceedance probabilities for prescribed ash concentration or mass accumulation thresholds (Titos et al. , 2022; Jenkins et al. , 2022), for which confidence intervals can be computed. Figure 5 maps the probability that the ground-level ash concentration exceeds a value of 500 $\mu$g m$^{-3}$ for 24 h or more for different ensemble sizes. As the number of samples increases, the variance is reduced in both proximal and distal locations relative to the source.

Figures 6 and 7 illustrate the relationship between CI widths and threshold for specific locations at different distances from the volcanic source. The exceedance probabilities are calculated using the full ensemble of 6000 simulations, so the lowest probability that can be represented is 1/6000 or about $1.67 \times 10^{-4}$. As the threshold increases, the estimated exceedance probability Eq. 1 decreases; then the associated variance Eq. 2 also decreases, and hence the CIs shrink (most easily seen in Fig. 6b). Figure 7 shows how the variance Eq. 2 and relative variance Eq. 8 of the probabilities vary with threshold for the same locations. As the variance of the estimator decreases at a slower rate than the exceedance probability estimator itself, the relative variance increases with threshold and dramatically increases at around 1000 $\mu$g m$^{-3}$ (Fig. 7b), where probabilities get very small (Fig. 6b).

Figure 8 displays hazard curves for each location in Table 1, where exceedance probability is shown as a function of threshold on a double-logarithmic scale. These plots clearly show how CI width increases relative to the exceedance probability itself as it decreases, and these CIs become masked when the hazard curve appears to become vertical, as the estimate of the exceedance probability decreases rapidly towards zero due to the finite number of samples.

Given the straightforward calculation of CIs for exceedance probabilities described, we can also calculate how many samples are required in order to restrict the expected size of the CI. This is illustrated in Fig. 9, where we show the minimum number of samples needed to expect the width of the 95% CI to be 50% of the exceedance probability itself (calculated through using the estimates obtained for each threshold in Fig. 6). We note that the number of samples needed increases with threshold (and hence decreasing exceedance probability) and also with distance from the volcanic source. For example, for the width of the 95% CI for the probability of exceeding an ash concentration of 10$^{4}$   $\mu$g m$^{-3}$ to be 50% of the exceedance probability itself, we require approximately 450 samples for the proximal Reykjavik location and approximately 37,000 samples for the distal Berlin location.

Fig. 7

a Sample variance of exceedance against threshold for each location in Table 1. b Relative variance against threshold for the same locations

The effect of stratified sampling on estimates

In the context of probabilistic volcanic ash dispersion, stratified sampling aims to reduce the variance in an estimate compared to that made with the same number of stochastic samples or to obtain an estimate with the same variance as an estimate constructed through stochastic sampling but using fewer samples. In this study, we stratify our meteorological input data using GWL regimes. In Fig. 10, we see how exceedance probabilities vary for different GWL regimes with threshold. Notice that there is greater variability in exceedance probability between regimes at lower thresholds because of the different directions of wind fields that make up each regime.

Figure 11 shows, as a percentage, the difference in variance of exceedance probability estimates achieved through the use of proportional stratified sampling using GWL regimes, as compared to stochastic sampling. For all locations and thresholds, proportional sampling from weighted GWL regimes leads to a reduction in the variance of the estimate. The greatest reduction in variance is seen for the lower thresholds, and this benefit decreases with increasing threshold as the exceedance probabilities are lower. We obtain an indication of the percentage reduction in ensemble size that would be required to obtain the same (or lower) variance as the stochastic sampling estimate. For example, for thresholds below 1000 $\mu$g m$^{-3}$, 5 to 17% fewer samples in the ensemble of weighted GWL regimes (i.e. about 5000 to 5700 samples) will give an estimate with the same or lower variance as the set of 6000 stochastic samples. For the FALL3D simulations presented in this study (Table 2), this corresponds to saving up to approximately 1000 h of computational time.

Fig. 8

Hazard curves showing exceedance probability estimates for each location in Table 1 on a double-logarithmic scale, with shaded regions indicating 95% confidence intervals

Discussion

In this paper, we have introduced statistical methods for quantifying the uncertainty of probabilistic volcanic ash hazard assessments that are widely used to inform operational decision-makers and risk managers. We have used these approaches to show that using synoptic scale weather regimes, where available, can reduce the number of simulations needed to compute exceedance probabilities to a required degree of confidence, compared to purely stochastic sampling of the wind fields.

When estimating the value of an expectation, a confidence interval can be straightforwardly calculated from the sample mean and variance and the number of samples. We have demonstrated how the use of confidence intervals can enable comparison of the results of ensemble simulations of different sizes. Given that this is not computationally intensive and does not require additional simulations to be performed, we recommend that computing and presenting confidence intervals becomes standard practice when communicating the results of probabilistic volcanic ash hazard assessments. This information provides a measure of uncertainty in the forecast results that can be used by decision-makers, and expressing results with confidence intervals allows the uncertainty in hazard estimation to be propagated through the full risk equation, where typically hazard is considered without any uncertainty. We have shown results for the calculation of confidence intervals for metrics of volcanic ash hazard and for exceedance probabilities and provide an R package for making these calculations whose link is provided in the Supplementary Material section at the end of the paper. These tools can also be straightforwardly implemented within or applied to the results of software packages that make probabilistic volcanic ash calculations, such as TephraProb (Biass et al. , 2016). While we have focused on the One Eruption Scenario and explored stochastic sampling of the forcing wind field only, the methods can be applied in exactly the same way to varying eruption source parameters (the Eruption Range Scenario; Bonadonna 2006). When considering the effects of the wind and the source parameters together, we expect the confidence intervals would typically be larger than we have shown here for the One Eruption Scenario (Fig. 6), reflecting the increased variation in the controls on ash dispersion.

Fig. 9

The minimum number of samples needed for the expected width of the 95% confidence interval of the exceedance probability for a threshold to be 50% of the exceedance probability itself for each location in Table 1

Fig. 10

Exceedance probability estimates against threshold for select (12 out of 29) GWL regimes at Heathrow airport. An ensemble size of 6000 is used

Fig. 11

Difference in variance of exceedance probability estimates from using proportional stratified sampling with GWL regimes compared to stochastic sampling, with the same location, expressed as a percentage. Differences are shown for each location in Table 1, and an ensemble size of 6000 is used

Our presentation of the statistical background to confidence interval calculation highlights some important consequences for ensemble design. The exceedance probability estimates that can be computed are directly related to the number of samples in the ensemble. For example, if the ensemble size is 1000, the smallest exceedance probability that can be resolved is 1/1000 or 0.1%. This resolution may be sufficient for some applications, such as assessment of ash impacts to inhabited areas or agricultural land, but may not be for potential impacts to critical infrastructure, which can require exceedance probability thresholds of $10^{-4}$ (0.0001%) or lower (ONR , 2020). Recognising this relationship between ensemble size and the exceedance probability that can be resolved provides a first step in ensemble design: is the ensemble size sufficient to provide the information needed by decision-makers? Furthermore, the confidence interval for an estimate reduces with increasing sample size (Figs. 4 and 9), so it is also possible to design an ensemble with the number of samples matched to a particular confidence interval range. For example, if repeated laboratory testing identified that an item of equipment failed within a given time period if its exposure to volcanic ash exceeded some concentration threshold, one could specify the number of samples required for an ensemble forecast to calculate the probability of exceeding this threshold for that time period to a desired level of confidence. We provide in Appendix B an accessible and minimal set of statistical results that justify the methods used in this paper. While not touched on in this paper, further improvements to ensemble size selection could be achieved through consideration of stopping rules for stochastic sampling. These require computation of a stopping criteria at each step, or every number of steps (Ata , 2007; Gilman , 1968), and hence facilitate a more complicated sampling process with further computations.

In many cases, it could be helpful for decision-makers to be able to identify where in ensemble simulation results there is greater or lower uncertainty in those results. Confidence interval maps such as presented in Fig. 5 provide an important visual indication of the variability within an ensemble of a given size, as well as quantitative information about the confidence of estimated ash thickness. The confidence interval width plots presented in Fig. 5 provide an immediate indication of regions for which variability of estimates is greatest (further from the volcanic source and in directions different from the dominant wind direction) and also how the variability changes with ensemble size.

We also use the variance of an estimate to quantitatively compare results from two sets of simulations, in this case between wind fields sampled stochastically and those sampled from wind fields corresponding to particular synoptic-scale weather patterns. The purpose of this example of stratified sampling was to investigate whether the use of weather patterns could increase the efficiency of probabilistic ash hazard assessments by reducing the number of samples required in an ensemble to compute an exceedance probability at a given confidence interval. For our simulations over scales of  1000 km, we find that proportional stratified sampling of wind fields corresponding to GWL regimes reduces the variance of estimates, and hence the required number of samples, by 5 to 20% for typical ground-level ash concentration thresholds. Although modest, this reduction could represent a significant saving of computational time when using time-dependent simulators. The ability to use a weather pattern approach relies on allocating each day in the wind field record to a particular regime, which may still need to be done for weather regimes used in other global settings.

The reduction in the number of samples required to compute an exceedance probability with a given degree of confidence using proportional stratified sampling of GWL regimes is achieved because the variance of the stratified sampling estimator is bounded above by the weighted sum of within-stratum variances, which we expect to be dominated by the between-stratum variances when samples from the same stratum are typically similar to each other. Each set of dispersion simulations for a particular regime could be used to calculate exceedance probability estimates of ground-level ash concentration or ash deposit thickness for a given size eruption occurring into a particular weather pattern. This set of simulations could be used to inform future preparedness and to anticipate the impacts of an event in real-time. In addition, post-stratification can be used to compute approximations with reweighted strata to better reflect environmental conditions for a specific eruption.

We have focused on the estimation of expectations and in their confidence intervals. This is partly to avoid confusion with other sources of uncertainty. In particular, the results presented do not provide information about the variability arising from the capability of the model used. For example, in Fig. 4a, the shaded region indicates uncertainty associated with the sample mean of the ash concentration at each point in time, which is due to the number of samples. With 5000 samples, there is very little uncertainty about the mean, but there is variability in ash concentrations themselves that cannot be quantified by looking at its expected value. Plainly, the quantity being presented is not the ‘true’ expected value of the quantity given the eruption event in the real world, but that of the quantity output by the simulator given some parameterisations. It is simple to reduce the width of an estimate’s CI further by increasing the ensemble size, but this will not reduce the inherent bias which arises from using an imperfect model. In operational environments, the results obtained from using the methods in this paper should always be presented with the caveat that these are based on model assumptions and that ‘true’ CIs will be larger than the numerical values obtained due to unmodelled variability.

We finally note that, although we used a 95% confidence level in our examples the methods presented in this paper extend to any choice of confidence level. A 95% confidence level is fairly traditional in situations where data is scarce or expensive to collect, as is usually the case in probabilistic volcanic hazard assessment. In practice, choice of confidence level should be context-specific and determined by the application and data. We note also that specialised corrections exist for CIs for Bernoulli probabilities that achieve marginal improvements upon the coverage obtained by the commonly used CI presented in this paper. In operational environments where ensemble size is large enough (typically $n > 40$; Brown et al. (2001)), it can be beneficial to instead use the modified version of Eq. 5 presented in Agresti and Coull (1998). For smaller ensembles ($n < 40$), the Wilson interval may be recommended instead due to its higher coverage (Wilson , 1927; Brown et al. , 2001). These minor corrections will result in small improvements in the coverage for an exceedance probability CI.

Table 3 GWL regime abbreviations and their brief descriptions (James , 2007)

The use of confidence intervals to compare probabilistic ensembles highlights the need to consider ensemble design across different types of volcanic ash forecasts and identify consistent standards for their presentation to unify probabilistic volcanic ash hazard assessment practice and communicate variability in forecasts. As a starting point, the volcanology community, in collaboration with operational end users, needs to choose the confidence intervals for different forecast applications such as airborne ash concentration or deposited ash thickness.

Appendices

Appendix A: GWL regime descriptions

Appendix B: Statistical background

The works collected here present some results for a deeper understanding of the ‘Statistical background’ section in the main text of the paper. This is not a presentation of new results: it is intended to collate the background information that is typically found in undergraduate statistics courses in an accessible way. Much of the information presented in this section can be found in DeGroot and Schervish (2012).

Estimators and estimates

Consider a general random variable X taking values in $\mathcal {X}$ with probability density function (PDF) $f(\cdot ; \theta ): \mathcal {X} \rightarrow \mathbb {R}$, characterised by some parameter $\theta \in \Theta \subseteq \mathbb {R}$. We write $X \sim f(\cdot ; \theta )$, or simply $X \sim f(\theta )$, to show that the distribution of X is described by f for some given value of the parameter $\theta \in \Theta$.

If we consider n random samples from the distribution of X for some unknown value $\theta ^{*} \in \Theta$, we write $\textbf{X} \sim f_n (\theta ^{*})$ with $\textbf{X}:= (X_1, \dots , X_n)$, where $f_n$ describes the joint distribution of $\textbf{X}$. In particular, if $X_1, \dots , X_n$ are independent and identically distributed (i.i.d.), we denote this by $\textbf{X} \overset{\text {iid}}{\sim }f_n(\theta ^{*})$, where the joint density of $\textbf{X}$ is the product of the densities of the $X_i$:

$$\begin{aligned} f_n (\textbf{x}; \theta ^{*}) = \prod _{i=1}^n f(x_i; \theta ^{*}). \end{aligned}$$

(B1)

Definition 1

(Estimate and estimator). Suppose that $\textbf{X} \sim f_n (\theta ^{*})$ for some unknown $\theta ^{*} \in \Theta$ and let $\textbf{x}$ be a realisation of $\textbf{X}$. For some function $\hat{\theta }: \mathcal {X}^n \rightarrow \Theta$ of $\textbf{x}$ that is intended to provide an approximation of $\theta ^{*}$, $\hat{\theta }(\textbf{x})$ is an estimate of $\theta ^{*}$. Then $\hat{\theta }$, or $\hat{\theta }(\textbf{X})$, is referred to as an estimator of $\theta ^{*}$.

We emphasise that the estimator is a random variable and the estimate a realisation of this random variable, but the terms may be used interchangeably in the main text of the paper.

Definition 2

(Unbiased). $\hat{\theta }$ is an unbiased estimator of $\theta$ if, for all values $\theta \in \Theta$, its expected value is the true value $\theta$: $\mathbb {E}_{}\!\left[ \hat{\theta }(\textbf{X})\right] = \theta$.

An unbiased estimator $\hat{\theta }$ thus provides us with unbiased estimates of $\theta$ given data $x_1, \dots , x_n$. The performance of an estimator, in terms of the discrepancy between the estimated value and its true value, can be measured via a loss function such as the mean squared error.

Definition 3

(Mean squared error). The mean squared error (MSE) of an estimator $\hat{\theta }$, given $\textbf{X} \sim f_n(\theta ^{*})$ for some $\theta ^{*} \in \Theta$, is a loss function defined by

$$\begin{aligned} \textrm{MSE}\left( \hat{\theta }(\textbf{X}) \right) := \mathbb {E}_{}\!\left[ \left( \hat{\theta }(\textbf{X}) - \theta ^{*} \right) ^2\right] , \end{aligned}$$

(B2)

the mean of the expected squared difference between the estimator and the true value $\theta ^{*}$.

Equation B2 can be decomposed into the variance and squared bias of the estimator, referred to as the bias-variance decomposition:

$$\begin{aligned} \text {MSE} \left( \hat{\theta } ({\textbf {X}}) \right) = \text {Var}_{}\! \left( \hat{\theta } ({\textbf {X}}) \right) + \left( \text {bias} \left( \hat{\theta } ({\textbf {X}}) \right) \right) ^2, \end{aligned}$$

(B3)

where we define the bias as the expected difference between the value of the estimator and the true value of the parameter:

$$\begin{aligned} \textrm{bias}\left( \hat{\theta }(\textbf{X}) \right) := \mathbb {E}_{}\!\left[ \hat{\theta }(\textbf{X}) - \theta ^{*}\right] = \mathbb {E}_{}\!\left[ \hat{\theta }(\textbf{X})\right] - \theta ^{*}. \end{aligned}$$

(B4)

Remark 1

Noting that $\textrm{bias}\left( \hat{\theta }(\textbf{X})\right) = 0$ when the estimator is unbiased, the bias-variance decomposition illustrates that the MSE of an unbiased estimator is its variance.

Asymptotic behaviour of estimators

Let us denote by $\{X_n\}$ a sequence $X_1, X_2, \dots$ of random variables taking values in $\mathcal {X}$ with the same distribution, indexed by n. In this section, we introduce the notion of probabilistic convergence of random variables and their distributions. This is key to understanding the reasoning behind why we can construct approximate confidence intervals for sufficiently large n using a standard normal distribution.

Definition 4

(Convergence in probability). $\{X_n\}$ is said to converge in probability to the random variable X if, for all $\varepsilon > 0$,

$$\begin{aligned} \lim _{n \rightarrow \infty } \mathbb {P}\!\left( \left| X_n - X \right| > \varepsilon \right) = 0, \end{aligned}$$

(B5)

which we write as $X_n \rightarrow _{\mathbb {P}} X$.

Definition 5

(Convergence in distribution). $\left\{ X_n \right\}$ is said to converge in distribution to a random variable X if, for all x where the cumulative distribution function (CDF) $F_X(x):= \mathbb {P}\!\left( X \le x\right)$ is continuous,

$$\begin{aligned} \lim _{n \rightarrow \infty } \mathbb {P}\!\left( X_n \le x\right) = \mathbb {P}\!\left( X \le x\right) . \end{aligned}$$

(B6)

Then, the distribution of X is referred to as the asymptotic distribution of $\left\{ X_n \right\}$, and we write this as $X_n \rightarrow _{\mathcal {D}} X$.

We present the following theorems in relation to the asymptotic distributions of sequences of random variables.

Theorem 1

(Weak Law of Large Numbers) If $\{X_n\}$ are i.i.d. random variables with common expectation $\mathbb {E}_{}\!\left[ X_1\right] = \mu < \infty$, then

$$\begin{aligned} \frac{1}{n} \sum _{i=1}^n X_i \rightarrow _{\mathbb {P}} \mu . \end{aligned}$$

(B7)

Theorem 2

(Central Limit Theorem) If $X_1, \dots , X_n$ are i.i.d. random variables such that $\mathbb {E}_{}\!\left[ X_i\right] = \mu < \infty$ and $\textrm{Var}_{}\!\left( X_i\right) = \sigma ^2 < \infty$ for all $i \in \left\{ 1, \dots , n \right\}$, then

$$\begin{aligned} \frac{\sqrt{n} (S_n - \mu )}{\sigma } \rightarrow _{\mathcal {D}} Z \sim \mathcal {N}(0,1), \end{aligned}$$

(B8)

where $S_n:= \frac{1}{n}\sum _{i=1}^n X_i$.

Remark 2

We may write $\sqrt{n}(S_n - \mu )/\sigma \rightarrow _{\mathcal {D}} Z \sim \mathcal {N}(0,1)$ as $\sqrt{n}(S_n - \mu )/\sigma \rightarrow _{\mathcal {D}} \mathcal {N}(0,1)$, a slight abuse of notation, for simplicity.

Theorem 3

Convergence in probability implies convergence in distribution.

Theorem 4

(Slutsky’s theorem) If $Y_n \rightarrow _{\mathcal {D}} Y$ and $Z_n \rightarrow _{\mathcal {D}} c$, where $c \in \mathbb {R}$ is a constant, then

• 1. $Y_n + Z_n \rightarrow _{\mathcal {D}} Y + c$.

• 2. $Y_n Z_n \rightarrow _{\mathcal {D}} Y c$.

• 3. $Y_n / Z_n \rightarrow _{\mathcal {D}} Y / c$, provided $c \ne 0$.

Theorem 5

(Continuous Mapping Theorem) Let $g: \mathcal {X} \rightarrow \mathcal {G}$ be continuous. Then,

• 1. If $Z_n \rightarrow _{\mathbb {P}} Z$, then $g(Z_n) \rightarrow _{\mathbb {P}} g(Z)$.

• 2. If $Z_n \rightarrow _{\mathcal {D}} Z$, then $g(Z_n) \rightarrow _{\mathcal {D}} g(Z)$.

Furthermore, we define the notions of consistency for a sequence of estimators $\hat{\theta }_1, \hat{\theta }_2, \dots$, which we denote by $\{\hat{\theta }_n\}$, and of asymptotic normality. This is essential for the construction of asymptotically exact confidence intervals for $\theta$.

Definition 6

(Consistent). A sequence of estimators $\{\hat{\theta }_n\}$ is consistent if, for all $\theta \in \Theta$ with $\textbf{X}\sim f_n (\theta )$,

$$\begin{aligned} \hat{\theta }_n (\textbf{X}) \rightarrow _{\mathbb {P}} \theta . \end{aligned}$$

(B9)

Definition 7

(Asymptotic normality). Let $\{\hat{\theta }_n \}$ denote a consistent sequence of estimators for some parameter $\theta \in \Theta$. $\{ \hat{\theta }_n \}$ is asymptotically normal if, for some $\sigma ^2 > 0$,

$$\begin{aligned} \frac{\sqrt{n} (\hat{\theta }_{n}(\textbf{X}) - \theta )}{\sigma } \rightarrow _{\mathcal {D}} \mathcal {N}(0,1). \end{aligned}$$

(B10)

The delta method illustrates that an asymptotically normal estimator remains asymptotically normal under transformation by a continuously differentiable function (Doob , 1935).

Theorem 6

(Delta method) Suppose $\{\hat{\theta }_n\}$ is a sequence of consistent and asymptotically normal estimators and $g: \Theta \rightarrow \mathcal {G}$ is a continuously differentiable function whose first derivative $g^{\prime }(\theta )$ is continuous and non-zero for all $\theta \in \Theta$. Then,

$$\begin{aligned} \frac{\sqrt{n} \left( g ( \hat{\theta }_n(\textbf{X}) ) - g(\theta ) \right) }{\sigma g^{\prime }(\theta )} \rightarrow _{\mathcal {D}} \mathcal {N}(0,1), \end{aligned}$$

(B11)

i.e. $\{ g(\hat{\theta }_n(\textbf{X}) \}$ is asymptotically normal.

Asymptotically exact confidence intervals

Definition 8

(Confidence interval). Let $\textbf{X} \sim f_n(\theta )$ for some $\theta \in \Theta$ and let $L: \mathcal {X}^n \rightarrow \Theta$ and $U: \mathcal {X}^n \rightarrow \Theta$ be functions satisfying $L(\textbf{x}) < U(\textbf{x})$ for all $\textbf{x} \in \mathcal {X}^n$. For some $\alpha \in [0,1]$, we say that a random interval $[L(\textbf{X}), U(\textbf{X})]$ is a $1-\alpha$ confidence interval if, for all $\theta \in \Theta$,

$$\begin{aligned} \mathbb {P}\!\left( \theta \in [L(\textbf{X}), U(\textbf{X})]\right)&= \mathbb {P}\!\left( L(\textbf{X}) \le \theta \le U(\textbf{X})\right) \\ {}&\ge 1-\alpha . \end{aligned}$$

We refer to $\mathbb {P}\!\left( \theta \in [L(\textbf{X}), U(\textbf{X})]\right)$ as the coverage of $[L(\textbf{X}),$ $U(\textbf{X})]$.

Remark 3

The above definition of a confidence interval is a probability statement about the joint distribution of the random variables $L({\textbf {X}})$ and $U({\textbf {X}})$, given a particular value of $\theta$. Once the values of $X_1, \dots , X_n$ are observed to be $x_1, \dots , x_n$, we compute the values of $L({\textbf {X}})$ and $U({\textbf {X}})$ to obtain an observed confidence interval $[L_n({\textbf {x}}), U_n({\textbf {x}})]$.

The following theorem tells us how to compute an observed confidence interval such that the coverage of the interval approaches $1-\alpha$ as the sample size increases.

Theorem 7

(Asymptotically exact confidence intervals) Suppose $\{\hat{\theta }_n\}$ is a consistent sequence of estimators of $\theta$ that is asymptotically normal, and also that $\{\hat{\sigma }_n^2\}$ is a consistent sequence of estimators of $\sigma ^2$. Then, for all $\alpha \in (0,1)$, $\left[ L_n (\textbf{x}), U_n (\textbf{x}) \right]$ is an asymptotically exact $1-\alpha$ confidence interval for $\theta$, where

$$\begin{aligned} L_n (\textbf{x})&= \hat{\theta }_n (\textbf{x}) - z_{\alpha /2} \sqrt{\frac{\hat{\sigma }_n^2(\textbf{x})}{n}}, \end{aligned}$$

(B12)

$$\begin{aligned} U_n (\textbf{x})&= \hat{\theta }_n (\textbf{x}) + z_{\alpha /2} \sqrt{\frac{\hat{\sigma }_n^2(\textbf{x})}{n}}. \end{aligned}$$

(B13)

The confidence interval is only asymptotically exact, so in practice, the coverage of the confidence interval will be different from $1-\alpha$. However, as n increases, the coverage will tend towards $1-\alpha$.

Suppose we parameterise the problem in terms of $\tau := g(\theta )$, where g is a bijective and continuously differentiable function. In order to find a $1-\alpha$ confidence interval for $\tau$, we might first consider a direct transformation of the confidence interval $[L(\textbf{x}), U(\textbf{x})]$ for $\theta ^{*}$ through noting that

$$\begin{aligned}&\left\{ \textbf{x} \in \mathcal {X}^n : L(\textbf{x}) \le \theta ^{*} \le U(\textbf{x}) \right\} \nonumber \\ {}&= \left\{ \textbf{x} \in \mathcal {X}^n : g(L(\textbf{x})) \le \tau ^{*} = g(\theta ^{*}) \le g(U(\textbf{x})) \right\} , \end{aligned}$$

(B14)

if g is an increasing function. We find that, as $n \rightarrow \infty$,

$$\begin{aligned}&\mathbb {P}\!\left( L(\textbf{x}) \le \theta ^{*} \le U(\textbf{x})\right) \nonumber \\ {}&= \mathbb {P}\!\left( g(L(\textbf{x})) \le \tau ^{*} = g(\theta ^{*}) \le g(U(\textbf{x}))\right) \rightarrow 1-\alpha , \end{aligned}$$

(B15)

so $[g(L(\textbf{x})), g(U(\textbf{x}))]$ is an asymptotically exact $1-\alpha$ confidence interval for $\tau ^{*}$. For decreasing g, we simply reverse the directions of the inequalities in the above. Note that this approach does not necessarily obtain a confidence interval that is centred at $\hat{\tau }_n(\textbf{x})$.

Alternatively, we note from Theorem 6 that if $\{\hat{\theta }_n\}$ is a consistent sequence of estimators that is asymptotically normal with mean $\theta$ and variance $\sigma ^2$, then $\{\hat{\tau }_{n}\}$ is also a consistent and asymptotically normal sequence of estimators with mean $g(\theta )=\tau$ and variance $\sigma ^2 (g^{\prime }(\theta ))^2$. Then, we can simply reapply Theorem 7 to $\{\hat{\tau }_n\}$, yielding an asymptotically exact $1-\alpha$ confidence interval $[\bar{L}(\textbf{x}), \bar{U}(\textbf{x})]$ for $\tau$:

$$\begin{aligned} \bar{L}(\textbf{x})&:= \hat{\tau }_n(\textbf{x}) - z_{\alpha /2} \sqrt{\frac{\sigma ^2_n(\textbf{x}) (g^{\prime }(\theta _n(\textbf{x}))^2}{n}}, \end{aligned}$$

(B16)

$$\begin{aligned} \bar{U}(\textbf{x})&:= \hat{\tau }_n(\textbf{x}) + z_{\alpha /2} \sqrt{\frac{\sigma ^2_n(\textbf{x}) (g^{\prime }(\theta _n(\textbf{x}))^2}{n}}. \end{aligned}$$

(B17)

Example 1

For a random variable X with distribution function f, a common exercise is to estimate the expected value of X, $\mu =\mathbb {E}_{}\!\left[ X\right]$. We sample n times from the distribution of $X_1, \dots , X_n$ and estimate $\mu$ by $\hat{\mu }_n=\frac{1}{n}\sum _{i=1}^n X_i$. A consistent estimator for $\sigma ^2=\textrm{Var}_{}\!\left( X\right)$ is then $\hat{\sigma }^2_n = \frac{1}{n} \sum _{i=1}^n (X_i-\hat{\mu }_n)^2$, so that a $1-\alpha$ confidence interval for $\mu$ is given by

$$\begin{aligned} \hat{\mu }_n \pm z_{\alpha /2} \sqrt{\frac{\sum _{i=1}^n (X_i - \hat{\mu }_n)^2}{n}}. \end{aligned}$$

(B18)

Suppose we now wish to find an estimate for $\log \mu$ and a corresponding confidence interval. From Theorem 5, we know that $\log \hat{\mu }_n \rightarrow _{\mathbb {P}} \log \mu$, so that ${\log \hat{\mu }_n}$ is consistent. Furthermore, since $\log \mu$ is continuously differentiable with non-zero first derivative $1/\mu$, we can apply Theorem 6 to show that the sequence of estimators is asymptotically normal and use Eqs. B16 and B17 to obtain a confidence interval for $\log \mu$:

$$\begin{aligned} \log \hat{\mu }_n \pm z_{\alpha /2} \sqrt{\frac{\sum _{i=1}^n (X_i - \hat{\mu }_n)^2}{n \hat{\mu }_n}}. \end{aligned}$$

(B19)

Estimation of Bernoulli probabilities

For the $\textrm{Bernoulli}\!\left( p\right)$ random variable X, which we define in the main text to represent exceedance for some threshold c, we aim to estimate the value of the exceedance probability $p \in (0,1)$ given some realised observations $\textbf{x}$ drawn from the distribution of $\textbf{X} \overset{\text {iid}}{\sim }f_n(p)$, where

$$\begin{aligned} f(x; p) = p^x (1-p)^x \end{aligned}$$

(B20)

for $x \in \{0,1\}$, and hence

$$\begin{aligned} f_n(\textbf{x}; p) = \prod _{i=1}^n f(x;p) = p^{x_i} (1-p)^{1-x_i} \end{aligned}$$

(B21)

for $\textbf{x} = (x_1, \dots , x_n) \in \mathcal {X}^n$. X has expectation $\mathbb {E}_{}\!\left[ X\right] =p$ and variance $\sigma ^2 = \textrm{Var}_{}\!\left( X\right) = p(1-p)$, and we define the simple estimator of p as

$$\begin{aligned} p_{\text {simple}}^n := \frac{1}{n} \sum _{i=1}^n X_i, \end{aligned}$$

(B22)

which is unbiased,

$$\begin{aligned} \mathbb {E}_{}\!\left[ p_{\text {simple}}^n\right] = \frac{1}{n} \sum _{i=1}^n \mathbb {E}_{}\!\left[ X_i\right] = \frac{1}{n} np = p, \end{aligned}$$

(B23)

with variance given by

$$\begin{aligned} \textrm{Var}_{}\!\left( p_{\text {simple}}^n\right)&= \frac{1}{n^2} \sum _{i=1}^n \textrm{Var}_{}\!\left( X_i\right) = \frac{1}{n^2} n p (1 - p) \nonumber \\ {}&= \frac{p(1-p)}{n}. \end{aligned}$$

(B24)

Since $p_{\text {simple}}^n = \frac{1}{n} \sum _{i=1}^n X_i$, where the $X_i$ are i.i.d. with $\mathbb {E}_{}\!\left[ X_{i}\right] =p$ for all $i = 1, \dots , n$, it follows from Theorem 1 that $p_{\text {simple}}^n \rightarrow _{\mathbb {P}} p$, i.e. it is a consistent estimator of p. Furthermore, by Theorem 2, $p_{\text {simple}}^n$ is asymptotically normal.

Using Theorem 7, we obtain the asymptotically exact confidence intervals Eq. 5 for p:

$$\begin{aligned} p_{\text {simple}}^n \pm z_{\alpha /2} \sqrt{\frac{p_{\text {simple}}^{n} (1 - p_{\text {simple}}^{n})}{n}}. \end{aligned}$$

(B25)

Remark 4

To obtain the confidence intervals for $\log p$, we define the reparameterisation $\tau := g(p) = \log p$. We use the result in Example 1 to obtain the asymptotically exact confidence intervals Eq. 6 for $\log p$:

$$\begin{aligned} \log \left( p_{\text {simple}}^n \right) \pm z_{\alpha /2} \sqrt{\frac{1-p_{\text {simple}}}{n p_{\text {simple}}}}. \end{aligned}$$

(B26)

Appendix C: Results related to stratified sampling

Variance decomposition into within- and between-stratum components

We show that Eq. 17 holds, i.e. the variance of a $\textrm{Bernoulli}\!\left( p\right)$ random variable X can be decomposed into within- and between-stratum components. Let Z be the random variable representing the start date of the wind field data drawn uniformly at random from $\mathcal {Z}$, where $\mathcal {Z}$ is partitioned into J strata $\mathcal {Z}_1, \dots , \mathcal {Z}_J$. For ease of notation, we represent the event $\left\{ \mathcal {Z} \in \mathcal {Z}_j \right\}$ by $\left\{ Y = j \right\}$, where Y is a random variable drawn from $\left\{ 1, \dots , J \right\}$ with probability

$$\begin{aligned} \mathbb {P}\!\left( Y=j\right) = \mathbb {P}\!\left( \mathcal {Z} \in \mathcal {Z}_j\right) = w_j, \end{aligned}$$

(C1)

for all $j \in \left\{ 1, \dots , J \right\}$, and $\sum _{j=1}^J w_j = 1$. Noting that

$$\begin{aligned} \mathbb {E}_{}\!\left[ X\vert Y=j\right]&= p_j, \end{aligned}$$

(C2)

$$\begin{aligned} \textrm{Var}_{}\!\left( X\vert Y=j\right)&= p_j (1 - p_j), \end{aligned}$$

(C3)

for all $j \in \left\{ 1, \dots , J \right\}$, we obtain

$$\begin{aligned} \mathbb {E}_{}\!\left[ \textrm{Var}_{}\!\left( X\vert Y\right) \right]= & {} \sum _{j=1}^J \mathbb {P}\!\left( Y=j\right) \textrm{Var}_{}\!\left( X \vert Y=j\right) \nonumber \\= & {} \sum _{j=1}^J w_j p_j (1 - p_j); \end{aligned}$$

(C4)

$$\begin{aligned} \textrm{Var}_{}\!\left( \mathbb {E}_{}\!\left[ X\vert Y\right] \right)= & {} \mathbb {E}_{}\!\left[ \left( \mathbb {E}_{}\!\left[ X\vert Y\right] - \mathbb {E}_{}\!\left[ \mathbb {E}_{}\!\left[ X\vert Y\right] \right] \right) ^2\right] \nonumber \\= & {} \mathbb {E}_{}\!\left[ \left( \mathbb {E}_{}\!\left[ X\vert Y\right] - \mathbb {E}_{}\!\left[ X\right] \right) ^2\right] \nonumber \\= & {} \sum _{j=1}^J \mathbb {P}\!\left( Y=j\right) \left( \mathbb {E}_{}\!\left[ X\vert Y=j\right] - \mathbb {E}_{}\!\left[ X\right] \right) ^2 \nonumber \\= & {} \sum _{j=1}^J w_{j} (p_j - p)^2. \end{aligned}$$

(C5)

Then, by the law of total variance,

$$\begin{aligned} \textrm{Var}_{}\!\left( X\right)&= \mathbb {E}_{}\!\left[ \textrm{Var}_{}\!\left( X\vert Y\right) \right] + \textrm{Var}_{}\!\left( \mathbb {E}_{}\!\left[ X\vert Y\right] \right) \end{aligned}$$

(C6)

$$\begin{aligned}&= \sum _{j=1}^J w_j p_j (1 - p_j) + \sum _{j=1}^J w_j (p_j - p)^2. \end{aligned}$$

(C7)

Unbiasedness and variance of the stratified sampling estimator

For the stratified sampling estimator $p_{\text {strat}}^n$ defined in Eq. 14, we show that it is an unbiased estimator of p. Noting that the samples $X_{j,1}, \dots , X_{j, n_j}$ are independent and identically distributed so that $\mathbb {E}_{}\!\left[ X_{j,i}\right] = \mathbb {E}_{}\!\left[ X_{j,1}\right]$ for all $j \in \left\{ 1, \dots , J \right\}$, we have

$$\begin{aligned} \mathbb {E}_{}\!\left[ p_{\text {strat}}^n\right]&= \mathbb {E}_{}\!\left[ \sum _{j=1}^J w_j \frac{1}{n_{j}} \sum _{i=1}^{n_{j}} X_{j,i} \right] \nonumber \\ {}&= \sum _{j=1}^J w_j p_j = p, \end{aligned}$$

(C8)

so it is unbiased for all $p \in (0,1)$. Furthermore, the variance of $p_{\text {strat}}^n$ is given by

$$\begin{aligned} \textrm{Var}_{}\!\left( p_{\text {strat}}^n\right)&= \sum _{j=1}^J w_j^2 \textrm{Var}_{}\!\left( p_j^n\right) \nonumber \\ {}&= \sum _{j=1}^J \frac{w_j^2}{n_j} p_j (1-p_j). \end{aligned}$$

(C9)

In particular, if $n_j=n w_j$ for all $j \in \{1, \dots , J\}$, as in proportional stratum allocation, we find that the variance of the estimator is guaranteed to be less than or equal to that of $p_{\text {simple}}^n$:

$$\begin{aligned} \textrm{Var}_{}\!\left( p_{\text {strat}}^n\right)&= \sum _{j=1}^J \frac{w_{j}^{2}}{n w_{j}} p_j (1-p_j) \nonumber \\ {}&= \frac{1}{n} \sum _{j=1}^J w_j p_j (1 - p_j) \nonumber \\&\le \frac{1}{n} \sum _{j=1}^J w_j \left( p_j (1-p_j) + (p_j - p)^2 \right) \nonumber \\&= \frac{1}{n} \textrm{Var}_{}\!\left( X\right) = \textrm{Var}_{}\!\left( p_{\text {simple}}^n\right) , \end{aligned}$$

(C10)

where the final line follows from Eq. 17.

Asymptotic normality of the stratified sampling estimator

We show that the stratified sampling estimator is asymptotically normal. Let $q_j:= \lim _{n \rightarrow \infty } n_j / n$.

$$\begin{aligned} \sqrt{n} \left( p_{\text {strat}}^n - p \right)&= \sqrt{n} \left( \sum _{j=1}^J \frac{w_j}{n_{j}} \sum _{i=1}^{n_{j}} X_{j,i} - \sum _{j=1}^J w_j p_j \right) \nonumber \\&= \sqrt{n} \left( \sum _{j=1}^J w_j \left( \frac{1}{n_{j}} \sum _{j=1}^J X_{j,i} - p_j \right) \right) \nonumber \\&= \sqrt{n} \left( \sum _{j=1}^J \frac{w_{j}}{\sqrt{n_{j}}} \left( \frac{1}{\sqrt{n_{j}}} S_j \right) \right) \nonumber \\&= \sum _{j=1}^J \frac{w_{j}}{\sqrt{n_{j} / n}} \left( \frac{1}{\sqrt{n_{j}}} S_j \right) , \end{aligned}$$

(C11)

where we denote $S_j:= \sum _{i=1}^{n_{j}} X_{j,i} - p_j$. By Theorem 2, $S_j / \sqrt{n_j} \rightarrow _{\mathcal {D}} \mathcal {N}( 0, \sigma _j^2)$. It follows that

$$\begin{aligned} \frac{w_{j}}{\sqrt{n_{j} / n}} \frac{1}{n_{j}} S_j \rightarrow _{\mathcal {D}} \mathcal {N}\left( 0, \frac{w_{j}^2}{q_j} \sigma _j^2 \right) . \end{aligned}$$

(C12)

Then, since the J terms in the summation in Eq. C11 are independent, we obtain

$$\begin{aligned} \sqrt{n} \left( p_{\text {strat}}^n - p\right)&= \sum _{j=1}^J \frac{w_{j}}{\sqrt{n_{j} / n}} \frac{1}{n_{j}} S_j \nonumber \\ {}&\rightarrow _{\mathcal {D}} \mathcal {N}\left( 0, \sum _{j=1}^J \frac{w_{j}^2}{q_j} \sigma _j^2 \right) . \end{aligned}$$

(C13)

That is, the stratified sampling estimator is asymptotically normal with mean p and variance $\frac{1}{n} \sum _{j=1}^J w_j^2 \sigma _j^2 / q_j$, where $q_j = \lim _{n \rightarrow \infty } n_j / n$.

Optimal stratum allocation

It is possible to define an optimum stratification which will always reduce the variance of the estimate, where the number of samples is allocated proportionally to both the weights $w_j$ and the stratum standard deviations $\sigma _j$, where $\sigma _j^2:= p_j \, (1-p_j)$ for Bernoulli probabilities $p_j$ (see Etore and Jourdain 2010). The variance of the optimal stratified estimator is guaranteed to be less than that of proportional allocation, but requires knowledge of the stratum variances. Since these are usually unknown, approximately optimal stratified estimators can be constructed using accurate approximations of the stratum variances. In the setting of exceedance probability estimation, stratum variances are linked to the exceedance threshold of interest; if a range of thresholds are considered, optimal allocation using any one threshold may not necessarily provide better results overall. Therefore, in this paper, we did not pursue optimal stratification, but here, we note its benefit in variance reduction if sufficiently accurate approximations of stratum variances are available.

Post-stratification

If our samples have already been drawn according to random sampling, it is possible to post-hoc reduce the variance of our probability estimates through a variant of stratified sampling called post-stratification (Jagers et al. , 1985). The method has applications in areas such as political polling, where survey responses are biased and require debiasing to be representative of the entire population (Jagers , 1986). An example application of post-stratification to the use of weather regimes in volcanic ash hazard assessment would be if the frequency of the weather regimes changed in the future (without a change in the variation within patterns), or perhaps if there were known seasonal changes in the frequencies. Post-stratification would allow re-weighting of the patterns without needing to resample individual wind fields from their distribution.

In particular, using the notation described in the ‘Statistical background’ section of the main paper, if the simulation start dates $Z_1, \dots , Z_n$ have been drawn independently with probabilities $q_1, \dots , q_J$, we may allocate each sample to the appropriate stratum according to their classification to obtain stratum sizes

$$\begin{aligned} n_j = \left| \left\{ i : Z_i \in \mathcal {Z}_j, \, i = 1, \dots , n \right\} \right| \end{aligned}$$

(C14)

for $j \in \left\{ 1, \dots , J \right\}$, which we note are now random. We then denote by $X_{j,1}, \dots , X_{j, n_j}$ the corresponding $\textrm{Bernoulli}\!\left( p_j\right)$ random variables representing exceedance for some threshold. Stratum sample means can then be computed by Eq. 13 and the stratified sampling estimator of p by Eq. 14, which we refer to as the post-stratified estimator.

The caveat of this method, however, is that the post-stratified estimate cannot be computed if $n_j = 0$ for some $j \in \left\{ 1, \dots , J \right\}$ (Jagers et al. , 1985). As the $n_j$ are random, the probability of this event is

$$\begin{aligned} \mathbb {P}\!\left( \min _j \, n_j = 0\right) = \sum _{j=1}^J (1-q_j)^{n}, \end{aligned}$$

(C15)

which decreases exponentially quickly in n with a rate depending on the smallest weight and hence becomes very small as n increases.

In the following section, we show that the post-stratified estimator is unbiased whenever the stratum sizes are non-zero. Moreover, the estimator is asymptotically normal which allows us to construct asymptotically exact confidence intervals.

Unbiasedness and asymptotic normality of the post-stratified estimator

We view post-stratification as a situation in which the stratum sizes $n_1, \dots , n_J$ are given positive integers. Given $n_j > 0$ for each $j \in \left\{ 1, \dots , J \right\}$, $X_{j,i} \sim \textrm{Bernoulli}\!\left( p_j\right)$ for each $i \in \left\{ 1, \dots , n_j \right\}$. Then, conditional on the $n_j$ being positive, we are in the standard stratified sampling setting, and the post-stratified estimator is unbiased with the same asymptotic distribution as in the previous section, provided that $\lim _{n \rightarrow \infty } n_j / n = q_j$.

If $n_j = 0$ for some $j \in \left\{ 1, \dots , J \right\}$, then the post-stratified estimator is not defined. It is possible to define the estimator in some other way in this case; however, this would introduce bias. Therefore, the post-stratified estimator is unbiased whenever $\min _{j \in \left\{ j, \dots , J \right\} } n_j > 0$.

An alternative approach is to treat the $n_1, \dots , n_j$ as realisations of random variables $N_1, \dots , N_J$ as in Jagers et al. (1985). Let $Z_1, \dots , Z_n$ be independent random variables drawn from $\mathcal {Z}$ such that $q_j:= \mathbb {P}\!\left( Z \in \mathcal {Z}_j\right)$ for all $j \in \left\{ 1, \dots , J \right\}$, where $\sum _{j=1}^J q_j = 1$. Then,

$$\begin{aligned} N_j = \sum _{i=1}^n \mathbbm {1}\left\{ Z_i \in \mathcal {Z}_j \right\} , \end{aligned}$$

(C16)

and we see that $(N_1, \!\dots \!, N_J) \sim \text {Multinomial} \left( n, (q_1, \!\dots \!, q_J) \right)$. Letting $f(Z_i) = \mathbbm {1}\left\{ \psi \circ \phi (Z_i) \ge c \right\} \sim \textrm{Bernoulli}\!\left( p\right)$ represent the exceedance event, we write the post-stratified estimator as

$$\begin{aligned} p_{\text {post}}^n := \sum _{j=1}^J w_j \frac{1}{N_j} \sum _{i=1}^n f(Z_i) \, \mathbbm {1} \left\{ Z_i \in \mathcal {Z}_j \right\} . \end{aligned}$$

(C17)

Then,

$$\begin{aligned}&\sqrt{n} \left( p_{\text {post}}^n - p \right) \nonumber \\ {}&= \sqrt{n} \left( \sum _{j=1}^J w_j \frac{1}{N_j} \sum _{i=1}^n \mathbbm {1} \left\{ Z_i \in \mathcal {Z}_j \right\} \left( f(Z_i) - p_j \right) \right) \nonumber \\ {}&= \sum _{j=1}^J \frac{n w_j}{N_j} \frac{1}{\sqrt{n}} S_j, \end{aligned}$$

(C18)

where we define

$$\begin{aligned} S_j = \sum _{i=1}^n \mathbbm {1} \left\{ Z_i \in \mathcal {Z}_j \right\} \left( f(Z_i) - p_j \right) =: \sum _{i=1}^n \varphi _j(Z_i). \end{aligned}$$

(C19)

Noting that

$$\begin{aligned} \varphi _j (Z_i)&= \left\{ \begin{array}{cl} -p_j &{} \text {if } Z_i \in \mathcal {Z}_j \text { and } X_i = 0, \\ 1-p_j &{} \text {if } Z_i \in \mathcal {Z}_j \text { and } X_i = 1, \\ 0 &{} \text {if } Z_i \notin \mathcal {Z}_j, \end{array}\right. \nonumber \\ {}&= \left\{ \begin{array}{cl} -p_j &{} \text {w.p. } q_j (1-p_j), \\ 1-p_j &{} \text {w.p. } q_j p_j, \\ 0 &{} \text {w.p. } 1-q_{j}, \end{array}\right. \end{aligned}$$

(C20)

we find that

$$\begin{aligned} \mathbb {E}_{}\!\left[ \varphi _j(Z_i)\right] = (1-p_j) q_j p_j - p_j q_j (1-p_j) = 0 \end{aligned}$$

(C21)

and

$$\begin{aligned} \mathbb {E}_{}\!\left[ \left( \varphi _j (Z_i) \right) ^2\right]&= (1-p_j)^2 q_j p_j + p_j^2 q_j (1-p_j) \nonumber \\ {}&= q_j p_j (1-p_j) = q_j \sigma _j^2, \end{aligned}$$

(C22)

giving

$$\begin{aligned} \textrm{Var}_{}\!\left( \varphi _j (Z_i)\right)&= \mathbb {E}_{}\!\left[ \left( \varphi _j(Z_i) \right) ^2\right] - \left( \mathbb {E}_{}\!\left[ \varphi _j (Z_i)\right] \right) ^2 \nonumber \\ {}&= \mathbb {E}_{}\!\left[ \left( \varphi _j (Z_i) \right) ^2\right] = q_j \sigma _j^2. \end{aligned}$$

(C23)

It follows from Theorem 2 that $\frac{1}{\sqrt{n}} S_j \rightarrow _{\mathcal {D}} \bar{S}_j \sim \mathcal {N} \left( 0, q_j \sigma _j^2 \right)$, for all $j\, {\in }\, \{1, \dots , J\}$. Noting that $\mathbb {E} [\varphi _j (Z_i) \varphi _k$ $(Z_i)] = 0$ for all $j \ne k$, we show that the $\varphi _j(Z_i)$ are uncorrelated for all $i \in \{1, \dots , n\}$:

$$\begin{aligned}&\textrm{Cov} \left( \varphi _j (Z_i), \varphi _j (Z_i) \right) \nonumber \\ {}&= \mathbb {E}_{}\!\left[ \left( \varphi _j (Z_i) - \mathbb {E}_{}\!\left[ \varphi _j (Z_i)\right] \right) \left( \varphi _k (Z_i ) - \mathbb {E}_{}\!\left[ \varphi _k (Z_i)\right] \right) \right] \nonumber \\&= \mathbb {E}_{}\!\left[ \varphi _j (Z_i) \varphi _k (Z_i)\right] = 0, \end{aligned}$$

(C24)

which follows from Eq. C21. Using this result, we arrive at

$$\begin{aligned} \textrm{Cov} \left( \frac{1}{\sqrt{n}} S_j, \frac{1}{\sqrt{n}} S_k \right) = \mathbb {E}_{}\!\left[ S_j S_k\right] = 0, \end{aligned}$$

(C25)

for $j \ne k$. Then, $\frac{1}{\sqrt{n}} S_1, \dots , \frac{1}{\sqrt{n}} S_J$ are uncorrelated and converge in distribution to $\bar{S}_1, \dots , \bar{S}_J$ which are normal and uncorrelated, and hence independent. Furthermore, by Theorem 1, $n w_j / N_j \rightarrow _{\mathbb {P}} w_j / q_j$. It then follows from Theorem 4 that

$$\begin{aligned} \frac{n w_j}{N_j} \frac{1}{\sqrt{n}} S_j \rightarrow _{\mathcal {D}} \mathcal {N} \left( 0, \frac{w_j^2}{q_j} \sigma _j^2 \right) . \end{aligned}$$

(C26)

Since there is joint convergence in distribution of $\frac{1}{\sqrt{n}}S_1, \dots \!,$ $\frac{1}{\sqrt{n}} S_J$ to independent normal random variables, and in $n w_1 / N_1, \dots , n w_J / N_J$ to constants, we can apply Theorem 5 to show that

$$\begin{aligned} \sqrt{n} \left( p_{\text {post}}^n - p \right)&= \sum _{j=1}^J \frac{n w_j}{N_j} \frac{1}{\sqrt{n}} S_j \nonumber \\ {}&\rightarrow _{\mathcal {D}} \mathcal {N} \left( 0, \sum _{j=1}^J \frac{w_j^2}{q_j} \sigma _j^2 \right) , \end{aligned}$$

(C27)

which is the same as Eq. C13. That is, the post-stratified estimator has the same asymptotic distribution as the original stratified sampling estimator despite the samples $Z_1, \dots , Z_n$ being drawn from some other distribution.

Supplementary information

An R package for carrying out the statistical methods discussed is available on GitHub (https://github.com/shannon-wms/stratsampling).