Introduction

Dynamic processes in the interior of the Earth that ultimately lead to volcanic eruptions leave their imprints in the chemical compositions of volcanic minerals and melts. As material is transferred from the source regions (partial melting, melt segregation) through residence in multiple reservoirs in the crust and the mantle (with processes such as magma mixing, mingling, and assimilation in transcrustal magma plumbing systems) to eruption (conduit processes, processes during cooling in lava flows or bombs), minerals are exposed to different thermodynamic magmatic environments (the overall chemical environment defined by chemical potentials of different components as well as temperature and pressure—see Kahl et al. 2015 for a detailed description and definition) for different durations of time. The chemical signature of each thermodynamic environment is distinct, and superposition of different chemical compositions in a given mineral grain leads to the development of compositionally zoned crystals. Chemical diffusion is effective in high-temperature magmatic systems and attempts to remove such disequilibrium, either by erasing existing compositional differences or by forming new gradients in order to reset the chemical composition of a mineral inherited from a different thermodynamic environment (e.g., different temperature or pressure). If the rate of diffusion of an element or isotope in a mineral is known, then the extent of such diffusive modification may be used to determine the duration of time spent by a crystal in a given environment (e.g., a particular magma reservoir). This is illustrated in Fig. 1. The basic principle is embodied in the relationship X2 ~ Dt, where X is the length scale over which diffusion occurs, D is the relevant diffusion coefficient, and t is the timescale of interest. Following the first applications in meteorites in the 1960s (Wood 1964), this principle has been applied to practically all kinds of rocks to obtain different parameters related to timescales (e.g., residence times, cooling rates, ascent rates) under different names (e.g., diffusion chronometry, geospeedometry, thermochronology). It is important to note at this point that the method yields a duration, and not an age of an event and that the method should be applied to compositional gradients only after it is established that these formed by diffusion and not crystal growth (e.g., see below as well as Costa et al. 2008; Shea et al. 2015a).

Fig. 1
figure 1

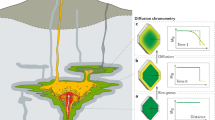
Illustration of the general principles of diffusion chronometry for a simple scenario where a rim of a different composition is overgrown on a crystal with orthorhombic symmetry (e.g., olivine or orthopyroxene), and subsequently diffusion of atoms occurs between the core and the rim. The simplified schematic drawing of a volcanic plumbing system to the left illustrates a deeper source region where magma is generated, a storage region at intermediate depths consisting of many interconnected smaller magma reservoirs, and the volcanic edifice at the top with an eruption center. The deeper source region is one magmatic environment (ME2, characterized by one set of values of pressure, temperature, and chemical potential of different chemical components), the shallow storage location is a second magmatic environment, ME1. It is highlighted that a magmatic environment may be made up of several physical reservoirs (assumption: these are so close to each other that the pressure difference cannot be discerned using standard tools of barometry). Magma from the source region with its crystal cargo (Stage I, at time tI) moves to the intermediate storage location (Stage II, time tII, “Intrusion”). The colors in the different reservoirs and crystals indicate different chemical compositions of the crystals in the different magmatic environments. In this case, the overgrowth of a new composition is triggered by the intrusion of the crystal cargo from ME2 into ME1 as part of a magma mixing event. A critical assumption is that the overgrowth is produced instantaneously after the arrival of the magma with its crystal cargo in ME1. Once the chemical contrast between the core and the rim of a crystal is produced, diffusion of atoms attempts to erase the concentration gradient (i.e., the diffusion clock starts ticking) and the process continues until it is quenched by cooling at eruption (Stage III). How fast the clock ticks depends on the diffusion coefficient of the element of interest in the mineral, and a variety of other parameters that characterize the ME. Modeling the diffusion process yields the time interval between the time of intrusion/magma mixing (tII) and eruption (tIII), which is the residence time of the crystal in ME1. The shape of the concentration profile that would be measured at each stage and the calculated profile shape that should match the measurements are shown on the sides. The equation that is solved to obtain the timescale is shown on the bottom right, and arrows on concentration profiles underscore other concentration parameters (initial condition = shape of concentration profile at the start of the diffusion process, boundary condition = how concentration change/stay constant at the boundaries of the domain where diffusion occurs) that need to be defined. More complex initial conditions such as non-homogeneous concentration distribution, boundary conditions such as concentrations at the rim changing with time, and multiple-stage processes can be modeled using the same principles iteratively (see Kahl et al. 2011 for an illustration) 

Full size image

There are a number of reasons for the growth in popularity of diffusion modelling to obtain timescales in recent years:

  1. (i)

    After the first pioneering studies, it became obvious that timescales in igneous systems (like residence times of crystals, cooling rates) were short and often covered ranges of days to years (e.g., Coish and Taylor 1979; Onorato et al. 1981; Gerlach and Grove 1982; Ozawa 1984; Grove et al. 1984; Koyaguchi 1986; Snow and Yund 1988; Nakamura 1995). Such short timescales are inaccessible to other methods (e.g., short-lived radionuclides), particularly for older rocks (the time-resolution of diffusion chronometry is independent of age).

  2. (ii)

    The advances in experimental and analytical techniques, particularly the ability to determine concentration gradients over micro- to nano-scales for a range of elements and isotopes, have made the determination of many diffusion coefficients as well as applications to many more situations possible. In addition to the conventional electron microprobe, tools such as SIMS or LA-ICP-MS for trace elements (e.g., Beck et al. 2006; Spandler et al. 2007; Qian et al. 2010), FTIR and Raman spectroscopy for H-species (e.g., Ingrin et al. 1995; Kohlstedt and Mackwell 1998; Demouchy et al. 2006), nano-SIMS ( e.g., Saunders et al. 2014; Seitz et al. 2018; Shamloo and Till 2019) or Atomprobe for ultrahigh spatial resolution (Valley et al. 2015), and femtosecond LA-ICP-MS for isotopic gradients of heavy elements are being used (e.g., Oeser et al. 2014, 2015; Steinmann et al. 2019).

  3. (iii)

    Numerical computation of diffusion processes can now be carried out on any ordinary laptop computer, making the tool accessible to even real-time monitoring (Gansecki et al. 2019; Re et al. 2021). Such programs should also include corrections for spatial averaging effects of the analytical tools (“Convolution correction”) (e.g., Hofmann 1994; Ganguly et al. 1988; Bradshaw and Kent 2017; Jollands 2020). A few user-friendly numerical tools are available where a user may directly determine timescales without the need for programming (e.g., DIPRA: Girona and Costa 2013; An Excel spreadsheet of Dan Morgan, pers. comm.; Hesse 2012, NIDIS: Petrone et al. 2016; DFENS: Mutch et al. 2021); more such tools should be forthcoming soon.

Examples of diffusion chronometry

Over the past 20 years, diffusion chronometry in volcanic rocks has been carried out using a number of elements and minerals that include:

  1. (i)

    Fe–Mg, Ni, Ca, and Mn in olivine;

  2. (ii)

    Mg, Sr in plagioclase;

  3. (iii)

    Mg, Ba, Sr, Na–K in sanidine;

  4. (iv)

    Ti in quartz

  5. (v)

    Fe–Mg, Fe-Ti, and Cr-Al in ilmenite/spinels;

  6. (vi)

    Fe–Mg in pyroxenes;

  7. (vii)

    H diffusion in olivine or pyroxenes;

  8. (viii)

    Li diffusion in olivine, plagioclase, pyroxenes or zircons;

  9. (ix)

    H2O (volatile) diffusion in melt embayments;

  10. (x)

    H2O (volatile) diffusive loss from melt inclusions via their host mineral (olivine);

  11. (xi)

    Cl in apatite.

A complete list of references with studies applying these different diffusion chronometers is provided as supplemental bibliography. Two points are worth noting in this context: (i) diffusion of some elements occur obeying equations that deviate from the conventional forms (e.g., Mg in plagioclase, see Costa et al. 2003), and (ii) timescales determined with older diffusion coefficients are often revised, or at least re-discussed, as newer, more robust diffusion data become available (consequence of improved technology as well as improved understanding of diffusion mechanisms in minerals).

These tools have been used in practically all known volcanic settings such as subduction zones (SZ), oceanic hot spots (OHS), mid ocean ridge systems (MOR), intracontinental rift zones (IRZ), hot spots (HS), or flood basalts (FB) as well as continental silicic volcanic systems (SVS); in the entire range of magmatic compositions from basaltic through rhyolitic/dacitic (including alkaline as well as sub-alkaline magmas); geographically spread over the entire globe and indeed, including samples from the Moon, Mars, and various meteorites; the applications span a range of ages from contemporary volcanic products to samples that are about as old as the Earth in meteorites (e.g., Ganguly et al. 1994; Miyamoto and Takeda 1994; McCallum and OBrien 1996; Fisler and Cygan 1998; Mikouchi et al. 2001; Fagan et al. 2002; Beck et al. 2006; Ganguly et al. 2013; Richter et al. 2021). There are some indications that timescales of evolution of silicic magma reservoirs are somewhat longer than storage and residence times in mafic systems (Cooper 2019, 2017; Costa 2021). Input of new, usually hotter, more mafic magmas shortly (weeks to months) before eruption is quite common and may have a triggering effect (Kent et al. 2020). Diffusion chronometry using faster diffusing elements like H has been used to determine ascent rates (inferred depth of the magma/duration of the ascent). These studies indicate that rapid exhumation is more often associated with explosion (Charlier et al. 2012; Barth et al. 2019; Myers et al. 2018; Barth and Plank 2021).

A number of reviews are available that discuss the details of the methods of such applications in volcanic systems (see Costa et al. 2008; Dohmen et al. 2017), strengths and weaknesses of diffusion modelling (see Chakraborty 2006, 2008), available diffusion coefficients in different minerals up to 2010 (see Zhang and Cherniak 2010), and the kinds of information relevant to volcanic systems that are obtained from diffusion chronometry (Cooper 2019; Costa et al. 2020; Costa 2021; Petrone and Mangler 2021). Short summaries of different aspects may be found in various articles in Elements (Costa and Turner 2007; Putirka 2017; Cooper 2017). While we refer readers to these reviews and original papers for details, we highlight a few practical aspects of diffusion chronometry and advanced approaches for volcanic systems.

Diffusion anisotropy and sectioning effects

Most applications so far have used one-dimensional concentration profiles (see Fig. 1). To obtain a correct duration from such a profile, it is necessary to consider that.

  1. (i)

    diffusion is anisotropic in non-cubic minerals and therefore the crystallographic direction of the profile needs to be measured (for example using EBSD, as shown in Costa and Chakraborty 2004) and

  2. (ii)

    the profile could be affected by diffusion fluxes from other directions oblique to the direction of the profile (Costa et al. 2003 provide an example). Shea et al. (2015b) discuss these aspects in detail for olivine (see also Krimer and Costa 2016, for orthopyroxene and Couperthwaite et al. 2021 for olivine) and make recommendations for the number of profile measurements that are necessary for obtaining statistically robust results.

Ganguly et al. (2000) discuss a way for correcting for oblique sectioning effects in isotropic minerals. Measurement of compositional gradients in three dimensions using serial sectioning or tomographic image analysis tools is a possible direction of future development (Lubbers et al. 2022); some related tools have recently been developed in the study of metamorphic rocks (George and Gaidies 2017; Gaidies and George 2021).

Fitting procedures and related errors

Uncertainties in fitting diffusion profiles arise from many sources (e.g., sectioning effects) and it is not possible to quantify all of them—therefore, reproducibility and spread of timescales obtained from a statistically significant number of multiple determinations remains the most reliable measure of uncertainties. However, this approach needs to account for the fact that not all crystals of the same mineral in a rock (e.g., olivines) experienced the same history. The tool of systems analysis of zoning profiles developed by Kahl et al. (2011, 2015) can help to identify crystal populations that experienced the same history, and reproducibility of timescales obtained from one such group of crystals is indicative of uncertainties. The different sources from which errors can arise in fitting diffusion profiles have been listed and discussed for experimental samples (where at least some of the variables are well constrained) in the Appendix of Faak et al. (2013). In natural samples, the additional and largest source of uncertainty is in the knowledge of the temperature(s) at which diffusion occurred and inferred uncertainty of the respective diffusion coefficient. These aspects have been considered in Gualda et al. (2012) and in the reviews by Costa (2021) and Petrone and Mangler (2021). New tools for addressing these are emerging from recent work (such as the DFENS method, Mutch et al. 2021).

It is worth noting here that the solutions of the diffusion equations are of the form C (x,t), so that it is necessary to determine a C(x)—a profile, and not a single composition at some point within a crystal (e.g., the core, or the rim)—for obtaining information on timescales. The same composition may result at the core of a crystal, for example, from different sets of initial and boundary conditions on different timescales; it is the profile shapes (more precisely—the curvatures of the profile, ∂2C/∂x2, at each position x along the profile, see diffusion equation in Fig. 1) that are unique functions of time. This important aspect has been discussed with illustrations in Faak and Gillis (2016).

Finally, incorrect choice of initial and boundary conditions can lead to errors (see, for example, Costa et al. 2003; Shamloo et al. 2021). The emerging recognition that (Welsch et al. 2013, 2014) crystals do not always grow radially from core outwards like tree-rings is an aspect that needs to be considered in this regard—analysis of stable isotopes can help.

Stable isotopes as diffusion fingerprint

Light isotopes diffuse faster than heavier ones and therefore they leave a fingerprint of the diffusive process (e.g., Richter et al. 2003; Beck et al. 2006; Sio et al. 2013). Recent advances using femtosecond-Laser ablation ICP-MS allow such isotopic fractionation and resulting zoning of elements like Li, Fe, and Mg in minerals like olivine or plagioclase (Oeser et al. 2015; Steinmann et al. 2020) to be determined. This gives us the opportunity to (a) distinguish between compositional gradients formed by diffusion from those that develop during crystal growth, and (b) define the correct initial and boundary conditions under which diffusion occurred (e.g., Oeser et al. 2015; Sio and Dauphas 2016; Steinmann et al. 2020).

Image analysis

As diffusion modelling relies on the measurement of concentration gradients and profile shapes, the time and cost of measurement of concentration profiles or element concentration maps is considerable and there have been efforts to reduce these. One approach relies on image analysis—for example, the brightness contrast in a BSE or CL image (collected in seconds) is calibrated for element concentrations and the resulting gradients are used for diffusion modelling (e.g., BSE for Ba in sanidine: Morgan et al. 2006, Rout and Worner 2020; or Fe–Mg in pyroxene: Morgan et al. 2004; CL and Ti in quartz: Gualda and Sutton 2016).

Multiple element/mineral approach

The occurrence of different minerals with many different major and trace elements offers several “clocks” in any given rock (each element in each mineral, with a different diffusion coefficient and likely different initial and boundary conditions under which diffusion occurs, is a separate “clock”). These can be used to verify internal consistency, as well as to access a wide range of timescales (e.g., use slow diffusing species, such as REE in some minerals: long timescales, such as source region events; rapidly diffusing species, such as Li or H in some minerals: rapid processes such as magma ascent and conduit processes). Note that each grain of a mineral, and even each crystallographic direction in a mineral with anisotropic diffusion, is an independent clock for determination of timescales. It is the consistency of such multiple determinations (i.e., enough statistical robustness) that compensates for many of the inherent shortcomings of the method (e.g., knowledge of initial conditions, the thermodynamic variables and uncertainties in diffusion coefficients), some illustrative examples include Costa and Dungan (2005), Kahl et al. (2011, 2016). On the other hand, discrepancies in obtained timescales using different “clocks” point to either shortcomings of one or more methods (providing a means of internal cross calibration), or to more nuanced non-linear thermal histories (see Chamberlain et al. 2014 for an example).

Many crystals go through multiple magmatic environments before eruption, and the tool of sequential kinetic analysis (Kahl et al. 2011) can help to determine the timescales of residence of the crystal in each of the environments.

Connection to other volcanological tools

The storage times at different reservoirs and the times of transfer (in units of “time before eruption”) between them may be related to various kinds of monitoring signals, thereby allowing observations on the surface to be related to processes in the interior, and at the same time providing a means of validating the timescales obtained from diffusion chronometry. Kahl et al. (2011) related timescales obtained from their sequential kinetic analysis to signals from seismic monitoring, variations in ground tilt and SO2-flux, and lava fountaining events in Mt. Etna between 1991 and 1993. These results showed how different signals observed on the surface are related to events occurring at different depths below the volcanic edifice at different times. Saunders et al. (2012) related timescales obtained from diffusion chronometry to seismic events observed at Mt. St. Helens, and subsequently other studies have related timescales from diffusion chronometry to various monitoring signals (e.g., Kahl et al. 2013; Marti et al. 2013; Kilgour et al. 2014; Viccaro et al. 2016; Rasmussen et al. 2018; Pankhurst et al. 2018; Albert et al. 2019; Giuffrida et al. 2021). Such studies lead to a better understanding of processes that occur within a plumbing system at depth. This, in turn, would enable (a) a more detailed understanding of past eruptions, where no monitoring signals are available, and (b) better interpretation of monitoring signals that are observed in the future.

Combination of geochronology and diffusion chronometry

A combination of geochronology (based on zircons or monazites, for example) and diffusion chronometry (based on olivines and plagioclase, for example, but also zircon) is a powerful tool (Cooper 2019). See Cooper (2019) and Cooper and Kent (2014) for details of how the tools are combined. These have revealed that magma reservoirs (locations where magma pools physically, which is often governed by long-term tectonics such as location of zones of faulting or other weakness) or by rheology (e.g., the crust—mantle boundary) may be long lived; residence times of magmas, i.e., molten entities in such locations, may occur on much shorter timescales, governed by thermal parameters. These have triggered the question and debate on whether magma is stored at near or sub-solidus conditions (warm storage) or cold between successive pulses of magma input (see Cooper 2019, and Costa 2021, for a discussion of pros and cons, as well as Bachmann and Huber 2019, for a review of physical modelling of different possible timescales).

Future directions and problems to address

  • Non-isothermal and non-isobaric diffusion models, with constantly adaptive boundary conditions should become more common as multistage and magma ascent related processes are studied. There will be a coupled need for high-resolution thermometry and barometry.

  • Combination of isotopic fractionation caused by diffusion (of light elements such as H or Li, as well as heavier elements such as Fe, Mg, or Ca) will be used increasingly to model diffusion under better constrained (more clearly defined initial and boundary conditions) conditions. Such models should integrate the diffusion of elements, isotopes and the fractionation in an internally consistent manner. The use of reaction–diffusion equations (to address homogeneous reactions) and multicomponent diffusion (coupling between different isotopes and overall elemental flux) will be necessary. We expect the specialized (and expensive) tool of isotopic fractionation to guide the modelling (e.g., identify concentration gradients formed by diffusion rather than growth, choice of boundary conditions) while the bulk of the data will be generated from more rapid and accessible tools (e.g., image analysis, see above).

  • An aspect that has been suppressed in the applications of diffusion chronometry in volcanic systems so far, implicitly or explicitly, has been the role of growth and dissolution coupled with diffusion. However, it is an important aspect in systems where crystals grown in one environment are constantly exposed to other environments in a dynamic system. Modelling such systems require reaction–diffusion equation (see the previous point as well) as well as an understanding of how the diffusion process is itself modified by moving boundaries that result from growth and/or dissolution. Note that solutions to reaction–diffusion equations have behavior that is not seen in simple diffusion equations, such as the attainment of time-independent, steady-state concentration gradients. It is important to evaluate this possibility in the application of diffusion chronometry, because otherwise erroneous timescales may be obtained by fitting such steady-state concentration profiles.

  • A related important aspect is the question of the lifetime of a crystal. Until now, it is assumed that a mineral grain exists in a system governed by its chemical thermodynamic phase relations (e.g., the temperature at which olivine forms). However, processes of recrystallization, governed by considerations of textural equilibrium (e.g., interfacial and surface energy effects) and facilitated by the presence of non-hydrostatic stress or fluids, determine the actual lifetime of a given grain of a mineral. This sets an upper limit to timescales that may be accessed by diffusion chronometry (i.e., olivine may be stable in a given system for a long duration, but if recrystallization of grains occurs on timescales of a few hundred years, then diffusion chronometry with olivine, no matter using which element, cannot access any timescale longer than a few hundred years). Some of the discrepancy between timescales obtained from geochronology and diffusion chronometry may be related to this effect. Studies that combine kinetics of evolution of crystal size distributions (CSD) with diffusion modelling will provide insights in this area.

  • Diffusion of many trace elements (e.g., Li, H, REE) in different rock forming silicates occur by more than one mechanism (e.g., Mackwell and Kohlstedt 1990; Dohmen et al. 2010; Bloch et al. 2020). Modelling these adequately requires an understanding of diffusion mechanisms and the use of reaction–diffusion equations that account for homogeneous reactions between different species, and these would become more common as more detailed measurements become available. Multicomponent diffusion equations that account for exchange between different species simultaneously will be necessary (e.g., Cl-F-OH in apatite, Li et al. 2020).

  • Connections of timescales obtained from diffusion chronometry to various physical phenomena (e.g., seismic events, changes in gas flux, or ground deformation) have so far been made empirically, by a “pattern matching” approach (see the examples above). Physics-based multi-stage models that are being increasingly developed (see, for example, lectures on the MCS RCN website: https://www.sz4dmcs.org/volcano-workshop; Bachmann and Huber 2019) should be coupled with diffusion modelling (Cheng et al. 2020) to obtain a more holistic view of processes occurring on various timescales in a volcanic system. We reiterate here that diffusion chronometry relates timescales to magmatic environments (ME); an associated next step that is very important is to relate those ME to physical entities/processes. For example, recorded changes in volatile contents relate to changes in volatile fugacities, but these may be caused by decompression, degassing, or by changes in fluid composition—the interpretation of timescales obtained from profiles of volatile species would be very different depending on which of these interpretations hold in a specific case.

As application of diffusion chronometry becomes more widespread, there will be a need for (a) quick, inexpensive but robust analytical tools for the determination of concentration gradients, (b) user-friendly software for making the tool accessible to a large group of volcanologists who are not specialists in diffusion chronometry, (c) benchmarks that allow users to test results they obtain, and (d) improved evaluation of various sources of errors and uncertainties in a probabilistic sense.