Abstract
A positive effect of (meta)population density on emigration has been predicted by many theoretical models and confirmed empirically in various organisms. However, in butterflies, the most popular species for dispersal studies, the evidence for its existence has so far been equivocal, with negative relationships between density and emigration being reported more frequently. We analysed dispersal in sympatric metapopulations of two Maculinea butterflies, intensively surveyed with mark–release–recapture methods for 7 years. Dispersal parameters, derived using the virtual migration model, were assessed against butterfly densities, which fluctuated strongly over the study period. Emigration was positively correlated with density, and this effect was particularly strong at densities above carrying capacity, when emigration increased up to threefold in females and twofold in males compared with the normal levels. In turn, density had little impact on other dispersal parameters analysed. Our findings provide good evidence for positive density-dependence of emigration in butterflies. Emigrating at high densities is particularly beneficial for females, because it gives them a chance to lay part of their egg-load in less crowded patches, where offspring survival is higher due to lower intraspecific competition. Even though the rise in emigration becomes considerable at densities exceeding carrying capacity, i.e. relatively infrequently, it still has serious implications for many ecological phenomena, such as species range expansions, gene flow, and metapopulation persistence. Consequently, instead of treating emigration as a fixed trait, it is worth allowing for its density-dependence in applications such as population viability analyses, genetic models or metapopulation models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Positive density-dependent emigration has been postulated by many numerous theoretical models as a regulatory mechanism in population dynamics (Poethke and Hovestadt 2002; Enfjäll and Leimar 2009, and references therein). Empirical evidence for its existence, however, has so far been highly inconsistent (see reviews in Lambin et al. 2001; Matthysen 2005; Bowler and Benton 2005). Although studies in various invertebrate species have documented increased emigration triggered by high population densities (e.g. Byers 2000; Doak 2000), for vertebrates, both positive and negative relationships between density and emigration have been frequently reported (Matthysen 2005; Kim et al. 2009).
Notably, the group in which the least indication of positive density-dependent emigration has been found are butterflies. This is remarkable, because of the large number of studies involving butterflies, which are the most common models for dispersal analyses (Stevens et al. 2010). In fact, more convincing evidence has been gathered for negative density-dependence of emigration in butterflies (Gilbert and Singer 1973; Brown and Ehrlich 1980; Kuussaari et al. 1996; Roland et al. 2000). This is typically due to the fact that individuals leave their patches more frequently at low population density in order to search for mating partners. Alternatively, low individual density may indicate low-quality habitat patches that butterflies tend to avoid. In turn, a positive effect of density on emigration rate has been demonstrated almost exclusively in already-mated females fleeing from harassment by overabundant males (Shapiro 1970; Odendaal et al. 1989; Baguette et al. 1998). The only case in which density-dependent emigration has been shown to act as a mechanism of avoiding overcrowding and the resulting intraspecific competition is, to our knowledge, the cage experiment by Enfjäll and Leimar (2005).
The aim of the present study was to assess density-dependence of emigration as well as other dispersal parameters in natural conditions. For this purpose, we analysed dispersal within metapopulations of two sympatric species of Maculinea butterflies, in which emigration triggered by sexual harassment is unlikely, but in turn strong intraspecific competition should be expected (Hochberg et al. 1994; Nowicki et al. 2009). Both species were investigated with intensive mark–release–recapture (MRR) surveys for 7 years, and over this period, their numbers experienced strong fluctuations. We were interested not only in establishing whether the relationship between density and emigration rate is positive or negative but also in evaluating its shape, particularly versus carrying capacity of the habitat. In addition, we focused on intersexual differences in density-dependent patterns of dispersal parameters. Sex-biased density-dependence of dispersal may be theoretically predicted, yet empirical evidence in this respect is even more equivocal than in the case of positive density-dependent emigration (Gros et al. 2008).
Materials and methods
Study species and area
We investigated metapopulations of two univoltine butterfly species, Maculinea nausithous and M. teleius (Lycaenidae), occurring sympatrically in the Elbe lowland near the town of Přelouč, central Czech Republic (50°03′N, 15°34′E; 207 m a.s.l.). Maculinea butterflies are highly specialised myrmecophilous butterflies, requiring specific foodplants and specific host ants of the genus Myrmica in their larval period (Thomas et al. 1998). Intraspecific competition between larvae in ant nests induces density-dependent regulation in Maculinea, and temporal changes in ant nest abundance result in strong fluctuations of Maculinea (meta)populations (Hochberg et al. 1994; Nowicki et al. 2009). Larval foodplants are also primary nectar sources for adult butterflies (Thomas et al. 1998). There is a controversy surrounding the fact whether adult butterflies can detect the presence of host ants, with most of the studies suggesting they cannot (Thomas and Elmes 2001; Fürst and Nash 2010; but see van Dyck et al. 2000). Regardless of this controversy, foodplant patches can be defined as habitats of local populations, because host ant occurrence usually coincides spatially with foodplant occurrence (Thomas and Elmes 2001).
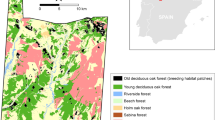
The foodplant of M. nausithous and M. teleius, the great burnet Sanguisorba officinalis, typically grows in very high densities (Nowicki et al. 2007, 2009) and consequently its patches are easy to map, which was the case also for the Přelouč metapopulations. We identified ten patches of Sanguisorba officinalis with the areas from 0.21 to 1.57 ha (7.73 ha in total) (Fig. 1). Inter-patch distances range from 80 to 1,200 m, and the matrix is a mosaic of meadows lacking the foodplant and agricultural fields with rare wooded strips.
Mark–release–recapture survey
All the local populations have been intensively surveyed with MRR methods for 7 years (2004–2010). Each year, the surveys covered the entire flight period of both species, which in this region lasts from early July to mid-August. Sampling was conducted daily, with few (<6 each year) days missed due to unfavourable weather, between 0900 and 1700 hours. Sampling intensity on particular habitat patches was adjusted to their area and butterfly numbers in order to ensure uniform capture probabilities across all the patches. Butterflies captured were individually marked with numbers written on the underside of their hind wing using a fine-tipped waterproof pen, and immediately released at the place of capture.
Statistical analysis
Seasonal metapopulation sizes in each year (\( \hat{N}_{t} \)) were obtained with constrained open population models of the program MARK 5.1 (White and Burnham 1999), according to procedure described by Schtickzelle et al. (2002; see this reference for the details of the procedure). First, Cormack–Jolly–Seber (CJS) models (Schwarz and Arnason 1996; Schwarz and Seber 1999) were applied to assess the patterns in survival and capture probability for each dataset, i.e. a single species in a single season. The best supported pattern in survival and capture probability subsequently served as a fixed basis for modelling recruitment with help of Jolly–Seber (JS) models (Arnason and Schwarz 1999). Finally, the super-population size derived for the best Jolly–Seber model was adopted as the metapopulation size estimate. The performance of candidate CJS and JS models was evaluated with the Akaike Information Criterion corrected for small sample size (AICc) (Akaike 1973; Hurvich and Tsai 1989). In each case, we followed the principle of parsimony (Burnham and Anderson 1998), i.e. as the best model, we regarded the one with the smallest number of parameters from among those with AICc differing from the minimal one by <2 (see Table S1 in the electronic appendix).
Based on the 7-year time series obtained, we estimated carrying capacities for both species through fitting a simplified Hassell density-dependence model: \( \hat{N}_{t + 1} = {{xr\hat{N}_{t} } \mathord{\left/ {\vphantom {{xr\hat{N}_{t} } {(x + r\hat{N}_{t} )}}} \right. \kern-\nulldelimiterspace} {(x + r\hat{N}_{t} )}} \), as in previous studies on Maculinea (Nowicki et al. 2007, 2009). In the model, r represents basic reproductive rate and x is a parameter related to carrying capacity (K) that can be derived as \( {{K = x(r - 1)} \mathord{\left/ {\vphantom {{K = x(r - 1)} r}} \right. \kern-\nulldelimiterspace} r} \). Since estimating basic reproductive rate from such short time-series would most likely lead to underestimation of this parameter, we decided to set its values to 4.3, which is equivalent to the maximum year-to-year population growths recorded in the aforementioned studies for both M. teleius and M. nausithous.
Dispersal parameters were estimated using the virtual migration (VM) model and program VM2 (Hanski et al. 2000), which represents a well-established standard for analysing dispersal in metapopulations on the basis of MRR data. It has been presented in detail elsewhere (Hanski et al. 2000; Wahlberg et al. 2002), and thus here we only briefly outline its rationale. The model assumes that individuals staying in habitat patches experience a certain dispersal-independent and constant mortality μp. Emigration rate from a natal patch (ε j ) depends on its area (A j ):
where η defines emigration propensity (here expressed as daily emigration rate from a 1-ha patch), while ζem is emigration scaling with patch area. Survival of dispersing individuals (φmj ) is a sigmoid function of their natal patch connectivity (S j ):
The square root of the scaling parameter λ represents the connectivity level at which half of the dispersers successfully reach other patches. Patch connectivity is measured as:
with d jk being the Euclidean distance between patches, A k referring to target patch area, and finally α and ζim scaling, respectively, distance-dependence of dispersal and immigration probability. Successful dispersers are distributed among target patches proportionally to their contributions to the natal patch connectivity.
The VM model allows the estimation of its six parameters (μp, η, ζem, λ, α, ζim) together with their 95% confidence intervals. It should be stressed that the VM model dispersal estimates, although based on the same MRR data, are independent of the metapopulation size estimates. The VM model also makes it possible to simulate dispersal within a metapopulation for the estimated parameter values (Hanski et al. 2000). We produced parameter estimates separately for both sexes as well as for all individuals pooled together. Only in the case of 2004 data small sample sizes precluded deriving separate estimates for both sexes in either of the two species investigated.
Additionally, in order to check whether sample size may induce bias in VM model parameter estimates (which could imitate the effects of density, because higher butterfly abundances corresponded with larger sample sizes), we also applied the model to artificially extended datasets. These were produced by triplicating each individual capture history so that three times higher butterfly numbers were achieved without altering the dispersal patterns. As this procedure left all the parameters values virtually unchanged, we present only the results obtained for the original datasets.
We used the negative exponential dispersal kernel in the VM model (as in Hanski et al. 2000) rather than the inverse power one (applied, e.g., by Schtickzelle et al. 2006). Hence, average dispersal distance (measured in km) corresponds to 1/α. The negative exponential kernel fitted our empirical data much better as revealed by the VM model goodness-of-fit tests. Earlier studies also found that a negative exponential dispersal kernel described movements by M. teleius and M. nausithous quite well (Hovestadt and Nowicki 2008). Nevertheless, it is worth noting that with inverse power kernel attempted for comparison we obtained almost identical estimates of all the VM model parameters (obviously apart from α) for each species and sex.
The main difficulty in testing the effect of density on dispersal parameters was the low precision of the VM model estimates and, to a lesser extent, of metapopulation size estimates. Consequently, we applied the non-parametric Kendal’s rank correlation coefficients. In addition, we conducted simulations, drawing 10,000 random values for all the VM model parameters and density estimates according to their likelihood distributions. Subsequently, we evaluated the strength of the relationship between butterfly densities and dispersal parameters, using the proportion of cases in which their simulated values produced a statistically significant outcome (P < 0.05) when tested with linear and exponential regression analyses. All the aforementioned statistical tests were conducted using Statistica 8.0 software (StatSoft 2008).
Results
Over the 7 years of the study, 1,880 M. nausithous and 2,935 M. teleius individuals were captured 4,680 and 7,479 times, respectively, with 591 and 390 inter-patch movements recorded. Estimated sex ratio was close to 1:1 in each case, i.e. species and year. Overall metapopulation size of both species fluctuated substantially in the course of the study (Fig. 2), which resulted in the considerable range of densities found: 19–126 M. nausithous/ha and 31–151 M. teleius/ha (coefficients of variation: CV = 0.61 for M. nausithous; CV = 0.47 for M. teleius). Fluctuations of M. nausithous and M. teleius were apparently asynchronous (Kendal’s correlation coefficient τ = 0.24, P = 0.4527). The simplified Hassell model fitted time-series of the investigated butterflies relatively well (R 2 = 0.32, P = 0.0159 for M. nausithous; R 2 = 0.41, P = 0.0054 for M. teleius), indicating density-dependent dynamics of their metapopulations. The carrying capacities were estimated at 67 (±SE = 19) M. nausithous adults and 111 (±SE = 24) M. teleius adults per ha.
Reliable MRR population size estimates could not be produced separately for each habitat patch, because sample sizes were too small in most cases. However, the numbers of individuals captured in each patch per season may well serve as indices of local abundances, because capture probabilities were fairly uniform (ca. 0.4–0.5) across species and years as well as across the few patches for which they could be estimated, while for the remaining patches they are also likely to be similar, taking into consideration the standardised sampling effort. Based on the seasonal numbers of individuals captured in each patch, it can be ascertained that in both species fluctuations of the local populations were much stronger than those of the entire metapopulation (average CV = 0.83 and 0.89 for M. nausithous and M. teleius, respectively), and poorly synchronised between one another (Pearson’s correlation coefficient r calculated for 45 population pairs averaged 0.361 for M. nausithous and 0.153 for M. teleius, with, respectively, 4 and 2 values significant at 0.05, but none of them remained significant after Bonferroni corrections were applied).
Emigration propensity, estimated with the VM model, was 0.08–0.10 in M. nausithous and 0.06–0.08 in M. teleius in years when the butterfly densities were at low to medium levels. Once the carrying capacity was exceeded, however, it rose sharply, doubling in males and rising threefold in females (Fig. 3). The estimates of emigration propensity reflect the proportion of individuals emigrating per day, scaled to an imaginary 1-ha patch. With real areas of habitat patches in Přelouč accounted for, they correspond to the seasonal proportions of emigrants of roughly 20–30% in ‘normal’ years, and up to 55% when the metapopulations reached their peaks (Fig. 4).
The virtual migration model estimates of emigration propensity (η; shown with 95% confidence intervals) in the investigated metapopulations of Maculinea butterflies presented against their densities (d) in a given year. Broken vertical lines indicate carrying capacities for both species. Solid lines represent best-fit regression lines based on simulations, in which the values of butterfly density and their emigration propensity were drawn 10,000 times according to the likelihood distributions of their estimates
Seasonal proportions of butterflies emigrating from their natal patches based on the virtual migration model simulations: a M. nausithous; b M. teleius. Dark bars indicate the fractions of unsuccessful dispersers. In the simulations, we assumed that numbers of butterflies living in particular patches are proportional to the numbers of individuals captured there
The effect of Maculinea density on their emigration was the most prominent above carrying capacity, but it could also be traced at lower densities. The clearly positive relationship between density and emigration propensity (Kendal’s correlation coefficient τ = 1.00, P = 0.0016 for both species) remained significant even if we treated the single years with the highest response as potential outliers and removed them from the analysis (Kendal’s correlation coefficient τ = 1.00, P = 0.0048 for both species). Similarly, the analyses conducted separately for both sexes also brought a significant outcome (Kendal’s correlation coefficient τ = 1.00, P = 0.0048 in females, and τ = 0.87, P = 0.0146 in males of both species) despite their smaller sample sizes due to the fact that sex-specific estimates of emigration propensity were not available for the first year of our study.
The simulations, in which parameter values were drawn from their likelihood distributions, revealed that density-dependence of emigration reached statistical significance in more than 99% cases in M. nausithous and more than 97% cases in M. teleius when tested with exponential regression (Table 1). Linear regression performed slightly worse, especially for the latter species. In the simulations conducted separately for each sex, the proportions of significant cases were considerably lower, which is understandable due to the lower precision of sex-specific emigration propensity estimates and their unavailability in 2004 (thus, one less data point in the analyses). Nevertheless, these proportions were still well above 50%, implying that the existence of an effect of density on emigration is more likely than its lack (Table 1).
Just like the fluctuations in butterfly densities, the fluctuations in emigration propensity of both species were not synchronised (Kendal’s correlation coefficient τ = 0.24, P = 0.4527), i.e. the proportions of emigrants in M. nausithous and M. teleius peaked in different years. In the context of the intersexual difference in emigration propensity, it should be noted that female emigration triggered by sexual harassment appears unlikely in Maculinea. Although we did occasionally observe individuals leaving their habitat patches, none of such cases resulted from female fleeing male harassment. Instead, adopting a rejection position, i.e. bending its abdomen, was typically enough for a female to deter male courtship.
VM model estimates of dispersal mortality scaling indicated relatively low mortality during dispersal (Fig. S2 in the electronic appendix). The overall proportion of unsuccessful dispersers within a metapopulation per season reached at maximum 12% in M. nausithous, and 28% in M. teleius. In most years, however, zero mortality during dispersal was the most likely. This result cannot be explained by small sample sizes, because the VM analyses of artificially triplicated datasets brought identical outcomes. Interestingly, dispersal-related mortality that was significantly above zero was only recorded for M. teleius in 2007–2008, when the species reached its highest densities (Fig. S2 in the electronic appendix). No such pattern was found for M. nausithous.
Maculinea density had little impact on any other parameter of their dispersal (Fig. S2 in the electronic appendix). Mortality of non-dispersers experienced in habitat patches ranged between ca. 0.10 and 0.25 per day, regardless of the species and sex. Natal patch area had a minor effect on emigration in M. nausithous (scaling parameter ζem = 0 to −0.7) and a moderate one in M. teleius (ζem = −0.7 to −1.7). In turn, the effect of target patch area on immigration was moderate in M. nausithous (scaling parameter ζim = 0.5–1.5) and strong in M. teleius (ζim = 1.1–2.5). The above area effects were usually, though not consistently, weaker in females. The average dispersal distance (1/α of Fig. S2 in the electronic appendix) was ca. 150–270 m in M. nausithous and ca. 80–220 m in M. teleius, with no indication of intersexual differences.
Discussion
All the parameter estimates obtained in our study are highly realistic. While our VM analysis is the only one conducted so far for Maculinea, its results resemble those yielded by the VM models for other butterflies (e.g. Wahlberg et al. 2002; Wang et al. 2004). Similarly, average dispersal distances of M. nausithous and M. teleius that we found as well as their adult densities and carrying capacities fit well within the typical value range recorded for both species (cf. Nowicki et al. 2005a, b, c, 2007; van Langevelde and Wynhoff 2009). The relatively low carrying capacity estimated for M. nausithous, as compared with that for M. teleius, is likely to stem from lower abundance of its host ants in Přelouč (cf. Witek et al. 2008).
Our analysis provided good evidence for the existence of density-dependent emigration in Maculinea butterflies. The positive effect of density on emigration propensity was weak but detectable at moderate densities, and fairly strong at densities above carrying capacity. Moreover, the temporal variation in emigration that we detected cannot be explained by environmental stochasticity, e.g. weather patterns, because the fluctuations in emigration propensity of both species were not synchronised.
Regretfully, we were able to estimate emigration only for entire metapopulations, while its density-dependence may be expected to be driven at the scale of local populations. Even the simplest patch-specific measure of emigration, i.e. the recorded proportion of individuals that changed patch among all butterflies that were marked in a particular patch and subsequently recaptured (Hill et al. 1996), could not be reliably derived because of the too small size of the investigated local populations—merely a single M. teleius population had >30 recaptured individuals each year. However, the positive density-dependence of emigration documented at the metapopulation scale should be regarded as the effect averaged across ten local populations. In other words, increases in metapopulation size reflected the fact that several local population peaked in these years, and our observations indicate (although as explained above the pattern cannot be properly quantified) that the pool of emigrants was then dominated by disproportionally high numbers of individuals leaving such populations, while very few emigrants originated from the populations experiencing decline in a particular year.
The fact that the impact of density on emigration becomes strong only above carrying capacity is in good agreement with theoretical predictions that emigration at times when conspecific density exceeds carrying capacity increases individual fitness (Hovestadt et al. 2010). It allows avoiding strong intraspecific competition (in our study system, the competition among butterfly larvae) even if we consider density measured for entire metapopulation rather than for a particular population. As long as the dynamics of local population are asynchronous, which is likely to be the rule rather than the exception (see, e.g., Nowicki et al. 2007 and Hanski 1999 for the theoretical background), the emigrants from peaking populations have chances to find a few relatively little populated patches.
Sex-biased effect of density on emigration is also well grounded in the theory, which predicts higher emigration in the sex that experiences stronger competition and lower dispersal mortality (Perrin and Mazalov 2000; Gros et al. 2008). In butterflies, dispersal-related mortality is similar for both sexes (Petit et al. 2001; Rabasa et al. 2007; see also Fig. S2 in the electronic appendix), while intra-specific competition is typically the most severe in the larval period, and the tendency to reduce it for their offspring should be expected to drive higher emigration in females. Furthermore, female emigration becomes more and more beneficial with increasing density in natal patches, because it allows laying at least a part of the egg-load in other patches, where the offspring survival may be higher. In males, the same can also be achieved through mating with subsequently dispersing females, while, on the other hand, staying in densely populated patches may allow more mating opportunities.
The actual mechanism that triggers emigration when adult density exceeds carrying capacity is unclear. In particular, the way in which Maculinea are able to assess their density remains a puzzle. Nevertheless, it is important to point out that the proximate factors do not necessarily act during the adult stage. One can imagine that density-dependent emigration may for instance stem from more dispersive behaviour of butterflies that developed in the presence of conspecifics in the final stage of their larval period. The number of full-grown larvae and pupae per infected Myrmica nest, which corresponds well with the number of subsequently eclosing butterflies, is ca. 1.5–2 on average, but it shows strong variation (Witek et al. 2008, 2010), and obviously it increases in years of high butterfly abundance.
In contrast to emigration propensity, our study provided no support for the impact of butterfly density on any other parameters of their dispersal, possibly with the exception of slightly increased dispersal mortality. This may reflect the fact that at high densities, when emigration is undertaken by a larger proportion of individuals than in normal years, some of these individuals may be less adapted to dispersal. An alternative explanation may be that some individuals tend to leave the metapopulation when it is at peak, because in the VM model dispersal beyond the investigated system (even if occasionally successful) cannot be distinguished from the true mortality during dispersal within the system. However, since we found such a pattern in one of the species investigated (M. teleius), and not in the other, both above explanations should be treated with caution until they are confirmed by further research.
To our knowledge, the present study is the first in which density-dependent emigration, unrelated to sexual harassment, has been so well documented in butterflies. Nevertheless, indication for such a phenomenon can be traced in some other recent papers. The results presented by Cassel-Lundhagen and Sjögren-Gulve (2007) showed over fivefold rise in emigration rate corresponding to the substantial increase in adult numbers of Coenonympha hero, although the authors themselves did not underline this finding, concentrating on the conservation implications of limited dispersal. Enfjäll and Leimar (2005) recorded a positive effect of density on Melitaea cinxia inter-cage movement frequency in their cage experiment. Density-dependent emigration results in low numbers of dispersers in ‘normal’ years, and very high numbers when a (meta)population is at its peak, because a great abundance of individuals is then combined with their increased emigration propensity. The latter situation may be infrequent, but it has tremendous consequences for many ecological phenomena. Density-dependent emigration has been found to accelerate the rate of species range expansions (Travis et al. 2009; but see Best et al. 2007), stimulate gene flow (Aars and Ims 2000), and to enhance metapopulation persistence (Nachman 2000; Hovestadt and Poethke 2006). Therefore, it is regretful that, in various applications, such as population viability analyses, genetic models or metapopulation models, emigration propensity is assumed to be a fixed trait (Clobert et al. 2004; Bowler and Benton 2005), although this is far from the reality. Just as Schtickzelle et al. (2006) demonstrated that emigration propensity is affected by habitat fragmentation and thus varies strongly between different metapopulations of the same species, our research proves that it is also highly variable in time within a single metapopulation.
High intraspecific variability does not preclude the existence of genuine interspecific differences in dispersal. If our data had been restricted to a single season, one could have easily concluded that either M. nausithous (e.g. in the case of the data from 2006) or M. teleius (e.g. in the case of the data from 2008) is the more mobile of the two closely related species. However, gathering the results for several years and analysing them against density fluctuations made it possible to establish that M. nausithous is better adapted to dispersal. This is reflected not only in its slightly, but consistently higher, emigration propensity but also in lower dispersal mortality and longer dispersal distances. Consequently, we would argue that it is not necessarily that “the existence of species-specific dispersal function is probably a myth” (as stated by Clobert et al. 2004; and repeated by Stevens et al. 2010), but rather that such functions are more complicated than it has been previously thought and applied.
References
Aars J, Ims RA (2000) Population dynamic and genetic consequences of spatial density-dependent dispersal in patchy populations. Am Nat 155:252–265
Akaike H (1973) Information theory and an extension of the maximum likelihood principle. In: Petrov BN, Csaki F (eds) Second international symposium on information theory. Akademiai Kiado, Budapest, pp 267–281
Arnason AN, Schwarz CJ (1999) Using POPAN-5 to analyse banding data. Bird Study 46:157–168
Baguette M, Vansteenwegen C, Convie I, Neve G (1998) Sex-biased density-dependent migration in a metapopulation of the butterfly Proclossiana eunomia. Acta Oecol 19:17–24
Best AS, Johst K, Münkemüller T, Travis JMJ (2007) Which species will successfully track climate change? The influence of intraspecific competition and density dependent dispersal on range shifting dynamics. Oikos 116:1531–1539
Bowler DE, Benton TG (2005) Causes and consequences of animal dispersal strategies: relating individual behaviour to spatial dynamics. Biol Rev 80:205–225
Brown IL, Ehrlich PR (1980) Population biology of the checkerspot butterfly, Euphydryas chalcedona. Structure of the Jasper Ridge colony. Oecologia 47:239–251
Burnham KP, Anderson DR (1998) Model selection and inference. Springer, Berlin
Byers JE (2000) Effects of body size and resource availability on dispersal in a native and a non-native estuarine snail. J Exp Mar Biol Ecol 248:133–150
Cassel-Lundhagen A, Sjögren-Gulve P (2007) Limited dispersal by the rare scarce heath butterfly—potential consequences for population persistence. J Ins Conserv 11:113–121
Clobert J, Ims RA, Rousset F (2004) Causes, mechanisms and consequences of dispersal. In: Hanski I, Gaggiotti OE (eds) Ecology, genetics and evolution of metapopulation. Elsevier, San Diego, pp 307–335
Doak P (2000) Population consequences of restricted dispersal for an insect herbivore in a subdivided habitat. Ecology 81:1828–1841
Enfjäll K, Leimar O (2005) Density-dependent dispersal in the Glanville fritillary, Melitaea cinxia. Oikos 108:465–472
Enfjäll K, Leimar O (2009) The evolution of dispersal–the importance of information about population density and habitat characteristics. Oikos 118:291–299
Fürst MA, Nash DR (2010) Host ant independent oviposition in the parasitic butterfly Maculinea alcon. Biol Lett 6:174–176
Gilbert LE, Singer MC (1973) Dispersal and gene flow in a butterfly species. Am Nat 107:58–72
Gros A, Hovestadt T, Poethke HJ (2008) Evolution of sex-biased dispersal: The role of sex-specific dispersal costs, demographic stochasticity, and inbreeding. Ecol Model 219:226–233
Hanski I (1999) Metapopulation ecology. Oxford University Press, Oxford
Hanski I, Alho J, Moilanen A (2000) Estimating the parameters of survival and migration of individuals in metapopulations. Ecology 81:239–251
Hill JK, Thomas CD, Lewis OT (1996) Effects of habitat patch size and isolation on dispersal by Hesperia comma butterflies: implications for metapopulation structure. J Anim Ecol 65:725–735
Hochberg ME, Clarke RT, Elmes GW, Thomas JA (1994) Population dynamic consequences of direct and indirect interactions involving a large blue butterfly and its plant and red ant hosts. J Anim Ecol 63:375–391
Hovestadt T, Nowicki P (2008) Investigating movement within irregularly shaped patches: Analysis of MRR data using randomisation procedures. Isr J Ecol Evol 54:137–154
Hovestadt T, Poethke HJ (2006) The control of emigration and its consequences for the survival of populations. Ecol Model 190:443–453
Hovestadt T, Kubisch A, Poethke HJ (2010) Information processing in models for density-dependent emigration: a comparison. Ecol Model 221:405–410
Hurvich CM, Tsai C (1989) Regression and time series model selection in small samples. Biometrika 76:297–307
Kim SY, Torres R, Drummond H (2009) Simultaneous positive and negative density-dependent dispersal in a colonial bird species. Ecology 90:230–239
Kuussaari M, Nieminen M, Hanski I (1996) An experimental study of migration in the Glanville fritillary butterfly Melitaea cinxia. J Anim Ecol 65:791–801
Lambin X, Aars J, Piertney SB (2001) Dispersal, intraspecific competition, kin competition and kin facilitation: a review of the empirical evidence. In: Clobert J, Danchin E, Dhondt AA, Nichols JD (eds) Dispersal. Oxford University Press, Oxford, pp 110–122
Matthysen E (2005) Density-dependent dispersal in birds and mammals. Ecography 28:403–416
Nachman G (2000) Effects of demographic parameters on metapopulation size and persistence: an analytical stochastic model. Oikos 91:51–65
Nowicki P, Richter A, Glinka U, Holzschuh A, Toelke U, Henle K, Woyciechowski M, Settele J (2005a) Less input same output—simplified approach for population size assessment in Lepidoptera. Popul Ecol 47:203–212
Nowicki P, Settele J, Thomas JA, Woyciechowski M (2005b) A review of population structure of Maculinea butterflies. In: Settele J, Kuhn E, Thomas JA (eds) Studies in the ecology and conservation of butterflies in Europe. vol 2. Species ecology along a European gradient: Maculinea butterflies as a model. Pensoft, Sofia–Moscow, pp 144–149
Nowicki P, Witek M, Skórka P, Settele J, Woyciechowski M (2005c) Population ecology of the endangered butterflies Maculinea teleius and M. nausithous, and its implications for conservation. Popul Ecol 47:193–202
Nowicki P, Pepkowska A, Kudlek J, Skórka P, Witek M, Settele J, Woyciechowski M (2007) From metapopulation theory to conservation recommendations: Lessons from spatial occurrence and abundance patterns of Maculinea butterflies. Biol Conserv 140:119–129
Nowicki P, Bonelli S, Barbero F, Balletto E (2009) Relative importance of density-dependent regulation and environmental stochasticity for butterfly population dynamics. Oecologia 161:227–239
Odendaal FJ, Turchin P, Stermitz FR (1989) Influence of host-plant density and male harassment on the distribution of female Euphydryas anicia (Nymphalidae). Oecologia 78:283–288
Perrin N, Mazalov M (2000) Local competition, inbreeding, and the evolution of sex-biased dispersal. Am Nat 155:116–127
Petit S, Moilanen A, Hanski I, Baguette M (2001) Metapopulation dynamics of the bog fritillary butterfly: movements between habitat patches. Oikos 92:491–500
Poethke HJ, Hovestadt T (2002) Evolution of density- and patch-size-dependent dispersal rates. Proc R Soc Lond B 269:637–646
Rabasa SG, Gutierrez D, Escudero A (2007) Metapopulation structure and habitat quality in modelling dispersal in the butterfly Iolana iolas. Oikos 116:793–806
Roland J, Keyghobadi N, Fownes S (2000) Alpine Parnassius butterfly dispersal: effects of landscape and population size. Ecology 81:1642–1653
Schtickzelle N, Le Boulenge E, Baguette M (2002) Metapopulation dynamics of the bog fritillary butterfly: demographic processes in a patchy population. Oikos 97:349–360
Schtickzelle N, Mennechez G, Baguette M (2006) Dispersal depression with habitat fragmentation in the bog fritillary butterfly. Ecology 87:1057–1065
Schwarz CJ, Arnason AN (1996) A general methodology for the analysis of capture-recapture experiments in open populations. Biometrics 52:860–873
Schwarz CJ, Seber GAF (1999) Estimating animal abundance: review III. Stat Sci 14:427–456
Shapiro AM (1970) The role of sexual behavior in density-related dispersal of pierid butterflies. Am Nat 104:367–372
StatSoft (2008) STATISTICA (data analysis software system), version 8.0. StatSoft, Tulsa
Stevens VM, Turlure C, Baguette M (2010) Filling in the tapestry: a meta-analysis of dispersal in butterflies. Biol Rev 85:625–642
Thomas JA, Elmes GW (2001) Food-plant niche selection rather than the presence of ant nests explains oviposition patterns in the myrmecophilous butterfly genus Maculinea. Proc R Soc Lond B 268:471–477
Thomas JA, Clarke RT, Elmes GW, Hochberg ME (1998) Population dynamics in the genus Maculinea (Lepidoptera: Lycaenidae). In: Dempster JP, McLean IFG (eds) Insect population dynamics in theory and practice. Symposia of the Royal Entomological Society 19. Chapman & Hall, London, pp 261–290
Travis JMJ, Mustin K, Benton TG, Dytham C (2009) Accelerating invasion rates result from the evolution of density-dependent dispersal. J Theor Biol 259:151–158
van Dyck H, Oostermeijer JGB, Talloen W, Feenstra V, van der Hidde A, Wynhoff I (2000) Does the presence of ant nests matter for oviposition to a specialized myrmecophilous Maculinea butterfly? Proc R Soc Lond B 267:861–866
van Langevelde F, Wynhoff I (2009) What limits the spread of two congeneric butterfly species after their reintroduction: quality or spatial arrangement of habitat? Anim Conserv 12:540–548
Wahlberg N, Klemetti T, Selonen V, Hanski I (2002) Metapopulation structure and movements in five species of checkerspot butterflies. Oecologia 130:33–43
Wang R, Wang Y, Chen J, Lei GC, Rumei X (2004) Contrasting movement patterns in two species of chequerspot butterflies, Euphydryas aurinia and Melitaea phoebe, in the same patch network. Ecol Entomol 29:367–374
White GC, Burnham KP (1999) Program MARK: survival estimation from populations of marked animals. Bird Study 46:120–138
Witek M, Sliwinska E, Skórka P, Nowicki P, Wantuch M, Vrabec V, Settele J, Woyciechowski M (2008) Host ant specificity of large blue butterflies Phengaris (Maculinea) (Lepidoptera: Lycaenidae) inhabiting humid grasslands in East-central Europe. Eur J Entomol 105:871–877
Witek M, Nowicki P, Sliwinska E, Skórka P, Settele J, Schönrogge K, Woyciechowski M (2010) Local host ant specificity of Phengaris (Maculinea) teleius butterfly, an obligatory social parasite of Myrmica ants. Ecol Entomol 35:557–564
Acknowledgments
Field surveys were conducted with a proper permission from the Kokořínsko Protected Landscape Area Authority (on behalf of the Czech Ministry of Environment). The data analysis has been funded by the European Commission within its project SCALES (FP7 Contract No. 226852), and by the Polish Ministry of Science and Higher Education (Grant No. N304 064139). We are grateful to Jiří Cibulka, who initiated the research in Přelouč, as well as to Pavla Antošová, Jana Bouberlová, Lenka Cibulková, Jana Hatlapatková, Helena Lálová, Kristýna Marušáková, Hana Potočková, Jana Pravdová, Hana Rychlíková, Milena Spalová, Žaneta Vávrová, and Hana Veselá, who helped in the fieldwork. Michel Baguette, Elizabeth Crone, Klaus Fischer, Karsten Schörogge, and two anonymous reviewers provided valuable comments on the manuscript, while Christine Richards improved its English.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Klaus Fischer.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Nowicki, P., Vrabec, V. Evidence for positive density-dependent emigration in butterfly metapopulations. Oecologia 167, 657–665 (2011). https://doi.org/10.1007/s00442-011-2025-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00442-011-2025-x