Introduction

A long-standing challenge in ecological research is the development of a theoretical framework that explains how emerging properties at the level of plant communities or ecosystems (i.e., vegetation structure, productivity and other ecosystem functions) arise from basic physiological processes and plant functional traits. Physiological and structural traits generally define the functioning of plant parts (e.g., leaves, stems, roots, etc.), but their fitness consequences are expressed at the individual and population level. Similarly, direct effects of climate change are mediated through physiological responses, but the interest of the global change community is in processes acting at the ecosystem level, such as carbon uptake or transpiration of vegetation stands (e.g., Sellers et al. 1992). The scaling from leaf to canopy is of special interest in this respect, because photosynthesis provides the structural substrates for growth and reproduction and because it is a primary element of the global carbon cycle (Mooney and Gulmon 1979; Sellers et al. 1992).

Based on our current physiological and biophysical knowledge of leaf photosynthesis and plant structure, complicated models are available that can simulate canopy photosynthesis if the leaf properties of all plants in the canopy are known. These models have been especially successful in agronomy as components of models that predict crop yields (see van Ittersum et al. 2003), but they are less effective in natural vegetation where such data are hard to obtain. Optimality theory provides a simple but potentially more powerful alternative (Dewar et al. 2009). Optimality theory is based on the concept that some performance measure is maximized with respect to one or more plant traits and considering one or more limiting factors. Optimal values of traits such as leaf N content, LAI (leaf area index, the amount of leaf area per unit soil area), stomatal conductance or leaf photosynthetic capacity are emergent outcomes rather than input parameters or subroutines (McMurtrie et al. 2008).

Optimization models are increasingly being used to assess the adaptive significance of canopy traits such as leaf nitrogen distribution, leaf angles, stomatal conductance and leaf area indices. Yet their ability to accurately predict vegetation structure and functioning is still open to debate. This is largely due to the fact that the optimization criterion that should be used is unclear; in other words, what do models assume plants to maximize, and over what time span? Most studies that apply optimization theory to analyze plant canopies (see reviews by Kull 2002; Hirose 2005) make two assumption. First, plant traits are considered to be optimal when they maximize whole-stand daily photosynthesis. This assumes that maximized individual fitness manifests itself as optimal characteristics at the stand level (Hikosaka and Hirose 1997; Anten 2005). Second, plant canopies are treated as being static; the dynamics of growth and associated changes in canopy structure and position that plants occupy in vegetation stands are not quantitatively considered (Franklin and Ågren 2002; Hikosaka 2003).

This review deals with the abovementioned debate about optimization criteria. First, it discusses static-plant simple optimization models that assume trait values to be optimal when whole-canopy daily carbon gain is maximized. Second, it deals with evolutionary game theoretical models, which consider that trait optimization of a given individual plant depends on the traits and density of its neighbors (Parker and Maynard-Smith 1990). We then discuss dynamic-plant simple optimization models that consider long-term photosynthesis, net primary production (NPP) or net biomass increment. As an example, we will focus on studies that consider the optimization of nitrogen use at the canopy level. Nitrogen is a primary part of the photosynthetic system, with photosynthetic rates generally being strongly positively correlated with leaf N contents (Evans 1989). It is also the primary growth limiting factor in many habitats (see Kull 2002). We will argue that the maximization of daily canopy photosynthesis, though widely used, is an inadequate optimization criterion to analyze the adaptive significance of traits associated with nitrogen use in plant canopies, and that a combination of evolutionary game theory and dynamic modeling should be used for this purpose.

Static-plant simple optimization models

As mentioned above, we denote models that consider plant trait values to be optimal when they result in maximum daily net canopy photosynthesis and that consider plant canopies to be static as “static-plant simple optimization models” (“SSO models” hereafter). Canopy photosynthesis of a vegetation stand is determined by the photosynthetic properties of different layers and by the size of the canopy (often denoted “LAI,” Saeki 1960). The former in turn is determined by the distribution of light and by the total amount and vertical distribution of nitrogen, a key component of the photosynthetic system, in the canopy. Thus, considerations concerning the optimal use of nitrogen for maximizing canopy photosynthesis typically address two characteristics: the optimal nitrogen distribution and the optimal LAI (Field 1983; Sands 1995).

Optimization of nitrogen distribution in the canopy

A large number of studies (e.g., Field 1983; Hirose and Werger 1987; Anten et al. 1995a; Posada et al. 2009) have analyzed distribution patterns of leaf nitrogen content per unit area (N area) in the canopy (see Kull 2002; Niinemets 2007). It was theoretically derived that if A max is linearly related to N area, and if other characteristics of the light response of leaf photosynthesis do not differ between leaves, canopy photosynthesis is maximized if plants allocate more nitrogen to higher, more illuminated leaves and less to lower, more shaded ones in such a way that the N area distribution parallels the light distribution in the canopy (Farquhar 1989; Anten et al. 1995a). This can be described mathematically as

$$ N_{\text{area}} \left( f \right) = N_{\text{o}} I\left( f \right) /I_{\text{o}}, $$
(1a)

so that

$$ A_{ \max } \left( f \right) = A_{\text{o}} I\left( f \right) /I_{\text{o}}, $$
(1b)

where N o and A o are the N area and A max of an unshaded leaf at the top of the canopy, I o and I(f) are the light intensities incident on leaves at the top or at a depth f (measured in LAI units) in the canopy, respectively. In accordance with this prediction, nonuniform patterns of N area distribution have been found in canopies of a wide variety of plants (see review by Hirose 2005). In all cases, canopy photosynthesis for the actual distribution was estimated to be 6–30% higher than the canopy photosynthesis of a stand with the same amount of nitrogen but with the nitrogen uniformly distributed among all leaves (see Hirose 2005; Niinemets 2007). However, actual N area distributions were also consistently more uniform than the predicted optimal distribution, with actual rates of canopy photosynthesis being 4–15% lower than the maximum values predicted in these canopies (Kull 2002, but see Koyama and Kikuzawa 2010).

Optimal leaf area indices

Assuming that only light limits canopy photosynthesis, it was derived that the LAI of a vegetation stand is optimal if the lowest leaves receive an amount of light that is equal to their compensation point, since any additional leaf would respire more than it photosynthesizes (Saeki 1960). This model was later expanded to include not only leaf respiration but also the additional costs associated with producing and maintaining structures that support a leaf (Givnish 1988; Reich et al. 2009). For a set of shrub species, Reich et al. (2009) estimated that these plants did indeed drop their leaves when the net carbon balance of these leaves (including support costs) was zero. Other studies (Oikawa et al. 2005, 2006), however, documented that leaves are often dropped well before their carbon balance reaches zero, especially at low nitrogen availability from the soil.

As noted in the “Introduction,” leaf area growth is often strongly limited by the availability of nutrients, especially nitrogen (Albaugh et al. 1998). An increase in the LAI indicates that more light is being intercepted, albeit with decreasing marginal returns as a result of self-shading. However, for a fixed total amount of canopy nitrogen (N t per m2 ground surface), it also implies that leaves will have lower N area (i.e., average N area in the canopy equals N t/LAI) and thus also a lower photosynthetic capacity (A max). Considering this, it was shown that there is an optimal LAI and thus an optimal mean N area at which canopy photosynthesis is maximized (Anten et al. 1995b). This model was tested for stands of a variety of herbaceous species varying widely in leaf photosynthetic and structural traits. A strong positive correlation was found between predicted and actual LAIs, with more than 70% of the variation in LAI between these stands being explained by the model (Fig. 1).

Fig. 1
figure 1

Predicted and measured LAI values for 12 herbaceous plant stands. Predictions were made using either SSO models (closed symbols) or EGT models (open symbols). Thick solid line is the one-to-one correspondence, the thin solid and dashed lines are the predicted and the measured regression lines for the SSO and EGT models, respectively. The following stands were studied: Sorghum bicolor, Oryza sativa, Amaranthus cruentus (all three at high and low N availability) and Glycine max (raw data from Anten et al. 1995b), Leersia hexandra, Hymenachne amplexicaulis, Paspalum fasciculatum and Hyparrhenia rufa (raw data taken from Anten et al. 1998). Figure redrawn from Anten (2002)

Full size image

An important application of SSO models for LAI has been to predict the effects of elevated CO2 on canopy development and photosynthesis (Hirose et al. 1997; Anten et al. 2004; Hikosaka et al. 2005; McMurtrie et al. 2008). The LAI of a vegetation stand is an important component of CO2 sink capacity, and there has thus been a debate on whether elevated CO2 will lead to increases in LAI (DeLucia et al. 2002). SSO models were able to accurately predict the relative effects of CO2 elevation on LAIs and leaf N contents obtained in field-applied elevated-CO2 experiments (FACE) with rice (Anten et al. 2004) and with a number of tree species (McMurtrie et al. 2008).

However, while the qualitative predictions from SSO LAI models were consistent with real observations, measured LAIs were consistently larger and N area consistently lower than predicted optimal values. As a result, canopy photosynthesis has been calculated to be 2–20% lower than the values at optimal LAIs derived from SSO models (Anten et al. 1998; Hirose et al. 1997).

Limitations associated with SSO models

Evidently, while SSO models provide good qualitative predictions, there are consistent deviations between predicted and actual trait values. Several explanations have been forwarded to explain this supposed “nonoptimality” of plant canopies, most of which deal with simplifying assumptions in the models regarding the structure, environment or physiology of plants. For example, models for optimal N allocation ignore energetic costs associated with the reallocation process (Field 1983). There are also questions as to whether the relatively high N area values and associated photosynthetic capacities predicted for leaves at the top of the canopy are biologically possible (Pons et al. 1989). Very high N area values may also make leaves more prone to herbivory (Stockhoff 1994).

The SSO models discussed above consider the maximization of canopy photosynthesis relative to the amount of N in the canopy (i.e., maximizing canopy-level PNUE), which assumes that photosynthesis is primarily limited by N. This assumption may not always hold true. For example, in most wet tropical rain forests, plant growth is probably limited by either light (Nemani et al. 2003) or phosphorus (Lambers et al. 1998). Posada et al. (2009) analyzed the N distributions in canopies of rain forest trees and argued that the distribution patterns that they found were similar to those that would maximize photosynthesis per unit captured light and not per unit N. Optimization of LAI can also be defined relative to water availability. Considering a fixed amount of water that is taken up from the soil, increased leaf area production and associated light capture will entail a lower mean stomatal conductance and thus a lower leaf-level photosynthesis. Similar to the case of N limitation, an optimal LAI can be defined at which the benefits of increased light capture no longer compensate for the negative effect of a lower stomatal conductance (McMurtrie et al. 2008). McMurtrie et al. (2008) developed an SSO model that determines the optimal LAI relative to both water and N availability, and obtained a reasonably accurate prediction of N area values in Liquidambar styraciflua grown at different CO2 levels.

All of these arguments are probably important and should be considered in future modeling. However, we will argue in the sections “Evolutionary game theoretical models” and “Dynamic-plant simple optimization models” that the principal problem with SSO models lies with the optimization criterion chosen, and the assumption of a static canopy.

Evolutionary game theoretical models

Simple optimization, with trait values being optimal if they result in maximum whole-canopy carbon gain, implicitly makes the assumption that characteristics maximizing individual fitness manifest themselves as optimal trait values at the canopy level. This either assumes some occurrence of group or kin selection, or it means that the performance of a plant is independent of the characteristics of its neighbors (Parker and Maynard-Smith 1990). The latter obviously does not hold true in most vegetation stands where plants compete both for light and soil resources. In such cases, evolutionary game theory (EGT), in which individual plant-based optimization is considered relative to the characteristics of neighbors (Riechert and Hammerstein 1983), might be a more appropriate approach.

Schieving and Poorter (1999) were the first to use EGT to analyze the distribution of N area, leaf area to mass ratios [specific leaf area (SLA)], and the resultant LAI values of vegetation stands. If one assumes that not only the total canopy nitrogen but also total leaf mass are fixed, changes in N area can only arise through changes in SLA. Schieving and Poorter (1999) showed that stands with an optimal N area and SLA distribution, and concomitant optimal LAI (all based on SSO models), can be invaded by mutant individuals that are the same as the resident population in all respects except that they produce leaves with a larger SLA and thus have lower N area values, a more uniform N area distribution (Fig. 2a), and a larger LAI (Fig. 2b). Because plants interact and thus compete for light, an increase in the leaf area of one individual entails that this plant captures a greater fraction of the available light, and its direct neighbors therefore capture less. Thus, even though whole-canopy photosynthesis is reduced, the mutant plant can increase its individual photosynthesis at the expense of its neighbors.

Fig. 2
figure 2

a Simulated distribution of leaf nitrogen content per unit leaf area (Narea) as a function of the relative height in the canopy, b the leaf area index, and c the associated canopy photosynthesis as functions of the total amount of nitrogen in the canopy. Simulations were conducted using either a simple static optimization model (closed symbols “SSO model”) or a evolutionary game theoretical model (open symbols “EGT model”). Modified from Schieving and Poorter (1999)

Full size image

Schieving and Poorter (1999) also showed theoretically that an evolutionarily stable (ES) vegetation stand (i.e., one that can not be invaded by a mutant with a different SLA distribution and leaf area) has a larger LAI and lower canopy photosynthesis than an optimal stand. Similar model results were obtained in several other studies (Anten and Hirose 2001; Anten 2002). Anten (2002) calculated the ES-LAI values for herbaceous vegetation stands of a variety of herbaceous species, and in all cases there appeared to be a very close correspondence between the predicted and observed LAIs (Fig. 1). Lloyd et al. (2010) also found for tropical rain forest stands that ES-LAIs were closer to measured values than the simple optimal LAIs.

Evolutionary game theory has been applied to canopy characteristics other than the N distribution and LAI. It has been shown that ES vegetation stands are taller (Givnish 1982; Falster and Westoby 2003; Pronk et al. 2007), have more horizontally projected leaves (Hikosaka and Hirose 1997), are less well defended (Broom et al. 2005), and produce more roots (Gersani et al. 2001) than optimal stands. As a result, plants in vegetation stands are believed to have a lower than maximum performance in terms of growth, seed production and defense. This clearly suggests that plant canopy traits can be subject to a so-called tragedy of the commons, sensu Hardin (1968); allocation to increase resource acquisition benefit the individual that employs this strategy, but the costs of this (e.g., increased shading in the canopy) are shared by the whole population.

Potential application of evolutionary game theory (EGT) as a scaling principle

EGT models appear to give better predictions of the structure, physiological characteristics and productivity of vegetation than static-plant simple optimization models. EGT thus provides a sophisticated yet simple theoretical framework to scale from leaf to canopy, and thus has the potential to be a useful predictive tool to help understand canopy responses to a globally changing environment. Yet, in contrast to simple optimization (see Dewar et al. 2009), EGT has rarely been used in global change research. This is probably partly due to the fact that EGT models come with their own set of problems.

First, model outcomes are very sensitive to the assumed degree of interaction between plants. For example, the payoff of increasing leaf area increases strongly with the degree to which the light gradient that a plant experiences is determined by the leaves of its neighbors. Anten (2002), for example, showed that the predicted ES-LAI decreases strongly with the assumed degree of self- versus non-self-shading (β), while predicted canopy photosynthesis showed the opposite trend (note that β = 1 gives the same solution as SSO models, Fig. 3). The value of β is hard to determine and may differ between plant types. For example, trees have relatively wide canopies and may experience relatively strong self-shading. Herbaceous plants typically have narrower canopies and thus interact more strongly with their neighbors. Finally, climbers may experience only minimal self-shading, with their climate being almost entirely created by leaves of neighbor plants (Takenaka 1994; Hikosaka et al. 2001). Very few studies have estimated β values in plant canopies (Hikosaka et al. 2001), or addressed the question of whether plants with different growth forms and associated degrees of neighbor interaction also exhibit different patterns of nitrogen allocation and leaf area growth (but see Schmid and Bazzaz 1994, discussed below).

Fig. 3
figure 3

The dependence of the evolutionarily stable (ES) leaf area index (closed symbols) and associated canopy photosynthesis (open symbols) on the ratio between the contributions of a target individual and its direct neighbors to the total leaf area index and the associated effect on the light climate (β). β = 1 indicates that an individual only interacts with itself, and the predicted LAI is the same as that predicted by SSO models. The degree of non-self-interaction increases with decreasing β. Recalculated from Anten (2002)

Full size image

Second, while EGT models correctly assume that genotypic changes occur as a result of natural selection, repeated mutations and invasions, they do not usually consider the potential time lag involved. Usually genotypic changes take place over several generations, which—depending on the life cycle of the plants—may take considerable time. This raises the question of the extent to which plants are able to adapt to fast and directional changes in the environment, such as the current rise in atmospheric CO2 and associated climate change.

Finally, by implicitly assuming that changes in trait values occur only through mutations, EGT models do not usually consider phenotypic plasticity. This evidently contradicts with the strong degree of phenotypic plasticity exhibited by plants (Schmitt et al. 1999), and an important challenge is to implement plasticity into EGT models such that they can predict plant responses to rapid environmental changes.

Dynamic-plant simple optimization models

The models discussed so far are “static” in the sense that they treat the N distribution in the canopy and the leaf area index as static characteristics. Yet, leaf canopies are dynamic: new leaves are produced, resources including nitrogen are allocated from older to newer leaves to partly sustain this production, and old leaves are dropped from the plants. Changes in the amount of N in the canopy thus depend on the rate of N uptake from the soil, leaf longevity, and the fraction of N that is resorbed from senescing leaves. This entails that these traits, together with the abovementioned leaf photosynthetic traits, leaf geometry and SLA determine whole-plant photosynthetic nitrogen-use efficiency.

Franklin and Ågren (2002) developed a dynamic-plant simple optimization (DSO) model to analyze photosynthetic nitrogen-use efficiency in plant canopies, including leaf turnover and nitrogen resorption. This model was simple in the sense that it did not consider neighbor interactions. Franklin and Ågren (2002) proposed that it is beneficial for a plant to drop a leaf if the increase in plant photosynthesis that can be achieved elsewhere in the plant with the nitrogen that is resorbed from that leaf exceeds its own photosynthesis. The model predicted that the optimal LAI decreases with increasing resorption efficiency r eff (the fraction of N that plants resorb from senescing leaves). However, for any r eff < 1, the model predicted larger optimal LAI values than the static-plant optimization (SSO) model of Anten et al. (1995b), and these values were reasonably close to the measured values (Fig. 4). Hikosaka (2003, 2005) developed a more elaborate DSO model that explicitly considered N uptake by plants and obtained qualitatively similar results; i.e., their optimal LAI was larger than the SSO-based one. However, he also showed that predicted LAI values are highly sensitive to changes in the values of N uptake rates and N contents of dead leaves.

Fig. 4
figure 4

Dynamic optimal leaf area indices calculated as a function of the fraction of nitrogen resorbed from senescing leaves for stands of four species: Amaranthus cruentus, Glycine max, Oryza sativa and Sorghum bicolor. Note that the LAI increases with a decreasing resorption fraction, as dropping leaves becomes less efficient when more N is lost. The LAI calculated for a resorption fraction of 1 (complete resorption) is equivalent to the optimal LAI, sensu Anten et al. (1995b). Large symbols indicate measured LAI values. Figure redrawn from Franklin and Ågren (2002)

Full size image

Why do DSO models predict larger LAIs than SSO models? Say the LAI of a vegetation stand exceeds the optimal as defined by SSO (Anten et al. 1995b). To reduce LAI, some leaves need to be dropped, but in doing so the plant also loses some nitrogen and thus indirectly part of its photosynthetic capacity. As shown by Hikosaka (2003), the negative effect of this loss on carbon gain depends on the rate of N uptake and thus implicitly on N availability from the soil.

Franklin (2007) scaled his canopy photosynthesis model (Franklin and Ågren 2002) up to simulate the dynamics of tree growth in forests, including respiration and turnover of nonphotosynthetic tissue. He considered maximization of net mass increment—the difference between photosynthetic carbon gain and carbon losses through respiration and turnover—as an optimization criterion, rather than maximization of net canopy photosynthesis. The rationale behind this was that plant size, which is the accumulation of net mass increment, is closely related to reproductive success. Unlike previous models that considered N costs only in terms of leaf maintenance respiration, he also considered costs associated with the production and maintenance of roots (Franklin et al. 2009). The model gave reasonably good predictions for biomass increment, as well as the relative effects of CO2 elevation on LAI, canopy photosynthesis and NPP (photosynthesis—whole-plant respiration), as obtained from elevated CO2 (FACE) experiments conducted for several tree species in the field (Fig. 5).

Fig. 5
figure 5

Modeled versus observed relative effects of elevated CO2 on net primary productivity (NPP, open symbols), canopy photosynthesis (gross primary productivity GPP, black symbols) and leaf area index (LAI, grey symbols) obtained at four different elevated CO2 (FACE) experiments conducted in the field: POPFACE (three different poplar species, circles), aspen birch (triangles), sweetgum (diamonds) and Loblolly pine (squares). r 2 = 0.83 for all observed versus modeled data. Figure redrawn from Franklin (2007)

Full size image

Mäkelä et al. (2008) considered the optimization of three traits: canopy-average leaf N content per unit mass, canopy leaf mass, and the amount of fine-root biomass at which NPP was maximized. They further assumed steady-state conditions with respect to both C (growth equals litter production) and N (N uptake equals N loss). This model provided reasonable predictions of both leaf and fine root biomass in stands of Pinus silvestris and Picea abies.

Dynamic-plant simple optimization models have thus taken an important step by scaling up from static analyses of canopy photosynthesis to the dynamics of plant growth. In so doing, they have introduced leaf turnover and N resorption rates and N uptake from the soil to optimality models, and have expanded the performance measure from photosynthesis to growth. However, current DSO models for optimal nitrogen use in canopies are still based on simple optimization, and ignore neighbor interactions as in game theoretical models; a combination of the two approaches is still lacking.

Validation of optimization criteria

The method most commonly used to validate optimization models has been to compare their predicted trait values to observed ones. Most authors consider a good quantitative agreement between the two as support for the assumptions underlying their model. In this context, it is somewhat disconcerting to note that field observations of key canopy traits can fit predictions of different models that are based on different assumptions. For example, observed patterns of N distribution in vegetation stands fit predictions from some SSO models (e.g., Pons et al. 1989; Posada et al. 2009) as well as predictions from game theoretical (EGT) models (Schieving and Poorter 1999). Similarly, as discussed above, both static EGT models (Anten 2002) and different DSO models (Franklin and Ågren 2002; Franklin 2007; Mäkelä et al. 2008) predict values for LAI and other vegetation properties that correspond closely to actual field measurements. In fact, the models of Anten (2002) and Franklin and Ågren (2002) give accurate predictions of the LAIs of the same vegetation stands (compare results for Amaranthus, Glycine, Oryza and Sorghum in Figs. 1 and 4). Evidently, one set of observations cannot be considered to support two clearly different assumptions regarding the adaptive significance of canopy traits, and experiments testing the response of these traits to changes in environmental conditions will be required to determine which model is correct.

What is lacking from the studies mentioned above is experimental evidence for the fitness benefit implicitly associated with an optimization criterion. In what way do differences in leaf turnover, N distribution, SLA and leaf area influence plant performance, and is this effect density dependent? Conducting such tests ideally entails comparing plants that are the same in all respects except the trait that is being optimized in the model. This can be achieved through either phenotypic manipulation or genetic transformation. An example is provided by studies that used these techniques to successfully test the supposed density dependence of fitness consequences of stem elongation (see Schmitt et al. 1999; Vermeulen et al. 2008).

Similar tests of the adaptive significance of different patterns of canopy N use have long been impossible, as suitable plant material was unavailable. However, so-called “stay-green” varieties recently developed for several crops (e.g., sorghum, maize and tobacco) may provide a solution, as these genotypes exhibit delayed senescence, and thus slower leaf turnover and potentially a more uniform N distribution in the canopy (Subedi and Ma 2005). For example, genetically modified PSAG12-IPT (SAG) tobacco plants have a pronounced delay in leaf senescence caused by increased cytokinin production at the onset of senescence (Gan and Amasino 1995).

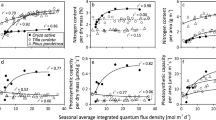
Boonman et al. (2006) conducted a competition experiment in which wild-type (WT) and SAG tobacco were grown in mono (WT or SAG) and mixed (WT and SAG) stands. The SAG did indeed maintain more leaves at the bottom of the canopy, and it had higher leaf N contents (N area) in the lower canopy layers (Fig. 6). Interestingly, WT used the additional N reallocated from lower (senescing) leaves to produce more leaf area at the top of the canopy than did the SAG plants, rather than producing leaves with a higher N area (Fig. 6). If N reallocation serves simply to maximize daily net photosynthesis, as predicted by SSO models, a higher N area would have been expected (Hirose and Werger 1987; Sands 1995).

Fig. 6
figure 6

The distribution of a leaf area and b leaf nitrogen content (N area) within the canopies of wild-type (WT) and PSAG12-IPT (SAG) tobacco plants grown in a mixture. The plants were clipped into five equal layers (1 bottom to 5 top) which each constituted 1/5 of the stand height. Redrawn from Boonman et al. (2006)

Full size image

In a second experiment, Boonman et al. (2006) grew SAG and WT target plants surrounded by WT plants in two densities and measured their lifetime performance in terms of growth and reproduction. Increased density tended to negatively affect the performances of both genotypes, but significantly more so in the SAG than in WT plants, though the results were not very clear, possibly due to the relatively small difference in plant density between the two density treatments (6.3 and 9.5 plants m−2).

Together these results suggest that the fitness consequences of variation in N reallocation and associated leaf turnover are density dependent, and should thus be analyzed in a game theoretical context. One could hypothesize that a relatively slow leaf turn over is probably the optimal strategy for maximizing whole-stand photosynthetic NUE, as it entails small losses in terms of mass and nitrogen (Aerts and Chapin 2000). However, such a stand could potentially be invaded by mutants that have faster leaf senescence, because in doing so they have more nitrogen available to produce leaves at the top of the canopy, giving rise to a tragedy of the commons. The eventual effectiveness of this strategy for plant performance might be restricted by the payback time of a leaf (the amount of time needed for leaf to assimilate the amount of energy used in its construction), and the turnover rate may be lower in harsh environments where photosynthetic rates are limited (Aerts and Chapin 2000). Unfortunately, this hypothesis—that selection for fast N reallocation and leaf turnover in dense vegetation leads to a tragedy of the commons—has not yet been tested adequately.

The results discussed above clearly indicate the need for models that combine evolutionary game theory with the modeling of canopy dynamics. As noted by Hikosaka (2005), “no one has analyzed the evolutionarily stable leaf turnover rate.” Research on the adaptive significance of N dynamics in plant canopies urgently needs such types of models (Fig. 7).

Fig. 7
figure 7

Flow diagram showing the different optimization criteria that have been used to analyze the adaptive significance of N utilization in plant canopies. Solid arrows indicate advances in the past, while dotted arrows with question marks indicate potential future steps. Plants with gray leaves are neighbor plants that are explicitly considered in the case of EGT models

Full size image

Choice of optimization criterion: the case of clonal plants

Clonal plants (plants that can reproduce through the production of vegetative offspring) are an especially interesting group of plants when considering group versus individual level optimization. Growth forms of clonal plants can be roughly divided into either phalanx or guerilla. In the former case, plants produce short runners (stolons or rhizomes) and dense patches of ramets all belonging to the same clone. The latter is characterized by the formation of long runners whereby ramets are placed further apart, resulting in greater interclonal mixing (Lovett-Doust 1981). Due to this variation in self-/non-self-interactions between these growth forms, one might predict that plants with the phalanx growth form have evolved traits that conform more with the predictions of simple optimization models (maximization of stand-level performance), whereas traits of plants with the guerilla growth form would tend to lead to a tragedy of the commons. Yet very few studies that we know of have tested this prediction.

Schmid and Bazzaz (1994) compared leaf traits and canopy dynamics in stands of two species: Solidago canadense with a typical phalanx growth form and Aster lanceolata with a guerilla growth form. Both species occur in the same habitat. The results supported the above contention. A. lanceolata exhibited an exponential increase in leaf production during the season, a fast leaf turnover, short leaf longevity, a shallow canopy and a relatively steep N distribution, indicating that enhanced N reallocation in dense stands is indeed important for competition in this species. S. canadense exhibited the opposite characteristics: slow leaf turnover, longer leaf longevity, a more uniform N distribution and a deeper canopy. These traits may be more in line with predictions derived from DSO models (Franklin and Ågren 2002; Hikosaka 2003, 2005). A. lanceolata also had more horizontal leaves than S. canadense, which again confirms that the former species exhibited more competitive traits at the expense of whole-stand productivity (Hikosaka and Hirose 1997).

This idea that the degree to which plants exhibit traits leading to a tragedy of the commons depends on the pattern of ramet placement and associated intergenotypical interaction seems to be confirmed by other studies. Semchenko et al. (2007) found that shoots of Glechoma hederacea—a species which they considered to have a phalanx growth form—tended to allocate roots away from each other, thus avoiding competition, and that they did this irrespective of the genetic identity of neighboring shoots. Conversely, shoots of Fragaria vesca, with a more guerilla-type growth form, tended to allocate roots equally away and towards each other, and allocation towards neighbors was greater when they interacted with shoots of another species. Phalanx species also tend to keep a tighter control on shoot production than guerilla species, and are thus better able to regulate shoot density (De Kroon and Kalliola 1995). This could potentially be interpreted in a game theoretical context, with phalanx but not guerilla species possibly optimizing shoot production to maximize resource acquisition at the stand level. Yet, in spite of these promising results, no study that we know of has formally applied optimization theory to analyze the differences in photosynthetic traits between species with the phalanx and guerilla growth forms.

Conclusion

Static-plant simple optimization—plants exhibiting traits that maximize the daily carbon gain of a vegetation stand—has long been the default optimization criterion used in canopy modeling, but it ignores competitive interactions between plants as well as the growth dynamics of plant canopies. Recently, these aspects have been separately introduced into game theoretical and dynamic models, but they have not yet been applied in combination (see Fig. 7). Such a combined approach is necessary. We also stress the need for more experiments with which optimization criteria can be tested, and note that both genetically modified plants and the phalanx versus guerilla dichotomy among clonal plants are interesting study subjects in this respect.