Abstract
For a d-dimensional random vector X, let \(p_{n, X}(\theta )\) be the probability that the convex hull of n independent copies of X contains a given point \(\theta \). We provide several sharp inequalities regarding \(p_{n, X}(\theta )\) and \(N_X(\theta )\) denoting the smallest n for which \(p_{n, X}(\theta )\ge 1/2\). As a main result, we derive the totally general inequality \(1/2 \le \alpha _X(\theta )N_X(\theta )\le 3d + 1\), where \(\alpha _X(\theta )\) (a.k.a. the Tukey depth) is the minimum probability that X is in a fixed closed halfspace containing the point \(\theta \). We also show several applications of our general results: one is a moment-based bound on \(N_X(\mathbb {E}\!\left[ X\right] )\), which is an important quantity in randomized approaches to cubature construction or measure reduction problem. Another application is the determination of the canonical convex body included in a random convex polytope given by independent copies of X, where our combinatorial approach allows us to generalize existing results in random matrix community significantly.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider generating independent and identically distributed d-dimensional random vectors. How many vectors do we have to generate in order that a point \(\theta \in \mathbb {R}^d\) is contained in the convex hull of the sample with probability at least 1/2? More generally, what is the probability of the event with an n-point sample for each n? These questions were first solved for a general distribution which has a certain symmetry about \(\theta \) by Wendel [45]. Let us describe the problem more formally.
Let X be a d-dimensional random vector and \(X_1,X_2,\ldots \) be independent copies of X. For each \(\theta \in \mathbb {R}^d\) and positive integer n, define
where \({{\,\textrm{conv}\,}}A:=\{\sum _{i=1}^m\lambda _ix_i\mid m\ge 1,\ x_i\in A,\ \lambda _i\ge 0,\ \sum _{i=1}^m\lambda _i = 1\}\) denotes the convex hull of a set \(A\subset \mathbb {R}^d\). We also define
as the reasonable number of observations we need. As \(p_{n, X}\) and \(N_X\) are only dependent on the probability distribution of X, we also write \(p_{n, \mu }\) and \(N_\mu \) when X follows the distribution \(\mu \). We want to evaluate \(p_{n,X}\) as well as \(N_X\) for a general X.
Wendel [45] showed that
holds for an X such that X and \(-X\) have the same distribution and \(X_1,\ldots ,X_d\) are almost surely linearly independent. In particular, \(N_X(0) = 2d\) holds for such random vectors. For an X with an absolutely continuous distribution with respect to the Lebesgue measure, Wagner and Welzl [44] showed more generally that the right-hand side of (1) is indeed an upper bound of \(p_{n, X}\), and they also characterized the condition for equality (see Theorem 6). Moreover, Kabluchko and Zaporozhets [20] recently gave an explicit formula for \(p_{n, X}\) when X is a shifted Gaussian.
In this paper, our aim is to give generic bounds of \(p_{n, X}\) and \(N_X\), and we are particularly interested in the upper bound of \(N_X\), which is opposite to the bound given by [44]. Estimating \(p_{n, X}\) and \(N_X\) is of great interest from application, which ranges from numerical analysis to statistics, and compressed sensing. As a by-product, we also give a general result explaining the deterministic body included in the random polytope \({{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\), which is a sharp generalization of a recent work in the random matrix community [15]. The remainder of this section will explain more detailed motivation from related fields and implications of our results.
Throughout the paper, let \(\left\langle \cdot , \cdot \right\rangle \) be any inner product on \(\mathbb {R}^d\), and \(\Vert \cdot \Vert \) be the norm it induces.
1.1 Cubature and measure reduction
Let \(\mu \) be a Borel probability measure on some topological space \(\mathcal {X}\). Consider d integrable functions \(f_1, \ldots , f_d : \mathcal {X}\rightarrow \mathbb {R}\). Then, we know the existence of “good reduction" of \(\mu \) by Tchakaloff’s theorem [3, 40]:
Theorem 1
(Tchakaloff) There are \(d+1\) points \(x_1, \ldots , x_{d+1}\in {{\,\textrm{supp}\,}}\mu \) and weights \(w_1, \ldots , w_{d+1}\ge 0\) such that \(w_1+\cdots +w_{d+1} = 1\) and
holds for each \(i = 1, \ldots , d\).
The proof is essentially given by classical Carathéodory’s theorem. The points and weights treated in Tchakaloff’s theorem is an important object in the field of numerical integration, called cubature [39]. An equivalent problem is also treated as a beneficial way of data compression in the field of data science [8, 26]. A typical choice of test function \(f_i\) is monomials when \(\mathcal {X}\) is a subset of an Euclidean space, so the integration with respect to the measure \(\sum _{j=1}^{d+1}w_j\delta _{x_j}\) is a good approximation of \(\int _\mathcal {X}f\,\textrm{d}\mu \) for a smooth integrand f. However, constructions under general setting are also useful; for example, in the cubature on Wiener space [25], \(\mathcal {X}\) is the space of continuous paths, \(\mu \) is the Wiener measure, and the test functions are iterated integrals of paths.
To this generalized cubature construction (or measure reduction) problem, there are efficient deterministic approaches [22, 26, 41] when \(\mu \) is discrete. Using randomness for construction is recently considered [8, 17] and it is important to know \(p_{n, X}(\mathbb {E}\!\left[ X\right] )\) for the d-dimensional random variable
where Y is drawn from \(\mu \). Indeed, once we have \(\mathbb {E}\!\left[ X\right] \in {{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\) (\(X_i = \varvec{f}(Y_i)\) are independent copies of X), then we can choose \(d+1\) points and weights satisfying (2) by solving a simple linear programming problem. Evaluation of \(N_X\) is sought for estimating the computational complexity of this naive scheme.
1.2 Statistical depth
From the statistical context, \(p_{d+1, X}(\theta )\) for a d-dimensional X is called the simplicial depth of \(\theta \in \mathbb {R}^d\) with respect to the (population) distribution of X [5, 24], which can be used for mathematically characterizing the intuitive “depth” of each point \(\theta \) when we are given the distribution of X. For an empirical measure, it corresponds to the number of simplices (whose vertices are in the data) containing \(\theta \).
There are also a various concepts measuring depth, all called statistical depth [5, 31]. One of the first such concepts is the halfspace depth proposed by [42]:
which can equivalently defined as the minimum measure of a halfspace containing \(\theta \). Donoho and Gasko [11] and Rousseeuw and Ruts [36] extensively studied general features of \(\alpha _X\). We call it the Tukey depth throughout the paper.
Our finding is that these two depth notions are indeed deeply related. We prove the rate of convergence \(p_{n, X}\rightarrow 1\) is essentially determined by \(\alpha _X\) (Proposition 13), and we have a beautiful relation \(1/2\le \alpha _XN_X\le 3d+1\) in Theorem 16.
1.3 Inclusion of deterministic convex bodies
Although we have seen the background of the \(p_{n, X}(\theta )\), which only describes the probability of a single vector contained in the random convex polytope, several aspects of such random polytopes have been studied [19, 27]. In particular, people also studied deterministic convex bodies associated with the distribution of a random vector. For example, one consequence of well-known Dvoretzky–Milman’s Theorem (see, e.g., [43, Chapter 11]) is that the convex hull of n independent samples from the d-dimensional standard normal distribution is “approximately” a Euclidean ball of radius \(\sim \sqrt{\log n}\) with high probability for a sufficiently large n.
Mainly from the context of random matrices, there have been several researches on the interior convex body of \({{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\) or its “absolute” version \({{\,\textrm{conv}\,}}\{\pm X_1,\ldots , \pm X_n\}\) for various classes of X such as Gaussian, Rademacher or vector with i.i.d. subgaussian entries [10, 13, 14, 16, 23]. One result about the Rademacher vector is the following:
Theorem 2
[13] Let d be a sufficiently large positive integer and \(X_1, X_2, \ldots \) be independent samples from the uniform distribution over the set \(\{-1, 1\}^d\subset \mathbb {R}^d\). Then, there exists an absolute constant \(c>0\) such that, for each integer \(n\ge d(\log d)^2\), we have
with probability at least \(1 - e^{-d}\). Here, \(B_2^d\) is the Euclidean unit ball in \(\mathbb {R}^d\) and \(B_\infty ^d = [-1, 1]^d\).
Although each of those results in literature was based on its specific assumptions on the distribution of X, Guédon et al. [15] found a possible way of treating the results in a unified manner under some technical assumptions on X. They introduced the floating body associated with X
to our context (the notation here is slightly changed from the original one), and argued that, under some assumptions on X, with high probability, \({{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\) includes a constant multiple of the polar body of \(\tilde{K}^\alpha (X)\) with \(\log (1/\alpha )\sim 1 + \log (n/ d)\). Note that their main object of interest is the absolute convex hull, but their results can be extended to the ordinary convex hull (see [15, Remark 1.7]).
Let us explain more formally. Firstly, for a set \(A\subset \mathbb {R}^d\), the polar body of A is defined as
Secondly, we shall describe the assumptions used in [15]. Let  be a norm on \(\mathbb {R}^d\) and \(\gamma , \delta , r, R > 0\) be constants. Their assumptions are as follows:
be a norm on \(\mathbb {R}^d\) and \(\gamma , \delta , r, R > 0\) be constants. Their assumptions are as follows:
-
\((\gamma , \delta )\) small-ball condition:
 holds for all \(t\in \mathbb {R}^d\).
holds for all \(t\in \mathbb {R}^d\). -
\(L_r\) condition with constant R:
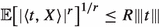 holds for all \(t\in \mathbb {R}^d\).
holds for all \(t\in \mathbb {R}^d\).
Under these conditions, they proved the following assertion by using concentration inequalities.
Theorem 3
[15] Let X be a d-dimensional symmetric random vector that satisfies the small-ball condition and \(L_r\) condition for a norm \({\left| \left| \left| \cdot \right| \right| \right| }\) and constants \(\gamma , \delta , r, R>0\). Let \(\beta \in (0, 1)\) and set \(\alpha = (en/d)^{-\beta }\). Then, there exist a constant \(c_0 = c_0(\beta , \delta , r, R/\gamma )\) and an absolute constant \(c_1>0\) such that, for each integer \(n\ge c_0 d\),
holds with probability at least \(1 - 2\exp ( - c_1 n^{1-\beta }d^\beta )\), where \(X_1, X_2, \ldots \) are independent copies of X.
Though computing \(\bigl (\tilde{K}^\alpha (X)\bigr )^\circ \) for individual X is not necessarily an easy task, this gives us a unified understanding of existing results in terms of the polar of the floating body \(\tilde{K}^\alpha (X)\). However, its use is limited due to the technical assumptions. In this paper, we show that we can completely remove the assumptions in Theorem 3 and obtain a similar statement only with explicit constants (see Proposition 22 and Corollary 25, or the next section).
Finally, we add that this interior body of random polytopes or its radius is recently reported to be essential in the robustness of sparse recovery [15] and the convergence rate of greedy approximation algorithms [6, 29] when the data is random.
1.4 Organization of the paper
In this paper, our aim is to derive general inequalities for \(p_{n, X}\) and \(N_X\). The main part of this paper is Sects. 2, 3, 4 and 5. The following is a broad description of the contents of each section.
-
Section 2: General bounds of \(p_{n, X}\) without specific quantitative assumptions
-
Section 3: Bounds of \(p_{n, X}\) uniformly determined by \(\alpha _X\)
-
Section 4: Bounds of \(N_X(\mathbb {E}\!\left[ X\right] )\) uniformly determined by the moments of X
-
Section 5: Results on deterministic convex bodies included in random polytopes
Let us give more detailed explanation about each section. Section 2 provides generalization of the results of [44], and we give generic bounds of \(p_{n, X}(\theta )\) under a mild assumption \(p_{d, X}(\theta ) = 0\), which is satisfied with absolutely continuous distributions as well as typical empirical distributions. Our main result in Sect. 2 is as follows (Theorem 8):
Theorem
Let X be an arbitrary d-dimensional random vector and \(\theta \in \mathbb {R}^d\). If \(p_{d, X}(\theta )=0\) holds, then, for any \(n\ge m\ge d+1\), inequalities
hold.
In Sect. 3, we introduce \(p_{n, X}^\varepsilon \) and \(\alpha _X^\varepsilon \) for an \(\varepsilon \ge 0\), which are “\(\varepsilon \)-relaxation" of \(p_{n, X}\) and \(\alpha _X\) in that \(p_{n, X}^0 = p_{n, X}\) and \(\alpha _X^0 = \alpha _X\) hold. For this generalization, we prove that the convergence of \(p^\varepsilon _{n, X} \rightarrow 1\) is uniformly evaluated in terms of \(\alpha _X^\varepsilon \) (Proposition 13), and obtain the following result (Theorem 14):
Theorem
Let X be an arbitrary d-dimensional random vector and \(\theta \in \mathbb {R}^d\). Then, for each \(\varepsilon \ge 0\) and positive integer \(n\ge 3d/\alpha _X^\varepsilon (\theta )\), we have
Although we do not define \(\varepsilon \)-relaxation version here, we can see from the case \(\varepsilon = 0\) that, for example, \(N_X(\theta ) \le \lceil 3d/\alpha _X(\theta ) \rceil \) generally holds (see also Theorem 16).
In Sect. 4, we derive upper bounds of \(N_X\) without relying on \(\alpha _X\), which may also be unfamiliar. By using the result in the preceding section and the Berry–Esseen theorem, we show some upper bounds of \(N_X\) in terms of the (normarized) moments of X as follows (Theorem 19):
Theorem
Let X be a centered d-dimensional random vector with nonsingular covariance matrix V. Then,
holds.
Here, \(\Vert \cdot \Vert _2\) denotes the usual Euclidean norm on \(\mathbb {R}^d\). Note that the right-hand side can easily be replaced by the moment of \(\Vert V^{-1/2}X\Vert _2\) (see also Corollary 20).
Section 5 asserts that \(K^\alpha (X):=\{\theta \in \mathbb {R}^d \mid \alpha _X(\theta ) \ge \alpha \}\) (\(\alpha \in (0, 1)\)) is a canonical deterministic body included in the random convex polytope \({{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\). We see in Proposition 22 that this body is essentially equivalent to the \(\bigl (\tilde{K}^\alpha (X)\bigr )^\circ \) mentioned in Sect. 1.3, and prove the following (Theorem 24):
Theorem
Let X be an arbitrary symmetric d-dimensional random vector, and let \(\alpha , \delta , \varepsilon \in (0, 1)\). If a positive integer n satisfies
then we have, with probability at least \(1 - \delta \),
where \(X_1, X_2, \ldots \) are independent copies of X.
A consequence of this theorem (Corollary 25) enables us to remove the technical assumption of Theorem 3.
Note that all these results give explicit constants with reasonable magnitude, which is because of our combinatorial approach typically seen in the proof of Proposition 10 and Proposition 15. After these main sections, we give some implications of our results on motivational examples (introduced in Sects. 1.1, 1.2) in Sect. 6, and we finally give our conclusion in Sect. 7.
2 General bounds of \(p_{n,X}\)
In this section, we denote \(p_{n, X}(0)\) by only \(p_{n, X}\). As we always have \(p_{n, X}(\theta ) = p_{n, X-\theta }(0)\), it suffices to treat \(p_{n, X}(0)\) unless we consider properties of \(p_{n, X}\) as a function.
Let us start with easier observations. Proposition 4 and Proposition 5 are almost dimension-free. Firstly, as one expects, the following simple assertion holds.
Proposition 4
For an arbitrary d-dimensional random vector X with \(\mathbb {E}\!\left[ X\right] = 0\) and \(\mathbb {P}\!\left( X\ne 0\right) >0\), we have
The conclusion still holds if we only assume \(p_{n, X}>0\) for some n instead of \(\mathbb {E}\!\left[ X\right] =0\).
Proof
For the proof of \(p_{2d, X} > 0\), see, e.g., [17]. From this and Carathéodory’s theorem, we also have \(p_{d+1, X} > 0\). We clearly have \(p_{n+1, X} \ge p_{n, X}\) for each \(n\ge d+1\).
The strict inequality also seems trivial, but we prove this for completeness. Assume \(p_{n+1, X} = p_{n, X}\) for some n. This implies that \(0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\Rightarrow 0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^{n+1}\) holds almost surely. By symmetry, for any \(J\subset \{1, \ldots , n+2\}\) with \(|J|= n + 1\), \(0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^{n+1}\Rightarrow 0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i\in J}\) holds almost surely. Therefore, we have \(0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\Rightarrow 0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^{n+2}\) with probability one. By repeating this argument, we obtain
with probability one, but this is only possible when \(\mathbb {P}\!\left( 0\not \in {{\,\textrm{conv}\,}}\{X_1,\ldots , X_n\}\right) = 0\) as \(p_{d+1, X} > 0\) and the variables \(X_{n+1},\ldots , X_{n+d+1}\) are independent from the others. This is of course impossible from the assumption \(\mathbb {P}\!\left( X\ne 0\right) >0\) (there exists a unit vector \(c\in \mathbb {R}^d\) such that \(\mathbb {P}\!\left( \left\langle c, X \right\rangle> 0\right) > 0\)), so we finally obtain \(p_{n, X} < p_{n+1, X}\).
Proving \(p_{n, X}\rightarrow 1\) is also easy. From the independence, we have
This leads to the conclusion combined with the monotonicity of \(p_{n, X}\).
Note that we have used the condition \(\mathbb {E}\!\left[ X\right] =0\) only to ensure \(p_{d+1}>0\). Hence the latter statement readily holds from the same argument. \(\square \)
The next one includes a little quantitative relation among \(p_{n, X}\) and \(N_X\).
Proposition 5
For an arbitrary d-dimensional random vector X and integers \(n \ge m \ge d+1\),
hold.
Proof
Let M be the number of m-point subsets of \(\{X_1,\ldots ,X_n\}\) whose convex hull contains 0. Then, we have
As \(p_{n, X}=\mathbb {P}\!\left( M\ge 1\right) \le \mathbb {E}\!\left[ M\right] \), we obtain the first inequality.
For the second part, we carry out the following rough estimate: For the minimum integer k satisfying \((1-p_{n, X})^k \le 1/2\), we have \(N_X \le kn\). If \(p_{n, X}\ge 1/2\) holds, then \(N_X\le n\) immediately holds. Thus it suffices to prove \(k\le \left\lceil \frac{1-p_{n, X}}{p_{n, X}}\right\rceil \) when \(p_{n, X}<1/2\). Indeed, by the motonicity of \((1+1/x)^x\) over \(x>0\), we have

so the conclusion follows. \(\square \)
Remark 1
Although the estimate \(N_X\le \frac{n}{p_{n, X}}\) looks loose in general, \(N_X\le \frac{2d}{p_{2d, X}}\) is a sharp uniform bound for each dimension d up to a universal constant. Indeed, in Examples 34 and 35 (Appendix B), we prove that
holds for each positive integer d. In contrast, the other inequality \(p_{n, X}\le \left( {\begin{array}{c}n\\ m\end{array}}\right) p_{m, X}\) is indeed very loose and drastically improved in Proposition 7.
In Propositions 4 and 5, we have never used the information of dimension except for observing \(p_{d+1, X}>0\) in Proposition 4. However, when the distribution of X has a certain regularity, there already exists a strong result that reflects the dimensionality.
Theorem 6
[44] When the distribution of X is absolutely continuous with respect to the Lebesgue measure on \(\mathbb {R}^d\),
holds for each \(n\ge d+1\). The equality is attained if and only if the distribution is balanced, i.e., \(\mathbb {P}\!\left( \left\langle c, X \right\rangle \le 0\right) =1/2\) holds for all the unit vectors \(c\in \mathbb {R}^d\).
The authors of [44] derived this result by showing the existence of a nonnegative continuous function \(h_X\) on [0, 1] such that \(h_X(t)=h_X(1-t)\), \(h_X(t)\le \frac{d+1}{2}\min \{t^d, (1-t)^d\}\) and
We shall provide an intuitive description of the function \(h_X\). Let us consider a one-dimensional i.i.d. sequence \(Y_1, Y_2, \ldots \) (also independent from \(X_1, X_2, \ldots \)), where each \(Y_i\) follows the uniform distribution over (0, 1). If we consider the \((d+1)\)-dimensional random vectors \(\tilde{X}_i:=(X_i, Y_i)\), then, for each n, \(0\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\subset \mathbb {R}^d\) is obviously equivalent to the condition that the \((d+1)\)-th coordinate axis (denoted by \(\ell \)) intersects the convex set \(\tilde{C}_n:={{\,\textrm{conv}\,}}\{\tilde{X}_1,\ldots ,\tilde{X}_n\}\subset \mathbb {R}^{d+1}\).
Under a certain regularity condition, there are exactly two facets (a d-dimensional face of \(C_n\)) respectively composed of a \((d+1)\)-point subset of \(\{\tilde{X}_1,\ldots ,\tilde{X}_n\}\) that intersects \(\ell \). Let us call them top and bottom, where the top is the facet whose intersection with \(\ell \) has the bigger \((d+1)\)-th coordinate. Let us define another random variable H as
-
0 if \(\ell \) does not intersect \({{\,\textrm{conv}\,}}\{\tilde{X}_1,\ldots , \tilde{X}_{d+1}\}\),
-
otherwise the probability that 0 and \(\tilde{X}_{d+2}\) are on the same side of the hyperplane supporting \({{\,\textrm{conv}\,}}\{\tilde{X}_1,\ldots ,\tilde{X}_{d+1}\}\) (conditioned by \(\tilde{X}_1, \ldots , \tilde{X}_{d+1}\)).
Then, for a given realization of \(\{\tilde{X}_1,\ldots ,\tilde{X}_n\}\), the probability that \({{\,\textrm{conv}\,}}\{\tilde{X}_1,\ldots ,\tilde{X}_{d+1}\}\) becomes the top of \(\tilde{C}_n\) is \(H^{n-d-1}\). As there are \(\left( {\begin{array}{c}n\\ d+1\end{array}}\right) \) choice of (equally) possible “top," we can conclude that
A similar observation shows \(p_{n, X} = \left( {\begin{array}{c}n\\ d+1\end{array}}\right) \mathbb {E}\!\left[ (1-H)^{n-d-1},\ H>0\right] \), and so we can understand \(h_X\) as the density of a half mixture of H and \(1-H\) over \(\{H>0\}\). This has been a simplified explanation of \(h_X\). For more rigorous arguments and proofs, see [44].
By using this “densit” function, we can prove the following interesting relationship.
Proposition 7
Let X be an \(\mathbb {R}^d\)-valued random variable with an absolutely continuous distribution. Then, for any integers \(n\ge m \ge d+1\), we have
Proof
The right inequality is clear from (4). For the left inequality, by using \(h_X(t)=h_X(1-t)\), we can rewrite (4) as
We can prove for \(a\ge b\ge 0\) that \(\frac{t^a+(1-t)^a}{t^b+(1-t)^b}\) attains its minimum at \(t=1/2\), e.g., by using the method of Lagrange multipliers. Accordingly, we obtain
which is equivalent to the inequality to prove. \(\square \)
Remark 2
The left inequality has nothing to say when n and m are large so \(2^{n-m}\) is faster than \((n/m)^d\). However, for small n and m, it works as a nice estimate. Consider the case \(n=2d\) and \(m=d+1\). Then, the proposition and the usual estimate for central binomial coefficients yield
This is comparable to the symmetric case, where \(p_{d+1,X}=1/2^d\) and \(p_{2d, X}=1/2\) hold.
The right inequality is an obvious improvement of the dimension-free estimate given in Proposition 5.
We next generalize these results to general distributions including discrete ones such as empirical measures. However, at least we have to assume \(p_{d, X}=0\). Note that it is weaker than the condition that X has an absolutely continuous distribution, as it is satisfied with usual empirical measures (see Proposition 9).
From smoothing arguments, we obtain the following generalization of inequalities (3) and (5).
Theorem 8
Let X be an arbitrary d-dimensional random vector with \(p_{d, X}=0\). Then, for any \(n\ge m\ge d+1\), inequalities
hold.
Proof
Let U be a uniform random variable over the unit ball of \(\mathbb {R}^d\) which is independent from X. Let also \(U_1, U_2 \ldots \) be independent copies of U, which is independent from \(X_1, X_2, \ldots \). We shall prove that \(\lim _{\varepsilon \searrow 0}p_{n, X+\varepsilon U} = p_{n, X}\) for each n. Note that the distribution of \(X+\varepsilon U\) has the probability density function
where V denotes the volume of the unit ball. Therefore, once we establish the limit \(\lim _{\varepsilon \searrow 0}p_{n, X+\varepsilon U} = p_{n, X}\) the statement of the theorem is clear.
From \(p_{d, X}=0\), we know that
For each \(n\ge d+1\), consider the event \(A_n:=\{0\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\}\). If the closed \(\varepsilon \)-ball centered at 0 is included in \({{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\), then 0 is also contained in \({{\,\textrm{conv}\,}}\{X_i+\varepsilon U_i\}_{i=1}^n\) as \(\Vert \varepsilon U_i\Vert \le \varepsilon \) for all i (more precisely, we can prove this by using the separating hyperplane theorem). Therefore, by considering the facets of the convex hull, we have
By using (6), we have
and so we obtain \(\liminf _{\varepsilon \searrow 0} p_{n, X+\varepsilon U} \ge p_{n, X}\).
On the other hand, if we have \(0\in {{\,\textrm{conv}\,}}\{X_i+\varepsilon U_i\}_{i=1}^n\) and \(0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\) at the same time, then there exsits \(J\subset \{1,\ldots ,n\}\) such that \(|J|=d\) and \(\inf _{y\in {{\,\textrm{conv}\,}}\{X_i\}_{i\in J}}\Vert y\Vert \le \varepsilon \). Indeed, we can write 0 as a convex combination \(\sum _{i=1}^n \lambda _i(X_i+\varepsilon U_i) =0\), so
As \(0\not \in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\), there is a facet within \(\varepsilon \)-distance from 0. Therefore, we obtain
and similarly it follows that
Thus we finally obtain \(\lim _{\varepsilon \searrow 0}p_{n, X+\varepsilon U} = p_{n, X}\). \(\square \)
We should remark that \(p_{d, X}=0\) is naturally satisfied with (centered) empirical measures.
Proposition 9
Let \(\mu \) be an absolutely continuous probability distribution on \(\mathbb {R}^d\) and \(Y_1, Y_2, \ldots \) be an i.i.d. samplings from \(\mu \). Then, with probability one, for each \(M\ge d+1\), distributions
satisfy \(p_{d, \mu _M} = p_{d, \tilde{\mu }_M} = 0\). \(p_{d, \mu _M} = 0\) also holds for \(1\le M\le d\) and requires only \(p_{d, \mu } = 0\).
Proof
For \(\mu _M\), it suffices to prove that with probability one there are no \(J\subset \{1,\ldots ,M\}\) with \(|J|= d\) such that \(0\in {{\,\textrm{conv}\,}}\{Y_i\}_{i\in J}\). This readily follows from the absolute continuity of the original measure \(\mu \). The extension to the case \(\mu \) satisfies only \(p_{d,\mu }=0\) is immediate.
For the centered version \(\tilde{\mu }_M\), what to prove is that with probability one there are no \(J\subset \{1,\ldots ,M\}\) with \(|J|= d\) such that \(\frac{1}{M}\sum _{i=1}^M Y_j \in {{\,\textrm{conv}\,}}\{Y_i\}_{i\in J}\). Suppose this occurs for some J. Then, we have that \(\frac{1}{M-d}\sum _{i\ne J}Y_i\) is on the affine hull of \(\{Y_i\}_{i\in J}\). However, as \(\{Y_i\}_{i\not \in J}\) is independent from \(\{Y_i\}_{i\in J}\) for a fixed J, this probability is zero again from the absolute continuity of \(\mu \). Therefore, we have the desired conclusion. \(\square \)
3 Uniform bounds of \(p_{n, X}^\varepsilon \) via the relaxed Tukey depth
We have not used any quantitative assumption on the distribution of X in the previous section. In this section, however, we shall evaluate \(p_{n, X}\) and its \(\varepsilon \)-approximation version by using the Tukey depth and its relaxation. We shall fix an arbitrarily real inner product \(\left\langle \cdot , \cdot \right\rangle \) on \(\mathbb {R}^d\), and use the induced norm \(\Vert \cdot \Vert \) and the notation \({{\,\textrm{dist}\,}}(x, A):=\inf _{a\in A}\Vert x - a\Vert \) for an \(x\in \mathbb {R}^d\) and \(A\subset \mathbb {R}^d\).
For a d-dimensional random vector X and \(\theta \in \mathbb {R}^d\), define an \(\varepsilon \)-relaxation version of the Tukey depth by
We also define, for a positive integer n,
where \(X_1, \ldots , X_n\) are independent copies of X. Note that \(p_{n, X} = p_{n, X}^0\). Although we regard them as functions of \(\theta \) in Sect. 5, we only treat the case \(\theta = 0\) and omit the argument \(\theta \) in this section.
Proposition 10
Let X be a d-dimensional random vector with an absolutely continuous distribution with respect to the Lebesgue measure. Then, for each \(\varepsilon \ge 0\) and positive integer \(n \ge d + 1\), we have
Before going into details of quantitative results, we note the following equivalence of the positivity of \(\alpha _X^\varepsilon \) and \(p_{n, X}^\varepsilon \) which immediately follows from this assertion.
Proposition 11
Let X be an arbitrary d-dimensional random vector and let \(\varepsilon \ge 0\). Then, \(p_{n, X}^\varepsilon > 0\) for some \(n\ge 1\) implies \(\alpha _X^\varepsilon > 0\). Reciprocally, \(\alpha _X^\varepsilon > 0\) implies \(p_{n, X}^\varepsilon > 0\) for all \(n\ge d+1\).
Proof
If \({{\,\textrm{dist}\,}}(0, {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n)\le \varepsilon \), there exists a point \(x\in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\) with \(\Vert x\Vert \le \varepsilon \). Then, for each \(c\in \mathbb {R}^d\) with \(\Vert c\Vert =1\), we have \(\left\langle c, x \right\rangle \le \varepsilon \) and so \(\left\langle c, X_i \right\rangle \le \varepsilon \) for at least one \(i\in \{1,\ldots ,n\}\). Hence we have a uniform evaluation
and the first assertion follows.
For the latter, if \(\alpha _X^\varepsilon \) is positive, we have \(p_{n, X}^\varepsilon > 0\) for a sufficiently large n from Proposition 10. Finally, Carathéodory’s theorem yields the positivity for all \(n\ge d+1\). \(\square \)
Let us prove Proposition 10.
Proof of Proposition 10
Let \(m\ge d\) be an integer. We first consider the quantity \(q_m:=1-p_{n, X}^\varepsilon \). Let \(A_m\) be the event given by
Also, let \(B_m\) be the event that \(\{X_1, \ldots , X_m\}\) is in general position. Then, we have \(\mathbb {P}\!\left( B_m\right) = 1\) and \(q_m = \mathbb {P}\!\left( A_m\cap B_m\right) \).
Under the event \(A_m\cap B_m\), we have a unique point \(h_m\in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^m\) that minimizes \(\Vert h_m\Vert \). Let \(H_m\) be the open halfspace defined by \(H_m:=\{x\in \mathbb {R}^d\mid \left\langle x - h_m, h_m \right\rangle > 0\}\). Then, the boundary \(\partial H_m\) is the hyperplane going through \(h_m\) and perpendicular to \(h_m\). From the general-position assumption, there are at most d points on \(\partial H_m\). Let \(I_m\) be the set of indices i satisfying \(\partial H_m\), then \(I_m\) is a random subset of \(\{1, \ldots , m\}\) with \(1\le |I_m|\le d\) under the event \(A_m\cap B_m\). Note also that \(X_i \in H\) for each \(i\in \{1, \ldots , d\}{\setminus } I_m\). For simplicity, define \(I_m = \emptyset \) for the event \((A_m\cap B_m)^c\).
As \(I_m\) is a random set determined uniquely, we can decompose the probability \(\mathbb {P}\!\left( A_m\cap B_m\right) \) as follows by symmetry:
Hence, we want to evaluate the probability \(\mathbb {P}\!\left( I_m = \{1, \ldots , k\}\right) \). Note that we can similarly define \(h_k\) as the unique point in \({{\,\textrm{conv}\,}}\{X_i\}_{i=1}^k\) that minimizes the distance from the origin. Then, \(H_k\) is the open halfspace \(H_k=\{x\in \mathbb {R}^d\mid \left\langle x - h_{m, k}, h_{m, k} \right\rangle > 0\}\). Then, we have
where \(X^\prime \) is a copy of X independent from \(X_1, X_2, \ldots \). As \(\mathbb {P}\!\left( X^\prime \in H_k \mid {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^k\right) \le 1 - \alpha _X^\varepsilon \) under the event \(\{\Vert h_k\Vert > \varepsilon ,\ {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^k\subset \partial H_k\}\), we have
Therefore, we have
By letting \(n = m+1\), we obtain the conclusion. \(\square \)
If we define \(g_{d, n}(\alpha )\) by \(g_{d, n} := 1\) for \(n = 1,\ldots , d\) and
for \(n = d+1, d+2, \ldots \), we clearly have \(1-p_{n, X}^\varepsilon \le g_{d, n}(\alpha _X^\varepsilon )\) from Proposition 10 for a d-dimensional X having density. We can actually generalize this to a general X.
Lemma 12
Let X be an arbitrary d-dimensional random vector. Then, for each \(\varepsilon \ge 0\) and positive integer n, we have \(1 - p_{n, X}^\varepsilon \le g_{d, n}(\alpha _X^\varepsilon )\).
Proof
Note first that \(g_{d, n}(\alpha )\) is non-increasing with respect to \(\alpha \in [0, 1]\). Let \(\tilde{X}\) be a d-dimensional random vector such that \(\Vert X-\tilde{X}\Vert \le \delta \) for some \(\delta >0\). Then, for an arbitrary \(c\in \mathbb {R}^d\) with \(\Vert c\Vert =1\), we have
so \(\mathbb {P}\!\left( \left\langle c, X \right\rangle \le \varepsilon \right) \le {\mathbb {P}}(\langle c, \tilde{X} \rangle \le \varepsilon + \delta )\). Hence we have \(\alpha _X^\varepsilon \le \alpha _{\tilde{X}}^{\varepsilon +\delta }\).
Consider generating i.i.d. pairs \((X_1, \tilde{X}_1), \ldots , (X_n, \tilde{X}_n)\) that are copies of \((X, \tilde{X})\). Then, for each \(x\in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\), there is a convex combination such that \(x = \sum _{i=1}^n\lambda _iX_i\) with \(\lambda _i\ge 0\) and \(\sum _{i=1}^n\lambda _i=1\). Then, we have
It means that \(\inf _{y\in {{\,\textrm{conv}\,}}\{\tilde{X}_i\}_{i=1}^n}\Vert x - y\Vert \le \delta \) holds for every \(x\in {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\), and we can deduce that \(p_{n, X}^{\varepsilon +2\delta } \ge p_{n, \tilde{X}}^{\varepsilon +\delta }\) holds.
In particular, we can choose \(\tilde{X}\) having density, so that we have \(1 - p_{n, X}^{\varepsilon +\delta } \le g_{d, n}(\alpha _{\tilde{X}}^{\varepsilon +\delta })\). Therefore, from the monotonicity of \(g_{d, n}\), we have
As \(\delta >0\) can be taken arbitrarily, we finally obtain
by letting \(\delta \rightarrow 0\). The \(\delta \)-relaxation technique used in this proof is a big advantage of introducing \(p_{n, X}^\varepsilon \) extending \(p_{n, X}\). \(\square \)
From this lemma, we obtain the following general bound.
Proposition 13
Let X be an arbitrary d-dimensional random vector. Then, for each \(\varepsilon \ge 0\) and positive integer \(n\ge d/\alpha _X^\varepsilon \), we have
Proof
From Lemma 12, it suffices to prove that
holds for each \(\alpha \in (0, 1)\) and \(n\ge d/\alpha \). From the definition of \(g_{d, n}\) (see (7)), if we set \(n_0:=\lceil d/\alpha \rceil \), then we have
As we know \(d/\alpha \le n_0 < d/\alpha +1\) by definition, we have
This is indeed the desired inequality (8). \(\square \)
Remark 3
As \(\frac{1}{\alpha }\log \frac{1}{1-\alpha }\ge 1\) holds on (0, 1) for \(n\ge \frac{(1+\alpha )d}{\alpha }\), the bound (8) yields a looser but more understandable variant
Note that we have a trivial lower bound of \(1 - p_{n, X}^\varepsilon \ge (1 - \alpha _X^\varepsilon )^n\), which is proven by fixing a separating hyperplane between the origin and sample points.
For a special choice \(n=\lceil 3d/\alpha \rceil \), the following is readily available:
Theorem 14
Let X be an arbitrary d-dimensional random vector. Then, for each \(\varepsilon \ge 0\) and positive integer \(n\ge 3d/\alpha _X^\varepsilon \), we have
Proof
From Proposition 13, it suffices to prove
for all \(\alpha \in (0, 1)\). If we let \(f(x) = \frac{x-2}{x}\log \frac{1}{1-x}\) for \(x\in (0, 1)\), then we have
If we set \(t:=\log \frac{1}{1-x}\), t takes positive reals and we have
Therefore, it suffices to consider the limit \(\alpha \searrow 0\). In this limit, the left-hand side of (9) is equal to \(3e^{-2}\), which is smaller than 1/2 since \(e>\sqrt{6}\) holds. \(\square \)
We complete this section with a stronger version of Proposition 10 only for \(\varepsilon = 0\). Indeed, by summing up the following inequality, we can immediately obtain the \(\varepsilon = 0\) case in Proposition 10.
Proposition 15
Let X be a d-dimensional random vector with an absolutely continuous distribution with respect to the Lebesgue measure. Then,
holds for all \(n\ge d+1\).
Proof
First, observe that \(p_{n+1, X}-p_{n, X}=\mathbb {P}\!\left( 0\right) \in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_{n+1}\}{\setminus }{{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) for \(n\ge d+1\) and independent copies \(X_1,X_2,\ldots \) of X. Assume \(0\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_{n+1}\}{\setminus }{{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) holds and no \(d+1\) points of \(\{0, X_1,\ldots ,X_{n+1}\}\) lie on the same hyperplane (the latter is satisfied almost surely as X is absolutely continuous). Then, there exists an expression such that
Here \(0<\lambda _{n+1}<1\) must hold as \(0\not \in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) and \(X_{n+1}\ne 0\). Therefore, we can rewrite
and this left-hand side is a convex combination of \(\{X_1,\ldots ,X_n\}\). Therefore, the line \(\ell \) passing through \(X_{n+1}\) and 0 intersects \({{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) after 0 (if directed from \(X_{n+1}\) to 0). Also, \(\ell \) never intersects \({{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) before 0. Indeed, if \(\lambda X_{n+1}\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) for some \(\lambda >0\), then \(0\in {{\,\textrm{conv}\,}}\{\lambda X_{n+1}, -\frac{\lambda _{n+1}}{1-\lambda _{n+1}}X_{n+1}\} \subset {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) holds and it contradicts the assumption.
Hence, we can define the first hitting point of \(\ell \) and \({{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) after 0. More formally, let P be the minimum-normed point in \(\ell \cap {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\). Then, by the general-position assumption, there exists a unique \(J\subset \{1,\ldots ,n\}\) with \(|J|=d\) such that \(P\in {{\,\textrm{conv}\,}}\{X_i\}_{i\in J}\) (more strongly, P is in the relative interior of \({{\,\textrm{conv}\,}}\{X_i\}_{i\in J}\)). In other words, \({{\,\textrm{conv}\,}}\{X_i\}_{i\in J}\) is the unique facet which intersects \(\ell \) first. Then, there exists a unique normal vector \(c_J\) that defines the hyperplane supporting \(\{X_i\}_{i\in J}\), i.e., \(\left\langle c_J, X_i \right\rangle =1\) for each \(i\in J\). Since \(\left\langle c_J, P \right\rangle =1\) also holds, we have \(\left\langle c_J, X_{n+1} \right\rangle < 0\). We can also prove \(\left\langle c_J, X_i \right\rangle > 1\) for each \(i\in \{1,\ldots ,n\}{\setminus } J\). Indeed, if we have \(\left\langle c_J, X_j \right\rangle < 1\) for some \(j\in \{1,\ldots ,n\}{\setminus } J\), then there are interior points of \({{\,\textrm{conv}\,}}\{X_i\}_{i\in J\cup \{j\}}\) that belongs to \(\ell \) and this contradicts the minimality of the norm of P.
Therefore, for a fixed \(J\subset \{1,\ldots ,n\}\) with \(|J|=d\), the probability that \(0\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_{n+1}\}{\setminus }{{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) holds and \({{\,\textrm{conv}\,}}\{X_i\}_{i\in J}\) becomes the first facet intersecting \(\ell \) after 0 is, from the independence,
where \(X'\) is a copy of X independent from \(\{X_i\}_{i\ge 1}\). By symmetry, this J is chosen with equal probability given \(0\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_{n+1}\}{\setminus }{{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\) (almost surely without overlapping). Hence, we obtain
where \(I=\{1,\ldots ,d\}\). Observe that this representation is still valid for \(n=d\). From the definition of \(\alpha _X\), we have \(\mathbb {P}\!\left( \left\langle c_I, X' \right\rangle > 1 \mid \{X_i\}_{i\in I}\right) \le 1-\alpha _X\), so finally obtain, for \(n\ge d+1\),
This is the desired inequality. \(\square \)
4 Bounds of \(N_X\) via Berry–Esseen theorem
In this section, we discuss upper bounds of \(N_X\) for a centered X, which are of particular interest from the randomized measure reduction (see Sect. 1.1).
We know the following assertion as a consequence of Theorem 14.
Theorem 16
Let X be an arbitrary d-dimensional random vector. Then, we have
Proof
The right inequality is an immediate consequence of Theorem 14. To prove the left one, let n be a positive integer satisfying \(\frac{1}{2n} > \alpha _X\). Then, there exists a vector \(c\in \mathbb {R}^d{\setminus }\{0\}\) such that \(\mathbb {P}\!\left( c^\top X\le 0\right) < \frac{1}{2n}\). Then, for \(X_1, X_2,\ldots , X_n\) (i.i.d. copies of X), we have
Therefore, \(N_X\) must satisfy \(\frac{1}{2N_X} \le \alpha _X\). \(\square \)
Remark 4
The above theorem states that \(1/2\le \alpha _X N_X\le 3d + 1\). This evaluation for \(\alpha _X N_X\) is indeed tight up to a universal constant. For example, if X is a d-dimensional standard Gaussian, we have \(\alpha _X=\frac{1}{2}\) and \(N_X=2d\), so \(\alpha _XN_X = d\). Moreover, for a small \(\varepsilon \in (0, 1)\), if we consider \(X=(X^1, \ldots , X^d)\) such that
-
\(\mathbb {P}\!\left( X^d = 1\right) = \varepsilon \) and \(\mathbb {P}\!\left( X^d = -1\right) = 1- \varepsilon \),
-
\((X^1, \ldots , X^{d-1})|_{X^d = 1}\) is a standard Gaussian,
-
\(X^1 = \cdots = X^{d-1} = 0\) if \(X^d = -1\),
then we can see \(\alpha _X = \varepsilon /2\) and \(N_X = \varOmega ((d-1)/\varepsilon )\) as \((0, \ldots , 0, 1)\) has to be in the convex hull of samples to include the origin in it. Hence the bound \(\alpha _X N_X = \mathcal {O}\!\left( d\right) \) is sharp even for a small \(\alpha _X\).
On the contrary,
holds (even when requiring \(p_{d, X}=0\)) for each positive integer d from Example 34 and Example 35 in the appendix (Sect. B).
Although Theorem 16 has strong generality, in many situations we have little information about the Tukey depth \(\alpha _X\). Indeed, approximately computing the Tukey depth itself is an important and difficult problem [9, 47]. However, if we limit the argument to a centered X, we can obtain various moment-based bounds as shown below. In this section, we use the usual Euclidean norm \(\Vert \cdot \Vert _2\) given by \(\Vert x\Vert _2 = \sqrt{x^\top x}\) for simplicity.
Let X be a d-dimensional centered random vector whose covariance matrix \(V:=\mathbb {E}\!\left[ XX^\top \right] \) is nonsingular. We also define \(V^{-1/2}\) as the positive-definite square root of \(V^{-1}\). Then, for each unit vector \(c\in \mathbb {R}^d\) (namely \(\Vert c\Vert _2 = 1\)), we have
We have the following simple result for a bounded X.
Proposition 17
Let X be a centered d-dimensional random vector with nonsingular covariance matrix V. If \(\Vert V^{-1/2}X\Vert _2\le B\) holds almost surely for a positive constant B, then we have
Proof
For a one-dimensional random variable Y with \(\mathbb {E}\!\left[ Y\right] = 0\), \(\mathbb {E}\!\left[ Y^2\right] = 1\) and \(|Y|\le B\), we have
and so
By observing this inequality for each \(Y = c^\top V^{-1/2}X\) with \(\Vert c\Vert _2 = 1\), we obtain the bound of \(\alpha _X\). The latter bound then follows from Theorem 16. \(\square \)
Let us consider the unbounded case. The Berry–Esseen theorem evaluates the speed of convergence in the central limit theorem [4, 12]. The following is a recent result with an explicit small constant.
Theorem 18
[21] Let Y be a random variable with \(\mathbb {E}\!\left[ Y\right] =0\), \(\mathbb {E}\!\left[ Y^2\right] =1\), and \(\mathbb {E}\!\left[ |Y|^3\right] <\infty \), and let \(Y_1, Y_2, \ldots \) be independent copies of Y. Also let Z be one-dimensional standard Gaussian. Then, we have
for arbitrary \(x\in \mathbb {R}\) and \(n\ge 1\).
We can apply the Berry–Esseen theorem for evaluating the probability \(\mathbb {P}\!\left( c^\top S_n\le 0\right) \) from (10), where \(S_n\) is the normalized i.i.d. sum \(\frac{1}{\sqrt{n}}V^{-1/2}(X_1+\cdots +X_n)\). By elaborating this idea, we obtain the following bound of \(N_X\).
Theorem 19
Let X be a centered d-dimensional random vector with nonsingular covariance matrix V. Then,
holds.
Proof
Let n be an integer satisfying
Then, for an arbitrary \(\Vert c\Vert _2=1\), from Theorem 18, we have
where \(X_1,X_2,\ldots \) are independent copies of X. Hence \(\alpha _{n^{-1}(X_1+\cdots +X_n)}\ge 9/50\) holds. Then we can use Theorem 16 to obtain
Since \(N_X \le nN_{n^{-1}(X_1+\cdots +X_n)}\) holds, we have
which is the desired conclusion. \(\square \)
Remark 5
The bound in Theorem 19 is sharp up to constant as a uniform bound in terms of \(\mathbb {E}\!\left[ \left|c^\top V^{-1/2} X\right|^3\right] \). Indeed, if X is d-dimensional standard Gaussian, then \(\mathbb {E}\!\left[ \left|c^\top V^{-1/2} X\right|^3\right] = \frac{2\sqrt{2}}{\sqrt{\pi }}\) holds for all \(\Vert c\Vert _2=1\) while \(N_X = 2d\), so we have
From Theorem 19, we can also obtain several looser but more tractable bounds.
Corollary 20
Let X be a centered d-dimensional random vector with nonsingular covariance matrix V. \(N_X\) can be bounded as
Proof
From Theorem 19, it suffices to prove
for each unit vector \(c\in \mathbb {R}^d\). The first bound is clear from
The second bound can also be derived as
where we have used the Cauchy–Schwarz inequality. \(\square \)
Remark 6
In the order notation, the first bound in this corollary states
This estimate is also sharp up to \(\mathcal {O}\!\left( d\right) \) factor in the sense that we can prove
for each positive integer d. For the proof of this fact, see Example 34 and Example 35 in the appendix (Sect. B).
We finally remark that there are multivariate versions of the Berry–Esseen theorem [35, 46] and we can use them to derive a bound of \(N_X\) in a different approach which does not use \(\alpha _X\). However, their bounds only gives the estimate
which is far worse than the bounds obtained in Theorem 19 and Corollary 20. However, it is notable that this approach from multidimensional Berry–Esseen formulas is applicable to non-identical \(X_i\)’s if the second and third moments are uniformly bounded, while the combinatorial approach based on \(\alpha _X\) seems to be fully exploiting the i.i.d. assumption. Therefore, we provide the details of this alternative approach in the appendix (Sect. A).
5 Deterministic interior body of random polytopes
For each \(\alpha > 0\), define a deterministic set defined by the level sets of Tukey depth
This set is known to be compact and convex [36]. We can also naturally generalize this set for the \(\varepsilon \)-relaxation of Tukey depth, and the generalization also satisfies the following:
Proposition 21
Let X be a d-dimensional random vector. Then, for each \(\varepsilon \ge 0\) and \(\alpha > 0\), the set \(\{\theta \in \mathbb {R}^d\mid \alpha _X^\varepsilon (\theta ) \ge \alpha \}\) is compact and convex, and satisfies
Proof
We fix \(\alpha \) and denote
Note that \(K_0 = K^\alpha (X)\). Let \(c\in \mathbb {R}^d\) satisfy \(\Vert c\Vert = 1\). Define t(c) by
If \(t(c) = \infty \), i.e., the right-hand set is empty for some c, then each set \(K_\varepsilon \) is empty. \(t(c) > -\infty \) is clear from \(\alpha > 0\). Suppose \(t(c)\in \mathbb {R}\) for all c. From the continuity of probability, the infimum can actually be replaced by minimum, so we have
for each \(\theta \in \mathbb {R}^d\). Hence, if \(\theta _0\in K_0\) and \(\Vert \theta - \theta _0\Vert \le \varepsilon \), then we have \(\theta \in K_\varepsilon \), so we obtain the inclusion statement.
Let us prove that \(K_\varepsilon \) is compact and convex. Define \(H_\varepsilon (c):=\{\theta \in \mathbb {R}^d \mid \left\langle c, \theta \right\rangle \ge t(c) - \varepsilon \}\) for each \(c\in \mathbb {R}^d\) with \(\Vert c\Vert = 1\). From (12), we have \(K_\varepsilon = \bigcap _{\Vert c\Vert = 1}H_\varepsilon (c)\). As \(H_\varepsilon (c)\) is closed and convex, \(K_\varepsilon \) is also closed and convex. To prove compactness, we shall prove \(K_\varepsilon \) is bounded. As X is a random vector, there is an \(R > 0\) such that \(\mathbb {P}\!\left( \Vert X\Vert \ge R\right) < \alpha \). Then, for each \(\theta \in \mathbb {R}^d\) satisfying \(\Vert \theta \Vert \ge R+\varepsilon \), we have
Therefore, we have \(\Vert \theta \Vert < R + \varepsilon \) for each \(\theta \in K_\varepsilon \) and so \(K_\varepsilon \) is bounded. \(\square \)
Remark 7
Note that the inclusion stated in Proposition 21 can be strict. For example, if X is a d-dimensional standard Gaussian, \(K^\alpha (X)\) is empty for each \(\alpha > 1/2\), but the \(\varepsilon \)-relaxation of Tukey depth can be greater than 1/2 for \(\varepsilon > 0\).
From this proposition, we can naturally generalize the arguments given in this section to the \(\varepsilon \)-relaxation case; natural interior bodies of \(\varepsilon \)-neighborhood of \({{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\) are given by the \(\varepsilon \)-relaxation of Tukey depth. However, to keep the notation simple, we only treat \(K^\alpha (X)\) the interior body of usual convex hull in the following.
We next prove that the polar body \(\bigl (\tilde{K}^\alpha (X)\bigr )^\circ \) used in [15], which we have introduced in Sect. 1.3, is essentially the same as \(K^\alpha (X)\) in their setting, i.e., when X is symmetric. Recall that \(\tilde{K}^\alpha (X)\) is defined as
Note that the following proposition is not surprising if we go back to the original background of \(\tilde{K}^\alpha \) [37], where X is uniform from some deterministic convex set, and recent reseaches on its deep relation to the Tukey depth [32].
Proposition 22
Let X be a d-dimensional symmetric random vector. Then, for each \(\alpha \in (0, 1/2)\), we have
Proof
Consider the set
Then, we clearly have \(A^\alpha \subset \tilde{K}^\alpha (X)\) and so \((A^\alpha )^\circ \supset \bigl (\tilde{K}^\alpha (X)\bigr )^\circ \). We first prove that \((A^\alpha )^\circ = K^\alpha (X)\) actually holds. From the definition of a polar, \(\theta \in (A^\alpha )^\circ \) if and only if
holds for each \(s\in \mathbb {R}^d{\setminus }\{0\}\). If we represent \(s = r^{-1}c\) by \(r>0\) and \(c\in \mathbb {R}^d\) with \(\Vert c\Vert = 1\), this is equivalent to
for each \(r > 0\) and \(\Vert c\Vert = 1\). As we have assumed that X is symmetric and \(\alpha < 1/2\), (13) is still equivalent even if we allow r to take all reals.
We shall prove that, for a fixed c, (13) is equivalent to \(\mathbb {P}\!\left( \left\langle c, X - \theta \right\rangle \ge 0\right) \ge \alpha \). Indeed, if
holds, there exists a \(\delta > 0\) such that \(\mathbb {P}\!\left( \left\langle c, X \right\rangle \ge \left\langle c, \theta \right\rangle - \delta \right) < \alpha \). Then, we have the negation of (13) by letting \(r = \left\langle c, \theta \right\rangle - \delta \). For the opposite direction, if we assume \(\mathbb {P}\!\left( \left\langle c, X \right\rangle \ge \left\langle c, \theta \right\rangle \right) \ge \alpha \), we have \(\mathbb {P}\!\left( \left\langle c, X \right\rangle \ge r\right) \ge \alpha \) for all \(r < \left\langle c, \theta \right\rangle \) and so (13) is true. Therefore, we obtain \((A^\alpha )^\circ = K^\alpha (X)\).
For each \(\beta \in (\alpha , 1/2)\), we clearly have \(\tilde{K}^\alpha (X) \subset A^{\beta }\). Therefore, we have
which is the desired assertion. \(\square \)
We are going to prove the extension of Theorem 3 by finding a finite set of points whose convex hull approximates \(K^\alpha (X)\). The following statement is essentially well-known [2, 34], but we give the precise statement and a brief proof for completeness.
Proposition 23
Let K be a compact and convex subset of \(\mathbb {R}^d\) such that \(K = -K\). Then, for each \(\varepsilon \in (0, 1)\), there is a finite set \(A\subset \mathbb {R}^d\) such that
Proof
We can only consider the case K has full dimension, i.e., K has a nonempty interior. Then, the Minkowski functional of K (e.g., see [7, IV.1.14])

defines a norm on \(\mathbb {R}^d\) (note that all norms are equivalent on \(\mathbb {R}^d\)). For this norm, it is known that there is a finite subset \(A\subset S\) such that  for all \(x\in B\) and \(|A| \le (1 + 2/\varepsilon )^d\) [34, Lemma 4.10]. It suffices to prove \((1-\varepsilon )K\subset {{\,\textrm{conv}\,}}A\). Assume the contrary, i.e., let \(x_0\) be a point such that
for all \(x\in B\) and \(|A| \le (1 + 2/\varepsilon )^d\) [34, Lemma 4.10]. It suffices to prove \((1-\varepsilon )K\subset {{\,\textrm{conv}\,}}A\). Assume the contrary, i.e., let \(x_0\) be a point such that  and \(x_0\not \in {{\,\textrm{conv}\,}}A\). Then, there exists a \((d-1)\)-dimensional hyperplane \(H\subset \mathbb {R}^d\) such that \(x_0\in H\) and all the points in A lie (strictly) on the same side as the origin with respect to H. Let
and \(x_0\not \in {{\,\textrm{conv}\,}}A\). Then, there exists a \((d-1)\)-dimensional hyperplane \(H\subset \mathbb {R}^d\) such that \(x_0\in H\) and all the points in A lie (strictly) on the same side as the origin with respect to H. Let  . Then, we have
. Then, we have  , and
, and  satisfies
satisfies  . Hence, we have
. Hence, we have  and it contradicts the assumption for A. \(\square \)
and it contradicts the assumption for A. \(\square \)
Theorem 24
Let X be an arbitrary symmetric d-dimensional random vector, and let \(\alpha , \delta , \varepsilon \in (0, 1)\). If a positive integer n satisfies
then we have, with probability at least \(1 - \delta \),
where \(X_1, X_2, \ldots \) are independent copies of X.
Proof
As \(K^\alpha (X)\) is symmetric and convex, there is a set \(A\subset K^\alpha (X)\) with cardinality at most \((1+2/\varepsilon )^d\) such that \((1-\varepsilon )K^\alpha (X)\subset {{\,\textrm{conv}\,}}A\) from Proposition 23. We shall evaluate the probability of \(A\subset {{\,\textrm{conv}\,}}\{X_i\}_{i=1}^n\). As each point \(\theta \in A\) satisfies \(\alpha _X(\theta )\ge \alpha \), from Remark 3, we have
for each \(\theta \in A\). Hence, it suffices to prove the right-hand side of (14) is bounded by \((1 + 2/\varepsilon )^{-d}\delta \). By taking the logarithm, it is equivalent to showing
Let us denote \(x:=n\alpha /d\). For \(x\ge 12\), as \(x/2-\log x\) is increasing, we have
by a simple computation. Therefore, from \(\log (1+2/\varepsilon ) \le \log 3 + \log (1/\varepsilon )\) and the assumption for n, we obtain the inequality (14). \(\square \)
Remark 8
Although the bound given in Theorem 24 requires \(n\ge 12d/\alpha \), it can be loosened for moderate \(\delta \) and \(\varepsilon \). For example, if we want to obtain a bound for the case \(\delta = \varepsilon = 1/2\), then we can prove \(n \ge 5d/\alpha \) to be sufficient by using the bound in Proposition 13. Moreover, we should note that we have used the assumption that X is symmetric only for assuring that \(K^\alpha (X)\) is symmetric so that we can use Proposition 23. If we take a symmetric convex subset \(K\subset K^\alpha (X)\), we can prove a similar inclusion statement for K even for a nonsymmetric X.
If we want a generalized version of Theorem 3, we can prove the following:
Corollary 25
Let X be an arbitrary d-dimensional symmetric random vector. Let \(\beta \in (0, 1)\) and set \(\alpha = (en/d)^{-\beta }\). Then, there exists an absolute constant \(c>0.45\) such that, for each integer n satisfying \(n\ge (12e^\beta )^{1/(1-\beta )}d\), we have
with probability at least \(1 - \exp (-ce^{-\beta } n^{1-\beta }d^\beta )\), where \(X_1, X_2, \ldots \) are independent copies of X.
Proof
For \(\alpha = (en/d)^{-\beta }\), we have
so \(n\ge 12d/\alpha \) is equivalent to \(n\ge (12e^\beta )^{1/(1-\beta )}d\). Hence, from Theorem 24, it suffices to determine how small \(\delta \) can be taken so as to satisfy
As \(n\ge 12d\) holds for all \(\beta \), for \(a:=\frac{\log 2}{6} < 0.1\), we have \(an \ge \frac{2d}{\alpha }\log 2\). Therefore, we can take \(\delta \) as small as
Therefore, we can take \(c = \frac{1-a}{2} > 0.45\) as desired. \(\square \)
6 Application
We discuss implications of the results of this paper in two parts. The first part discusses the use of the bounds we gave on \(p_{n, X}\), while the second part gives implication of \(N_X\)’s bounds on the randomized cubature construction.
6.1 Bounds of \(p_{n, X}\)
Firstly, the inequality between \(p_{n, X}\) and \(p_{m, X}\) given in Proposition 7 provides the inequality
as it is mentioned in Remark 2.
Measure reduction Consider a discrete (probability) measure \(\mu = \sum _{x\in {\mathcal {X}}}w_x\delta _{x}\) for a finite subset of \({\mathcal {X}}\subset \mathbb {R}^d\). In [8], randomized algorithms for constructing a convex combination satisfying \({\mathbb {E}}_{X\sim \mu }[X] = \sum _{i=1}^{d+1}\lambda _i x_i\) (\(x_i\in {\mathcal {X}}\)), whose existence is assured by Tchakaloff’s theorem [3, 40], are considered. As a basic algorithm, the authors consider the following scheme:
-
(a.1)
Randomly choose d points \(A = \{x_1,\ldots ,x_d\}\) from \({\mathcal {X}}\).
-
(a.2)
For each \(x\in {\mathcal {X}}\subset A\), determine if \({\mathbb {E}}_{X\sim \mu }[X]\in {{\,\textrm{conv}\,}}(A\cup \{x\})\) or not, and finish the algorithm and return \(A\cup \{x\}\) if it holds.
-
(a.3)
Go back to (a.1).
Although we can execute the decision for each x in (a.2) with \(\mathcal {O}\!\left( d^2\right) \) computational cost with an \(\mathcal {O}\!\left( d^3\right) \) preprocessing for a fixed A, the overall expected computational cost until the end of the algorithm is at least \(\varOmega \!\left( d^2/p_{d+1,X}\right) \) under some natural assumption on \(\mu \) (see Proposition 9).
However, we can also consdier the following naive procedure:
-
(b.1)
Randomly choose 2d points \(B = \{x_1,\ldots ,x_{2d}\}\) from \({\mathcal {X}}\).
-
(b.2)
Return B if \({\mathbb {E}}_{X\sim \mu }[X]\in {{\,\textrm{conv}\,}}B\), and go back to (b.1) if not.
By using an LP solver with the simplex method we can execute (b.2) in (empirically) \(\mathcal {O}\!\left( d^3\right) \) time [33, 38]. Hence the overall computational cost can be heuristically bounded above by \(\mathcal {O}\!\left( d^3/p_{2d,X}\right) \), which is faster than the former by \(\varOmega \!\left( d^{-3/2}2^d \right) \) from the evaluation in (15). Note also that we have rigorously polynomial bounds via other LP methods (e.g., an infeasible-interior-point method [30]), and so the latter scheme is preferable even in worst-case when the dimension d becomes large.
Relation between two depths We can also deduce an inequality between two depth concepts in statistics. As is mentioned in Introduction, for a random vector \(X\in \mathbb {R}^d\), \(p_{d+1, X}\) is called the simplicial depth whereas \(\alpha _X\) is the Tukey depth of the origin with respect to X.
Naively, we have \(\alpha _X \ge \frac{p_{n, X}}{n}\) for each n, so \(\alpha _X \ge \frac{p_{d+1, X}}{d+1}\) holds. However, by using (15) here, we obtain a sharper estimate
In contrast, deriving a nontrivial upper bound of \(\alpha _X\) in terms of \(p_{d+1, X}\) still seems difficult.
6.2 Bounds of \(N_X\)
Secondly, we give applications of the bounds of \(N_X\) given in Sect. 4.
Random trigonometic cubature Consider a d-dimensional random vector
for a positive integer d, where \(\theta \) is a uniform random variable over \((-\pi , \pi )\). Then, from an easy computation, we have \(V:= \mathbb {E}\!\left[ XX^\top \right] = \frac{1}{2}I_d\), and so we obtain
almost surely. Therefore, from Proposition 17, we have
This example is equivalent to a random construction of the so-called Gauss–Chebyshev quadrature [28, Chapter 8]. Although we can bound as above the number of observations required in a random construction, concrete constructions with fewer points are already known.
Deriving a bound for random construction of cubature without any know deterministic construction, such as cubature on Wiener space [18, 25], which is more important, is still unsolved and left for future work.
Beyond naive cubature construction Recall the cubature construction problem described in Sect. 1.1. We consider a random variable of the form \(X = \varvec{f}(Y)\), where Y is a random variable on some topological space \(\mathcal {X}\) and \(\varvec{f}=(f_1,\ldots ,f_d)^\top : \mathcal {X}\rightarrow \mathbb {R}^d\) is a d-dimensional vector valued integrable function. Our aim is to find points \(y_1, \ldots , y_{d+1} \in \mathcal {X}\) and weights \(w_1, \ldots , w_{d+1} \ge 0\) whose total is one such that
A naive algorithm proposed by [17] was to generate independent copies \(Y_1, Y_2, \ldots \) of Y and choose \(y_j\) from these random samples. Without any knowledge of \(N_X\), the algorithm would be of the form
-
(c.1)
Take \(k = 2d\).
-
(c.2)
Randomly generate \(Y_i\) up to \(i = k\) and determine if (16) can be satisfied with \(y_j\in \{Y_i\}_{i = 1}^k\) by using an LP solver.
-
(c.3)
If we find a solution, stop the algorithm. Otherwise, go to (c.2) after replacing k by 2k.
This procedure ends at \(k\le 2N_X(\mathbb {E}\!\left[ X\right] )\) with probability more than half. We can then heuristically estimate the computational cost by \(\varTheta (C(d, N_X(\mathbb {E}\!\left[ X\right] )))\), where we denote by C(d, n) the computational complexity of a linear programming problem finding the solution of (16) from n sample points. Empirically, this is estimated as \(\varOmega (d^2n)\) or more when we use the simplex method [38].
However, our analysis on \(N_X\) via the Berry–Esseen bound tells us the possibility of an alternative (Algorithm 1).

Although the pseudocode may seem a little long, this is just uses \(\ell d\) random vectors of the form \(n^{-1}(X_1 + \cdots + X_n)\) as the possible vertices of the convex combination, which is used for deriving bounds of \(N_X\) in Sect. 4. After executing Algorithm 1, we can use any algorithm for deterministic measures (typically called recombination; [22, 26, 41]) to obtain an actual \(d+1\) points cubature rule, whose time complexity is rigorously bounded by \(\mathcal {O}\!\left( kd^3 + 2^kd^2\right) \) by using the final value of k in the above algorithm.
As we can carry out Algorithm 1 within \(\mathcal {O}\!\left( 2^k\ell d^2 + kC(d, \ell d)\right) \), the overall computational cost is \(\mathcal {O}\!\left( k C(d, \ell d) + 2^k\ell d^2\right) \). Then we heuristically have the bound \(\mathcal {O}\!\left( k\ell d^3 + 2^k\ell d^2\right) \) for a small \(\ell \). By using the number \(N = 2^k\ell d\), which is the number of randomly generated copies of Y, this cost is rewritten as
As our bound for \(N_X(\mathbb {E}\!\left[ X\right] )\) in Theorem 19 is applicable for this N because of the use of Berry–Esseen type estimate (\(\ell = 17\) is used in the proof), we can also give an estimate for this alternative algorithm. If the N is not as large as \(\varOmega (dN_X(\mathbb {E}\!\left[ X\right] ))\) for an appropriate choice of \(\ell \), we indeed have a better scheme, though the comparison itself may be a nontrivial problem in general. In any event, the fact that we can avoid solving a large LP problem is an obvious advantage.
7 Concluding remarks
In this paper, we have investigated inequalities regarding \(p_{n, X}, N_X\) and \(\alpha _X\), which is motivated from the fields of numerical analysis, data science, statistics and random matrix. We generalized the existing inequalities for \(p_{n, X}\) in Sect. 2. After pointing out that the convergence rate of \(p_{n, X}\) is determined by \(\alpha _X\) in Sect. 3 with introduction of \(\varepsilon \)-relaxation of both quantities, we proved that \(N_X\) and \(1/\alpha _X\) are of the same magnitude up to an \(\mathcal {O}\!\left( d\right) \) factor in Theorem 16. We also gave estimates of \(N_X\) based on the moments of X in Sect. 4 by using Berry–Esseen type bounds. Although arguments have been based on whether a given vector is included in the random convex polytope \({{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\), in Sect. 4, we extended our results to the analysis of deterministic convex bodies included in the random convex hull, which immediately led to a technical improvement on a result from the random matrix community. We finally discussed several implications of our results on application in Sect. 6.
Data availibility
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Ball, K.: The reverse isoperimetric problem for Gaussian measure. Discrete Comput. Geom. 10(4), 411–420 (1993)
Barvinok, A.: Thrifty approximations of convex bodies by polytopes. Int. Math. Res. Not. 2014(16), 4341–4356 (2014)
Bayer, C., Teichmann, J.: The proof of Tchakaloff’s theorem. Proc. Am. Math. Soc. 134(10), 3035–3040 (2006)
Berry, A.C.: The accuracy of the Gaussian approximation to the sum of independent variates. Trans. Am. Math. Soc. 49(1), 122–136 (1941)
Cascos, I.: Depth functions based on a number of observations of a random vector. Working paper 07–07, Statistics and Econometrics Series, Universidad Carlos III de Madrid (2007). https://hdl.handle.net/10016/700
Combettes, C.W., Pokutta, S.: Revisiting the approximate Carathéodory problem via the Frank–Wolfe algorithm. Math. Program. (2021). https://doi.org/10.1007/s10107-021-01735-x
Conway, J.B.: A Course in Functional Analysis. Springer, Berlin (2007)
Cosentino, F., Oberhauser, H., Abate, A.: A randomized algorithm to reduce the support of discrete measures. In: Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H. (eds.) Advances in Neural Information Processing Systems, vol. 33, pp. 15100–15110, Curran Associates, Inc (2020)
Cuesta-Albertos, J.A., Nieto-Reyes, A.: The random Tukey depth. Comput. Stat. Data Anal. 52(11), 4979–4988 (2008)
Dafnis, N., Giannopoulos, A., Tsolomitis, A.: Asymptotic shape of a random polytope in a convex body. J. Funct. Anal. 257(9), 2820–2839 (2009)
Donoho, D.L., Gasko, M.: Breakdown properties of location estimates based on halfspace depth and projected outlyingness. Ann. Stat. 20(4), 1803–1827 (1992)
Esseen, C.G.: On the Liapunoff limit of error in the theory of probability. Arkiv for Matematik, Astronomi och Fysik, A 1–19 (1942)
Giannopoulos, A., Hartzoulaki, M.: Random spaces generated by vertices of the cube. Discrete Comput. Geom. 28(2), 255–273 (2002)
Gluskin, E.D.: Extremal properties of orthogonal parallelepipeds and their applications to the geometry of Banach spaces. Math. USSR-Sbornik 64(1), 85–96 (1989)
Guédon, O., Krahmer, F., Kümmerle, C., Mendelson, S., Rauhut, H.: On the geometry of polytopes generated by heavy-tailed random vectors. Commun. Contemp. Math. 24(03), 2150056 (2022)
Guédon, O., Litvak, A.E., Tatarko, K.: Random polytopes obtained by matrices with heavy-tailed entries. Commun. Contemp. Math. 22(04), 1950027 (2020)
Hayakawa, S.: Monte Carlo cubature construction. Jpn. J. Ind. Appl. Math. 38, 561–577 (2021)
Hayakawa, S., Tanaka, K.: Monte Carlo construction of cubature on Wiener space. Jpn. J. Ind. Appl. Math. 39(2), 543–571 (2022)
Hug, D.: Random polytopes. In: Spodarev, E. (ed.) Stochastic Geometry, Spatial Statistics and Random Fields, pp. 205–238. Springer, Berlin (2013)
Kabluchko, Z., Zaporozhets, D.: Absorption probabilities for Gaussian polytopes and regular spherical simplices. Adv. Appl. Probab. 52(2), 588–616 (2020)
Korolev, V., Shevtsova, I.: An improvement of the Berry-Esseen inequality with applications to Poisson and mixed Poisson random sums. Scand. Actuar. J. 2012(2), 81–105 (2012)
Litterer, C., Lyons, T.: High order recombination and an application to cubature on Wiener space. Ann. Appl. Probab. 22(4), 1301–1327 (2012)
Litvak, A., Pajor, A., Rudelson, M., Tomczak-Jaegermann, N.: Smallest singular value of random matrices and geometry of random polytopes. Adv. Math. 195(2), 491–523 (2005)
Liu, R.Y.: On a notion of data depth based on random simplices. Ann. Stat. 18(1), 405–414 (1990)
Lyons, T., Victoir, N.: Cubature on Wiener space. Proc. R. Soc. Lond. Ser. A 460, 169–198 (2004)
Maalouf, A., Jubran, I., Feldman, D.: Fast and accurate least-mean-squares solvers. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché Buc, F., Fox, E., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 32. Curran Associates Inc., Red Hook (2019)
Majumdar, S.N., Comtet, A., Randon-Furling, J.: Random convex hulls and extreme value statistics. J. Stat. Phys. 138(6), 955–1009 (2010)
Mason, J.C., Handscomb, D.C.: Chebyshev Polynomials. CRC Press, Boca Raton (2002)
Mirrokni, V., Leme, R.P., Vladu, A., Wong, S.C.W.: Tight bounds for approximate Carathéodory and beyond. In: International Conference on Machine Learning, pp. 2440–2448. PMLR (2017)
Mizuno, S.: Polynomiality of infeasible-interior-point algorithms for linear programming. Math. Program. 67(1–3), 109–119 (1994)
Mosler, K.: Depth statistics. In: Becker, C., Fried, R., Kuhnt, S. (eds.) Robustness and Complex Data Structures, pp. 17–34. Springer, Berlin (2013)
Nagy, S., Schütt, C., Werner, E.M.: Halfspace depth and floating body. Stat. Surv. 13(1), 52–118 (2019)
Pan, V.: On the complexity of a pivot step of the revised simplex algorithm. Comput. Math. Appl. 11(11), 1127–1140 (1985)
Pisier, G. (ed.): The Volume of Convex Bodies and Banach Space Geometry, vol. 94. Cambridge University Press, Cambridge (1999)
Raič, M.: A multivariate Berry–Esseen theorem with explicit constants. Bernoulli 25(4A), 2824–2853 (2019)
Rousseeuw, P.J., Ruts, I.: The depth function of a population distribution. Metrika 49(3), 213–244 (1999)
Schütt, C., Werner, E.: The convex floating body. Math. Scand. 66(2), 275–290 (1990)
Shamir, R.: The efficiency of the simplex method: a survey. Manag. Sci. 33(3), 301–334 (1987)
Stroud, A.H.: Approximate Calculation of Multiple Integrals. Prentice-Hall, Hoboken (1971)
Tchakaloff, V.: Formules de cubature mécanique à coefficients non négatifs. Bulletin des Sciences Mathématiques 81, 123–134 (1957)
Tchernychova, M.: Carathéodory cubature measures. Ph.D. thesis, University of Oxford (2015)
Tukey, J.W.: Mathematics and the picturing of data. In: Proceedings of the International Congress of Mathematicians, Vancouver, 1975, vol. 2, pp. 523–531 (1975)
Vershynin, R.: High-Dimensional Probability: An Introduction with Applications in Data Science, vol. 47. Cambridge University Press, Cambridge (2018)
Wagner, U., Welzl, E.: A continuous analogue of the upper bound theorem. Discrete Comput. Geom. 26(2), 205–219 (2001)
Wendel, J.G.: A problem in geometric probability. Math. Scand. 11(1), 109–111 (1963)
Zhai, A.: A high-dimensional CLT in \(\cal{W} _2\) distance with near optimal convergence rate. Probab. Theory Relat. Fields 170(3–4), 821–845 (2018)
Zuo, Y.: A new approach for the computation of halfspace depth in high dimensions. Commun. Stat. Simul. Comput. 48(3), 900–921 (2019)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is supported by the DataSıg Program [EP/S026347/1], the Alan Turing Institute [EP/N510129/1], and the Hong Kong Innovation and Technology Commission (InnoHK Project CIMDA).
Appendices
A Bounds of \(N_X\) via Multivariate Berry–Esseen theorem
In this section, we provide two different estimates of \(N_X\). Although we can prove that the first bound (Sect. A.2) is strictly stronger than the second one (Sect. A.3), we also give the proof of the second as there seems to be more room for improvement in the second approach than in the first.
The following first bound is the one mentioned in (11). The proof is given in Sect. A.2.
Theorem 26
Let X be an \(\mathbb {R}^d\)-valued random vector which is centered and of nonsingular covariance matrix V. Then,
holds.
Note that
holds so we can ignore the \({\mathcal {O}}(d)\) term. In the case \(\sup \left\| V^{-1/2}X\right\| _2<\infty \), we have
Therefore, the following proposition, which only states \(N_X=\tilde{{\mathcal {O}}}\!\Bigg (d^{15/2}\sup \left\| V^{-1/2}X\right\| _2^2\Bigg )\), is weaker than Theorem 26. However, the approach of proofs is different and there seems to remain some room for improvement in the proof of Proposition 27, so we give the proof in Sect. 1.
Proposition 27
Let X be an \(\mathbb {R}^d\)-valued random vector which is centered, bounded and of nonsingular covariance matrix V. Then, for all n satisfying
\(N_X\le 6dn\) holds.
1.1 A.1 Multivariate Berry–Esseen bounds
Before proceeding to the evaluation of \(N_X\), we briefly review multivariate Berry–Esseen type theorems. The following theorem should be the best known bound with explicit constants and dependence with respect to the dimension.
Theorem 28
[35] Let \(Y_1,\ldots ,Y_n\) be i.i.d. D-dimensional independent random vectors with mean zero and covariance \(I_D\). For any convex measurable set \(A\subset \mathbb {R}^D\), it holds
where Z is a D-dimensional standard Gaussian.
Note that the original statement is not limited to the i.i.d. case. However, similarly to the other existing Berry–Esseen type bounds, Theorem 28 only gives information about convex measurable sets. Thus we cannot use this result directly. However, Sect. A.2 gives a creative use of Theorem 28.
Unlike the usual Berry–Esseen results, the next theorem can be used for nonconvex case with reasonable dependence on dimension. We denote by \({\mathcal {W}}_2(\mu , \nu )\) the Wasserstein-2 distribution between two probability measures \(\mu \) and \(\nu \) on the same domain. This is defined formally as
where the infimum is taken for all the joint distribution (Y, Z) with the marginal satisfying \(Y\sim \mu \) and \(Z\sim \nu \). Although it is an abuse of notation, we also write \({\mathcal {W}}_2(Y, Z)\) to represent \({\mathcal {W}}_2(\mu , \nu )\) when \(Y\sim \mu \) and \(Z\sim \nu \) for some random variables Y and Z.
Theorem 29
[46] Let \(Y_1,\ldots ,Y_n\) be D-dimensional independent random vectors with mean zero, covariance \(\varSigma \), and \(\Vert Y_i\Vert _2\le B\) almost surely for each i. If we let Z be a Gaussian with covariance \(\varSigma \), then we have
For a set \(A\subset \mathbb {R}^D\) and an \(\varepsilon >0\), define
By combining the following assertion with Theorem 29, we derive another bound of \(N_X\) in Sect. 1.
Proposition 30
Let Y, Z be D-dimensional random vectors. Then, for any measurable set \(A\subset \mathbb {R}^d\) and any \(\varepsilon >0\), the following estimates hold:
Proof
This proof is essentially the same as the argument given in the proof of [46, Proposition 1.4]. Let \((Y', Z')\) be an arbitrary couple of random variables such that \(Y'\sim Y\) and \(Z'\sim Z\). Then, we have

By taking the infimum of the right-hand side with respect to all the possible couples \((Y', Z')\), we obtain the former result. The latter can also be derived by evaluating
and again taking the infimum. \(\square \)
1.2 A.2 The first bound
In this section, we prove Theorem 26. We shall set \(D=d\) and make use of Theorem 28.
First, fix a set \(S\subset \mathbb {R}^d\) and consider the set \(C(S):=\{x\in \mathbb {R}^d\mid 0\in {{\,\textrm{conv}\,}}(S\cup \{x\})\}\). We can prove this set is convex for any S. Indeed, if \(0\in {{\,\textrm{conv}\,}}S\), then clearly \(C(S)=\mathbb {R}^d\). Otherwise, \(x\in C(S)\) is equivalent to the existence of some \(k\ge 0\) and \(x_1, \ldots , x_k\in S\), \(\lambda >0\), \(\lambda _1,\ldots , \lambda _k\ge 0\) such that
Here, \(\lambda >0\) comes from the assumption \(0\not \in {{\,\textrm{conv}\,}}S\). This occurs if and only if x is contained in the negative cone of S, i.e., \(C(S)=\{\sum _{i=1}^k\tilde{\lambda }_ix_i\mid k\ge 0,\ \tilde{\lambda }_i\le 0,\ x_i\in S\}\). In both cases C(S) is convex, so \(S_0\) is always convex (and of course measurable).
Let X be an \(\mathbb {R}^d\)-valued random vector with mean 0 and nonsingular covariance V. Suppose \(\mathbb {E}\!\left[ \left\| V^{-1/2}X\right\| _2^3\right] <\infty \). Let \(X_1,X_2,\ldots \) be independent copies of X, and for a fixed positive integer n, define
for \(i=1,\ldots ,2d\). We also let \(Z_1,\ldots , Z_{2d}\) be independent d-dimensional standard Gaussian which is also independent from \(X_1,X_2,\ldots \). Then, by using Theorem 28 and the above-mentioned convexity of C(S), we have
By repeating similar evaluations, we obtain
Therefore, by letting
we have \(\mathbb {P}\!\left( 0\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_{2dn}\}\right) \ge 1/6\). Since \((1-1/6)^4<1/2\) holds, we finally obtain \(N_X\le 8dn\).
1.3 A.3 The second bound
In this section, we provide a proof of Sect. 27 in a different manner from the one given in the previous section. We set \(D=2d^2\) and define \(A_d\subset \mathbb {R}^D\) as follows:
Then, it suffices to find a suitable upper bound of \(\mathbb {P}\!\left( Z\in A_d{\setminus } A_d^{-\varepsilon }\right) \) for a D-dimensional standard Gaussian Z for our purpose. For an \(\varepsilon >0\), \(B_{d,\varepsilon }:=A_d{\setminus } A_d^{-\varepsilon }\) can be explicitly written as
For a (finite) set \(S=\{v_1,\ldots , v_j\}\subset \mathbb {R}^d\), define the negative box \(N(S)\subset \mathbb {R}^d\) by
N(S) is obviously a convex set.
Lemma 31
For an arbitrary \(x=(x_1,\ldots ,x_{2d})\in B_{d,\varepsilon }\), there exists an index \(k\in \{1,\ldots ,2d\}\) such that \(x_k\in N(\{x_i\mid i\ne k\}){\setminus } N(\{x_i\mid i\ne k\})^{-\varepsilon \sqrt{2d}}\).
Proof
As \(0\in {{\,\textrm{conv}\,}}\{x_i\}_{i=1}^{2d}\), there exist nonnegative weights \(\lambda _1,\ldots ,\lambda _{2d}\) such that \(\lambda _1x_1+\cdots +\lambda _{2d}x_{2d}=0\) with the total weight one. Let k be an index such that \(w_k\) is the maximum weight. Then, \(\lambda _k\) is clearly positive and we have \(x_k=\sum _{i\ne k} -\frac{\lambda _i}{\lambda _k}x_i\). Therefore, we obtain \(x_k\in N(\{x_i\mid i\ne k\})\).
By (17), there exists an \(\tilde{x}=(\tilde{x}_i)_{i=1}^{2d}\in \mathbb {R}^D\) such that \(\sum _{i=1}^{2d}\Vert x_i-\tilde{x}_i\Vert _2^2<\varepsilon ^2\) and \(0\not \in {{\,\textrm{conv}\,}}\{\tilde{x}_i\}_{i=1}^{2d}\). We can prove that \(\tilde{x}_k\not \in N(\{\tilde{x}_i\mid i\ne k\})\). Indeed, if we can write \(\tilde{x}_k= - \sum _{i\ne k} a_i\tilde{x}_i\) with \(a_i\in [0, 1]\), then
is a convex combination and it contradicts the assumption \(0\not \in {{\,\textrm{conv}\,}}\{\tilde{x}_i\}_{i=1}^{2d}\). Therefore, we can take a unit vector \(c\in \mathbb {R}^d\) such that
Let us assume the closed ball with center \(x_k\) and radius \(\delta \) is included in \(N(\{x_i\mid i\ne k\})\) for a \(\delta >0\). Then, if \(\delta > \Vert x_k-\tilde{x}_k\Vert _2\), the closed ball with center \(\tilde{x}_k\) and radius \(\delta ^\prime :=\delta -\Vert x_k-\tilde{x}_k\Vert _2\) is included in \(N(\{x_i\mid i\ne k\})\). In particular, we have some coefficients \(a_i\in [-1,0]\) such that \(\tilde{x}_k + \delta ^\prime c = \sum _{i\ne k} a_ix_i\). By the inequality (18), we have
so by arranging
Therefore, from the definition of \(\delta ^\prime \), we obtain
by Cauchy-Schwarz and the assumption. It immediately implies the desired assertion. \(\square \)
Proposition 32
\(\mathbb {P}\!\left( Z\in B_{d,\varepsilon }\right) \le 8\sqrt{2}d^{7/4}\varepsilon \) holds.
Proof
By Lemma 31, we have \(B_{d,\varepsilon }\subset \bigcup _{k=1}^{2d}\{x\mid x_k\in N(\{x_i\mid i\ne k\}) {\setminus } N(\{x_i\mid i\ne k\})^{-\varepsilon \sqrt{2d}}\}\). Therefore, letting \(Z=(Z_1,\ldots ,Z_{2d})\) be a standard Gaussian in \(\mathbb {R}^D\) (where each \(Z_i\) is a independent standard Gaussian in \(\mathbb {R}^d\)), we can evaluate
For each k, \(Z_k\) is independent from the random convex set \(N(\{Z_i\mid i\ne k\})\). Therefore, we can use the result of [1] to deduce \(\mathbb {P}\!\left( Z_k\in N(\{Z_i\mid i\ne k\}){\setminus } N(\{Z_i\mid i\ne k\})^{-\varepsilon \sqrt{2d}}\}\right) \le 4d^{1/4}\cdot \varepsilon \sqrt{2d}\). Therefore, we finally obtain
\(\square \)
By letting \(\varepsilon =2^{-13/2}d^{-7/4}\), we have \(\mathbb {P}\!\left( Z\in B_{d, \varepsilon }\right) \le 1/8\). Under this value of \(\varepsilon \), if we let n satisfy
for a constant B, then we have
Now consider a bounded and centered \(\mathbb {R}^d\)-valued random vector X with \(V=\mathbb {E}\!\left[ XX^\top \right] \) nonsingular. Then \(B':=\sup \left\| V^{-1/2}X\right\| _2\) is finite. Let \(X_1, X_2, \ldots \) be independent copies of X. Define \(\mathbb {R}^D\)-valued random vectors \(Y_1, Y_2, \ldots \) by \(Y_i:=(V^{-1/2}X_{(2i-1)d+1}, \ldots , V^{-1/2}X_{2id})^\top \) for each i. Then, note that \(\Vert Y_i\Vert _2\le \sqrt{2d}B'\). By taking \(B=\sqrt{2d}B'\) in (19), we have from Theorem 29 that (for \(\varepsilon =2^{-13/2}d^{-7/4}\))
From Proposition 30, we obtain
Therefore, 0 is contained in the convex hull of \(\{X_1,\ldots , X_{2dn}\}\) with probability at least 1/4. Since \((1-1/4)^3<1/2\), \(N_X\le 6dn\) holds. Therefore, our proof of Proposition 27 is complete.
B Extreme examples
Before treating concrete examples, we prove a proposition which is useful for evaluating \(N_X\).
Lemma 33
For a random vector X and its independent copies \(X_1,X_2,\ldots \), define \(\tilde{N}_X\) as the minimum index n satisfying \(0\in {{\,\textrm{conv}\,}}\{X_1, \ldots , X_n\}\). Then, we have
Proof
From the definition of \(N_X\), \(\mathbb {P}\!\left( 0\in \{X_1, \ldots , X_{N_X-1}\}\right) <1/2\) holds. Thus \(\mathbb {P}\!\left( \tilde{N}_X\ge N_X\right) \ge 1/2\), and so we obtain \(\mathbb {E}\!\left[ \tilde{N}_X\right] \ge \frac{1}{2}N_X\).
For the other inequality, we use the evaluation \(\mathbb {P}\!\left( \tilde{N}_X \ge kN_X\right) \le 2^{-k}\) for each nonnegative integer k. As \(\tilde{N}_X\) is a nonnegative discrete random variable, we have
\(\square \)
Note that all the examples given below satisfy \(p_{d, X} = 0\). They are given as one of the worst-case examples for uniform estimates of \(N_X\) in Proposition 5 or Theorem 26. Let us start with the simplest extreme case.
Example 34
Let \(d=1\). For an \(\varepsilon \in (0, 1)\), let X be a random variable such that \(\mathbb {P}\!\left( X=1/\varepsilon \right) = \varepsilon \) and \(\mathbb {P}\!\left( X=-1/(1-\varepsilon )\right) = 1-\varepsilon \). Then \(\mathbb {E}\!\left[ X\right] =0\).
In this example, we can explicitly calculate \(p_{n, X}\) as
In particular, \(p_{2, X} = 2\varepsilon - 2\varepsilon ^2\). We have \(\lim _{\varepsilon \searrow 0}(1-\varepsilon )^{1/2\varepsilon }=e^{-1/2}=0.60\ldots \), so \(p_{\lceil 1/2\varepsilon \rceil , X} < 1/2\) holds for a sufficiently small \(\varepsilon \). For such an \(\varepsilon \), we have
and so \(N_X\le \frac{2}{p_{2, X}}\) in Proposition 5 is sharp up to constant.
For \(\varepsilon \in (0, 1/2)\), \(N_X\) can also be evaluated above as \(N_X \le 2\mathbb {E}\!\left[ \tilde{N}_X\right] \le 2\left( \frac{1}{\varepsilon }+ \frac{1}{(1-\varepsilon )}\right) \) by using Proposition 33. We also have \(\alpha _X = \varepsilon \) for \(\varepsilon \in (0, 1/2)\), so
As the variance is \(V=\mathbb {E}\!\left[ X^2\right] =\frac{1}{\varepsilon }+ \frac{1}{1-\varepsilon } = \frac{1}{\varepsilon (1-\varepsilon )}\), we have
Therefore, from (20), we obtain
which is what is mentioned in Remark 6 when \(d=1\).
The next example is a multi-dimensional version of the previous one.
Example 35
Let \(d\ge 2\). Let \(\{e_1,\ldots ,e_d\}\subset \mathbb {R}^d\) be the standard basis of \(\mathbb {R}^d\). Let us first consider, for an arbitrary \(\varepsilon \in (0, 1)\), a random vector X given by
where \(\mathbb {P}\!\left( Y=1\right) =1-\varepsilon \), \(\mathbb {P}\!\left( Y=0\right) =\varepsilon \) and \(Z^1,\ldots ,Z^{d-1}\) are independent uniform random variables over \([-1, 1]\). (also independent from Y). Namely, X is \(\varepsilon ^{-1} e_d\) with probability \(\varepsilon \) and a \((d-1)\)-dimensional uniform vector over a box on the hyperplane \(\{x\in \mathbb {R}^d\mid e_d^\top x = - (1-\varepsilon )^{-1}\}\) otherwise. \(\mathbb {E}\!\left[ X\right] =0\) also holds.
Let us estimate \(p_{d+1,X}, p_{2d, X}\) and \(N_X\) for this X. To contain the origin in the convex hull, we have to observe at least one \(X_i\) with \(Y=0\). Therefore, for an \(\varepsilon \ll 1/d\), we have
where \(X'\) represents a \((d-1)\)-dimensional uniform random vector over the box \([-1, 1]^{d-1}\). We can see that \(p_{2d, X}\gtrsim 2^{d-1}p_{d+1, X}\) holds for a small \(\varepsilon \) as Remark 2 suggests.
For the calculation of \(N_X\), we can exploit Proposition 33. We first bound the expectation of \(\tilde{N}_X\). For independent copies \(X_1, X_2, \ldots \) of X, let \(N_1\) be the minimum integer n satisfying \(X_n = \varepsilon ^{-1}e_d\). We also define \(N_2\) as the minimum integer n satisfying \(-(1-\varepsilon )^{-1}e_d\in {{\,\textrm{conv}\,}}\{X_1,\ldots ,X_n\}\). Then, \(\tilde{N}_X = \max \{N_1, N_2\}\) holds. Thus we have \(N_1 \le \tilde{N}_X \le N_1 + N_2\). \(\mathbb {E}\!\left[ N_1\right] =1/\varepsilon \) clearly holds. For \(N_2\), we can evaluate (again using \(X'\)) as
where we have used Proposition 33 for the inequality. Therefore, from Proposition 33, we obtain
We finally compare the naive general estimate \(N_X\le \frac{n}{p_{n, X}}\) in Proposition 5 with this example. From (21), we have
Therefore, the evaluation \(N_X\le \frac{2d}{p_{2d, X}}\) is sharp even for small \(p_{2d, X}\) up to constant in the sense that
holds.
Also in this example, we have \(\alpha _X = \varepsilon \) for \(\varepsilon \in (0, 1/3)\). Hence, combined with (21), we have
Therefore, we have \(\inf _{X:d\text {-dim}}\alpha _XN_X\le 2\).
We next evaluate the value of \(\mathbb {E}\!\left[ \left\| V^{-1/2}X\right\| _2^3\right] \), where \(V=(V^{ij})\) is the covariance matrix of X with respect to the basis \(\{e_1,\ldots ,e_d\}\). Then, for \((i,j)\in \{1,\ldots ,d-1\}^2\), we obtain

by using the independence of Y, \(Z_1,\ldots , Z_{d-1}\). For the \(V^{dd}\), we have
Therefore, \(V^{-1/2}X\) can be explicitly written as
Thus we have
and so
holds when \(0<\varepsilon <1/2\). By using (21), we obtain
Therefore, by taking \(\varepsilon \rightarrow 0\), we finally obtain the estimate
as mentioned in Remark 6.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hayakawa, S., Lyons, T. & Oberhauser, H. Estimating the probability that a given vector is in the convex hull of a random sample. Probab. Theory Relat. Fields 185, 705–746 (2023). https://doi.org/10.1007/s00440-022-01186-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-022-01186-1




 holds for all
holds for all 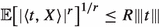 holds for all
holds for all