Abstract
We consider point-to-point last-passage times to every vertex in a neighbourhood of size \(\delta N^{\nicefrac {2}{3}}\) at distance N from the starting point. The increments of the last-passage times in this neighbourhood are shown to be jointly equal to their stationary versions with high probability that depends only on \(\delta \). Through this result we show that (1) the \(\text {Airy}_2\) process is locally close to a Brownian motion in total variation; (2) the tree of point-to-point geodesics from every vertex in a box of side length \(\delta N^{\nicefrac {2}{3}}\) going to a point at distance N agrees inside the box with the tree of semi-infinite geodesics going in the same direction; (3) two point-to-point geodesics started at distance \(N^{\nicefrac {2}{3}}\) from each other, to a point at distance N, will not coalesce close to either endpoint on the scale N. Our main results rely on probabilistic methods only.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Planar last-passage percolation (LPP) belongs to the KPZ universality class where models of random surface growth exhibit height and transversal fluctuation exponents of order \(\nicefrac {1}{3}\) and \(\nicefrac {2}{3}\), respectively. The different models in the KPZ universality class are believed to have the same limiting behaviour under this scaling. The LPP with exponential weights belongs to the set of models in the KPZ universality class that are exactly solvable, or integrable. For models in this group, one can obtain closed form expressions for their prelimiting statistics. Coupling this with techniques from combinatorics, representation theory and random matrix theory, one can take the limits of the prelimiting expressions to obtain the statistics of the limiting object. By the KPZ universality conjecture, these statistics should be valid for all models in the KPZ universality class.
One of the interesting questions about the model involves its prelimiting local fluctuations. To make this more concrete, let \(G_x\) be the last-passage time between the points (0, 0) and x. Define
If \(|x|,|y|=O(1)\), then \(L^N\) is close to a stationary cocycle called the Busemann function [17]. In fact, these stationary cocycles are defined as, roughly speaking, the limits when N is taken to infinity in (1.1). Busemann functions extend the stationary LPP process to the whole lattice \(\mathbb {Z}^2\) and play a major role in the study of infinite geodesics.
The main contribution of this paper is the total variation convergence of \(L^N\) to the Busemann function when \(|x|,|y|\le \delta N^\frac{2}{3}\), first \(N\rightarrow \infty \) and then \(\delta \rightarrow 0\). Moreover, the results are quantitative; we show that the decay of the error is polynomial in \(\delta \). We stress that this cannot be obtained simply from the “crossing lemma” (Lemma B.2) which says that difference of geodesics along an edge is monotone in the starting point of the geodesics. Indeed, to compare the LPP increments to those of the stationary LPP one must tweak the intensity of the stationary LPP by order of \(N^{-\frac{1}{3}}\) so that the error of the approximation along each edge is of the order of \(N^{-\frac{1}{3}}\) as well. Therefore a simple union bound over \(N^\frac{2}{3}\) edges gives \(N^\frac{2}{3}N^{-\frac{1}{3}}=N^\frac{1}{3}\) and will not work. In a recent work, Fan and Seppäläinen [12] obtained a coupling of different Busemann functions using queueing mappings. We use new insights about this coupling to obtain a result we call local stationarity. Our other results are applications of local stationarity to questions about the \(\text {Airy}_2\) process and geodesics.
LPP can be viewed as a \(1+1\) dimensional growing surface, and also as a Markov process that takes values in the space of continuous functions. Using the 1:2:3 KPZ scaling, the conjectural limit of this Markov process is believed to be the KPZ-fixed point [26]. An extension of this limiting object was shown to exist recently in [9]. In [23] Johansson showed the convergence of the spatial fluctuations to the \(\text {Airy}_2\) process minus a parabola and that the limit is continuous. As was mentioned previously, the fact that LPP has stationary counterparts whose spatial fluctuations are that of a simple random walk suggests that locally, the \(\text {Airy}_2\) process should have a Brownian behaviour around a fixed point.
Known results on the Brownian behaviour of the \(\text {Airy}_2\) process fall roughly into two types:
-
1.
on a small interval \([0,\epsilon ]\) the \(\text {Airy}_2\) process should be close to the Brownian motion in some sense;
-
2.
on the interval [0, 1] the law of the \(\text {Airy}_2\) process can be related to that of the Brownian motion.
Under point (1), Pimentel [29] showed, in the LPP setup, that locally the \(\text {Airy}_2\) process converges weakly to a Brownian motion in the Skorohod topology. The proof relied on the comparison lemma, also called the crossing lemma (Lemma B.2). The idea is that the spatial increments of the last-passage time can be compared with high probability to stationary increments with a small drift. In [26, Theorem 4.14], Matetski, Quastel and Remenik showed that the \(\text {Airy}_2\) process has Brownian regularity and its finite-dimensional distributions converges to those of two-sided Brownian motion. In [30] (that contains results under both points (1) and (2)) Pimentel extended the results in [29], though the convergence is still in the weak sense.
Under point (2), Corwin and Hammond [7] showed that the Airy line ensemble (the top line of which is the \(\text {Airy}_2\) process) minus a parabola, conditioned on its values at the boundaries, has the distribution of Brownian bridges conditioned not to meet. Building on these ideas, Calvert, Hammond and Hedge obtained through the Brownian LPP [6, 18], among other things, control on the moment of the Radon-Nikodym derivative of the law of the Airy line ensemble with respect to the Brownian bridge and a modulus of continuity of the \(\text {Airy}_2\) process. In LPP on the lattice, control on the modulus of continuity of the prelimiting spatial fluctuations was obtained in [1] by Basu and Ganguly. In [10] Dauvergne and Virág, using better insight on the sampled Airy line ensemble, managed to show that the Airy line ensemble can be approximated, in total variation, by Brownian bridges, conditioned on not intersecting, without the conditioning on the lower boundary that appears in the Brownian Gibbs property.
Our work compares the \(\text {Airy}_2\) process with Brownian motion on a small interval. Our result on the Brownian regularity of \(\text {Airy}_2\) process belongs to point (1). In Theorem 2.2 we show that the \(\text {Airy}_2\) process is close in total variation to a rate 2 Brownian motion. This improves similar results under point (1). Our Corollary 2.3 shows that the regularity of the \(\text {Airy}_2\) process cannot be better than that of Brownian motion. This corollary can also be deduced from [6, Theorem 1.1].
Next we apply local stationarity to study two aspects of the behaviour of geodesics, their behaviour close to the endpoints which we refer to as stabilization, and the coalescence of point-to-point geodesics started from two points whose distance scales with N. Let us start with the latter.
The first suite of methods for studying geodesics of growth models came from Newman and co-authors in planar first-passage percolation (FPP) [20, 21, 25, 28]. FPP is another random growth model believed to be in the KPZ universality class. These methods were then used by Ferrari and Pimentel [14] and Coupier [8] to show that in exponential LPP, for a fixed direction, from any point on the lattice there exists a.s. a unique infinite geodesic and all these geodesics coalesce.
The first quantitive coalescence result in LPP came from Pimentel [29], who showed that two semi-infinite geodesics with the same direction, coming out of two points distance k apart, coalesce after about \(k^{\nicefrac {3}{2}}\) steps. The tail of the decay was conjectured to be of exponent \(-\nicefrac {2}{3}\). The proof used the distributional equality of the geodesic tree and its dual tree, and drew on existing bounds on the exit point of a geodesic in stationary LPP, derived with probabilistic proofs. The question of showing that the geodesics will not coalesce too far compared to k i.e. a matching upper bound, was left open. This question was then taken up by Basu, Sarkar and Sly [3] who proved the \(-\nicefrac {2}{3}\) exponent for the lower bound and a matching upper bound. In that paper, the authors also proved a polynomial upper bound for point-to-point coalescence. In [33] Seppäläinen and Shen studied coalescence of semi-infinite geodesics. Without relying on integrable probability methods, they reproved the results of [3] up to a logarithmic error and obtained new upper and lower bounds of matching order on abnormally fast coalescence. In [36] Zhang proved the optimal bounds of \(-\nicefrac {2}{3}\) for coalescence of two point-to-point geodesics from two points at distance k. The proof relies on diffusive concentration of geodesic fluctuations coming from integrable probability.
The first coalescence question we consider is the following: if \(\pi ^1\) and \(\pi ^2\) are the geodesics from (0, 0) and \((0,N^\frac{2}{3})\), respectively, that terminate at (N, N), what is the typical distance of the coalescence point from the three endpoints? Results of that flavour were proved in [19] and [2] for Brownian LPP, and in [13] for Poissonian LPP. We show in Theorem 2.8 and Theorem 2.9 that the coalescence point will not be too close, on the macroscopic scale N, to any of the end points. We emphasize that the methods used in [29] and [33] cannot be used here, as they rely on a well understood duality principle for stationary LPP geodesics [32].
We turn to stabilization. Let \(\pi \) be the geodesic from (0, 0) to (N, N). Since the work of Johansson in [22] it is known that the fluctuations of \(\pi \) around the diagonal at any macroscopic point should be of order \(N^{\nicefrac {2}{3}}\). If \(1 \le l \ll N\), as the geodesic is expected to have a self-similarity property, one would expect the fluctuation of \(\pi \) in a square of size \(l^2\) around the origin to be of order \(l^{\nicefrac {2}{3}}\). A proof of this was given in [3, Theorem 3] with diffusive concentration bounds. In [18] Hammond considered the regularity of the spatial fluctuation around the point (l, l) for the Brownian LPP while for the lattice LPP with exponential weights this was proved in [1, Theorem 3] by Basu and Ganguly.
The behaviour of semi-infinite geodesics is somewhat better understood because they can be defined locally in terms of the Busemann functions, through the minimum gradient principle [16, 17, 32]. This implies that a link between point-to-point geodesics and infinite ones should provide better insight on the former. Consider a small square of side length M around the origin. Denote by \(\mathcal {T}^{pp}\) the tree consisting of all the geodesics from points in the \(M\times M\) square to the point (N, N). Let \(\mathcal {T}^{\infty }\) be the tree of semi-infinite geodesics in direction \(45^\circ \) started from the \(M\times M\) square. Our stabilization result, Theorem 2.4, shows that on a square of side \(M=\delta N^\frac{2}{3}\), the trees \(\mathcal {T}^{pp}\) and \(\mathcal {T}^{\infty }\) agree outside an event whose probability decays as a power of \(\delta \).
We use this to show in (2.5), for example, that the fluctuations of the point-to-point geodesic in a small box of side l around the origin are, with high probability, the same as those of a stationary geodesic for which the fluctuations are known to be of the order \(l^\frac{2}{3}\).
Finally, we use stabilization to study coalescence of point-to-point geodesics to (N, N) from two fixed starting points. For fixed \(k>0\) let \(\pi ^1\) and \(\pi ^2\) be the geodesics to (N, N) started from (0, 0) and \((0,k^\frac{2}{3})\), respectively. Let \(p_c\) be the coalescence point of \(\pi ^1\) and \(\pi ^2\). Let \(p^{\infty }_c\) be the coalescence point of the two semi-infinite geodesics in direction (1, 1) started at the points (0, 0) and \((0,k^\frac{2}{3})\). Theorem 2.6 shows that \(p_c\) converges weakly to \(p^{\infty }_c\). In this theorem we also show how our stabilization result gives an alternative route from the bounds on \(p^{\infty }_c\) given in [3] to the tail decay of \(\vert p_c\vert \) earlier derived in [36].
Evidence to the strength of the methods developed in this work can be seen in a recent work of one of the authors and Ferrari [5]. Precisely, in [5, Theorem 2.2] they obtain a lower bound on the probability of stabilization of the point to point profile increments to that of the stationary one in a neighbourhood of o(N) in the time direction (as opposed to \(o(N^{2/3})\) in this work) around the endpoint (N, N). The main step towards such result is Theorem 2.4 in this paper. The idea is to show that geodesics terminating at (N, N), with high probability, will cross a small spatial interval of size \(o(N^{2/3})\) at time \(N-o(N)\). Our Theorem 2.4 would then imply that these geodesics must have coalesced by that time. To execute this scheme, [5] employs a chaining argument from [4], that shows that geodesics fluctuations around their characteristic along a time interval of size O(N) is of order \(O(N^{2/3})\). Moreover, [5, Theorem 2.6] gives an upper bound on the probability of stabilization in the setup of [5, Theorem 2.2]. This was done using the heavy traffic picture of the difference of Busemann functions developed in Sect. 5 and the Appendix of this work.
The correct exponent of stabilization of any geodesic leaving from a neighbourhood of (0, 0) of size \(O(N^{2/3})\) in space and O(N) in time is 1/2, as was shown in [5]. It is not hard to verify that using concentration results from [24] one could improve the exponent in Theorem 2.4 from 3/8 to 1/2. However, the authors of this paper opt for simple probabilistic arguments for concentration bounds and therefore use suboptimal polynomial concentration bounds as in Lemma 5.5. Sharper concentration bounds using simple probabilistic arguments were developed in [11] and [5, Theorem 2.8].
The main body of our arguments only uses probabilistic methods. The only integrable-probability input used is the emergence of the \(\text {Airy}_2\) process as the limit of the increments of the last-passage time.
1.1 Some general notation and terminology
\(\mathbb {Z}_{\ge 0}=\{0,1,2,3, \dotsc \}\) and \(\mathbb {Z}_{>0}=\{1,2,3,\dotsc \}\). For \(n\in \mathbb {Z}_{>0}\) we abbreviate \([n]=\{1,2,\dotsc ,n\}\). A sequence of n points is denoted by \(x_{0,n}=(x_k)_{k=0}^n=\{x_0,x_1,\dotsc ,x_n\}\), and in case it is a path of length n also by  . \(a\vee b=\max \{a,b\}\), \(a\wedge b=\min \{a,b\}\). \(x^+=x1_{x>0}\) and \(x^-=\vert x\vert 1_{x<0}\). C is a constant whose value can change from line to line.
. \(a\vee b=\max \{a,b\}\), \(a\wedge b=\min \{a,b\}\). \(x^+=x1_{x>0}\) and \(x^-=\vert x\vert 1_{x<0}\). C is a constant whose value can change from line to line.
The standard basis vectors of \(\mathbb {R}^2\) are \(e_1=(1,0)\) and \(e_2=(0,1)\). For a point \(x=(x_1,x_2)\in \mathbb {R}^2\) the \(\ell ^1\)-norm is \(\vert x\vert =\vert x_1\vert + \vert x_2\vert \) . We call the x-axis occasionally the \(e_1\)-axis, and similarly the y-axis and the \(e_2\)-axis are the same thing. Inequalities on \(\mathbb {R}^2\) are interpreted coordinatewise: for \(x=(x_1,x_2)\in \mathbb {R}^2\) and \(y=(y_1,y_2)\in \mathbb {R}^2\), \(x\le y\) means \(x_1\le y_1\) and \(x_2\le y_2\). Notation [x, y] represents both the line segment \([x,y]=\{tx+(1-t)y: 0\le t\le 1\}\) for \(x,y\in \mathbb {R}\) and the rectangle \([x,y]=\{(z_1,z_2)\in \mathbb {R}^2: x_i\le z_i\le y_i \text { for }i=1,2\}\) for \(x=(x_1,x_2), y=(y_1,y_2)\in \mathbb {R}^2\). The context will make clear which case is used. 0 denotes the origin of both \(\mathbb {R}\) and \(\mathbb {R}^2\).
If \(x<y\) we write \(\llbracket x,y \rrbracket \) for the set of integers \([x,y]\cap \mathbb {Z}\). If \(x,y\in \mathbb {R}^2\) such that \(x\le y\) we denote by \(\llbracket x,y \rrbracket =[x,y]\cap \mathbb {Z}^2\). Nearest-nieghbor edges \((x,x+e_i)\) are generically denoted by e. For \(A\subset \mathbb {Z}^2\), \(\mathcal {E}(A)\) is the set of nearest-neighbor edges between points of A.
\(X\sim \) Exp(\(\lambda \)) for \(0<\lambda <\infty \) means that random variable X has exponential distribution with rate \(\lambda \), in other words \(\mathbb {P}(X>t)=e^{-\lambda t}\) for \(t\ge 0\). The mean is \(\mathbb {E}(X)=\lambda ^{-1}\) and variance \({{\,\mathrm{Var}\,}}(X)=\lambda ^{-2}\). In general, \({\overline{X}}=X-\mathbb {E}(X)\) denotes a random variable X centered at its mean.
To lighten on notation we generally ignore integer parts and treat for example \(N\xi \) when \(\xi \in \mathbb {R}^2\) as if it were a point on the lattice \(\mathbb {Z}^2\) close to \(N\xi \).
2 Main results
Let \(\omega =\{\omega _x\}_{x\in \mathbb {Z}^2}\) be i.i.d. \(\text {Exp}(1)\)-distributed random weights on the vertices of \(\mathbb {Z}^2\). For \(o\in \mathbb {Z}^2\), define the last-passage percolation (LPP) process on \(o+\mathbb {Z}_{\ge 0}^2\) by

\(\Pi _{o,y}\) is the set of paths  that start at \(x_0=o\), end at \(x_n=y\) with \(n=\vert y-o\vert \), and have increments \(x_{k+1}-x_k\in \{e_1,e_2\}\). The a.s. unique path \(\pi ^{o,y}\in \Pi _{o,y}\) that attains the maximum in (2.1) is the geodesic from o to y. A stationary LPP process \(G^{\frac{1}{2}}_{o,y}\) associated with the direction (1, 1) is defined similarly, but with altered weights on the boundary of the quadrant \( o+\mathbb {Z}_{\ge 0}^2\) (precise definition follows below in (3.7)).
that start at \(x_0=o\), end at \(x_n=y\) with \(n=\vert y-o\vert \), and have increments \(x_{k+1}-x_k\in \{e_1,e_2\}\). The a.s. unique path \(\pi ^{o,y}\in \Pi _{o,y}\) that attains the maximum in (2.1) is the geodesic from o to y. A stationary LPP process \(G^{\frac{1}{2}}_{o,y}\) associated with the direction (1, 1) is defined similarly, but with altered weights on the boundary of the quadrant \( o+\mathbb {Z}_{\ge 0}^2\) (precise definition follows below in (3.7)).
Let \(\widehat{R}^c=[N-cN^\frac{2}{3},N]\) be the rectangle whose lower left corner is \((N-cN^\frac{2}{3},N-cN^\frac{2}{3})\) and whose upper right corner is (N, N). Let \(\mathcal {E}(\widehat{R}^c)\) be the set of directed edges in the subgraph of \(\mathbb {Z}^2\) induced by the vertices in \(\widehat{R}^c\). Define the increment random variables indexed by the edges in \(\mathcal {E}(\widehat{R}^c)\) by
and then the configurations of increment variables:
Let \(d_\text {TV}(\cdot ,\cdot )\) denote the total variation distance between two probability distributions. If \(X\sim \mu \) and \(Y\sim \nu \), we also write \(d_\text {TV}(X,Y)=d_\text {TV}(\mu ,\nu )\). The following is the main result of the paper. It shows that on the scale of \(N^\frac{2}{3}\), around the point (N, N), local increments of G jointly equal those of \(G^{\frac{1}{2}}\) with high probability. The choice of direction (1, 1) which determines the parameter \(\frac{1}{2}\) in \(G^{\frac{1}{2}}\), is made only to simplify exposition. The same result works for any direction vector \(\xi \), with a different stationary process \(G^\rho \) and constants that depend on \(\xi \).
Theorem 2.1
There exists \(c_0>0\) and \(C(c_0)>0\) such that, for \(c\in (0, c_0]\) and \(N\ge 1\),
Let \({\mathcal {A}}_2(x)\) denote the \(\text {Airy}_2\) process and
the process of LPP values on the antidiagonal at distance 2N from the origin. A continuous interpolation of \(x\mapsto L^N_x\) converges in distribution to \({\mathcal {A}}_2(x)-x^2\) as \(N\rightarrow \infty \), in the uniform topology of continuous functions on compact sets. This was proved by Johansson [23] for LPP with geometric weights and in [15, Cor. 2.4] for the case of exponential weights we use here. Set
Let \({\mathcal {B}}\) be a two-sided Brownian motion of variance 2 on \(\mathbb {R}\). As a consequence of Theorem 2.1, our next result shows that locally, the \(\text {Airy}_2\) process looks like a Brownian motion in a strong sense. The proof is given at the end of Sect. 5.
Theorem 2.2
There exists \(c_0>0\) and \(C(c_0)>0\), such that for \(c\le c_0\)
By the transportation cost representation of the total variation distance [34, Thm. 1.27, p. 44], as a corollary we have the existence of a coupling between \({\mathcal {A}}'_2|_{[-c,c]}\) and \({\mathcal {B}}|_{[-c,c]}\) such that
Precisely, \(\mathbf {P}\) is a probability measure on the product space \(C([-c,c])^2\) of pairs of continuous functions on \([-c,c]\) and the marginals of \(\mathbf {P}\) are the distributions of \({\mathcal {A}}'_2|_{[-c,c]}\) and \({\mathcal {B}}|_{[-c,c]}\).
Let \(I\subset \mathbb {R}\) be a compact interval containing the origin, and let
be the modulus of continuity of the Brownian motion. In [18, Theorem 1.11] Hammond showed that the regularity of the Airy process is not worse than that of a Brownian motion i.e.
As a corollary of Theorem 2.2, we show that the regularity of the \(\text {Airy}_2\) process is not better than that of a Brownian motion. As was mentioned earlier, this can also be deduced from [6, Theorem 1.1].
Corollary 2.3
We turn to the stabilization results. The set of possible asymptotic velocities or direction vectors of semi-infinite up-right paths is \(\mathcal U=\{(t, 1-t): 0\le t\le 1\}\), with relative interior \({{\,\mathrm{ri}\,}}\mathcal U=\{(t, 1-t): 0< t<1\}\). For \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\), let \(\mathcal {R}^{\xi ,M}=[0,M\xi ]\) be the rectangle whose lower left corner is (0, 0) and upper right corner is \(M\xi \). Let \(\pi \) be an up-right path whose origin is (0, 0). Let \(I^\pi =\{i:\pi _i\in \mathcal {R}^{\xi ,M}\}\) be the set of indices of \(\pi \) for which \(\pi \) is in \(\mathcal {R}^{\xi ,M}\). We define \(\mathcal {P}^{\xi ,M}(\pi )\) to be the restriction of the path \(\pi \) to the rectangle \(\mathcal {R}^{\xi ,M}\), that is, \(\mathcal {P}^{\xi ,M}(\pi )\) is a finite path defined by
Let \(\pi ^{x,\infty \xi }\) be the infinite geodesic started from x whose direction is \(\xi \) [32]. For \(M<N\), define the following event
\(\mathcal {S}^{\xi ,M}\) is the event on which any geodesic leaving from any site \(x\in \mathcal {R}^{\xi ,M}\) and terminating at \(\xi N\) agree with the infinite geodesic \(\pi ^{x,\infty \xi }\) on \(\mathcal {R}^{\xi ,M}\) (see Fig. 1). Our first result gives a lower bound on the probability of stabilization on small enough rectangles.
Theorem 2.4
For any \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(c>0\) there exists a constant \(C=C(\xi ,c)>0\), locally bounded in c, such that the following holds: whenever \(0<M\le cN^\frac{2}{3}\),
The infinite geodesic \(\pi ^{0, \infty \xi }\) and the geodesic \(\pi ^{0,N\xi }\) agree in the box \(\mathcal {R}^{\xi ,f}\). On the event \(\mathcal {S}^{\xi ,f}\) for any \(x\in \mathcal {R}^{\xi ,f}\) the geodesics \(\pi ^{x, \infty \xi }\) and \(\pi ^{x,N\xi }\) have the same restriction on the small square \(\mathcal {R}^{\xi ,f}\)
As was mentioned earlier, stabilization can be used to study the behaviour of point-to-point geodesics close to their endpoints. The following result shows that around the origin, on the scale of o(N) the geodesic has transversal fluctuations of exponent 2/3. A result of that flavour was obtained in [3, Theorem 3].
Corollary 2.5
There exists \(C(\xi )>0\) such that for \(l\in \mathbb {Z}_{> 0}\)
Proof
For fixed M, on \(\mathcal {R}^{\xi ,M}\) consider the stationary backward LPP \(\widehat{G}^{\rho }_{M\xi +e_1+e_2,0}\) (precise definition below in (3.14)), starting from the point \(M\xi +e_1+e_2\) and terminating at the origin. Let us denote its geodesic by \(\widehat{\pi }^\rho \). Let \(\pi ^{0,N\xi }\) be the geodesic of LPP starting from the origin 0 and terminating at \(N\xi \). Theorem 2.4 and the fact that the distribution of an infinite geodesic going backwards is that of a stationary one (see the proof of Theorem 2.4) imply that
(2.7) follows from (2.8) and well known bounds on the fluctuations of stationary geodesics [31, Theorem 5.3]. \(\square \)
Stabilization relates results on semi-infinite geodesics with results on point-to-point geodesics. Consider the points \(q_1=(0,0)\) and \(q_2=k^{\nicefrac {2}{3}}e_2\) for some \(k\ge 1\). Let \(\pi ^{q_1, \infty \xi }\) and \(\pi ^{q_2, \infty \xi }\) be the semi-infinite geodesics in direction \(\xi \) started from \(q_1\) and \(q_2\), respectively. Let \(p^{\infty }_c\) be the point in \(\pi ^{q_1, \infty \xi }\cap \pi ^{q_2, \infty \xi }\) that is closest to the origin. Similarly let \(p_c=(p_c(1),p_c(2))\) be the closest point to the origin in \(\pi ^{q_1, N\xi }\cap \pi ^{q_2, N\xi }\). In [3] Basu, Sarkar and Sly showed that there exist universal constants \(C_1,C_2,R_0\) such that for every \(k>0\) and \(R>R_0\)
Moreover, they showed that there exist \(C,R_0,c>0\) such that for every \(k>0\) and \(R>R_0\)
The exponent c in (2.10) was not identified but was conjectured to be \(\nicefrac {2}{3}\). This was recently settled by Zhang in [36]. The theorem below shows how our stabilization result transfers the bounds (2.9) from \(p^{\infty }_c\) to \(p_c\).
Theorem 2.6
The sequence \(|p_c|\) converges weakly to \(|p^{\infty }_c|\). Moreover, there exist universal constants \(C_1,C_2,R_0>0\) such that for \(R>R_0\), for any \(k\ge 1\) and \(N>(Rk)^5\)
Proof
If exactly one of the events \(\{|p^{\infty }_c|>Rk\},\{|p_c|>Rk\}\) occurs then paths must not have coalesced in \(\mathcal {R}^{\xi ,\frac{1}{2} Rk}\), in other words, \(\mathcal {S}^{\xi ,\frac{1}{2} Rk}\) does not occur. Therefore, via the symmetric difference and using Theorem 2.4,
which shows that \(|p_c|\) converges weakly to \(|p^{\infty }_c|\). Taking \(N=(Rk)^{5}\) and using Theorem 2.4
As \(\nicefrac {7}{8}> \nicefrac {2}{3}\), (2.11) and (2.9) imply the result. \(\square \)
Remark 2.7
We note here that in terms of the conditions on N, the results in [36, Theorem 1.1] are sharper. Indeed, in [36, Theorem 1.1] the requirement on N is \(N>RK\) while in Theorem 2.6\(N>(Rk)^5\).
We turn to coalescence results where the distance between the starting point is of order \(N^{2/3}\). In \(\mathcal {R}^{\xi , N}=[0, N\xi ]\), consider the points \(o=\xi N\), \(q^1=(0,0)\) and \(q^2=aN^\frac{2}{3}e_2\) where \(a>0\) and where we assume that N is large enough so that \(q^2\in \mathcal {R}^{\xi , N}\). Let

be the points shared by the geodesics starting from \(q_i\) and terminating at \(o\) for \(i\in \{1,2\}\). We define the coalescence point \(p_c\) to be the unique point such that
as in Fig. 2. Our next result shows that the point \(p_c\) is not likely to be too close to the point \(o\) on a macroscopic scale.
Theorem 2.8
For every \(a>0\) and \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\), there exists a constant \(C(\xi ,a)>0\), locally bounded in a, such that for every \(0<\alpha <1\) and \(N>N(\alpha )\)
The following complementary result shows that the geodesics  and
and  do not coalesce too close to their origins on a macroscopic scale. Although the proof does not require local stationarity, we state it for completeness.
do not coalesce too close to their origins on a macroscopic scale. Although the proof does not require local stationarity, we state it for completeness.
Theorem 2.9
For every \(a>0\) and \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\), there exists a constants \(C(\xi ,a)>0\) such that for every \(0<\alpha <1\) and \(N>N(\alpha )\)
3 Preliminaries
3.1 Ordering of paths
We construct a partial order on directed paths in \(\mathbb {Z}^2\). For \(x,y\in \mathbb {Z}^2\) we write \(x \preceq y\) if y is below and to the right of x, i.e.
We also write \(x{\prec }y\) if
If \(A,B\subset \mathbb {Z}^2\), we write \(A \preceq B\) if
A down-right path is a bi-infinite sequence \(\mathcal {Y}=(y_k)_{k\in \mathbb {Z}}\) in \(\mathbb {Z}^2\) such that \(y_k-y_{k-1}\in \{e_1,-e_2\}\) for all \(k\in \mathbb {Z}\). Let \(\mathcal {DR}\) be the set of infinite down-right paths in \(\mathbb {Z}^2\). For two up-right paths \(\gamma _1,\gamma _2\) in \(\mathbb {Z}^2\),
where we take the inequality to be vacuously true if one of the intersections in (3.4) is empty (see Fig. 3).
3.2 Stationary LPP
For a base point \(o=(o_1,o_2)\in \mathbb {Z}^2\) and a parameter value \(\rho \in (0,1)\) we introduce the stationary last-passage percolation process  on \(o+\mathbb {Z}_{\ge 0}^2\). This process has boundary conditions given by two independent sequences
on \(o+\mathbb {Z}_{\ge 0}^2\). This process has boundary conditions given by two independent sequences
of i.i.d. random variables with marginal distributions \(I^\rho _{o+e_1}\sim \text {Exp}(1-\rho )\) and \(J^\rho _{o+e_2}\sim \text {Exp}(\rho )\). Put \(G^\rho _{o,o}=0\) and on the boundaries
Then in the bulk for \(x=(x_1,x_2)\in o+ \mathbb {Z}_{>0}^2\),
For a northeast endpoint \(p\in o+\mathbb {Z}_{>0}^2\), let \(Z^\rho _{o,p}\) be the signed exit point of the geodesic  of \(G^\rho _{o,p}\) from the west and south boundaries of \(o+\mathbb {Z}_{>0}^2\). More precisely,
of \(G^\rho _{o,p}\) from the west and south boundaries of \(o+\mathbb {Z}_{>0}^2\). More precisely,
The value \(G^\rho _{o,x}\) can be determined by (3.6) and the recursion
Relation (3.9) implies that one can backtrack the geodesic \(\pi ^{o,p}\) in the box \([o+e_1+e_2,p]\) in the following way; for each (directed) edge (x, y) in \([o+e_1+e_2,p]\) assign the weight \({w}_{x,y}=G^\rho _{o,y}-G^\rho _{o,x}\). Let \(m=|p-o|\), and \(p_i=\pi ^{o,p}_{i}\). Then
In other words, we trace the geodesic \(\pi ^{o,p}\) backwards up to the exit point from the boundaries, by following the edges of minimal \(G^\rho _{o,p}\) increments.
The following result will be used repeatedly in this paper.
Lemma 3.1
[31, Corollary 5.10] Fix \(0<\rho <1\) and let \((m,n)=\big ( N(1-\rho )^2 , N\rho ^2 \big )\). There exists \(C(\rho )>0\) such that for \(N>0\) such that \(m\wedge n \ge 1\) and \(r>0\)
The constant C is locally bounded in its parameter. Similar results hold for the exit point of the stationary geodesic going from the origin to the points \((m+rN^{2/3},n)\) and \((m-rN^{2/3},n)\).
3.3 Backward LPP
Next we consider LPP maximizing down-left paths. For \(y\le o\), define
For each \(o\in \mathbb {Z}^2\) and a parameter value \(\rho \in (0,1)\) define a stationary last-passage percolation processes \(\widehat{G}^\rho \) on \(o+\mathbb {Z}^2_{\le 0}\), with boundary variables on the north and east, in the following way. Let
be mutually independent sequences of i.i.d. random variables with marginal distributions \(I^\rho _{o-ie_1}\sim \text {Exp}(1-\rho )\) and \(J^\rho _{o-je_2}\sim \text {Exp}(\rho )\). The boundary variables in (3.5) and those in (3.12) are taken independent of each other. Put \(\widehat{G}^\rho _{o,\,o}=0\) and on the boundaries
Then in the bulk for \(x=(x_1,x_2)\in o+ \mathbb {Z}_{<0}^2\),
For a southwest endpoint \(p\in o+\mathbb {Z}_{<0}^2\), let \(\widehat{Z}^\rho _{o,p}\) be the signed exit point of the geodesic  of \(\widehat{G}^\rho _{o,p}\) from the north and east boundaries of \(o+\mathbb {Z}_{<0}^2\). Precisely,
of \(\widehat{G}^\rho _{o,p}\) from the north and east boundaries of \(o+\mathbb {Z}_{<0}^2\). Precisely,
Similar to (3.10), one can backtrack the geodesic \(\pi ^{o,p}\) in the box \([p,o-e_1-e_2]\) in the following way; for each edge (x, y) (where \(y\le x\)) in \([p,o-e_1-e_2]\) assign the weight
Letting \(p_i=\pi ^{o,p}_i\), we have
Since
we see that (3.17) can be written as
3.4 Nested LPP processes
The following is a construction we shall refer to often. For general weights \(\{Y_x\}_{x\in \mathbb {Z}^2}\) on the lattice and a point \(u\in \mathbb {Z}^2\), let \(G_{u,x}\) be the LPP defined by

Now let \(v\in \mathbb {Z}^2\) be such that \(u\le v\). One can construct a new LPP on \(\mathbb {Z}^2_{> v}\) as follows. Define the south-west boundary weights
Let \(\{G^{[u]}_{v,x}\}_{x\in \mathbb {Z}_{> v}}\) be the LPP defined through relations (3.6)–(3.7) using the base point \(o=v\), the boundary conditions (3.20) and the bulk weights \(\{Y_x\}_{x\in \mathbb {Z}_{> v}}\). We call \(G^{[u]}\) the induced LPP at v by \(G_{u,x}\). The superscript [u] indicates that \(G^{[u]}\) uses boundary weights determined by the process  with base point u. Figure 4 illustrates the next lemma. The proof of the lemma is elementary.
with base point u. Figure 4 illustrates the next lemma. The proof of the lemma is elementary.
Illustration of Lemma 3.2. Path u-x-y is a geodesic of \(G_{u,y}\) and path v-x-y is a geodesic of \(G^{[u]}_{v,y}\)
Lemma 3.2
Let \(u\le v\le y\) in \(\mathbb {Z}^2\). Then \(G_{u,y}=G_{u,v}+G^{[u]}_{v,y}\). The restriction of any geodesic of \(G_{u,y}\) to \(v+\mathbb {Z}_{\ge 0}^2\) is part of a geodesic of \(G^{[u]}_{v,y}\). The edges with one endpoint in \(v+\mathbb {Z}_{>0}^2\) that belong to a geodesic of \(G^{[u]}_{v, y}\) extend to a geodesic of \(G_{u,y}\).
In case the process inherited is associated to a stationary process \(G^\rho \) we shall use the notation \(G^{\rho ,[u]}\) to indicate the density \(\rho \) as well. Similarly, if \(\widehat{G}_{u,x}\) is a LLP on \(\mathbb {Z}^2_{<u}\) for some \(u\in \mathbb {Z}^2\), if \(v<u\), we can construct the induced process \(\widehat{G}^{[u]}_{v,x}\) on \(\mathbb {Z}^2_{<v}\). A result similar to Lemma 3.2 holds for \(\widehat{G}_{u,x}\) and \(\widehat{G}^{[u]}_{v,x}\).
4 Busemann functions
4.1 Existence and properties of Busemann functions
Let \((\Omega ,\mathcal {F},\mathbb {P})\) be a probability space and let \(\{\tau _z\}_{z\in \mathbb {Z}^2}\) be a group of translations on \(\Omega \).
Definition 4.1
A measurable function \(B:\Omega \times \mathbb {Z}^2 \times \mathbb {Z}^2\rightarrow \mathbb {R}\) is a covariant cocycle if it satisfies these two conditions for \(\mathbb {P}\)-a.e. \(\omega \) and all \(x,y,z\in \mathbb {Z}^2\):
Given a down-right path \(\mathcal {Y}\in \mathcal {DR}\), the lattice decomposes into a disjoint union \(\mathbb {Z}^2=\mathcal {G}_-\cup \mathcal {Y}\cup \mathcal {G}_+\) where the two regions are
and
Definition 4.2
Let \(0<\alpha <1\). Let us say that a process

is an exponential-\(\alpha \) last-passage percolation system if the following properties (a)–(b) hold.
-
(a)
The process is stationary with marginal distributions
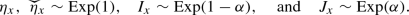 (4.4)
(4.4)For any down-right path \(\mathcal {Y}=(y_k)_{k\in \mathbb {Z}}\) in \(\mathbb {Z}^2\), the random variables
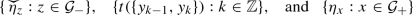 (4.5)
(4.5)are all mutually independent, where the undirected edge variables \(t(e)\) are defined as
$$\begin{aligned} t(e)= {\left\{ \begin{array}{ll} I_x &{}\text {if } e=\{x-e_1,x\}\\ J_x &{}\text {if } e=\{x-e_2,x\}. \end{array}\right. } \end{aligned}$$(4.6) -
(b)
The following equations are in force at all \(x\in \mathbb {Z}^2\):
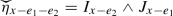 (4.7)
(4.7)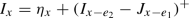 (4.8)
(4.8)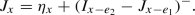 (4.9)
(4.9)
The following theorem can be found in the lecture notes [31]. The Busemann limit (4.14) below uses the characteristic direction associated with the parameter \(\rho \in (0,1)\), defined by
When \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) is given, \(\rho (\xi )\) denotes the unique parameter value \(\rho \) that satisfies (4.10).
Theorem 4.3
For each \(0<\alpha <1\) there exist a stationary cocycle \(B^\alpha \) and a family of random weights \(\{X^\alpha _x\}_{x\in \mathbb {Z}^2}\) on \((\Omega , \mathcal {F}, \mathbb {P})\) with the following properties.
-
(i)
For each \(0<\alpha <1\), process
$$\begin{aligned} \{ X^\alpha _x, \, B^\alpha _{x-e_1,x}, \, B^\alpha _{x-e_2,x}, \,\omega _x: x\in \mathbb {Z}^2\} \end{aligned}$$(4.11)is an exponential-\(\alpha \) last-passage system as described in Definition 4.2.
-
(ii)
There exists a single event \(\Omega _2\) of full probability such that for all \(\omega \in \Omega _2\), all \(x\in \mathbb {Z}^2\) and all \(\lambda <\rho \) in (0, 1) we have the inequalities
$$\begin{aligned} B^\lambda _{x,x+e_1}(\omega ) \le B^\rho _{x,x+e_1}(\omega ) \quad \text {and}\quad B^\lambda _{x,x+e_2}(\omega ) \ge B^\rho _{x,x+e_2}(\omega ). \end{aligned}$$(4.12)Furthermore, for all \(\omega \in \Omega _2\) and \(x,y\in \mathbb {Z}^2\), the function \(\lambda \mapsto B^\lambda _{x,y}(\omega )\) is right-continuous with left limits.
-
(iii)
For each fixed \(0<\alpha <1\) there exists an event \(\Omega ^{(\alpha )}_2\) of full probability such that the following holds: for each \(\omega \in \Omega ^{(\alpha )}_2\) and any sequence \(v_n\in \mathbb {Z}^2\) such that \(\vert v_n\vert \rightarrow \infty \) and
$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{v_n}{\vert v_n\vert } \, = \,\xi (\alpha ) \end{aligned}$$(4.13)we have the limits
$$\begin{aligned} B^\alpha _{x,y}(\omega ) =\lim _{n\rightarrow \infty } [ G_{x, v_n}(\omega )-G_{y,v_n}(\omega )] \qquad \forall x,y\in \mathbb {Z}^2. \end{aligned}$$(4.14)The LPP process \(G_{x,y}\) is now defined by (2.1). Furthermore, for all \(\omega \in \Omega ^{(\alpha )}_2\) and \(x,y\in \mathbb {Z}^2\),
$$\begin{aligned} \lim _{\lambda \rightarrow \alpha }B^\lambda _{x,y}(\omega )=B^\alpha _{x,y}(\omega ). \end{aligned}$$(4.15)
4.2 Busemann functions and infinite geodesics
Fix \(x\in \mathbb {Z}^2\). An infinite up-right path  originating at x is called a geodesic if for all \(m,n\in \mathbb {Z}_{>0}\) such that \(m<n\), the path \(\{\pi ^{x,\infty }_l\}_{l\in \llbracket m,n\rrbracket }\) is a geodesic. We say a geodesic has direction \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) if
originating at x is called a geodesic if for all \(m,n\in \mathbb {Z}_{>0}\) such that \(m<n\), the path \(\{\pi ^{x,\infty }_l\}_{l\in \llbracket m,n\rrbracket }\) is a geodesic. We say a geodesic has direction \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) if
It is known that for a given \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\), with probability one, from every point \(x\in \mathbb {Z}^2\) there is a unique semi-infinite geodesic \(\pi ^{x,\infty \xi }\) in direction \(\xi \). Busemann functions can be used to construct these semi-infinite geodesics. Consider the family of random variables
defined in (4.11). Let \(\xi :=\xi (\alpha )\) be the characteristic direction associated with \(\alpha \). One can trace the infinite geodesic \(\pi ^{x,\infty }\) by following the gradient of the Busemann function \(B^\alpha \). (This is developed for example in [16].) Let \(\{p_i\}_{i\in \mathbb {Z}_{\ge 0}}\) be an enumeration of the vertices in \(\pi ^{x,\infty \xi }\), i.e.
where \(p_0=x\). Then the vertices \(\{p_i\}_{i\in \mathbb {Z}_{> 0}}\) are given recursively through
(Equality happens with probability zero on the right, due to the independence of \(B^\alpha _{x,x+e_1}\) and \(B^\alpha _{x,x+e_2}\).) Note that in (4.18) \(p_i\) is attained by taking an up \(\backslash \) right step from the point \(p_{i-1}\) in the direction of the minimal increment of the Busemann function. Since \(\omega _x=B^\alpha _{x,x+e_1}\wedge B^\alpha _{x,x+e_2}\), \(\pi ^{x,\infty \xi }\) is the unique path that satisfies
The monotonicity (4.12) of Busemann functions implies a spatial ordering of geodesics:
Lemma 4.4
Let \(x\in \mathbb {Z}^2\) and \(\xi _1,\xi _2\in {{\,\mathrm{ri}\,}}\mathcal U\) such that \(\xi _1{\preceq }\xi _2\). For \(i\in \{1,2\}\) let \(\pi ^{x,\xi _i\infty }\) be the infinite geodesic starting from x in direction \(\xi _i\). Then
4.3 Coupling Busemann functions
In [12, Theorem 3.2] a coupling between Busemann functions of different densities was developed, expressed in terms of queueing mappings.
Lemma 4.5
Let \(0<{\underline{\rho }}<{\bar{\rho }}<1\). The coupling of \(B^{{\underline{\rho }}}\) and \(B^{{\bar{\rho }}}\) in Theorem 4.3 has the following properties.
-
(i)
For every \(x\in \mathbb {Z}^2\)
$$\begin{aligned} B^{{\underline{\rho }}}_{x,x+e_2}&\ge B^{{\bar{\rho }}}_{x,x+e_2}\nonumber \\ B^{{\bar{\rho }}}_{x,x+e_1}&\ge B^{{\underline{\rho }}}_{x,x+e_1}. \end{aligned}$$(4.22) -
(ii)
For every \(x\in \mathbb {Z}^2\) we have the joint distributions
$$\begin{aligned} \big (B^{{\bar{\rho }}}_{x+ie_1,x+(i+1)e_1},B^{{\underline{\rho }}}_{x+ie_1,x+(i+1)e_1}\big )_{i\in \mathbb {Z}}&\sim \nu ^{1-{\bar{\rho }},1-{\underline{\rho }}}\\ \big (B^{{\underline{\rho }}}_{x+ie_2,x+(i+1)e_2},B^{{\bar{\rho }}}_{x+ie_2,x+(i+1)e_2}\big )_{i\in \mathbb {Z}}&\sim \nu ^{{\underline{\rho }},{\bar{\rho }}}, \end{aligned}$$where \(\nu ^{\lambda ,\rho }\) is the distribution defined in (A.4).
5 Stabilization
In this section we prove Theorems 2.1 and 2.4. Recall (3.11) and define the event
\({\mathcal {H}}^{\xi ,M}\) is the event where the increments of \(\widehat{G}\) along the edges in \(\mathcal {E}(\mathcal {R}^{\xi ,M})\) coincide with those of the Busemann function associated with the direction \(\xi \).
5.1 Bounds on \(\mathbb {P}(\mathcal {S}^{\xi ,M})\) and \(\mathbb {P}({\mathcal {H}}^{\xi ,M})\)
Recall definition (4.10) that connects directions and parameter values. Fix a direction vector \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) with its parameter \(\rho (\xi )\). For \(r>0\) define perturbed parameters
with characteristic directions
Set a northeast base vertex at \(\widehat{o}_N=\xi N+e_1+e_2\). Assign weights on the edges of the north and east outer boundaries of \(\mathcal {R}^{\xi ,N}\) by
Use the boundary weights \(\{I^{\bar{\rho }}_i\}_{0\le i \le N\xi _1},\{J^{\bar{\rho }}_i\}_{0\le i \le N\xi _2}\) and the bulk weights \(\{\omega _x\}_{x\in \mathcal {R}^{\xi ,N}}\) to construct the stationary LPP \(\widehat{G}^{\bar{\rho }}\) as in (3.13)–(3.14). Similarly we construct \(\widehat{G}^{\underline{\rho }}\). As in (3.15) we let \(\widehat{Z}^{\bar{\rho }}_{\widehat{o}_N,x}\) (resp. \(\widehat{Z}^{\underline{\rho }}_{\widehat{o}_N,x}\)) denote the exit point of the geodesic \(\pi ^{{\bar{\rho }},\widehat{o}_N,x}\) of \(\widehat{G}^{\bar{\rho }}\) (resp. geodesic \(\pi ^{{\underline{\rho }},\widehat{o}_N,x}\) of \(\widehat{G}^{\underline{\rho }}\)). For \(0<M<N\) let
\(\widehat{A}^{\xi ,M}\) is the event that for each \(x\in \mathcal {R}^{\xi ,M}\), the geodesic \(\pi ^{{\bar{\rho }}, \widehat{o}_N,x}\) of \(\widehat{G}^{\bar{\rho }}_{\widehat{o}_N,x}\) (and geodesic \(\pi ^{{\underline{\rho }}, \widehat{o}_N,x}\) of \(\widehat{G}^{\underline{\rho }}_{\widehat{o}_N,x}\)) crosses the boundary of \(\mathcal {R}^{\xi ,N}\)(not to be confused with \(\mathcal {R}^{\xi ,M}\)!) from the north (from the east).
Lemma 5.1
Let \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(N>M>0\). On the event \(\widehat{A}^{\xi ,M}\) the following ordering of geodesics holds in the rectangle \(\mathcal {R}^{\xi , N}\):
Proof
We show the first inequality in (5.5), the second one being analogous. Because the boundary conditions (5.3) come from the Busemann functions, the geodesic \(\pi ^{{\bar{\rho }}, \widehat{o}_N,x}\) of the stationary LPP process \(\widehat{G}^{\bar{\rho }}_{\widehat{o}_N,x}\) follows the semi-infinite geodesic \(\pi ^{x,\infty {\bar{\xi }}}\) from x until they hit together the north/east boundary of the rectangle \([x,\widehat{o}]\). (This is a version of Lemma 3.2 where Fig. 4 is rotated 180 degrees and then the base point u is taken to infinity in direction \(\xi \).) Event \(\widehat{A}^{\xi ,M}\) constrains this hit to happen on the north boundary, that is, to the left of the point \(N\xi \). Uniqueness of point-to-point geodesics then forces \(\pi ^{x,N\xi }\) to stay to the right of \(\pi ^{{\bar{\rho }}, \widehat{o}_N,x}\). \(\square \)
Let \(\widehat{o}_M=M\xi +e_1+e_2\) be the outer upper right corner of \(\mathcal {R}^{\xi ,M}\). Assign weights on the edges of the north-east outer boundary of \(\mathcal {R}^{\xi ,M}\) from the Busemann function:
Define the event where the increment variables for \({\bar{\rho }}\) and \({\underline{\rho }}\) agree on the north and east boundaries of the rectangle \([0,\widehat{o}_M]\):
Lemma 5.2
On the event \(C^{\xi ,M}\),
Proof
The values \(\{B^\rho _e: e\in \mathcal {E}(\mathcal {R}^{\xi ,M})\}\) are determined by the bulk weights \(\{\omega \}_{x\in \mathcal {R}^{\xi ,M}}\) and the boundary weights in (5.6) through the recursion (4.8)–(4.9):
As both \(\{B^{\bar{\rho }}_e\}_{e\in \mathcal {E}(\mathcal {R}^{\xi ,M})}\) and \(\{B^{\underline{\rho }}_e\}_{e\in \mathcal {E}(\mathcal {R}^{\xi ,M})}\) use the same bulk weights and the event \(C^{\xi ,M}\) forces their boundary conditions to agree, \( B^{\bar{\rho }}_e=B^{\underline{\rho }}_e \ \forall e\in \mathcal {E}(\mathcal {R}^{\xi ,M}). \) Equality (5.8) follows from the monotonicity (4.12) of Busemann functions. (5.9) follows from (5.8) because the geodesics \(\mathcal {P}^{\xi ,M}(\pi ^{x,\infty {\bar{\xi }}})\) and \(\mathcal {P}^{\xi ,M}(\pi ^{x,\infty {\underline{\xi }}})\) are determined by the Busemann function increments through (4.18). \(\square \)
Corollary 5.3
On the event \(C^{\xi ,M}\cap \widehat{A}^{\xi ,M}\),
Proof
By Lemma B.2, on the event \(\widehat{A}^{\xi ,M}\)
which implies (5.10), using (5.8). By Lemma 4.4 we see that
By Lemma 5.1, on \(\widehat{A}^{\xi ,M}\)
Lemma 5.2 along with (5.12) and (5.13) imply the result. \(\square \)
For \(M>0\), recall the event \(\mathcal {S}^{\xi ,M}\) in (2.5). Using Corollary 5.3 we have the following.
Corollary 5.4
Proof
The first inequality comes from
which is true because last-passage and Busemann increments determine the geodesics. The second inequality comes from Corollary 5.3. \(\square \)
5.2 Upper bound on \(\mathbb {P}((\widehat{A}^{\xi ,M})^c)\)
Lemma 5.5
For \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(c>0\) there exist finite constants \(C=C(c,\xi )\) and \(N_0=N_0(\xi ,c)\), locally bounded in c, such that the following hold: whenever \(N\ge N_0\), \(0<M\le cN^\frac{2}{3}\) and \(1\le r \le N^\frac{1}{3}(\log (N))^{-1}\),
and
where \(\widehat{o}_N=N\xi +e_1+e_2\), \({\underline{\rho }}(\xi )=\rho (\xi )-rN^{-\frac{1}{3}}\) and \({\bar{\rho }}(\xi )=\rho (\xi )+rN^{-\frac{1}{3}}\).
Proof
We only prove (5.16) as (5.15) is similar. Given \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\), abbreviate \(\rho =\rho (\xi )\) and \({\bar{\rho }}={\bar{\rho }}(\xi )\). Let \(x^0=(M\xi _1,0)\) be the lower-right corner of \(\mathcal {R}^{\xi ,M}\). By the order on geodesics we have
which implies
In order to upper bound (5.17) we must show that the characteristic line of direction \(-\xi ({\bar{\rho }})\) that leaves from \(\widehat{o}_N\) goes, on the scale of \(N^\frac{2}{3}\), well below the point \(x^0=(x^0(1),x^0(2))=(M\xi _1 ,0)\). We have, via (4.10),
where in the first inequality we used that \(M\le cN^{2/3}\) and in the second inequality the definition of \({\bar{\rho }}\). For large enough N and \(r\le N^\frac{1}{3}(\log (N))^{-1}\) plug into (5.19) to obtain
such that for N large enough
For
the right hand side of (5.20) is smaller than \(-N^\frac{2}{3}\). This in turn implies that there exists a constant \(C'(\xi ,c)>0\) (locally bounded in c) such that
It then follows by Lemma 3.1 that there exists a constant \(C_1(\xi ,c)>0\)
which proves the result. \(\square \)
Corollary 5.6
Fix \(\xi \in (0,1)\) and \(c>0\). There exists \(C(c,\xi )>0\), locally bounded in c, such that for every \(0<M\le cN^\frac{2}{3}\) and \(1\le r \le N^\frac{1}{3}(\log (N))^{-1}\)
Proof
By the definition of \(\widehat{A}^{\xi ,M}\) we see that
Taking probability on both sides of (5.22) and using (5.15) and (5.16) we obtain the result. \(\square \)
5.3 Upper bound on \(\mathbb {P}((C^{\xi ,M})^c)\)
Express \(C^{\xi ,M}\) from (5.7) as
where
This subsection proves the following.
Proposition 5.7
For \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(c>0\) there exists a constant \(C(\xi ,c)>0\), locally bounded in c, such that for \(0< M\le cN^\frac{2}{3}\), there exists \(r(\xi ,M,N)>0\) for which the following holds
Before we prove Proposition 5.7 we obtain some auxiliary results. As was noted in Lemma 4.5[ii], for \({\bar{\xi }}{\preceq }{\underline{\xi }}\) (and therefore \({\underline{\rho }} \le {\bar{\rho }}\))
where \(\mathbf{d}=D(\mathbf{a},\mathbf{s})\) from “Appendix A”, and \(\mathbf{a}=(a_j)_{j\in \mathbb {Z}}\) and \(\mathbf{s}=(s_j)_{j\in \mathbb {Z}}\) are two independent i.i.d sequences of exponential random variables of intensity \(1-{\bar{\rho }}\) and \(1-{\underline{\rho }}\) respectively, such that \(0<{\underline{\rho }}<{\bar{\rho }}<1\). Using (A.9)
It follows that
and similarly
Altogether, plugging (5.25) and (5.26) into (5.23) we obtain
Let us now try to explain the idea behind the proof. Let \(x_j=s_{j-1}-a_j\), from (A.6) we see that
Define the stopping time
so that
Using this recursion and (A.10)
The dynamics behind (5.28) is as follows. The waiting time \(w_j\) increases when the service times are longer then usual and the interarrival times are shorter i.e. when the random walk \(S^{0,j}\) goes up. Similarly, the \(w_j\) decreases when the service times are fast compared to the arrival of customers i.e. \(S^{0,j}\) goes down. This dynamics hold until the random walk goes below \(-w_0\) where the waiting time at the queue vanishes. The r.v. \(\sum _{i=1}^{\xi _1 M} e_i\) can be thought of as the local time of the queue at zero, i.e. the accumulated time of the queue being empty. The main idea behind the proof of Proposition 5.7 is the observation that when \({\bar{\rho }}-{\underline{\rho }}\sim N^{-\frac{1}{3}}\), that is when the queue is in the so-called heavy traffic regime, at stationarity, the waiting time \(w_0\) of customer 0, is of order \(N^\frac{1}{3}\). As the difference between the average service time rate and the average inter-arrival time rate is of order \({\bar{\rho }}-{\underline{\rho }}\sim N^{-\frac{1}{3}}\), the simple random walk \(S^{0,j}\) has drift \(-N^{-\frac{1}{3}}\). (5.28) implies that the queue’s waiting time vanishes by time of order \(N^\frac{2}{3}\). Over time \(t=o(N^{\frac{2}{3}})\) the random walk \(S_t\) will not change the waiting time at the queue by much so that with high probability \(w_t\) will be of order \(N^{\frac{1}{3}}\) and the r.v. \(\sum _{i=1}^{t} e_i\) will be zero (see Fig. 5). The proof of the following result is deferred to the appendix.
The two cases of a queue at stationarity. \(S_t\) is the random walk whose incremental step is \(x_t=s_{t-1}-a_t\). As the rate of service at the queue is higher than the rate of interarrival \(\mathbb {E}(x_t)<0\) and so \(S_t\) is a simple random walk with a negative drift. The waiting time at the queue decreases by \(S_t\) until it vanishes
Lemma 5.8
Let \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and let \(M>0\). For \(0<\beta<\alpha <1\)
Lemma 5.9
Let \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and let \(M>0\). For \({\underline{\rho }}(\xi )=\rho (\xi )-rN^{-\frac{1}{3}}\), \({\bar{\rho }}(\xi )=\rho (\xi )+rN^{-\frac{1}{3}}\) and \(0<\theta <{\bar{\rho }}\),
Proof
Set \(\beta ={\underline{\rho }}\) and \(\alpha ={\bar{\rho }}\) so that
and that
Using (5.31) and (5.32) in (5.29) and the change of variable \(2rN^{-\frac{1}{3}}w\mapsto w\)
\(\square \)
Lemma 5.10
Let \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and let \(M>0\) such that \(M\le cN^\frac{2}{3}\). There exists \(C(\xi ,c)>0\) such that
Proof
Let \(r=(\xi _1M)^{-\frac{1}{8}}N^{\frac{1}{12}}\) and \(\theta =(\xi _1M)^{-\frac{1}{2}}\) in (5.30) to obtain
where
and
where
There exists \(C_A(\rho )>0\) such that
Note that by our assumption on M the numerator in (5.37) is dominated by \(2cN^\frac{2}{3} \vee (\xi _1M)^{-1}\) and
where \(C(c)>0\) is locally bounded in c. In particular, there exists \(C_{B_2}(\rho )>0\) such that
Plugging (5.36), (5.40) and (5.38) into (5.35) we see that there exists \(C_B(\rho )>0\) such that
Plugging now (5.39) and (5.41) into (5.34) and using (5.25) we obtain the result. \(\square \)
Proof of Proposition 5.7
Similar to Lemma 5.10 one can show that for \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(M>0\) such that \(M\le cN^\frac{2}{3}\), there exists \(C(\xi ,c)>0\) such that
(5.33) and (5.42) imply the result. \(\square \)
Proof of Theorem 2.1
Plugging (5.21) and (5.24) into (5.14) we see that there exists \(c_0>0\) such that for every \(c\le c_0\)
By the definition (5.1) of \({\mathcal {H}}^{\xi ,cN^\frac{2}{3}}\), (5.43) shows that there exists a coupling between
and \(B^{\xi (\rho )}|_{\mathcal {E}(R^{\xi ,cN^{2/3}})}\), the Busemann function \(B^{\xi (\rho )}\) restricted to the edges in \(\mathcal {E}(R^{\xi ,cN^{2/3}})\), such that
In general, the coupling inequality above bounds the total variation distance. Hence
As the distribution of \(B^{\xi (\rho )}|_{\mathcal {E}(R^{\xi ,cN^{2/3}})}\) equals that of
(5.45) also gives
With \(\xi =(\tfrac{1}{2},\tfrac{1}{2})\) and \(\rho =\tfrac{1}{2}\), (5.46) is the same as (2.2) after rotating the LPP picture by 180 degrees. \(\square \)
Proof of Theorem 2.4
Plugging (5.21) and (5.24) into (5.14) we obtain the result. \(\square \)
Proof of Theorem 2.2
Define
By Theorem 2.1 there exists \(c_0>0\) and \(C(c_0)>0\) such that for any \(|c|\le c_0\), with probability at least \(1-Cc^\frac{3}{8}\), simultaneously for all \(|x|\le c\)
Defining
we conclude that with probability at least \(1-Cc^\frac{3}{8}\), simultaneously for all \(|x|\le c\)
This coupling implies the bound
The following limits are in distribution in the topology of continuous functions on \([-c,c]\).
To see that (5.50) holds, note that by Theorem 4.3 and Definition 4.2, \(\Delta L^{\frac{1}{2},N}\) is an unbiased random walk, Donsker’s invariance principal implies (5.50). Using Lemma C.2 with (5.49)–(5.50) and (5.48) implies that
which implies the result. \(\square \)
Proof of Corollary 2.3
By the stationarity of the \({\mathcal {A}}_2\), it is enough to verify the claim for \(I=[0,a]\) for some \(a>0\). For every \(\epsilon >0\), let \(\Omega ^\epsilon =C[0,\epsilon ]\) be the space of continuous functions on the interval \([0,\epsilon ]\). Let \(\mathcal {F}^\epsilon \) be the Borel sigma algebra associated with the supremum metric on \(\Omega ^\epsilon \). By Theorem 2.2, for every \(\delta >0\) there exists \(0<\epsilon \le a\) and a probability space \((\Omega ^\epsilon ,\mathbb {P}^\epsilon )\) such that
For \(\epsilon \in (0,a]\), (5.51) implies that with probability larger than \(1-\delta \)
where the last equality comes from Lévy’s modulus of continuity [27, Theorem 10.1] and the self-similarity of Brownian motion. Taking \(\delta \rightarrow 0\)
Note that
6 Coalescence of point-to-point geodesics
In this section we prove Theorem 2.8 and Theorem 2.9. For technical reasons, namely the direction in which we send \(v_n\) to infinity in (4.13), we prove the results for a setup that is a bit different, yet equivalent, to the one in Fig. 2 i.e. we set \(q^1=\xi N,q^2=\xi N-aN^{2/3}e_2\) and \(o=(0,0)\) (see Fig. 6).
6.1 Upper bound on \(\mathbb {P}(|o-p_c|\le \alpha N)\)
Let \(\widehat{G}^{\bar{\rho }}\) and \(\widehat{G}^{\underline{\rho }}\) be the stationary LPP with \({\bar{\rho }}=\rho +rN^{-\frac{1}{3}}\) and \({\underline{\rho }}=\rho -rN^{-\frac{1}{3}}\) constructed through (3.13)–(3.14) with the boundary weights on the north-east boundaries of \(\mathcal {R}^{ \xi ,N}\) as in (5.6) (with \(M=N\)) and the bulk weights \(\{\omega _x\}_{x\in \mathcal {R}^{ N\xi }}\). Recall (3.15). Similarly to (5.4) define
Similarly to Corollary 5.6 we have
Lemma 6.1
Fix \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(a>0\). There exist \(C(\xi ,a)>0\), locally bounded in a, and \(N_0(\xi ,r)>0\) such that
Proof
By definition of \(\widehat{A}^{r}\)
The bound on \(\mathbb {P}\big (\widehat{Z}^{{\bar{\rho }}(\xi )}_{q^1,o}<0\Big )\) comes from (5.16), it remains to bound \(\mathbb {P}\big (\widehat{Z}^{{\underline{\rho }}(\xi )}_{q^1,o}\ge -aN^\frac{2}{3}\big )\). Let \(u=(u_1,u_2)=\xi N-aN^\frac{2}{3}e_2\), and let \(\widehat{G}^{{\underline{\rho }},[q^1]}_{u,x}\) be the LPP induced by \(\widehat{G}^{\underline{\rho }}_{q^1,x}\) at u. By Lemma 3.2 we see that
where \(\widehat{Z}^{[q^1]}_{u,x}\) is the exit point of \(\widehat{G}^{{\underline{\rho }},[q^1]}_{u,x}\). Compute
where
It follows that there exists \(N_0(\xi ,r)\) such that for \(N>N_0\)
where
It then follows by Lemma 3.1 that there exists a constant \(C_1(\xi )>0\) such that
the proof is now complete. Taking \(C>0\) large enough implies (6.1) \(\square \)
Let \(0<\alpha <1\) and \(o_\alpha =o+\alpha \xi N=\alpha \xi N\). We define \(\mathfrak {R}_\alpha =[o,o_\alpha ]\) to be the rectangle whose left bottom corner is \(o\) and whose upper right corner is \(o_\alpha \). We shall need the following result.
Lemma 6.2
Fix \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\), \(0<\alpha <1\) and \(r>0\). There exists \(C(\xi )>0\) such that for \(t>\alpha r\) and \(N>N_0(\xi ,r)\)
Proof
We prove (6.6) as (6.7) is similar. In fact we only prove here the upper bound for \(\mathbb {P}\big (\widehat{Z}^{\bar{\rho }}_{o_\alpha ,o}>tN^\frac{2}{3}\big )\) as the bound on \(\mathbb {P}\big (\widehat{Z}^{\bar{\rho }}_{o_\alpha ,o}<tN^\frac{2}{3}\big )\) is similar. Let \(\widehat{G}^{{\bar{\rho }},[o_\alpha ]}_{u,x}\) be the LPP induced by \(\widehat{G}^{\bar{\rho }}_{o_\alpha ,x}\) at u where \(u=\alpha \xi N-A_1tN^\frac{2}{3}e_1\), and
By Lemma 3.2 we see that
where \(\widehat{Z}^{[o_\alpha ]}_{u,x}\) and \(\widehat{Z}^{\bar{\rho }}_{o_\alpha ,x}\) are the exit points of \(\widehat{G}^{{\bar{\rho }},[o_\alpha ]}_{u,x}\) and \(\widehat{G}^{\bar{\rho }}_{o_\alpha ,x}\) respectively. We would like to show that the characteristic \(\xi ({\bar{\rho }})\) emanating from the point \(u=(u_1,u_2)\) goes well above the point \(o\) on the scale of \(N^\frac{2}{3}\). Compute
By (6.8), for \(t\ge r\alpha \)
It follows that there exists \(N_0(r)>0\) such that for \(N>N_0\)
It then follows by Lemma 3.1 that there exists a constant \(C'_1(\xi )>0\)
Plugging (6.9) in (6.10) implies that
Applying the change of variables \(A_1t\mapsto t\), there exists \(C_1(\xi )>0\) such that
Similarly we show that there exists \(C_2(\xi )\) such that
Setting \(C=C_1\vee C_2\) implies the result. \(\square \)
Define the sets
In words, \(\partial ^{\alpha }\) is the north-east boundary of \(\mathfrak {R}_\alpha \), \(\partial ^{\alpha ,t}_c\) are all the points in \(\partial ^{\alpha }\) whose \(l_1\) distance from \(o_\alpha \) is less or equal to \(t N^\frac{2}{3}\) while \(\partial ^{\alpha ,t}_f\) are the set of points in \(\partial ^{\alpha }\) whose \(l_1\) distance from \(o_\alpha \) is larger or equal to \(t N^\frac{2}{3}\). Let \({\bar{\pi }}^{q^1,o}\) and \({\underline{\pi }}^{q^1,o}\) be the stationary geodesics that start from \(q^1\) and terminate at \(o\), associated to \(\widehat{G}^{\bar{\rho }}\) and \(\widehat{G}^{\underline{\rho }}\) respectively. Define
The superscript r in \(\mathcal {B}^{r,\alpha ,t}\) appears implicitly in \({\bar{\rho }},{\underline{\rho }}\). The following result shows that with high probability the geodesics \({\bar{\pi }}^{q^1,o}\) and \({\underline{\pi }}^{q^1,o}\) will not wonder too far from the point \(o_\alpha \).
Corollary 6.3
Fix \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\), \(0<\alpha <1\) and \(r>0\). There exists \(C(\xi )>0\) such that for \(t>\alpha r\) and \(N>N_0(\xi ,r)\)
Proof
Note that it is possible to couple \(\widehat{Z}^{\bar{\rho }}_{o_\alpha ,o},\widehat{Z}^{\underline{\rho }}_{o_\alpha ,o},{\underline{\pi }}^{q^1,o}\) and \({\bar{\pi }}^{q^1,o}\) so that
Taking probabilities on both sides of (6.14) and (6.15), using Lemma 6.2 and union bound we obtain (6.13). \(\square \)
Define the sets
where the superscript r is implicit in \({\bar{\rho }},{\underline{\rho }}\) ((5.2)).
Lemma 6.4
For every \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(0<\alpha <1\), there exists \(C(\xi )>0\) so that for every \(r\ge 1\) and \(t\le r^{-2}\) there exists \(N_0(r)>0\) such that for \(N\ge N_0\)
Proof
We show (6.16) for \(\mathcal {D}^{r,\alpha ,t}_2\) the result then follows by union bound. As in (5.26) we have
Using (5.30) with \(\theta =t^{-\frac{1}{2}}N^{-\frac{1}{3}}\)
Sending N to \(\infty \), the right hand site of (6.18) converges to
Plugging (6.19) in (6.17), by our assumption on t, \(rt^{\frac{1}{2}}\le 1\), and so we see that there exists \(C_2(\xi )>0\) such that for every \(r\ge 1\), there exists \(N_0(r)>0\) such that for \(N\ge N_0\)
Similar bound can be obtained for \(\mathcal {D}_1^{r,\alpha ,t}\) the result then follows by union bound. \(\square \)
Proof of Theorem 2.8
We first claim that on the event \(\widehat{A}^{r} \cap \mathcal {B}^{r,\alpha ,t}\cap \mathcal {D}^{r,\alpha ,t}\) the geodesics  and
and  must coalesce outside \(\mathfrak {R}_\alpha \) (see Fig. 6). On the event \(\widehat{A}^{r}\)
must coalesce outside \(\mathfrak {R}_\alpha \) (see Fig. 6). On the event \(\widehat{A}^{r}\)

This means that coalescence of the geodesics \({\bar{\pi }}_{q^1,o}\) and \({\underline{\pi }}_{q^1,o}\) outside \(\mathfrak {R}_\alpha \) implies the coalescence of the geodesics  and
and  outside \(\mathfrak {R}_\alpha \). It is therefore enough to show that on the set \(\mathcal {B}^{r,\alpha ,t}\cap \mathcal {D}^{r,\alpha ,t}\)
outside \(\mathfrak {R}_\alpha \). It is therefore enough to show that on the set \(\mathcal {B}^{r,\alpha ,t}\cap \mathcal {D}^{r,\alpha ,t}\)
On the event \(\mathcal {B}^{r,\alpha ,t}\) the geodesics \({\bar{\pi }}_{q^1,o}\) and \({\underline{\pi }}_{q^1,o}\) do not cross \(\partial ^{\alpha ,t}_f\) and therefore use only the weights \(B^{\bar{\rho }}_e,B^{\underline{\rho }}_e\) where \(e\in \mathcal {E}(\partial ^{\alpha ,t}_c)\) and the bulk weights \(\{\omega _x\}_{x\in \mathfrak {R}_\alpha }\). It follows that on \(\mathcal {B}^{r,\alpha ,t}\cap \mathcal {D}^{r,\alpha ,t}\) (6.21) holds. Set \(r=\alpha ^{-\frac{2}{27}},t=\alpha ^\frac{16}{27}\) so that \(t=\alpha ^{\frac{16}{27}}\ge \alpha ^{\frac{25}{27}}=\alpha r\) holds (since \(0<\alpha <1\)). Note that under this choice of parameters \(t^{1/2}r<1\). Use (6.1), (6.13) and (6.16) to see that there exists \(C'(\xi ,a)>0\) such that
The result now follows. \(\square \)
6.2 Upper bound on \(\mathbb {P}(|q^2-p_c|\le \alpha N)\)
For every \(\xi \in {{\,\mathrm{ri}\,}}\mathcal U\) and \(m\in \mathbb {Z}\), define the set
Let \(\xi ^1=\xi \) and \(\xi ^2=\xi -(0,aN^{-\frac{1}{3}})\) be two vectors whose direction is that of the characteristics emanating from \(o\) associated with the point \(q^1\) and \(q^2\) respectively. Let \({\bar{\rho }}=\rho (\xi )+rN^{-\frac{1}{3}}\), \({\underline{\rho }}=\rho (\xi )-rN^{-\frac{1}{3}}\) and consider \(G^{\bar{\rho }}_{o,x}\) and \(G^{\underline{\rho }}_{o,x}\) on \(\mathcal {R}^{ N\xi }\) as in (3.7). For \(x\in o+\mathbb {Z}^2_{>0}\), let \({\bar{\pi }}^{o,x}\) and \({\underline{\pi }}^{o,x}\) be the geodesics associated with the last-passage time \(G^{\bar{\rho }}_{o,x}\) and \(G^{\underline{\rho }}_{o,x}\) respectively. We shall need the following auxiliary result.
Lemma 6.5
Let \(0<\alpha <1\) and \(r\ge 1\). There exists \(N_0(\xi ,r),C(\xi ),A(\xi )>0\) such that for \(N>N_0\) and \(t\ge A\alpha r\)


Proof
We prove only (6.22) as the proof of (6.23) is similar. We would first like to show that there exist \(N_0(\xi ,r),C_1(\xi ),A(\xi )>0\) such that for \(N>N_0\) and \(t\ge A\alpha r\) (see Fig. 7)
To see that (6.24) holds, let \(u=\big ((1-\alpha ) \xi _1N,(1-\alpha ) \xi _2N-tN^\frac{2}{3}\big )\) and consider \(G^{{\bar{\rho }},[o]}_{u,x}\). Note that
We compute
If
then there for \(C'(\xi )>0\)
so that there exists \(N_0(\xi ,r)\) such that for \(N>N_0\) the left hand side of (6.26) is greater of equal to
It then follows by Lemma 3.1 that there exists a constant \(C_1(\xi )>0\) such that for \(N>N_0\)
(6.24) now follows from (6.27) using (6.25). Next we use (6.24) to obtain (6.22). To see that, we first note that (similar to (5.16)) there exists \(C_2(\xi )>0\) such that
which implies that

Note that

Taking probability in (6.29) and using (6.24) and (6.28) we arrive at (6.22). \(\square \)
Proof of Theorem 2.9
Fix \(0<\alpha <1\). Note that
Let \(t=\frac{a}{3}(1-\alpha )\) and \(r=\frac{t}{A}\alpha ^{-\frac{2}{3}}\) where A is the constant from Lemma 6.5, so that \(t\ge A\alpha r=t\alpha ^{\frac{1}{3}}\). By Lemma 6.5, there exists \(C(\xi ,a)>0\)

Let  and
and  be the lowest and highest intersection points of the vertical line at \((1-\alpha )\xi _1 N\) with
be the lowest and highest intersection points of the vertical line at \((1-\alpha )\xi _1 N\) with  and
and  respectively (Fig. 8). (6.30) implies that
respectively (Fig. 8). (6.30) implies that
It follows that
(6.31) implies the result. \(\square \)
References
Basu, R., Ganguly, S.: Time correlation exponents in last passage percolation. arXiv preprint arXiv:1807.09260, (2018)
Basu, R., Ganguly, S., Hammond, A.: Fractal geometry of Airy\_2 processes coupled via the airy sheet. arXiv preprint arXiv:1904.01717, (2019)
Basu, R., Sarkar, S., Sly, A.: Coalescence of geodesics in exactly solvable models of last passage percolation. J. Math. Phys. 60(9), 093301,22, (2019)
Basu, R., Sidoravicius, V., Sly, A.: Last passage percolation with a defect line and the solution of the slow bond problem. (2014). arXiv:1408.3464
Busani, O., Ferrari, P.: Universality of the geodesic tree in last passage percolation. arXiv preprint arXiv:2008.07844, (2020)
Calvert, J., Hammond, A., Hegde, M.: Brownian structure in the KPZ fixed point. arXiv preprint arXiv:1912.00992, (2019)
Corwin, I., Hammond, A.: Brownian Gibbs property for Airy line ensembles. Invent. Math. 195(2), 441–508 (2014)
Coupier, D.: Multiple geodesics with the same direction. Electron. Commun. Probab. 16, 517–527 (2011)
Dauvergne, D., Ortmann, J., Virág, B.: The directed landscape. arXiv preprint arXiv:1812.00309, (2018)
Dauvergne, D., Virág, B.: Basic properties of the Airy line ensemble. arXiv preprint arXiv:1812.00311, (2018)
Emrah, E., Janjigian, C., Seppäläinen, T.: Right-tail moderate deviations in the exponential last-passage percolation. arXiv:2004.04285, (2020)
Wai-Tong (Louis) F., Timo S.: Joint distribution of Busemann functions in the exactly solvable corner growth model. (2018). arXiv:1808.09069, to appear in Probab. Math. Phys
Ferrari, P.L., Spohn, H.: Last branching in directed last passage percolation. vol. 9, pp. 323–339 (2003). Inhomogeneous random systems (Cergy-Pontoise, 2002)
Ferrari, P.A., Pimentel, L.P.R.: Competition interfaces and second class particles. Ann. Probab. 33(4), 1235–1254 (2005)
Ferrari, P.L., Occelli, A.: Universality of the GOE Tracy-Widom distribution for TASEP with arbitrary particle density. Electron. J. Probab., 23: Paper No. 51, 24, (2018)
Georgiou, N., Rassoul-Agha, F., Seppäläinen, T.: Geodesics and the competition interface for the corner growth model. Probab. Theory Related Fields 169(1–2), 223–255 (2017)
Georgiou, N., Rassoul-Agha, F., Seppäläinen, T.: Stationary cocycles and Busemann functions for the corner growth model. Probab. Theory Related Fields 169(1–2), 177–222 (2017)
Hammond, A.: Brownian regularity for the Airy line ensemble, and multi-polymer watermelons in brownian last passage percolation. arXiv preprint arXiv:1609.02971, (2016)
Hammond, A.: Exponents governing the rarity of disjoint polymers in brownian last passage percolation. Proce. London Math. Soc. 120(3), 370–433 (2020)
Howard, C.D., Newman, C.M.: Euclidean models of first-passage percolation. Probab. Theory Related Fields 108(2), 153–170 (1997)
Howard, C.D., Newman, C.M.: Geodesics and spanning trees for Euclidean first-passage percolation. Ann. Probab. 29(2), 577–623 (2001)
Johansson, K.: Transversal fluctuations for increasing subsequences on the plane. Probab. Theory Related Fields 116(4), 445–456 (2000)
Johansson, K.: Discrete polynuclear growth and determinantal processes. Comm. Math. Phys. 242(1–2), 277–329 (2003)
Ledoux, M., Rider, B.: Small deviations for beta ensembles. Electron. J. Probab. 15(41), 1319–1343 (2010)
Licea, C., Newman, C.M.: Geodesics in two-dimensional first-passage percolation. Ann. Probab. 24(1), 399–410 (1996)
Matetski, K., Quastel, J., Remenik, D.: The KPZ fixed point. arXiv preprint arXiv:1701.00018, (2016)
Mörters, P., Peres, Y.: Brownian Motion, vol. 30. Cambridge University Press, Cambridge (2010)
Newman, C.M.: A surface view of first-passage percolation. In: Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Zürich, 1994), pp. 1017–1023, Basel, (1995). Birkhäuser
Pimentel, L.P.R.: Duality between coalescence times and exit points in last-passage percolation models. Ann. Probab. 44(5), 3187–3206 (2016)
Pimentel, L.P.R.: Brownian aspects of the KPZ fixed point. arXiv preprint arXiv:1912.11712, (2019)
Seppäläinen, T.: The corner growth model with exponential weights. In: Random growth models, volume 75 of Proceeding of Symposia in Applied Mathematics, pp. 133–201. Amer. Math. Soc., Providence, RI, (2018). arXiv:1709.05771
Seppäläinen, Timo: Existence, uniqueness and coalescence of directed planar geodesics: proof via the increment-stationary growth process. Ann. Inst. Henri Poincaré Probab. Stat. 56(3), 1775–1791 (2020)
Seppäläinen, T., Shen, X.: Coalescence estimates for the corner growth model with exponential weights. Electron. J. Probab., 25: Paper No. 85, 31, (2020)
Villani, C.: Topics in Optimal Transportation. Graduate Studies in Mathematics, vol. 58. American Mathematical Society, Providence, RI (2003)
Whitt, W.: Stochastic-Process Limits. Springer Series in Operations Research. Springer-Verlag, New York (2002)
Zhang, L.: Optimal exponent for coalescence of finite geodesics in exponential last passage percolation. Electron. Commun. Probab. 25, 14 (2020)
Acknowledgements
The authors thank Bálint Tóth for useful discussions and comments and Alan Hammond for guidance to the literature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
M. Balázs was partially supported by EPSRC’s EP/R021449/1 Standard Grant.
O. Busani was supported by EPSRC’s EP/R021449/1 Standard Grant.
T. Seppäläinen was partially supported by National Science Foundation grant DMS-1854619 and by the Wisconsin Alumni Research Foundation.
All data generated or analysed during this study are included in this published article [and its supplementary information files].
Appendices
Appendix A. Queues
We formulate last-passage percolation over a bi-infinite strip as a queueing operator. The inputs are two bi-infinite sequences: the inter-arrival process \(\mathbf{a}=(a_j)_{j\in \mathbb {Z}}\) and the service process \(\mathbf{s}=(s_j)_{j\in \mathbb {Z}}\). The queueing interpretation is that \(a_j\) is the time between the arrivals of customers \(j-1\) and j and \(s_j\) is the service time of customer j. The operations below are well-defined as long as \(\lim _{m\rightarrow -\infty } \sum _{i=m}^0 (s_i-a_{i+1})=-\infty .\)
From inputs \((\mathbf{a},\mathbf{s})\) three output sequences

are constructed through explicit mappings: the inter-departure process \(\mathbf{d}=(d_j)_{j\in \mathbb {Z}}\), the sojourn process \(\mathbf{t}=(t_j)_{j\in \mathbb {Z}}\), and the dual service times  .
.
The formulas are as follows. Choose a sequence \(G=(G_j)_{j\in \mathbb {Z}}\) that satisfies \(a_j=G_j-G_{j-1}\). Define the sequence \(\widetilde{G}=(\widetilde{G}_j)_{j\in \mathbb {Z}}\) by
The supremum above is taken at some finite k. Then set

The outputs (A.3) are independent of the choice of G. Note that to compute  , only inputs \(\{ a_j , s_j : j\le m\}\) are needed. Let \(\mathbf{a}=(a_j)_{j\in \mathbb {Z}}\) and \(\mathbf{s}=(s_j)_{j\in \mathbb {Z}}\) be two independent sequences of i.i.d. exponential r.v. of intensity \(\lambda \) and \(\rho \) respectively, where \(0<\lambda<\rho <1\). We denote by \(\nu ^{\lambda ,\rho }\) the distribution of \((D(\mathbf{a},\mathbf{s}),\mathbf{s})\) on \(\mathbb {R}_+^\mathbb {Z}\times \mathbb {R}_+^\mathbb {Z}\), i.e.
, only inputs \(\{ a_j , s_j : j\le m\}\) are needed. Let \(\mathbf{a}=(a_j)_{j\in \mathbb {Z}}\) and \(\mathbf{s}=(s_j)_{j\in \mathbb {Z}}\) be two independent sequences of i.i.d. exponential r.v. of intensity \(\lambda \) and \(\rho \) respectively, where \(0<\lambda<\rho <1\). We denote by \(\nu ^{\lambda ,\rho }\) the distribution of \((D(\mathbf{a},\mathbf{s}),\mathbf{s})\) on \(\mathbb {R}_+^\mathbb {Z}\times \mathbb {R}_+^\mathbb {Z}\), i.e.
By Burke’s Theorem \(D(\mathbf{a},\mathbf{s})\) is sequences of i.i.d. Exponential r.v. of intensity \(\lambda \), consequently, the measure \( \nu ^{\lambda ,\rho }\) is referred to as a stationary measure of the queue. The waiting time of the j’th customer is given by
The random variables \(\{w_j\}_{j\in \mathbb {Z}}\) satisfy
The distribution of \(w_0\) (and by stationarity the distribution of any \(w_j\) for \(j\in \mathbb {Z}\)) is given by
One can write
where \(e_j\) is called the j’th idle time and is given by
\(e_j\) is the time between the departure of customer \(j-1\) and the arrival of customer j in which the sever is idle. Define
and the summation operator
Summing \(e_j\) we obtain the cumulative idle time [35][Chapter 9.2, Eq. 2.7] as in the following lemma.
Lemma A.1
For any \(k\le l\)
Proof
For simpler exposition we set \(k=1\). By (A.5)
To see that the last equality holds, note that
It follows that
where
where the last equality in (A.12) follows since
It follows that
where we dropped the positive part because
By (A.6) and (A.9) we see that
Summing on both sides of (A.14) and using (A.13)
\(\square \)
Proof of Lemma 5.8
By (A.11)
where
Next we bound from above the probability that the infimum of the path of \(\{S_x^{1,i}\}_{1 \le i\le \xi _1 M}\) drops too low. Let \(C>0\), then
As \(-S^{1,i}_x\) is a submartingale and \(\phi _\theta (x)=e^{\theta x}\) is a strictly increasing convex function for \(\theta >0\) \(\phi _{\theta }(-S^{1,i}_x)\) is again a submartingale. By Doob’s inequality
Note that by the independence of \(\mathbf{a}=(a_j)_{j\in \mathbb {Z}}\) and \(\mathbf{s}=(s_j)_{j\in \mathbb {Z}}\), for \(0<\theta <\beta \)
By (A.15)
and so
Note that by the definition of \(w_0\) ((A.5)), \(w_0\) is independent of \(\{S_x^{1,i}\}_{i\in \mathbb {Z}_{> 0}}\) and so
where \(f_w\) is given by (see (A.7))
so that
Plugging (A.18) in (A.22) we obtain the result. \(\square \)
Appendix B. Coupling and monotonicity in last-passage percolation
In this section \(\omega =(\omega _x)_{x\in \mathbb {Z}^2}\) is a fixed assignment of real weights. \(G_{x,y}\) is the last-passage value defined by (2.1). No probability is involved.
Lemma B.1
Suppose weights \(\omega \) and \(\widetilde{\omega }\) satisfy \(\omega _{o+ie_1}\ge \widetilde{\omega }_{o+ie_1}\), \(\omega _{o+je_2}\le \widetilde{\omega }_{o+je_2}\), and \(\omega _x=\widetilde{\omega }_x\) for \(i,j\ge 1\) and \(x\in o+\mathbb {Z}_{>0}^2\). As in (2.1) define LPP processes

Then for all \(y\in o+\mathbb {Z}_{\ge 0}^2\), the increments over nearest-neighbor edges satisfy
Proof
The statements are true by construction for edges \((y, y+e_i)\) that lie on the axes \(o+\mathbb {Z}_{\ge 0}e_i\). Proceed by induction: assuming the inequalities hold for the edges \((y,y+e_2)\) and \((y, y+e_1)\) , deduce them for the edges \((y+e_2, y+e_1+e_2)\) and \((y+e_1, y+e_1+e_2)\). \(\square \)
Lemma B.2
(Crossing Lemma) The inequalities below are valid whenever the last-passage values are defined.
Proof
The proofs of all parts are similar. We prove the second inequality in (B.1), that is,
The geodesics \(\pi _{o,\,x+e_2}\) and \(\pi _{o+e_2,\,x}\) must cross. Let u be the first point where they meet. Note that
Add the two inequalities in (B.4) and rearrange to obtain (B.3).
This inequality can be proved also from Lemma B.1, by writing \(G_{o+e_2,\,x+e_2}-G_{o+e_2,\,x}=\widetilde{G}_{o,\,x+e_2}-\widetilde{G}_{o,\,x}\) with environment \(\widetilde{\omega }_{o+y}=\omega _{o+y}\) when \(y_2>0\) and \(\widetilde{\omega }_{o+ie_1}=-M\) for large enough M. \(\square \)
Appendix C. Convergence of distributions
Let \((\mathbb {X}, \rho )\) be a complete, separable metric space and let \(\mathcal {M}_1(\mathbb {X})\) be the space of Borel probability distributions on \(\mathbb {X}\). For \(\mu ,\nu \in \mathcal {M}_1(\mathbb {X})\) and \(\epsilon \ge 0\) we define
For \(\epsilon =0\) we obtain exactly the definition of total variation distance of distributions.
Lemma C.1
Let \(\mu _1,\mu _2,\mu _3\in \mathcal {M}_1(\mathbb {X})\). Suppose that for some \(\delta >0\)
Then
Proof
Let \(\mathbb {X}_1,\mathbb {X}_2\) and \(\mathbb {X}_3\) be three copies of \(\mathbb {X}\) and let \(\Omega =\mathbb {X}_1\times \mathbb {X}_2 \times \mathbb {X}_3\). By (C.1), there exist \(f_{\mu _1,\mu _2},f_{\mu _1,\mu _3}\in \mathcal {M}_1(\mathbb {X}^2)\) s.t.
For \(i\in \{2,3\}\) let \(df_{\mu _i|\mu _1}\) be the conditional distribution of \(\mu _i\) given \(\mu _1\) w.r.t. \(f_{\mu _1,\mu _i}\). Define the distribution F on \(\Omega \) by
Note that the marginals of F are \(\mu _1,\mu _2\) and \(\mu _3\). Let \(\mathcal {P}_{2,3}:\Omega \rightarrow \mathbb {X}^2\) be the projection map of the last two coordinates in \(\Omega \) and let \(F'\) be the pushforward measure of F with respect to \(\mathcal {P}_{2,3}\). Then \(F'\) is a coupling of \(\mu _2\) and \(\mu _3\) and
(C.2) implies the result. \(\square \)
Lemma C.2
Let \(\{\mu _n\}_{n\in \mathbb {N}}\) and \(\{\nu _n\}_{n\in \mathbb {N}}\) be two sequences of distributions on \(\mathbb {X}\). Suppose that
Assume that for every \(n\in \mathbb {N}\)
Then
Proof
Fix \(k\in \mathbb {N}\). The convergences in (C.3) can be realized a.s. and so, there exists N(k) such that for \(n>N(k)\)
Using Lemma C.1 twice with (C.4) implies that for \(n>N(k)\)
and so there must be a coupling \(F^k\) of \(\mu \) and \(\nu \) such that
The sequence \(\{F^{k}\}_{k\in \mathbb {N}}\) is tight with respect to the product metric as the marginals of \(F^{k}\) are independent of k. It follows that there must be a weakly convergent subsequence \(F^{k_m}\) such that
where F is a coupling of \(\mu \) and \(\nu \) and that for every \(k\in \mathbb {N}\)
Sending k to infinity implies the result. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Balázs, M., Busani, O. & Seppäläinen, T. Local stationarity in exponential last-passage percolation. Probab. Theory Relat. Fields 180, 113–162 (2021). https://doi.org/10.1007/s00440-021-01035-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-021-01035-7
Keywords
- Local stationarity
- Coalescence
- Corner growth model
- Directed percolation
- Geodesic
- Random growth model
- Last-passage percolation
- Queues


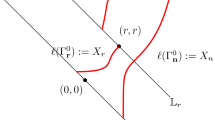





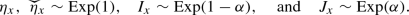
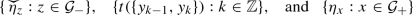
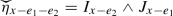
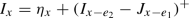
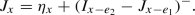


 and
and  . The stationary geodesics (in red) use the same weights on edges in
. The stationary geodesics (in red) use the same weights on edges in 
