Anisotropic $(2+1)$d growth and Gaussian limits of q-Whittaker processes

Abstract

We consider a discrete model for anisotropic $(2+1)$-dimensional growth of an interface height function. Owing to a connection with q-Whittaker functions, this system enjoys many explicit integral formulas. By considering certain Gaussian stochastic differential equation limits of the model we are able to prove a space–time limit of covariances to those of the $(2+1)$-dimensional additive stochastic heat equation (or Edwards–Wilkinson equation) along characteristic directions. In particular, the bulk height function converges to the Gaussian free field which evolves according to this stochastic PDE.

Appendices

Generalities of Gaussian processes

Here we recall some basics of Gaussian processes as we will use them (see e.g. [25, Section VIII.6]) An n-dimensional diffusion process $X_t$ with linear drift, say drift $\mu =A X_t$ for a given matrix A (possibly time-dependent), and space-independent dispersion matrix $\sigma$ is a solution of a system of SDE’s

$$\begin{aligned} dX^k_t= A(t) X_t dt+\sigma (t) dW_t \end{aligned}$$

with $W_t$ being a standard n-dimensional Brownian motion. Then, the probability density P(x, t) that the process X is at x at time t satisfies the Fokker–Planck equation

$$\begin{aligned} \frac{d P(x,t)}{dt} = -\sum _{i,j} A_{i,j} \frac{d}{dx_i} (x_j P(x,t)) +\frac{1}{2} \sum _{i,j} B_{i,j} \frac{d^2 P(x,t)}{dx_i dx_j}, \end{aligned}$$

where $B=\sigma ^{\mathrm {T}}\sigma$ is the diffusion matrix.

In particular, if one starts with $\delta$-initial condition at x(0), i.e., $P(x,0)=\prod _{i=1}^r \delta (x_i-x_i(0))$, then

$$\begin{aligned} {\mathbb {E}}(X(t))= Y(t) X(0), \end{aligned}$$

where Y(t) is the evolution matrix satisfying

(A.1)

Further, the solution of the Fokker–Plank equation is given by

$$\begin{aligned} P(x,t)=\frac{1}{[(2\pi )^n\det (\varXi )]^{1/2}} \exp \left( -\frac{1}{2} (x-{\mathbb {E}}(X(t))^{\mathrm {T}} \varXi ^{-1} (x-{\mathbb {E}}(X(t))\right) \end{aligned}$$

where $\varXi (t)$ is the covariance matrix given by

$$\begin{aligned} \varXi (t)=\int _0^t ds Y(t) Y^{-1}(s) B(s) Y^{-{\mathrm {T}}}(s) Y^{\mathrm {T}}(t). \end{aligned}$$

Further, $\varXi$ can be characterized as the solution of the equation

$$\begin{aligned} \frac{d\varXi }{dt}=A \varXi + \varXi A^{\mathrm {T}}+B,\quad \varXi (0)=0. \end{aligned}$$

We compute the two-time distribution when such a Gaussian transition probability is applied to a Gaussian distribution with covariance matrix $C_1:=\varXi (t_1)$, i.e., with density given by $\mathrm{const}\cdot e^{-\frac{1}{2} x^{\mathrm {T}} C_1^{-1} x}$. Denote as well $C_{1,2}=\varXi (t_2,t_1)$ and $t=t_2-t_1$. Then,

$$\begin{aligned}&{\mathbb {P}}(x(t_1)\in dx, x(t_2)\in dy)\\&\quad =\mathrm{const} \exp \left( -\frac{1}{2} \left[ x^{\mathrm {T}} C_1^{-1} x+(y-Y(t))^{\mathrm {T}} C_{1,2}^{-1} (y-Y(t)x)\right] \right) dx dy. \end{aligned}$$

The quadratic form in the parenthesis can be written as

$$\begin{aligned} (x^{\mathrm {T}},y^{\mathrm {T}}) \left( \begin{array}{cc} C_1^{-1}+ Y(t)^{\mathrm {T}} C_{1,2}^{-1} Y(t) &{} -Y^{\mathrm {T}}(t)\\ -C_{1,2}^{-1} Y(t) &{} C_{1,2}^{-1} \end{array}\right) \left( \begin{array}{c} x \\ y \end{array}\right) . \end{aligned}$$

We use the block matrix inversion formula

$$\begin{aligned} \left( \begin{array}{cc} a &{} b \\ c &{} d \end{array}\right) ^{-1} = \left( \begin{array}{cc} -m^{-1} &{} m^{-1} b d^{-1} \\ d^{-1} c m^{-1} &{} d^{-1}-d^{-1} c m^{-1} b d^{-1} \end{array}\right) \end{aligned}$$

with $m=b d^{-1} c -a$ and obtain

$$\begin{aligned} \left( \begin{array}{cc} C_1^{-1}+ Y(t)^{\mathrm {T}} C_{1,2}^{-1} Y(t) &{} -Y^{\mathrm {T}}(t)\\ -C_{1,2}^{-1} Y(t) &{} C_{1,2}^{-1} \end{array}\right) ^{-1} = \left( \begin{array}{cc} C_1 &{} C_1 Y^{\mathrm {T}}(t) \\ Y(t) C_1 &{} C_{1,2}+Y(t)C_1Y^{\mathrm {T}}(t). \end{array}\right) \end{aligned}$$

Thus this is the covariance matrix for the two-time distribution. In particular, the covariance between a site $x(t_1)$ and $y(t_2)$ is given by the application of the propagator $Y(t_2-t_1)$ to the covariance $C_1$ at time $t_1$.

Additional q-Whittaker dynamics

1.1 Alpha dynamics

In addition to the push-block alpha dynamics, there is also an RSK type dynamic (see [29, Section 6.2], or [32]). Considering interlacing partitions $\bar{\lambda }$, we define a Markov transition matrix $P^{\mathrm{RSK}}_{\mathbf {a};\alpha }\big (\bar{\lambda }\rightarrow \bar{\nu }\big )$ to a new set of interlacing partition $\bar{\nu }$ according to the following update procedure. For $k=1,\ldots , N$ choose independent random variables $v_k$ distributed according to the q-geometric law with parameter $\alpha a_k$ (see Sect. 2.1). For $1\le k\le n-1$, let $c_k = \nu ^{(n-1)}_{k}-\lambda ^{(n-1)}_k$. Choose $w_1,\ldots , w_{n-1}$ independently so that $w_k\in \{0,1,\ldots , c_k\}$ is distributed according to

$$\begin{aligned} {\mathbb {P}}(w_k = s)= \varphi _{q^{-1}, q^{\lambda ^{(n)}_k - \lambda ^{(n-1)}_{k}}, q^{\lambda ^{(n-1)}_{k-1}-\lambda ^{(n-1)}_{k}}} \big (s | c_k\big ), \end{aligned}$$

where we recall the convention that $\lambda ^{(n)}_0=+\infty$ for all n.

Now update

$$\begin{aligned} \nu ^{(n)}_1 = \lambda ^{(n)}_1 + w_1 +v_n,\qquad \text {and for}\, k\ge 2\quad \nu ^{(n)}_k = \lambda ^{(n)}_{k} +w_k + c_{k-1}-w_{k-1}. \end{aligned}$$

Proposition B.1

Define a Markov process indexed by t on interlacing partitions $\bar{\lambda }(t)$ with packed initial data and Markov transition between time $t-1$ and t given by $P^{\mathrm{RSK}}_{\mathbf {a};\alpha _{t}}\big (\bar{\lambda }(t-1) \rightarrow \bar{\lambda }(t)\big )$. Then, for any $t\in \{0,1,\ldots \}$, $\bar{\lambda }(t)$ is marginally distributed according to the q-Whittaker measure ${\mathbb {P}}_{\mathbf {a};\mathbf {\alpha }(t)}$ with $\mathbf {\alpha }(t) = (\alpha _1,\ldots , \alpha _t)$.

Proof

This follows from [29, Theorem 6.4]. $\square$

In Sect. 3.3.1 we probe the limiting difference equation which arises from the push-block dynamics as $q\rightarrow 1$. There should be difference equations for the RSK type dynamics above, though we do not pursue this here. We also do not pursue any fluctuation limits.

1.2 Plancherel dynamics

We consider two additional dynamics besides the push-block Plancherel dynamics.

The “right-pushing dynamics” were introduced as [10, Dynamics 9]. For $2\le k\le n\le N$, each $\lambda ^{(n)}_{k}$ evolves according to the push-block dynamics. The only difference is in the behavior of $\lambda ^{(n)}_1$. For $1\le n\le N$, each $\lambda ^{(n)}_1$ jumps (i.e., increases value by one) at rate $a_n q^{\lambda ^{(n-1)}_{1}-\lambda ^{(n)}_{2}}$. When $\lambda ^{(n)}_{1}$ jumps it deterministically forces $\lambda ^{(n+1)}_1,\ldots , \lambda ^{(N)}_1$ to likewise increase by one. It is clear that these dynamics preserve the interlacing structure of $\bar{\lambda }$.

The “RSK type dynamics” were introduced as [10, Dynamics 8] (see also [32]). For $1\le n\le N$, each $\lambda ^{(n)}_1$ has its own independent exponential clock with rate $a_n$. When the clock rings, the particle $\lambda ^{(n)}_1$ jumps (i.e., increases value by one). These are all of the independent jumps, however there are certain triggered moves. When a particle $\lambda ^{(n-1)}_k$ jumps, it triggers a single jump from some coordinate of $\lambda ^{(n)}$. Let $\xi (k)$ represent the maximal index less than k for which increasing $\lambda ^{(n)}_{\xi (k)}$ by one does not violate the interlacing rules between the new $\lambda ^{(n)}$ and $\lambda ^{(n-1)}$. With probability

$$\begin{aligned} q^{\lambda ^{(n)}_k-\lambda ^{(n-1)}_k} \frac{1- q^{\lambda ^{(n-1)}_{k-1}-\lambda ^{(n)}_k}}{1- q^{\lambda ^{(n-1)}_{k-1}-\lambda ^{(n-1)}_k}} \end{aligned}$$

(recall the convention that $\lambda ^{(n)}_0\equiv +\infty$) $\lambda ^{(n)}_{\xi (k)}$ jumps; and with complementary probability $\lambda ^{(n)}_{k+1}$ jumps. It is clear that these dynamics maintain the interlacing structure of $\bar{\lambda }$.

Proposition B.2

For each of the right-pushing and RSK type dynamics described above, define continuous time Markov processes, all denoted by $\bar{\lambda }(\gamma )$, started from packed initial data. Then, for any $\gamma >0$, $\bar{\lambda }(\gamma )$ is marginally distributed according to the Plancherel specialized q-Whittaker process ${\mathbb {P}}_{\mathbf {a};\gamma }$.

Proof

This follows from a combination of [10, Proposition 8.2 and Theorem 6.13]. $\square$

In the same manner as in Sect. 3.3.2, we can derive ODEs for the LLN from the above continuous time dynamics. In the right-pushing case, the dynamics are the same as in the push-block case aside from $\lambda ^{(n)}_1$. Hence by the same reasoning that for $k\ge 2$, (3.14) still holds. From the right-pushing rule, we similarly deduce that the following should hold

$$\begin{aligned} \frac{d x^{(n)}_{1}(\tau )}{d\tau } = a_n e^{-x^{(n-1)}_1(\tau ) + x^{(n)}_2(\tau )} + \sum _{\ell =1}^{n-1}\frac{d x^{(\ell )}_1(\tau )}{d\tau }. \end{aligned}$$

For the RSK type dynamics, let us assume that all particles are well-spaced (as they surely will be after a short amount of time). Then we need not worry about transferring jumps in the RSK type dynamics. Thus, by similar reasoning as in the push-block case we find that

$$\begin{aligned} \frac{d}{d\tau } x^{(1)}_{1}(\tau ) = a_1, \qquad \frac{d}{d\tau } x^{(n)}_{1}(\tau ) = a_n + \frac{d}{d\tau }x^{(n-1)}_1(\tau ) \, \cdot \, e^{-x^{(n)}_1(\tau )+x^{(n-1)}_{1}(\tau )} \end{aligned}$$

and for $k\ge 2$,

$$\begin{aligned} \frac{d}{d\tau } x^{(n)}_{k}(\tau )&= \frac{d}{d\tau } x^{(n-1)}_{k}(\tau ) e^{-x^{(n)}_k(\tau )+x^{(n-1)}_k(\tau )}\, \frac{1-e^{-x^{(n-1)}_{k-1}(\tau )+x^{(n)}_k(\tau )}}{1-e^{-x^{(n-1)}_{k-1}(\tau )+x^{(n-1)}_k(\tau )}}\\&\quad + \frac{d}{d\tau } x^{(n-1)}_{k-1}(\tau ) \bigg (1- e^{-x^{(n)}_{k-1}(\tau )+x^{(n-1)}_{k-1}(\tau )}\, \frac{1-e^{-x^{(n-1)}_{k-2}(\tau )+x^{(n)}_{k-1}(\tau )}}{1-e^{-x^{(n-1)}_{k-2}(\tau )+x^{(n-1)}_{k-1}(\tau )}}\bigg ). \end{aligned}$$

In these equations, on the right-hand side the differential term $d/d\tau$ gives the rate of jumps from below whereas the terms multiplying that correspond to the proportion of this jump rate which is transferred to $x^{(n)}_k$.

We do not pursue these alternative dynamics any further, though note that they may yield different fluctuation SDEs than in the push-block case (though they will all have the same marginals).

1.3 Positivity in determinantal expressions

Recall that in Corollary 3.3, equation (3.10) provides the determinantal formula

$$\begin{aligned} e^{-(x^{(n)}_{n}(\tau ) +\cdots + x^{(n)}_{n-r+1}(\tau ))} = e^{-\tau r} \det \Big [G_{r,\tau }(n+1-r+j-i)\Big ]_{i,j=1}^r. \end{aligned}$$

We show below that

$$\begin{aligned} e^{-\tau r} \det \Big [G_{r,\tau }(n+1-r+j-i)\Big ]_{i,j=1}^r =e^{-\tau r} p^{n}_r(\tau ), \end{aligned}$$

where $p^{n}_r(\tau )$ is a polynomial in $\tau$ with positive coefficients. This positivity is surprising and its origins warrants further investigation.

The above representation is shown by realizing the determinant as a partition function for a certain system of non-intersecting paths with positive weights. We explain this for the above determinant, Eq. (3.10) in the main text, as well as the alpha version, Eq. (3.9) in the main text.

Fig. 15

Karlin–McGregor interpretation of the determinant in (3.9) and (3.10)

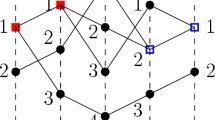
It is possible to represent the determinant in (3.9) in terms of the partition function for a collection of r non-intersecting paths on a certain weighted lattice. Consider the lattice on the left of Fig. 15 which has width n and height $r+t$. The bottom r portion of the lattice is the standard square lattice, and every edge (horizontal and vertical) has a weight of 1. The top t portion of the lattice is composed of vertical edges and diagonal up-right edges. Each diagonal edge between level $r+\ell$ and $r+\ell +1$ has weight $1-\alpha _{\ell }$ and each vertical edge between those levels has weight $\alpha _\ell$. The weight of a directed path (only taking up or right edges for the first r levels and then up or up-right edge for the remaining levels) from level 1, position i to level $r+t$, position j ($1\le i\le j\le n$) is the product of the weights along the path. The partition function is the sum of these weights over all such paths and is readily computed as

$$\begin{aligned} \sum _{c=i}^{j}\left( {\begin{array}{c}r\\ c-i\end{array}}\right) e_{j-c}(1-\mathbf {\alpha };\mathbf {\alpha }) = \sum _{\ell =0}^{j-i}e_{\ell }(1-\mathbf {\alpha };\mathbf {\alpha }) \frac{(r)_{j-i-\ell }}{(j-i-\ell )!}=G_{r,j-i}(j-i+1). \end{aligned}$$

(B.1)

The Lindström–Gessel–Viennot theorem implies that the partition function for a collection of r non-intersecting paths is written as an r-by-r determinant. In particular, taking the starting points on level one of the r paths to be $(1,\ldots , r)$ and the ending points on level $r+t$ to be $(n+1-r,\ldots , n)$ we find that this partition function is exactly $\det [G_{r,t}(n+1-r+j-i)]_{i,j=1}^r$.

Similarly, in the Plancherel case of (3.10) (see the right part of Fig. 15) we consider r non-intersecting paths from positions $(1,\ldots ,r)$ to $(n+1-r,\ldots ,n)$ such that in the first part they either go up or to the right until reaching level $r-1$, in the second part they perform one-sided continuous simple random walk with jump rate $\tau$ during a time span of 1. A combination of the Lindström–Gessel–Viennot and Karlin–McGregor theorems imply that the probability that these r paths do not intersect is proportional to $e^{-\tau r} \det [G_{r,\tau }(n+1-r+j-i)]_{i,j=1}^r$. On the other hand, for a single path, the probability of going from a fixed starting point to fixed ending point is proportional to $e^{-\tau }$ times a polynomial in $\tau$ with positive coefficients. Therefore the probability of the r non-intersecting paths also takes the form $e^{-\tau r}$ times a polynomial in $\tau$ with positive coefficients, which shows the positivity of the polynomial $p^{n}_r(\tau )$.

Proof of Proposition 3.6

Let us first prove (3.16). Doing linear combinations of columns and using the relation (3.15), the determinants in (3.16) can be rewritten as follow:

$$\begin{aligned} \begin{aligned} Q_1&:=\det [B_{i,j}]_{1\le i,j\le M+1} = \left| \left( \begin{array}{cccc} C_{1,1} &{} \cdots &{} C_{1,M} &{} B_{1,M+1} \\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ C_{M+1,1} &{} \cdots &{} C_{M+1,M} &{} B_{M+1,M+1} \\ \end{array} \right) \right| ,\\ Q_2&:= \det [C_{i+1,j+1}]_{i,j=1}^M, \end{aligned} \end{aligned}$$

(C.1)

and

$$\begin{aligned} \begin{aligned} Q_3&:=\det [C_{i,j}]_{i,j=1}^{M+1}, \\ Q_4&:=\det [B_{i+1,j+1}]_{i,j=1}^M = \left| \left( \begin{array}{cccc} C_{2,2} &{} \cdots &{} C_{2,M} &{} B_{2,M+1} \\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ C_{M+1,1} &{} \cdots &{} C_{M+1,M} &{} B_{M+1,M+1} \\ \end{array} \right) \right| , \end{aligned} \end{aligned}$$

(C.2)

and finally

$$\begin{aligned} \begin{aligned} Q_5&:=\gamma \det [B_{i,j+1}]_{i,j=1}^{M+1} = -\left| \left( \begin{array}{cccc} C_{1,2} &{} \cdots &{} C_{1,M+1} &{} B_{1,M+1} \\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ C_{M+1,2} &{} \cdots &{} C_{M+1,M+1} &{} B_{M+1,M+1} \\ \end{array} \right) \right| ,\\ Q_6&:=\det [C_{i+1,j}]_{i,j=1}^M. \end{aligned} \end{aligned}$$

(C.3)

With these notations we have (3.16)$=Q_1 Q_2 -Q_3 Q_4 + Q_5 Q_6$.

Let us define the following $(2M+1)\times (2M+1)$ matrix,

$$\begin{aligned} Q=\left( \begin{array}{ccccccccc} C_{1,2} &{} \cdots &{} C_{1,M} &{} C_{1,M+1} &{} B_{1,M+1} &{} C_{1,1} &{}0 &{} \cdots &{} 0\\ \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{}\vdots &{} \ddots &{} \vdots \\ C_{M+1,2} &{} \cdots &{} C_{M+1,M} &{} C_{M+1,M+1} &{} B_{M+1,M+1} &{}C_{M+1,1} &{}0 &{} \cdots &{} 0\\ 0 &{} \cdots &{} 0 &{} C_{2,M+1} &{} B_{2,M+1} &{} C_{2,1} &{}C_{2,2} &{} \cdots &{} C_{2,M} \\ \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{}\vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} 0 &{} C_{M+1,M+1} &{} B_{M+1,M+1} &{}C_{M+1,1} &{}C_{M+1,2} &{} \cdots &{} C_{M+1,M} \\ \end{array} \right) . \end{aligned}$$

(C.4)

Next, notice that for a square block matrix of the form $\left( \begin{array}{cc} \alpha &{} 0\\ 0 &{}\beta \end{array}\right)$, its determinant is always zero unless $\alpha$ (and thus $\beta$) are square matrices. Adding the block of the last $M-1$ columns to the first $M-1$ columns and then subtracting rows $1+j$ from $M+1+j$, $j=1,\ldots ,M$, we obtain a matrix block matrix with zeroes but with $\alpha$ of size $(M+2)\times (M+1)$. Thus $\det (Q)=0$.

In Q there are three columns without zero entries. Call the first block with C’s above the zeroes as $A_1$ and the last block below the zeroes as $A_2$. Then we can write Q in the following form

$$\begin{aligned} Q=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} A_1 &{} U_1 &{} U_2 &{} U_3 &{}0\\ 0 &{} L_1 &{} L_2 &{} L_3 &{} A_2 \end{array} \right) , \end{aligned}$$

(C.5)

where $U_i$ are $(M+1)$-vectors and $L_i$ are M-vectors. By multi-linearity of the determinant, we have that $\det (Q)$ equals the sum of the determinants of the matrices obtained by replacing for each pair $(U_i,L_i)$, $i=1,2,3$, one of the elements by the vector of zeroes. Thus obtained matrices are of the block matrix form with zero corners as described above but, except if one sets exactly one of the $U_i=0$, the $\alpha$ matrix is not square. Thus we have

$$\begin{aligned} \begin{aligned} 0=\det (Q)&=\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} A_1 &{} 0 &{} U_2 &{} U_3 &{}0\\ 0 &{} L_1 &{} 0 &{} 0 &{} A_2 \end{array} \right) + \det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} A_1 &{} U_1 &{}0 &{} U_3 &{}0\\ 0 &{} 0&{} L_2 &{} 0 &{} A_2 \end{array} \right) \\&\quad +\det \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} A_1 &{} U_1 &{} U_2 &{}0 &{}0\\ 0 &{} 0&{} 0 &{} L_3 &{} A_2 \end{array} \right) = -Q_1 Q_2 + Q_3 Q_4 - Q_5 Q_6\\&= - (3.16). \end{aligned} \end{aligned}$$

(C.6)

Next we prove (3.17). In the first step, using linear combinations of columns, we can replace in the determinants of (3.17), the $B_{i,j}$’s with $C_{i,j}$’s except for the last column. This gives

$$\begin{aligned} \begin{array}{ll} P_1:=\gamma \det [B_{i,j}]_{i,j=1}^{M+1} = Q_1, &{}P_2:=\det [C_{i+1,j+1}]_{i,j=1}^{M-1},\\ P_3:=\det [C_{i,j}]_{i,j=1}^{M}, &{}P_4:=\det [B_{i+1,j+1}]_{i,j=1}^{M}=Q_4, \end{array} \end{aligned}$$

(C.7)

and finally

$$\begin{aligned} \begin{aligned} P_5&:=\det [B_{i,j+1}]_{i,j=1}^{M} = \left| \left( \begin{array}{cccc} C_{1,2} &{} \cdots &{} C_{1,M} &{} B_{1,M+1} \\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ C_{M,2} &{} \cdots &{} C_{M,M} &{} B_{M,M+1} \\ \end{array} \right) \right| ,\\ P_6&:=\det [C_{i+1,j}]_{i,j=1}^M. \end{aligned} \end{aligned}$$

(C.8)

We have to prove (3.17) $=P_1 P_2 - P_3 P_4 + P_5 P_6 =0$. Now we have written all the $P_i$’s in terms of $C_{i,j}$’s and sometimes one single column of $B_{k,M+1}$’s. Let us show that the factor multiplying $B_{k,M+1}$ equals zero for all $k=1,\ldots ,M+1$. First, for $k=1$ (resp. $k=M+1$), it is immediate to see that the factors are zero, since there are only two contributing terms: one from $P_1$ and the other one from $P_4$ (resp. $P_5$). Now take a fixed $k\in \{2,\ldots ,M\}$. Then, the factor in (3.17) which multiplies $B_{k,M+1}$ is given by the sum of these three terms:

$$\begin{aligned} A_1=\left| \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} C_{2,2} &{} \cdots &{} C_{2,M} &{} &{} &{}\\ \vdots &{} \ddots &{} \vdots &{} &{} 0 &{}\\ C_{M+1,2} &{} \cdots &{} C_{M+1,M} &{} &{} &{}\\ &{} &{} &{} C_{1,1} &{} \cdots &{} C_{1,M}\\ &{} 0 &{} &{} \vdots &{}\text {No }C_{k,\cdot } &{} \\ &{} &{} &{} C_{M,2} &{} \cdots &{} C_{M,M}\\ \end{array} \right) \right| , \end{aligned}$$

(C.9)

where $\text {No }C_{k,\cdot }$ means that the row with the $C_{k,j}$’s is missing,

$$\begin{aligned} A_2=-\left| \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} C_{1,1} &{} \cdots &{} C_{1,M} &{} &{} &{}\\ \vdots &{} \ddots &{} \vdots &{} &{} 0 &{}\\ C_{M,1} &{} \cdots &{} C_{M,M} &{} &{} &{}\\ &{} &{} &{} C_{2,2} &{} \cdots &{} C_{2,M}\\ &{} 0 &{} &{} \vdots &{}\text {No }C_{k,\cdot } &{} \\ &{} &{} &{} C_{M+1,2} &{} \cdots &{} C_{M+1,M}\\ \end{array} \right) \right| , \end{aligned}$$

(C.10)

and

$$\begin{aligned} A_3=\left| \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} C_{2,1} &{} \cdots &{} C_{2,M} &{} &{} &{}\\ \vdots &{} \ddots &{} \vdots &{} &{} 0 &{}\\ C_{M+1,1} &{} \cdots &{} C_{M+1,M} &{} &{} &{}\\ &{} &{} &{} C_{1,2} &{} \cdots &{} C_{1,M}\\ &{} 0 &{} &{} \vdots &{}\text {No }C_{k,\cdot } &{} \\ &{} &{} &{} C_{M,2} &{} \cdots &{} C_{M,M}\\ \end{array} \right) \right| . \end{aligned}$$

(C.11)

We need to show that $A_1+A_2+A_3=0$. Define the matrix

$$\begin{aligned} P=\left| \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} C_{1,1} &{} \cdots &{} C_{1,M} &{} C_{1,2} &{} \cdots &{} C_{1,M}\\ \vdots &{} \ddots &{} \vdots &{} &{} 0 &{}\\ C_{k,1} &{} \cdots &{} C_{k,M} &{} C_{k,2} &{} \cdots &{} C_{k,M}\\ \vdots &{} \ddots &{} \vdots &{} &{} 0 &{}\\ C_{M+1,1} &{} \cdots &{} C_{M+1,M} &{} C_{M+1,2}&{} \cdots &{} C_{M+1,M}\\ &{} &{} &{} C_{2,2} &{} \cdots &{} C_{2,M}\\ &{} 0 &{} &{} \vdots &{}\text {No }C_{k,\cdot } &{} \\ &{} &{} &{} C_{M,2} &{} \cdots &{} C_{M,M}\\ \end{array} \right) \right| , \end{aligned}$$

(C.12)

where the top-right $(M+1)\times (M-1)$ block contains only three non-zero rows. It is easy to verify that $\det (P)=0$, since by linear combinations of rows and columns we can delete the three lines in the just mentioned block. Expanding the determinant by multi-linearity, for each of the three rows of P without zeroes, we can decide whether to keep the first M terms or the last $M-1$. Only when we replace with zeroes exactly one set of the M terms and the other two sets of $M-1$ terms we get a non-zero determinant by the same argument with block matrices with zero corners as used above. Up to reordering the columns, we have a block diagonal determinant, leading (up to a $(-1)^M$ factor) to $A_1$ when we keep $(C_{k,2},\ldots ,C_{k,M})$, to $A_2$ when we keep $(C_{M+1,2},\ldots ,C_{M+1,M})$ and $A_3$ when we keep $(C_{1,2},\ldots ,C_{1,M})$. This finishes the proof of the identity (3.17).